the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A methodology to constrain carbon dioxide emissions from coal-fired power plants using satellite observations of co-emitted nitrogen dioxide
Bryan N. Duncan
Nickolay A. Krotkov
Lok N. Lamsal
Steffen Beirle
Debora Griffin
Chris A. McLinden
Daniel L. Goldberg
Zifeng Lu
We present a method to infer CO2 emissions from individual power plants based on satellite observations of co-emitted nitrogen dioxide (NO2), which could serve as complementary verification of bottom-up inventories or be used to supplement these inventories. We demonstrate its utility on eight large and isolated US power plants, where accurate stack emission estimates of both gases are available for comparison. In the first step of our methodology, we infer nitrogen oxides (NOx) emissions from US power plants using Ozone Monitoring Instrument (OMI) NO2 tropospheric vertical column densities (VCDs) averaged over the ozone season (May–September) and a “top-down” approach that we previously developed. Second, we determine the relationship between NOx and CO2 emissions based on the direct stack emissions measurements reported by continuous emissions monitoring system (CEMS) programs, accounting for coal quality, boiler firing technology, NOx emission control device type, and any change in operating conditions. Third, we estimate CO2 emissions for power plants using the OMI-estimated NOx emissions and the CEMS NOx∕CO2 emission ratio. We find that the CO2 emissions estimated by our satellite-based method during 2005–2017 are in reasonable agreement with the US CEMS measurements, with a relative difference of 8 %±41 % (mean ± standard deviation). The broader implication of our methodology is that it has the potential to provide an additional constraint on CO2 emissions from power plants in regions of the world without reliable emissions accounting. We explore the feasibility by comparing the derived NOx∕CO2 emission ratios for the US with those from a bottom-up emission inventory for other countries and applying our methodology to a power plant in South Africa, where the satellite-based emission estimates show reasonable consistency with other independent estimates. Though our analysis is limited to a few power plants, we expect to be able to apply our method to more US (and world) power plants when multi-year data records become available from new OMI-like sensors with improved capabilities, such as the TROPOspheric Monitoring Instrument (TROPOMI), and upcoming geostationary satellites, such as the Tropospheric Emissions: Monitoring Pollution (TEMPO) instrument.
- Article
(2949 KB) -
Supplement
(205 KB) - BibTeX
- EndNote
Thermal power plants, particularly coal-fired power plants, are among the largest anthropogenic CO2 emitters, contributing ∼40 % of energy-related CO2 emissions globally in 2010 (Janssens-Maenhout et al., 2017). Coal-fired power plants are expected to be one of the primary contributors of CO2 emissions in the coming decades because of abundant world coal reserves (Shindell and Faluvegi, 2010). Therefore, it is important to accurately monitor global CO2 emissions from power production in order to better predict climate change (Shindell and Faluvegi, 2010) and to support the development of effective climate mitigation strategies.
CO2 emissions from power plants are typically quantified based on bottom-up approaches using fuel consumption and fuel quality, though fuel properties are not always well known, resulting in uncertainties in the estimated CO2 emissions for individual plants (Wheeler and Ummel, 2008). Even for US power plants that are considered to have the most accurate information on fuel usage among world nations, the difference between emissions estimated based on fuel usage and those reported as part of continuous emissions monitoring system (CEMS) programs is typically about 20 % (Ackermann and Sundquist, 2008). Thus, emission estimates based on independent data sources, such as satellite observations, are a desirable complement for the validation and improvement of the current CO2 emissions inventories, especially in countries without CEMS data, which is the case in most of the world.
Anthropogenic CO2 emissions have been estimated from space-based CO2 observations, but the existing satellite CO2 sensors are designed to provide constraints on natural CO2 sources and sinks (Basu et al., 2013; Houweling et al., 2015) and thus their capability for monitoring anthropogenic point sources is limited (Nassar et al., 2017). Observations from sensors, including the Scanning Imaging Absorption Spectrometer for Atmospheric Chartography (SCIAMACHY; Burrows et al., 1995), Greenhouse gases Observing SATellite (GOSAT; Yokota et al., 2009), and Orbiting Carbon Observatory-2 (OCO-2; Crisp, 2015), show statistically significant enhancements over metropolitan regions (Kort et al., 2012; Schneising et al., 2013; Janardanan et al., 2016; Buchwitz et al., 2018; Reuter et al., 2019; Wang et al., 2018). However, very few studies have focused on individual point sources. Bovensmann et al. (2010) and Velazco et al. (2011) presented a promising satellite remote-sensing concept to infer CO2 emissions for power plants based on the atmospheric CO2 column distribution. Nassar et al. (2017) presented the first quantification of CO2 emissions from individual power plants using OCO-2 observations. However, because of the narrow swath (∼10 km at nadir) and 16 d repeat cycle of the OCO-2 sensor, the number of clear-day overpasses is too small to allow for the development of a global CO2 emissions database.
In contrast to CO2, inferring NOx emissions from individual power plants using satellite NO2 column retrievals has been done with a higher degree of confidence (e.g., Duncan et al., 2013; de Foy et al., 2015). The Dutch-Finnish Ozone Monitoring Instrument (OMI) on NASA's Earth Observing System Aura spacecraft (Schoeberl et al., 2006) provides near-daily, global NO2 tropospheric vertical column densities (VCDs) at a spatial resolution of 13×24 km2 (at nadir) (Levelt et al., 2006, 2018; Krotkov et al., 2017), which allows emission signals from individual power plants to be resolved. Beirle et al. (2011) first analyzed isolated large sources (i.e., megacities and the US Four Corners power plant) by averaging OMI NO2 tropospheric VCDs separately for different wind directions, which allows for the estimation of NOx emissions and lifetimes by fitting an exponentially modified Gaussian function. Several follow-up studies (e.g., de Foy et al., 2015; Lu et al., 2015 and Goldberg et al., 2019a) further developed this approach and inferred NOx emissions from isolated power plants and cities. More recently, we advanced this approach for sources located in polluted areas to infer NOx emissions for 17 power plants and 53 cities across China and the US (Liu et al., 2016, 2017).
Since NOx is co-emitted with CO2, NOx emissions inferred from satellite data may be used to estimate CO2 emissions from thermal power plants. Previous analyses estimated regional CO2 emissions based on satellite-derived NOx emissions and the NOx to CO2 emission ratios from bottom-up emission inventories (Berezin et al., 2013; Konovalov et al., 2016; Goldberg et al., 2019b) or co-located satellite retrievals of CO2 and NO2 (Reuter et al., 2014). Hakkarainen et al. (2016) confirmed the spatial correlation between CO2 spatial anomalies and OMI NO2 VCD enhancements at the regional scale using satellite observations at higher resolution. Hakkarainen et al. (2019) also showed how overlapping OCO-2 CO2 data and data of NO2 from the recently launched (October 2017) European Union Copernicus Sentinel-5 precursor TROPOspheric Monitoring Instrument (TROPOMI; Veefkind et al., 2012) can be used to identify small-scale anthropogenic CO2 signatures.
More recently, the co-located regional enhancements of CO2 observed by OCO-2 and NO2 observed by TROPOMI were analyzed to infer localized CO2 emissions for six hotspots including one power plant globally (Reuter et al., 2019). As emissions plumes are significantly longer than the swath width of OCO-2 (10 km), OCO-2 sees only cross sections of plumes, which may not be sufficient to infer emission strengths. Because power plant emissions can have substantial temporal variations (Velazco et al., 2011) and the cross-sectional CO2 fluxes are valid only for OCO-2 overpass times, the cross-sectional fluxes may not adequately represent the annual or monthly averages, which are required for the development of climate mitigation strategies. In addition, the cross-sectional fluxes may not be a good approximation for emission strengths if meteorological conditions are not taken into account (Varon et al., 2018). As compared to the method proposed in this study, Reuter's method has the advantage of not requiring a priori emission information. However, there are currently no satellite instruments with a wide enough swath to allow wider application of Reuter's method.
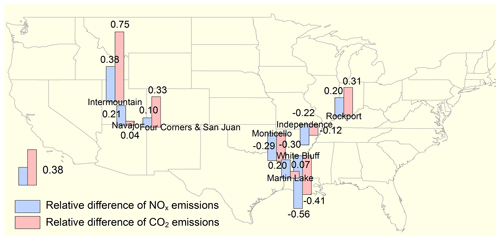
Figure 1Locations of the power plants investigated in this study. The bar charts denote the relative differences, defined as (, averaged over 2005–2017 for NOx (blue) and CO2 (red) emissions. The upward and downward bars represent positive and negative differences, respectively. The Monticello power plant installed SNCR to control NOx emissions in 2008. The other power plants are not equipped with post-combustion NOx control devices.
In this study, we present a method to estimate CO2 emissions from individual power plants using OMI NO2 observations and auxiliary CEMS information necessary to estimate NOx to CO2 emission ratios. Such estimates could serve as complementary verification of bottom-up CO2 inventories or as a supplement to these inventories. For instance, Liu et al. (2018) used satellite data of SO2 to identify large SO2 sources that were missing from a bottom-up emissions inventory and created a merged bottom-up and top-down SO2 emissions inventory. We apply our approach to US power plants, which have an exceptionally detailed CEMS database of NOx and CO2 emissions, in order to validate our method. Using auxiliary CEMS information, we explore the relationship between NOx and CO2 emissions for individual power plants, assessing variations in the ratio associated with coal quality, boiler firing type, NOx emission control device technology, and changes in operating conditions. Understanding the causes of these variations will allow for better-informed assumptions when applying our method to power plants that have no or uncertain information on the factors that affect their emissions ratios. We discuss the uncertainties and applications of our approach and the potential of NO2 datasets from new and upcoming satellite instruments, which will improve the utility of our method for inferring CO2 emissions from power plants around the world. Finally, we discuss future research directions.
In this section, we present our method to infer CO2 emissions () from satellite-derived NOx emissions () for individual coal-fired power plants using the following equation:
where i represents coal type and y represents the target year. We demonstrate our method on US power plants since there are accurate CEMS stack measurements of NOx and CO2 emissions with which to validate . In Sect. 2.1, we describe how we estimate from OMI NO2 tropospheric VCD observations. In Sect. 2.2, we discuss how we estimate the ratio of NOx to CO2 emissions () from CEMS stack measurements in the US Emissions and Generation Resource Integrated Database (eGRID; USEPA, 2018). Since post-combustion NOx control systems, including selective non-catalytic reduction (SNCR) and selective catalytic reduction (SCR), change the relationship between and , we present separate methods to determine for power plants without and with post-combustion NOx control systems in Sect. 2.2.1 and 2.2.2, respectively. We discuss the validation of the estimated in Sect. 3.
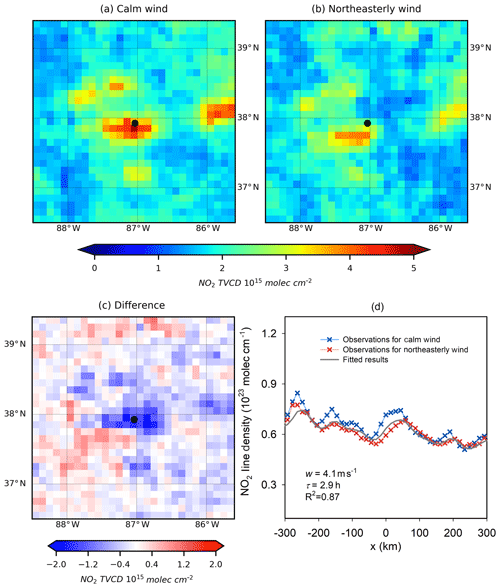
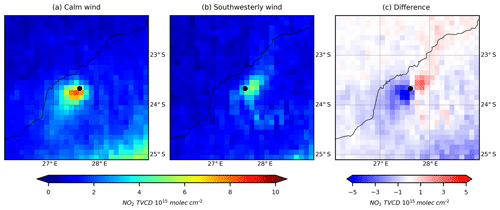
Figure 2Mean OMI NO2 tropospheric VCDs around the Rockport power plant (Indiana, USA) for (a) calm conditions, (b) northeasterly wind and (c) their difference (northeasterly minus calm) for the period of 2005–2017. The location of Rockport is labeled by a black dot. (d) NO2 line densities around Rockport. Crosses are NO2 line densities for calm (blue) and northeasterly winds (red) as function of the distance x to Rockport center. The grey line is the fitted results for NO2 line densities for northeasterly winds. The numbers indicate the net mean wind velocities (windy minus calm) from MERRA-2 (w), the fitted lifetime (τ), and the coefficient of determination (R2) of the fit.
2.1 Estimating satellite-derived NOx emissions ()
From all US coal-fired power plants, we selected 21 power plants for estimating . We chose these plants based on the magnitude of their annual emissions (i.e., > 10 Gg yr−1 in 2005) and relative isolation from other large sources to avoid “contamination” of a power plant's NOx plume. Power plants located in urban areas (i.e., within a radius of 100 km from a city center), or clustered in close proximity (i.e., 50 km) with other large industrial plants were excluded by visual inspection using satellite imagery from Google Earth. We used the top 200 largest US cities (ranked by 2018 population as estimated by the United States Census Bureau, available at https://en.wikipedia.org/wiki/List_of_United_States_cities_by_population, last access: 10 December 2019) to select power plants. As discussed below, we were able to estimate for 8 of the 21 plants. The locations of the 8 plants are shown in Fig. 1 and given in Table S1 in the Supplement.
We followed the method of Liu et al. (2016, 2017) to estimate for 2005 to 2017. In our analysis, we used OMI NO2 tropospheric VCDs from the NASA OMI standard product, version 3.1 (Krotkov et al., 2017), together with meteorological wind information from the Modern-Era Retrospective Analysis for Research and Applications, version 2 (MERRA-2; Gelaro et al., 2017). We only analyzed data for the ozone season (May–September), in order to exclude winter data, which have larger uncertainties and longer NOx lifetimes. As in our previous study (Liu et al., 2017), we calculated one-dimensional NO2 “line densities”, i.e., NO2 cm−1, as function of distance for each wind direction separately by integration of the mean NO2 VCDs (i.e., NO2 cm−2) perpendicular to the wind direction. We then used the changes of NO2 line densities under calm wind conditions (wind speed < 2 m s−1 below 500 m) and windy conditions (wind speed > 2 m s−1) to fit the effective NOx lifetime. We then estimated the average NO2 total mass integrated around a power plant on the basis of the 3-year mean VCDs, in agreement with previous studies (Fioletov et al., 2011; Lu et al., 2015). The NO2 total mass was scaled by a factor of 1.32 in order to derive total NOx mass, following Beirle et al. (2011). The uncertainty associated with the NOx∕NO2 ratio has been discussed in detail in Sect. 3 of the Supplement to Liu et al. (2016). The 3-year average was derived from the corresponding 3-year average NOx mass divided by the average NOx lifetime of the entire study period (Liu et al., 2017). Fitting results of insufficient quality (e.g., correlation coefficient of the fitted and observed NO2 distributions < 0.9) were excluded from this analysis, consistent with the criteria in Sect. 2.2 of Liu et al. (2016). This final filtering left 18 power plants, of which 8 had valid results for all consecutive 3-year periods between 2005 and 2017. More details of the approach are documented in Liu et al. (2017). The fitted lifetimes and other fitting parameters for all power plants are given in Table S1.
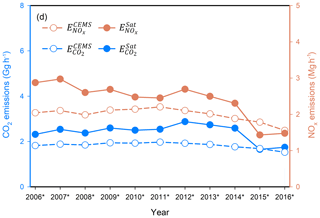
We use the Rockport power plant (37.9∘ N, 87.0∘ W) in Indiana to demonstrate our approach. This power plant is particularly well suited for estimating because it is a large and isolated NOx point source. Figure 2 presents the NO2 VCD map around Rockport and the fitted results. Figure 3 displays based on 3-year mean VCDs. Each 3-year period is represented by the middle year with an asterisk (e.g., 2006* denotes the period from 2005 to 2007). For comparison to , is from Air Markets Program Data (available at: https://ampd.epa.gov/ampd/, last access: 1 May 2019) and averaged over the period of May to September. For this particular plant, is always higher than during the entire period, except the last 2 years. The coefficient of determination for the entire period is R2=0.68. The relative differences for individual 3-year means (defined as ( )/) range from −20 % to 41 % because of the uncertainties of , as discussed in Sect. 3.2. Both datasets present a declining trend from 2012∗. The total declines of 45 % and 26 % since 2012* in and are attributed to the 25 % decrease in net electricity generation for the plant. The average relative difference of and for the eight plants in this study is 0 %±33 %, ranging from −58 % to 72 % for individual 3-year periods (Fig. 1).
2.2 Estimating NOx to CO2 emission ratios using CEMS data (ratioCEMS)
We determined the relationship between and for coal-fired power plants using eGRID information about each plant's net electric generation, boiler firing technology (e.g., tangential or wall-fired boiler), NOx control device type, fossil fuel category (i.e., coal, oil, gas, and other), and coal quality (i.e., bituminous, lignite, subbituminous, refined, and waste coal). We used data of power plants with more than 99 % of the fuel burned being coal, as reported in eGRID. We analyzed the relationship between and by coal type, as emission characteristics vary widely by coal type.
The eGRID includes two datasets of emissions for NOx and CO2: (1) calculated from fuel consumption data and (2) observed by stack monitoring (i.e., and ). Here we focus on eGRID CEMS data, as are reported to be highly accurate with an error of less than 5 % (e.g., Glenn et al., 2003). may have larger uncertainties than fuel-based emissions estimates because of uncertainties in the calculation of flue gas flow (Majanne et al., 2015). Nevertheless, we used to relate NOx emissions to CO2 emissions, since the primary uncertainty of and arises from the calculation of the flue gas flow, which will cancel in ratioCEMS.
Table 1The slope (), coefficient of determination, standard deviation, and sample number of the linear regression of and by year for all US power plants without post-combustion NOx control devices from 2005 to 2016.
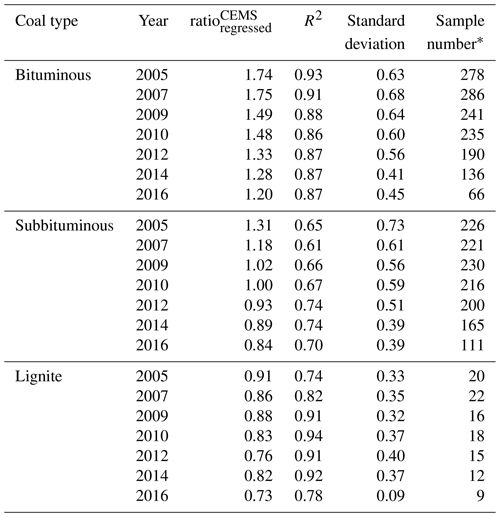
* The sample number generally decreases from 2005 to 2016 as power plants installed post-combustion NOx control devices over time.
2.2.1 Coal-fired power plants without post-combustion NOx control systems
We initially limited our analysis to and from coal-fired power plants without post-combustion NOx control systems in operation in a given year (Table 1). We find that and have a strong linear relationship (Fig. 4). In Fig. 4a, we compare and from power plants (using bituminous coal) by boiler firing type in 2005. We use bituminous coal-fired plants for illustration, as bituminous coal is the most widely used coal in US power plants. We analyzed power plants that use cyclone or cell burner boilers separately and exclude them in Fig. 4 because they typically produce higher NOx emissions than other boiler types (USEPA, 2009; available at: https://www3.epa.gov/ttn/chief/ap42/ch01/index.html, last access: 1 April 2019). A strong linear relationship between and is evident with excellent correlation (R2=0.93, N=278), regardless of boiler firing type. Similar linear relationships exist for other years (e.g., year 2016 in Fig. 4b) and other types of coal (Table 1). The slope of the regression of and , , is assumed by setting the intercept to zero. Table 1 shows by coal type and year. In Sect. 3.1, will be applied to approximate when estimating from for the eight plants (Fig. 1) for years before post-combustion control systems were in operation.
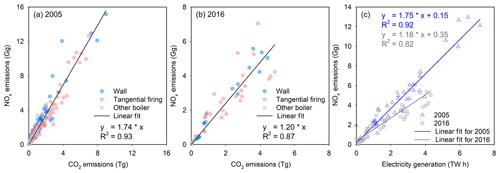
Figure 4Scatterplots of versus for all the US bituminous coal-fired electric generating units for (a) 2005 and (b) 2016. Values are color coded by firing type. (c) Scatterplot of versus electricity generation of the same units for years 2005 (triangle) and 2016 (square). Only plants without post-combustion NOx control devices within a given year are used. The electricity generation data are also from eGRID. The lines in all three panels represent the computed linear regressions.
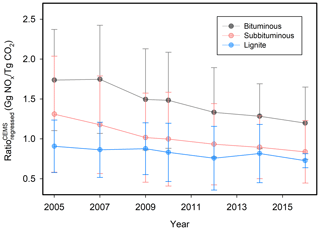
The value for power plants using bituminous coal decreased from 2005 (Fig. 4a) to 2016 (Fig. 4b) by 31 % on average because of reductions in NOx emission factors associated with improvements in boiler operations, such as by optimizing furnace design and operating conditions. The NOx emissions factors, defined as NOx emission rates per net electricity generation (Gg TW h−1), declined by 33 % from 2005 to 2016 (Fig. 4c). We interpolated to get year-specific ratios by coal type for the entire study period, as eGRID data are only available for some years (i.e., 2005, 2007, 2009, 2010, 2012, 2014, and 2016).
In addition, shows significant variation by coal type and year (Fig. 5). The value is 1.7, 1.3, and 0.91 Gg NOx∕TgCO2 for bituminous, subbituminous, and lignite coal types in 2005, respectively. A reduction over time in is observed for all coal types (Fig. 5). The value displays a large decrease of 31 %, 36 % and 20 % from 2005 to 2016 for bituminous, subbituminous, and lignite coal types, respectively.
2.2.2 Coal-fired power plants with post-combustion NOx control systems
Here, we describe how we estimated ratioCEMS for the entire study period for plants that had post-combustion NOx control systems installed at some time during our study period, 2005–2017. The estimation is based on derived in Sect. 2.2.1 for plants without post-combustion control systems in operation. We introduce a NOx removal efficiency parameter, f, to adjust for years after the installation of post-combustion control systems, ratioCEMS-estimated:
f is commonly measured for individual power plants to describe the performance of their post-combustion NOx control systems. It is directly reported by some power plant databases, such as the China coal-fired Power plant Emissions Database (CPED; Liu et al., 2015). For databases that do not report f, like eGRID used in this study, one can estimate it for an individual power plant by first estimating the unabated emissions per electricity generation, eunabated, which is the emission factor before the flue gas enters the post-combustion control system:
where eCEMS denotes the actual emission factor in terms of CEMS NOx emissions per net electricity generation (Gg TW h−1).
eunabated for a given year, eunabated,y, is estimated based on the emission per electricity generation for years prior, p, to the installation of the post-combustion control system, eunabated,p:
where the scaling factor, ky, is used to account for the change over time in eunabated associated with improvements in boiler operations discussed in Sect. 2.2.1. ky is calculated as the ratio of the averaged eunabated (i.e., the slope of the regression of NOx emissions on electricity generation) in year t to that in year p.
To assess the reliability of ratioCEMS-estimated, we selected all power plants that had post-combustion devices installed between 2005 and 2016. Figure 6 shows a scatterplot of ratioCEMS (i.e., the ratio of to for individual plants) and ratioCEMS-estimated. We used the NOx emissions factor in 2005, eunabated,2005, to predict the unabated emission factor in 2016, eunabated,2016, following Eqs. (3) and (4) in order to quantify the removal efficiencies for 2016, f2016. The value is based on the estimated f2016 and from Sect. 2.2.1. ratioCEMS and ratioCEMS-estimated show good correlation (R2=0.64), which increases our confidence that the estimated removal efficiencies approximate the actual efficiencies. The slight underestimation suggested by the slope of 0.85 arises from uncertainties in estimating unabated NOx emission factors (eunabated,y) using Eq. (4) and thus removal efficiencies (f), which is a major source of error of for power plants that install post-combustion NOx control systems (see details in Sect. 3.2).
Table 2Summary of effective NOx lifetimes, satellite-derived NOx emissions () and CO2 emissions (), bottom-up NOx emissions (), and CO2 emissions () for eight US power plants during May to September from 2005 to 2017. The 3-year periods are represented by the middle year with an asterisk.
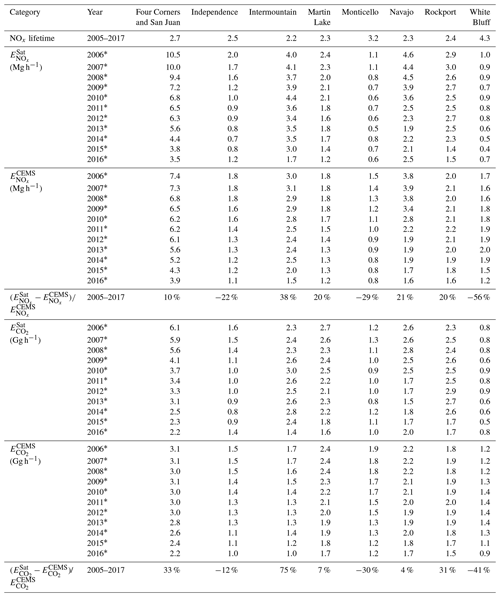
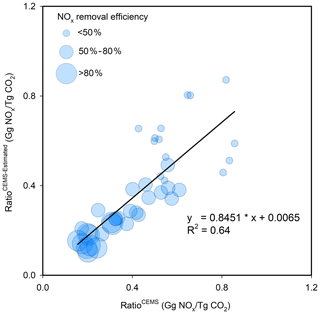
Figure 6Scatterplot of ratioCEMS-estimated as compared to ratioCEMS for 2016. All 44 coal-fired power plants that operated post-combustion devices after 2005 and before 2016 (including 2016) are used in the plot. The sizes of the circles denote the magnitude of the NOx reduction efficiency of post-combustion control devices estimated in this study. The line represents the linear regression of ratioCEMS to ratioCEMS-estimated.
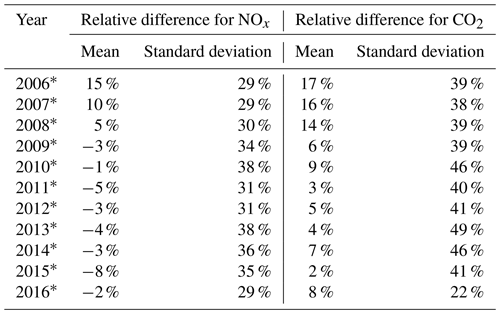
In Sect. 3.1, we present for our eight selected power plants and, in Sect. 3.2, we discuss the uncertainties associated with . In Sect. 3.3, we compare the US ratios derived in this study with those from a bottom-up inventory for other regions to explore the potential of applying our method to regions outside the US. We finally apply our approach to one power plant in South Africa, which has several independent estimates for its CO2 emissions as presented in the scientific literature. Table 2 shows 3-year means of , , , and for eight power plants (Fig. 1). Table 3 lists the mean and the standard deviation of the relative differences between and , and , and for all eight power plants.
Table 3Summary of relative difference between satellite-derived NOx emissions (), bottom-up NOx emissions (), satellite-derived CO2 emissions (), and bottom-up CO2 emissions () for eight US power plants during May to September from 2005 to 2017. The 3-year periods are represented by the middle year with an asterisk.
3.1 Satellite-derived CO2 emissions ()
Figure 7a is a scatterplot of and for the eight power plants (Fig. 1), seven of which did not have post-combustion NOx control systems installed during the study period, 2005–2017. The comparison shows a good correlation, R2, of 0.66. The average for all power plants is 2.0 Gg h−1 and the average is 1.8 Gg h−1. The relative difference for individual 3-year means (defined as ( )/) is 8 %±41 % (mean ± standard deviation). For example, Fig. 3 shows for the Rockport power plant, which typically has a positive bias as compared to because of a positive bias in .
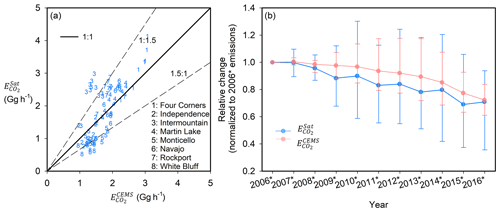
Figure 7(a) Scatterplot of for eight power plants, as compared to from 2006* to 2016*. The solid lines represent the ratio of 1:1. The dashed lines represent the ratios of 1:1.5 and 1.5:1, respectively. (b) Interannual trends of the averaged (blue lines) and (pink lines) are for all power plants analyzed in this study from 2006* to 2016*, as normalized to the 2006* value. The whiskers denote the maximum and minimum values.
Figure 7b presents the generally consistent time series between and , with their annual averages for the eight power plants exhibiting a declining trend of 5 % yr−1 and 3 % yr−1 from 2006* to 2016* for and , respectively. The reduction in net electricity generation is the driving force underlying the emission changes, which decreased by 37 % for the eight power plants from 2005 to 2016, as power producers shut down coal-fired units in favor of cheaper and more flexible natural gas as well as solar and wind (USEIA, 2018). It is interesting to note that the temporal variations in are not as “smooth” as those in , which results from fluctuations in . Such fluctuations are caused by uncertainties associated with , as discussed in Sect. 3.2. For example, changes in VCDs do not necessarily relate linearly with NOx emissions (e.g., Fig. 2 in Duncan et al., 2013) because of temporal variations in meteorology, and nonlinear NOx chemistry (Valin et al., 2013) and transport. Averaging VCDs for a long-term period (3 years in this study) helps reduce those influences, but small fluctuations may still exist.
3.2 Uncertainties
We estimated the uncertainty of based on the fit performance of and comparison with . The major sources of uncertainty are (a) (Liu et al., 2016), (b) , and (c) f. We give the estimated uncertainties of each source for individual power plants in Table S2.
3.2.1
The uncertainty of is quantified following the method described in Liu et al. (2017), accounting for errors arising from the fit procedure, the NOx∕NO2 ratio, and OMI NO2 VCD observations (Liu et al., 2016). The number 1.32, used for scaling the NOx∕NO2 ratio, is based on assumptions presented in Sect. 6.5.1 of Seinfeld and Pandis (2006) for “typical urban conditions and noontime sun”. Note that conditions are quite similar in this study because of the overpass time of OMI close to noon, the selection of cloud-free observations, the focus on the ozone season, and the focus on polluted regions. A case study of chemical transport model (CTM) simulations shows an identical value of 1.32 for Paris in summer (Shaiganfar et al., 2017). The simulated NOx∕NO2 ratio at the OMI overpass time within the boundary layer (up to 2 km) in a chemistry–climate model, European Centre for Medium-Range Weather Forecasts – Hamburg (ECHAM)/Modular Earth Submodel System (MESSy) Atmospheric Chemistry (EMAC)(Jöckel et al., 2016), was 1.28±0.08 for polluted (NOx > 1×1015 molec cm−2) regions for the 1 July 2005, and 1.32±0.06 on average for the ozone season. However, the coarse grid of EMAC ( in latitude and longitude) may not capture the true range of variation in the NOx∕NO2 ratio. Therefore, we assumed an uncertainty of 20 % arising from the NOx∕NO2 ratio, double the standard deviation of the EMAC ratio.
Additionally, the tropospheric air mass factors (AMFs) used in NO2 retrievals are based on relatively coarsely resolved surface albedo data and a priori NO2 vertical profile shapes, likely causing low-biased VCDs over strong emission sources (e.g., Russell et al., 2011; McLinden et al., 2014; Griffin et al., 2019). The average AMF uncertainty of ∼30 % (see Table 2 in Boersma et al., 2007) likely contributes to the underestimation of emissions from some power plants in this study. Both random and systematic (bias) uncertainties in VCDs directly propagate into the uncertainty of (see details in the Supplement of Liu et al., 2016 and Sect. 3.4 of Liu et al., 2017).
The overall uncertainties of range from 57 % to 64 % for all power plants in our analysis, which is comparable with the level of differences between and . We expect this uncertainty to be less for new (e.g., TROPOMI) and upcoming (e.g., NASA Tropospheric Emissions: Monitoring Pollution, TEMPO) OMI-like sensors, which have enhanced capabilities relative to OMI. Further details are provided in Sect. S1 of the Supplement.
3.2.2
For power plants without post-combustion devices, derived from the regression (Fig. 4a and b) and the plant-specific CEMS measurements are within 15 %, which is assumed as the uncertainty of the ratio for all power plants.
3.2.3 f
For power plants with post-combustion devices, an additional uncertainty of 20 % is applied to reflect the difference between the predicted and the true removal efficiency as suggested by Fig. 6.
We assume that their contributions to the overall uncertainty are independent. We then define the total uncertainty, expressed as a 95 % confidence interval, as the sum of the root of the quadratic sum of the aforementioned contribution. The overall uncertainties of are ∼60 % for all power plants in our analysis.
3.2.4 Summary of uncertainties
However, it is worth noting that this uncertainty estimate is rather conservative. The mean and the standard deviation of the relative differences between and , and and for all eight power plants provide a good alternative measure of uncertainties (Table 3). The relative differences are rather small, which are 0 %±33 % and 8 %±41 % (mean ± standard deviation) for NOx and CO2, respectively. We additionally calculate the geometric standard deviations (GSDs) of the difference between and from 2006* to 2016* for individual power plants in Table S2. The small values of GSDs ranging from 1.07 to 1.31 further improve our confidence in the accuracy of the derived emissions in this study.
3.3 Application
In this section, we assess the feasibility of applying our method to infer CO2 emissions () for power plants outside the US. We first compare the NOx to CO2 emission ratios derived from this study with those from a bottom-up emission database in Sect. 3.3.1. We then apply the US ratio to a power plant in South Africa in Sect. 3.3.2.
3.3.1 Comparison with bottom-up ratios
Figure 8 shows the NOx to CO2 emission ratios for 2010 from the global power emissions database (GPED; Tong et al., 2018a), which is the only publicly available bottom-up emission database that reports both NOx and CO2 emissions for individual power plants for every country. All countries with over 30 coal-fired power plants in the GPED are shown in Fig. 8. Not surprisingly, countries with more strict standards in place for NOx emissions from power plants (i.e., NOx emission limit value, ELV, < 200 mg m−3; hereafter referred to as “more strict countries”) have smaller NOx to CO2 ratios (i.e., 1.0 versus 2.5 on average) than countries with less strict standards (i.e., NOx ELV > 200 mg m−3; hereafter referred to as “less strict countries”). Additionally, the correlation coefficients are smaller for more strict countries (i.e., 0.82 on average) as compared to less strict countries (i.e., 0.96 on average) because power plants in more strict countries are more likely to have installed post-combustion NOx control systems, which likely lowered , similar to what occurred in the US over our analysis period (Sect. 2.2.2).
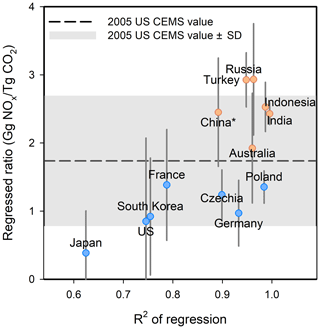
Figure 8Comparison of the regressed NOx to CO2 emission ratios derived from the global power emissions database (GPED) for different regions versus the correlation coefficient of the regression. The blue and red circles denote regions that are subject to more strict standards for NOx emissions from power plants (i.e., a NOx ELV of 200 mg m−3 or less) and other regions, respectively. The y axis is the slope of the regression of the NOx to CO2 emissions with an assumed y-intercept of zero. Error bars show the standard deviations for the NOx to CO2 emission ratios for individual power plants. The x axis is correlation coefficient of the regression. The dashed line represents 2005 US for bituminous coal derived in this study. The grey shadow represents 2005 US ± standard deviation. * China switched from being a less strict country to a more strict country in 2014, when most coal-fired power plants in China were required to comply with its new emission standards (GB13223-2011).
We further compare the 2005 US in Table 1 with the GPED NOx to CO2 emission ratios for less strict countries. We chose the 2005 value for comparison based on the following considerations. In 2005, the US EPA issued the Clean Air Interstate Rule (CAIR) to address the interstate transport of ozone and fine particulate matter pollution for eastern US states, which reduced NOx emissions and thus NOx to CO2 ratios (). However, similar comprehensive control strategies have not been adopted in less strict countries. In this way, the 2005 values are expected to show better consistency with the NOx to CO2 ratios of less strict countries than values for more recent years. Note that the GPED database does not give information on ratios by coal type. Therefore, we use for bituminous coal, which is the most widely used coal type in coal-fired power plants in most countries.
The ratios for individual power plants in less strict countries tend to be larger than the US for 2005, considering that power plants in those countries may not be equipped with any NOx control devices or even low-NOx burners, a technology which is widely installed in US power plants with and without post-combustion NOx control devices. Most ratios range from US 2005 to 2005 standard deviation (Fig. 8). It is no surprise that some less strict countries have ratios higher than this range, which also occurs for some US power plants without post-combustion emission controls (Fig. 4). However, there are considerable uncertainties in the GPED database given the scarcity of reliable emissions information in less strict countries. For example, the GPED NOx and CO2 emissions estimates for Turkey and Russia, which are outliers in Fig. 8, are subject to more assumptions and thus larger uncertainties than countries with high-quality country-specific emission data, such as China, which has a high-resolution emissions database (CPED; Liu et al., 2015), and India, which has a database developed by Argonne National Laboratory (Lu et al., 2012).
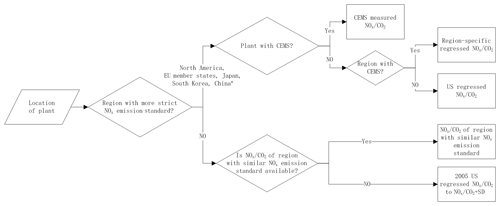
Figure 9Schematic of our methodology to estimate the NOx to CO2 emission ratios for power plants outside the US. * China switched from being a less strict country to a more strict country in 2014, when most coal-fired power plants in China were required to comply with its new emission standards (GB13223-2011).
Figure 9 shows a schematic of our methodology to estimate the NOx to CO2 emission ratios for power plants outside the US. We adopt different approaches for more and less strict countries. More strict countries, including Canada, European Union (EU) member states, Japan, South Korea, and, more recently, China, usually use CEMS to monitor emissions, particularly from the largest emitters. For power plants with CEMS measurements for both NOx and CO2 emissions, it is straightforward to use the measured ratios. However, there is still a significant number of power plants in those countries without CEMS technology, particularly for CO2 measurements. For example, EU member states do not require power plants to use CEMS for CO2 reporting and the majority of plants in the EU therefore reports CO2 emissions based on emission factors (Sloss, 2011). Therefore, we recommend applying our method described in Sect. 2.2 to infer region-specific ratios for those power plants. The US could be a less accurate but reasonable approximation when no CEMS data are available, considering those countries share NOx ELVs for power plants that are similar to the US. For less strict countries, we recommend using the 2005 US values by coal type when ratios from countries with similar NOx emission standards are not available. We also recommend assigning a range from 2005 to 2005 standard deviation, instead of a fixed value, to the ratio for inferring CO2 emissions, considering the knowledge about ratios from those regions is too low to narrow the constraint.
As demonstrated in Sect. 2.2, our method presented in this study provides a reasonable estimate of the ratio for power plants without post-combustion NOx control devices with only knowing coal type. Even for regions without reliable emission information, the information on coal type, particularly for large power plants, are very likely publicly available. For power plants that install post-combustion NOx control technology, we additionally require the removal efficiency of the device to derive the ratio. The removal efficiency of post-combustion NOx control devices is usually directly reported, as the operation of such devices is very expensive and is expected to be subject to strict quality control and assurance standards. In contrast to bottom-up approaches, many details are required for calculating NOx and CO2 emissions, including coal type, coal quality, boiler firing type, NOx emission control device type, and operating condition of boiler and emission control device.
3.3.2 Application to Matimba power plant in South Africa
We apply the methodology shown in Fig. 9 to estimate CO2 emissions from a South African power plant, Matimba, which is a strong isolated NOx point source (Fig. 10). It is a well-studied power plant, having had its emissions estimated using several different methods as reported in the literature. We estimate for Matimba from 2005 to 2017 based on OMI NO2 observations following the approach in Sect. 2.1. Matimba uses subbituminous coal with a calorific value of ∼20 MJ kg−1 (Makgato and Chirwa, 2017). We apply the ratio ranging from 2005 to 2005 standard deviation to Matimba, following the methodology in Fig. 9, considering that South Africa is a less strict country without any post-combustion NOx control devices (Pretorius et al., 2015). Our derived is shown in Fig. 11 and fluctuates over time. The growth after 2008* is most likely caused by the increased unit operating hours driven by the desire to meet fully the demand for electricity in South Africa after a period of rolling blackouts (2007–2008) (Duncan et al., 2016). The decline afterwards may be associated with the tripping of generating units at the Matimba because of overload and shortage of coal as reported by South African government news agency (available at: https://www.sanews.gov.za/south-africa/eskom-alone-cannot-solve-our-energy-challenges, last access: 1 March 2019). The increase in 2016* may be associated with a newly built power plant, Medupi, which began limited operations in 2015. Note that the range of (grey band) in Fig. 11 represents the emissions based on a range of NOx-to-CO2 ratios and not the uncertainty. We calculate the uncertainty of for Matimba following Sect. 3.2 with an additional uncertainty of ∼50 % to reflect the fact that the ratio may range from to standard deviation. The overall uncertainty of for Matimba is 81 %, as shown by the error bars in Fig. 11.
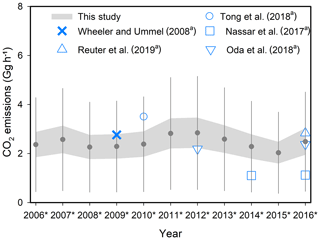
Figure 11Comparison of (Gg h−1) derived in this study, with existing estimates for the Matimba power plant during 2005 to 2017. is inferred based on the NOx to CO2 emissions ratio ranging from to standard deviation of ratio. The upper and lower grey bands denote the emissions inferred from and standard deviation of ratio, respectively. The grey dots and error bars show the mean of the upper and lower grey bands and their uncertainties, respectively. a Emissions are estimated for 2009 by Wheeler and Ummel (2008), for 2010 by Tong et al. (2018a), for 2014 and 2016 by Nassar et al. (2017), for 2016 by Reuter et al. (2019), and for 2012 and 2016 by Oda et al. (2018).
Figure 11 shows derived in this study and other independent estimates reported in the literature, including two top-down (Nassar et al., 2017; Reuter et al., 2019) and three bottom-up estimates (Wheeler and Ummel, 2008; Tong et al., 2018a; Oda et al., 2018). Despite the uncertainties associated with each of these methods, the CO2 emissions estimates agree reasonably well, but we do not have sufficient information to understand the differences between these estimates. However, Tong et al. (2018a) present in their CPED database both CO2 and NOx emissions, which allows us to determine that the difference between and the CPED bottom-up estimate contributes significantly to the difference in CO2 estimates from the two methods. for Matimba is 3.8 Mg h−1 for 2010*, which is 65 % smaller than the estimate by Tong et al. (2018a) for 2010. It is not surprising to see such differences considering the uncertainties of satellite-derived NOx emissions and bottom-up estimates for power plants without reliable CEMS measurements. For instance, is potentially underestimated because of the bias in the OMI NO2 standard product (version 3.1) associated with a low-resolution static climatology of surface Lambert-Equivalent Reflectivity (OMLER) (Kleipool et al., 2008). We perform a sensitivity analysis by using the preliminary new version of the OMI NO2 product, which uses new geometry-dependent Moderate Resolution Imaging Spectroradiometer (MODIS)-based surface reflectivity. The inferred based on the new product is over 10 % higher than version 3.1. The bottom-up estimates for Matimba are subject to significant uncertainties as well. For example, Tong et al. (2018a) used national total fuel consumption of the power sector for South Africa as reported by the International Energy Agency to estimate fuel consumption at the plant level, as detailed fuel consumption for each plant is not currently available. Additionally, they used default NOx emission factors obtained from the literature because of the absence of country-specific measurement data.
In our study, we investigated the feasibility of using satellite data of NO2 from power plants to infer co-emitted CO2 emissions, which could serve as complementary verification of bottom-up inventories or be used to supplement these inventories that are highly uncertain in many regions of the world. For example, our estimates will serve as an independent check of CO2 emissions that will be inferred from satellite retrievals of future CO2 sensors (Bovensmann et al., 2010). Currently, uncertainties in CO2 emissions from power plants confound national and international efforts to design effective climate mitigation strategies.
We estimate NO2 and CO2 emissions during the “ozone season” from individual power plants from satellite observations of NO2 and demonstrate its utility for US power plants, which have accurate CEMS with which to evaluate our method. We systematically identify the sources of variation, such as types of coal, boiler, and NOx emission control device, and change in operating conditions, which affect the NOx to CO2 emissions ratio. Understanding the causes of these variations will allow for better-informed assumptions when applying our method to power plants that have no or uncertain information on the factors that affect their emissions ratios. For example, we estimated CO2 emissions from the large and isolated Matimba power plant in South Africa, finding that our emissions estimate shows reasonable agreement with other independent estimates.
We found that it is feasible to infer CO2 emissions from satellite NO2 observations, but limitations of the current satellite data (e.g., spatiotemporal resolution or signal-to-noise) only allow us to apply our method to eight large and isolated U.S. power plants. Looking forward, we anticipate that these limitations will diminish for the recently launched (October 2017) TROPOMI and three upcoming (launches expected in the early 2020s) geostationary instruments (NASA TEMPO, European Space Agency and Copernicus Programme Sentinel-4, Korea Meteorological Administration Geostationary Environment Monitoring Spectrometer, GEMS), which are designed to have superior capabilities to OMI. High-resolution TROPOMI observations are capable of describing the spatiotemporal variability of NO2, even in a relatively small city like Helsinki (Ialongo et al., 2019) and allow estimates of NOx emissions to be calculated for shorter timeframes (Goldberg et al., 2019c). Higher spatial and temporal resolutions will likely reduce uncertainties in estimates of NOx emissions as well as allow for the separation of more power plant plumes from nearby sources, thus increasing the number of power plants available for analysis. Therefore, future work will be to apply our method to these new datasets, especially after several years of vetted data become available. Additional future work will include applying our method to other regions of the world with reliable CEMS information, such as Europe, Canada and, more recently, China, to develop a more reliable and complete database with region-specific ratios.
The OMI NO2 and MERRA-2 wind data can be downloaded from the Goddard Earth Sciences Data and Information Services Center (GES DISC). The OMI NO2 data are available at https://doi.org/10.5067/Aura/OMI/DATA2017; Krotkov et al. (2018). The MERRA-2 wind data are available at https://doi.org/10.5067/Aura/OMI/DATA2033; Joiner (2018). The CEMS emissions data can be downloaded from Air Markets Program Data (available at https://ampd.epa.gov/ampd/, US EPA, 2017). The GPED data are available at http://www.meicmodel.org/dataset-gped.html; Tong et al. (2018b).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-20-99-2020-supplement.
FL, BND, and NAK designed the framework. FL, SB, LNL, DG, CAM, and DLG developed the NOx emission fitting algorithm and FL carried it out. FL and ZL analyzed the NOx∕CO2 emission ratio. FL and BND prepared the manuscript with contributions from all co-authors.
The authors declare that they have no conflict of interest.
The Dutch-Finnish built OMI instrument is part of the NASA EOS Aura satellite payload. KNMI and the Netherlands Space Agency (NSO) manage the OMI project. We thank the US EPA for making the Emissions and Generation Resource Integrated Database (eGRID) available online. We thank the two anonymous reviewers for helpful comments during ACP discussions.
This research has been supported by the NASA (Earth Science Division Atmospheric Composition: Modeling and Analysis Program, ACMAP) and the NASA Aura Science team.
This paper was edited by Aijun Ding and reviewed by two anonymous referees.
Ackerman, K. V. and Sundquist, E. T.: Comparison of two U.S. power-plant carbon dioxide emissions data sets, Environ. Sci. Technol., 42, 5688–5693, https://doi.org/10.1021/es800221q, 2008.
Basu, S., Guerlet, S., Butz, A., Houweling, S., Hasekamp, O., Aben, I., Krummel, P., Steele, P., Langenfelds, R., Torn, M., Biraud, S., Stephens, B., Andrews, A., and Worthy, D.: Global CO2 fluxes estimated from GOSAT retrievals of total column CO2, Atmos. Chem. Phys., 13, 8695–8717, https://doi.org/10.5194/acp-13-8695-2013, 2013.
Beirle, S., Boersma, K. F., Platt, U., Lawrence, M. G., and Wagner, T.: Megacity emissions and lifetimes of nitrogen oxides probed from space, Science, 333, 1737–1739, 2011.
Berezin, E. V., Konovalov, I. B., Ciais, P., Richter, A., Tao, S., Janssens-Maenhout, G., Beekmann, M., and Schulze, E.-D.: Multiannual changes of CO2 emissions in China: indirect estimates derived from satellite measurements of tropospheric NO2 columns, Atmos. Chem. Phys., 13, 9415–9438, https://doi.org/10.5194/acp-13-9415-2013, 2013.
Boersma, K. F., Eskes, H. J., Veefkind, J. P., Brinksma, E. J., van der A, R. J., Sneep, M., van den Oord, G. H. J., Levelt, P. F., Stammes, P., Gleason, J. F., and Bucsela, E. J.: Near-real time retrieval of tropospheric NO2 from OMI, Atmos. Chem. Phys., 7, 2103–2118, https://doi.org/10.5194/acp-7-2103-2007, 2007.
Bovensmann, H., Buchwitz, M., Burrows, J. P., Reuter, M., Krings, T., Gerilowski, K., Schneising, O., Heymann, J., Tretner, A., and Erzinger, J.: A remote sensing technique for global monitoring of power plant CO2 emissions from space and related applications, Atmos. Meas. Tech., 3, 781–811, https://doi.org/10.5194/amt-3-781-2010, 2010.
Buchwitz, M., Reuter, M., Schneising, O., Noël, S., Gier, B., Bovensmann, H., Burrows, J. P., Boesch, H., Anand, J., Parker, R. J., Somkuti, P., Detmers, R. G., Hasekamp, O. P., Aben, I., Butz, A., Kuze, A., Suto, H., Yoshida, Y., Crisp, D., and O'Dell, C.: Computation and analysis of atmospheric carbon dioxide annual mean growth rates from satellite observations during 2003–2016, Atmos. Chem. Phys., 18, 17355–17370, https://doi.org/10.5194/acp-18-17355-2018, 2018.
Burrows, J. P., Hölzle, E., Goede, A. P. H., Visser, H., and Fricke, W.: SCIAMACHY – scanning imaging absorption spectrometer for atmospheric chartography, Acta Astronaut., 35, 445–451, https://doi.org/10.1016/0094-5765(94)00278-T, 1995.
Crisp, D.: Measuring atmospheric carbon dioxide from space with the Orbiting Carbon Observatory-2 (OCO-2), Proc. SPIE, 9607, 960702, https://doi.org/10.1117/12.2187291, 2015.
de Foy, B., Lu, Z., Streets, D. G., Lamsal, L. N., and Duncan, B. N.: Estimates of power plant NOx emissions and lifetimes from OMI NO2 satellite retrievals, Atmos. Environ., 116, 1–11, 2015.
Duncan, B. N., Yoshida, Y., de Foy, B., Lamsal, L. N., Streets, D. G., Lu, Z., Pickering, K. E., and Krotkov, N. A.: The observed response of Ozone Monitoring Instrument (OMI) NO2 columns to NOx emission controls on power plants in the United States: 2005–2011, Atmos. Environ., 81, 102–111, 2013.
Duncan, B. N., Lamsal, L. N., Thompson, A. M., Yoshida, Y., Lu, Z., Streets, D. G., Hurwitz, M. M., and Pickering, K. E.: A spacebased, high-resolution view of notable changes in urban NOx pollution around the world (2005–2014), J. Geophys. Res., 121, 976–996, https://doi.org/10.1002/2015jd024121, 2016.
Fioletov, V. E., McLinden, C. A., Krotkov, N., Moran, M. D., and Yang, K.: Estimation of SO2 emissions using OMI retrievals, Geophys. Res. Lett., 38, L21811, https://doi.org/10.1029/2011gl049402, 2011.
Gelaro, R., McCarty, W., Suárez, M. J., Todling, R., Molod, A., Takacs, L., Randles, C. A., Darmenov, A., Bosilovich, M. G., Reichle, R., Wargan, K., Coy, L., Cullather, R., Draper, C., Akella, S., Buchard, V., Conaty, A., Silva, A. M. d., Gu, W., Kim, G.-K., Koster, R., Lucchesi, R., Merkova, D., Nielsen, J. E., Partyka, G., Pawson, S., Putman, W., Rienecker, M., Schubert, S. D., Sienkiewicz, M., and Zhao, B.: The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2), J. Climate, 30, 5419–5454, https://doi.org/10.1175/jcli-d-16-0758.1, 2017.
Glenn, C., Logan, T., Vu, B., Walsh, M., and Williams, P.: Evaluation of NOx Flue Gas Analyzers for Accuracy and Their Applicability for Low-Concentration Measurements AU – Gluck, Steven, J. Air Waste Manage., 53, 749–758, https://doi.org/10.1080/10473289.2003.10466208, 2003.
Goldberg, D. L., Saide, P. E., Lamsal, L. N., de Foy, B., Lu, Z., Woo, J.-H., Kim, Y., Kim, J., Gao, M., Carmichael, G., and Streets, D. G.: A top-down assessment using OMI NO2 suggests an underestimate in the NOx emissions inventory in Seoul, South Korea, during KORUS-AQ, Atmos. Chem. Phys., 19, 1801–1818, https://doi.org/10.5194/acp-19-1801-2019, 2019a.
Goldberg, D. L., Lu, Z., Oda, T., Lamsal, L. N., Liu, F., Griffin, D., McLinden, C. A., Krotkov, N. A., Duncan, B. N., and Streets, D. G.: Exploiting OMI NO2 satellite observations to infer fossil-fuel CO2 emissions from U.S. megacities, Sci. Total Environ., 695, 133805, https://doi.org/10.1016/j.scitotenv.2019.133805, 2019b.
Goldberg, D. L., Lu, Z., Streets, D. G., de Foy, B., Griffin, D., McLinden, C. A., Lamsal, L. N., Krotkov, N. A., and Eskes, H.: Enhanced Capabilities of TROPOMI NO2: Estimating NOx from North American Cities and Power Plants, Environ. Sci. Technol., 53, 12594–12601, https://doi.org/10.1021/acs.est.9b04488, 2019c.
Griffin, D., Zhao, X., McLinden, C. A., Boersma, F., Bourassa, A., Dammers, E., Degenstein, D., Eskes, H., Fehr, L., Fioletov, V., Hayden, K., Kharol, S. K., Li, S.-M., Makar, P., Martin, R. V., Mihele, C., Mittermeier, R. L., Krotkov, N., Sneep, M., Lamsal, L. N., Linden, M. t., Geffen, J. v., Veefkind, P., and Wolde, M.: High-resolution mapping of nitrogen dioxide with TROPOMI: First results and validation over the Canadian oil sands, Geophys. Res. Lett., 46, 1049–1060, https://doi.org/10.1029/2018gl081095, 2019.
Hakkarainen, J., Ialongo, I., and Tamminen, J.: Direct space-based observations of anthropogenic CO2 emission areas from OCO-2, Geophys. Res. Lett., 43, 11400–11406, https://doi.org/10.1002/2016GL070885, 2016.
Hakkarainen, J., Ialongo, I., Maksyutov, S., and Crisp, D.: Analysis of Four Years of Global XCO2 Anomalies as Seen by Orbiting Carbon Observatory-2, Remote Sens., 11, 850, https://doi.org/10.3390/rs11070850, 2019.
Houweling, S., Baker, D., Basu, S., Boesch, H., Butz, A., Chevallier, F., Deng, F., Dlugokencky, E. J., Feng, L., Ganshin, A., Hasekamp, O., Jones, D., Maksyutov, S., Marshall, J., Oda, T., O'Dell, C. W., Oshchepkov, S., Palmer, P. I., Peylin, P., Poussi, Z., Reum, F., Takagi, H., Yoshida, Y., and Zhuravlev, R.: An intercomparison of inverse models for estimating sources and sinks of CO2 using GOSAT measurements, J. Geophys. Res.-Atmos., 120, 5253–5266, https://doi.org/10.1002/2014JD022962, 2015.
Ialongo, I., Virta, H., Eskes, H., Hovila, J., and Douros, J.: Comparison of TROPOMI/Sentinel 5 Precursor NO2 observations with ground-based measurements in Helsinki, Atmos. Meas. Tech. Discuss., https://doi.org/10.5194/amt-2019-329, in review, 2019.
Janardanan, R., Maksyutov, S., Oda, T., Saito, M., Kaiser, J. W., Ganshin, A., Stohl, A., Matsunaga, T., Yoshida, Y., and Yokota, T.: Comparing GOSAT observations of localized CO2 enhancements by large emitters with inventory-based estimates, Geophys. Res. Lett., 43, 3486–3493, https://doi.org/10.1002/2016GL067843, 2016.
Janssens-Maenhout, G., Crippa, M., Guizzardi, D., Muntean, M., Schaaf, E., Dentener, F., Bergamaschi, P., Pagliari, V., Olivier, J. G. J., Peters, J. A. H. W., van Aardenne, J. A., Monni, S., Doering, U., and Petrescu, A. M. R.: EDGAR v4.3.2 Global Atlas of the three major Greenhouse Gas Emissions for the period 1970–2012, Earth Syst. Sci. Data Discuss., https://doi.org/10.5194/essd-2017-79, 2017.
Jöckel, P., Tost, H., Pozzer, A., Kunze, M., Kirner, O., Brenninkmeijer, C. A. M., Brinkop, S., Cai, D. S., Dyroff, C., Eckstein, J., Frank, F., Garny, H., Gottschaldt, K.-D., Graf, P., Grewe, V., Kerkweg, A., Kern, B., Matthes, S., Mertens, M., Meul, S., Neumaier, M., Nützel, M., Oberländer-Hayn, S., Ruhnke, R., Runde, T., Sander, R., Scharffe, D., and Zahn, A.: Earth System Chemistry integrated Modelling (ESCiMo) with the Modular Earth Submodel System (MESSy) version 2.51, Geosci. Model Dev., 9, 1153–1200, https://doi.org/10.5194/gmd-9-1153-2016, 2016.
Joiner, J.: GEOS-5 FP-IT Assimilation Geo-colocated to OMI/Aura VIS 1-Orbit L2 Support Swath 13x24km V3, https://doi.org/10.5067/Aura/OMI/DATA2033, 2018.
Kleipool, Q. L., Dobber, M. R., de Haan, J. F., and Levelt, P. F.: Earth surface reflectance climatology from 3 years of OMI data, J. Geophys. Res.-Atmos., 113, D18, https://doi.org/10.1029/2008jd010290, 2008.
Konovalov, I. B., Berezin, E. V., Ciais, P., Broquet, G., Zhuravlev, R. V., and Janssens-Maenhout, G.: Estimation of fossil-fuel CO2 emissions using satellite measurements of “proxy” species, Atmos. Chem. Phys., 16, 13509–13540, https://doi.org/10.5194/acp-16-13509-2016, 2016.
Kort, E. A., Frankenberg, C., Miller, C. E., and Oda, T.: Space-based observations of megacity carbon dioxide, Geophys. Res. Lett., 39, L17806, https://doi.org/10.1029/2012GL052738, 2012.
Krotkov, N. A., Lamsal, L. N., Celarier, E. A., Swartz, W. H., Marchenko, S. V., Bucsela, E. J., Chan, K. L., Wenig, M., and Zara, M.: The version 3 OMI NO2 standard product, Atmos. Meas. Tech., 10, 3133–3149, https://doi.org/10.5194/amt-10-3133-2017, 2017.
Krotkov, N. A., Lamsal, L. N., Marchenko, S. V., Celarier, E. A., Bucsela, E. J., Swartz, W. H., Joiner, J., and the OMI core team: OMI/Aura Nitrogen Dioxide (NO2) Total and Tropospheric Column 1-orbit L2 Swath 13x24 km V003, https://doi.org/10.5067/Aura/OMI/DATA2017, 2018.
Levelt, P. F., van den Oord, G. H. J., Dobber, M. R., Malkki, A., Huib, V., Johan de, V., Stammes, P., Lundell, J. O. V., and Saari, H.: The ozone monitoring instrument, IEEE T. Geosci. Remote, 44, 1093–1101, 2006.
Levelt, P. F., Joiner, J., Tamminen, J., Veefkind, J. P., Bhartia, P. K., Stein Zweers, D. C., Duncan, B. N., Streets, D. G., Eskes, H., van der A, R., McLinden, C., Fioletov, V., Carn, S., de Laat, J., DeLand, M., Marchenko, S., McPeters, R., Ziemke, J., Fu, D., Liu, X., Pickering, K., Apituley, A., González Abad, G., Arola, A., Boersma, F., Chan Miller, C., Chance, K., de Graaf, M., Hakkarainen, J., Hassinen, S., Ialongo, I., Kleipool, Q., Krotkov, N., Li, C., Lamsal, L., Newman, P., Nowlan, C., Suleiman, R., Tilstra, L. G., Torres, O., Wang, H., and Wargan, K.: The Ozone Monitoring Instrument: overview of 14 years in space, Atmos. Chem. Phys., 18, 5699–5745, https://doi.org/10.5194/acp-18-5699-2018, 2018.
Liu, F., Zhang, Q., Tong, D., Zheng, B., Li, M., Huo, H., and He, K. B.: High-resolution inventory of technologies, activities, and emissions of coal-fired power plants in China from 1990 to 2010, Atmos. Chem. Phys., 15, 13299–13317, https://doi.org/10.5194/acp-15-13299-2015, 2015.
Liu, F., Beirle, S., Zhang, Q., Dörner, S., He, K., and Wagner, T.: NOx lifetimes and emissions of cities and power plants in polluted background estimated by satellite observations, Atmos. Chem. Phys., 16, 5283–5298, https://doi.org/10.5194/acp-16-5283-2016, 2016.
Liu, F., Beirle, S., Zhang, Q., van der A, R. J., Zheng, B., Tong, D., and He, K.: NOx emission trends over Chinese cities estimated from OMI observations during 2005 to 2015, Atmos. Chem. Phys., 17, 9261–9275, https://doi.org/10.5194/acp-17-9261-2017, 2017.
Liu, F., Choi, S., Li, C., Fioletov, V. E., McLinden, C. A., Joiner, J., Krotkov, N. A., Bian, H., Janssens-Maenhout, G., Darmenov, A. S., and da Silva, A. M.: A new global anthropogenic SO2 emission inventory for the last decade: a mosaic of satellite-derived and bottom-up emissions, Atmos. Chem. Phys., 18, 16571–16586, https://doi.org/10.5194/acp-18-16571-2018, 2018.
Lu, Z. and Streets, D. G.: Increase in NOx emissions from Indian thermal power plants during 1996–2010: Unit-based inventories and multisatellite observations, Environ. Sci. Technol., 46, 7463–7470, https://doi.org/10.1021/es300831w, 2012.
Lu, Z., Streets, D. G., de Foy, B., Lamsal, L. N., Duncan, B. N., and Xing, J.: Emissions of nitrogen oxides from US urban areas: estimation from Ozone Monitoring Instrument retrievals for 2005–2014, Atmos. Chem. Phys., 15, 10367–10383, https://doi.org/10.5194/acp-15-10367-2015, 2015.
Majanne, Y., Korpela, T., Judl, J., Koskela, S., Laukkanen, V., and Häyrinen, A.: Real Time Monitoring of Environmental Efficiency of Power Plants, IFAC-PapersOnLine, 48, 495–500, https://doi.org/10.1016/j.ifacol.2015.12.428, 2015.
Makgato, S. and Chirwa, E.: Characteristics of Thermal Coal used by Power Plants in Waterberg Region of South Africa, Chem. Engineer. Trans., 57, 511–516, 10.3303/CET1757086, 2017.
McLinden, C. A., Fioletov, V., Boersma, K. F., Kharol, S. K., Krotkov, N., Lamsal, L., Makar, P. A., Martin, R. V., Veefkind, J. P., and Yang, K.: Improved satellite retrievals of NO2 and SO2 over the Canadian oil sands and comparisons with surface measurements, Atmos. Chem. Phys., 14, 3637–3656, https://doi.org/10.5194/acp-14-3637-2014, 2014.
Nassar, R., Hill, T. G., McLinden, C. A., Wunch, D., Jones, D. B. A., and Crisp, D.: Quantifying CO2 Emissions From Individual Power Plants From Space, Geophys. Res. Lett., 44, 10045–10053, https://doi.org/10.1002/2017GL074702, 2017.
Oda, T., Maksyutov, S., and Andres, R. J.: The Open-source Data Inventory for Anthropogenic CO2, version 2016 (ODIAC2016): a global monthly fossil fuel CO2 gridded emissions data product for tracer transport simulations and surface flux inversions, Earth Syst. Sci. Data, 10, 87–107, https://doi.org/10.5194/essd-10-87-2018, 2018.
Pretorius, I., Piketh, S., Burger, R., and Neomagus, H.: A perspective on South African coal fired power station emissions, J. Energy South. Afr., 26, 27–40, https://doi.org/10.17159/2413-3051/2015/v26i3a2127, 2015.
Reuter, M., Buchwitz, M., Hilboll, A., Richter, A., Schneising, O., Hilker, M., Heymann, J., Bovensmann, H., and Burrows, J. P.: Decreasing emissions of NOx relative to CO2 in East Asia inferred from satellite observations, Nat. Geosci., 7, 792–795, https://doi.org/10.1038/ngeo2257, 2014.
Reuter, M., Buchwitz, M., Schneising, O., Krautwurst, S., O'Dell, C. W., Richter, A., Bovensmann, H., and Burrows, J. P.: Towards monitoring localized CO2 emissions from space: co-located regional CO2 and NO2 enhancements observed by the OCO-2 and S5P satellites, Atmos. Chem. Phys., 19, 9371–9383, https://doi.org/10.5194/acp-19-9371-2019, 2019.
Russell, A. R., Perring, A. E., Valin, L. C., Bucsela, E. J., Browne, E. C., Wooldridge, P. J., and Cohen, R. C.: A high spatial resolution retrieval of NO2 column densities from OMI: method and evaluation, Atmos. Chem. Phys., 11, 8543–8554, https://doi.org/10.5194/acp-11-8543-2011, 2011.
Schneising, O., Heymann, J., Buchwitz, M., Reuter, M., Bovensmann, H., and Burrows, J. P.: Anthropogenic carbon dioxide source areas observed from space: assessment of regional enhancements and trends, Atmos. Chem. Phys., 13, 2445–2454, https://doi.org/10.5194/acp-13-2445-2013, 2013.
Schoeberl, M. R., Douglass, A. R., Hilsenrath, E., Bhartia, P. K., Beer, R., Waters, J. W., Gunson, M. R., Froidevaux, L., Gille, J. C., and Barnett, J. J.: Overview of the EOS Aura mission, IEEE T. Geosci. Remote, 44, 1066–1074, 2006.
Seinfeld, J. H. and Pandis, S. N.: Atmospheric chemistry and physics: From air pollution to climate change, John Wiley and Sons, New York, 204–275, 2006.
Shaiganfar, R., Beirle, S., Denier van der Gon, H., Jonkers, S., Kuenen, J., Petetin, H., Zhang, Q., Beekmann, M., and Wagner, T.: Estimation of the Paris NOx emissions from mobile MAX-DOAS observations and CHIMERE model simulations during the MEGAPOLI campaign using the closed integral method, Atmos. Chem. Phys., 17, 7853–7890, https://doi.org/10.5194/acp-17-7853-2017, 2017.
Shindell, D. and Faluvegi, G.: The net climate impact of coal-fired power plant emissions, Atmos. Chem. Phys., 10, 3247–3260, https://doi.org/10.5194/acp-10-3247-2010, 2010.
Sloss, L.: Efficiency and emissions monitoring and reporting, CCC/188, 40, IEA Clean Coal Centre, London, UK, 2011.
Tong, D., Zhang, Q., Davis, S. J., Liu, F., Zheng, B., Geng, G., Xue, T., Li, M., Hong, C., Lu, Z., Streets, D. G., Guan, D., and He, K.: Targeted emission reductions from global super-polluting power plant units, Nature Sustainability, 1, 59–68, https://doi.org/10.1038/s41893-017-0003-y, 2018a.
Tong, D., Zhang, Q., Davis, S. J., Liu, F., Zheng, B., Geng, G., Xue, T., Li, M., Hong, C., Lu, Z., Streets, D. G., Guan, D., and He, K.: The Global Power Emissions Database, available at: http://www.meicmodel.org/dataset-gped.html (last access: 1 April 2019), 2018b.
U.S. Energy Information Administration (US EIA): Electric Power Annual 2017, available at: https://www.eia.gov/electricity/annual/pdf/epa.pdf (last access: 11 April 2019), 2018.
U.S. Environmental Protection Agency (US EPA): Compilation of Air Pollutant Emission Factors, AP-42, Fifth Edition, Volume 1, Chapter 1, Washington, D. C., available at: https://www3.epa.gov/ttn/chief/ap42/ch01/index.html (last access: 20 March 2019), 2009.
U.S. Environmental Protection Agency (US EPA), Air Markets Program Data, available at: https://ampd.epa.gov/ampd/ (last access: 10 March 2019), 2017.
U.S. Environmental Protection Agency (US EPA): Technical support document for eGRID with year 2016 data (the Emissions & Generation Resource Integrated Database), Washington, D.C., 2018.
Valin, L. C., Russell, A. R., and Cohen, R. C.: Variations of OH radical in an urban plume inferred from NO2 column measurements, Geophys. Res. Lett., 40, 1856–1860, https://doi.org/10.1002/grl.50267, 2013.
Varon, D. J., Jacob, D. J., McKeever, J., Jervis, D., Durak, B. O. A., Xia, Y., and Huang, Y.: Quantifying methane point sources from fine-scale satellite observations of atmospheric methane plumes, Atmos. Meas. Tech., 11, 5673–5686, https://doi.org/10.5194/amt-11-5673-2018, 2018.
Veefkind, J. P., Aben, I., McMullan, K., Förster, H., de Vries, J., Otter, G., Claas, J., Eskes, H. J., de Haan, J. F., Kleipool, Q., van Weele, M., Hasekamp, O., Hoogeveen, R., Landgraf, J., Snel, R., Tol, P., Ingmann, P., Voors, R., Kruizinga, B., Vink, R., Visser, H., and Levelt, P. F.: TROPOMI on the ESA Sentinel-5 Precursor: A GMES mission for global observations of the atmospheric composition for climate, air quality and ozone layer applications, Remote Sens. Environ., 120, 70–83, 2012.
Velazco, V. A., Buchwitz, M., Bovensmann, H., Reuter, M., Schneising, O., Heymann, J., Krings, T., Gerilowski, K., and Burrows, J. P.: Towards space based verification of CO2 emissions from strong localized sources: fossil fuel power plant emissions as seen by a CarbonSat constellation, Atmos. Meas. Tech., 4, 2809–2822, https://doi.org/10.5194/amt-4-2809-2011, 2011.
Wang, S., Zhang, Y., Hakkarainen, J., Ju, W., Liu, Y., Jiang, F., and He, W.: Distinguishing anthropogenic CO2 emissions From different energy intensive industrial sources using OCO-2 observations: A case study in Northern China, J. Geophys. Res.-Atmos., 123, 9462–9473, https://doi.org/10.1029/2018jd029005, 2018.
Wheeler, D. and Ummel, K.: Calculating CARMA: Global estimation of CO2 emissions from the power sector, Center for Global Development, Working Paper 145, 2008.
Yokota, T., Yoshida, Y., Eguchi, N., Ota, Y., Tanaka, T., Watanabe, H., and Maksyutov, S.: Global Concentrations of CO2 and CH4 Retrieved from GOSAT: First Preliminary Results, SOLA, 5, 160–163, https://doi.org/10.2151/sola.2009-041, 2009.