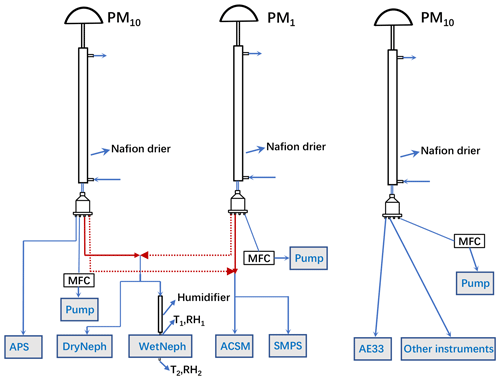
2.1 Inlet system and instruments

During this field campaign, all instruments were housed in an air-conditioned container, with the temperature held almost constant near 24^∘. The schematic diagram of the inlet systems for the aerosol sampling instruments is displayed in Fig. 1. Three inlet impactors are used for aerosol sampling, two PM₁₀ inlets and one PM₁ inlet, respectively sampling ambient aerosol particles with an aerodynamic diameter less than 10 and 1 µm. Nafion driers with lengths of 1.2 m were placed downstream of each PM impactor inlet, which can drop the RH of sampled air below 15 %; thus, sampled aerosol particles can be treated as being in the dry state. Additionally, downstream of every PM impactor inlet, an MFC (mass flow controller) and a pump were added for automatic flow compensation to ensure that each impactor reaches its required flow rate of 16.7 L min⁻¹ and guarantee the right cut diameters.

Figure 1Schematic diagram of the inlet systems for aerosol sampling instruments.

Download

Aerosol sampling instruments can be categorized into four groups according to their inlet routes. The first group (group 1) downstream of the first PM₁₀ inlet is comprised of only one instrument, the Aerodynamic Particle Sizer (APS, TSI Inc., Model 3321), measuring the size distribution of ambient aerosol particles with an aerodynamic diameter ranging from 700 nm to 20 µm at a temporal resolution of 20 s. The second group (group 2) includes a humidified nephelometer system (consisting of two nephelometers and a humidifier) that measures aerosol optical properties (scattering and backscattering coefficients at three wavelengths: 450, 525, and 635 nm) of ambient aerosol particles in the dry state (DryNeph) and under 85 % RH condition (WetNeph). The third group (group 3) includes two instruments, an ACSM and a scanning mobility particle sizer (SMPS; TSI model 3080). The CV-ToF-ACSM measures non-refractory particulate matter (NR-PM) species including organics, ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$, ${\mathrm{NO}}_{\mathrm{3}}^{-}$, ${\mathrm{NH}}_{\mathrm{4}}^{+}$, and Cl⁻, with an air flow of 0.1 L min⁻¹ and a time resolution of 2 min. Since the CV-ToF-ACSM instrument comes with a PM_2.5 impactor, when the impactor of upstream is PM₁₀, chemical compositions of PM_2.5 rather than of PM₁₀ were measured.

The SMPS measures particle mobility diameter size distributions with a diameter range of 12 to 760 nm. The inlets of group 2 and group 3 switch every 15 min, as denoted by the dashed and solid red lines in Fig. 1, enabling the instruments of these two groups to alternately measure the chemical and optical properties of PM₁₀ and PM₁. The fourth group (group 4) includes an AE33 aethalometer (Drinovec et al., 2015) and other aerosol instruments. Due to technical issues with the humidifier, the humified nephelometer system started to operate continuously on the 30 November.

2.2 The humidified nephelometer system

The humidified nephelometer system we built was set up to measure dry-state aerosol optical properties at a fixed RH of 85 %. The RH of the air sample is increased by a humidifier that consists of two layers. The inner layer is a Gore-Tex tube layer passing through sampled air, while the outer layer is a stainless-steel tube with circulating liquid water. The water vapor penetrates through the Gore-Tex tube and humidifies the sample air, while liquid water is kept from the inner layer by the Gore-Tex material. Upon the switch of inlets between group 2 and group 3, delays in valve switching caused instantaneous low pressure in the sample air, which broke the humidifier with the Gore-Tex tube after 4 d of continuous operation (3 December) and flooded the WetNeph. The WetNeph was fixed and recalibrated, and a commercial Nafion drier (60 cm long; Perma Pure company) replaced the Gore-Tex tube, which works the same way but is more resistant to low pressure. The temperature of the circulating water layer is controlled by a water bath and specified by an algorithm that adjusts the water temperature to maintain a relatively constant RH in the sensing volume of the WetNeph. To monitor the RH in the sensing volume of the WetNeph, two temperature and RH sensors (Vaisala HMP110, with accuracies of ±0.2^∘ and ±1.7 % for RH between 0 % to 90 %, respectively, and ±2.5 % for RH between 90 % to 100 %) were placed at the inlet and outlet of the WetNeph. Defining measured RHs and temperatures at the inlet and outlet of the WetNeph as RH₁/T₁ and RH₂/T₂, the according dew point temperatures T_d1 and T_d2 can be calculated, and the average value $\stackrel{\mathrm{‾}}{T_{\mathrm{d}}}$ was treated as the dew point of the sample air in the sensing volume of WetNeph. The sample RH is calculated using $\stackrel{\mathrm{‾}}{T_{\mathrm{d}}}$ and the sample temperature measured by a sensor inside the sample cavity of the nephelometer.

2.3 ACSM measurements and data analysis

The mass concentration and chemical composition of NR-PM species were measured with the Aerodyne ToF-ACSM, which is equipped with a PM_2.5 aerodynamic lens (Williams et al., 2010) and a capture vaporizer (CV; Xu et al., 2017; Hu et al., 2017) to extend the measured particle size to 2.5 µm. Detailed instrument descriptions were given in Fröhlich et al. (2013) and Xu et al. (2017). The CV-ToF-ACSM data were analyzed with the standard data analysis software (Tofware v2.5.13; https://sites.google.com/site/ariacsm/, last access: 21 January 2020) within Igor Pro (v6.37; WaveMetrics, Inc., Oregon, USA). The CV was designed with an enclosed cavity to increase particle collection efficiency (CE) at the detector (Xu et al., 2017). Field measurements indicate that the CE of CV was fairly robust and was roughly equivalent to 1. Therefore, a CE of 1 was applied to all measured species in this study (Hu et al., 2017, 2018b). Relative ionization efficiencies (RIEs) of 3.06 and 1.09 were used for ammonium and sulfate quantification, respectively, and the default values of 1.1 and 1.4 were used for nitrate and organic aerosol (OA), respectively. Compared with the AMS with a standard vaporizer, the CV-ToF-ACSM reports higher fragments at smaller m∕z values due to additional thermal decomposition associated with increased residence time and hot surface collisions (Hu et al., 2018a). As a result, f₄₄ values from CV-ToF-ACSM measurements are often much higher than those previously reported from AMS, yet they are well correlated (Hu et al., 2018a).

The organic mass spectra from m∕z 12 to 214 were analyzed by positive matrix factorization (PMF; Paatero and Tapper, 1994) with an Igor Pro-based PMF evaluation tool (v3.04; Ulbrich et al., 2009). The ion fragments m∕z of 38, 49, 63, and 66 were removed from both PM₁ and PM_2.5 PMF inputs, considering their small contributions to the total organic signals yet high signal-to-noise ratios. The PMF results were then evaluated following the procedures detailed in Zhang et al. (2011). After carefully evaluating the mass spectral profiles, diurnal patterns, and temporal variations in the OA factors and comparing them with other collocated measurements, a five-factor solution was selected for both PM₁ and PM_2.5. The five factors include four primary factors, i.e., hydrocarbon-like OA (HOA), cooking OA (COA), biomass burning OA (BBOA), coal combustion OA (CCOA), and a secondary factor, oxygenated OA (OOA). More detailed descriptions on the PMF results will be given elsewhere.

2.4 Data reprocessing

The size distributions measured by APS were converted to mobility-equivalent size distributions using spherical shape assumptions and an effective particle density of 1.7 g cm⁻³. Note that the designations of PM₁₀ and PM₁ are with respect to aerosol aerodynamic diameters, while the corresponding mobility-equivalent cut diameters of the two impactors are approximately 7669 and 767 nm, respectively. For simplicity and consistency, we will continue to refer to them as the PM₁₀ and PM₁ based on their aerodynamic diameter. For the case of PM₁ measurements, the mobility-equivalent cut diameter is quite near the upper range of the SMPS size range. Considering that the cut diameter of the impactor corresponds to the diameter of aerosol particles in the ambient state (aerosol hygroscopic growth effect needs to be taken into account) and the SMPS measures the size distributions of aerosol particles in the dry state, the SMPS measurements should be able to cover the full size range of PM₁. When the SMPS was sampling aerosol particles of PM₁₀, the size distributions measured by SMPS and APS were merged together and truncated to an upper limit of 7669 nm to provide a full range of particle number size distributions (PNSDs). In addition, the AE33 measures the aerosol absorption coefficient at several wavelengths; the mass concentrations of black carbon (BC) were converted from measured aerosol absorption coefficients at 880 nm with a mass absorption coefficient of 7.77 m² g⁻¹ (Drinovec et al., 2015).

Since group 2 and 3 switched between PM₁ and PM₁₀ inlets every 15 min, all measurements were averaged over each 15 min observation episode, resulting in valid time resolutions of 15 min for APS and BC PM₁₀ measurements and of 30 min for SMPS, CV-ToF-ACSM, and the humidified nephelometer system PM₁ and PM₁₀ measurements, respectively. This resulted in a 15 min time lag between the averaged datasets of group 2 and group 3. To match the time of all the measurement data, the measurements of SMPS, ACSM, and the humidified nephelometer system were linearly interpolated to the 15 min time resolution of the APS data.

3.1 Calculations of hygroscopicity parameters κ_sca and κ from measurements of the humidified nephelometer system

The humidified nephelometer system measures aerosol light-scattering coefficients and backscattering coefficients at three wavelengths under the dry state and 85 % RH condition, providing measurements of the light-scattering enhancement factor f(RH, λ), which is defined as $f\left(\mathrm{RH}=\mathrm{85}\mathit{\%},\mathit{\lambda }\right)=\frac{{\mathit{\sigma }}_{\mathrm{sp}}(\mathrm{RH},\mathit{\lambda })}{{\mathit{\sigma }}_{\mathrm{sp}}(\mathrm{dry},\mathit{\lambda })}$, with λ being the light wavelength. In this study, we only calculate f(RH, 525 nm) and refer to it hereinafter as f(RH) for simplicity. Brock et al. (2016) proposed a single parameter formula to describe f(RH, λ) as a function of RH. Kuang et al. (2017) further developed this parameterization scheme to better describe measured f(RH) by including the reference RH (RH₀) in the dry nephelometer as shown in Eq. (1), using which the optical hygroscopicity parameter κ_sca can be derived from f(RH)_measured:

An overall hygroscopicity parameter κ, referred to as κ_f(RH), can be retrieved from the measured f(RH) with the addition of a simultaneously measured PNSD and BC mass concentration (Chen et al., 2014; Kuang et al., 2017). The idea is to conduct an iterative calculation using the Mie theory and the κ-Köhler theory together to find a κ_f(RH) that closes the gap between the simulated and the measured f(RH). Details on the calculations of κ_f(RH) can be found in Kuang et al. (2017).

3.2 Calculations of κ_chem from aerosol chemical-composition measurements

For the calculation of aerosol hygroscopicity parameter κ based on measured chemical-composition data (κ_chem), detailed information on the chemical species is needed. The CV-ToF-ACSM can only provide bulk mass concentrations of ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$, ${\mathrm{NO}}_{\mathrm{3}}^{-}$, ${\mathrm{NH}}_{\mathrm{4}}^{+}$, and Cl⁻ ions and organic components. For the inorganic ions, a simplified ion pairing scheme (as listed in Table 1) was used to convert ion mass concentrations to mass concentrations of corresponding inorganic salts (Gysel et al., 2007; Wu et al., 2016).

Table 1Densities (ρ) and hygroscopicity parameters (κ) of inorganic salts used in this study.

Download Print Version | Download XLSX

Mass concentrations of ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$, ${\mathrm{NO}}_{\mathrm{3}}^{-}$, ${\mathrm{NH}}_{\mathrm{4}}^{+}$, and Cl⁻ are thus specified as ammonium sulfate (AS), ammonium nitrate (AN), ammonium chloride (AC), and ammonium bisulfate (ABS), with the κ values of these salts specified according to Wu et al. (2016) and Liu et al. (2014; Table 1). For a given internal mixture of different aerosol chemical species, a simple mixing rule called Zdanovskii–Stokes–Robinson (ZSR) can be used for predicting the overall κ_chem on the basis of volume fractions of different chemical species (ε_i; Petters and Kreidenweis, 2007):

where κ_i and ε_i represent the hygroscopicity parameter κ and volume fraction of chemical component i in the mixture. Based on Eq. (2), κ_chem can be calculated as follows:

where κ_OA and ε_OA represent the κ and volume fraction of total organics. Since black carbon is hydrophobic, κ_BC is assumed to be zero. With known κ_chem, κ_OA can be calculated using the following formula:

The volume concentration of organics was calculated by assuming that the density of POA is 1 g cm⁻³ and density of OOA is 1.4 g cm⁻³ (Wu et al., 2016). For the calculation of the total volume concentration (V_tot), we have three approaches. The first approach is to sum up the volume concentrations of all chemical species (AS, AN, ABS, AC, BC, and organics), where the volume concentration of BC was calculated by assuming a density of 1.7 g cm⁻³ (Wu et al., 2016). We refer to the calculated total volume concentration of aerosol particles as V_tot, Chem. The second approach is to integrate V_tot from the measured PNSD using the equation $V_{\mathrm{tot},\mathrm{PNSD}}=\int \frac{\mathrm{4}}{\mathrm{3}}\mathit{\pi }{r}^{\mathrm{3}}n\left(r\right)\mathrm{d}r$, where r is the particle radius and n(r) is the measured particle number concentrations. The third approach is to use the trained machine-learning estimator to estimate the V_tot based on measurements of the dry nephelometer (V_tot, Neph), as was introduced in Kuang et al. (2018). V_tot values of PM₁ calculated using these three methods were compared to each other and shown in Fig. S2 in the Supplement. V_tot, Chem correlates well with V_tot, PNSD, but it is on average 30 % lower than that of V_tot, PNSD. Chemical components within aerosol particles such as dust, sea salt, and metal ions cannot be detected by CV-ToF-ACSM. Since the Gucheng site is far from the ocean, sea salt should have negligible impacts on the total mass of PM₁. However, mineral dust can extend into the submicron range (Shao et al., 2007), which might be the cause for the low V_tot, Chem calculated using CV-ToF-ACSM and BC data. V_tot, Neph also correlates well with V_tot, PNSD but is on average 16 % lower than that of V_tot, PNSD. Closure studies between modeled and measured σ_sp and σ_bsp at 525 nm for PM₁ and PM₁₀ aerosol particles all showed good agreement between theoretical modeling results and measurements (Fig. S1), with most points falling within the 20 % relative deviation lines. However, modeled σ_sp values for both PM₁ and PM₁₀ were obviously higher than measured σ_sp, with an average relative difference of 22 % and 13 % between them for PM₁₀ and PM₁, respectively. The result for PM₁ explains why V_tot, Neph was lower than V_tot, PNSD. Two reasons might have contributed to this discrepancy. (1) Both PNSD and aerosol optical property measurements carry non-negligible uncertainties, with the SMPS bearing measurement uncertainty of 30 % for particles larger than 200 nm, which contribute most to V_tot (Wiedensohler et al., 2012), and the nephelometer measured σ_sp having an uncertainty of 9 % (Sherman et al., 2015; Titos et al., 2016). (2) The sampling tube length, valves, tube angles, and flow rates are different for the dry nephelometer and SMPS (e.g., much shorter tube and smaller flow rate for SMPS than those for the dry nephelometer), leading to different wall loss and loss in semi-volatile aerosol components. ACSM and the dry nephelometer had a similar tube length, and nephelometer measurements bear less uncertainty than SMPS. Thus, V_tot, Neph was chosen as V_tot in the calculations of Eq. (4). Based on the calculated V_tot, the material unidentified by CV-ToF-ACSM accounts for 19 % of V_tot on average, which could not be neglected in the κ_OA calculation. Thus, Eq. (4) was modified as follows:

where κ_X and ε_X are the hygroscopicity parameter κ and volume fraction of the unidentified material. Previous studies using V_tot, Chem as the total volume concentration of aerosol particles have avoided the discussion about influences of unidentified material by the CV-ToF-ACSM or other aerosol mass spectrometer instruments. The hygroscopicity of these unidentified materials, which might be dust or other components in continental regions, was not discussed before. Dust is nearly hydrophobic, with mineral dust showing κ values in range of 0.01 to 0.08 (Koehler et al., 2009). In this paper, we arbitrarily specified κ_X to be 0.05.

3.3 Can κ_f(RH) represent κ_chem?

According to Eq. (5), the measured bulk κ_chem values are needed to derive κ_OA. When bulk aerosol chemical compositions and aerosol hygroscopicity κ_f(RH) measurements are available, one might naturally jump to the conclusion of treating κ_f(RH) as κ_chem to derive κ_OA because both κ_f(RH) and κ_chem are from bulk aerosol measurements. However, the relationship between κ_chem, κ_f(RH) and the size-resolved κ distribution needs to be clarified in order to answer the question of whether κ_f(RH) can accurately represent κ_chem. The physical meanings of different κ representations used in the following discussions are listed in Table 2.

Table 2Different κ and their physical meanings.

Download Print Version | Download XLSX

Using V_i to represent volume concentrations of chemical species i and V_i(D_p) to represent volume concentrations of species i with a diameter of D_p, κ_chem can be derived as follows based on Eq. (2):

By swapping the order of summation and integration, Eq. (6) can be written as

Considering that ${\mathit{\kappa }}_{D_{\mathrm{p}}}=\sum _i\frac{\mathrm{d}{V}_i\left(D_{\mathrm{p}}\right)}{\mathrm{d}V\left(D_{\mathrm{p}}\right)}\cdot {\mathit{\kappa }}_i$, Eq. (7) can be rewritten as

The result of Eq. (8) indicates that κ_chem calculated using Eq. (3) represents the overall hygroscopicity of aerosol particles with volume contribution as the weighting function of ${\mathit{\kappa }}_{D_{\mathrm{p}}}$.

As for κ_f(RH), a detailed analysis is performed here to facilitate its physical understanding. The differential form of σ_sp of aerosol particles in the dry state can be expressed as follows:

Based on the definition of f(RH), the σ_sp of aerosol particles under different RH conditions can be written as

Therefore, the differential form of observed overall f(RH) can be formulated as

Figure 2(a) Simulated $\frac{\partial f_{D_{\mathrm{p}}}\left(\mathrm{RH}\right)}{\partial {\mathit{\kappa }}_{D_{\mathrm{p}}}}$; (b) simulated $\frac{\mathrm{1}}{\mathrm{d}\log D_{\mathrm{p}}}\cdot \frac{\partial f\left(\mathrm{RH}\right)}{\partial {\mathit{\kappa }}_{D_{\mathrm{p}}}}$.

Download

Based on this formula, the sensitivity of f(RH) on the hygroscopicity of aerosol particles with the diameter D_p can be derived as

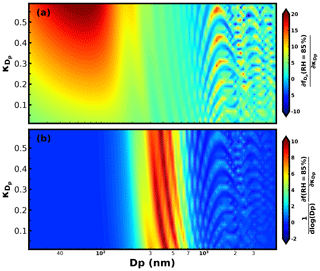
The sensitivity of f(RH) to ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ is determined together by the two terms in Eq. (12): (1) $\frac{\mathrm{1}}{{\mathit{\sigma }}_{\mathrm{sp}}}\cdot \frac{\mathrm{d}{\mathit{\sigma }}_{\mathrm{sp}}}{\mathrm{d}\log D_{\mathrm{p}}}$, which represents the contribution of σ_sp of aerosol particles in the dry state with the diameter D_p to total σ_sp, and (2) $\frac{\partial f_{D_{\mathrm{p}}}\left(\mathrm{RH}\right)}{\partial {\mathit{\kappa }}_{D_{\mathrm{p}}}}$, which represents the sensitivity of $f_{D_{\mathrm{p}}}\left(\mathrm{RH}\right)$ to ${\mathit{\kappa }}_{D_{\mathrm{p}}}$. Based on the Mie theory and the κ-Köhler theory, we simulated the second term under the 85 % RH condition for varying D_p and ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ values (Fig. 2a). In the diameter range below 200 nm, $\frac{\partial f_{D_{\mathrm{p}}}\left(\mathrm{RH}\right)}{\partial {\mathit{\kappa }}_{D_{\mathrm{p}}}}$ is very high, displaying a maximum near 60 nm. In this diameter range, a larger ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ generally corresponds to a higher $\frac{\partial f_{D_{\mathrm{p}}}\left(\mathrm{RH}\right)}{\partial {\mathit{\kappa }}_{D_{\mathrm{p}}}}$. For $\mathrm{200}\mathrm{nm}<D_{\mathrm{p}}<\mathrm{800}$ nm, higher and lower $\frac{\partial f_{D_{\mathrm{p}}}\left(\mathrm{RH}\right)}{\partial {\mathit{\kappa }}_{D_{\mathrm{p}}}}$ values appear alternatively, with all values staying positive. For D_p>800 nm, maxima and minima regions appear alternatively, and $f_{D_{\mathrm{p}}}\left(\mathrm{RH}\right)$ might decrease with increasing ${\mathit{\kappa }}_{D_{\mathrm{p}}}$. This is because, at this diameter range, the aerosol scattering efficiency has a non-monotonic response to the particle diameter increase (see Fig. 2a of Kuang et al., 2018).

The first term of Eq. (9), representing size-resolved σ_sp contributions of particles with the diameter in the dry state, mainly depends on the PNSD. The average PNSD of PM₁₀ was applied in the simulation of the first term using Mie theory (Fig. S3). Combining results of the first term and second term, the sensitivity of f(RH) to ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ was obtained and depicted in Fig. 2b. Results reveal that f(RH) is quite sensitive to the ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ of particles within the 200 to 800 nm diameter range but almost insensitive to ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ of particles with diameters below 200 nm and above 800 nm (corresponding aerodynamic diameter of about 1 µm). For particles smaller than 200 nm, the first term was quite small, especially for particles smaller than 100 nm (Fig. S3), while for particles larger than 800 nm, in addition to a small first term, the second term fluctuated between negative and positive values, which is why f(RH) was not sensitive to the overall hygroscopicity of these larger aerosol particles. These results suggest that although κ_f(RH) was derived from f(RH) measurements of PM₁₀, it mainly represents the overall hygroscopicity of aerosol particles with dry diameters between 200 and 800 nm for continental aerosol. This result indicates that κ_f(RH) values derived from f(RH) measurements of PM₁₀ and PM₁ should differ little from each other for measurements conducted in continental regions.

However, the quantitative relationship between the κ_f(RH) and size-resolved ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ is still not clear. Based on Eq. (11), $f_{D_{\mathrm{p}}}\left(\mathrm{RH}\right)$ can be expressed as

where g is the growth factor of aerosol particles which is a function of ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ and RH (Brock et al., 2016), i.e., $g=(\mathrm{1}+{\mathit{\kappa }}_{D_{\mathrm{p}}}\cdot \frac{\mathrm{RH}}{\mathrm{100}-\mathrm{RH}}{)}^{\mathrm{1}/\mathrm{3}}$, dN is differential form of aerosol number concentration, and Q_sca is the scattering efficiency as a function of D_p and g. The results of Kuang et al. (2018) indicate that, under the dry state, Q_sca can be expressed as $Q_{\mathrm{sca}}=k\cdot D_{\mathrm{p}}$, with k varying as a function of D_p. Here, we follow this idea and express the Q_sca under the humidified condition as $Q_{\mathrm{sca}}\left(D_{\mathrm{p}},g\right)=C\cdot D_{\mathrm{p}}\cdot g$, where C is a function of D_p, ${\mathit{\kappa }}_{D_{\mathrm{p}}}$, and RH. Replacing g and Q_sca in Eq. (13), we yield

which we can substitute into Eq. (8) to obtain a new expression for f(RH):

If we define $X_c(D_{\mathrm{p}},{\mathit{\kappa }}_{D_{\mathrm{p}}},\mathrm{RH})=C(D_{\mathrm{p}},{\mathit{\kappa }}_{D_{\mathrm{p}}},\mathrm{RH})/k$, and considering that $\mathrm{d}{\mathit{\sigma }}_{\mathrm{sp}}=\frac{\mathrm{1}}{\mathrm{4}}\cdot \mathit{\pi }\cdot D_{\mathrm{p}}^{\mathrm{2}}\cdot Q_{\mathrm{sca}}\cdot \mathrm{d}N=\frac{\mathrm{1}}{\mathrm{4}}\cdot \mathit{\pi }\cdot D_{\mathrm{p}}^{\mathrm{3}}\cdot k\cdot \mathrm{d}N$, Eq. (14) can be written as

The κ_f(RH) is a uniform κ for aerosol particle sizes that can yield a simulated f(RH) equal to the measured one. Thus, f(RH) can also be expressed as

Combining Eqs. (16) and (17), the relationship between κ_f(RH) and size-resolved ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ can be derived as

X_c values under 85 % RH for different D_p and ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ values are simulated and shown in Fig. 3; based on this result of X_c the second term of Eq. (18) (which depends on the PNSD and size-resolved ${\mathit{\kappa }}_{D_{\mathrm{p}}})$ could be calculated using the average PNSD during this field campaign and two assumed extreme cases of size-resolved ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ (solid and dashed black lines in Fig. 3). For PM₁, the second term corresponding to the two size-resolved ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ cases was −0.007 and 0.008, respectively. Corresponding values simulated for PM₁₀ were −0.005 and 0.004, respectively. To further investigate the possible contribution range of the second term to κ_f(RH), size-resolved ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ values derived by Liu et al. (2014) based on size-resolved chemical-composition measurements in ambient atmosphere in the NCP region (Fig. S4) were used with the average PNSD during this campaign to calculate values of the second term. Calculated values of second term ranged from −0.005 to 0.009, with its contribution to κ_f(RH) ranging from −1.5 % to 2 % (0.3 % on average). These results indicate that the second term was negligible in most cases, and Eq. (18) could be approximated as

X_c values shown in Fig. 3 indicate that for aerosol particles in the diameter range of 200 to 800 nm (which contribute most to σ_sp and are the part of the aerosol population that κ_f(RH) is most sensitive to) and for the observed ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ range of continental aerosol (${\mathit{\kappa }}_{D_{\mathrm{p}}}$usually less than 0.5), X_c mainly ranged from 0.7 to 1. Considering this, we might approximately assume X_c in Eq. (18) to be a constant value. Then, Eq. (19) can be further simplified to

This result suggests that κ_f(RH) can be approximately understood as the overall hygroscopicity of aerosol particles with the σ_sp contribution as the weighting function of ${\mathit{\kappa }}_{D_{\mathrm{p}}}$.

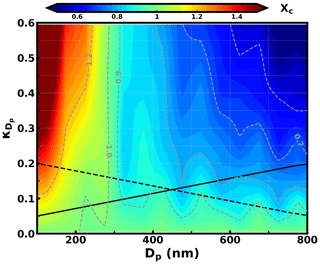
Figure 3Simulated values of X_c under 85 % RH for different D_p and ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ values. Black solid and dashed lines are two assumed size-resolved ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ distributions.

Download

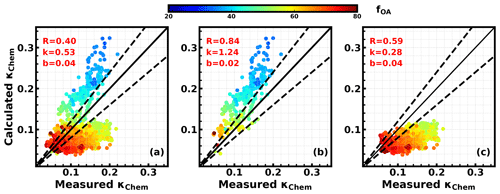
Based on results of Eqs. (8) and (20), both κ_f(RH) and κ_chem represent the overall hygroscopicity of bulk aerosol particles; however, their weighting functions of ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ are different. Within a certain D_p range, aerosol σ_sp is approximately proportional to aerosol volume (Kuang et al., 2018), resulting in little difference between κ_f(RH) and κ_chem. In this study, bulk κ_f(RH) was measured for both PM₁ and PM₁₀. How much does κ_chem differ from κ_f(RH) for PM₁ and PM₁₀ samples? Both PNSD and size-resolved ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ distributions contribute to the difference between κ_chem and κ_f(RH). To study their influences in a simple and apparent way, κ_chem and κ_f(RH) were simulated based on the two extreme cases of size-resolved ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ distributions in Fig. 3 and five average PNSDs corresponding to five ranges of the aerosol Ångström exponent (0.9–1.1, 1.1–1.3, 1.3–1.5, 1.5–1.7, and 1.7–1.9) during this field campaign. In the instance of PM₁, as can be seen in Fig. 4a, assuming a ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ increasing as a function of D_p resulted in κ_chem<κ_f(RH) (squares in Fig. 4a), especially for PNSDs corresponding to larger Ångström exponents. This is because the volume contributions of small particles (e.g., particles with D_p between 100 to 300 nm) to V_tot are larger than their light-scattering coefficient contributions to σ_sp (as shown in Fig. S6); thus the hygroscopicity of small particles had larger impacts on κ_chem than κ_f(RH). Higher Ångström exponents generally correspond to a shift in PNSD towards smaller D_p, which exacerbates the contribution of small particles, further increasing the difference between κ_chem and κ_f(RH). For the case with ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ decreasing as a function of D_p (circle markers in Fig. 4a), the opposite applies, resulting in κ_chem>κ_f(RH). In general, for these two extreme cases of size-resolved ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ distributions, the absolute value of the relative difference between κ_chem and κ_f(RH) ranged from 2.8 % to 7.5 %, with an average of 4.8 %. This result indicates that for PM₁, κ_chem might differ little from κ_f(RH), since ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ usually varies less with D_p in ambient atmosphere than in the two assumed cases (Liu et al., 2014). The average size-resolved ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ distribution from the Haze in China campaign (Liu et al., 2014) indicates that ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ varies significantly for D_p<250 nm, while it varies less within the diameter range of 250 nm to 1 µm. To further study the variation range of the relative difference between κ_chem and κ_f(RH) under ambient conditions, the size-resolved ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ distributions derived from measured size-resolved chemical compositions in the NCP region (Liu et al., 2014; shown in Fig. S5) were used in simulations, and results are shown in Fig. 4b. The absolute value of the relative difference between κ_chem and κ_f(RH) ranged from 0.04 % to 8 %, with an average and standard deviation of 2.8±2 %, which further confirms that for PM₁, κ_f(RH) can accurately represent κ_chem in most cases.

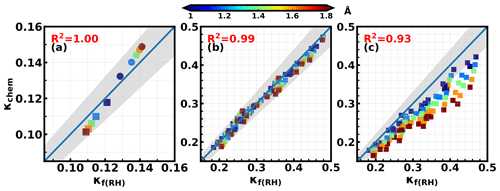
Figure 4κ_chem versus κ_f(RH); colors represent average Ångström exponent (Å) values of corresponding PNSD (a) corresponding to size-resolved ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ distributions shown in Fig. 3 (squares correspond to the solid line in Fig. 3, and circles correspond to the dashed line in Fig. 3). (b) and (c) correspond to size-resolved ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ distributions shown in Fig. S4 for PM₁ and PM₁₀, respectively. Gray areas represent the absolute relative differences between κ_chem and κ_f(RH) less than 10 %.

Download

For PM₁₀, values of κ_chem and κ_f(RH) using ${\mathit{\kappa }}_{D_{\mathrm{p}}}$ size distributions derived from ambient measurements (Fig. S5, similar to Fig. 4b) were simulated and displayed in Fig. 4c. The simulated absolute values of the relative difference between κ_chem and κ_f(RH) ranged from 0.2 % to 41 %, with an average and standard deviation of 16±8 % and with all κ_chem values lower than κ_f(RH). This is because, for PM₁₀, supermicron particles, typically with low hygroscopicity (Fig. S5), contribute much more to V_tot than to σ_sp (as shown in Fig. S7). These results indicate that, for PM₁₀, κ_f(RH) cannot accurately represent κ_chem.

Above analysis results indicate that κ_f(RH) retrieved from light-scattering measurements of PM₁ represent the κ_chem of PM₁ accurately and can be used in Eq. (5) as measured κ_chem for deriving κ_OA.

4.1 Overview of the campaign data

The time series of ambient RH, chemical compositions of PM_2.5 and PM₁, σ_sp at 525 nm of PM₁₀ and PM₁ in the dry state, and calculated κ_sca and κ_f(RH) values of PM₁₀ and PM₁ are shown in Fig. 5. Overall, the mass concentrations of NR-PM₁ and NR-PM_2.5 ranged from 1 to 221 µg m⁻³ and from 1.8 to 326 µg m⁻³, with average concentrations of 63 and 93 µg m⁻³, respectively. Measured σ_sp at 525 nm of PM₁ and PM₁₀ ranged from 11 to 1875 Mm⁻¹ and from 18 to 2732 Mm⁻¹, with average values of 550 and 814 Mm⁻¹, respectively. These results demonstrate that this campaign was carried out at a site that is overall highly polluted, where quite clean conditions as well as extremely polluted conditions were experienced during the measurement period. The mass contributions of ammonium, nitrate, sulfate, and organics to NR-PM_2.5 and NR-PM₁ are listed in Table 3, with organics being the major fraction of NR-PM₁ and NR-PM_2.5.

Table 3Average (range) mass contribution of ammonium, nitrate, sulfate, and organics to NR-PM_2.5 and NR-PM₁ during different periods.

Download Print Version | Download XLSX

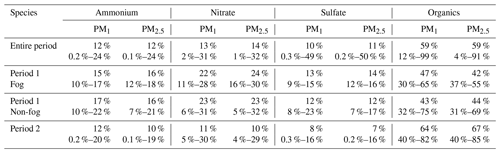
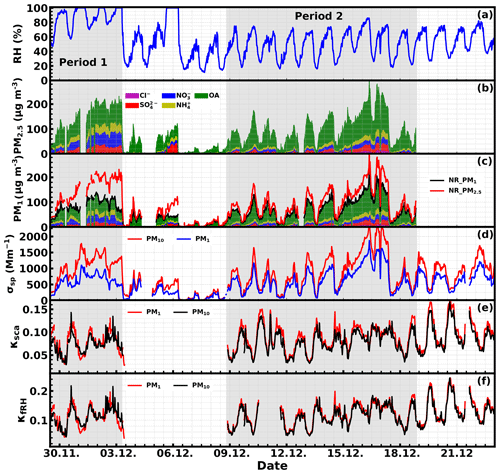
Figure 5Time series of ambient RH (a), chemical compositions of PM_2.5 (b) and PM₁ (c), σ_sp at 525 nm of PM₁₀ and PM₁ (d), and calculated κ_sca (e) and κ_f(RH) (f) values of PM₁₀ and PM₁.

Download

During Period 1 shown in Fig. 5, nitrate contributed most to inorganics, while inorganics contribute most to mass concentrations of NR-PM_2.5 and NR-PM₁. During Period 2, shown in Fig. 5, the ambient RH is relatively lower than that of the first period, ranging from 16 % to 86 % with an average of 49 %. During this period, organics contributed most to mass concentrations of NR-PM_2.5 and NR-PM₁, with the NR mass concentrations of PM_2.5 and σ_sp at 525 nm of PM₁₀ being only 33 % and 40 % higher than those of PM₁.

The time series of calculated κ_sca and κ_f(RH) are shown in Fig. 5e–f. The κ_sca of PM₁ and PM₁₀ ranged from 0.01 to 0.2 and from 0.02 to 0.17, with corresponding averages of 0.09 and 0.08, respectively. The κ_f(RH) was not available from 12:00 on 10 December to 12:00 LT on 11 December due to the absence of PNSD measurements. The κ_f(RH) of PM₁ and PM₁₀ ranged from 0.02 to 0.27 and from 0.03 to 0.26, with corresponding averages of 0.12 and 0.12, respectively. These results indicate that the hygroscopicity during this campaign was generally low, which could be associated with the high mass contributions of organics. The range as well as the average level of κ_f(RH) is quite consistent with the results obtained at the same site in winter 2016, suggesting the prevalent low aerosol hygroscopicity conditions in winter at this site. Additionally, it can be noted that, except for fog events, κ_sca and κ_f(RH) values of PM₁ are generally higher than those of PM₁₀, yet the differences are small (10 % and 3.5 % for κ_sca and κ_f(RH), respectively). Although particles with diameters above 800 nm have an almost negligible impact on retrieved κ_f(RH) (refer to discussions in Sect. 3.3), it can still cause a small difference between κ_f(RH) of PM₁₀ and PM₁. Results of previous studies indicate that the overall hygroscopicity of aerosol particles larger than 800 nm is usually low and is typically lower than the overall hygroscopicity of accumulation-mode particles (Liu et al., 2014), which may explain why κ_f(RH) values of PM₁ are generally higher than those of PM₁₀ during non-fog periods (periods with RH < 100 %).

During fog periods, a large number of submicron particles in the dry state will be activated into fog droplets, which are supermicron particles in the ambient state (see PNSD examples in Fig. S4a), exerting substantial impacts on f(RH) measurements of PM₁₀, which are not detectable in the PM₁ measurements. Since for a certain particle diameter and fog supersaturation, particles with higher hygroscopicity are more readily activated, the observed PM₁₀ κ_f(RH) increased during fog events and often exceeded those of PM₁ in contrast to non-fog periods (Fig. 5f).

Figure 6Comparison between measured and calculated κ_chem by assuming a κ_OA of 0.06. (a) The whole period. (b) Only Period 1. (c) Only Period 2. Colors represents the mass fractions of organic aerosol in NR-PM₁ (f_OA), and the color bar is shown on the top.

Download

4.2 κ_OA derivations and its relationship with organic aerosol oxidation state

The results in Sect. 3.3 demonstrate that the κ_f(RH) of PM₁ accurately represents the κ_chem in most cases; thus a closure study between calculated κ_chem values of PM₁ based on measured chemical compositions and measured κ_chem values (represented by PM₁ κ_f(RH)) can be conducted using Eq. (3) if κ_OA is known. A κ_OA of 0.06 was used in this closure test, which was calculated by Wu et al. (2016) based on aerosol chemical composition and aerosol hygroscopicity measurements. As shown in Fig. 6a, the comparison between measured and calculated κ_chem has not achieved very good agreements. We notice that the calculated κ_chem was overestimated when the mass fraction of organic aerosol (f_OA) was lower than 45 %, while it was underestimated when f_OA was higher than 45 %. As described in Sect. 4.1, these two situations roughly correspond to Period 1 and 2, respectively. Separating the data points shown in Fig. 6a into Period 1 (Fig. 7b) and 2 (Fig. 7c), it can be seen that all low f_OA data points are found in Period 1, with most of the data points showing a f_OA of less than 50 %. Although the calculated κ_chem values during this period were on average 25 % higher than the measured κ_chem values, they were highly correlated (R=0.84). A similar case was also found in Wu et al. (2013), and they concluded that the loss of semi-volatile ammonium nitrate in the HTDMA might be the reason. The relationship between nitrate concentration and the difference between calculated and measured κ_chem were investigated, which confirmed the influence of nitrate on this discrepancy (Fig. S7) and the overestimation of calculated κ_chem due to the volatile loss of ammonium nitrate. Since the tube length (from the splitter to inlet of instrument) of the wet nephelometer was about 1 m longer than that of the CV-ToF-ACSM, there was probably more loss in ammonium nitrate in the wet nephelometer.

Figure 7(a) The relationship between derived κ_OA and f₄₄. (b) Comparison with previous studies.

Download

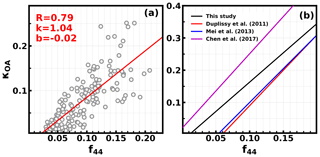
During Period 2, the average mass fraction of nitrate was low (11 %), and the loss of ammonium nitrate had a minor influence on κ_chem estimations (Fig. S7). However, when organic aerosol was dominant during Period 2, the calculated κ_chem was underestimated in most cases (Fig. 6c). Previous studies have shown a larger κ_OA for OA with a higher oxidation level (Chang et al., 2010; Duplissy et al., 2011; Wu et al., 2013), which might have contributed to the underestimation in κ_chem. This gave us the hint that Period 2 might provide us a good opportunity to study κ_OA. Following the method in Sect. 3.2, κ_OA was derived using Eq. (5), resulting in a κ_OA ranging from 0.0 to 0.25, with an average of 0.08±0.06. This indicates that using a constant κ_OA value in the calculation of κ_chem would result in a large bias. To further investigate the impact of OA oxidation level on κ_OA, we compared the derived κ_OA against f₄₄, which is often used to represent the oxidation level of OA. Results show a clear positive correlation (R=0.79) and a statistical relationship of ${\mathit{\kappa }}_{\mathrm{OA}}=\mathrm{1.04}\cdot f_{\mathrm{44}}-\mathrm{0.02}$ (Fig. 7a), indicating that the degree of the oxidation level is a crucial parameter determining the OA hygroscopicity. Based on the relationship between f₄₄ and the O∕C ratio for CV-ACSM (Hu et al., 2018b), $\mathrm{O}:\mathrm{C}=\mathrm{3.47}\times f_{\mathrm{44}}+\mathrm{0.01}$, the relationship between κ_OA and O:C can be expressed as ${\mathit{\kappa }}_{\mathrm{OA}}=\mathrm{0.3}\times \mathrm{O}:\mathrm{C}-\mathrm{0.02}$. The derived empirical relationship between κ_OA and f₄₄ was compared to results in previous studies (Fig. 7b). As mentioned in Sect. 2.3, the f₄₄ from CV-ToF-ACSM measurements is much higher than that previously reported from AMS, but they are well correlated, and the ratio between the f₄₄ of CV-ToF-ACSM and previous AMS instruments for ambient aerosol ranges from 1.5 to 2, with an average of 1.75. Therefore, to be consistent with the f₄₄ in previous studies, the empirical relationship in Fig. 7b is changed to ${\mathit{\kappa }}_{\mathrm{OA}}=\mathrm{1.79}\cdot f_{\mathrm{44}}-\mathrm{0.03}$. The κ_OA values are lower than those from the scheme of Chen et al. (2017) but higher than those in Duplissy et al. (2011) and Mei et al. (2013a). In general, results of most published studies about κ_OA demonstrate that hygroscopicity of organic aerosol generally increases as the oxidation level of organic aerosol increases; however, the empirical mathematical relationship differs much among different studies (Hong et al., 2018). These results highlight that more studies are required to study the influence of the OA oxidation level on κ_OA and to derive a more universal parameterization scheme that can be used in chemical transport models.

4.3 Distinct diurnal variations in κ_OA and its relationship with OOA

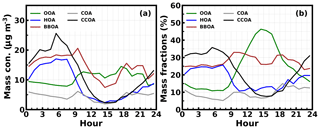
The time series of derived κ_OA are depicted in Fig. 8a, which showed large fluctuations in a day. The average κ_OA (Fig. 8b) displays a distinct diurnal variation, with κ_OA reaching its minimum (0.02) in the morning (near 07:30 LT) and increasing quickly to a maximum (0.16) near 14:30 LT. As a consequence, the water uptake abilities of organic aerosol particles changed from nearly hydrophobic to moderately hygroscopic within 7 h during the day. Previous results from observations in Japan also revealed significant κ_OA diurnal variations, though with daily minima in the afternoon hours due to the increase in less oxygenated OA mass fractions (Deng et al., 2018, 2019). Such large variability and significant diurnal variations in κ_OA were observed for the first time on the NCP. We found that the diurnal profile of the mass fraction OOA in OA (f_OOA) was remarkably similar to that of κ_OA (R=0.8; Fig. 8a and c), suggesting that OOA is very likely the determining factor of κ_OA in winter on the NCP.

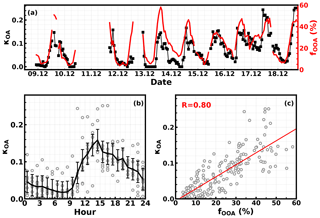
Figure 8(a) Time series of derived κ_OA and OOA mass fraction in NR-PM₁ (f_OOA) on the right y axis. (b) Average diurnal profile of κ_OA. (c) Scatter points of κ_OA versus f_OOA (%), and red line is the fitting line with linear regression.

Download

The correlation coefficient between the average diurnal profiles of κ_OA and f_OOA was 0.95, which suggests that the variations in f_OOA were driving the significant diurnal variations in κ_OA. The average diurnal variations in mass concentrations of identified OOA, HOA, COA, CCOA, BBOA, and their mass fractions in total organic mass are shown in Fig. 9a and b, respectively. The mass concentrations of HOA, CCOA, and BBOA decreased rapidly from the morning to 15:00 LT due to the rising boundary layer height and also to the decreased primary source emissions. The mass concentrations of COA increased a little in the morning and then decreased quickly after 09:30 LT. This transitory increase in COA in the morning might be associated with cooking for breakfast. However, the OOA mass increased rapidly from about 07:30 to 10:30 LT despite the boundary layer development during period of time and then remained almost constant thereafter. The rapid decreases in primary organic aerosol components and the increases in OOA concentration together resulted in a dramatic increase in f_OOA, from ∼10 % at 09:00 LT to ∼45 % at 13:30 LT in the afternoon, which also corresponds to the similar increase in κ_OA. After 14:30 LT, the OOA mass concentration remained relatively unchanged; however, of the large increases in primary organic aerosol components, it also led to considerable decreases in f_OOA and κ_OA.

Figure 9(a) Average diurnal profiles of mass concentrations of OOA, HOA, COA, CCOA, and BBOA. (b) Average diurnal variations in mass fractions of OOA, HOA, COA, CCOA, and BBOA.

Download