2.1 Experimental approach

The CERN CLOUD chamber is a 26.1 m³ stainless steel aerosol chamber that can be kept at a constant temperature within 0.1 K precision. It offers the possibility to study new particle formation under different ionization levels. Two high-voltage electrode grids inside the chamber can efficiently clear ions and charged particles from the chamber within seconds, ensuring neutral conditions. When there is no electric field in the chamber, galactic cosmic rays lead to an ion production rate of ∼ 2–4 ion pairs cm⁻³ s⁻¹. Ion concentrations can also be elevated to upper tropospheric conditions by the illumination of the chamber with a pion beam from the CERN Proton Synchrotron. The dry air supply for the chamber is provided by boil-off oxygen and boil-off nitrogen mixed at the atmospheric ratio of 79 : 21. This ensures extremely low contaminant levels, especially from organics and sulfuric acid. This was verified by a PTR3 proton transfer reaction time-of-flight mass spectrometer (Breitenlechner et al., 2017) and a nitrate chemical ionization atmospheric pressure interface time-of-flight (nitrate CI-APi-ToF) mass spectrometer (Jokinen et al., 2012). The absence of any contamination from amines was confirmed by measurements with a water cluster CI-APi-ToF (Pfeifer et al., 2020), which did not register dimethylamine mixing ratios above the detection limit of 0.1 pptv.

We performed measurements of particle growth from sulfuric acid and ammonia at either +20 or +5 ^∘C with the relative humidity kept constant at either 38 % or 60 %. SO₂ (5 ppb), O₃ (∼120 ppb) and ammonia (varied between 3 and 1000 pptv) were injected into the chamber. The experiments were initiated by homogeneous illumination of the chamber at constant O₃ and SO₂ levels. The UV light of four Hamamatsu UV lamps guided into the chamber with fibre optics induced the photo-dissociation of O₃ and the production of OH• radicals. Thus, SO₂ was oxidized, leading to the formation of sulfuric acid (varied between 10⁷ and 10⁹ cm⁻³). A typical experiment is shown in Fig. S1 in the Supplement. Sulfuric acid monomer concentrations were measured with the nitrate CI-APi-ToF. Calibration of the instrument's response to sulfuric acid (Kürten et al., 2012) was performed before and after the measurement campaign and yielded comparable results. Compared with previous studies, the measurement of gas-phase NH₃ also significantly improved due to the deployment of the calibrated water cluster CI-APi-ToF. The protonated water cluster reagent ions selectively ionize ammonia and amines at ambient pressure reaching a detection limit of approximately 0.5 pptv for ammonia.

Particle growth was monitored using a differential mobility analyser-train (DMA-train; Stolzenburg et al., 2017) for the main size range from 1.8 to 8 nm. We also include measurements from a Caltech nano-radial DMA (Brunelli et al., 2009) with a custom-built diethylene glycol (DEG) counter for sizes between 4 and 8 nm and a TSI Scanning Mobility Particle Sizer (nano-SMPS; model 3936) for sizes larger than 5 nm when investigating the size dependence of the growth. For the growth of the charged fraction, we use a neutral cluster and air ion spectrometer (NAIS; Manninen et al., 2009). All four instruments use electrical mobility classification, and the measured mobility diameters are corrected to mass diameters (Larriba et al., 2011) for the calculation of collision kinetics. Compared with the scanning particle size magnifier (see e.g. Lehtipalo et al., 2014), which was used in Lehtipalo et al. (2016), these instruments that use direct mobility analysis have less systematic uncertainty on the actual size classification. The size ranges of both studies are also not directly comparable. We show the measurements in the lower size interval of the DMA-train (1.8–3.2 nm mobility diameter) as well as the earlier results (size range between 1.5 and 2.5 nm mobility diameter) in Fig. S2.

Another difference between the instruments is the treatment of the sample relative humidity. In the DMA-train, the aerosol sheath flow is dried using silica gel, achieving a relative humidity measured at the sheath inlet of the DMA below 5 % for all experiments in this study. The nano-SMPS uses a water trap to keep the relative humidity of the DMA sheath flow below 20 % during the reported experiments. The Caltech nano-radial DMA, the NAIS and the particle size magnifier used in Lehtipalo et al. (2016) do not deploy any humidity conditioning for the sheath or sample flow, except for the possible decrease in relative humidity as a result of a temperature increase between the measurement device and chamber. This effect occurred for all instruments to some extent, even if the sampling lines were insulated. The effect of aerosol dehydration during the measurement is usually described by the hygroscopic growth factor gf, relating the measured diameter d_p,m to the actual diameter d_p as follows: $d_{\mathrm{p}}=\mathrm{gf}\cdot d_{\mathrm{p},\mathrm{m}}$.

From the measured aerosol size distributions, we inferred particle growth rates using two complementary methods in order to limit systematic biases in the analysis. In the first method, particle growth rates were measured with the appearance time method, which requires a growing particle population that can be clearly identified (Dada et al., 2020; Lehtipalo et al., 2014; Stolzenburg et al., 2018). Figure S1d demonstrates how the signal in each size channel is fitted by an empirical sigmoidal shape curve estimating the time at which 50 % of the maximum signal intensity is reached. These appearance times are fitted with a linear function over the size intervals from 1.8 to 3.2 and from 3.2 to 8 nm, with the slope yielding an average growth rate over the interval (shown in Fig. S1b). In the second method, we applied the size- and time-resolving growth rate analysis method “INSIDE” (INterpreting the change rate of the Size-Integrated general Dynamic Equation; Pichelstorfer et al., 2018) to cross-check our results. The INSIDE method uses the measured particle size distribution at a time t₁ and simulates the expected aerosol dynamics (coagulation, wall losses and dilution) until time t₂. By comparing this to the measured data at t₂ and evaluating the general dynamics equation, it infers the condensational growth rate at specified diameters for this time step. The time- and size-resolved growth rates for each experiment were time-averaged for all sizes to yield a statistically more robust result. Compared to the appearance time method, INSIDE requires accurate absolute number size distributions, whereas the appearance time method only depends on the relative signal increase. However, INSIDE can confirm the absence of systematic biases like changing precursor vapour concentrations or coagulation and wall loss effects. Therefore, a combined assessment with both methods should yield a solid estimate of the observed growth rates.

2.2 Growth model description

If the evaporation rates of the growing particles are effectively zero due to the extremely low vapour pressure of the condensing vapour, particle growth rates are limited by the collision frequencies of vapour molecules with the growing particles. Our description of particle growth follows the approach of Nieminen et al. (2010), which, in comparison to the equations of mass transfer that can be found in e.g. Seinfeld and Pandis (2016), include the non-negligible effect of vapour molecular size using a collision frequency between vapour and particle in analogy to coagulation theory (Lehtinen and Kulmala, 2003):

where d_p is the growing particle mass diameter, V_p and V_v are the volume of the particle and vapour molecule respectively, C_v is the vapour monomer concentration and k_coll(d_v,d_p) is the kinetic collision frequency between particle and vapour. Following Fuchs and Sutugin (1971), the collision frequency for the transition regime is defined by

where, according to Lehtinen and Kulmala (2003), the Knudsen number (Kn) and mean free path (λ) need to be specified as $\mathit{Kn}=\mathrm{2}\mathit{\lambda }\cdot {\left(d_{\mathrm{v}}+d_{\mathrm{p}}\right)}^{-\mathrm{1}}$ and $\mathit{\lambda }=\mathrm{3}\left(D_{\mathrm{v}}+D_{\mathrm{p}}\right)\cdot {\left({\stackrel{\mathrm{‾}}{c}}_{\mathrm{v}}^{\mathrm{2}}+{\stackrel{\mathrm{‾}}{c}}_{\mathrm{p}}^{\mathrm{2}}\right)}^{-\mathrm{1}/\mathrm{2}}$, which depend on the diameters d_v∕p, the masses m_v∕p (within the calculation of the mean thermal velocities ${\stackrel{\mathrm{‾}}{c}}_{\mathrm{v}/\mathrm{p}})$ and the diffusion coefficients D_v∕p of the colliding vapour molecules or particles respectively. Assuming that the accommodation coefficient α is unity and relating the volume V_v of the condensing monomer to its molecular mass and (bulk) density $V_{\mathrm{v}}=m_{\mathrm{v}}/{\mathit{\rho }}_{\mathrm{v}}$, Eqs. (1) and (2) determine the hard-sphere kinetic limit for particle growth.

We then additionally consider a collision enhancement of neutral vapour monomers and particles due to attractive van der Waals forces, where the collision frequency can be described according to Sceats (1989):

with the enhanced collision frequency for the continuum regime described by

and the enhanced collision frequency for the kinetic regime described by

Equation (3) is designed such that it reaches the correct limits of the free molecular and diffusion regime which is comparable to the approach of Fuchs and Sutugin (1971), i.e. Eq. (2). However, it includes the collision enhancement factors E(∞) and E(0). These factors can be linked to the attractive potential of van der Waals forces. For the continuum regime, this is done by solving the following integral:

Here, x is the relative distance between the centres of the two colliding entities, and ϕ(x) is the van der Waals potential (Hamaker, 1937), which is expressed in terms of the vapour and particle radii r_v∕p:

Chan and Mozurkewich (2001) provide a fit to the solution of the numerically evaluated integral from Sceats (1989):

where a_n are the fit parameters, and A^′ is the reduced Hamaker constant, which relates to the Hamaker constant A by $A^{\prime }=\mathrm{4}A\cdot k^{-\mathrm{1}}{T}^{-\mathrm{1}}\cdot d_{\mathrm{v}}{d}_{\mathrm{p}}\cdot {\left(d_{\mathrm{v}}+d_{\mathrm{p}}\right)}^{-\mathrm{2}}$ (Chan and Mozurkewich, 2001; Hamaker, 1937). However, the measurements of this study are conducted completely in the free molecular regime; thus, the derivation of the continuum case will not significantly affect our results. For the free molecular regime enhancement factor E(∞), an overview of its relation to the Hamaker constant is given in Ouyang et al. (2012). Chan and Mozurkewich (2001) also used a fit to the solution from Sceats (1989) with the fit parameters b_n:

In this study, we compare the results of Sceats (1989), who used Brownian coagulation to describe the collisions, to the simple ballistics approach of Fuchs and Sutugin (1965). In that approach, the minimum distance x_min along the trajectory of two colliding particles with impact parameter b is calculated from the conservation of angular momentum and energy:

where ϕ is the interaction potential, μ is the reduced mass of the colliding entities and v is their relative speed. The critical impact parameter b_crit is obtained as the minimum value of b for which the minimum distance still takes a real value larger than (r_v+r_p). The enhancement factor is than related to the critical impact parameter b_crit :

Note, that this approach is oversimplified, as the initial velocity of the colliding entities is assumed to be fixed but should actually follow a (Maxwell–Boltzmann) distribution. However, Ouyang et al. (2012) concluded that the difference in the derived Hamaker constant is almost negligible.

Using the description of an enhanced collision kernel, the particle growth rates measured with the DMA-train can be fitted with the Hamaker constant as the single free parameter of the fit. As the theoretical growth rates are compared to the appearance time growth rates, which are measured as a time difference in signal appearance Δt over a certain size interval Δd_p (ranging from d_init to d_final), a comparison with experimental values requires the integration of Eq. (1):

Equation (12) includes several properties of the condensing vapour and the growing particles. Sulfuric acid molecules are usually hydrated at typical ambient relative humidity. While the thermodynamic model E-AIM (Extended Aerosol Inorganics Model; Wexler et al., 2002) predicts an average of two water molecules attached to a sulfuric acid monomer at 298 K and 40 %–60 % relative humidity, quantum chemical studies predict an average hydration of one to two water molecules for these conditions (Henschel et al., 2014; Kurtén et al., 2007; Temelso et al., 2012). Moreover, the hydration state of the particles in the chamber is also not directly measured and might be altered during the sampling process, which requires information on the hygroscopic growth factor (see Sect. 2.1).

We examine the effect of hydration using three different approaches. In the first naïve approach, we assume that no dehydration occurs during measurement and that the particle sulfuric acid mass fraction is equal to the vapour mass fraction, i.e. $w=M_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}/m_{\mathrm{v}}$, with $m_{\mathrm{v}}=M_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}+\mathrm{2}{M}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ (assuming two water molecules attached to the sulfuric acid monomer), where $M_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$ and $M_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ are the molecular mass of sulfuric acid and water respectively. In the second approach, we assume a dry measurement, and in this case the growth of the measured dry particles is described by uptake of sulfuric monomers only, i.e. $m_{\mathrm{v}}=M_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$. However, for the actual vapour and particle size used in the collision kernel k_coll(d_v,d_p), the hydrated sizes are used. We again assume an average hydration for the monomer with two water molecules as above and an average hygroscopic growth factor of 1.25 for all particle sizes and RH values in our experiments. The latter is an average value of the results of Biskos et al. (2009) for highly acidic sulfuric acid sub-10 nm particles at 40 %–60 % relative humidity. In the third approach, we consider that the extent of hydration might vary with size and relative humidity. We use modelled composition data from MABNAG (Model for Acid–Base chemistry in Nanoparticle Growth; Yli-Juuti et al., 2013) in order to predict the sulfuric acid mass fraction w(RH,T) (see Fig. S4a) and calculate the hygroscopic growth factor:

where ρ_sol is a parametrization of the density of the sulfuric acid–water solution (Myhre et al., 1998), and w(RH,T) and w(RH_mT_m) are the mass fractions of sulfuric acid in the growing and measured particles respectively. We follow the considerations of Verheggen and Mozurkewich (2002) in order to separate the growth by sulfuric acid addition and water uptake by differentiating the hydrated particle volume $V_{\mathrm{p}}=m_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}/\left(w{\mathit{\rho }}_{\mathrm{sol}}\right)$. Both the numerator (particle sulfuric acid mass $m_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$) and the denominator (sulfuric acid mass fraction and solution density) depend on time. The addition of sulfuric acid is again described in analogy to coagulation theory, resulting in

Equation (14) contains a first term for the addition of pure sulfuric acid and a second term for water uptake. It can be solved for the particle growth rate $\frac{\mathrm{d}{d}_{\mathrm{p}}}{\mathrm{d}t}$:

In this case, we assume $m_{\mathrm{v}}=M_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}$, but we use the hydrated monomer diameter d_v in the collision kernel. For the particles, we now use the hydrated size, i.e. $d_{\mathrm{p}}=\mathrm{gf}\cdot d_{\mathrm{p},\mathrm{m}}$ with gf and w(RH,T) taken from the model. We compare the MABNAG predictions in Fig. S4b with SAWNUC (Sulfuric Acid Water Nucleation model; Ehrhart et al., 2016), which only takes sulfuric acid and water into account, whereas MABNAG also includes ammonia. MABNAG predicts a significantly lower water content at larger sizes (>2.5 nm), even at 3 pptv ammonia. In addition, previous experiments in the CLOUD chamber have suggested that even background level ammonia has an influence on the hygroscopic growth factor (Kim et al., 2016); this is similar to Biskos et al. (2009), who also indicated some extent of neutralization for sub-10 nm particles at low ammonia. Due to the presumably better prediction of the particle hydration by MABNAG for sizes larger than 2.5 nm, we choose the results from Fig. S4a, even if they might overestimate the hydration at small sizes. We have neglected the effect of ammonia addition on collisions in all three approaches so far, but we test the assumption $m_{\mathrm{v}}=M_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}+\mathrm{2}{M}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}+\mathrm{1}{M}_{{\mathrm{NH}}_{\mathrm{3}}}$ and different vapour hydrations in our systematic uncertainties estimate in Fig. S5. All of the parameters for vapour and particles used for all approaches are summarized in Table S1 in the Supplement.

2.3 Global model description

We implement the results of our growth rate measurements for sulfuric-acid-driven growth in a global model (Mann et al., 2010; Mulcahy et al., 2018), which includes sulfuric acid–water binary nucleation. However, the model does not include ternary nucleation schemes (Dunne et al., 2016) and pure biogenic nucleation (Gordon et al., 2016) and will, therefore, underestimate the impact of nucleation on the global aerosol and CCN budget. In the model, growth between the nucleation size and 3 nm is treated with the equation from Kerminen and Kulmala (2002), which gives the fraction of particles surviving to 3 nm at a given growth and loss rate. Here, as a baseline case, we use the geometric hard-sphere kinetic growth rate based on bulk density (Eqs. 1–2) and compare this to the collision-enhanced growth (Eqs. 3–9). For larger sizes, aerosol growth in the model is calculated by solving the condensation equations. Therefore, no direct growth parametrization can be altered, but as condensational growth scales linearly with the diffusion coefficient of the condensing vapour, we increased sulfuric acid diffusion for condensation in the nucleation mode (2–10 nm) and in the Aitken mode (10–100 nm). The enhancement factors are derived for the median diameters of the modes (7.6 and 57 nm respectively) at the cloud-base level (1 km). However, this constant factor of increase in the diffusion coefficient (and, hence, flux onto particles) for all particles of the entire mode might underestimate the impact of the collision enhancement. Rapid growth is increasingly important for the smallest particles, which actually have a higher collision enhancement than particles with the size of the mode median diameters.

3.1 Collision enhancement

Figure 1 shows the particle growth rates for two size intervals (Fig. 1a, 1.8–3.2 nm mobility diameter; Fig. 1b, 3.2–8.0 nm mobility diameter) versus the sulfuric acid monomer concentration, which correlate linearly. No significant dependence on temperature, ionization levels in the chamber or the concentration of ammonia is evident. While the effect of temperature expected from theory is small and cannot be discerned within the statistical uncertainties of our measurements (Nieminen et al., 2010), the insignificant influence of ammonia and the ionization level on the growth rate differs from previous findings (Lehtipalo et al., 2016).

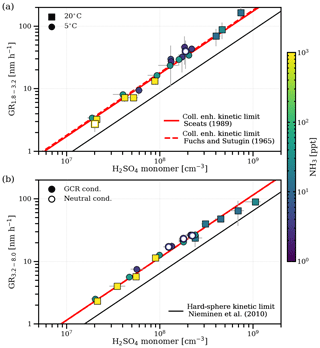
Figure 1Growth rates of nanoparticles in two size intervals versus the measured gas-phase sulfuric acid monomer concentration. Panel (a) shows growth rates for the size interval between 1.8 and 3.2 nm (mobility diameter; 1.5–2.9 nm in mass diameter), and panel (b) shows growth rates for the size interval between 3.2 and 8.0 nm (mobility diameter; 2.9–7.7 nm in mass diameter). The colour code represents the measured NH₃ concentration during the growth period. Squares are measurements at 20 ^∘C, and circles are measurements at 5 ^∘C. Filled symbols represent runs under ambient galactic cosmic ray ionization levels, and open symbols represent runs under neutral conditions. Error bars for the data points represent the statistical uncertainty in the appearance time growth rate measurements and the maximum variation of the sulfuric acid concentration during the growth period, also explaining the slight deviations from linearity at high sulfuric acid concentrations, where stable conditions are not fully reached. The black line shows the geometric limit of kinetic condensation assuming the same hydration for the condensing cluster and the measured particles (Nieminen et al., 2010). The red solid line shows the fit of Eq. (12) to the data with the Hamaker constant as the free parameter assuming a Brownian coagulation model for the enhanced collision kernel (Sceats, 1989), whereas the red dashed line uses a ballistics approach (Fuchs and Sutugin, 1965).

Download

We compare the measured growth rates from this study with the results from Lehtipalo et al. (2016) in Fig. S2. In contrast to our results, elevated ammonia (∼1000 pptv) led to increased growth rates in that study. The major difference is the narrower size range for the growth rate measurements (1.5–2.5 nm mobility diameter) due to different instrumentation. For smaller sizes and at low ammonia, sulfuric acid evaporation likely plays a role due to an increased Kelvin term. The stabilizing effect of ammonia is certainly relevant at the sizes of the nucleating clusters (Kirkby et al., 2011). For our results, we confirm the absence of significant evaporation rates above 2 nm using an independent experiment presented in Fig. 2. This demonstrates that, in the absence of gas-phase sulfuric acid, the coagulation- and dilution-corrected loss rates of particles ($k_{\mathrm{tot}}^{\mathrm{meas}}-k_{\mathrm{dil}}-k_{\mathrm{coag}}^{\mathrm{avg}}$) over all sizes follow the expected size dependence of wall losses which is inferred from the sulfuric acid monomer decay. Evaporation would cause another term and would distort the balance equation (also depending on the relative abundances of the particles during the decay), causing a deviation from the expected wall loss rate.

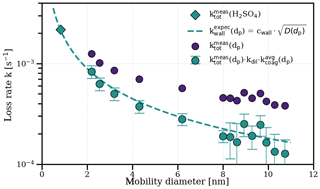
Figure 2Measurement of zero sulfuric acid evaporation rates. The total loss rates of sulfuric acid and ammonia particles (with the mobility diameter shown on the x axis) were measured during a decay experiment (5 ^∘C, 60 % relative humidity, 1000 pptv NH₃) by switching off the UV lights after a particle growth stage, which stops the production of sulfuric acid and, subsequently, nucleation and growth. After sulfuric acid was reduced to the background level, the exponential decay rate of the remaining particles in the chamber was measured ($k_{\mathrm{tot}}^{\mathrm{meas}}$, blue circles), which was not possible for the 1.8 nm channel due to low statistics. Decay of particles in the chamber is dominated by wall loss, dilution loss and coagulation loss to other particles. Particle loss rates are corrected for an averaged coagulation loss during the decay ($k_{\mathrm{coag}}^{\mathrm{avg}}$) to all particles larger than d_p and for the dilution loss (k_dil; turquoise circles). They agree well with the expected wall loss rate $k_{\mathrm{wall}}\left(d_{\mathrm{p}}\right)=C_{\mathrm{wall}}\cdot \sqrt{D_{\mathrm{p}}\left(d_{\mathrm{p}}\right)}$ (red dashed line) with C_wall=0.0077 s^−0.5 cm⁻¹ inferred from an independent sulfuric acid decay experiment in the absence of a particle sink, where the mobility diameter is assumed to be 0.82 nm (Ehrhart et al., 2016; turquoise diamond). This suggests that there is negligible evaporation from the sulfuric acid particles above ca. 2 nm under the above-mentioned experimental conditions, which would introduce another term that disturbs the balance equation at each size. As all of our growth rate measurements, independent of the ammonia concentration and temperature, fall on the same line (see Fig. 1), this also points towards negligible evaporation effects at reduced ammonia levels (below 10 pptv) and up to 20 ^∘C.

Download

The insignificant effect of ammonia on growth (Fig. 1) and the same high ratio (>100, Fig. S3a) between sulfuric acid monomer and dimer concentrations for all experiments point towards a negligible influence of clustering on our measured growth rates (Li and McMurry, 2018). Moreover, in Fig. S3b, using a model including sulfuric acid/ammonia clustering and evaporation, we show that no cluster contribution is indeed expected, even at elevated ammonia concentrations (Kürten, 2019).

In the absence of evaporation and strong clustering, our growth rate data provide a direct measurement of the condensational growth at the kinetic limit caused by sulfuric acid monomers only. We find the measured growth rates both with and without the addition of ammonia to be significantly above the geometric hard-sphere limit (Eqs. 1–2) of kinetic condensation (Nieminen et al., 2010). For this comparison, we followed a naïve approach, assuming an average hydration of the monomer by two water molecules and applied the resulting mass fraction to find the bulk density (Myhre et al., 1998). The observed enhancement is similar to Lehtipalo et al. (2016) in the case where evaporation was suppressed by ammonia (see Fig. S2). We also measure a growth rate enhancement for the larger size range (Fig. 1b), which should be less sensitive to evaporation. The faster growth rates might be due to an enhanced collision frequency, which can be attributed to van der Waals forces, either permanent dipole–(induced) dipole interactions between polar sulfuric acid molecules and particles or London dispersion forces (London, 1937). The magnitude of the enhancement is described by the Hamaker constant A (Hamaker, 1937), which we use as the single free parameter to fit a collision-enhanced kinetic limit. For the Brownian coagulation model linking the Hamaker constant to the collision kernel, i.e. Eqs. (3)–(9) (Sceats, 1989), we find $A=\left(\mathrm{4.6}\pm \mathrm{1.5}\left(\mathrm{stat}.\right)\right)\times {\mathrm{10}}^{-\mathrm{20}}$ J. If we apply a ballistics approach in the free molecular regime (Fuchs and Sutugin, 1965; Ouyang et al., 2012), we derive a slightly higher value of $A=\mathrm{8.7}\times {\mathrm{10}}^{-\mathrm{20}}$ J, but both yield comparable values to previous results (Chan and Mozurkewich, 2001; McMurry, 1980).

An enhancement due to charge–dipole interactions between the polar sulfuric acid monomers and charged particles is not significant in our total (neutral plus charged particle) growth rate measurements (as shown in Fig. 1), where we observe no difference between growth rates under neutral and galactic cosmic ray ionization levels. From average dipole orientation theory (Su and Bowers, 1973), a small enhancement is expected in the collision frequency for charged particles above 2 nm (Nadykto and Yu, 2003), which should affect the growth rate (Laakso et al., 2003; Lehtipalo et al., 2016). We find an enhancement factor of 1.45 by comparing the total to the ion growth rate (as shown in Fig. 3), which is in good agreement with theory. However, the total growth rate is influenced on a minor level by faster ion growth because, at the representative galactic cosmic ray ionization levels and sulfuric acid concentrations in our experiments, most (more than 75 %) of the growing particles are neutral (see Fig. 3). However, the effects of ion condensation and charge–dipole enhancement might be stronger at lower sulfuric acid concentrations (Svensmark et al., 2017).

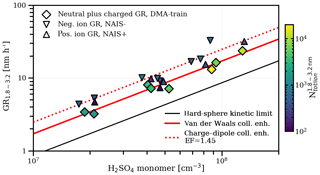
Figure 3The effect of charge on growth. Measured growth rates of 1.8–3.2 nm (mobility diameter) particles and ions in experiments with ammonia above 25 pptv. The DMA-train measures both neutral and charged particles (diamonds), whereas the NAIS$+/-$ (Manninen et al., 2009) measures purely charged particles (triangles). Both the positively and negatively charged particle population have a faster apparent growth rate than the total particle population due to an enhanced collision rate from charge–dipole interactions. We measure a multiplicative charge enhancement factor of 1.45 in this size range with a combined fit to both polarities (red dotted line), which is consistent with estimates from average dipole orientation theory (Nadykto and Yu, 2003). At galactic cosmic rays ionization levels in the chamber, the charged fraction of the growing particles in the size range from 1.8 to 3.2 nm (mobility diameter) is between 5 % and 25 %. This is demonstrated by the colour code which indicates the integrated total or ion number concentration over the growth rate size interval averaged during the growth period. Therefore, the fit of the appearance time for the total particle population is affected on a minor level by the small, earlier appearing charged fraction.

Download

3.2 Size dependence and hydration effects

Condensational growth at the geometric kinetic limit predicts increasing growth rates with decreasing particle sizes due to the non-negligible effect of vapour molecule size on the collision cross section (Nieminen et al., 2010), which has not yet been shown experimentally. Furthermore, the collision enhancement due to van der Waals forces and the collision enhancement due to charge–dipole interactions also depend on the comparative size of the condensing vapour and the growing particle. Figure 4a illustrates the theoretical predictions of the size dependence of the collision rate of sulfuric acid monomers with larger particles, including van der Waals forces and charge–dipole interactions. The enhancement factor compared to the hard-sphere kinetic limit is shown for both the Brownian coagulation model (Sceats, 1989) and the ballistics approach (Fuchs and Sutugin, 1965), which is 2.1 and 2.3 for the free molecular regime respectively, and is comparable to previous experimental results (Kürten et al., 2014; Lehtipalo et al., 2016) and quantum chemical calculations (Halonen et al., 2019).

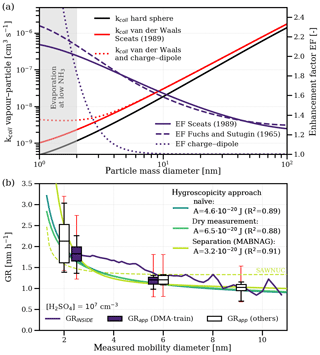
Figure 4The size dependence of sulfuric acid growth. Panel (a) shows the theoretical collision rate of hydrated sulfuric acid vapour molecules ($m_{\mathrm{v}}=M_{{\mathrm{H}}_{\mathrm{2}}{\mathrm{SO}}_{\mathrm{4}}}+\mathrm{2}{M}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$) with particles of a certain mass diameter. The black line represents the hard-sphere limit, the red solid line also includes a collision enhancement due to van der Waals forces based on the approach of Sceats (1989; $A=\mathrm{4.6}\times {\mathrm{10}}^{-\mathrm{20}}$ J), and the red dashed line is based on the approach of Fuchs and Sutugin (1965; $A=\mathrm{8.7}\times {\mathrm{10}}^{-\mathrm{20}}$ J). The red dotted line additionally includes charge–dipole interactions based on average dipole orientation theory. The blue lines show the enhancement factor of a single attractive force compared to the hard-sphere limit. Panel (b) shows the measured size dependence of growth rates normalized to a sulfuric acid concentration of 10⁷ cm⁻³. The solid blue line shows the growth rates inferred using the INSIDE method. Filled boxes represent the appearance time growth rates from the DMA-train used to fit the Hamaker constant. Empty boxes represent the appearance time growth rates from other instruments, including the results from Lehtipalo et al. (2016) with high (>100 pptv) NH₃ concentrations. The boxes indicate the median and the 50 % interquartile range of the data, whereas the whiskers represent the 90 % quantile. The small red error bars indicate the −33 %/+50 % systematic uncertainty in the sulfuric acid measurement. We show the size dependence of three different approaches for particle hygroscopicity: the naïve approach (solid turquoise line), assuming the same hydration for vapour and particle; the dry measurement approach (solid light green line), assuming that the DMA-train measures completely dehydrated particles; and the separation approach (solid yellow line), assuming that available composition data from MABNAG can disentangle water uptake from sulfuric acid condensation. The separation approach using SAWNUC composition data is also shown as a dashed yellow line.

Download

In addition to the approach for calculating the kinetic enhancement factor, the description of particle hydration might also play a crucial role. Until now, we have used the naïve assumption that vapour and particle hydration are the same and that particles are measured at their hydrated size. However, during sampling the measured particles are potentially dried. To investigate the effect of particle hydration, we use the DMA-train data from Fig. 1 to fit the collision enhancement for two alternative approaches: one approach where we assume that particles are measured dry and one approach where we separate the uptake of water and sulfuric acid condensation (Verheggen and Mozurkewich, 2002) using modelled particle composition data from SAWNUC (Ehrhart et al., 2016) or MABNAG (Yli-Juuti et al., 2013). We compare the predictions for the size dependence of all approaches with the measured growth rates of all instruments normalized to a sulfuric acid concentration of 10⁷ cm⁻³ in Fig. 4b. In addition, we show the growth rates using the time- and size-resolving growth rate analysis method INSIDE (Pichelstorfer et al., 2018), which agrees with the appearance time method, demonstrating a minor systematic bias in our growth rate determination. All approaches reproduce the size dependence at an acceptable level (R² larger than 0.87). The separation approach yields higher growth rates at the smallest sizes due to the overestimation of hydration by MABNAG below 2.5 nm. However, for SAWNUC composition data, which presumably describe the cluster hydration better, the R² is only 0.66 and does not reproduce the observed size dependence. This is possibly caused by the overly high hydration assumed for larger sizes. Thus, the simple dry measurement approach might be a good approximation for the predictions of both MABNAG and SAWNUC for the size range of interest (see Fig. S4b). We estimate the systematic uncertainty of the results in Fig. S5, including the effects of different vapour hydration, ammonia addition and sulfuric acid measurement uncertainty. All approaches overlap largely within their systematic uncertainties with $A=\left({\mathrm{5.2}}_{-\mathrm{3.4}}^{+\mathrm{9.7}}\left(\mathrm{syst}.\right)\right)\times {\mathrm{10}}^{-\mathrm{20}}$ J as the best estimate of a combined assessment (assuming the Brownian coagulation model). We also give a first-order approximation for our measured growth rates and their size dependence for the conditions in our experiments:

3.3 Global implications

The observed steep increase of the growth rates with decreasing size shows that the collision enhancement due to van der Waals forces is especially important for the smallest particles. As these are the most vulnerable for losses to pre-existing aerosols, their survival probability in the atmosphere is directly affected, altering the CCN budget (Pierce and Adams, 2007) or promoting NPF in urban environments (Kulmala et al., 2017). In order to test the effects of collision enhancement on sulfuric acid growth on a global scale, we use the atmosphere-only configuration of the United Kingdom Earth System Model (UKESM1; Mulcahy et al., 2018; Walters et al., 2019) which includes the GLOMAP (Global Model of Aerosol Processes) aerosol microphysics module describing nucleation and growth (Mann et al., 2010). Figure 5 illustrates the global model results comparing the baseline case (no collision enhancement) with a collision enhancement simulation (with enhancement factors of 2.2, 1.8 and 1.3 for the cluster, nucleation and Aitken modes respectively) for the present-day atmosphere. The absolute particle number concentrations averaged over all longitudes are shown in Fig. 5a, indicating changes of more than 50 %, especially at high altitudes (> 10 km; Fig. 5b) where most aerosol particles originate from pure sulfuric-acid-driven NPF. The importance of the nucleation process and, therefore, the growth rate enhancement is lower at lower altitudes and in the Northern Hemisphere, which is mainly due to the higher condensation sink and the restriction of the model to sulfuric acid–water binary nucleation. However, the significant enhancement of sulfuric-acid-driven nanoparticle growth in the upper troposphere may be important in quantifying sources of stratospheric aerosols and cirrus CCN (Brock et al., 1995; Deshler, 2008) and needs to be accounted for in future model development.

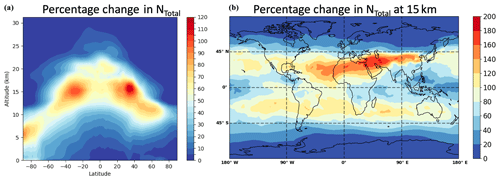
Figure 5Increased global aerosol number concentrations due to collision enhancement. Results from a global modelling study of the present-day atmosphere. Panel (a) shows the relative change in the total aerosol number concentration (particles larger 3 nm) averaged over all longitudes in a vertical profile if collision enhancement is considered in sulfuric acid growth. Panel (b) shows the relative increase at an altitude of 15 km on a global scale where the effects are most significant. Higher relative changes would also be expected at lower altitudes if the model is adjusted for ternary sulfuric acid–water–ammonia nucleation.