the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Modelling the effect of condensed-phase diffusion on the homogeneous nucleation of ice in ultra-viscous particles
Kathryn Fowler
Paul Connolly
David Topping
Computational models of cloud formation typically use homogeneous nucleation to predict the ice nucleated in supercooled water. However, the existence of ultra-viscous organic aerosol in the upper troposphere has offered alternative ice nucleation pathways, which have been observed in laboratory studies. The possible effects of aerosol viscosity on cloud microphysical properties have traditionally been interpreted from simple model simulations of an individual aerosol particle based on equilibration timescales. In this study, to gain insight into the formation of ice in an ensemble of ultra-viscous aerosol particles, we have developed the first cloud parcel model with bin microphysics to simulate condensed phase diffusion through each individual aerosol particle. Our findings demonstrate, for the first time, the complex relationship between the rate of ice formation and the viscosity of secondary organic aerosol, driven by two competing effects – which cannot be explained using existing modelling approaches. The first is inhibition of homogeneous ice nucleation below 200 K, due to restricted particle growth and low water volume. The second occurs at temperatures between 200 and 220 K, where water molecules are slightly more mobile, and a layer of water condenses on the outside of the particle, causing an increase in the number of frozen aerosol particles. Our new model provides a basis to better understand and simulate ice cloud formation on a larger scale, addressing a major source of uncertainty in climate modelling through the representation of microphysical cloud processes.
Clouds in the upper troposphere play an important role in climatic processes, interacting with long-wave radiation leaving the Earth's troposphere, controlling moisture entering the stratosphere and ensuring the overall stability of the Earth's atmosphere (Fueglistaler et al., 2009). Cirrus clouds are often modelled using homogeneous ice nucleation theory (Kärcher, 2002; Kärcher and Lohmann, 2002). Subvisible cirrus clouds have a low optical depth of less than 0.03, their large horizontal extents mean that they interact with a large amount of radiation entering the Earth's atmosphere, which means accurate modelling of these systems is essential to better understand their climatic effects. In situ studies of low-temperature (< 205 K) and subvisible cirrus clouds in the upper troposphere near to the tropical tropopause have found evidence of an order of magnitude fewer than expected ice crystal numbers compared to predictions from traditional homogeneous theory (ranging from 0.005 to 0.1 cm−3) and higher than expected supersaturations with respect to ice (Jensen et al., 2005; Krämer et al., 2009; Jensen et al., 2013, 2017; Spichtinger and Krämer, 2013). These observations suggested that the current understanding of ice formation mechanisms and therefore methods of modelling the formation of low-temperature cirrus clouds are incorrect or incomplete (Peter et al., 2006; Krämer et al., 2009; Jensen et al., 2010). The uncertainties related to low-temperature ice formation are related to both our ability to sample high in the atmosphere and relate these observations to laboratory experiments (Krämer et al., 2016). A number of different mechanisms have been proposed for the discrepancies observed between atmospheric observations of ice number densities and ice supersaturations with those predicted in model simulations, which can be described by a microphysical process such as suppression in the rate of ice nucleation, by suppression in ice crystal growth (Peter et al., 2006) or by a mesoscale process such as convective hydration (Lee et al., 2018). Due to the size and inaccessibility of the tropical tropopause layer there are relatively few studies that have been able to characterise both physical and chemical aerosol properties in the region (Lawson et al., 2008; Krämer et al., 2009; Jensen et al., 2017). Although one study has reported that aerosol particles in the region are composed of an internal mixture of organic material and sulfates, based on the composition of ice residuals collected from subvisible cirrus clouds (Froyd et al., 2010).
Since the discovery that organic aerosol particles could exist in an amorphous or a viscous state under atmospheric conditions (Zobrist et al., 2008; Virtanen et al., 2010), there has been a push to better predict the atmospheric implications of the aerosol phase (Reid et al., 2018) and to characterise the global phase distributions of aerosol particles (Shiraiwa et al., 2017; Maclean et al., 2017). Modelling studies have suggested that in the cold, dry regions of the upper troposphere, aerosols were most likely to exist in a glassy state (Shiraiwa et al., 2017). It has been suggested that the ice nucleating ability or inability of viscous biogenic secondary organic aerosols could provide a crucial mechanism for the formation of cirrus clouds high in the tropical tropopause layer (Froyd et al., 2010; Wilson et al., 2012).
The role of organic aerosol in the formation of ice has been a rapidly progressing area of research since the publication of a review of laboratory experiments (Hoose and Möhler, 2012). In particular, the role of viscous organic aerosol on ice nucleation at low temperatures has been a contested subject (Wagner et al., 2017; Reid et al., 2018). Initially, laboratory studies suggested that viscous aerosol may inhibit homogeneous ice nucleation (Zobrist et al., 2008; Murray, 2008; Murray and Bertram, 2008). Further cloud chamber studies have concluded that glassy aerosol cores could act as heterogeneous ice nuclei (Murray et al., 2010; Wang et al., 2012; Baustian et al., 2013; Berkemeier et al., 2014; Ignatius et al., 2016). α-pinene is a biogenic precursor to secondary organic aerosol (SOA), creating particles that have the potential to exist in an amorphous state under atmospheric conditions. Experiments testing the ice nucleating ability of α-pinene-derived secondary organic aerosol have produced conflicting results, both through homogeneous nucleation (Möhler et al., 2008; Ladino et al., 2014; Wagner et al., 2017) and heterogeneous nucleation (Wagner et al., 2017; Ignatius et al., 2016). However, it is important to acknowledge that in these experiments, secondary organic aerosols were produced through various methods, including ozonolysis and OH oxidation of α-pinene, therefore, both chemical and physical properties of the aerosol could vary between studies (Huang et al., 2018).
A combination of laboratory studies (Lienhard et al., 2015; Price et al., 2015) and computational models (Zobrist et al., 2011; Shiraiwa et al., 2013; O'Meara et al., 2016) have used equilibration times though viscous secondary organic aerosol particles, produced from the oxidation products of α-pinene, to extract diffusion coefficients at low temperatures through inverse modelling. Diffusion coefficients were then used in single particle simulations to interpret how equilibration timescales could interact with microphysical cloud properties and modes of ice formation (Lienhard et al., 2015). At low temperatures, less than 195 K, the viscosity of α-pinene SOA particles is such that homogeneous ice nucleation may be inhibited due to restricted particle growth (Lienhard et al., 2015). However, at temperatures greater than 200 K and low cooling rates, less than 1 K s−1, α-pinene SOA particles are expected to be in equilibrium with atmospheric conditions and to freeze homogeneously. Further studies have suggested that between the temperatures of 195 and 220 K, deliquescence is slowed to the extent where a glassy core forms and may act as a heterogeneous ice nucleus (Price et al., 2015).
Measurements of ice formation in chamber studies do not automatically disclose the mechanism of ice nucleation, rather, the relative humidity and temperature conditions will indicate whether ice has formed above or below the limit of homogeneous freezing (Koop et al., 2000; Wagner et al., 2017). Therefore, there is a need for modelling studies to be developed and to allow comparison with the chamber studies to ensure that the underlying physical mechanisms producing ice are understood. However, only recently have computational models been developed to treat diffusion through a distribution of aerosol particles (Zaveri et al., 2018), and therefore direct comparisons to cloud chamber studies on the ice nucleating ability of viscous aerosol particles have not been attempted.
The task of this study is to develop a simple cloud parcel model, that takes into account water transport through particle bulk using an aerosol diffusion framework (Fowler et al., 2018) to better understand the effect of aerosol viscosity on ice nucleation. To appreciate the possible atmospheric implications of aerosol viscosity on ice nucleation, atmospherically relevant diffusion coefficients that depend on both temperature and water content should be used to ensure that evolving particle growth and morphology is taken into account (Lienhard et al., 2015; O'Meara et al., 2016). The overall aim of this study is to better understand the underlying physical mechanisms of ice formation in low-temperature clouds and consider whether by including aerosol viscosity effects, our model is better able to simulate their formation high in the troposphere.
The article contains a short model description, followed by a methodology detailing the range of initial conditions used to test the model. To consider whether the new modelling approach is appropriate for gaining a better insight into ice formation mechanisms in amorphous aerosol particles at low temperatures, we ensure that the initial conditions used in the study are comparable to both in situ and laboratory studies (Möhler et al., 2008; Wagner et al., 2017; Yu et al., 2017). Then the sensitivity of model simulations over a range of atmospherically relevant initial conditions are given in the results, followed by a few specific examples to highlight subtleties observed during extensive model testing. Finally, the implications for the low-temperature clouds formed through homogeneous ice nucleation on ultra-viscous aerosol particles are discussed and brought together with conclusions.
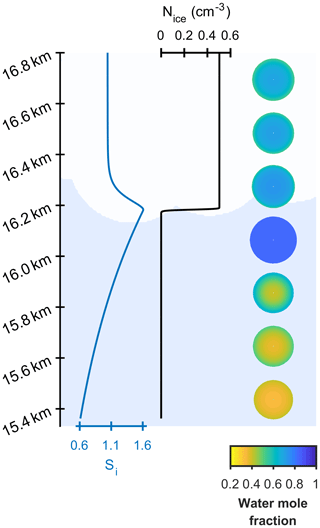
Two different models are referred to in this study, the new model and the control model. The new model has been developed to investigate the effect of aerosol viscosity on ice nucleation and is the first to solve condensed phase diffusion of water through individual aerosol particles within a particle size-resolved cloud parcel model with adiabatic ascent. The control model is also a particle size-resolved cloud parcel model, but it assumes that individual aerosol particles are uniformly mixed and does not solve for condensed phase diffusion. The schematic in Fig. 1a and b corresponds to the control model and the new model including diffusion, respectively, and shows the effect of slowed condensed phase diffusion on particle morphology and growth, hence possibly affecting the number and size of ice crystals nucleated in the simulation.
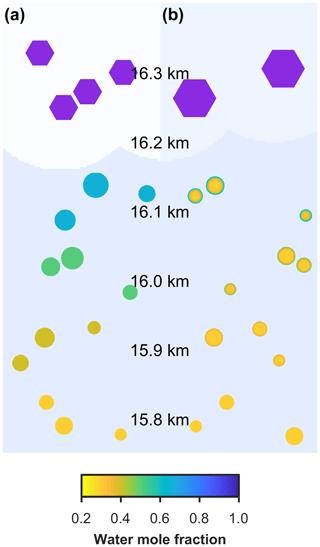
Figure 1A schematic of changing particle composition in a rising cloud parcel initiated with viscous α-pinene SOA particles, where the water mole fraction of condensed phase particles is given by the colour bar and purple hexagons represent frozen particles in a low-temperature cirrus cloud. Panel (a) is the control model output, which does not take into account condensed phase diffusion and (b) is the output from the new bin microphysics cloud model, which includes condensed phase diffusion through individual aerosol particles.
The models are initiated with a log-normal size distribution (Seinfeld and Pandis, 2006)
where N is the number density of aerosol particles, r is particle radius, NT is the total number of aerosol particles, rm is the median radius and σ is the geometric standard deviation of the logarithmic distribution, details of which are found in the methods section. At the start of the simulation, the individual aerosol size bins are assumed to be in equilibrium with the surrounding gas phase. It is at this stage that the new model initiates each aerosol size bin with a diffusion framework of logarithmically spaced shells (Fowler et al., 2018).
Both models solve a system of four coupled differential equations for height, z, water vapour mass mixing ratio, rv, pressure, p, and temperature, T, for a rising moist air parcel in hydrostatic balance, such that the ascent is adiabatic. However, the new and control model differ in their calculation of the droplet growth rate (Pruppacher and Klett, 2010)
where mw,i the mass of water in each size bin i, t is time, ri the radius of the particles in bin i, S is the saturation ratio of water vapour, Seq,i is the equilibrium vapour pressure of aerosol bin i with respect to liquid, ρi is the particle density in bin i, ρw is the density of water, Lv the latent heat of vaporisation, es is the saturation vapour pressure, T is temperature, R is the gas constant and Mw is the molar mass of water. The effects of mass accommodation are taken into account through a modified diffusivity, D*, and conductivity, k* (Pruppacher and Klett, 2010). The two models differ in the calculation of the droplet growth because the equilibrium saturation ratio, Seq,i, is found at the droplet's surface, which depends upon particle morphology. In the control model case, concentration is uniform throughout the particle radius and at the surface. The new model solves for condensed phase diffusion, which means concentration can vary along particle radius. A more detailed model description, along with open source code, will be available in an accompanying model development paper.
As well as the difference in calculation of the droplet growth equation, through the equilibrium saturation ratio, there are a couple of other differences between the two models. The new model assumes particle viscosity does not affect its ability to take up water through the surface accommodation coefficient because the diffusional limit of condensation is removed when water is able to mix through the outer aerosol layers (Rothfuss et al., 2018). The second difference is that the new model calculates the nucleation rate in the individual concentric aerosol shells, which means freezing can occur in layers of high water mole fraction on the surface of an amorphous aerosol core. The rate of homogeneous ice nucleation is calculated using temperature and the water activity of the mixture in both models (Koop et al., 2000).
For this study, Fick's second law of diffusion (Fick, 1855)
where c is concentration, D the condensed phase diffusion coefficient, r the particle radius, is solved numerically for each individual aerosol size bin using the backward Euler method (Fowler et al., 2018). Initially the Euler backward method was chosen because it conserves mass and is stable over the longer time periods associated with cloud development. However, during model testing it became apparent that diffusion would need to be solved simultaneously with droplet growth, and sufficiently small time steps would be needed to ensure model stability. Therefore, it is expected that alternative diffusion frameworks incorporated into the bin parcel model would give similar solutions as little variability was found in a study comparing the sensitivity of diffusion timescales to the model framework (O'Meara et al., 2016).
Throughout our study, simulations from the new model are compared with a control simulation, which does not include an aerosol diffusion framework and assumes individual particle bins have a constant concentration along the particle radius. The comparison between the new and control models allows us to assess the impact on the current understanding of ice nucleation processes and the specific conditions where aerosol viscosity has the greatest influence on cloud microphysics. The method section contains details of initial conditions and the metric defined as the fractional difference in ice nucleation used to compare the output from the new and control models.
3.1 Initial conditions
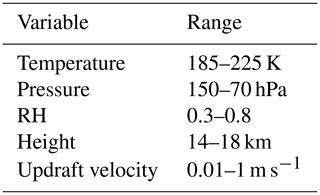
The study has been motivated by the evidence of viscous secondary organic aerosols found in the upper troposphere. However, to fully investigate where the formation of atmospheric ice is sensitive to aerosol viscosity, initial conditions have been selected to represent the conditions where secondary organic aerosols are likely to exist in glassy and amorphous states (Zobrist et al., 2008; Virtanen et al., 2010; Shiraiwa et al., 2017). Table 1 shows the full parameter space of atmospheric conditions tested with the cloud parcel models.
Figure 2 and the corresponding Table 2, show three aerosol size distributions used to initialise model simulations. Size distribution 1 corresponds to organic aerosol data collected near the tropical tropopause (Yu et al., 2017) and size distributions 2 and 3 correspond to two laboratory studies investigating the ice nucleating ability of α-pinene SOA (Möhler et al., 2008; Wagner et al., 2017). Although size distribution 3 is from a laboratory study, and concentrations are much higher than size distribution 1 taken from in situ measurements, extremely high number concentrations of organic aerosol have been observed in the troposphere near to regions of deep convective outflow in the tropics (Andreae et al., 2018). Aerosol size bins used in simulations ranged from 10nm to 7 µm to ensure the full size range of aerosol particles were accounted for and the edges of each size bin were defined once the particles were evenly distributed between all bins. This study used 60 particle size bins as it gave a balance between detail in the results and computational expense, since solving for diffusion in every bin and time step meant increasing the number of bins greatly increased the model run time. The molecular weight (136.2 g mol−1) and density (1260 kg m−3) of α-pinene SOA were kept constant throughout the study.
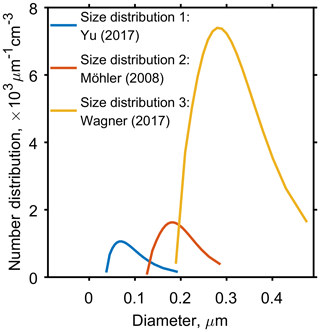
Figure 2Three aerosol particle size distributions used to initiate the cloud parcel models, which have been taken from published studies. Yu et al. (2017), corresponds to secondary organic aerosol data collected near the tropopause in Kunming, China, and both Möhler et al. (2008) and Wagner et al. (2017) correspond to aerosol size distributions used in cloud chamber experiments. Table 2 found in the Appendix gives specific parameter values for the log-normal size distributions.
Table 2Parameters used to plot the aerosol size distributions in Fig. 2, where the size distributions 1, 2 and 3 correspond to the studies by Yu et al. (2017), Möhler et al. (2008) and Wagner et al. (2017) respectively.
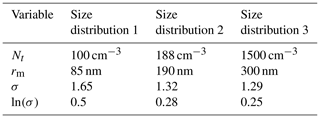
Nt, the total number density of aerosol particles; rm, the median radius; and σ, the geometric standard deviation of a log-normal distribution correspond to the aerosol size distributions used throughout the study.
A number of studies have aimed to quantify the effect of aerosol viscosity on equilibration timescales through α-pinene SOA by estimating coefficients of water diffusion (Renbaum-Wolff et al., 2013; Price et al., 2015; Lienhard et al., 2015). The water diffusion coefficients for α-pinene SOA from Lienhard et al. (2015) were specifically used in this study because the parameterisation is valid down to the low temperatures observed high in the troposphere and covers the large temperature range appropriate for our experiment as indicated by the initial conditions in Table 1. Figure 3 shows the diffusion coefficient as a function of temperature and water activity; highlighting how temperature conditions for homogeneous freezing, shown by the grey shaded region, interact with the published α-pinene SOA diffusion coefficients. Figure 3 indicates that at low temperatures, below 200 K, slow diffusion could influence homogeneous ice formation. It is important to acknowledge that published α-pinene SOA diffusion coefficients vary by orders of magnitude (Price et al., 2015), and that aerosols produced in laboratory studies may differ in composition to those produced in the atmosphere (Huang et al., 2018). The model simulations are initiated just below cloud base so we envisage that there will be no further co-condensation of volatile vapours with decreasing temperature as the cloud parcel begins to rise.
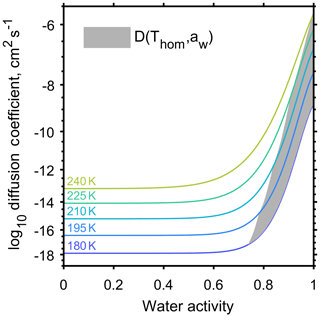
Figure 3Water diffusion coefficient through α-pinene secondary organic aerosol as a function of temperature and water activity adapted from Viscous organic aerosol particles in the upper troposphere: diffusivity-controlled water uptake and ice nucleation? by Lienhard et al. (2015). The grey region shows where the conditions of homogeneous freezing and diffusion coefficient interact.
3.2 Metric for model testing
To compare the number of ice crystals formed by the new and control model we chose to define the fractional difference between the number of ice produced by the two simulations to be
where, is the number density of ice produced by our new model and is the number density of ice produced by the control model. The fractional difference in Nice was chosen as the metric to compare ice nucleation rates, as the values are limited between −1 for no ice produced in the new model and 1 no ice produced by the control model.
4.1 Model sensitivities
The results of this study begin with a sensitivity analysis, comparing the outputs from both the new and control models to investigate how specific input variables effect aerosol viscosity and ice formation. The parameter space which the models are tested over is introduced in Table 1. Both rates of diffusion and ice nucleation depend upon temperature and water activity or concentration, therefore much of the discussion in this section concentrates on factors that directly or indirectly affect the temperature and the rate of water uptake by the individual aerosol size bins.
Figure 4 shows three different parcel trajectories: typical cirrus (T∼225 K), colder cirrus (T∼210 K) and very cold cirrus (T∼200 K). As the cloud parcels rise in simulations, the temperature decreases and ice saturation ratio increases until conditions for homogeneous ice nucleation are met. As aerosol particles freeze and ice crystals grow, the parcel of air dehydrates, shown by the rapid decrease in ice saturation ratio. The fractional difference in the number of ice crystals frozen between the new and control model simulations is given as a function of the initial temperature and ice saturation conditions. The blue colours represent a suppression in the number of ice crystals formed by our new model in comparison to the control model, and red colours represent an enhancement in the number of ice crystals formed by our new model in comparison to the control model. For each cloud parcel simulation in Fig. 4, a representative aerosol particle concentration profile shows that as initial temperature decreases, the equilibration timescale increases.
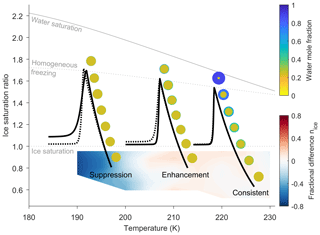
Figure 4A schematic showing the effect of initial temperature on particle composition, ice formation and ice saturation ratio, highlighting the effects of temperature-dependant diffusion on ice nucleation for three specific cloud parcel trajectories. The solid black lines show a cloud parcel trajectory for our new model and the broken black line for the control simulation. The changing water mole fraction for a single particle is shown next to each of the parcel trajectories. The fractional difference in number of frozen particles is shown at the initial conditions of ice saturation ratio and temperature, where the blue areas show that ice formation is suppressed in the new model simulations in comparison to the control model, and red regions show an enhancement in the number of frozen particles in new model simulations. At the lowest temperatures, below 200 K water molecules are immobile and particle growth is restricted, leading to a suppression in ice formation. As temperature increases, water molecules become more mobile and diffuse through the viscous SOA particle, so that between 200 and 220 K there is an increase in the number of particles frozen as a result of the thicker layer of water on the aerosol surface. At higher temperatures, above 220 K an aerosol core is still visible, however the core shrinks in relation to the outer liquid water layer until the aerosol particle is almost totally mixed as the parcel reaches the conditions for homogeneous freezing, which results in a consistent number of particles freezing in both the new and control model. Simulations from both the new and control model have been initiated with a size distribution 3, given in Fig. 2, under a constant updraft velocity of 0.6 ms−1.
In model simulations initiated under very cold cirrus conditions, Fig. 4 shows a very thin layer of water on the outside of the individual particles. The immobility of water molecules through the aerosol particle is due to the high viscosity or small diffusion coefficients of water through α-pinene SOA at temperatures below 200 K. The small volume of water on the aerosol particles in the cold temperature simulations results in a suppression of ice formation rate in comparison to the control model simulations. Cold cloud chamber studies investigating the ice nucleating ability of α-pinene SOA have not been taken down to the temperatures used in these model simulations. However, inhibited homogeneous ice nucleation at high cooling rates has been observed in citric acid particles (Murray, 2008), which are viscous at higher temperatures than α-pinene SOA (Price et al., 2014). In the cold cirrus case, aerosol particles are less viscous and water molecules more mobile, which means there is a larger layer of water on the surface of the aerosol particles. The larger volume of high water activity in the outer layer of aerosol particles results in an enhanced rate of ice formation in comparison to the control model. Under the temperature conditions of a typical cirrus cloud, we predict that α-pinene SOA particles are almost in equilibrium with their surroundings by the time conditions for homogeneous ice nucleation are reached, and only a small aerosol core is still visible in the larger particles of the size distribution. Hence, under typical cirrus conditions the models do not predict any difference in the number of aerosol particles frozen whether viscosity or accounted for or not.
Aerosol particles in all three parcel trajectories from Fig. 4 exhibit a boundary between the outer layer of water and the highly viscous α-pinene SOA core, represented by the contrast in water mole fraction. These steep gradients in concentration between the core and outer layer of water have been observed using Mie resonances in levitated highly viscous aerosol particles (Bastelberger et al., 2018) and reproduced in model simulations (O'Meara et al., 2016). Diffusion fronts are formed as a result of the plasticising effect of water, where a small increase in the volume of water greatly reduces the viscosity of a solution. The evolution of the diffusion front through the aerosol particle is limited by the aerosol viscosity ahead of the diffusion front. The diffusion front is recreated by the model using a sigmoidal relationship between water activity and diffusion coefficient for α-pinene SOA (Lienhard et al., 2015).
Current models simulate the changing composition of a single viscous aerosol particle under changing atmospheric conditions (Lienhard et al., 2015), however our new model allows the cumulative effect of particle viscosity on ice formation within a cloud parcel to be studied. Figure 5 extends the investigation of the effect of particle viscosity on ice nucleation by taking into account both updraft velocity and aerosol size distribution. The fractional difference in the number of ice crystals nucleated between the bin diffusion model and a control model is given as a function of initial temperature and ice saturation ratio. As with Fig. 4, blue colours represent a suppression in the number of ice crystals by our new model compared to control model runs and red an enhancement in the number of ice crystals by the new model compared to control model runs. To reproduce a wide range of atmospheric conditions, the simulations are initiated with temperatures, pressures, relative humidities and updraft velocities from Table 1.
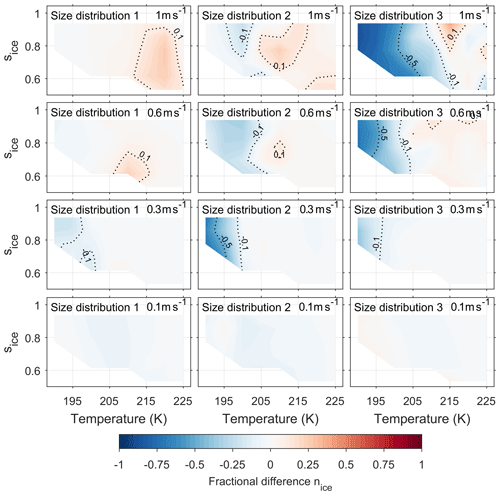
Figure 5Shows the effect of initial conditions on the fractional difference in number of frozen particles between the new and control model simulations. The blue areas show that ice formation is suppressed in the new model simulations in comparison to the control model, and red regions show an enhancement in the number of frozen particles in new model simulations. Contours on the graph are labelled and highlight the 0.1 and 0.5 fractional suppression and enhancements by the new model compared to the control model. The models have been initiated with three different size distributions, which are given in Fig. 2, and with constant updraft velocities ranging from 0.1 to 1 ms−1. Figures showing the number density of ice crystals formed in the new and the control model simulations are available in the Appendix.
As updraft velocity increases in Fig. 5, in general, there is a greater fractional difference in the number frozen aerosol particles between the new model and control model simulations apart from the low-temperature suppression from simulations using size distribution 2 with an updraft speed of 0.3 ms−1. The observed suppression in the case of size distribution 2 with an updraft speed of 0.3 ms−1 is the result of a combination of effects; the lower number concentration means that water vapour is distributed between fewer particles, and the larger mean radii cause diffusion timescales (and growth) to be slower, which results in fewer particles growing large enough to freeze below 200 K. However, in general, at higher updraft speeds there is less time for the diffusion front to move through the aerosol to its centre, therefore the viscous α-pinene SOA particles do not have time to equilibrate with parcel conditions. Hence at updraft speeds of 0.6 ms−1 or greater, both the low-temperature suppression of ice nucleation and the higher temperature enhancement of ice nucleation are amplified. In the case of size distribution 3, a fractional difference in the number of ice crystals of up to 0.8 is found, which corresponds to a suppression of over 50 cm−3 of ice between the new and control model. The enhancement of ice nucleation by α-pinene SOA at temperatures greater than 200 K or the colder cirrus conditions only occurs at updraft velocities of 0.6 ms−1 or greater. The enhancement is a result of a layer of water forming on the viscous aerosol core, as shown by the schematic in Fig. 4. For the number of ice crystals formed by the new model to be greater than the number produced by the control model conditions need to be optimal, allowing for enough liquid water to condense for homogeneous ice nucleation to occur in the outer liquid water layer. At lower updraft velocities, 0.3 ms−1 and below, the diffusion front moves through the particle before the conditions for homogeneous ice nucleation are reached, therefore an enhancement in the number of frozen particles does not occur. At the lowest updraft velocities of 0.1 ms−1, viscosity has much less of an effect on ice nucleation given that the fractional difference in frozen particles is less than 0.1. At low updraft velocities droplet growth is predicted to be similar in both the new and control models as viscous particles have plenty of time to equilibrate with the parcel conditions, which results in a very similar number of ice crystals forming.
Figure 5 shows an enhanced suppression of ice nucleation in the simulations initiated with the size distribution 3 compared size distributions 1 and 2. We suggest that the amplified suppression of ice by the new model simulations in comparison to the control for size distribution 3 is because condensed phase water is distributed between a greater number of particles in the high aerosol number concentrations as indicated by Fig. 2. Therefore, under the very cold cirrus conditions, or the most viscous cases, less liquid water condenses on the outer layer of individual aerosol particles and fewer aerosol particles freeze.
Figure 5 shows that the smallest fractional difference in the number of frozen aerosol particles between the new and control models was in simulations initiated with size distribution 1. There are a couple of reasons why aerosol viscosity has a limited effect on ice nucleation from the in situ case of size distribution 1 (Yu et al., 2017). The first is the smaller number concentration of aerosol particles, shown in Fig. 2, which means liquid water is distributed between fewer aerosol particles resulting in a higher water activity in the outer aerosol shells. The high water activity in the outer shells causes particles to equilibrate before the conditions for homogeneous ice nucleation are reached, due to the plasticising effect of water on viscous aerosols (O'Meara et al., 2016). Secondly, the median diameter of size distribution 1 is the smallest used in this study. A particle with a smaller diameter is expected to equilibrate with the gas phase in a shorter amount of time in comparison to a larger particle, since diffusion timescales are proportional to the square of the diameter over the diffusion coefficient (Price et al., 2015). Therefore, simulations initiated with size distribution 1 are likely to have equilibrated before reaching the conditions of homogeneous ice nucleation.
Our findings suggest that viscous organic aerosols, such as α-pinene SOA, are expected to have no effect on the rate of homogeneous ice nucleation even at the highest limit of updraft velocities found in the tropical tropopause layer as shown in the lower left panel of Fig. 5 (size distribution 1, 0.1 ms−1). Previous studies using single particle simulations have also concluded that aerosol viscosity may have a limited effect on homogeneous ice nucleation under certain atmospheric conditions (Lienhard et al., 2015). However, the investigation into the effect of viscous aerosol on ice nucleation in low-temperature cirrus should not end there as the new model could be used to gain further insights into how cloud processing could make alternative ice nucleation mechanisms possible under atmospheric conditions.
4.2 Processing of viscous aerosol particles
Figure 6 shows how ice saturation ratio and number of ice crystals formed depends upon cloud parcel temperature for four model simulations, all initiated on the same parcel trajectory but at different initial ice saturation ratios. Only one control model run, shown by the black line, has been plotted on the graph, since both the ice saturation ratio and number of ice crystals formed are consistent for the different initial ice saturation ratios. The upper panel shows that parcels initiated in equilibrium with atmospheric conditions, closer to cloud base result in a higher steady state ice saturation ratio after homogeneous freezing takes place, which is a result of fewer aerosol particles freezing, as shown in the lower panel. Figure 6 contains simple plots, but they show that as the timescales of diffusion become a limiting factor in cloud droplet growth, the history of individual particles needs to be considered in relation to parcel vapour content and ice nucleation.
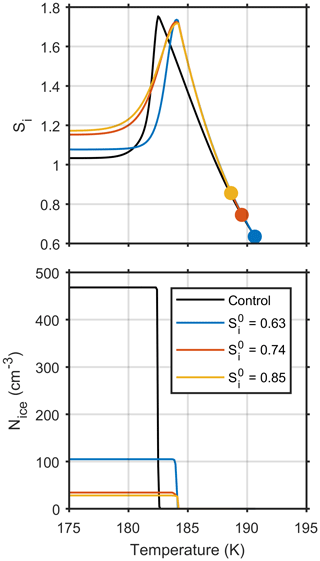
Figure 6The effect of different initial ice supersaturations, Si, on model simulations initiated with aerosol size distribution 3 and a constant updraft velocity of 0.6 ms−1.
Pre-activation of ice nuclei has been discussed in relation to the modes of ice nucleation in amorphous secondary organic aerosols (Wagner et al., 2012) and in particular α-pinene SOA (Wagner et al., 2017; Ladino et al., 2014). As water is removed, ice residuals could be left inside the core of the particle or within a glassy porous structure leading to a nucleation event (Wagner et al., 2017). We did not intend to investigate pre-activation, however on closer inspection of model runs initiated with low updraft speeds (0.1 ms−1), such as Fig. 7, we noticed that after a freezing event and the drop in the cloud ice saturation ratio, water was removed from the outer layers of the aerosol particle, leaving high water activity in the aerosol core. In noticing the formation of an organic shell we wonder if under further model development the effect of aerosol viscosity on ice nucleation during multiple cooling cycles could be investigated. The further model development that we envisage would be required to investigate cloud processing, includes tracking changes in state through individual cloud particles and solving for diffusion through a solid lattice.
The current understanding of ambient aerosol particle viscosity and the implications this has for atmospheric processes is underpinned by laboratory studies (Reid et al., 2018). These laboratory studies have enabled the researchers to probe single aerosol particles both as samples deposited of substrates and as levitated particles over a wide range of temperature and viscosity (Krieger et al., 2012). However, few studies have investigated the effect of viscosity on a population of aerosol particles (Yli-Juuti et al., 2017; Ye et al., 2016; Zaveri et al., 2018). Using the new cloud parcel model that solves for condensed phase diffusion through individual aerosol particles enables a different insight to the atmospheric implications of viscous aerosol on ice nucleation processes.
The suppression of homogeneous ice nucleation at low temperatures by ultra-viscous aerosol has been suggested as a reason for the high in cloud supersaturations observed in low-temperature cirrus clouds or subvisible cirrus (Murray, 2008; Peter et al., 2006; Krämer et al., 2009; Froyd et al., 2010). Figure 4 shows both the parcel trajectories for our new model and control simulations, which are given by the solid and broken black lines respectively. In the highly viscous regime, where model simulations are initiated below 200 K, the suppression in the number of ice particles by the new model causes the parcel of air to dehydrate at a slower rate in comparison to the control model, which can be seen in the gradient of the parcel trajectories after ice nucleation. There is a clear difference between the steady state relative humidities with respect to ice, where the control model predicts a value close to ice saturation and the new model predicts an ice saturation ratio of 1.1.
In this study we consider the effect of aerosol particle viscosity on the homogeneous nucleation of ice; however, it is important to acknowledge that there is evidence that viscous aerosols can nucleate ice heterogeneously. Laboratory experiments have shown that a variety of viscous substances nucleated ice well below the homogeneous limit in a cloud chamber study (Murray et al., 2010; Wilson et al., 2012), and a more recent study has found evidence that α-pinene SOA also acts as a heterogeneous ice nucleus (Ignatius et al., 2016).
The modes of heterogeneous ice nucleation are less well understood and modelled in comparison to homogeneous ice nucleation. Despite this, under low-temperature cirrus conditions, where highly viscous organic aerosols can exist in a glassy phase, there is evidence that these particles could nucleate ice in the deposition mode of freezing (Wang et al., 2012). As temperatures increase, water molecules become more mobile forming a thicker outer shell with a high water activity; in this regime it has been suggested that ice nucleation could occur through the immersion mode on the viscous organic aerosol core (Murray et al., 2010). Using diffusion coefficients, our model replicates the cold and warm regimes observed in laboratory experiments through totally inhibited growth and the formation of a condensed liquid phase outer shell. Other studies have investigated the regimes of ice nucleation under cold cirrus conditions using metrics such as glass transition temperature (Wang et al., 2012), the limit between an amorphous substance being in a glassy state and a viscous state.
To better understand how our approach differs with standard methods of modelling cirrus cloud development in the upper troposphere, we compare cloud parcel simulations with a parameterisation for homogeneous ice formation used in large-scale general circulation models (Kärcher and Lohmann, 2002). Figure 8 shows how ice crystal number concentrations depend upon temperature and updraft. Model simulations have been initiated just below ice saturation, with an aerosol number density of 1000 cm−3 at temperatures of 230, 210 and 190 K, and a range of constant updraft speeds from 0.01 to 1 ms−1. At low updraft speeds, where aerosol particles are able to equilibrate with the surrounding gas, the number density of ice crystals formed in both the models and predicted by the parameterisation agree. However, at higher updraft speeds, greater than 0.5 ms−1, we notice that the number of ice crystals formed by the new model, initiated at 190 K, deviate from both the control and the general circulation model parameterisation by an order of magnitude. The parameterisation, control and new model all simulate the great range in magnitude of measured ice crystal concentrations, which range from 0.005 to 60 cm−3 (Krämer et al., 2009). By taking into account particle viscosity, through condensed phase diffusion, the upper limit of homogeneous ice nucleation in the coldest cases is limited by the new model as shown in Fig. 8. However, neither model well reproduces the lowest ice crystal concentrations observed during in situ studies.
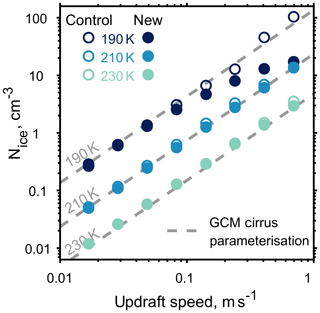
Figure 8The effect of updraft speed and temperature on the formation of ice for both the new and control cloud parcel models is shown by the filled and outlined circles respectively. The grey dashed line represents a parameterisation for ice number density in cirrus clouds used in a large-scale general circulation model (Kärcher and Lohmann, 2002).
The model analysis presented in this paper suggests that there are two competing effects as a result of the immobility of water molecules through viscous α-pinene secondary organic aerosol particles. The first is the inhibition of homogeneous ice nucleation at the lowest temperatures, below 200 K, due to restricted particle growth and low water volume. The second effect occurs at warmer temperatures, between 200 and 220 K, where water molecules are more mobile and a layer of water condenses on the outside of the particle, leading to an increase in the homogeneous nucleation rate. The new cloud parcel model that solves for condensed phase diffusion through individual aerosol particles provides a platform to further investigate the effect of condensed phase diffusion on cloud microphysical processes and addresses some of the problems associated with modelling cirrus clouds in larger-scale general circulation models. Initial research, addressed in this study, has focused on how viscous secondary organic aerosol particles, such as α-pinene SOA, effect ice nucleation in low-temperature cirrus clouds. However, recent work has highlighted that anthropogenic sources also produce highly viscous aerosols that exist at much higher temperatures and relative humidities (Reid et al., 2018), which could have implications under the conditions of mixed phase cloud formation (Charnawskas et al., 2017). Then there are more complex multi-component systems to consider, containing a mixture of SOA and inorganic salts have been observed to form liquid–liquid phase separations, which can effect cloud particle growth and activation at higher temperatures and relative humidities (Renbaum-Wolff et al., 2016). There is scope to further develop our new model to investigate how the solubility of aerosol particles within multi-component systems could affect cloud microphysical properties using a Maxwell–Stefan diffusion framework (Fowler et al., 2018).
The code used in this study is available through open access at https://doi.org/10.5281/zenodo.3355545 (Connolly and Fowler, 2019).
Figures A1 and A2 have been included in the appendix to quantify the number of ice crystals nucleated by both the new model and control model respectively. The colour scale shows the frozen fraction of total aerosol particles in the simulations and contour lines give the number of particles nucleated per cubic centimetre. The fractional difference in Nice, from Eq. (4) and represented by the colour scale in Fig. 5, corresponds to the difference between Figs. A1 and A2 divided by their sum. By comparing the contour lines in the simulations run with size distribution 3 and updraft speeds of 0.6 ms−1 and above we are able quantify the difference that viscosity could have on the number of ice crystals formed.
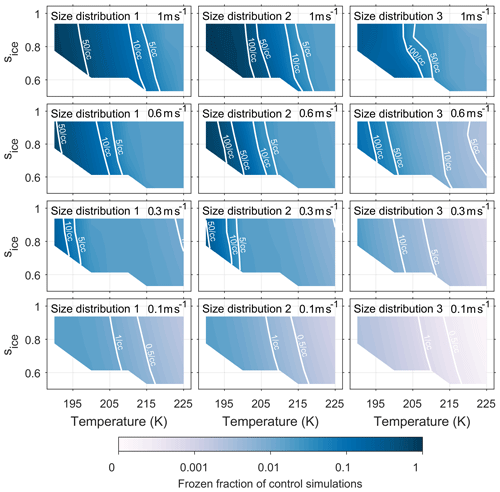
Figure A1Quantifying the number of aerosol particles frozen in control model simulations. The colour scale represents the frozen fraction of total aerosol particles and the labelled contour lines give the number of frozen aerosol particles per cubic centimetre. The model run have been initiated with three different size distributions, which are given in Fig. 2, and with constant updraft velocities ranging from 0.1 to 1 ms−1.
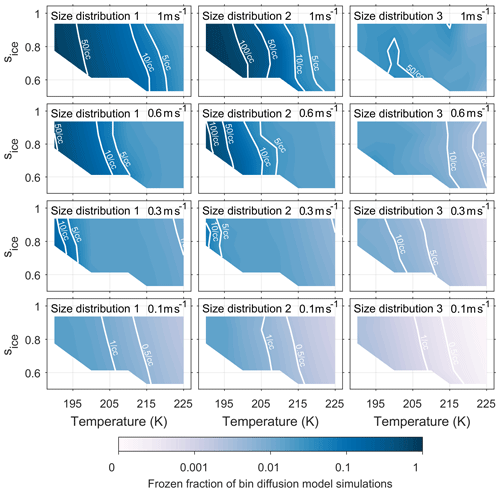
Figure A2Quantifying the number of aerosol particles frozen in bin diffusion model simulations. The colour scale represents the frozen fraction of total aerosol particles and the labelled contour lines give the number of frozen aerosol particles per cubic centimetre. The model run have been initiated with three different size distributions, which are given in Fig. 2, and with constant updraft velocities ranging from 0.1 to 1 ms−1.
PC and KF conceived and designed the research and developed the model code. KF led the analysis and figure preparation and wrote the paper. KF, PC and DT contributed to scientific discussions and to the preparation of the paper.
The authors declare that they have no conflict of interest.
This publication contains work conducted during the PhD studentship of Kathryn Fowler, supported by the Natural Environment Research Council (NERC) EAO Doctoral Training Partnership. Paul Connolly acknowledges support from the European Union's Seventh Framework Programme (FP7/2007-2013), under grant agreement no. 603445.
This research has been supported by the Natural Environment Research Council (grant no. NE/L002469/1).
This paper was edited by Ottmar Möhler and reviewed by two anonymous referees.
Andreae, M. O., Afchine, A., Albrecht, R., Holanda, B. A., Artaxo, P., Barbosa, H. M. J., Borrmann, S., Cecchini, M. A., Costa, A., Dollner, M., Fütterer, D., Järvinen, E., Jurkat, T., Klimach, T., Konemann, T., Knote, C., Krämer, M., Krisna, T., Machado, L. A. T., Mertes, S., Minikin, A., Pöhlker, C., Pöhlker, M. L., Pöschl, U., Rosenfeld, D., Sauer, D., Schlager, H., Schnaiter, M., Schneider, J., Schulz, C., Spanu, A., Sperling, V. B., Voigt, C., Walser, A., Wang, J., Weinzierl, B., Wendisch, M., and Ziereis, H.: Aerosol characteristics and particle production in the upper troposphere over the Amazon Basin, Atmos. Chem. Phys., 18, 921–961, https://doi.org/10.5194/acp-18-921-2018, 2018. a
Bastelberger, S., Krieger, U. K., Luo, B. P., and Peter, T.: Time evolution of steep diffusion fronts in highly viscous aerosol particles measured with Mie resonance spectroscopy, J. Chem. Phys., 149, 244506, https://doi.org/10.1063/1.5052216, 2018. a
Baustian, K. J., Wise, M. E., Jensen, E. J., Schill, G. P., Freedman, M. A., and Tolbert, M. A.: State transformations and ice nucleation in amorphous (semi-)solid organic aerosol, Atmos. Chem. Phys., 13, 5615–5628, https://doi.org/10.5194/acp-13-5615-2013, 2013. a
Berkemeier, T., Shiraiwa, M., Pöschl, U., and Koop, T.: Competition between water uptake and ice nucleation by glassy organic aerosol particles, Atmos. Chem. Phys., 14, 12513–12531, https://doi.org/10.5194/acp-14-12513-2014, 2014. a
Charnawskas, J. C., Alpert, P. A., Lambe, A. T., Berkemeier, T., O'Brien, R. E., Massoli, P., Onasch, T. B., Shiraiwa, M., Moffet, R. C., Gilles, M. K., Davidovits, P., Worsnop, D. R., and Knopf, D. A.: Condensed-phase biogenic-anthropogenic interactions with implications for cold cloud formation, Faraday Discuss., 200, 165–194, https://doi.org/10.1039/c7fd00010c, 2017. a
Connolly, P. J. and Fowler, K.: UoM-maul1609/bin-diffusion-model: Full working version, https://doi.org/10.5281/zenodo.3355545, 2019. a
Fick, A.: Ueber Diffusion, Ann. Phys. Chem., 170, 59–86, https://doi.org/10.1002/andp.18551700105, 1855. a
Fowler, K., Connolly, P. J., Topping, D. O., and O'Meara, S.: Maxwell-Stefan diffusion: a framework for predicting condensed phase diffusion and phase separation in atmospheric aerosol, Atmos. Chem. Phys., 18, 1629–1642, https://doi.org/10.5194/acp-18-1629-2018, 2018. a, b, c, d
Froyd, K. D., Murphy, D. M., Lawson, P., Baumgardner, D., and Herman, R. L.: Aerosols that form subvisible cirrus at the tropical tropopause, Atmos. Chem. Phys., 10, 209–218, https://doi.org/10.5194/acp-10-209-2010, 2010. a, b, c
Fueglistaler, S., Dessler, A. E., Dunkerton, T. J., Folkins, I., Fu, Q., and Mote, P. W.: Tropical tropopause layer, Rev. Geophys., 47, RG1004, https://doi.org/10.1029/2008RG000267, 2009. a
Hoose, C. and Möhler, O.: Heterogeneous ice nucleation on atmospheric aerosols: a review of results from laboratory experiments, Atmos. Chem. Phys., 12, 9817–9854, https://doi.org/10.5194/acp-12-9817-2012, 2012. a
Huang, W., Saathoff, H., Pajunoja, A., Shen, X., Naumann, K.-H., Wagner, R., Virtanen, A., Leisner, T., and Mohr, C.: α-Pinene secondary organic aerosol at low temperature: chemical composition and implications for particle viscosity, Atmos. Chem. Phys., 18, 2883–2898, https://doi.org/10.5194/acp-18-2883-2018, 2018. a, b
Ignatius, K., Kristensen, T. B., Järvinen, E., Nichman, L., Fuchs, C., Gordon, H., Herenz, P., Hoyle, C. R., Duplissy, J., Garimella, S., Dias, A., Frege, C., Höppel, N., Tröstl, J., Wagner, R., Yan, C., Amorim, A., Baltensperger, U., Curtius, J., Donahue, N. M., Gallagher, M. W., Kirkby, J., Kulmala, M., Möhler, O., Saathoff, H., Schnaiter, M., Tomé, A., Virtanen, A., Worsnop, D., and Stratmann, F.: Heterogeneous ice nucleation of viscous secondary organic aerosol produced from ozonolysis of α-pinene, Atmos. Chem. Phys., 16, 6495–6509, https://doi.org/10.5194/acp-16-6495-2016, 2016. a, b, c
Jensen, E. J., Smith, J. B., Pfister, L., Pittman, J. V., Weinstock, E. M., Sayres, D. S., Herman, R. L., Troy, R. F., Rosenlof, K., Thompson, T. L., Fridlind, A. M., Hudson, P. K., Cziczo, D. J., Heymsfield, A. J., Schmitt, C., and Wilson, J. C.: Ice supersaturations exceeding 100 % at the cold tropical tropopause: implications for cirrus formation and dehydration, Atmos. Chem. Phys., 5, 851–862, https://doi.org/10.5194/acp-5-851-2005, 2005. a
Jensen, E. J., Pfister, L., Bui, T.-P., Lawson, P., and Baumgardner, D.: Ice nucleation and cloud microphysical properties in tropical tropopause layer cirrus, Atmos. Chem. Phys., 10, 1369–1384, https://doi.org/10.5194/acp-10-1369-2010, 2010. a
Jensen, E. J., Diskin, G., Lawson, R. P., Lance, S., Bui, T. P., Hlavka, D., McGill, M., Pfister, L., Toon, O. B., and Gao, R.: Ice nucleation and dehydration in the Tropical Tropopause Layer, P. Natl. Acad. Sci. USA, 110, 2041–6, https://doi.org/10.1073/pnas.1217104110, 2013. a
Jensen, E. J., Thornberry, T. D., Rollins, A. W., Ueyama, R., Pfister, L., Bui, T., Diskin, G. S., DiGangi, J. P., Hintsa, E., Gao, R.-S., Woods, S., Lawson, R. P., and Pittman, J.: Physical processes controlling the spatial distributions of relative humidity in the tropical tropopause layer over the Pacific, J. Geophys. Res.-Atmos., 122, 6094–6107, https://doi.org/10.1002/2017JD026632, 2017. a, b
Kärcher, B.: Properties of subvisible cirrus clouds formed by homogeneous freezing, Atmos. Chem. Phys., 2, 161–170, https://doi.org/10.5194/acp-2-161-2002, 2002. a
Kärcher, B. and Lohmann, U.: A parameterization of cirrus cloud formation: Homogeneous freezing of supercooled aerosols, J. Geophys. Res., 107, 4010, https://doi.org/10.1029/2001JD000470, 2002. a, b, c
Koop, T., Luo, B., Tsias, A., and Peter, T.: Water activity as the determinant for homogeneous ice nucleation in aqueous solutions, Nature, 406, 611–4, https://doi.org/10.1038/35020537, 2000. a, b
Krämer, M., Schiller, C., Afchine, A., Bauer, R., Gensch, I., Mangold, A., Schlicht, S., Spelten, N., Sitnikov, N., Borrmann, S., de Reus, M., and Spichtinger, P.: Ice supersaturations and cirrus cloud crystal numbers, Atmos. Chem. Phys., 9, 3505–3522, https://doi.org/10.5194/acp-9-3505-2009, 2009. a, b, c, d, e
Krämer, M., Rolf, C., Luebke, A., Afchine, A., Spelten, N., Costa, A., Meyer, J., Zöger, M., Smith, J., Herman, R. L., Buchholz, B., Ebert, V., Baumgardner, D., Borrmann, S., Klingebiel, M., and Avallone, L.: A microphysics guide to cirrus clouds – Part 1: Cirrus types, Atmos. Chem. Phys., 16, 3463–3483, https://doi.org/10.5194/acp-16-3463-2016, 2016. a
Krieger, U. K., Marcolli, C., and Reid, J. P.: Exploring the complexity of aerosol particle properties and processes using single particle techniques, Chem. Soc. Rev. 41, 6631–62, https://doi.org/10.1039/c2cs35082c, 2012. a
Ladino, L. A., Zhou, S., Yakobi-Hancock, J. D., Aljawhary, D., and Abbatt, J. P. D.: Factors controlling the ice nucleating abilities of α-pinene SOA particles, J. Geophys. Res.-Atmos., 119, 9041–9051, https://doi.org/10.1002/2014JD021578, 2014. a, b
Lawson, R. P., Pilson, B., Baker, B., Mo, Q., Jensen, E., Pfister, L., and Bui, P.: Aircraft measurements of microphysical properties of subvisible cirrus in the tropical tropopause layer, Atmos. Chem. Phys., 8, 1609–1620, https://doi.org/10.5194/acp-8-1609-2008, 2008. a
Lee, K.-O., Dauhut, T., Chaboureau, J.-P., Khaykin, S., Krämer, M., and Rolf, C.: Convective hydration in the tropical tropopause layer during the StratoClim aircraft campaign: pathway of an observed hydration patch, Atmos. Chem. Phys., 19, 11803–11820, https://doi.org/10.5194/acp-19-11803-2019, 2019. a
Lienhard, D. M., Huisman, A. J., Krieger, U. K., Rudich, Y., Marcolli, C., Luo, B. P., Bones, D. L., Reid, J. P., Lambe, A. T., Canagaratna, M. R., Davidovits, P., Onasch, T. B., Worsnop, D. R., Steimer, S. S., Koop, T., and Peter, T.: Viscous organic aerosol particles in the upper troposphere: diffusivity-controlled water uptake and ice nucleation?, Atmos. Chem. Phys., 15, 13599–13613, https://doi.org/10.5194/acp-15-13599-2015, 2015. a, b, c, d, e, f, g, h, i
Maclean, A. M., Butenhoff, C. L., Grayson, J. W., Barsanti, K., Jimenez, J. L., and Bertram, A. K.: Mixing times of organic molecules within secondary organic aerosol particles: a global planetary boundary layer perspective, Atmos. Chem. Phys., 17, 13037–13048, https://doi.org/10.5194/acp-17-13037-2017, 2017. a
Möhler, O., Benz, S., Saathoff, H., Schnaiter, M., Wagner, R., Schneider, J., Walter, S., Ebert, V., and Wagner, S.: The effect of organic coating on the heterogeneous ice nucleation efficiency of mineral dust aerosols, Environ. Res. Lett., 3, 025007, https://doi.org/10.1088/1748-9326/3/2/025007, 2008. a, b, c, d, e
Murray, B. J.: Inhibition of ice crystallisation in highly viscous aqueous organic acid droplets, Atmos. Chem. Phys., 8, 5423–5433, https://doi.org/10.5194/acp-8-5423-2008, 2008. a, b, c
Murray, B. J. and Bertram, A. K.: Inhibition of solute crystallisation in aqueous H+---H2O droplets, Phys. Chem. Chem. Phys., 10, 3287, https://doi.org/10.1039/b802216j, 2008. a
Murray, B. J., Wilson, T. W., Dobbie, S., Cui, Z., Al-Jumur, S. M. R. K., Möhler, O., Schnaiter, M., Wagner, R., Benz, S., Niemand, M., Saathoff, H., Ebert, V., Wagner, S., and Kärcher, B.: Heterogeneous nucleation of ice particles on glassy aerosols under cirrus conditions, Nat. Geosci., 3, 233–237, https://doi.org/10.1038/ngeo817, 2010. a, b, c
O'Meara, S., Topping, D. O., and McFiggans, G.: The rate of equilibration of viscous aerosol particles, Atmos. Chem. Phys., 16, 5299–5313, https://doi.org/10.5194/acp-16-5299-2016, 2016. a, b, c, d, e
Peter, T., Marcolli, C., Spichtinger, P., Corti, T., Baker, M. B., and Koop, T.: When Dry Air Is Too Humid, Science, 314, 1399–1402, https://doi.org/10.1126/science.1135199, 2006. a, b, c
Price, H. C., Murray, B. J., Mattsson, J., O'Sullivan, D., Wilson, T. W., Baustian, K. J., and Benning, L. G.: Quantifying water diffusion in high-viscosity and glassy aqueous solutions using a Raman isotope tracer method, Atmos. Chem. Phys., 14, 3817–3830, https://doi.org/10.5194/acp-14-3817-2014, 2014. a
Price, H. C., Mattsson, J., Zhang, Y., Bertram, A. K., Davies, J. F., Grayson, J. W., Martin, S. T., O'Sullivan, D., Reid, J. P., Rickards, A. M. J., and Murray, B. J.: Water diffusion in atmospherically relevant α-pinene secondary organic material, Chem. Sci., 6, 4876–4883, https://doi.org/10.1039/C5SC00685F, 2015. a, b, c, d, e
Pruppacher, H. and Klett, J.: Microphysics of Clouds and Precipitation, Vol. 18, Atmospheric and Oceanographic Sciences Library, Springer Netherlands, Dordrecht, https://doi.org/10.1007/978-0-306-48100-0, 2010. a, b
Reid, J. P., Bertram, A. K., Topping, D. O., Laskin, A., Martin, S. T., Petters, M. D., Pope, F. D., and Rovelli, G.: The viscosity of atmospherically relevant organic particles, Nat. Commun., 9, 956, https://doi.org/10.1038/s41467-018-03027-z, 2018. a, b, c, d
Renbaum-Wolff, L., Grayson, J. W., Bateman, A. P., Kuwata, M., Sellier, M., Murray, B. J., Shilling, J. E., Martin, S. T., and Bertram, A. K.: Viscosity of α-pinene secondary organic material and implications for particle growth and reactivity, P. Natl. Acad. Sci. USA, 110, 8014–9, https://doi.org/10.1073/pnas.1219548110, 2013. a
Renbaum-Wolff, L., Song, M., Marcolli, C., Zhang, Y., Liu, P. F., Grayson, J. W., Geiger, F. M., Martin, S. T., and Bertram, A. K.: Observations and implications of liquid-liquid phase separation at high relative humidities in secondary organic material produced by α-pinene ozonolysis without inorganic salts, Atmos. Chem. Phys., 16, 7969–7979, https://doi.org/10.5194/acp-16-7969-2016, 2016. a
Rothfuss, N. E., Marsh, A., Rovelli, G., Petters, M. D., and Reid, J. P.: Condensation Kinetics of Water on Amorphous Aerosol Particles, J. Phys. Chem. Lett., 9, 3708–3713, https://doi.org/10.1021/acs.jpclett.8b01365, 2018. a
Seinfeld, J. H. and Pandis, S. N.: Atmospheric Chemistry And Physics, John Wiley & Sons, Hoboken, New Jersey, 2nd Edn., 408–834, 2006. a
Shiraiwa, M., Zuend, A., Bertram, A. K., and Seinfeld, J. H.: Gas-particle partitioning of atmospheric aerosols: interplay of physical state, non-ideal mixing and morphology, Phys. Chem. Chem. Phys., 15, 11441, https://doi.org/10.1039/c3cp51595h, 2013. a
Shiraiwa, M., Li, Y., Tsimpidi, A. P., Karydis, V. A., Berkemeier, T., Pandis, S. N., Lelieveld, J., Koop, T., and Pöschl, U.: Global distribution of particle phase state in atmospheric secondary organic aerosols, Nat. Commun., 8, 15002, https://doi.org/10.1038/ncomms15002, 2017. a, b, c
Spichtinger, P. and Krämer, M.: Tropical tropopause ice clouds: a dynamic approach to the mystery of low crystal numbers, Atmos. Chem. Phys., 13, 9801–9818, https://doi.org/10.5194/acp-13-9801-2013, 2013. a
Virtanen, A., Joutsensaari, J., Koop, T., Kannosto, J., Yli-Pirilä, P., Leskinen, J., Mäkelä, J. M., Holopainen, J. K., Pöschl, U., Kulmala, M., Worsnop, D. R., and Laaksonen, A.: An amorphous solid state of biogenic secondary organic aerosol particles, Nature, 467, 824–827, https://doi.org/10.1038/nature09455, 2010. a, b
Wagner, R., Möhler, O., Saathoff, H., Schnaiter, M., Skrotzki, J., Leisner, T., Wilson, T. W., Malkin, T. L., and Murray, B. J.: Ice cloud processing of ultra-viscous/glassy aerosol particles leads to enhanced ice nucleation ability, Atmos. Chem. Phys., 12, 8589–8610, https://doi.org/10.5194/acp-12-8589-2012, 2012. a
Wagner, R., Höhler, K., Huang, W., Kiselev, A., Möhler, O., Mohr, C., Pajunoja, A., Saathoff, H., Schiebel, T., Shen, X., and Virtanen, A.: Heterogeneous ice nucleation of α-pinene SOA particles before and after ice cloud processing, J. Geophys. Res.-Atmos., 122, 4924–4943, https://doi.org/10.1002/2016JD026401, 2017. a, b, c, d, e, f, g, h, i, j
Wang, B., Lambe, A. T., Massoli, P., Onasch, T. B., Davidovits, P., Worsnop, D. R., and Knopf, D. A.: The deposition ice nucleation and immersion freezing potential of amorphous secondary organic aerosol: Pathways for ice and mixed-phase cloud formation, J. Geophys. Res., 117, D16209, https://doi.org/10.1029/2012JD018063, 2012. a, b, c
Wilson, T. W., Murray, B. J., Wagner, R., Möhler, O., Saathoff, H., Schnaiter, M., Skrotzki, J., Price, H. C., Malkin, T. L., Dobbie, S., and Al-Jumur, S. M. R. K.: Glassy aerosols with a range of compositions nucleate ice heterogeneously at cirrus temperatures, Atmos. Chem. Phys., 12, 8611–8632, https://doi.org/10.5194/acp-12-8611-2012, 2012. a, b
Ye, Q., Robinson, E. S., Ding, X., Ye, P., Sullivan, R. C., and Donahue, N. M.: Mixing of secondary organic aerosols versus relative humidity, P. Natl. Acad. Sci. USA, 113, 12649–12654, https://doi.org/10.1073/pnas.1604536113,2016. a
Yli-Juuti, T., Pajunoja, A., Tikkanen, O.-P., Buchholz, A., Faiola, C., Väisänen, O., Hao, L., Kari, E., Peräkylä, O., Garmash, O., Shiraiwa, M., Ehn, M., Lehtinen, K., and Virtanen, A.: Factors controlling the evaporation of secondary organic aerosol from α-pinene ozonolysis, Geophys. Res. Lett., 44, 2562–2570, https://doi.org/10.1002/2016GL072364, 2017. a
Yu, P., Rosenlof, K. H., Liu, S., Telg, H., Thornberry, T. D., Rollins, A. W., Portmann, R. W., Bai, Z., Ray, E. A., Duan, Y., Pan, L. L., Toon, O. B., Bian, J., and Gao, R.-S.: Efficient transport of tropospheric aerosol into the stratosphere via the Asian summer monsoon anticyclone, P. Natl. Acad. Sci. USA, 114, 6972–6977, https://doi.org/10.1073/pnas.1701170114, 2017. a, b, c, d, e
Zaveri, R. A., Shilling, J. E., Zelenyuk, A., Liu, J., Bell, D. M., D’Ambro, E. L., Gaston, C. J., Thornton, J. A., Laskin, A., Lin, P., Wilson, J., Easter, R. C., Wang, J., Bertram, A. K., Martin, S. T., Seinfeld, J. H., and Worsnop, D. R.: Growth Kinetics and Size Distribution Dynamics of Viscous Secondary Organic Aerosol, Environ. Sci. Technol., 52, 1191–1199, https://doi.org/10.1021/acs.est.7b04623, 2018. a, b
Zobrist, B., Marcolli, C., Pedernera, D. A., and Koop, T.: Do atmospheric aerosols form glasses?, Atmos. Chem. Phys., 8, 5221–5244, https://doi.org/10.5194/acp-8-5221-2008, 2008. a, b, c
Zobrist, B., Soonsin, V., Luo, B. P., Krieger, U. K., Marcolli, C., Peter, T., and Koop, T.: Ultra-slow water diffusion in aqueous sucrose glasses, Phys. Chem. Chem. Phys., 13, 3514–26, https://doi.org/10.1039/c0cp01273d, 2011. a