the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Heterogeneous oxidation of amorphous organic aerosol surrogates by O3, NO3, and OH at typical tropospheric temperatures
Jienan Li
Seanna M. Forrester
Daniel A. Knopf
Typical tropospheric temperatures render possible phase states of amorphous organic aerosol (OA) particles of solid, semisolid, and liquid. This will affect the multiphase oxidation kinetics involving the organic condensed-phase and gaseous oxidants and radicals. To quantify this effect, we determined the reactive uptake coefficients (γ) of O3, NO3, and OH by substrate films composed of single and binary OA surrogate species under dry conditions for temperatures from 213 to 313 K. A temperature-controlled coated-wall flow reactor coupled to a chemical ionization mass spectrometer was applied to determine γ with consideration of gas diffusion transport limitation and gas flow entrance effects, which can impact heterogeneous reaction kinetics. The phase state of the organic substrates was probed via the poke-flow technique, allowing the estimation of the substrates' glass transition temperatures. γ values for O3 and OH uptake to a canola oil substrate, NO3 uptake to a levoglucosan and a levoglucosan / xylitol substrate, and OH uptake to a glucose and glucose / 1,2,6-hexanetriol substrate have been determined as a function of temperature. We observed the greatest changes in γ with temperature for substrates that experienced the largest changes in viscosity as a result of a solid-to-liquid phase transition. Organic substrates that maintain a semisolid or solid phase state and as such a relatively higher viscosity do not display large variations in heterogeneous reactivity. From 213 to 293 K, γ values of O3 with canola oil, of NO3 with a levoglucosan / xylitol mixture, and of OH with a glucose / 1,2,6-hexanetriol mixture and canola oil, increase by about a factor of 34, 3, 2, and 5, respectively, due to a solid-to-liquid phase transition of the substrate. These results demonstrate that the surface and bulk lifetime of the OA surrogate species can significantly increase due to the slowed heterogeneous kinetics when OA species are solid or highly viscous in the middle and upper troposphere. This experimental study will further our understanding of the chemical evolution of OA particles with subsequent important consequences for source apportionment, air quality, and climate.
- Article
(4055 KB) -
Supplement
(772 KB) - BibTeX
- EndNote
Organic aerosol (OA) particles are ubiquitous and can represent 20 %–90 % of the mass fraction of the submicron aerosol (particles ≤1 µm in diameter) in the atmosphere. The significance of OA has long been established, influencing air quality, human health, cloud formation processes, and the radiative budget, on a regional and global scale, and thus climate (Hallquist et al., 2009; Jimenez et al., 2009; Seinfeld and Pandis, 2016; Stocker et al., 2013; Knopf et al., 2018; Abbatt et al., 2019; Shiraiwa et al., 2017b; Kanakidou et al., 2005; Pachauri et al., 2014; Pöschl and Shiraiwa, 2015). Characterizing these impacts crucially depends on our ability to determine and quantify aerosol sources and strengths (Bai et al., 2013; Robinson et al., 2006; McFiggans et al., 2019; Hopke, 2016) and to understand the physical and chemical transformation of aerosol particles during atmospheric transport by multiphase chemical processes (George and Abbatt, 2010; Rudich et al., 2007; Laskin et al., 2015; Springmann et al., 2009; Kaiser et al., 2011; Ervens et al., 2011; Zhou et al., 2019; Moise et al., 2015). Gas-to-particle, also termed heterogeneous, reactions can involve organic components in the condensed-phase and gas-phase oxidants such as O3, NO3, and OH. These reactions, which can include multiple phases, change the physicochemical properties of particles including composition, density, and hygroscopicity, thereby defining their chemical lifetime, optical properties, and ice nucleating ability (Jimenez et al., 2009; Kroll et al., 2015; Katrib et al., 2005b; Knopf et al., 2018; Slade et al., 2017; Robinson et al., 2007; Shiraiwa et al., 2012, 2017a; Moise et al., 2015; Murray et al., 2010; Wang et al., 2012).
It is now well established that OA can exhibit amorphous phase states (Mikhailov et al., 2009; Virtanen et al., 2010; Koop et al., 2011; Reid et al., 2018; Renbaum-Wolff et al., 2013; Kidd et al., 2014). Depending on the viscosity and microstructure, the amorphous phases can be classified as glasses, rubbers, gels, or ultra-viscous liquids (Mikhailov et al., 2009; Riemer et al., 2019). The glass transition temperature, Tg, is a characteristic parameter to describe the viscosity of a liquid on the order of 1012 Pa s (Koop et al., 2011; Angell, 1995; Zobrist et al., 2011; Dette and Koop, 2015; Zhang et al., 2019). At this temperature, the molecular motion of the species is so slow that it can be considered a solid. The phase state of OA can be modulated by particle composition and environmental conditions such as relative humidity (RH) and temperature (Koop et al., 2011; Zobrist et al., 2008; Shiraiwa et al., 2017a; Petters et al., 2019). Particle viscosity will influence the diffusion of atmospheric oxidants and other small gas molecules (e.g., O3, OH, NO3, H2O) entering the organic matrix (Price et al., 2015; Zobrist et al., 2011; Slade et al., 2017; Davies and Wilson, 2016; Moridnejad and Preston, 2016) as well as the transport and mixing of the condensed-phase organic species (Rothfuss and Petters, 2017; Marsh et al., 2018; Lienhard et al., 2015; Abramson et al., 2013; Chenyakin et al., 2017; Kiland et al., 2019; Shiraiwa and Seinfeld, 2012; Renbaum-Wolff et al., 2013). Therefore, it can be expected that the particle phase state will significantly affect the rate of multiphase chemical kinetics (Slade and Knopf, 2014; Kolesar et al., 2014; Knopf et al., 2005; Katrib et al., 2005a; Pöschl and Shiraiwa, 2015; Davies and Wilson, 2015; Gaston et al., 2014; Zhang et al., 2018; Houle et al., 2018b). The heterogeneous reaction kinetics are often expressed by the reactive uptake coefficient (γ), which represents the fraction of gas collisions with a substrate surface that yield uptake or reaction (Pöschl et al., 2007; Schwartz, 1986).
As has been demonstrated for heterogeneous ozonolysis reactions, the composition of the condensed phase can alter the phase state, thereby significantly altering the reactive uptake kinetics (Knopf et al., 2005; Hearn et al., 2005; de Gouw and Lovejoy, 1998; Ziemann, 2005). In general, the solid condensed phase showed significantly lower γ values compared to the ozonolysis of the liquid phase. Recent experimental studies focused on how relative humidity (RH) influences the reactive uptake of gas oxidants via its impact on the phase state of the organic species (Berkemeier et al., 2016; Steimer et al., 2015; Shiraiwa et al., 2011; Slade and Knopf, 2014; Li et al., 2018; Davies and Wilson, 2015; Hu et al., 2016; Marshall et al., 2018; Pajunoja et al., 2016). The heterogeneous oxidation of a typical component of biomass burning aerosol (BBA) particles, levoglucosan (LEV) by OH yielded γ values in the range from 0.008 to 1 with implications for the lifetime of LEV ranging from weeks at dry conditions (Slade and Knopf, 2013, 2014; Kessler et al., 2010; Arangio et al., 2015) to a couple of days when LEV is in a more liquid-like state in response to ambient RH (Yang et al., 2013; Bai et al., 2013; Slade and Knopf, 2014). The general conclusion is that at lower RH, the reactive uptake can be dominated by surface reactions when the condensed phase is in a solid state, whereas at higher RH, the condensed phase can be semisolid or liquid and the oxidation process can commence at the surface and in the bulk. For the latter scenario, the gaseous oxidants can access greater depths of the condensed phase, and the oxidized organic species at the surface can be readily replenished by unreacted molecules from the bulk (Arangio et al., 2015; Slade and Knopf, 2014). Davies and Wilson (2015) investigated how the viscosity change in citric acid, due to changes in water content, governs the reactive uptake of OH radicals. They observed that the depletion of citric acid and the formation of reaction products are confined near the aerosol–gas interface on the order of 8 nm at 20 % RH, and the reaction depth increases to ∼50 nm at 50 % RH. Recently, Li et al. (2018) observed that the heterogeneous aging of secondary organic aerosol (SOA) by OH radicals at 89 % RH and 25 % RH resulted in ∼60 % and 20 % loss of particle mass, respectively. The authors concluded that this difference in particle mass degradation is attributed to a larger OH uptake coefficient and/or larger fragmentation probability at higher RH.
The temperature in the troposphere ranges approximately from 200 to 300 K (Wallace and Hobbs, 2006), with subsequent impact on the OA phase state (Shiraiwa et al., 2017a; Koop et al., 2011) and multiphase reaction kinetics. However, only a few laboratory studies investigated the temperature dependence of heterogeneous oxidation reactions while considering the phase transition of organic substrates and aerosol particles (de Gouw and Lovejoy, 1998; Edebeli et al., 2019; Gross et al., 2009; Knopf et al., 2005; Moise and Rudich, 2002, 2000; Slade et al., 2017; Moise et al., 2002). Moise and Rudich (2002) demonstrated that the uptake of ozone by oleic and linoleic acid is a strong function of temperature, where γ decreases by about an order of magnitude with decreasing temperature when both substrates transformed from a liquid to a solid state. Similarly, Gross et al. (2009) observed a decrease of 70 % to 90 % in γ of NO3, as oleic acid, diethyl sebacate, and conjugated linoleic acid substrates solidified as the temperature decreased from 302 to 263 K. The authors suggested that the net liquid phase reaction involves both a surface reaction and a bulk reaction, whereas solidification of the substrate greatly minimizes the significance of any bulk reactions. This is in line with results of a kinetic flux model applied to NO3 exposure studies of solid LEV and abietic acid substrates, further indicating that under shorter timescales reactive uptake was dominated by surface reaction, whereas for timescales greater than ∼100 s, even for a solid organic substrate, bulk processes can impact the overall reactive uptake kinetics (Shiraiwa et al., 2012) Very recently, Edebeli et al. (2019) investigated the temperature dependence of bromide oxidation by ozone in a citric acid / bromide mixture and observed that γ decreases from at 289 K to at 245 K. Their analysis indicated that the humidity-driven acceleration in uptake reactivity decreased due to the increased viscosities of the citric acid / bromide mixture and decreased diffusivity of ozone as the temperature was lowered. The effect of temperature on uptake kinetics via its impact on the condensed-phase state has also been highlighted in a recent modeling study (Mu et al., 2018), which showed that low-temperature conditions can substantially increase the lifetime of polycyclic aromatic hydrocarbons (PAHs) against O3 and enhance their dispersion through both the planetary boundary layer and the free troposphere. Temperature also impacts the other processes involved in multiphase kinetics (Schwartz, 1986; Pöschl et al., 2007) including the collision flux of gas-phase species, the desorption rate, and surface and bulk reaction rates, both typically expressed by an Arrhenius factor (Laidler et al., 1940; Pöschl et al., 2007; Baetzold and Somorjai, 1976). Clearly, the temperature dependency of the reaction kinetics and the role of the condensed-phase state pose a challenge for detangling the underlying physicochemical processes governing multiphase chemical kinetics of OA under typical tropospheric conditions.
To add to our understanding of multiphase chemical kinetics at low temperatures, we determined the reactive uptake of O3, NO3, and OH by OA surrogates for temperatures ranging from 213 to 293 K under dry conditions. We employed a chemical ionization mass spectrometer (CIMS) coupled to a coated-wall flow-tube reactor. As OA proxies, we applied substrates of canola oil (CA), levoglucosan (LEV), a levoglucosan / xylitol mixture (LEV / XYL), glucose (GLU), and a glucose/1,2,6-hexanetriol mixture (GLU / HEX). CA is a mixture of multiple saturated and unsaturated fatty acids, dominated by unsaturated oleic and linoleic acid however, and serves as an OA surrogate for both marine and terrestrial organic aerosol including anthropogenic emissions like cooking (Kawamura et al., 2003; Schauer et al., 2002; Limbeck and Puxbaum, 1999; Liu et al., 2017; Rogge et al., 1991). LEV serves as a surrogate for biomass burning aerosol (BBA) including natural sources such as forest fires and anthropogenic sources such as heating and cooking BBA (Schauer et al., 2001; Iinuma et al., 2007). GLU can serve as a tracer to characterize and apportion primary biogenic organic aerosols (PBOAs) (Zhu et al., 2015; Samaké et al., 2019). XYL and HEX are used in compound mixtures to modify the glass transition temperature and thus condensed-phase viscosity. O3 and OH radicals reflect typical gas oxidants present in photochemically active regions and during long-range transport. NO3 radicals reflect an effective oxidant participating in the nighttime chemistry of typically polluted regions (Finlayson-Pitts and Pitts, 1999; Brown et al., 2006). Some of the examined substrates undergo a phase transition from liquid to solid in the probed temperature regime with subsequent consequences for the heterogeneous uptake kinetics. The substrate's phase state was qualitatively verified by conducting film poke-flow experiments. The results of our reactive uptake experiments emphasize the importance of the temperature-induced phase changes of the OA surrogates when describing the chemical degradation of OA during atmospheric transport.
2.1 Apparatus
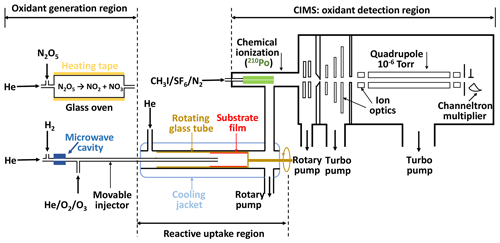
The experimental system is based on our previous setups (Slade and Knopf, 2013; Knopf et al., 2005, 2011) and includes a temperature-controlled coated-wall flow reactor and a custom-built CIMS, as shown in Fig. 1. It consists of three parts: gas-phase oxidant generation, multiphase chemical reaction, and oxidant detection. The gas-phase oxidant (O3, NO3, or OH) enters the coated-wall flow reactor via a movable injector, where it can react with the organic substrate film coating on the inner wall of a rotating tube. The changes in oxidant concentration are measured by CIMS via soft ionization in the chemical ionization region.
The uptake measurements are conducted in a temperature range of 213 to 313 K. The axial temperature variation in the flow reactor is smaller than 1 K for all our experimental conditions, which is determined with a thermocouple that is fixed at the tip of the injector, as discussed in the Supplement Sect. S1. The rotating tube fits snugly inside the flow tube that is enclosed by a cooling jacket for temperature control. The rotating speed of the substrate tube is set to ∼5–10 rpm to keep the liquid film evenly distributed on its inner surface. The pressure in flow reactor ranges from 2 to 5 hPa depending on the applied oxidant gases.
For OH radical uptake experiments, an additional rotatory pump is directly connected to the flow reactor. The pump is used to lower the flow reactor pressure to < 2.5 hPa, thus minimizing gas transport limitation due to diffusion (Knopf et al., 2015; Zasypkin et al., 1997) while simultaneously maintaining a high flow rate. Two sizes of rotating glass cylinders with diameters of 1.75 and 1.2 cm are used in these uptake experiments. The latter one is designed specifically for OH heterogeneous reactions to avoid limitation of gas transport by diffusion. For O3 and NO3 uptake experiments, gas transport limitations due to diffusion can be neglected under applied flow conditions because of a slower reactive uptake.
The pseudo-first-order loss of the oxidant species to the organic substrate is determined by monitoring the loss of the gaseous oxidants as the injector is pulled back in 1 or 2 cm increments until reaching 10 cm. The flow rate of gas oxidants in the movable injector ranges from 2 to 100 cm3 min−1 STP (standard temperature and pressure). The flow rate of the carrier gas He in the flow reactor ranges from 30 to 900 cm3 min−1 STP. As a result, the residence time varies 2 orders of magnitude in these experiments, ranging from ∼2 ms for OH uptake to 100 ms for O3 uptake. The Reynolds number (Re) for all experiments is below 20, indicating laminar flow conditions. Care has been taken to ensure a carrier-to-injector gas velocity ratio of > 1.33, in order to avoid the disruption of the gas flow by a fast gas flow exiting the injector, as pointed out by Davis (2008). This condition is also a necessity to accurately account for the gas flow entrance effect, which is important for fast-uptake kinetics, as further discussed in the Appendix. The γ value at each temperature reported in this study is derived from at least six reactive uptakes, with a freshly prepared organic substrate employed for each.
2.2 Oxidant formation, detection, and flow conditions
A carbon filter (Supelco Supelcarb HC hydrocarbon trap) and a Drierite cold trap cooled with liquid nitrogen or an ethanol / dry ice mixture are used to purify ultra-high-purity (UHP) gases of N2, He, and O2. O3 is generated by introducing a flow of O2 through a UV source (Jelight, model no. 600) prior to the injector. The flow rate of the O2∕O3 mixture ranged between 2 and 7 cm3 min−1 (STP). A carrier He gas flow of 30–85 cm3 min−1 (STP) enters the flow reactor, mixes with the injector O2∕O3 gas flow, and results in a laminar flow with Re < 3. O3 is detected as after charge transfer reaction with . is generated by passing a minor amount of SF6 in N2(g) through a 210Po source. The O3 concentrations ranged between 1.5×1011 and 2.1×1012 molec. cm−3, reflecting typical atmospheric concentrations (Wallace and Hobbs, 2006; Finlayson-Pitts and Pitts, 1999).
NO3 is generated by thermal dissociation of N2O5 gas at 433 K in a glass oven prior to the injector, as previously described (Knopf et al., 2006, 2011). N2O5 is generated via reaction of NO2 and O3 and stored as pure N2O5 crystals in a glass container at 193 K. A gas flow of N2O5 in He of about 12–18 cm3 min−1 STP is further diluted by 100–120 cm3 min−1 (STP) He(g) flow before entering the injector. The flow reactor carrier gas is composed of He and O2 at ∼500 and ∼100 cm3 min−1 (STP), respectively. This results in laminar flow conditions (Re < 10). NO3 is detected as after chemical ionization by I−. NO3 concentrations are obtained via titration of a known amount of NO, resulting in 8×109 to 7×1011 molec. cm−3, representing typical atmospheric NO3 nighttime concentrations (Finlayson-Pitts and Pitts, 1999; Brown et al., 2006).
OH radicals are produced following previously established methods (Bertram et al., 2001; Slade and Knopf, 2014) via the reaction of H atoms with O2. A 2.45 GHz Evenson microwave cavity powered by a microwave generator is utilized to maintain an H plasma. The H atoms are formed by flowing a mixture of H2(g) (1–2 cm3 min−1, STP) and He(g) (40–80 cm3 min−1, STP) through a 1∕4 in. o.d. (outer diameter) Pyrex tube that runs through the center of the microwave cavity. The generated H atoms then pass through a 1∕8 in. o.d. Pyrex tube directed down the center of a 1∕4 in. o.d. Pyrex injector where OH production occurs with H radicals reacting with O2(g) at 2–22 cm3 min−1 (STP). Complete reaction to OH is ensured by monitoring the formation of OH− via charge transfer with in the CIMS. At colder flow reactor temperatures, the usable injector length is shortened to avoid artifacts in OH concentration due to temperature gradients in the injector tube which can impact OH formation (Atkinson et al., 2004). A He gas flow of 700–900 cm3 min−1 (STP) enters the flow reactor and further mixes with the injector flow, yielding a laminar gas flow with Re < 20. Employed OH concentrations ranged between 5×107 and 1×109 molec. cm−3, which are higher than typical background OH concentrations of 106 molec. cm−3 (Finlayson-Pitts and Pitts, 1999).
2.3 Substrate film preparation and characterization
The film substrate preparation method when using a coated-wall flow reactor has been discussed in detail in previous studies (Knopf et al., 2011; Slade and Knopf, 2013). Canola oil is liquid and thus can be directly applied to the inner surface of the rotating tube. The other organic substrates, i.e., LEV, LEV / XYL mixture, GLU, and GLU / HEX mixture, are first dissolved in water, and then 1–2 mL of the aqueous solution is evenly distributed inside the rotating glass tube. The concentration of the LEV solution is 5 % (w∕w) due to its relatively lower solubility, and all other solutions are 10 % (w∕w). The organic mass ratios of the LEV / XYL and GLU / HEX films are 1:1 and 4:1, respectively. As outlined further below, these mass ratios were chosen to set the expected glass transition temperature within the examined temperature range. During the entire process, a dry He or N2 purging gas flow is applied to avoid contamination by room air. The glass tube rotates in the flow reactor until a smooth coating is established. To dry the substrate, the substrate is exposed to rough vacuum conditions (1–2 hPa) resulting in the evaporation of water. Surface solidification of single-component saccharide films may result in trapping of condensed-phase water and thus impact the film composition and its viscosity. The remaining water content for all substrate films after the drying process was determined to be 13 %–16 % (w∕w) by measuring the mass change of the organic substrate films before and after the drying process with an ultra-microbalance (Mettler Toledo XP2U), as detailed in Sect. S2. The thickness of the applied organic film is estimated to be around 50–100 µm. We assume a smooth surface morphology and use the geometric surface area of the film to derive γ.
The phase state of the applied organic substrates at different temperatures can be qualitatively verified by using the poking experiments outlined below. The “poke-flow” technique has been applied to quantitatively estimate the viscosity of amorphous organic particles (Murray et al., 2012) including secondary organic material (SOM) produced by α-pinene ozonolysis (Renbaum-Wolff et al., 2013). A similar setup is used here to qualitatively investigate the phase state of applied amorphous substrates at different temperatures ranging from 213 to 313 K. A temperature-controlled cooling stage (Linkam BSC 196) is coupled to an optical microscope (Olympus BX51) (Fig. 2). Images of the film substrate are recorded at 230 magnification and the depth of field of the 10X objective is 15.9 µm. The organic film substrate, generated from a volume of 2 µL liquid applied to a glass slide, is first placed into the flow reactor, undergoing the same preparation method as the substrate films employed for reactive uptake experiments. This results in a film with a thickness of about 50–100 µm. The substrate film is then moved into the poke-flow experiment. In the cooling stage, the organic substrate film is sealed against room air and resides in an atmosphere of dry N2 at positive pressure during the entire poking process. After poking with a needle, the phase states and flow characteristics of the organic substrate films at different temperatures are determined under the microscope as a function of time. Images are recorded with the film surface in focus to monitor the flow of the organic substrate and to probe film viscosity. Under the applied resolution, all film substrates appeared to be smooth and transparent. The calibration of the cooling stage was performed via measurements of the melting points of octane (216.35 K), decane (243.5 K), and water (273.15 K). Before each experiment, the temperature was verified by measuring the melting temperature of three 2 µL water droplets (273.15 K). The difference from the expected melting temperature difference is always smaller than 1 K. We measured Tg with at least five independently prepared substrate films.
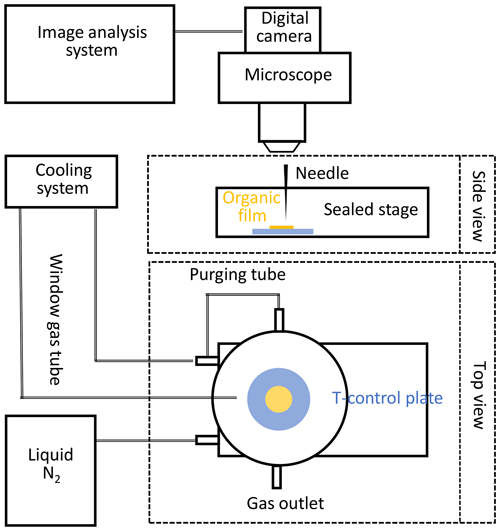
Figure 2Schematic of the experimental poke-flow setup. This includes a temperature-controlled Linkam cooling stage coupled to a microscope equipped with a digital camera and an image analysis system.
2.4 Chemicals
Listed below are the chemicals we used in our study and corresponding purities and manufactures. N2 (ultra-high purity, UHP), O2 (UHP), H2 (UHP), and He (UHP) were purchased from Airgas East. SF6 (99.998 %) was acquired from Praxair. NO2 (99.5 %) was purchased from Mathenson. 1,6-Anhydro-β-D-glucopyranose (99 %) was purchased from Acros Organics. Glucose (99 %) and xylitol (99 %) were acquired from Alfa Aesar. 1,2,6-Hexanetriol (96 %) and iodomethane (99 %) were purchased from Sigma-Aldrich. Purity of canola oil was not determined. Millipore water (resistivity > 18.2 MΩ cm) was applied to prepare aqueous solutions for generation of organic substrates.
3.1 Characterization of substrate phase state
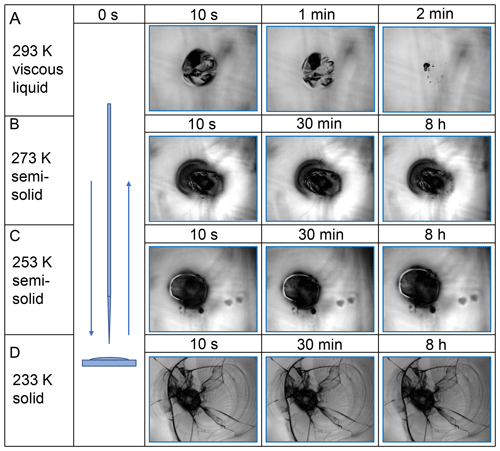
Images of the film surfaces in Fig. 3 show the flow characteristics and the morphologies of a GLU / HEX substrate mixture when subject to poking by a needle. In the experiment at T=293 K (Fig. 3a), the film surface is deformed after being poked, leaving a black dent. The area around the dent reflects the smooth morphology of the film substrate before poking it. The slightly darker shades within the imaged area do not represent any morphology features but the unfocused scratches from the silver substrate holder beneath the film. The film flowed at an observable rate to restore a smooth surface, minimizing the surface energy of the system (Fig. 3a). At 273 K, the same deformed film did not show observable changes within 30 min (Fig. 3b). Only after 8 h can minor changes in film morphology be identified, clearly demonstrating greater substrate viscosity at this temperature compared to 293 K. At 253 K, the notch by poking on the surface maintains its shape for 8 h, indicative of a semisolid phase state (Fig. 3c). At T=233 K, which is below the predicted Tg=248 K, the surface shattered when poked with a needle (Fig. 3d). Furthermore, over the experimental observation time of 8 h, no restorative flow was observed at 233 K. The fragments have clear glass-like cracks, and no smoothing of the edges was observed over the course of the experiment. Based on our poke-flow experiments as shown in Figs. S2–S7 in the Supplement, the applied GLU and LEV substrates remain in a solid or semisolid phase state within the temperature range of 213 to 313 K. However, the mixtures of GLU / HEX and LEV / XYL exist as liquids at 293 K and experience a glass phase transition with decreasing temperature.
Table 1Estimated Tg of the applied substrate films. is the measured Tg using the poke-flow technique. is the literature-reported Tg. is predicted Tg for mixtures with the Gordon–Taylor equation using and kGT. kGT is the solute-specific constant in the Gordon–Taylor equation. D is fragility.
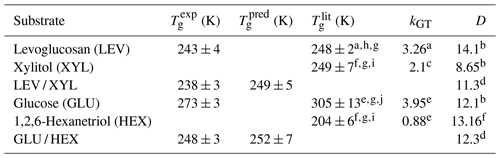
a Lienhard et al. (2012). b DeRieux et al. (2018). c Elamin et al. (2012). d Interpolated values based on mass fraction. e Zobrist et al. (2008). f Nakanishi et al. (2011). g Rothfuss (2019). h Tombari and Johari (2015). i Dorfmüller et al. (1979). j Diogo and Ramos (2008).
By monitoring the substrate surface morphology, we can estimate Tg of the applied substrates as the highest temperature when shattering occurs. Viscosity greater than 1012 Pa s indicates the presence of a glassy phase. Thus, we ascribe the observed shattering of the substrate film a viscosity of 1012 Pa s, although the exact value cannot be assessed with the poke-flow technique. All images of the poke-flow experiment are documented in Figs. S2–S7. Table 1 gives the estimated values of applied substrates compared to literature and predicted values. for substrate mixtures is derived from the Gordon–Taylor equation (Gordon and Taylor, 2007) assuming literature Tg values and no residual water present. The uncertainties in values are derived by Gaussian error propagation. Except for the GLU substrate film, we achieve agreement or close agreement with either or . Since Tg determination depends on cooling or drying rates, we do not expect agreement with literature values or predicted values. In addition, if 10 %–16 % residual water is considered while using the Gordon–Taylor equation, would be roughly 30 K lower than , assuming the residual water is homogeneously distributed in the film. This discrepancy is very likely due to our substrate film preparation process where under slow drying (evaporation) the outermost layers of the film contain less water than the deeper layers. Thus, the substrate surface represents the experimental conditions more closely. Furthermore, the microscope focus in our poke-flow experiments is on the substrate surface, thereby monitoring the substrate morphology that is governed by the film viscosity most closely representing the desired conditions.
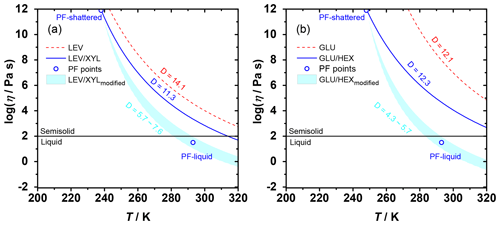
Figure 4The Angell plot of viscosity as a function of temperature for LEV, LEV / XYL, GLU, and GLU / HEX substrates. The lines represent predicted viscosities as a function of and applied D values (see Table 1). PF-shattered and PF-liquid (blue circles) indicate the conditions for which the poke-flow (PF) experiment detected a solid (glassy) and liquid phase state of the substrate, respectively. The shaded areas represent predicted viscosities by using the VTF equation with modified D values as indicated in the panels based on the estimated viscosities derived from the poke-flow experiment. The horizontal black line at η=102 Pa s indicates the threshold of liquid and semisolid phase states.
The temperature dependence of the substrate viscosity can be predicted by using the modified Vogel–Tammann–Fulcher (VTF) equation (Angell, 1991):
where T0 is the Vogel temperature and T is the ambient temperature. The fragility parameter, D, is defined in terms of the deviation of the temperature dependence of the viscosity from the simple Arrhenius behavior. Assuming T=Tg, η=1012 Pa s, T0 can be represented by Tg (DeRieux et al., 2018):
Therefore, the temperature dependence of substrate viscosity can be predicted using our measured as illustrated in Fig. 4. For our calculations, we use literature D values for pure sugars and a mass-weighted interpolation of D values for the mixtures as shown in Table 1. In Fig. 4a, LEV maintains a relatively higher viscosity compared to the LEV / XYL mixture throughout the studied temperature. The poke-flow experiments indicate the presence of a liquid phase at 293 K and solid phase at 238 K. In contrast to our poke-flow experiments, Fig. 4a suggests that the LEV / XYL mixture does not show a liquid phase in the examined temperature regime. Capturing this phase transition with the modified VTF equation (Angell, 1991) can only be achieved when using lower D values of 5.7–7.6 (compared to the interpolated D value of the LEV / XYL mixture), a reasonable assumption when considering the presence of residual water in the substrate. The addition of water increases the steepness of the glass transition and decreases D values by potentially reducing the thermal energy necessary to promote the cooperative chain motions (Angell, 2002; Borde et al., 2002). Furthermore, a study of the trehalose–water system corroborates that the presence of water lowers D values to 3.32–4.85 as a lower limit (Elias and Elias, 1999). For GLU and the GLU / HEX mixture shown in Fig. 4b, adding HEX to GLU greatly lowers the Tg of the mixture and thus decreases its viscosity. Also, in this case, the predicted substrate viscosity of GLU / HEX disagrees with our observations when interpolating the D values of the pure compounds. A D value between 4.3 and 5.7 better represents the observed phase transition of the GLU / HEX mixture.
3.2 Reactive uptake kinetics
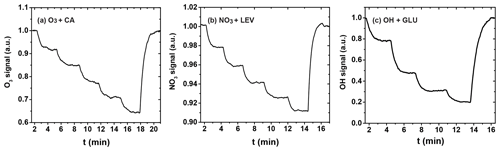
The uptake coefficient is determined experimentally from the loss of the gas-phase oxidant to the organic substrate as the substrate area or corresponding reaction time is changed. Figure 5 shows three exemplary uptakes of O3 by the canola oil (CA) film, NO3 by LEV film, and OH radical by the GLU film, indicating the stepwise irreversible removal of the gas oxidants. Taking O3 uptake as an example, the injector is pulled back in 2 cm increments until reaching 10 cm and is then pushed back to its original position (0 cm), with normalized O3 signals recovering to unity.
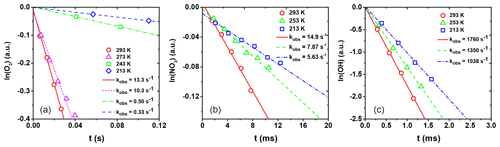
Figure 6Natural logarithm of the change in gas-phase oxidant signal as a function of reaction time for (a) O3 uptake by CA, (b) NO3 uptake by the LEV / XYL mixture, and (c) OH uptake by the GLU / HEX mixture. Open circles, triangles, squares, and diamonds correspond to uptake measurements at different temperatures. Lines represent the corresponding linear fits to the data and corresponding slopes. kobs values are given in the legend.
From these data, the observed first-order wall loss rate, kobs, is determined as the slope of the change in the natural logarithm of the oxidant signal as a function of reaction time, i.e., the residence time of the oxidants in the flow reactor (Knopf et al., 2011; Slade and Knopf, 2013). Figure 6 shows exemplary kobs derived for uptakes of O3, NO3, and OH for various temperatures. kobs is obtained from the slope of the linear fit to the data. The good linear regression indicates that the reported uncertainties for γ are likely due to the variability of organic substrates and uncertainty in the diffusion coefficient. In the case of O3 uptake (Fig. 6a), we can identify two different regimes of kobs, where the linear regression with a larger slope at higher temperatures indicates greater reactivity. As discussed in detail further below, the large difference in kobs between these two temperature regimes coincides with the CA substrates being in a liquid and solid phase state. For the cases of NO3 and OH (Fig. 6b and c), the gradual change of kobs coincides with a phase transition for both substrates from a highly viscous liquid to a semisolid and solid (glassy) phase.
The change in concentration of oxidant X along the flow tube due to reactive uptake can be expressed using the effective uptake coefficient
Following the Knopf–Pöschl–Shiraiwa (KPS) method (Knopf et al., 2015), actual γ can be derived as
where Dtube is the diameter of the coated-wall tube, and ωX (X= O3, NO3 or OH radical) is the mean molecular velocity of the respective gas-phase oxidant. is the effective Sherwood number which represents an effective dimensionless mass-transfer coefficient to account for changes in the radial concentration profile of the entry region (Knopf et al., 2015; Davis, 2008), and KnX is the Knudsen number that characterizes the flow regime (Wutz, 1989; Fuchs and Sutugin, 1971). The Sherwood number departs from under conditions of fast flows and short tubes. The KPS method is advantageous over the correction approach by Brown (1978) since it accounts for entrance effects that can result in the overestimation of reactive uptake coefficients as outlined by Davis (2008) and discussed in more detail in the Appendix. The Cooney–Kim–Davis (CKD) method (Cooney et al., 1974) also accounts for the flow entrance effects as discussed in Murphy and Fahey (1987). This is crucial for fast uptakes involving the OH radical, however, less so for the uptakes involving O3 and NO3 radicals. The uncertainty in derived γ values represents the greater value of either a 20 % uncertainty in the diffusion coefficient or variation in measurements expressed as ±1σ.
The gas-phase diffusion coefficient of O3 in He () is taken as 394 Torr cm2 s−1 at 298 K (Moise and Rudich, 2000). Diffusion coefficients of NO3 in He and O2 are taken as 345 and 80 Torr cm2 s−1 at 273 K, respectively (Rudich et al., 1996). The method introduced by Fuller et al. (1966) was utilized for O3 and NO3 to derive the diffusion coefficients at other temperatures. The diffusion coefficients of OH in He and O2 gas (DOH−He and ) for different temperatures are theoretically calculated based on a method reported by Mason and Monchick (1962). A reference value of DOH−He measured at room temperature is 662±33 Torr cm2 s−1 (Ivanov et al., 2007; Liu et al., 2009). To calculate the diffusion coefficient of an oxidant (DX) in a mixture of He and O2, we applied the following equation with PHe and representing pressures derived from experimental flow rates and pressure measurements (Hanson and Ravishankara, 1991):
The pressure in the flow reactor is maintained at less than 2.5 hPa to avoid transport limitations by diffusion of OH radicals that undergo fast reactive uptake kinetics. Diffusion limitation can be estimated by using the additivity formula for kinetic resistances as (Gershenzon et al., 1995)
where kobs (s−1) is the observed wall loss rate of heterogeneous uptake, and kk and kd represent its kinetic and diffusion limits, respectively. R is the radius of the flow tube. Gershenzon et al. (1995) proposed that kk∕kd should be < 3–5 to obtain an accurate γ value. Some of the highest temperature OH uptake experiments involving liquid canola oil were conducted under diffusion limitation with –30. However, for all the remaining experiments and, thus, are not diffusion limited.
As outlined in Sect. S4, for semisolid and solid substrate films, the fraction of the unoxidized reaction sites is always larger than 90 % due to short reaction time and low concentrations of gas oxidants (Bertram et al., 2001), implying no significant surface saturation effect on γ. In other words, during the typical duration of a reactive uptake experiment, the oxidant exposure does not lead to complete oxidation of the substrate surface.
3.3 Temperature-modulated reactive O3 uptake
Figure 7 shows γ of O3 reacting with canola oil as a function of temperature. The reactive uptake is determined under dry conditions in the presence of O2. Both Brown and KPS methods were used to derive γ (Brown, 1978; Knopf et al., 2015). Both methods yield the same results due to the slow uptake kinetics as further discussed in the Appendix. Around 90 % of canola oil is made up of oleic acid, linoleic acid, and α-linolenic acid (Ghazani and Marangoni, 2013), and it solidifies readily around its melting point (de Gouw and Lovejoy, 1998). γ decreases sharply by a factor of ∼18 from (5.65±0.89) to (3.23±0.74) as the temperature decreases from 267 to 258 K, a temperature range in which the canola oil experiences a phase transition from liquid to solid (Fasina et al., 2008). In this temperature regime, the bulk diffusion coefficients of both ozone and canola oil are expected to decrease by several orders of magnitude due to the transition from a viscous liquid to a solid (Koop et al., 2011). Our O3 reactive uptake coefficients agree with previous literature data by de Gouw and Lovejoy (1998) and extend those to lower temperatures. A study by Berkemeier et al. (2016) showed that the uptake of O3 by shikimic acid is at low RH conditions and increases by a factor of ∼16 at higher RH due to a decrease in viscosity as a result of a RH-induced phase transition, similar to our observations. Our results are consistent with previous studies (Shiraiwa et al., 2009, 2010; Steimer et al., 2015), which showed that the O3 uptake is slower and restricted to near the particle surface if the organic is in a solid phase, while the uptake is dominated by bulk reaction if the organic is in a liquid phase.
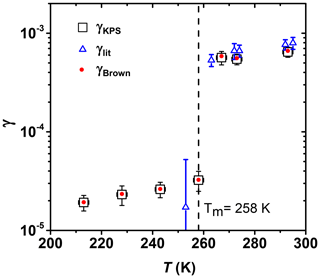
Figure 7Reactive uptake coefficients of O3 by canola oil as a function of temperature. Squares and red circles represent γ values derived using the KPS and Brown methods, respectively. See text for more details. γlit represents values reported by de Gouw et al. (1998).
In the low-temperature regime, from 213 to 258 K, γ only increases by about a factor of 1.7 (Fig. 6). If we consider the gas-phase reaction kinetics of O3 with an unsaturated bond having an activation energy of 15 kJ mol−1 (Atkinson et al., 2006), an increase in the reaction rate by a factor of 4.4 would be expected over a temperature of 45 K. This less-than-expected temperature dependency of γ may be due to the combined temperature effects on both the underlying reaction kinetics and the desorption lifetime (Pöschl et al., 2007). As the temperature decreases and reactivity decreases, the desorption lifetime increases, potentially resulting in a compensating effect on the overall uptake kinetics. In the temperature regime above the phase transition, between 267 and 293 K, γ is significantly larger than when the canola oil substrate is solid, likely due to greater reaction rates and greater O3 and condensed-phase diffusion coefficients.
3.4 Temperature-modulated reactive NO3 uptake
The uptake coefficient of NO3 by levoglucosan (LEV) decreases from (4.2±0.6) to (2.8±0.3) as the temperature decreases from 293 to 213 K, thus displaying only a slight change in γ within the experimental temperature range (Fig. 8a). Based on our poke-flow experiment, LEV substrates maintained a semisolid or solid phase state for all examined temperatures. The slight increase in γ with temperature may be due to the combined effects of changes in substrate viscosity (see Fig. 4), the counteracting effect of the temperature dependence of the reaction rate (Atkinson et al., 2006), and the desorption lifetime (Pöschl et al., 2007). Assessment of these various impacts on the observed uptake kinetics necessitates an in-depth analysis, e.g., by application of kinetic flux modeling (Shiraiwa et al., 2012; Arangio et al., 2015). Note the γ of NO3 by LEV in this experiment is smaller than the value of (1.3±0.9) determined in our previous study at 298 K, although the data agree within uncertainties (Knopf et al., 2011). A possible explanation for the lower γ value in this study is that the substrates have undergone longer drying to remove residual water. Presence of water would render the film less viscous, thereby increasing reactivity.
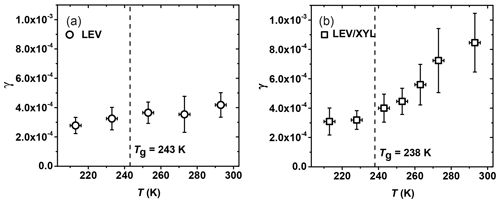
Figure 8Reactive uptake coefficients, γ, of NO3 reacting with (a) levoglucosan (LEV) and (b) 1:1 by mass LEV and xylitol (XYL) mixture as a function of temperature. The dashed line represents the glass transition temperature (Tg) measured in the poke-flow experiment.
Table 2Comparison of uptake coefficients of NO3 on liquid and solid substrates of saturated and unsaturated organics.
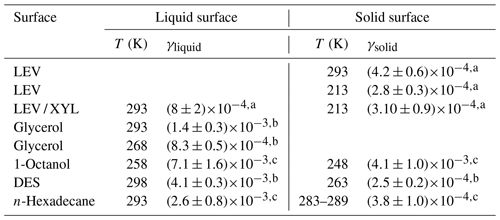
a This study. b Gross et al. (2009). c Moise et al. (2002).
For the mixture of LEV / XYL (Fig. 8b), γ at 293 K is , about a factor of 2 larger than for pure LEV (see Table 2). As the temperature decreases, γ reaches a value of at 213 K, similar to the γ value derived for solid LEV (Fig. 8a). Our poke-flow experiment yielded Tg=238 K for the applied LEV / XYL film. The largest change of γ is observed above the expected Tg (Fig. 8b). Therefore, the significant change in NO3 uptake reactivity in the investigated temperature range can be attributed to the transition of a solid or highly viscous substrate film to a liquid substrate film. As such, the underlying reaction mechanism changes; i.e., at higher temperatures, the kinetic uptake is likely governed by surface and bulk reactions and at lower temperatures only surface reaction dominates. As shown in Shiraiwa et al. (2012), for highly viscous and solid LEV films, the transport of bulk LEV towards the interface is strongly limited, slowing the reactive uptake kinetics. At higher temperatures, with decreasing viscosity of LEV, the diffusivity of LEV and NO3 increases, likely facilitating transport and thus reaction.
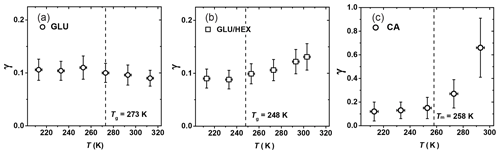
Figure 9Reactive uptake coefficients, γ, of OH radicals reacting with (a) glucose (GLU), (b) 1:4 by mass glucose and 1,2,6-hexanetriol (GLU / HEX) mixture, and (c) canola oil (CA) as a function of temperature. Tg is the glass transition temperature determined in the poke-flow experiment.
Gross et al. (2009) reported that γ of NO3 by liquid glycerol (GLY) is (14±3) at 293 K and decreases to at 268 K, representing a decrease of 41 % in γ over 25 K. The Tg of glycerol is 193 K, and the viscosity decreases from 20 Pa s at 268 K to 1.32 Pa s at 293 K (Schröter and Donth, 2000). For the same temperature difference of 25 K, γ for the viscous liquid LEV / XYL substrate decreases by about 24 %. The viscosity of LEV / XYL film is around 101 to 102 Pa s based on our poke-flow experiments and viscosity prediction as outlined in Sect. 3.1. We hypothesize that the lesser change in γ with temperature for the LEV / XYL substrate compared to a GLY substrate (Gross et al., 2009) may be due to the viscosity difference between both substrates. Moise et al. (2002) studied the uptake of NO3 by a saturated alcohol, 1-octanol, in the liquid and solid phases. They derived at 258 K for the liquid phase of 1-octanol and at 248 K for the solid phase as shown in Table 2. The change in γ is a factor 1.73 over 10 K, mainly because of the rapid phase transition of 1-octanol. In our LEV / XYL uptake experiment, γ changes by a factor 2.74 over a temperature range of 80 K; however, γ measured here is about 1 order of magnitude lower. We suggest that the different sensitivity in γ over these different temperature ranges is due to the continuous amorphous phase transition of the LEV / XYL mixture compared to the abrupt phase transition of 1-octanol.
At low temperatures, γ for NO3 uptake by LEV and LEV / XYL films is similar within our experimental uncertainties, as shown in Table 2. This is in contrast to expectations derived from the gas-phase structure activity relationships (SARs) (Atkinson, 1987; Kerdouci et al., 2014), which predict that the reaction NO3 + LEV occurs 6.7 times faster than the reaction of NO3 + XYL. Also, γ of solid LEV and LEV / XYL is similar to NO3 uptake by solid alkane substrates and monolayers, e.g., n-hexadecane given in Table 2 (Knopf et al., 2006, 2011; Gross and Bertram, 2009; Moise et al., 2002). However, an alcohol is expected to be more reactive with NO3 compared to an alkane, as the α-hydrogen atom at the OH group is more labile and thus facilitates the hydrogen abstraction. These measurements indicate that the presence of labile α-hydrogen atoms in solid substrate films does not significantly yield higher γ. A possible explanation may be that the number density of labile α-hydrogen atoms at the interface is not sufficiently different between LEV, the LEV / XYL mixture, and alkane substrate films. Furthermore, considering that NO3 concentrations are too low to saturate the substrate surface, the probability of collisions with the most reactive hydrogen may also be low. This may result in similar γ within our uncertainties, for both substrates. In conclusion, our study demonstrates a strong positive correlation between temperature, substrate phase state, and NO3 uptake reactivity for saturated alcohols.
3.5 Temperature-modulated reactive OH uptake
Figure 9a shows γ of OH reacting with GLU as a function of temperature, indicating no significant change in reactivity over the examined temperature range. As the temperature increases from 250 K on, γ appears to slightly decrease from 0.11±0.03 to 0.09±0.03, although this change is within experimental uncertainties. GLU substrates maintain a solid or highly viscous phase state for all examined temperatures. The gas-phase structure activity relationship (SAR) predicts that the gas-phase reaction rate of OH radicals with GLU () decreases by a factor of 2.5 from 213 to 298 K (Atkinson, 1987; Kwok and Atkinson, 1995). We also observe a decrease in reactivity (Fig. 9a), however, not as strong as for gas-phase reactions. This implies that other factors may also play a role in the observed heterogeneous reactivity. Since different chemical bonds have different reactivity and temperature dependence (Kwok and Atkinson, 1995), the reaction probability of OH radicals can be affected by the molecular orientation at the surface. SAR suggests that tertiary C–H bonds contribute to this negative temperature dependency of the reactivity. Hence, if more C–OH bonds are exposed to the surface compared to tertiary C–H bonds, this negative temperature dependency of reactivity weakens. A similar steric argument was given by Nah et al. (2014), who suggested that the increased surface density of C=C double bonds due to the formation of oleic acid dimers possibly leads to a faster surface reaction involving OH radicals. Also, the remaining amount of water in these substrates may impact the surface structure and the viscosity of the near-surface region, thereby potentially counteracting the decreasing reaction rate with increasing temperature predicted with the SAR method.
For the GLU / HEX mixture (Fig. 9b), γ at 303 K is 0.13±0.03, ∼1.5 times larger than that at 233 K. The larger γ at higher temperature can be attributed to the viscosity change of the substrate film with increasing temperature. Tg is estimated as (248±3) K by our poke-flow experiment. Judging by the morphology and the flow characteristics of the organic film, it experiences a glass phase transition within the investigated temperature range. The major change in γ occurs above the expected Tg of the GLU / HEX mixture. γ by GLU / HEX at low temperatures, i.e., between 213 and 233 K, is lower than γ by GLU, and this is likely related to the lower reaction rate of HEX with OH radicals. For example, SAR predicts the reaction rate for HEX + OH to be 2.6 times slower than that for GLU + OH at 213 K.
Figure 9c shows that γ of CA increases by a factor of 5 within the experimental temperature range, from 0.13±0.08 at 213 K to 0.66±0.24 at 293 K. This increase in γ is particularly significant above the melting point of canola oil, Tm=258 K (Fasina et al., 2008). Above the melting point, γ increases by a factor of ∼2.4 between 273 and 293 K, where the viscosity of canola oil changes from 0.185 to 0.079 Pa s (Fasina et al., 2006). Therefore, we attribute this large change in γ to the phase and viscosity change of the canola oil. We observed that as the canola oil is in a solid or viscous liquid (grease) state at temperatures between 213 and 253 K, γ is less sensitive to temperature changes compared to when the canola oil is in a liquid phase. γ by CA is larger than γ by GLU at low temperatures, although both are in the solid phase, thus implying that OH reacts faster with C=C bonds than with C–H bonds and OH groups present on solid surfaces. Waring et al. (2011) measured the reactive loss of gas-phase OH radicals on squalene surfaces at room temperature, reporting . These measurements suggest that γ by CA can be larger than γ by squalene, although squalene has more double bonds compared to canola oil and both organics have similar viscosity (e.g., μSqe is 0.012 Pa s at 298 K; Comunas et al., 2013). Different accessibility of C=C bonds on the substrate surfaces could be one reason for different γ values. X-ray diffraction studies on liquid oleic acid showed that the unsaturated acid molecules exist primarily as dimers through hydrogen bonding of the carbonyl oxygen and the acidic hydrogen (Iwahashi and Kasahara, 2011; Iwahashi et al., 2000), and this possibly leads to more C=C double bonds at the substrate surface (Hearn et al., 2005). However, whether or not this phenomenon can compensate for the more numerous C=C double bonds present in squalene molecules is uncertain. Lastly, gas-phase reaction kinetics suggest that unsaturated oxygenated organics (e.g., acids, alcohols, ketones) are more reactive toward OH radicals than their alkene equivalents due to the formation of a hydrogen-bonded complex that facilities the formation of stable reaction products via interactions between the OH radical and the oxygenated functional group of the molecule (Mellouki et al., 2003; Orlando et al., 2001).
Temperature varies greatly in the troposphere, in both the latitudinal and altitudinal directions. The zonal average surface temperature changes approximately 0.86 K per degree latitude in the Northern Hemisphere (Gates et al., 1999), and the vertical temperature gradient is typically defined by the lapse rate of ∼10 K km−1 for dry air and ∼7 K km−1 for wet air (Wallace and Hobbs, 2006). Globally, the temperature will greatly influence the phase state and the heterogeneous oxidation of OA particles, especially for SOA particles that can exist in a liquid phase state in the warmer planetary boundary layer but can be mostly solid in the colder middle and upper troposphere (Shiraiwa et al., 2017a).
The determined γ values can be used to estimate the oxidation lifetime for a solid organic surface with the following equation (Moise and Rudich, 2001):
where τ is the lifetime of one monolayer of coverage, i.e., how long it takes for 63 % of surface molecules to be oxidized. Ntot represents the concentration of reaction sites on the organic substrate surface. Here, we apply this idealized approach to assess the degree of surface oxidation of OA particles in a solid or highly viscous phase state and when the oxidation reactions are confined to the surface. However, given that the surface-active organics are ubiquitous in tropospheric aerosols and organic films can exist on aerosol surfaces with potentially significant effects on atmospheric chemistry and climate, e.g., heterogeneous reactions, particle hygroscopicity, optical properties, and cloud-forming activity (Jimenez et al., 2009; Kroll et al., 2015; Katrib et al., 2005b; Knopf et al., 2007, 2018; Slade et al., 2017; Robinson et al., 2007; Shiraiwa et al., 2017a; Cosman and Bertram, 2008; McNeill et al., 2006; Knopf and Forrester, 2011; Moise et al., 2015), this approach can further our understanding of the chemical evolution of atmospheric OA. We assume Ntot= 1015 cm−2 (Bertram et al., 2001). The concentration of gas oxidants O3, NO3, and OH is based on ambient conditions of 1×1012, 1.25×109, and 1×106 molec. cm−3, respectively (Finlayson-Pitts and Pitts, 1999). Figure 10 shows the effect of temperature on the surface species' lifetime for the different examined heterogeneous oxidation reactions. Oxidation of CA by O3 proceeds within minutes to hours for typical tropospheric temperatures. Thus, degradation of unsaturated fatty acids is expected to proceed efficiently, even at colder temperatures. Despite the OH radical being the most effective oxidizer, Fig. 10 suggests that for middle- and upper-tropospheric conditions, oxidation of the particle surface by OH can take 1 to 2 weeks, emphasizing the slow physicochemical changes of the particle properties during transport at high altitudes. However, closer to the surface, degradation can proceed almost an order of magnitude faster. Degradation of the particle surface by NO3 may proceed by about a factor of 2 slower at the coldest tropospheric temperatures compared to boundary layer conditions. Clearly, these datasets indicate that the topmost organic layers for most of the investigated OA surrogates can be oxidized within 1 week for lower- and middle-tropospheric conditions. However, as soon as OA particles reach higher altitudes and lower temperatures by, e.g., pyro-convection (Andreae et al., 2004; Jost et al., 2004; Fromm and Servranckx, 2003), their atmospheric lifetime increases significantly. For example, aerosol particles originating from extreme wildfires, like Australia bushfires, can circumnavigate the globe in weeks and can even reach the stratosphere, existing for weeks or months (Ribeiro et al., 2020).
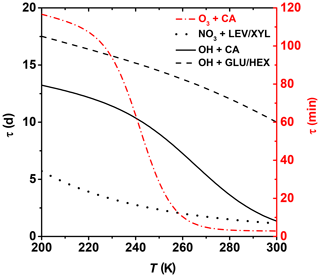
Figure 10Lifetime estimates of one monolayer of examined OA surrogates for typical background concentrations of O3, NO3, and OH. See text for more details.
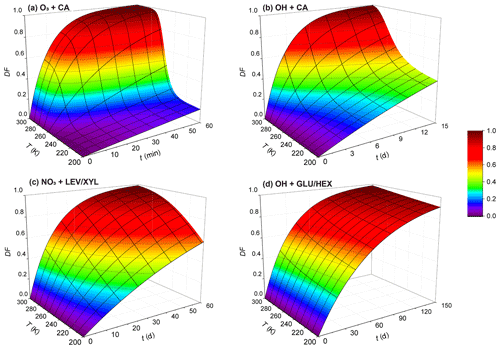
Figure 11Exposure- and temperature-dependent particle degraded fraction (DF) for particles 200 nm in diameter for (a) O3 oxidation of canola oil, (b) OH oxidation of canola oil, (c) NO3 oxidation of the LEV / XYL mixture, and (d) OH oxidation of the GLU / HEX mixture. Note the different scales on the time axis.
For OA particles, the lifetime (τp) and particle degraded fraction (DF) can be estimated by the equations below (George et al., 2007):
and
where R is the radius of the particle, chosen here as 100 nm, Na is Avogadro's number, M is the molecular weight of the condensed-phase species, and t is time. We derive DF as a function of temperature and oxidant exposure time for oxidant concentrations given above. However, we note that this DF estimate is a simplified approach, since we assume that measured oxidation kinetics proceed throughout the entire particle with the same rate. This ignores the slow gas diffusion in the condensed phase and the hindered internal mixing of organic species, particularly when the OA particle is in a solid or highly viscous phase state. For OH oxidation, previous studies indicate that the oxidation reaction is confined to near the surface of a liquid or solid organic substrate, even for longer OH exposure periods at lower OH concentrations (Slade and Knopf, 2014; George and Abbatt, 2010; Lee and Wilson, 2016; Shiraiwa et al., 2011). However, whether bulk processes may significantly change the reactivity under long oxidant exposure as encountered in the atmosphere still needs to be examined. In the case of O3 and NO3 oxidation of organic substrates, the results by Shiraiwa et al. (2011, 2012) indicate that the reactive uptake coefficients decrease with increasing exposure. Therefore, we probably underestimate the chemical lifetime. As such, the DF values at lower temperatures likely represent upper limits. In other words, degradation in ambient particles is expected to be less. Keeping this limitation in mind, Fig. 11 displays the estimated DF for the examined oxidant–surrogate systems. As expected, for the lowest temperatures, the DF values are lowest, implying the longest lifetimes. The stronger the particle viscosity change with temperature, the greater the change in DF; e.g., viscosity of CA decreases from 1012 to 10−2 Pa s over the temperature range from 213 to 293 K. This yields the largest change in DF over this temperature range compared to the other investigated systems (considering the same exposure time period). Figure 11c and d display a small DF within 1 month for LEV / XYL and GLU / HEX mixtures in the upper troposphere. This is consistent with previous aircraft observations reporting a large number of biomass burning aerosol particles in aged plumes at higher altitudes of the troposphere (Cubison et al., 2011). This also supports the hypothesis that aerosol particles originating from large wildfires (e.g., Australian bushfires) can be transported into the Northern Hemisphere from the stratosphere within a time period of 1 year (Deshler, 2008; Peterson et al., 2018). The presence of water vapor will significantly impact the phase state, in particular, of hygroscopic species such as LEV and GLU (Zobrist et al., 2008; Koop et al., 2011; Mikhailov et al., 2009), where increasing humidity yields lower condensed-phase viscosity and, in turn, faster reaction kinetics (Slade and Knopf, 2014; Slade et al., 2017; Davies and Wilson, 2015). Neglecting this effect will lead to an underestimation of DF. This discussion neglects the chemical complexity of ambient OA where different condensed-phase species can result in different reactivities and reaction pathways (Zhang et al., 2015; Surratt et al., 2010; Ziemann and Atkinson, 2012; Knopf et al., 2005; Davies and Wilson, 2015). Those in turn can change the multiphase kinetics and its dependency on temperature and particle phase state. Furthermore, heterogeneous particle composition and morphology can result in matrix effects or liquid–liquid phase separation, where, for example, more reactive organic species are shielded by less reactive species (Lignell et al., 2014; Lee and Wilson, 2016; Charnawskas et al., 2017; Bertram et al., 2011). Those effects were not assessed in this study but necessitate additional experimental investigations.
In this study, we measured γ for several systems of oxidant and organic aerosol surrogate combinations including O3 and OH+CA, NO3+ LEV and LEV / XYL, and OH + GLU and GLU / HEX, under dry conditions and for temperatures ranging from 213 to 313 K. For the case of OH, this is the first low-temperature reactive uptake study of which the authors are aware. The phase states of the organic substrate films were examined using the poke-flow technique, allowing for an estimation of Tg and substrate flow characteristics to constrain the magnitude of the substrate viscosity at different temperatures using the VTF equation.
The strongest changes in heterogeneous reactivity observed for the examined oxidant–substrate systems correlate with the largest change in organic substrate viscosity with temperature associated with a solid-to-liquid phase transition. The largest reactivity occurs between O3 and CA, exhibiting a change by a factor of 34, due to the phase transition of CA. In general, we attribute the faster heterogeneous kinetics in the semisolid and liquid phase states to surface and bulk reactions, the latter enabled by increased diffusion coefficients of gas and condensed species resulting from lower viscosity. Furthermore, once in the liquid phase, as temperature increases viscosity decreases and diffusivity increases, leading to potentially strong increases in reactivity. LEV and GLU substrates display a semisolid and solid phase state over the entire probed temperature range, with estimated viscosities larger than 104 Pa s. As a result, the overall reactivity is lower compared to liquid substrate films and does not change significantly with temperature. Although viscosity in the semisolid phase regime can change substantially with temperature, viscosity can still be too high to allow for significant bulk processes to play a role. In this case, surface reactions likely dominate, and replenishment of unoxidized molecules to the surface is hindered. Application of organic substrate mixtures to control Tg to induce a solid-to-liquid phase transition as temperature increases is accompanied by an increase in reactivity.
Our results are consistent with previous studies reporting the significance of particle phase state for the reactive uptake kinetics (Arangio et al., 2015; Knopf et al., 2005; Kolesar et al., 2014; Slade and Knopf, 2014; Davies and Wilson, 2015; Shiraiwa et al., 2012). To resolve the molecular processes of the measured heterogeneous kinetics, detailed modeling studies (Pöschl et al., 2007; Shiraiwa et al., 2010; Arangio et al., 2015; Houle et al., 2015; Houle et al., 2018a; Pöschl and Shiraiwa, 2015) extended to lower temperatures are needed. A crucial aspect of this study is the interplay between the temperature dependence of the reaction kinetics and the desorption lifetime. At lower temperatures when an organic substrate is in the solid state, over a wide temperature range the reactivity does not change significantly. Desorption lifetime will likely increase significantly with decreasing temperature with subsequent effects on the reaction kinetics. Changes in substrate viscosity with temperature may also play a role in the overall heterogeneous kinetics when the substrate is in a semisolid phase state. However, to what extent the particle viscosity will influence the diffusion and reaction kinetics is still not resolved. The comprehensive dataset presented here will allow application of a more detailed kinetic multi-layer model to constrain the temperature dependency of reaction and transport parameters. This study did not address the role of water vapor acting as a plasticizer concurrent to phase changes induced by temperature changes (Zobrist et al., 2008; Koop et al., 2011; Mikhailov et al., 2009). The role of humidity in amorphous phase state and resulting multiphase kinetics has been studied at room temperature (Shiraiwa et al., 2011; Slade and Knopf, 2014; Davies and Wilson, 2015; Li et al., 2018). Most of these studies suggest that increasing humidity leads to faster reactive uptake kinetics. However, at lower temperatures, diffusivity is slower, leading to kinetically hindered adjustments of the condensed-phase state (Berkemeier et al., 2014; Knopf et al., 2018; Charnawskas et al., 2017; Wang et al., 2012). Future experimental studies should focus on how the coupled effects of ambient temperature and humidity on the amorphous phase state of OA particles modulate the multiphase oxidation kinetics.
Our study demonstrates unambiguously that the chemical reactivity of organic matter towards atmospheric oxidants can vary significantly in response to ambient temperature, which, in turn, modulates the organic phase state. Ambient OA, however, displays greater chemical and morphological complexity (Laskin et al., 2016, 2019), and as such we expect varying multiphase reaction pathways having different reactivity towards atmospheric gas-phase oxidants which will translate into different reactivity dependencies on temperature and phase state. Despite this caveat, due to lower temperatures at higher altitudes, we can expect OA particles during transport in the free troposphere to have significantly longer lifetimes with respect to chemical degradation. This is important information for our understanding of the chemical evolution of OA particles and their impact on source apportionment, air quality, and climate.
The KPS method (Knopf et al., 2015), similar to the Cooney–Kim–Davis (CKD) method applied by Murphy and Fahey (1987), accounts for gas flow entrance effects into the flow reactor, i.e., the establishment of concentration profiles, that impact the derivation of the reactive uptake coefficient as pointed out by Davis (2008). When considering the establishment of gas concentration profiles for correction of observed pseudo-first-order wall loss rates, slower uptake reaction kinetics (e.g., the uptake of O3) typically represent conditions of either having a slow gas flow or long flow tube, and thus the as shown in Fig. A1 (Davis, 2008). In this case, the different approaches (Brown, CKD, and KPS) to correct observed wall loss rate for transport limitations by diffusion yield the same γ values as illustrated in Fig. 7 (CKD approach is not shown but yields the same results as KPS). However, reactive OH uptake exerts faster reaction kinetics and thus resembles conditions of a fast gas flow or a short flow tube (Fig. A1) where can significantly depart from 3.66 (Knopf et al., 2015; Murphy and Fahey, 1987; Davis, 2008). In this case, γ values derived by the Brown method always yield larger values compared to those derived by the KPS method as illustrated in Fig. A2 for the uptake of OH by glucose. Hence, for fast uptake kinetics, we recommend using either the KPS or CKD methods to derive accurate uptake kinetics when using a coated-wall flow reactor.
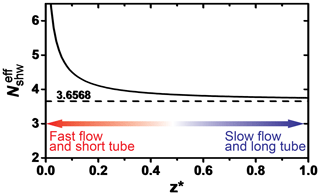
Figure A1Dependence of the effective Sherwood number () on the dimensionless axial distance of the flow reactor. Smaller dimensionless axial distance represents the scenario of a fast flow or short tube. Adapted from Davies (2008) and Knopf et al. (2015).
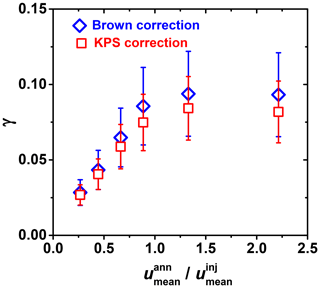
Figure A2Differences in reactive uptake coefficient (γ) derived from two gas transport correction methods for fast heterogeneous kinetics involving OH uptake by glucose as a function of flow velocity ratio between mean gas flow velocity in the annular section of the flow reactor () and the gas flow exiting the movable injector (). Red squares and blue diamonds represent the KPS and Brown methods, respectively.
The gas flow velocity ratio between mean flow velocities in the flow reactor () and the gas flow exiting the movable injector () also impacts the derivation of γ. If , reactive uptake experiments are ambiguous, potentially resulting in an underestimation of the uptake kinetics, as pointed out by Davis (2008). This flow condition can lead to a jet-like exit gas flow from the movable injector. Figure A2 displays this effect when < 1, where the measured γ values can deviate by a factor of 3 from the actual value.
For all experimentally derived γ values, we set > 1.27 for the flow tube with 1.758 cm inner diameter and > 1.33 for the flow tube with an inner diameter of 1.2 cm, based on the theoretical calculation below. The velocity profile and volume flow rate Q of a Poiseuille flow in the annular section can be described by the equations (Rosenhead, 1988)
and
where u(r) is the flow velocity profile as a function of the radius r. G is a constant pressure gradient, μ is the dynamic viscosity, R1 is the inner cylinder radius, R2 is the outer cylinder radius, and r is a radius value between R1 and R2. If R1, R2, and constant parameters (G and μ) are known, the maximum flow velocity umax is obtained by setting , and the mean flow velocity in the annular section umean is derived from Q∕Aann, where Aann is the cross-sectional area of the annular section.
Using the flow tube with a diameter of 1.758 cm as an example, and setting R1=0.325 and R2=0.879 cm, the ratio of maximum flow velocity over the average flow velocity in the annular section is . The ratio of the mean flow velocity over the maximum velocity in a tubular injector is as the injector flow is laminar (Rogers, 1992). Therefore, even when adjusting the gas flows in the injector and flow reactor to yield the same mean flow velocities, the difference in the maximum flow velocities can still differ significantly. In this case, the difference can be up to 27 %, potentially resulting in a jet-like gas flow profile. For this reason, we set > 1.27 to avoid this effect. In the case of using a flow tube with a diameter of 1.2 cm, > 1.33.
All data needed to draw the conclusions in the present study are shown in the paper and/or the Supplement. For additional data related to this study, please contact the corresponding author.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-20-6055-2020-supplement.
JL conducted O3, NO3, and OH uptake experiments. SMF performed N2O5 synthesis and conducted NO3 uptake experiments. JL conducted the poke-flow experiments. JL performed all analysis of data. SMF conducted analysis of NO3 uptake data and contributed to the writing of the manuscript. JL led the writing of the manuscript. DAK oversaw the project, envisioned the analysis, and contributed to the writing of the manuscript.
The authors declare that they have no conflict of interest.
Support from the National Science Foundation and partial support from the U.S. Department of Energy, Office of Science (BER), Atmospheric System Research, are acknowledged.
This research has been supported by the U.S. National Science Foundation (grant no. AGS-1446286) and the U.S. Department of Energy, Office of Science (BER), Atmospheric System Research (grant no. DE-SC0016370).
This paper was edited by Jason Surratt and reviewed by two anonymous referees.
Abbatt, J. P. D., Leaitch, W. R., Aliabadi, A. A., Bertram, A. K., Blanchet, J.-P., Boivin-Rioux, A., Bozem, H., Burkart, J., Chang, R. Y. W., Charette, J., Chaubey, J. P., Christensen, R. J., Cirisan, A., Collins, D. B., Croft, B., Dionne, J., Evans, G. J., Fletcher, C. G., Galí, M., Ghahremaninezhad, R., Girard, E., Gong, W., Gosselin, M., Gourdal, M., Hanna, S. J., Hayashida, H., Herber, A. B., Hesaraki, S., Hoor, P., Huang, L., Hussherr, R., Irish, V. E., Keita, S. A., Kodros, J. K., Köllner, F., Kolonjari, F., Kunkel, D., Ladino, L. A., Law, K., Levasseur, M., Libois, Q., Liggio, J., Lizotte, M., Macdonald, K. M., Mahmood, R., Martin, R. V., Mason, R. H., Miller, L. A., Moravek, A., Mortenson, E., Mungall, E. L., Murphy, J. G., Namazi, M., Norman, A.-L., O'Neill, N. T., Pierce, J. R., Russell, L. M., Schneider, J., Schulz, H., Sharma, S., Si, M., Staebler, R. M., Steiner, N. S., Thomas, J. L., von Salzen, K., Wentzell, J. J. B., Willis, M. D., Wentworth, G. R., Xu, J.-W., and Yakobi-Hancock, J. D.: Overview paper: New insights into aerosol and climate in the Arctic, Atmos. Chem. Phys., 19, 2527–2560, https://doi.org/10.5194/acp-19-2527-2019, 2019.
Abramson, E., Imre, D., Beranek, J., Wilson, J., and Zelenyuk, A.: Experimental determination of chemical diffusion within secondary organic aerosol particles, Phys. Chem. Chem. Phys., 15, 2983–2991, https://doi.org/10.1039/c2cp44013j, 2013.
Andreae, M. O., Rosenfeld, D., Artaxo, P., Costa, A. A., Frank, G. P., Longo, K. M., and Silva-Dias, M. A.: Smoking rain clouds over the Amazon, Science, 303, 1337–1342, https://doi.org/10.1126/science.1092779, 2004.
Angell, C. A.: Relaxation in liquids, polymers and plastic crystals – strong fragile patterns and problems, J. Non-Cryst. Solids, 131, 13–31, https://doi.org/10.1016/0022-3093(91)90266-9, 1991.
Angell, C. A.: Formation of glasses from liquids and biopolymers, Science, 267, 1924–1935, https://doi.org/10.1126/science.267.5206.1924, 1995.
Angell, C. A.: Liquid fragility and the glass transition in water and aqueous solutions, Chem. Rev., 102, 2627–2650, https://doi.org/10.1021/cr000689q, 2002.
Arangio, A. M., Slade, J. H., Berkemeier, T., Pöschl, U., Knopf, D. A., and Shiraiwa, M.: Multiphase chemical kinetics of OH radical uptake by molecular organic markers of biomass burning aerosols: humidity and temperature dependence, surface reaction, and bulk diffusion, J. Phys. Chem. A, 119, 4533–4544, https://doi.org/10.1021/jp510489z, 2015.
Atkinson, R.: A structure-activity relationship for the estimation of rate constants for the gas-phase reactions of OH radicals with organic compounds, Int. J. Chem. Kinet., 19, 799–828, https://doi.org/10.1002/kin.550190903, 1987.
Atkinson, R., Baulch, D. L., Cox, R. A., Crowley, J. N., Hampson, R. F., Hynes, R. G., Jenkin, M. E., Rossi, M. J., and Troe, J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Volume I – gas phase reactions of Ox, HOx, NOx and SOx species, Atmos. Chem. Phys., 4, 1461–1738, https://doi.org/10.5194/acp-4-1461-2004, 2004.
Atkinson, R., Baulch, D. L., Cox, R. A., Crowley, J. N., Hampson, R. F., Hynes, R. G., Jenkin, M. E., Rossi, M. J., Troe, J., and IUPAC Subcommittee: Evaluated kinetic and photochemical data for atmospheric chemistry: Volume II – gas phase reactions of organic species, Atmos. Chem. Phys., 6, 3625–4055, https://doi.org/10.5194/acp-6-3625-2006, 2006.
Baetzold, R. and Somorjai, G. A.: Preexponential factors in surface reactions, J. Catal., 45, 94–105, https://doi.org/10.1016/0021-9517(76)90059-2, 1976.
Bai, J., Sun, X., Zhang, C., Xu, Y., and Qi, C.: The OH-initiated atmospheric reaction mechanism and kinetics for levoglucosan emitted in biomass burning, Chemosphere, 93, 2004–2010, https://doi.org/10.1016/j.chemosphere.2013.07.021, 2013.
Berkemeier, T., Shiraiwa, M., Pöschl, U., and Koop, T.: Competition between water uptake and ice nucleation by glassy organic aerosol particles, Atmos. Chem. Phys., 14, 12513–12531, https://doi.org/10.5194/acp-14-12513-2014, 2014.
Berkemeier, T., Steimer, S. S., Krieger, U. K., Peter, T., Pöschl, U., Ammann, M., and Shiraiwa, M.: Ozone uptake on glassy, semi-solid and liquid organic matter and the role of reactive oxygen intermediates in atmospheric aerosol chemistry, Phys. Chem. Chem. Phys., 18, 12662–12674, https://doi.org/10.1039/c6cp00634e, 2016.
Bertram, A. K., Ivanov, A. V., Hunter, M., Molina, L. T., and Molina, M. J.: The reaction probability of OH on organic surfaces of tropospheric interest, J. Phys. Chem. A, 105, 9415–9421, https://doi.org/10.1021/jp0114034, 2001.
Bertram, A. K., Martin, S. T., Hanna, S. J., Smith, M. L., Bodsworth, A., Chen, Q., Kuwata, M., Liu, A., You, Y., and Zorn, S. R.: Predicting the relative humidities of liquid-liquid phase separation, efflorescence, and deliquescence of mixed particles of ammonium sulfate, organic material, and water using the organic-to-sulfate mass ratio of the particle and the oxygen-to-carbon elemental ratio of the organic component, Atmos. Chem. Phys., 11, 10995–11006, https://doi.org/10.5194/acp-11-10995-2011, 2011.
Borde, B., Bizot, H., Vigier, G., and Buleon, A.: Calorimetric analysis of the structural relaxation in partially hydrated amorphous polysaccharides. I. Glass transition and fragility, Carbohyd. Polym., 48, 83–96, https://doi.org/10.1016/s0144-8617(01)00217-x, 2002.
Brown, R.: Tubular flow reactors with first-order kinetics, J. Res. Nat. Bur. Stand., 83, 1–8, 1978.
Brown, S. S., Ryerson, T. B., Wollny, A. G., Brock, C. A., Peltier, R., Sullivan, A. P., Weber, R. J., Dube, W. P., Trainer, M., Meagher, J. F., Fehsenfeld, F. C., and Ravishankara, A. R.: Variability in nocturnal nitrogen oxide processing and its role in regional air quality, Science, 311, 67–70, https://doi.org/10.1126/science.1120120, 2006.
Charnawskas, J. C., Alpert, P. A., Lambe, A. T., Berkemeier, T., O'Brien, R. E., Massoli, P., Onasch, T. B., Shiraiwa, M., Moffet, R. C., Gilles, M. K., Davidovits, P., Worsnop, D. R., and Knopf, D. A.: Condensed-phase biogenic-anthropogenic interactions with implications for cold cloud formation, Faraday Discuss., 200, 165–194, https://doi.org/10.1039/c7fd00010c, 2017.
Chenyakin, Y., Ullmann, D. A., Evoy, E., Renbaum-Wolff, L., Kamal, S., and Bertram, A. K.: Diffusion coefficients of organic molecules in sucrose–water solutions and comparison with Stokes–Einstein predictions, Atmos. Chem. Phys., 17, 2423–2435, https://doi.org/10.5194/acp-17-2423-2017, 2017.
Comunas, M. J. P., Paredes, X., Gacino, F. M., Fernandez, J., Bazile, J. P., Boned, C., Daridon, J. L., Galliero, G., Pauly, J., Harris, K. R., Assael, M. J., and Mylona, S. K.: Reference Correlation of the Viscosity of Squalane from 273 to 373 K at 0.1 MPa, J. Phys. Chem. Ref. Data, 42, 033101, https://doi.org/10.1063/1.4812573, 2013.
Cooney, D. O., Kim, S.-S., and James Davis, E.: Analyses of mass transfer in hemodialyzers for laminar blood flow and homogeneous dialysate, Chem. Eng. Sci., 29, 1731–1738, https://doi.org/10.1016/0009-2509(74)87031-4, 1974.
Cosman, L. M. and Bertram, A. K.: Reactive uptake of N2O5 on aqueous H2SO4 solutions coated with 1-component and 2-component monolayers, J. Phys. Chem. A, 112, 4625–4635, https://doi.org/10.1021/jp8005469, 2008.
Cubison, M. J., Ortega, A. M., Hayes, P. L., Farmer, D. K., Day, D., Lechner, M. J., Brune, W. H., Apel, E., Diskin, G. S., Fisher, J. A., Fuelberg, H. E., Hecobian, A., Knapp, D. J., Mikoviny, T., Riemer, D., Sachse, G. W., Sessions, W., Weber, R. J., Weinheimer, A. J., Wisthaler, A., and Jimenez, J. L.: Effects of aging on organic aerosol from open biomass burning smoke in aircraft and laboratory studies, Atmos. Chem. Phys., 11, 12049–12064, https://doi.org/10.5194/acp-11-12049-2011, 2011.
Davies, J. F. and Wilson, K. R.: Nanoscale interfacial gradients formed by the reactive uptake of OH radicals onto viscous aerosol surfaces, Chem. Sci., 6, 7020–7027, https://doi.org/10.1039/c5sc02326b, 2015.
Davies, J. F. and Wilson, K. R.: Raman Spectroscopy of Isotopic Water Diffusion in Ultraviscous, Glassy, and Gel States in Aerosol by Use of Optical Tweezers, Anal. Chem., 88, 2361–2366, https://doi.org/10.1021/acs.analchem.5b04315, 2016.
Davis, E. J.: Interpretation of uptake coefficient data obtained with flow tubes, J. Phys. Chem. A, 112, 1922–1932, https://doi.org/10.1021/jp074939j, 2008.
de Gouw, J. A. and Lovejoy, E. R.: Reactive uptake of ozone by liquid organic compounds, Geophys. Res. Lett., 25, 931–934, https://doi.org/10.1029/98gl00515, 1998.
DeRieux, W.-S. W., Li, Y., Lin, P., Laskin, J., Laskin, A., Bertram, A. K., Nizkorodov, S. A., and Shiraiwa, M.: Predicting the glass transition temperature and viscosity of secondary organic material using molecular composition, Atmos. Chem. Phys., 18, 6331–6351, https://doi.org/10.5194/acp-18-6331-2018, 2018.
Deshler, T.: A review of global stratospheric aerosol: Measurements, importance, life cycle, and local stratospheric aerosol, Atmos. Res., 90, 223–232, https://doi.org/10.1016/j.atmosres.2008.03.016, 2008.
Dette, H. P. and Koop, T.: Glass Formation Processes in Mixed Inorganic/Organic Aerosol Particles, J. Phys. Chem. A, 119, 4552–4561, https://doi.org/10.1021/jp5106967, 2015.
Diogo, H. P. and Ramos, J. J. M.: Slow molecular mobility in the crystalline and amorphous solid states of glucose as studied by thermally stimulated depolarization currents (TSDC), Carbohyd. Res., 343, 2797–2803, https://doi.org/10.1016/j.carres.2008.07.002, 2008.
Dorfmüller, T., Dux, H., Fytas, G., and Mersch, W.: A light scattering study of the molecular motion in hexanetriol 1,2,6, J. Chem. Phys., 71, 366–375, https://doi.org/10.1063/1.438079, 1979.
Edebeli, J., Ammann, M., and Bartels-Rausch, T.: Microphysics of the aqueous bulk counters the water activity driven rate acceleration of bromide oxidation by ozone from 289–245 K, Environ. Sci.-Proc. Imp., 21, 63–73, https://doi.org/10.1039/c8em00417j, 2019.
Elamin, K., Sjostrom, J., Jansson, H., and Swenson, J.: Calorimetric and relaxation properties of xylitol-water mixtures, J. Chem. Phys., 136, 104508, https://doi.org/10.1063/1.3692609, 2012.
Elias, M. E. and Elias, A. M.: Trehalose plus water fragile system: properties and glass transition, J. Mol. Liq., 83, 303–310, https://doi.org/10.1016/s0167-7322(99)00094-x, 1999.
Ervens, B., Turpin, B. J., and Weber, R. J.: Secondary organic aerosol formation in cloud droplets and aqueous particles (aqSOA): a review of laboratory, field and model studies, Atmos. Chem. Phys., 11, 11069–11102, https://doi.org/10.5194/acp-11-11069-2011, 2011.
Fasina, O. O., Hallman, H., Craig-Schmidt, M., and Clements, C.: Predicting temperature-dependence viscosity of vegetable oils from fatty acid composition, J. Am. Oil Chem. Soc., 83, 899–903, https://doi.org/10.1007/s11746-006-5044-8, 2006.
Fasina, O. O., Craig-Schmidt, M., Colley, Z., and Hallman, H.: Predicting melting characteristics of vegetable oils from fatty acid composition, LWT-Food Sci. Technol., 41, 1501–1505, https://doi.org/10.1016/j.lwt.2007.09.012, 2008.
Finlayson-Pitts, B. J. and Pitts Jr., J. N.: Chemistry of the upper and lower atmosphere: theory, experiments, and applications, Academic, San Diego, 969 pp., 1999.
Fromm, M. D. and Servranckx, R.: Transport of forest fire smoke above the tropopause by supercell convection, Geophys. Res. Lett., 30, 1542, https://doi.org/10.1029/2002gl016820, 2003.
Fuchs, N. and Sutugin, A. G.: High-dispersed aerosols, in: Topics in current aerosol research, Pergamon Press, Oxford, 1, https://doi.org/10.1016/B978-0-08-016674-2.50006-6, 1971.
Fuller, E. N., Schettler, P. D., and Giddings, J. C.: New Method for Prediction of Binary Gas-Phase Diffusion Coefficients, Ind. Eng. Chem., 58, 18–27, https://doi.org/10.1021/ie50677a007, 1966.
Gaston, C. J., Thornton, J. A., and Ng, N. L.: Reactive uptake of N2O5 to internally mixed inorganic and organic particles: the role of organic carbon oxidation state and inferred organic phase separations, Atmos. Chem. Phys., 14, 5693–5707, https://doi.org/10.5194/acp-14-5693-2014, 2014.
Gates, W. L., Boyle, J. S., Covey, C., Dease, C. G., Doutriaux, C. M., Drach, R. S., Fiorino, M., Gleckler, P. J., Hnilo, J. J., Marlais, S. M., Phillips, T. J., Potter, G. L., Santer, B. D., Sperber, K. R., Taylor, K. E., and Williams, D. N.: An Overview of the Results of the Atmospheric Model Intercomparison Project (AMIP I), B. Am. Meteorol. Soc., 80, 29–55, https://doi.org/10.1175/1520-0477(1999)080<0029:Aootro>2.0.Co;2, 1999.
George, I. J. and Abbatt, J. P.: Heterogeneous oxidation of atmospheric aerosol particles by gas-phase radicals, Nat. Chem., 2, 713–722, https://doi.org/10.1038/nchem.806, 2010.
George, I. J., Vlasenko, A., Slowik, J. G., Broekhuizen, K., and Abbatt, J. P. D.: Heterogeneous oxidation of saturated organic aerosols by hydroxyl radicals: uptake kinetics, condensed-phase products, and particle size change, Atmos. Chem. Phys., 7, 4187–4201, https://doi.org/10.5194/acp-7-4187-2007, 2007.
Gershenzon, Y. M., Grigorieva, V. M., Ivanov, A. V., and Remorov, R. G.: O3 and OH sensitivity to heterogeneous sinks of HOx and CH3O2 on aerosol particles, Faraday Discuss., 100, 83–100, https://doi.org/10.1039/fd9950000083, 1995.
Ghazani, S. M. and Marangoni, A. G.: Minor Components in Canola Oil and Effects of Refining on These Constituents: A Review, J. Am. Oil Chem. Soc., 90, 923–932, https://doi.org/10.1007/s11746-013-2254-8, 2013.
Gordon, M. and Taylor, J. S.: Ideal copolymers and the second-order transitions of synthetic rubbers. i. non-crystalline copolymers, J. Appl. Chem., 2, 493–500, https://doi.org/10.1002/jctb.5010020901, 2007.
Gross, S. and Bertram, A. K.: Products and kinetics of the reactions of an alkane monolayer and a terminal alkene monolayer with NO3 radicals, J. Geophys. Res., 114, D02307, https://doi.org/10.1029/2008jd010987, 2009.
Gross, S., Iannone, R., Xiao, S., and Bertram, A. K.: Reactive uptake studies of NO3 and N2O5 on alkenoic acid, alkanoate, and polyalcohol substrates to probe nighttime aerosol chemistry, Phys. Chem. Chem. Phys., 11, 7792–7803, https://doi.org/10.1039/b904741g, 2009.
Hallquist, M., Wenger, J. C., Baltensperger, U., Rudich, Y., Simpson, D., Claeys, M., Dommen, J., Donahue, N. M., George, C., Goldstein, A. H., Hamilton, J. F., Herrmann, H., Hoffmann, T., Iinuma, Y., Jang, M., Jenkin, M. E., Jimenez, J. L., Kiendler-Scharr, A., Maenhaut, W., McFiggans, G., Mentel, Th. F., Monod, A., Prévôt, A. S. H., Seinfeld, J. H., Surratt, J. D., Szmigielski, R., and Wildt, J.: The formation, properties and impact of secondary organic aerosol: current and emerging issues, Atmos. Chem. Phys., 9, 5155–5236, https://doi.org/10.5194/acp-9-5155-2009, 2009.
Hanson, D. R. and Ravishankara, A. R.: The reaction probabilities of ClONO2 and N2O5 on polar stratospheric cloud materials, J. Geophys. Res., 96, 5081–5090, https://doi.org/10.1029/90jd02613, 1991.
Hearn, J. D., Lovett, A. J., and Smith, G. D.: Ozonolysis of oleic acid particles: evidence for a surface reaction and secondary reactions involving Criegee intermediates, Phys. Chem. Chem. Phys., 7, 501–511, https://doi.org/10.1039/b414472d, 2005.
Hopke, P. K.: Review of receptor modeling methods for source apportionment, J. Air Waste Manage., 66, 237–259, https://doi.org/10.1080/10962247.2016.1140693, 2016.
Houle, F. A., Hinsberg, W. D., and Wilson, K. R.: Oxidation of a model alkane aerosol by OH radical: the emergent nature of reactive uptake, Phys. Chem. Chem. Phys., 17, 4412–4423, https://doi.org/10.1039/c4cp05093b, 2015.
Houle, F. A., Wiegel, A. A., and Wilson, K. R.: Predicting Aerosol Reactivity Across Scales: from the Laboratory to the Atmosphere, Environ. Sci. Technol., 52, 13774–13781, https://doi.org/10.1021/acs.est.8b04688, 2018a.
Houle, F. A., Wiegel, A. A., and Wilson, K. R.: Changes in Reactivity as Chemistry Becomes Confined to an Interface. The Case of Free Radical Oxidation of C30H62 Alkane by OH, J. Phys. Chem. Lett., 9, 1053–1057, https://doi.org/10.1021/acs.jpclett.8b00172, 2018b.
Hu, W., Palm, B. B., Day, D. A., Campuzano-Jost, P., Krechmer, J. E., Peng, Z., de Sá, S. S., Martin, S. T., Alexander, M. L., Baumann, K., Hacker, L., Kiendler-Scharr, A., Koss, A. R., de Gouw, J. A., Goldstein, A. H., Seco, R., Sjostedt, S. J., Park, J.-H., Guenther, A. B., Kim, S., Canonaco, F., Prévôt, A. S. H., Brune, W. H., and Jimenez, J. L.: Volatility and lifetime against OH heterogeneous reaction of ambient isoprene-epoxydiols-derived secondary organic aerosol (IEPOX-SOA), Atmos. Chem. Phys., 16, 11563–11580, https://doi.org/10.5194/acp-16-11563-2016, 2016.
Iinuma, Y., Bruggemann, E., Gnauk, T., Muller, K., Andreae, M. O., Helas, G., Parmar, R., and Herrmann, H.: Source characterization of biomass burning particles: The combustion of selected European conifers, African hardwood, savanna grass, and German and Indonesian peat, J. Geophys. Res., 112, D08209, https://doi.org/10.1029/2006jd007120, 2007.
Ivanov, A. V., Trakhtenberg, S., Bertram, A. K., Gershenzon, Y. M., and Molina, M. J.: OH, HO2, and ozone gaseous diffusion coefficients, J. Phys. Chem. A, 111, 1632–1637, https://doi.org/10.1021/jp066558w, 2007.
Iwahashi, M. and Kasahara, Y.: Dynamic molecular movements and aggregation structures of lipids in a liquid state, Curr. Opin. Colloid In., 16, 359–366, https://doi.org/10.1016/j.cocis.2011.06.005, 2011.
Iwahashi, M., Kasahara, Y., Matsuzawa, H., Yagi, K., Nomura, K., Terauchi, H., Ozaki, Y., and Suzuki, M.: Self-Diffusion, Dynamical Molecular Conformation, and Liquid Structures of n-Saturated and Unsaturated Fatty Acids, J. Phys. Chem. B, 104, 6186–6194, https://doi.org/10.1021/jp000610l, 2000.
Jimenez, J. L., Canagaratna, M. R., Donahue, N. M., Prevot, A. S., Zhang, Q., Kroll, J. H., DeCarlo, P. F., Allan, J. D., Coe, H., Ng, N. L., Aiken, A. C., Docherty, K. S., Ulbrich, I. M., Grieshop, A. P., Robinson, A. L., Duplissy, J., Smith, J. D., Wilson, K. R., Lanz, V. A., Hueglin, C., Sun, Y. L., Tian, J., Laaksonen, A., Raatikainen, T., Rautiainen, J., Vaattovaara, P., Ehn, M., Kulmala, M., Tomlinson, J. M., Collins, D. R., Cubison, M. J., Dunlea, E. J., Huffman, J. A., Onasch, T. B., Alfarra, M. R., Williams, P. I., Bower, K., Kondo, Y., Schneider, J., Drewnick, F., Borrmann, S., Weimer, S., Demerjian, K., Salcedo, D., Cottrell, L., Griffin, R., Takami, A., Miyoshi, T., Hatakeyama, S., Shimono, A., Sun, J. Y., Zhang, Y. M., Dzepina, K., Kimmel, J. R., Sueper, D., Jayne, J. T., Herndon, S. C., Trimborn, A. M., Williams, L. R., Wood, E. C., Middlebrook, A. M., Kolb, C. E., Baltensperger, U., and Worsnop, D. R.: Evolution of organic aerosols in the atmosphere, Science, 326, 1525–1529, https://doi.org/10.1126/science.1180353, 2009.
Jost, H. J., Drdla, K., Stohl, A., Pfister, L., Loewenstein, M., Lopez, J. P., Hudson, P. K., Murphy, D. M., Cziczo, D. J., Fromm, M., Bui, T. P., Dean-Day, J., Gerbig, C., Mahoney, M. J., Richard, E. C., Spichtinger, N., Pittman, J. V., Weinstock, E. M., Wilson, J. C., and Xueref, I.: In-situ observations of mid-latitude forest fire plumes deep in the stratosphere, Geophys. Res. Lett., 31, L11101, https://doi.org/10.1029/2003gl019253, 2004.
Kaiser, J. C., Riemer, N., and Knopf, D. A.: Detailed heterogeneous oxidation of soot surfaces in a particle-resolved aerosol model, Atmos. Chem. Phys., 11, 4505–4520, https://doi.org/10.5194/acp-11-4505-2011, 2011.
Kanakidou, M., Seinfeld, J. H., Pandis, S. N., Barnes, I., Dentener, F. J., Facchini, M. C., Van Dingenen, R., Ervens, B., Nenes, A., Nielsen, C. J., Swietlicki, E., Putaud, J. P., Balkanski, Y., Fuzzi, S., Horth, J., Moortgat, G. K., Winterhalter, R., Myhre, C. E. L., Tsigaridis, K., Vignati, E., Stephanou, E. G., and Wilson, J.: Organic aerosol and global climate modelling: a review, Atmos. Chem. Phys., 5, 1053–1123, https://doi.org/10.5194/acp-5-1053-2005, 2005.
Katrib, Y., Biskos, G., Buseck, P. R., Davidovits, P., Jayne, J. T., Mochida, M., Wise, M. E., Worsnop, D. R., and Martin, S. T.: Ozonolysis of mixed oleic-acid/stearic-acid particles: reaction kinetics and chemical morphology, J. Phys. Chem. A, 109, 10910–10919, https://doi.org/10.1021/jp054714d, 2005a.
Katrib, Y., Martin, S. T., Rudich, Y., Davidovits, P., Jayne, J. T., and Worsnop, D. R.: Density changes of aerosol particles as a result of chemical reaction, Atmos. Chem. Phys., 5, 275–291, https://doi.org/10.5194/acp-5-275-2005, 2005b.
Kawamura, K., Ishimura, Y., and Yamazaki, K.: Four years' observations of terrestrial lipid class compounds in marine aerosols from the western North Pacific, Global Biogeochem. Cy., 17, 1003, https://doi.org/10.1029/2001gb001810, 2003.
Kerdouci, J., Picquet-Varrault, B., and Doussin, J.-F.: Structure–activity relationship for the gas-phase reactions of NO3 radical with organic compounds: Update and extension to aldehydes, Atmos. Environ., 84, 363–372, https://doi.org/10.1016/j.atmosenv.2013.11.024, 2014.
Kessler, S. H., Smith, J. D., Che, D. L., Worsnop, D. R., Wilson, K. R., and Kroll, J. H.: Chemical sinks of organic aerosol: kinetics and products of the heterogeneous oxidation of erythritol and levoglucosan, Environ. Sci. Technol., 44, 7005–7010, https://doi.org/10.1021/es101465m, 2010.
Kidd, C., Perraud, V., Wingen, L. M., and Finlayson-Pitts, B. J.: Integrating phase and composition of secondary organic aerosol from the ozonolysis of alpha-pinene, P. Natl. Acad. Sci. USA, 111, 7552–7557, https://doi.org/10.1073/pnas.1322558111, 2014.
Kiland, K. J., Maclean, A. M., Kamal, S., and Bertram, A. K.: Diffusion of Organic Molecules as a Function of Temperature in a Sucrose Matrix (a Proxy for Secondary Organic Aerosol), J. Phys. Chem. Lett., 10, 5902, https://doi.org/10.1021/acs.jpclett.9b02182, 2019.
Knopf, D. A. and Forrester, S. M.: Freezing of water and aqueous NaCl droplets coated by organic monolayers as a function of surfactant properties and water activity, J. Phys. Chem. A, 115, 5579–5591, https://doi.org/10.1021/jp2014644, 2011.
Knopf, D. A., Anthony, L. M., and Bertram, A. K.: Reactive uptake of O3 by multicomponent and multiphase mixtures containing oleic acid, J. Phys. Chem. A, 109, 5579–5589, https://doi.org/10.1021/jp0512513, 2005.
Knopf, D. A., Mak, J., Gross, S., and Bertram, A. K.: Does atmospheric processing of saturated hydrocarbon surfaces by NO3 lead to volatilization?, Geophys. Res. Lett., 33, L17816, https://doi.org/10.1029/2006gl026884, 2006.
Knopf, D. A., Cosman, L. M., Mousavi, P., Mokamati, S., and Bertram, A. K.: A novel flow reactor for studying reactions on liquid surfaces coated by organic monolayers: methods, validation, and initial results, J. Phys. Chem. A, 111, 11021–11032, https://doi.org/10.1021/jp075724c, 2007.
Knopf, D. A., Forrester, S. M., and Slade, J. H.: Heterogeneous oxidation kinetics of organic biomass burning aerosol surrogates by O3, NO2, N2O5, and NO3, Phys. Chem. Chem. Phys., 13, 21050–21062, https://doi.org/10.1039/c1cp22478f, 2011.
Knopf, D. A., Pöschl, U., and Shiraiwa, M.: Radial diffusion and penetration of gas molecules and aerosol particles through laminar flow reactors, denuders, and sampling tubes, Anal. Chem., 87, 3746–3754, https://doi.org/10.1021/ac5042395, 2015.
Knopf, D. A., Alpert, P. A., and Wang, B.: The Role of Organic Aerosol in Atmospheric Ice Nucleation: A Review, ACS Earth Space Chem., 2, 168–202, https://doi.org/10.1021/acsearthspacechem.7b00120, 2018.
Kolesar, K. R., Buffaloe, G., Wilson, K. R., and Cappa, C. D.: OH-initiated heterogeneous oxidation of internally-mixed squalane and secondary organic aerosol, Environ. Sci. Technol., 48, 3196–3202, https://doi.org/10.1021/es405177d, 2014.
Koop, T., Bookhold, J., Shiraiwa, M., and Pöschl, U.: Glass transition and phase state of organic compounds: dependency on molecular properties and implications for secondary organic aerosols in the atmosphere, Phys. Chem. Chem. Phys., 13, 19238–19255, https://doi.org/10.1039/c1cp22617g, 2011.
Kroll, J. H., Lim, C. Y., Kessler, S. H., and Wilson, K. R.: Heterogeneous Oxidation of Atmospheric Organic Aerosol: Kinetics of Changes to the Amount and Oxidation State of Particle-Phase Organic Carbon, J. Phys. Chem. A, 119, 10767–10783, https://doi.org/10.1021/acs.jpca.5b06946, 2015.
Kwok, E. and Atkinson, R.: Estimation of hydroxyl radical reaction rate constants for gas-phase organic compounds using a structure-reactivity relationship: An update, Atmos. Environ., 29, 1685–1695, https://doi.org/10.1016/1352-2310(95)00069-b, 1995.
Laidler, K. J., Glasstone, S., and Eyring, H.: Application of the Theory of Absolute Reaction Rates to Heterogeneous Processes I. The Adsorption and Desorption of Gases, J. Chem. Phys., 8, 659–667, https://doi.org/10.1063/1.1750736, 1940.
Laskin, A., Laskin, J., and Nizkorodov, S. A.: Chemistry of atmospheric brown carbon, Chem. Rev., 115, 4335–4382, https://doi.org/10.1021/cr5006167, 2015.
Laskin, A., Gilles, M. K., Knopf, D. A., Wang, B. B., and China, S.: Progress in the Analysis of Complex Atmospheric Particles, in: Annual Review of Analytical Chemistry, Vol 9, edited by: Bohn, P. W. and Pemberton, J. E., Annu. Rev. Anal. Chem., 9, 117–143, https://doi.org/10.1146/annurev-anchem-071015-041521, 2016.
Laskin, A., Moffet, R. C., and Gilles, M. K.: Chemical Imaging of Atmospheric Particles, Accounts Chem. Res., 52, 3419–3431, https://doi.org/10.1021/acs.accounts.9b00396, 2019.
Lee, L. and Wilson, K.: The Reactive-Diffusive Length of OH and Ozone in Model Organic Aerosols, J. Phys. Chem. A, 120, 6800–6812, https://doi.org/10.1021/acs.jpca.6b05285, 2016.
Li, Z., Smith, K. A., and Cappa, C. D.: Influence of relative humidity on the heterogeneous oxidation of secondary organic aerosol, Atmos. Chem. Phys., 18, 14585–14608, https://doi.org/10.5194/acp-18-14585-2018, 2018.
Lienhard, D. M., Bones, D. L., Zuend, A., Krieger, U. K., Reid, J. P., and Peter, T.: Measurements of thermodynamic and optical properties of selected aqueous organic and organic-inorganic mixtures of atmospheric relevance, J. Phys. Chem. A, 116, 9954–9968, https://doi.org/10.1021/jp3055872, 2012.
Lienhard, D. M., Huisman, A. J., Krieger, U. K., Rudich, Y., Marcolli, C., Luo, B. P., Bones, D. L., Reid, J. P., Lambe, A. T., Canagaratna, M. R., Davidovits, P., Onasch, T. B., Worsnop, D. R., Steimer, S. S., Koop, T., and Peter, T.: Viscous organic aerosol particles in the upper troposphere: diffusivity-controlled water uptake and ice nucleation?, Atmos. Chem. Phys., 15, 13599–13613, https://doi.org/10.5194/acp-15-13599-2015, 2015.
Lignell, H., Hinks, M. L., and Nizkorodov, S. A.: Exploring matrix effects on photochemistry of organic aerosols, P. Natl. Acad. Sci. USA, 111, 13780–13785, https://doi.org/10.1073/pnas.1322106111, 2014.
Limbeck, A. and Puxbaum, H.: Organic acids in continental background aerosols, Atmos. Environ., 33, 1847–1852, https://doi.org/10.1016/s1352-2310(98)00347-1, 1999.
Liu, T., Li, Z., Chan, M., and Chan, C. K.: Formation of secondary organic aerosols from gas-phase emissions of heated cooking oils, Atmos. Chem. Phys., 17, 7333–7344, https://doi.org/10.5194/acp-17-7333-2017, 2017.
Liu, Y., Ivanov, A. V., and Molina, M. J.: Temperature dependence of OH diffusion in air and He, Geophys. Res. Lett., 36, L03816, https://doi.org/10.1029/2008gl036170, 2009.
Marsh, A., Petters, S. S., Rothfuss, N. E., Rovelli, G., Song, Y. C., Reid, J. P., and Petters, M. D.: Amorphous phase state diagrams and viscosity of ternary aqueous organic/organic and inorganic/organic mixtures, Phys. Chem. Chem. Phys., 20, 15086–15097, https://doi.org/10.1039/c8cp00760h, 2018.
Marshall, F. H., Berkemeier, T., Shiraiwa, M., Nandy, L., Ohm, P. B., Dutcher, C. S., and Reid, J. P.: Influence of particle viscosity on mass transfer and heterogeneous ozonolysis kinetics in aqueous-sucrose-maleic acid aerosol, Phys. Chem. Chem. Phys., 20, 15560–15573, https://doi.org/10.1039/c8cp01666f, 2018.
Mason, E. A. and Monchick, L.: Transport Properties of Polar-Gas Mixtures, J. Chem. Phys., 36, 2746–2757, https://doi.org/10.1063/1.1732363, 1962.
McFiggans, G., Mentel, T. F., Wildt, J., Pullinen, I., Kang, S., Kleist, E., Schmitt, S., Springer, M., Tillmann, R., Wu, C., Zhao, D., Hallquist, M., Faxon, C., Le Breton, M., Hallquist, A. M., Simpson, D., Bergstrom, R., Jenkin, M. E., Ehn, M., Thornton, J. A., Alfarra, M. R., Bannan, T. J., Percival, C. J., Priestley, M., Topping, D., and Kiendler-Scharr, A.: Secondary organic aerosol reduced by mixture of atmospheric vapours, Nature, 565, 587–593, https://doi.org/10.1038/s41586-018-0871-y, 2019.
McNeill, V. F., Patterson, J., Wolfe, G. M., and Thornton, J. A.: The effect of varying levels of surfactant on the reactive uptake of N2O5 to aqueous aerosol, Atmos. Chem. Phys., 6, 1635–1644, https://doi.org/10.5194/acp-6-1635-2006, 2006.
Mellouki, A., Le Bras, G., and Sidebottom, H.: Kinetics and mechanisms of the oxidation of oxygenated organic compounds in the gas phase, Chem. Rev., 103, 5077–5096, https://doi.org/10.1021/cr020526x, 2003.
Mikhailov, E., Vlasenko, S., Martin, S. T., Koop, T., and Pöschl, U.: Amorphous and crystalline aerosol particles interacting with water vapor: conceptual framework and experimental evidence for restructuring, phase transitions and kinetic limitations, Atmos. Chem. Phys., 9, 9491–9522, https://doi.org/10.5194/acp-9-9491-2009, 2009.
Moise, T. and Rudich, Y.: Reactive uptake of ozone by proxies for organic aerosols: Surface versus bulk processes, J. Geophys. Res., 105, 14667–14676, https://doi.org/10.1029/2000jd900071, 2000.
Moise, T. and Rudich, Y.: Uptake of Cl and Br by organic surfaces-A perspective on organic aerosols processing by tropospheric oxidants, Geophys. Res. Lett., 28, 4083–4086, https://doi.org/10.1029/2001gl013583, 2001.
Moise, T. and Rudich, Y.: Reactive Uptake of Ozone by Aerosol-Associated Unsaturated Fatty Acids: Kinetics, Mechanism, and Products, J. Phys. Chem. A, 106, 6469–6476, https://doi.org/10.1021/jp025597e, 2002.
Moise, T., Talukdar, R. K., Frost, G. J., Fox, R. W., and Rudich, Y.: Reactive uptake of NO3 by liquid and frozen organics, J. Geophys. Res., 107, 4014, https://doi.org/10.1029/2001jd000334, 2002.
Moise, T., Flores, J. M., and Rudich, Y.: Optical properties of secondary organic aerosols and their changes by chemical processes, Chem. Rev., 115, 4400–4439, https://doi.org/10.1021/cr5005259, 2015.
Moridnejad, A. and Preston, T. C.: Models of Isotopic Water Diffusion in Spherical Aerosol Particles, J. Phys. Chem. A, 120, 9759–9766, https://doi.org/10.1021/acs.jpca.6b11241, 2016.
Mu, Q., Shiraiwa, M., Octaviani, M., Ma, N., Ding, A. J., Su, H., Lammel, G., Pöschl, U., and Cheng, Y. F.: Temperature effect on phase state and reactivity controls atmospheric multiphase chemistry and transport of PAHs, Sci. Adv., 4, eaap7314, https://doi.org/10.1126/sciadv.aap7314, 2018.
Murphy, D. M. and Fahey, D. W.: Mathematical treatment of the wall loss of a trace species in denuder and catalytic converter tubes, Anal. Chem., 59, 2753–2759, https://doi.org/10.1021/ac00150a006, 1987.
Murray, B. J., Wilson, T. W., Dobbie, S., Cui, Z. Q., Al-Jumur, S., Mohler, O., Schnaiter, M., Wagner, R., Benz, S., Niemand, M., Saathoff, H., Ebert, V., Wagner, S., and Karcher, B.: Heterogeneous nucleation of ice particles on glassy aerosols under cirrus conditions, Nat. Geosci., 3, 233–237, https://doi.org/10.1038/ngeo817, 2010.
Murray, B. J., Haddrell, A. E., Peppe, S., Davies, J. F., Reid, J. P., O'Sullivan, D., Price, H. C., Kumar, R., Saunders, R. W., Plane, J. M. C., Umo, N. S., and Wilson, T. W.: Glass formation and unusual hygroscopic growth of iodic acid solution droplets with relevance for iodine mediated particle formation in the marine boundary layer, Atmos. Chem. Phys., 12, 8575–8587, https://doi.org/10.5194/acp-12-8575-2012, 2012.
Nah, T., Kessler, S. H., Daumit, K. E., Kroll, J. H., Leone, S. R., and Wilson, K. R.: Influence of molecular structure and chemical functionality on the heterogeneous OH-initiated oxidation of unsaturated organic particles, J. Phys. Chem. A, 118, 4106–4119, https://doi.org/10.1021/jp502666g, 2014.
Nakanishi, M. and Nozaki, R.: Systematic study of the glass transition in polyhydric alcohols, Phys. Rev. E, 83, 051503, https://doi.org/10.1103/PhysRevE.83.051503, 2011.
Orlando, J. J., Tyndall, G. S., and Ceazan, N.: Rate Coefficients and Product Yields from Reaction of OH with 1-Penten-3-ol, (Z)-2-Penten-1-ol, and Allyl Alcohol (2-Propen-1-ol), J. Phys. Chem. A, 105, 3564–3569, https://doi.org/10.1021/jp0041712, 2001.
Pachauri, R. K., Allen, M. R., Barros, V. R., Broome, J., Cramer, W., Christ, R., Church, J. A., Clarke, L., Dahe, Q., and Dasgupta, P.: Climate change 2014: synthesis report. Contribution of Working Groups I, II and III to the fifth assessment report of the Intergovernmental Panel on Climate Change, IPCC, Geneva, 151 pp., 2014.
Pajunoja, A., Hu, W., Leong, Y. J., Taylor, N. F., Miettinen, P., Palm, B. B., Mikkonen, S., Collins, D. R., Jimenez, J. L., and Virtanen, A.: Phase state of ambient aerosol linked with water uptake and chemical aging in the southeastern US, Atmos. Chem. Phys., 16, 11163–11176, https://doi.org/10.5194/acp-16-11163-2016, 2016.
Peterson, D. A., Campbell, J. R., Hyer, E. J., Fromm, M. D., Kablick, G. P., Cossuth, J. H., and DeLand, M. T.: Wildfire-driven thunderstorms cause a volcano-like stratospheric injection of smoke, NPJ Clim. Atmos. Sci., 1, 30, https://doi.org/10.1038/s41612-018-0039-3, 2018.
Petters, S. S., Kreidenweis, S. M., Grieshop, A. P., Ziemann, P. J., and Petters, M. D.: Temperature- and Humidity-Dependent Phase States of Secondary Organic Aerosols, Geophys. Res. Lett., 46, 1005–1013, https://doi.org/10.1029/2018gl080563, 2019.
Pöschl, U. and Shiraiwa, M.: Multiphase chemistry at the atmosphere-biosphere interface influencing climate and public health in the anthropocene, Chem. Rev., 115, 4440–4475, https://doi.org/10.1021/cr500487s, 2015.
Pöschl, U., Rudich, Y., and Ammann, M.: Kinetic model framework for aerosol and cloud surface chemistry and gas-particle interactions – Part 1: General equations, parameters, and terminology, Atmos. Chem. Phys., 7, 5989–6023, https://doi.org/10.5194/acp-7-5989-2007, 2007.
Price, H. C., Mattsson, J., Zhang, Y., Bertram, A. K., Davies, J. F., Grayson, J. W., Martin, S. T., O'Sullivan, D., Reid, J. P., Rickards, A. M. J., and Murray, B. J.: Water diffusion in atmospherically relevant alpha-pinene secondary organic material, Chem. Sci., 6, 4876–4883, https://doi.org/10.1039/c5sc00685f, 2015.
Reid, J. P., Bertram, A. K., Topping, D. O., Laskin, A., Martin, S. T., Petters, M. D., Pope, F. D., and Rovelli, G.: The viscosity of atmospherically relevant organic particles, Nat. Commun., 9, 956, https://doi.org/10.1038/s41467-018-03027-z, 2018.
Renbaum-Wolff, L., Grayson, J. W., Bateman, A. P., Kuwata, M., Sellier, M., Murray, B. J., Shilling, J. E., Martin, S. T., and Bertram, A. K.: Viscosity of alpha-pinene secondary organic material and implications for particle growth and reactivity, P. Natl. Acad. Sci. USA, 110, 8014–8019, https://doi.org/10.1073/pnas.1219548110, 2013.
Ribeiro, L. M., Viegas, D. X., Almeida, M., McGee, T. K., Pereira, M. G., Parente, J., Xanthopoulos, G., Leone, V., Delogu, G. M., and Hardin, H.: Extreme wildfires and disasters around the world, in: Extreme Wildfire Events and Disasters, Elsevier, 31–51, https://doi.org/10.1016/b978-0-12-815721-3.00002-3, 2020.
Riemer, N., Ault, A. P., West, M., Craig, R. L., and Curtis, J. H.: Aerosol Mixing State: Measurements, Modeling, and Impacts, Rev. Geophys., 57, 187–249, https://doi.org/10.1029/2018rg000615, 2019.
Robinson, A. L., Subramanian, R., Donahue, N. M., Bernardo-Bricker, A., and Rogge, W. F.: Source apportionment of molecular markers and organic aerosol. 2. Biomass smoke, Environ. Sci. Technol., 40, 7811–7819, https://doi.org/10.1021/es060782h, 2006.
Robinson, A. L., Donahue, N. M., Shrivastava, M. K., Weitkamp, E. A., Sage, A. M., Grieshop, A. P., Lane, T. E., Pierce, J. R., and Pandis, S. N.: Rethinking organic aerosols: semivolatile emissions and photochemical aging, Science, 315, 1259–1262, https://doi.org/10.1126/science.1133061, 2007.
Rogers, D. F.: Laminar flow analysis, Cambridge University Press, Edinburgh Building, Cambridge, 422 pp., 1992.
Rogge, W. F., Hildemann, L. M., Mazurek, M. A., Cass, G. R., and Simonelt, B. R. T.: Souces of fine organic aerosol. 1. Charbroilers and meat cooking operations, Environ. Sci. Technol., 25, 1112–1125, https://doi.org/10.1021/es00018a015, 1991.
Rosenhead, L.: Laminar boundary layers, Dover, New York, 687 pp., 1988.
Rothfuss, N. E.: Toward Better Characterization of the Viscosity of Organic Aerosol, PhD thesis, North Carolina State University, NC, 485 pp., 2019.
Rothfuss, N. E. and Petters, M. D.: Characterization of the temperature and humidity-dependent phase diagram of amorphous nanoscale organic aerosols, Phys. Chem. Chem. Phys., 19, 6532–6545, https://doi.org/10.1039/c6cp08593h, 2017.
Rudich, Y., Talukdar, R. K., Imamura, T., Fox, R. W., and Ravishankara, A. R.: Uptake of NO3 on KI solutions: rate coefficient for the NO3 + I− reaction and gas-phase diffusion coefficients for NO3, Chem. Phys. Lett., 261, 467–473, https://doi.org/10.1016/0009-2614(96)00980-3, 1996.
Rudich, Y., Donahue, N. M., and Mentel, T. F.: Aging of organic aerosol: bridging the gap between laboratory and field studies, Annu. Rev. Phys. Chem., 58, 321–352, https://doi.org/10.1146/annurev.physchem.58.032806.104432, 2007.
Samaké, A., Jaffrezo, J.-L., Favez, O., Weber, S., Jacob, V., Albinet, A., Riffault, V., Perdrix, E., Waked, A., Golly, B., Salameh, D., Chevrier, F., Oliveira, D. M., Bonnaire, N., Besombes, J.-L., Martins, J. M. F., Conil, S., Guillaud, G., Mesbah, B., Rocq, B., Robic, P.-Y., Hulin, A., Le Meur, S., Descheemaecker, M., Chretien, E., Marchand, N., and Uzu, G.: Polyols and glucose particulate species as tracers of primary biogenic organic aerosols at 28 French sites, Atmos. Chem. Phys., 19, 3357–3374, https://doi.org/10.5194/acp-19-3357-2019, 2019.
Schauer, J. J., Kleeman, M. J., Cass, G. R., and Simoneit, B. R. T.: Measurement of emissions from air pollution sources. 3. C-1-C-29 organic compounds from fireplace combustion of wood, Environ. Sci. Technol., 35, 1716–1728, https://doi.org/10.1021/es001331e, 2001.
Schauer, J. J., Kleeman, M. J., Cass, G. R., and Simoneit, B. R. T.: Measurement of emissions from air pollution sources. 5. C-1-C-32 organic compounds from gasoline-powered motor vehicles, Environ. Sci. Technol., 36, 1169–1180, https://doi.org/10.1021/es0108077, 2002.
Schröter, K. and Donth, E.: Viscosity and shear response at the dynamic glass transition of glycerol, J. Chem. Phys., 113, 9101–9108, https://doi.org/10.1063/1.1319616, 2000.
Schwartz, S. E.: Mass-transport considerations pertinent to aqueous phase reactions of gases in liquid-water clouds, in: Chemistry of multiphase atmospheric systems, Springer, Berlin, Heidelberg, Germany, 415–471, https://doi.org/10.1007/978-3-642-70627-1, 1986.
Seinfeld, J. H. and Pandis, S. N.: Atmospheric chemistry and physics: from air pollution to climate change, 3rd ed., John Wiley & Sons, Hoboken, New Jersey, 1152 pp., 2016.
Shiraiwa, M. and Seinfeld, J. H.: Equilibration timescale of atmospheric secondary organic aerosol partitioning, Geophys. Res. Lett., 39, L24801 https://doi.org/10.1029/2012gl054008, 2012.
Shiraiwa, M., Garland, R. M., and Pöschl, U.: Kinetic double-layer model of aerosol surface chemistry and gas-particle interactions (K2-SURF): Degradation of polycyclic aromatic hydrocarbons exposed to O3, NO2, H2O, OH and NO3, Atmos. Chem. Phys., 9, 9571–9586, https://doi.org/10.5194/acp-9-9571-2009, 2009.
Shiraiwa, M., Pfrang, C., and Pöschl, U.: Kinetic multi-layer model of aerosol surface and bulk chemistry (KM-SUB): the influence of interfacial transport and bulk diffusion on the oxidation of oleic acid by ozone, Atmos. Chem. Phys., 10, 3673–3691, https://doi.org/10.5194/acp-10-3673-2010, 2010.
Shiraiwa, M., Ammann, M., Koop, T., and Pöschl, U.: Gas uptake and chemical aging of semisolid organic aerosol particles, P. Natl. Acad. Sci. USA, 108, 11003–11008, https://doi.org/10.1073/pnas.1103045108, 2011.
Shiraiwa, M., Pöschl, U., and Knopf, D. A.: Multiphase Chemical Kinetics of NO3 Radicals Reacting with Organic Aerosol Components from Biomass Burning, Environ. Sci. Technol., 46, 6630–6636, https://doi.org/10.1021/es300677a, 2012.
Shiraiwa, M., Li, Y., Tsimpidi, A. P., Karydis, V. A., Berkemeier, T., Pandis, S. N., Lelieveld, J., Koop, T., and Pöschl, U.: Global distribution of particle phase state in atmospheric secondary organic aerosols, Nat. Commun., 8, 15002, https://doi.org/10.1038/ncomms15002, 2017a.
Shiraiwa, M., Ueda, K., Pozzer, A., Lammel, G., Kampf, C. J., Fushimi, A., Enami, S., Arangio, A. M., Frohlich-Nowoisky, J., Fujitani, Y., Furuyama, A., Lakey, P. S. J., Lelieveld, J., Lucas, K., Morino, Y., Pöschl, U., Takaharna, S., Takami, A., Tong, H. J., Weber, B., Yoshino, A., and Sato, K.: Aerosol Health Effects from Molecular to Global Scales, Environ. Sci. Technol., 51, 13545–13567, https://doi.org/10.1021/acs.est.7b04417, 2017b.
Slade, J. H. and Knopf, D. A.: Heterogeneous OH oxidation of biomass burning organic aerosol surrogate compounds: assessment of volatilisation products and the role of OH concentration on the reactive uptake kinetics, Phys. Chem. Chem. Phys., 15, 5898–5915, https://doi.org/10.1039/c3cp44695f, 2013.
Slade, J. H. and Knopf, D. A.: Multiphase OH oxidation kinetics of organic aerosol: The role of particle phase state and relative humidity, Geophys. Res. Lett., 41, 5297–5306, https://doi.org/10.1002/2014gl060582, 2014.
Slade, J. H., Shiraiwa, M., Arangio, A., Su, H., Pöschl, U., Wang, J., and Knopf, D. A.: Cloud droplet activation through oxidation of organic aerosol influenced by temperature and particle phase state, Geophys. Res. Lett., 44, 1583–1591, https://doi.org/10.1002/2016gl072424, 2017.
Springmann, M., Knopf, D. A., and Riemer, N.: Detailed heterogeneous chemistry in an urban plume box model: reversible co-adsorption of O3, NO2, and H2O on soot coated with benzo[a]pyrene, Atmos. Chem. Phys., 9, 7461–7479, https://doi.org/10.5194/acp-9-7461-2009, 2009.
Steimer, S. S., Berkemeier, T., Gilgen, A., Krieger, U. K., Peter, T., Shiraiwa, M., and Ammann, M.: Shikimic acid ozonolysis kinetics of the transition from liquid aqueous solution to highly viscous glass, Phys. Chem. Chem. Phys., 17, 31101–31109, https://doi.org/10.1039/c5cp04544d, 2015.
Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M.: Climate change 2013: The physical science basis. Contribution of Working Groups I to the fifth assessment report of the Intergovernmental Panel on Climate Change, IPCC, Cambridge University Press, Cambridge, UK and New York, NY, USA, 1535 pp., 2013.
Surratt, J. D., Chan, A. W. H., Eddingsaas, N. C., Chan, M. N., Loza, C. L., Kwan, A. J., Hersey, S. P., Flagan, R. C., Wennberg, P. O., and Seinfeld, J. H.: Reactive intermediates revealed in secondary organic aerosol formation from isoprene, P. Natl. Acad. Sci. USA, 107, 6640–6645, https://doi.org/10.1073/pnas.0911114107, 2010.
Tombari, E. and Johari, G. P.: Structural fluctuations and orientational glass of levoglucosan-High stability against ordering and absence of structural glass, J. Chem. Phys., 142, 104501, https://doi.org/10.1063/1.4913759, 2015.
Virtanen, A., Joutsensaari, J., Koop, T., Kannosto, J., Yli-Pirila, P., Leskinen, J., Makela, J. M., Holopainen, J. K., Pöschl, U., Kulmala, M., Worsnop, D. R., and Laaksonen, A.: An amorphous solid state of biogenic secondary organic aerosol particles, Nature, 467, 824–827, https://doi.org/10.1038/nature09455, 2010.
Wallace, J. M. and Hobbs, P. V.: Atmospheric science: an introductory survey, 2nd ed., Elsevier, 504 pp., 2006.
Wang, B. B., Lambe, A. T., Massoli, P., Onasch, T. B., Davidovits, P., Worsnop, D. R., and Knopf, D. A.: The deposition ice nucleation and immersion freezing potential of amorphous secondary organic aerosol: Pathways for ice and mixed-phase cloud formation, J. Geophys. Res., 117, D16209, https://doi.org/10.1029/2012jd018063, 2012.
Waring, C., King, K. L., Bagot, P. A., Costen, M. L., and McKendrick, K. G.: Collision dynamics and reactive uptake of OH radicals at liquid surfaces of atmospheric interest, Phys. Chem. Chem. Phys., 13, 8457–8469, https://doi.org/10.1039/C0CP02734K, 2011.
Wutz, M.: Theory and practice of vacuum technology, Vieweg, Braunschweig, Germany, 667 pp., 1989.
Yang, Z., Liu, X., Yang, Z., Zhuang, G., Bai, Z., Zhang, H., and Guo, Y.: Preparation and formation mechanism of levoglucosan from starch using a tubular furnace pyrolysis reactor, J. Anal. Appl. Pyrol., 102, 83–88, https://doi.org/10.1016/j.jaap.2013.03.012, 2013.
Zasypkin, A. Y., Grigor'eva, V. M., Korchak, V. N., and Gershenson, Y. M.: A formula for summing of kinetic resistances for mobile and stationary media: I. Cylindrical reactor, Kinet. Catal.+, 38, 772–781, 1997.
Zhang, X., McVay, R. C., Huang, D. D., Dalleska, N. F., Aumont, B., Flagan, R. C., and Seinfeld, J. H.: Formation and evolution of molecular products in alpha-pinene secondary organic aerosol, P. Natl. Acad. Sci. USA, 112, 14168–14173, https://doi.org/10.1073/pnas.1517742112, 2015.
Zhang, Y., Chen, Y. Z., Lambe, A. T., Olson, N. E., Lei, Z. Y., Craig, R. L., Zhang, Z. F., Gold, A., Onasch, T. B., Jayne, J. T., Worsnop, D. R., Gaston, C. J., Thornton, J. A., Vizuete, W., Ault, A. P., and Surratt, J. D.: Effect of the Aerosol-Phase State on Secondary Organic Aerosol Formation from the Reactive Uptake of Isoprene-Derived Epoxydiols (IEPDX), Environ. Sci. Tech. Let., 5, 167–174, https://doi.org/10.1021/acs.estlett.8b00044, 2018.
Zhang, Y., Nichman, L., Spencer, P., Jung, J. I., Lee, A., Heffernan, B. K., Gold, A., Zhang, Z. F., Chen, Y. Z., Canagaratna, M. R., Jayne, J. T., Worsnop, D. R., Onasch, T. B., Surratt, J. D., Chandler, D., Davidovits, P., and Kolb, C. E.: The Cooling Rate- and Volatility-Dependent Glass-Forming Properties of Organic Aerosols Measured by Broadband Dielectric Spectroscopy, Environ. Sci. Technol., 53, 12366–12378, https://doi.org/10.1021/acs.est.9b03317, 2019.
Zhou, S., Hwang, B. C. H., Lakey, P. S. J., Zuend, A., Abbatt, J. P. D., and Shiraiwa, M.: Multiphase reactivity of polycyclic aromatic hydrocarbons is driven by phase separation and diffusion limitations, P. Natl. Acad. Sci. USA, 116, 11658–11663, https://doi.org/10.1073/pnas.1902517116, 2019.
Zhu, C. M., Kawamura, K., and Kunwar, B.: Organic tracers of primary biological aerosol particles at subtropical Okinawa Island in the western North Pacific Rim, J. Geophys. Res., 120, 5504–5523, https://doi.org/10.1002/2015jd023611, 2015.
Ziemann, P. J.: Aerosol products, mechanisms, and kinetics of heterogeneous reactions of ozone with oleic acid in pure and mixed particles, Faraday Discuss., 130, 469–490, https://doi.org/10.1039/b417502f, 2005.
Ziemann, P. J. and Atkinson, R.: Kinetics, products, and mechanisms of secondary organic aerosol formation, Chem. Soc. Rev., 41, 6582–6605, https://doi.org/10.1039/c2cs35122f, 2012.
Zobrist, B., Marcolli, C., Pedernera, D. A., and Koop, T.: Do atmospheric aerosols form glasses?, Atmos. Chem. Phys., 8, 5221–5244, https://doi.org/10.5194/acp-8-5221-2008, 2008.
Zobrist, B., Soonsin, V., Luo, B. P., Krieger, U. K., Marcolli, C., Peter, T., and Koop, T.: Ultra-slow water diffusion in aqueous sucrose glasses, Phys. Chem. Chem. Phys., 13, 3514–3526, https://doi.org/10.1039/c0cp01273d, 2011.
- Abstract
- Introduction
- Experimental methods
- Results and discussion
- Atmospheric implications
- Conclusions
- Appendix A: The impact of gas flow entrance effects and velocity profiles on the reactive uptake kinetics
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Experimental methods
- Results and discussion
- Atmospheric implications
- Conclusions
- Appendix A: The impact of gas flow entrance effects and velocity profiles on the reactive uptake kinetics
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement