the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The sub-adiabatic model as a concept for evaluating the representation and radiative effects of low-level clouds in a high-resolution atmospheric model
Hartwig Deneke
Andreas Macke
The realistic representation of low-level clouds, including their radiative effects, in atmospheric models remains challenging. A sensitivity study is presented to establish a conceptual approach for the evaluation of low-level clouds and their radiative impact in a highly resolved atmospheric model. Considering simulations for six case days, the analysis supports the notion that the properties of clouds more closely match the assumptions of the sub-adiabatic rather than the vertically homogeneous cloud model, suggesting its use as the basis for evaluation. For the considered cases, 95.7 % of the variance in cloud optical thickness is explained by the variance in the liquid water path, while the droplet number concentration and the sub-adiabatic fraction contribute only 3.5 % and 0.2 % to the total variance, respectively. A mean sub-adiabatic fraction of 0.45 is found, which exhibits strong inter-day variability. Applying a principal component analysis and subsequent varimax rotation to the considered set of nine properties, four dominating modes of variability are identified, which explain 97.7 % of the total variance. The first and second components correspond to the cloud base and top height, and to liquid water path, optical thickness, and cloud geometrical extent, respectively, while the cloud droplet number concentration and the sub-adiabatic fraction are the strongest contributors to the third and fourth components. Using idealized offline radiative transfer calculations, it is confirmed that the shortwave and longwave cloud radiative effects exhibit little sensitivity to the vertical structure of clouds. This reconfirms, based on an unprecedented large set of highly resolved vertical cloud profiles, that the cloud optical thickness and the cloud top and bottom heights are the main factors dominating the shortwave and longwave radiative effect of clouds and should be evaluated together with radiative fluxes using observations to attribute model deficiencies in the radiative fluxes to deficiencies in the representation of clouds. Considering the different representations of cloud microphysical processes in atmospheric models, the analysis has been further extended and the deviations between the radiative impact of the single- and double-moment schemes are assessed. Contrasting the shortwave cloud radiative effect obtained from the double-moment scheme to that of a single-moment scheme, differences of about ∼40 W m−2 and significant scatter are observed. The differences are attributable to a higher cloud albedo resulting from the high values of droplet number concentration in particular in the boundary layer predicted by the double-moment scheme, which reach median values of around ∼600 cm−3.
Clouds play a crucial role in the global energy budget and climate. One important aspect is their strong influence on the shortwave (SW) and longwave (LW) radiation budgets. Despite significant progress over the past decades, the relevant processes and resulting climate feedbacks of clouds have not been fully understood and cannot be reliably represented in climate projections (IPCC, 2013). The representation of boundary layer clouds (i.e., shallow cumulus, stratiform) is particularly problematic (Turner et al., 2007) due to their high spatiotemporal variability. In addition, the coarse resolution of general circulation models (GCMs) (∼100 km) is not sufficient to resolve processes taking place at subgrid scale, nor does it allow us to explicitly take vertical and horizontal heterogeneity into consideration.
Clouds are characterized by complicated three-dimensional (3-D) shapes with highly variable macrophysical, microphysical, and radiative properties. Full 3-D radiative transfer calculations in complex cloudy atmospheres are computationally expensive, and hence a number of simplifications are commonly adopted for calculating their radiative effect in atmospheric models. The plane-parallel (PP) approximation is often utilized, which implies that radiative transfer simulations are conducted assuming horizontally homogeneous clouds covering a fraction of the model grid (Di Giuseppe and Tompkins, 2003; Chosson et al., 2007). One particular shortcoming of this assumption is the so-called plane-parallel albedo bias, which refers to the fact that inhomogeneous clouds reflect less solar radiation than otherwise identical homogeneous clouds (Werner et al., 2014). To account for this bias, and to consider horizontal heterogeneities in GCMs, several correction schemes have been developed over the last years, e.g., scaling the liquid water path by a constant reduction factor, renormalization techniques, among others (e.g., Cahalan et al., 1994; Barker, 2000; Cairns et al., 2000; Barker and Räisänen, 2004; Pincus et al., 2003; Shonk and Hogan, 2008).
The optical properties of a cloudy layer are largely determined by two of their physical properties: the liquid water content (qL) and the effective radius (reff) (Slingo, 1989; Collins et al., 2006). The latter is mostly obtained by assuming a fixed droplet size distribution (Chosson et al., 2007). Double-moment cloud microphysical schemes, which also constrain the effective radius through prognostic equations, are only recently becoming more widespread in use in operational forecasting.
To improve the scientific understanding of clouds and their representation in models, high-quality observations from active (i.e., lidar and cloud radar) and passive (i.e., radiometers) instruments from both ground and space are essential. Currently, such instrumentation is available, i.e., from the Cloudnet program (Illingworth et al., 2007), the A-Train constellation (Stephens et al., 2002), and the geostationary satellite Meteosat Second Generation (MSG) (Roebeling et al., 2006), while upcoming missions comprise the Earth Cloud Aerosol Radiation Explorer (EarthCARE) satellite mission (Illingworth et al., 2015) and Meteosat Third Generation (MTG) (Stuhlmann et al., 2005). A variety of algorithms have been developed for inferring cloud properties from these observations (e.g., Nakajima and King, 1990; Bennartz, 2007; Roebeling et al., 2013). However, the underlying observational techniques often rely heavily on assumptions about the cloud vertical structure.
High-resolution atmospheric models at cloud-resolving scales are another promising avenue to gain insights into cloud processes and the effects of small-scale cloud variability, and to improve their representation in GCMs. They can resolve relevant processes up to a much smaller scale (∼100 m for large eddy simulations) and can thus serve as the basis for developing more accurate parameterizations. Enabled by the exponential growth in computer power over the past decades, they are increasingly utilized for simulations covering larger domains and longer time periods. In contrast to observations, they also offer the opportunity to assess the interplay of all relevant state variables simultaneously, while instrumental capabilities are generally limited to a small subset, sometimes affected by large measurement uncertainties (Miller et al., 2016).
It is, however, crucial to also critically evaluate the performance of high-resolution models with observations. Like coarse-resolution models, they include various assumptions and parameterizations, and their shortcomings need to be identified and mitigated. Given the complexity of atmospheric models and the level of detail available from the output of such models, it is, though, often a daunting task to identify the physical reasons for model shortcomings. Inconsistent or even conflicting assumptions made in observation-based products add further complications to the evaluation of models with observations. Examples of such assumptions include a vertically homogeneous or a sub-adiabatic cloud that is often made in satellite retrievals (Brenguier et al., 2000; Chosson et al., 2007) or the assumption of a vertically constant cloud droplet number concentration commonly used in ground-based remote sensing of clouds, which is a significant simplification of the profiles available from in situ observations or double-moment cloud microphysical schemes.
In this work, the highly resolved ICON-LEM atmospheric model (ICOsahedral Non-hydrostatic Large-Eddy Model) is employed, which was recently developed within the HD(CP)2 (High Definition Clouds and Precipitation for advancing Climate Prediction) project (Dipankar et al., 2015; Heinze et al., 2017). We introduce a conceptual approach for evaluating the representation of low-level clouds in this and other high-resolution atmospheric models, with a particular focus on the correct representation of their radiative effect. A sensitivity study is conducted in order to investigate the relevance of the vertical distribution of microphysical properties for their radiative effect, aiming for the identification of suitable column-effective cloud properties for the purpose of model evaluation. The suitability of the sub-adiabatic cloud model is compared to that of the vertically homogeneous cloud model, both of which are commonly used in remote sensing. In addition, differences in cloud radiative properties arising from the availability of the cloud droplet number concentration provided by the double-moment cloud microphysical scheme of Seifert and Beheng (2006) compared to a single-moment scheme are highlighted.
2.1 ICON-LEM
The ICON unified modeling framework was co-developed by the German meteorological service (DWD) and the Max Planck Institute for Meteorology (MPI-M) in order to support climate research and weather forecasting. Within the HD(CP)2 project, ICON was further extended towards large eddy simulations with realistic topography and open boundary conditions. This resulted in ICON-LEM deployed in restricted areas that are centered on Germany and the tropical Atlantic (Heinze et al., 2017). The equations utilized by the model are based on the prognostic variables given by Gassmann and Herzog (2008). Concerning turbulence parameterization, the three-dimensional Smagorinsky scheme is employed (Dipankar et al., 2015). These variables comprise the horizontal and vertical velocity components, the density of moist air, the virtual potential temperature, and the mass and number densities of traces, e.g., specific humidity, liquid water, and different ice hydrometeors. A comprehensive description of the model and its governing equations is found in Dipankar et al. (2015) and Wan et al. (2013). The activation of cloud condensation nuclei (CCN) is based on the parameterization of Seifert and Beheng (2006) and modified in order to account for the consumption of CCN due to their activation into cloud droplets. The CCN concentration is then parameterized following the pressure profile and the vertical velocity (Hande et al., 2016).
ICON-LEM utilizes the double-moment mixed-phase bulk microphysical parameterization scheme introduced by Seifert and Beheng (2006). Following their comprehensive description, a generalized gamma distribution is utilized to describe the mass (xm) of hydrometeors:
The coefficients ν, ξ are constants taken from Table 1 in Seifert and Beheng (2006), while the coefficients Am and Bm are prognostic quantities expressed by the number and mass densities (see Appendix A).
Simulations are carried out for three different domains with 624, 312, and 156 m horizontal resolution. The model domains consist of 150 vertical levels, with resolutions ranging from ∼25 to 70 m within the boundary layer, and from 70 to 355 m further up until the top of the domain at 21 km. For each of the aforementioned grids, data are stored as one-dimensional (1-D) profiles every 10 s, two-dimensional (2-D), and 3-D snapshots (Heinze et al., 2017). In the case of the 3-D output, the simulation data are interpolated from the original grids (e.g., 156 m) to a 1 km grid, the 3-D coarse data, and 300 m grid, the so-called HD(CP)2 Observational Prototype Experiment (HOPE) data. The latter output has been created for the purpose of model evaluation with ground-based observations from HOPE, which took place near Jülich (Macke et al., 2017) and is limited to a domain size of about ∼45 km2. Note here that for the 2-D and 3-D output, data are stored at day- and nighttime frequencies. Daytime frequency begins at 06:00 UTC and lasts until 00:00 UTC, while nighttime starts at midnight and lasts until 06:00 UTC. The 2-D data are stored with a daytime and nighttime frequency of 10 s and 5 min, respectively. The 3-D coarse data have a daytime frequency of 10 min (1 h at nighttime). In this study, the 3-D HOPE data that are stored only at a daytime frequency of 15 min have been used.
2.2 RRTMG
For radiative transfer simulations, ICON-LEM employs the Rapid Radiative Transfer Model (RRTM) for GCM applications (RRTMG) (Mlawer et al., 1997; Iacono et al., 2008). For the purpose of this investigation, an interface of the RRTMG for use with the Python programming language has been developed, which allows the offline calculation of the radiative fluxes using ICON-LEM outputs as the basis.
RRTMG is a fast and accurate broadband radiative transfer model developed by Atmospheric Environmental Inc. The model employs the correlated-k approach for efficient fluxes and heating rate computations (Mlawer et al., 1997). Molecular absorption information for the k distributions is taken from the line-by-line radiative transfer model (LBLRTM) (Clough et al., 2005). Fluxes and heating rates are derived for 14 bands in the SW and 16 bands in the LW. RRTMG considers major absorbing gases, i.e., water vapor, ozone, and carbon dioxide, but also minor absorbing species, i.e., methane, oxygen, nitrogen, and aerosols. Optical properties (optical thickness, single-scattering albedo, and asymmetry parameter) of liquid water clouds are parameterized according to Hu and Stamnes (1993). Note that the RRTMG is a 1-D plane-parallel radiative transfer model. For the representation of the subgrid cloud variability, a Monte Carlo independent column approximation (McICA) method is used (Pincus et al., 2003). Multiple scattering is considered employing a two-stream algorithm (Oreopoulos and Barker, 2006).
RRTMG provides the SW and LW radiative fluxes for both upward (F↑) and downward (F↓) radiation. These two components can be combined to define the net flux (Fnet):
Accordingly, the cloud radiative effect (CRE) is defined as the difference between the cloudy and clear-sky net radiative fluxes:
The CRE can be computed for the LW, SW, or the net CRE, defined by the sum of the SW and LW radiation.
2.3 Case days
In this study, the 3-D HOPE data have been used, and a set of 6 d of simulations has been considered, including 24–25 April and 5 May 2013, 29 July and 14 August 2014, and 3 June 2016. Only a limited subset of variables is stored, including the specific humidity, cloud water, ice, rain and snow mixing ratio, wind, vertical velocity, temperature, pressure, cloud cover, and turbulent diffusion coefficient for heat. These days have been selected from the total set of available case days by the presence of suitable liquid water cloud fields and no known bugs in the used model version, which affect the representation of low-level clouds.
2.4 Column selection
In order to investigate the characteristics of liquid water clouds in ICON-LEM, only idealized cloud profiles (i.e., stratiform and cumulus) are considered, corresponding to single-layer non-drizzling clouds. The selection of such cloudy columns has been conducted according to the following threshold criteria:
-
For each cloudy layer, there is a liquid water content of qL>0.01 g m−3. For each cloudy column, there is a liquid water path (QL) larger than 20 g m−2.
-
There is no occurrence of rain/drizzle, with a rain water path below 0.1 g m−2 and dBZ, denoting the maximum radar reflectivity (see Eq. 6) within the cloud profile (Rémillard et al., 2013; Merk et al., 2016).
-
A cloud geometrical extent (H) larger than 100 m (at least two subsequent model layers) is present.
-
Clouds are located between 300 and 4000 m.
-
No vertical gaps are allowed.
-
Mixed-phase clouds are excluded. The ice water content for the first 4000 m must be zero.
-
Superadiabatic clouds have been excluded.
The cloud bottom height (CBH) and cloud top height (CTH) are determined by the bottom and top of the lowermost and uppermost layers for the aforementioned ideal low-level clouds, respectively.
2.5 Cloud property diagnostics
The model outputs the droplet number concentration and liquid water content for each model layer representing the zeroth and the first moments of the mass size distribution (MSD; see Eq. 1). Following Petty and Huang (2011), the mass size distribution is transformed into a droplet size distribution (DSD). For details on the derivation of the moments of DSD and the cloud microphysical properties, the reader is referred to Appendix A.
Following Hansen and Travis (1974), the effective radius, reff, is defined as the ratio of the third to second moments of the DSD:
The division by 2 is carried out for diameter-to-radius conversion. The effective radius is linked to the volume-equivalent radius (rV) by the k2 factor, which depends only on the effective variance (υ) of the droplet size distribution:
For ICON-LEM, the effective variance of the reconstructed gamma DSD is υ=0.052, corresponding to k2=0.849. Typical values of k2 reported in the literature vary between 0.5 and 1 (e.g., Brenguier et al., 2000; Zeng et al., 2014; Merk et al., 2016). Furthermore, the radar reflectivity is defined as the sixth moment of the size distribution:
Note that, in ICON-LEM, the droplet number concentration varies with height, but the width of the DSD is assumed invariant.
2.6 Cloud models
2.6.1 Vertically homogeneous cloud model
A widely used assumption for passive satellite and ground-based retrievals is the vertically homogenous cloud model. Accordingly, a vertically homogeneous DSD is assumed, meaning vertically constant microphysical properties. It follows that the cloud liquid water path is given by
describing a positive linear relationship between QL and both the cloud optical thickness (τ) and effective radius (reff). Here, ρw stands for the water density, while the factor 2∕3 is a scale factor resulting from the constant liquid water content and effective radius with height (Lebsock and Su, 2014). Assuming a vertically constant cloud droplet number concentration additionally implies that the cloud geometric extent depends linearly on the cloud water path for a fixed effective radius.
2.6.2 Sub-adiabatic cloud model
The sub-adiabatic cloud model describes the evolution of a convective closed parcel of moist air. According to Albrecht et al. (1990), the liquid water content (qL) of such an air parcel increases linearly with height:
where Γad is the adiabatic increase of the liquid water content (Bennartz, 2007), z is the height over the cloud base, fad denotes the sub-adiabatic fraction, T is the temperature, and P is the pressure. fad describes the deviation from the linear increase with height of qL caused by entrainment of dry air resulting in evaporation and fad<1 (sub-adiabaticity). In the case of a pure adiabatic cloud, fad=1 and Eq. (8) yields to the adiabatic liquid water content (qL, ad). For low-level liquid water clouds, typical values of fad found in the literature are in the range of 0.3 to 0.9 (Boers et al., 2006). An alternative definition for the liquid water content accounting for the depletion of the liquid water content due to entrainment, precipitation, and freezing drops is described by
following a modified sub-adiabatic profile (Karstens et al., 1994; Foth and Pospichal, 2017).
Γad depends on temperature (weak function of pressure) following the first law of thermodynamics and the Clausius–Clapeyron relationship. For low-level clouds, Γad varies slightly (∼20 %). Consequently, in most studies, Γad is assumed constant (e.g., Albrecht et al., 1990; Boers et al., 2006) or it is calculated from cloud bottom temperature and pressure (e.g., Merk et al., 2016) or cloud top information (e.g., Zeng et al., 2014). For this study, an average value of Γad between cloud bottom and cloud top has been used.
Integrating the liquid water content between cloud base height and cloud top height, the cloud liquid water path is obtained:
Hereby, H denotes the cloud geometrical extent. Compared to Eq. (7), Eq. (10) leads to a factor of 5∕9, meaning that the sub-adiabatic liquid water path is 5∕6 times the one of the vertically homogeneous model (Wood and Hartmann, 2006). Dividing QL by its adiabatic value (inserting fad=1 into Eq. 10), the sub-adiabatic fraction can be computed:
For low-level liquid water clouds, the droplet number concentration (Nd) depends on the availability of cloud condensation nuclei (CCN) that could get activated at cloud base (Bennartz, 2007). Considering the adiabatic increase of the liquid water content, it follows that at any given height, qL is distributed over the activated CCN (per unit volume). Consequently, there is no dependency of the mean volume radius rV on the shape of the droplet size distribution but only on Nd and qL:
Combining Eqs. (5) and (12), the effective radius for the uppermost cloud layer can be written in terms of the liquid water path, the droplet number concentration, and the adiabatic fraction:
In the geometric optics regime, the extinction coefficient, bext, can be written as a function of the liquid water content and the effective radius. Consequently, the cloud optical thickness can be computed by integrating bext over the cloud geometrical extent, i.e., from cloud base height to cloud top height:
For vertically constant qL and reff, this can be interpreted as the cloud optical thickness coming from the vertical homogeneous model (see Eq. 7). According to the sub-adiabatic cloud model, the cloud optical thickness is linked to the liquid water path and the effective radius (Wood, 2006):
Alternatively, substituting reff from Eq. (13) in Eq. (15), the cloud optical thickness is given by
3.1 General features
Table 1 lists the statistics of the cloud properties for all the case days individually and on average as simulated by ICON-LEM, while Fig. 1 illustrates the corresponding histograms for the latter case only. Note that for the droplet number concentration and the effective radius, results are presented as follows:
-
Droplet number concentration weighted over the cloud geometrical extent is given by
-
effective radius weighted over the extinction coefficient at each layer is given by
It can be shown that the latter equation reduces to Eq. (7), which implies that the calculated effective radius corresponds to that of a vertically homogeneous cloud with identical liquid water path and optical thickness. The different cloud properties are characterized by a large variability from day to day but even within the same day driven by entrainment processes. In addition, the differences are also subject to the sample size (n) for each day depending on the column selection filter that applied to ICON-LEM output. Recall here that a cloudy column is taken under consideration when qL>0.01 g m−3 for each cloud model level, while the liquid water path for the entire column should be larger than 20 g m−2. Subsequently, the fraction of clouds (FC) selected in this study is quite low (FC<3 %). Alternatively, if only a liquid water path filter is applied to the data, defining as cloudy the columns with QL larger than 1 g m−2, the actual cloud fraction (CF) is obtained. The rather large value of the CF found for 3 June 2016 is associated with very low (with m) overcast cloudy conditions in the early hours.
Table 1Statistics of cloud properties of low-level clouds for all the case days individually and on average as simulated by ICON-LEM. n stands for the sample size. For the fraction of clouds, two values are presented: values in brackets denote the fraction of selected clouds (FC) according to the column selection (see Sect. 2.4), while values outside brackets stand for the actual cloud fraction (CF) in terms of the following threshold for the liquid water path, QL>1 g m−2.
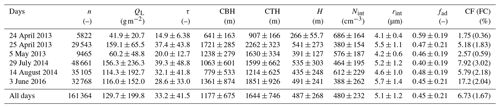
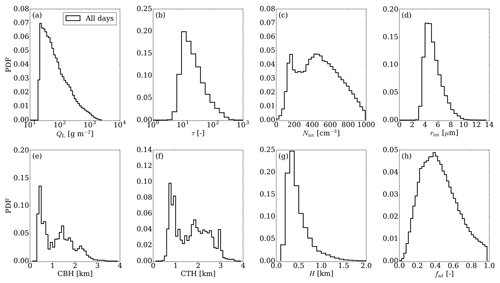
Figure 1Histograms of cloud properties for all the case days on average as simulated by ICON-LEM: (a) QL, (b) τ, (c) Nint, (d) rint, (e) CBH, (f) CTH, (g) H, and fad.
Looking at the mean histograms of CTH and CBH, one can identify multimodal distributions. Note here that, in this study, all low-level clouds are considered (i.e., cumuli-like, stratiform) increasing the variability of the different properties.
The double-moment microphysical scheme adopted in ICON-LEM is reflected on the histograms of the droplet number concentration. The mean histogram of Nint for all the case days on average suggests a bimodal distribution with peaks centered around 200 and 450 cm−3. These two modes are clearly found for 29 July and 14 August 2014, and 3 June 2016. Especially for 3 June 2016, the peak around 200 cm−3 is even more notable (not shown here). Note here that this value is close to the fixed droplet number concentration profile suggested by single-moment microphysical schemes adopted by atmospheric models, such as ECHAM (Giorgetta et al., 2013) and ICON-NWP, which is the global numerical weather prediction (NWP) version of the ICON model (Heinze et al., 2017). For 5 May 2013, the corresponding histogram is characterized by a right-skewed distribution, with a rather long tail towards large values of Nint and a very small peak that appears around 800 cm−3. On the contrary, for 24–25 April 2013, the distributions of Nint are described by skewed distributions (not shown here) with well-defined single peaks. For 24 April, the peak veers towards large Nint values (left skewed), while, for 25 April, the peak is located at small Nint values (right skewed), which are centered around 686 and 380 cm−3, respectively. A close relation between the effective radius and the droplet number concentration exists. On average, the larger the Nint, the smaller the rint.
3.2 Vertical variability
Figure 2 shows a box-and-whisker plot of the droplet number concentration for all the case days on average, describing the histograms of Nd simulated for different model levels by the double-moment scheme of ICON-LEM. For comparison, the red line shows the climatology-based droplet number concentration profile adopted by ECHAM (Giorgetta et al., 2013). While above 2 km altitude, the modeled values match the climatology well, much larger median values up to 600 cm−3 are found in the boundary layer. Compared to satellite estimates of Nd, these values seem rather high (Quaas et al., 2006; Grosvenor et al., 2018). On the contrary, in situ observations suggest higher values of Nd and, accordingly, closer to those simulated by ICON-LEM. Hence, efforts should be undertaken to further validate the cloud droplet number concentrations predicted by the double-moment scheme.
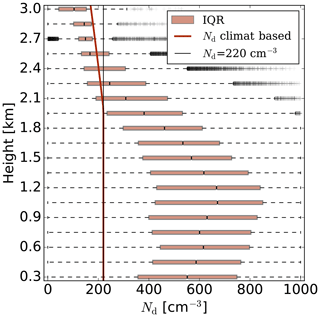
Figure 2Box-and-whisker plot of the droplet number concentration for all the case days on average, describing the histograms of Nd simulated for different model levels by the double-moment scheme of ICON-LEM. Boxes illustrate interquartile range (IQR), dark red line denotes the climatology-based Nd profile adopted by ECHAM, and the thin black line demonstrates the constant Nd profile of 220 cm−3.
Figure 3 depicts the mean profiles of qL and Nd normalized over the cloud geometrical extent (from CBH to CTH) for all the case days on average. The ICON-LEM simulated liquid water profile follows a linear increase from cloud bottom to around 50 %–60 % of the cloud height, in agreement with the adiabatic cloud model. Thereafter, the liquid water content decreases towards the cloud top due to evaporation induced by entrainment of dry air mass from cloud top. Furthermore, the mean profile of the droplet number concentration is found roughly constant at vertical depths between 30 % and 70 % of H (∼480 cm−3) and decreases towards the cloud top at values ∼100 cm−3 characterized by a large variability.
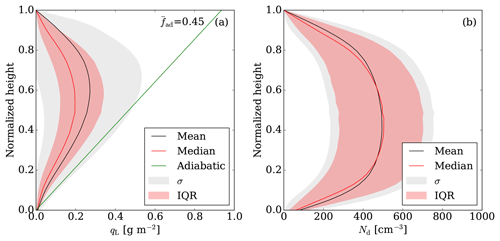
Figure 3ICON-LEM simulated mean (a) qL and (b) Nd profiles for all the case days on average. Profiles are normalized over height from the CBH to the CTH. Black lines denote the mean, solid red lines the median, gray shaded areas the standard deviation, red shaded areas the interquartile range (IQR), and the solid green line outlines the mean adiabatic qL profile characterized by a mean adiabatic fraction () of 0.45.
3.3 Adiabaticity of liquid water clouds
Following the sub-adiabatic cloud model, higher values of the liquid water path are linked with geometrically thicker clouds (see Eq. 10). For all the days, the distribution of the cloud geometrical extent follows a similar pattern, except for 24 April and 5 May 2013. For the latter two days, only optically thinner clouds are simulated as compared to the rest of days, with τ values of 14.9 and 20, respectively. However, this could also be subject to the very small sample size as compared to the other simulated days. The highest mean value of the sub-adiabatic fraction is found for 24 April 2013, whereby only optically and geometrically thin clouds are simulated located at the lowermost altitudes (mean CTH of 907 m). One could expect the same findings for 5 May 2013, but the smaller values of fad are partly associated with the higher values of H, together with their vertical location, where entrainment processes can be more pronounced. The lowest mean values of fad are found for 29 July 2014 reflected by the high frequency of occurrence of larger values of the cloud geometrical extent. Overall, the statistics of fad for the six days under investigation (161 364 liquid water cloudy columns) over Germany introduces a mean value of about fad=0.45 (see Table 1), while the interquartile range (IQR) is [0.29,0.59]. There is a wide range of values of fad from nearly 0 to 1. The latter is in agreement with the findings of Boers et al. (2006) and Merk et al. (2016). Especially Merk et al. (2016) derived the fad from ground-based observations over Germany and reported a mean value of 0.45 for the period of 2012–2015, with an IQR of [0.29,0.61]; Boers et al. (2006) reported fad values within [0.3,0.9].
3.3.1 Cloud optical thickness
One of the fundamental cloud properties describing the SW radiative effect is the cloud optical thickness. In this section, we focus on its derivation and its dependencies.
Table 2Prediction of cloud optical thickness by an ordinary least squares regression method: regressor coefficients (a), Y intercept (a0), squared correlations (R2), and root mean square error (RMSE). Theoretical (Th.) values according to the sub-adiabatic model are also included.

With this intention, an effort has been conducted to predict the cloud optical thickness derived from Eq. (14) by employing the sub-adiabatic model and Eq. (16). On a logarithmic scale, Eq. (16) suggests that τ is a linear function of QL, fad, and Nd, and it can be seen as a linear regression model. Here, the droplet number concentration weighted over the cloud geometrical extent (Nint) is used. An advantage of the logarithmic scale is that the variance of the cloud optical thickness can be decomposed into the contributions from each of the regressors (QL, fad, and Nint). This enables us to attribute the relative importance of the regressors in explaining the variance in τ. In our framework, we employed the ordinary least squares (OLS) regression method. This method finds the projection direction for which QL, fad, and Nint are maximally correlated with τ and provides the values of the coefficients that minimize the error in the prediction of τ. Results are compiled in Table 2.
Firstly, we focus on the relative importance of QL in τ. Model Y1(QL) suggests that the liquid water path explains 95.7 % of the variance in cloud optical thickness and it follows an excellent linear relationship with a 5∕6 slope (α=0.849) and a root mean square error (RMSE) of 0.175. In agreement with the sub-adiabatic model, τ is proportional to and not to QL as suggested by the vertically homogeneous model; otherwise, a value of α=1 would be expected. Comparing the models Y2(QL,Nint) and Y3(QL,fad), Y2 has a higher R2 value (0.992 compared to 0.959) and a lower RMSE (0.075 compared to 0.172), while the regression coefficients are much closer to the sub-adiabatic theory.
All in all, the liquid water path is able to explain 95.7 % of the variance in cloud optical thickness, while the droplet number concentration and the sub-adiabatic fraction additionally contribute 3.5 % and 0.2 % to the variance, respectively.
Variability caused by Γad is insignificant and thus is not shown here. This is confirmed by model , which, even though it excludes Γad, explains 99.9 % of the variance in cloud optical thickness. In fact, model supports the applicability of the sub-adiabatic model since it is able to approximate the cloud optical thickness with high accuracy (RMSE=0.027).
To identify the minimum set of parameters for the representation of low-level clouds towards the computation of the CREs, the dominating modes of variability among the different cloud properties have been investigated. Cloud properties from all the case days have been considered. Γad is not a cloud property, but since it is considered by the sub-adiabatic model, we decided to include it in the analysis. Towards this direction, one should first map the correlation of the different properties. Figure 4 identifies groups of variables that tend to covary together. The first group comprises τ, QL, and H, which are strongly positively correlated with one another (Pearson>0.837), while in the second group, CTH and CBH are positively correlated (Pearson>0.934), albeit inversely correlated with Γad (). Alternatively, these two groups could be partly noted as the SW and LW (excluding Γad) properties, respectively. Last but not least, only a weak to mediocre correlation was found between rint, Nint, fad, and the other properties.
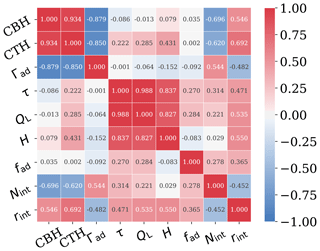
Figure 4Correlation plot between all the properties (CBH, CTH, Γad, τ, QL, H, fad, Nint, and rint). The color bar indicates the values of the corresponding Pearson correlations.
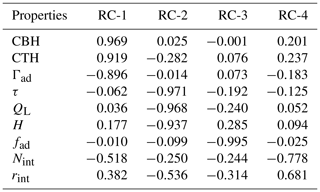
A principal component analysis (PCA) and a subsequent varimax rotation (hereafter rotational component analysis) are applied to reveal systematic covariations among the cloud properties, reducing the degrees of freedom, while preserving the maximum amount of information towards redundancy. This analysis has been conducted by employing the logarithm of the properties. Since our aim is to retain as few degrees of freedom as possible, the first step is to estimate the optimal number of components needed. As a primary solution, we used the same number of components as the original variables (nine in number) and we estimated the fraction of variance explained by each component. Table 3 illustrates the resulting cumulative explained variance as a function of each rotational component (RC). The cumulative explained variance suggests the use of four RCs (97.7 %), going from a nine-dimensional space to a four-dimensional space; the variance contributed by the fifth component is 2.1 %. The interpretation of the principal components (not shown here) is based on finding which properties are correlated with each principal component (PC). However, PCs are hard to interpret. Although each new dimension is clearly dominated by some of the cloud properties, the PCs are found moderately or strongly correlated with other properties. However, the rotational component analysis associates each cloud property to at most one RC by maximizing the sum of the variance of the squared correlations between the cloud properties and the PCs (Stegmann et al., 2006).
Table 3Explained variance and cumulative explained variance by different components obtained from the RC analysis.

Table 4 summarizes the quality of reduction in Pearson correlations by comparing the residual correlations to the logarithm of the original cloud properties. These correlations are either close to unity or zero, allowing only a few moderate correlations and pointing to how each cloud property loads on each component. RC-2, responsible for 35.5 % of the total variance, is strongly correlated with three of the original variables, i.e., τ, QL, and H, with Pearson correlations of −0.971, −0.968, and −0.937, respectively. Considering the strong correlation found between τ and QL (see Fig. 4) and their robust linear relation (Pearson=0.988), they can be considered interchangeable. In the same direction are the findings for RC-1 and CBH (Pearson=0.969), CTH (Pearson=0.919), and Γad (), with an explained variance of about 33.8 %. RC-3 and RC-4 are clearly a function of fad () and Nint (), respectively. They explain 14.8 % and 13.6 % of the total variance (see Table 4), pointing to two clear degrees of freedom. Effective radius is the only property that shows a moderate or strong importance in more than one RC, namely RC-2 and RC-4, but it could be substituted as a degree of freedom from a well-defined DSD, with Nint as a primary component and k2. Note here that the first two components account for more than 69.3 % of the variance of the cloud properties, with the first component related to those that dominate in the SW CRE, while the second component is related to those that are of great importance in the LW CRE.
Table 4Pearson correlations between the logarithm of the cloud properties and the RCs. Degree of correlation (absolute values): (a) very weak: below 0.2, (b) weak: [0.2,0.4), (c) moderate: [0.4,0.6), (d) strong: [0.6,0.8), and (e) very strong [0.8,1.0].
The aforementioned analysis points to the reduced set of parameters for the representation of low-level clouds towards the computation of the CREs: Nint, QL, fad, H, and one of the CTH or CBH.
5.1 Radiative transfer simulations
The input for the radiative transfer simulations was constructed on the basis of ICON-LEM. In other words, temperature, pressure, and water vapor profiles, surface temperature and pressure, and cloud liquid water content and droplet number concentration are taken from the high-resolution model. For ozone, the profile of the US standard atmosphere is adopted (Anderson et al., 1986). Note here that ICON-LEM profiles reach approximately 21 km altitude. Hence, we further extended the atmosphere up to 120 km height according to the US standard atmosphere. Considering the focus of this study, the effects of aerosols are neglected and a maximum cloud overlap of cloudy layers is assumed, since only idealized single-layer water clouds are considered. Table 5 compiles the rest of the input parameters for the radiative transfer simulations that are not adopted by ICON-LEM.
5.1.1 Simulated scenarios
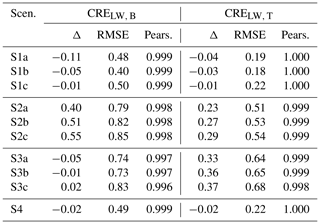
In order to estimate the effects of the bulk microphysical parameterizations and the vertical stratification of the cloud properties on the CREs, the double-moment scheme (ICON-LEM; hereafter reference simulation, ref.) is confronted against the following scenarios: S1, single-moment scheme, whereby the droplet number concentration follows a fixed profile that varies according to pressure profile (P), sharing the same liquid water content profiles as in the reference simulation:
with
Here, Nd, 2 is the droplet number concentration in the boundary layer, cm−3 denotes the corresponding value in the free troposphere, and Pb is the boundary layer height (800 hPa) (Giorgetta et al., 2013). Two different scenarios are considered, where the liquid water path is preserved within the vertical column, but the water content profile is redistributed: in S2, a constant liquid water content profile is used, with a fixed droplet number concentration representing the vertically homogeneous cloud model, and scenario S3 denotes the equivalent sub-adiabatic profile. Finally, scenario S4 employs the mean vertical profile of Nd over all case days (see Fig. 2). For scenarios S1–S3, three individual simulations have been conducted according to the following droplet number concentration:
-
Nd following the climatology of ECHAM, 220 cm−3;
-
Nd weighted over H, Nint; and
-
Nd=480 cm−3, employing the mean Nint for all case days.
Note here that all scenarios share the same QL and k2 parameters. The different scenarios are summarized in Table 6.
5.1.2 Modeled CREs
For the reference run, the mean and the standard deviation of the modeled CREs for the SW, LW, and NET (SW plus LW) radiation are summarized in Table 7. The atmospheric cloud radiative effect (ATM), defined as the difference between CREs at the top of the atmosphere (TOA) and bottom of the atmosphere (BOA), is also included. Results are presented for all the case days. Low-level clouds induce a strong negative SW CRE, driven by vigorous scattering, and a positive LW CRE, due to absorption of upward radiation, resulting in a net cooling effect. The warming of the atmosphere due to absorption of SW radiation (∼32.9 W m−2) is recompensed by the atmospheric LW cooling ( W m−2), leading to a net cooling of the atmosphere ( W m−2). The net CRE is characterized by high variability depending on the distribution of the microphysical and optical cloud properties (see Sect. 5.1.3).
Table 7Mean and standard deviation of modeled CREs (W m−2) for the SW, LW, and NET (SW plus LW) radiation for the reference simulation over all case days. ATM stands for the atmospheric cloud radiative effect, defined as the difference between the CREs at the TOA and BOA.

Table 8 lists the difference of the mean CREs between the reference and the rest of the simulated scenarios for the SW radiation for both TOA and BOA. In the LW, all the scenarios are able to reproduce the reference mean CREs (see Table C1 in Appendix C); the difference of the mean CRE is below ∼0.55 W m−2 (in absolute values), with the vertically homogeneous run leading to the largest differences. Note here that the deviations in the CREs for the BOA and the TOA are of the same magnitude.
Table 8Mean CRE (W m−2) for the SW radiation. Results are given as differences between the new scenario and the reference simulation (Δ). The RMSE in W m−2 and the Pearson (Pears.) correlation between the new scenarios and the reference simulation are also given.
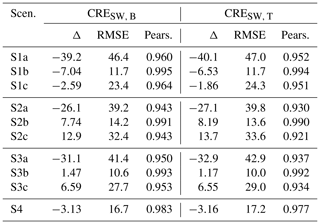
Overall, the single-moment radiative transfer simulations underestimate the SW CREs for both the TOA and BOA. Starting from S1a (220 cm−3), the CRE in the single-moment run is −40.1 W m−2 less than the double-moment one, with a RMSE up to 47 W m−2. The latter differences are attributed to the very low droplet number climatology adopted by coarse climate models (such as ECHAM, ICON-NWP) as compared to ICON-LEM. For a given liquid water path, the smaller the droplet number concentration, the larger the resulting effective radius and, accordingly, the smaller the cloud reflectance. In other words, this can be seen as the magnitude of the cloud albedo effect, the so-called first indirect effect (e.g., Twomey, 1977; Ackerman et al., 2000; Werner et al., 2014). For all the case days, a mean value of 480±232 cm−3 is found for the droplet number concentration, and a fixed Nd profile of 220 cm−3 (in the boundary layer) can only represent a small fraction of the bimodal distribution of the droplet number concentration yielded from ICON-LEM (see also Fig. 1). A single-moment run with a more representative value for the droplet number concentration approximates the SW CRE with more accuracy. By employing the mean Nint (S1c), the differences in the CRE between the single- and the double-moment runs are considerably smaller but with quite large scatter; for the BOA (TOA), a RMSE of 23.4 W m−2 (24.3 W m−2) and a Pearson correlation of 0.964 (0.951) are yielded. The best scenario is found to be S1b, which is supplied by the droplet number concentration weighted over the cloud geometrical extent, i.e., Nint. The differences of the mean CREs between S1b and the reference simulations lead to a RMSE of 11.7 W m−2 and a Pearson correlation of at least 0.994 for both the BOA and TOA. The latter small differences are no surprise considering the quite realistic representation of the droplet number concentration in each profile.
Having preserved the liquid water path profile (but redistributed scenarios 2–3), one can regard the changes in the CREs to the vertical stratification of low-level clouds within ICON-LEM. Comparing the SW CREs yielded by the vertically homogeneous (S2) and the sub-adiabatic (S3) runs, it follows that the shape of the liquid water content profile, and thus the other cloud properties, can be well represented by the sub-adiabatic model. This is in agreement with our findings in Sect. 3.2 and 3.3. In brief, for the simulations with the more representative droplet number concentration values (sub-cases), i.e., Nint (b) and mean Nint for all case days (c), the differences in the mean CREs are more pronounced for the vertically homogeneous equivalent simulation (S2), as compared to the sub-adiabatic one (S3) for both BOA and TOA: for S2b (for S2c) of about 8.19 W m−2 (13.7 W m−2) with a RMSE up to 14.2 W m−2 (33.6 W m−2) and for S3b (S3c) of about 1.47 W m−2 (6.59 W m−2) with a RMSE up to 10.6 W m−2 (29 W m−2), respectively. The dependency of the latter deviations on the different droplet number concentration values follows the same pattern as that for the single- vs. double-moment schemes. For instance, in the case of the sub-adiabatic scenario (S3) and, going from the least to the most accurate ones, errors (in terms of the RMSE) up to 42.9 W m−2 for S3a (220 cm−3), 29 W m−2 for S3c (mean Nint), and 10.6 W m−2 for S3b (Nint) are found for both BOA and TOA.
Last but not least, replacing the vertical profile of Nd by the mean profile of Nd over all case days (see Fig. 2) emulates the cloud radiative effects of the reference simulation quite well. Accordingly, scenario S4 slightly underestimates the mean SW CREs, with a mean error up to −3.16 W m−2 and a RMSE up to 17.2 W m−2 for both BOA and TOA. In fact, this scenario outperforms the rest of the scenarios (S1–S3), except from the sub-case b (Nint) in all scenarios. For an illustration of the excellent linear correlation between the reference simulation and S4 by means of a bivariate kernel density (BKD) plot, the reader is referred to Fig. B1 in Appendix B. One can see that the CREs computed by these scenarios are in a very good agreement almost everywhere except towards larger values of the CREs in the case of the SW radiation, with Pearson correlations larger than 0.977 for both BOA and TOA.
Note here that the RRTMG model is able to derive the radiative fluxes only for effective radius between 2.5 and 60 µm. For all scenarios, all columns with effective radius outside this range have been excluded.
5.1.3 Impact of the cloud properties on the CREs
For a better assessment of the impact of the different cloud properties on both the SW and LW CREs, their correlations have been investigated (in the case of ref.). Table 9 summarizes the corresponding correlations. Due to the monotonic relation between the SW CREs and the cloud properties and the linear relation between the LW CREs and the cloud properties, results are presented only in terms of the Spearman (monotonic) and Pearson (linear) correlations, respectively. To demonstrate, Figs. 5 and 6 illustrate the resulting bivariate kernel density between the cloud radiative effects and the cloud properties that are essential to describe the SW and LW radiation, respectively. Considering the small differences between BOA and TOA, results are only presented for the latter one.
Table 9Correlations between the cloud radiative effects for the reference simulation (ref.) and the cloud properties. For the SW (LW) radiation, results are presented in the case of the Spearman (Pearson) correlation.
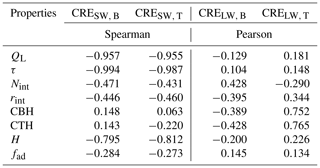
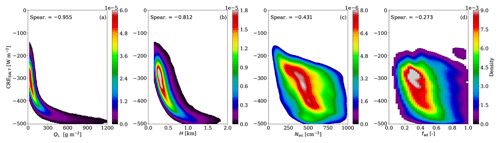
Figure 5BKD between the reference simulation (ref.) and the cloud properties that are essential for the derivation of the cloud optical thickness, which is one of the fundamental properties describing the SW cloud radiative effect. Panels illustrate the BKD between the CRESW,T and (a) QL, (b) H, (c) Nint, and (d) fad. The corresponding Spearman (Spear.) correlations are highlighted.
In the SW radiation, there is an excellent monotonic relation between the CREs and τ, QL, and H for both BOA and TOA, with Spearman correlations higher than −0.987, −0.955, and −0.795, respectively (see Table 9 and Fig. 5), following the second rotational component (RC-2; see Table 4). In particular, the SW CREs increase monotonically with the liquid water path. The latter monotonic relation that is found stronger for lower values of the liquid water path saturates at QL>300 g m−2. In the same direction are the findings for τ (not shown here) and H with the saturation occurring at ∼ 60 and ∼ 0.75 km, respectively. This is no surprise considering their relation to QL (see Eqs. 10 and 16). From Eq. (14), one could expect a similar correlation between the SW cloud radiative effect and the effective radius, but a Spearman correlation below 0.46 (in absolute values) is found for both the BOA and TOA. The latter can be explained by the way the droplet number concentration is derived (see Eq. 4) and the two modes that can be seen in Fig. 5c. The Spearman correlations of the SW CRE with the cloud borders and fad are very weak.
In the LW radiation, changes in QL (and thus in τ and H) possess only a minor influence on CREs (see Table 9) with Pearson correlations below 0.226 (in absolute values). In addition, effective radius and droplet number concentration have a moderate effect on the CRE; Pearson correlations are below 0.428 (in absolute values). The cloud radiative effect in the LW is mostly dependent on the macrophysical cloud properties, namely the cloud position and vertical extension that impacts the cloud temperature, following the first rotational component (RC-1; see Table 4). Thus, we would expect a strong linear correlation with CBH and CTH. This holds true but only in the case of the TOA, whereby a Pearson correlation above 0.752 was yielded (see Table 9 and Fig. 6). For the BOA, the correlations are below 0.428 (in absolute values) for both CBH and CTH. This can be explained by the large variability in CBH and CTH among the different case days (see Table 1). It follows that CRE at the BOA is much more sensitive to the macrophysical cloud properties as compared to the CRE at the TOA.
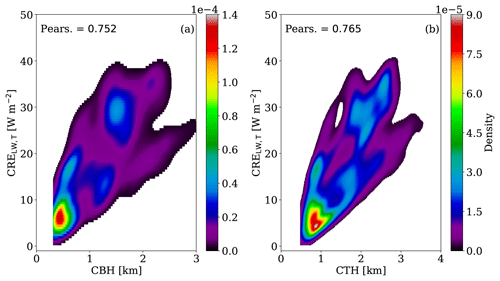
Figure 6BKD between the reference simulation (ref.) and the cloud properties describing the LW cloud radiative effect at the TOA, and (a) CBH and (b) CTH. The corresponding Pearson (Pears.) correlations are highlighted.
Finally, we further examined the relation between the first two rotational components and the cloud radiative effects. Confirming our assumption, in Fig. 7, an excellent monotonic relation is found between SW CRE and RC-2 that is comprised by τ, QL, and H, while a strong linear relation is obtained between LW CRE and RC-1 in the case of the TOA, which is described by CBH and CTH. The resulting Spearman and Pearson correlations are larger than 0.948 for the SW and 0.86 for the LW (for TOA only), respectively. Once again, low linear correlation is found between the LW CRE and RC-1 for the BOA. In Fig. 7d, one can clearly identify several clusters that correspond to different days. With this in mind, we further investigated the latter correlation for each day individually (not shown here). For example, the two lower clusters, with CRE W m−2, are linked to 29 July 2014, while the two upper clusters (CRE W m−2) are regarded to 5 May 2013.
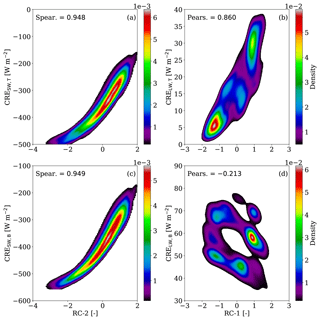
Figure 7For the reference simulation (ref.), BKD between CRESW and the second rotational component (RC-2) at (a) TOA and (c) BOA, and between CRELW and the first rotational component (RC-1) at (b) TOA and (d) BOA. The corresponding Spearman (Spear.) and Pearson (Pears.) correlations are highlighted for the SW and LW radiation, respectively.
To this end, based on the robust evidence over all case days, such a statistical approach, i.e., rotational component analysis, can be employed as an alternative concept for describing the low-level clouds and, consequently, their radiative impact.
By analyzing simulations of the high-resolution model ICON-LEM, a sensitivity study has been carried out to investigate the suitability of the vertically homogeneous and the sub-adiabatic cloud models to, firstly, serve as conceptual models for the evaluation of the representation of low-level clouds in ICON-LEM and similar high-resolution models, and to, secondly, capture the relevant properties which determine the cloud radiative effect. Considering the representation of the cloud microphysical processes in ICON-LEM, we have additionally highlighted the differences in cloud radiative effect resulting from the use of a double- instead of a single-moment cloud microphysics scheme.
ICON-LEM, with its high vertical resolution, ranging from 25 to 70 m within the boundary layer, and from 70 to 100 m further up to the altitude limit for the occurrence of low-level clouds selected for this study (4000 m), enables a significantly improved investigation of the vertical distribution of microphysical properties of these clouds. Based on six case days, we find that the behavior of modeled liquid water clouds over Germany more closely resembles the sub-adiabatic than the vertically homogeneous one, in agreement with ground-based observational studies over the same area of interest (Merk et al., 2016). A rather large number of vertical profiles of modeled low-level clouds have been considered in this study and support the use of the sub-adiabatic model as a conceptual tool for the evaluation of these profiles in high-resolution models, in agreement with previous studies that supported its use in parameterizations in GCMs (Brenguier et al., 2000). According to the sub-adiabatic model, the key cloud properties which determine the cloud optical thickness and thus the SW CRE are the liquid water path, the vertically integrated droplet number concentration (over the cloud geometrical extend, in agreement with Han et al., 1998), the sub-adiabatic fraction, and the cloud geometrical extent, which provide a simplified approximation of the vertical structure of clouds. Consistent with this model, we have demonstrated that the cloud optical thickness varies proportionally to and not linearly with QL, as predicted by the vertically homogeneous model that further supports both observational and theoretical studies (e.g., Brenguier et al., 2000; Merk et al., 2016). In addition, an effort has been conducted to predict the cloud optical thickness resulting from ICON-LEM by the formulation suggested by the sub-adiabatic model. We employed the ordinary least squares (OLS) regression method and we show that, for all case days, the sub-adiabatic model approximates the cloud optical thickness with high accuracy (RMSE=0.027). In brief, in this prediction, 95.7 % of the variance in cloud optical thickness is explained by the variance in the liquid water path, while the droplet number concentration and the sub-adiabatic fraction contribute 3.5 % and 0.2 % to the total variance, respectively. The sub-adiabatic fraction of clouds is characterized by a large variability () that strongly varies from day to day, but also within the same day, likely driven by entrainment processes. The latter is in agreement with previous studies based on ground-based observations (e.g., Boers et al., 2006; Kim et al., 2008; Merk et al., 2016), and the identification of influential factors is an important goal for future research. Furthermore, our results confirm the findings of Min et al. (2012) and Merk et al. (2016) that the highest values of adiabaticity are linked with optically and geometrically thin clouds. Considering the aforementioned variability of entrainment, the constant and comparatively high values of fad, which are often adopted in satellite retrievals of cloud droplet number concentration or cloud geometric thickness (e.g., Zeng et al., 2014), are not supported and might lead to discrepancies in model validation. Therefore, a much lower value of fad ranging from 0.4 to 0.6 should be utilized in the sub-adiabatic model to link the cloud optical thickness to the prognostic quantities utilized in GCM parameterizations and determine the indirect effect and cloud feedbacks. The latter value of the sub-adiabatic fraction is close to the one adopted by Grosvenor et al. (2018) for the error assessment of the retrieved Nd.
The vertical variability of the droplet number concentration was examined. For all the case days, above an altitude of about 2 km, values of Nd are about 200 cm−3 and are thus close to climatological values, while in the boundary layer, the double-moment scheme predicts Nd values above 600 cm−3. Such values are regarded as rather high compared to satellite remote sensing estimates (Quaas et al., 2006; Grosvenor et al., 2018), but such comparison is rather vague considering, firstly, the large uncertainties of the satellite-derived estimates of cloud droplet number concentration (Grosvenor et al., 2018) and, secondly, they are not available in high resolution. However, in situ observations, which are considered to be the most accurate approach to determine Nd, suggest higher values and hence lie closer to those simulated by ICON-LEM. Thus, by means of in situ observations, evaluation activities should be conducted for a better characterization of the droplet number concentration from remote sensing techniques. The latter will scrutinize the double-moment scheme implemented in ICON-LEM and could potentially lead to better simulations of cloud processes and radiation.
A principal component analysis and a subsequent varimax rotation (rotational component analysis) of cloud properties have been conducted to explore the covariance of cloud properties and radiative effects, and to identify the dominating modes of variability. The goal was ultimately to uncover potential shortcomings in the representation of clouds towards the computation of the cloud radiative effects. This analysis reveals that, out of the set of nine parameters considered by us, only four components are sufficient to explain 97.7 % of the total variance. The first component comprises the cloud bottom and top heights, and thus corresponds to the vertical location of the cloud layer in the atmosphere. The second component combines liquid water path, optical thickness, and geometric extent of the clouds, while the third and fourth components are functions of the sub-adiabatic fraction and the cloud droplet number concentration, respectively. By means of such a statistical approach, we offer an alternative concept for describing the CREs, with the first and second components representing the main modes of variability determining the LW and SW CREs explaining 33.8 % and 35.5 %, respectively. The third and fourth components, while having smaller contributions to the total variance (14.8 % and 13.6 %, respectively), point to clear degrees of freedom. Moreover, they potentially capture signatures of the second (cloud geometric extent; Pincus and Baker, 1994) and first indirect aerosol effects (e.g., Twomey, 1977; Ackerman et al., 2000; Werner et al., 2014). This analysis points to the reduced set of parameters for the representation of low-level clouds towards the computation of the CREs: the column effective properties, i.e., Nint, QL, fad, H, and one of the CTH or CBH. A similar attempt to provide an alternative concept for the description of the CREs was reported by Schewski and Macke (2003); they tried to correlate domain-averaged radiative fluxes from 3-D fields with domain-averaged properties of cloudy atmospheres.
By means of an offline version of the RRTMG radiative transfer model, idealized simulations have been carried out to estimate the effect of the representation of cloud microphysics in ICON-LEM on the cloud radiative effect; the double-moment scheme implemented in ICON-LEM (Seifert and Beheng, 2006) has been compared to that of a single-moment scheme. Special emphasis was given on the characterization of the droplet number concentration and thus an effective radius that could approximate the microphysical and radiative properties of the modeled low-level clouds as simulated by ICON-LEM (reference scenario). Utilizing a droplet number concentration profile that follows the climatology of a coarse atmospheric model (ECHAM), the single-moment scheme would yield values of the SW CRE which are up to ∼40.1 W m−2 less than those of the double-moment scheme, with a RMSE of ∼47 W m−2. By employing a more representative profile for the Nd, i.e., a mean vertical profile of Nd, for all case days leads to a rather good approximation; the RMSE is below 17.2 W m−2. This points to the need to better account for prognostic Nd calculations.
Finally, we investigated the reliability of the vertically homogeneous and the sub-adiabatic model to determine the cloud radiative effects. Overall, the sub-adiabatic cloud model outperforms the vertically homogeneous one for the representation of low-level clouds for calculating their radiative effects.
Based on our results, the following approach is recommended to evaluate the representation of clouds and their radiative effects as simulated by high-resolution atmospheric models: for the shortwave, the vertically integrated water path should be targeted primarily, which is quite reliably retrieved from remote sensing; recent advances in correcting the PP bias enable the retrieval of the liquid water path with high accuracy (Zhang et al., 2016; Werner et al., 2018). In addition, the cloud droplet number concentration and the sub-adiabatic fraction are of relevance and deserve attention, but their reliable derivation remains challenging both due to the limitations of current remote sensing methods and the lack of validation data on the basis of in situ observations (Grosvenor et al., 2018). In this respect, the rather large values of cloud droplet number concentration reported here as predicted by the two-moment scheme of Seifert and Beheng (2006), Nd, should be scrutinized on the basis of in situ observations. For the computation of the cloud radiative effects, a more representative vertical profile for the droplet number concentration could be used, as long as they can represent the different magnitudes in Nd within and above the boundary layer as shown here. For the LW CRE, the cloud base and top heights are the determining factors that are rather well derived from ground- and satellite-based observations, respectively. It has be noted, however, that the reliable determination of cloud base height from satellites remains challenging. The sub-adiabatic fraction is also of interest, as it controls the geometric extent of clouds for a given value of liquid water path. Based on our findings, the sub-adiabatic model seems to be better suited than the vertically homogeneous model for the evaluation of the representation of clouds in models.
In future work, the results presented here should be combined with efforts to also take into account the impact of horizontal cloud variability and in particular of the cloud fraction, which are well-known factors of relevance for the cloud radiative effect. In order to link deficiencies in the CRE to the model representation of cloud properties, an effort should be made to simultaneously evaluate the ICON-LEM-based fluxes and cloud properties discussed here to observations, e.g., through the combined use of irradiance observed at the top of atmosphere by the Geostationary Earth Radiation Budget (GERB) and at the ground together with measurements of liquid water path, cloud top and bottom height, cloud droplet number concentration, and solar fluxes. This requires the synergistic combination of active and passive remote sensing instruments.
The Python RRTMG interface (pyRRTMG) used in this study is available at https://github.com/hdeneke/pyRRTMG (last access: 5 June 2018).
The full 3-D large eddy simulation fields used for this paper are stored at the Deutsche Klima Rechenzentrum archive (DKRZ) as part of the HD(CP)2 project.
In Sect. 2.1, the generalized gamma distribution describing the mass of hydrometeors was introduced (see Eq. 1). The ηth moment is computed by
Γ stands for the gamma function. For cloud droplets (see Table 1 in Seifert and Beheng, 2006), the zeroth and first moments of the mass size distribution that denote the droplet number concentration and the liquid water content, respectively, are derived:
and
Dividing Eq. (A2) by Eq. (A3), one can obtain
Inserting Eq. (A4) in Eq. (A2) and rearranging gives
According to Seifert and Beheng (2006) and Petty and Huang (2011), a power law is applied for the mass–size relation:
D denotes the geometrical diameter. In the case of spherical particles, and b=3, with ρw being the water density. In Table 2 in Petty and Huang (2011), one can find the transformation factors between the mass of hydrometeors and the diameter of the hydrometeors:
Given the aforementioned relations, the formula describing the modified gamma distribution of the DSD is
Accordingly, the ηth moments of the DSD are given by
For the reconstructed DSD, n(D), the zeroth moment (M0) stands for the droplet number concentration. The volume-equivalent radius, rV, is derived from the third moment:
In Sect. 5.1.2, by conducting idealized radiative transfer simulations, we estimated the impact of the representation of cloud properties in ICON-LEM on the CREs. Special emphasis was given on identifying the droplet number concentration (Nd), which approximates the microphysical and radiative properties of low-level clouds as simulated by ICON-LEM (reference scenario). A radiative transfer simulation, which employs a mean vertical profile of Nd of all case days (scenario S4), approximates the CREs of the reference scenario quite well. Figure B1 depicts the excellent linear correlation between the reference simulation and S4 by means of BKD.
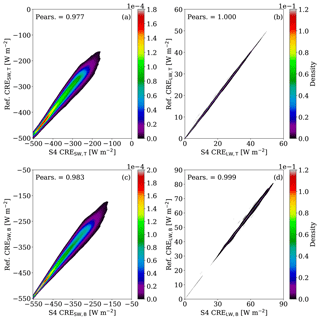
Figure B1BKD between the reference simulation (ref.) and the scenario that employs the mean vertical Nd profile (S4). For the CREs, BKDs are presented for the SW radiation at the TOA (a) and BOA (c), and for the LW radiation at the TOA (b) and BOA (d). The corresponding Pearson (Pears.) correlations are highlighted.
Table C1 lists the difference of the mean CREs between the reference and the rest of the simulated scenarios for the LW radiation for both TOA and BOA. All scenarios are able to reproduce the reference mean CREs; the difference of the mean CREs is below ∼0.55 W m−2 (in absolute values).
VB conceived and refined the overall structure of the investigation, based on discussions with and feedback from all co-authors. VB carried out and refined the data analysis. HD implemented the Python interface to RRTMG used in the analysis. VB wrote the draft manuscript, with all authors contributing to the interpretation of the results and to its improvement.
The authors declare that they have no conflict of interest.
This work has been conducted in the framework of the High Definition Clouds and Precipitation for Advancing Climate Prediction (HD(CP)2), funded by the German Federal Ministry of Education and Research (BMBF; http://www.fona.de/, last access: 9 February 2019) under grant no. 01LK1504B. We thank our colleagues, Anja Hünerbein and Frank Werner, for the many thoughtful comments that led to the improvement of the manuscript.
This research has been supported by the German Federal Ministry of Education and Research (BMBF) (grant no. 01LK1504B).
The publication of this article was partially funded by the
Open Access Fund of the Leibniz Association.
This paper was edited by Toshihiko Takemura and reviewed by three anonymous referees.
Ackerman, A., Toon, O., Taylor, J., Johnson, D., Hobbs, P., and Ferek, R.: Effects of aerosols on cloud albedo: Evaluation of Twomey's parameterization of cloud susceptibility using measurements of ship tracks, J. Atmos. Sci., 57, 2684–2695, 2000. a, b
Albrecht, B. A., Fairall, C. W., Thomson, D. W., White, A. B., Snider, J. B., and Schubert, W. H.: Surface-based remote sensing of the observed and the Adiabatic liquid water content of stratocumulus clouds, Geophys. Res. Lett., 17, 89–92, https://doi.org/10.1029/GL017i001p00089, 1990. a, b
Anderson, G., Clough, S., Kneizys, F., Chetwynd, J., and Shettle, E.: AFGL Atmospheric Constituent Profiles (0–120 km), Tech. Rep. AFGL-TR-86-0110, AFGL (OPI), Hanscom AFB, MA 01736, 1986. a
Barker, H. W.: Indirect Aerosol Forcing by Homogeneous and Inhomogeneous Clouds, J. Climate, 13, 4042–4049, https://doi.org/10.1175/1520-0442(2000)013<4042:IAFBHA>2.0.CO;2, 2000. a
Barker, H. W. and Räisänen, P.: Neglect by GCMs of subgrid-scale horizontal variations in cloud-droplet effective radius: A diagnostic radiative analysis, Q. J. Roy. Meteor. Soc., 130, 1905–1920, https://doi.org/10.1256/qj.03.116, 2004. a
Bennartz, R.: Global assessment of marine boundary layer cloud droplet number concentration from satellite, J. Geophys. Res., 112, D02201, https://doi.org/10.1029/2006JD007547, 2007. a, b, c
Boers, R., Acarreta, J. R., and Gras, J. L.: Satellite monitoring of the first indirect aerosol effect: Retrieval of the droplet concentration of water clouds, J. Geophys. Res., 111, D22208, https://doi.org/10.1029/2005JD006838, 2006. a, b, c, d, e
Brenguier, J.-L., Pawlowska, H., Schüller, L., Preusker, R., Fischer, J., and Fouquart, Y.: Radiative Properties of Boundary Layer Clouds: Droplet Effective Radius versus Number Concentration, J. Atmos. Sci., 57, 803–821, https://doi.org/10.1175/1520-0469(2000)057<0803:RPOBLC>2.0.CO;2, 2000. a, b, c, d
Cahalan, R. F., Ridgway, W., Wiscombe, W. J., Gollmer, S., and Harshvardhan: Independent Pixel and Monte Carlo Estimates of Stratocumulus Albedo, J. Atmos. Sci., 51, 3776–3790, https://doi.org/10.1175/1520-0469(1994)051<3776:IPAMCE>2.0.CO;2, 1994. a
Cairns, B., Lacis, A. A., and Carlson, B. E.: Absorption within Inhomogeneous Clouds and Its Parameterization in General Circulation Models, J. Atmos. Sci., 57, 700–714, https://doi.org/10.1175/1520-0469(2000)057<0700:AWICAI>2.0.CO;2, 2000. a
Chosson, F., Brenguier, J.-L., and Schüller, L.: Entrainment-Mixing and Radiative Transfer Simulation in Boundary Layer Clouds, J. Atmos. Sci., 64, 2670–2682, https://doi.org/10.1175/JAS3975.1, 2007. a, b, c
Clough, S., Shephard, M., Mlawer, E., Delamere, J., Iacono, M., Cady-Pereira, K., Boukabara, S., and Brown, P.: Atmospheric radiative transfer modeling: a summary of the AER codes, J. Quant. Spectrosc. Ra., 91, 233–244, https://doi.org/10.1016/j.jqsrt.2004.05.058, 2005. a
Collins, W. D., Rasch, P. J., Boville, B. A., Hack, J. J., McCaa, J. R., Williamson, D. L., Briegleb, B. P., Bitz, C. M., Lin, S.-J., and Zhang, M.: The Formulation and Atmospheric Simulation of the Community Atmosphere Model Version 3 (CAM3), J. Climate, 19, 2144–2161, https://doi.org/10.1175/JCLI3760.1, 2006. a
Di Giuseppe, F. and Tompkins, A. M.: Effect of Spatial Organization on Solar Radiative Transfer in Three-Dimensional Idealized Stratocumulus Cloud Fields, J. Atmos. Sci., 60, 1774–1794, https://doi.org/10.1175/1520-0469(2003)060<1774:EOSOOS>2.0.CO;2, 2003. a
Dipankar, A., Stevens, B., Heinze, R., Moseley, C., Zängl, G., Giorgetta, M., and Brdar, S.: Large eddy simulation using the general circulation model ICON, J. Adv. Model. Earth Sy., 7, 963–986, https://doi.org/10.1002/2015MS000431, 2015. a, b, c
Foth, A. and Pospichal, B.: Optimal estimation of water vapour profiles using a combination of Raman lidar and microwave radiometer, Atmos. Meas. Tech., 10, 3325–3344, https://doi.org/10.5194/amt-10-3325-2017, 2017. a
Gassmann, A. and Herzog, H.-J.: Towards a consistent numerical compressible non-hydrostatic model using generalized Hamiltonian tools, Q. J. Roy. Meteor. Soc., 134, 1597–1613, https://doi.org/10.1002/qj.297, 2008. a
Giorgetta, M., Roeckner, E., Mauritsen, T., Bader, J., Crueger, T., Esch, M., Rast, S., Kornblueh, L., Schmidt, H., Kinne, S., Hohenegger, C., Möbis, B., Krismer, T., Wieners, K.-H., and Stevens, B.: The atmospheric general circulation model ECHAM6 – Model description, Max-Planck-Institut für Meteorologie, 135, 173 pp., https://doi.org/10.17617/2.1810480, 2013. a, b, c
Grosvenor, D. P., Sourdeval, O., Zuidema, P., Ackerman, A., Alexandrov, M. D., Bennartz, R., Boers, R., Cairns, B., Chiu, J. C., Christensen, M., Deneke, H., Diamond, M., Feingold, G., Fridlind, A., Hünerbein, A., Knist, C., Kollias, P., Marshak, A., McCoy, D., Merk, D., Painemal, D., Rausch, J., Rosenfeld, D., Russchenberg, H., Seifert, P., Sinclair, K., Stier, P., van Diedenhoven, B., Wendisch, M., Werner, F., Wood, R., Zhang, Z., and Quaas, J.: Remote Sensing of Droplet Number Concentration in Warm Clouds: A Review of the Current State of Knowledge and Perspectives, Rev. Geophys., 56, 409–453, https://doi.org/10.1029/2017RG000593, 2018. a, b, c, d, e
Han, Q., Rossow, W. B., Chou, J., and Welch, R. M.: Global variation of column droplet concentration in low-level clouds, Geophys. Res. Lett., 25, 1419–1422, https://doi.org/10.1029/98GL01095, 1998. a
Hande, L. B., Engler, C., Hoose, C., and Tegen, I.: Parameterizing cloud condensation nuclei concentrations during HOPE, Atmos. Chem. Phys., 16, 12059–12079, https://doi.org/10.5194/acp-16-12059-2016, 2016. a
Hansen, J. E. and Travis, L. D.: Light scattering in planetary atmospheres, Space Sci. Rev., 16, 527–610, https://doi.org/10.1007/BF00168069, 1974. a
Heinze, R., Dipankar, A., Henken, C. C., Moseley, C., Sourdeval, O., Trömel, S., Xie, X., Adamidis, P., Ament, F., Baars, H., Barthlott, C., Behrendt, A., Blahak, U., Bley, S., Brdar, S., Brueck, M., Crewell, S., Deneke, H., Di Girolamo, P., Evaristo, R., Fischer, J., Frank, C., Friederichs, P., Göcke, T., Gorges, K., Hande, L., Hanke, M., Hansen, A., Hege, H.-C., Hoose, C., Jahns, T., Kalthoff, N., Klocke, D., Kneifel, S., Knippertz, P., Kuhn, A., van Laar, T., Macke, A., Maurer, V., Mayer, B., Meyer, C. I., Muppa, S. K., Neggers, R. A. J., Orlandi, E., Pantillon, F., Pospichal, B., Röber, N., Scheck, L., Seifert, A., Seifert, P., Senf, F., Siligam, P., Simmer, C., Steinke, S., Stevens, B., Wapler, K., Weniger, M., Wulfmeyer, V., Zängl, G., Zhang, D., and Quaas, J.: Large-eddy simulations over Germany using ICON: a comprehensive evaluation, Q. J. Roy. Meteor. Soc., 143, 69–100, https://doi.org/10.1002/qj.2947, 2017. a, b, c, d
Hu, Y. X. and Stamnes, K.: An Accurate Parameterization of the Radiative Properties of Water Clouds Suitable for Use in Climate Models, J. Climate, 6, 728–742, https://doi.org/10.1175/1520-0442(1993)006<0728:AAPOTR>2.0.CO;2, 1993. a
Iacono, M. J., Delamere, J. S., Mlawer, E. J., Shephard, M. W., Clough, S. A., and Collins, W. D.: Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models, J. Geophys. Res., 113, D13103, https://doi.org/10.1029/2008JD009944, 2008. a
Illingworth, A. J., Hogan, R. J., O'Connor, E., Bouniol, D., Brooks, M. E., Delanoë, J., Donovan, D. P., Eastment, J. D., Gaussiat, N., Goddard, J. W. F., Haeffelin, M., Baltink, H. K., Krasnov, O. A., Pelon, J., Piriou, J.-M., Protat, A., Russchenberg, H. W. J., Seifert, A., Tompkins, A. M., van Zadelhoff, G.-J., Vinit, F., Willén, U., Wilson, D. R., and Wrench, C. L.: Cloudnet, B. Am. Meteorol. Soc., 88, 883–898, https://doi.org/10.1175/BAMS-88-6-883, 2007. a
Illingworth, A. J., Barker, H. W., Beljaars, A., Ceccaldi, M., Chepfer, H., Clerbaux, N., Cole, J., Delanoë, J., Domenech, C., Donovan, D. P., Fukuda, S., Hirakata, M., Hogan, R. J., Huenerbein, A., Kollias, P., Kubota, T., Nakajima, T., Nakajima, T. Y., Nishizawa, T., Ohno, Y., Okamoto, H., Oki, R., Sato, K., Satoh, M., Shephard, M. W., Velázquez-Blázquez, A., Wandinger, U., Wehr, T., and van Zadelhoff, G.-J.: The EarthCARE Satellite: The Next Step Forward in Global Measurements of Clouds, Aerosols, Precipitation, and Radiation, B. Am. Meteorol. Soc., 96, 1311–1332, https://doi.org/10.1175/BAMS-D-12-00227.1, 2015. a
IPCC: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, https://doi.org/10.1017/CBO9781107415324.004, 2013. a
Karstens, U., Simmer, C., and Ruprecht, E.: Remote sensing of cloud liquid water, Meteorol. Atmos. Phys., 54, 157–171, https://doi.org/10.1007/BF01030057, 1994. a
Kim, B.-G., Miller, M. A., Schwartz, S. E., Liu, Y., and Min, Q.: The role of adiabaticity in the aerosol first indirect effect, J. Geophys. Res., 113, D05210, https://doi.org/10.1029/2007JD008961, 2008. a
Lebsock, M. and Su, H.: Application of active spaceborne remote sensing for understanding biases between passive cloud water path retrievals, J. Geophys. Res.-Atmos., 119, 8962–8979, https://doi.org/10.1002/2014JD021568, 2014. a
Macke, A., Seifert, P., Baars, H., Barthlott, C., Beekmans, C., Behrendt, A., Bohn, B., Brueck, M., Bühl, J., Crewell, S., Damian, T., Deneke, H., Düsing, S., Foth, A., Di Girolamo, P., Hammann, E., Heinze, R., Hirsikko, A., Kalisch, J., Kalthoff, N., Kinne, S., Kohler, M., Löhnert, U., Madhavan, B. L., Maurer, V., Muppa, S. K., Schween, J., Serikov, I., Siebert, H., Simmer, C., Späth, F., Steinke, S., Träumner, K., Trömel, S., Wehner, B., Wieser, A., Wulfmeyer, V., and Xie, X.: The HD(CP)2 Observational Prototype Experiment (HOPE) – an overview, Atmos. Chem. Phys., 17, 4887–4914, https://doi.org/10.5194/acp-17-4887-2017, 2017. a
Merk, D., Deneke, H., Pospichal, B., and Seifert, P.: Investigation of the adiabatic assumption for estimating cloud micro- and macrophysical properties from satellite and ground observations, Atmos. Chem. Phys., 16, 933–952, https://doi.org/10.5194/acp-16-933-2016, 2016. a, b, c, d, e, f, g, h, i
Miller, D. J., Zhang, Z., Ackerman, A. S., Platnick, S., and Baum, B. A.: The impact of cloud vertical profile on liquid water path retrieval based on the bispectral method: A theoretical study based on large-eddy simulations of shallow marine boundary layer clouds, J. Geophys. Res.-Atmos., 121, 4122–4141, https://doi.org/10.1002/2015JD024322, 2016. a
Min, Q., Joseph, E., Lin, Y., Min, L., Yin, B., Daum, P. H., Kleinman, L. I., Wang, J., and Lee, Y.-N.: Comparison of MODIS cloud microphysical properties with in-situ measurements over the Southeast Pacific, Atmos. Chem. Phys., 12, 11261–11273, https://doi.org/10.5194/acp-12-11261-2012, 2012. a
Mlawer, E. J., Taubman, S. J., Brown, P. D., Iacono, M. J., and Clough, S. A.: Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave, J. Geophys. Res., 102, 16663–16682, https://doi.org/10.1029/97JD00237, 1997. a, b
Nakajima, T. and King, M. D.: Determination of the Optical Thickness and Effective Particle Radius of Clouds from Reflected Solar Radiation Measurements. Part I: Theory, J. Atmos. Sci., 47, 1878–1893, https://doi.org/10.1175/1520-0469(1990)047<1878:DOTOTA>2.0.CO;2, 1990. a
Oreopoulos, L. and Barker, H. W.: Accounting for subgrid-scale cloud variability in a multi-layer 1d solar radiative transfer algorithm, Q. J. Roy. Meteor. Soc., 125, 301–330, https://doi.org/10.1002/qj.49712555316, 2006. a
Petty, G. W. and Huang, W.: The Modified Gamma Size Distribution Applied to Inhomogeneous and Nonspherical Particles: Key Relationships and Conversions, J. Atmos. Sci., 68, 1460–1473, https://doi.org/10.1175/2011JAS3645.1, 2011. a, b, c
Pincus, R. and Baker, M. B.: Effect of precipitation on the albedo susceptibility of clouds in the marine boundary layer, Nature, 372, 250–252, https://doi.org/10.1038/372250a0, 1994. a
Pincus, R., Barker, H. W., and Morcrette, J.-J.: A fast, flexible, approximate technique for computing radiative transfer in inhomogeneous cloud fields, J. Geophys. Res., 108, 4376, https://doi.org/10.1029/2002JD003322, 2003. a, b
Quaas, J., Boucher, O., and Lohmann, U.: Constraining the total aerosol indirect effect in the LMDZ and ECHAM4 GCMs using MODIS satellite data, Atmos. Chem. Phys., 6, 947–955, https://doi.org/10.5194/acp-6-947-2006, 2006. a, b
Rémillard, J., Kollias, P., and Szyrmer, W.: Radar-radiometer retrievals of cloud number concentration and dispersion parameter in nondrizzling marine stratocumulus, Atmos. Meas. Tech., 6, 1817–1828, https://doi.org/10.5194/amt-6-1817-2013, 2013. a
Roebeling, R., Baum, B., Bennartz, R., Hamann, U., Heidinger, A., Thoss, A., and Walther, A.: Outcome of the third cloud retrieval evaluation workshop, AIP Conf. Proc., 1531, 416–419, https://doi.org/10.1063/1.4804795, 2013. a
Roebeling, R. A., Feijt, A. J., and Stammes, P.: Cloud property retrievals for climate monitoring: Implications of differences between Spinning Enhanced Visible and Infrared Imager (SEVIRI) on METEOSAT-8 and Advanced Very High Resolution Radiometer (AVHRR) on NOAA-17, J. Geophys. Res., 111, D20210, https://doi.org/10.1029/2005JD006990, 2006. a
Schewski, M. and Macke, A.: Correlation between domain averaged cloud properties, and solar radiative fluxes for three-dimensional inhomogeneous mixed phase clouds, Meteorol. Z., 12, 293–299, https://doi.org/10.1127/0941-2948/2003/0012-0293, 2003. a
Seifert, A. and Beheng, K. D.: A two-moment cloud microphysics parameterization for mixed-phase clouds. Part 1: Model description, Meteorol. Atmos. Phys., 92, 45–66, https://doi.org/10.1007/s00703-005-0112-4, 2006. a, b, c, d, e, f, g, h
Shonk, J. K. P. and Hogan, R. J.: Tripleclouds: An Efficient Method for Representing Horizontal Cloud Inhomogeneity in 1D Radiation Schemes by Using Three Regions at Each Height, J. Climate, 21, 2352–2370, https://doi.org/10.1175/2007JCLI1940.1, 2008. a
Slingo, A.: A GCM Parameterization for the Shortwave Radiative Properties of Water Clouds, J. Atmos. Sci., 46, 1419–1427, https://doi.org/10.1175/1520-0469(1989)046<1419:AGPFTS>2.0.CO;2, 1989. a
Stegmann, M. B., Sjöstrand, K., and Larsen, R.: Sparse modeling of landmark and texture variability using the orthomax criterion, Proc. SPIE 6144, Medical Imaging 2006: Image Processing, San Diego, California, USA, 11–16 February 2006, 61441G, https://doi.org/10.1117/12.651293, 2006. a
Stephens, G. L., Vane, D. G., Boain, R. J., Mace, G. G., Sassen, K., Wang, Z., Illingworth, A. J., O'connor, E. J., Rossow, W. B., Durden, S. L., Miller, S. D., Austin, R. T., Benedetti, A., and Mitrescu, C. a.: THE CLOUDSAT MISSION AND THE A-TRAIN, B. Am. Meteorol. Soc., 83, 1771–1790, https://doi.org/10.1175/BAMS-83-12-1771, 2002. a
Stuhlmann, R., Rodriguez, A., Tjemkes, S., Grandell, J., Arriaga, A., Bézy, J.-L., Aminou, D., and Bensi, P.: Plans for EUMETSAT's Third Generation Meteosat geostationary satellite programme, Adv. Space Res., 36, 975–981, https://doi.org/10.1016/j.asr.2005.03.091, 2005. a
Turner, D. D., Vogelmann, A. M., Austin, R. T., Barnard, J. C., Cady-Pereira, K., Chiu, J. C., Clough, S. A., Flynn, C., Khaiyer, M. M., Liljegren, J., Johnson, K., Lin, B., Long, C., Marshak, A., Matrosov, S. Y., McFarlane, S. A., Miller, M., Min, Q., Minimis, P., O'Hirok, W., Wang, Z., and Wiscombe, W.: Thin Liquid Water Clouds: Their Importance and Our Challenge, B. Am. Meteorol. Soc., 88, 177–190, https://doi.org/10.1175/BAMS-88-2-177, 2007. a
Twomey, S.: The influence of pollution on the shortwave albedo of clouds, J. Atmos. Sci., 34, 1149–1152, https://doi.org/10.1175/1520-0469(1977)034<1149:TIOPOT>2.0.CO;2, 1977. a, b
Wan, H., Giorgetta, M. A., Zängl, G., Restelli, M., Majewski, D., Bonaventura, L., Fröhlich, K., Reinert, D., Rípodas, P., Kornblueh, L., and Förstner, J.: The ICON-1.2 hydrostatic atmospheric dynamical core on triangular grids – Part 1: Formulation and performance of the baseline version, Geosci. Model Dev., 6, 735–763, https://doi.org/10.5194/gmd-6-735-2013, 2013. a
Werner, F., Ditas, F., Siebert, H., Simmel, M., Wehner, B., Pilewskie, P., Schmeissner, T., Shaw, R. A., Hartmann, S., Wex, H., Roberts, G. C., and Wendisch, M.: Twomey effect observed from collocated microphysical and remote sensing measurements over shallow cumulus, J. Geophys. Res.-Atmos., 119, 1534–1545, https://doi.org/10.1002/2013JD020131, 2014. a, b, c
Werner, F., Zhang, Z., Wind, G., Miller, D. J., Platnick, S., and Di Girolamo, L.: Improving Cloud Optical Property Retrievals for Partly Cloudy Pixels Using Coincident Higher-Resolution Single Band Measurements: A Feasibility Study Using ASTER Observations, J. Geophys. Res.-Atmos., 123, 12253–12276, https://doi.org/10.1029/2018JD028902, 2018. a
Wood, R.: Relationships between optical depth, liquid water path, droplet concentration, and effective radius in adiabatic layer cloud, University of Washington, 3 pp., available at: https://atmos.uw.edu/~robwood/papers/chilean_plume/optical_depth_relations.pdf (last access: 18 December 2019), 2006. a
Wood, R. and Hartmann, D. L.: Spatial Variability of Liquid Water Path in Marine Low Cloud: The Importance of Mesoscale Cellular Convection, J. Climate, 19, 1748–1764, https://doi.org/10.1175/JCLI3702.1, 2006. a
Zeng, S., Riedi, J., Trepte, C. R., Winker, D. M., and Hu, Y.-X.: Study of global cloud droplet number concentration with A-Train satellites, Atmos. Chem. Phys., 14, 7125–7134, https://doi.org/10.5194/acp-14-7125-2014, 2014. a, b, c
Zhang, Z., Werner, F., Cho, H.-M., Wind, G., Platnick, S., Ackerman, A. S., Di Girolamo, L., Marshak, A., and Meyer, K.: A framework based on 2-D Taylor expansion for quantifying the impacts of subpixel reflectance variance and covariance on cloud optical thickness and effective radius retrievals based on the bispectral method, J. Geophys. Res.-Atmos., 121, 7007–7025, https://doi.org/10.1002/2016JD024837, 2016. a
- Abstract
- Introduction
- Data and methods
- Cloud characteristics
- Principal component analysis
- Cloud radiative effects of low-level clouds
- Discussion and conclusions
- Code and data availability
- Data availability
- Appendix A: Derivation of moments of the droplet size distribution
- Appendix B: Correlation between reference simulation and scenario S4
- Appendix C: Differences of the mean CREs between the reference simulation and the new scenarios for the LW radiation
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Data and methods
- Cloud characteristics
- Principal component analysis
- Cloud radiative effects of low-level clouds
- Discussion and conclusions
- Code and data availability
- Data availability
- Appendix A: Derivation of moments of the droplet size distribution
- Appendix B: Correlation between reference simulation and scenario S4
- Appendix C: Differences of the mean CREs between the reference simulation and the new scenarios for the LW radiation
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References