the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Optimization of process models for determining volatility distribution and viscosity of organic aerosols from isothermal particle evaporation data
Väinö Hämäläinen
Grazia Rovelli
Antti Lipponen
Manabu Shiraiwa
Jonathan P. Reid
Kari E. J. Lehtinen
Taina Yli-Juuti
The composition of organic aerosol under different ambient conditions as well as their phase state have been a subject of intense study in recent years. One way to study particle properties is to measure the particle size shrinkage in a diluted environment at isothermal conditions. From these measurements it is possible to separate the fraction of low-volatility compounds from high-volatility compounds. In this work, we analyse and evaluate a method for obtaining particle composition and viscosity from measurements using process models coupled with input optimization algorithms. Two optimization methods, the Monte Carlo genetic algorithm and Bayesian inference, are used together with process models describing the dynamics of particle evaporation. The process model optimization scheme in inferring particle composition in a volatility-basis-set sense and composition-dependent particle viscosity is tested with artificially generated data sets and real experimental data. Optimizing model input so that the output matches these data yields a good match for the estimated quantities. Both optimization methods give equally good results when they are used to estimate particle composition to artificially test data. The timescale of the experiments and the initial particle size are found to be important in defining the range of values that can be identified for the properties from the optimization.
- Article
(955 KB) -
Supplement
(1035 KB) - BibTeX
- EndNote
It has been estimated that organic aerosols (OAs) comprise a large fraction of global aerosol particle mass (Kanakidou et al., 2005; Jimenez et al., 2009). A significant fraction of OA is of secondary origin (secondary organic aerosol, SOA), i.e. OA formed from oxidation of volatile organic compounds and their subsequent condensation onto pre-existing particles (Hallquist et al., 2009). Especially in SOA systems, there are gaps of knowledge in the composition and phase state of the particles and their response to atmospheric conditions such as relative humidity or temperature (Hallquist et al., 2009; Virtanen et al., 2010; Pajunoja et al., 2015). These properties are important since they control the evolution of atmospheric organic particles and their subsequent effect on climate (Tsigaridis et al., 2014; Shiraiwa et al., 2017).
The volatilities of particle-phase compounds in OA and the viscosity of the particles can be inferred by measuring the size change of particles during their evaporation (Vaden et al., 2011; Wilson et al., 2015; Yli-Juuti et al., 2017). In addition, if the shrinking stops after a certain time, the particles can be inferred to contain organic compounds, which are nonvolatile with respect to the ambient conditions. The phase state of OA particles can be studied in these experiments by comparing evaporation at different relative humidity conditions. New techniques have also been developed to infer the viscosity of the particles directly (Abramson et al., 2013; Renbaum-Wolff et al., 2013; Reid et al., 2018). The benefit of the evaporation technique over direct measurement of viscosity is the possibility of using freshly formed, suspended OA particles without a need, for example, for filter collection and further treatment.
In addition to experimental methods, increasing attention has also been given to modelling the evaporation process to better understand the measurements (Vaden et al., 2011; Liu et al., 2016; Yli-Juuti et al., 2017). Usually, the model results obtained by assuming distinct OA properties are compared to experimental data and conclusions are drawn from the differences or similarities of the two. However, an inverse approach is also possible where some of the OA properties are fit such that the model output is matched to the experimental observations. This approach allows the estimation of the properties that are challenging to measure directly with available instruments. For example, Arangio et al. (2015) used this concept to derive kinetic parameters for multiphase chemical reactions of the hydroxyl radical with levoglucosan and abietic acid. Berkemeier et al. (2016) derived kinetic parameters influencing ozone uptake of shikimic acid by fitting to multiple measurements of ozone uptake by the acid at different relative humidities. Lowe et al. (2016) studied the sensitivity of various parameters of Köhler theory by studying the goodness of fit to artificial cloud condensation nucleus spectra. Yli-Juuti et al. (2017) inferred volatility distribution of compounds in SOA particles by searching for an optimal input to a process model such that the model produces similar particle size change as was measured.
Even though the optimization of models to replicate experimental data is a widely used method in other fields (e.g., Kaipio et al., 2000; Hernández et al., 2017; Varvia et al., 2018), such an approach is yet to be commonly utilized in studies probing organic aerosol volatility and viscosity. The current challenges of accurately estimating OA component volatility and particle viscosity raises a need for studies that assess how accurately they can be inferred by fitting process model output to time-dependent evaporation measurements, which is the aim of this study.
The rest of the article is organized as follows. In the second section the evaporation data and computational methods are described. In the third section two different approaches for performing the optimization are tested. In sections four and five, the particle volatility distribution is optimized to match artificial data sets and then the optimization method is tested by applying it to experimental data sets where the composition and viscosity of generated particles are known. In the last section the findings are summarized and conclusions are drawn.
The optimization method described here is based on process models that simulate the evaporation of OA particles and an optimization algorithm that is used for finding the desired properties. Two evaporation models which have different levels of detail in their representation of the aerosol particle evaporation process are used. Additionally, two different optimization algorithms are tested.
2.1 Process models
Evaporation at high relative humidity (RH) is modelled with a liquid-like evaporation model (hereafter LLEVAP) (Yli-Juuti et al., 2017) and evaporation at low RH with a modified version of the kinetic multilayer model for gas–particle interactions in aerosols and clouds (KM-GAP) model (Shiraiwa et al., 2012; Yli-Juuti et al., 2017). Both models and variations from their typical implementations are described below.
In LLEVAP the evaporation of an organic compound i is controlled by the difference in its gas-phase concentration Ci and the equilibrium concentration Ceq,i (Vesala et al., 1997; Lehtinen and Kulmala, 2003), equivalent to the gas-phase diffusional gradient between the infinite distance and particle surface, respectively. Therefore, the mass transport between the gas and the particle phases is assumed to be the limiting phenomenon and the diffusion timescales within the particle are assumed to be negligible. The mixture of organics and water is assumed to behave ideally. When performing optimization to interpret real measurements, as described in Sect. 2.3.2, a flow of N2 maintains a near-zero background gas-phase concentration of the volatilizing components. This nitrogen flow is taken into account by including the Sherwood number correction to the mass flux equations (Kulmala et al., 1995).
In KM-GAP, the particle-phase mass transport is modelled by dividing the particle into concentric layers (Shiraiwa et al., 2012, 2013). The composition-dependent viscosity η in layer j is assumed to have the form
where is the mole fraction of the ith compound in the jth layer and bi is a coefficient that describes the contribution of compound i to the viscosity ηj (O'Meara et al., 2016). The particle-phase diffusion coefficients are calculated from the viscosities based on the Stokes–Einstein relation (Einstein, 1905). The molecular diffusion inside the particle is calculated based on Fick's law of diffusion. As with LLEVAP, an ideal mixture is assumed in the KM-GAP model implementation.
During an evaporation simulation the particle size decreases. This shrinkage is modelled by allowing the quasi-static surface layer (the outermost layer of the particle) to shrink so that its thickness deviates from the thicknesses of other layers. If the thickness of the quasi-static surface layer is less than 0.3 nm it is combined with the first bulk layer, which is the layer directly beneath the quasi-static surface layer. This approach is the same as that used by Yli-Juuti et al. (2017).
In both models, equilibrium partitioning of water in the gas and particle phases is assumed. In LLEVAP, this controls the mole fraction of water in the entire particle. In KM-GAP, this assumption controls the mole fraction of water in the particle surface layer while the composition of the inner layers is based on the kinetics of water transport. Moreover, the coefficient b for water in Eq. (1) is set to the literature value for the viscosity of pure water, Pa s (Rumble et al., 2018) when calculating the viscosity of a mixture in a layer.
In most of the model simulations the organic compounds are represented by a one-dimensional volatility basis set (Donahue et al., 2006) (1D-VBS, hereafter VBS). Organic compounds are grouped into distinct “bins” in a VBS, described by their saturation (mass) concentration (Csat) value and the amount of that bin in the gas and particle phases. The saturation concentration of a compound can be used interchangeably with the effective saturation concentration (Csat,i times the activity coefficient of compound i) because the organic–water mixture is assumed to behave ideally.
The volatilities of the compounds in the particle are modelled with either a “full VBS” or with a “sparse VBS”. The full VBS consists of bins from minimum defined Csat to maximum defined Csat with a decadal difference in Csat between two adjacent bins; the sparse VBS consists of a predefined number of bins whose saturation concentration is not constrained relative to each other. The sparse VBS is used to present the properties of the organic compounds where the number of evaporating compounds is known. Hereafter the terms compound and VBS bin are used interchangeably in the text. The gas phase is assumed to be infinitely diluted of organic compounds in the particle evaporation data sets described in Sect. 2.3 and, thus, the mass or mole fraction presented in the VBS is always the fraction in the particle phase.
2.2 Optimization methods
2.2.1 Monte Carlo genetic algorithm
The Monte Carlo genetic algorithm (MCGA) is an optimization method developed by Berkemeier et al. (2017). MCGA has been previously used in estimating atmospheric multiphase chemistry parameters such as reaction rate coefficients and bulk-phase diffusion coefficients (Table 1 in Berkemeier et al., 2017).
The algorithm divides the optimization process into two different parts: a random sampling of the parameter space (MC part) and a genetic algorithm (GA part) with an initial population from the MC sampling. Random sampling means that a predetermined number of parameter sets, named candidate solutions or candidates, are created by randomly choosing values for the free parameters (Berkemeier et al., 2017). These candidates form a population. The free parameter values are drawn from a uniform distribution between 0.01 and 1 for the mole or mass fraction of a compound and from a log-uniform distribution for the saturation concentrations and b parameters of Eq. (1), with clearly defined minimum and maximum values (see Tables 1 and 5). Below the fitness of a candidate is determined as the inverse of its goodness-of-fit statistic. The goodness of fit in this work is calculated as a mean squared error (MSE) between the evaporation simulation produced with the candidate's parameter set and the measured evaporation. A lower value for goodness-of-fit statistic, i.e. lower MSE, means higher value for fitness and a better candidate.
The initial population to the GA part is chosen from the MC part so that 5 % of the best-fit candidates are chosen and the remaining 95 % of the population is chosen randomly. The computation times of the MC and GA parts are divided, so that both parts require about half of the total computation time (Berkemeier et al., 2017).
The GA part employs a survival-of-the-fittest scheme to improve the parameter sets drawn in the MC part. The GA part consists of evolving the initial population by forming generations. Each new generation is created by first choosing a number of elite candidates from the previous generation whose fitness is the highest. The rest of the generation is created in a crossover process. First two candidates, called parents, are chosen. A new candidate is created from the two parents' parameter sets. A new parameter for the new candidate is chosen from the parents' parameters randomly (Berkemeier et al., 2017).
The version of the algorithm used in this work differs from the version described in Berkemeier et al. (2017) in how a new candidate is accepted to the next generation and how parents are chosen. Once the new candidate has all its free parameters drawn, it is accepted to the new generation if its fitness is higher than the lowest fitness in the previous generation or if the candidate's fitness divided by the lowest fitness in the previous generation is lower than a uniform random number between 0 and 1. If neither of the criteria for accepting the candidate is met, a parent survives to the next generation with probability proportional to their MSE values. The additional criterion for accepting the candidate is similar to the Metropolis algorithm (Metropolis et al., 1953). Lastly in the GA, once a new candidate is created and before its fitness is compared against the previous generation, the candidate can undergo mutation with a preset probability. If mutation happens the values for all the fitting parameters are chosen again randomly. In genetic algorithms the goal is to keep the population as variable as possible while at the same time improving the fitness of the candidates when new generations are calculated. If only the candidates that best produce the observations were chosen, the algorithm might get stuck in a local minimum, and, conversely, if new random parameters were drawn too often the genetic algorithm would not converge. The mutation step together with the Metropolis criterion ensure that the values of the fitting parameters stay variable in the population.
The probability to be chosen to be a parent was set to be proportional to the candidate's fitness. This way the parameters that produce better fits to the data are more likely chosen than those candidates that produce worse fits. The number of elite candidates was set to be 5 % of the generation size and the mutation probability was set to 20 %. The number of generations was set to 10. To obtain statistics of the estimated parameters the optimization process was always repeated at least 100 times. These consecutive optimization runs are hereafter referred to as optimization rounds. All the MCGA parameters for each data set in this work are listed in Supplement Table S1.
When showing estimates from the distribution of fitted parameters, the mode of the estimate is used as a point estimate and the uncertainty is characterized by the 10th and 90th percentiles of the distribution.
2.2.2 Bayesian inference
Bayesian inference is a class of statistical inference that can be used in finding estimates for unknown parameters in a model. In Bayesian inference, the estimates of the unknown parameters are based on statistical prior information, observed data and an observation model. Statistical prior information is encoded into prior probability distribution and it can be used, for example, to constrain the unknown parameter values to a physically feasible range (e.g. nonnegativity). The observation model describes the dependency between the observed data and unknown parameters, and statistical models for the observation noise and model uncertainties are used to construct the so-called likelihood probability distribution. The solution of a Bayesian inference problem is a posterior probability distribution that is a conditional probability distribution for the unknown parameters given the observations and prior information. The posterior probability according to the Bayes' rule (Bayes et al., 1763; Gelman et al., 2013) is proportional to the product of likelihood and prior probabilities. Usually in practical applications, the posterior probability distribution is not used as it is, but it is used to derive point or interval estimates for the unknown parameters.
Analytic derivation of the posterior probability distribution is often difficult or even impossible and, therefore, feasible numerical methods have been developed to explore the posterior probability distribution. These numerical methods are typically used to draw random samples from the posterior probability distribution. The random samples are further used to compute point estimates and credible intervals for the unknown parameters. A well-known class of sampling algorithms are the Markov chain Monte Carlo (MCMC) algorithms. In MCMC algorithms, random samples from the posterior probability distributions are drawn and, for example, the most probable values for the unknown parameters are computed.
The evaporation of an organic aerosol particle is modelled using the LLEVAP model described in Sect. 2.1. This method is applied to data set 1 described in Sect. 2.3. The prior probability models for the three organic compounds in data set 1 are set to positive parts of normal distributions with means of 0, 0 and 500 µg m−3 and standard deviations of 10, 10 and 500 µg m−3, respectively, for the saturation concentrations of the three organic compounds. For the molar fraction the mean is one-third, standard deviation is one-third and the distributions' Gaussian for every compound with the negative part of the distribution function is removed. A Hamiltonian MCMC algorithm the No-U-Turn Sampler (NUTS) (Hoffman and Gelman, 2014) is employed using the Stan software (Carpenter et al., 2017) to draw 2000 samples from the posterior probability distribution. Finally, the most probable random sample according to the posterior distribution is taken as the point estimate for the unknown parameters. This point estimate is called the maximum a posteriori (MAP) estimate. Furthermore, the 90 % credible interval for the unknown parameters is calculated to reflect the uncertainty of the estimates.
2.3 Test data
Altogether, 10 different data sets were used to test how well the volatility and viscosity of OA particles can be estimated using the techniques described above. First, four artificially created data sets were used to test the accuracy of the estimated VBS in case of no particle-phase diffusion limitations. Second, particle evaporation data measured with an electrodynamic balance (EDB) (see Sect. 2.3.2) were used to characterize how well the volatility of compounds can be estimated from experimental data on particles consisting of few compounds. Finally, measured evaporation data were used to test the simultaneous estimation of volatility and viscosity of particles generated from two compound mixtures.
2.3.1 Artificial data sets generated with the LLEVAP model
All four artificial data sets were generated using the LLEVAP model. In every case the data sets were created by a different person than the one performing the optimization. This prevented subconscious bias of the operator altering the estimates towards correct values. Table 1 shows the properties of the particles or the organic compounds that change between data sets and the free parameters. Table 2 shows the properties of the organic compounds and ambient conditions that are the same between the data sets and Table 3 shows the mole fractions and saturation concentrations of each compound in every data set. The optimization results of these data sets are described and discussed in Sect. 4. Additionally, the first artificial data set is also used to compare the Bayesian inference and MCGA methods in Sect. 3.
Table 1Characteristics for the artificial data sets. Properties from top to bottom are number of VBS compounds (bins), particle diameter at the start of the evaporation, saturation concentrations of the VBS compounds and dry mole fraction of the compounds at the start of the evaporation. For Csat and Xmole,dry “fitted” means that the parameter value was used as a fitting parameter and the value was constrained between the reported minimum and maximum values.

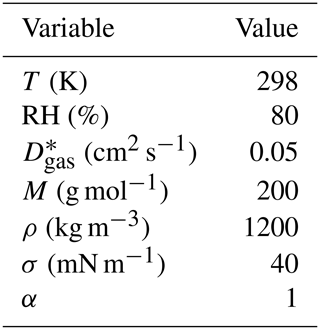
Table 2The ambient conditions and properties of the organic compounds in the artificial test data that are the same for all compounds in artificial data sets 1–4. The variables are, from top to bottom, temperature, relative humidity, gas-phase diffusion coefficient, molar mass, particle-phase density of the pure compound , particle surface tension and mass accommodation coefficient.
∗ The gas-phase diffusion coefficients are scaled to correct temperatures by multiplying with a factor of (T∕273.15)1.75 (Reid et al., 1987).
Table 3The correct parameters that are fitted in the optimization process for every artificial data set. The order of the mole fractions is from the least volatile to the most volatile compound for artificial data sets 3 and 4.

∗ The mole fractions are lumped into six volatility classes. See Table S2 for the exact values.
The artificial data sets 1, 3 and 4 mimic evaporation of monodisperse particle population in the University of Eastern Finland residence time chamber similar to the measurements reported in Yli-Juuti et al. (2017). The data sets differ in their number of organic compounds and their saturation concentration values. In data set 1, three organic compounds were used and their Csat values were chosen from the appropriate range. Both saturation concentrations and initial dry mole fractions of the compounds in the particle were treated as free parameters in optimization. In data set 3, six organic compounds, i.e. a full VBS, were used. The saturation concentrations were set to their correct values (see Table 1) and only dry particle mole fractions at the start of the evaporation were optimized. Data set 4 was generated by simulating evaporation of a mixture of 40 compounds with a range of Csat and mole fractions. In optimization a full VBS with fixed saturation concentrations was used.
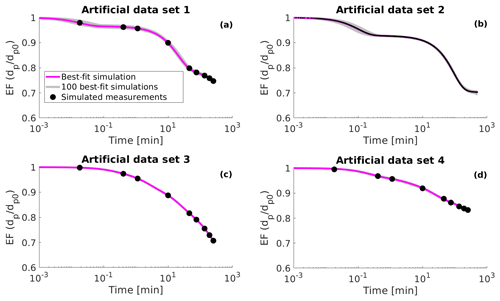
Figure 1Simulated evaporation factors (EF, particle diameter dp divided by the initial diameter dp0) (black circles), 100 best-fit simulations (grey lines) and the best-fit simulation (magenta line) for (a) artificial data set 1, (b) artificial data set 2, (c) artificial data set 3 and (d) artificial data set 4. The best-fit simulation is determined as the evaporation simulation that produces the smallest mean squared error relative to the measurement data.
Artificial data set 2 mimics the evaporation of a single particle in an electrodynamic balance (see next subsection). This data set simulates the particle evaporation measurements performed at the University of Bristol (Davies et al., 2012; Rovelli et al., 2016). Data set 2 differs from the other data sets as the particle diameter is larger by several orders of magnitude at the start of the evaporation and the particle size is sampled at a higher frequency. The number of organic compounds in data set 2 was set to three and both the values of saturation concentration and the initial fraction of each organic compound was optimized to fit the data (similar to data set 1). The artificial evaporation data are shown in Fig. 1 as well as in the Supplement (Figs. S1, S2, S3 and S4).
2.3.2 Experimental OA evaporation data
An electrodynamic balance (EDB) was used to trap single aerosol droplets generated from aqueous mixtures of organic components with known chemical composition. The evaporative loss of semi-volatile organic components was observed by measuring changes in the droplet radius over timescales of ∼105 s. The experimental setup and the sizing of trapped droplets is extensively described in previous publications (Davies et al., 2013; Rovelli et al., 2016; Marsh et al., 2017) and briefly presented below.
Charged droplets are generated by means of a microdispenser (Microfab MJ-ABP-01) and confined within the electrodynamic field generated by a set of concentric cylindrical electrodes. Once trapped, a single particle sits in a nitrogen flow (200 mL min−1, gas flow velocity of 3 cm s−1) of controlled RH and T. The RH is measured by fitting either the size vs. time profile of an evaporating probe water droplet (at RHs above 80 %) or the equilibrated radius of a NaCl or NaNO3 aqueous solution probe droplet (below 80 %) by applying a literature evaporation–condensation kinetic model (Kulmala et al., 1993). The procedure is described in Rovelli et al. (2016), where the uncertainties associated with the measured RH are also discussed (typically % at RH >90 % and % below 90 %). The temperature is measured by means of a thermocouple (NI-USB-TC01, thermocouple type K, uncertainty of ±1.5 K) placed between the inner and the outer bottom electrodes, directly within the gas flow. All the measurements in this work have been taken at 293 K. The droplet is illuminated with a 532 nm laser light (Laser Quantum Ventus CW laser) and the angularly resolved elastically scattered light is collected with a camera (Thorlabs CMOS camera, DCC1545M). The scattering pattern is used to retrieve the evolving radius of the confined droplet, by applying the geometric optics approximation (Glantschnig and Chen, 1981), with a time resolution up to 10 ms.
Table 4Composition of mixtures 1–4 in EDB measurements and the literature values for the saturation concentrations.
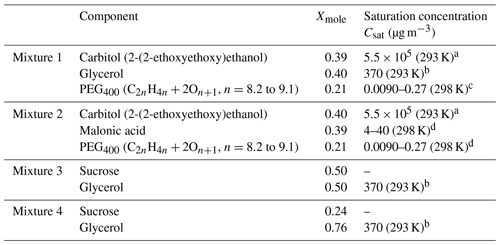
a Data from unpublished EDB measurements, same experimental approach as in Krieger et al. (2018). b Saturation concentration of glycerol at 298 K from Haynes (2009) was converted to 293 K using the Clausius–Clapeyron equation. The enthalpy of vaporization at boiling point (T=562 K) was taken from Rumble et al. (2018) and corrected to 298 K using Eq. 7-12-1 from Reid et al. (1987) resulting in ΔHvap=78.4 kJ mol−1. c Krieger et al. (2018). d Bilde et al. (2015).
Four different aqueous mixtures of organic components were considered; their detailed chemical composition can be found in Table 4. Mixtures 1 and 2 include three components of variable volatility, whereas mixtures 3 and 4 are sucrose–glycerol–water ternary solutions. Considering that the water-activity-dependent viscosity of binary sucrose spans over 10−3–1012 Pa s (Power et al., 2013) and that pure glycerol has a viscosity of 1.46 Pa s (Haynes, 2009), the viscosity of mixtures 3 and 4 is expected to be significant and to increase over time as glycerol evaporates from the trapped droplet. For each of these mixtures, a single droplet was trapped into two different RHs (low and high RH; see Sect. 5.2).
The artificial data set 1 was used to compare the two estimation methods, MCGA and Bayesian inference. Estimates for three saturation concentrations and dry particle mole fractions at the start of the evaporation were calculated. For MCGA, the total number of optimization rounds was 500. For Bayesian inference, 2000 samples were generated after a burn-in period of 500 samples where the parameters of the NUTS algorithm were tuned (Hoffman and Gelman, 2014). Every fourth estimated parameter set was selected from these 2000 samples for the final analysis, allowing the two methods to be compared.
Additionally, the MCGA method was used with two different sampling schemes. In the uniform sampling scheme, the fitting parameter values were drawn from a uniform distribution (log-uniform distribution for Csat). In the second scheme the values for saturation concentration and mole fractions at the start of the evaporation are drawn from a normal distribution with preset means and standard deviations similar to the Bayesian inference method (see Sect. 2.2.2). The two MCGA schemes are later referenced as MCGA with uniform sampling and Gaussian sampling, respectively.
Bayesian inference fundamentally assumes that experimental values are always associated with an uncertainty. This uncertainty is needed as an a priori knowledge before any Bayesian analysis can take place. The artificial data set 1, however, did not include any uncertainty. When optimizing the particle composition with the Bayesian inference method, a 1 % uncertainty in the evaporation factor (EF) (particle diameter divided by the initial diameter) was assumed.
The Bayesian inference and the MCMC algorithm assume estimated parameters are random variables with probability distributions, whereas the MCGA algorithm tries to find a single set of input parameters that best fit to the observations. The MCMC algorithm explores the posterior distribution by randomly drawing samples from it. The samples are drawn such that the parameter values that better fit to the data and thus are more probable are drawn more often than the lower probability parameter values that produce worse fits. Because of this fundamental difference between these two approaches, it would not be appropriate to compare how the model–output data residuals evolve during the execution of both algorithms, and only the distributions of parameter estimates from MCMC and MCGA over multiple optimization rounds are used to compare the two methods.
Overall the three methods are able to produce similar, reliable estimates that are close to the correct values (Fig. 2). Figure S1 shows the relative evaporation curve densities for all three optimization methods together with the artificial evaporation data. Relative curve density is calculated by dividing the time and EF space into grids and calculating how many of the simulated evaporation curves go through a specific grid point and dividing this count by the maximum count in the same time column. The relative curve densities are similar for the three methods (Fig. S1).
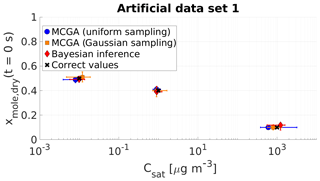
Figure 2Parameter estimates from the three different optimization methods applied to artificial data set 1. Shown are MCGA with uniform sampling (blue circles), MCGA with sampling distributions similar to the Bayesian inference (Gaussian sampling, yellow squares) and Bayesian inference (red diamonds). The markers show the modes of the estimated variable distributions for MCGA methods and the maximum a posteriori estimate of the fitting variable distributions for the Bayesian inference. The whiskers show the 10th and 90th percentiles of the variable distributions for the MCGA methods and 90 % credible interval for the Bayesian inference.
The differences between the methods are the most obvious with the most volatile compound. While the mole fraction estimates are all close to the correct value, the saturation concentration estimates show deviation from the correct value. The Bayesian inference estimate (1230 µg m−3) narrowly misses the correct saturation concentration (1000 µg m−3). The MCGA method with Gaussian sampling produces an estimate of 800 µg m−3, a difference opposite in direction to the Bayesian inference method. The estimate with the MCGA method with uniform sampling deviates the most from the correct value (600 µg m−3). The absolute uncertainties of all three methods span over several hundreds of microgrammes per cubic metre. The reason for this high uncertainty is due to the evaporation timescale of the highest-volatility compound and is discussed more thoroughly in Sect. 4.1.
Since all of the studied optimization methods yielded similar results, only the MCGA scheme with uniform sampling is used in the rest of this study, first to test the optimization method with different artificial data sets and then with the experimental data.
The estimates of the compounds with the highest and lowest volatility in data set 1 are more uncertain than the estimates of the other compounds. In this section the reasons for this behaviour are examined. Further, the process model optimization scheme is tested in estimating volatility for the three remaining artificial data sets. With data set 2, the goal is to inspect the performance of the process model input optimization approach when the evaporation conditions change in terms of particle diameter, evaporation timescale and measurement sampling frequency. With data set 3, the target is to evaluate the performance of the optimization in the case of a full VBS and the method's ability to distinguish VBS bins from each other. With data set 4 the optimization method is tested against evaporation data where the particle contains more evaporating compounds than what are used in the optimization, which is the case with real OA. A total of 500 optimization rounds were calculated for every data set.
The range of saturation concentrations that can be determined from the data with the optimization method varies with initial particle diameter and with the time span of the evaporation data. The former is due to the dependence of the mass flux between the gas and particle phases on particle size. To assess the range of minimum and maximum possible saturation concentrations that can be identified with the method from data sets, the LLEVAP model was run multiple times with particles that consist solely of one evaporating component and are characterized by variable size. The minimum identifiable saturation concentration was determined to be the concentration that shows at least 1 % shrinkage in terms of particle diameter in the timescale of an experiment. Similarly, the maximum identifiable saturation concentration was determined to correspond to a concentration that left 10 % of the particle size remaining at first data point. These minimum and maximum values are shown in Table 1. The evaporation rate of a compound also depends on its mole fraction, but this simple analysis already gives a reasonable range of possible saturation concentrations for the optimization process.
4.1 Data set 1
The values of estimated variables in Fig. 2 show the largest uncertainty for the lowest- and highest-volatility compound whereas the middle saturation concentration compound has a relatively small uncertainty. The reason for this behaviour lies in the nature of the evaporation process. For the least volatile compound, the correct value of the estimated saturation concentration was 0.01 µg m−3. The 10th and 90th percentiles of the obtained estimate were 0.004 and 0.012 µg m−3. The lower end of the estimated saturation concentrations corresponds to evaporation curves which do not show practically any evaporation once the middle-volatility compound has evaporated from the particles. The higher end corresponds to curves which follow the slow evaporation pattern also observed in the data. To constrain the saturation concentration and mole fraction estimates of the least volatile compound better, more data would be needed after ca. 50 min, when the evaporation of the least volatile compound dominates the particle shrinkage.
A similar analysis can be applied to the most volatile compound, for which the obtained values of saturation concentration span from around 400 to over 3000 µg m−3. In the case of data set 1, the amount of the most volatile compound decreases by 99 % during the first 5 s of the evaporation. As there is only one data point before 5 s, the estimated values of the most volatile compound contribute relatively little compared to the other two compounds when the goodness of fit is calculated. In all simulations there exists a distinct high-volatility compound as the shape of the evaporation curve dictates that the particle must shrink 10 % by diameter during the first 10 min. This shrinkage can only be achieved with a compound that has a relatively high saturation concentration. More accurate estimates of the most volatile compound would require more data points at the very beginning of the evaporation. As data set 1 mimics evaporation experiments which require filling of an evaporation chamber as reported in Yli-Juuti et al. (2017), it might not be straightforward to obtain more data points at the start of the evaporation.
4.2 Data set 2
There exist three key differences in data set 2 compared to other data sets. First, the data extend almost twice as long in time. Second, the particle diameter is 125 times larger and, third, the time resolution is higher, resulting in more data points, especially at the start of the evaporation. The first two differences mean that the range of identifiable Csat values changes compared to data sets 1, 3 and 4 (see Table 1).
The MCGA estimates agree well with the correct values for data set 2 (Fig. 3). For the least volatile compound the saturation concentration and mole fraction estimates match exactly with the correct values. The uncertainty in the mole fraction estimate is small. While at first the uncertainty in the saturation concentration might seem high for the least volatile component, the absolute values are between 0.4 and 20 µg m−3 and organics with these saturation concentrations do not evaporate at all or evaporate only very slowly in the timescale of the simulated evaporation.
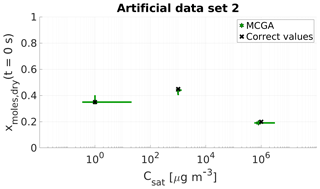
Figure 3Parameter estimates for artificial data set 2; dry particle mole fraction at the start of the evaporation and saturation concentrations of three model compounds were optimized to match the data. Green stars show the MCGA estimates and black crosses the correct values. The whiskers show the 10th and 90th percentiles of the estimated variable distributions.
The estimates for the second compound match the correct values well. The behaviour is similar to data set 1, for which it was found that the compound whose saturation concentration lies between the two other compounds' saturation concentration was characterized the best.
For the most volatile compounds the estimates are close to the correct values and the uncertainty in mole fraction is negligible. The uncertainty in the Csat estimate is high and arises from the fact that only ca. 8 % of the data points are recorded before the most volatile compound is gone (over the timescale of ca. 30 s). However, the increased number in data points that influence the Csat value makes the estimate more certain when compared to the estimate of the most volatile compound calculated with MCGA and uniform sampling of the parameters in data set 1 for which only one data point is encountered before the compound has practically evaporated.
4.3 Data set 3
Artificial data set 3 describes the evaporation of organic aerosol in conditions similar to those in data set 1. The difference from data set 1 is that the particle composition consists of a “full VBS”; i.e. all VBS bins between minimum and maximum identifiable Csat are present in the particle at the start of the evaporation. From the optimization point of view, the saturation concentrations of the organic compounds are fixed during the optimization and only the mole fractions of each compound at the start of the evaporation are optimized to the data. This mimics the analysis that would be performed for SOA particles to derive their composition in terms of a full volatility distribution. The estimated mole fractions together with the correct values are shown in Fig. 4. The estimated values show that when the saturation concentrations are discretized into six bins, optimizing only the mole fractions is more accurate compared to data set 1 where saturation concentrations and mole fractions were estimated.
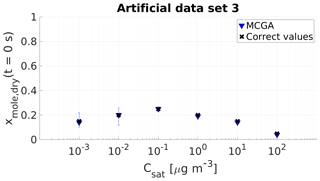
Figure 4Parameter estimates for artificial data set 3; dry particle mole fraction at the start of the evaporation of six model compounds with predefined saturation concentration were optimized to match the data. Blue triangles show the MCGA estimates and black crosses the correct values. The whiskers show the 10th and 90th percentiles of the estimated variable distributions.
For the three compounds with saturation concentration higher than or equal to 10−1 µg m−3 in data set 3, the estimated mole fractions deviate only by 0.02 from the correct values. The estimates for the two least volatile compounds are different compared with the other compounds in terms of uncertainty. The estimated mole fraction for the compound with µg m−3 matches the correct value and the uncertainty is . For the least volatile compound the estimated mole fraction is 0.01 lower than the correct value and the uncertainty is .
The evaporation curves calculated with the LLEVAP model using the MCGA estimates as input variables show that all the curves match artificial data set 3 extraordinarily well (Figs. 1c and S3) compared to data set 1 (Figs. 1a and S1) where the curves calculated from estimates show much higher variance around the data points. This demonstrates that the uncertainty in the mole fraction estimates is not due to the MCGA algorithm itself but to the ability to distinguish low-volatility VBS bins. In fact, the same evaporation curve can be simulated by switching the numbers of molecules between the two least volatile bins. This indistinguishability is also seen in that the summed mole fraction of the two least volatile compounds is always in the range 0.35±0.01.
4.4 Data set 4
In terms of evaporation characteristics, the artificial data set 4 is similar to data sets 1 and 3. However, the evaporating particle is made of 40 different compounds for data set 4 with distinct saturation concentrations and amounts in the particle. The correct values for all the evaporating compounds can be found in Table S2, whereas the correct values in Fig. 5 show these 40 compounds lumped into six VBS bins.
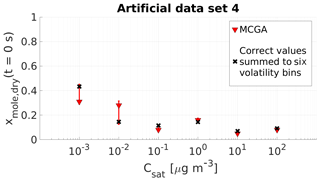
Figure 5Parameter estimates for artificial data set 4 dry particle mole fraction at the start of the evaporation of six model compounds with predefined saturation concentration were optimized to match the data. Red triangles show the MCGA estimates and the whiskers show the 10th and 90th percentiles of the estimated variable distributions. Black crosses are the correct values summed to six volatility bins. All the correct values for the 40 evaporating compounds are listed in Table S2.
When optimizing the particle composition of data set 4, the compounds are presented with a full VBS similar to data set 3 and the free parameters are set the same way.
Figure 5 compares the MCGA estimates for the mole fraction with the correct values. The accuracy of the estimates is similar to the results obtained with data set 3. For the four highest volatility classes, the estimates deviate at most by 0.04 from the correct lumped values. For the two lowest-volatility groups the estimates deviate more from the correct values, by approximately 0.12 for the group with µg m−3 and by 0.13 for the lowest-volatility group. There is no consistent over- or underestimation associated with these low-volatility bins. The estimate for the group with µg m−3 is higher than the correct value and the estimate for the lowest-volatility group is lower than the correct value. In both cases, the correct lumped value is included in the uncertainties of the estimates that are higher compared to the other compounds. This behaviour was also seen with data set 3 and again shows the indistinguishability that is associated with the two least volatile bins and the timescale of this data set. When the sums of the two least volatile compounds are compared, the correct mole fraction would be approximately 0.58 and the 10th and 90th percentiles of the estimates are 0.58 and 0.61, respectively.
4.5 Discussion on estimating the volatility from artificial data
While all the estimates capture the correct values with reasonable accuracy, the number of data points and their temporal distribution clearly affect the estimates. When the data are sparse, the uncertainty of the estimated variables increases as the optimization process is designed to weight each data point equally. In the case of data set 1 and data set 2, the compounds with saturation concentration between the other two saturation concentrations always have the smallest uncertainty. This is because the middle compound evaporates during almost the whole duration of the data and thus its saturation concentration and mole fraction influences the evaporation curve the most. If the goal is to reduce uncertainties of the least volatile compound, measurements should be carried out over longer timescales. Similarly, if the goal is to study compounds that evaporate quickly, the very start of the evaporation needs to be measured at a higher frequency.
The above results show the particle size and timescale of the experiment affect the range of possible saturation concentrations that can be estimated from the data. When the particle size is small and the measurement timescales long, lower saturation concentrations can be distinguished from the data; when the particle size is large, higher saturation concentrations are distinguished from the data. The time of the first data point and the time resolution at the start of the evaporation also matter. With higher sampling frequency and earlier data points, the higher-volatility compounds can be identified from the data with the optimization method.
An interesting remark concerns the choice of the variables that are optimized. From Figs. S1 and S2 it can be seen that the simulated evaporation curves show more variance around the data points when the saturation concentrations and mole fractions are optimized than in Figs. S3 and S4, where only mole fractions at the start of the evaporation of a full VBS are optimized. The mole fractions are an easier task to optimize because each new VBS bin creates a new dimension to the parameter space, which can take values between 0 and 1. By contrast, adding a new saturation concentration dimension increases the parameter space significantly more as possible values span over several orders of magnitude.
It should be noted that it is not always better to fit a full VBS as illustrated by data set 3. If the number of evaporating compounds is known, fixing the number of compounds and optimizing their relative amount and saturation concentration gives more information about the experiment than optimizing only the mole fractions of a full VBS.
So far, this study has considered only artificial evaporation data calculated with the LLEVAP model. Next, the process model optimization scheme is applied to real experimental data. In the following discussion, “low viscosity” refers to particles where particle-phase diffusivity is fast enough so that it does not pose a limitation to the evaporation of the volatile compounds, and “high viscosity” refers to particles where the particle-phase diffusivity is low enough to affect the particles' evaporation rate. Compositions are estimated for two low viscosity (mixtures 1 and 2) and two high viscosity mixtures (mixtures 3 and 4 at low RH). For the latter two, the viscosities are also estimated by using evaporation profiles measured at two different relative humidities. The organic properties in the model and conditions of evaporation for all four mixtures are listed in Table 5. For every mixture, 100 different parameter sets that fit to the measured data were calculated. The measured and modelled evaporation curves are shown in Fig. 6 as well as in the Supplement (Figs. S5, S6, S7 and S8)
Table 5The properties of the organic compounds for the particles generated from mixtures 1–4. The variables are, from top to bottom, particle diameter at the start of the evaporation, molar mass, particle-phase density, gas-phase diffusion coefficient, relative humidity, temperature, saturation concentrations of the VBS compounds, mole fraction of the compounds at the start of the evaporation and viscosity parameters b in Eq. (1).
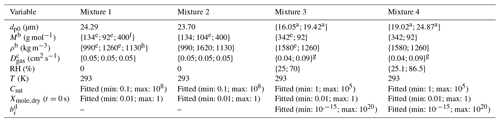
a First value is for measurement at low RH and second for measurement at
high RH.
b For mixtures 1 and 2 only for the optimization runs where exact compound
properties were
used. The order of the compounds is the same as in Table 4.
c The order of the compounds is the same as in Table 4. The gas-phase
diffusion coefficients are scaled to correct
temperatures by multiplying
by a factor of (T∕273.15)1.75.
d Only for low RH.
e Rumble et al. (2018).
f Mean molar mass from Krieger et al. (2018).
g Calculated using data
and Eq. 11-3-2 from Reid et al. (1987).
h Sigma-Aldrich.
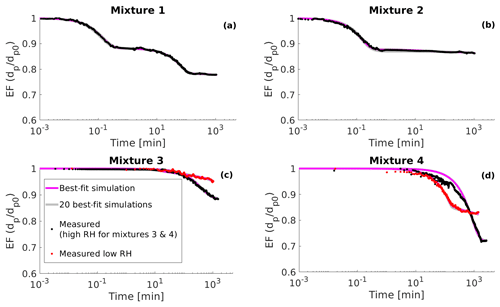
Figure 6(a) Measured evaporation factors (EF, particle diameter dp divided by the initial diameter dp0) of mixture 1 from the determined point of water equilibrium (see Sect. 5) (black circles), 20 best-fit simulations (grey lines) and the best-fit simulation (magenta line). (b) Same as panel (a) but for mixture 2. (c) Measured evaporation factors of mixture 3 from the determined point of water equilibrium under high RH conditions (RH = 70 %, black circles) and low RH conditions (RH = 25 %, red circles). Grey lines show 20 best-fit simulations and magenta line the best-fit simulation; (d) same as panel (c) but for mixture 4 for which the high RH is 86.5 % and low RH is 25.1 %. The best-fit simulation is determined as the evaporation simulation that produces the smallest mean squared error relative to the measurement data.
In the EDB the particle- and gas-phase water are not fully in equilibrium when the measurement starts. This creates a period of very rapid evaporation when water evaporates from the particle. As both process models used in this study assume that the water is in equilibrium at the start of the evaporation, these rapid evaporation periods were removed from the data. The point at which water is in equilibrium was determined to be the point where the rate of change of particle squared radius is constantly higher than 1 µm2 s−1 for mixtures 1, 2, 4 and 3 at high RH and 0.1 µm2 s−1 for mixture 3 at low RH. The reason for the higher threshold for mixture 3 at low RH is that the mixture has the highest viscosity and the excess water evaporation the slowest of all the organic–water mixtures.
The sampling frequency varied across the measurements. After removing the period where water evaporates from the particle, the start of the data sets contained a period where the particle size was sampled at higher frequency than at later times. For mixture 3 at low RH and for mixture 4 at both RH values this led the MCGA algorithm to weight more strongly in fitting the start of the evaporation where there were more data. As this was not the desired behaviour, only one data point for every minute was taken into account when calculating the goodness of fit for these experimental data sets.
The correct values presented here are mole or mass fraction in the actual mixture and the literature values for the pure compound saturation concentrations (Table 4). However, the saturation concentration estimates obtained from the optimization process are effective saturation concentrations because the evaporation models assume ideal behaviour. Any nonideal behaviour of the mixtures will cause the estimated Csat to differ from the literature values. The possible deviation from ideality of every mixture is assessed by performing AIOMFAC (http://www.aiomfac.caltech.edu, last access: 11 January 2019; Zuend et al., 2008, 2011) calculations with the composition at the start of the evaporation as the input.
5.1 Evaporation of low viscosity mixtures
The correct mole fractions and saturation vapour pressures for the low viscosity mixtures 1 and 2 are listed in Table 4 and shown for mixture 1 in Fig. 7 and for mixture 2 in Fig. 8. In both figures, two different MCGA estimates are shown. The darker squares represent optimization results where the literature values for molar masses and particle-phase densities were used. The light diamond markers represent optimization where the same molar mass and particle-phase density (M=200 g mol−1; ρ=1200 kg m−3) were used for every model compound. The vertical axis in Figs. 7 and 8 is mass fraction of a compound at the start of the evaporation since it is less sensitive to the assumed molar masses compared to mole fraction.
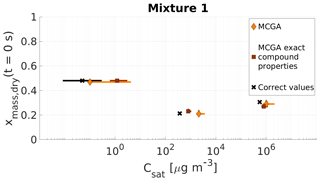
Figure 7Parameter estimates for particles generated from mixture 1. Dry particle mass fraction at the start of the evaporation of three compounds and their saturation concentrations were optimized to match the evaporation data. Orange diamonds show the MCGA estimates calculated by assuming equal molar mass and particle-phase density for all compounds and brown squares show the MCGA estimates calculated by setting the molar mass and particle-phase density to their literature values. Black crosses show the literature values. The whiskers of the estimates show the 10th and 90th percentiles of the estimated variable distributions and the whiskers of the corrected values show the range of literature values (see Table 4 for references).
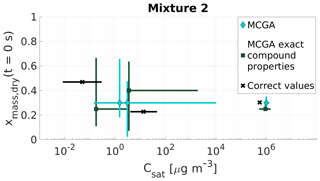
Figure 8Parameter estimates for particles generated from mixture 2. Dry particle mass fraction at the start of the evaporation of three compounds and their saturation concentrations were optimized to match the evaporation data. Cyan diamonds show the MCGA estimates calculated by assuming equal molar mass and particle-phase density for all compounds, and teal squares show the MCGA estimates calculated by setting the molar mass and particle-phase density to their literature values. Black crosses show the correct values. The whiskers of the estimates show the 10th and 90th percentiles of the estimated variable distributions and the whiskers of the correct values show the range of literature values (see Table 4 for references)
5.1.1 Mixture 1
The mass fraction estimates are close to the correct values for all three compounds (Fig. 7). The correct value is within the uncertainty of the estimates for all the compounds except for the highest-volatility compound (MCGA, exact compound properties) for which the 90th percentile corresponds to a mass fraction of approximately 0.28, 0.02 away from the correct value.
The saturation concentration estimates are slightly overestimated with both methods for the highest-volatility compound (Carbitol) and for the middle-volatility compound (glycerol). For glycerol the MCGA estimate with literature properties (800 µg m−3) is closer to the literature saturation concentration (370 µg m−3; see Table 4 for references) than the MCGA estimate with equal compound properties (2100 µg m−3). With equal compound properties for the estimates to produce comparable evaporation rates to measurements, a higher saturation concentration is needed to compensate for the larger molar mass.
For the least volatile compound (PEG400), the estimated saturation concentrations show the largest variation. In fact, both estimates do not include the literature value in their distribution. This is again because of the low sensitivity of the evaporation curve to the least volatile compound. It does not make a significant difference to the overall goodness of fit if the saturation concentration is 3 or 0.1 µg m−3, as in the timescales of the measurements all these saturation concentrations lead to practically no evaporation from the particle.
Figure S5a shows all the simulated and measured evaporation curves and Fig. 6a shows 20 best-fit-simulated evaporation curves and the measured one. The simulated curves show similar spread as with artificial data sets 1 and 2. In Fig. S5b the literature values are used as input to the LLEVAP model and the resulting evaporation curve is compared with the measurements to show that with parameters from the literature and with correct mole fractions the model would produce evaporation rates similar to measurements everywhere except in the middle of the measurement where the simulated rate of evaporation is slower. This discrepancy could be explained by the nonideality of the mixture as the AIOMFAC-calculated activity coefficients are 1.12 and 1.88, respectively, for Carbitol and glycerol. Neglecting the nonideality in the model may have caused an overestimation of the saturation concentration of glycerol in the optimization.
5.1.2 Mixture 2
The estimated mass fractions and saturation concentrations for mixture 2 (Fig. 8) show different behaviour to the estimated properties of mixture 1. The only satisfactory estimates are the saturation concentration and mass fraction of the highest-volatility compound (Carbitol), for which both MCGA methods marginally overestimate the saturation concentration. The optimization performed with exact compound properties produces a mass fraction estimate that is 0.05 smaller than the correct value (0.30). In the MCGA runs with exact compound properties, the uncertainties are higher than in the MCGA runs with equal compound properties for all the compounds, especially in the saturation concentration estimate. The AIOMFAC calculations give an activity coefficient of 1.06 for Carbitol, which could explain some of the overestimation in the saturation concentration.
The estimates of the saturation concentrations and mass fractions for the two other compounds (malonic acid and PEG400) are problematic when compared with all of the other systems encountered so far. For both MCGA approaches the estimates clearly deviate from the values that were sought. The uncertainties of the estimated values with both approaches span over a wide range in the parameter space, from 0.03 to 0.66 in mass fraction and from 0.15 to almost 9500 µg m−3 in saturation concentration. The reason for this inaccuracy in the optimization method is discussed in Sect. 5.3.
5.2 Evaporation of high-viscosity mixtures 3 and 4
Finally, the results concerning the evaporation of high-viscosity mixtures 3 and 4 are described. For these optimization runs the correct molar masses, particle-phase densities and gas-phase diffusion coefficients were used for sucrose and glycerol. With both mixtures two different evaporation measurements were performed, one measured at high RH and one at lower RH. For the high-RH case, it was assumed that the particles behave like well-mixed ideal liquids and, thus, the LLEVAP model was used to model the evaporation. For low-RH measurements with significant particle-phase diffusion limitations, KM-GAP was used to model the evaporation. The optimization to both relative humidities was performed simultaneously. In this case the goodness of fit was calculated as a sum of individual measurement–simulation MSEs.
Two restrictions were set for the new candidate creation. The candidate was not accepted if the overall particle viscosity was below 0.01 Pa s at the start of the evaporation. Such a low viscosity does not produce slower evaporation at low RH, which is observed in the measurements, and a low viscosity greatly increases the computation time of a single KM-GAP simulation. In addition, during the candidate creation, the free parameters were sorted based on the saturation concentrations. Effectively, this guides the optimization algorithm away from values that would produce wrong evaporation as the higher-volatility compound (glycerol) was prevented from becoming associated with the preset properties of lower-volatility compound (sucrose) (e.g. molar mass, gas-phase diffusion coefficient) or vice versa. Ultimately the choice leads to a smaller number of iterations that must be calculated in order to obtain a reliable estimate for the free parameters.
Table 6The median b parameter which describes the contribution of glycerol and sucrose to the particle viscosity from optimizing the KM-GAP model to match the low RH measurement of mixtures 3 and 4. The literature values for viscosity of glycerol are also reported. For sucrose the reported literature value is an experimental fit calculated from viscosity measurements of sucrose–water mixtures evaluated at RH = 0 %.

a Rumble et al. (2018). b Song et al. (2016).
The estimates for the saturation concentration of sucrose and glycerol and their mole fractions are shown in Fig. 9 for mixture 3 and in Fig. 10 for mixture 4. Table 6 shows the median and 10th and 90th percentiles of the estimated bi factors with which the particle viscosity is calculated in the KM-GAP simulations. In addition, the spread of the simulations together with the measured evaporation of particles are reported in Fig. S7a (mixture 3) and Fig. S8a (mixture 4). In Figs. S7b and S8b, the KM-GAP and LLEVAP simulations made with the literature values are compared with the evaporation measurements. Figure 6c and d show the 20 best-fit simulations together with the measured evaporation.
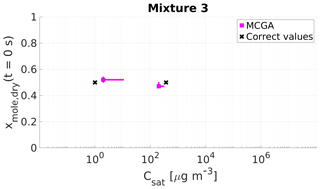
Figure 9Parameter estimates for particles generated from mixture 3. Dry particle mole fraction at the start of the evaporation of two compounds and their saturation concentrations and the viscosity parameters bi were optimized to match the evaporation data. Magenta squares show the MCGA estimates and black crosses show the literature values. The whiskers show the 10th and 90th percentiles of the estimated variable distributions. Sucrose Csat is marked at the lower limit of the Csat range due to its assumed low value.
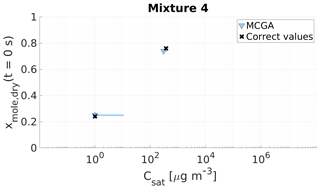
Figure 10Parameter estimates for particles generated from mixture 4. Dry particle mole fraction at the start of the evaporation of two compounds and their saturation concentrations and the viscosity parameters bi were optimized to match the evaporation data. Light blue triangles show the MCGA estimates and black crosses show the literature values. The whiskers show the 10th and 90th percentiles of the estimated variable distributions. Sucrose Csat is marked at the lower limit of the Csat range due to its assumed low value.
The saturation concentration of sucrose is presumably so low that practically no sucrose evaporates from the particle. For this reason, it is marked in Figs. 9 and 10 at Csat=1 µg m−3, which was identified as the lower limit that can be reliably fitted considering the experimental timescale (see Sect. 4). The estimated saturation concentrations for sucrose are comparable to this value: for mixture 3 the estimated saturation concentrations are between 2 and 11 µg m−3 and for mixture 4 between 1 and 10 µg m−3. The mole fraction estimates for sucrose are excellent as the deviation from the correct value is at a maximum of 0.02 for mixture 3 and 0.01 for mixture 4.
For the higher-volatility compound glycerol, the optimization yields slightly lower saturation concentrations (200–285 µg m−3) than the literature value (370 µg m−3) for mixture 3. For mixture 4 the estimated saturation concentration matches the literature value better, although the literature value is at the high end of the estimated Csat (260–380 µg m−3). For the mole fraction of each compound at the start of the evaporation, the estimates are close to the real values.
Lastly, with mixtures 3 and 4 the contribution of each compound to the particle viscosity was estimated. If an ideal mixture is assumed, these contribution parameters (bi in Eq. 1) can be compared to the pure compound viscosities. The estimated contribution parameters b together with pure component viscosity of sucrose and glycerol found from the literature are shown in Table 6. For sucrose the estimated bsucrose values are on the lower end of the literature values and for glycerol the bglycerol estimates are several magnitudes smaller than the literature value.
5.3 Discussion on estimating the volatility and viscosity from EDB measurements
Overall, it can be said that the estimated properties are captured well when the process model optimization scheme is applied to real experiments. However, some aspects merit further discussion on the limitations of the method.
Among the 10 artificial and experimental data sets considered in this work, the method fails to estimate the correct mass fractions at the start of the evaporation and the saturation concentrations only for malonic acid and PEG400 in mixture 2. This exception can be understood by looking at Fig. S6a. The measured evaporation curve is shaped like the letter L. There is a clear faster period of evaporation when mainly the highest-volatility compound (Carbitol) evaporates followed by evaporation of at least one other compound. If more than one compound characterized by low volatility is present (in this case two, with Csat≈10 µg m−3 or smaller) the evaporation curve will look the same as in the case of one low-volatility compound; i.e. the particle size remains practically constant towards the end, and it is difficult for an optimization algorithm to distinguish between the two. This is an important finding because it provides information on the sensitivity of the model to low-volatility chemical species; in addition, it provides an estimate of what range in volatility can be accessible as a function of the experimental timescale. When optimizing the LLEVAP model input to particles produced from mixture 2, MCGA was set to find saturation concentrations and mass fractions for exactly three compounds. When one compound is needed to produce the fast evaporation and one compound the slow evaporation the third compound is left over. In this case MCGA finds solutions where the third compound's saturation concentration is close to either of the two other compounds or its mass fraction at the start of the evaporation is insignificant. Fundamentally this result shows a limit to the optimization method. If the properties of two compounds are close to each other so that they produce similar measurable quantities as they would produce alone, the optimization method might not find a clearly defined estimate for these properties. This shortcoming was encountered when finding an optimal set of mass fractions and saturation concentrations for three compounds. With artificial data set 4 it was shown that lumping 40 compounds into six volatility classes produced a good fit, meaning that the impact of such a shortcoming is expected to be limited when performing the optimization to “real” OA evaporation data sets.
Another aspect concerns the lower estimate for the saturation concentration of glycerol compared to the literature value and the estimated values for the bi parameters of sucrose and glycerol. Figures S7b and S8b show the simulated curves when the real properties of the organics are used as input values. The simulated evaporation is faster than the measured one, which means that the properties estimated by optimizing the model to match measured data are not expected to match with the literature values. AIOMFAC calculations give water activity coefficients of 0.50, 0.86 and 0.59 for mixture 3 at low and high RH and for mixture 4 at low RH, respectively, when using the start of the evaporation composition as input. The activity coefficients for glycerol are all close to unity for these mixtures. Water activity coefficients smaller than unity mean that there is more water partitioned in the particle phase than calculated based on the ideality assumption. Due to Raoult's law the rate of evaporation of glycerol might be hindered, which might explain why the optimization method underestimates glycerol's saturation concentration and why the literature values produce too fast evaporation when used as a model input. AIOMFAC calculations produce a near-unity (0.97) water activity coefficient for the high-RH experiment of mixture 4. With this experiment the AIOMFAC activity coefficient of glycerol is 0.68, which again might explain the discrepancy.
When optimizing the viscosity, the overall particle viscosity is optimized, which is made up of the individual contribution parameters of sucrose and glycerol. These contribution parameters can be compared to the pure compound viscosities, if the mixture is ideal. While at first the estimated b parameters seem to be too high for sucrose and too low for glycerol, the range of possible contribution parameter values allowed in the optimization was large, from 10−15 to 1020. At a closer inspection of the estimated bi parameters (Fig. S9), it is clear that the high bsucrose values are always associated with low bglycerol values. However, the literature values reported in Table 6 do not fit to the trend observed in Fig. S9. If the literature values were input to Eq. (1), they would produce higher viscosity than what is estimated with the process model optimization method. This discrepancy could be explained by the nonideality of mixtures 3 and 4 at low RH where AIOMFAC-calculated activity coefficients for water were 0.50 and 0.59, respectively (i.e. there could be more water in the particle phase than what is calculated based on the ideality assumption). This additional water could decrease the particle-phase viscosity.
In this study, process model optimization methods were tested as a possible way of quantifying some of the physicochemical properties of organic aerosol particles that are challenging to measure directly. More specifically, the particle compounds' volatilities and particle viscosity were estimated by searching for those values that when used as an input to a detailed evaporation model produce an evaporation curve similar to the evaporation test data. Additionally, two different ways of stating the optimization problem were tested. Both the Monte Carlo genetic algorithm and Bayesian inference method yielded similar optimization results.
The process model optimization scheme was tested for both artificially generated and measured isothermal evaporation data. When fitting the model to artificial data, accurate estimates for both mole fraction and saturation concentrations of the components were obtained. With real experimental data the method produced good estimates given the fact that the models assumed ideal behaviour and thermodynamic equilibrium calculations with AIOMFAC showed that the mixtures might be slightly nonideal.
For some of the tested data sets, the few shortcomings of the method could be largely attributed to the fact that the model output was not sensitive to the changes in the estimated parameters with respect to the experimental timescale and parameter range. If some parameters are uninfluential (or have a small influence over the observed timescales) to the model output or if the parameter is coupled to another parameter, they cannot be estimated precisely. This was the case with artificial data sets 3 and 4, in which the two least volatile compounds were almost interchangeable as both produce slow evaporation, and with the estimated viscosity of glycerol and sucrose in mixtures 3 and 4 where the b parameters were coupled to produce the overall viscosity of the particle. This overall viscosity could be achieved by many combinations of the allowed values of the b parameter in Eq. (1).
In addition, if the estimated properties of two different compounds were close to each other the studied method might not be able to discriminate between them. This was observed with the evaporation of particles produced from mixture 2 as the saturation concentrations of malonic acid and PEG400 were close to each other and produced nearly constant rates of evaporation over the considered experimental timescale.
The process model optimization scheme also depends on the process models that are used. If the model output with literature values deviates from the measurements, the obtained estimates will not be exact. This kind of drawback was encountered when estimating the saturation concentration of glycerol in evaporation of mixtures 3 and 4. This can be the case if the model does not describe the system accurately, e.g. due to ignored nonideality.
Optimizing process model input to match measured data is a promising method for the quantification of the volatility of OA particle constituents and viscosity from evaporation experiments which are challenging properties to measure directly. Further studies using this method should be accompanied by a clearly defined range of values for each estimated parameter. This range should take into account what can be inferred from the data with respect to the experimental conditions and model assumptions. Based on the analysis shown here, various parameters can be obtained from experimental data using this method and the design of the experiments can be used to focus experiments on properties of interest. For instance, in order to distinguish between saturation concentrations of low-volatile compounds, small particles and hours-long evaporation times are required. Conversely, to distinguish between semivolatile or intermediate-volatility compounds, larger particles and/or high sampling time resolution for the short evaporation timescales are needed.
The process models and the version of the MCGA used in this study can be acquired upon request from the corresponding author.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-9333-2019-supplement.
OPT developed the MCGA code with support from TYJ. VH and AL developed the Bayesian inference code with support from KEJL. MS developed the KM-GAP model. OPT, TYJ and KEJL designed the simulations and OPT and VH performed them. GR and JPR designed and performed the measurements. All authors participated in the interpretation of the data. OPT prepared the paper with contributions from all co-authors.
The authors declare that they have no conflict of interest.
This research has been supported by the Academy of Finland (grant nos. 307331 and 299544), the NERC Environmental Bioinformatics Centre (grant no. NE/M004600/1), the US National Science Foundation (grant no. AGS-1654104), and the University of Eastern Finland Doctoral Program in Environmental Physics, Health and Biology.
This paper was edited by Barbara Ervens and reviewed by two anonymous referees.
Abramson, E., Imre, D., Beránek, J., Wilson, J., and Zelenyuk, A.: Experimental determination of chemical diffusion within secondary organic aerosol particles, Phys. Chem. Chem. Phys., 15, 2983–2991, https://doi.org/10.1039/C2CP44013J, 2013.
Arangio, A. M., Slade, J. H., Berkemeier, T., Pöschl, U., Knopf, D. A., and Shiraiwa, M.: Multiphase Chemical Kinetics of OH Radical Uptake by Molecular Organic Markers of Biomass Burning Aerosols: Humidity and Temperature Dependence, Surface Reaction, and Bulk Diffusion, J. Phys. Chem. A, 119, 4533–4544, https://doi.org/10.1021/jp510489z, 2015.
Bayes, T., Price, R., and Canton, J.: An essay towards solving a problem in the doctrine of chances, Philos. T. Roy. Soc., https://doi.org/10.1098/rstl.1763.0053, 1763.
Berkemeier, T., Steimer, S. S., Krieger, K. U., Peter, T., Pöschl, U., Ammann, M., and Shiraiwa, M.: Ozone uptake on glassy, semi-solid and liquid organic matter and the role of reactive oxygen intermediates in atmospheric aerosol chemistry, Phys. Chem. Chem. Phys., 18, 12662–12674, https://doi.org/10.1039/C6CP00634E, 2016.
Berkemeier, T., Ammann, M., Krieger, U. K., Peter, T., Spichtinger, P., Pöschl, U., Shiraiwa, M., and Huisman, A. J.: Technical note: Monte Carlo genetic algorithm (MCGA) for model analysis of multiphase chemical kinetics to determine transport and reaction rate coefficients using multiple experimental data sets, Atmos. Chem. Phys., 17, 8021–8029, https://doi.org/10.5194/acp-17-8021-2017, 2017.
Bilde, M., Barsanti, K., Booth, M., Cappa, C. D., Donahue, N. M., Emanuelsson, E. U., McFiggans, G., Krieger, U. K., Marcolli, C., Topping, D., Ziemann, P., Barley, M., Clegg, S., Dennis-Smither, B., Hallquist, M., Hallquist, Åsa M, Khlystov, A., Kulmala, M., Mogensen, D., Percival, C. J., Pope, F., Reid, J. P., V Ribeiro da Silva, M. A., Rosenoern, T., Salo, K., Pia Soonsin, V., Yli-Juuti, T., Prisle, N. L., Pagels, J., Rarey, J., Zardini, A. A., and Riipinen, I.: Saturation Vapor Pressures and Transition Enthalpies of Low- Volatility Organic Molecules of Atmospheric Relevance: From Dicarboxylic Acids to Complex Mixtures, Chem. Rev., 115, 4115–4156, https://doi.org/10.1021/cr5005502, 2015.
Carpenter, B., Gelman, A., Hoffman, M. D., Lee, D., Goodrich, B., Betancourt, M., Brubaker, M., Guo, J., Li, P., and Riddell, A.: Stan: A probabilistic programming language, J. Stat. Softw., 76, 1–32, https://doi.org/10.18637/jss.v076.i01, 2017.
Davies, J. F., Haddrell, A. E., and Reid, J. P.: Time-Resolved Measurements of the Evaporation of Volatile Components from Single Aerosol Droplets, Aerosol Sci. Tech., 46, 666–677, https://doi.org/10.1080/02786826.2011.652750, 2012.
Davies, J. F., Haddrell, A. E., Rickards, A. M. J., and Reid, J. P.: Simultaneous Analysis of the Equilibrium Hygroscopicity and Water Transport Kinetics of Liquid Aerosol, Anal. Chem., 85, 5819–5826, https://doi.org/10.1021/ac4005502, 2013.
Donahue, N. M., Robinson, A. L., Stanier, C. O., and Pandis, S. N.: Coupled partitioning, dilution, and chemical aging of semivolatile organics, Environ. Sci. Technol., 40, 2635–2643, https://doi.org/10.1021/es052297c, 2006.
Einstein, A.: Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen, Ann. Phys., 322, 549–560, https://doi.org/10.1002/andp.19053220806, 1905.
Gelman, A., Stern, H. S., Carlin, J. B., Dunson, D. B., Vehtari, A., and Rubin, D. B.: Bayesian data analysis, Chapman and Hall/CRC, Boca Raton, FL, USA, 2013.
Glantschnig, W. J. and Chen, S.-H.: Light scattering from water droplets in the geometrical optics approximation, Appl. Optics, 20, 2499, https://doi.org/10.1364/AO.20.002499, 1981.
Hallquist, M., Wenger, J. C., Baltensperger, U., Rudich, Y., Simpson, D., Claeys, M., Dommen, J., Donahue, N. M., George, C., Goldstein, A. H., Hamilton, J. F., Herrmann, H., Hoffmann, T., Iinuma, Y., Jang, M., Jenkin, M. E., Jimenez, J. L., Kiendler-Scharr, A., Maenhaut, W., McFiggans, G., Mentel, Th. F., Monod, A., Prévôt, A. S. H., Seinfeld, J. H., Surratt, J. D., Szmigielski, R., and Wildt, J.: The formation, properties and impact of secondary organic aerosol: current and emerging issues, Atmos. Chem. Phys., 9, 5155–5236, https://doi.org/10.5194/acp-9-5155-2009, 2009.
Haynes, W. M.: CRC handbook of chemistry and physics, 6th ed., CRC press, Boca Raton, FL, USA, 2009.
Hernández, W. P., Castello, D. A., Roitman, N., and Magluta, C.: Thermorheologically simple materials: A bayesian framework for model calibration and validation, J. Sound Vib., 402, 14–30, https://doi.org/10.1016/j.jsv.2017.05.005, 2017.
Hoffman, M. D. and Gelman, A.: The No-U-turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo., J. Mach. Learn. Res., 15, 1593–1623, 2014.
Jimenez, J. L., Canagaratna, M. R., Donahue, N. M., Prevot, A. S. H., Zhang, Q., Kroll, J. H., DeCarlo, P. F., Allan, J. D., Coe, H., Ng, N. L., Aiken, A. C., Docherty, K. S., Ulbrich, I. M., Grieshop, A. P., Robinson, A. L., Duplissy, J., Smith, J. D., Wilson, K. R., Lanz, V. A., Hueglin, C., Sun, Y. L., Tian, J., Laaksonen, A., Raatikainen, T., Rautiainen, J., Vaattovaara, P., Ehn, M., Kulmala, M., Tomlinson, J. M., Collins, D. R., Cubison, M. J., Dunlea, E. J., Huffman, J. A., Onasch, T. B., Alfarra, M. R., Williams, P. I., Bower, K., Kondo, Y., Schneider, J., Drewnick, F., Borrmann, S., Weimer, S., Demerjian, K., Salcedo, D., Cottrell, L., Griffin, R., Takami, A., Miyoshi, T., Hatakeyama, S., Shimono, A., Sun, J. Y., Zhang, Y. M., Dzepina, K., Kimmel, J. R., Sueper, D., Jayne, J. T., Herndon, S. C., Trimborn, A. M., Williams, L. R., Wood, E. C., Middlebrook, A. M., Kolb, C. E., Baltensperger, U., Worsnop, D. R., and Worsnop, D. R.: Evolution of organic aerosols in the atmosphere, Science, 326, 1525–1529, https://doi.org/10.1126/science.1180353, 2009.
Kaipio, J. P., Kolehmainen, V., Somersalo, E., and Vauhkonen, M.: Statistical inversion and Monte Carlo sampling methods in electrical impedance tomography, Inverse Probl., 16, 1487, https://doi.org/10.1088/0266-5611/16/5/321, 2000.
Kanakidou, M., Seinfeld, J. H., Pandis, S. N., Barnes, I., Dentener, F. J., Facchini, M. C., Van Dingenen, R., Ervens, B., Nenes, A., Nielsen, C. J., Swietlicki, E., Putaud, J. P., Balkanski, Y., Fuzzi, S., Horth, J., Moortgat, G. K., Winterhalter, R., Myhre, C. E. L., Tsigaridis, K., Vignati, E., Stephanou, E. G., and Wilson, J.: Organic aerosol and global climate modelling: a review, Atmos. Chem. Phys., 5, 1053–1123, https://doi.org/10.5194/acp-5-1053-2005, 2005.
Krieger, U. K., Siegrist, F., Marcolli, C., Emanuelsson, E. U., Gøbel, F. M., Bilde, M., Marsh, A., Reid, J. P., Huisman, A. J., Riipinen, I., Hyttinen, N., Myllys, N., Kurtén, T., Bannan, T., Percival, C. J., and Topping, D.: A reference data set for validating vapor pressure measurement techniques: homologous series of polyethylene glycols, Atmos. Meas. Tech., 11, 49–63, https://doi.org/10.5194/amt-11-49-2018, 2018.
Kulmala, M., Vesala, T., and Wagner, P. E.: An analytical expression for the rate of binary condensational particle growth, Proc. R. Soc. Lon. Ser.-A, 441, 589–605, https://doi.org/10.1098/rspa.1993.0081, 1993.
Kulmala, M., Vesala, T., Schwarz, J., and Smolik, J.: Mass transfer from a drop – II. Theoretical analysis of temperature dependent mass flux correlation, Int. J. Heat Mass Tran., 38, 1705–1708, https://doi.org/10.1016/0017-9310(94)00302-C, 1995.
Lehtinen, K. E. J. and Kulmala, M.: A model for particle formation and growth in the atmosphere with molecular resolution in size, Atmos. Chem. Phys., 3, 251–257, https://doi.org/10.5194/acp-3-251-2003, 2003.
Liu, P., Li, Y. J., Wang, Y., Gilles, M. K., Zaveri, R. A., Bertram, A. K., and Martin, S. T.: Lability of secondary organic particulate matter, P. Natl. Acad. Sci. USA, 113, 12643–12648, https://doi.org/10.1073/pnas.1603138113, 2016.
Lowe, S., Partridge, D. G., Topping, D., and Stier, P.: Inverse modelling of Köhler theory – Part 1: A response surface analysis of CCN spectra with respect to surface-active organic species, Atmos. Chem. Phys., 16, 10941–10963, https://doi.org/10.5194/acp-16-10941-2016, 2016.
Marsh, A., Miles, R. E. H., Rovelli, G., Cowling, A. G., Nandy, L., Dutcher, C. S., and Reid, J. P.: Influence of organic compound functionality on aerosol hygroscopicity: dicarboxylic acids, alkyl-substituents, sugars and amino acids, Atmos. Chem. Phys., 17, 5583–5599, https://doi.org/10.5194/acp-17-5583-2017, 2017.
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., and Teller, E.: Equation of State Calculations by Fast Computing Machines, J. Chem. Phys., 21, 1087–1092, https://doi.org/10.1063/1.1699114, 1953.
O'Meara, S., Topping, D. O., and McFiggans, G.: The rate of equilibration of viscous aerosol particles, Atmos. Chem. Phys., 16, 5299–5313, https://doi.org/10.5194/acp-16-5299-2016, 2016.
Pajunoja, A., Lambe, A. T., Hakala, J., Rastak, N., Cummings, M. J., Brogan, J. F., Hao, L., Paramonov, M., Hong, J., Prisle, N. L., Malila, J., Romakkaniemi, S., Lehtinen, K. E. J., Laaksonen, A., Kulmala, M., Massoli, P., Onasch, T. B., Donahue, N. M., Riipinen, I., Davidovits, P., Worsnop, D. R., Petäjä, T., and Virtanen, A.: Adsorptive uptake of water by semisolid secondary organic aerosols, Geophys. Res. Lett., 42, 3063–3068, https://doi.org/10.1002/2015GL063142, 2015.
Power, R. M., Simpson, S. H., Reid, J. P., and Hudson, A. J.: The transition from liquid to solid-like behaviour in ultrahigh viscosity aerosol particles, Chem. Sci., 4, 2597, https://doi.org/10.1039/c3sc50682g, 2013.
Reid, J. P., Bertram, A. K., Topping, D. O., Laskin, A., Martin, S. T., Petters, M. D., Pope, F. D., and Rovelli, G.: The viscosity of atmospherically relevant organic particles, Nat. Commun., 9, 956, https://doi.org/10.1038/s41467-018-03027-z, 2018.
Reid, R. C., Prausnitz, J. M. and Poling, B. E.: The properties of gases and liquids, 4th ed., McGraw Hill Book Co, New York, NY, USA, 1987.
Renbaum-Wolff, L., Grayson, J. W., Bateman, A. P., Kuwata, M., Sellier, M., Murray, B. J., Shilling, J. E., Martin, S. T., and Bertram, A. K.: Viscosity of α-pinene secondary organic material and implications for particle growth and reactivity, P. Natl. Acad. Sci. USA, 110, 8014–8019, https://doi.org/10.1073/pnas.1219548110, 2013.
Rovelli, G., Miles, R. E. H., Reid, J. P., and Clegg, S. L.: Accurate Measurements of Aerosol Hygroscopic Growth over a Wide Range in Relative Humidity, J. Phys. Chem. A, 120, 4376–4388, https://doi.org/10.1021/acs.jpca.6b04194, 2016.
Rumble, J., R., Lide, D., R., and Bruno, T., J.: CRC handbook of chemistry and physics, 99th ed., CRC press, Taylor & Francis Group, Boca Raton, FL., USA, 2018.
Shiraiwa, M., Pfrang, C., Koop, T., and Pöschl, U.: Kinetic multi-layer model of gas-particle interactions in aerosols and clouds (KM-GAP): linking condensation, evaporation and chemical reactions of organics, oxidants and water, Atmos. Chem. Phys., 12, 2777–2794, https://doi.org/10.5194/acp-12-2777-2012, 2012.
Shiraiwa, M., Zuend, A., Bertram, A. K., and Seinfeld, J. H.: Gas–particle partitioning of atmospheric aerosols: interplay of physical state, non-ideal mixing and morphology, Phys. Chem. Chem. Phys., 15, 11441, https://doi.org/10.1039/c3cp51595h, 2013.
Shiraiwa, M., Li, Y., Tsimpidi, A. P., Karydis, V. A., Berkemeier, T., Pandis, S. N., Lelieveld, J., Koop, T., and Pöschl, U.: Global distribution of particle phase state in atmospheric secondary organic aerosols, Nat. Commun., 8, 15002, https://doi.org/10.1038/ncomms15002, 2017.
Song, Y. C., Haddrell, A. E., Bzdek, B. R., Reid, J. P., Bannan, T., Topping, D. O., Percival, C., and Cai, C.: Measurements and Predictions of Binary Component Aerosol Particle Viscosity, J. Phys. Chem. A, 120, 8123–8137, https://doi.org/10.1021/acs.jpca.6b07835, 2016.
Tsigaridis, K., Daskalakis, N., Kanakidou, M., Adams, P. J., Artaxo, P., Bahadur, R., Balkanski, Y., Bauer, S. E., Bellouin, N., Benedetti, A., Bergman, T., Berntsen, T. K., Beukes, J. P., Bian, H., Carslaw, K. S., Chin, M., Curci, G., Diehl, T., Easter, R. C., Ghan, S. J., Gong, S. L., Hodzic, A., Hoyle, C. R., Iversen, T., Jathar, S., Jimenez, J. L., Kaiser, J. W., Kirkevåg, A., Koch, D., Kokkola, H., Lee, Y. H., Lin, G., Liu, X., Luo, G., Ma, X., Mann, G. W., Mihalopoulos, N., Morcrette, J.-J., Müller, J.-F., Myhre, G., Myriokefalitakis, S., Ng, N. L., O'Donnell, D., Penner, J. E., Pozzoli, L., Pringle, K. J., Russell, L. M., Schulz, M., Sciare, J., Seland, Ø., Shindell, D. T., Sillman, S., Skeie, R. B., Spracklen, D., Stavrakou, T., Steenrod, S. D., Takemura, T., Tiitta, P., Tilmes, S., Tost, H., van Noije, T., van Zyl, P. G., von Salzen, K., Yu, F., Wang, Z., Wang, Z., Zaveri, R. A., Zhang, H., Zhang, K., Zhang, Q., and Zhang, X.: The AeroCom evaluation and intercomparison of organic aerosol in global models, Atmos. Chem. Phys., 14, 10845–10895, https://doi.org/10.5194/acp-14-10845-2014, 2014.
Vaden, T. D., Imre, D., Beránek, J., Shrivastava, M., and Zelenyuk, A.: Evaporation kinetics and phase of laboratory and ambient secondary organic aerosol, P. Natl. Acad. Sci. USA, 108, 2190–2195, https://doi.org/10.1073/pnas.1013391108, 2011.
Varvia, P., Rautiainen, M., and Seppänen, A.: Bayesian estimation of seasonal course of canopy leaf area index from hyperspectral satellite data, J. Quant. Spectrosc. Ra., 208, 19–28, https://doi.org/10.1016/j.jqsrt.2018.01.008, 2018.
Vesala, T., Kulmala, M., Rudolf, R., Vrtala, A., and Wagner, P. E.: Models for condensational growth and evaporation of binary aerosol particles, J. Aerosol Sci., 28, 565–598, https://doi.org/10.1016/S0021-8502(96)00461-2, 1997.
Virtanen, A., Joutsensaari, J., Koop, T., Kannosto, J., Yli-Pirilä, P., Leskinen, J., Mäkelä, J. M., Holopainen, J. K., Pöschl, U., Kulmala, M., Worsnop, D. R., and Laaksonen, A.: An amorphous solid state of biogenic secondary organic aerosol particles, Nature, 467, 824–827, https://doi.org/10.1038/nature09455, 2010.
Wilson, J., Imre, D., Beraek, J., Shrivastava, M., and Zelenyuk, A.: Evaporation Kinetics of Laboratory-Generated Secondary Organic Aerosols at Elevated Relative Humidity, Environ. Sci. Technol., 49, 243–249, https://doi.org/10.1021/es505331d, 2015.
Yli-Juuti, T., Pajunoja, A., Tikkanen, O.-P., Buchholz, A., Faiola, C., Väisänen, O., Hao, L., Kari, E., Peräkylä, O., Garmash, O., Shiraiwa, M., Ehn, M., Lehtinen, K., and Virtanen, A.: Factors controlling the evaporation of secondary organic aerosol from α-pinene ozonolysis, Geophys. Res. Lett., 44, 2562–2570, https://doi.org/10.1002/2016GL072364, 2017.
Zuend, A., Marcolli, C., Luo, B. P., and Peter, T.: A thermodynamic model of mixed organic-inorganic aerosols to predict activity coefficients, Atmos. Chem. Phys., 8, 4559–4593, https://doi.org/10.5194/acp-8-4559-2008, 2008.
Zuend, A., Marcolli, C., Booth, A. M., Lienhard, D. M., Soonsin, V., Krieger, U. K., Topping, D. O., McFiggans, G., Peter, T., and Seinfeld, J. H.: New and extended parameterization of the thermodynamic model AIOMFAC: calculation of activity coefficients for organic-inorganic mixtures containing carboxyl, hydroxyl, carbonyl, ether, ester, alkenyl, alkyl, and aromatic functional groups, Atmos. Chem. Phys., 11, 9155–9206, https://doi.org/10.5194/acp-11-9155-2011, 2011.
- Abstract
- Introduction
- Methods
- Comparison of MCGA and Bayesian inference methods for fitting volatility
- Evaluation of process model optimization method for fitting OA properties to artificial test data
- Volatility and viscosity estimates from the EDB evaporation measurements
- Summary and conclusions
- Code availability
- Author contributions
- Competing interests
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Methods
- Comparison of MCGA and Bayesian inference methods for fitting volatility
- Evaluation of process model optimization method for fitting OA properties to artificial test data
- Volatility and viscosity estimates from the EDB evaporation measurements
- Summary and conclusions
- Code availability
- Author contributions
- Competing interests
- Financial support
- Review statement
- References
- Supplement





