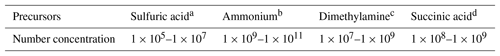the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Interaction between succinic acid and sulfuric acid–base clusters
Yixin Li
Jeremiah Secrest
Fei Xu
Yuan Wang
Taicheng An
Dicarboxylic acids likely participate in the formation of pre-nucleation clusters to facilitate new particle formation in the atmosphere, but the detailed mechanism leading to the formation of multicomponent critical nuclei involving organic acids, sulfuric acid (SA), base species, and water remains unclear. In this study, theoretical calculations are performed to elucidate the interactions between succinic acid (SUA) and clusters consisting of SA-ammonia (AM)∕dimethylamine (DMA) in the presence of hydration of up to six water molecules. Formation of the hydrated SUA•SA• base clusters is energetically favorable, triggering proton transfer from SA to the base molecule to form new covalent bonds or strengthening the preexisting covalent bonds. The presence of SUA promotes hydration of the SA•AM and SA•AM•DMA clusters but dehydration of the SA•DMA clusters. At equilibrium, SUA competes with the second SA molecule for addition to the SA• base clusters at atmospherically relevant concentrations. The clusters containing both the base and organic acid are capable of further binding with acid molecules to promote subsequent growth. Our results indicate that the multicomponent nucleation involving organic acids, sulfuric acid, and base species promotes new particle formation in the atmosphere, particularly under polluted conditions with a high concentration of diverse organic acids.
- Article
(6068 KB) -
Supplement
(667 KB) - BibTeX
- EndNote
Atmospheric aerosols are important to several issues, including climate, visibility, and human health (IPCC, 2013; Zhang et al., 2015). In particular, aerosols influence the Earth energy budget directly by absorbing/scattering incoming solar radiation and indirectly by acting as cloud condensation nuclei (CCN)/ice nuclei (IN), which impact the lifetime, coverage, precipitation efficiency, and albedo of clouds (Andreae et al., 2004; Fan et al., 2007; Li et al., 2008). Currently, the indirect radiative forcing of aerosols represents the largest uncertainty in climate predictions (IPCC, 2013). In addition, ultrafine aerosols likely cause adverse human health outcomes (Rychlik et al., 2019; Wu et al., 2019). New particle formation (NPF) has been observed under diverse environmental conditions (Kulmala and Kerminen, 2008; Zhang et al., 2012; Wang et al., 2013, 2016; Guo et al., 2014; Bianchi et al., 2016) and contributes up to half of the CCN population in the troposphere (Merikanto et al., 2009; Yue et al., 2011). NPF involves two distinct steps, i.e., nucleation to form a critical nucleus and subsequent growth of newly formed nanoparticles to a larger size (>3 nm). Currently, the identities and the roles of chemical species involved in NPF are not fully understood at the molecular level, hindering the development of physically based parameterization to include NPF in atmospheric models (Zhang, 2010; Cai and Jiang, 2017). Sulfuric acid (SA) is believed to be the most common atmospheric nucleation species, and ammonia (AM)/amines further stabilize the hydrated sulfuric acid clusters and enhance the nucleation (Kuang et al., 2010; Yue et al., 2010; Erupe et al., 2011; Yu et al., 2012; Qiu et al., 2013; Wang et al., 2018; Yao et al., 2018). However, neither the sulfuric acid–water binary nucleation nor ammonia/amine-containing ternary nucleation sufficiently explains the measured NPF rates in the lower troposphere (Xu et al., 2010a; Zhang et al., 2012), suggesting the role of other chemical species, such as organic acids, in NPF (Zhang et al., 2004; McGraw and Zhang, 2008).
The role of organic species in assisting aerosol nucleation and growth has been demonstrated by both experimental and theoretical studies (Zhang et al., 2009; Zhao et al., 2009; Wang et al., 2010; Xu et al., 2010b; Xu and Zhang, 2012, 2014; Elm et al., 2014; Weber et al., 2014; Zhu et al., 2014; Tröstl et al., 2016). However, the interactions between organic acids and the other nucleation precursors are still elusive, due to the large variability in the physicochemical nature of organic acids, e.g., the wide range of volatility and functionality (Zhang et al., 2012; Riccobono et al., 2014). In addition, most previous theoretical studies focus on the enhancement effects of organic acids on the SA–H2O binary nucleation or the role of organic acids in clustering basic species such as ammonia or amines with hydration (Zhao et al., 2009; Xu et al., 2010a; Xu and Zhang, 2013; Elm et al., 2014; Weber et al., 2014; Zhu et al., 2014). Several recent studies have been conducted on the underlying mechanisms of organic acids in large pre-nucleation clusters (e.g., ammonia/amine-containing ternary nucleation) (Xu et al., 2010b; Xu and Zhang, 2012; Elm et al., 2016a; Zhang et al., 2017), but most of these studies treated the clusters without the consideration of hydration. Because of the ubiquitous presence of water (W) in the atmosphere and its much higher abundance than other nucleation precursors, the hydration effect on aerosol nucleation is significant (Loukonen et al., 2010; Xu and Zhang, 2013; Henschel et al., 2014, 2016; Zhu et al., 2014).
Atmospheric measurements have shown that the presence of dicarboxylic acids, including succinic acid (SUA), is prevalent in ambient particles (Kawamura and Kaplan, 1987; Decesari et al., 2000; Legrand et al., 2005; Hsieh et al., 2007; Blower et al., 2013). The effect of dicarboxylic acids on aerosol nucleation involving SA or base molecules has been recognized in theoretical studies. Xu and Zhang (2012) showed that dicarboxylic acids promote aerosol nucleation with other nucleating precursors in two directions via hydrogen bonding to the two carboxylic groups on dicarboxylic acids, which is distinct from monocarboxylic acids. Elm et al. (2014) indicated that clustering of a single pinic acid with SA molecules leads to closed structures because of no available sites for additional hydrogen bonding. In addition, Elm et al. (2017) suggested that more than two carboxylic acid groups are required for a given organic oxidation product to efficiently stabilize sulfuric-acid containing clusters. The interaction between SUA and dimethylamine (DMA) is strengthened by hydration via forming aminium carboxylate ion pairs (Xu and Zhang, 2013), while hydration of oxalic acid–AM cluster is unfavorable under atmospheric conditions (Weber et al., 2014). Clearly, the interactions of dicarboxylic acids with other nucleation precursors depend on the type of dicarboxylic acids and the number of the molecules involved in clustering. Presently, theoretical studies on the effect of dicarboxylic acids on nucleation from multicomponent systems are lacking (Xu et al., 2010a; Xu and Zhang, 2013). In particular, the role of organic acids as well as their participation in stabilizing larger pre-nucleation clusters of the SA-ammonia/amine systems needs to be evaluated with the presence of hydration in order to better understand NPF.
In this study, we performed theoretical calculations to evaluate the effect of SUA on hydrated SA•base clusters. Two base species, ammonia and dimethylamine (DMA), were considered. The basin-paving Monte Carlo (BPMC) method was employed to sample stable cluster conformers, and quantum calculations were performed to predict the thermochemical properties of the multicomponent clusters. Geometric and topological analyses were carried out to investigate the structures and binding between SUA and SA•base clusters in the presence of hydration. The implications of the interaction of SUA with hydrated SA–base clusters for atmospheric NPF are discussed.
The methodology of the BPMC conformational sampling combined with quantum calculations using density functional theory (DFT) were employed to assess the role of SUA in clustering of SA with base compounds in the presence of water (Xu and Zhang, 2013). Briefly, the local energy minima in BPMC simulations was searched by using the Amber11 package, and the basin-hopping Monte Carlo (BHMC) approach was employed to increase the Monte Carlo transition probability, which allows the clustering system to escape from the traps of the local energy minimum. We employed the generalized AMBER force field (GAFF) for AM, DMA, and SUA following Wang et al. (2004, 2016). The force field parameters from Loukonen et al. (2010) were adapted for SUA and bisulfate ion. Hydration of the clustering system was evaluated by employing the TIP3P model. The geometric optimization and frequency calculations of the BPMC sampled cluster complexes were further performed at the PW91PW91 level of theory with the basis set 6-311G(2d, 2p) using the Gaussian 09 software package (Frisch et al., 2009). Thermodynamic quantities, such as the electronic energy (ΔE with ZPE), enthalpy (ΔH), and Gibbs free energies (ΔG), were obtained on the basis of unscaled density functional frequencies at a temperature of 298.15 K and pressure of 1 atm. Several basic cluster systems were also examined at the M06-2X/6-311G(3df, 3pd) level of theory, which has been suggested to be more reliable in predicting binary and ternary cluster formation (Elm et al., 2012; Leverentz et al., 2013; Zhang et al., 2017). Comparisons of the free energies with the two different DFT levels of theories between this study and previous available theoretical and experimental studies are presented in Table 1. The energies derived at the PW91PW91/6-311G(2d, 2p) are consistent with those of the M06-2X/6-311G(3df, 3pd) method, and the differences between our calculations and previous studies are within 1.6 kcal mol−1. The thermochemical quantities calculated at the PW91PW91/6-311G(2d, 2p) level of theory for the most stable cluster configurations are summarized in Table 2.
Table 1Theoretical and experimental values of the free energy change for several basic reactions in kilocalories per mole.
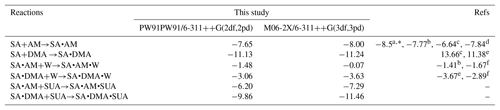
a From Hanson and Eisele (2002).
b From Nadykto and Yu (2007).
c From Kurtén and Kerminen (2008).
d From Elm et al. (2012).
e From Nadykto et al. (2011).
f From Henschel et al. (2014).
∗ Corresponds to experimental results.
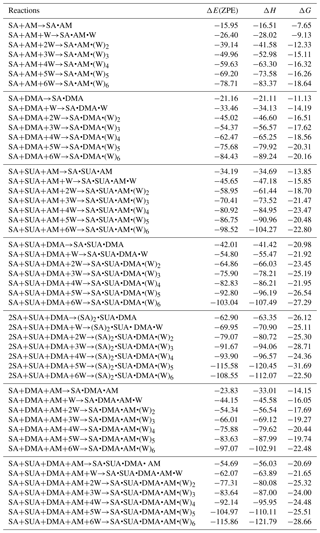
Table 2Calculated binding energy ΔE(ZPE), enthalpy ΔH, and Gibbs free energy ΔG (at T=298.15 K and p=1 atm) at the PW91PW91/6-311G(2d, 2p) level of theory for the hydrated clusters. Energies are in kilocalories per mole.
Topological analysis on the SA•base clusters with hydration and SUA was performed by employing the multifunctional wavefunction analyzer (Multiwfn) 3.3.8 program (Lu and Chen, 2012). The topological characteristics at the bond critical points (BCPs) were calculated for electron density (ρ), Laplacian of electron density (Δρ), and potential energy density (V). Since the electron density is highly correlated to bonding strength (Lane et al., 2013), the potential energy density is an indicator of hydrogen bond energies (Espinosa et al., 1998). The occurrence of proton transfer in the clusters was determined using the localized orbital locator (LOL). A high LOL value denotes greatly localized electrons and indicates the existence of a covalent bond (Lu and Chen, 2012). The covalent bond is characterized by a negative Δρ, while a positive Δρ is associated with a hydrogen bond. In addition, a newly formed covalent bond via proton transfer was quantitatively examined in terms of the bond strength using the Laplacian bond order (LBO) as an indicator (Lu and Chen, 2012). Both LOL and LBO were calculated with the Multiwfn 3.3.8 program (Lu and Chen, 2012).
The extent to which clusters are hydrated (or the hydrophilicity of the clusters) is affected by humidity conditions in the atmosphere (Loukonenet al., 2010; Henschel et al., 2014, 2016). To examine the influence of SUA on cluster hydration under different humidity conditions, the relative hydrate distributions over the number of water molecules contained in clusters were calculated at different relative humidity (RH) levels. The distribution was calculated according to Henschel et al. (2014), in which the Gibbs free energies of hydration obtained from DFT calculations are converted to equilibrium constants for the formation of the respective hydrate by
and the relative hydrate population xn of the hydrate-containing n water molecules is determined by
where p(H2O) is the water partial pressure, p0 is the pressure of water at 1 atm, x0 is the population of the dry cluster for , T is the standard temperature (298.15 K), and R is the molar gas constant. p(H2O) is related to RH through
where p(H2O)eq is the water saturation vapor pressure, which is a function of the temperature (Wexler, 1976). Note that only the Gibbs free energy for the lowest energy structure for each hydration was considered and the Boltzmann averaging effect over configurations on comparable clusters was negligible for the free energies of hydration (Erupe et al., 2011; Xu and Zhang, 2013; Tsona et al., 2015).
To assess the importance of uptake of SUA on the SA•base clusters under atmospheric conditions, the ratio in the concentrations SA•X•SUA to (SA)2•X (X denotes either AM or DMA) is estimated under equilibrium conditions,
and the equilibrium constants K1 and K2 for Reactions (R1) and (R2) are expressed as
The ratio between SA•X•SUA and (SA)2•X concentrations is derived by dividing K1 and K2,
where Δ(ΔG) is the difference in the Gibbs free energies between Reactions (R1) and (R2) at 298 K. As listed in Table 3, the concentrations of sulfuric acid, ammonia, and dimethylamine in the atmosphere are typically in the range of 105–107, 109–1011, and 107–109 molecules cm−3 (Zhang et al., 2012), and the SUA concentration is in the range of 108–109 molecules cm−3 (Ho et al., 2007), resulting in a SUA∕SA ratio from 10 to 104. In addition, the concentration for the cluster (SA)m•(AM)n•(DMA)l•(SUA)k, [cluster], is estimated from the atmospheric concentrations of the various precursors,
where ΔG corresponds to the Gibbs free energy change for the reaction, mSA +nAM +lDMA +kSUA → (SA)m• (AM)n• (DMA)l• (SUA)k.
3.1 Structures and topology
The most stable structures (in terms of ΔG at T=298.15 K and p=1 atm) of the hydrated SA•base clusters are shown in Figs. 1–3. Addition of SUA to hydrated SA•base clusters alters the hydrogen bonding and rearranges the cluster structure, affecting the free energy and stability for the cluster formation. Proton transfer occurs with SUA addition to SA•base, leading to a conversion from the hydrogen bond to covalent bond within the cluster. Proton transfer is absent in the SA•AM cluster (Fig. 1a), consistent with the previous studies (Kurtén et al., 2006; Loukonen et al., 2010; Henschel et al., 2014), while the occurrence of proton transfer with SUA addition (Fig. 1b) is confirmed by the relocation of the LOL high value (Fig. 4a). For the SA•AM cluster, a large value of LOL is adjacent to the SA molecule, indicating that electrons attained with the hydrogen atom (H1) on the S–O–H group are localized on the SA molecule side. In contrast, a large LOL region is located near the nitrogen atom (N1) on the AM molecule with the addition of SUA, suggesting that electrons are greatly localized on the AM side. Proton transfer converts the N1–H1 hydrogen bonding to a covalent bond, leading to the formation of ammonium bisulfate with a value of 0.464 for LBO. The formation of the covalent bond is also confirmed by the negative sign of ∇ρ at the BCP of the N1–H1 bond (Table S1 in the Supplement). The electron density (potential energy density) at the BCP of the N1–H1 bond exhibits a significant increase (decrease), from 0.091 (−0.087) atomic units (a.u.) in the SA•AM cluster to 0.271 (−0.424) a.u. in the SA•AM•SUA cluster. The structures of SA•AM and SA•DMA hydrates with up to five water molecules in our calculations are consistent with those of Henschel et al. (2014). The interactions between SA and AM/DMA in the presence of hydration were previously studied (DePalma et al., 201; Yu et al., 2012; Qiu and Zhang, 2013; Xu and Zhang, 2013; Tsona et al., 2015), showing strong hydrogen bonding among SA, base compound, and water molecules. Another study on glycolic acid found that addition of one glycolic acid molecule to the SA•AM cluster does not result in proton transfer, unless a second glycolic acid molecule is added (Zhang et al., 2017). Clearly, SUA is more efficient than glycolic acid to stabilize the SA•AM clusters.
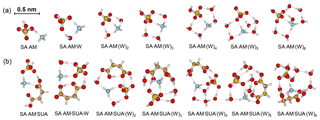
Figure 1Most stable configurations of the hydrated SA•AM clusters and the clusters with one SUA addition. The hydration is with zero to six water molecules. The sulfur (carbon) atoms are depicted as large (small) yellow balls, oxygen atoms in red, nitrogen atoms in blue, and hydrogen atoms in white. The dashed line denotes the hydrogen bond.
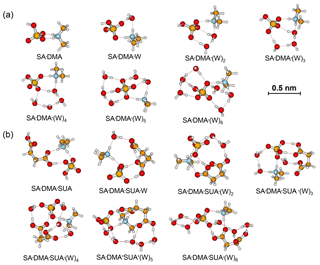
Figure 2Most stable configurations of the hydrated SA•DMA clusters and the clusters with one SUA addition. The hydration is with zero to six water molecules.
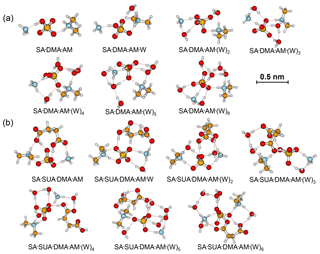
Figure 3Most stable configurations of the hydrated SA•DMA•AM clusters and the clusters with one SUA addition. The hydration is with zero to six water molecules.
In contrast to the SA•AM cluster, proton transfer occurs for the SA•DMA cluster without water or SUA (Figs. 2 and 4b) because of stronger basicity of DMA than AM (Anderson et al., 2008). Similarly, proton transfer occurs for the SA•AM•DMA cluster, leading to the formation of the aminium bisulfate () ion pair. Addition of SUA to SA•DMA•AM•(W)n results in additional proton transfer between the bisulfate ion and AM, leading to the formation of sulfate ions () (Figs. 3 and 4c).
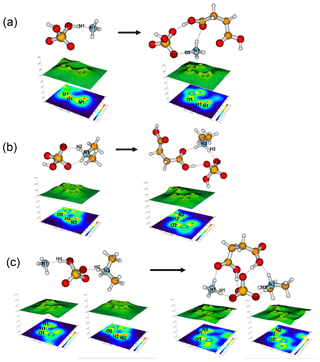
Figure 4Relief maps with the projection of a localized orbital locator for clusters of (a) SA•AM and SA•AM•SUA, (b) SA•DMA, SA•DMA•SUA, and (c) SA•DMA•AM and SA•DMA•AM•SUA. Hydrogen bonds are shown as dashed lines. A large LOL value reflects that electrons are greatly localized, indicating the existence of a covalent bond.
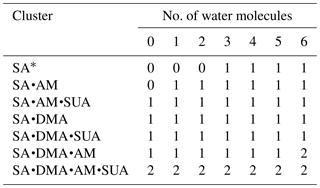
The dependence of the number of proton transfers on hydration is summarized in Table 4. For comparison, the results of hydration of SA clusters by Xu and Zhang (2013), who employed a similar method for the structure sampling and quantum calculations, are also included in this table. Both hydration and addition of SUA promote proton transfer in the SA•base clusters. Previous studies identified facile proton transfer by hydration (Ding et al., 2003; Al Natsheh et al., 2004; Loukonen et al., 2010; Xu and Zhang, 2013), and the dependence of proton transfer on the hydration level was also indicated by Tsona et al. (2015). For the SA cluster, Xu and Zhang (2013) found that proton transfer in the hydrated SA clusters only occurs with more than two water molecules. In our study, proton transfer due to hydration occurs in the monohydrate of SA•AM. A second proton transfer also occurs due to hydration, for example, when SA•AM•DMA•(W)5 clusters are hydrated with one more water molecule (Figs. 1a and 3a). The formation of the covalent bond in the monohydrate of SA•AM and the sixth hydrate of SA•AM•DMA is confirmed by the LOL relocation (Fig. S1 in the Supplement). Loukonen et al. (2010) also found that proton transfer occurs in SA•AM for the hydrated cluster with two water molecules. Our results show that neither water molecules nor SUA induce the second proton transfer in SA•DMA clusters. In contrast, Loukonon et al. (2010) showed that the second proton transfer occurs when the SA•DMA cluster is hydrated with five water molecules. The difference in proton transfer with hydration between this study and Loukonen et al., is attributable to the different sampling methodologies used to obtain the most stable conformers of the clusters. Note that the findings of Loukonen et al., are also in contrast to those by Henschel et al. (2014).
Table 5 summarizes the available LBO values for the covalent bonds in the SA•base clusters with hydration. The dependence of LBO on the hydration level varies with the clusters. For SA•AM without SUA, additional water molecules result in a higher LBO of N1–H1 bonds, while for SA•DMA LBO of the N2–H2 bond generally increases at all hydration levels except for the dihydrate. With addition of SUA to SA•AM and SA•DMA, the LBO values of the preexisting covalent bonds of SUA-containing clusters are higher than those of the clusters without SUA at all hydration levels except for the sixth hydration. This indicates that, although addition of SUA to the two hydrated clusters does not result in additional proton transfer, the presence of SUA enhances the covalent bonds at the hydration levels of 0 to 5. The electron and the potential energy densities at BCPs of the N–H bonds are somewhat higher and lower, respectively, in the SUA-containing clusters than in those without SUA for most hydration cases (Tables S2 and S3).
Table 5Laplacian bond order (LBO) of the newly formed covalent bond (nitrogen–hydrogen bond) between in the clusters (a.u.).
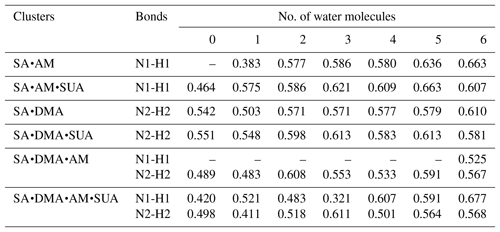
Note: N1 is the nitrogen atom on the ammonia (AM) molecule; N2 is the nitrogen atom on the dimethylamine (DMA) molecule; H1 is the hydrogen atom on one of the hydroxyl functions of the sulfuric acid (SA) molecule and bound to N1; H2 is the hydrogen atom on one of the hydroxyl functions of the SA (SA) molecule and bound to N2.
Addition of SUA to SA•base results in cleavage of the hydrogen bond between the base and SA molecules (Figs. 1b, 2b, and 3b). Note that the carbon chain of SUA tends to bend accordingly as the hydration degree increases because the carboxylic groups at the two ends of the carbon chain are involved in hydrogen bonding. As expected, the number of hydrogen bonds by AM in SA•AM•SUA clusters increases with the hydration degree, which is always equal to or larger than that of the corresponding clusters without SUA and is closely related to the free energy changes in SUA addition to SA•AM clusters (see detailed discussions below on the energetics). For the DMA-containing clusters, the nitrogen atom is saturated by two hydrogen bonds, and the presence of the two free methyl groups likely corresponds to another factor affecting the stability (Ortega et al., 2012). The complexity of the cluster structures is partially ascribed by intramolecular hydrogen bonding associated with SUA, as illustrated by SA•AM•SUA•W, SA•DMA•SUA•W, or SA•AM•DMA• SUA•(W)5 (Fis. 1b, 2b, and 3b).
3.2 Energetics
The stepwise hydration free energies for the clusters, along with the number of water molecules in the clusters, are presented in Fig. 5a and Table 2. For SA•AM and SA•DMA with up to five water molecules, the free energies are in agreement with those by Henschel et al. (2014) using the RICC2/aug-cc-pV(T+d)Z level for sulfur and the RICC2/aug-cc-pVTZ level for all other atoms, but differ from those by Loukonen et al. (2010) at the RI-MP2/aug-cc-pV(T+d)Z level of theory. Note that the structures of the hydrates in this study and Henschel et al. (2014) are different from those of Loukonen et al. (2010), explaining the differences in the energies among the various studies.
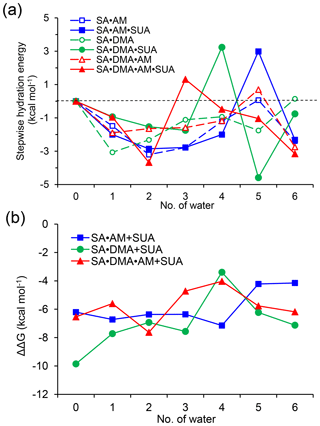
Figure 5Stepwise hydration free energies (a) and the relative Gibbs free energy changes due to addition of one SUA molecule to SA•base clusters (b) at T=298.15 K and p=1 atm. The free energy is calculated at the PW91PW91/6-311G(2d, 2p) level.
Figure 5a shows that the stepwise hydration energies are negative at most hydration degrees, suggesting that hydration is thermodynamically favorable. Without SUA, the fifth hydration of SA•AM and SA•DMA•AM and the sixth hydration of SA•DMA exhibit positive or nearly zero one-step hydration free energies. These endergonic steps are ascribed because of the saturation by water molecules of the SA•base clusters (Henschel et al., 2013). For SUA-containing clusters, the addition of one more water molecule increases the free energy, resulting in a larger positive hydration energy. For example, the one-step free energies are 2.99, 3.24, and 1.32 kcal mol−1 for the fifth hydration for SA•AM•SUA, the fourth hydration for SA•DMA•SUA, and the third hydration of SA•DMA•AM•SUA, respectively. The large increases in free energies for SA•AM•SUA and SA•DMA•SUA are explained by structural rearrangement. The positive one-step hydration energy for the third hydration of SA•DMA•AM•SUA is likely because of the formation of the stable dihydrate.
The relative changes in the free energy due to addition of SUA to the SA•base clusters are depicted along with hydration degree (Fig. 5b). For all hydration levels except the fourth one, the free energy changes for the SA•DMA cluster by SUA addition are more negative than that for the SA•AM cluster, suggesting that the addition of SUA to SA•DMA is more favorable than that to SA•AM. The largest change in the free energy (−7.15 kcal mol−1) between SA•AM•SUA and SA•AM occurs at the fourth hydration step, which is attributable to the structure change due to SUA addition, i.e., an additional hydrogen bond formed on AM in the fourth hydrate of SA•AM•SUA. However, such a hydrogen bond is absent in the SA•AM cluster until the fifth hydration (Fig. 1). The largest negative free energy change (−9.86 kcal mol−1) in SA•DMA corresponds to the unhydrated form. The strong hydrogen bonds between DMA and the two acids formed in the unhydrated SA•DMA•SUA cluster undergo cleavage due to water uptake, leading to a smaller free energy difference between the SA•DMA•SUA and SA•DMA clusters with hydration. In addition, stabilization by hydration for the SA•base clusters is weakened by addition of SUA, particularly for the SA•DMA and SA•DMA•AM clusters, with much smaller hydration energies for SA•DMA•SUA and SA•DMA•AM•SUA than the corresponding clusters without SUA (Fig. 5a). It is evident that the Gibbs free energy changes of SUA addition to the multicomponent clusters are relevant to the hydration degree and the base types.
The role of SUA in the subsequent growth of the SA•base clusters was examined by comparing the differences in free energies for adding SA to SA•DMA and SA•DMA•SUA. Computations were also performed for the unhydrated (SA)2•DMA, (SA)3•DMA, and (SA)2•DMA•SUA clusters (Table 6). The optimized clusters containing more than one SA molecule are depicted in Fig. 6. The free energies of SA addition to SA•DMA and (SA)2•DMA are −10.5 and −6.1 kcal mol−1, respectively. The free energy for adding SA to SA•DMA•SUA is −5.14 kcal mol−1, higher than that of SA addition to SA•DMA. With hydration (i.e., (SA)2•DMA•SUA•(W)x), the free energies for adding SA to SA•DMA•SUA•(W)x clusters are all negative (Table 2).
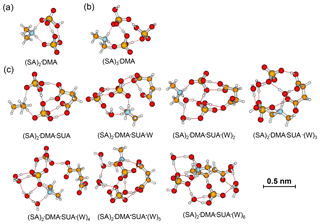
Figure 6Most stable configurations of (a) unhydrated (SA)2•DMA, (b) (SA)2•DMA, and (c) the hydrated (SA)2•DMA•SUA clusters. The hydration is with zero to six water molecules (W).
Table 6Gibbs free energy (ΔG, kcal mol−1), interaction energy (ΔH0, kcal mol−1), and cluster concentration at equilibrium for basic clustering reactions. The right-hand side of clustering reactions are the product clusters in Eq. (7), and the core clusters and addition molecules in Eq. (7) are listed here as well.
3.3 Hydration profiles
The equilibrium hydrate distributions were calculated for the SA•base clusters with and without the presence of SUA. Figure 7 displays the relative hydrate distributions under three typical atmospheric RH values, i.e., 20 %, 50 %, and 80 %. The SA•base cluster shows an increasing hydration with increasing RH, although the different clusters exhibit distinct characteristics in the hydrate distribution.
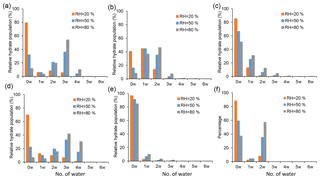
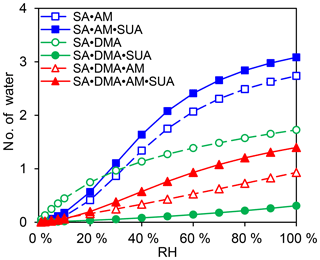
Figure 7Hydrate distributions of clusters under different RH levels (20 %, 50 %, and 80 %). Panels (a), (b), and (c) show clusters for SA•AM, SA•DMA, and SA•DMA•AM, respectively. Panels (d), (e), and (f) show clusters with one SUA addition on the basis of (a), (b), and (c) clusters. In all RH cases, T=298 K.
Our results for the SA•AM hydrate distribution are consistent with the previous studies (Loukonen et al., 2010; Henschel et al., 2014), showing that the hydrate distribution of SA•AM is sensitive to RH (Fig. 7a). The completely dry SA•AM cluster dominates the hydrate distribution under low RH (<40 %), while the trihydrate is most prevalent as RH exceeds 40 % because of higher stability of the trihydrate than the monohydrate and dihydrate. Since the change in the free energies is almost identical for addition of one or two water molecules, the SA•DMA clusters of the unhydrated form, monohydrate, and dihydrate are evenly distributed (Fig. 7b) and account for 85 % of the total population at all RH levels. The peak of the hydrate distribution for SA•DMA shows a continuous shift from the unhydrated cluster to dihydrate with increasing RH. The SA•DMA•AM cluster tends to be dehydrated, as reflected by the fact that the relative population of dry SA•DMA•AM clusters exceeds 50 % even under highly humid conditions (Fig. 7c). Hence, addition of DMA or AM considerably lowers the hydrophilicity of SA•AM or SA•DMA. The dehydration trend of the SA•DMA•AM cluster in our work is consistent with the previous investigations, in which the base-containing clusters with SA were found to be less hydrophilic than the SA clusters.
Addition of SUA alters the hydrate distribution of the SA•base clusters. For example, the hydrate distribution is broader for SA•AM•SUA than for SA•AM (Fig. 7a, d), with a considerably high population of the fourth hydrate for SA•AM•SUA at high RH to promote hydration. The broader hydrate distribution is consistent with the more negative hydration energy at the fourth hydration step for SA•AM•SUA for SA•AM. However, the peaks of the distribution exhibit a similar pattern with varying RH for SA•AM and SA•AM•SUA, i.e., with unhydrated and trihydrate clusters, as the most populated forms. The hydrate distributions for SA•DMA•SUA and SA•DMA exhibit distinct characteristics. In the presence of SUA, over 80 % of the clusters exist in a dry state independent of RH (Fig. 7e), indicating that hydration of SA•DMA•SUA is less favorable than that of SA•DMA. The hydrate distribution peak for SA•DMA•SUA at the unhydrated cluster is consistent with the fact that addition of SUA greatly reduces the free energy of the dry clusters and the changes in hydration free energy are relatively small at all hydration levels. The SA•DMA•AM•SUA clusters are likely dehydrated or hydrated with two water molecules dependent on RH (Fig. 7f), as the distribution peak shifts between the unhydrated (RH <70 %) and the dihydrate (RH >70 %) clusters and does not exhibit a peak in monohydrate at any RH level. Clearly, hydration is more favorable for SA•DMA•AM•SUA than for SA•DMA•AM.
The hydration profiles are shown in Fig. 8 as functions of RH for the clusters with SA•base. The maximal numbers of water molecules for SA•AM, SA•DMA, and SA•DMA•AM are 2.7, 1.7, and 0.9, respectively, as RH approaches 100 %. The calculated degrees of hydration for SA•AM and SA•DMA are slightly higher in this study than those by Henschel et al. (2014). Addition of SUA considerably enhances the hydrophilicity of SA•AM and SA•DMA•AM, leading to high degrees of hydration for SUA-containing clusters. In contrast, the number of water molecules bound to SA•DMA is greatly reduced with SUA addition since the most populated cluster of SA•DMA•SUA is unhydrated for different RH values (Fig. 7e).
3.4 Atmospheric implications
The cluster growth can be represented by a reversible, stepwise kinetic process in a single- or multicomponent system (Zhang et al., 2012),
where Ai−1 denotes a monomer species to be added to the cluster Ci−1 at the (i−1)th step and and represent the association and decomposition rate constants of the cluster, respectively. Hence, whether cluster Ci grows or decomposes is dependent on the competition between the forward and backward reactions for Ci, which are dependent on the rate constant and monomer concentration [Ai] and (i.e., the thermal stability of Ci), respectively. The time-dependent concentration of cluster Ci is derived according to Zhang et al. (2012),
Note that Eq. (7) is the steady-state expression of Eq. (9) summed over all reaction steps.
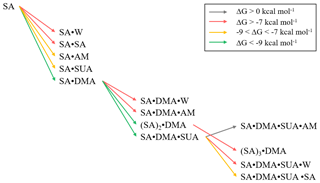
Addition of SUA to SA or SA•base is thermodynamically favorable (Fig. 5b), as reflected by large negative free energies. The estimated cluster concentrations using Eq. (7) and the atmospherically relevant concentrations of the precursor species are 10−3–102 cm−3 for SA•DMA•SUA and 100–103 cm−3 for SA•SUA (Table 6), suggesting that SUA likely contributes to the further growth of the SA and SA•base clusters. Furthermore, the dipole moments of SA•DMA•SUA and SA•AM•SUA are 7.5 and 8.8 debye, respectively (Table 6), which are the largest among those of the trimers. The calculated ratios of [SA•X•SUA]∕[(SA)2•X] (X denotes AM, DMA, water molecule, or none) under atmospherically relevant concentrations are presented in Table 7. The estimated ratio of [SA•DMA•SUA] to [(SA)2•DMA] is in the range from 3:1 to 3000:1 under atmospherically relevant concentrations for the precursor species, i.e., [SUA] ∕ [SA] in the range from 10:1 to 104:1, indicating that SA•DMA•SUA is prevalent in the atmosphere. The ratios of [SA• SUA]∕[(SA)2] and [SA•W•SUA]∕[(SA)2•W] are both higher than 103:1, indicating that the SUA-containing clusters are prevalent for both unhydrated and hydrated SA clusters with one water molecule. While the sulfuric acid dimer is believed to be an important precursor for NPF (Zhang et al., 2012), our study shows that SUA, which is one of the most abundant dicarboxylic acids in the atmosphere, competes with the formation and further growth of the sulfuric acid dimer because of the strong interaction of SUA with SA to form the unhydrated or hydrated clusters. The effect of SUA on the formation and further growth of the sulfuric acid dimer is more pronounced than that by ketodiperoxy acid (Elm et al., 2016b). Figure 9 depicts the relative stability of cluster formation from the interaction among SUA, SA, base, and W molecules, showing SA•DMA as the most stable dimer and (SA)2•DMA as most stable trimer, followed by SA•DMA•SUA.
It should be pointed out that steady-state equilibrium for pre-nucleation clusters is rarely established under atmospheric conditions for each intermediate step (i.e., Eq. 9) and the overall cluster growth (i.e., Eq. 7) because of continuous forward reactions by adding monomers to form larger clusters during NPF. Whether a cluster grows to form a nanoparticle is dependent on the competition between the forward reaction by adding a monomer and the backward reaction by losing a monomer (evaporation) at each intermediate step. For example, at step i the cluster grows (or evaporates) when the term of is larger (smaller) than that of (Eq. 9). While the evaporation rate relies on the thermodynamic stability of the cluster, the forward rate constant is kinetically controlled, dependent on the interaction (i.e., the natural charges and dipole moments) and kinetic energies between the colliding cluster and monomer (Zhang et al., 2012). For neutral clusters, electrostatically induced dipole-dipole interaction plays a key role in facilitating the forward reaction rate. The presence of organic acids typically increases the dipole moment of clusters (Zhao et al., 2009). Furthermore, in addition to SUA, there are many other organic acids present under ambient conditions. In particular, organic acids with multifunctionality, i.e., more carboxylic acid groups and the presence of hydroxyl groups, likely contribute more importantly to aerosol nucleation.
We have investigated the molecular interactions between SUA and SA•base clusters in the presence of hydration, including AM and DMA. SUA addition promotes proton transfer in the SA•base clusters, which is confirmed by formation of new covalent bonds and relocation of the high LOL value from the SA side to the AM side and a shift from positive to negative for the Laplacian of electron density. The presence of SUA in SA•AM and SA•DMA clusters generally strengthens the existing covalent bonds in SA•base•SUA•(W)n clusters at the various hydration levels, since the LBO values of the covalent bonds in SUA-containing clusters are higher than those in the clusters without SUA. The hydrate distribution is broader for SA•AM•SUA than for SA•AM. Also, the peak in the distribution of SA•DMA•AM•SUA hydrates occurs at the two-water molecule level under high RH, but the peak in the distribution for SA•DMA•AM corresponds to the unhydrated cluster. The peak hydrate distribution shifts toward a larger number of water molecules in SUA-containing clusters than in clusters without SUA, suggesting that the addition of SUA enhances the hydrophilicity of SA•AM and SA•DMA•AM. However, the presence of SUA causes dehydration to the SA•DMA clusters since the most prevalent cluster for SA•DMA•SUA is in a dry state. At equilibrium and atmospherically typical abundances of SUA and SA, SUA•SA•base (AM or DMA) is the most dominant form among the three-molecule clusters, indicating that SUA competes with SA for the growth of the SA•base dimers.
Various organic acids are produced from atmospheric oxidation of volatile organic compounds from biogenic (i.e., pinenes) and anthropogenic sources (i.e., aromatics). Our results indicate that the multicomponent molecular interaction involving organic acids, sulfuric acid, and base species promotes NPF in the atmosphere, particularly under polluted environments because of elevated concentrations of these species. The role of different organic acids with distinct functionality in NPF needs to be further assessed. In particular, future studies are necessary to evaluate both the kinetics and thermodynamics of the interactions of organic acids with SA and base species, i.e., the forward and reverse rates as well as the potential energy surfaces for cluster formation, in order to develop physically based parameterizations of NPF in atmospheric models.
The data used in this study are available from the corresponding author upon request (renyi-zhang@tamu.edu).
Supplementary material contains additional relief maps for the sulfuric acid–base clusters and lists of topological properties for the most stable conformers of each cluster category. The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-8003-2019-supplement.
YuL, YJ, and RZ designed the research. YuL, YJ, YiL, WX, and FX performed simulations. YuL, YW, YJ, YiL, TA, and JS analyzed data. YuL, YJ, YiL, and RZ wrote the paper.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Multiphase chemistry of secondary aerosol formation under severe haze”. It is not associated with a conference.
The research was partially conducted with the advanced computing resources provided by Texas A&M High Performance Research Computing. The authors acknowledged the Laboratory for Molecular Simulations at Texas A&M University.
This work was supported by the National Natural Science Foundation of China (41675122, 41425015, U1401245, and 41373102), Science and Technology Program of Guangzhou City (201707010188), Team Project from the Natural Science Foundation of Guangdong Province, China (S2012030006604), Special Program for Applied Research on Super Computation of the NSFC-Guangdong Joint Fund (the second phase), National Supercomputing Center in Guangzhou (NSCC-GZ), and Robert A. Welch Foundation (A-1417).
This paper was edited by Jingkun Jiang and reviewed by three anonymous referees.
Al Natsheh, A., Nadykto, A. B., Mikkelsen, K. V., Yu, F., and Ruuskanen, J.: Sulfuric acid and sulfuric acid hydrates in the gas phase: A DFT investigation, J. Phys. Chem. A, 108, 8914–8929, https://doi.org/10.1021/jp048858o, 2004.
Anderson, K. E., Siepmann, J. I., McMurry, P. H., and VandeVondele, J.: Importance of the Number of Acid Molecules and the Strength of the Base for Double-Ion Formation in (H2SO4)m•Base•(H2O)6 Clusters, J. Am. Chem. Soc., 130, 14144–14147, https://doi.org/10.1021/ja8019774, 2008.
Andreae, M. O., Rosenfeld, D., Artaxo, P., Costa, A. A., Frank, G. P., Longo, K. M., and Silva-Dias, M. A. F.: Smoking rain clouds over the Amazon, Science, 303, 1337–1342, 2004.
Bianchi, F., Tröstl, J., Junninen, H., Frege, C., Henne, S., Hoyle, C. R., Molteni, U., Herrmann, E., Adamov, A., Bukowiecki, N., Chen, X., Duplissy, J., Gysel, M., Hutterli, M., Kangasluoma, J., Kontkanen, J., Kürten, A., Manninen, H. E., Münch, S., Peräkylä, O., Petäjä, T., Rondo, L., Williamson, C., Weingartner, E., Curtius, J., Worsnop, D. R., Kulmala, M., Dommen, J., and Baltensperger, U.: New particle formation in the free troposphere: A question of chemistry and timing, Science, 352, 1109–1112, https://doi.org/10.1126/science.aad5456, 2016.
Blower, P. G., Ota, S. T., Valley, N. A., Wood, S. R., and Richmond, G. L.: Sink or Surf: Atmospheric Implications for Succinic Acid at Aqueous Surfaces, J. Phys. Chem., 117, 7887–7903, https://doi.org/10.1021/jp405067y, 2013.
Cai, R. and Jiang, J.: A new balance formula to estimate new particle formation rate: reevaluating the effect of coagulation scavenging, Atmos. Chem. Phys., 17, 12659–12675, https://doi.org/10.5194/acp-17-12659-2017, 2017.
Decesari, S., Facchini, M. C., Fuzzi, S., and Tagliavini, E., Characterization of water-soluble organic compounds in atmospheric aerosol: A new approach, J. Geophys. Res.-Atmos., 105, 1481–1489, https://doi.org/10.1029/1999JD900950, 2000.
DePalma, J. W., Bzdek, B. R., Doren, D. J., and Johnston, M. V.: Structure and energetics of nanometer size clusters of sulfuric acid with ammonia and dimethylamine, J. Phys. Chem. A, 116, 1030–1040, https://doi.org/10.1021/jp210127w, 2012.
Ding, C.-G., Laasonen, K., and Laaksonen, A.: Two sulfuric acids in small water clusters, J. Phys. Chem., 107, 8648–8658, https://doi.org/10.1021/jp022575j, 2003.
Elm, J., Bilde, M., and Mikkelsen, K. V.: Assessment of density functional theory in predicting structures and free energies of reaction of atmospheric prenucleation clusters, J. Chem. Theory Comput., 8, 2071–2077, https://doi.org/10.1021/ct300192p, 2012.
Elm, J., Kurten, T., Bilde, M., and Mikkelsen, K. V.: Molecular interaction of pinic acid with sulfuric acid: exploring the thermodynamic landscape of cluster growth, J. Phys. Chem. A, 118, 7892–7900, https://doi.org/10.1021/jp503736s, 2014.
Elm, J., Jen, C. N., Kurtén, T., and Vehkamäki, H.: Strong hydrogen bonded molecular interactions between atmospheric diamines and sulfuric acid, J. Phys. Chem., 120, 3693–3700, https://doi.org/10.1021/acs.jpca.6b03192, 2016a.
Elm, J., Myllys, N., Luy, J.-N., Kurtén, T., and Vehkamäki, H.: The Effect of Water and Bases on the Clustering of a Cyclohexene Autoxidation Product C6H8O7 with Sulfuric Acid, J. Phys. Chem., 120, 2240–2249, https://doi.org/10.1021/acs.jpca.6b00677, 2016b.
Elm, J., Myllys, N., and Kurtén, T.: What is required for highly oxidized molecules to form clusters with sulfuric acid?, J. Phys. Chem., 121, 4578–4587, https://doi.org/10.1021/acs.jpca.7b03759, 2017.
Erupe, M. E., Viggiano, A. A., and Lee, S.-H.: The effect of trimethylamine on atmospheric nucleation involving H2SO4, Atmos. Chem. Phys., 11, 4767–4775, https://doi.org/10.5194/acp-11-4767-2011, 2011.
Espinosa, E., Molins, E., and Lecomte, C.: Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities, Chem. Phys. Lett., 285, 170–173, https://doi.org/10.1016/S0009-2614(98)00036-0, 1998.
Fan, J., Zhang, R., Li, G., and Tao, W.-K.: Effects of aerosols and relative humidity on cumulus clouds, J. Geophys. Res., 112, D14204, https://doi.org/10.1029/2006JD008136, 2007.
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., Scalmani, G., Barone, V., Petersson, G. A., Nakatsuji, H., Li, X., Caricato, M., Marenich, A., Bloino, J., and Janesko, R. G. B. G., Mennucci, B., Hratchian, H. P., Ortiz, J. V., Izmaylov, A. F., Sonnenberg, J. L., Williams-Young, D., Ding, F., Lipparini, F., Egidi, F., Goings, J., Peng, B., Petrone, A., Henderson, T., Ranasinghe, D., Zakrzewski, V. G., Gao, J., Rega, N., Zheng, G., Liang, W., Hada, M., Ehara, M., Toyota, K., Fukuda, R., Hasegawa, J., Ishida, M., Nakajima, T., Honda, Y., Kitao, O., Nakai, H., Vreven, T., Throssell, K., Montgomery Jr., J. A., Peralta, J. E., Ogliaro, F., Bearpark, M., Heyd, J. J., Brothers, E., Kudin, K. N., Staroverov, V. N., Keith, T., Kobayashi, R., Normand, J., Raghavachari, K., Rendell, A., Burant, J. C., Iyengar, S. S., Tomasi, J., Cossi, M., Millam, J. M., Klene, M., Adamo, C., Cammi, R., Ochterski, J. W., Martin, K. R. L., Morokuma, Farkas, O., Foresman, J. B., and Fox, D. J.: Gaussia, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009.
Ge, X., Wexler, A. S., Clegg, S. L.: Atmospheric amines – Part I. A review, Atmos. Environ., 45, 524, https://doi.org/10.1016/j.atmosenv.2010.10.012, 2011.
Guo, S., Hu, M., Zamora, M. L., Peng, J., Shang, D., Zheng, J., Du, Z., Wu, Z., Shao, M., Zeng, L., Molina, M. J., and Zhang, R.: Elucidating severe urban haze formation in China, P. Natl. Acad. Sci. USA, 111, 17373–17378, https://doi.org/10.1016/10.1073/pnas.1419604111, 2014.
Hanson, D. R. and Eisele, F. L.: Acid–base chemical reaction model for nucleation rates in the polluted atmospheric boundary layer, J. Geophys. Res.-Atmos., 107, 18713–18718, https://doi.org/10.1073/pnas.1210285109, 2002.
Henschel, H., Ortega, I. K., Kupiainen, O., Olenius, T., Kurtén, T., and Vehkamäki, H.: Hydration of pure and base-Containing sulfuric acid clusters studied by computational chemistry methods, AIP Conference Proceedings, 1527, 218–221, https://doi.org/10.1063/1.4803243, 2013.
Henschel, H., Navarro, J. C., Yli-Juuti, T., Kupiainen-Maatta, O., Olenius, T., Ortega, I. K., Clegg, S. L., Kurten, T., Riipinen, I., and Vehkamaki, H.: Hydration of atmospherically relevant molecular clusters: Computational chemistry and classical thermodynamics, J. Phys. Chem. A, 118, 2599–2611, https://doi.org/10.1021/jp500712y, 2014.
Henschel, H., Kurtén, T., and Vehkamäki, H.: Hydration of Atmospherically Relevant Molecular Clusters: Computational Chemistry and Classical Thermodynamics, J. Phys. Chem., 120, 2599–2611, https://doi.org/10.1021/jp500712y, 2016.
Ho, K. F., Cao, J. J., Lee, S. C., Kawamura, K., Zhang, R. J., Chow, J. C., and Watson, J. G.: Dicarboxylic acids, ketocarboxylic acids, and dicarbonyls in the urban atmosphere of China, J. Geophys. Res., 112, D22S27, https://doi.org/10.1029/2006JD008011, 2007.
Hsieh, L.-Y., Kuo, S.-C., Chen, C.-L., and Tsai, Y. I.: Origin of Low-molecular-weight Dicarboxylic Acids and their Concentration and Size Distribution Variation in Suburban Aerosol, Atmos. Environ., 41, 6648–6661, https://doi.org/10.1016/j.atmosenv.2007.04.014 2007.
IPCC: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, available at: http://www.ipcc.ch/report/ar5/wg1/ (last access: 1 June 2019), 2013.
Kawamura, K. and Kaplan, I. R.: Motor exhaust emissions as a primary source for dicarboxylic acids in Los Angeles ambient air, Environ. Sci. Technol., 21, 105–110, 1987.
Kuang, C., Riipinen, I., Sihto, S.-L., Kulmala, M., McCormick, A. V., and McMurry, P. H.: An improved criterion for new particle formation in diverse atmospheric environments, Atmos. Chem. Phys., 10, 8469–8480, https://doi.org/10.5194/acp-10-8469-2010, 2010.
Kulmala, M. and Kerminen, V. M.: On the formation and growth of atmospheric nanoparticles, Atmos. Res., 90, 132–150, https://doi.org/10.1016/j.atmosres.2008.01.005, 2008.
Kurtén, T., Sundberg, M. R., Vehkamäki, H., Noppel, M., Blomqvist, J., and Kulmala, M.: Ab initio and density functional theory reinvestigation of gas-phase sulfuric acid monohydrate and ammonium hydrogen sulfate, J. Phys. Chem., 110, 7178–7188, https://doi.org/10.1021/jp0613081, 2006.
Lane, J. R., Contreras-García, J., Piquemal, J.-P., Miller, B. J., and Kjaergaard, H. G.: Are bond critical points really critical for hydrogen bonding?, J. Chem. Theory Comput. 9, 3263–3266, https://doi.org/10.1021/ct400420r, 2013.
Legrand, M., Preunkert, S., Galy-Lacaux, C., Liousse, C., and Wagenbach, D.: Atmospheric year-round records of dicarboxylic acids and sulfate at three French sites located between 630 and 4360 m elevation, J. Geophys. Res.-Atmos., 110, D13302, https://doi.org/10.1029/2004JD005515, 2005.
Leverentz, H. R., Siepmann, J. I., Truhlar, D. G., Loukonen, V., and Vehkamäki, H.: Energetics of atmospherically implicated clusters made of sulfuric acid, ammonia, and dimethyl amine, J. Phys. Chem. A, 117, 3819–3825, https://doi.org/10.1021/jp402346u, 2013.
Li, G., Wang, Y., and Zhang, R.: Implementation of a two-moment bulk microphysics scheme to the WRF model to investigate aerosol-cloud interaction, J. Geophys. Res., 113, D15211, https://doi.org/10.1029/2007JD009361, 2008.
Loukonen, V., Kurtén, T., Ortega, I. K., Vehkamäki, H., Pádua, A. A. H., Sellegri, K., and Kulmala, M.: Enhancing effect of dimethylamine in sulfuric acid nucleation in the presence of water – a computational study, Atmos. Chem. Phys., 10, 4961–4974, https://doi.org/10.5194/acp-10-4961-2010, 2010.
Lu, T. and Chen, F.: Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 33, 580–592, https://doi.org/10.1002/jcc.22885, 2012.
Lu, T. and Chen, F.: Bond order analysis based on the Laplacian of electron density in fuzzy overlap space, J. Phys. Chem. A, 117, 3100–3108, https://doi.org/10.1021/jp4010345, 2013.
McGraw, R. and Zhang, R.: Multivariate analysis of homogeneous nucleation rate measurements: I. Nucleation in the p-toluic acid/sulfuric acid/water system, J. Chem. Phys., 128, 064508, https://doi.org/10.1063/1.2830030, 2008.
Merikanto, J., Spracklen, D. V., Mann, G. W., Pickering, S. J., and Carslaw, K. S.: Impact of nucleation on global CCN, Atmos. Chem. Phys., 9, 8601–8616, https://doi.org/10.5194/acp-9-8601-2009, 2009.
Nadykto, A. B. and Yu, F.: Strong hydrogen bonding between atmospheric nucleation precursors and common organics, Chem. Phys. Lett., 435, 14–18, https://doi.org/10.1016/j.cplett.2006.12.050, 2007.
Nadykto, A. B., Yu, F., Jakovleva, M. V., Herb, J., and Xu, Y.: Amines in the Earth's Atmosphere: A Density Functional Theory Study of the Thermochemistry of Pre-Nucleation Clusters, Entropy, 13, 554–569, https://doi.org/10.3390/e13020554, 2011.
Ortega, I. K., Kupiainen, O., Kurtén, T., Olenius, T., Wilkman, O., McGrath, M. J., Loukonen, V., and Vehkamäki, H.: From quantum chemical formation free energies to evaporation rates, Atmos. Chem. Phys., 12, 225–235, https://doi.org/10.5194/acp-12-225-2012, 2012.
Qiu, C. and Zhang, R.: Multiphase chemistry of atmospheric amines, Phys. Chem. Chem. Phys., 15, 5738–5752, https://doi.org/10.1039/C3CP43446J, 2013.
Riccobono, F., Schobesberger, S., Scott, C. E., Dommen, J., Ortega, I. K., Rondo, L., Almeida, J., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Downard, A., Dunne, E. M., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Hansel, A., Junninen, H., Kajos, M., Keskinen, H., Kupc, A., Kürten, A., Kvashin, A. N., Laaksonen, A., Lehtipalo, K., Makhmutov, V., Mathot, S., Nieminen, T., Onnela, A., Petäjä, T., Praplan, A. P., Santos, F. D., Schallhart, S., Seinfeld, J. H., Sipilä, M., Spracklen, D. V., Stozhkov, Y., Stratmann, F., Tomeì, A., Tsagkogeorgas, G., Vaattovaara, P., Viisanen, Y., Vrtala, A., Wagner, P. E., Weingart- ner, E., Wex, H., Wimmer, D., Carslaw, K. S., Curtius, J., Donahue, N. M., Kirkby, J., Kulmala, M., Worsnop, D. R., and Baltensperger, U.: Oxidation products of biogenic emissions contribute to nucleation of atmospheric particles, Science, 344, 717–721, https://doi.org/10.1126/science.1243527, 2014.
Rychlik, K., Secrest, J. R., Lauc, C., Pulczinski, J., Zamora, M. L., Leal, J., Langleya, R., Myatt, L., Raju, M., Chang, R. C.-A., Li, Y., Golding, M. C., Rodrigues-Hoffmann, A., Molina, M. J., Zhang, R., and Johnson, N. M.: In utero ultrafine particulate matter exposure causes offspring pulmonary immunosuppression, P. Natl. Acad. Sci. USA, 116, 3443–3448, https://doi.org/10.1073/pnas.1816103116, 2019.
Tröstl, J., Chuang, W. K., Gordon, H., Heinritzi, M., Yan, C., Molteni, U., Ahlm, L., Frege, C., Bianchi, F., Wagner, R., Simon, M., Lehtipalo, K., Williamson, C., Craven, J. S., Duplissy, J., Adamov, A., Almeida, J., Bernhammer, A.-K., Breitenlechner, M., Brilke, S., Dias, A., Ehrhart, S., Flagan, R. C., Franchin, A., Fuchs, C., Guida, R., Gysel, M., Hansel, A., Hoyle, C. R., Jokinen, T., Junninen, H., Kangasluoma, J., Kesk- inen, H., Kim, J., Krapf, M., Kürten, A., Laaksonen, A., Lawler, M., Leiminger, M., Mathot, S., Möhler, O., Nieminen, T., Onnela, A., Petäjä, T., Piel, F. M., Miettinen, P., Rissanen, M. P., Rondo, L., Sarnela, N., Schobesberger, S., Sengupta, K., Sipilä, M., Smith, J. N., Steiner, G., TomeÌ, A., Virtanen, A., Wagner, A. C., Weingartner, E., Wimmer, D., Winkler, P. M., Ye, P., Carslaw, K. S., Curtius, J., Dommen, J., Kirkby, J., Kulmala, M., Riipinen, I., Worsnop, D. R., Donahue, N. M., and Baltensperger, U.: The role of low-volatility organic compounds in initial particle growth in the atmosphere, Nature, 533, 527–531, https://doi.org/10.1038/nature18271, 2016.
Tsona, N. T., Henschel, H., Bork, N., Loukonen, V., and Vehkamäki, H.: Structures, Hydration, and Electrical Mobilities of Bisulfate Ion–Sulfuric Acid–Ammonia/Dimethylamine Clusters: A Computational Study, J. Phys. Chem. A, 119, 9670–9679, https://doi.org/10.1021/acs.jpca.5b03030, 2015.
Wang, C.-Y., Jiang, S., Liu, Y.-R., Wen, H., Wang, Z.-Q., Han, Y.-J., Huang, T., and Huang, W.: Synergistic Effect of Ammonia and Methylamine on Nucleation in the Earth's Atmosphere. A Theoretical Study, J. Phys. Chem. A, 122, 3470–3479, https://doi.org/10.1021/acs.jpca.8b00681, 2018.
Wang, J., Krejci, R., Giangrande, S., Kuang, C., Barbosa, H. M. J., Brito, J., Carbone, S., Chi, X., Comstock, J., Ditas, F., Lavric, J., Manninen, H. E., Mei, F., Moran-Zuloaga, D., Pöhlker, C., Pöh- lker, M. L., Saturno, J., Schmid, B., Souza, R. A. F., Springston, S. R., Tomlinson, J. M., Toto, T., Walter, D., Wimmer, D., Smith, J. N., Kulmala, M., Machado, L. A. T., Artaxo, P., Andreae, M. O., Petäjä, T., and Martin, S. T.: Amazon boundary layer aerosol concentration sustained by vertical transport during rainfall, Nature, 539, 416–419, https://doi.org/10.1038/nature19819, 2016.
Wang, L., Khalizov, A.F., Zheng, J., Xu, W., Lal, V., Ma, Y., and Zhang, R.: Atmospheric nanoparticles formed from heterogeneous reactions of organics, Nat. Geosci., 3, 238–242, https://doi.org/10.1038/ngeo778, 2010.
Wang, Z. B., Hu, M., Mogensen, D., Yue, D. L., Zheng, J., Zhang, R. Y., Liu, Y., Yuan, B., Li, X., Shao, M., Zhou, L., Wu, Z. J., Wiedensohler, A., and Boy, M.: The simulations of sulfuric acid concentration and new particle formation in an urban atmosphere in China, Atmos. Chem. Phys., 13, 11157–11167, https://doi.org/10.5194/acp-13-11157-2013, 2013.
Weber, K. H., Liu, Q., and Tao, F.-M.: Theoretical study on stable small clusters of oxalic acid with ammonia and water, J. Phys. Chem. A, 118, 1451–1468, https://doi.org/10.1021/jp4128226, 2014.
Wexler, A.: Vapor pressure formulation for water in range 0 to 100 C. A revision, J. Res. Nat. Bur. Stand., 80A, 775–785, 1976.
Wu, G., Brown, J., Zamora, M. L., Miller, A., Satterfield, M. C., Meininger, C. J., Steinhauser, C. B., Johnson, G. A., Burghardt, R. C., Bazer, F. W., Li, Y., Johnson, N. M., Molina, M. J., and Zhang, R.: Adverse organogenesis and predisposed long-term metabolic syndrome from prenatal exposure to fine particulate matter, P. Natl. Acad. Sci. USA, 116, 11590–11595, https://doi.org/10.1073/pnas.1902925116, 2019.
Xu, W. and Zhang, R.: Theoretical investigation of interaction of dicarboxylic acids with common aerosol nucleation precursors, J. Phys. Chem., 116, 4539-4550, https://doi.org/10.1021/jp301964u, 2012.
Xu, W. and Zhang, R.: A theoretical study of hydrated molecular clusters of amines and dicarboxylic acids, J. Chem. Phys., 139, 064312, https://doi.org/10.1063/1.4817497, 2013.
Xu, W., Gomez-Hernandez, M., Guo, S., Secrest, J., Marrero-Ortiz, W., Zhang, A. L., and Zhang, R.: Acid-catalyzed reactions of epoxides for atmospheric nanoparticle growth, J. Am. Chem. Soc., 136, 15477–15480, https://doi.org/10.1021/ja508989a, 2014.
Xu, Y., Nadykto, A. B., Yu, F., Jiang, L., and Wang, W.: Formation and properties of hydrogen-bonded complexes of common organic oxalic acid with atmospheric nucleation precursors, J. Mol. Struct.-Theochem., 951, 28–33, https://doi.org/10.1016/j.theochem.2010.04.004, 2010a.
Xu, Y., Nadykto, A. B., Yu, F., Herb, J., and Wang, W.: Interaction between common organic acids and trace nucleation species in the Earth's atmosphere, J. Phys. Chem. A, 114, 387–396, https://doi.org/10.1021/jp9068575, 2010b.
Yao, L., Garmash, O., Bianchi, F., Zheng, J., Yan, C., Kontkanen, J., Junninen, H., Mazon, B. S., Ehn, M., Paasonen, P., Sipila, M., Wang, M., Wang, X., Xiao, S., Chen, H., Lu, Y., Zhang, B., Wang, D., Fu, Q., Geng, F., Li, L., Wang, H., Qiao, L., Yang, X., Chen, J., Kerminen, V., PetajÁ, T., Worsnop, D., Kulmala, M., and Wang, L.: Atmospheric new particle formation from sulfuric acid and amines in a Chinese megacity, Science, 361, 278–281, https://doi.org/10.1126/science.aao4839, 2018.
Yu, H., McGraw, R., and Lee, S.-H.: Effects of amines on formation of sub-3 nm particles and their subsequent growth, Geophys. Res. Lett., 39, L02807, https://doi.org/10.1029/2011GL050099, 2012.
Yue, D. L., Hu, M., Zhang, R. Y., Wang, Z. B., Zheng, J., Wu, Z. J., Wiedensohler, A., He, L. Y., Huang, X. F., and Zhu, T.: The roles of sulfuric acid in new particle formation and growth in the mega-city of Beijing, Atmos. Chem. Phys., 10, 4953–4960, https://doi.org/10.5194/acp-10-4953-2010, 2010.
Yue, D. L., Hu, M., Zhang, R. Y., Wu, Z. J., Su, H., Wang, Z. B., and Wiedensohler, A.: Potential contribution of new particle formation to cloud condensation nuclei in Beijing, Atmos. Environ., 45, 6070–6077, https://doi.org/10.1016/j.atmosenv.2011.07.037, 2011.
Zhang, H., Kupiainen-Määttä, O., Zhang, X., Molinero, V., Zhang, Y., and Li, Z., The enhancement mechanism of glycolic acid on the formation of atmospheric sulfuric acid–ammonia molecular clusters, J. Chem. Phys., 146, 184308, https://doi.org/10.1063/1.4982929, 2017.
Zhang, R.: Getting to the critical nucleus of aerosol formation, Science, 328, 1366–1367, https://doi.org/10.1126/science.1189732, 2010.
Zhang, R., Suh, I., Zhao, J., Zhang, D., Fortner, E. C., Tie, X., Molina, L. T., and Molina, M. J.: Atmospheric new particle formation enhanced by organic acids, Science, 304, 1487–1490, https://doi.org/10.1126/science.1095139, 2004.
Zhang, R., Wang, L., Khalizov, A. F., Zhao, J., Zheng, J., McGraw, R. L., and Molina, L. T.: Formation of nanoparticles of blue haze enhanced by anthropogenic pollution, P. Natl. Acad. Sci. USA, 106, 17650–17654, https://doi.org/10.1073/pnas.0910125106, 2009.
Zhang, R., Khalizov, A. F., Wang, L., Hu, M., and Xu, W.: Nucleation and growth of nanoparticles in the atmosphere, Chem. Rev., 112, 1957–2011, https://doi.org/10.1021/cr2001756, 2012.
Zhang, R., Wang, G., Guo, S., Zamora, M. L., Ying, Q., Lin, Y., Wang, W., Hu, M., and Wang Y.: Formation of urban fine particulate matter, Chem. Rev., 115, 3803–3855, https://doi.org/10.1021/acs.chemrev.5b00067, 2015.
Zhao, J., Khalizov, A., Zhang, R., and McGraw, R.: Hydrogen bonding interaction of molecular complexes and clusters of aerosol nucleation precursors, J. Phys. Chem. A, 113, 680–689, https://doi.org/10.1021/jp806693r, 2009.
Zhu, Y. P., Liu, Y. R., Huang, T., Jiang, S., Xu, K. M., Wen, H., Zhang, W. J., and Huang, W.: Theoretical study of the hydration of atmospheric nucleation precursors with acetic acid, J. Phys. Chem. A, 118, 7959–7974, https://doi.org/10.1021/jp506226z, 2014.