the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Can downwelling far-infrared radiances over Antarctica be estimated from mid-infrared information?
Christophe Bellisario
Helen E. Brindley
Simon F. B. Tett
Rolando Rizzi
Gianluca Di Natale
Luca Palchetti
Giovanni Bianchini
Far-infrared (FIR: , ν<667 cm−1) radiation emitted by the Earth and its atmosphere plays a key role in the Earth's energy budget. However, because of a lack of spectrally resolved measurements, radiation schemes in climate models suffer from a lack of constraint across this spectral range. Exploiting a method developed to estimate upwelling far-infrared radiation from mid-infrared (MIR: cm−1) observations, we explore the possibility of inferring zenith FIR downwelling radiances in zenith-looking observation geometry, focusing on clear-sky conditions in Antarctica. The methodology selects a MIR predictor wavenumber for each FIR wavenumber based on the maximum correlation seen between the different spectral ranges. Observations from the REFIR-PAD instrument (Radiation Explorer in the Far Infrared – Prototype for Application and Development) and high-resolution radiance simulations generated from co-located radio soundings are used to develop and assess the method. We highlight the impact of noise on the correlation between MIR and FIR radiances by comparing the observational and theoretical cases. Using the observed values in isolation, between 150 and 360 cm−1, differences between the “true” and “extended” radiances are less than 5 %. However, in spectral bands of low signal, between 360 and 667 cm−1, the impact of instrument noise is strong and increases the differences seen. When the extension of the observed spectra is performed using regression coefficients based on noise-free radiative transfer simulations the results show strong biases, exceeding 100 % where the signal is low. These biases are reduced to just a few percent if the noise in the observations is accounted for in the simulation procedure. Our results imply that while it is feasible to use this type of approach to extend mid-infrared spectral measurements to the far-infrared, the quality of the extension will be strongly dependent on the noise characteristics of the observations. A good knowledge of the atmospheric state associated with the measurements is also required in order to build a representative regression model.
Defined here as wavelengths above 15 µm or wavenumbers below 667 cm−1, the far-infrared (FIR) spectral band plays a key role in energetic exchanges between the Earth's surface, atmosphere and space (Harries et al., 2008). Under clear-sky conditions, absorption in the FIR is dominated by water vapour such that typically very little FIR radiation emitted from the surface directly escapes to space. However, the very cold, dry conditions commonly found in polar regions simultaneously shift the peak of surface emission towards longer wavelengths and, under clear-skies, allow as much as 45 % of FIR radiation emitted from the ground to escape directly to space, making the clear-sky FIR outgoing longwave radiation sensitive to surface properties (Feldman et al., 2014). A corollary of this enhanced atmospheric transmissivity is the increased sensitivity of downward clear-sky FIR radiation at the surface to conditions at higher levels in the atmosphere than would normally be the case in warmer, wetter environments.
Despite its role in the energy budget, due to the inherent difficulties involved, only a few instruments have measured hyperspectral radiances across the FIR. Aircraft and ground-based measurements available from the Tropospheric Airborne Fourier Transform Spectrometer (TAFTS) (Canas et al., 1997) have been used to probe water vapour spectroscopy, upper tropospheric humidity, the radiative properties of cirrus and snow–ice surface emissivity (Green et al., 2012; Fox et al., 2015; Cox et al., 2007, 2010; Bellisario et al., 2017). Balloon and ground-based observations from the Radiation Explorer in the Far InfraRed – Prototype of Applications and Development (REFIR-PAD; Bianchini et al., 2006) have been exploited to determine precipitable water (Bianchini et al., 2011), investigate the spectral signature of cirrus (Maestri et al., 2014) and provide simultaneous retrievals of water vapour, temperature and cirrus properties (Di Natale et al., 2017). The Far-InfraRed Spectroscopy of the Troposphere (FIRST) instrument (Mlynczak et al., 2006) has participated in both balloon and ground-based campaigns, providing a rigorous test of the ability of radiative transfer models to match the spectroscopic signals measured in the far infrared (Mlynczak et al., 2016; Mast et al., 2017). All three of these instruments participated in one or both of the Radiative Heating in Underexplored Bands Campaigns (RHUBC), providing a robust dataset which has been used to improve our knowledge of the underlying far-infrared water vapour spectroscopy (Turner and Mlawer, 2010).
Almost all of the available FIR radiance measurements originate from limited field campaigns. Recognising the key role that the FIR plays in determining the Earth's energy budget, the information that may be contained in the spectrum and the lack of available measurements, Turner et al. (2015, hereafter T15) describe a methodology designed to estimate FIR radiances by exploiting correlated behaviour in the mid-infrared (MIR). They applied this method to nadir radiance measurements from the Infrared Atmospheric Sounding Interferometer (IASI; Clerbaux et al., 2009) and evaluated their approach by comparing spectrally integrated radiances across the infrared with measurements from the Clouds and the Earth's Radiant Energy System (CERES; Wielicki et al., 1996) broadband radiometers taken during simultaneous nadir overpasses. Overall mean broadband agreement is encouraging, but the evaluation technique precludes the identification of any compensating biases within the FIR itself. In essence, the T15 methodology, and similar methods that seek to create synthetic FIR top-of-atmosphere spectra from mid-infrared observations (e.g. Huang et al., 2008) have not been evaluated with real spectral observations due to the absence of such measurements. As shown by Huang et al. (2008, 2013), estimates of spectrally resolved fluxes across the infrared can provide a powerful tool for climate model evaluation.
REFIR-PAD has been measuring spectral downwelling longwave radiances at Dome-C Antarctica since 2011, providing a long-term database covering the spectral range from 100 to 1400 cm−1 (Palchetti et al., 2015). In this study we exploit the availability of these observations to test whether a similar methodology to that described by T15 can be developed and applied to the REFIR-PAD measurements. Unlike T15, our goal is not to create an algorithm that can be applied on the global scale but simply to evaluate the performance of such an approach under the very specific conditions sampled by REFIR-PAD during its deployment. We focus on clear-sky conditions, essentially providing a test of the unique information contained in the FIR relating to water vapour spectroscopy and concentration. Because spectrally resolved observations covering much of the infrared are available, inferred FIR spectral radiances can be compared to the real observations, providing a thorough evaluation of the success of the technique. Radiative transfer simulations utilising radiosonde measurements of the atmospheric state can also be used to assess the impact of instrumental and sampling noise on the robustness of the relationships seen. In this way we are able to assess to what level it is possible to use information in the MIR (within the constraint of the REFIR-PAD wavenumber range and location) to infer FIR spectral behaviour using actual observations.
Given the constrained nature of the REFIR-PAD dataset, if the results show that the approach fails to capture the observed spectral behaviour, it would cast serious doubt on whether our ability to model the full infrared spectrum is sufficient for us to expect a similar approach to give a robust spectral prediction over a wider range of conditions and/or viewing geometries. Conversely, while a successful implementation does not directly imply that a similar level of agreement will be seen in other locations and for other viewing geometries, it does give confidence that the general principle is robust.
In Sect. 2, the instrumental data are described along with the radiative transfer model used to produce simulated spectra for comparisons. We also describe the distinct steps of the spectral extension method. Section 3 displays the results, with comparison between instrumental and theoretical extensions, which are discussed in Sect. 4. We also investigate the impact of spectral averaging, consistent with the type of resolution currently employed in global climate models as a key potential use of such data for model evaluation. Finally we draw conclusions in Sect. 5.
2.1 REFIR-PAD
The REFIR-PAD instrument is currently located at the Italian–French Concordia research station in Antarctica (75∘06′ S, 123∘23′ E) at 3230 m above sea level. It was installed in the Physics Shelter, south of the main station buildings for the PRANA project (Proprietà Radiative dell' Atmosfera e delle Nubi in Antartide), financed by the Italian PNRA (Programma Nazionale di Ricerche in Antartide). The PRANA project aimed to supply the first multi-year dataset of spectral downwelling longwave radiances, including the unique measurements in the FIR over a polar region, and the instrument has been recording data autonomously since 2011 (Palchetti et al., 2015), with further support from projects CoMPASS (COncordia Multi-Process Atmospheric StudieS), the currently active DoCTOR (DOme C Tropospheric ObserveR) and FIRCLOUDS (Far Infrared Radiative Closure Experiment For Antarctic Clouds). A protective chimney separates the instrument from the outside temperature, and the ingress of wind and snow is prevented by a barrier on the rooftop.
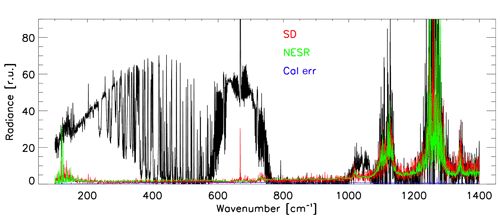
The instrument, fully described in Bianchini et al. (2006), is composed of a Fourier transform spectroradiometer (Mach–Zehnder type) with an operating spectral bandwidth of 100–1400 cm−1 (100–7.1 µm) at a resolution of 0.4 cm−1 and with an acquisition time of 80 s. One calibrated spectrum is based on the average of four zenith observations for an overall measurement time of 6.5 min every 14 min. The noise equivalent spectral radiance (NESR) due to detector noise is approximately 1 at 400 cm−1. In addition to the radiometric NESR, the calibration error and the standard deviation of the four observations composing the calibrated spectrum are calculated. The standard deviation is an a posteriori estimation that includes the NESR and possible scene variations (Palchetti et al., 2015).
The selection of the clear-sky spectra uses the classification outlined in Rizzi et al. (2016) to discriminate between clear and cloudy scenes for 2013. A total of 24 spectral intervals are selected, and seven tests are applied, comparing the mean radiances, the standard deviation and the brightness temperature in the specified spectral intervals. This approach yields 5126 clear-sky spectra for 2013.
We choose to focus only on clear-sky conditions because this gives us a reasonably well-constrained dataset to use in testing the extension approach. Including cloudy conditions would require a successful detection of cloud type, height and microphysics to incorporate into the radiative transfer modelling described in Sect. 2.3, adding significant complexity to the study. From previous theoretical studies and ongoing work analysing the REFIR-PAD spectra, we also expect unique information related to ice crystal habit to be contained within the FIR micro-windows (Yang et al., 2003; Maestri et al., 2014; Di Natale et al., 2017).
An example of a clear-sky spectrum is displayed in Fig. 1 and shows unphysically high radiances and standard deviations in two bands within the atmospheric window region, from 1095 to 1140 and from 1230 to 1285 cm−1. These are a manifestation of absorption by the polyethylene terephthalate (Mylar) substrate which composes the wideband beam splitter, and hence radiances within these bands are not used in this study. Outside these two regions and where the downwelling signal is typically high (below 400 cm−1 and between 600 and 800 cm−1), the standard deviations are relatively small. However, in the most transparent regions, where the radiance is low (micro-windows between 400 and 600 cm−1 and in the atmospheric window from 800 to 1000 cm−1, for example), the standard deviations can exceed the measured radiances with values around 2 (radiance unit), where 1 is equivalent to 1 .
2.2 Radiosonde profiles
Since 2005, the radiosonde system routinely operative at Dome C has provided atmospheric pressure, temperature and humidity profiles at 12:00 UTC. From 2009 onwards these observations have been made using the Vaisala RS-92SPGW. The daily profiles are available at http://www.climantartide.it (last access: 27 May 2019).
During a radiosonde launch, data are recorded every 2 s, corresponding to around 800 measurements in the troposphere and between 900 and 1900 measurements in the stratosphere, reaching up to 26–30 km (Tomasi et al., 2011). However, the relative humidity is only measured up to 15 km. Due to the balloon ascent rate (5–6 m s−1) and the recording rate, the vertical resolution is about 10–12 m. Raw water vapour profiles are provided in relative humidity, and the conversion to mixing ratio assumes saturation over water as advised by the World Meteorological Organisation (WMO) guide to meteorological instruments and methods of observation (https://www.wmo.int/pages/prog/www/IMOP/CIMO-Guide.html, last access: 27 May 2019).
2.3 LBLRTM
We use the Line-By-Line Radiative Transfer Model (LBLRTM; Clough et al., 2005) to simulate the downwelling radiance. The version used in this study is LBLRTM v12.7, with an updated line parameter database AER version 3.5 (following HITRAN 2012; Rothman et al., 2013) and a continuum code MT_CKD_3.0, which includes up-to-date representation of the H2O foreign continuum from 0 to 600 cm−1 and of the self continuum in the microwave that resulted from an analysis of measurements taken at the ARM RHUBC-II campaign and a reanalysis of RHUBC-I measurements (not included in T15).
The radiosonde profiles described in Sect. 2.2 provide the temperature and water vapour inputs for the radiative transfer simulations. The radiosonde profiles are interpolated onto 100 levels, with the highest vertical resolution being 26 m near the surface. Additional levels extending up to 50 km in altitude are included, using temperature and humidity data from the closest ERA-Interim (Dee et al., 2011) profiles in space and time, scaled to the highest altitude where reliable temperature and water vapour values were recorded by the given radiosonde. Ozone concentrations are extracted from the same ERA-Interim profile. Minor species are taken from the AFGL sub-Arctic winter and summer profiles (Anderson, 1986), and CO2 has been scaled to 2013 values as reported by NOAA's Global Monitoring Division, Earth System Research Laboratory (https://www.esrl.noaa.gov/gmd/ccgg/trends/, last access: 27 May 2019). To achieve consistency with the REFIR-PAD instrumental characteristics, each simulated spectrum is Fourier-transformed, and a maximum optical path difference of 1.25 cm is applied in the interferogram domain. The truncated interferogram is then retransformed, and the resulting spectrum is sampled at the REFIR-PAD sampling frequency.
2.4 Extension methodology
Based on the methodology developed by T15, FIR wavenumbers between 100 and 667 cm−1 are correlated with (predictor) wavenumbers from 667 to 1400 cm−1. The estimated radiance in the FIR Iν,FIR can be written as a function of the predictor radiance Iν,predictor and two regression coefficients, a0 and a1, using
given the assumption of a logarithmic relationship between the predictor and estimated radiances and
for a linear assumption.
We start by selecting the REFIR-PAD spectra that will be used to calculate the regression coefficients. All clear-sky spectra that are closest in time to the daily radiosonde measurement at 12:00 UTC are selected. If the closest spectrum on a given day is measured more than 2 h before or after 12:00 UTC, the spectrum is discarded. 125 d during 2013 are retained using this criterion. These spectra are randomly divided into two sets. The first set is used as a creation set, from which the regression coefficients are derived, and the second is used as a test set, with which the regression coefficients derived from the creation set are tested.
To choose the predictor wavenumbers, we select a FIR wavenumber and create a vector composed of all radiances in the creation set at this wavenumber. We compute the correlation of this vector with a similar vector at a MIR wavenumber. We repeat this analysis for all MIR wavenumbers and select the MIR wavenumber that shows the highest correlation as the predictor for the given FIR wavenumber. Finally, the linear (or logarithmic) regression coefficients are calculated. The whole process is repeated for each FIR wavenumber. We emphasise that the methodology described here is only based on analytical considerations with the computation of the correlation. No spectral assumptions are made, and as a consequence the MIR predictor wavenumbers can be associated either with, for example, a CO2 line or a H2O line or a combination of both.
3.1 Application to observed spectra
Figure 2a displays the correlation between FIR and MIR radiances using the REFIR-PAD creation set, displayed at the nominal instrument spectral resolution of 0.4 cm−1. As noted previously, the bands corresponding to regions of high noise due to the absorption by the beam splitter (1095–1140 and 1230–1285 cm−1) have been removed from the analysis.
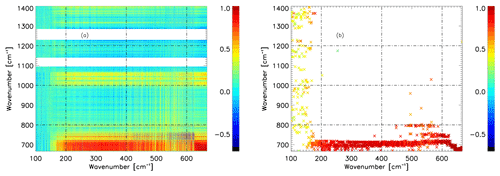
Figure 2(a) Correlation map using REFIR-PAD clear-sky spectral radiances with MIR wavenumbers on the y axis and FIR wavenumbers on the x axis. (b) MIR wavenumbers that maximise the correlation for each FIR wavenumber. Colour scales indicate the correlation.
We observe specific spectral regions that maximise the correlation. A large portion of the spectral region between 150 and 500 cm−1 is highly correlated with wavenumbers between 667 and 720 cm−1. Figure 2b indicates the MIR predictor wavenumber selected for each FIR wavenumber using the approach described in Sect. 2.4. Below 150 cm−1, the predictor wavenumbers are scattered between 700 and 1400 cm−1, with low correlation values between 0.2 and 0.5. This can be explained by a high NESR at the edge of the REFIR-PAD detector, as seen in Fig. 1 in green. Between 200 and 470 cm−1, the predictor wavenumbers are clustered around 700 cm−1, within the wing of the 667 cm−1 CO2 band, with correlations of between 0.84 and 0.94. Figure 2a shows lower, more varied correlations in the 470 and 570 cm−1 region: here the MIR predictor wavenumber also shows more variability, taking values varying between 696 and 799 cm−1. The correlation values in this region lie between 0.71 and 0.92. Moving towards the centre of the 667 cm−1 CO2 band, MIR predictors are typically clustered at 682 cm−1 and show a narrower range of higher correlations of between 0.96 and 0.98. We note that the predictor wavenumbers are mainly localised in a spectral area dominated by the CO2 band coexisting with typically weaker vapour lines.
As noted in Sect. 2.4, regression coefficients a0 and a1 in Eqs. (1) and (2) are computed between each FIR wavenumber and the corresponding predictor MIR wavenumber. Figure 3 shows an example of the relationship between a predictor wavenumber at 698.4 cm−1 and its corresponding predictand wavenumber at 301.6 cm−1 across all creation set spectra. Logarithmic (Eq. 1) and linear (Eq. 2) fits between the radiances are also displayed.
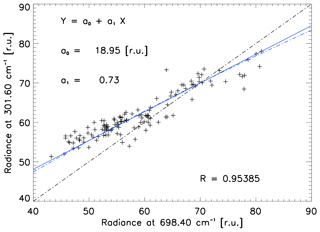
Figure 3FIR radiances at 301.6 cm−1 against predictor MIR radiance at 698.4 cm−1 for all creation set spectra. The solid blue line is the linear fit of the points using Eq. (2), with regression coefficients a0 and a1. The linear correlation value R is indicated. For completeness, the logarithmic fit is also shown by the dashed blue line. The dashed–dotted black line represents 1:1.
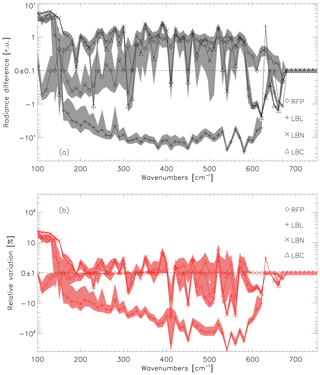
Using the test set of spectra we examined the robustness of the extension method. An example of a single REFIR-PAD observation (in black) and its extension (in blue) is displayed in Fig. 4a, with the radiance and relative differences in Fig. 4b at 10 cm−1 resolution. In this case, linear regressions have been used to perform all the extensions. Displaying the results at 10 cm−1 allows a clearer picture to emerge in terms of the performance of the extension.
At 10 cm−1 resolution the absolute difference mean across the FIR over the entire test set is relatively small at less than 0.6 It is worth nothing that below 370 cm−1 the mean error fluctuates around zero, but at higher wavenumbers ( cm−1) there does appear to be a small positive bias of ∼0.5 r.u. Under clear-sky conditions this region is generally more transmissive than the lower wavenumber regime – as evidenced by the comparatively lower radiances in Fig. 4a. These lower radiances, particularly between 400 and 570 cm−1, contribute to slightly higher relative differences and variability across this range in Fig. 4b. Above 570 cm−1, both absolute and relative differences diminish as the radiance increases.
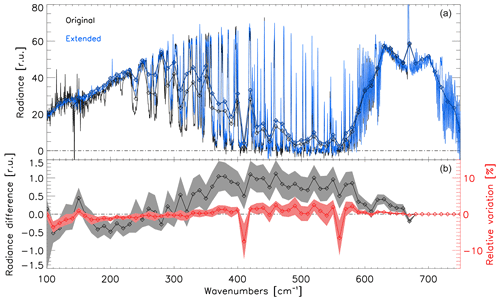
Figure 4Far-infrared extension based on REFIR-PAD data (linear case). (a) Example of a spectrum (black) and its extension (blue) below 667 cm−1. The same spectra integrated over 10 cm−1 bands are also shown by the diamond lines. (b) Mean difference (black) and relative variation (red) between the original and the extended spectra at 10 cm−1 resolution calculated over the entire test set. Shaded areas are the associated standard deviations.
3.2 Application to simulated spectra
The previous section suggests that a reasonable reconstruction of observed clear-sky downwelling FIR surface spectral radiances at a moderate (10 cm−1) resolution can be obtained using simultaneous observations of MIR radiances. In this section we explore whether similar results are obtained using simulations.
Therefore, we apply the same process of extension using simulated LBLRTM spectra. For each clear-sky case used to build the creation and test sets for REFIR-PAD data, the corresponding radiosonde profile is selected and used as input for LBLRTM as described in Sect. 2.2. The output spectra are used to generate the equivalent simulated creation and test sets.
We consider two cases. The first uses the LBLRTM spectra as directly simulated, while the second adds noise in order to be more representative of the REFIR-PAD observations. Noise is introduced using the following equation:
where is the spectral radiance from LBLRTM with noise, Iν,LBLRTM is the “noise-free” spectral radiance directly simulated by LBLRTM, r is a normally distributed random number between −1 and 1 and σν,REFIR-PAD, NESRν,REFIR-PAD and CalErrν,REFIR-PAD are respectively the standard deviation, the noise equivalent spectral radiance and the calibration error from the corresponding REFIR-PAD spectrum.
The correlation maps of LBLRTM with and without noise are displayed in Fig. 5a and b respectively. Taking the no-noise case first, most wavenumbers show a strong correlation with all others, with values typically above 0.5. The FIR band sees an enhanced correlation with the MIR between 667 and 950 cm−1 and wavenumbers between 1300 and 1400 cm−1. When noise is added, the correlations reduce and show a much greater spectral variation, which is more consistent with the observational case. The same bands seen in Fig. 2a which maximise the correlation appear.
The predictor wavenumbers are displayed in Fig. 5 without noise (c) and with noise (d). In the case of a perfect simulation, the number of predictor wavenumbers is relatively small, indicating a high degree of correlation in the spectra. Below 600 cm−1, most of the predictor wavenumbers are located between 1340 and 1400 cm−1. As a comparison, T15 find predictor wavenumbers outside the REFIR-PAD spectral range, between 1500 and 1600 cm−1 towards the centre of the ν2 water vapour vibration–rotation band. Below 300 cm−1, a second band is visible around 700 cm−1. Between 600 and 667 cm−1, the predictor wavenumbers are spread over a range of discrete values close to 700 cm−1. When the LBLRTM simulations are perturbed with noise, consistent with the change in the correlation map, the selected predictor channels show similar behaviour to REFIR-PAD (Fig. 2b). Below 160 cm−1, the predictor wavenumbers are located in a wide band between 667 and 1400 cm−1 but with a correlation of about 0.5. Between 200 and 400 cm−1, the predictor wavenumbers are distributed in a band centred at 700 cm−1. Above 400 cm−1, predictor wavenumbers up to 800 cm−1 also begin to appear, while between 500 and 600 cm−1 the spread in predictors again extends across the whole 667–1400 cm−1 range, with typically lower correlations.
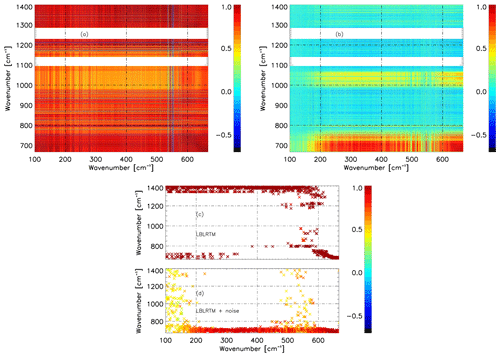
Figure 5Correlation map using noiseless LBLRTM spectra (a) and LBLRTM spectra with realistic noise added (b). Panels (c) and (d) are as Fig. 2b, showing predictor wavenumbers for LBLRTM without noise and with noise respectively.
At the time of writing there are only very limited spectrally resolved data in the FIR. The goal of this research is thus to see whether the LBLRTM simulations are able to provide coefficients to correctly map the observed MIR data into the FIR. So we now test the accuracy of going from observed MIR to FIR radiances using three different approaches. All predictions are then compared against the REFIR-PAD FIR observations. The three different sets of regression coefficients we use are
-
LBLRTM simulations (LBL);
-
LBLRTM simulations with added realistic noise (LBN);
-
coupled LBLRTM (LBC), whereby predictor wavenumbers are generated from LBLRTM with added realistic noise, but regression coefficients are generated from LBLRTM without noise.
By coupling the predictor wavenumbers from LBLRTM with added noise and the regression coefficients from LBLRTM without noise in the last approach, we obtain the best estimate of regression coefficients at the wavenumbers at which the expected relationship is strongest.
In all cases shown, a linear regression is used, although the findings are essentially unchanged if a logarithmic fit is employed (see Table 1). Figure 6 displays the mean differences (a) and mean relative variations (b) between the “true” and “extended” FIR radiances for all cases, with their associated standard deviations. For ease of comparison, the extension of REFIR-PAD based on REFIR-PAD-derived regression coefficients (previously shown in Fig. 4b) is also included. The extension to the FIR using regression coefficients based on noise-free simulations (LBL) fails to capture the observed FIR behaviour. A strong bias is visible, with a mean difference of −45 %. In this case, the selected predictor wavenumbers are close to 1400 cm−1 (Fig. 5c); however, at these wavenumbers, the observed correlation for REFIR-PAD is very low (Fig. 2a), due to increased noise (Fig. 1), leading to large differences between the extended spectra and observations. If the predictor wavenumbers are selected from the noise adjusted simulations (LBN and LBC), the mean differences and standard deviations show a marked decrease, reducing the mean difference to 1.1 % and −0.4 % for LBN and LBC respectively.
Noise-free simulations of downwelling spectrally resolved clear-sky radiances over Antarctica imply a high level of correlation between the MIR and FIR. However, the prediction model based on these simulations fails to adequately capture observed behaviour under clear skies as exhibited by REFIR-PAD. Instrumental noise characteristics strongly affect the choice of predictor wavenumbers. Including the effects of this noise in the simulations markedly improves the prediction model, which is capable of capturing the observed mean radiance in the FIR to within 2 %, except in selected bands where the downwelling radiance is low (for example 410 and 490 cm−1, with the largest discrepancy at 540 cm−1; see Fig. 6a and b).
More specific to this study, it is worth noting that the temperature and water vapour profiles very close to the ground (within 2 m) may also be affected by the presence of the chimney connecting the physics shelter to the outside environment. Palchetti et al. (2015) perform a least squares minimisation of the radiance differences between the observation and the simulation, with the addition of a first level inside the chimney into the fitted profiles. Rizzi et al. (2016) include a first level inside the chimney based on the average between the internal PAD temperature and the shelter temperature. We performed tests on the first profile level in our simulations, adding a temperature point corresponding to the chimney mean temperature (of available year 2016). The differences between our vertical resolution and this test showed differences up to 0.2 , peaking in the centre of the CO2 band. In the absence of measurements of temperature inside the chimney for 2013, and bearing in mind the limited sensitivity seen, we choose to keep our vertical profiles. With this approach, biases between the observations and the corresponding simulations are within 2 , consistent with Rizzi et al. (2018).
In this study, the extension of REFIR-PAD has been performed on its native grid (Δν=0.4 cm−1), and the results have been predominantly presented over averaged bands of Δν=10 cm−1. At present, climate and Earth system models do not operate at such a high spectral resolution. It is thus of interest to investigate how the differences presented in Figs. 4 and 6 are affected by integration over the wider spectral bands more typical of these general circulation models. As an exemplar, we consider the Met Office Unified Model (UM). In the UM, there are three bands with FIR contributions, from 1 to 400, 400 to 550 and 550 to 800 cm−1.
The extensions of REFIR-PAD using the various prediction models described in Sect. 3.2 were integrated over these bands, and the corresponding results are shown in Table 1. For each band and each case, the median value of the variations is provided, along with the corresponding 1σ standard deviations across the spectra in the test set. Because of the boundaries of the extension, the bands from 1 to 400 and from 550 to 800 cm−1 are reduced to 100.4–400 and 550–667 cm−1 respectively.
Table 1Distribution of the differences and relative variations between the extension and the original spectra within the three bands (100.4–400, 400–550 and 550–667 cm−1) for REFIR-PAD extension itself, REFIR-PAD extension based on LBLRTM (LBL), based on LBLRTM with added noise (LBN) and based on coupled LBLRTM (LBC). The first and second lines correspond to a linear and a logarithmic extension respectively. The values correspond to the median value ±1σ.
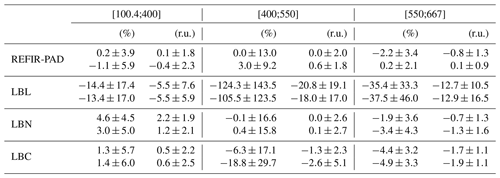
Using the REFIR-PAD prediction model, integrating over wide spectral bands results in relatively small differences between the observed and extended spectra, below 3 %. However, as described earlier, the extension using simulated noise-free regression coefficients leads to strong biases, with maximum percentage differences (up to −124 %) seen in the 400–550 cm−1 region, the most transparent of the three bands and hence the most susceptible to noise due to the low radiance level. When looking at LBN and LBC cases, the extension shows median biases which are only marginally larger than those seen using the observations themselves. In addition, the difference between using a linear or logarithmic extension is small.
In this study we have used REFIR-PAD downwelling radiance observations covering the spectral range 100–1400 cm−1 for clear-sky cases from 2013 over Dome C in Antarctica to assess whether it is currently possible to build a model which uses MIR spectral radiances to predict spectral values in the FIR to an acceptable level of accuracy. The motivation for this work comes from a number of studies that have estimated the FIR spectrum from satellite observations of MIR radiances (Huang et al., 2008; Turner et al., 2015). While these have shown encouraging agreement with broadband observations, the results have not been tested with spectrally resolved measurements due to the lack of such observations. We have described a correlation- and regression-based methodology based on Turner et al. (2015), which we have used to search for predictor wavenumbers and to extract regression coefficients at these specified wavenumbers. In addition to the observations, radiosonde soundings are used to create a corresponding simulated spectral database with the radiative transfer model LBLRTM.
Correlation maps between the observed FIR and MIR radiances show peak values at wavenumbers around 700 cm−1. In contrast, noise-free simulated spectra show peak correlations at wavenumbers between 1340 and 1400 cm−1. With the addition of realistic noise to the simulations, the pattern of the correlation map alters and looks more similar to the one created using the REFIR-PAD observations, with reduced correlations at wavenumbers <180 cm−1, between 470 and 570 cm−1 and between 1340 and 1400 cm−1. This indicates that the selected wavenumbers and the associated MIR to FIR correlation are both highly dependent on instrumental noise. One possible way of at least partially mitigating these noise effects would be to combine channels showing the highest correlations such that the predictors for a given FIR channel comprise contributions from more than one MIR measurement. This could certainly be an area for future investigation.
Using a prediction model built solely with REFIR-PAD observations, the extension from the MIR to the FIR works satisfactorily, with mean relative variations below 5 % over most of the spectral range. Between 400 and 570 cm−1, where the atmosphere is highly transparent, and the downwelling radiances are very low, the relative variation can reach up to 10 %, but the absolute variation is of the same order to the rest of the spectrum (0.5 ). Using a prediction model based on noise-free simulations, the extension to the FIR shows markedly poorer fidelity with the observed behaviour. However, when we add realistic instrument noise to the simulations, the prediction model is able to satisfactorily estimate the REFIR-PAD FIR measurements. Where the radiance is low, higher relative differences can arise as for the REFIR-PAD-only case. Notable differences are also seen at wavenumbers below 150 cm−1, which can be explained by the enhanced instrument noise close to the edge of the REFIR-PAD detector.
Our results show that while it is feasible to use the type of approach we have outlined here to extend mid-infrared spectral measurements to the far infrared, the quality of the extension is strongly dependent on the noise characteristics of the observations. This in turn implies that if a similar approach is developed to extend existing mid-infrared ground- or satellite-based observations, the instrument noise must be explicitly accounted for in building the model due to its potential role in altering the choice of predictor wavenumbers from the noise-free case. In addition, the quality of any extension using this type of method will also be critically dependent on whether the creation set of atmospheric profiles correctly represents the conditions which are actually sampled by the MIR instruments.
An obvious next step for this work would be to include cloudy conditions in the approach. However, this is challenging, as, given the results here, one would anticipate that a good knowledge of cloud microphysics and optical properties as well as vertical location, including any impact on the associated temperature and water vapour profiles, would be required to perform the forward modelling with the requisite accuracy. The frequency of radiosonde ascents at Concordia precludes knowledge of the last effect. Cloud microphysics are not measured directly, and cirrus bulk optical properties are poorly constrained in the FIR (Baran et al., 2014). Previous campaigns highlight the difficulty in matching radiance measurements across the infrared in the presence of cirrus cloud (Cox et al., 2010). However, retrievals directly from the REFIR-PAD measurements themselves may provide a means to circumvent some of these issues in future (Di Natale et al., 2017; Maestri et al., 2019).
More generally, one would want to test whether such a synthetic approach could be applied at the global scale and for potentially more interesting satellite viewing geometries. If selected, the candidate ESA Earth Explorer 9 mission, the Far infrared Outgoing Radiation Understanding and Monitoring concept (FORUM; Palchetti et al., 2016), could provide the extensive, simultaneous FIR and MIR observational database needed to build and validate such a prediction model at the spectrally resolved level. With a correct appreciation of the role of instrument noise, such a model could then be applied retrospectively to existing MIR hyperspectral measurements (such as IASI) to derive a long-term record of spectrally resolved radiances suitable for climate model evaluation.
The REFIR-PAD data are available at http://refir.fi.ino.it/refir-pad-domeC (Palchetti et al., 2015, last access: 27 May 2019). Radiosounding measurements are part of the IPEV/PNRA project “Routine Meteorological Observation” at Station Concordia (http://www.climantartide.it/index.php?lang=enea; Tomasi et al., 2011, last access: 27 May 2019). ECMWF data were acquired from https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era-interim (Dee et al., 2011, last access: 27 May 2019).
CB, HEB and SFBT designed and carried out the study. RR provided clear-sky data. GDN, LP and GB provided REFIR-PAD data. All co-authors contributed to the preparation of the article.
The authors declare that they have no conflict of interest.
The analysis was supported by the NERC-funded International Consortium for the Exploitation of Infrared Measurements of PolAr ClimaTe (ICE-IMPACT) project (grant NE/N01376X/1) and by the National Centre for Earth Observation, UK. The deployment of REFIR-PAD in Antarctica was supported by the Italian National Program for Research in Antarctica PNRA (Programma Nazionale di Ricerche in Antartide) under the following projects: 2009/A04.03, 2013/AC3.01 and 2013/AC3.06.
This research was supported by the NERC (grant no. NE/N01376X/1).
This paper was edited by Qiang Fu and reviewed by three anonymous referees.
Anderson, G., Clough, S., Kneizys, F., Chetwynd, J., and Shettle, E.: AFGL Atmospheric Constituent Profiles (0–120 km), Tech. Rep. AFGL-TR-86-0110, 1986. a
Baran, A. J., Hill, P., Furtado, K., Field, P., and Manners, J.: A Coupled Cloud Physics–Radiation Parameterization of the Bulk Optical Properties of Cirrus and Its Impact on the Met Office Unified Model Global Atmosphere 5.0 Configuration, J. Climate, 27, 7725–7752, https://doi.org/10.1175/JCLI-D-13-00700.1, 2014. a
Bellisario, C., Brindley, H. E., Murray, J. E., Last, A., Pickering, J., Harlow, R. C., Fox, S., Fox, C., Newman, S. M., Smith, M., Anderson, D., Huang, X., and Chen, X.: Retrievals of the Far Infrared Surface Emissivity Over the Greenland Plateau Using the Tropospheric Airborne Fourier Transform Spectrometer (TAFTS), J. Geophys. Res.-Atmos., 122, 12152–12166, https://doi.org/10.1002/2017JD027328, 2017. a
Bianchini, G., Palchetti, L., and Carli, B.: A wide-band nadir-sounding spectroradiometer for the characterization of the Earth's outgoing long-wave radiation, Proc. SPIE 6361, Sensors, Systems, and Next-Generation Satellites X, 63610A, https://doi.org/10.1117/12.689260, 2006. a, b
Bianchini, G., Palchetti, L., Muscari, G., Fiorucci, I., Di Girolamo, P., and Di Iorio, T.: Water vapor sounding with the far infrared REFIR-PAD spectroradiometer from a high-altitude ground-based station during the ECOWAR campaign, J. Geophys. Res.-Atmos., 116, d02310, https://doi.org/10.1029/2010JD014530, 2011. a
Canas, T. A., Murray, J. E., and Harries, J. E.: Tropospheric airborne Fourier transform spectrometer (TAFTS), in: Satellite Remote Sensing of Clouds and the Atmosphere II, edited by: Haigh, J. D., Proc. SPIE, 3220, 91–102, https://doi.org/10.1117/12.301139, 1997. a
Clerbaux, C., Boynard, A., Clarisse, L., George, M., Hadji-Lazaro, J., Herbin, H., Hurtmans, D., Pommier, M., Razavi, A., Turquety, S., Wespes, C., and Coheur, P.-F.: Monitoring of atmospheric composition using the thermal infrared IASI/MetOp sounder, Atmos. Chem. Phys., 9, 6041–6054, https://doi.org/10.5194/acp-9-6041-2009, 2009.. a
Clough, S., Shephard, M., Mlawer, E., Delamere, J., Iacono, M., Cady-Pereira, K., Boukabara, S., and Brown, P.: Atmospheric radiative transfer modeling: a summary of the AER codes, J. Quant. Spectrosc. Ra., 91, 233–244, https://doi.org/10.1016/j.jqsrt.2004.05.058, 2005. a
Cox, C. V., Murray, J. E., Taylor, J. P., Green, P. D., Pickering, J. C., Harries, J. E., and Last, A. E.: Clear-sky far-infrared measurements observed with TAFTS during the EAQUATE campaign, September 2004, Q. J. Roy. Meteor. Soc., 133, 273–283, https://doi.org/10.1002/qj.159, 2007. a
Cox, C. V., Harries, J. E., Taylor, J. P., Green, P. D., Baran, A. J., Pickering, J. C., Last, A. E., and Murray, J.: Measurement and simulation of mid- and far-infrared spectra in the presence of cirrus, Q. J. Roy. Meteor. Soc., 136, 718–739, https://doi.org/10.1002/qj.596, 2010. a, b
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011. a
Di Natale, G., Palchetti, L., Bianchini, G., and Del Guasta, M.: Simultaneous retrieval of water vapour, temperature and cirrus clouds properties from measurements of far infrared spectral radiance over the Antarctic Plateau, Atmos. Meas. Tech., 10, 825–837, https://doi.org/10.5194/amt-10-825-2017, 2017. a, b, c
Feldman, D. R., Collins, W. D., Pincus, R., Huang, X., and Chen, X.: Far-infrared surface emissivity and climate, P. Natl. Acad. Sci. USA, 111, 16297–16302, https://doi.org/10.1073/pnas.1413640111, 2014. a
Fox, C., Green, P. D., Pickering, J. C., and Humpage, N.: Analysis of far-infrared spectral radiance observations of the water vapor continuum in the Arctic, J. Quant. Spectrosc. Ra., 155, 57–65, https://doi.org/10.1016/j.jqsrt.2015.01.001, 2015. a
Green, P. D., Newman, S. M., Beeby, R. J., Murray, J. E., Pickering, J. C., and Harries, J. E.: Recent advances in measurement of the water vapour continuum in the far-infrared spectral region, Phil. T. Roy. Soc. Lond. A, 370, 2637–2655, https://doi.org/10.1098/rsta.2011.0263, 2012. a
Harries, J., Carli, B., Rizzi, R., Serio, C., Mlynczak, M., Palchetti, L., Maestri, T., Brindley, H., and Masiello, G.: The Far-infrared Earth, Rev. Geophys., 46, RG4004, https://doi.org/10.1029/2007RG000233, 2008. a
Huang, X., Yang, W., Loeb, N. G., and Ramaswamy, V.: Spectrally resolved fluxes derived from collocated AIRS and CERES measurements and their application in model evaluation: Clear sky over the tropical oceans, J. Geophys. Res.-Atmos., 113, d09110, https://doi.org/10.1029/2007JD009219, 2008. a, b, c
Huang, X., Cole, J. N. S., He, F., Potter, G. L., Oreopoulos, L., Lee, D., Suarez, M., and Loeb, N. G.: Longwave Band-By-Band Cloud Radiative Effect and Its Application in GCM Evaluation, J. Climate, 26, 450–467, https://doi.org/10.1175/JCLI-D-12-00112.1, 2013. a
Maestri, T., Rizzi, R., Tosi, E., Veglio, P., Palchetti, L., Bianchini, G., Girolamo, P. D., Masiello, G., Serio, C., and Summa, D.: Analysis of cirrus cloud spectral signatures in the far infrared, J. Quant. Spectrosc. Ra., 141, 49–64, https://doi.org/10.1016/j.jqsrt.2014.02.030, 2014. a, b
Maestri, T., Arosio, C., Rizzi, R., Palchetti, L., Bianchini, G., and Del Guasta, M.: Antarctic ice cloud identification and properties using downwelling spectral radiance from 100 to 1,400 cm−1, J. Geophys. Res.-Atmos., 124, 4761–4781, https://doi.org/10.1029/2018JD029205, 2019. a
Mast, J. C., Mlynczak, M. G., Cageao, R. P., Kratz, D. P., Latvakoski, H., Johnson, D. G., Turner, D. D., and Mlawer, E. J.: Measurements of downwelling far-infrared radiance during the RHUBC-II campaign at Cerro Toco, Chile and comparisons with line-by-line radiative transfer calculations, J. Quant. Spectrosc. Ra., 198, 25–39, https://doi.org/10.1016/j.jqsrt.2017.04.028, 2017. a
Mlynczak, M. G., Johnson, D. G., Latvakoski, H., Jucks, K., Watson, M., Kratz, D. P., Bingham, G., Traub, W. A., Wellard, S. J., Hyde, C. R., and Liu, X.: First light from the Far-Infrared Spectroscopy of the Troposphere (FIRST) instrument, Geophys. Res. Lett., 33, L07704, https://doi.org/10.1029/2005GL025114, 2006. a
Mlynczak, M. G., Cageao, R. P., Mast, J. C., Kratz, D. P., Latvakoski, H., and Johnson, D. G.: Observations of downwelling far-infrared emission at Table Mountain California made by the FIRST instrument, J. Quant. Spectrosc. Ra., 170, 90–105, https://doi.org/10.1016/j.jqsrt.2015.10.017, 2016. a
Palchetti, L., Bianchini, G., Di Natale, G., and Del Guasta, M.: Far-Infrared Radiative Properties of Water Vapor and Clouds in Antarctica, B. Am. Meteorol. Soc., 96, 1505–1518, https://doi.org/10.1175/BAMS-D-13-00286.1, 2015. a, b, c, d
Palchetti, L., Di Natale, G., and Bianchini, G.: Remote sensing of cirrus cloud microphysical properties using spectral measurements over the full range of their thermal emission, J. Geophys. Res.-Atmos., 121, 10804–10819, https://doi.org/10.1002/2016JD025162, 2016. a
Rizzi, R., Arosio, C., Maestri, T., Palchetti, L., Bianchini, G., and Guasta, M. D.: One year of downwelling spectral radiance measurements from 100 to 1400 cm−1 at Dome Concordia: Results in clear conditions, J. Geophys. Res.-Atmos., 121, 10937–10953, https://doi.org/10.1002/2016JD025341, 2016. a, b
Rizzi, R., Maestri, T., and Arosio, C.: Estimate of Radiosonde Dry Bias From Far-Infrared Measurements on the Antarctic Plateau, J. Geophys. Res.-Atmos., 123, 3205–3211, https://doi.org/10.1002/2017JD027874, 2018. a
Rothman, L. S., Gordon, I. E., Babikov, Y., Barbe, A., Chris Benner, D., Bernath, P. F., Birk, M., Bizzocchi, L., Boudon, V., Brown, L. R., Campargue, A., Chance, K., Cohen, E. A., Coudert, L. H., Devi, V. M., Drouin, B. J., Fayt, A., Flaud, J.-M., Gamache, R. R., Harrison, J. J., Hartmann, J.-M., Hill, C., Hodges, J. T., Jacquemart, D., Jolly, A., Lamouroux, J., Le Roy, R. J., Li, G., Long, D. A., Lyulin, O. M., Mackie, C. J., Massie, S. T., Mikhailenko, S., Müller, H. S. P., Naumenko, O. V., Nikitin, A. V., Orphal, J., Perevalov, V., Perrin, A., Polovtseva, E. R., Richard, C., Smith, M. A. H., Starikova, E., Sung, K., Tashkun, S., Tennyson, J., Toon, G. C., Tyuterev, V. G., and Wagner, G.: The HITRAN2012 molecular spectroscopic database, J. Quant. Spectrosc. Ra., 130, 4–50, https://doi.org/10.1016/j.jqsrt.2013.07.002, 2013. a
Tomasi, C., Petkov, B., Benedetti, E., Valenziano, L., and Vitale, V.: Analysis of a 4 year radiosonde data set at Dome C for characterizing temperature and moisture conditions of the Antarctic atmosphere, J. Geophys. Res.-Atmos., 116, d15304, https://doi.org/10.1029/2011JD015803, 2011. a
Turner, D. and Mlawer, E.: The Radiative Heating in Underexplored Bands Campaigns, B. Am. Meteorol. Soc., 91, 911–923, https://doi.org/10.1175/2010BAMS2904.1, 2010. a
Turner, E. C., Lee, H.-T., and Tett, S. F. B.: Using IASI to simulate the total spectrum of outgoing long-wave radiances, Atmos. Chem. Phys., 15, 6561–6575, https://doi.org/10.5194/acp-15-6561-2015, 2015. a, b, c
Wielicki, B. A., Barkstrom, B. R., Harrison, E. F., III, R. B. L., Smith, G. L., and Cooper, J. E.: Clouds and the Earth's Radiant Energy System (CERES): An Earth Observing System Experiment, B. Am. Meteorol. Soc., 77, 853–868, https://doi.org/10.1175/1520-0477(1996)077<0853:CATERE>2.0.CO;2, 1996. a
Yang, P., Mlynczak, M. G., Wei, H., Kratz, D. P., Baum, B. A., Hu, Y. X., Wiscombe, W. J., Heidinger, A., and Mishchenko, M. I.: Spectral signature of ice clouds in the far-infrared region: Single-scattering calculations and radiative sensitivity study, J. Geophys. Res.-Atmos., 108, 4569, https://doi.org/10.1029/2002JD003291, 2003. a