the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Estimation of rate coefficients and branching ratios for reactions of organic peroxy radicals for use in automated mechanism construction
Michael E. Jenkin
Richard Valorso
Bernard Aumont
Andrew R. Rickard
Organic peroxy radicals (RO2), formed from the degradation of hydrocarbons and other volatile organic compounds (VOCs), play a key role in tropospheric oxidation mechanisms. Several competing reactions may be available for a given RO2 radical, the relative rates of which depend on both the structure of RO2 and the ambient conditions. Published kinetics and branching ratio data are reviewed for the bimolecular reactions of RO2 with NO, NO2, NO3, OH and HO2; and for their self-reactions and cross-reactions with other RO2 radicals. This information is used to define generic rate coefficients and structure–activity relationship (SAR) methods that can be applied to the bimolecular reactions of a series of important classes of hydrocarbon and oxygenated RO2 radicals. Information for selected unimolecular isomerization reactions (i.e. H-atom shift and ring-closure reactions) is also summarized and discussed. The methods presented here are intended to guide the representation of RO2 radical chemistry in the next generation of explicit detailed chemical mechanisms.
- Article
(1832 KB) - Companion paper 1
- Companion paper 2
-
Supplement
(1790 KB) - BibTeX
- EndNote
Organic peroxy radicals (RO2) are important intermediates in the tropospheric degradation of hydrocarbons and other volatile organic compounds (VOCs). It is well established that their chemistry plays a key role in the mechanisms that generate ozone (O3), secondary organic aerosol (SOA) and other secondary pollutants (e.g. Lightfoot et al., 1992; Jenkin and Clemitshaw, 2000; Tyndall et al., 2001; Archibald et al., 2009; Orlando and Tyndall, 2012; Ehn et al., 2017), and rigorous representation of their chemistry is therefore essential for chemical mechanisms used in chemistry-transport models. As discussed in the preceding papers in this series (Jenkin et al., 2018a, b), they are formed rapidly and exclusively from the reactions of O2 with the majority of carbon-centred organic radicals (R) (Reaction R1), these in turn being produced from the reactions that initiate VOC degradation (e.g. reaction with OH radicals), or from other routes such as decomposition of larger oxy radicals (M denotes a third body, most commonly N2 or O2 under atmospheric conditions):
Under tropospheric conditions, a given RO2 radical may have several competing reactions available, the relative rates of which are dependent both on the prevailing ambient conditions and on the structure of RO2. These include a series of bimolecular reactions (i.e. with NO, NO2, NO3, OH and HO2; and the self-reaction and cross-reactions with the multitude of other RO2 radicals present in the atmosphere), which are generally available for all RO2 radicals; and specific unimolecular isomerization reactions (i.e. H-atom shift or ring-closure reactions) that are potentially available for some classes of RO2.
The propagating channel of the reaction of RO2 with NO (Reaction R2a) plays a key role in tropospheric O3 formation, through oxidizing NO to NO2, and also usually represents the major reaction for RO2 radicals under comparatively polluted conditions:
The efficiency of this reaction is influenced by the relative importance of the other reactions available for a given RO2 radical. The contribution of the terminating channel of the reaction of RO2 with NO (forming an organic nitrate product, RONO2) depends on the structure and size of RO2; and the reaction of NO2 with selected RO2 radicals forms stable peroxynitrate products, ROONO2. The formation, transport and degradation of these oxidized organic nitrogen reservoirs from the RO2+NO and RO2+NO2 reactions has potential impacts in a number of ways, ranging from the inhibition of O3 formation on local/regional scales to influencing the global budget and distribution of NOx and O3 (e.g. Perring et al., 2013). The reactions of RO2 radicals with NO3 primarily play a role during the nighttime in moderately polluted air, providing a radical propagation route that potentially supplements nighttime chain oxidation processes (e.g. Carslaw et al., 1997; Bey et al., 2001a, b; Geyer et al., 2003; Walker et al., 2015).
The reactions with OH, HO2 and the pool of RO2 radicals gain in importance as the availability of NOx becomes more limited, and therefore also inhibit O3 formation by competing with Reaction (R2a). In many cases, the reactions are significantly terminating and collectively make a major contribution to controlling atmospheric free radical concentrations under NOx-limited conditions, although the branching ratios for the propagating and terminating reaction channels depend on the structure of RO2. For some classes of RO2, unimolecular isomerization reactions can compete with (or dominate over) the bimolecular reactions. These reactions therefore potentially play an important role in HOx radical recycling under NOx-limited conditions, and in rapid chain oxidation mechanisms generating highly oxidized multifunctional molecules, HOMs (e.g. Peeters et al., 2009, 2014; Crounse et al., 2013; Ehn et al., 2014, 2017; Jokinen et al., 2014; Rissanen et al., 2015; Bianchi et al., 2019). The relative contributions of the various reactions available for RO2 thus influence the distribution and functional group content of the oxidized products formed, and their physicochemical properties (e.g. volatility and solubility), and therefore the SOA formation propensity of the chemistry.
In this paper, published data on the kinetics and branching ratios for the above bimolecular reactions of hydrocarbon and oxygenated RO2 radicals are reviewed and discussed. Preliminary information is also presented for selected unimolecular isomerization reactions, which continue to be considered in ongoing work. The information on bimolecular reactions is used to define and document a set of rules and structure–activity relationship (SAR) methods (a chemical protocol) to guide the representation of the RO2 reactions in future detailed chemical mechanisms (Vereecken et al., 2018). In particular, the methods presented below are being used to design the next generation of explicit mechanisms based on the Generator for Explicit Chemistry and Kinetics of Organics in the Atmosphere, GECKO-A (Aumont et al., 2005), and the Master Chemical Mechanism, MCM (Saunders et al., 2003). Application of the methods is illustrated with examples in the supporting information provided in the Supplement.
2.1 The reactions of RO2 with NO
2.1.1 Kinetics
Rate coefficients for the reactions of NO with a variety of specific hydrocarbon and oxygenated RO2 radicals have been reported, as summarized in Table 1. For the vast majority of the RO2 radicals formed in detailed mechanisms, however, kinetic data are unavailable and it is therefore necessary to assign generic rate coefficients based on the reported data.
Table 1Kinetic data for the reactions of hydrocarbon and oxygenated peroxy radicals with NO. Where available, the temperature dependence is given by .
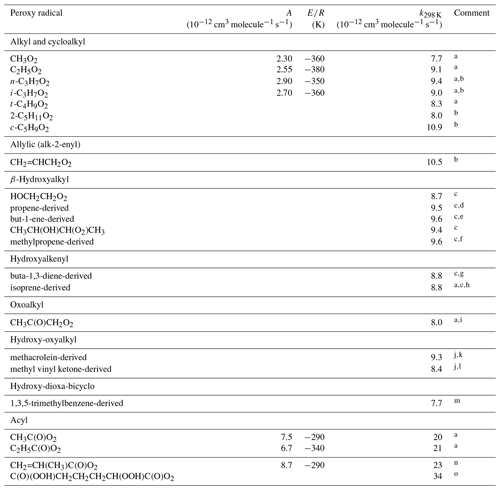
Comments: a IUPAC Task Group recommendation (http://iupac.pole-ether.fr/, last access: January 2019). b Based on Eberhard and Howard (1996, 1997), Eberhard et al. (1996). c Based on Miller et al. (2004). d Mixture of CH2(OH)CH(O2)CH3 and CH2(O2)CH(OH)CH3. e Mixture of CH2(OH)CH(O2)C2H5 and CH2(O2)CH(OH)C2H5. f Mixture of CH2(OH)C(O2)(CH3)2 and CH2(O2)C(OH)(CH3)2. g Mixture of CH2(OH)CH(O2)CH=CH2, CH2(OH)CH=CHCH2O2 and CH2(O2)CH(OH)CH=CH2. h Mixture of CH2(OH)C(O2)(CH3)CH=CH2, CH2(OH)C(CH3)=CHCH2O2, CH2(O2)C(CH3)(OH)CH=CH2, CH2(OH)CH(O2)C(CH3)=CH2, CH2(OH)CH=C(CH3)CH2O2 and CH2(O2)CH(OH)C(CH3)=CH2. i Based on Sehested et al. (1998). j Based on Hsin and Elrod (2007). k Mixture of CH2(OH)C(O2)(CH3)CHO and CH2(O2)C(OH)(CH3)CHO. l Mixture of CH2(OH)CH(O2)C(=O)CH3 and CH2(O2)CH(OH)C(=O)CH3. m Elrod (2011). Mixture of two complex radicals of molecular formula HOC9H12[OO]O2, although with one isomer likely dominant. n De Gouw and Howard (1997). o Berndt et al. (2015). Inferred to be the complex oxo-di-hydroperoxy acyl peroxy radical shown, on the basis of its molecular mass and a proposed mechanism.
For acyl peroxy radicals (i.e. of structure RC(O)O2), a generic rate coefficient (kAPNO) is applied:
This is based on the IUPAC Task Group1 recommendation for the reaction of NO with CH3C(O)O2. As shown in Table 1, this is also close to the rate coefficients recommended for the less studied acyl peroxy radicals, C2H5C(O)O2 and CH2=CH(CH3)C(O)O2. The 298 K value reported for C(O)(OOH)CH2CH2CH2CH(OOH)C(O)O2 (Berndt et al., 2015) is also broadly consistent with kAPNO, although further studies of highly oxygenated acyl peroxy radicals would help to establish the effects of additional substituent groups.
For other classes of hydrocarbon and oxygenated peroxy radical, a generic rate coefficient () is applied:
The value of at 298 K ( cm3 molecule−1 s−1) is based on a rounded average of the 298 K rate coefficients listed for the ≥C2 alkyl, cycloalkyl, hydroxyalkyl, hydroxyalkenyl, oxoalkyl, hydroxy-oxyalkyl and hydroxy-dioxa-bicyclo RO2 radicals in Table 1, which show no significant trends related to the identity and structure of R. The temperature dependence is similarly based on the rounded average of the available values within this group, which are limited to those for C2H5O2, n-C3H7O2 and i-C3H7O2. In practice, the preferred values for all the ≥C2 (non-acyl) RO2 radicals in Table 1 are also equivalent to within the reported uncertainties, such that the generic rate coefficient can reasonably be applied for simplicity in all cases except CH3O2. Although derived from a more extensive dataset, the expression for in Eq. (2) is identical to that recommended previously by Atkinson (1997).
2.1.2 Product branching ratios
The following channels are considered for the reactions of RO2 with NO:
It is well established that the branching ratio for alkyl peroxy radicals depends on temperature, pressure, and the size and degree of substitution of the peroxy radical (e.g. Carter and Atkinson, 1989; Arey et al., 2001; Yeh and Ziemann, 2014a). The branching ratio has also been reported to be influenced by the presence of oxygenated substituents, with most systematic information reported for β- and δ-hydroxy groups (e.g. O'Brien et al., 1998; Matsunga and Ziemann, 2009, 2010; Yeh and Ziemann, 2014b; Teng et al., 2015).
The fraction of the reaction forming a nitrate product (RONO2) via the terminating channel, , is calculated following the method originally reported for secondary alkyl peroxy radicals by Carter and Atkinson (1989), and subsequently updated by Arey et al. (2001) and Teng et al. (2015). Based on this method, the reference branching ratio for secondary alkyl peroxy radicals, , is calculated as follows.
with , , F=0.41 and . Variable nCON is the number of carbon, oxygen and nitrogen atoms in the organic group (R) of the peroxy radical (i.e. excluding the peroxy radical oxygen atoms and equivalent to the carbon number in alkyl peroxy radicals), T is the temperature (in kelvin) and [M] is the gas density (in molecule cm−3).
The fractions of the reaction proceeding via the terminating channel, R2b, and the propagating channel, R2a (), for a specific peroxy radical are then given by
The effect of the degree of substitution (i.e. whether the radical is primary, secondary or tertiary) is described by fa, with a unity value applied to secondary peroxy radicals by definition. A further scaling factor, fb, is used to describe systematic variations in the yields of RONO2 resulting from the presence of oxygenated substituents (e.g. the effect of hydroxyl substituents, as indicated above), or for specific peroxy radical classes, with a value of fb being required to account for the effect of each relevant substituent. The applied values of fa and fb are summarized in Tables 2 and 3, and example calculations are provided in Sect. S1 in the Supplement.
Table 2Values of the scaling factor, fa, applied to the branching ratio calculation for the reaction of RO2 with NO.
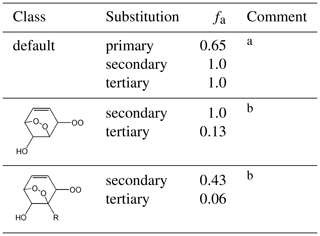
Comments: a Applied in all cases, except for those covered by comment b. fa=1 for secondary peroxy radicals by definition. The equivalent value for tertiary peroxy radicals, and the lower value for primary peroxy radicals, is based on a consensus of information from Cassanelli et al. (2007), Orlando and Tyndall (2012) and Teng et al. (2015) and on previous consideration of the OH + isoprene system (Jenkin et al., 2015); b Inhibition of nitrate formation has been reported for complex hydroxy-dioxa-bicyclo peroxy radicals derived from aromatics, relative to comparably sized alkyl peroxy radicals by Rickard et al. (2010) and Elrod (2011), with a particular impact from the presence of alkyl substituents reported by Elrod (2011). The reduced values of fa for tertiary peroxy radicals, and the general reduction in fa for peroxy radicals with a neighbouring alkyl substituent (as shown), is inferred from the trend in nitrate yields reported for benzene, toluene, p-xylene and 1,3,5-trimethylbenzene by Elrod (2011).
Table 3Values of the scaling factor, fb, applied to the branching ratio calculation for the reaction of RO2 with NOa.
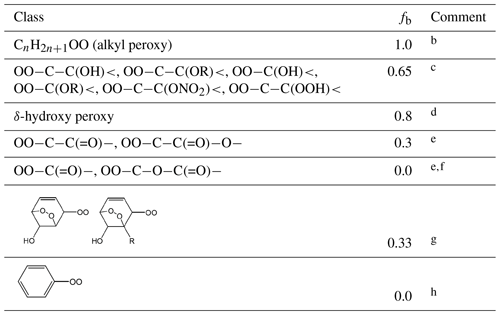
Comments: a A value of fb needs to be applied to account for the effect of each relevant substituent (see Sect. S1 in the Supplement for further information). b fb=1 for alkyl peroxy radicals, by definition, and also used as a default in all cases other than those covered by comments . c Based on a compromise of information from Matsunaga and Ziemann (2009, 2010), Yeh and Ziemann (2014b) and Teng et al. (2015) for β-hydroxy substituents, but also taking account of information reported for a number of other oxygenated systems (e.g. Tuazon et al., 1998a; Crounse et al., 2012; Lee et al., 2014) and previous consideration of the OH + isoprene system (Jenkin et al., 2015). < assumed to be in this category by analogy. d Based on the relative impacts of β-OH and δ-OH substituents reported by Yeh and Ziemann (2014a) and previous consideration of the OH + isoprene system (Jenkin et al., 2015). e fb value for informed by reported studies of ketone oxidation (Lightfoot et al., 1992; Praske et al., 2015); fb values for and informed by reported studies of ester and dibasic ester oxidation (Tuazon et al., 1998b, 1999; Cavalli et al., 2001; Picquet-Varrault et al., 2001, 2002; Pimentel et al., 2010). f fb=0 for is based on the general lack of observation of acyl nitrate products in systems where acyl peroxy radicals are formed. g Value set to recreate the hydroxy-dioxa-bicyclo nitrate yield reported for benzene by Elrod (2011); In conjunction with the values of fa in Table 2, this also allows a consistent representation of the yields in the toluene, p-xylene and 1,3,5-trimethylbenzene systems (Elrod, 2011; Rickard et al., 2010); h fb=0 for phenyl (and other aryl) peroxy radicals is based on the general lack of observation of aryl nitrate products during the oxidation of aromatic hydrocarbons.
It is also recognized that reaction channel (R2a) is significantly exothermic, such that prompt decomposition or isomerization of a fraction of the initially formed chemically activated oxy radicals has been reported to occur in some cases; with the remainder being collisionally deactivated to form thermalized RO (e.g. Orlando et al., 2003; Calvert et al., 2015). This is particularly important for β-hydroxy-oxy radicals (e.g. Orlando et al., 1998; Vereecken et al., 1999; Vereecken and Peeters, 1999; Caralp et al., 2003) and some other oxygenated oxy radicals (e.g. Christensen et al., 2000; Orlando et al., 2000a; Wallington et al., 2001). The contributions and treatment of these reactions is summarized in Sect. S2.
2.2 The reaction of RO2 with NO2
The reactions of RO2 with NO2 have generally been reported to proceed via a reversible association reaction in each case to form a peroxy nitrate (ROONO2):
Rate coefficients for the forward and reverse reactions for a number of RO2 radicals are summarized in Table 4. Those for CH3O2 and C2H5O2 – and for the two simplest acyl peroxy radicals, CH3C(O)O2 and C2H5C(O)O2 – are based on (or informed by) the IUPAC Task Group recommendations, and describe the pressure and temperature dependences of the reactions. In all other cases, the reactions are assumed to be at the high-pressure limit under atmospheric conditions, and generic parameters are applied. The parameters kf PN and kb PN (given in Table 4) can reasonably be applied to reactions involving non-acyl peroxy radicals, being based on the high-pressure limiting rate coefficients (k∞) for the forward and reverse reactions of C2H5O2 and those reported for a number of higher alkyl peroxy radicals at close to atmospheric pressure (see Table 4 comments). This assumption is also broadly consistent with the limited information available for the forward or reverse reactions of other non-acyl oxygenated peroxy radicals (e.g. Orlando and Tyndall, 2012). In practice, however, these reactions are often omitted from atmospheric chemical mechanisms, owing to the instability of the ROONO2 products under lower tropospheric conditions (lifetime ≈0.2 s at 298 K). As a result, only the formation and decomposition of methyl peroxy nitrate, CH3OONO2, from the most abundant non-acyl peroxy radical, CH3O2, have previously been represented in the MCM (Saunders et al., 2003). This approach remains advocated here for application for lower tropospheric conditions.
Table 4Rate coefficients for the reactions of hydrocarbon and oxygenated RO2 radicals with NO2 and for the reverse decomposition of the RO2NO2 products. Generic rate coefficients for specified RO2 classes are shown in bold font.

Comments: a Rate coefficient for a pressure-dependent reaction is calculated using the expression: , where log and N=[0.75–1.27 log10(Fc)] (see http://iupac.pole-ether.fr/, last access: January 2019); b Based on the evaluation of Golden (2005); c Recommended by the IUPAC Task Group (http://iupac.pole-ether.fr/, last access: January 2019); d Reported by McKee et al. (2016) for a mixture of n-C4H9O2 and sec-C4H9O2 formed from reaction of Cl with butane; e Pressure-independent generic rate coefficient. f k∞ assumed equivalent to that for CH3C(O)O2+NO2 reaction. k0 scaled relative to that for CH3C(O)O2 to preserve the C2H5C(O)O2+NO2 ⇌ C2H5C(O)OONO2 equilibrium constant, kf∕kb, over the pressure range 100–760 Torr. Fc is equivalent to that recommended for kb. g Forward reaction rate coefficient, kf PAN, is based on k∞ for the CH3C(O)O2+NO2 reaction. h Based on Zabel et al. (1989), as recommended by Lightfoot et al. (1992), for isomeric mixtures formed from reactions of Cl with butane, hexane or octane. Assumed to be at high-pressure limit at 800 Torr. i kb PN is rounded average of the reported rate coefficients for C2-C8 alkyl peroxy radicals. j Based on Roberts and Bertman (1992). Assumed to be at high-pressure limit at 760 Torr. k kb PAN, is based on a value of s−1 at 298 K, which is the average of those reported for n-C3H7C(O)OONO2, n-C4H9C(O)OONO2 and n-C5H11C(O)OONO2 (Kabir et al., 2014) and CH2=C(CH3)C(O)O2 (Roberts and Bertman, 1992) (see Fig. 1). E∕R is based on the average of the high-pressure limit values for CH3C(O)O2NO2, C2H5C(O)O2NO2 and CH2=C(CH3)C(O)O2, and also consistent with the approximate value for n-C5H11C(O)OONO2 (Kabir et al., 2014). l Pressure-independent generic rate coefficient for thermal decomposition of ROC(O)O2 is a factor of 2 greater, based on data for CH3OC(O)O2 and C6H5OC(O)O2 (Kirchner et al., 1999), with reduced thermal stability also consistent with data for C2H5OC(O)O2 (Bossolasco et al., 2011).
Table 5Kinetic data for the reactions of alkyl and oxygenated peroxy radicals with NO3. Where available, the temperature dependence is given by .

Comments: a IUPAC Task Group recommendation (http://iupac.pole-ether.fr/, last access: January 2019). b k298 K based on an average of the values reported by Biggs et al. (1995), Ray et al. (1996), Vaughan et al. (2006) and Laversin et al. (2016). E∕R taken from Laversin et al. (2016). c Taken from Vaughan et al. (2006). d Taken from Kalalian et al. (2018). e Taken from Doussin et al. (2003). Canosa-Mas et al. (1996) reported a comparable value of cm3 molecule−1 s−1 over the range 403–443 K.
The reactions are generally represented for acyl peroxy radicals, for which the product peroxyacyl nitrates, RC(O)OONO2, are particularly stable (lifetime ≈40–50 min at 298 K). The generic parameters, kf PAN and kb PAN, are applied in the majority of cases (see Table 4). As shown in Fig. 1, larger acyl peroxy radicals have been reported to be slightly more stable than those derived from CH3C(O)O2 and C2H5C(O)O2 (Roberts and Bertman, 1992; Kabir et al., 2014), and the assigned value of kb PAN is consistent with the data for the larger species.
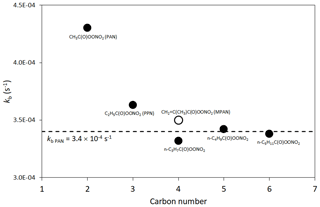
Figure 1Reported thermal decomposition rates of selected peroxyacyl nitrates at 298 K and 760 Torr. Values for PAN, PPN and MPAN (defined in the figure) are the IUPAC Task Group recommendations (http://iupac.pole-ether.fr/, last access: January 2019). The other values are taken from the systematic study of Kabir et al. (2014), which also reports consistent values for PAN and PPN. The broken line is the generic rate coefficient, kb PAN, for the decomposition of RC(O)OONO2 structures (see Sect. 2.2 and Table 4).
Reported data for CH3OC(O)O2, C6H5OC(O)O2 and C2H5OC(O)O2 (Kirchner et al., 1999; Bossolasco et al., 2011) indicate a reduced thermal stability of peroxyacyl nitrates derived from formate esters, and an increased decomposition rate (2×kb PAN) is therefore applied to ROC(O)OONO2 species in general.
In a limited number of cases, the reaction of RO2 with NO2 has been reported to oxidize NO2 to NO3 in an irreversible reaction:
These cases include HC(O)C(O)O2 (Orlando and Tyndall, 2001), CH3C(O)C(O)O2 (Jagiella and Zabel, 2008) and the phenylperoxy radical, C6H5O2 (Jagiella and Zabel, 2007). Reaction (R3b) is therefore applied generally to HC(O)C(O)O2, RC(O)C(O)O2, C6H5O2 and other aryl peroxy radicals, using the generic rate coefficient kf PAN.
2.3 The reaction of RO2 with NO3
On the basis of reported information for CH3O2 and C2H5O2 (e.g. Biggs et al., 1995; Kukui et al., 1995), the reactions of RO2 with NO3 are assumed to proceed via a single channel in each case as follows:
Reported rate coefficients are summarized in Table 5. The reaction of C2H5O2 with NO3 is the most studied, with consistent 298 K rate coefficients reported in a number of studies (Biggs et al., 1995; Ray et al., 1996; Vaughan et al., 2006; Laversin et al., 2016) and with the temperature dependence systematically investigated (Laversin et al., 2016). The corresponding parameters in Table 5 therefore form the basis of a generic rate coefficient for the reactions of non-acyl peroxy radicals with NO3:
Within the reported uncertainties, the value of the rate coefficient at 298 K is consistent with that for c-C6H11O2 and with the approximate value for c-C5H9O2 reported by Vaughan et al. (2006); and the temperature dependence expression for is consistent with those reported for the oxygenated primary peroxy radicals, (CH3)2C(OH)CH2O2, CH3OCH2O2 and CH3C(O)CH2O2, by Kalalian et al. (2018). is therefore currently considered appropriate for application to all ≥C2 non-acyl peroxy radicals. For CH3O2, the reaction has been well studied at 298 K, and the value in Table 5 is applied in conjunction with the pre-exponential factor, leading to
The generic rate coefficient for acyl peroxy radicals is based on data for CH3C(O)O2, which have been shown to react slightly more rapidly with NO3 (Canosa-Mas et al., 1996; Doussin et al., 2003). The value at 298 K in Table 5 (based on that reported by Doussin et al., 2003) is once again applied in conjunction with the pre-exponential factor, leading to
The resultant weak temperature dependence yields a value of in the range 403–443 K that is fully consistent with that reported by Canosa-Mas et al. (1996).
2.4 The reaction of RO2 with OH
Kinetics determinations have been reported for the reactions of OH with C1–C4 alkyl peroxy radicals. As shown in Table 6, these reactions are reported to occur rapidly at room temperature, with the rate coefficients for all the reactions being essentially equivalent at 298 K, within the reported uncertainties. Based on the study by Yan et al. (2016), a weak temperature dependence is recommended for the reaction of CH3O2 with OH, and the resultant expression,
is also adopted in the present work as a generic rate coefficient for the reactions of RO2 with OH.
Table 6Kinetic data for the reactions of peroxy radicals with OH. Where available, the temperature dependence is given by .

Comments: a IUPAC Task Group recommendation (http://iupac.pole-ether.fr/, last access: January 2019) based on Assaf et al. (2016) and Yan et al. (2016) with an uncertainty factor of 2 assigned to k298 K; b IUPAC Task Group recommendation (http://iupac.pole-ether.fr/, last access: January 2019) based on Faragó et al. (2015) with an uncertainty factor of 1.6 assigned to k298 K. A consistent value of cm3 molecule−1 s−1 has more recently been reported by Assaf et al. (2017b); c Global rate coefficients, and ( cm3 molecule−1 s−1, reported by Assaf et al. (2017b) for isomeric mixtures of peroxy radicals formed from reactions of Cl atoms with propane and butane, respectively.
The following product channels are considered, but with their branching ratios being strongly dependent on the size of R:
In their theoretical studies of the reaction of CH3O2 with OH, Bian et al. (2015), Müller et al. (2016) and Assaf et al. (2018) calculated reaction channel (R5a) to be the most favourable, with experimental confirmation of a dominant contribution from this channel reported for CH3O2 by Assaf et al. (2017a, 2018). A number of alternative channels have been considered in modelling assessments (e.g. Archibald et al., 2009), including formation of CH2O2 and H2O or CH3OH and O2. However, no evidence for formation of CH2O2 and H2O has been observed at room temperature, indicating that this product channel is at most minor (<5 %) (Yan et al., 2016; Assaf et al., 2017a; Caravan et al., 2018); this is also consistent with theoretical data (e.g. Müller et al., 2016). The formation of CH3OH and O2 via channel (R5b) has been shown to make a minor contribution (6 %– 9 %) in the experimental study of Caravan et al. (2018), consistent with the theoretical estimate of ∼7 % by Müller et al. (2016). It is noted that Caravan et al. (2018) also reported evidence for minor CH3OOOH formation at atmospheric pressure, via channel (R5c); although this was calculated to be formed with a low yield (1.7 %) by Assaf et al. (2018). As a result, values of and are currently assigned to the reaction of CH3O2 with OH in the present work.
The experimental and theoretical study of Assaf et al. (2018) for a series of C1–C4 alkyl peroxy radicals has demonstrated that the reaction can more generally be regarded as proceeding by either channel (R5a) or (R5c). Formation of the thermalized hydrotrioxide, ROOOH, via channel (R5c) was found to be increasingly important for the larger RO2. Based approximately on their theoretical calculations for 298 K and 1 atm of pressure, k5c∕k5 is thus currently assigned a value of 0.0 for CH3O2, 0.8 for RO2 for which nCON=2 (e.g. C2H5O2 and HOCH2O2) and 1.0 for all other RO2 radicals. In the nCON=2 case, the balance of the reaction is assigned to channel (R5a), i.e. with . As discussed by Assaf et al. (2018), detailed experimental and theoretical studies of the atmospheric fate of ROOOH are therefore clearly required for the effect of the RO2+OH reaction to be fully assessed and represented. A provisional treatment is provided in Sect. S3, based mainly on rate coefficients reported in the theoretical studies of Müller et al. (2016), Assaf et al. (2018) and Anglada and Solé (2018).
2.5 The reaction of RO2 with HO2
2.5.1 Kinetics
Rate coefficients for the reactions of HO2 with a variety of specific hydrocarbon and oxygenated RO2 radicals have been reported, as summarized in Table 7. For the vast majority of the RO2 radicals formed in detailed mechanisms, however, kinetic data are unavailable, and it is therefore necessary to assign generic rate coefficients based on the reported data.
Table 7Kinetic data for the reactions of hydrocarbon and oxygenated peroxy radicals with HO2. Where available, the temperature dependence is given by .
Comments: a IUPAC Task Group recommendation (http://iupac.pole-ether.fr/, last access: January 2019). b Based on Rowley et al. (1992a, b) and Boyd et al. (2003a). c Taken from Boyd et al. (2003a). d Mixture of C10H21O2 radicals derived from the reaction of OH with decane. e Mixture of C14H29O2 radicals derived from the reaction of OH with tetradecane. f Approximate value from Boyd et al. (1996a), based on extrapolation of higher temperature data (393–426 K) using assumed value of K. g Taken from Jenkin and Hayman (1995). h Derived from the reaction of OH with cyclohexene. RO2 population dominated by β-hydroxy peroxy radical, HO-c-C6H10-O2, formed from OH addition. i RO2 population dominated by hydroxy peroxy radicals formed from OH addition to the given monoterpene. j Mixture of HOC5H8O2 radicals derived from the reaction of OH with isoprene. k Approximate value from Jenkin et al. (1993a), based on steady state concentration of HO2 formed from the self-reaction of CH3OCH2O2 during modulated photolysis. l Based on Bridier et al. (1993). m k298 K based on Groß et al. (2014), Winiberg et al. (2016) and Hui et al. (2019). E∕R based on Hui et al. (2019) (see Sect. S4). n Based on Roth et al. (2010).
As discussed previously (Jenkin et al., 1997; Saunders et al., 2003; Boyd et al., 2003a; Orlando and Tyndall, 2012; Wennberg et al., 2018), the 298 K rate coefficients tend to increase with the size of the organic group. Figure 2 shows the data plotted as a function of nCON. The data for alkyl peroxy radicals and β-hydroxyalkyl peroxy radicals (the most systematically studied groups) show comparable values across the nCON range. Based on optimization to these data, the following expression is derived for application to non-acyl peroxy radicals:
The temperature dependence is typical of that reported for >C2 alkyl and β-hydroxy RO2 radicals and remains unchanged from that applied previously by Saunders et al. (2003).
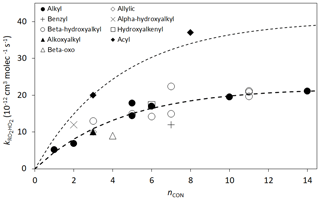
Figure 2Rate coefficients for the reactions of various classes of RO2 radicals with HO2 as a function of nCON at 298 K. The heavy broken line is the best fit to the data for alkyl and β-hydroxyalkyl RO2 on the basis of the assumed function . The light broken line is the same function with the 298 K value of k increased by a factor of 1.84 (see Sect. 2.5).
Based on the limited data for acyl peroxy radicals (see Fig. 2 and Table 7), and specifically that for CH3C(O)O2, the 298 K rate coefficients are assigned values that are almost a factor of 2 greater than those defined by Eq. (9). The temperature dependences reported for acyl peroxy radicals appear to be weaker than those for similar-sized radicals in other classes, and the temperature coefficient is again based on that recommended for CH3C(O)O2. The following expression is therefore assigned to acyl peroxy radicals:
2.5.2 Product branching ratios
On the basis of reported information, the following channels are considered for the reactions of RO2 with HO2:
Formation of a hydroperoxide product (ROOH) and O2 via terminating channel (R6a) is reported to be dominant for reactions of alkyl peroxy radicals, and this is also taken to be the default where no information is available (see Table 8). However, the reactions of HO2 with oxygenated peroxy radicals have received considerable attention and evidence has been reported for several additional channels leading to both radical termination, Reactions (R6b) and (R6c), and radical propagation, Reactions (R6d) and (R6e). Table 8 summarizes the 298 K branching ratios that are applied to several classes of oxygenated peroxy radical based on reported information.
Table 8Branching ratios assigned to reaction channels (R6a)–(R6e) for reactions of hydrocarbon and oxygenated peroxy radical classes with HO2 at 298 K.
Comments: a Based on studies of CH3O2 and C2H5O2 (as summarized by Orlando and Tyndall, 2012), and also used as a default in all cases other than those covered by comments . b Based on studies of CH3C(O)O2 (Niki et al., 1985; Horie and Moortgat, 1992; Hasson et al., 2004; Jenkin et al., 2007; Dillon and Crowley, 2008; Groß et al., 2014; Winiberg et al., 2016; Hui et al., 2019); see Sect. S4. Hasson et al. (2012) also reported broadly comparable branching ratios for C2H5C(O)O2 and C3H7C(O)O2. c Based on studies of C6H5C(O)O2. k6d∕k6 based on Dillon and Crowley (2008) and Roth et al. (2010), with other branching ratios based on those reported by Roth et al. (2010). d Based on studies of CH3C(O)CH2O2 (Jenkin et al., 2008; Dillon and Crowley, 2008; Hasson et al., 2012). e Based on studies of CH3C(O)CH(O2)CH3 (Dillon and Crowley, 2008; Hasson et al., 2012) and of CH3C(O)CH(O2)CH2OH Praske et al. (2015). Praske et al. (2015) also reported possible minor contribution of channel (R6e) and/or (R6c) for CH3C(O)CH(O2)CH2OH. f Based on studies of HOCH2O2 (Jenkin et al., 2007) and CH3OCH2O2 (Jenkin et al., 2010). Contribution of OH formation in those studies was originally attributed to channel (R6d), but is allocated here to channel (R6e) on the basis of the theoretical study of Nguyen et al. (2010). g Full reaction is assigned to channel (R6a), because channels (R6c) and (R6e) are unavailable for tertiary radicals owing to the absence of an α-H atom. h Based on study of hydroxyallylic peroxy radicals formed in isoprene system by Liu et al. (2013), with support from the studies of Paulot et al. (2009) and Navarro et al. (2013). i Based on study of nitrooxyallylic radicals formed in isoprene system by Schwantes et al. (2015).
The temperature dependences of the reaction channels have generally not been studied, and the branching ratios in Table 8 are thus applied independent of temperature in most cases. The only exception is the reaction of HO2 with (non-aryl) acyl peroxy radicals. This class of reaction (in particular the reaction of HO2 with CH3C(O)O2) has received the most attention and is also a class for which radical propagation is reported to be particularly important at temperatures near 298 K. As shown in Table 8, channels (R6a), (R6b) and (R6d) are reported to contribute. The temperature dependence of k6d∕k is based on the recent study of the CH3C(O)O2 + HO2 reaction reported by Hui et al. (2019). The contributions and temperature dependences of k6a∕k and k6b∕k also take account of the wider database for the same reaction, in particular the experimental characterization of k6a∕k6b reported by Horie and Moortgat (1992). This procedure (described in detail in Sect. S4) results in the following fitted Arrhenius expressions for the individual channel rate coefficients:
The corresponding temperature dependences of the channel rate coefficients, derived from the CH3C(O)O2 data, are thus applied to all (non-aryl) acyl peroxy radicals. The variation of the branching ratios and channel rate coefficients are illustrated for the CH3C(O)O2 + HO2 reaction in Figs. S2 and S3 for the 230–300 K temperature range. Summation of the channel rate coefficients given in Eqs. (11)–(13) reproduces the values of calculated for the overall reaction using Eq. (10) to within 5 % over this temperature range (see Sect. S4 for further details).
2.6 The permutation reactions of RO2
The “permutation” reactions of a given RO2 radical are its self-reactions (R7) and its cross-reactions (R8) with other peroxy radicals, R′O2, for which a number of product channels may occur:
In view of the large number of RO2 radicals generated in a detailed chemical mechanism, however, it is unrealistic to represent these reactions explicitly, and the use of simplified parameterizations is essential (Madronich and Calvert, 1990). As described in detail previously (Jenkin et al., 1997), a very simplified approach has traditionally been adopted in the MCM, in which each peroxy radical is assumed to react with all other peroxy radicals (i.e. the peroxy radical “pool”) at a single, collective rate. This is achieved by defining a parameter “∑[RO2]” which is the sum of the concentrations of all peroxy radicals, excluding HO2. The collective rate of all the permutation reactions of a particular peroxy radical is then represented by a single pseudo-unimolecular reaction, which has an assigned rate coefficient equal to [RO2],
with the value of k9 depending on the structure of the reacting RO2 radical. A similar, but more detailed, approach has been applied in GECKO-A, in which the peroxy radical population is divided into a number of reactivity classes (Aumont et al., 2005). This requires the inclusion of a pseudo-unimolecular reaction (analogous to Reaction R9) for reaction of a given peroxy radical with each peroxy radical class, but has the advantage that differential reactivity with each of those classes can be represented, as appropriate. The following subsections describe the basis for assigning rate parameters to the single parameterized permutation reactions (Reaction R9) for each peroxy radical in the more simplified MCM approach. Extension of the method to reactions with a number of reactivity classes (as traditionally applied with GECKO-A) is described in Sect. S5.
2.6.1 Kinetics of self-reactions
Rate coefficients for the self-reactions and cross-reactions of a variety of specific hydrocarbon and oxygenated RO2 radicals have been reported (as summarized in Tables 9–11), and these form the basis of assigning rate parameters to the parameterized permutation reaction (Reaction R9) for each peroxy radical. The data show that the self-reaction reactivity, relative to that of alkyl peroxy radicals, is activated by the presence of numerous functional groups (including allyl-, benzyl-, hydroxy-, alkoxy-, oxo- and acyl-groups), and that the rate coefficients follow the general trend of decreasing reactivity, primary > secondary > tertiary, for peroxy radicals containing otherwise similar functionalities. It also appears that reactivity tends to increase with the size of the organic group towards a “plateau” value, as most clearly demonstrated by the systematic study of secondary alkyl peroxy radicals reported by Boyd et al. (1999). Based on optimization to the complete secondary alkyl peroxy radical dataset, an expression almost identical to that recommended by Boyd et al. (1999) is thus derived as a reference rate coefficient for secondary peroxy radicals at 298 K, as illustrated in Fig. 3 (units of k are cm3 molecule−1 s−1):
The data for primary alkyl peroxy radicals are more limited. Those for C2H5O2, n-C3H7O2, i-C4H9O2 and neo-C5H11O2 suggest a similar trend for primary alkyl peroxy radicals, and an analogous expression to Eq. (14) is therefore derived as a reference rate coefficient at 298 K (see Fig. 3):
It is noted, however, that rate coefficients for the self-reactions of n-C4H9O2 and n-C5H11O2 are reported to be comparable to that for n-C3H7O2, and a factor of 2 to 3 lower than those for i-C4H9O2 and neo-C5H11O2 (see Table 9), suggesting that there may be sensitivity to whether the alkyl group is linear or branched. In the absence of additional data (and noting that the kinetics of neo-C5H11O2 were the most directly determined of the set of C4 and C5 primary alkyl peroxy radicals), the above (stronger) size dependence is provisionally applied here.
Table 9Kinetic data for the self-reactions of hydrocarbon peroxy radicals. Where available, the temperature dependence is given by .
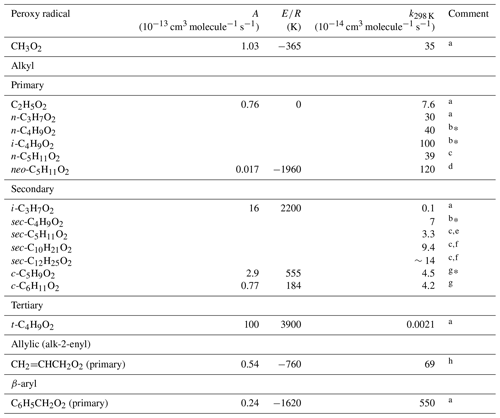
Comments: * Reported rate coefficient not corrected for the effects of secondary chemistry, which can lead to either an overestimate or underestimate of the rate coefficient. a IUPAC Task Group recommendation (http://iupac.pole-ether.fr/, last access: January 2019). b Taken from Glover and Miller (2005). c Taken from Boyd et al. (1999). d Based on Lightfoot et al. (1990). e Mixture of 2-pentyl and 3-pentyl peroxy radicals. f Mixture of secondary peroxy radicals of given formula. g Based Rowley et al. (1991, 1992c). h Based on Jenkin et al. (1993b) and Boyd et al. (1996a).
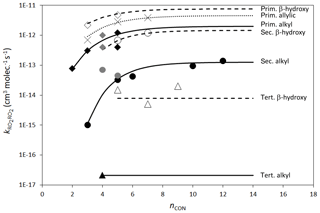
Figure 3Rate coefficients for the self-reactions of alkyl (filled points), β-hydroxyalkyl (open points) and allylic (×) RO2 at 298 K as a function of nCON. Grey filled points indicate where the reported rate coefficient has not been corrected for secondary chemistry. Where available, data are shown for primary, secondary and tertiary radicals containing the given functionalities. Primary, secondary and tertiary alkyl and β-hydroxyalkyl radicals are shown as diamonds, circles and triangles, respectively. The “allylic” peroxy radical group contains only primary radicals and includes “δ-hydroxyallylic” peroxy radicals. The lines represent the calculated rate coefficients fitted to the data using the methods described in Sect. 2.6.
Table 10Kinetic data for the self-reactions of oxygenated peroxy radicals. Where available, the temperature dependence is given by .
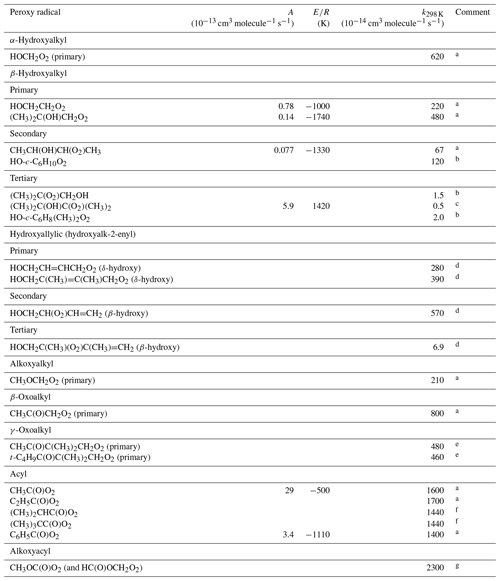
Comments: a IUPAC Task Group recommendation (http://iupac.pole-ether.fr/, last access: January 2019). b Taken from on Boyd et al. (2003b). c Based on Jenkin and Hayman (1995) and Boyd and Lesclaux (1997). d Taken from Jenkin et al. (1998). e Based on Le Crâne and Lesclaux (2006). f Based on Tomas and Lesclaux (2000) and Le Crâne et al. (2004). g Taken from Hansen et al. (2003). The kinetics of the two peroxy radicals formed from the reaction of Cl or F with methyl formate reported to possess indistinguishable kinetics.
Table 11Kinetic data for the cross-reactions of hydrocarbon or oxygenated peroxy radicals at 298 K. Where available, the temperature dependence expression is given in the comments.

Comments: a IUPAC Task Group recommendation (http://iupac.pole-ether.fr/, last access: January 2019). b Taken from Villenave and Lesclaux (1996). c Based on Villenave and Lesclaux (1996) and Nozière and Hanson (2017). d Temperature dependence expression is . e Temperature dependence expression is . f Temperature dependence expression is . g Taken from Villenave et al. (1998). h Taken from Boyd et al. (2003b). The structures refer to the isomeric secondary and tertiary peroxy radicals formed from the addition of OH to 1-methylcyclohexene. i Taken from Jenkin et al. (1998). Presented values are limited to those reported for the cross-reactions of the major radicals formed from the terminal addition of OH to buta-1,3-diene and the terminal addition of OH to 2,3-dimethyl-buta-1,3-diene.
Data for tertiary alkyl peroxy radicals are currently limited to t-C4H9O2, and the corresponding rate coefficient is currently applied as the reference rate coefficient at 298 K, independent of radical size (see Fig. 3):
Figure 3 also shows data for allylic and β-hydroxyalkyl RO2, demonstrating that the presence of both these functionalities has an activating effect on self-reaction reactivity. The allylic peroxy radical category includes two δ-hydroxyallylic peroxy radicals, and the assumption is made here that the δ-hydroxy group is too remote to have an influence. Table 12 summarizes a series of activation factors (defined in terms of the parameters α and β) for allylic-, β-aryl-, hydroxy-, alkoxy- and oxo-groups, optimized on the basis of the data in Tables 9 and 10. These are used in conjunction with the reference rate coefficients in Eqs. (14)–(16) to calculate the self-reaction rate coefficient for a given peroxy radical at 298 K, , as follows:
Here, represents the appropriate reference rate coefficient (i.e. for primary, secondary or tertiary RO2, as appropriate) as defined by Eqs. (14)–(16); and the term describes the level of activation from the given substituent. The inclusion of within this activation term is required because the relative enhancement of reactivity resulting from a given substituent appears to decrease as the reactivity increases, as illustrated for the β-hydroxyalkyl group data in Fig. 3. Based on this method, the estimated rate coefficients correlate well with those observed for the series of peroxy radicals for which data are currently available (summarized in Tables 9 and 10), as shown in Fig. 4. It is emphasized, however, that the parameters for several of the substituent groups are based on data for very limited sets of peroxy radicals, and additional data would be valuable to test and constrain the method.
Table 12Substituent activation factors applied to self-reaction rate coefficients, based on Eq. (17).
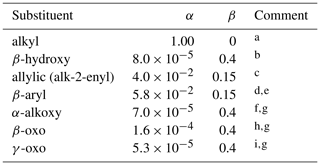
Comments: a α=1.00 and β=0 by definition for alkyl peroxy radicals. These are also used as a default for peroxy radical classes not covered by comments b to i, with the exception of acyl peroxy radicals (discussed in Sect. 2.6); b Based on data for β-hydroxyalkyl peroxy radicals in Table 10; c Based on data for allylic and δ-hydroxyallylic peroxy radicals in Tables 9 and 10; d Based on data for C6H5CH2O2 (Table 9); e β assumed equivalent to that for allylic substituent; f Based on data for CH3OCH2O2 (Table 10); g β assumed equivalent to that for β-hydroxy substituent; h Based on data for CH3C(O)CH2O2 (Table 10); i Based on data for γ-oxoalkyl peroxy radicals in Table 10.
Information on the effects of multiple substituents is limited to the data for the secondary and tertiary β-hydroxyallylic peroxy radicals, HOCH2CH(O2)CH=CH2 and HOCH2C(CH3)(O2)C(CH3)=CH2, given in Table 10. The reported rate coefficients are consistent with the activating impacts of the β-hydroxy and allylic substituents being approximately cumulative, suggesting that an activation factor should be applied for each relevant organic substituent. However, this would lead to unreasonably large estimated values of for secondary and tertiary peroxy radicals containing two or three of the most activating substituents, such that the impact needs to be limited. In multifunctional peroxy radicals, therefore, an activating factor is only applied for the most activating oxygenated substituent in a given peroxy radical, with an additional factor also applied only for the specific cases of an allylic or a β-aryl substituent, again limited to one (i.e. the most activating) factor if the peroxy radical contains more than one allylic or β-aryl group. In these specific cases, therefore,
where α1 and β1 refer to the oxygenated substituent, and α2 and β2 refer to either the allylic substituent or the β-aryl substituent. Further information is required to allow the impacts of multiple substituents to be defined more rigorously.
2.6.2 Parameterized representation
The rate coefficients for cross-reactions of peroxy radicals (Reaction R8) have often been inferred from those for the self-reactions of the participating peroxy radicals, using a geometric mean rule as first suggested by Madronich and Calvert (1990), i.e.
where k8 is the cross-reaction rate coefficient, and k7 and are the self-reaction rate coefficients for the participating peroxy radicals, RO2 and R′O2. Figure 5 shows that such a correlation provides a reasonable guide in many cases (although a clear deviation from the rule occurs for the particular case of reactions involving acyl peroxy radicals). In the very simplified MCM approach, the rate coefficient for the single parameterized permutation reaction of a given peroxy radical (Reaction R9) is based on that estimated for the cross-reaction of the peroxy radical with CH3O2. This is regarded as a logical choice because CH3O2 is the most abundant organic peroxy radical in the atmosphere (and therefore most commonly the major reaction partner), and also possesses a self-reaction rate coefficient that is in the middle of the range of reported values (see Tables 9 and 10). Taking account of the correlations in Fig. 5, the rate coefficients (in cm3 molecule−1 s−1) for the parameterized permutation reactions at 298 K are defined as follows.
Here, k298(CH3O2+CH3O2) is the rate coefficient for the self-reaction of CH3O2 at 298 K ( cm3 molecule−1 s−1) and is the 298 K self-reaction rate coefficient, estimated as described above (Sect. 2.6.1). is a scaling factor that is introduced to describe systematic deviations from the geometric mean rule, if required. Based on the correlations in Fig. 5, a unity value of is considered acceptable for primary and secondary peroxy radicals (i.e. no deviation from the geometric mean rule), whereas a value of is applied to tertiary peroxy radicals. This elevated scaling factor is based on observation of Jenkin et al. (1998) for complex tertiary RO2 cross-reactions.
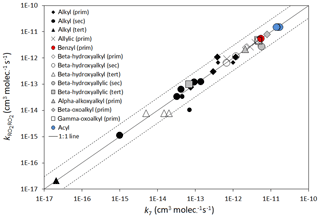
Figure 4Scatter plot of estimated rate coefficients () for peroxy radical self-reactions with those reported (k7), as listed in Tables 9 and 10. Those shown with reduced size symbols are where the reported value of k7 was not corrected for secondary chemistry (see Table 9 comments). The broken lines show the factor of 3 range.
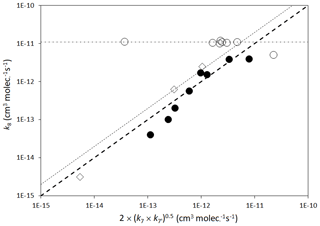
Figure 5Scatter plot of rate coefficients for peroxy radical cross-reactions (k8) with the geometric mean of the self-reaction rate coefficients (denoted k7 and ) for the participating peroxy radicals, RO2 and R′O2. Open circles are reactions involving an acyl peroxy radical and a non-acyl peroxy radical; closed circles are reactions involving combinations of primary and secondary peroxy radicals; open diamonds are reactions involving a tertiary peroxy radical and a primary or secondary peroxy radical. The heavy broken line is a 1:1 relationship; the light broken line is a 2:1 relationship; the dot–dash line is cm3 molecule−1 s−1.
Based on the reported temperature dependences of peroxy radical self- and cross-reactions (see Tables 9 and 10, and Table 11 comments), kAP and are assigned respective pre-exponential factors of and cm3 molecule−1 s−1. For acyl peroxy radicals, this is consistent with the temperature dependence reported for the reaction of CH3C(O)O2 with CH3O2, and results in the following temperature-dependent expression in all cases:
For , the pre-exponential factor is a rounded value, based on the geometric mean of those for the self-reactions of non-acyl peroxy radicals given in Tables 9 and 10. This results in the following temperature dependence expression for non-acyl peroxy radicals (except CH3O2),
with having a case-dependent value of , where is defined by Eq. (22). Examples of specific rate coefficients estimated using this method are given in Sect. S5 for the peroxy radicals formed from the sequential addition of OH and O2 to isoprene. As indicated above, the collective rate of all the permutation reactions of a particular peroxy radical is then represented by a pseudo-unimolecular reaction (Reaction R9), which has an assigned rate coefficient equal to [RO2] for acyl peroxy radicals, and [RO2] for all other peroxy radicals (except CH3O2). For the specific case of CH3O2, the applied rate coefficient () is twice the self-reaction rate coefficient given in Table 9,
with the pseudo-unimolecular reaction rate coefficient equal to [RO2]. This representation is therefore consistent with CH3O2 being lost via its self-reaction with the recommended rate coefficient when it is the dominant radical.
Each reaction potentially has up to four product channels, the branching ratios of which depend on the structure of the radical, as shown in Table 13:
Channels (R9a)–(R9c) have been considered previously in the MCM (Jenkin et al., 1997; Saunders et al., 2003). They are the pseudo-unimolecular representation of the self-reaction channels (R7a) and (R7b) and the cross-reaction channels (R8a)–(R8c), which are reported to account for most of the reaction, particularly for smaller peroxy radicals (e.g. Lightfoot et al., 1992; Orlando and Tyndall, 2012). As shown in Table 13, channels (R9a)–(R9c) continue to represent the complete reaction in the current parameterized methodology.
Table 13Branching ratios assigned to parameterized permutation reactions of RO2 (see text).
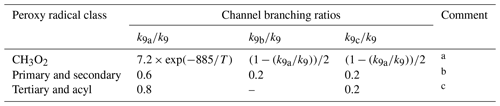
Comments: a Based on IUPAC Task Group recommendation for the CH3O2 self-reaction (http://iupac.pole-ether.fr/, last access: January 2019). An alternative representation using temperature-dependent channel rate coefficients is provided in Sect. S5. b Based on a rounded mean of the reported 298 K branching ratios for the self-reactions of C2H5O2, i-C3H7O2, HOCH2CH2O2, (CH3)2C(OH)CH2O2, CH3C(O)CH2O2, CH3OCH2O2 and C6H5CH2O2 based on IUPAC Task Group recommendations (http://iupac.pole-ether.fr/, last access: January 2019); neo-C5H11O2, c-C6H11O2 and CH2=CHCH2O2 based on Lightfoot et al. (1990), Rowley et al. (1991), Jenkin et al. (1993a, b) and Boyd et al. (1996a); and for the self- and cross-reactions of primary and secondary RO2 formed from reactions of OH with conjugated dienes (Jenkin et al., 1998). c Based on a rounded mean of the reported 298 K branching ratios for the following cross-reactions: CH3C(O)O2 + CH3O2, C2H5C(O)O2 + C2H5O2 and CH3C(O)O2 + CH3C(O)CH2O2 based on IUPAC Task Group recommendations (http://iupac.pole-ether.fr/, last access: January 2019); and HOCH2C(CH3)(O2)C(CH3)=CH2 + HOCH2C(CH3)=C(CH3)CH2O2 formed from reaction of OH with 2,3-dimethyl-buta-1,3-diene (Jenkin et al., 1998).
Although not currently included in the parameterized representation, channel (R9d) is listed to acknowledge the potential formation of peroxide products (i.e. Reactions R7c and R8d). Although these channels have generally been reported to be minor for small peroxy radicals (e.g. Lightfoot et al., 1992; Orlando and Tyndall, 2012), recent studies suggest that they may be more significant for larger peroxy radicals containing oxygenated substituents, and they have been reported to play a role in the formation of low-volatility products in a number of studies (Ziemann, 2002; Ng et al., 2008; Ehn et al., 2014; Jokinen et al., 2014; Mentel et al., 2015; Rissanen et al., 2015; Berndt et al., 2015, 2018a, b; Zhang et al., 2015; McFiggans et al., 2019). These reactions may therefore play a potentially important role in particle formation and growth in the atmosphere. The product denoted “RO(peroxide)” in the pseudo-unimolecular approach represents the monomeric contribution the given peroxy radical makes to the total formation of (dimeric) peroxide products, but is not an independent species for which subsequent gas-phase chemistry can be rigorously defined. In principle, channel (R9d) can be included for the permutation reactions of a subset of larger peroxy radicals, with the RO(peroxide) product assumed to transfer completely to the condensed phase (i.e. not participating in gas-phase reactions). However, there is currently insufficient information on the structural dependence of the contributions of channels (R7c) or (R8d) to the overall self- and cross-reactions to allow the branching ratio of channel (R9d) to be defined reliably. Further systematic studies of these channel contributions are therefore required as a function of peroxy radical size and functional group content.
Unimolecular isomerization reactions are potentially available for some classes of RO2. These generally fall into the category of either ring-closure reactions (where the peroxy radical adds intra-molecularly to an unsaturated linkage to form a peroxide-bridged radical product) or reactions involving the migration of a hydrogen atom to the peroxy radical group (e.g. forming a hydroperoxy-substituted organic radical product when abstraction from a C−H bond occurs). For some RO2 structures, these reactions have been shown to compete with (or dominate over) the bimolecular reactions under some atmospheric conditions, as discussed further below in Sect. 3.1 and 3.2. Evidence for the operation of peroxy radical isomerization reactions has been reported in numerous theoretical and laboratory studies (e.g. Vereecken and Peeters, 2004; Peeters et al., 2009; 2014; Crounse et al., 2013; Ehn et al., 2014, 2017; Jokinen et al., 2014; Rissanen et al., 2015; Jørgensen et al., 2016; Praske et al., 2017, 2019; Otkjær et al., 2018; Mohammed et al., 2018), and new information is constantly emerging on this important aspect of peroxy radical chemistry (e.g. Bianchi et al., 2019; Xu et al., 2019; Møller et al., 2019). The present section provides a summary of selected classes of isomerization reactions that are currently being considered and represented in ongoing mechanism development work. However, it does not currently attempt to provide a full treatment of unimolecular reactions of RO2 radicals, which will be considered further in future work as more new information becomes available.
3.1 Ring-closure reactions of RO2
Table 14 shows representative rate coefficients for selected template ring-closure reactions. The first entry relates to the β-hydroxy cyclohexadienylperoxy radicals formed from the addition of O2 to OH-aromatic hydrocarbon adducts. As discussed in the companion paper on the OH-initiated oxidation of aromatic VOCs (Jenkin et al., 2018b), these peroxy radicals are represented to undergo rapid and exclusive ring closure to produce a hydroxy-dioxa-bicyclo or “peroxide-bicyclic” radical. This reaction has been calculated to dominate over alternative bimolecular reactions of the peroxy radicals under atmospheric conditions (see Table 14), although evidence for competitive loss via bimolecular reactions has been characterized in experimental studies using high concentrations of NO and/or RO2 (e.g. Birdsall et al., 2010; Birdsall and Elrod, 2011).
Table 14Representative rate coefficients for template ring-closure reactions of peroxy radicalsa.
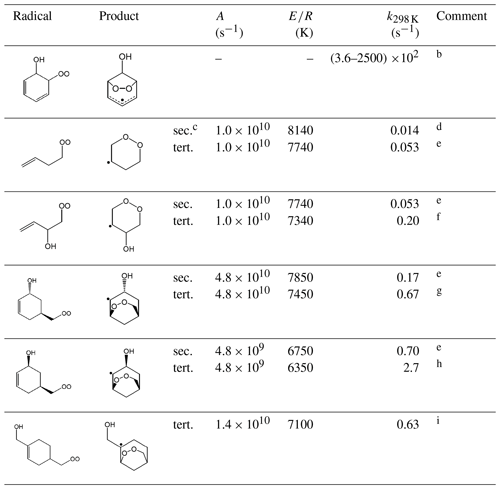
Comments: a Temperature dependence of rate coefficient given by . Rapid reaction of the product radical with O2 dominates over the reverse ring-opening reaction under atmospheric conditions. Entries in bold font are based on reported data for the specific or closely related structures, with other entries inferred using assumptions given in the following comments. b Range of 298 K values based on the calculations of Raoult et al. (2004), Glowacki et al. (2009) and Olivella et al. (2009) for the dominant conformer of the example peroxy radical, formed during the oxidation of benzene. Based on these data, and data for other aromatic systems, analogous ring-closure reactions are assumed to be the exclusive fates of corresponding peroxy radicals formed during the oxidation of aromatic hydrocarbons (Jenkin et al., 2018b). c Denotes substitution of product radical. d Based on information reported by Vereecken and Peeters (2004) for calculations for the given peroxy radical. e E∕R for formation of a tertiary radical assumed to be 400 K lower than for formation of a secondary radical, corresponding to a difference in E of ≈3.3 kJ mol−1. This is consistent with differences in energy barriers reported for formation of secondary and tertiary radicals (Vereecken and Peeters, 2004). f Based on the calculations of Vereecken and Peeters (2004) for a relevant tertiary peroxy radical formed during the oxidation of isoprene. g Based on the calculations of Vereecken and Peeters (2004) for a relevant tertiary peroxy radical formed during the oxidation of α-pinene. Applies specifically to anti-conformers, when the OH and peroxy radical groups on the opposite sides of the ring (as shown), which were calculated to account for 60 % of the anti- + syn-population (Vereecken and Peeters, 2004). h Based on the calculations of Vereecken and Peeters (2004) for a relevant tertiary peroxy radical formed during the oxidation of α-pinene. Applies specifically to syn-conformers, when the OH and peroxy radical groups on the same side of the ring (as shown), which were calculated to account for 40 % of the anti- + syn- population (Vereecken and Peeters, 2004). i Based on the calculations of Vereecken and Peeters (2004) for the a relevant tertiary peroxy radical, formed during the oxidation of β-pinene.
The remaining reactions in Table 14 are based on information presented by Vereecken and Peeters (2004) for specific peroxy radicals formed from the sequential addition of OH and O2 to isoprene, α-pinene and β-pinene. That information has been used to assign or infer representative rate coefficients to the series of related template peroxy radical structures presented in Table 14. In these cases, the reactions are expected to occur at rates that can compete to varying extents with loss via bimolecular reactions (or other unimolecular reactions discussed below) under atmospheric conditions. It is noted that Xu et al. (2019) have also very recently reported information for a series of isomerization reactions (including ring-closure reactions) for the α- and β-pinene systems, which are being considered in ongoing work.
3.2 Hydrogen atom migration reactions of RO2
Table 15 shows selected hydrogen atom migration reactions that are currently considered. The rate coefficient assigned generally to the 1,4-formyl H-shift reaction of α-formyl peroxy radicals is based on that determined for the methacrolein-derived peroxy radical, HOCH2C(CH3)(O2)C(=O)H, in the experimental study of Crounse et al. (2012). It is noted that this is slightly higher than, but comparable with, the range of values reported for α-formyl peroxy radicals in the preliminary calculations of Peeters and Nguyen (2012).
Table 15Representative rate coefficients for selected H-shift isomerization reactions of peroxy radicals.
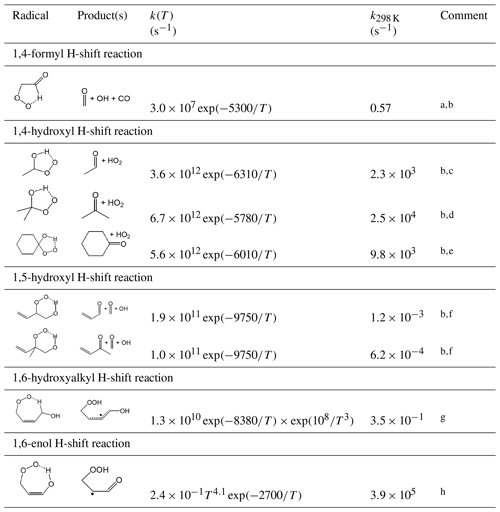
Comments: a Based on rate coefficient reported for the methacrolein-derived peroxy radical, HOCH2C(CH3)(O2)C(=O)H by Crounse et al. (2012). Applied to primary, secondary and tertiary α-formyl peroxy radicals. b The initially formed hydroperoxy-substituted product radical decomposes spontaneously to produce the displayed products. c Based on the rate coefficient estimated for CH3CH(OH)O2 by Hermans et al. (2005); applied to secondary α-hydroxyl peroxy radicals. d Based on the rate coefficient estimated for (CH3)2C(OH)O2 by Hermans et al. (2005); applied to tertiary α-hydroxy peroxy radicals. e Based on the rate coefficient estimated for cyclo-C6H10(OH)O2 by Hermans et al. (2005); applied generally to cyclic α-hydroxy peroxy radicals (i.e. where the OH and OO groups are substituents to a ring). f Based on rate coefficients reported by Peeters et al. (2014) for corresponding unsaturated secondary and tertiary β-hydroxy peroxy radicals formed in isoprene oxidation. Applied generally to unsaturated β-hydroxy peroxy radicals containing the substructures shown. g Based on the geometric mean of rate coefficients applied to (Z)-CH(OH)C(CH3)=CHCH2O2 (CISOPAO2) and (Z)-CH(OH)CH=C(CH3)CH2O2 (CISOPCO2) in MCM v3.3.1 (Jenkin et al., 2015) based on the calculations of Peeters et al. (2014) and observations of Crounse et al. (2011). Applied generally to unsaturated δ-hydroxy peroxy radicals containing the substructure shown, except for CISOPAO2 and CISOPCO2 themselves for which the species-specific rate coefficients are applied (see Table S5). Rapid reaction of the product radical with O2 dominates over the reverse isomerization reaction under atmospheric conditions. h Based on the geometric mean of rate coefficients reported for (Z)-HOCH=C(CH3)CH(O2)CH2OH and (Z)-HOCH=CHC(CH3)(O2)CH2OH in the calculations of Peeters and Nguyen (2012). Applied to peroxy radicals containing the substructure shown. Rapid reaction of the product radical with O2 dominates over the reverse isomerization reaction under atmospheric conditions.
The rate coefficients assigned to the 1,4-hydroxyl H-shift reactions of (thermalized) α-hydroxy peroxy radicals are based on those estimated for secondary, tertiary and cyclic peroxy radicals in the theoretical study of Hermans et al. (2005). As discussed in the companion paper on the OH-initiated oxidation of aliphatic VOCs (Jenkin et al., 2018a), thermalized α-hydroxy peroxy radicals are represented to be increasingly formed from the reactions of O2 with larger α-hydroxy organic radicals (i.e. those with nCON>5). At the assigned rates, the 1,4-hydroxyl H-shift reaction is likely to be the major fate of the majority of thermalized α-hydroxy peroxy radicals under atmospheric conditions, and therefore indistinguishable from that of the chemically activated α-hydroxy peroxy radical adducts that are formed predominantly from the reactions of O2 with small α-hydroxy organic radicals (see Sect. 6.2 of Jenkin et al., 2018a). However, the rates of the 1,4-hydroxyl H-shift reactions are formalized in the present work to allow for the representation of competing rapid isomerization reactions for specific structurally complex peroxy radicals (e.g. the 1,6-enol H-shift reaction discussed below), or with bimolecular reactions under appropriate conditions. It is noted that evidence for competitive loss via bimolecular reactions has been characterized in experimental studies using high concentrations of NO (e.g. Orlando et al., 2000b; Jenkin et al., 2005; Aschmann et al., 2010), leading to the formation of organic acids.
The remaining reactions in Table 15 are inferred from information reported for specific unsaturated peroxy radicals formed during the OH-initiated oxidation of isoprene, taking particular account of the work of Peeters et al. (2009, 2014) on the Leuven isoprene mechanism (LIM1), which has been largely verified by experimental study (e.g. Wennberg et al., 2018; and references therein). The rate coefficients for the 1,5-hydroxyl H-shift reactions are those reported by Peeters et al. (2014) for the corresponding unsaturated secondary and tertiary β-hydroxy peroxy radicals formed from the sequential addition of OH and O2 to isoprene, with these also being generally consistent with those reported by da Silva et al. (2010). The rate coefficient assigned to the 1,6-hydroxyalkyl H-shift reaction is the geometric mean of rate coefficients applied to (Z)-CH2(OH)C(CH3)=CHCH2O2 (CISOPAO2) and (Z)-CH2(OH)CH=C(CH3)CH2O2 (CISOPCO2) in MCM v3.3.1. As discussed by Jenkin et al. (2015), those rate coefficients are derived from the LIM1 calculations of Peeters et al. (2014), but with some scaling to recreate the observations of Crounse et al. (2011, 2014). The generic rate coefficient is applied generally to unsaturated δ-hydroxy peroxy radicals containing the substructure shown, but with the exceptions of CISOPAO2 and CISOPCO2 themselves, for which the species-specific rate coefficients are applied (see Sect. S6 and Table S5). Similarly, the rate coefficient for the rapid 1,6-enol H-shift reaction is the geometric mean of those calculated for (Z)-HOCH=C(CH3)CH(O2)CH2OH and (Z)-HOCH=CHC(CH3)(O2)CH2OH by Peeters and Nguyen (2012). Once again, the 1,6-enol H-shift reaction is likely to be the major fate of the majority of peroxy radicals containing the relevant substructure (see Table 15) under atmospheric conditions, but the rate is formalized in the present work to allow for the representation of competing rapid isomerization reactions for specific structurally complex peroxy radicals, e.g. the 1,4-hydroxyl H-shift reaction discussed above, or other reactions that may be considered and represented in future work.
As indicated above, the present paper does not attempt to provide a full treatment of unimolecular reactions of RO2 radicals, which ideally require systematic information on the rates of a series of 1,n-H-shift reactions from C−H and O−H bonds in different environments. In this respect, it is noted that the systematic influence of a series of neighbouring functional groups and transition state sizes have been considered in theoretical studies of a number of model systems (e.g. Crounse et al., 2013; Jørgensen et al., 2016; Praske et al., 2017; Otkjær et al., 2018). Such studies provide the basis for defining systematic structure–activity methods for a wide range of RO2 radicals and their potential isomerization reactions, and are being considered in ongoing work. A further consideration, highlighted in those studies, is that the rates of the reverse isomerization reactions are sometimes sufficiently rapid that the product radical may not be fully trapped by onward reaction (e.g. addition of O2) under atmospheric conditions. It is noted that the explicit representation of a very large number of rapid reversible reactions in detailed mechanisms can have implications for computational efficiency, and needs to be considered carefully in method development and implementation.
Published kinetics and branching ratio data have been reviewed for the bimolecular reactions of organic peroxy radicals (RO2), with information for selected unimolecular isomerization reactions also summarized and discussed. The information has been used to define generic rate coefficients and structure–activity relationship (SAR) methods for the reactions of a series of important classes of hydrocarbon and oxygenated RO2 radicals, for application in the next generation of explicit detailed chemical mechanisms, based on GECKO-A and the MCM.
The availability of kinetic and mechanistic data for peroxy radical reactions has increased substantially since the appraisals of Saunders et al. (2003) and Aumont et al. (2005), on which the previous treatments of peroxy radical chemistry in the MCM and GECKO-A were mainly based. These advances have allowed improved and updated methods to be defined and summarized in the present work for an extended set of peroxy radical reactions. Nevertheless, there are still a number of specific areas (commented on in Sects. 2 and 3) where information is lacking and further studies would be beneficial. These include the following.
-
Kinetics studies of the reactions with NO have only been reported for a limited number of acyl peroxy radicals. Further studies, particularly for larger and highly oxygenated acyl peroxy radicals, would help to establish whether size and/or the presence of additional substituent groups has an effect on reactivity.
-
Further systematic data on RONO2 yields from the reactions with NO are required to help improve branching ratio parameterizations. These include additional data for a variety of acyclic and cyclic oxygenated RO2 as a function of size and structure.
-
For the reactions with NO3, studies for ≥C2 (non-acyl) RO2 are dominated by primary peroxy radicals. Further studies are therefore required for secondary and tertiary radicals, and product information is generally required for a variety of peroxy radical classes to test assumption that the reaction proceeds via a single channel forming RO, NO2 and O2.
-
The reactions of ≥C2 hydrocarbon RO2 with OH are believed to produce a thermalized hydrotrioxide, ROOOH, as the major product. Detailed experimental and theoretical studies are therefore required to establish the atmospheric fate of these ROOOH species. Studies of the reactions of oxygenated RO2 with OH are also required.
-
The reactions of HO2 with several oxygenated RO2 classes have been shown to proceed via multiple channels, although the temperature dependences of the product channels have generally not been studied. Additional studies of their temperature dependences would therefore be valuable, in addition to information for larger sets of oxygenated RO2 within some classes. Kinetics studies have only been reported for a limited number of acyl peroxy radicals. Further studies, particularly for larger and highly oxygenated acyl peroxy radicals, would help to establish whether size and/or the presence of additional substituent groups has an effect on reactivity.
-
For the self- and cross-reactions of peroxy radicals, further information is required to allow the impacts of multiple substituents on the kinetics to be defined more rigorously. Further systematic studies of the formation of ROOR + O2 (from the self-reaction of RO2) and (from the cross-reaction of RO2 with R′O2) are also required as a function of peroxy radical size and functional group content.
-
For unimolecular isomerization reactions, further systematic studies are required for the rates of 1,n-H-shift reactions from C−H and O−H bonds in different chemical environments, and for the effect of ring size and substituents on ring-closure reactions, to build upon recently reported data for these reaction classes.
All relevant data have been tabulated or provided as supporting information in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-7691-2019-supplement.
All authors defined the scope of the work. MEJ developed and revised the estimation methods and drafted the manuscript. The estimation methods were tested, evaluated and refined by all authors. The manuscript was reviewed and revised by all authors.
The authors declare that they have no conflict of interest.
This work was performed as part of the MAGNIFY project, with funding from the UK Natural Environment Research Council (NERC) and the French National Research Agency (ANR). It was also partially funded by the European Commission through EUROCHAMP-2020. Paul Wennberg (California Institute of Technology), Luc Vereecken (Forschungszentrum Jülich), Geoff Tyndall (NCAR, Boulder), John Crounse (California Institute of Technology) and an anonymous referee are gratefully acknowledged for review and discussion comments that helped to improve the paper.
This research has been supported by the UK Natural Environment Research Council (NERC) (grant no. NE/M013448/1), the French National Research Agency (ANR) (grant no. ANR-14-CE01-0010), and the European Commission through EUROCHAMP-2020 (grant no. 730997).
This paper was edited by Dwayne Heard and reviewed by Paul O. Wennberg, Geoffrey Tyndall, and one anonymous referee.
Anglada, J. M. and Solé, A.: Tropospheric oxidation of methyl hydrotrioxide (CH3OOOH) by hydroxyl radical, Phys. Chem. Chem. Phys., 20, 27406–27417, 2018.
Archibald, A. T., Petit, A. S., Percival, C. J., Harvey, J. N., and Shallcross, D. E.: On the importance of the reaction between OH and RO2 radicals, Atmos. Sci. Let., 10, 102–108, 2009.
Arey, J., Aschmann, S. M., Kwok, E. S. C., and Atkinson, R.: Alkyl nitrate, hydroxyalkyl nitrate, and hydroxycarbonyl formation from the NOx–air photooxidations of C5–C8 n-alkanes, J. Phys. Chem. A, 105, 1020–1027, https://doi.org/10.1021/jp003292z, 2001.
Aschmann, S. M., Tuazon, E. C., Arey, J., and Atkinson, R.: Products and mechanisms of the gas-phase reactions of OH radicals with 1-octene and 7-tetradecene in the presence of NO, Environ. Sci. Technol., 44, 3825–3831, 2010.
Assaf, E., Song, B., Tomas, A., Schoemaecker, C., and Fittschen, C.: Rate constant of the reaction between CH3O2 radicals and OH radicals revisited, J. Phys. Chem. A, 120, 8923–8932, 2016.
Assaf, E., Sheps, L., Whalley, L., Heard, D., Tomas, A., Schoemaecker, C., and Fittschen, C.: The reaction between CH3O2 and OH radicals: product yields and atmospheric implications, Environ. Sci. Technol., 51, 2170–2177, 2017a.
Assaf, E., Tanaka, S., Kajii, Y., Schoemaecker, C., and Fittschen, C.: Rate constants of the reaction of C2–C4 peroxy radicals with OH radicals, Chem. Phys. Lett., 684, 245–249, 2017b.
Assaf, E., Schoemaecker, C., Vereecken, L., and Fittschen, C.: Experimental and theoretical investigation of the reaction of RO2 radicals with OH radicals: Dependence of the HO2 yield on the size of the alkyl group, Int. J. Chem. Kinet., 50, 670–680, 2018.
Aumont, B., Szopa, S., and Madronich, S.: Modelling the evolution of organic carbon during its gas-phase tropospheric oxidation: development of an explicit model based on a self generating approach, Atmos. Chem. Phys., 5, 2497–2517, https://doi.org/10.5194/acp-5-2497-2005, 2005.
Berndt, T., Richters, S., Kaethner, R., Voigtländer, J., Stratmann, F., Sipilä, M., Kulmala, M. and Herrmann, H.: Gas-phase ozonolysis of cycloalkenes: formation of highly oxidized RO2 radicals and their reactions with NO, NO2, SO2, and other RO2 radicals, J. Phys. Chem. A, 119, 10336–10348, 2015.
Berndt, T., Scholz, W., Mentler, B., Fischer, L., Herrmann, H., Kulmala, M., and Hansel, A.: Accretion product formation from self- and cross-reactions of RO2 radicals in the atmosphere, Angew. Chem. Int. Edit., 57, 3820–3824, 2018a.
Berndt, T., Mentler, B., Scholz, W., Fischer, L., Herrmann, H., Kulmala, M. and Hansel, A.: Accretion product formation from ozonolysis and OH radical reaction of α-pinene: mechanistic insight and the influence of isoprene and ethylene, Environ. Sci. Technol., 52, 11069–11077, 2018b.
Bian, H., Zhang, S. and Zhang, H.: Theoretical study on the atmospheric reaction of CH3O2 with OH, Int. J. Quantum. Chem., 115, 1181–1186, 2015.
Bianchi, F., Kurtén, T., Riva, M., Mohr, C., Rissanen, M. P., Roldin, P., Berndt, T., Crounse, J. D., Wennberg, P. O., Mentel, T. F., Wildt, J., Junninen, H., Jokinen, T., Kulmala, M., Worsnop, D. R., Thornton, J. A., Donahue, N., Kjaergaard, H. G., and Ehn, M.: Highly oxygenated organic molecules (HOM) from gas-phase autoxidation involving peroxy radicals: A key contributor to atmospheric aerosol, Chem. Rev., 119, 3472–3509, 2019.
Birdsall, A. W. and Elrod, M. J.: Comprehensive NO-dependent study of the products of the oxidation of atmospherically relevant aromatic compounds, J. Phys. Chem. A, 115, 5397–5407, 2011.
Birdsall, A. W., Andreoni, J. F., and Elrod, M. J.: Investigation of the role of bicyclic peroxy radicals in the oxidation mechanism of toluene, J. Phys. Chem. A, 114, 10655–10663, 2010.
Bey, I., Aumont, B., and Toupance, G.: A modeling study of the nighttime radical chemistry in the lower continental troposphere: 1 – Development of a detailed chemical mechanism including nighttime chemistry, J. Geophys. Res., 106, 9959–9990, 2001a.
Bey, I., Aumont, B. and Toupance, G.: A modeling study of the nighttime radical chemistry in the lower continental troposphere: 2 – Origin and evolution of HOx”, J. Geophys. Res., 106, 9990–10001, 2001b.
Biggs, P., Canosa-Mas, C., Fracheboud, J. M., Shallcross, D. E., and Wayne, R. P.: Rate constants for the reactions of C2H5, C2H5O and C2H5O2 radicals with NO3 at 298 K and 2.2 Torr, J. Chem. Soc. Faraday T., 91, 817–825, 1995.
Bossolasco, A. G., Malanca, F. E., and Argüello, G. A.: Peroxy ethoxyformyl nitrate, CH3CH2OC(O)OONO2. Spectroscopic and thermal characterization, J. Photochem. Photobio. A, 221, 58–63, 2011.
Boyd, A. A. and Lesclaux, R.: The temperature dependence of the rate coefficients for β-hydroxyperoxy radical self reactions, Int. J. Chem. Kinet., 29, 323–331, 1997.
Boyd, A. A., Noziere, B., and Lesclaux, R.: Kinetic studies of the allylperoxyl radical self-reaction and reaction with HO2, Chem. Soc. Faraday T., 92, 201–206, 1996a.
Boyd, A. A., Lesclaux, R., Jenkin, M. E., and Wallington, T. J.: A spectroscopic, kinetic, and product study of the (CH3)2C(OH)CH2O2 radical self reaction and reaction with HO2, J. Phys. Chem., 100, 6594–6603, 1996b.
Boyd, A. A., Villenave, E., and Lesclaux, R.: Structure-reactivity relationships for the self-reactions of linear secondary alkylperoxy radicals: an experimental investigation, Int. J. Chem. Kinet., 31, 37–46, 1999.
Boyd, A. A., Flaud, P.-M., Daugey, N., and Lesclaux, R.: Rate constants for RO2+HO2 reactions measured under a large excess of HO2, J. Phys. Chem. A, 107, 818–821, 2003a.
Boyd, A. A., Villenave, E., and Lesclaux, R.: Self- and cross-reactions of β-hydroxyperoxy radicals of relevance to tropospheric monoterpene oxidation: structure-activity relationships for rate coefficients, Atmos. Environ., 37, 2751–2760, 2003b.
Bridier, I., Veyret, B., Lesclaux, R., and Jenkin, M. E.: Flash-photolysis study of the uv spectrum and kinetics of reactions of the acetonylperoxy radical, J. Chem. Soc. Faraday T., 89, 2993–2997, 1993.
Calvert, J. G., Orlando, J. J., Stockwell, W. R., and Wallington, T. J.: The mechanisms of reactions influencing atmospheric ozone, Oxford University Press, Oxford, ISBN 978-0-19-023301-0, 2015.
Canosa-Mas, C. E., King, M. D., Lopez, R., Percival, C. J., Wayne, R. P., Shallcross, D. E., Pyle, J. A., and Daele, V.: Is the reaction between CH3C(O)O2 and NO3 important in the night-time troposphere?, J. Chem. Soc. Faraday T., 92, 2211–2222, 1996.
Caralp, F., Forst, W., and Rayez, M. T.: Chemical activation in OH radical-oxidation of 1-n-alkenes, Phys. Chem. Chem. Phys., 5, 476–486, 2003.
Caravan, R. L., Khan, M. A. H., Zádor, J., Sheps, L., Antonov, I. O., Rotavera, B., Ramasesha, K., Kendrew, A., Chen, M., Rösch, D., Osborn, D. L., Fittschen, C., Schoemaecker, C., Duncianu, M., Grira, A., Dusanter, S., Tomas, A., Percival, C., Shallcross, D. E., and Taatjes, C. A.: The reaction of hydroxyl and methylperoxy radicals is not a major source of atmospheric methanol, Nat. Commun., 9, 4343, https://doi.org/10.1038/s41467-018-06716-x, 2018.
Carslaw, N., Carpenter, L. J., Plane, J. M. C., Allan, B. J., Burgess, R. A., Clemitshaw, K. C., Coe, H., and Penkett, S. A.: Simultaneous measurements of nitrate and peroxy radicals in the marine boundary layer, J. Geophys. Res., 102, 18917–18933, 1997.
Carter, W. P. L. and Atkinson, R.: Alkyl nitrate formation from the atmospheric photoxidation of alkanes; a revised estimation method, J. Atmos. Chem., 8, 165–173, 1989.
Cassanelli, P., Fox, D. J., and Cox, R. A.: Temperature dependence of pentyl nitrate formation from the reaction of pentyl peroxy radicals with NO, Phys. Chem. Chem. Phys., 9, 4332–4337, 2007.
Cavalli, F., Barnes, I., and Becker, K.-H.: FT-IR kinetic and product study of the OH radical and Cl-atom–initiated oxidation of dibasic esters, Int. J. Chem. Kinet., 33, 431–439, 2001.
Christensen, L. K., Ball, J. C., and Wallington, T. J.: Atmospheric oxidation mechanism of methyl acetate, J. Phys. Chem. A, 104, 345–351, 2000.
Crounse, J. D., Paulot, F., Kjaergaard, H. G., and Wennberg, P. O.: Peroxy radical isomerization in the oxidation of isoprene, Phys. Chem. Chem. Phys., 13, 13607–13613, 2011.
Crounse, J. D., Knap, H. C., Ørnsø, K. B., Jørgensen, S., Paulot, F., Kjaergaard, H. G., and Wennberg, P. O.: Atmospheric fate of methacrolein. 1. Peroxy radical isomerization following addition of OH and O2, J. Phys. Chem. A, 116, 5756–5762, 2012.
Crounse, J. D., Nielsen, L. B., Jørgensen, S., Kjaergaard, H. G., and Wennberg, P. O.: Autoxidation of organic compounds in the atmosphere, J. Phys. Chem. Lett., 4, 3513–3520, 2013.
Crounse, J. D., Teng, A., and Wennberg, P. O.: Experimental constraints on the distribution and fate of peroxy radicals formed in reactions of isoprene + OH + O2, presented at Atmospheric Chemical Mechanisms: Simple Models – Real World Complexities, University of California, Davis, USA, 10–12 December 2014.
Da Silva, G., Graham, C., and Wang, Z.-F.: Unimolecular β-hydroxyperoxy radical decomposition with OH recycling in the photochemical oxidation of isoprene, Environ. Sci. Technol., 44, 250–256, 2010.
De Gouw, J. A. and Howard, C. J.: Direct measurement of the rate coefficient for the CH2C(CH3)C(O)O2 + NO reaction using chemical ionization mass spectrometry, J. Phys. Chem. A, 101, 8662–8667, 1997.
Dillon, T. J. and Crowley, J. N.: Direct detection of OH formation in the reactions of HO2 with CH3C(O)O2 and other substituted peroxy radicals, Atmos. Chem. Phys., 8, 4877–4889, https://doi.org/10.5194/acp-8-4877-2008, 2008.
Doussin, J. F., Picquet-Varrault, B., Durand-Jolibois, R., Loirat, H. and Carlier, P.: A visible and FTIR spectrometric study of the nighttime chemistry of acetaldehyde and PAN under simulated atmospheric conditions, J. Photochem. Photobio. A, 157, 283–293, 2003.
Eberhard, J. and Howard, C. J.: Temperature-dependent kinetics studies of the reactions of C2H5O2 and n-C3H7O2 radicals with NO, Int. J. Chem. Kinet., 28, 731–740, 1996.
Eberhard, J. and Howard, C. J.: Rate coefficients for the reactions of some C3 to C5 hydrocarbon peroxy radicals with NO, J. Phys. Chem. A, 101, 3360–3366, 1997.
Eberhard, J., Villalta, P. W., and Howard, C. J.: Reaction of isopropyl peroxy radicals with NO over the temperature range 201–401 K, J. Phys. Chem., 100, 993–997, 1996.
Ehn, M., Thornton, J. A., Kleist, E., Sipilä, M., Junninen, H., Pullinen, I., Springer, M., Rubach, F., Tillmann, R., Lee, B., Lopez-Hilfiker, F., Andres, S., Acir, I.-H., Rissanen, M., Jokinen, T., Schobesberger, S., Kangasluoma, J., Kontkanen, J., Nieminen, T., Kurtén, T., Nielsen, L. B., Jørgensen, S., Kjaergaard, H. G., Canagaratna, M., Maso, M. D., Berndt, T., Petäjä, T., Wahner, A., Kerminen, V.-M., Kulmala, M., Worsnop, D. R., Wildt, J., and Mentel, T. F.: A large source of low-volatility secondary organic aerosol, Nature, 506, 476–479, https://doi.org/10.1038/nature13032, 2014.
Ehn, M., Berndt, T., Wildt, J., and Mentel, T.: Highly oxygenated molecules from atmospheric autoxidation of hydrocarbons: a prominent challenge for chemical kinetics studies, Int. J. Chem. Kinet., 49, 821–831, 2017.
Elrod, M. J.: Kinetics study of the aromatic bicyclic peroxy radical + NO Reaction: overall rate constant and nitrate product yield measurements, J. Phys. Chem. A, 115, 8125–8130, 2011.
Faragó, E. P., Schoemaecker, C., Viskolcz, B., and Fittschen, C.: Experimental determination of the rate constant of the reaction between C2H5O2 and OH radicals, Chem. Phys. Lett., 619, 196–200, 2015.
Geyer, A., Bächmann, K., Hofzumahaus, A., Holland, F., Konrad, S., Klüpfel, T., Pätz, H.W., Perner, D., Mihelcic, D., Schäfer, H. J., Volz-Thomas, A., and Platt, U.: Nighttime formation of peroxy and hydroxyl radicals during the BERLIOZ campaign: Observations and modeling studies, J. Geophys. Res., 108, 8249, https://doi.org/10.1029/2001JD000656, 2003.
Glover, B. G. and Miller, T. J.: Near-IR cavity ringdown spectroscopy and kinetics of the isomers and conformers of the butyl peroxy radical, J. Phys. Chem. A, 109, 11191–11197, 2005.
Glowacki, D. R., Wang, L., and Pilling, M. J.: Evidence of formation of bicyclic species in the early stages of atmospheric benzene oxidation, J. Phys. Chem. A, 113, 5385–5396, 2009.
Groß, C. B. M., Dillon, T. J., Schuster, G., Lelieveld, J., and Crowley, J. N.: Direct kinetic study of OH and O3 formation in the reaction of CH3C(O)O2 with HO2, J. Phys. Chem. A, 118, 974–985, https://doi.org/10.1021/jp412380z, 2014.
Hansen, J. C., Li, Y., Rosado-Reyes, C. M., Francisco, J. S., Szente, F. J., and Maricq, M. M.: Theoretical and experimental investigation of the UV cross section and kinetics of the methyl formate peroxy radical, J. Phys. Chem. A, 107, 5306–5316, 2003.
Hasson, A. S., Tyndall, G. S., and Orlando, J. J.: A product yield study of the reaction of HO2 Radicals with ethyl peroxy (CH3CH2O2), acetyl peroxy (CH3C(O)O2), and acetonyl peroxy (CH3C(O)CH2O2) radicals, J. Phys. Chem. A, 108, 5979–5989, 2004.
Hasson, A. S., Tyndall, G. S., Orlando, J. J., Singh, S., Hernandez, S. Q., Campbell, S., and Ibarra, Y.: Branching ratios for the reaction of selected carbonyl-containing peroxy radicals with hydroperoxy radicals, J. Phys. Chem., 116, 6264–6281, 2012.
Hermans, I., Muller, J. F., Nguyen, T. L., Jacobs, P. A., and Peeters, J.: Kinetics of α-hydroxy-alkylperoxyl radicals in oxidation processes. HO2-initiated oxidation of ketones/aldehydes near the tropopause, J. Phys. Chem. A, 109, 4303–4311, 2005.
Horie, O. and Moortgat, G. K.: Reactions of CH3C(O)O2 radicals with CH3O2 and HO2 between 263 K and 333 K, J. Chem. Soc. Faraday T., 88, 3305–3312, 1992.
Hsin, H. Y. and Elrod, M. J.: Overall rate constant measurements of the reaction of hydroxy- and chloroalkylperoxyradicals derived from methacrolein and methyl vinyl ketone with nitric oxide, J. Phys. Chem. A, 111, 613–619, 2007.
Hui, A. O., Fradet, M., Okumura, M., and Sander, S. P.: Temperature dependence study of the kinetics and product yields of the HO2 + CH3C(O)O2 reaction by direct detection of OH and HO2 radicals using 2f-IR wavelength modulation spectroscopy, J. Phys. Chem. A, 123, 3655–3671, https://doi.org/10.1021/acs.jpca.9b00442, 2019.
Jagiella, S. and Zabel, F.: Reaction of phenylperoxy radicals with NO2 at 298 K, Phys. Chem. Chem. Phys., 9, 5036–5051, 2007.
Jagiella, S. and Zabel, F.: Thermal stability of carbonyl radicals. Part II. Reactions of methylglyoxyl and methylglyoxylperoxy radicals at 1 bar in the temperature range 275–311 K, Phys. Chem. Chem. Phys., 10, 1799–1808, 2008.
Jenkin, M. E. and Clemitshaw, K. C.: Ozone and other secondary photochemical pollutants: chemical processes governing their formation in the planetary boundary layer, Atmos. Environ., 34, 2499–2527, 2000.
Jenkin, M. E. and Hayman, G. D.: Kinetics of reactions of primary, secondary and tertiary β-hydroxy peroxyl radicals: application to isoprene degradation, J. Chem. Soc. Faraday T., 91, 433–446, 1995.
Jenkin, M. E., Hayman, G. D., Wallington, T. J., Hurley, M. D., Ball., J. C., Nielsen, O. J., and Ellerman, T.: Kinetic and mechanistic study of the self reaction of CH3OCH2O2 radicals at room temperature, J. Phys. Chem, 97, 11712–11723, 1993a.
Jenkin, M. E., Murrells, T. P., Shalliker, S. J., and Hayman, G. D.: Kinetics and product study of the self-reactions of allyl and allyl peroxy radicals at 296 K, J. Chem. Soc. Faraday T., 89, 433–446, 1993b.
Jenkin, M. E., Saunders, S. M., and Pilling M. J.: The tropospheric degradation of volatile organic compounds: a protocol for mechanism development, Atmos. Environ., 31, 81–104, 1997.
Jenkin, M. E., Boyd, A. A., and Lesclaux, R.: Peroxy radical kinetics resulting from the OH-initiated oxidation of 1,3-butadiene, 2,3-dimethyl-1,3-butadiene and isoprene, J. Atmos. Chem., 29, 267–298, 1998.
Jenkin, M. E., Sulbaek Andersen, M. P., Hurley, M. D., Wallington, T. J., Taketani, F., and Matsumi, Y.: A kinetics and mechanistic study of the OH and NO2 initiated oxidation of cyclohexa-1,3-diene in the gas phase, Phys. Chem. Chem. Phys., 7, 1194–1204, 2005.
Jenkin, M. E., Hurley, M. D., and Wallington, T. J.: Investigation of the radical product channel of the CH3C(O)O2 + HO2 reaction in the gas phase, Phys. Chem. Chem. Phys., 9, 3149–3162, 2007.
Jenkin, M. E., Hurley, M. D., and Wallington, T. J.: Investigation of the radical product channel of the CH3C(O)CH2O2 + HO2 reaction in the gas phase, Phys. Chem. Chem. Phys., 10, 4274–4280, 2008.
Jenkin, M. E., Hurley, M. D., and Wallington, T. J.: Investigation of the radical product channel of the CH3OCH2O2 + HO2 reaction in the gas phase, J. Phys. Chem., 114, 408–416, 2010.
Jenkin, M. E., Young, J. C., and Rickard, A. R.: The MCM v3.3.1 degradation scheme for isoprene, Atmos. Chem. Phys., 15, 11433–11459, https://doi.org/10.5194/acp-15-11433-2015, 2015.
Jenkin, M. E., Valorso, R., Aumont, B., Rickard, A. R., and Wallington, T. J.: Estimation of rate coefficients and branching ratios for gas-phase reactions of OH with aliphatic organic compounds for use in automated mechanism construction, Atmos. Chem. Phys., 18, 9297–9328, https://doi.org/10.5194/acp-18-9297-2018, 2018a.
Jenkin, M. E., Valorso, R., Aumont, B., Rickard, A. R., and Wallington, T. J.: Estimation of rate coefficients and branching ratios for gas-phase reactions of OH with aromatic organic compounds for use in automated mechanism construction, Atmos. Chem. Phys., 18, 9329–9349, https://doi.org/10.5194/acp-18-9329-2018, 2018b.
Jokinen, T., Sipilä, M., Richters, S., Kerminen, V.-M., Paasonen, P., Stratmann, F., Worsnop, D., Kulmala, M., Ehn, M., Herrmann, H. and Berndt, T.: Rapid autoxidation forms highly oxidized RO2 radicals in the atmosphere, Angew. Chem. Int. Ed., 53, 14596–14600, https://doi.org/10.1002/anie.201408566, 2014.
Jørgensen, S., Knap, H. C., Otkjær, R. V., Jensen, A. M., Kjeldsen, M. L. H., Wennberg, P. O., and Kjaergaard, H. G.: Rapid hydrogen shift scrambling in hydroperoxy-substituted organic peroxy radicals, J. Phys. Chem. A, 120, 266–275, https://doi.org/10.1021/acs.jpca.5b06768, 2016.
Kabir, M., Jagiella, S., and Zabel, F: Thermal stability of n-acyl peroxynitrates, Int. J. Chem. Kinet., 46, 462–469, 2014.
Kalalian, C., Roth, E., and Chakir, A.: Atmospheric reactivity of nitrate radicals: reaction with peroxy radicals, Atmos. Environ., 190, 308–316, 2018.
Kirchner, K., Mayer-Figge, A., Zabel, F., and Becker, K.-H.: Thermal stability of peroxynitrates, Int. J. Chem. Kinet., 31, 127–144, 1999.
Kukui, A. S., Jungkamp, T. P. W., and Schindler, R. N.: Aldehyde formation in the reaction of methoxy radicals with NO3, Ber. Bunsen. Phys. Chem., 99, 1565–1567, 1995.
Laversin, H., Cousin, J., Joly, L., Roth, E., Durry, G., and Chakir, A.: Kinetic study of the reaction of nitrate radicals with ethylperoxyradicals between 277 and 358 K, Chem. Phys. Lett., 644, 14–19, 2016.
Le Crâne, J. P. and Lesclaux, R.: UV absorption spectra and self-reaction rate constants for primary peroxy radicals arising from the chlorine-initiated oxidation of carbonyl compounds, Int. J. Chem. Kinet., 38, 276–283, 2006.
Le Crâne, J. P., Villenave, E., Hurley, M. D., Wallington, T. J., Nishida, S., Takahashi, K., and Matsumi, Y.: Atmospheric chemistry of pivalaldehyde and isobutyraldehyde: kinetics and mechanisms of reactions with Cl atoms, fate of (CH3)3CC(O) and (CH3)2CHC(O) radicals, and self-reaction kinetics of (CH3)3CC(O)O2 and (CH3)2CHC(O)O2 radicals, J. Phys. Chem. A, 108, 795–805, 2004.
Lee, L., Teng, A. P., Wennberg, P. O., Crounse, J. D., and Cohen, R. C.: On rates and mechanisms of OH and O3 reactions with isoprene-derived hydroxy nitrates, J. Phys. Chem. A, 118, 1622–1637, 2014.
Lightfoot, P. D., Cox, R. A., Crowley, J. N., Destriau, M., Hayman, G. D., Jenkin, M. E., Moortgat, G. K., and Zabel, F.: Organic peroxy radicals: kinetics, spectroscopy and tropospheric chemistry, Atmos. Environ., 26A, 1805–1964, 1992.
Liu, Y. J., Herdlinger-Blatt, I., McKinney, K. A., and Martin, S. T.: Production of methyl vinyl ketone and methacrolein via the hydroperoxyl pathway of isoprene oxidation, Atmos. Chem. Phys., 13, 5715–5730, https://doi.org/10.5194/acp-13-5715-2013, 2013.
Madronich, S. and Calvert, J. G.: Permutation reactions of organic peroxy radicals in the troposphere, J. Geophys. Res., 95, 5697–5715, 1990.
Matsunaga, A. and Ziemann, P. J.: Yields of beta-hydroxynitrates and dihydroxynitrates in aerosol formed from OH radical initiated reactions of linear alkenes in the presence of NOx, J. Phys. Chem. A, 113, 599–606, https://doi.org/10.1021/jp807764d, 2009.
Matsunaga, A. and Ziemann, P. J.: Yields of beta-hydroxynitrates, dihydroxynitrates, and trihydroxynitrates formed from OH radical-initiated reactions of 2-methyl-1-alkenes, P. Natl. Acad. Sci. USA, 107, 6664–6669, https://doi.org/10.1073/pnas.0910585107, 2010.
McFiggans, G., Mentel, T. F., Wildt, J., Pullinen, I., Kang, S., Kleist, E., Schmitt, S., Springer, M., Tillmann, R., Wu, C., Zhao, D., Hallquist, M., Faxon, C., Le Breton, M., Hallquist, Å. M., Simpson, D., Bergström, R., Jenkin, M. E., Ehn, M., Thornton, J. A., Alfarra, M. R., Bannan, T. J., Percival, C. J., Priestley, M., Topping, D., and Kiendler-Scharr, A.: Secondary organic aerosol reduced by mixture of atmospheric vapours, Nature, 565, 587–593, 2019.
McKee, K., Blitz, M. A., and Pilling, M. J.: Temperature and pressure studies of the reactions of CH3O2, HO2 and 1,2-C4H9O2 with NO2, J. Phys. Chem. A, 120, 1408–1420, 2016.
Mentel, T. F., Springer, M., Ehn, M., Kleist, E., Pullinen, I., Kurtén, T., Rissanen, M., Wahner, A., and Wildt, J.: Formation of highly oxidized multifunctional compounds: autoxidation of peroxy radicals formed in the ozonolysis of alkenes – deduced from structure-product relationships, Atmos. Chem. Phys., 15, 6745-6765, https://doi.org/10.5194/acp-15-6745-2015, 2015.
Miller, A. M., Yeung, L. Y., Kiep, A. C., and Elrod, M. J.: Overall rate constant measurements of the reactions of alkene-derived hydroxyalkylperoxy radicals with nitric oxide, Phys. Chem. Chem. Phys., 6, 3402–3407, 2004.
Mohammed, S. Y., Davis, A. A., Al Rashidi, M. J., and Sarathy, S. M.: High-pressure limit rate rules for α-H isomerization of hydroperoxyalkylperoxy radicals, J. Phys. Chem. A., 122, 3626–3639, https://doi.org/10.1021/acs.jpca.7b11955, 2018.
Møller, K. H., Bates, K. H., and Kjaergaard, H. G.: The importance of peroxy radical hydrogen-shift reactions in atmospheric isoprene oxidation, J. Phys. Chem. A., 123, 920–932, https://doi.org/10.1021/acs.jpca.8b10432, 2019.
Müller, J. F., Liu, Z., Nguyen, V. S., Stavrakou, T., Harvey, J. N., and Peeters, J.: The reaction of methyl peroxy and hydroxyl radicals as a major source of atmospheric methanol, Nat. Commun., 7, 13213, https://doi.org/10.1038/ncomms13213, 2016.
Navarro, N. A., Dusanter, S., and Stevens, P. S.: Temperature dependence of the yields of methacrolein and methyl vinyl ketone from the OH-initiated oxidation of isoprene under NOx-free conditions, Atmos. Environ., 79, 59–66, 2013.
Ng, N. L., Kwan, A. J., Surratt, J. D., Chan, A. W. H., Chhabra, P. S., Sorooshian, A., Pye, H. O. T., Crounse, J. D., Wennberg, P. O., Flagan, R. C., and Seinfeld, J. H.: Secondary organic aerosol (SOA) formation from reaction of isoprene with nitrate radicals (NO3), Atmos. Chem. Phys., 8, 4117–4140, https://doi.org/10.5194/acp-8-4117-2008, 2008.
Nguyen, T. L., Vereecken, L., and Peeters, J.: Theoretical study of the HOCH2OO+ HO2 reaction: detailed molecular mechanisms of the three reaction channels, Z. Phys. Chem., 224, 1081–1093, 2010.
Niki, H., Maker, P. D., Savage, C. M., and Breitenbach, L. P.: FTIR study of the kinetics and mechanism for Cl-atom-initiated reactions of acetaldehyde, J. Phys. Chem., 89, 588–591, 1985.
Nozière, B. and Hanson, D.: Speciated monitoring of gas-phase organic peroxy radicals by chemical ionization mass spectrometry: Cross-reactions between CH3O2, CH3(CO)O2, (CH3)3CO2, and c-C6H11O2, J. Phys. Chem. A, 121, 8453–8464, 2017.
O'Brien, J. M., Czuba, E., Hastie, D. R., Francisco, J. S., and Shepson, P. B.: Determination of the hydroxy nitrate yields from the reaction of C2–C6 alkenes with OH in the presence of NO, J. Phys. Chem. A, 102, 8903–8908, https://doi.org/10.1021/jp982320z, 1998.
Olivella, S., Solé, A., and Bofill, J. M.: Theoretical mechanistic study of the oxidative degradation of benzene in the troposphere: reaction of benzene−HO radical adduct with O2, J. Chem. Theory Comput., 5, 1607–1623, 2009.
Orlando, J. J. and Tyndall, G. S: The atmospheric chemistry of the HC(O)CO radical, Int. J. Chem. Kinet., 33, 149–156, 2001.
Orlando, J. J. and Tyndall, G. S.: Laboratory studies of organic peroxy radical chemistry: an overview with emphasis on recent issues of atmospheric significance, Chem. Soc. Rev., 41, 6294–6317, 2012.
Orlando, J. J., Tyndall, G. S., Bilde, M., Ferronato, C., Wallington, T. J., Vereecken, L., and Peeters, J.: Laboratory and theoretical study of the oxy radicals in the OH- and Cl-initiated oxidation of ethene, J. Phys. Chem. A, 102, 8116–8123, 1998.
Orlando, J. J., Tyndall, G. S., Vereecken, L., and Peeters, J.: The atmospheric chemistry of the acetonoxy radical, J. Phys. Chem. A, 104, 11578–11588, 2000a.
Orlando, J. J., Nozière, B., Tyndall, G. S., and Orzechowska, G. E.: Paulson, S. E., and Rudich, Y.: Product studies of the OH and ozone-initiated oxidation of some monoterpenes, J. Geophys. Res., 105, 11561–11572, 2000b.
Orlando, J. J., Tyndall, G. S., and Wallington, T. J.: The atmospheric chemistry of alkoxy radicals, Chem. Rev., 103, 4657–4689, 2003.
Otkjær, R. V., Jakobsen, H. H., Tram, C. M., and Kjaergaard, H. G.: Calculated hydrogen shift rate constants in substituted alkyl peroxy radicals, J. Phys. Chem. A., 122, 8665–8673, https://doi.org/10.1021/acs.jpca.8b06223, 2018.
Paulot, F., Crounse, J. D., Kjaergaard, H. G., Kurten, A., St Clair, J. M., Seinfeld, J. H., and Wennberg, P. O.: Unexpected epoxide formation in the gas-phase photooxidation of isoprene, Science, 325, 730–733, https://doi.org/10.1126/science.1172910, 2009.
Peeters, J. and Nguyen, T. L: Unusually fast 1,6-H shifts of enolic hydrogens in peroxy radicals: formation of the first-generation C2 and C3 carbonyls in the oxidation of isoprene, J. Phys. Chem. A, 116, 6134–6141, 2012.
Peeters, J., Nguyen, T. L., and Vereecken, L.: HOx radical regeneration in the oxidation of isoprene, Phys. Chem. Chem. Phys., 28, 5935–5939, 2009.
Peeters, J., Müller, J.-F., Stavrakou, T., and Nguyen, V. S.: Hydroxyl radical recycling in isoprene oxidation driven by hydrogen bonding and hydrogen tunneling: the upgraded LIM1 mechanism, J. Phys. Chem. A, 118, 8625–8643, 2014.
Perring, A. E., Pusede, S. E., and Cohen, R. C.: An observational perspective on the atmospheric impacts of alkyl and multifunctional nitrates on ozone and secondary organic aerosol, Chem. Rev., 113, 5848–5870, 2013.
Picquet-Varrault, B., Doussin, J.-F., Durand-Jolibois, R., and Carlier, P.: FTIR spectroscopic study of the OH-induced oxidation of two linear acetates: ethyl and n-propyl acetates, Phys. Chem. Chem. Phys., 3, 2595–2606, 2001.
Picquet-Varrault, B., Doussin, J.-F., Durand-Jolibois, R. and Carlier, P.: FTIR spectroscopic study of the OH-induced oxidation of isopropyl, isobutyl, and tert-butyl acetates, J. Phys. Chem. A, 106, 2895–2902, 2002.
Pimentel, A. S., Tyndall, G. S., Orlando, J. J., Hurley, M. D., Wallington, T. J., Sulbaek Andersen, M. P., Marshall, P., and Dibble, T. S.: Atmospheric chemistry of isopropyl formate and tert-butyl formate, Int. J. Chem. Kinet., 42, 479–498, 2010.
Praske, E., Crounse, J. D., Bates, K. H., Kurtén, T., Kjaergaard, H. G., and Wennberg, P. O.: Atmospheric fate of methyl vinyl ketone: peroxy radical reactions with NO and HO2, J. Phys. Chem. A, 119, 4562–4572, 2015.
Praske, E., Otkjær, R. V., Crounse, J. D., Hethcox, J. C., Stoltz, B. M., Kjaergaard, H. G., and Wennberg, P. O.: Atmospheric autoxidation is increasingly important in urban and suburban North America, P. Natl. Acad. Sci. USA, 115, 64–69, https://doi.org/10.1073/pnas.1715540115, 2017.
Praske, E., Otkjær, R. V., Crounse, J. D., Hethcox, J. C., Stoltz, B. M., Kjaergaard, H. G., and Wennberg, P. O.: Intramolecular hydrogen shift chemistry of hydroperoxy-substituted peroxy radicals, J. Phys. Chem. A., 123, 590–600, https://doi.org/10.1021/acs.jpca.8b09745, 2019.
Raoult, S., Rayez, M.-T. , Rayez, J.-C., and Lesclaux, R.: Gas phase oxidation of benzene: Kinetics, thermochemistry and mechanism of initial steps, Phys. Chem. Chem. Phys., 6, 2245–2253, 2004.
Ray, A., Daele, V., Vassalli, I., Poulet, G., and LeBras, G.: Kinetic study of the reactions of C2H5O and C2H5O2 with NO3 at 298 K, J. Phys. Chem., 100, 5737–5744, 1996.
Rickard, A. R., Wyche, K. P., Metzger, A., Monks, P. S., Ellis, A. M., Dommen, J., Baltensperger, U., Jenkin, M. E., and Pilling, M. J.: Gas phase precursors to anthropogenic secondary organic aerosol: using the Master Chemical Mechanism to probe detailed observations of 1,3,5-trimethylbenzene photo-oxidation, Atmos. Environ., 44, 5423–5433, 2010.
Rissanen, M. P., Kurtén, T., Sipilä, M., Thornton, J. A., Kausiala, O., Garmash, O., Kjaergaard, H. G., Petäjä, T., Worsnop, D. R., Ehn, M., and Kulmala, M.: Effects of chemical complexity on the autoxidation mechanisms of endocyclic alkene ozonolysis products: from methylcyclohexenes toward understanding α-pinene, J. Phys. Chem. A, 119, 4633–4650, https://doi.org/10.1021/jp510966g, 2015.
Roberts, J. M. and Bertman, S. B.: Measurement of the thermal decomposition of peroxyacetic nitric anhydride (PAN) and peroxymethacrylic nitric anhydride (MPAN), Int. J. Chem. Kinet., 24, 297–307, 1992.
Roth, E., Chakir, A., and Ferhati, A.: Study of a peroxybenzoyl radical in the gas phase: ultraviolet spectrum and C6H5C(O)O2+ HO2 reaction between 295 and 357 K, J. Phys. Chem. A, 114, 10367–10379, 2010.
Rowley, D. M., Lightfoot, P. D., Lesclaux, R., and Wallington, T. J.: UV Absorption spectrum and self-reaction of cyclohexylperoxy radicals, J. Chem. Soc. Faraday T., 87, 3221–3226, 1991.
Rowley, D. M., Lesclaux, R., Lightfoot, P. D., Hughes, K., Rudy, S., Hurley, M. D., and Wallington, T. J.: A kinetic and mechanistic study of the reaction of neopentylperoxy radicals with HO2, J. Phys. Chem., 96, 7043–7048, 1992a.
Rowley, D. M., Lesclaux, R., Lightfoot, P. D., Noziere, B., Wallington, T. J., and Hurley, M. D.: Kinetic and mechanistic studies of the reactions of cyclopentylperoxy and cyclohexylperoxy radicals with HO2, J. Phys. Chem., 96, 4889–4894, 1992b.
Rowley, D. M., Lightfoot, P. D., Lesclaux, R., and Wallington, T. J.: Ultraviolet absorption spectrum and self-reaction of cyclopentylperoxy radicals, J. Chem. Soc. Faraday T., 88, 1369–1376, 1992c.
Saunders, S. M., Jenkin, M. E., Derwent, R. G., and Pilling, M. J.: Protocol for the development of the Master Chemical Mechanism, MCM v3 (Part A): tropospheric degradation of non-aromatic volatile organic compounds, Atmos. Chem. Phys., 3, 161–180, https://doi.org/10.5194/acp-3-161-2003, 2003.
Schwantes, R. H., Teng, A. P., Nguyen, T. B., Coggon, M. M., Crounse, J. D., St. Clair, J. M., Zhang, X., Schilling, K. A., Seinfeld, J. H., and Wennberg, P. O.: Isoprene NO3 oxidation products from the RO2+ HO2 pathway, J. Phys. Chem. A, 119, 10158–10171, 2015.
Sehested, J., Christensen, L. K., Nielsen, O. J., Bilde, M., Wallington, T. J., Schneider, W. F., Orlando, J. J., and Tyndall, G. S: Atmospheric chemistry of acetone: kinetic study of the reactions and decomposition of CH3C(O)CH2O2NO2, Int. J. Chem. Kinet., 30, 475–489, 1998.
Teng, A. P., Crounse, J. D., Lee, L., St. Clair, J. M., Cohen, R. C., and Wennberg, P. O.: Hydroxy nitrate production in the OH-initiated oxidation of alkenes, Atmos. Chem. Phys., 15, 4297–4316, https://doi.org/10.5194/acp-15-4297-2015, 2015.
Tomas, A. and Lesclaux, R.: Self-reaction kinetics of the (CH3)2CHC(O)O2 and (CH3)3CC(O)O2 acylperoxy radicals between 275 and 363 K, Chem. Phys. Lett., 319, 521–528, 2000.
Tuazon, E. C., Aschmann, S. M., Atkinson, R., and Carter, W. P. L.: The reactions of selected acetates with the OH radical in the presence of NO: novel rearrangement of alkoxy radicals of structure RC(O)OCH′R, J. Phys. Chem. A, 102, 2316–2321, 1998a.
Tuazon, E. C., Aschmann, S. M., and Atkinson, R.: Products of the gas-phase reactions of the OH radical with 1-methoxy-2-propanol and 2-butoxyethanol, Environ. Sci. Technol., 32, 3336–3345, 1998b.
Tyndall, G. S., Cox, R. A., Granier, C., Lesclaux, R., Moortgat, G. K., Pilling, M. J., Ravishankara, A. R., and Wallington, T. J.: Atmospheric chemistry of small organic peroxy radicals, J. Geophys. Res., D106, 12157–12182, 2001.
Vaughan, S., Canosa-Mas, C. E., Pfrang, C., Shallcross, D. E., Watson, L., and Wayne, R. P.: Kinetic studies of reactions of the nitrate radical (NO3) with peroxy radicals (RO2): an indirect source of OH at night?, Phys. Chem. Chem. Phys., 8, 3749–3760, 2006.
Vereecken, L. and Peeters, J.: Theoretical investigation of the role of intramolecular hydrogen bonding in β-hydroxyethoxy and β-hydroxyethylperoxy radicals in the tropospheric oxidation of ethene, J. Phys. Chem. A, 103, 1768–1775, 1999.
Vereecken, L. and Peeters, J.: Non-traditional (per)oxy ring-closure paths in the atmospheric oxidation of isoprene and monoterpenes, J. Phys. Chem. A, 108, 5197–5204, 2004.
Vereecken, L., Peeters, J., Orlando, J. J., Tyndall, G. S., and Ferronato, C.: Decomposition of β-hydroxypropoxy radicals in the OH-initiated oxidation of propene. A theoretical and experimental study J. Phys. Chem. A, 103, 4693–4702, 1999.
Vereecken, L., Aumont, B., Barnes, I., Bozzelli, J. W., Goldman, M. J., Green, W. H., Madronich, S., McGillen, M. R., Mellouki, A., Orlando, J. J., Picquet-Varrault, B., Rickard, A. R., Stockwell, W. R., Wallington, T. J., and Carter, W. P. L.: Perspective on mechanism development and structure-activity relationships for gas-phase atmospheric chemistry, Int. J. Chem. Kinet., 50, 435–469, 2018.
Villenave, E. and Lesclaux, R.: Kinetics of the cross reactions of CH3O2 and C2H5O2 radicals with selected peroxy radicals, J. Phys. Chem., 100, 14372–14382, 1996.
Villenave, E., Lesclaux, R., Seefeld, S., and Stockwell, W. R.: Kinetics and atmospheric implications of peroxy radical cross reactions involving the CH3C(O)O2 radical, J. Geophys. Res., 103, 25273–25285, 1998.
Walker, H. M., Stone, D., Ingham, T., Vaughan, S., Cain, M., Jones, R. L., Kennedy, O. J., McLeod, M., Ouyang, B., Pyle, J., Bauguitte, S., Bandy, B., Forster, G., Evans, M. J., Hamilton, J. F., Hopkins, J. R., Lee, J. D., Lewis, A. C., Lidster, R. T., Punjabi, S., Morgan, W. T., and Heard, D. E.: Night-time measurements of HOx during the RONOCO project and analysis of the sources of HO2, Atmos. Chem. Phys., 15, 8179–8200, https://doi.org/10.5194/acp-15-8179-2015, 2015.
Wallington, T. J., Hurley, M. D., Maurer, T., Barnes, I., Becker, K. H., Tyndall, G. S., Orlando, J. J., Pimentel, A. S., and Bilde, M.: Atmospheric oxidation mechanism of methyl formate, J. Phys. Chem. A, 105, 5146–5154, 2001.
Wennberg, P. O., Bates, K. H., Crounse, J. D., Dodson, L. G., McVay, R. C., Mertens, L. A., Nguyen, T. B., Praske, E., Schwantes, R. H., Smarte, M. D., St Clair, J. M., Teng A. P., Zhang, X., and Seinfeld, J. H.: Gas-phase reactions of isoprene and its major oxidation products, Chem. Rev., 118, 3337–3390, 2018.
Winiberg, F. A. F., Dillon, T. J., Orr, S. C., Groß, C. B. M., Bejan, I., Brumby, C. A., Evans, M. J., Smith, S. C., Heard, D. E., and Seakins, P. W.: Direct measurements of OH and other product yields from the HO2+CH3C(O)O2 reaction, Atmos. Chem. Phys., 16, 4023–4042, https://doi.org/10.5194/acp-16-4023-2016, 2016.
Xu, L., Møller, K. H., Crounse, J. D., Otkjær, R. V., Kjaergaard, H. G., and Wennberg, P. O.: Unimolecular reactions of peroxy radicals formed in the oxidation of α-pinene and β-pinene by hydroxyl radicals, J. Phys. Chem. A., 123, 1661–1674, https://doi.org/10.1021/acs.jpca.8b11726, 2019.
Yan, C., Kocevska, S., and Krasnoperov, L. N.: Kinetics of the reaction of CH3O2 radicals with OH studied over the 292–526 K temperature range, J. Phys. Chem. A, 120, 6111–6121, 2016.
Yeh, G. K. and Ziemann, P. J.: Alkyl nitrate formation from the reactions of C8-C14 n-alkanes with OH radicals in the presence of NOx: measured yields with essential corrections for gas-wall partitioning. J. Phys. Chem. A, 118, 8147–8157, https://doi.org/10.1021/jp500631v, 2014a.
Yeh, G. K. and Ziemann, P. J.: identification and yields of 1,4-hydroxynitrates formed from the reactions of C8-C16 n-alkanes with OH radicals in the presence of NOx, J. Phys. Chem. A, 118, 8797–8806, https://doi.org/10.1021/jp500631v, 2014b.
Zabel, F., Reimer, A., Becker, K. H., and Fink, E. H.: Thermal decomposition of alkyl peroxynitrates, J. Phys. Chem., 93, 5500–5507, 1989.
Zhang, X., McVay, R., Huang, D. D., Dalleska, N. F., Aumont, B., Flagan, R. C., and Seinfeld, J. H.: Formation and evolution of molecular products in alpha-pinene secondary organic aerosol, P. Natl. Acad. Sci. USA, 112, 14168–14173, 2015.
Ziemann, P. J.: Evidence for low-volatility diacyl peroxides as a nucleating agent and major component of aerosol formed from reactions of O3 with cyclohexene and homologous compounds, J. Phys. Chem. A, 106, 4390–4402, https://doi.org/10.1021/jp012925m, 2002.
The “IUPAC Task Group on Atmospheric Chemical Kinetic Data Evaluation” is abbreviated to “IUPAC Task Group” for simplicity. The evaluation is available at http://iupac.pole-ether.fr/ (last access: January 2019).
- Article
(1832 KB) - Full-text XML





