the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Significant decline of mesospheric water vapor at the NDACC site near Bern in the period 2007 to 2018
Klemens Hocke
Ellen Eckert
Niklaus Kämpfer
The middle atmospheric water vapor radiometer MIAWARA is located close to Bern in Zimmerwald (46.88∘ N, 7.46∘ E; 907 m) and is part of the Network for the Detection of Atmospheric Composition Change (NDACC). Initially built in the year 2002, a major upgrade of the instrument's spectrometer allowed middle atmospheric water vapor to be continuously measured since April 2007. Thenceforward to May 2018, a time series of more than 11 years has been gathered, that makes a first trend estimate possible. For the trend estimation, a robust multilinear parametric trend model has been used. The trend model encompasses a linear term, a solar activity tracker, the El Niño–Southern Oscillation (ENSO) index and the Quasi-Biennial Oscillation (QBO) as well as the annual and semi-annual oscillation. In the time period April 2007 to May 2018 we find a significant decline in water vapor by ppm per decade between 61 and 72 km. Below the stratopause level (∼48 km) a smaller reduction of H2O of up to ppm per decade is detected.
Water vapor is the most important greenhouse gas in the atmosphere (Kiehl and Trenberth, 1997) and has a dominant feedback role in the Earth's climate system. In the troposphere it provides the main source of moisture for the formation process of precipitation in the atmosphere. While global warming progresses, the amount of moisture is expected to increase faster than the overall amount of precipitation, that is controlled by evaporation and the heat budget at the surface (Trenberth et al., 2003).
Long-term changes in the abundance of atmospheric water vapor can be used to characterize climate change. One region of the atmosphere which is very sensitive to those changes is the upper troposphere, but the actual impact on climate change is poorly understood (Held and Soden, 2000). Some direct anthropogenic changes in water vapor are due to emissions by aviation and the possible subsequent formation of contrails that freeze-dry the air and exert a strong radiative forcing (RF) effect. Contrails that persist for several hours and lose their line-shaped form are known as contrail cirrus. Globally averaged (1999 to 2016) annual mean RF estimates with uncertainty ranges are about 0.01 (0.005–0.03) W m−2 for long-lived contrails alone and together with contrail cirrus RF they reach about 0.05 (0.02–0.15) W m−2 (Kärcher, 2018). In contrast, total aviation RF for instance in the year 2000 is about 0.048 W m−2 (Sausen et al., 2005).
Compared to the troposphere, the stratosphere is very dry, and the amount of H2O is commonly indicated in volume mixing ratios (parts per million) like for ozone. Water vapor from the troposphere can enter the stratosphere mainly through convective processes at the Equator. The cold tropical tropopause acts as a cold trap for ascending tropospheric air and causes most of the water vapor to freeze out. Nevertheless, water vapor in the stratosphere has a high impact on ozone chemistry, and it is of importance to a global warming feedback process. Further, water vapor provides the main source of hydrogen radicals (OH, H,HO2), which are involved in the catalytic destruction cycle of ozone in the stratosphere (Brasseur and Solomon, 2006). An important long-term data set of lower free tropospheric (2 km) up to middle stratospheric (28 km) water vapor has been available from Boulder (Colorado) since 1980. These data come from balloon frost-point hygrometer (FPH) measurements that are launched usually once per month. A weighted, piecewise regression analysis of the 30-year record from 1980 to 2010 by Hurst et al. (2011) revealed an average increase of 1.0±0.2 ppm in the altitude range between 16 and 26 km. About a quarter of the H2O increase could be attributed to changes in the methane (CH4) concentration. Methane can easily be transported from the surface upward into the stratosphere, where its oxidation is a major in situ source of water vapor.
Compared to water vapor, stratospheric ozone has attracted much higher scientific attention in regard of its long-term development after the detection of the Antarctic ozone hole in 1985 (Farman et al., 1985). Two years later in 1987, the Montreal Protocol was signed to protect the ozone layer by banning and regulating the production of numerous substances that are responsible for ozone depletion. Numerous trend studies on ozone have been published in recent years (e.g., Eckert et al., 2014; Moreira et al., 2015; Steinbrecht et al., 2017; Ball et al., 2018), showing how ozone has developed in the course of time. Drift-corrected ozone trends from MIPAS (Michelson Interferometer for Passive Atmospheric Sounding) space-borne observations (July 2002 to April 2012) range from negative (up to −0.41 ppm per decade) in the tropical stratosphere to positive (+0.55 ppm per decade) at southern midlatitudes (Eckert et al., 2014). A 20-year continuous mapping of the stratospheric ozone layer at the NDACC site Bern could be achieved. A recent trend analysis by Moreira et al. (2015) showed that ozone recovered by about 3 % per decade at an altitude of 40 km within the time period 1997 to 2015. Steinbrecht et al. (2017) calculated ozone trends for a larger number of ground-based NDACC site observations using different techniques such as FTIR (Fourier transform infrared spectroscopy), microwave radiometry or lidar. They found positive trends between 35 and 48 km altitude in the tropics as well as in the 35 to 65∘ latitude belts of the Northern and Southern Hemisphere. More specifically, ozone mixing ratios at 42 km increased by 1.5 % (tropics) and 2–2.5 % (midlatitudes) per decade, respectively. Although total column measurements of ozone show that the ozone layer has stopped declining across the globe, there is some evidence from satellite observations that lower stratospheric ozone has continued to decline within 60∘ N to 60∘ S after 1998, resulting in a downward trend of stratospheric ozone columns (Ball et al., 2018).
In order to understand detected water vapor trends in the middle atmosphere, models and measurements are both important. A 40-year (1960–1999) model simulation with the coupled chemistry–climate model (CCM) ECHAM resulted in a global mean stratospheric H2O increase of 0.7 ppm between 1980 and 1999 (Stenke and Grewe, 2005). Trend estimates in lower stratospheric water vapor strongly differentiate between the NOAA (National Oceanic and Atmospheric Administration) FPH observations at Boulder and merged zonal mean satellite measurements as pointed out by Lossow et al. (2018). The differences reach up to 0.5 ppm per decade and change signs from positive for the in situ observations to negative for the processed satellite data. But not only do the observations not agree, but also extensive trend estimates from simulations show discrepancies for the location of Boulder and the corresponding zonal mean latitude band around 40∘ N. An intercomparison of ground-based microwave and satellite linear trends in the lower mesosphere at an altitude of about 53 km (0.46 hPa) within different extended periods shows no consistent picture between the different observations. The following stations were considered in the study by Nedoluha et al. (2017): Lauder, Mauna Loa, Table Mountain, Seoul, Bern and Onsala. Satellite retrievals that were integrated in the intercomparison include ACE-FTS (Advanced Composition Explorer – Fourier Transform Spectrometer), HALOE (Halogen Occultation Experiment), MIPAS (Michelson Interferometer for Passive Atmospheric Sounding), MLS (Microwave Limb Sounder), SCIAMACHY (Scanning Imaging Absorption Spectrometer for Atmospheric Chartography), SMR (Sub-Millimeter Radiometer), SOFIE (Solar Occultation For Ice Experiment) and different data subversions of these. At none of the comparison sites could a uniform result of only positive or negative trends be retrieved. This might be related to the problem that the time periods cover different ranges. Regarding Fig. 8 in Nedoluha et al. (2017), the trends at Bern range from +16 to −5 % per decade. However, the majority of H2O time series, including Aura/MLS, exhibit small positive relative trends in the range between 1 % and 7 % per decade. At the 0.46 hPa pressure level the multilinear regression model used in our study does not produce a significant trend at the 95 % confidence level.
On a seasonal timescale mesospheric water vapor is changing its concentration, mainly due to the vertical advection caused by the meridional circulation. As shown by Chandra et al. (1997), within the solar cycle timescale, the modulation of the Lyman-α radiation intensity is forcing changes of up to 30 %–40 % near the mesopause level. An in situ source of H2O is the oxidation of methane. The long-term increase in methane accounts thus for an increase in H2O and estimates yield values of about 0.4 % per year (Chandra et al., 1997). It is clear that the actual long-term development of mesospheric H2O is related to a complex mixture of different processes, and it is still not certain how mesospheric water vapor develops in a changing climate of the earth. Therefore it is very important to continue the observations, especially from those instruments that already have long records such as the microwave NDACC instruments at Mauna Loa (Hawaii), Table Mountain (USA) or Bern (Switzerland). In this study we report on a detected decline of H2O in the mesosphere from the NDACC ground-based microwave measurement site near Bern in the time period between 2007 and 2018.
Section 2 introduces the NDACC measurement site Bern with the MIAWARA radiometer in more detail and presents the water vapor data set that is processed in the trend model which is introduced in Sect. 3 later. The final results of the trend study are handled in Sect. 3.2, while conclusions are given in Sect. 4.
The MIddle Atmospheric WAter vapor RAdiometer (MIAWARA) measures the intensity of the pressure broadened emission of H2O molecules at a center frequency of 22.235 GHz (Kämpfer et al., 2012). Atmospheric pressure decreases exponentially with altitude, and this information is reflected in the H2O line shape. The obtained spectra are used to retrieve water vapor profiles by means of radiative transfer calculations and the optimal estimation method as described in Rodgers (2000) using the retrieval software package ARTS/Qpack (Eriksson et al., 2005; Buehler et al., 2018). As a spectroscopic H2O model, a combination of the H2O-MPM93 model from Liebe et al. (1993), for the pressure-broadened half line width, and recent entries in the JPL (Jet Propulsion Laboratory) line catalog, for the lower state energy and line strength at 300 K, is taken. MIAWARA has been continuously operated on the roof of the building for Atmospheric Remote Sensing in Zimmerwald (46.88∘ N, 7.46∘ E; ), which is close to Bern, since September 2006. The reason why we only use data from April 2007 onwards is a major upgrade of the instrument from optoacoustic to fast Fourier transform (FFT) spectrometry. In the course of this upgrade the spectral resolution increased from 600 to 61 kHz. Other technical instrumental parameters are summarized in Table 1.
In recent years, data from the MIAWARA radiometer have been used to detect a solar-induced variability of mesospheric H2O (Lainer et al., 2016); further they have been used to investigate planetary 16 d, subdiurnal and 2 d atmospheric wave activities by using H2O as a dynamical tracer (Scheiben et al., 2014; Lainer et al., 2017, 2018).
2.1 Measurement stability
The total FFT spectrometer bandwidth of MIAWARA is 1 GHz, but only a narrow part of maximal 250 MHz is in general usable in the retrieval procedure due to baseline artifacts at the wings of the H2O line spectrum. However, the reduced bandwidth is sufficient for the retrieval of water vapor in the middle atmosphere, and even less is needed for the mesosphere. In order to guarantee a high stability of the spectral measurements we further constrain the bandwidth to 80 MHz around the central line frequency of MIAWARA. The calibration of the radiometer is done via a tipping curve scheme, using different sky elevation angles, to derive tropospheric opacities and receiver temperatures every 20 min (Fig. 1). At several times per year a manual liquid nitrogen calibration is performed as a verification method. Figure 1 demonstrates that the tipping curve calibration performed well during the whole investigated time period. The seasonal changes in tropospheric opacity are due to the local weather variability and affect the sensitive altitude region of the water vapor retrieval. In order to reduce the effect of tropospheric conditions on the retrieval, we use a variable integration scheme of the spectral information to reach a stable measurement noise of 0.01±0.0005 K. Further, we set the measurement response to 80 % to derive a quite stable upper and lower limit of the measurements. This approach generates profiles with a time resolution of typically a few hours in winter and up to 1–2 d during summer.
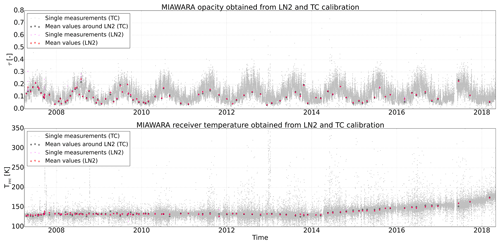
Figure 1Development of the tropospheric opacities and the MIAWARA receiver temperatures as obtained from tipping curve (TC) (operational, grey dots) and regular liquid nitrogen (LN2) verification calibrations (mean values shown by red markers). The mean values around LN2 can be compared to the mean values around TC that are shown by the black markers. The time period between April 2007 and May 2018 is shown.
The change of a broken pre-amplifier in the MIAWARA frontend in early 2014 resulted in a continuously increase of the receiver temperature afterwards. As shown in the bottom plot of Fig. 1, the receiver temperatures were at a rather constant level below 150 K before the amplifier change, while thereafter an increase up to about 200 K until 2018 was observed. However this increase obviously does not effect the derivation of the tropospheric opacities which do not show any pattern change or increase after 2014. The increasing receiver temperatures also lead to higher noise levels of MIAWARA. But with the application of a dynamic integration scheme, this effect is fully compensated for.
The a priori water vapor information is derived from a monthly mean zonal mean climatology using Aura/MLS v2.2 data over 4 years between 2004 and 2008. The most recent Level2 Aura/MLS data (v.4.2) are used to initialize pressure, temperature and geopotential height within the MIAWARA H2O retrieval. The vertical resolution of the instrument varies between 11 km in the stratosphere and 14 km in the mesosphere (Deuber et al., 2005). An instrument validation against Aura/MLS v3.3 with more than 1000 seasonal separated profile comparisons can be found in Lainer et al. (2015). An area of 800 km × 400 km (E/W × N/S) has been used as a spatial coincident criterion for the satellite overpasses. In the pressure range of 2–10 hPa the relative differences are below 3 %, and between 0.05 and 2 hPa the analysis revealed negative biases of MIAWARA compared to Aura/MLS of up to −10 %.
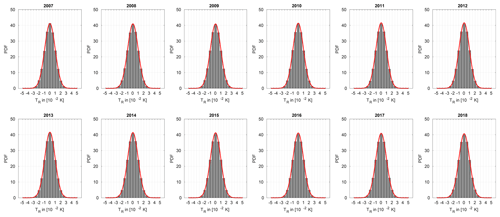
Figure 2Yearly averaged histograms of the MIAWARA residuals (difference between measured difference spectrum and modeled spectrum) as residuum brightness temperature fluctuations TR in 10−2 K within the frequency range of 22.195 to 22.275 GHz (80 MHz bandwidth) from 2007 to 2018, showing the evolution of the PDF (probability density function). The red curve is the fit of the corresponding normal distribution. The chosen bin width is .
In Fig. 2 we show the overall yearly statistics of the MIAWARA residuals in a bandwidth of 80 MHz. The residuals are defined as the difference between the observed difference spectrum and the modeled spectrum from the retrieved profile, illustrated as residuum brightness temperature fluctuations TR. Especially measurements at lower altitudes like in the stratosphere are particularly dependent on a good baseline fitting over a broad frequency range. Overall two different baseline fittings are performed. A fifth-order polynomial fit and a sinus fit with six coefficients guarantee a stable removal of baseline artifacts on our calibrated spectra. In particular, the histograms show the PDF (probability density function) of the binned (bin width: ) brightness temperature fluctuations TR of the yearly cumulated MIAWRARA measurement noise ,together with the fit of a normal distribution. Overall, the maxima of the normal distribution fits are centered at 0 K, and the changes between the years are negligible.
The two plots in Fig. 3 show the monthly and yearly averaged time series of TR at 22.235 GHz valid for the time period between April 2007 and May 2018. In the monthly mean overview it is visible that the range of the noise varies between 0.0102 and 0.0097 K. Starting from autumn 2010 an improvement of the residual temperature patterns could be achieved according to an upgrade of the measurement cycle scheme, resulting in more measurement data per time interval, while maintaining the same thermal noise level of the measured difference spectrum. The upgrade of the measurement cycle had no effect on the overall homogeneity of the water vapor time series, also because the measurements were always conducted with the same FFT spectrometer. In both plots no trend pattern can be found, concluding that no frequency shift of MIAWARA occurred within the investigated time period.
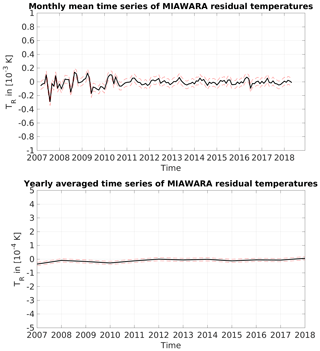
Figure 3Monthly and yearly averaged MIAWARA TR residuals within the time period of the trend analysis (April 2007 to May 2018). The red dashed lines mark the respective standard deviations.
Beside baseline artifacts which are not fitted correctly, it is known that the retrieval averaging kernels A can have an impact on the H2O profile product. For a long-term measurement-based trend study it is of importance that any variability of A does not imply a data drift, which could induce an artificial trend. Accordingly we investigate this issue through a sensitivity trend test in Sect. 3.1.
2.2 H2O data and error handling
Figure 4 presents the derived monthly mean H2O data time series from the MIAWARA instrument at the northern midlatitude observation site Bern. From 1 April 2007 to 30 April 2018 a total of 133 months are available. The white horizontal lines indicate the pressure level at which the measurement response (MR) drops below 80 %. A nonsignificant variability of MR can be seen at the lower altitude limit at around 3 hPa. A larger but stable variability can be found in the upper mesosphere between 0.02 and 0.04 hPa. We find a high correlation between the variability of tropospheric opacity (Fig. 1) and the MR at the upper altitude limit. That the MR variability is not critical for trend estimates is explained in Sect. 3.1.
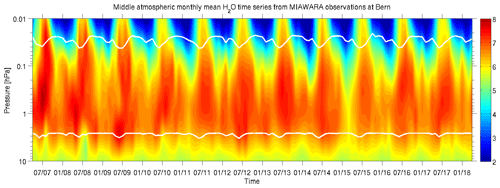
Figure 4Monthly mean water vapor time series in parts per million (ppm) obtained by the MIAWARA instrument located at the Zimmerwald observatory near Bern between April 2007 and May 2018. The horizontal upper and lower white lines indicate the pressure layer within which the measurement response is higher than 80 %. This data set is used as input for the trend model.
The annual cycle of water vapor is the most obvious signature in Fig. 4 and mainly originates from dynamics. In the summer midlatitude mesosphere an upwelling motion of water vapor rich air, caused by the Brewer–Dobson circulation, determines the seasonal variability. The photodissociation by Lyman-α radiation, which is stronger during summer, only has a minor impact on the abundance of water vapor. This is predominantly the case in the upper mesosphere and mesopause region at about 80 km.
For the trend model it is very important to assess a reasonable uncertainty of the microwave radiometer measurements and thus the overall error of the monthly mean water vapor profiles. Two different types of errors were considered. The first type is the natural variability, which can be approximated by the standard error σstd of the monthly mean H2O profiles. The second type is the instrument-related observational error σobs that belongs to the random error and depends on the thermal noise on the water vapor spectra. The observational error is calculated during the retrieval computation. Both errors were then combined in the following way to get a total monthly mean error profile σtot for the initialization of the trend model:
Figure 5c shows the temporal evolution of the total error at an altitude of 70 km. At this altitude the error predominantly fluctuates around 0.3 ppm.
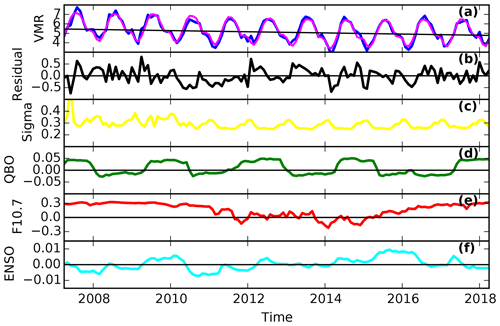
Figure 5Panel (a) shows the trend fit at 0.04 hPa (70 km), with the MIAWARA monthly mean H2O data (blue line), the calculated model fit (magenta line) and the related linear trend (black line). Panel (b) shows the residual, and in the following panels (c), (d), (e) and (f) the evolution of the σ uncertainty (yellow line), the fitted signals of the QBO (green line), F10.7 (red line) and ENSO (cyan line) proxies at 0.04 hPa are shown.
We performed the trend analyses of the water vapor data through a robust multilinear parametric trend estimation method developed by von Clarmann et al. (2010). The trend program finds a linear trend of the data time series by minimizing a cost function.
The cost function includes a quadratic norm of the residual between a regression model and the analyzed monthly H2O profile time series, weighted by the inverse covariance matrix of the data errors. The data errors are based on the monthly standard deviation and observational errors of the instruments as described in Sect. 2.2. In addition, error correlations between data points are supported, which makes the method suitable for consideration of autocorrelated residuals. The regression function Y(t) itself consists of an axis intercept, a linear trend, sine waves and different proxies:
where t represents the time and a and b the constant term and the slope of the fit. The terms qbo1 and qbo2 are the normalized Singapore winds at 30 and 50 hPa pressure levels as provided by the Free University of Berlin via http://www.geo.fu-berlin.de/met/ag/strat/produkte/qbo/index.html (last access: 1 April 2019). According to Kyrölä et al. (2010), the Singapore zonal wind series at the two altitudes are in good approximation orthogonal to each other so that the combination of both can reproduce the Quasi-Biennial Oscillation (QBO) phase shift. Fitting against the solar irradiance variability is accounted for by the solar radio flux at 10.7 cm, hereafter denoted as F10.7, which is a good proxy for this variability. The MEI term in the regression function is the multivariate ENSO index. It describes the strength of the El Niño–Southern Oscillation (ENSO) with six parameters consisting of surface winds (zonal and meridional), sea surface temperature, sea level pressure, surface air temperature and the sky cloudiness fraction. Both the solar activity and MEI index lists are available from the following web page: https://www.esrl.noaa.gov/psd/data/climateindices/list/ (last access: 1 April 2019).
The sum term consists of two sine and cosine functions with the period length ln, including the annual and semi-annual oscillations (l1=182.5 d and l2=365 d). All coefficients (a, b, c1, c2, c3, d1, d2, d3, e and f) are fitted against the water vapor monthly mean time series in order to estimate the linear variations.
For the water vapor trend analyses, the multilinear regression model needs the monthly mean profiles together with their uncertainties as input. Figure 5a represents the H2O model fit (magenta line) on top of the monthly mean time series (blue line) derived by MIAWARA and the linear variation (black line) on 0.04 hPa. Overall, the temporal H2O variability could be very well reproduced by the model fit, which is also revealed by the residual between the measurements and fit (Fig. 5b) rarely exceeding 0.5 ppm. Overall, the regression model is able to explain about 90 % of the variance of the measurements between 0.02 and 3 hPa. The three other panels display the H2O fitted signals of the QBO (green line), F10.7 (red line) and ENSO (cyan line) proxies at 0.04 hPa (70 km).
3.1 Averaging kernel sensitivity test
Here we describe a test performed on an artificial water vapor profile time series in order to check if the variability of the MIAWARA averaging kernels can induce a data drift that might be misinterpreted as a trend. The averaging kernel matrix A is defined as
It represents the sensitivity of the retrieved state to the difference in the true atmospheric state x. The measured microwave spectrum is denoted as y. In our case we use a time series of one constant artificial H2O profile xart of 5 ppm at 50 pressure levels between 10 and 0.01 hPa at the same time steps as the original MIAWARA profiles as follows:
A has to be given on the grid of xa and is interpolated to the grid of x, conserving the measurement response. The artificial convolved water vapor time series (beginning of April 2007 to the end of April 2018) was then used to calculate monthly mean profiles that could be used as input to the trend model described in Sect. 3. No significant trend has been generated by the convolution process with the MIAWARA v301 averaging kernels, the retrieval version for the main trend analysis. In conclusion this means that neither a variability of A nor a variability in the measurement response (white lines in Fig. 4), which is derived from A, can have an effect on the result of the trend estimate presented in Sect. 3.2.
3.2 H2O trend estimate
After having shown that MIAWARA is measuring with a high instrumental stability, we are confident about presenting the trend result from the multilinear parametric trend model (von Clarmann et al., 2010). Figure 6 shows the estimated water vapor trend profiles in absolute (panel a) and relative (panel b) units. The latter is calculated relative to the mean H2O profile between April 2007 and May 2018. Although the pressure range of the trend profile goes from 0.01 to 10 hPa in the two plots, equivalent to 30–80 km, we restrict the trustworthy trend results to the altitudes of the MIAWARA radiometer, which are to a degree of 80 % a priori-independent. These lower and upper limits are marked by the horizontal red lines and are located at 0.03 and 2.5 hPa. At higher and lower altitudes the trend turns towards zero, which is to be expected due to the fact that the MIAWARA mixing ratios gradually approach the climatology of Aura/MLS a priori values and those exhibit no long-term variability. Further, a significant trend result between the red lines could not be obtained at every pressure level. This circumstance is expressed by the green dashed boxes by encompassing two altitude regions in which the trend is 2 times larger than the uncertainty. According to Tiao et al. (1990) this is equivalent to a significance on the 95 % confidence level.
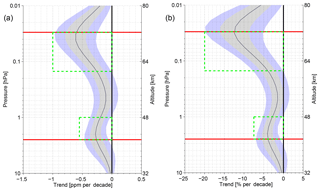
Figure 6Estimated water vapor trend profile in parts per million (ppm) per decade (a) and percent (%) per decade (b), for the time period between April 2007 and May 2018, observed by the MIAWARA instrument at the Zimmerwald observatory close to Bern, Switzerland. The black line represents the trend profile; the grey and violet shaded areas represent the 1σ and 2σ uncertainties of the trend estimate. The green boxes show where the trend is statistically significant on the 95 % confidence level. The horizontal red lines mark the pressure range (0.03–2.5 hPa) where the MIAWARA data is to ∼80 % a priori independent.
Below the stratopause from 1 to 2.5 hPa (42–48 km) a small but still significant negative trend, maximizing at 2 hPa, could be determined. A mean linear decline rate of ppm per month results in ppm per decade (in relative units: % per decade) or a total loss of ≈0.33 ppm in the analyzed measurement period. This result is contradictory to explanations presented in North et al. (2015), whereby the increase of methane in the last decades is expected to also increase the water vapor content in the stratosphere through photodissociation and oxidation. On the other hand it has been pointed out that the current understanding of the total stratospheric water vapor budget and the mechanisms involved in controlling the entry and mixing of H2O into the lower stratosphere is still under investigation.
The second statistically significant pressure layer in the MIAWARA trend profile is located in the mesosphere between 0.03 and 0.15 hPa (61–72 km). Although the 1σ error in the trend estimate is roughly doubled, the negative trend is clearly strengthened to ppm per decade at 0.03–0.04 hPa. In relative terms, we see a decrease between −12 and % per decade. The impact of the included extra month of H2O data on the trend estimate was found to be below a change of ±0.05 ppm. It is difficult to find other water vapor trend studies in the literature that investigate mesospheric altitudes and cover a comparable time period. Satellite data from Aura/MLS, which have existed since August 2004, could be a basis for trend investigations. Lately MLS data have been globally analyzed by Froidevaux et al. (2019), and in the case of water vapor a positive trend was derived between 100 and 0.03 hPa for northern and southern latitudes up to 60∘. However, Aura/MLS H2O data below 20 hPa could be problematic for estimating trends due to detected data drifts (Hurst et al., 2016).
Robust measurements by the water vapor radiometer MIAWARA, which belongs to the NDACC network, were performed between April 2007 and May 2018 and used to obtain a middle atmospheric trend profile by means of a multilinear parametric regression trend model fit of prior derived monthly mean profile and uncertainty data time series.
With this study, we demonstrated the high stability of the MIAWARA residuals and outlined that any variability of the averaging kernels or measurement response fluctuations do not induce a measurement drift. Hence we rely on the computed trend results with the presented multilinear parametric regression trend model. Overall two altitude regions exhibit a significant (95 % confidence) negative water vapor trend during the time period of April 2007 to May 2018.
-
0.03–0.15 hPa (61–72 km): % per decade.
-
1–2.5 hPa (42–48 km): % per decade.
We are not able to give an explanation for the reasons for the detected H2O decline below the stratopause and in the mesosphere. The complexity of interactions between dynamics and chemistry is hard to address using observations alone. Numerical investigations will be needed to unravel the impacts of the different processes, like the long-term development of methane concentrations, temperature trends, H2O advection within Brewer–Dobson circulation or changes in photodissociation rates.
Because of the fact that a lot of inconsistent results are published regarding the evolution of middle atmospheric water vapor, it will be of great importance to continue with measurements from various ground-based observation sites. Satellite missions, like EOS Aura, can provide data for almost the whole globe (82∘ S to 82∘ N); however the maintenance of the long-term stability and lifetime is limited and complicates trend studies.
Data from the ground-based microwave instrument MIAWARA are publicly available from the NDACC database as monthly files with a diurnal temporal resolution (ftp://ftp.cpc.ncep.noaa.gov/ndacc/station/bern, last access: 1 May 2019).
ML was responsible for the ground-based water vapor measurements, performed the trend analysis and prepared the paper. KH contributed to the interpretation of the results. EE was involved in the development of the trend model. NK led the microwave project group at the University of Bern and he took care of the operation and funding of MIAWARA.
The authors declare that they have no conflict of interest.
The study presented was supported by the Swiss National Science Foundation and MeteoSwiss in the framework of the GAW project “Fundamental GAW parameters measured by microwave radiometry”.
This research was supported by the Swiss National Science Foundation (grant no. 200020-160048) and MeteoSwiss.
This paper was edited by Farahnaz Khosrawi and reviewed by three anonymous referees.
Ball, W. T., Alsing, J., Mortlock, D. J., Staehelin, J., Haigh, J. D., Peter, T., Tummon, F., Stübi, R., Stenke, A., Anderson, J., Bourassa, A., Davis, S. M., Degenstein, D., Frith, S., Froidevaux, L., Roth, C., Sofieva, V., Wang, R., Wild, J., Yu, P., Ziemke, J. R., and Rozanov, E. V.: Evidence for a continuous decline in lower stratospheric ozone offsetting ozone layer recovery, Atmos. Chem. Phys., 18, 1379–1394, https://doi.org/10.5194/acp-18-1379-2018, 2018. a, b
Brasseur, G. and Solomon, S.: Aeronomy of the Middle Atmosphere: Chemistry and Physics of the Stratosphere and Mesosphere, vol. 32, Springer, Dordrecht, the Netherlands, 2006. a
Buehler, S. A., Mendrok, J., Eriksson, P., Perrin, A., Larsson, R., and Lemke, O.: ARTS, the Atmospheric Radiative Transfer Simulator – version 2.2, the planetary toolbox edition, Geosci. Model Dev., 11, 1537–1556, https://doi.org/10.5194/gmd-11-1537-2018, 2018. a
Chandra, S., Jackman, C. H., Fleming, E. L., and Russell III, J. M.: The Seasonal and Long Term Changes in Mesospheric Water Vapor, Geophys. Res. Lett., 24, 639–642, https://doi.org/10.1029/97GL00546, 1997. a, b
Deuber, B., Haefele, A., Feist, D. G., Martin, L., Kämpfer, N., Nedoluha, G. E., Yushkov, V., Khaykin, S., Kivi, R., and Vomel, H.: Middle Atmospheric Water Vapour Radiometer – MIAWARA: Validation and first results of the LAUTLOS/WAVVAP campaign, J. Geophys. Res., 110, D13306, https://doi.org/10.1029/2004JD005543, 2005. a
Eckert, E., von Clarmann, T., Kiefer, M., Stiller, G. P., Lossow, S., Glatthor, N., Degenstein, D. A., Froidevaux, L., Godin-Beekmann, S., Leblanc, T., McDermid, S., Pastel, M., Steinbrecht, W., Swart, D. P. J., Walker, K. A., and Bernath, P. F.: Drift-corrected trends and periodic variations in MIPAS IMK/IAA ozone measurements, Atmos. Chem. Phys., 14, 2571–2589, https://doi.org/10.5194/acp-14-2571-2014, 2014. a, b
Eriksson, P., Jiménez, C., and Buehler, S. A.: Qpack, a general tool for instrument simulation and retrieval work, J. Quant. Spectrosc. Ra., 91, 47–64, https://doi.org/10.1016/j.jqsrt.2004.05.050, 2005. a
Farman, J. C., Gardiner, B. G., and Shanklin, J. D.: Large losses of total ozone in Antarctica reveal seasonal ClOx∕NOx interaction, Nature, 315, 207–210, https://doi.org/10.1038/315207a0, 1985. a
Froidevaux, L., Kinnison, D. E., Wang, R., Anderson, J., and Fuller, R. A.: Evaluation of CESM1 (WACCM) free-running and specified dynamics atmospheric composition simulations using global multispecies satellite data records, Atmos. Chem. Phys., 19, 4783–4821, https://doi.org/10.5194/acp-19-4783-2019, 2019. a
Held, I. M. and Soden, B. J.: Water Vapor Feedback And Global Warming, Annu. Rev. Energ. Env., 25, 441–475, https://doi.org/10.1146/annurev.energy.25.1.441, 2000. a
Hurst, D. F., Oltmans, S. J., Vömel, H., Rosenlof, K. H., Davis, S. M., Ray, E. A., Hall, E. G., and Jordan, A. F.: Stratospheric water vapor trends over Boulder, Colorado: Analysis of the 30 year Boulder record, J. Geophys. Res.-Atmos., 116, D02306, https://doi.org/10.1029/2010JD015065, 2011. a
Hurst, D. F., Read, W. G., Vömel, H., Selkirk, H. B., Rosenlof, K. H., Davis, S. M., Hall, E. G., Jordan, A. F., and Oltmans, S. J.: Recent divergences in stratospheric water vapor measurements by frost point hygrometers and the Aura Microwave Limb Sounder, Atmos. Meas. Tech., 9, 4447–4457, https://doi.org/10.5194/amt-9-4447-2016, 2016. a
Kämpfer, N., Nedoluha, G., Haefele, A., and De Wachter, E.: Microwave Radiometry, vol. 10 of ISSI Scientific Report Series, Springer New York, https://doi.org/10.1007/978-1-4614-3909-7, 2012. a
Kärcher, B.: Formation and radiative forcing of contrail cirrus, Nat. Commun., 9, 1824, https://doi.org/10.1038/s41467-018-04068-0, 2018. a
Kiehl, J. T. and Trenberth, K. E.: Earth's Annual Global Mean Energy Budget, B. Am. Meteorol. Soc., 78, 197–208, https://doi.org/10.1175/1520-0477(1997)078<0197:EAGMEB>2.0.CO;2, 1997. a
Kyrölä, E., Tamminen, J., Sofieva, V., Bertaux, J. L., Hauchecorne, A., Dalaudier, F., Fussen, D., Vanhellemont, F., Fanton d'Andon, O., Barrot, G., Guirlet, M., Fehr, T., and Saavedra de Miguel, L.: GOMOS O3, NO2, and NO3 observations in 2002–2008, Atmos. Chem. Phys., 10, 7723–7738, https://doi.org/10.5194/acp-10-7723-2010, 2010. a
Lainer, M., Kämpfer, N., Tschanz, B., Nedoluha, G. E., Ka, S., and Oh, J. J.: Trajectory mapping of middle atmospheric water vapor by a mini network of NDACC instruments, Atmos. Chem. Phys., 15, 9711–9730, https://doi.org/10.5194/acp-15-9711-2015, 2015. a
Lainer, M., Hocke, K., and Kämpfer, N.: Variability of mesospheric water vapor above Bern in relation to the 27-day solar rotation cycle, J. Atmos. Sol.-Terr. Phy., 143–144, 71–87, https://doi.org/10.1016/j.jastp.2016.03.008, 2016. a
Lainer, M., Hocke, K., Rüfenacht, R., and Kämpfer, N.: Quasi 18 h wave activity in ground-based observed mesospheric H2O over Bern, Switzerland, Atmos. Chem. Phys., 17, 14905–14917, https://doi.org/10.5194/acp-17-14905-2017, 2017. a
Lainer, M., Hocke, K., and Kämpfer, N.: Long-term observation of midlatitude quasi 2-day waves by a water vapor radiometer, Atmos. Chem. Phys., 18, 12061–12074, https://doi.org/10.5194/acp-18-12061-2018, 2018. a
Liebe, H., Hufford, G., and Cotton, M.: Propagation modeling of moist air and suspended water/ice particles at frequencies below 1000 GHz, in: AGARD, Atmospheric Propagation Effects Through Natural and Man-Made Obscurants for Visible to MM-Wave Radiation, 11 pp. (SEE N94-30495 08-32), AGARD Conference Proceedings 542, May 1993, Palma de Mallorca, Spain, 1993. a
Lossow, S., Hurst, D. F., Rosenlof, K. H., Stiller, G. P., von Clarmann, T., Brinkop, S., Dameris, M., Jöckel, P., Kinnison, D. E., Plieninger, J., Plummer, D. A., Ploeger, F., Read, W. G., Remsberg, E. E., Russell, J. M., and Tao, M.: Trend differences in lower stratospheric water vapour between Boulder and the zonal mean and their role in understanding fundamental observational discrepancies, Atmos. Chem. Phys., 18, 8331–8351, https://doi.org/10.5194/acp-18-8331-2018, 2018. a
Moreira, L., Hocke, K., Eckert, E., von Clarmann, T., and Kämpfer, N.: Trend analysis of the 20-year time series of stratospheric ozone profiles observed by the GROMOS microwave radiometer at Bern, Atmos. Chem. Phys., 15, 10999–11009, https://doi.org/10.5194/acp-15-10999-2015, 2015. a, b
Nedoluha, G. E., Kiefer, M., Lossow, S., Gomez, R. M., Kämpfer, N., Lainer, M., Forkman, P., Christensen, O. M., Oh, J. J., Hartogh, P., Anderson, J., Bramstedt, K., Dinelli, B. M., Garcia-Comas, M., Hervig, M., Murtagh, D., Raspollini, P., Read, W. G., Rosenlof, K., Stiller, G. P., and Walker, K. A.: The SPARC water vapor assessment II: intercomparison of satellite and ground-based microwave measurements, Atmos. Chem. Phys., 17, 14543–14558, https://doi.org/10.5194/acp-17-14543-2017, 2017. a, b
North, G. R., Pyle, J., and Zhangi, F., eds.: Stratospheric Chemistry Topics: Stratospheric Water Vapor, second edn., Academic Press, Oxford, UK, https://doi.org/10.1016/B978-0-12-382225-3.00393-5, 2015. a
Rodgers, C. D.: Inverse methods for atmospheric sounding: theory and practice, vol. 2, World Scientific Publishing Co Pte. Ltd., Singapore, 2000. a
Sausen, R., Isaksen, I., Grewe, V., Hauglustaine, D., Lee, D. S., Myhre, G., Köhler, M. O., Pitari, G., Schumann, U., Stordal, F., and Zerefos, C.: Aviation radiative forcing in 2000: An update on IPCC (1999), Meteorol. Z., 14, 555–561, https://doi.org/10.1127/0941-2948/2005/0049, 2005. a
Scheiben, D., Tschanz, B., Hocke, K., Kämpfer, N., Ka, S., and Oh, J. J.: The quasi 16-day wave in mesospheric water vapor during boreal winter 2011/2012, Atmos. Chem. Phys., 14, 6511–6522, https://doi.org/10.5194/acp-14-6511-2014, 2014. a
Steinbrecht, W., Froidevaux, L., Fuller, R., Wang, R., Anderson, J., Roth, C., Bourassa, A., Degenstein, D., Damadeo, R., Zawodny, J., Frith, S., McPeters, R., Bhartia, P., Wild, J., Long, C., Davis, S., Rosenlof, K., Sofieva, V., Walker, K., Rahpoe, N., Rozanov, A., Weber, M., Laeng, A., von Clarmann, T., Stiller, G., Kramarova, N., Godin-Beekmann, S., Leblanc, T., Querel, R., Swart, D., Boyd, I., Hocke, K., Kämpfer, N., Maillard Barras, E., Moreira, L., Nedoluha, G., Vigouroux, C., Blumenstock, T., Schneider, M., García, O., Jones, N., Mahieu, E., Smale, D., Kotkamp, M., Robinson, J., Petropavlovskikh, I., Harris, N., Hassler, B., Hubert, D., and Tummon, F.: An update on ozone profile trends for the period 2000 to 2016, Atmos. Chem. Phys., 17, 10675–10690, https://doi.org/10.5194/acp-17-10675-2017, 2017. a, b
Stenke, A. and Grewe, V.: Simulation of stratospheric water vapor trends: impact on stratospheric ozone chemistry, Atmos. Chem. Phys., 5, 1257–1272, https://doi.org/10.5194/acp-5-1257-2005, 2005. a
Tiao, G. C., Reinsel, G. C., Xu, D., Pedrick, J. H., Zhu, X., Miller, A. J., DeLuisi, J. J., Mateer, C. L., and Wuebbles, D. J.: Effects of autocorrelation and temporal sampling schemes on estimates of trend and spatial correlation, J. Geophys. Res.-Atmos., 95, 20507–20517, https://doi.org/10.1029/JD095iD12p20507, 1990. a
Trenberth, K. E., Dai, A., Rasmussen, R. M., and Parsons, D. B.: The Changing Character of Precipitation, B. Am. Meteorol. Soc., 84, 1205–1218, https://doi.org/10.1175/BAMS-84-9-1205, 2003. a
von Clarmann, T., Stiller, G., Grabowski, U., Eckert, E., and Orphal, J.: Technical Note: Trend estimation from irregularly sampled, correlated data, Atmos. Chem. Phys., 10, 6737–6747, https://doi.org/10.5194/acp-10-6737-2010, 2010. a, b






