the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A potential source of atmospheric sulfate from O2−-induced SO2 oxidation by ozone
Narcisse Tchinda Tsona
It was formerly demonstrated that O2SOO− forms at collisions rate in the gas phase as a result of SO2 reaction with . Here, we present a theoretical investigation of the chemical fate of O2SOO− by reaction with O3 in the gas phase, based on ab initio calculations. Two main mechanisms were found for the title reaction, with fundamentally different products: (i) formation of a van der Waals complex followed by electron transfer and further decomposition to O2 + SO2 + and (ii) formation of a molecular complex from O2 switching by O3, followed by SO2 oxidation to within the complex. Both reactions are exergonic, but separated by relatively low energy barriers. The products in the former mechanism would likely initiate other SO2 oxidations as shown in previous studies, whereas the latter mechanism closes a path wherein SO2 is oxidized to . The latter reaction is atmospherically relevant since it forms the ion, hereby closing the SO2 oxidation path initiated by . The main atmospheric fate of is nothing but sulfate formation. Exploration of the reactions kinetics indicates that the path of reaction (ii) is highly facilitated by humidity. For this path, we found an overall rate constant of cm3 molecule−1 s−1 at 298 K and 50 % relative humidity. The title reaction provides a new mechanism for sulfate formation from ion-induced SO2 oxidation in the gas phase and highlights the importance of including such a mechanism in modeling sulfate-based aerosol formation rates.
- Article
(1231 KB) -
Supplement
(308 KB) - BibTeX
- EndNote
The chemistry of sulfur is highly important in the atmosphere. Through its oxidation products, sulfur participates in the formation of secondary atmospheric aerosols, clouds, and acid rain. Sulfur dioxide (SO2), the most abundant sulfur-containing molecule in the atmosphere, is known to react both in the gas phase and in multiphase oxidation processes following different mechanisms to form sulfate as the final oxidation species. The main SO2 oxidizers in the gas phase include the hydroxyl radical (OH) (Seinfeld and Pandis, 2016), stabilized Criegee intermediates (Welz et al., 2012; Mauldin III et al., 2012; Vereecken et al., 2012), and atmospheric ions (Fehsenfeld and Ferguson, 1974; Enghoff et al., 2012; Tsona et al., 2015). The main routes for SO2 heterogeneous/multiphase oxidation include reactions with mineral dust (Harris et al., 2013), O3 and H2O2 in cloud droplets (Caffrey et al., 2001; Hoyle et al., 2016; Harris et al., 2012; Hegg et al., 1996), and NO2 and O2 in aerosol water and on CaCO3 particles (Cheng et al., 2016; Wang et al., 2016; Zhang et al., 2018; Yu et al., 2018; Zhao et al., 2018). In the gas phase, the SO2 oxidation by OH and Criegee intermediates leads to SO3 that ultimately forms H2SO4 (Larson et al., 2000), whereas reactions with ions are generally more complex. In the aqueous phase, is formed as the terminal oxidation species. Sulfate is known to be the main driving species in atmospheric aerosols formation and its formation is critical in the determination of aerosol formation rates (Nieminen et al., 2009; Sipilä et al., 2010; Kuang et al., 2008; Kulmala et al., 2000). The role of ions in this formation has been well established (Yu, 2006; Yu and Turco, 2000, 2001; Enghoff and Svensmark, 2008; Kirkby et al., 2011; Wagner et al., 2017; Yan et al., 2018), although relatively minor compared to the mechanism involving neutral particles exclusively (Eisele et al., 2006; Manninen et al., 2010; Kirkby et al., 2011; Hirsikko et al., 2011; Wagner et al., 2017).
The immediate products of SO2 oxidation by ions are mostly sulfur oxide ion intermediates (Fehsenfeld and Ferguson, 1974; Möhler et al., 1992; Bork et al., 2012; Tsona et al., 2014) that are susceptible to the triggering of new reactions or recombination with oppositely charged counterparts to form neutral species. Some of these ions, namely , , and , were detected at relatively high concentrations in the ambient atmosphere (Ehn et al., 2010) and in chamber experiments of SO2 ionic oxidation studies (Nagato et al., 2005; Hvelplund et al., 2013; Kirkby et al., 2011, 2016). The chemical fate of most sulfur oxides anions is relatively known. Bork et al. (2012) showed that can form SO3, the precursor for H2SO4, through electron transfer to ozone (O3) (Bork et al., 2012). can equally react with O2 to form , whose atmospheric outcome by reaction with O3 is H2SO4 formation (Bork et al., 2013). It was also speculated from chamber studies that could form and stabilize clusters with sulfuric acid in the gas phase (Kirkby et al., 2011). Reliable predictions of the outcomes of these ions require an exact knowledge of their chemical structures since interactions between molecules or ions depend both on their physical and chemical properties. A previous study demonstrated that two forms of separated by a high energy barrier may exist in the atmosphere (Tsona et al., 2014): the sulfate radical ion henceforth indicated as , and the peroxy form, O2SOO−, in which the O2S–OO− bond nature is more dative than covalent. Formerly, the two isomers were often misleadingly attributed exclusively to the sulfate radical ion, the most stable form of . However, their reactive properties greatly differ (Fehsenfeld and Ferguson, 1974).
The formation mechanisms of in the gas phase have been largely unknown but, recent studies showed that this ion can be formed by reaction with O3 (Bork et al., 2013) and in a O2SOO− isomerization process catalyzed by NO (Tsona et al., 2018). can also be produced during the chemical transformation of organic compounds, triggered by sulfate salts (Noziere et al., 2010), whereas O2SOO− is formed at collision rates upon SO2 reaction with (Fahey et al., 1982; Tsona et al., 2014).
The sulfate radical ion is believed to react with unsaturated compounds to form organosulfates, a major component of secondary organic aerosol (Surratt et al., 2007, 2008; Schindelka et al., 2013). Using first-principle calculations, was shown to act as a catalyst in SO2 oxidation to SO3 by O3 in the gas phase and, hence, plays a role in atmospheric aerosol formation (Tsona et al., 2015, 2016). The chemistry of O2SOO− is largely unknown, although potentially important for sulfur chemistry and atmospheric aerosol formation. Fehsenfeld and Ferguson found that O2SOO− can be decomposed by NO2 into and SO3 (Fehsenfeld and Ferguson, 1974) and a recent study showed that in the presence of nitrogen oxides (NOx = NO2 + NO), O2SOO− can be converted into sulfate (Tsona et al., 2018). In mildly polluted environments, the concentration of O3 can be a few orders of magnitude higher than that of NOx and the chemical fate of O2SOO− would then also greatly depend on collisions with O3. In such environments, O2SOO− could experience much more collisions with O3 than with NOx.
Hereby, we investigate the reaction between O2SOO− ⋯ (H2O)0−1 and O3 using ab initio calculations. By determining the reactions' thermodynamics and kinetics, we examine the possible pathways for the reaction and propose the most probable outcome of O2SOO− ⋯ (H2O)0−1 based on the O3 reaction. Implications of the most relevant pathways for aerosol formation are discussed.
2.1 Geometry optimizations and thermochemical and charge analysis
As the substrate in this study is a radical anion, all stationary points in the energy surface were optimized using density functional theory (DFT) based on the UM06-2X density functional (Zhao and Truhlar, 2008) and the aug-cc-pVTZ basis set (Dunning Jr. et al., 2001), setting the charge to −1 and the spin multiplicity to 2. The use of UM06-2X implies the use of unrestricted wave functions to describe the quantum state of the system. Spin contamination often arises from unrestricted DFT calculations and it is not guaranteed that the electronic states from these calculations are eigenstates of the operator. The spin contamination was then evaluated for all electronic states as , where is the actual value of the expectation value of the operator from DFT calculations and is the ideal expectation value. For systems explored in this study, .
The UM06-2X functional has successfully proven to be adequate for reactions involving transition state (TS) configurations (Elm et al., 2012, 2013a, b). Harmonic vibrational frequency analyses on the optimized structures were performed (at 298 K and 1 atm) using the UM06-2X/aug-cc-pVTZ method under the harmonic oscillator–rigid rotor approximation. These calculations ensured that the stationary points obtained were minima or TS and, also, provided the thermal contributions to the Gibbs free energy and the enthalpy.
Transition-state structures were initially located by scanning the reactants configurations. The best TS guesses from the scans were then refined using the synchronous transit quasi-Newton method (Peng et al., 1996), and the final TS structures underwent internal reaction coordinate calculations (Fukui, 1981) to ensure they connected the reactants to desired products.
The electronic energies of the UM06-2X/aug-cc-pVTZ optimized geometries were corrected using the UCCSD(T) method (Purvis and Bartlett, 1982) in conjunction with the aug-cc-pVTZ basis set. The Gibbs free energies, G, of all relevant species were then calculated as
where EUCCSD(T) is the electronic energy calculated using the UCCSD(T)/aug-cc-pVTZ method and Gtherm is the thermal contribution to the Gibbs free energy, calculated at the UM06-2X/aug-cc-pVTZ level of theory. All geometry optimizations, harmonic vibrational frequency analysis, and electronic energy correction calculations were carried out in the Gaussian 09 package (Frisch et al., 2013).
To analyze the distribution of the excess electronic charge over different species and fragments in the optimized systems, we used the atoms-in-molecules charge partitioning method presented by Bader (Bader, 1998). This is an intuitive way of dividing the molecules of a system into atoms, which are purely defined in terms of electronic charge density. The Bader charge partitioning assumes that the charge density between atoms of a molecular system reaches a minimum, which is an ideal place to separate atoms from each other. As input, this method requires electronic density and nuclear coordinates from electronic structure calculations. We used the approach implemented in the algorithm developed by Henkelman and co-workers, which has been shown to work well both for charged and water-containing systems (Tang et al., 2009; Bork et al., 2011; Henkelman et al., 2006).
2.2 Reactions kinetics
Regardless of the presence of water, the reaction between O2SOO− and O3 begins by forming different van der Waals pre-reactive intermediates, depending on the orientation of the reactants at impact. The pre-reactive intermediate could either decompose to different species or react further through a transition state configuration to form new products:
The traditional approach to determine the rate constant of Reaction (R1) relies on the steady-state approximation and leads to the following equation:
where kcoll is the collision frequency for O2SOO−–O3 collisions, kevap is the rate constant for the evaporation of the pre-reactive intermediate back to initial reactants, and kreac is the unimolecular rate constant for the reaction of the pre-reactive intermediate to the products. Moreover, assuming that kevap≫kreac, the rate constant of Reaction (R1) becomes k=Keqkreac over a range of temperatures, with Keq being the equilibrium constant of formation of the pre-reactive intermediate from the reactants. This consideration is, however, not valid for reactions with a submerged barrier, since the pre-reactive intermediate seldom thermally equilibrates. For such reactions, a two-transition-state theory has been introduced, treating two distinct transition state bottlenecks that define the net reactive flux (Klippenstein et al., 1988; Georgievskii and Klippenstein, 2005; Greenwald et al., 2005). The first bottleneck, the “outer” transition state, occurs in the association of the initial reactants to form the pre-reactive intermediate, whereas the second bottleneck, the “inner” transition state, occurs in the transformation of the pre-reactive intermediate to the products. Based on this theory, the overall rate constant (k) for a reaction channel is expressed in terms of the outer (kout) and inner (kin) rate constants as
The outer transition state is treated by the long-range transition state theory approach (Georgievskii and Klippenstein, 2005), while the inner transition state is resolved by the transition state theory. It was shown that for interactions between ions and neutral molecules, due to their long-range attraction, the collision cross section is larger than would be measured from the physical dimensions of the colliding species (Kupiainen-Määttä et al., 2013). To account for this phenomenon, the outer rate constant was determined from the ion–dipole parametrization of Su and Chesnavich, who performed trajectory simulations of collisions between a point charge and a rigidly rotating molecule (Su and Chesnavich, 1982). This parametrization is equivalent to a Langevin capture rate constant (kL) scaled by a temperature-dependent term and was found to provide good agreement with experiments (Kupiainen-Määttä et al., 2013). It is given as
where , , q is the charge of the ion, μ is the reduced mass of the colliding species, ε0 is the vacuum permittivity, α and μD are the polarizability and dipole moment of the neutral molecule (ozone), kB is Boltzmann's constant, and T is the absolute temperature. The inner rate constant can be written as
where ΔG‡ is the Gibbs free energy barrier separating the pre-reactive intermediate and the products, h is the Planck's constant, R is the molar gas constant, and c0 is the standard gas-phase concentration. The constants and variables in Eqs. (4) and (5) are given in the centimeter-gram-second (CGS) system of units and International System (SI) units, respectively. Details on these units are given in the Supplement.
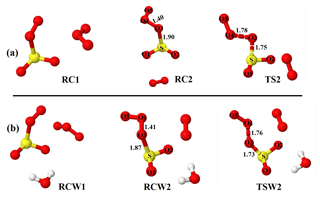
Figure 1Optimized structures of the most stable intermediates in the O2SOO− + O3 reaction (a) in the absence and (b) in the presence of a single water molecule. Optimizations were performed at the UM06-2X/aug-cc-pVTZ level of theory. Lengths (in Å) of some descriptive bonds are indicated. The color coding is yellow for sulfur, red for oxygen, and white for hydrogen.
Starting with optimized structures of O2SOO− ⋯ (H2O)0−1 and O3 shown in Fig. S1 in the Supplement, a series of geometry optimizations was performed on the O2SOO− ⋯ (H2O)0−1 + O3 system, taking into account different spatial orientations of the reactants at impact. These optimizations led to two main chemical processes, depending on the initial orientation of the reactants, with potentially different outcomes. The first process is the formation of a van der Waals complex followed by its direct decomposition to other species. The second process is the low-lying formation of a molecular complex in which the SO2 entity of O2SOO− ⋯ (H2O)0−1 is oxidized to .
3.1 Cluster formation and decomposition of O2SOO− ⋯ (H2O)0−1
As O3 approaches O2SOO− ⋯ (H2O)0−1 towards the oxygen atoms of the peroxy fragment or the oxygen atom of the SO2 moiety, the immediate outcome of O2SOO− ⋯ (H2O)0−1 and O3 collisions is the formation of the van der Waals O3 ⋯ O2SOO− ⋯ (H2O)0−1 complex in which O3 interacts with O2SOO−. Among the different stable configurations found upon optimization, we solely report the most stable one with respect to the Gibbs free energy, which is henceforth denoted RC1 and RCW1 for the unhydrated and monohydrated reactions, respectively, shown in Fig. 1. Exploration of the RC1 and RCW1 structures reveals that O2SOO− ⋯ (H2O)0−1 basically keeps its configuration upon clustering with O3. The spin contaminations for RC1 and RCW1 are negligible, being 0.0086 and 0.0081, respectively. The electronic energies of formation of RC1 and RCW1 are −5.1 and −4.6 kcal mol−1, respectively. Despite the fact that these complexes may form at 0 K, the Gibbs free energies of their formation under atmospheric pressure and 298 K (4.5 and 4.7 kcal mol−1, respectively) indicate that their formation is endergonic under atmospherically relevant conditions. These Gibbs free energy values indicate that, if formed, these complexes would not live long and will rather decompose either to initial reactants or to different species. Hence, the Gibbs free energies of formation of RC1 and RCW1 define the lowest states at which O2SOO− can interact with O3 to allow electron transfer and O2S–OO decomposition, and thus represent the energy barrier towards O2 + SO2 + formation. Inspecting the vibrational modes of RC1 and RCW1, two vibrations are found that would clearly lead to the dissociation of O2SOO− within the complex. The analysis of the charge distribution over O3 ⋯ O2SOO− ⋯ (H2O)0−1 shows that the extra electron initially located on O2SOO in the reactants has migrated to the O3 molecule in the van der Waals product complex, as can be observed in Fig. S2. This is as expected, given the high electronegativity of O3 relative to that of O2 and SO2 (Rothe et al., 1975). The charge distribution over the different atoms of the optimized complex is weakly affected by the presence of water, as previously demonstrated by Bork and co-workers (Bork et al., 2011).
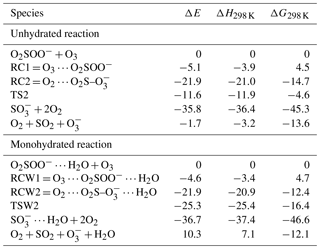
Table 1Electronic energies (ΔE), enthalpies (ΔH298 K), and Gibbs free energies (ΔG298 K) of the different states in the O2SOO− + O3 reaction both in the absence and in the presence of water, calculated relative to the energy of initial reactants at the UCCSD(T)/aug-cc-pVTZ//UM06-2X/aug-cc-pVTZ level of theory.
The most likely fates of RC1 and RCW1 are, therefore, decomposition into O2, SO2, and as follows:
The numerical values of the formation energies of all intermediate species in Reaction (R2) are given in Table 1, and the energy surfaces are plotted in Fig. 2. RC1 and RCW1 decompositions are highly exergonic at 298 K, occurring with −18.1 and −16.7 kcal mol−1 Gibbs free energy changes, respectively. These processes are, therefore, likely to occur in the atmosphere upon formation of O3 ⋯ O2SOO− ⋯ (H2O)0−1.
The limiting step in Reaction (R2) is the formation of RC1 and RCW1, whose formation energies indicated above can then be considered as the only barrier to the formation of O2 + SO2 + . This leads to overall rate constants (according to Eq. 5) of and cm3 molecule−1 s−1 at 298 K for the unhydrated and monohydrated reactions, respectively. Both reactions are, in principle, collision-limited and the effect of hydration on the kinetics is found to be negligible. The atmospheric relevance of Reaction (R2) has been determined already (Bork et al., 2012, 2013; Enghoff et al., 2012).
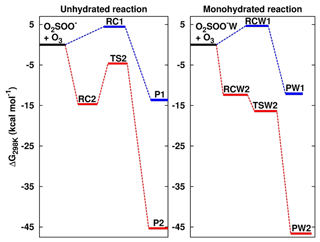
Figure 2Formation Gibbs free energies of the most stable intermediate species in the O2SOO− + O3 reaction in the absence and in the presence of water. “W” is the shorthand notation for water. RC1, RC2, TS2, RCW1, RCW2, and TSW2 structures are shown in Fig. 1. P1 = O2 + SO2 + , P2 = + 2O2, PW1 = O2 + SO2 + + H2O, and PW2 = ⋯ H2O + 2O2. Calculations were performed at the UCCSD(T)/aug-cc-pVTZ//UM06-2X/aug-cc-pVTZ level of theory.
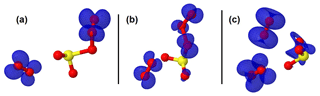
Figure 3Representation of the spin density (in blue color) on intermediate structures in the O2SOO− + O3 reaction. The spin density clearly indicates that the extra electron is progressively distributed over all the atoms from (a) the pre-reactive complex through (b) the transition state to (c) the product complex.
3.2 O2SOO− ⋯ (H2O)0−1 reaction with O3
When O3 approaches O2SOO− ⋯ (H2O)0−1 from the sulfur atom side, the formation of a more stable cluster than found above prevails. The incoming O3 molecule strongly interacts with O2SOO− ⋯ (H2O)0−1 by forming a coordination bond with the sulfur atom and hereby inducing the ejection of the O2 molecule that remains in interaction with the remainder of the system. This process leads to the formation of the O2 ⋯ O2S– ⋯ (H2O)0−1 complex which further transforms, through an intramolecular SO2 oxidation, into ⋯ (H2O)0−1 + 2O2 according to the following equation:
The configurations of the most stable intermediate structures in Reaction (R3) are given in Fig. 1. The charge analysis on this system indicates that the electronic charge on the pre-reactive complex is essentially on two oxygen atoms of the O3 moiety that is coordinated to SO2 as can be seen in Fig. 3a. The net charge on these two oxygen atoms is 1.04e, whereas the net charge on the free O2 molecule is 0.01e. The latter value shows that the O2 molecule formed in the pre-reactive complex has no unpaired electrons, and hence is a singlet. Although the charge is still on the O3 moiety in the transition state configuration, it is mostly located on the oxygen atom bound to sulfur (Fig. 3b). The net charge on the two outer oxygen atoms of the O3 moiety in the transition state has substantially decreased to 0.30e, while the charge on the free O2 molecule has slightly increased to 0.04e. The strong decrease in the charge of the two outer oxygen atoms of O3 from the pre-reactive complex to the transition state suggests that the O2 molecule to form in the product will likely be a singlet. In the products (Fig. 3c), the old free O2 molecule has a net charge of 1.99e, whereas the charge on the newly formed O2 is 0.06e. The 1.99e charge on the old free O2 molecule indicates the presence of unpaired electrons in its configuration, meaning that the singlet O2 has been transformed into a triplet. This clearly shows that a spin flip has occurred in O2 during further optimization of the products. The newly formed O2 with 0.06e charge is obviously a singlet. This analysis shows for the unhydrated system that the singlet O2 initially formed in the pre-reactive complex transforms into a triplet in the product state, while a new singlet O2 is also formed. In the monohydrated system, the singlet O2 initially formed in the pre-reactive complex remains as a singlet in the product state and a triplet O2 is also released. Overall, the two forms of O2 (singlet and triplet) are formed in the studied reaction, despite following different mechanisms. Although the water molecule in the monohydrated system does not retain any electric charge, it most likely stabilizes the initially formed singlet O2 and prevents the spin flip.
Though the necessity to determine the electronic structure of the O2 molecule in the singlet state (1Δg) has been demonstrated to be useful (Buttar and Hirst, 1994), obtaining a reliable electronic energy for O2(1Δg) is difficult (Drougas and Kosmas, 2005). An alternative approach to determine this energy is to add the experimental energy spacing (22.5 kcal mol−1) between triplet and singlet states of O2 to the computed electronic energy of the triplet O2 (Schweitzer and Schmidt, 2003; Drougas and Kosmas, 2005). We used this approach to determine the energies of the products of Reaction (R3). The numerical values of the formation energies of all intermediate species in Reaction (R3) are thus given in Table 1 and the energy surfaces are plotted in Fig. 2. The most stable optimized structures of O2 ⋯ O2S– ⋯ (H2O)0−1 according to our calculations are denoted as RC2 and RCW2 for the unhydrated and monohydrated systems, respectively, and are shown in Fig. 1. Regardless of the presence of water, the O2 ⋯ O2S– configuration results from O2 being switched by O3 in the O2SOO− molecular ion. In the optimized O2 ⋯ O2S– structure, the O3 atom (labeled in Fig. 1) of O3 points towards the S atom of O2SOO−, forming S–O3 bonds at distances of 1.90 and 1.87 Å in the absence and in the presence of water, respectively. These bonds are coordination bonds in nature since the S–O covalent bond is, e.g., 1.43 Å in SO3 and 1.4 Å in H2SO4. The S–O3 coordination bond distances in RC2 and RCW2 are shorter by 0.04 and 0.03 Å than O2S–OO− bond distances in unhydrated and monohydrated O2SOO− forms. This indicates stronger interaction between O3 and SO2, and hence higher stability of O2 ⋯ O2S– relative to O2SOO−.
The formations of RC2 and RCW2 are highly exergonic, with Gibbs free energy changes at 298 K of −14.7 and −12.4 kcal mol−1, respectively. These values, with corresponding electronic energies and enthalpies, are shown in Table 1. These Gibbs free energy changes for the formation of RC2 and RCW2 are about 19 kcal mol−1 lower than those of RC1 and RCW1 at similar conditions, indicating the higher stability of RC2 and RCW2 and the highly favorable switching reaction at ambient conditions. SO2 oxidation can readily occur within the O2 ⋯ O2S– ⋯ (H2O)0−1 cluster and lead to formation. In principle, to form the products of Reaction (R3), the O3 atom of the O3 moiety in O2 ⋯ O2S– ⋯ (H2O)0−1 is transferred through transition state configurations, to SO2 and forms followed by the ejection of the O2 molecule. The transition states are denoted TS2 and TSW2 for the unhydrated and monohydrated systems, respectively, and their structures are presented in Fig. 1. While RC2 and RCW2 are formed with similar Gibbs free energies within 2 kcal mol−1 difference, the formation Gibbs free energies of their transition states at similar conditions greatly differ. TS2 is located at 10 kcal mol−1 Gibbs free energy above RC2, while TSW2 is located at −4 kcal mol−1 below RCW2. It is speculated that the low energy barrier in the monohydrated reaction is the result of a strong stabilization of the transition state due to hydration, with the S–O3 bonds in RCW2 and TSW2 shorter by ∼0.03 Å than in RC2 and TS2. Another reason for this substantial drop in the energy barrier is the difference in the electronic configurations of the two outer oxygen atoms of the O3 moiety in the two transition states that form O2 with different multiplicities in the products.
Based on the TS2 energy, the unimolecular decomposition of O2 ⋯ O2S– at 298 K in the absence of water was found to occur at a rate constant of 3.1×105 s−1, corresponding to an atmospheric lifetime of 3.3 µs. Both this short lifetime and the negative energy barrier of the monohydrated reaction indicate that O2 ⋯ O2S– would not live long enough to experience collisions with other atmospheric oxidants. It should be noted that few to no collisions with nitrogen can, however, be achieved. It follows that the most likely outcome of O2 ⋯ O2S– is decomposition to the products of Reaction (R3), which are formed with about −46 kcal mol−1 overall Gibbs free energy at 298 K. The net reaction is an -initiated SO2 oxidation to by O3.
The spin contamination for electronic states in Reaction (R3) is quite significant, being 1.0122, 1.4666, and 2.0374 for the pre-reactive complex, transition state, and product, respectively, and is almost insensitive to the presence of water. The actual values of the expectation values of the operator for all electronic states obtained from our calculations are given in the Supplement, along with their Cartesian coordinates. The high values of spin contamination likely reflect the formation of O2 with different multiplicities within the system. As the charge analysis indicates, starting with singlet O2 in the pre-reactive complexes of Reaction (R3), both singlet and triplet O2 are formed in the final products.
The overall rate constants of Reaction (R3), determined at 298 K using Eq. (3), are and cm3 molecule−1 s−1 for the unhydrated and monohydrated reactions, respectively. The values of the different components (kout and kin) of these rate constants are listed in Table S1 of the Supplement. It is observed from Table S1 that the inner transition state provides the dominant bottleneck to the rate constant of the unhydrated reaction, whereas the outer transition state provides the dominant bottleneck to the rate constant of the monohydrated reaction.
The effective effect of water on the rate constant can be evaluated by taking into account the stability of O2SOO− ⋯ H2O (which is formed at the entrance channel of the reaction in the presence of water before colliding with O3) and the equilibrium vapor pressure of water. Starting from the definition of the reaction rate for the hydrated reaction,
where k(R3w) is the overall rate constant for the hydrated reaction, determined using Eq. (3), and is the effective reaction rate constant calculated as . Keq is the equilibrium constant for the O2SOO− + H2O ↔ O2SOO− ⋯ H2O reaction and the actual water vapor pressure. Details on the determination of Keq and are given in the Supplement.
At 298 K and 50 % relative humidity, the effective rate constant of the monohydrated reaction is cm3 molecule−1 s−1, 4 orders of magnitude higher than the rate constant of the unhydrated reaction. Therefore, water plays a catalytic role in the kinetics of Reaction (R3). The net rate constant of Reaction (R3) can be obtained by weighing the rate constants of the unhydrated and monohydrated reactions to corresponding equilibrium concentrations of O2 ⋯ O2S– hydrates. Using the law of mass action, we find that O2 ⋯ O2S–O mostly exists as a dry species, constituting 77 % of the total population, whereas the monohydrated species forms 23 % of the total population. The net rate constant of Reaction (R3) is then determined to be cm3 molecule−1 s−1 at 298 K.
Considering only the unhydrated process of Reaction (R3), the rate constant is 4–5 orders of magnitude lower than the rate constant obtained for the SO2 + → + O2 reaction (Fehsenfeld and Ferguson, 1974; Bork et al., 2012). Despite this difference, the oxidation process follows a similar mechanism to the one presented by Bork et al. for the SO2 + → + O2 reaction, consisting of the oxygen transfer from O3 to SO2 (Bork et al., 2012). The discrepancy between the two results is associated with the effect of the presence of the O–O fragment initially coordinated to SO2 in the current study, which tends to stabilize the O2 ⋯ O2S– pre-reactive complex. The presence of the O–O fragment seemingly deactivates SO2 for the upcoming O transfer from O3 to form . However, this situation is rapidly reversed with the presence of water as the reaction becomes much faster, proceeding nearly at collision rate.
3.3 Further chemistry
In real atmospheric and ionized conditions, despite O2 having lower electron affinity than O3, it would likely ionize faster than O3, owing to its much higher concentration. Considering, for example, chamber experiments, upon interaction of ionizing particles with the gas, electrons can transfer from one species to another and, e.g., can form and rapidly hydrate within 1 ns (Svensmark et al., 2007; Fahey et al., 1982). Furthermore, Fahey et al. (1982) showed that the ⋯ (H2O)0−1 association reaction with SO2 is faster than the electron transfer from ⋯ (H2O)0−1 to O3 (Fahey et al., 1982). This means that in an ionized environment containing O2, O3, and SO2, the formation of O2SOO− resulting from SO2 and association will happen faster than formation. O2SOO− would react thereafter with O3 and the following stepwise process could take place:
The Gibbs free energy change of this net reaction at 298 K is about −40 kcal mol−1 more negative than that of the SO2 + → + O2 reaction at similar conditions. Given that the intermediate steps of Reaction (R4) are significantly fast, this reaction is believed to be an important process in most environments of SO2 ion-induced oxidation to or more oxidized species. The limiting step in the process of Reaction (R4) is Reaction (R4c) for which an energy barrier has to be overcome before the products are released.
is an identified stable ion detected in the atmosphere and in experiments (Ehn et al., 2010; Kirkby et al., 2011, 2016). The chemical fate of is fundamentally different from that of SO3 that forms H2SO4 by hydration. Likely outcomes of are hydrolysis, electron transfer by collision with O3, reaction with O2 and H2O, and, possibly, radicals, according to the following equations:
Fehsenfeld and Ferguson showed that H2SO4 formation could occur in the ⋯ H2O cluster, releasing a free electron (Reaction R5) (Fehsenfeld and Ferguson, 1974). Owing to the high electron affinity of O3 relative to SO3 (Rothe et al., 1975), the electron can transfer from to O3 and lead to the formation of SO3, the precursor for sulfuric acid in the atmosphere. Moreover, the free electron released and the formed in Reactions (R5) and (R6), respectively, are potential triggers of new SO2 oxidations with implication for aerosol formation (Svensmark et al., 2007; Enghoff and Svensmark, 2008; Bork et al., 2013). Reactions (R7) and (R8) are potential outcomes for as well, forming the highly stable species that would terminate the oxidation process of SO2 initiated by a free electron. Reactions (R5)–(R8) are likely competitive processes upon formation in the gas phase, and their different rates would determine the number of SO2 oxidations induced by a free electron. However, they have no other fate than or H2SO4, the most oxidized sulfur species in the atmosphere, which both share many properties and play a central role in atmospheric particle formation.
Experimental studies have shown that in atmospheres heavily enriched in SO2 and O3, a free electron could initiate SO2 oxidation and induce the formation of ∼107 cm−3 sulfates in the absence of UV light, clearly indicating the importance of other ionic SO2 oxidation mechanisms than UV-induced oxidation (Enghoff and Svensmark, 2008). To evaluate the importance of the mechanism presented in this study in the formation of sulfate, it is necessary to identify the scavengers that terminate the SO2 oxidation initiated by . Possible scavengers include radicals, NOx, acids, cations, and other particles. The main ones are likely NOx, OH, HO2, and organic acids, which lead to the formation of the stable , , and species. If the ion concentration was known, the contribution of Reaction (R4) to H2SO4 formation could be determined by comparing its formation rates from ionic and electrically neutral mechanisms. Alternatively, it can be assumed that Reaction (R4) is terminated when the ion cluster hits a scavenger. The free electron which acts as a catalyst is then scavenged. The average catalytic turnover number (TON) is defined as follows (Kozuch and Martin, 2012):
The concentration of the catalyst can be approximated to the concentration of the scavengers and, considering that at most atmospheric conditions [O3] > [SO2], SO2 is the limiting species in Reaction (R4). Equation (8) can then be re-written as
The catalytic efficiency of SO2 ion-induced oxidation is then given as
where kion is the ion production rate. Depending on the tropospheric temperature and altitude, measurements at the Cosmics Leaving Outdoor Droplets chamber at CERN found kion=2–100 cm−3 s−1, covering the typical ionization range in the troposphere (Franchin et al., 2015). We assume nearly pristine conditions with [SO2] = 5 ppb = 1.2×1011 molecule cm−3, [NOx] = 200 ppt = 4.9×109 molecule cm−3, [OH] = 5.0×105 molecule cm−3 (day and night average), and [HO2] = 108 molecule cm−3 (Dusanter et al., 2009; Holland et al., 2003). Noting that formic acid and acetic acid are the most abundant organic acids in the atmosphere, their concentrations are considered in Eq. (9) as representative examples for organic acids, [organic acids] = 110 ppt = 2.7×109 molecule cm−3 (Le Breton et al., 2012; Baasandorj et al., 2015). We then determine Jion in the range 3.2×101–1.6×103 cm−3 s−1. The rate of the UV-induced SO2 oxidation by OH is
With cm3 molecule−1 s−1 (Atkinson et al., 2004), molecule cm−3 s−1, the proportion of H2SO4 formed from ion-induced oxidation can be estimated from the following equation:
We find that the contribution of ion-induced SO2 oxidation to H2SO4 formation can range from 0.1 % to 2.0 % of the total formation rate. This estimate could be improved by also considering the rate of SO2 oxidation by Criegee intermediates, another important channel for H2SO4 formation.
This study highlights the role of the superoxide ions () in SO2 oxidation. Our previous study demonstrated that SO2 interacts with and forms O2SOO−, whose atmospheric fate remains unelucidated (Tsona et al., 2014). In this study, we used ab initio calculations to assess the chemical fate of O2SOO− by collisions with O3. Regardless of the presence of water, two main mechanisms are observed, leading to fundamentally different products. The first mechanism is characterized by electron transfer followed by O2SOO− decomposition, leading to formation and releasing SO2. The chemistry of SO2 + has been explored elsewhere. The second mechanism is characterized by SO2 oxidation and proceeds through formation of a pre-reactive complex that subsequently reacts to form the products by overcoming a relatively low energy barrier. The overall reaction, + SO2 + O3 → + 2O2, is faster and more energetically favorable than the SO2 + → + O2 reaction, thereby highlighting the positive role of in SO2 ionic oxidation. Hence, the two reactions may compete in chamber experiments and in the atmosphere.
While for the electron transfer and O2SOO− decomposition process the reaction is hindered by the presence of water, the oxidation reaction is catalyzed instead, as the rate constant is increased by 6 orders of magnitude with the presence of water. Weighing the rate constants of unhydrated and monohydrated reactions to the equilibrium concentrations of hydrates of corresponding pre-reactive complexes leads to the net rate constant of cm3 molecule−1 s−1 at 298 K for the oxidation reaction. Hence, this reaction proceeds nearly at collision rate. The main species () in the end products of the studied reaction has been proved to form both in the atmosphere and in experiments, whereby it definitely plays a role in atmospheric sulfur chemistry and particle formation. The contribution of this mechanism to the total atmospheric sulfuric acid formation is estimated. The studied reaction further deepens the understanding of ion-induced SO2 oxidation, with implications for aerosol formation.
The results presented in this article are from Gaussian calculations, exclusively, and they are obtained by exploiting the output files from these calculations. These files can be obtained by contacting the authors.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-649-2019-supplement.
NTT and LD designed the work. NTT performed all calculations and analyzed the data. NTT wrote the whole manuscript and LD edited it.
The authors declare that they have no conflict of interest.
This work was supported by the National Natural Science Foundation of China
(21707080, 91644214), the Postdoctoral Science Foundation of China
(2017M612276), the Shandong Natural Science Fund for Distinguished Young
Scholars (JQ201705), and the International Postdoctoral Exchange Fellowship
Program. We acknowledge the High-Performance Computing Center of Shandong
University for providing the computational resources.
Edited by: Sergey A. Nizkorodov
Reviewed by: two anonymous referees
Atkinson, R., Baulch, D. L., Cox, R. A., Crowley, J. N., Hampson, R. F., Hynes, R. G., Jenkin, M. E., Rossi, M. J., and Troe, J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Volume I – gas phase reactions of Ox, HOx, NOx and SOx species, Atmos. Chem. Phys., 4, 1461–1738, https://doi.org/10.5194/acp-4-1461-2004, 2004.
Baasandorj, M., Millet, D. B., Hu, L., Mitroo, D., and Williams, B. J.: Measuring acetic and formic acid by proton-transfer-reaction mass spectrometry: sensitivity, humidity dependence, and quantifying interferences, Atmos. Meas. Tech., 8, 1303–1321, https://doi.org/10.5194/amt-8-1303-2015, 2015.
Bader, R. F. W.: A Bond Path: A Universal Indicator of Bonded Interactions, J. Phys. Chem. A, 102, 7314–7323, https://doi.org/10.1021/jp981794v, 1998.
Bork, N., Kurtén, T., Enghoff, M., Pedersen, J. O. P., Mikkelsen, K. V., and Svensmark, H.: Ab initio studies of (H2O)n and (H2O)n anionic molecular clusters, n=12, Atmos. Chem. Phys., 11, 7133–7142, https://doi.org/10.5194/acp-11-7133-2011, 2011.
Bork, N., Kurtén, T., Enghoff, M., Pedersen, J. O. P., Mikkelsen, K. V., and Svensmark, H.: Structures and reaction rates of the gaseous oxidation of SO2 by an (H2O)0−5 cluster – a density functional theory investigation, Atmos. Chem. Phys., 12, 3639–3652, https://doi.org/10.5194/acp-12-3639-2012, 2012.
Bork, N., Kurtén, T., and Vehkamäki, H.: Exploring the atmospheric chemistry of O2 and assessing the maximum turnover number of ion-catalysed H2SO4 formation, Atmos. Chem. Phys., 13, 3695–3703, https://doi.org/10.5194/acp-13-3695-2013, 2013.
Buttar, D. and Hirst, D. M.: Ab initio quantum chemistry study of the gas-phase reaction of ClO with HO2, J. Chem. Soc. Faraday Trans., 90, 1811–1817, https://doi.org/10.1039/FT9949001811, 1994.
Caffrey, P., Hoppel, W., Frick, G., Pasternack, L., Fitzgerald, J., Hegg, D., Gao, S., Leaitch, R., Shantz, N., Albrechcinski, T., and Ambrusko, J.: In-cloud oxidation of SO2 by O3 and H2O2: Cloud chamber measurements and modeling of particle growth, J. Geophys. Res.-Atmos., 106, 27587–27601, https://doi.org/10.1029/2000jd900844, 2001.
Cheng, Y., Zheng, G., Wei, C., Mu, Q., Zheng, B., Wang, Z., Gao, M., Zhang, Q., He, K., Carmichael, G., Pöschl, U., and Su, H.: Reactive nitrogen chemistry in aerosol water as a source of sulfate during haze events in China, Sci. Adv., 2, e1601530, https://doi.org/10.1126/sciadv.1601530, 2016.
Drougas, E. and Kosmas, A. M.: Computational studies of (HIO3) isomers and the HO2 + IO reaction pathways, J. Phys. Chem. A, 109, 3887–3892, https://doi.org/10.1021/jp044197j, 2005.
Dunning Jr., T. H., Peterson, K. A., and Wilson, A. K.: Gaussian basis sets for use in correlated molecular calculations. X. The atoms aluminum through argon revisited, J. Chem. Phys., 114, 9244–9253, https://doi.org/10.1063/1.1367373, 2001.
Dusanter, S., Vimal, D., Stevens, P. S., Volkamer, R., Molina, L. T., Baker, A., Meinardi, S., Blake, D., Sheehy, P., Merten, A., Zhang, R., Zheng, J., Fortner, E. C., Junkermann, W., Dubey, M., Rahn, T., Eichinger, B., Lewandowski, P., Prueger, J., and Holder, H.: Measurements of OH and HO2 concentrations during the MCMA-2006 field campaign – Part 2: Model comparison and radical budget, Atmos. Chem. Phys., 9, 6655–6675, https://doi.org/10.5194/acp-9-6655-2009, 2009.
Ehn, M., Junninen, H., Petäjä, T., Kurtén, T., Kerminen, V.-M., Schobesberger, S., Manninen, H., Ortega, I., Vehkamäki, H., and Kulmala, M.: Composition and temporal behavior of ambient ions in the boreal forest, Atmos. Chem. Phys., 10, 8513–8530, https://doi.org/10.5194/acp-10-8513-2010, 2010.
Eisele, F. L., Lovejoy, E. R., Kosciuch, E., Moore, K. F., Mauldin III, R. L., Smith, J. N., McMurry, P. H., and Iida, K.: Negative atmospheric ions and their potential role in ion-induced nucleation, J. Geophys. Res.-Atmos., 111, D04305, https://doi.org/10.1029/2005jd006568, 2006.
Elm, J., Bilde, M., and Mikkelsen, K. V.: Assessment of Density Functional Theory in Predicting Structures and Free Energies of Reaction of Atmospheric Prenucleation Clusters, J. Chem. Theory Comput., 8, 2071–2077, https://doi.org/10.1021/ct300192p, 2012.
Elm, J., Bilde, M., and Mikkelsen, K. V.: Assessment of binding energies of atmospherically relevant clusters, Phys. Chem. Chem. Phys., 15, 16442–16445, https://doi.org/10.1039/c3cp52616j, 2013a.
Elm, J., Bilde, M., and Mikkelsen, K. V.: Influence of Nucleation Precursors on the Reaction Kinetics of Methanol with the OH Radical, J. Phys. Chem. A, 117, 6695–6701, https://doi.org/10.1021/jp4051269, 2013b.
Enghoff, M. and Svensmark, H.: The role of atmospheric ions in aerosol nucleation – a review, Atmos. Chem. Phys., 8, 4911–4923, https://doi.org/10.5194/acp-8-4911-2008, 2008.
Enghoff, M. B., Bork, N., Hattori, S., Meusinger, C., Nakagawa, M., Pedersen, J. O. P., Danielache, S., Ueno, Y., Johnson, M. S., Yoshida, N., and Svensmark, H.: An isotopic analysis of ionising radiation as a source of sulphuric acid, Atmos. Chem. Phys., 12, 5319–5327, https://doi.org/10.5194/acp-12-5319-2012, 2012.
Fahey, D., Böhringer, H., Fehsenfeld, F., and Ferguson, E.: Reaction rate constants for (H2O)n ions n=0 to 4, with O3, NO, SO2, and CO2, J. Chem. Phys., 76, 1799–1805, https://doi.org/10.1063/1.443220, 1982.
Fehsenfeld, F. and Ferguson, E.: Laboratory studies of negative ion reactions with atmospheric trace constituents, J. Chem. Phys., 61, 3181–3193, https://doi.org/10.1063/1.1682474, 1974.
Franchin, A., Ehrhart, S., Leppä, J., Nieminen, T., Gagné, S., Schobesberger, S., Wimmer, D., Duplissy, J., Riccobono, F., Dunne, E. M., Rondo, L., Downard, A., Bianchi, F., Kupc, A., Tsagkogeorgas, G., Lehtipalo, K., Manninen, H. E., Almeida, J., Amorim, A., Wagner, P. E., Hansel, A., Kirkby, J., Kürten, A., Donahue, N. M., Makhmutov, V., Mathot, S., Metzger, A., Petäjä, T., Schnitzhofer, R., Sipilä, M., Stozhkov, Y., Tome, A., Kerminen, V. M., Carslaw, K., Curtius, J., Baltensperger, U., and Kulmala, M.: Experimental investigation of ion-ion recombination under atmospheric conditions, Atmos. Chem. Phys., 15, 7203–7216, https://doi.org/10.5194/acp-15-7203-2015, 2015.
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., Scalmani, G., Barone, V., Mennucci, B., Petersson, G. A., Nakatsuji, H., Caricato, M., Li, X., Hratchian, H. P., Izmaylov, A. F., Bloino, J., Zheng, G., Sonnenberg, J. L., Hada, M., Ehara, M., Toyota, K., Fukuda, R., Hasegawa, J., Ishida, M., Nakajima, T., Honda, Y., Kitao, O., Nakai, H., Vreven, T., Montgomery Jr., J. A., Peralta, J. E., Ogliaro, F., Bearpark, M. J., Heyd, J., Brothers, E. N., Kudin, K. N., Staroverov, V. N., Kobayashi, R., Normand, J., Raghavachari, K., Rendell, A. P., Burant, J. C., Iyengar, S. S., Tomasi, J., Cossi, M., Rega, N., Millam, N. J., Klene, M., Knox, J. E., Cross, J. B., Bakken, V., Adamo, C., Jaramillo, J., Gomperts, R., Stratmann, R. E., Yazyev, O., Austin, A. J., Cammi, R., Pomelli, C., Ochterski, J. W., Martin, R. L., Morokuma, K., Zakrzewski, V. G., Voth, G. A., Salvador, P., Dannenberg, J. J., Dapprich, S., Daniels, A. D., Farkas, Ö., Foresman, J. B., J. Ortiz, V., Cioslowski, J., and Fox, D. J.: Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford, CT, USA, 2013.
Fukui, K.: The path of chemical reactions-the IRC approach, Acc. Chem. Res., 14, 363–368, https://doi.org/10.1021/ar00072a001, 1981.
Georgievskii, Y. and Klippenstein, S. J.: Long-range transition state theory, J. Chem. Phys., 122, 194103, https://doi.org/10.1063/1.1899603, 2005.
Greenwald, E. E., North, S. W., Georgievskii, Y., and Klippenstein, S. J.: A two transition state model for radical-molecule reactions: A case study of the addition of OH to C2H4, J. Phys. Chem. A, 109, 6031–6044, https://doi.org/10.1021/jp058041a, 2005.
Harris, E., Sinha, B., Hoppe, P., Crowley, J. N., Ono, S., and Foley, S.: Sulfur isotope fractionation during oxidation of sulfur dioxide: gas-phase oxidation by OH radicals and aqueous oxidation by H2O2, O3 and iron catalysis, Atmos. Chem. Phys., 12, 407–423, https://doi.org/10.5194/acp-12-407-2012, 2012.
Harris, E., Sinha, B., van Pinxteren, D., Tilgner, A., Fomba, K. W., Schneider, J., Roth, A., Gnauk, T., Fahlbusch, B., Mertes, S., Lee, T., Collett, J., Foley, S., Borrmann, S., Hoppe, P., and Herrmann, H.: Enhanced Role of Transition Metal Ion Catalysis During In-Cloud Oxidation of SO2, Science, 340, 727–730, https://doi.org/10.1126/science.1230911, 2013.
Hegg, D. A., Majeed, R., Yuen, P. F., Baker, M. B., and Larson, T. V.: The impacts of SO2 oxidation in cloud drops and in haze particles on aerosol light scattering and CCN activity, Geophys. Res. Lett., 23, 2613–2616, https://doi.org/10.1029/96gl02419, 1996.
Henkelman, G., Arnaldsson, A., and Jónsson, H.: A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 36, 354–360, https://doi.org/10.1016/j.commatsci.2005.04.010, 2006.
Hirsikko, A., Nieminen, T., Gagné, S., Lehtipalo, K., Manninen, H. E., Ehn, M., Hõrrak, U., Kerminen, V. M., Laakso, L., McMurry, P. H., Mirme, A., Mirme, S., Petäjä, T., Tammet, H., Vakkari, V., Vana, M., and Kulmala, M.: Atmospheric ions and nucleation: a review of observations, Atmos. Chem. Phys., 11, 767–798, https://doi.org/10.5194/acp-11-767-2011, 2011.
Holland, F., Hofzumahaus, A., Schafer, R., Kraus, A., and Patz, H. W.: Measurements of OH and HO2 radical concentrations and photolysis frequencies during BERLIOZ, J. Geophys. Res.-Atmos., 108, 8246, https://doi.org/10.1029/2001jd001393, 2003.
Hoyle, C. R., Fuchs, C., Järvinen, E., Saathoff, H., Dias, A., El Haddad, I., Gysel, M., Coburn, S. C., Tröstl, J., Bernhammer, A. K., Bianchi, F., Breitenlechner, M., Corbin, J. C., Craven, J., Donahue, N. M., Duplissy, J., Ehrhart, S., Frege, C., Gordon, H., Höppel, N., Heinritzi, M., Kristensen, T. B., Molteni, U., Nichman, L., Pinterich, T., Prévôt, A. S. H., Simon, M., Slowik, J. G., Steiner, G., Tomé, A., Vogel, A. L., Volkamer, R., Wagner, A. C., Wagner, R., Wexler, A. S., Williamson, C., Winkler, P. M., Yan, C., Amorim, A., Dommen, J., Curtius, J., Gallagher, M. W., Flagan, R. C., Hansel, A., Kirkby, J., Kulmala, M., Möhler, O., Stratmann, F., Worsnop, D. R., and Baltensperger, U.: Aqueous phase oxidation of sulphur dioxide by ozone in cloud droplets, Atmos. Chem. Phys., 16, 1693–1712, https://doi.org/10.5194/acp-16-1693-2016, 2016.
Hvelplund, P., Pedersen, J. O. P., Stochkel, K., Enghoff, M. B., and Kurten, T.: Experimental studies of the formation of cluster ions formed by corona discharge in an atmosphere containing SO2, NH3, and H2O, Int. J. Mass Spectrom., 341, 1–6, https://doi.org/10.1016/j.ijms.2013.03.001, 2013.
Kirkby, J., Curtius, J., Almeida, J., Dunne, E., Duplissy, J., Ehrhart, S., Franchin, A., Gagné, S., Ickes, L., Kürten, A., Kupc, A., Metzger, A., Riccobono, F., Rondo, L., Schobesberger, S., Tsagkogeorgas, G., Wimmer, D., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Dommen, J., Downard, A., Ehn, M., Flagan, R. C., Haider, S., Hansel, A., Hauser, D., Jud, W., Junninen, H., Kreissl, F., Kvashin, A., Laaksonen, A., Lehtipalo, K., Lima, J., Lovejoy, E. R., Makhmutov, V., Mathot, S., Mikkila, J., Minginette, P., Mogo, S., Nieminen, T., Onnela, A., Pereira, P., Petäjä, T., Schnitzhofer, R., Seinfeld, J. H., Sipilä, M., Stozhkov, Y., Stratmann, F., Tomé, A., Vanhanen, J., Viisanen, Y., Vrtala, A., Wagner, P. E., Walther, H., Weingartner, E., Wex, H., Winkler, P. M., Carslaw, K. S., Worsnop, D. R., Baltensperger, U., and Kulmala, M.: Role of sulphuric acid, ammonia and galactic cosmic rays in atmospheric aerosol nucleation, Nature, 476, 429–433, https://doi.org/10.1038/nature10343, 2011.
Kirkby, J., Duplissy, J., Sengupta, K., Frege, C., Gordon, H., Williamson, C., Heinritzi, M., Simon, M., Yan, C., Almeida, J., Tröstl, J., Nieminen, T., Ortega, I. K., Wagner, R., Adamov, A., Amorim, A., Bernhammer, A.-K., Bianchi, F., Breitenlechner, M., Brilke, S., Chen, X., Craven, J., Dias, A., Ehrhart, S., Flagan, R. C., Franchin, A., Fuchs, C., Guida, R., Hakala, J., Hoyle, C. R., Jokinen, T., Junninen, H., Kangasluoma, J., Kim, J., Krapf, M., Kürten, A., Laaksonen, A., Lehtipalo, K., Makhmutov, V., Mathot, S., Molteni, U., Onnela, A., Peräkylä, O., Piel, F., Petäjä, T., Praplan, A. P., Pringle, K., Rap, A., Richards, N. A. D., Riipinen, I., Rissanen, M. P., Rondo, L., Sarnela, N., Schobesberger, S., Scott, C. E., Seinfeld, J. H., Sipilä, M., Steiner, G., Stozhkov, Y., Stratmann, F., Tomé, A., Virtanen, A., Vogel, A. L., Wagner, A. C., Wagner, P. E., Weingartner, E., Wimmer, D., Winkler, P. M., Ye, P., Zhang, X., Hansel, A., Dommen, J., Donahue, N. M., Worsnop, D. R., Baltensperger, U., Kulmala, M., Carslaw, K. S., and Curtius, J.: Ion-induced nucleation of pure biogenic particles, Nature, 533, 521–526, https://doi.org/10.1038/nature17953, 2016.
Klippenstein, S. J., Khundkar, L. R., Zewail, A. H., and Marcus, R. A.: Application of unimolecular reaction-rate theory for highly flexible transition-states to the dissociation of NCNO into NC and NO, J. Chem. Phys., 89, 4761–4770, https://doi.org/10.1063/1.455670, 1988.
Kozuch, S. and Martin, J. M. L.: “Turning Over” Definitions in Catalytic Cycles, Acs Catalysis, 2, 2787–2794, https://doi.org/10.1021/cs3005264, 2012.
Kuang, C., McMurry, P. H., McCormick, A. V., and Eisele, F. L.: Dependence of nucleation rates on sulfuric acid vapor concentration in diverse atmospheric locations, J. Geophys. Res.-Atmos., 113, D10209, https://doi.org/10.1029/2007jd009253, 2008.
Kulmala, M., Pirjola, L., and Mäkelä, J. M.: Stable sulphate clusters as a source of new atmospheric particles, Nature, 404, 66–69, https://doi.org/10.1038/35003550, 2000.
Kupiainen-Määttä, O., Olenius, T., Kurtén, T., and Vehkamäki, H.: CIMS sulfuric acid detection efficiency enhanced by amines due to higher dipole moments: a computational study, J. Phys. Chem. A, 117, 14109–14119, https://doi.org/10.1021/jp4049764, 2013.
Larson, L. J., Kuno, M., and Tao, F.-M.: Hydrolysis of sulfur trioxide to form sulfuric acid in small water clusters, J. Chem. Phys., 112, 8830–8838, https://doi.org/10.1063/1.481532, 2000.
Le Breton, M., McGillen, M. R., Muller, J. B. A., Bacak, A., Shallcross, D. E., Xiao, P., Huey, L. G., Tanner, D., Coe, H., and Percival, C. J.: Airborne observations of formic acid using a chemical ionization mass spectrometer, Atmos. Meas. Tech., 5, 3029–3039, https://doi.org/10.5194/amt-5-3029-2012, 2012.
Manninen, H. E., Nieminen, T., Asmi, E., Gagné, S., Häkkinen, S., Lehtipalo, K., Aalto, P., Vana, M., Mirme, A., Mirme, S., Hõrrak, U., Plass-Dülmer, C., Stange, G., Kiss, G., Hoffer, A., Törő, N., Moerman, M., Henzing, B., de Leeuw, G., Brinkenberg, M., Kouvarakis, G. N., Bougiatioti, A., Mihalopoulos, N., O'Dowd, C., Ceburnis, D., Arneth, A., Svenningsson, B., Swietlicki, E., Tarozzi, L., Decesari, S., Facchini, M. C., Birmili, W., Sonntag, A., Wiedensohler, A., Boulon, J., Sellegri, K., Laj, P., Gysel, M., Bukowiecki, N., Weingartner, E., Wehrle, G., Laaksonen, A., Hamed, A., Joutsensaari, J., Petäjä, T., Kerminen, V. M., and Kulmala, M.: EUCAARI ion spectrometer measurements at 12 European sites – analysis of new particle formation events, Atmos. Chem. Phys., 10, 7907–7927, https://doi.org/10.5194/acp-10-7907-2010, 2010.
Mauldin III, R. L., Berndt, T., Sipilä, M., Paasonen, P., Petäjä, T., Kim, S., Kurtén, T., Stratmann, F., Kerminen, V.-M., and Kulmala, M.: A new atmospherically relevant oxidant of sulphur dioxide, Nature, 488, 193–196, https://doi.org/10.1038/nature11278, 2012.
Möhler, O., Reiner, T., and Arnold, F.: The formation of by gas phase ion–molecule reactions, J. Chem. Phys., 97, 8233–8239, https://doi.org/10.1063/1.463394, 1992.
Nagato, K., Kim, C. S., Adachi, M., and Okuyama, K.: An experimental study of ion-induced nucleation using a drift tube ion, mobility spectrometer/mass spectrometer and a cluster-differential mobility analyzer/Faraday cup electrometer, J. Aerosol Sci., 36, 1036–1049, https://doi.org/10.1016/j.jaerosci.2004.12.006, 2005.
Nieminen, T., Manninen, H., Sihto, S.-L., Yli-Juuti, T., Mauldin III, R. L., Petäjä, T., Riipinen, I., Kerminen, V.-M., and Kulmala, M.: Connection of sulfuric acid to atmospheric nucleation in boreal forest, Environ. Sci. Technol., 43, 4715–4721, https://doi.org/10.1021/es803152j, 2009.
Noziere, B., Ekstrom, S., Alsberg, T., and Holmstrom, S.: Radical-initiated formation of organosulfates and surfactants in atmospheric aerosols, Geophys. Res. Lett., 37, L05806, https://doi.org/10.1029/2009gl041683, 2010.
Peng, C., Ayala, P. Y., Schlegel, H. B., and Frisch, M. J.: Using redundant internal coordinates to optimize equilibrium geometries and transition states, J. Comput. Chem., 17, 49–56, 1996.
Purvis, G. D. and Bartlett, R. J.: A full coupled-cluster singles and doubles model – the inclusion of disconnected triples, J. Chem. Phys., 76, 1910–1918, https://doi.org/10.1063/1.443164, 1982.
Rothe, E. W., Tang, S. Y., and Reck, G. P.: Measurement of electron affinities of O3, SO2, and SO3 by collisional ionization, J. Chem. Phys., 62, 3829–3831, https://doi.org/10.1063/1.430941, 1975.
Schindelka, J., Iinuma, Y., Hoffmann, D., and Herrmann, H.: Sulfate radical-initiated formation of isoprene-derived organosulfates in atmospheric aerosols, Faraday Discuss., 165, 237–259, https://doi.org/10.1039/c3fd00042g, 2013.
Schweitzer, C. and Schmidt, R.: Physical mechanisms of generation and deactivation of singlet oxygen, Chem. Rev., 103, 1685–1757, https://doi.org/10.1021/cr010371d, 2003.
Seinfeld, J. H. and Pandis, S. N.: Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, 3rd Edn., John Wiley & Sons, Inc., New Jersey, 2016.
Sipilä, M., Berndt, T., Petäjä, T., Brus, D., Vanhanen, J., Stratmann, F., Patokoski, J., Mauldin III, R. L., Hyvarinen, A.-P., Lihavainen, H., and Kulmala, M.: The Role of Sulfuric Acid in Atmospheric Nucleation, Science, 327, 1243–1246, https://doi.org/10.1126/science.1180315, 2010.
Su, T. and Chesnavich, W. J.: Parametrization of the ion-polar molecule collision rate-constant by trajectory calculations, J. Chem. Phys., 76, 5183–5185, https://doi.org/10.1063/1.442828, 1982.
Surratt, J. D., Lewandowski, M., Offenberg, J. H., Jaoui, M., Kleindienst, T. E., Edney, E. O., and Seinfeld, J. H.: Effect of acidity on secondary organic aerosol formation from isoprene, Environ. Sci. Technol., 41, 5363–5369, https://doi.org/10.1021/es0704176, 2007.
Surratt, J. D., Gomez-Gonzalez, Y., Chan, A. W. H., Vermeylen, R., Shahgholi, M., Kleindienst, T. E., Edney, E. O., Offenberg, J. H., Lewandowski, M., Jaoui, M., Maenhaut, W., Claeys, M., Flagan, R. C., and Seinfeld, J. H.: Organosulfate formation in biogenic secondary organic aerosol, J. Phys. Chem. A, 112, 8345–8378, https://doi.org/10.1021/jp802310p, 2008.
Svensmark, H., Pedersen, J. O. P., Marsh, N. D., Enghoff, M. B., and Uggerhoj, U. I.: Experimental evidence for the role of ions in particle nucleation under atmospheric conditions, Proc. Roy. Soc. A, 463, 385–396, https://doi.org/10.1098/rspa.2006.1773, 2007.
Tang, W., Sanville, E., and Henkelman, G.: A grid-based Bader analysis algorithm without lattice bias, J. Phys. Condens. Matter, 21, 084204, https://doi.org/10.1088/0953-8984/21/8/084204, 2009.
Tsona, N., Bork, N., and Vehkamäki, H.: Exploring the chemical fate of the sulfate radical anion by reaction with sulfur dioxide in the gas phase, Atmos. Chem. Phys., 15, 495–503, https://doi.org/10.5194/acp-15-495-2015, 2015.
Tsona, N. T., Bork, N., and Vehkamäki, H.: On the gas-phase reaction between SO2 and (H2O)0−3 clusters – an ab initio study, Phys. Chem. Chem. Phys., 16, 5987–5992, https://doi.org/10.1039/c3cp54715a, 2014.
Tsona, N. T., Bork, N., Loukonen, V., and Vehkamäki, H.: A Closure Study of the Reaction between Sulfur Dioxide and the Sulfate Radical Ion from First-Principles Molecular Dynamics Simulations, J. Phys. Chem. A, 120, 1046–1050, https://doi.org/10.1021/acs.jpca.5b12395, 2016.
Tsona, N. T., Li, J., and Du, L.: From -Initiated SO2 oxidation to sulfate formation in the gas-phase, J. Phys. Chem. A, 122, 5781–5788, https://doi.org/10.1021/acs.jpca.8b03381, 2018.
Vereecken, L., Harder, H., and Novelli, A.: The reaction of Criegee intermediates with NO, RO2, and SO2, and their fate in the atmosphere, Phys. Chem. Chem. Phys., 14, 14682–14695, https://doi.org/10.1039/c2cp42300f, 2012.
Wagner, R., Yan, C., Lehtipalo, K., Duplissy, J., Nieminen, T., Kangasluoma, J., Ahonen, L. R., Dada, L., Kontkanen, J., Manninen, H. E., Dias, A., Amorim, A., Bauer, P. S., Bergen, A., Bernhammer, A. K., Bianchi, F., Brilke, S., Mazon, S. B., Chen, X., Draper, D. C., Fischer, L., Frege, C., Fuchs, C., Garmash, O., Gordon, H., Hakala, J., Heikkinen, L., Heinritzi, M., Hofbauer, V., Hoyle, C. R., Kirkby, J., Kürten, A., Kvashnin, A. N., Laurila, T., Lawler, M. J., Mai, H., Makhmutov, V., Mauldin Iii, R. L., Molteni, U., Nichman, L., Nie, W., Ojdanic, A., Onnela, A., Piel, F., Quéléver, L. L. J., Rissanen, M. P., Sarnela, N., Schallhart, S., Sengupta, K., Simon, M., Stolzenburg, D., Stozhkov, Y., Tröstl, J., Viisanen, Y., Vogel, A. L., Wagner, A. C., Xiao, M., Ye, P., Baltensperger, U., Curtius, J., Donahue, N. M., Flagan, R. C., Gallagher, M., Hansel, A., Smith, J. N., Tomé, A., Winkler, P. M., Worsnop, D., Ehn, M., Sipilä, M., Kerminen, V. M., Petäjä, T., and Kulmala, M.: The role of ions in new particle formation in the CLOUD chamber, Atmos. Chem. Phys., 17, 15181–15197, https://doi.org/10.5194/acp-17-15181-2017, 2017.
Wang, G., Zhang, R., Gomez, M. E., Yang, L., Levy Zamora, M., Hu, M., Lin, Y., Peng, J., Guo, S., Meng, J., Li, J., Cheng, C., Hu, T., Ren, Y., Wang, Y., Gao, J., Cao, J., An, Z., Zhou, W., Li, G., Wang, J., Tian, P., Marrero-Ortiz, W., Secrest, J., Du, Z., Zheng, J., Shang, D., Zeng, L., Shao, M., Wang, W., Huang, Y., Wang, Y., Zhu, Y., Li, Y., Hu, J., Pan, B., Cai, L., Cheng, Y., Ji, Y., Zhang, F., Rosenfeld, D., Liss, P. S., Duce, R. A., Kolb, C. E., and Molina, M. J.: Persistent sulfate formation from London Fog to Chinese haze, P. Natl. Acad. Sci. USA, 113, 13630, https://doi.org/10.1073/pnas.1616540113, 2016.
Welz, O., Savee, J. D., Osborn, D. L., Vasu, S. S., Percival, C. J., Shallcross, D. E., and Taatjes, C. A.: Direct kinetic measurements of Criegee intermediate (CH2OO) formed by reaction of CH2I with O2, Science, 335, 204–207, https://doi.org/10.1126/science.1213229, 2012.
Yan, C., Dada, L., Rose, C., Jokinen, T., Nie, W., Schobesberger, S., Junninen, H., Lehtipalo, K., Sarnela, N., Makkonen, U., Garmash, O., Wang, Y., Zha, Q., Paasonen, P., Bianchi, F., Sipilä, M., Ehn, M., Petäjä, T., Kerminen, V. M., Worsnop, D. R., and Kulmala, M.: The role of H2SO4–NH3 anion clusters in ion-induced aerosol nucleation mechanisms in the boreal forest, Atmos. Chem. Phys., 18, 13231–13243, https://doi.org/10.5194/acp-18-13231-2018, 2018.
Yu, F.: From molecular clusters to nanoparticles: second-generation ion-mediated nucleation model, Atmos. Chem. Phys., 6, 5193–5211, https://doi.org/10.5194/acp-6-5193-2006, 2006.
Yu, F. Q. and Turco, R. P.: Ultrafine aerosol formation via ion-mediated nucleation, Geophys. Res. Lett., 27, 883–886, https://doi.org/10.1029/1999gl011151, 2000.
Yu, F. Q. and Turco, R. P.: From molecular clusters to nanoparticles: Role of ambient ionization in tropospheric aerosol formation, J. Geophys. Res.-Atmos., 106, 4797–4814, https://doi.org/10.1029/2000jd900539, 2001.
Yu, T., Zhao, D., Song, X., and Zhu, T.: NO2-initiated multiphase oxidation of SO2 by O2 on CaCO3 particles, Atmos. Chem. Phys., 18, 6679–6689, https://doi.org/10.5194/acp-18-6679-2018, 2018.
Zhang, H., Chen, S., Zhong, J., Zhang, S., Zhang, Y., Zhang, X., Li, Z., and Zeng, X. C.: Formation of aqueous-phase sulfate during the haze period in China: Kinetics and atmospheric implications, Atmos. Environ., 177, 93–99, https://doi.org/10.1016/j.atmosenv.2018.01.017, 2018.
Zhao, D., Song, X., Zhu, T., Zhang, Z., Liu, Y., and Shang, J.: Multiphase oxidation of SO2 by NO2 on CaCO3 particles, Atmos. Chem. Phys., 18, 2481–2493, https://doi.org/10.5194/acp-18-2481-2018, 2018.
Zhao, Y. and Truhlar, D. G.: The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Account., 120, 215–241, https://doi.org/10.1007/s00214-007-0310-x, 2008.





