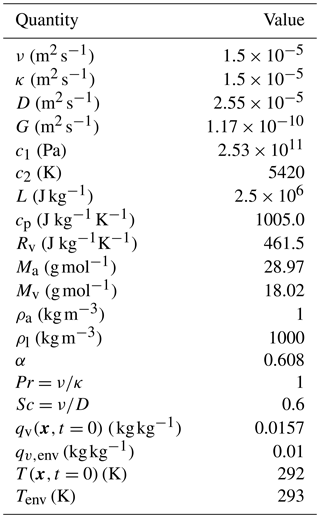the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Cloud-droplet growth due to supersaturation fluctuations in stratiform clouds
Gunilla Svensson
Axel Brandenburg
Nils E. L. Haugen
Condensational growth of cloud droplets due to supersaturation fluctuations is investigated by solving the hydrodynamic and thermodynamic equations using direct numerical simulations (DNS) with droplets being modeled as Lagrangian particles. The supersaturation field is calculated directly by simulating the temperature and water vapor fields instead of being treated as a passive scalar. Thermodynamic feedbacks to the fields due to condensation are also included for completeness. We find that the width of droplet size distributions increases with time, which is contrary to the classical theory without supersaturation fluctuations, where condensational growth leads to progressively narrower size distributions. Nevertheless, in agreement with earlier Lagrangian stochastic models of the condensational growth, the standard deviation of the surface area of droplets increases as t1∕2. Also, for the first time, we explicitly demonstrate that the time evolution of the size distribution is sensitive to the Reynolds number, but insensitive to the mean energy dissipation rate. This is shown to be due to the fact that temperature fluctuations and water vapor mixing ratio fluctuations increase with increasing Reynolds number; therefore the resulting supersaturation fluctuations are enhanced with increasing Reynolds number. Our simulations may explain the broadening of the size distribution in stratiform clouds qualitatively, where the mean updraft velocity is almost zero.
The growth of cloud droplets is dominated by two processes: condensation and collection. Condensation of water vapor on active cloud condensation nuclei is important in the size range from the activation size of aerosol particles to about a radius of 10 µm (Lamb and Verlinde, 2011; Pruppacher and Klett, 2012). Since the rate of droplet growth by condensation is inversely proportional to the droplet radius, large droplets grow slower than smaller ones. This generates narrower size distributions (Lamb and Verlinde, 2011). To form rain droplets in warm clouds, small droplets must grow to about 50 µm in radius within 15–20 min (Devenish et al., 2012; Grabowski and Wang, 2013; Pruppacher and Klett, 2012; Seinfeld and Pandis, 2016). Therefore, collection, a widely accepted microscopical mechanism, has been proposed to explain the rapid formation of rain droplets (Berry and Reinhardt, 1974; Grabowski and Wang, 2013; Saffman and Turner, 1956; Shaw, 2003). However, collection can only become active when the size distribution reaches a certain width.
Hudson and Svensson (1995) observed a broadening of the droplet size distribution in Californian marine stratus, which was contrary to the classical theory of condensational growth (Yau and Rogers, 1996). The increasing width of droplet size distributions was further observed by Pawlowska et al. (2006) and Siebert and Shaw (2017). The contradiction between the observed broadening width and the theoretical narrowing width in the absence of turbulence has stimulated several studies. The classical treatment of diffusion-limited growth assumes that supersaturation depends only on average temperature and water mixing ratio. Since fluctuations of temperature and the water mixing ratio are affected by turbulence, the supersaturation fluctuations are inevitably subjected to turbulence. Naturally, condensational growth due to supersaturation fluctuations became the focus (Cooper, 1989; Grabowski and Abade, 2017; Kabanov and Mazin, 1970; Khvorostyanov and Curry, 1999; Korolev, 1995; Sardina et al., 2015; Sedunov, 1965; Srivastava, 1989). The supersaturation fluctuations are particularly important for understanding the condensational growth of cloud droplets in stratiform clouds, where the updraft velocity of the parcel is almost zero (Hudson and Svensson, 1995; Korolev, 1995). When the mean updraft velocity is not zero, there could be a competition between mean updraft velocity and supersaturation fluctuations. This may diminish the role of supersaturation fluctuations (Sardina et al., 2018).
Condensational growth due to supersaturation fluctuations was first recognized by Srivastava (1989), who criticized the use of a volume-averaged supersaturation and proposed a randomly distributed supersaturation field. Cooper (1989) proposed that droplets moving in clouds are exposed to a varying supersaturation field. This results in a broadening of the droplet size distribution due to supersaturation fluctuations. Grabowski and Wang (2013) called the mechanism of Cooper (1989) the eddy-hopping mechanism, which was then investigated by Grabowski and Abade (2017). Using direct numerical simulations (DNS), Vaillancourt et al. (2002) found that the mean energy dissipation rate of turbulence has a negligible effect on condensational growth and attributed this to the decorrelation between the supersaturation and the droplet size. Paoli and Shariff (2009) considered three-dimensional (3-D) turbulence as well as stochastically forced temperature and vapor fields with a focus on statistical modeling for large-eddy simulations. They found that supersaturation fluctuations due to turbulence mixing are responsible for the broadening of the droplet size distribution. Lanotte et al. (2009) conducted 3-D DNS for condensational growth by only solving a passive scalar equation for the supersaturation and concluded that the width of the size distribution increases with increasing Reynolds number. Sardina et al. (2015) extended the DNS of Lanotte et al. (2009) to a higher Reynolds number and found that the variance of the size distribution increases in time. In a similar manner as Sardina et al. (2015), Siewert et al. (2017) modeled the supersaturation field as a passive scalar coupled to the Lagrangian particles and found that their results can be reconciled with those of earlier numerical studies by noting that the droplet size distribution broadens with increasing Reynolds number (Lanotte et al., 2009; Paoli and Shariff, 2009; Sardina et al., 2015). Neither Sardina et al. (2015) nor Siewert et al. (2017) solved the thermodynamics that determine the supersaturation field. Both Saito and Gotoh (2017) and Chen et al. (2018) solved the thermodynamics equations governing the supersaturation field. However, since collection was also included in their work, one cannot clearly identify the roles of turbulence on collection or condensational growth, nor can one compare their results with Lagrangian stochastic models (Sardina et al., 2015; Siewert et al., 2017) related to condensational growth.
Recent laboratory experiments and observations about cloud microphysics also confirm the notion that supersaturation fluctuations may play an important role in broadening the size distribution of cloud droplets. The laboratory studies of Chandrakar et al. (2016) and Desai et al. (2018) suggested that supersaturation fluctuations in the low aerosol number concentration limit are likely of leading importance for the onset of precipitation. The condensational growth due to supersaturation fluctuations seems to be more sensitive to the integral scale of turbulence (Götzfried et al., 2017). Siebert and Shaw (2017) measured the variability of temperature, water vapor mixing ratio, and supersaturation in warm clouds and support the notion that both aerosol particle activation and droplet growth take place in the presence of a broad distribution of supersaturation (Brenguier et al., 1998; Hudson and Svensson, 1995; Miles et al., 2000; Pawlowska et al., 2006). The challenge is now how to interpret the observed broadening of the droplet size distribution in warm clouds. How does turbulence drive fluctuations of the scalar fields (temperature and water vapor mixing ratio) and therefore affect the broadening of droplet size distributions (Siebert and Shaw, 2017)?
In an attempt to answer this question, we conduct 3-D DNS experiments of condensational growth of cloud droplets, where turbulence, thermodynamics, feedback from droplets to the fields via the condensation rate, and buoyancy force are all included. The main aim is to investigate how supersaturation fluctuations affect the droplet size distribution. We particularly focus on the time evolution of the size distribution f(r,t) and its dependency on small and large scales of turbulence. We then compare our simulation results with Lagrangian stochastic models (Sardina et al., 2015; Siewert et al., 2017). For the first time, the stochastic model and simulation results from the complete set of equations governing the supersaturation field are compared.
We now discuss the basic equations where we combine the Eulerian description of the density (ρ), turbulent velocity (u), temperature (T), and water vapor mixing ratio (qv) with the Lagrangian description of the ensemble of cloud droplets. The water vapor mixing ratio qv is defined as the ratio between the mass density of water vapor and dry air. Droplets are treated as superparticles. A superparticle represents an ensemble of droplets, whose mass, radius, and velocity are the same as those of each individual droplet within it (Johansen et al., 2012; Li et al., 2017; Shima et al., 2009). For condensational growth, the superparticle approach (Li et al., 2017) is the same as the Lagrangian point-particle approach (Kumar et al., 2014) since there is no interaction among droplets. Nevertheless, we still use the superparticle approach so that we can include more processes like collection (Li et al., 2017, 2018) in the future. Another reason to adopt the superparticle approach is that it can be easily adapted to conduct large-eddy simulations with appropriate sub-grid-scale models (Grabowski and Abade, 2017). To investigate the condensational growth of cloud droplets that experience fluctuating supersaturation, we track each individual superparticle in a Lagrangian manner. The motion of each superparticle is governed by the momentum equation for inertial particles. The supersaturation field in the simulation domain is determined by T(x,t) and qv(x,t) transported by turbulence. Lagrangian droplets are exposed in different supersaturation fields. Therefore, droplets either grow by condensation or shrink by evaporation depending on the local supersaturation field. This phase transition generates a buoyancy force, which in turn affects the turbulent kinetic energy, T(x,t), and qv(x,t). Pencil Code (Brandenburg, 2018) is used to conduct all the simulations.
2.1 Equations of motion for Eulerian fields
The background airflow is almost incompressible and thus obeys the Boussinesq approximation. Its density ρ(x,t) is governed by the continuity equation and velocity u(x,t) by the Navier–Stokes equation. The temperature T(x,t) of the background airflow is determined by the energy equation with a source term due to the latent heat release. The water vapor mixing ratio qv(x,t) is transported by the background airflow. The Eulerian equations are given by
where is the material derivative, f is a random forcing function (Haugen et al., 2004), ν is the kinematic viscosity of air, is the traceless rate-of-strain tensor, p is the gas pressure, ρ is the gas density, cp is the specific heat at constant pressure, L is the latent heat, κ is the thermal diffusivity of air, Cd is the condensation rate, B is the buoyancy, ez is the unit vector in the z direction (vertical direction), and D is the diffusivity of water vapor. To avoid global transpose operations associated with calculating Fourier transforms for solving the nonlocal equation for the pressure in strictly incompressible calculations, we solve here instead the compressible Navier–Stokes equations using high-order finite differences. The sound speed cs obeys , where is the ratio between specific heats, cp and cv, at constant pressure and constant volume, respectively. We set the sound speed as 5 m s−1 to simulate the nearly incompressible atmospheric airflow, resulting in a Mach number of 0.06 when urms=0.27 m s−1, where urms is the rms velocity. Such a configuration, with such a small Mach number, is almost equivalent to an incompressible flow. It is worth noting that the temperature determining the compressibility of the flow is constant and independent of the temperature field of the gas flow governed by Eq. (3). Also, since the gas flow is almost incompressible and its mass density is much smaller than the one of the droplet, there is no mass exchange between the gas flow and the droplet; i.e., the density of the gas flow ρ(x,t) is not affected by T(x,t). Thus, the source terms Sρ and Su in Eqs. (1) and (2) are neglected (Krüger et al., 2017). The buoyancy B(x,t) depends on the temperature T(x,t), water vapor mixing ratio qv(x,t), and the liquid mixing ratio ql (Kumar et al., 2014),
where when Ma and Mv are the molar masses of air and water vapor, respectively. The amplitude of the gravitational acceleration is given by g. The liquid water mixing ratio is the ratio between the mass density of liquid water and the dry air and is defined as
where ρl and ρa are the liquid water density and the reference mass density of dry air. N△ is the total number of droplets in a cubic grid cell with volume (Δx)3, where Δx is the one-dimensional size of the grid box. The temperature fluctuations are given by
and the water vapor mixing ratio fluctuations by
We adopt the same method as in Kumar et al. (2014), where the mean environmental temperature Tenv and water vapor mixing ratio qv,env do not change in time. This assumption is plausible in the circumstance that we do not consider the entrainment; i.e., there is only mass and energy transfer between liquid water and water vapor. The condensation rate Cd (Vaillancourt et al., 2001) is given by
where G is the condensation parameter (in units of m2 s−1), which depends weakly on temperature and pressure and is here assumed to be constant (Lamb and Verlinde, 2011). The supersaturation s is defined as the ratio between the vapor pressure ev and the saturation vapor pressure es,
Using the ideal gas law, Eq. (10) can be expressed as
In terms of the water vapor mixing ratio and saturation water vapor mixing ratio , Eq. (11) can be written as
Here ρv is the mass density of water vapor and ρvs the mass density of saturated water vapor, and qvs(T) is the saturation water vapor mixing ratio at temperature T and can be determined by the ideal gas law,
The saturation vapor pressure es over liquid water is the partial pressure due to the water vapor when an equilibrium state of evaporation and condensation is reached for a given temperature. It can be determined by the Clausius–Clapeyron equation, which determines the change in es with temperature T. Assuming constant latent heat L, es is approximated as (Götzfried et al., 2017; Yau and Rogers, 1996)
where c1 and c2 are constants adopted from page 14 of Yau and Rogers (1996). We refer to Table 1 for all the thermodynamics constants. In the present study, the updraft cooling is omitted. Therefore, the assumption of constant latent heat L is plausible.
2.2 Lagrangian model for cloud droplets
In addition to the Eulerian fields described in Sect. 2.1 we treat cloud droplets as Lagrangian particles. In the Pencil Code, they are invoked as non-interacting superparticles.
2.2.1 Kinetics of cloud droplets
Each superparticle is treated as a Lagrangian point particle, where one solves for the particle position xi,
and its velocity Vi via
in the usual way; see Li et al. (2017) for details. Here, u is the fluid velocity at the position of the superparticle, and τi is the particle inertial response or stopping time of a droplet i and is given by
The correction factor (Marchioli et al., 2008; Schiller and Naumann, 1933),
models the effect of the nonzero particle Reynolds number . This is a widely used approximation, although it does not correctly reproduce the small-Rei correction to the Stokes formula (Veysey II and Goldenfeld, 2007).
2.2.2 Condensational growth of cloud droplets
The condensational growth of the particle radius ri is governed by Lamb and Verlinde (2011); Pruppacher and Klett (2012)
3.1 Initial configurations
The initial values of the water vapor mixing ratio kg kg−1 and temperature are matched to the ones obtained in the CARRIBA experiments (Katzwinkel et al., 2014), which are the same as those in Götzfried et al. (2017). With this configuration, we obtain %, which means that the water vapor is initially supersaturated. The time step of the simulations presented here is governed by the smallest timescale in the present configuration, which is the particle stopping time defined in Eq. (17). The thermodynamic timescale is much larger than the turbulent one. Table 1 shows the list of thermodynamic parameters used in the present study.
Initially, 10 µm sized droplets with zero velocity are randomly distributed in the simulation domain. The mean number density of droplets, which is constant in time since droplet collections are not considered, is m−3. This gives an initial liquid water content, , which is 0.001 kg m−3. The simulation domain is a cube of size , the values of which are given in Table 2. The number of superparticles Ns satisfies , where Ngrid is the number of lattices depending on the spatial resolution of the simulations. Setting , on the one hand, is still within the convergence range (Li et al., 2018). On the other hand, it can mimic the diluteness of the atmospheric cloud system, where there are about 0.1 droplets per cubic Kolmogorov scale. This configuration results in when Ngrid=1283.
3.2 DNS
We conduct high-resolution simulations (Li et al., 2019) for the different Taylor micro-scale Reynolds number Reλ and mean energy dissipation rate (see Table 2 for details of the simulations). The Taylor micro-scale Reynolds number is defined as . For simulations with different values of at fixed Reλ, we vary both the domain size Lx () and the amplitude of the forcing f0. As for fixed , Reλ is varied by solely changing the domain size, which in turn changes urms. In all simulations, we use for the Prandtl number and for the Schmidt number . For our simulations with Ngrid=5123 mesh points, the code computes 55 000 time steps in 24 h wall-clock time using 4096 cores. For Ngrid=1283 mesh points, the code computes 4.5 million time steps in 24 h wall-clock time using 512 cores.
Figure 1a shows time-averaged turbulent kinetic-energy spectra for different values of at fixed Reλ≈130. Since the abscissa in the figures is normalized by , the different spectra shown in Fig. 1a collapse onto a single curve. Here, η is the Kolmogorov length scale. Fig. 1b shows the time-averaged turbulent kinetic-energy spectra for different values of Reλ at fixed . For larger Reynolds numbers the spectra extend to smaller wavenumbers. A flat profile corresponds to Kolmogorov scaling (Pope, 2000) when the energy spectrum is compensated by . For the largest Reλ in our simulations (Reλ=130), the inertial range extends for about a decade in k-space.
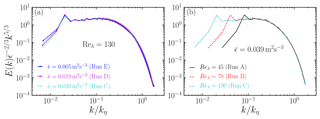
Figure 1Time-averaged kinetic-energy spectra of the turbulence gas flow for (a) different = 0.005 m2 s−3 (dash-dotted blue line), 0.019 (dash-dotted magenta line), and 0.039 (dashed cyan line) at fixed Reλ=130 (see runs C, D, and E in Table 2 for details) and for (b) different Reλ=45 (solid black line), 78 (dashed red line), and 130 (dashed cyan line) at fixed (see runs A, B, and C in Table 2 for details).
Next we inspect the response of thermodynamics to turbulence. In Fig. 2, we show time series of fluctuations of temperature Trms, water vapor mixing ratio qv,rms, buoyancy force Brms, and the supersaturation srms. All quantities reach a statistically steady state within a few seconds. The steady-state values of Trms, qv,rms, and srms increase with increasing Reλ approximately linearly and hardly vary at all with . On the other hand, Brms changes only by a few percent as Reλ or vary. Note, however, that the buoyancy force is only about 0.3 % of the fluid acceleration. This is because Trms is small (about 0.1 K in the present study). Therefore, the effect of the buoyancy force should indeed be small.
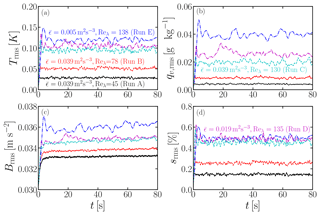
Figure 2Time series of the field quantities: (a) Trms, (b) qv,rms, (c) Brms, and (d) srms. Same simulations as in Fig. 1.
When changing while keeping Reλ fixed, the Kolmogorov scale of turbulence varies. Therefore, the various fluctuations quoted above are insensitive to the small scales of turbulence. However, when varying Reλ while keeping fixed, their rms values change, which is due to large scales of turbulence. Indeed, temperature fluctuations are driven by the large scales of turbulence, which affects the supersaturated vapor pressure qvs via the Clausius–Clapeyron equation; see Eq. (13). Therefore, supersaturation fluctuations result from both temperature fluctuations and water vapor fluctuations via Eq. (12). Both qv,rms and Trms increase with increasing Reλ, resulting in larger fluctuations of s. Supersaturation fluctuations, in turn, affect T and qv via the condensation rate Cd.
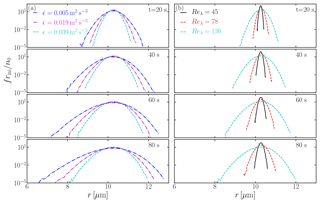
Our goal is to investigate the condensational growth of cloud droplets due to supersaturation fluctuations. Figure 3 shows the time evolution of droplet size distributions for different configurations. The conventional understanding is that condensational growth leads to a narrow size distribution (Lamb and Verlinde, 2011; Pruppacher and Klett, 2012). However, supersaturation fluctuations broaden the distribution. More importantly, the width of the size distribution increases with increasing Reλ, but decreases slightly with increasing over the range studied here. This is consistent with the results shown in Fig. 2 in that supersaturation fluctuations are sensitive to Reλ but are insensitive to . In atmospheric clouds, Reλ≈104, which may result in an even broader size distribution.
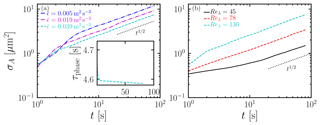
Figure 4Time evolution of σA for different (a) at Reλ=130 and (b) Reλ at . Same simulations as in Fig. 1.
We further quantify the variance of the size distribution by investigating the time evolution of the standard deviation of the droplet surface area σA for different configurations. In terms of the droplet surface area Ai (), Eq. (19) can be written as
It can be seen from Eq. (20) that the evolution of the surface area is analogous to Brownian motion, indicating that its standard deviation . A more detailed stochastic model for σA is developed by Sardina et al. (2015). Based on Eq. (19), σA is given by
Sardina et al. (2015) adopted a Langevin equation to model the supersaturation field and the vertical velocity of droplets, resulting in the scaling law:
where is a constant for given τL, τs, and Reλ. Under the assumptions that τs≪TL and a negligible influence on the macroscopic observables from small-scale turbulent motions, Sardina et al. (2015) obtained an analytical expression for σA as
where τs is the phase transition timescale given by
and τL is the turbulence integral timescale. The model proposed that condensational growth of cloud droplets depends only on Reλ and is independent of . In terms of the size distribution f(r,t), σA can be given as
where aζ is the moment of the size distribution, which is defined as
Here, ζ is a positive integer. As shown in Fig. 4, the time evolution of σA agrees with the prediction . Sardina et al. (2015) and Siewert et al. (2017) solved the passive scalar equation of s without considering fluctuations of T and qv. Feedbacks to flow fields from cloud droplets were also neglected. They found good agreement between the DNS and the stochastic model. Comparing with Sardina et al. (2015) and Siewert et al. (2017), our study solves the complete sets of the thermodynamics of supersaturation. It is remarkable that a good agreement between the stochastic model and our DNS is observed. This indicates that the stochastic model is robust. On the other hand, modeling supersaturation fluctuations using the passive scalar equation seems to be sufficient for the Reynolds numbers considered in this study. We recall that τs in Eq. (23) is constant. In the present study, τs is determined by Eq. (24). Therefore, τs varies with time as shown in the inset of Fig. 4a. Nevertheless, since the variation of τs is small, we still observe except for the initial phase of the evolution, where .
Comparing panels a and b of Fig. 4, it is clear that changing Reλ has a much larger effect on σA than changing . In fact, as is increased by a factor of about 8, σA decreases only by a factor of about 1.6, so the ratio of their logarithms is about 1∕5, i.e., . By contrast, σA changes by a factor of about 5 as Reλ is increased by a factor of nearly 3, so . This quantifies the high sensitivity of σA to changes in Reλ compared to .
Two comments are here in order. First, we emphasize that we observe here instead of σA∝Reλ. Therefore, there could be a critical Reλ, beyond which σA∝Reλ and below which . However, the highest Reλ in our DNS is 130. To verify this proposal, a large parameter range of Reλ is required. Second, we note that . This is because the Damköhler number increases with decreasing (see Table 2), which is defined as the ratio of the fluid timescale to the characteristic thermodynamic timescale associated with the evaporation process . Vaillancourt et al. (2002) also found that σA decreases with , even though the mean updraft cooling is included in their study.
Condensational growth of cloud droplets due to supersaturation fluctuations is investigated using DNS. Cloud droplets are tracked in a Lagrangian framework, where the momentum equation for inertial particles are solved. The thermodynamic equations governing the supersaturation field are solved simultaneously. Feedback from cloud droplets onto u, T, and qv is included through the condensation rate and buoyancy force. We resolve the smallest scale of turbulence in all simulations. Contrary to the classical condensation theory, which leads to a narrow distribution when supersaturation fluctuations are ignored, we find that droplet size distributions broaden due to supersaturation fluctuations. For the first time, we explicitly demonstrate that the size distribution becomes wider with increasing Reλ, which is, however, insensitive to . Supersaturation fluctuations are subjected to both temperature fluctuations and water vapor mixing ratio fluctuations.
We observe that when the complete sets of the thermodynamics equations governing the supersaturation are solved, which are consistent with the findings by Sardina et al. (2015) and Siewert et al. (2017) even though fluctuations of temperature and water vapor mixing ratio, buoyancy force, and droplets feedbacks to the field quantities are neglected in their studies. This indicates that the stochastic model of condensational growth developed by Sardina et al. (2015) is robust. For the first time, to our knowledge, the stochastic model (Sardina et al., 2015) and simulation results from the complete set of thermodynamics equations governing the supersaturation field are compared. The broadening size distribution with increasing Reλ demonstrates that condensational growth due to supersaturation fluctuations is an important mechanism for droplet growth. The maximum Reλ in the present study is 130, which is about 2 orders of magnitude smaller than the one in atmospheric clouds (Reλ=104). Since the width of the size distribution increases dramatically with increasing Reλ, the supersaturation-fluctuation-facilitated condensation may easily overcome the bottleneck barrier (Grabowski and Wang, 2013).
The stochastic model developed by Sardina et al. (2015) assumes that the width of droplet size distributions is independent of . Our result shows that the width decreases slightly with increasing . However, the largest in warm clouds is about (Grabowski and Wang, 2013). Therefore, neglecting the smallest scales in the stochastic model is indeed acceptable. Vaillancourt et al. (2002) also found that the width of the droplet size distribution decreases with increasing and attributed this to the decorrelation between supersaturation fluctuations and surface area of droplets. Sardina et al. (2015), however, found stronger correlation between supersaturation fluctuations and surface area of droplets with increasing Reλ. The present study is consistent with both the works of Vaillancourt et al. (2002) and Sardina et al. (2015). Therefore, we emphasize that there is no contradiction between both papers.
In the present study, the simulation box is stationary, which means that the volume is not exposed to cooling, as no mean updraft is considered. Therefore, the condensational growth is solely driven by supersaturation fluctuations. This is similar to the condensational growth of cloud droplets in stratiform clouds, where the updraft velocity of the parcel is close to zero (Hudson and Svensson, 1995; Korolev, 1995). The observational data show that the width of the size distribution is wider than the one expected from condensational growth with a mean supersaturation (Brenguier et al., 1998; Hudson and Svensson, 1995; Miles et al., 2000; Pawlowska et al., 2006; Siebert and Shaw, 2017). Qualitatively consistent with observations, we show that the width of droplet size distributions broadens due to supersaturation fluctuations.
Entrainment of dry air is not considered here. It may lead to rapid changes in the supersaturation fluctuations and result in an even faster broadening of the size distribution (Kumar et al., 2014). Activation of aerosols in a turbulent environment is omitted. This may provide a more physical and realistic initial distribution of cloud droplets. Incorporating all the cloud microphysical processes is computationally demanding and will have be explored in future studies.
The source code used for the simulations of this study, the Pencil Code (Brandenburg, 2018), is freely available on https://github.com/pencil-code/ (last access: 16 December 2018) The DOI of the code is https://doi.org/10.5281/zenodo.2315093. The DNS setup and the corresponding data (Li et al., 2019) are freely available at https://doi.org/10.5281/zenodo.2538027.
XYL developed the idea, coded the module, performed the simulations, and wrote the manuscript. AB and NELH contributed to the development of the module and commented on the manuscript. GS contributed to the development of the idea and commented on the manuscript.
The authors declare that they have no conflict of interest.
We thank Wojtek Grabowski, Andrew Heymsfield, Gaetano Sardina,
Igor Rogachevskii, and Dhrubaditya Mitra for stimulating discussions. This
work was supported through the FRINATEK grant 231444 under the Research
Council of Norway, SeRC, the Swedish Research Council grants 2012-5797 and
2013-03992, the University of Colorado through its support of the George
Ellery Hale visiting faculty appointment, and the grant “Bottlenecks for
particle growth in turbulent aerosols” from the Knut and Alice Wallenberg
Foundation, Dnr. KAW 2014.0048. The simulations were performed using
resources provided by the Swedish National Infrastructure for Computing
(SNIC) at the Royal Institute of Technology in Stockholm and Chalmers Centre
for Computational Science and Engineering (C3SE). This work also benefited
from computer resources made available through the Norwegian NOTUR program,
under award NN9405K.
The article processing charges for this
open-access
publication were covered by Stockholm University.
Edited by: Ryan Sullivan
Reviewed by: two anonymous referees
Berry, E. X. and Reinhardt, R. L.: An analysis of cloud drop growth by collection: Part I. Double distributions, J. Atmos. Sci., 31, 1814–1824, 1974. a
Brandenburg, A.: Pencil Code, https://doi.org/10.5281/zenodo.2315093, 2018. a, b
Brenguier, J.-L., Bourrianne, T., Coelho, A. A., Isbert, J., Peytavi, R., Trevarin, D., and Weschler, P.: Improvements of droplet size distribution measurements with the Fast-FSSP (Forward Scattering Spectrometer Probe), J. Atmos. Ocean. Tech., 15, 1077–1090, 1998. a, b
Chandrakar, K. K., Cantrell, W., Chang, K., Ciochetto, D., Niedermeier, D., Ovchinnikov, M., Shaw, R. A., and Yang, F.: Aerosol indirect effect from turbulence-induced broadening of cloud-droplet size distributions, P. Natl. Acad. Sci., 113, 14243–14248, 2016. a
Chen, S., Yau, M., and Bartello, P.: Turbulence effects of collision efficiency and broadening of droplet size distribution in cumulus clouds, J. Atmos. Sci., 75, 203–217, 2018. a
Cooper, W. A.: Effects of variable droplet growth histories on droplet size distributions. Part I: Theory, J. Atmos. Sci., 46, 1301–1311, 1989. a, b, c
Desai, N., Chandrakar, K., Chang, K., Cantrell, W., and Shaw, R.: Influence of Microphysical Variability on Stochastic Condensation in a Turbulent Laboratory Cloud, J. Atmos. Sci., 75, 189–201, 2018. a
Devenish, B., Bartello, P., Brenguier, J.-L., Collins, L., Grabowski, W., IJzermans, R., Malinowski, S., Reeks, M., Vassilicos, J., Wang, L.-P., and Warhaft, Z.: Droplet growth in warm turbulent clouds, Q. J. Roy. Meteor. Soc., 138, 1401–1429, 2012. a
Götzfried, P., Kumar, B., Shaw, R. A., and Schumacher, J.: Droplet dynamics and fine-scale structure in a shearless turbulent mixing layer with phase changes, J. Fluid Mech., 814, 452–483, 2017. a, b, c
Grabowski, W. W. and Abade, G. C.: Broadening of cloud droplet spectra through eddy hopping: Turbulent adiabatic parcel simulations, J. Atmos. Sci., 74, 1485–1493, 2017. a, b, c
Grabowski, W. W. and Wang, L.-P.: Growth of Cloud Droplets in a Turbulent Environment, Annu. Rev. Fluid Mech., 45, 293–324, 2013. a, b, c, d, e
Haugen, N. E. L., Brandenburg, A., and Dobler, W.: Simulations of nonhelical hydromagnetic turbulence, Phys. Rev. E, 70, 016308, https://doi.org/10.1103/PhysRevE.70.016308, 2004. a
Hudson, J. G. and Svensson, G.: Cloud microphysical relationships in California marine stratus, J. Appl. Meteorol., 34, 2655–2666, 1995. a, b, c, d, e
Johansen, A., Youdin, A. N., and Lithwick, Y.: Adding particle collisions to the formation of asteroids and Kuiper belt objects via streaming instabilities, Astron. Astrophys., 537, A125, https://doi.org/10.1051/0004-6361/201117701, 2012. a
Kabanov, A. and Mazin, I.: The effect of turbulence on phase transition in clouds, Tr. TsAO, 98, 113–121, 1970. a
Katzwinkel, J., Siebert, H., Heus, T., and Shaw, R. A.: Measurements of turbulent mixing and subsiding shells in trade wind cumuli, J. Atmos. Sci., 71, 2810–2822, 2014. a
Khvorostyanov, V. I. and Curry, J. A.: Toward the Theory of Stochastic Condensation in Clouds. Part I: A General Kinetic Equation, J. Atmos. Sci., 56, 3985–3996, https://doi.org/10.1175/1520-0469(1999)056<3985:TTTOSC>2.0.CO;2, 1999. a
Korolev, A. V.: The influence of supersaturation fluctuations on droplet size spectra formation, J. Atmos. Sci., 52, 3620–3634, 1995. a, b, c
Krüger, J., Haugen, N. E. L., and Løvås, T.: Correlation effects between turbulence and the conversion rate of pulverized char particles, Combust. Flame, 185, 160–172, 2017. a
Kumar, B., Schumacher, J., and Shaw, R. A.: Lagrangian Mixing Dynamics at the Cloudy–Clear Air Interface, J. Atmos. Sci., 71, 2564–2580, https://doi.org/10.1175/JAS-D-13-0294.1, 2014. a, b, c, d
Lamb, D. and Verlinde, J.: Physics and Chemistry of Clouds, Cambridge, England, Cambridge Univ. Press, 2011. a, b, c, d, e
Lanotte, A. S., Seminara, A., and Toschi, F.: Cloud Droplet Growth by Condensation in Homogeneous Isotropic Turbulence, J. Atmos. Sci., 66, 1685–1697, https://doi.org/10.1175/2008JAS2864.1, 2009. a, b, c
Li, X.-Y., Brandenburg, A., Haugen, N. E. L., and Svensson, G.: Eulerian and L agrangian approaches to multidimensional condensation and collection, J. Adv. Model. Earth Sy., 9, 1116–1137, 2017. a, b, c, d
Li, X.-Y., Brandenburg, A., Svensson, G., Haugen, N. E. L., Mehlig, B., and Rogachevskii, I.: Effect of Turbulence on Collisional Growth of Cloud Droplets, J. Atmos. Sci., 75, 3469–3487, https://doi.org/10.1175/JAS-D-18-0081.1, 2018. a, b
Li, X.-Y., Svensson, G., Brandenburg, A., and Haugen, N. E. L.: Cloud droplet growth due to supersaturation fluctuations in stratiform clouds, https://doi.org/10.5281/zenodo.2538027, 2019. a, b
Marchioli, C., Soldati, A., Kuerten, J., Arcen, B., Taniere, A., Goldensoph, G., Squires, K., Cargnelutti, M., and Portela, L.: Statistics of particle dispersion in direct numerical simulations of wall-bounded turbulence: Results of an international collaborative benchmark test, Intern. J. Multiphase Flow, 34, 879–893, 2008. a
Miles, N. L., Verlinde, J., and Clothiaux, E. E.: Cloud droplet size distributions in low-level stratiform clouds, J. Atmos. Sci., 57, 295–311, 2000. a, b
Paoli, R. and Shariff, K.: Turbulent condensation of droplets: direct simulation and a stochastic model, J. Atmos. Sci., 66, 723–740, 2009. a, b
Pawlowska, H., Grabowski, W. W., and Brenguier, J.-L.: Observations of the width of cloud droplet spectra in stratocumulus, Geophys. Res. Lett., 33, L19810, https://doi.org/10.1029/2006GL026841, 2006. a, b, c
Pope, S.: Turbulent Flows, Cambridge University Press, Cambridge, UK, 2000. a
Pruppacher, H. R. and Klett, J. D.: Microphysics of Clouds and Precipitation: Reprinted 1980, Springer Science & Business Media, Berlin, Germany, 2012. a, b, c, d
Saffman, P. G. and Turner, J. S.: On the collision of drops in turbulent clouds, J. Fluid Mech., 1, 16–30, https://doi.org/10.1017/S0022112056000020, 1956. a
Saito, I. and Gotoh, T.: Turbulence and cloud droplets in cumulus clouds, New J. Phys., 20, 023 001, 2017. a
Sardina, G., Picano, F., Brandt, L., and Caballero, R.: Continuous Growth of Droplet Size Variance due to Condensation in Turbulent Clouds, Phys. Rev. Lett., 115, 184501, https://doi.org/10.1103/PhysRevLett.115.184501, 2015. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r
Sardina, G., Poulain, S., Brandt, L., and Caballero, R.: Broadening of Cloud Droplet Size Spectra by Stochastic Condensation: Effects of Mean Updraft Velocity and CCN Activation, J. Atmos. Sci., 75, 451–467, 2018. a
Schiller, L. and Naumann, A.: Fundamental calculations in gravitational processing, Z. Ver. Dtsch. Ing., 77, 318–320, 1933. a
Sedunov, Y. S.: Fine cloud structure and its role in the formation of the cloud spectrum, Atmos. Oceanic Phys., 1, 416–421, 1965. a
Seinfeld, J. H. and Pandis, S. N.: Atmospheric chemistry and physics: from air pollution to climate change, John Wiley & Sons, New Jersey, US, 2016. a
Shaw, R. A.: Particle-turbulence interactions in atmospheric clouds, Annu. Rev. Fluid Mech., 35, 183–227, 2003. a
Shima, S., Kusano, K., Kawano, A., Sugiyama, T., and Kawahara, S.: The super-droplet method for the numerical simulation of clouds and precipitation: a particle-based and probabilistic microphysics model coupled with a non-hydrostatic model, Q. J. Roy. Meteor. Soc., 135, 1307–1320, 2009. a
Siebert, H. and Shaw, R. A.: Supersaturation fluctuations during the early stage of cumulus formation, J. Atmos. Sci., 74, 975–988, 2017. a, b, c, d
Siewert, C., Bec, J., and Krstulovic, G.: Statistical steady state in turbulent droplet condensation, J. Fluid Mech., 810, 254–280, 2017. a, b, c, d, e, f, g
Srivastava, R.: Growth of cloud drops by condensation: A criticism of currently accepted theory and a new approach, J. Atmos. Sci., 46, 869–887, 1989. a, b
Vaillancourt, P., Yau, M., and Grabowski, W. W.: Microscopic approach to cloud droplet growth by condensation. Part I: Model description and results without turbulence, J. Atmos. Sci., 58, 1945–1964, 2001. a
Vaillancourt, P., Yau, M., Bartello, P., and Grabowski, W. W.: Microscopic approach to cloud droplet growth by condensation. Part II: Turbulence, clustering, and condensational growth, J. Atmos. Sci., 59, 3421–3435, 2002. a, b, c, d
Veysey II, J. and Goldenfeld, N.: Simple viscous flows: From boundary layers to the renormalization group, Rev. Modern Phys., 79, 883–927, 2007. a
Yau, M. K. and Rogers, R.: A short course in cloud physics, Elsevier, Amsterdam, the Netherlands, 1996. a, b, c