the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Cloud droplet growth in shallow cumulus clouds considering 1-D and 3-D thermal radiative effects
Carolin Klinger
Graham Feingold
Takanobu Yamaguchi
The effect of 1-D and 3-D thermal radiation on cloud droplet growth in shallow cumulus clouds is investigated using large eddy simulations with size-resolved cloud microphysics. A two-step approach is used for separating microphysical effects from dynamical feedbacks. In step one, an offline parcel model is used to describe the onset of rain. The growth of cloud droplets to raindrops is simulated with bin-resolved microphysics along previously recorded Lagrangian trajectories. It is shown that thermal heating and cooling rates can enhance droplet growth and raindrop production. Droplets grow to larger size bins in the 10–30 µm radius range. The main effect in terms of raindrop production arises from recirculating parcels, where a small number of droplets are exposed to strong thermal cooling at cloud edge. These recirculating parcels, comprising about 6 %–7 % of all parcels investigated, make up 45 % of the rain for the no-radiation simulation and up to 60 % when 3-D radiative effects are considered. The effect of 3-D thermal radiation on rain production is stronger than that of 1-D thermal radiation. Three-dimensional thermal radiation can enhance the rain amount up to 40 % compared to standard droplet growth without radiative effects in this idealized framework.
In the second stage, fully coupled large eddy simulations show that dynamical effects are stronger than microphysical effects, as far as the production of rain is concerned. Three-dimensional thermal radiative effects again exceed one-dimensional thermal radiative effects. Small amounts of rain are produced in more clouds (over a larger area of the domain) when thermal radiation is applied to microphysics. The dynamical feedback is shown to be an enhanced cloud circulation with stronger subsiding shells at the cloud edges due to thermal cooling and stronger updraft velocities in the cloud center. It is shown that an evaporation–circulation feedback reduces the amount of rain produced in simulations where 3-D thermal radiation is applied to microphysics and dynamics, in comparison to where 3-D thermal radiation is only applied to dynamics.
- Article
(9156 KB) - Full-text XML
- BibTeX
- EndNote
Cloud droplets form in saturated environments by condensation of water vapor on cloud condensation nuclei (CCN). In the first phase of its lifetime, cloud droplet growth follows Köhler theory (Köhler, 1936). If a certain critical radius is reached a droplet can grow further, following diffusional droplet growth theory. From a certain droplet size onward, rain formation processes such as collision and coalescence dominate growth (Pruppacher and Klett, 2010).
The droplet size distribution in clouds has important implications for the Earth's atmosphere. The size distribution of droplets determines how much solar radiation is reflected back to space. Smaller droplet sizes reflect more radiation back to space (for constant liquid water), thus leading to a cooling of the atmosphere, while larger droplets allow radiation to penetrate more easily to the surface, thus allowing more radiation to be absorbed (Ramanathan et al., 1989; Stephens, 2005; Boucher et al., 2013).
Furthermore, the droplet size distribution determines the formation of rain in clouds. Droplets that reach the 10–30 µm radius range can lead to rain formation. Only very small numbers of droplets of this size (on the order of 1 per liter) are necessary to initiate the process of collision and coalescence. It is known that a broad droplet size spectrum is necessary for these processes to start; however, cloud droplet growth in the diffusional growth theory slows down when droplets reach 10 µm and collision and coalescence is not yet effective (the so-called collision–coalescence bottleneck Simpson, 1941; Langmuir, 1948; Mason, 1960; Pruppacher and Klett, 2010). Different processes can cause broadening of the droplet size spectra, e.g., turbulence (Grabowski and Wang, 2013), the associated supersaturation fluctuations (Cooper, 1989; Shaw et al., 1998; Lasher-Trapp et al., 2005; Grabowski and Abade, 2017), giant CCN (Feingold et al., 1999; Cheng et al., 2009) and radiation (Harrington et al., 2000; de Lozar and Muessle, 2016). As soon as rain is initiated, the cloud system morphology and intrinsic properties can change as the dynamics of the system change.
Radiative effects on cloud droplet growth have been studied in various ways in the past. Among the earliest are the studies by Roach (1976) and Barkstrom (1978). Both analyzed the growth of an individual droplet and showed that droplets can grow to 20 µm and larger by radiative cooling, even in a subsaturated environment.
Guzzi and Rizzi (1980) and Austin et al. (1995) studied the effect of radiation on the growth of a droplet population. Guzzi and Rizzi (1980) showed increased droplet growth in the diffusional droplet growth regime, while Austin et al. (1995) also included collision–coalescence and found earlier onset of rain by a factor of 4. An important issue of the application of radiation to droplet growth is the timescale of the temperature exchange. Davies (1985) estimated the time until droplets reach a steady state in temperature exchange. For most droplet sizes, the timescale was small enough to make the assumption of a steady state system feasible. Bott et al. (1990) simulated radiative fog, thus including microphysical and dynamical feedbacks. The inclusion of the radiative term in the droplet growth equation had important consequences for the lifetime of fog. The enhanced growth of larger droplets by radiation and associated gravitational settling caused a reduction of liquid water in the fog. The oscillation of liquid water (with a period of 15–20 min) could only be simulated by including radiative effects. Ackerman et al. (1995) simulated stratocumulus clouds, using a bin microphysical model including 1-D radiation. The stronger diffusional growth in the simulations with radiative effects reduced supersaturation and therefore the number of small droplets. The reduced number of droplets and the larger droplet size resulted in more drizzle and therefore a lower cloud optical thickness. Observations of nocturnal stratocumulus were remodeled with Lagrangian parcels by Caughey and Kitchen (1984). They stated that “a simple Lagrangian model suggested that the larger drops grew within the zone of high net radiative loss around cloud top”. Harrington et al. (2000) used a large eddy simulation (LES) and an independent parcel model, including bin microphysics and radiative effects on droplet growth. They showed that only parcel trajectories spending long periods of time at cloud top (10 min or more) can cause the droplet size spectrum to broaden via radiative cooling. They also found an earlier onset of drizzle production; however, this occurred along parcels that would produce drizzle anyhow. They concluded that radiative cooling may reduce the time for drizzle onset.
The recent theoretical study of Brewster (2015) and direct numerical simulations by de Lozar and Muessle (2016) re-emphasize the hypothesis that thermal radiation might influence droplet growth significantly and lead to a broadening of the droplet size spectra and thus enhance the formation of precipitation. Similarly, Zeng (2018) investigated the effect of thermal radiation on rain formation in a precipitating shallow cumulus case and found broadening of the droplet size spectrum and earlier rain formation.
In this study, we investigate the role of thermal radiation on cloud droplet growth in cumulus clouds. The limited lifetime of cumulus clouds changes the radiative impact compared to former studies where stratiform clouds where investigated. The finite size of the cumulus clouds and the high local cooling rates of several hundred kelvin per day (K d−1) at cloud top and at cloud sides (e.g., Kablick et al., 2011; Klinger and Mayer, 2014; Klinger et al., 2017) suggest that the investigation of 3-D thermal radiation effects might have a significant effect on droplet growth. Klinger and Mayer (2016) (their Fig. 11) showed that local peak differences in cooling rates between 1-D and 3-D thermal radiation in cumulus cloud fields can reach 20 %–120 %, depending on the cloud field resolution. But the differences between 1-D and 3-D thermal radiation are not only focused on local grid boxes. Kablick et al. (2011) and Črnivec and Mayer (2019) showed that layer averaged 1-D and 3-D heating and cooling differences can be up to 1 K d−1, which is the same order of magnitude as clear-sky cooling. Whether the stronger local 3-D cooling affects droplet growth compared to 1-D thermal cooling and if cooling in general causes changes in droplet growth in cumulus clouds are questions addressed in this study. The focus of this work is on thermal radiative effects on droplet growth. At the end of the study, we will briefly investigate thermal radiative effects on dynamics as shown by Guan et al. (1995, 1997), Mechem et al. (2008) or Klinger et al. (2017).
The paper is structured as follows: Sect. 2 provides the necessary theory and Sect. 3 the model setup. Section 4 analyzes the results of our study. Summary, conclusion and outlook are provided in Sect. 5.
The energy budget at a droplet surface is described by Eq. (1), which combines water vapor diffusion to the droplet and latent heat release, where lv is the latent heat, dm dt−1 the change in mass (m) over time (t), r the droplet radius, K the thermal diffusivity, and Td and Tinf the droplet temperature and the temperature of the surrounding air:
Following Roach (1976), the equation can be extended by a radiative term (Eq. 2), where HR Fnet,λ(r) is the emitted or absorbed power of an individual droplet. qabs,λ(r) is the absorption efficiency per droplet radius and wavelength (λ), and Fnet,λ(r) is the net radiative gain or loss of a droplet per radius and wavelength in watt per square meters (W m−2).
Harrington et al. (2000) transformed the equation to the notation of the bin microphysical model of Tzivion et al. (1989). We will follow their notation in the following, as we use the same bin microphysical model. Thus, Eq. (2) becomes
where l0 is a length scale representing gas kinetic effects, η(t) the excess specific humidity (qv-qs(T)) and ; , where D is the diffusion coefficient, Rv is the specific gas constant for moist air and es is the saturation vapor pressure. J(P,T) summarizes constants concerning the radiative term J(P,T)= with rs the saturation mixing ratio, αc= and ρl the liquid water density. We note that the radiative cooling is an increasing function of droplet mass.
HR(m) of a droplet is the wavelength band (i) integrated radiative gain or loss, weighted by the absorption efficiency for a mass size bin (k) for the bin microphysical model. Harrington et al. (2000) showed that the radiative term HR(m) can be approximated with the mean mass () of a drop size bin k:
This radiative term must be included in the equation for supersaturation and for droplet growth. The equation for the supersaturation, in our case water vapor excess η, is
where the function A(P,T) connects the integrated mass growth rate dMdt−1 to changes in η. Including the integrated radiative terms of the mass growth rate ℛ, Eq. (5) becomes
where D represents the increase or decrease in η due to dynamics, G is the contribution to η from the standard droplet growth and ℛ the contribution to η from radiatively driven droplet growth. Here it can be seen that the additional radiative term can increase or decrease η due to radiative heating or cooling. For a more detailed explanation the reader is referred to Harrington et al. (2000), their Eqs. (6)–(10).
For solving the condensation equation in the two-moment framework of Tzivion et al. (1989), where both mass and number in a bin k are predicted, Eq. (3) has to be integrated over one time step from t0 until tf. Again, we follow Harrington et al. (2000) to calculate the forcing τ (the gain or loss of mass of a droplet) of the droplet growth equation:
where τ is the combined dynamic (τd) and radiative (τr) forcing of the droplet growth equation, and m0 and mf are the initial and final mass of the droplet before and after condensation or evaporation.
What remains now is to derive the radiative term Fnet,λ(r) in Eq. (2) from the radiation scheme in the LES model. Heating rates in LES models are calculated spectrally from bulk water. These heating rates include contributions from liquid water (cloud water) as well as water vapor and other atmospheric gases. Former studies, e.g., Roach (1976) and Harrington et al. (2000), used a 1-D radiative transfer approximation and calculated the individual droplet absorption and emission from the upwelling and downwelling fluxes. We, however, include 3-D radiative effects. Our 3-D radiative transfer approximation is designed to provide 3-D heating rates. We estimate the individual droplet emission or absorption from a volume heating rate and therefore have to separate the heating or cooling from the liquid water phase (HRliquid) from the total heating or cooling (from liquid water and atmospheric gases, HRtot). We follow the approach of Mayer and Madronich (2004) which showed the relationship between heating or cooling rates and the actinic flux F0 to be
where kabs is the total absorption coefficient and kabs,liquid the absorption coefficient of liquid water.
Combining these two equations it follows that the heating or cooling rate resulting from the liquid water absorption is
This total heating rate now has to be distributed among all droplets in the volume. The total heating or cooling from the liquid water of a grid box (for a single wavelength λ or wavelength band i) is the sum of all droplet contributions to the heating or cooling:
where n(r) is the number of droplets of radius r per radius interval dr, and is the heating or cooling rate of each droplet at radius r with the absorption efficiency qabs,λ(r) and the net heating of each droplet Fnet,λ(r).
Assuming steady state (e.g., Davies, 1985), HRliquid,λ is equally distributed among all droplets, and the individual heating or cooling (Fnet,λ(r)) of a droplet of size r in Eq. (2) is therefore
To estimate the effect of 1-D and 3-D thermal radiation on cloud droplet growth we use a two-stage approach. First, to estimate the impact of thermal radiation on droplet growth and to gain insight into physical processes, we use Lagrangian parcels (Yamaguchi and Randall, 2012) recorded during a LES (System for Atmospheric Modeling, SAM; Khairoutdinov and Randall, 2003) with the bin-emulating two-moment bulk scheme of Feingold et al. (1998b). These parcel trajectories are then used to drive an independent (offline) parcel model including a bin-microphysics scheme (Tzivion et al., 1987; Feingold et al., 1999). We separate between 1-D (RRTMG, Mlawer et al., 1997; Iacono et al., 2000, 1DR) and 3-D thermal (Klinger and Mayer, 2016, 3DR) radiative effects and compare both results to the droplet growth without radiative impacts (NR) and to each other. This approach allows us to focus on the effect of thermal radiation on droplet growth, without the interaction of changing dynamics that would occur in a fully coupled LES.
Second, we run a fully coupled LES with the Tel Aviv University (TAU) bin-microphysics scheme (Tzivion et al., 1987; Feingold et al., 1988; Tzivion et al., 1989), where 1-D and 3-D thermal radiative effects (heating rates) are applied to the droplet growth and to the dynamics, or to just one of the two. We chose a shallow cumulus case with weak precipitation (BOMEX, Barbados Oceanographic and Meteorological EXperiment) where we expect the effects of thermal radiation on cloud droplet growth to be tangible and not overwhelmed by the rapid development of precipitation encountered in deeper trade-wind cumulus environments. We expect that it would be harder to discern these effects in a more strongly precipitating case.
In both cases the simulations were run with 75 m horizontal and 50 m vertical resolution for a 45 km×45 km domain. The simulations for the trajectories were run for 6 h in total; the last 2 h are used for evaluation. The coupled LES cases were run for 8 h in total.
For the first part of the study 2.7 million Lagrangian air parcel trajectories were recorded in the last 2 h of the BOMEX simulation with a 2 s time step. The simulation was driven by 1-D thermal radiation, but we recorded 3-D thermal radiation along the same parcels. This allows us to compare the same parcels, driven by the same variables (liquid water potential temperature, pressure, vertical velocity) in the later part of the study. The difference in the results of the independent parcel model ensemble is therefore only due to the difference in the 1-D and 3-D thermal heating or cooling rates and their impact on cloud droplet growth. (Changes to the approach of Harrington et al., 2000, were explained in Sect. 2.) The total number of aerosol particles (assumed to be ammonium sulfate) is 100 cm−3 with a median radius of 0.1 µm and a geometric standard deviation of 1.5 (assuming a log-normal distribution). The bin model includes diffusional growth and the growth by collision and coalescence and covers 33 size bins with a mass doubling from one bin to the next. The radius of the first bin (lower bound) is 1.56 µm. Aerosol particles are activated based on the locally calculated supersaturation and placed in the first bin. We neglect the solute and kelvin effect in this framework, because they have a minor impact for r>1.56 µm. Kinetic and ventilation effects are taken into account.
A few comments are in order regarding our approach. With the parcel model, we focus on the effects of thermal radiation on microphysics, neglecting any changes in cloud development that would occur due to feedbacks within a LES framework. A further advantage of this method is that spurious spectral broadening due to advection is avoided (Harrington et al., 2000). A key limitation of this method is that drop sedimentation is not represented; drops do not fall off a trajectory of interest, and drops from other trajectories do not fall onto that trajectory. Because all droplets follow the parcel trajectory, the liquid water content (qc) is not reduced as the parcels do not “rain out” and radiation does not change along the parcel trajectories when the size distribution (or qc) changes. The method is thus mostly useful for examining the onset of drizzle. One can consider the trajectory approach to be an imperfect but useful model (as documented in Stevens et al., 1996; Feingold et al., 1998a, 1999) for examining the combined effect of droplet growth and thermal radiation with and without the radiative effects in a framework that allows for realistic and quantifiable exposure to strong radiative cooling at cloud edges. The analysis of characteristic timescales of important processes for a droplet radius of 20 µm, such as diffusional droplet growth (χgrowth), diffusional droplet growth with radiation (χgrowth,rad) and sedimentation (χsed), supports our argument about the usefulness of the approach, despite the fact that sedimentation is not represented in the parcel model. The characteristic timescales for the three processes are on the order of minutes for the diffusional droplet growth (χgrowth=6 min 40 s and min 30 s) and on the order of an hour for sedimentation (χsed=1 h 23 min). For the full calculation of the timescales, the reader is referred to the appendix (Appendix A). This clear signal lends credence to the use of the parcel model.
In contrast, LES allows for a more faithful treatment of these processes because of the coupling of interactive components but at the expense of transparency of the radiative effects on droplet growth. In combination the two modeling approaches allow insights that neither could have produced by themselves.
As the microphysical schemes in our LES and in the offline parcel model are different (two-moment bulk vs. bin), small differences in the predicted liquid water can occur. Therefore, the calculated heating or cooling rates of the LES might occasionally be too high for the application in the parcel model, thus causing unrealistic droplet growth. We therefore applied a threshold to the cooling. Whenever the distributed droplet cooling (Fnet) was larger than the black body emission (σT4∕6; the factor 1∕6 accounting for the window regions and emission to only one hemispheric dimension) the cooling of the droplet was set to the black body emission value. Tests showed that the discrepancy between the liquid water content of the parcel model and the LES occurs most often at the edges of clouds where qc is very small. In this area, droplet cooling can be regarded as “black”, because droplets are exposed to clear sky.
The coupled LESs have a similar setup, but we used the bin-microphysics scheme from the beginning of the simulation. We restarted after 4 h from a base simulation with 1-D thermal radiation passed to dynamics only. We separate five cases:
-
1-D thermal radiation applied to dynamics only (1DD),
-
1-D thermal radiation applied to dynamics and droplet growth (1DD_1DM),
-
3-D thermal radiation applied to dynamics only (3DD),
-
3-D thermal radiation applied to dynamics and droplet growth (3DD_3DM), and
-
1-D thermal radiation applied to dynamics and 3-D radiation applied to droplet growth (1DD_3DM).
These five simulations allow us to (a) look at the effect of thermal radiation on droplet growth, (b) separate between 1-D and 3-D thermal radiative effects and (c) to separate the droplet growth effect from dynamical effects.
4.1 Parcel model – cloud field statistics and properties
Figure 1 shows a time snapshot of the cumulus field and selected time-dependent trajectories (red). From our 2.7 million parcel trajectories we selected about 340 000 that make contact with a cloud for further investigation. This number was chosen as it provides us with a statistically representative result and a number of parcels that could still be handled in a finite amount of time in the post-processing.
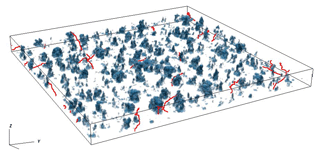
Figure 1Time snapshot of the BOMEX shallow cumulus cloud field. Displayed are qc and selected parcel trajectories (red).
The effect of 1-D and 3-D thermal radiation on the growth of cloud droplets depends (among other factors) on the length of time that a droplet is exposed to thermal cooling (in other words, that a droplet is located close to cloud edges or cloud top) and the strength of the cooling. Harrington et al. (2000) found that droplets have to spend about 10 min in a cooling area to experience a noticeable effect on the droplet size distribution. We therefore first investigated different properties of our trajectories:
-
in-cloud residence time and
-
time spent in the vicinity of cloud edges or cloud tops.
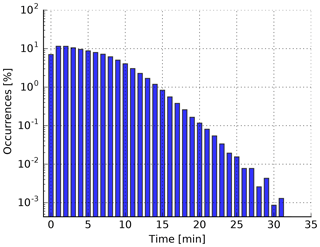
Figure 2Histogram of the time that parcels spend in a cloud. For the sampling of the data, a threshold of 0.01 g kg−1 of the qc was used to separate cloudy from non-cloudy regions.
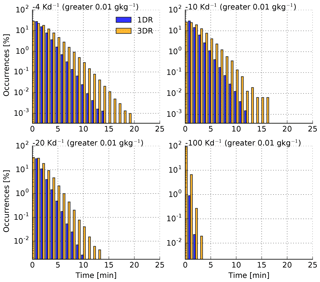
Figure 3Histogram of the time that parcels spend at cloud top or cloud side. For the sampling of the data, a threshold of 0.01 g kg−1 of the qc was used to separate cloudy from non-cloudy regions. To separate cloud edge regions from the cloud interior, four different thresholds of the cooling rates were used (4, 10, 20, 100 K d−1).
For the cloud residence time, we used a threshold of 0.01 g kg−1 to separate between cloudy and cloud-free areas. We then traced among our 340 000 parcel trajectories the time periods during which a parcel stays in a cloud. Inevitably, a parcel can contact a cloud more than once, in which case the hits were counted as multiple events. Figure 2 shows a histogram of the time that our parcels spend in clouds. Most of the parcels spend less than 15 min in a cloud, but we also find some rather long periods of more than 25 min. This is in agreement with former results (e.g., Jiang et al., 2010).
The time at cloud side was estimated by setting the same threshold for qc (0.01 g kg−1) and additionally setting four different thresholds in terms of heating rates (−4, −10, −20, −100 K d−1) for 1-D and 3-D thermal radiation. Again, multiple hits were possible for each parcel trajectory. The histograms are shown in Fig. 3. One-dimensional (blue) and three-dimensional (orange) thermal radiative transfer simulations show that most of the parcels spend less than 5 min in a certain cloud volume encompassing a cooling threshold. For the 100 K d−1 threshold, no parcel exceeds 3 min. However, there are some parcels which spend 10 min or longer, especially when 3-D radiative effects are considered in volumes experiencing cooling of 10–20 K d−1. This is simply due to the fact that a larger volume of each cloud experienced cooling rates in 3-D radiative transfer. The possibility that thermal radiation can affect cloud droplet growth is therefore given. In the following, we will take a closer look at individual parcel trajectories and the overall statistics of the 340 000 parcel trajectory ensemble.
4.2 Parcel model – cloud droplet growth including thermal radiative effects
4.2.1 Individual parcels
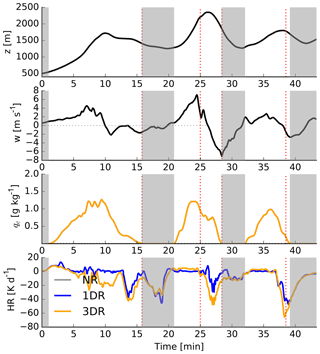
We now focus on individual parcels. An example of a parcel trajectory is given in Fig. 4. The qc is shown in color (Fig. 4a). This illustration of the trajectory includes a temporal dimension. Each data point is recorded at a different time step. The parcel rises in the beginning, enters an area of high qc (red, arrow (i)), followed by a decrease in qc (blue area, arrow (ii)), but never drops to zero, before entering again an area of high qc (red, arrow (iii)). Finally, qc decreases again and the parcel leaves the cloud.
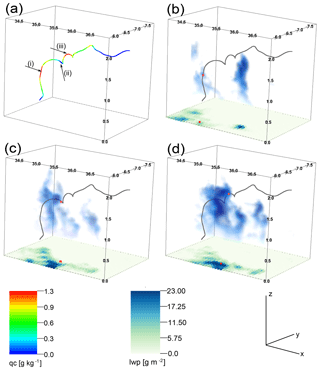
Figure 4The three-dimensional visualization of qc, the parcel position and liquid water path (lwp) of the selected scene. (a) shows the parcel trajectory. The qc at each time step of the selected parcel is colored. Three time intervals were selected for the following figures: time intervals where the parcel stays in high-qc areas (i, iii) and one where the qc drops substantially but does not reduce to zero (i). (b), (c) and (d) show the parcel trajectory (gray, again time dependent). For the time interval in focus, the qc is again colored. The displayed clouds are chosen at the center time of the interval, as is the lwp. The red marker displayed in the lwp field shows the projected location of the center time step.
The other three panels of Fig. 4 combine time snapshots of the cloud field and the temporal development of the parcel trajectory. The cloud field is shown at the time marked by the red dot on the trajectory. The surface shows the liquid water path, lwp, of the selected cloud field at that specific time. The red dot on the surface is the vertical projection of the location of the parcel at the time. Figure 4b shows the updraft area where the parcel first enters an area of high qc. The parcel (at that time) is located in the upper part of the cloud where it experiences cooling. In the following, the cloud grows, and at the next shown time step (Fig. 4c) a significantly larger cloud with more qc is encountered. The parcel is now located at the outer edge of the cloud (especially visible in the lwp field, red dot). qc has dropped below 0.01 g kg−1 but does not decrease to zero in the following, meaning the parcel never leaves the cloud. The cloud grows further (Fig. 4d)) and the parcel is located again in an area of high qc. We will see later that this “recirculation” of parcels occurs occasionally and can cause a broadening in the droplet size spectrum. It is likely that radiative effects become more important in this case, because parcels pass cloud edges where thermal cooling per droplet is strong.
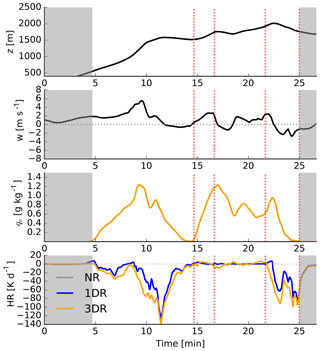
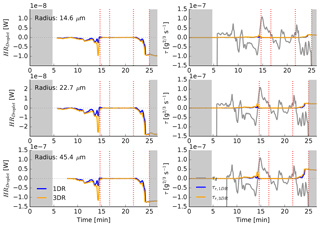
Figure 5Time series of different properties of the first selected parcel. Shown are height, vertical velocity, qc, heating or cooling rate, predominant radius and the heating or cooling rate per droplet. Gray areas show time intervals where the qc is below 0.01 g kg−1. The red dotted lines show selected time steps used in the following analysis.
4.2.2 Parcel trajectory 1
We now take a more detailed look at the same parcel trajectory shown in Fig. 4. Figure 5 shows this selected parcel, which is characterized by moderate vertical velocities (peaking at about 6 m s−1 in the beginning but not exceeding 2 m s−1 later on). The parcel stays in the cloud for about 20 min and twice experiences radiative cooling (for about 8 and 2 min). We chose four different time steps for further investigation (red dotted lines at 14, 16, 21 and 25 min). The first time step was chosen shortly after the parcel passes the first volume of strong cooling and is recirculating. Here, we defined “recirculation” loosely as an event where the qc along a parcel trajectory becomes very low (in this case 0.007 g kg−1). The second time step was chosen after qc has risen again, the third time step shortly before the second cooling phase and the fourth when the parcel leaves the cloud.
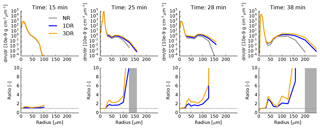
The drop distribution at these four time steps is shown in Fig. 6. Figure 6a–d show the drop size spectra (dm∕dr) themselves, and Fig. 6e–h show the ratio of the spectra of the 1DR and 3DR simulations and the NR simulation of the parcel.
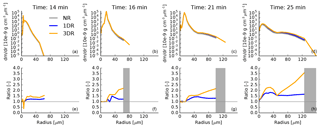
Figure 6Drop size distribution dm∕dr plot for the four selected time steps displayed by the red dotted line in Fig. 5. (a)–(d) show dm∕dr. The lower row shows the ratio between the NR case and the 1DR and 3DR case. Gray areas in (e)–(h) display size bins where mass occurs in the 1DR and 3DR case but not the 1DR case and therefore no ratio could be calculated.
In the beginning, hardly any differences can be seen in the drop spectra between the NR, 1DR and 3DR simulations. The spectrum broadens over time. Looking at the ratio of dm∕dr of the 1DR/3DR and the NR simulation reveals a decrease in mass in the small bins and an increase in the larger bins for the radiation simulations. This changes later in the simulation when the simulations with thermal radiation increase mass over the entire drop spectrum. dm∕dr for the 1DR and 3DR simulations exceeds the NR simulations up to 1.5 times for r>10 µm. The size spectrum broadens and a drizzle mode develops. The peak of the spectra remains at about 15 µm. The ratio for 3DR simulations always exceeds that for 1DR simulations. A factor of more than 2 is reached for dm∕dr of the 3-D radiation simulation compared to the NR simulation. The droplet concentration in the 20 µm bin (not shown) increases by up to 15 % for the 3DR case along this trajectory.
The possible increase in droplet growth by thermal radiation does not only depend on the time that a droplet is exposed to cooling, but also on the magnitude of the cooling and the size of the droplet. Recall that the larger the droplet, the more effectively radiation can act on it as the droplet absorbs and emits radiation more effectively. Radiative effects become stronger from a radius of about 10 µm on. Additionally, the radiative impact competes with the dynamical effects, which depend on the vertical velocity (see Eq. 7). It therefore follows that the larger the droplet and the weaker the updraft, the more radiation can affect droplet growth. Figure 7 shows the temporal development of the individual droplet heating or cooling rate for three different sizes (left column). This heating or cooling rate is the fraction of the spectrally and bin-integrated cooling rate per bin (Eq. 4), integrated over all wavelengths. The center radius of the corresponding bin is given in each figure. Gray shaded areas and the red lines are identical to those shown in Fig. 5 for comparison. Note the change in the y axis for these figures. We find that the cooling per droplet increases with increasing radius and that 3-D cooling is stronger than 1-D cooling.
The right column (Fig. 7) shows the forcing τ (Eq. 7), which is the total driving force for condensation in each bin. The gray line shows the dynamical forcing (τd), which if compared to Fig. 5 follows the vertical velocity trend. The radiative forcing (τr) is shown in yellow (3-D) and blue (1-D) for the same four size bins. Note that a cooling per droplet (left side) causes a positive contribution to the droplet growth and therefore a positive forcing (right side). The radiative forcing is smaller than the dynamical one but has the same order of magnitude. An additional boost is given to the droplet growth shortly before 15 min, after which the dynamical forcing rises again. This small radiative perturbation is sufficient to cause the increase in dm∕dr seen in Fig. 6b and f. The radiative forcing becomes strongest towards the end of the parcel trajectory, counteracting the negative dynamical forcing, especially for the larger size bins.
4.2.3 Parcel trajectory 2
This second parcel experiences stronger dynamical forcing. Vertical velocity rises and falls throughout the parcel's lifetime and peaks at more than ±6 m s−1. The parcel recirculates twice. During these two periods the parcel experiences radiative cooling, which causes a broadening of the droplet size spectrum (Figs. 8 and 9). Due to the strong dynamical forcing, the parcel shows broader spectra than the first trajectory. As before, a substantial increase in condensed water is found for the 1DR and 3DR simulations, peaking for the 3-D thermal radiation simulation.
These examples illustrate the variety of ways in which radiative effects can act on a cloud droplet. The time that a parcel spends in a certain cooling area, the magnitude of the cooling, the size of the droplets at the time of cooling and the dynamical forcing contribute to droplet growth with different magnitudes. The ideal situation for the radiative effects to enhance droplet growth would be droplets of size of about 10 µm or more, a cooling period of more than 5 min in a cooling of 20 K d−1 or more, and vertical velocities close to zero. Because these effects usually do not occur together, the overall effect on the droplet growth from these factors is small.
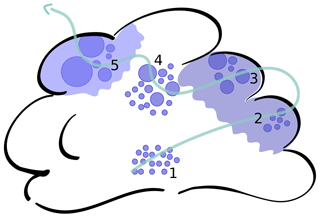
A strong effect is found when parcels recirculate. Whenever a parcel reaches cloud edge, the number of droplets is small. Yet, these droplets are exposed to cloud top or cloud edge cooling which, due to the limited number of droplets, is close to the maximum cooling that a droplet can experience (2 in Fig. 10). Additionally, these parcels already include larger droplets, where radiative effects are stronger. The droplets experience additional growth by radiative cooling during the recirculation time and return into the cloud with a slightly broadened size distribution (3 in Fig. 10). The droplet size distribution subsequently continues to broaden (4 in Fig. 10).
Summarizing, these analyses of individual parcel trajectories have shown that radiatively enhanced droplet growth can occur in “lucky situations” or when recirculation occurs. The increased droplet growth for recirculating parcels agrees well with prior results of enhanced droplet growth in areas of net radiative loss (see, e.g., Caughey and Kitchen, 1984). The radiative cooling does not seem to cause droplet growth in individual parcels beyond the NR case (as also found by Harrington et al., 2000), but thermal radiative effects enhance the mass per bin and occasionally allow droplets to grow into larger bins. In the following, we will take a more general look at the effects in our parcel trajectory ensemble.
4.2.4 Parcel model – ensemble results
As a next step, we evaluated our 340 000 parcel trajectory ensemble to see if we find changes in droplet size and rain amount, as represented by the local volume flux of water, or rain rate.
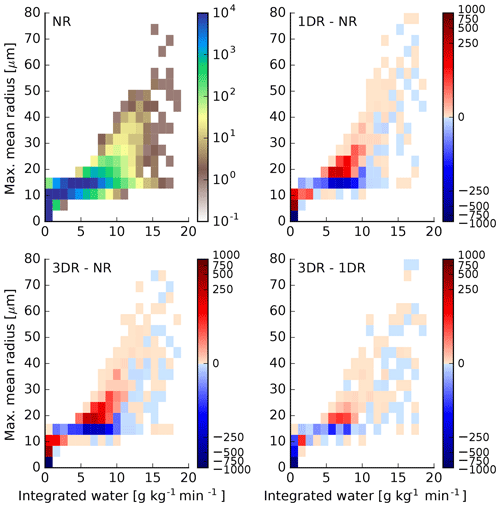
Figure 11Joint histogram of integrated water and maximum mean radius. The first figure shows all data from the NR simulation. The other figures show the difference of the number of occurrences of 1DR vs. NR, 3DR vs. NR and 3DR vs. 1DR.
Figure 11 shows a histogram of maximum mean radius along a parcel trajectory versus the integrated qc along the parcels. The first figure shows the number of occurrences for the NR case. Integrated qc mostly occurs in a range of 0–10 g kg−1 min−1 with maximum mean radii up to 20 µm. Larger droplets and integrated qc amounts exist but are comparatively small in number. When comparing the number of occurrences of the 1DR case to the NR case, we find an increase in the number of larger droplets for small qc amounts and for those between 5 and 10 g kg−1 min−1 and a decrease in the directly smaller bin. Radiation thus enhances the growth of droplets for a specific qc for very small droplets and for droplets in the 10–25 or 30 µm range. There is also a tendency for the larger drops to grow to larger sizes in the 1DR case. For 3-D thermal radiation we see a similar picture. The number of droplets growing to larger sizes is even higher than in the 1DR case. Comparing the results of the 3-D thermal radiative transfer simulation to the 1DR simulation shows the additional increase in the 3DR case. We confirm here that due to thermal radiation droplets in the critical range tend to grow to larger sizes.
Next, we calculate the total rain rate at each time step (accounting for drop radii >20 µm) for the entire trajectory ensemble. In the first hour, the absolute differences in the rain rate between the three setups is small. Absolute differences become larger over time and are clearly visible during the last 40 min of the analyzed time period (Fig. 12). Looking at the relative differences between either the 1DR simulation and the NR case, or 3-D thermal radiation simulation and the NR case, we find differences of 10 % for the 1DR case in the first hour and 20 % for the 3-D thermal radiation case. Relative differences increase commensurately with the absolute differences towards the end of the 2 h simulation and reach as high as 40 % for the 3-D thermal radiation case.
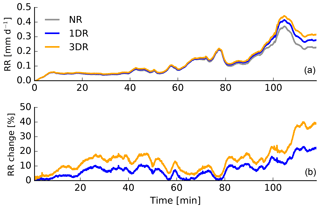
Figure 12Total parcel rain rate calculated from the trajectory ensemble simulation (accounting for drop radii >20 µm). (a) shows the absolute rain rate for the NR, the 1DR and the 3DR cases. (b) shows the relative differences of 1DR simulation and the NR case, as well as 3DR simulation and the NR cases.
We then separated the rain rates according to different factors that could affect droplet growth on our trajectories. Following on the results of our investigation of the individual trajectories, we calculated rain rates for parcels with certain thresholds of updraft speeds, cumulative cooling, or time spent at cloud side. About 50 % of the rain rate arises from parcels that are in an updraft region of 3 m s−1 or more (regions typically associated with higher qc), but differences between the NR and 1DR and 3DR cases are small. The largest radiative effect emerges from parcels that recirculate (see Fig. 14). We define “recirculation” by setting a threshold in terms of qc of 0.01 g kg−1.
The time periods for recirculation events are shown in Fig. 13. Most of the parcels spend a few minutes outside a cloud. More than 90 % of the recirculation events are shorter than 5 min. Up to 58 % of the parcel rain rate of the 3DR simulation arises from recirculating parcels, while in the case of NR about 45 % of the parcel rain rate arises from recirculating parcels. The largest increase is found within the last 20 min of the investigated timeframe. Differences of 5–10 % are found in the first 20 to 50 min, while in between there is no difference between the three simulation types. Setting an upper limit in time (e.g., 5 min, which includes more than 90 % of our recirculating parcels), the changes in our results are very small. The maximum contribution of the rain rate reduces to 56 %. For a time threshold of 2 min, the maximum reduces to 45 %. In this context it should be noted that only 6 %–7 % of our 340 000 parcel trajectories are classified as recirculating according to our definition. Remarkably, these 6 %–7 % can contribute up to 60 % of the total parcel rain rate. The parcel rain rate due to recirculation (when normalized to each of the corresponding simulations and therefore without considering radiative effects) is about 30 % in our study. Naumann and Seifert (2016) found a similar magnitude in their study. About 50 % of the rain rate emerged from recirculating parcels. These zones might be considered the birth place of precipitation embryos, which subsequently become important for accelerating collision and coalescence.
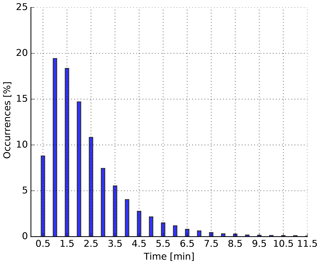
Figure 13Histogram of the time period of recirculation events. Recirculation events are defined by threshold in terms of qc of 0.01 g kg−1.
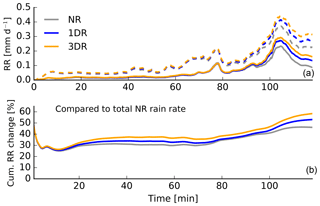
Figure 14Total rain rate calculated from the trajectory ensemble simulation from recirculating parcels with a threshold of 0.01 g kg−1. The dashed lines show the total rain rate, and the solid lines show the rain rate from recirculating parcels as well as the relative difference between the cumulated sum rain rates from recirculating parcels compared to the cumulated sum total NR rain rate.
4.3 Coupled LES – cloud droplet growth under the impact of thermal radiative effects
Next, we investigate the effect of 1-D and 3-D thermal radiation in a fully coupled system. To this end, we ran a set of BOMEX simulations as described in Sect. 3. Here we (a) look at the effects of thermal radiation on microphysics in a coupled system and (b) compare it to the effect on dynamics.
4.3.1 The effect of thermal radiative transfer on microphysics
We start with variables concerning rain and first focus on the microphysical effect. Figure 15 shows rain water path, surface precipitation fraction, domain-averaged surface precipitation rate and the cumulative surface precipitation rate of four of the five simulations. We take the simulation with 1-D radiation on dynamics (1DD) as our reference case. We focus first on the discussion of the rain water path. We find a small increase in rain water path an hour after restart in the case of 3-D radiation acting on microphysics and dynamics (3DD_3DM); however, differences among the four simulations never become significant. Surface precipitation fraction (over the total domain) shows an increase for all simulations where radiation is coupled to the diffusional droplet growth. The strongest increase is found for the 3DD_3DM case. This suggests that more clouds produce rain when radiation is coupled to the droplet growth, but the total amount of rain water produced does not change substantially.
The surface precipitation rate shows no clear changes, but in accumulation the simulations with the radiative–microphysical coupling produce more rain (10 % for 3DD_3DM). There is a subtle increase in the accumulated rain rate and rain water path when thermal radiation is coupled to the diffusional droplet growth. However, when comparing 1DD_3DM to 1DD_1DM, no difference can be found. Hence, the small increase in rain in the case of 3DD_3DM must arise from the effects of 3-D thermal radiation on dynamics, not on microphysics. We will investigate the 3-D effect further in the following.
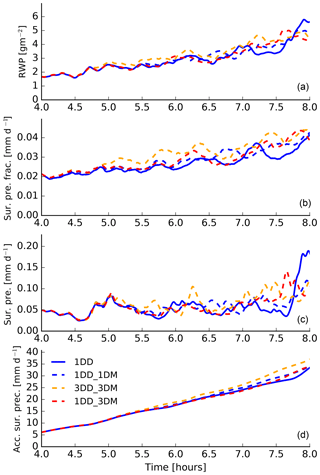
Figure 15Temporal development of rain water path (a), surface precipitation fraction (b), domain-averaged surface precipitation rate (c) and the accumulated domain-averaged surface precipitation rate (d). The time series is shown from the restart time of 4 h onward. We compare four of our five simulations here where thermal radiation was coupled to the diffusional droplet growth.
4.3.2 3-D thermal radiative effects
Figure 16 shows the same variables as Fig. 15 but now comparing the results of the 3DD_3DM and 3DD. In the beginning, rain water path and rain rate show no noticeable difference. After 7 h of the simulation, rain water increases for 3DD. Prior to 7 h, as also discussed in Sect. 4.3.1, the fraction of surface rain rate is slightly enhanced in 3DD_3DM compared to 3DD, which again suggests that the coupling to microphysics does not produce more rain but that more clouds produce small amounts of rain, while in the 3DD case changes in the dynamics cause somewhat stronger rain in fewer clouds. Figure 16d shows again the accumulated surface rain rate over time. The 3DD simulation produces more rain. This was counterintuitive at first, because it was expected that thermal radiative effects enhance droplet growth.
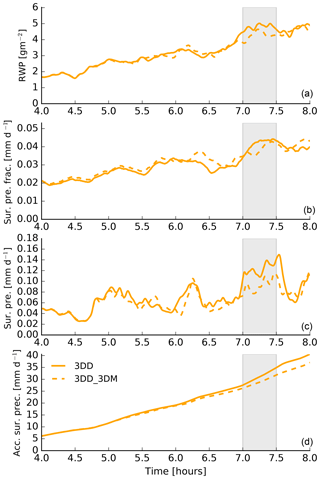
Figure 16Similar to Fig. 15 but for 3DD and 3DD_3DM. The gray shaded area shows the time period between 6.7 and 7.3 h which is investigated in the further analysis.
We pose the following hypothesis to explain this behavior:
enhanced droplet growth, due to 3-D thermal radiation at the cloud edges, decreases the evaporation at the cloud edges, causing weaker evaporative cooling and weaker downward motion, representing an evaporation–circulation feedback.
This hypothesis constitutes a negative feedback to changes in the cloud circulation found by Klinger et al. (2017) and will be explained in the following. It is analogous to the previously documented evaporation–circulation feedback due to changing aerosol concentrations in cumulus clouds (Xue and Feingold, 2006) and earlier studies that identified the relationship between the horizontal buoyancy gradient and the vortical circulation around a cloud; stronger cloud edge evaporation generates stronger horizontal buoyancy gradients, increased turbulence kinetic energy (TKE), and enhanced mixing and entrainment (Zhao and Austin, 2005).
Klinger et al. (2017) found an enhanced cloud circulation due to thermal radiative effects. It was shown that cloud top cooling caused stronger updraft velocities in the clouds and, due to the side cooling, stronger subsiding shells at the cloud edge. Due to the stronger updrafts, clouds were deeper, more turbulent and contained more qc. The results from Klinger et al. (2017) and the above posed hypothesis, can, if correct, explain the differences in surface rain fraction and rain rate between the two simulations. We will therefore investigate the profiles of cloud water mixing ratio, precipitation flux, evaporation rate and buoyancy production of TKE (Fig. 17), averaged over half an hour marked by the gray shading in Fig. 16. This time period is chosen as it is the period shortly before and at the beginning of the increase in rain production. All four variables show higher values for 3DD compared to 3DD_3DM.
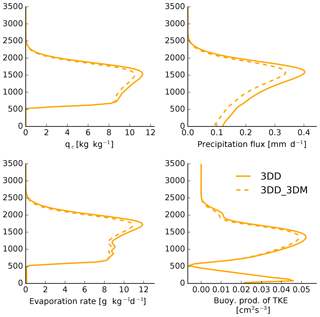
Figure 17Time-averaged profiles of cloud water mixing ratio, precipitation flux, evaporation rate and buoyancy production of the TKE averaged from 6.7 to 7.3 h.
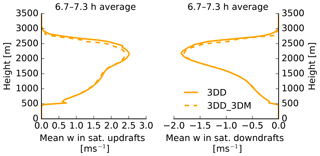
Finally, we look at the temporally averaged profiles of updraft and downdraft vertical velocities in saturated areas. Here we also find stronger downdraft and stronger updrafts in the 3DD case. These analyses lend credence to our hypothesis and Klinger et al. (2017) (Fig. 18).
4.3.3 1-D vs. 3-D thermal radiative effects
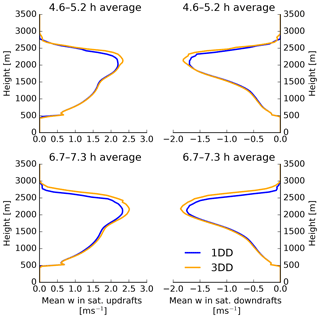
Finally, we compare the results of 1DD and 3DD to examine the effect of 3-D thermal radiation on dynamics. We focus again on rain production as this was not included in Klinger et al. (2017). As expected, 3-D radiation causes an increase in all the rain-related variables (shown in Fig. 19). To prove that a change in the cloud circulation is also causing the increase in rain, we look at the profiles of the updraft and downdraft vertical velocity in saturated areas, averaged over two time periods marked in gray in Fig. 19. The time periods were again chosen because they include the beginning of rain enhancement by 3-D thermal radiation compared to 1-D thermal radiation. For both time periods, Fig. 20 shows enhanced downdrafts and updrafts for the 3DD simulation compared to 1DD.
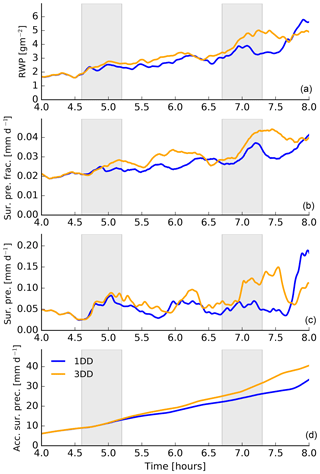
Figure 19Similar to Fig. 15 but for 1DD and 3DD. The gray shaded area shows the time period between 4.6 and 5.3 h as well as 6.7 and 7.3 h, which are investigated in the further analysis.
4.3.4 Summary
The coupling of thermal radiative effects to microphysics can lead to the formation of larger cloud droplets and drizzle droplets. For 3-D thermal radiative effects, additional cooling occurs at cloud edges, which can strengthen the effect. The coupled LESs showed the following.
-
When thermal radiation is coupled to microphysics, there is a small increase in rain production for 1-D radiative effects (1DD_1DM). This could be due to recirculation of droplets, as shown in the parcel model study. However, the change in rain in the coupled simulations is very small. When coupling radiation to droplet growth it matters little whether 3-D or 1-D thermal radiation is applied. The increase in the surface precipitation fraction suggests that rain is produced in more clouds distributed over the domain.
-
When 3-D thermal radiative effects are considered we find (counterintuitively) overall more rain in the simulation with dynamics only.
-
The fact that more rain is produced by the simulation coupled to dynamics only is hypothesized to be due to an evaporation–circulation feedback caused by the larger droplets in the 3DD_3DM simulation.
-
When comparing the 1-D and 3-D thermal radiative effects on dynamics we find an increase in the rain production for 3-D thermal radiation.
-
The dynamical effect caused by 1-D and 3-D thermal radiation is a change in the cloud circulation as already found by Klinger et al. (2017) where thermal radiation increases upward and downward vertical velocities in and in the near-cloud environment, which causes deepening and more rain.
Finally, we note that the overall differences concerning precipitation are small and might not be detectable relative to differences associated with perturbations to thermodynamical inputs in an ensemble of simulations (see, e.g., Lonitz et al., 2015).
In this study we investigated the effect of thermal radiation on cloud droplet growth and rain formation in shallow cumulus clouds. We used a two-stage approach, which allowed us to separate microphysical from dynamical effects.
First an offline parcel model was used to investigate the effect of 1-D and 3-D thermal radiation on cloud droplet growth. It was found that thermal radiation in general has the potential to enhance droplet growth and rain formation. Three-dimensional thermal radiation enhances droplet growth and rain formation more than one-dimensional thermal radiation. It was shown that thermal radiation enhances the formation of precipitation embryos in the 10–30 µm radius range. These embryos have the potential to enhance rain formation in real clouds. Thermal radiation can affect cloud droplet growth when one or more of the following conditions are fulfilled.
Droplets have already grown to a size of about 10 µm or more when being exposed to thermal cooling. A cooling period of more than 5 min at a cooling rate of 20 K d−1 or more and vertical velocities close to zero are favorable for radiative effects. If one or more of these factors occur, radiative cooling can enhance droplet growth. The main effect was found in recirculating parcels, which fulfill parts of the above-mentioned criteria. Recirculating parcels include droplets that have already grown to a certain size when passing a cloud edge area. At the cloud edge area cloud droplets are exposed to large cooling (close to black body emission), and this small number of droplets grows by thermal cooling, which counteracts evaporation. When reentering a cloud, droplet growth continues, generating a broader spectrum, which can enhance rain formation. Only 6 %–7 % of our simulated parcels are classified as recirculating, yet they can contribute up to 45 %–60 % of the local rain rate.
Second, in a more realistic framework we investigated large eddy simulations where thermal radiative effects were applied to droplet growth and dynamics. It was shown that the effect on droplet growth is small. However more clouds produce small amounts of rain when radiative effects are applied to the diffusional droplet growth; thus rain covers a larger area of the simulation domain. Three-dimensional thermal radiative effects exceed one-dimensional thermal radiative effects. The largest amount of rain is produced when 3-D thermal radiation is applied to dynamics only. This was initially considered to be counterintuitive since both microphysical and radiative effects tend to enhance rain. We hypothesize that an evaporation–circulation feedback is responsible for less rain in the simulation where radiation is also applied to droplet growth: 3-D thermal cooling rates at the cloud edges enhance droplet growth locally at the cloud edge, thus leading to weaker evaporation rates, which in turn reduces the strength of the subsiding shell and the horizontal buoyancy gradient, all leading to weaker cloud turbulence and lower rain production. In simulations with 3-D thermal cooling only applied to the dynamics, the enhanced cloud circulation causes stronger updrafts in the cloud center, a cloud deepening and more condensation or rain formation.
These results could have implications in terms of cloud field organization. As shown by Klinger et al. (2017), thermal radiation can cause mesoscale organization of shallow cumulus clouds by changing cloud circulation. It was shown that this change in cloud circulation also occurs in the simulation in this study. Furthermore, more rain produced by thermal radiation changes the dynamics of the system as a whole. The larger area of the domain covered by rain when radiative effects are applied to microphysics could also lead to a feedback in terms of dynamics and cloud field organization. Longer simulations are necessary to investigate the organization feedbacks. Finally, a trade-wind cumulus case that tends to deepen and generate more precipitation and organization would be worth investigating.
Input files and the model code for reproducing the simulations and data of this study are available from the corresponding author upon request.
The analysis of timescales supports our argument about the usefulness of the parcel model, even though it does not represent certain physical processes. The characteristic timescales for a number of processes involved in our study (diffusional droplet growth, diffusional droplet growth with radiation and sedimentation) are calculated in the following. The analysis is performed for a droplet of 20 µm radius. In order to avoid confusion, we use χ to represent timescales, because the standard abbreviation τ is already used as the forcing in the diffusional droplet growth equation (Eq. 7).
The analysis shows a clear signal: sedimentation occurs on much longer timescales than all the other processes. The timescale of sedimentation is on the order of 1 h, while the diffusional droplet growth timescales, with and without radiation, are on the order of a few minutes.
A1 Diffusional droplet growth
Diffusional droplet growth (which follows from Eq. 1) is defined as
It therefore follows that the characteristic timescale χgrowth is
with a droplet radius r of 20 µm, C=1e10 s m−2 and a supersaturation S=0.01.
A2 Diffusional droplet growth including thermal radiative effects
The diffusional droplet growth including radiative effects (see also Eq. 2, but defined in mass space) is
Therefore χgrowth,rad becomes (when assuming that r is constant over time in the radiative term)
with F≈1 and Wm−2 (one-third of the black body radiation occurring in the window region).
A3 Sedimentation
The timescale for sedimentation follows
with a typical length scale of L=100 m and a fall velocity at 20 µm of v(20 µm)=0.02 m s−1.
The authors declare that they have no conflict of interest.
CK implemented the 3-D radiative transfer scheme into the LES, ran the simulations and performed the analysis. TY implemented the bin-microphysics scheme into the LES. All authors contributed to developing the basic ideas, discussing the results and preparing the manuscript.
The authors acknowledge Bernhard Mayer and Jerry Harrington for useful discussion and Jan Kazil for help with SAM. We gratefully acknowledge Marat Khairoutdinov (Stony Brook University) for developing and making the System for Atmospheric Modeling (SAM) available. The authors acknowledge the NOAA Research and Development High Performance Computing Program for providing computing and storage resources that have contributed to the research results of this paper.
This research has been supported by the Deutsche Forschungsgemeinschaft (DFG) (grant no. KL-3035/1) and the Bundesministerium für Bildung und Forschung through the High Definition Clouds and Precipitation for advancing Climate Prediction project (HD(CP)2) phase 2 (grant no. 01LK1504D).
This paper was edited by Timothy Garrett and reviewed by two anonymous referees.
Ackerman, A. S., Hobbs, P. V., and Toon, O. B.: A Model for Particle Microphysics, Turbulent Mixing, and Radiative Transfer in the Stratocumulus-Topped Marine Boundary Layer and Comparisons with Measurements, J. Atmos. Sci., 52, 1204–1236, https://doi.org/10.1175/1520-0469(1995)052<1204:AMFPMT>2.0.CO;2, 1995. a
Austin, P. H., Siems, S., and Wang, Y.: Constraints on droplet growth in radiatively cooled stratocumulus clouds, J. Geophys. Res.-Atmos., 100, 14231–14242, https://doi.org/10.1029/95JD01268, 1995. a, b
Barkstrom, B. R.: Some Effects of 8–12 µm Radiant Energy Transfer on the Mass and Heat Budgets of Cloud Droplets, J. Atmos. Sci., 35, 665–673, https://doi.org/10.1175/1520-0469(1978)035<0665:SEORET>2.0.CO;2, 1978. a
Bott, A., Sievers, U., and Zdunkowski, W.: A Radiation Fog Model with a Detailed Treatment of the Interaction between Radiative Transfer and Fog Microphysics, J. Atmos. Sci., 47, 2153–2166, https://doi.org/10.1175/1520-0469(1990)047<2153:ARFMWA>2.0.CO;2, 1990. a
Boucher, O., Randall, D., Artaxo, P., Bretherton, C., Feingold, G., Forster, P., Kerminen, V.-M., Kondo, Y., Liao, H., Lohmann, U., Rasch, P., Satheesh, S., Sherwood, S., Stevens, B., and Zhang, X.: Clouds and aerosols, in: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, 571–657, Cambridge University Press, 2013. a
Brewster, M.: Evaporation and condensation of water mist/cloud droplets with thermal radiation, Int. J. Heat Mass Trans., 88, 695–712, https://doi.org/10.1016/j.ijheatmasstransfer.2015.03.055, 2015. a
Caughey, S. J. and Kitchen, M.: Simultaneous measurements of the turbulent and microphysical structure of nocturnal stratocumulus cloud, Q. J. Roy. Meteorol. Soc., 110, 13–34, https://doi.org/10.1002/qj.49711046303, 1984. a, b
Cheng, W. Y. Y., Carrió, G. G., Cotton, W. R., and Saleeby, S. M.: Influence of cloud condensation and giant cloud condensation nuclei on the development of precipitating trade wind cumuli in a large eddy simulation, J. Geophys. Res.-Atmos., 114, D08201, https://doi.org/10.1029/2008JD011011, 2009. a
Cooper, W. A.: Effects of Variable Droplet Growth Histories on Droplet Size Distributions. Part I: Theory, J. Atmos. Sci., 46, 1301–1311, https://doi.org/10.1175/1520-0469(1989)046<1301:EOVDGH>2.0.CO;2, , 1989. a
Črnivec, N. and Mayer, B.: Quantifying the bias of radiative heating rates in NWP models for shallow cumulus clouds, Atmos. Chem. Phys. Discuss., https://doi.org/10.5194/acp-2018-1247, in review, 2019. a
Davies, R.: Response of Cloud Supersaturation to Radiative Forcing, J. Atmos. Sci., 42, 2820–2825, https://doi.org/10.1175/1520-0469(1985)042<2820:ROCSTR>2.0.CO;2, 1985. a, b
de Lozar, A. and Muessle, L.: Long-resident droplets at the stratocumulus top, Atmos. Chem. Phys., 16, 6563–6576, https://doi.org/10.5194/acp-16-6563-2016, 2016. a, b
Feingold, G., Tzivion, S., and Levin, Z.: Evolution of Raindrop Spectra. Part I: Solution to the Stochastic Collection/Breakup Equation Using the Method of Moments, J. Atmos. Sci., 45, 3387–3399, https://doi.org/10.1175/1520-0469(1988)045<3387:EORSPI>2.0.CO;2, 1988. a
Feingold, G., Kreidenweis, S. M., and Zhang, Y.: Stratocumulus processing of gases and cloud condensation nuclei: 1. Trajectory ensemble model, J. Geophys. Res.-Atmos., 103, 19527–19542, https://doi.org/10.1029/98JD01750, 1998a. a
Feingold, G., Walko, R., Stevens, B., and Cotton, W.: Simulations of marine stratocumulus using a new microphysical parameterization scheme, Atmos. Res., 47, 505–528, https://doi.org/10.1016/S0169-8095(98)00058-1, 1998b. a
Feingold, G., Cotton, W. R., Kreidenweis, S. M., and Davis, J. T.: The Impact of Giant Cloud Condensation Nuclei on Drizzle Formation in Stratocumulus: Implications for Cloud Radiative Properties, J. Atmos. Sci., 56, 4100–4117, https://doi.org/10.1175/1520-0469(1999)056<4100:TIOGCC>2.0.CO;2, 1999. a, b, c
Grabowski, W. W. and Abade, G. C.: Broadening of Cloud Droplet Spectra through Eddy Hopping: Turbulent Adiabatic Parcel Simulations, J. Atmos. Sci., 74, 1485–1493, https://doi.org/10.1175/JAS-D-17-0043.1, 2017. a
Grabowski, W. W. and Wang, L.-P.: Growth of Cloud Droplets in a Turbulent Environment, Ann. Rev. Fluid Mechan., 45, 293–324, https://doi.org/10.1146/annurev-fluid-011212-140750, 2013. a
Guan, H., Davies, R., and Yau, M.: Longwave radiative cooling rates in axially symmetric clouds, J. Geophys. Res.-Atmos., 100, 3213–3220, 1995. a
Guan, H., Yau, M., and Davies, R.: The Effects of Longwave Radiation in a Small Cumulus Cloud, J. Atmos. Sci., 54, 2201–2214, 1997. a
Guzzi, R. and Rizzi, R.: The effect of radiative exchange on the growth by condensation of a population of droplets, Beitr. Phys. Atmos., 53, 351–365, 1980. a, b
Harrington, J. Y., Feingold, G., and Cotton, W. R.: Radiative Impacts on the Growth of a Population of Drops within Simulated Summertime Arctic Stratus, J. Atmos. Sci., 57, 766–785, https://doi.org/10.1175/1520-0469(2000)057<0766:RIOTGO>2.0.CO;2, 2000. a, b, c, d, e, f, g, h, i, j, k
Iacono, M. J., Mlawer, E. J., Clough, S. A., and Morcrette, J.-J.: Impact of an improved longwave radiation model, RRTM, on the energy budget and thermodynamic properties of the NCAR community climate model, CCM3, J. Geophys. Res.-Atmos., 105, 14873–14890, https://doi.org/10.1029/2000JD900091, 2000. a
Jiang, H., Feingold, G., and Sorooshian, A.: Effect of Aerosol on the Susceptibility and Efficiency of Precipitation in Warm Trade Cumulus Clouds, J. Atmos. Sci., 67, 3525–3540, https://doi.org/10.1175/2010JAS3484.1, 2010. a
Kablick, G., Ellingson, R., Takara, E., and Gu, J.: Longwave 3D Benchmarks for Inhomogeneous Clouds and Comparisons with Approximate Methods, J. Climate, 24, 2192–2205, 2011. a, b
Khairoutdinov, M. F. and Randall, D. A.: Cloud Resolving Modeling of the ARM Summer 1997 IOP: Model Formulation, Results, Uncertainties, and Sensitivities, J. Atmos. Sci., 60, 607–625, https://doi.org/10.1175/1520-0469(2003)060<0607:CRMOTA>2.0.CO;2, 2003. a
Klinger, C. and Mayer, B.: Three-dimensional Monte Carlo calculation of atmospheric thermal heating rates, J. Quant. Spectrosc. Rad. Trans., 144, 123–136, https://doi.org/10.1016/j.jqsrt.2014.04.009, 2014. a
Klinger, C. and Mayer, B.: The Neighboring Column Approximation (NCA) – A fast approach for the calculation of 3D thermal heating rates in cloud resolving models, J. Quant. Spectrosc. Rad. Trans., 168, 17–28, https://doi.org/10.1016/j.jqsrt.2015.08.020, 2016. a, b
Klinger, C., Mayer, B., Jakub, F., Zinner, T., Park, S.-B., and Gentine, P.: Effects of 3-D thermal radiation on the development of a shallow cumulus cloud field, Atmos. Chem. Phys., 17, 5477–5500, https://doi.org/10.5194/acp-17-5477-2017, 2017. a, b, c, d, e, f, g, h, i
Köhler, H.: The nucleus in and the growth of hygroscopic droplets, Trans. Faraday Soc., 32, 1152–1161, 1936. a
Langmuir, I.: The production of rain by a chain reaction in cumulus clouds at temperatures above freezing, J. Meteorology, 5, 175–192, https://doi.org/10.1175/1520-0469(1948)005<0175:TPORBA>2.0.CO;2, 1948. a
Lasher-Trapp, S. G., Cooper, W. A., and Blyth, A. M.: Broadening of droplet size distributions from entrainment and mixing in a cumulus cloud, Q. J. Roy. Meteorol. Soc., 131, 195–220, https://doi.org/10.1256/qj.03.199, 2005. a
Lonitz, K., Stevens, B., Nuijens, L., Sant, V., Hirsch, L., and Seifert, A.: The Signature of Aerosols and Meteorology in Long-Term Cloud Radar Observations of Trade Wind Cumuli, J. Atmos. Sci., 72, 4643–4659, https://doi.org/10.1175/JAS-D-14-0348.1, 2015. a
Mason, B.: The evolution of droplet spectra in stratus clouds, J. Meteor., 17, 459–462, 1960. a
Mayer, B. and Madronich, S.: Actinic flux and photolysis in water droplets: Mie calculations and geometrical optics limit, Atmos. Chem. Phys., 4, 2241–2250, https://doi.org/10.5194/acp-4-2241-2004, 2004. a
Mechem, D. B., Kogan, Y. L., Ovtchinnikov, M., Davis, A., Evans, K., and Ellingson, R.: Multi-Dimensional Longwave Forcing of Boundary Layer Cloud Systems, J. Atmos. Sci., 65, 3963–3977, 2008. a
Mlawer, E. J., Taubman, S. J., Brown, P. D., Iacono, M. J., and Clough, S. A.: Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave, J. Geophys. Res.-Atmos., 102, 16663–16682, https://doi.org/10.1029/97JD00237, 1997. a
Naumann, A. K. and Seifert, A.: Recirculation and growth of raindrops in simulated shallow cumulus, J. Adv. Model. Earth Syst., 8, 520–537, https://doi.org/10.1002/2016MS000631, 2016. a
Pruppacher, H. and Klett, J.: Microphysics of Clouds and Precipitation, Atmospheric and Oceanographic Sciences Library, Springer Netherlands, available at: https://books.google.de/books?id=0MURkyjuoGMC (last access: 5 March 2019), 2010. a, b
Ramanathan, V., Cess, R. D., Harrison, E. F., Minnis, P., Barkstrom, B. R., Ahmad, E., and Hartmann, D.: Cloud-Radiative Forcing and Climate: Results from the Earth Radiation Budget Experiment, Science, 243, 57–63, https://doi.org/10.1126/science.243.4887.57, 1989. a
Roach, W. T.: On the effect of radiative exchange on the growth by condensation of a cloud or fog droplet, Q. J. Roy. Meteorol. Soc., 102, 361–372, https://doi.org/10.1002/qj.49710243207, 1976. a, b, c
Shaw, R. A., Reade, W. C., Collins, L. R., and Verlinde, J.: Preferential Concentration of Cloud Droplets by Turbulence: Effects on the Early Evolution of Cumulus Cloud Droplet Spectra, J. Atmos. Sci., 55, 1965–1976, https://doi.org/10.1175/1520-0469(1998)055<1965:PCOCDB>2.0.CO;2, 1998. a
Simpson, G. C.: On the formation of cloud and rain, Q. J. Roy. Meteorol. Soc., 67, 99–133, https://doi.org/10.1002/qj.49706729002, 1941. a
Stephens, G. L.: Cloud Feedbacks in the Climate System: A Critical Review, J. Climate, 18, 237–273, https://doi.org/10.1175/JCLI-3243.1, 2005. a
Stevens, B., Feingold, G., Cotton, W. R., and Walko, R. L.: Elements of the Microphysical Structure of Numerically Simulated Nonprecipitating Stratocumulus, J. Atmos. Sci., 53, 980–1006, https://doi.org/10.1175/1520-0469(1996)053<0980:EOTMSO>2.0.CO;2, 1996. a
Tzivion, S., Feingold, G., and Levin, Z.: An Efficient Numerical Solution to the Stochastic Collection Equation, J. Atmos. Sci., 44, 3139–3149, https://doi.org/10.1175/1520-0469(1987)044<3139:AENSTT>2.0.CO;2, 1987. a, b
Tzivion, S., Feingold, G., and Levin, Z.: The Evolution of Raindrop Spectra. Part II: Collisional Collection/Breakup and Evaporation in a Rainshaft, J. Atmos. Sci., 46, 3312–3328, https://doi.org/10.1175/1520-0469(1989)046<3312:TEORSP>2.0.CO;2, 1989. a, b, c
Xue, H. and Feingold, G.: Large-Eddy Simulations of Trade Wind Cumuli: Investigation of Aerosol Indirect Effects, J. Atmos. Sci., 63, 1605–1622, https://doi.org/10.1175/JAS3706.1, 2006. a
Yamaguchi, T. and Randall, D. A.: Cooling of Entrained Parcels in a Large-Eddy Simulation, J. Atmos. Sci., 69, 1118–1136, https://doi.org/10.1175/JAS-D-11-080.1, 2012. a
Zeng, X.: Modeling the Effect of Radiation on Warm Rain Initiation, J. Geophys. Res.-Atmos., 123, 6896–6906, https://doi.org/10.1029/2018JD028354, 2018. a
Zhao, M. and Austin, P. H.: Life Cycle of Numerically Simulated Shallow Cumulus Clouds. Part I: Transport, J. Atmos. Sci., 62, 1269–1290, https://doi.org/10.1175/JAS3414.1, 2005. a