the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Ice nucleation activity of silicates and aluminosilicates in pure water and aqueous solutions – Part 3: Aluminosilicates
Claudia Marcolli
Thomas Peter
Aluminosilicates and quartz constitute the majority of airborne mineral dust. Despite similarities in structures and surfaces they differ greatly in terms of their ice nucleation (IN) efficiency. Here, we show that determining factors for their IN activity include surface ion exchange, NH3 or adsorption, and surface degradation due to the slow dissolution of the minerals. We performed immersion freezing experiments with the (Na-Ca)-feldspar andesine, the K-feldspar sanidine, the clay mineral kaolinite, the micas muscovite and biotite, and gibbsite and compare their IN efficiencies with those of the previously characterized K-feldspar microcline and quartz. Samples were suspended in pure water as well as in aqueous solutions of NH3, (NH4)2SO4, NH4Cl and Na2SO4, with solute concentrations corresponding to water activities aw equal to 0.88–1.0. Using differential scanning calorimetry (DSC) on emulsified micron-sized droplets, we derived onset temperatures of heterogeneous (Thet) and homogeneous (Thom) freezing as well as heterogeneously frozen water volume fractions (Fhet). Suspensions in pure water of andesine, sanidine and kaolinite yield Thet equal to 242.8, 241.2 and 240.3 K, respectively, while no discernable heterogeneous freezing signal is present in the case of the micas or gibbsite (i.e., K). The presence of NH3 and/or salts as solutes has distinct effects on the IN efficiency of most of the investigated minerals. When feldspars and kaolinite are suspended in very dilute solutions of NH3 or salts, Thet shifts to higher temperatures (by 2.6–7.0 K compared to the pure water suspension). Even micas and gibbsite develop weak heterogeneous freezing activities in ammonia solutions. Conversely, suspensions containing Na2SO4 cause the Thet of feldspars to clearly fall below the water-activity-based immersion freezing description (Δaw= const.) even in very dilute Na2SO4 solutions, while Thet of kaolinite follows the Δaw= constant curve. The water activity determines how the freezing temperature is affected by solute concentration alone, i.e., if the surface properties of the ice nucleating particles are not affected by the solute. Therefore, the complex behavior of the IN activities can only be explained in terms of solute-surface-specific processes. We suggest that the immediate exchange of the native cations (K+, Na+, Ca2+) with protons, when feldspars are immersed in water, is a prerequisite for their high IN efficiency. On the other hand, excess cations from dissolved alkali salts prevent surface protonation, thus explaining the decreased IN activity in such solutions. In kaolinite, the lack of exchangeable cations in the crystal lattice explains why the IN activity is insensitive to the presence of alkali salts (Δaw= const.). We hypothesize that adsorption of NH3 and on the feldspar surface rather than ion exchange is the main reason for the anomalous increased Thet in dilute solutions of NH3 or salts. This is supported by the response of kaolinite to NH3 or , despite lacking exchangeable ions. Finally, the dissolution of feldspars in water or solutions leads to depletion of Al and formation of an amorphous layer enriched in Si. This hampers the IN activity of andesine the most, followed by sanidine, then eventually microcline, the least soluble feldspar.
- Article
(3333 KB) - Companion paper 1
- Companion paper 2
-
Supplement
(2738 KB) - BibTeX
- EndNote
Clouds interacting with incoming solar radiation and outgoing longwave radiation influence the Earth's radiation budget (IPCC, 2013). Ice crystals are found in cold cirrus clouds as well as mixed-phase clouds, modulating their radiative properties (Sun and Shine, 1994; Sassen and Benson, 2001). Moreover, mixed-phase clouds are responsible for precipitation formation via the Wegener–Bergeron–Findeisen process (Rogers and Yau, 1989; Korolev and Field, 2008). Ice can either form homogeneously from liquid droplets supercooled to temperatures below about 237 K or heterogeneously at higher temperatures with the help of foreign particles, called ice nucleating particles (INPs), which lower the free energy required to form a critical ice embryo growing into crystalline ice (Vali et al., 2015). Heterogeneous ice nucleation (IN) can proceed via various pathways, namely (1) immersion freezing, when ice forms on an INP suspended inside a supercooled droplet; (2) condensation freezing, when IN is concurrent with the activation of an aerosol particle to a cloud droplet and (3) contact nucleation, when ice forms in a supercooled droplet upon collision with an INP (Pruppacher and Klett, 1994; Vali et al., 2015). These freezing mechanisms all occur under participation of a liquid phase. Ice may also form at conditions supersaturated with respect to ice but subsaturated with respect to liquid water, a process termed deposition nucleation (Vali et al., 2015). Traditionally, it has been ascribed to deposition of water molecules directly from the vapor phase onto a solid INP without involvement of a liquid phase. Though, it has been questioned whether this process actually occurs, or whether ice forms by pore condensation and freezing (PCF), after stabilizing water in pores by an inverse Kelvin effect (Marcolli, 2014). The most important IN mechanisms in mixed-phase clouds are viewed to be immersion and condensation freezing (Hoose et al., 2008; Ansmann et al., 2009; Twohy et al., 2010; de Boer et al., 2011).
Various studies have shown that mineral dust, typically composed of feldspars, clay minerals, quartz, micas, calcite and metal oxides, constitutes an important class of INPs (Pruppacher and Klett, 1994; Murray et al., 2011; Hoose and Möhler, 2012; Atkinson et al., 2013; Cziczo et al., 2013; Kanji et al., 2017). The impact of mineral dusts on cloud properties has been shown in several observational and modeling studies (Lohmann and Diehl, 2006; Hoose et al., 2010; Seifert et al., 2010). Feldspars have been reported to be the most IN active minerals although the individual members of the feldspar group exhibit very different IN efficiencies in immersion freezing mode (Atkinson et al., 2013; Zolles et al., 2015; Harrison et al., 2016; Kaufmann et al., 2016). During long-range transport in the atmosphere, mineral dust particles can acquire organic and inorganic coatings (Usher et al., 2003; Sullivan et al., 2007), which may change their IN efficiencies (Zuberi et al., 2002; Zobrist et al., 2008; Eastwood et al., 2009; Augustin-Bauditz et al., 2014, 2016; Kumar et al., 2018a; Kanji et al., 2019). When the INPs are fully covered by a water-soluble coating, IN may occur by an immersion freezing mechanism, typically after the aerosol particles experience increasing humidity (Augustin-Bauditz et al., 2014). Indeed, studies conducted with size-selected Arizona Test Dust (ATD, 300 nm) coated with sulfuric acid have shown irreversible impairment of its IN efficiency in both water-subsaturation and supersaturation regimes (Sullivan et al., 2010b; Niedermeier et al., 2011; Reitz et al., 2011). On the other hand, Sullivan et al. (2010a) also reported decreased IN efficiency of size-selected ATD particles (200 nm) coated with nitric acid at RHw<97 %, which recovered at conditions with RHw≥100 %. In addition, Sihvonen et al. (2014) discussed the hampering of IN efficiency of clay minerals (kaolinite and montmorillonite) treated with aqueous acids at conditions below water saturation on the basis of the reaction products and surface physicochemical changes generated on the mineral surface due to acid–mineral interaction. Although, Kanji et al. (2019) reported no effect of secondary organic aerosol (SOA) coating on the IN efficiency of two types of natural dust samples (Saharan and Asian) in immersion freezing mode.
Koop et al. (2000) provided observational evidence and theoretical underpinning that the homogeneous freezing temperatures of aqueous solution droplets can be described as a function of the water activity of solution (aw) alone, namely by shifting the ice melting curve by a constant Δaw to higher aw values. A similar approach has been used, with a suitably reduced Δaw, to describe the immersion freezing temperatures of various types of INPs as a function of aw. While the water-activity-based description of homogeneous IN is well established, for heterogeneous IN this description assumes implicitly that there is no interaction between particle surface and solute (Zobrist et al., 2008). Several studies suggest that the IN efficiency of various INPs can indeed be approximated by such a water-activity-based description (Archuleta et al., 2005; Zobrist et al., 2006, 2008; Koop and Zobrist, 2009; Knopf et al., 2011; Knopf and Forrester, 2011; Knopf and Alpert, 2013; Rigg et al., 2013). However, recent studies by Whale et al. (2018) and Kumar et al. (2018a) showed independently that the IN temperatures of some minerals – including the K-feldspars microcline and sanidine – deviate significantly from a freezing point line with Δaw= const., with a shift to higher temperatures in the presence of dilute NH3- and -containing solutions and a shift to lower temperatures in the presence of alkali salts.
In the companion paper Part 1 (Kumar et al., 2018a) we discussed the interactions of inorganic solutes with the microcline surface and the effects on its IN efficiency. In this and the companion paper Part 2 (Kumar et al., 2019) we relate IN on mineral surfaces with the mineral surface properties by investigating the differences in IN activity of chemically and/or structurally similar minerals in pure water and aqueous solutions. The analysis of our previous freezing experiments suggests that heterogeneous IN does not occur on the whole surface of INPs with a uniform probability. Rather, there are preferred locations, so-called active sites, which are responsible for the IN activity of a surface (Fletcher, 1969; Marcolli et al., 2007; Vali, 2014; Vali et al., 2015; Kaufmann et al., 2017). Estimates based on classical nucleation theory suggests that minimum surface areas of these sites need to cover about 10–50 nm2 (Kaufmann et al., 2017). In the present paper, for the discussion of IN activity of aluminosilicates we will assume that IN active surface structures need to be of such size. We will further assume that IN active sites exhibit surface functional groups that are characteristic of the mineral, but either occurring in a special 2-D arrangement (e.g., higher density of certain end groups on a flat surface) or with a special 3-D feature (e.g., a step, crack or wedge), making them IN active.
In our companion papers (Kumar et al., 2018a, 2019) we discuss the specific aluminosilicate microcline and various aluminum-free silicas (both amorphous and crystalline forms) with a special focus on quartz (a crystalline form of silica). The present study investigates the differences in IN activities of a number of other aluminosilicates, and offers an overall summary. The aluminosilicates investigated by immersion freezing include sanidine (K-feldspar), andesine (Na-Ca-feldspar), kaolinite, micas (muscovite and biotite) and gibbsite, dispersed in solution droplets containing ammonia or the inorganic salts ammonium sulfate, ammonium chloride and sodium sulfate.
2.1 Sources of samples, mineralogical composition and particle size distribution
Feldspar (sanidine and andesine) and mica (muscovite and biotite) samples were obtained from the Institute of Geochemistry and Petrology of ETH Zurich and milled with a tungsten carbide disc mill. Particle number size distributions were obtained with a TSI 3080 scanning mobility particle sizer (SMPS) and a TSI 3321 aerodynamic particle sizer (APS). The dry particles were dispersed using a fluidized bed. The detailed size distribution and mineralogical composition (using X-ray diffraction, XRD) of the feldspars, kaolinite and muscovite are given in Kaufmann et al. (2016). Rietveld refinement using Profex software (Döbelin and Kleeberg, 2015) was performed for a quantitative analysis. The microcline sample (Si : Al ≈ 3.1; Al : K ≈ 1.4) consists of 86.33 % (±1.71 %) microcline, mixed with orthoclase (6.18 % ± 0.72 %) and albite (7.49 % ± 0.48 %) (Kumar et al., 2018a). The sanidine sample proved to be pure sanidine with Si : Al ≈ 3.1 and Al : K ≈ 1.6 while andesine proved to be pure andesine with Si : Al ≈ 1.7 and Ca ∕ (Ca + Na) = 64 %. Note that andesine would be a labradorite based on the Ca ∕ (Ca + Na) ratio, but crystallographically it fits best with an andesine. Also note that the andesine sample is termed as “plagioclase” in Kaufmann et al. (2016). Biotite shows a bimodal particle size distribution with mode diameters of 241 nm and 1.7 µm (see Supplement). XRD analysis showed no traces of tungsten carbide in any of the milled samples. The kaolinite used in this study was KGa-1b from the Clay Mineral Society. Gibbsite (Al(OH)3⋅xH2O, < 45 µm) was obtained from Sigma-Aldrich.
2.2 Emulsion freezing experiments with mineral dusts freshly suspended in pure water or solutions
We described the general setup of immersion freezing experiments in Part 1 of this series of papers (Kumar et al., 2018a). Here we repeat essential aspects for convenience. The experiments were carried out with the differential scanning calorimetry (DSC; TA Instruments, Q10) setup (Zobrist et al., 2008). Sanidine and andesine suspensions (2 wt %), kaolinite suspensions (5 wt %), mica (muscovite and biotite; 5 wt % and 10 wt %) suspensions and gibbsite (10 wt %) suspensions in water (molecular biology reagent water from Sigma-Aldrich) were prepared with varying concentrations (0–20 wt %) of (NH4)2SO4 (Sigma-Aldrich, ≥ 99 %), NH4Cl (Sigma-Aldrich, ≥ 99.5 %), Na2SO4 (Sigma-Aldrich, ≥ 99 %) and diluted NH3 solutions (Merck, 25 %). To avoid particle aggregation, the suspensions were sonicated for 5 min before preparing the emulsions. The aqueous suspension and an oil/surfactant mixture (95 wt % mineral oil, Sigma-Aldrich, and 5 wt % lanolin, Fluka Chemical) taken in a ratio of 1 : 4 were mixed using a rotor–stator homogenizer (Polytron PT 1300D with a PT-DA 1307/2EC dispersing aggregate) for emulsification (40 s at 7000 rpm); 4–10 mg of this emulsion was placed in an aluminum pan, which was hermetically closed; and then, following the method developed and described by Marcolli et al. (2007), three freezing cycles in the DSC were performed. The first and the third freezing cycles were executed at a cooling rate of 10 K min−1 to control the stability of the emulsion. The second freezing cycle was run at 1 K min−1 cooling rate and used for evaluation (Zobrist et al., 2008; Pinti et al., 2012; Kaufmann et al., 2016; Kumar et al., 2018a). Emulsions prepared by this procedure exhibit droplet size distributions peaking at diameters of about 2–3 µm in number and a broad distribution in volume with highest contributions from particles with diameters between 4 and 12 µm similar to the ones shown in Fig. 1 of Marcolli et al. (2007), Pinti et al. (2012) and Kaufmann et al. (2016). For a clear heterogeneous signal, dust particles need to be of similar size or smaller than the droplets. Large particles (> 10 µm) present in dust samples contribute significantly to the dust mass but hardly to the heterogeneous freezing signal.
Typically, a DSC thermogram of the cooling cycle performed with an emulsion containing INPs features two freezing signals, as depicted in Kumar et al. (2018a). The first peak occurring at a warmer temperature displays the heat release accompanied by heterogeneous freezing and the second peak occurring at a colder temperature is due to homogeneous freezing. The freezing temperatures (Thet and Thom) are determined as the onset of the freezing peaks (i.e., intersection of the tangent drawn at the point of greatest slope at the leading edge of the thermal peak with the extrapolated baseline). Droplets with diameters of about 12 µm are considered to be relevant for the freezing onset. The loading of these droplets with particles depends on the particle size distribution and the suspension concentration. For 2 wt %–5 wt % suspensions, 12 µm droplets contain about 100–1000 particles (Kumar et al., 2018a). The melting temperature (Tmelt) was determined as the maximum of the ice melting peak. For the investigated samples, average precision in Thet was ±0.1 K with maximum deviations not exceeding 0.5 K. Precisions of Thom and Tmelt are precise within ±0.1 K.
The heat release is related to the frozen water volume and is given by the integral of the heat signal over time. Since the enthalpy of freezing is temperature dependent, this evaluation is only approximate (Speedy, 1987; Johari et al., 1994). Fhet is defined as the ratio of the heterogeneous freezing signal to the total freezing signal (heterogeneous and homogeneous). More details about the evaluation of Thet and Fhet can be found in Kumar et al. (2018a). Absolute uncertainties in Fhet are on average ±0.02 and do not exceed ±0.1 in cases where the heterogeneous freezing signal is clearly distinguishable from the homogeneous freezing signal. It is important to highlight that Fhet carries larger uncertainties (0.1) in cases where heterogeneous freezing signals are weak and overlap (forming a flattened shoulder; see the Supplement) with the homogeneous freezing signal (e.g., in case of strong hampering of IN ability of feldspars in alkali solutes; see Sect. 3.1.1). Spikes occurring before the appearance of the heterogeneous freezing signal are excluded from the evaluation as they originate from single droplets (mostly between 100 and 300 µm with some up to 500 µm in diameter) in the tail of the droplet size distribution, which are orders of magnitude larger in volume than the average droplets, and not representative for the sample.
For feldspars, freezing experiments were at least performed in duplicates with separate emulsions, prepared from a single suspension for each concentration and the means are reported. For kaolinite and micas, freezing experiments were performed with emulsions prepared from at least two separate suspensions for each solute concentration and means are reported. Representative DSC thermograms of all experiments are shown in the Supplement.
2.3 Aging experiments with kaolinite suspended in pure water or solutions
Similar to our experiments with microcline (Kumar et al., 2018a), we let kaolinite (5 wt % suspension) age in pure water, ammonia solution (0.005 molal), and ammonium sulfate solutions (0.1 wt % and 10 wt %) over a period of 5 days and its IN activity was tested during this period in emulsion freezing experiments with the DSC setup. For each solute concentration two separate suspensions were prepared and aged. Small portions were taken from the suspension and emulsified for freezing experiments (as described in the previous section) on the day of suspension preparation (fresh) and the subsequent 5 days in order to assess the long-term effect of ammonia- and ammonium-containing solutes on the IN efficiency of kaolinite.
3.1 Feldspars
Feldspars are crystalline aluminosilicates, primarily of igneous origin, with the general formula , often written as XT4O8 with T = (Al, Si) in tetrahedral coordination with oxygen. X represents an alkali or alkaline earth metal, acting as a charge-compensating cation. The tetrahedra with Al at the center carry single negative charges that are compensated by (for one Al atom) or Ca2+ (for two Al atoms). Microcline, sanidine and orthoclase (all K-rich feldspars) are polymorphs and form the potassium feldspar group (Hofmeister and Rossman, 1983). Ideally, all of them exhibit a Si : Al ratio of 3 : 1, while our microcline and sanidine samples exhibit a Si : Al ratio of 3.1. In sanidine, which forms at high temperatures, Al and Si are fully disordered with Al taking random positions in the aluminosilicate framework leading to monoclinic symmetry. In microcline, Al is fully ordered leading to triclinic symmetry while orthoclase takes an intermediate position with Al and Si being partially disordered (Brown and Parsons, 1989). Despite the difference in charge, Na+ and Ca2+ are sufficiently similar in ionic radius so that there is a complete solid solution series, the plagioclase series, between albite (NaAlSi3O8) and anorthite (CaAl2Si2O8), with intermediate members divided arbitrarily on the basis of anorthite contribution (see Fig. 1). In this series, the Ca : Na and Si : Al ratios are linked with the Al content that changes according to the Ca content. Andesine takes an intermediate position of (Na-Ca)-feldspars with a Ca ∕ (Ca + Na) = 30 %–50 % (Greenwood and Earnshaw, 1998). Our andesine (Si : Al ≈ 1.7) crystallographically fits best with an andesine though it exhibits Ca ∕ (Ca + Na) = 64 %.
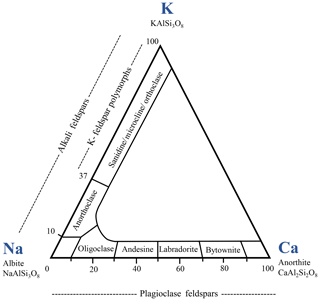
Figure 1Feldspar classification diagram. Numbers are contributions of the end-member minerals in wt % (adapted from Greenwood and Earnshaw, 1998).
3.1.1 Dependence of the heterogeneous freezing temperatures and heterogeneously frozen fractions on water activity
Figure 2a and b show mean heterogeneous (Thet) and homogeneous freezing onsets (Thom) and ice melting temperatures (Tmelt) of the feldspars sanidine and andesine for all investigated solutes (NH4Cl, (NH4)2SO4, Na2SO4) as a function of aw (water activity of solution). The water activity is defined as the ratio of the equilibrium vapor pressure of water over the flat surface of the solution and the saturation vapor pressure over the flat surface of pure water at the same temperature. We derive aw from the melting point depression measured by DSC during the heating cycle (thus, the measured melting points, Tmelt, lie by definition exactly on the melting curve). This procedure was not applicable to Na2SO4, because above the eutectic concentration of 4.6 wt % a hydrate of Na2SO4 crystallizes together with ice (Negi and Anand, 1985). Therefore, water activities for Na2SO4 solutions have been calculated based on the solute concentration using the AIOMFAC thermodynamic model at 298 K (Zuend et al., 2008, 2011). The homogeneous freezing curve (dotted black line) is obtained by a constant shift of the melting curve by , calculated to best fit the current dataset (see Kumar et al., 2018a, for more details of the derivation). This offset is in good agreement with found by Koop et al. (2000). Following Koop et al. (2000), we assume aw to be temperature independent between Thom and Tmelt.
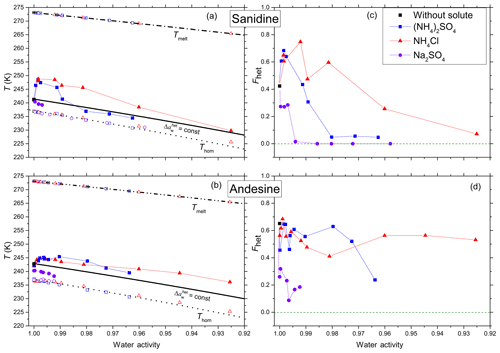
Figure 2Measured freezing temperatures (a, b) and heterogeneously frozen fractions (c, d) of emulsion freezing experiments with 2 wt % feldspar, namely sanidine (a, c) and andesine (b, d), in various solutions (color coded). (a, b) Heterogeneous freezing onset temperatures, Thet (filled solid symbols connected by thin lines to guide the eye); homogeneous freezing onset temperatures, Thom (open symbols at T<237 K); and ice melting temperatures, Tmelt (open symbols at T>265 K) as functions of water activity of solutions, aw, for various solutes (symbols and colors see insert). Dash-dotted black line: ice melting point curve. Dotted black line: homogeneous ice freezing curve for supercooled aqueous solutions obtained by horizontally shifting the ice melting curve by a constant offset . Solid black line: horizontally shifted from the ice melting curve by and 0.254 for sanidine (a) and andesine (b), respectively, with offsets derived from the heterogeneous freezing temperature of the suspension of the mineral in pure water (filled black square at aw=1). Symbols are the mean of at least two separate emulsion freezing experiments. Difference between the two measurements plus instrumental uncertainty in Thet and aw are smaller than the symbol size (see Sect. 2.2). (c, d) Heterogeneously frozen fraction, Fhet, as a function of aw, for sanidine (c) and andesine (d). Measurement difference and uncertainty in Fhet do not exceed ±0.1.
A constant offset is also applied to the heterogeneous freezing temperatures. Here, the offset in aw is chosen so that the heterogeneous freezing line passes through the freezing temperature of the pure water case. This yields the solid black lines with for sanidine and for andesine, which will be referred to as and , respectively. The heterogeneous freezing behavior would be expected to follow these curves if specific chemical interactions between the solute and the ice-nucleating surface were absent, so that the only effect of the solute is a freezing point depression. However, as can be seen from Fig. 2a and b, the measured heterogeneous freezing onset temperatures, Thet, deviate from the curves for both feldspars. For both solute cases ((NH4)2SO4 and NH4Cl), sanidine shows a strong increase in Thet (by up to ≈ 7 K with respect to the pure water case) at low solute concentrations (aw>0.99). This increase is followed by a decrease at higher concentrations back to in the case of NH4Cl solutions (aw≈0.925) and even slightly below in the case of (NH4)2SO4 solutions (aw≤0.98). Andesine also shows an increase in Thet, though smaller in magnitude (≈ 2.6 K with respect to the pure water case), but this enhancement persists to higher concentrations. The observed enhancements with respect to are ∼ 5.1 and ∼ 4.0 K for NH4Cl and (NH4)2SO4, respectively.
In contrast to solutions, freezing experiments in the presence of Na2SO4 as a non- solute show a strong decrease in Thet below by ∼ 1.7 K and ∼ 2.4 K for sanidine and andesine, respectively, at aw≈0.99. No discernible heterogeneous freezing signal was observed for higher Na2SO4 concentrations (aw<0.99).
Figure 2c and d show the heterogeneously frozen fraction Fhet (the ratio of the heterogeneous freezing signal to the total freezing signal) as a function of aw for sanidine and andesine. In dilute -containing solutions, sanidine shows an enhancement in Fhet up to ≈ 0.75 at aw≈0.99 compared to the suspension in pure water (Fhet≈0.42 at aw=1). With decreasing water activities, this enhancement reverses into a decline (for aw<0.99 in case of (NH4)2SO4 and for aw<0.98 in case of NH4Cl). In contrast, Fhet of andesine is less influenced by the presence of solutes since there is no significant enhancement at low concentrations and much less of a decrease at higher concentrations.
For both feldspars, the addition of Na2SO4 leads to a decrease of Fhet for the lowest solute concentration (aw≥0.99) and even to an almost complete inhibition of the IN activity for aw<0.99.
3.1.2 Comparison with previous IN studies performed with feldspars
Thet and Fhet trends for sanidine and andesine are similar to the ones of the K-feldspar microcline reported in our previous study, Kumar et al. (2018a), but with significant variations. All investigated feldspars show an increase in Thet at low concentrations of solutes (aw≥0.99). This increase is highest for sanidine and lowest for andesine. On the other hand, the decrease of Thet at higher solute concentration is most pronounced for microcline with values falling below the prediction from the water activity-based description. In case of non- solutes, Thet decreases below the prediction from the water activity-based approach for all investigated feldspars even at low solute concentrations. Similar trends among the feldspars are also observed for Fhet. These findings are also in general agreement with droplet freezing experiments by Whale et al. (2018) who observed an increase of active-site densities for microcline and sanidine in the presence of solutes and a decrease in alkali halide solutions.
The IN activity of feldspars has been investigated in numerous studies. All studies agree that the IN activity of K-feldspars is high among mineral dusts (Atkinson et al., 2013; Harrison et al., 2016; Kaufmann et al., 2016; Peckhaus et al., 2016; Welti et al., 2019). Kaufmann et al. (2016) and Welti et al. (2019) found that the IN activity of microcline is superior compared with other K-feldspars. Several studies have been dedicated to microcline. Niedermeier et al. (2015) and Burkert-Kohn et al. (2017) found frozen fractions of 0.5 at 244–245.5 K for condensation freezing on 300 nm microcline particles that were strongly reduced when the samples were aged under acidic conditions. A strong reduction of IN activity when feldspars were coated with sulfuric acid was also observed by Kulkarni et al. (2014). The IN activity of microcline after aging in pure water seems to depend on the specific sample. Samples with the highest onset freezing temperatures also show the strongest reduction in IN activity after aging, indicating that the best active sites might also be the most labile ones (Harrison et al., 2016; Peckhaus et al., 2016). Harrison et al. (2016) found that one sample of Na-feldspar (albite) was similarly active as microcline when freshly suspended in water, but lost its high IN activity after having been suspended for months in water, indicating that its IN activity may be related to sites with high solubility that are lost over time by dissolution. Kiselev et al. (2017) found that high-energy (100) surface patches of K-rich feldspars are best suited for deposition growth of aligned ice crystals below water saturation. However, it is not clear how resistant these high-energy sites are when immersed in water. Whale et al. (2017) related the exceptionally high IN ability of K-feldspars to microtextures, giving rise to topographic features with high IN temperatures. The IN site densities that they investigated with their setup were in the range from 10−1 to 103 cm−2 with IN temperatures up to 271 K. With the DSC emulsion freezing experiments, we investigate the properties of sites that are common to submicrometer particles, i.e., with surface densities in the range from 1010 to 105 cm−2 nucleating ice up to 252 K. While the sites investigated by Whale et al. (2017) may be well correlated with perthitic structures, it is unlikely that such features are common enough in submicrometer particles to account for the IN activity observed in our emulsion freezing experiments. Welti et al. (2019) found a clear decrease in IN activity for all investigated feldspars (microclines, orthoclases, sanidine, pericline and labradorites) with decreasing particle size from 800–50 nm, indicating the better active sites are rarer.
3.1.3 Surface ion exchange
In pure water, the native charge-balancing surface cations (K+, Na+, Ca2+) immediately undergo cation exchange by (Chardon et al., 2006; Lee et al., 2008), with hardly any simultaneous structural surface damage (Busenberg and Clemency, 1976). The native cation may also participate in ion exchange with an externally added cation depending on the size and charge compatibility of the latter with the crystal structure (Auerbach et al., 2003; Belchinskaya et al., 2013). Ammonium ions not only have a strong preference for cation exchange with K-feldspars and (Na-Ca)-feldspars but part of them remain fixed to the surface in nonexchangeable form (Nash and Marshall, 1957; Barker, 1964). In Kumar et al. (2018a), we have shown that the ion exchange is unlikely as a reason for the enhanced IN efficiency of microcline in dilute -containing solutions. Rather, hydrogen bonding of ammonia/ammonium with the surface hydroxyl groups seems to provide better ice-like template sites for the incoming water molecules (Anim-Danso et al., 2016), leading to an increase in IN efficiency.
3.1.4 Aluminum depletion and surface dissolution
When suspended in water or solutions, feldspars undergo slow dissolution, followed and accompanied by the precipitation of more stable phases like kaolinite, gibbsite or halloysite (Stillings and Brantley, 1995). Depending on the specific feldspar and solution pH, steady-state Si dissolution rates vary between 10−10 and 10−14 moles m−2 s−1 (Crundwell, 2015) with lowest values at near-neutral conditions. The solution pH during the emulsion freezing experiments reported in Fig. 2 are close to neutral with pH values ranging from 5.5 to 6.7. For the feldspars investigated in this study, steady-state dissolution rates are lowest for microcline with – moles m−2 s−1 at pH ∼ 6 (Crundwell, 2015) followed by sanidine with a rate of ∼ moles m−2 s−1 at near-neutral conditions (Crundwell, 2015), while dissolution of andesine occurs with a steady-state rate of 10−12–10−11 moles m−2 s−1 at pH ∼ 8 (Gudbrandsson et al., 2014). Hereby, initial dissolution rates of freshly suspended feldspar may be higher by up to 3 orders of magnitude than the rates at steady state (Zhu et al., 2016). With these rates, dissolution is in the range of one monolayer within the timescale of a DSC freezing experiment (1–1.5 h) for andesine, and below it for sanidine and microcline.
At near-neutral conditions, the dissolution proceeds via protonation of the oxygen of bridges with subsequent release of Al3+ resulting in an incongruent (deviation of ratio of released Si to Al from stoichiometric ratio) initial dissolution for most feldspars when they are freshly suspended in water (Oelkers and Schott, 1995; Oelkers et al., 2009), and leading to a rich surface (Oxburgh et al., 1994; Stillings and Brantley, 1995; Oelkers et al., 2009). Oelkers et al. (2009) found aluminum surface depletion to occur readily in their 20 min titration experiments with the Na-feldspar albite. Thus, the feldspar surfaces in pure water suspensions can be considered at least partly or even completely depleted in aluminum with the dangling bonds replaced by silanol groups within the timescales of our experiments. The dissolution incongruence with respect to Al atoms depends on the Si∕Al ordering and the Si : Al ratio of the feldspar lattice (Yang et al., 2014a, b). Yang et al. (2014b) investigated the stoichiometry of feldspar dissolution under acidic conditions (pH 1.8) and found that microcline with Si : Al = 3.0 dissolved with a ratio of Si : Al = 2.1. Their sanidine sample with Si : Al = 2.87 released Al with Si :Al = 1.36, while their andesine sample with Si : Al = 1.95 dissolved at a ratio Si : Al = 0.76 : 1. This dissolution incongruence leads to a layer leached in Al, with a thickness that depends on the specific feldspar and increases with decreasing pH. At steady state, this Al-depleted layer is 6.6–8.5 nm thick for microcline at pH 1 (Lee et al., 2008), but only 1–2 nm at pH 3 (Stillings and Brantley, 1995). For andesine, it reaches 60–120 nm at pH 3.5 and still 15–30 nm at pH 5.7 (Muir et al., 1990). Since Al dissolution at steady-state conditions needs to occur through this layer, the andesine surface is considered to consist of somewhat loosened and distorted feldspar chains resulting in a porous amorphous-like structure (Marshall, 1962; Stillings and Brantley, 1995; Zhang and Lüttge, 2007). At pH 1, the first 5 nm of surface layer of microcline were found to be amorphous (Lee et al., 2008). Since amorphous silica shows barely any IN activity (see also the companion paper, Kumar et al., 2019), the loss of IN activity of microcline in the presence of H2SO4 (Kumar et al., 2018a) may be explained by the presence of an amorphous silica layer. Since Thet correlates with the thickness of the leached layer reported for the investigated feldspars, we hypothesize that amorphous surface layers exceeding a few nanometers in depth hamper the IN activity of feldspars.
3.1.5 Surface charge and surface protonation
Feldspars exhibit a negative surface charge over a wide pH range with a point of zero charge (PZC) < 2 (Karagüzel et al., 2005; Vidyadhar and Hanumantha Rao, 2007). Bringing the feldspar surface closer to the PZC by adding H2SO4 did not increase Thet but decreases Fhet due to surface degradation as was shown for microcline (Kumar et al., 2018a). This shows that surface charge is only one among several factors influencing IN activity. We discuss the effect of surface charge on IN activity of mineral surfaces in more detail in Sect. 4.
Surface hydroxyl groups are considered to promote IN because they can form hydrogen bonds with water molecules and bring them in a suitable orientation for IN. In a recent molecular simulation study, Pedevilla et al. (2017) found that the OH density rather than a specific OH pattern is a useful descriptor of IN ability. The relevance of surface hydroxylation is in agreement with our observations that Na+ ions added to an aqueous feldspar suspension decrease Thet and Fhet for all investigated feldspars since they replace the protons (Oelkers et al., 2009) thus decreasing the surface hydroxylation (see Fig. 2 of this paper; Kumar et al., 2018a). Ammonium on the other hand, can form hydrogen bonds with water molecules and therefore does not reduce the IN activity. In addition, is not only involved in ion exchange but also binds to the feldspar surface (Kumar et al., 2018a). Therefore, it increases the capacity for hydrogen bonding even more and leads to an increased IN activity. A strong increase of proton concentration (low pH), on the other hand, hampers or even totally impedes IN because it promotes aluminum depletion and the formation of an amorphous silica surface layer.
3.1.6 Influence of sulfate
While we consider solute effects to be dominated by cations at low concentrations, the anions seem to become more relevant at higher concentrations. Aqueous phase complexes of dissolved aluminum with sulfate enhance the solubility of aluminum. Surface complexes of sulfate with surface aluminum can impede or enhance dissolution of aluminum. Bidentate surface complexes with sulfate do not enhance surface protonation and should stabilize aluminum at the surface, while the formation of mononuclear complexes should facilitate surface protonation and help dissolution of aluminum (Min et al., 2015). The effect of sulfate should therefore depend on the bonding strength of aluminum to the feldspar surface, which depends on the Si ∕ Al order and Si : Al ratio. Min et al. (2015) found that the dissolution rate of anorthite, a (Na-Ca)-feldspar with Si : Al = 1, is enhanced by the formation of monodentate complexes between the aluminum surface sites and sulfate. This seems to be also the case for the (Na-Ca)-feldspar andesine. On the other hand, surface complexation of aluminum sites with sulfate seems to decrease the removal of aluminum and block sites for IN in the case of microcline, while sanidine takes an intermediate position.
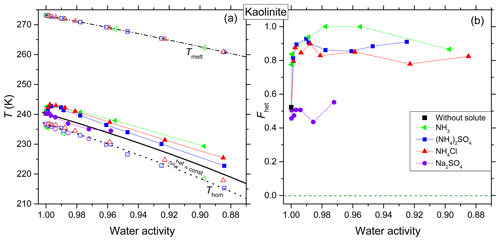
Figure 3Same as Fig. 2, but for kaolinite (5 wt %). (a) Homogeneous ice freezing curve (dotted black line) characterized by a constant offset . Ice melting curve (dash-dotted black line) and the heterogeneous freezing curve (solid black line) horizontally shifted from the ice melting curve by derived from the heterogeneous freezing temperature of the suspension of the mineral in pure water (filled black square at aw=1). Measured differences and instrumental uncertainties in Thet and aw are smaller than the symbol size (see Sect. 2.2). (b) Fhet (heterogeneously frozen fraction) as a function of water activity of the solutions. Measurement difference and uncertainty in Fhet do not exceed ±0.1.
3.2 Kaolinite and gibbsite
Kaolinite (Al4[Si4O10](OH)8) is a layered 1 : 1 (one tetrahedral sheet and one octahedral sheet forming stacked T–O layers) dioctahedral phyllosilicate and one of the most abundant clay minerals found in the Earth's crust (Murray, 1991). Each layer consists of a sheet of SiO4 tetrahedra forming six-membered silicate rings connected via common oxygen atoms to a sheet of AlO6 octahedra forming four-membered aluminate rings. Weak hydrogen bonds between Al−OH and Si–O–Si groups provide interlayer attraction preventing ions or molecules from entering the interlayer space and constituting the non-swelling nature of this mineral. Since ionic substitution of Si4+ with Al3+ is absent in the regular kaolinite lattice, exchangeable ions only occur at defects or at edges (Bibi et al., 2016). Cleavage of kaolinite preferentially occurs along the basal plane, resulting, on one side, in a hydroxylated Al surface with Al atoms arranged in a hexagonal pattern and on the other side in a siloxane surface with Si–O–Si bridges forming hexagonal rings (Bear, 1965).
Although particles of gibbsite are of rare abundance in atmospheric dusts (Boose et al., 2016; Kaufmann et al., 2016), we investigate this mineral because the hydroxylated Al sheets of kaolinite are structurally identical with gibbsite. Gibbsite is an aluminum hydroxide of the general formula Al(OH)3 that exists as different polymorphs. The basal surface of gibbsite is comparable to the aluminol surface of kaolinite and, therefore, often used as a model surface to elucidate the physicochemical properties of the Al surface of kaolinite (Liu et al., 2015; Kumar et al., 2016).
3.2.1 Dependence of the heterogeneous freezing temperatures and frozen water volume fraction on water activity
Figure 3a presents Thet, Thom and Tmelt as a function of aw for kaolinite. The offset in aw applied to shift the melting curve so that it passes through the freezing temperature of the pure water case for kaolinite is , here referred to as . In the presence of solutes, kaolinite shows an increase (≈ 2.4 K) in Thet compared to even at the lowest investigated solute concentration (0.1 wt %; aw>0.99). The influence of NH3 on the IN activity was found to be similar to the one of the -containing solutes. This enhancement relative to persists over the complete concentration range probed in this study, similar to the case of andesine. For aw<0.9, kaolinite shows an increase up to 2.9, 5.5 and 6.9 K in Thet compared to in solutions of (NH4)2SO4, NH4Cl and NH3, respectively. In contrast to the feldspars, in Na2SO4 solutions Thet follows within the error range for all investigated concentrations.
Figure 3b shows Fhet as a function of aw for kaolinite. Interestingly, kaolinite shows a strong enhancement in Fhet to 0.75–1.00 compared to the pure water case (Fhet≈0.52) in the presence of NH3 and solutes over the complete investigated concentration range (aw=1–0.88). This enhancement is strongest for ammonia solutions, reaching Fhet≈1 (Fhet≈1 was assumed when it was not possible to discern a homogeneous freezing signal; see Fig. 5) at aw=0.98–0.96, compared to Fhet≈0.5 in pure water. In contrast, Fhet seems to be unaffected by Na2SO4 within experimental uncertainties over the measured concentration range.
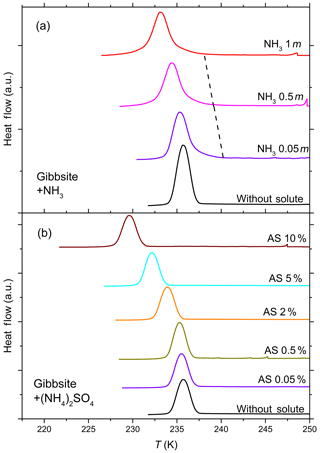
Figure 4DSC thermograms of 10 wt % gibbsite suspended in ammonia solution droplets (a) of concentrations from 0 to 1 molal (aw=1–0.981) and (NH4)2SO4 solution droplets (b) from 0 to 10 wt % (aw equal to 1–0.961). All curves are normalized such that the areas under the heterogeneous and homogeneous freezing curves sum up to the same value. Gibbsite shows no discernible heterogeneous freezing signal in pure water and starts to show a weak heterogeneous freezing signal when suspended in ammonia solution (dashed black line connects the onset of heterogeneous freezing signals), while no heterogeneous IN is observed for gibbsite suspended in (NH4)2SO4.
Figure 4 shows the DSC thermograms of the emulsion freezing experiments carried out with 10 wt % gibbsite suspensions in pure water, in NH3- (panel a) and in (NH4)2SO4-containing solutions (panel b). Gibbsite, exhibiting no heterogeneous freezing signal during emulsion freezing experiments in pure water, starts to show a weak heterogeneous freezing signal with increasing NH3 concentration (indicated by the dashed black line in Fig. 4a). On the other hand, no heterogeneous freezing signal can be observed for gibbsite suspended in (NH4)2SO4 solutions (0.05 wt %–10 wt %; aw equal to 0.996–0.961.
3.2.2 Previous studies on the IN activity of kaolinite
Kaolinite has shown IN activity in various freezing modes (Hoose and Möhler, 2012; Murray et al., 2012; Kanji et al., 2017). Many studies investigated K-SA kaolinite from Sigma-Aldrich (Zuberi et al., 2002; Lüönd et al., 2010; Burkert-Kohn et al., 2017), while others used the KGa-1b kaolinite from the Clay Mineral Society with high mineralogical purity (96 %, minor impurities of anatase, crandallite, mica, and illite) (Murray et al., 2011; Pinti et al., 2012; Wex et al., 2014; Kaufmann et al., 2016). Pinti et al. (2012) found with their emulsion freezing experiments that K-SA exhibits a second freezing peak at higher temperatures with onset at ∼248 K that could be related to impurities of feldspars (Atkinson et al., 2013). On the other hand, KGa-1b features only one heterogeneous freezing peak with an almost constant onset at ∼ 240 K in emulsion freezing experiments irrespective of the kaolinite concentration in the aqueous suspension (Pinti et al., 2012), which is an indication of the homogeneous composition and mineralogical purity of the sample. Kaufmann et al. (2016) evaluated the active particle fraction of kaolinite KGa-1b to be only about 0.04 compared to values of 0.54–0.64 determined for microcline. A lower active fraction of kaolinite compared with the feldspar microcline was also confirmed by single particle immersion freezing experiments (Burkert-Kohn et al., 2017).
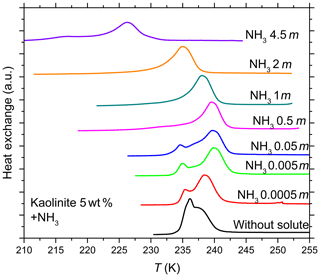
Figure 5DSC thermograms of 5 wt % kaolinite particles suspended in ammonia solution droplets (0–4.5 molal; aw equal to 1–0.922). All curves are normalized such that the areas under the heterogeneous and homogeneous freezing curves sum up to the same value.
The DSC curves for kaolinite suspended in NH3 solution (Fig. 5) show that for a certain NH3 concentration range (0.5–2 molal; aw equal to 0.988–0.955) the heterogeneous freezing signal totally dominates the homogeneous one, indicating that initially IN inactive particles (contributing to the homogeneous freezing DSC signal) became IN active after addition of ammonia. Salam et al. (2007, 2008) have previously reported improved IN efficiency of the clay mineral montmorillonite below and above water saturation after the particles were exposed to NH3 gas.
3.2.3 Which kaolinite surface is responsible for the IN activity?
As a sheet aluminosilicate, kaolinite exhibits two basal faces – the siloxane tetrahedral and the alumina octahedral – and hydroxylated edges. The overall surface charge of kaolinite in pure water is negative with a PZC < 2. The PZC increases when kaolinite is suspended in salt solutions (Yukselen-Aksoy and Kaya, 2011). However, this overall value determined from bulk experiments does not need to apply to the individual faces of kaolinite.
Recent surface force measurements have been able to probe the surface properties of the kaolinite faces individually. These measurements evidenced a negative charge of the siloxane surface with a PZC below pH 4 (Gupta and Miller, 2010). Isomorphic substitution of Si(IV) for Al(III) in tetrahedral layers is considered the main reason for the net permanent negative surface charge, which is balanced by the adsorption of cations (e.g., Na+, K+, Ca2+) (Cashen, 1959; Grim, 1968; Bolland et al., 1980). The oxygen atoms on the siloxane surface are relatively weak electron donors and incapable of forming hydrogen bonds with water molecules. Therefore, the near-surface water molecules interact predominantly with each other so that the surface is considered nearly hydrophobic (Jepson, 1984; Giese and van Oss, 1993; Braggs et al., 1994).
Unlike the siloxane surface, the hydroxyl-rich surface of the Al-octahedral layer is hydrophilic and forms hydrogen bonds with water (Schoonheydt and Johnston, 2006; Yin et al., 2012). The alumina face was found to be negatively charged at pH ≥ 8 and positively charged at pH ≤ 6 indicating a PZC of pH 6–8 (Gupta and Miller, 2010). The pH-dependent, nonpermanent surface charge arises from protonation or deprotonation of surface hydroxyl groups. While silanol groups mainly contribute to negative charge through the formation of SiO− by deprotonation, aluminol groups undergo both protonation at low pH and deprotonation at high pH (Abendroth, 1970; Bleam et al., 1993).
Disruption of the kaolinite sheets leads to dangling oxygen atoms at the crystal edges that take up water molecules to transform into hydroxyl groups. This process produces a surface rich in silanols and aluminols, which terminate tetrahedral and octahedral layers, respectively (Brady et al., 1996; Liu et al., 2013). The PZC of the kaolinite edge surface was found to be below pH 4. The negative charge is considered to arise from deprotonation of Si sites, which is only partly counteracted by positively charged Al sites (Brady et al., 1996). The reactive hydroxyl groups, due to their charge, have the potential to chemisorb certain other ionic species (Schoonheydt and Johnston, 2006, 2013). Such hydroxyl groups are also present at steps and cracks.
First principles calculations and molecular dynamics simulations have indicated that hydrogen bonding to surface hydroxyl groups is an essential factor for providing IN activity to mineral surfaces (Hu and Michaelides, 2007; Sosso et al., 2016a; Glatz and Sarupria, 2018). The absence of sites for hydrogen bonding make the regular siloxane surface an unlikely candidate for IN (Freedman, 2015). The alumina surface, on the other hand, is OH-rich and has been probed in several modeling studies for its capability to nucleate ice. Based on a density-functional theory study, Hu and Michaelides (2007) concluded that the basal surfaces of kaolinite do not support epitaxial multilayer ice growth, rather they may promote the growth of the prism face of ice (Cox et al., 2013). Monte Carlo simulations carried out by Croteau et al. (2008, 2009) suggested that a rigid Al surface of kaolinite (001) is incapable of orienting water molecules into ice-like configurations, instead trenches and surface defects were suggested to be responsible for IN (Croteau et al., 2010a, b). Zielke et al. (2015) showed that both the Al surface and the Si surface can nucleate ice, by reorientation of hydroxyl groups in the former case and by ordered arrangement of hexagonal and cubic ice layers joined at their basal planes in the latter case. Glatz and Sarupria (2018), based on molecular dynamics simulations on kaolinite-like surfaces, argued that lattice matching and hydrogen bonding are necessary but not sufficient conditions for IN. Sosso et al. (2016b) found that IN on the hydroxylated basal surface of kaolinite proceeds exclusively via the formation of the hexagonal ice polytype but that this process crucially depends on very small structural changes upon kaolinite surface relaxation in the molecular dynamics simulations.
While most of these studies focused on the basal planes, experimental evidence suggests that the edges are preferred locations for IN. Indeed, Wang et al. (2016) found in IN experiments with a cell coupled to an environmental scanning electron microscope that ice preferentially nucleates at the edges of kaolinite particles when they were exposed to increasing relative humidity. The similar response of kaolinite and feldspars to solutes indicates a similar chemical composition of IN active sites on the surfaces of these two mineral types, suggesting that the kaolinite edges, rich in both aluminol and silanol groups should be responsible for the observed IN activity.
Similar to the hydroxylated Al layers of kaolinite, gibbsite consists of stacked sheets of linked octahedra of aluminum hydroxide. Therefore, the gibbsite surface is often taken as a model for the Al surface of kaolinite (Liu et al., 2015; Kumar et al., 2016). The PZC of gibbsite falls in the pH range from 7.5 to 11.3 (Kosmulski, 2009; Liu et al., 2015), thus in a similar, yet somewhat higher, range than the one of the Al surface of kaolinite (pH 6–8). DSC thermograms of the emulsion freezing experiments with gibbsite (Fig. 4) show no heterogeneous freezing signal in pure water and (NH4)2SO4 solutions up to 10 wt %. Only when suspended in NH3 solutions (0.05–1 molal, aw equal to 0.996–0.981), a weak heterogeneous freezing signal developed. This indicates that NH3 hydrogen bonded to the hydroxylated Al surface provide IN activity to gibbsite, while the positively charged does not adsorb on the positively charged Al surface. Given the inability of gibbsite to nucleate ice in water and (NH4)2SO4, we conclude that the IN activity of kaolinite rather stems from the edges as suggested by Wang et al. (2016) and Croteau et al. (2010a). This conclusion is further supported by the finding that kaolinite indeed adsorbs NH3 by forming hydrogen bonds with the hydroxyl groups at the edges (James and Harward, 1962).
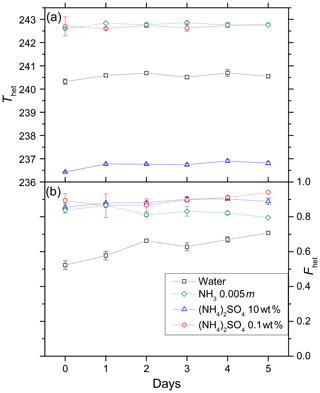
Figure 6Development of Thet (a) and Fhet (b) for 5 wt % kaolinite suspended in water, 10 wt % (NH4)2SO4, 0.1 wt % (NH4)2SO4, 0.005 molal ammonia solutions over a period of 5 days. Data points depict mean (with error bars representing min to max) for Thet and Fhet measured for two aging experiments performed with two independently aged suspensions.
3.2.4 Aging effect
We carried out immersion freezing experiments with kaolinite (5 wt %) suspended in pure water, NH3 solution (0.005 molal, aw=0.999), and (NH4)2SO4 solutions (0.1 wt % and 10 wt %; aw=0.996, aw=0.961, respectively) over a period of 5 days to assess the effect of aging on the IN efficiency of kaolinite. Figure 6 shows Thet (panel a) and Fhet (panel b) as a function of time. Thet remains stable over the measured time period within the experimental measurement uncertainties. Similarly, Fhet remains constant except in the pure water case where it shows a slight increase.
The dissolution rate of kaolinite depends on pH with the lowest values of 10−14–10−13 moles (of Si) m−2 s−1 realized at near-neutral conditions (Carroll and Walther, 1990; Huertas et al., 1999). At acidic conditions the dissolution increases because of H+ attack at the Si–O–Al linkages of the edges leading to the liberation of aluminum ions into the solution (Xiao and Lasaga, 1994; Fitzgerald et al., 1997). At alkaline conditions, dissolution is considered to occur dominantly at the basal octahedral face via deprotonation of aluminum sites (Huertas et al., 1999; Naderi Khorshidi et al., 2018). At near-neutral conditions, both mechanisms are inefficient leading to a minimum in the dissolution rate. Between pH 5 and 10, kaolinite dissolution is accompanied by the precipitation of an aluminum hydroxide phase (Huertas et al., 1999).
The pH of the solutions used for the aging experiments with kaolinite are in the slow dissolution near-neutral regime. Since there is no decrease in IN efficiency during the 5 days of aging in the aqueous solutions of ammonia and ammonium sulfate, surface alteration during this time period seems to be minor. Indeed, with a dissolution rate of 10−14–10−13 moles m−2 s−1, the Si dissolved during the 5 days of the experiments should be well below a monolayer and should not lead to a significant alteration of the surface composition. Nevertheless, when dissolution occurs preferentially on chemically more reactive sites that are likewise IN active, destruction of these sites might lead to a decrease in IN activity (Kumar et al., 2019). However, the increase of IN activity in pure water rather suggests the generation of new IN active sites due to surface changes in the presence of water.
3.3 Micas
Muscovite (KAl2(AlSi3O10)(OH)2) and biotite (K(Mg,Fe)3AlSi3O10(OH)2), both quite soft (on Mohs scale 2–3), are 2 : 1 layer phyllosilicates (one octahedral sheet sandwiched between two tetrahedral sheets, forming stacked T–O–T layers) belonging to the mica group with nearly perfect basal cleavage (Bower et al., 2016; Christenson and Thomson, 2016). The tetrahedral layer consists of Si and Al at a ratio of 3 : 1. The Al is randomly ordered avoiding Al–O–Al arrangements. The presence of Al in the tetrahedral layer introduces a negative charge that is neutralized by potassium ions acting as the bridge between the layers. Muscovite and biotite differ in their octahedral layers, which in the case of muscovite is dioctahedral and occupied by Al3+. Biotite is part of a solid solution series within the mica group with trioctahedral layers occupied by Fe2+ and Mg2+. The end-members of the series are pure iron biotite called annite and pure magnesium biotite called phlogopite (Bray et al., 2015), while biotites take intermediate positions in terms of Fe : Mg ratios (Fleet et al., 2003).
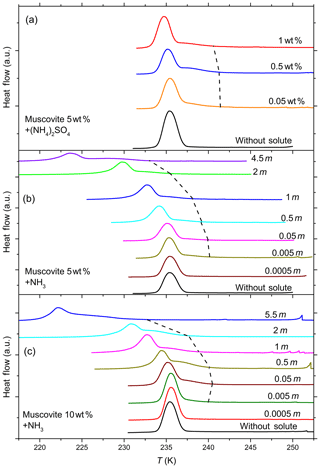
Figure 7DSC thermograms of 5 wt % (a, b) and 10 wt % (c) muscovite particles suspended in ammonia (0–5.5 molal; aw equal to 1–0.912) and ammonium sulfate (0–1 wt %; aw equal to 1–0.988) droplets of different solution concentrations (given as inserts). All curves are normalized such that the areas under the heterogeneous and homogeneous freezing curves sum up to the same value. The dashed black line connects the heterogeneous freezing onset temperatures (Thet) of the emulsions. With increasing ammonia concentration heterogeneous IN efficiency starts to develop, as can be noticed from the appearance of Thet, which was absent in pure water. The intensity of the heterogeneous freezing signal, hence Fhet, becomes more prominent in 10 wt % suspensions (see Table 1).
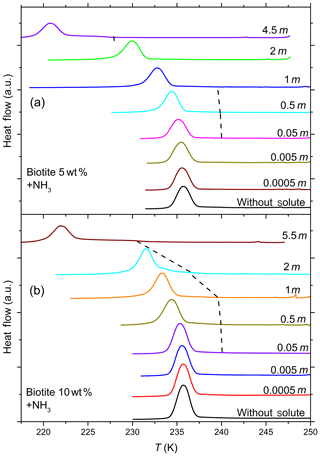
Figure 8DSC thermograms of 5 wt % (a) and 10 wt % (b) biotite particles suspended in ammonia solution droplets (0–5.5 molal; aw equal to 1–0.912). All curves are normalized such that the areas under the heterogeneous and homogeneous freezing curves sum up to the same value. In contrast to muscovite, biotite becomes IN active only at very high concentrations of ammonia. In addition, the intensity of the heterogeneous freezing signal (hence Fhet) is low, but becomes more prominent in 10 wt % suspensions (see Table 2).
3.3.1 Heterogeneous freezing of aqueous solution droplets containing micas
Figure 7 shows DSC thermograms of muscovite particles suspended in (NH4)2SO4 and NH3 solution droplets of increasing concentration, and Fig. 8 the same for biotite in NH3 solution droplets. Thet and Fhet from these measurements for muscovite and biotite are summarized in Tables 1 and 2, respectively. Interestingly, when suspended in pure water, neither muscovite nor biotite exhibit a discernible heterogeneous freezing signal in the DSC thermograms. Considering the particle size distributions of the two minerals, which peaks at about 335 nm in the case of the muscovite sample (Kaufmann et al., 2016) and is bimodal with maxima at 241 nm and 1.7 µm for biotite (see the Supplement), the lack of a heterogeneous freezing signal cannot be ascribed to the predominance of empty emulsion droplets. Indeed, both start to develop IN activity when immersed in ammonia or ammonium solutions (indicated by the dashed black lines in Figs. 7 and 8). The frozen fraction, Fhet, is a strong function of NH3 or concentration. For muscovite (5 wt %), Fhet increases from 0.138 in 0.005 molal NH3 (aw=0.997) to 0.387 in 4.5 molal NH3 (aw=0.922) solutions. In the case of biotite (5 wt %), suspensions do not reveal a heterogeneous freezing signal in pure water or in dilute ammonia solutions. A well discernable heterogeneous freezing signal appears only in concentrated ammonia (4.5 molal, aw=0.922, Fig. 8a). For 10 wt % biotite suspensions, the heterogeneous freezing signal becomes visible already in 2 molal ammonia (aw=0.968; Table 2), yet the signals are clearly weaker than those from muscovite suspensions at similar solute concentrations.
Table 1Summary of the freezing experiments with emulsified aqueous solution droplets containing muscovite (5 wt % and 10 wt %). Note that the absolute uncertainty in Fhet may be up to ±0.1. Only Fhet values above this threshold are clear evidence of heterogeneous IN.
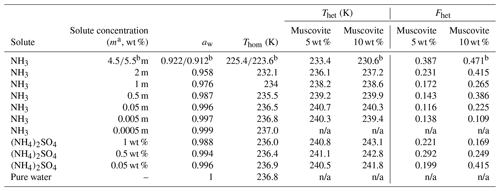
a molality; b 10 wt % muscovite suspended in 5.5 molal NH3 solution; n/a: no Thet and Fhet can be reported due to absence of a discernible heterogeneous freezing signal in the emulsion freezing experiments.
Table 2Summary of the freezing experiments with emulsified aqueous solution droplets containing biotite (5 wt % and 10 wt %). Note that the absolute uncertainty in Fhet may be up to ±0.1. Only Fhet above this threshold are clear evidence of heterogeneous IN.
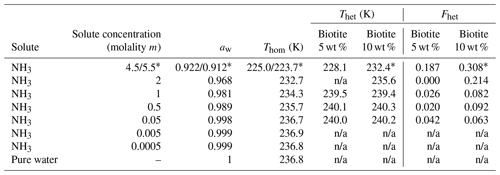
* 10 wt % biotite suspended in 5.5 molal NH3 solution; n/a: no Thet and Fhet can be reported due to absence of a discernible heterogeneous freezing signal in the emulsion freezing experiments
3.3.2 Previous studies on IN activities of micas
Micas have been tested for IN activity in numerous studies, but with very diverse outcomes. Older studies have reported dentritic ice growth on the basal planes of freshly cleaved micas (muscovite and fluorophlogopite: KMg3AlSi3O10F2) when they were exposed to water saturation at cold temperatures (Bryant et al., 1959; Hallett, 1961; Layton and Harris, 1963). Shen et al. (1977) showed that fluorophlogopite and muscovite particles (44–74 µm) induce IN in bulk freezing experiments with onset temperatures of 272 and 268 K, respectively. Steinke (2013) investigated the freezing of water droplets on a muscovite surface in a cold stage and found IN activity around 250 K but with a much lower active site density compared with clay minerals. Atkinson et al. (2013), on the other hand, observed hardly any IN activity in immersion mode for a non-specified mica. Campbell et al. (2015) found freezing close to the homogeneous freezing temperature for droplets on muscovite. Surface imperfections on the basal plane of muscovite were found to promote IN on muscovite exposed to water vapor below the threshold temperature for homogeneous IN but had no effect when the surface was immersed in water above this threshold temperature. Overall, the IN activity of micas seems to be much lower than that of clay minerals such as kaolinite despite their similar structure.
3.3.3 IN activity in relation to the surface properties of micas
The basal surfaces of micas are dominated by Si–O–Si and Al–O–Si bridges exhibiting little hydroxylation. Due to the isomorphic substitution of Si(IV) for Al(III) in the tetrahedral layer, the basal surfaces are hydrophilic and carry a permanent negative charge that is neutralized by K+ ions (Zhao et al., 2008; Yan et al., 2013). When suspended in electrolyte solutions, K+ exposed to the surface undergo ion exchange within seconds (Cho and Komarneni, 2009; de Poel et al., 2017; Lee et al., 2017). In pure water, surface K+, and to a lesser degree also interlayer potassium ions, are lost to the suspension and replaced by protons introducing hydroxylation to the basal surface and widening the muscovite lamellae (Banfield and Eggleton, 1990). At the edges of the plate-like particles, the broken bonds of the disrupted sheets are saturated by –OH, resulting in a hydrophilic, hydroxylated surface with a surface charge that depends on pH (Zhao et al., 2008).
Micas slowly dissolve when suspended in water accompanied by precipitation of metal (hydr)oxides and kaolinite, which may form nanometer coatings on the mica surface blocking active sites (Pachana et al., 2012). The dissolution occurs with similar pH dependence as observed for feldspars with the lowest rates at near-neutral conditions (Oelkers et al., 2008; Bray et al., 2015; Lammers et al., 2017). Dissolution may occur via etch pits on the basal surface, but the dominating process seems to be corrosion of the edge surfaces (Oelkers et al., 2008; Pachana et al., 2012).
The Si dissolution rate of muscovite is about 10−13 to 10−12 moles m−2 s−1 at neutral conditions (Brady and Walther, 1989; Lammers et al., 2017), which is sufficient to lead to surface alterations within the timescale of our experiments. The initial dissolution of Al is higher than the one of Si (Pachana et al., 2012), confirming that edges dissolve more readily than the basal faces. The basal plane of muscovite carries negative charge independent of pH while the edges carry a negative charge at high pH and a positive charge at low pH with a PZC at pH 7–8. The dissolution rate of biotite is 10−12 to 10−11 moles m−2 s−1 at neutral conditions. The initial dissolution at pH 6 was observed to be congruent with respect to Si and Al, but Mg and Fe positioned in the octahedral layer dissolved at a higher rate, resulting in a metal-depleted disordered octahedral layer (Pachana et al., 2012; Bray et al., 2015).
The absence of a heterogeneous freezing signal in emulsion freezing experiments suggests a low density of IN active sites. Thus, the IN activity seems to stem from very special features that are rare, while the regular mica surfaces are inactive despite the hydrophilicity of the basal surfaces and the dense hydroxylation of the edges, both characteristics of IN active surfaces. Indeed, sum-frequency-generation (SFG) spectra showed that water adsorbed at full monolayer coverage (90 % RH) forms an ice-like film on the basal muscovite surface (Miranda et al., 1998). Yet, this film does not seem to grow readily into bulk ice. The surface electric field of the negatively charged muscovite surface orders water molecules with the protons pointing towards the surface. SFG spectra show that this ordering decreases when the water freezes and increases again when the ice melts, suggesting that the ordered water layer adsorbed on the basal mica surface is unable to match ice (Anim-Danso et al., 2016). This finding is in line with Abdelmonem et al. (2017) who found that IN was not promoted by the presence of an ordered water layer on the hydroxylated sapphire (α-Al2O3) surface. On the contrary, IN was observed to occur at slightly warmer temperature close to the PZC when the water molecules were disordered. While at low and high pH, the aligning of the water molecules on the positively or negatively charged surface, respectively, was detrimental to IN.
While the absence of IN activity at the edges of biotite may be ascribed to the fast disintegration of this surface in the presence of water, it is not clear whether surface alteration at the edges of muscovite are sufficient to explain their lack of IN activity in pure water. In the presence of NH3 and (NH4)2SO4 solutions, both investigated micas show IN activity in the emulsion freezing experiments. This might be due to adsorption of on the basal planes increasing the number of sites available for hydrogen bonding or due to adsorption at the edges that may influence the dissolution rate.
Table 3IN activities in terms of Thet and Fhet together with surface properties of minerals investigated in this study at near-neutral conditions (representative for pure water), microcline from Kumar et al. (2018a) and quartz from Kumar et al. (2019).
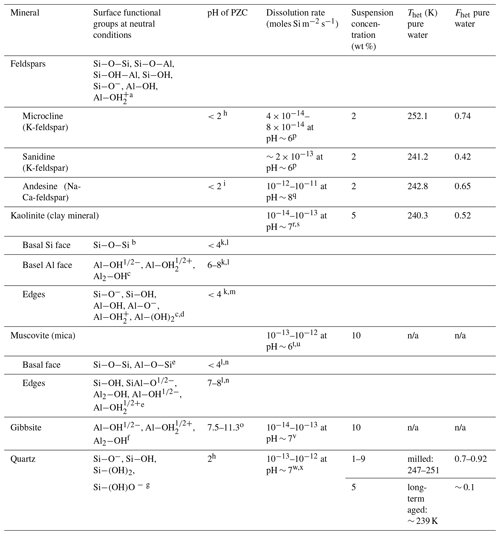
a: Teng et al., (2001); b: Schoonheydt and Johnston, (2006); c: Brady et al. (1996); d: Liu et al. (2013); e: Yan et al. (2011); f: Hiemstra et al. (1999); g: Liu et al. (2014); h: Vidyadhar and Hanumantha Rao (2007); i: Karagüzel et al. (2005); k: Gupta and Miller (2010); l: Kumar et al. (2017); m: Liu et al. (2014); n: Zhao et al. (2008); o: Kosmulski (2009); p: Crundwell (2015); q: Gudbrandsson et al. (2014); r: Carroll and Walther (1990); s: Huertas et al. (1999); t: Brady and Walther (1989); u: Lammers et al. (2017); v: Dietzel and Böhme (2005); w: Brady and Walther (1990); x: Berger et al. (1994); n/a: no Thet and Fhet can be reported due to the absence of a discernible heterogeneous freezing signal in the emulsion freezing experiments
4.1 Influence of surface properties
Table 3 summarizes the IN activity of the minerals investigated in this study together with results of microcline from Part 1 (Kumar et al., 2018a) and quartz results from Part 2 (Kumar et al., 2019) and relates them to selected surface properties of the investigated minerals, namely the prevalent surface groups, the dissolution rates at near-neutral conditions and the PZC.
Although all investigated minerals possess hydroxylated surfaces, which are generally thought to promote IN (Hu and Michaelides, 2007; Sosso et al., 2016a; Glatz and Sarupria, 2018) (see Table 3), not all of them proved to be IN active in our emulsion freezing experiments. Namely, the gibbsite and mica (muscovite and biotite) samples did not show any heterogeneous freezing signal in pure water. Zeta potential measurements of these minerals show that the hydroxylated edges of muscovite and the surface of gibbsite carry a positive charge at neutral conditions due to protonation of aluminol groups (see Table 3). This is in contrast to the surfaces of quartz, feldspars and the hydroxylated edges of kaolinite, which all carry negative charge at neutral conditions due to partial deprotonation of the silanol groups. Thus, positively charged (due to protonation) hydroxylated surfaces seem to have a tendency to be IN inactive, while negatively charged surfaces tend to be IN active. However, long-term aged quartz surfaces (7 months; see Kumar et al., 2019) show hardly any IN activity while milled quartz surfaces are highly IN active, although the quartz surface is in both cases negatively charged and highly hydroxylated (Turci et al., 2016). On the other hand, AgI (Edwards and Evans, 1962; Marcolli et al., 2016) and sapphire (Abdelmonem et al., 2017) show the highest IN activity close to the point of zero charge. Conversely, pyroelectric LiTaO3 and SrTiO3 promote IN when their surfaces are positively charged (Ehre et al., 2010). This shows that the OH surface density together with the surface charge are not sufficient to predict IN activity.
4.2 Dissolution and growth in pure water
The surfaces of the investigated feldspars exhibit similar chemical compositions although with different Si : Al ratios and Si ∕ Al ordering, which both influence the aluminum depletion and the dissolution rate. The initial dissolution of most feldspars is incongruent with preferential dissolution of aluminum, resulting in a Si-rich amorphous layer. We hypothesize that the surface remains well-ordered over a longer period of time for microcline due to its lowest dissolution rate (compared to the other investigated feldspars). Indeed, our emulsion freezing experiments on a microcline suspension (2 wt %) in pure water, which was aged for 6 months, showed no significant change in IN efficiency compared with a freshly prepared sample (aged sample: Thet=251.4 K, Fhet=0.71, see Fig. S15 in the Supplement; fresh sample: Thet=252.1 K, Fhet=0.74; Kumar et al., 2018a). Peckhaus et al. (2016) observed a decrease in IN activity by 2 K for a K-feldspar over a time span of 5 months. This implies that the high initial IN activity of microcline degrades only slowly within days or months (Kumar et al., 2018a). Hydrogen bonding to the feldspar surface is a prerequisite to arrange water molecules in a suitable configuration for IN, but at the same time it is the first step to the disintegration of the feldspar surface. Feldspar dissolution occurs via protonation of Al–O–Si bridges followed by removal of Al3+ and protonation of the dangling bonds resulting in a silanol-rich surface. As the dissolution proceeds, the Al-depleted Si layer becomes thicker and more amorphous-like.
When the surface of milled quartz grows or dissolves, active sites are lost and the IN activity decreases (Kumar et al., 2019). Under growth conditions, i.e., when the dissolved Si concentration exceeds the saturation concentration with respect to quartz, a siliceous layer forms on the quartz surface within about a day, which hampers the IN activity of quartz. When this layer is washed away with pure water after several days of aging, the IN activity is restored. On timescales of months, quartz slowly grows within this layer resulting in an intact, grown quartz surface that is barely IN active. This suggests that the IN activity of silica mainly stems from activation through grinding and is absent in regular, grown quartz surfaces. We ascribe the absence of IN on the highly hydroxylated grown quartz surface to networks of interconnected hydrogen bonds that are too strong to be disrupted by water molecules. This implies that for a hydroxylated surface to be IN active the hydrogen bonds must be available for bonding to water molecules in order to direct them into an ice-like pattern.
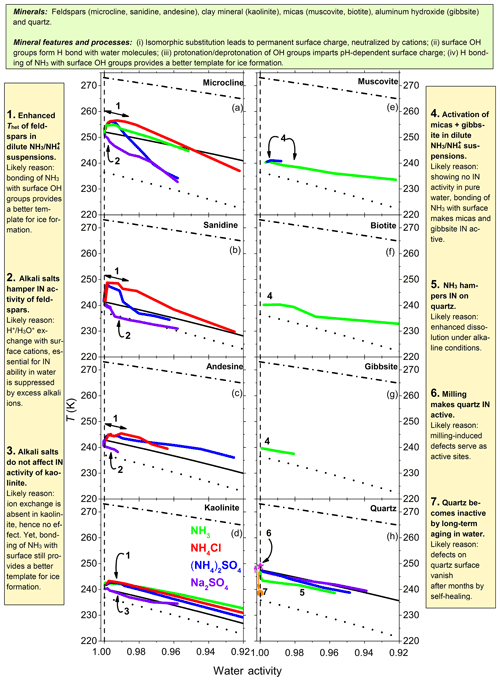
Figure 9Annotated summary: heterogeneous IN onset temperatures, Thet, of various mineral dusts (2 wt %–10 wt %) as a function of water activity in NH3, (NH4)2SO4, NH4Cl and Na2SO4 solutions (color coded) for aw equal to 1.0–0.92. (a) Results for microcline from Kumar et al. (2018a). (b–g) Feldspars, kaolinite, micas and gibbsite investigated in the present study. (h) Results for quartz from Kumar et al. (2019). Dash-dotted black lines: ice melting point curves. Dotted black lines: homogeneous ice freezing curves for supercooled aqueous solutions. Solid black lines: expected heterogeneous freezing curves if the presence of solutes did not change the mineral surface properties. Lines result by horizontally shifting from the ice melting curve by a constant emanating from the heterogeneous freezing temperatures of the suspensions of the minerals in pure water (at aw=1). Specifically, , , , and .
4.3 Influence of solutes
Figure 9 reviews the influence of solutes on the heterogeneous IN onset temperatures of the investigated aluminosilicates and quartz. The presence of in the suspensions increases Thet of all investigated feldspars and kaolinite (Fig. 9, point 1). Moreover, it provides IN activity to the investigated micas and gibbsite, which showed no IN activity in our emulsion freezing experiments performed in pure water (Fig. 9, point 4). The increase in Thet of kaolinite with no exchangeable cations confirms the findings from Kumar et al. (2018a) that the enhanced IN activity in the presence of is not due to ion exchange of with the native cations but stems from the adsorption of on the mineral surface. Water molecules can form hydrogen bonds with NH groups of adsorbed that may promote their arrangement into an ice-like pattern. Moreover, this adsorption can decrease the feldspar dissolution by stabilizing the surface. While also interact with silica surfaces, these interactions do not lead to an increase in Thet. Rather, a decrease is observed in the presence of NH3 due to the enhanced dissolution of quartz under alkaline conditions (Fig. 9, point 5).
The alkali salt Na2SO4 strongly decreases the IN activity of feldspars (Fig. 9, point 2) but does not influence that of kaolinite (Fig. 9, point 3). This indicates that alkali ions influence the IN activity of feldspars through ion exchange, which does not take place in kaolinite. Dissolved Na+ may take the positions of the protons on the surface and thus impede IN. This shows that the replacement of the charge balancing cations with protons taking place in pure water is crucial for the IN activity of feldspars.
4.4 Influence of milling
Milling increases the IN activity of quartz (Fig. 9, point 6), while the growth of an intact quartz layer on top of the milled quartz surface strongly hampers it (Fig. 9, point 7). Milling leads to an increase in surface irregularities and defects, which may lead to changes in the abundance and distribution of surface functional groups. These changes, in general, enhance IN efficiency but the enhancement depends on the type of mineral surface. Zolles et al. (2015) showed that additional milling of K-feldspar leads to only a slight increase in its high IN efficiency. Kaufmann et al. (2016) performed emulsion freezing experiments with a dust sample that was ground-collected in Antarctica (48 % feldspars, 24 % quartz) and observed an increase of the already high IN activity of the sieved sample when it was additionally milled. We ascribe the high IN activity of the sieved sample to the presence of the feldspars, whereas an additional increase after milling is most likely due to activation of the quartz component. Together with the finding that K-feldspars aged in pure water over months (see Sect. 4.2) kept their IN activity, we conclude that mechanical activation, e.g., due to milling, is not a prerequisite for the IN activity of feldspars. This is in contrast to our findings for quartz surfaces presented here (Fig. 9) and in Kumar et al. (2019). Boose et al. (2016) found a slightly higher active site density of the milled fraction of their Atacama dust sample (65 % feldspars, 10 % quartz) compared with the sieved fraction (51 % feldspars, 16 % quartz). On the other hand, they observed a decreased IN activity of their Israel dust sample after milling (80 % calcite, 6 % quartz) compared with the sieved fraction (67 % calcite, 7 % quartz). A natural quartz sample from Zolles et al. (2015) showed a very strong enhancement in IN efficiency due to milling. Moreover, milled samples from Boose et al. (2016) collected in Australia and Morocco, which primarily consisted of quartz, showed a very high IN activity, corroborating our results on quartz and amorphous silica in the companion paper (Kumar et al., 2019). Therefore, it seems likely that milling is a prerequisite for the IN activity of quartz. A natural process, closest to milling, would be dry erosion, yet it is unclear whether the forces exerted by fracturing during erosion are sufficient to generate similar defects as milling.
Immersion freezing experiments with aluminosilicates, namely feldspars, kaolinite, micas and gibbsite presented in this study and in Kumar et al. (2019) have shown that modifications of the mineral surfaces in the presence of water and solutes influence their IN activity.
The interaction of water with mineral surfaces is complex and manifold. It depends not only on the type of mineral but also on the exposure time of the surfaces to water and solutes. Factors influencing the IN ability of aluminosilicate surfaces are adsorption and ion exchange with solute molecules influencing the density of OH and NH groups that provide sites for hydrogen bonding with water molecules, permanent and pH-dependent surface charge influencing the orientation of water molecules and surface changes generated by the slow dissolution of the minerals. Therefore, for an improved understanding of IN, the specific surface properties of each mineral and the processes modifying the mineral surfaces in water and aqueous solutions need to be investigated by experimental surface techniques. In addition, molecular dynamics simulations of IN may contribute to clarifying these processes, but only if interactions of the mineral surface with water, e.g., surface ion exchange, protonation or deprotonation of the surface and slow dissolution, are taken into account.
Aluminosilicates constitute the majority of airborne mineral dust. Dust particles can be exposed to reactive gases like NH3 or SO2 during long-range transport, resulting in a coating and surface modification (Sullivan et al., 2007; Kolb et al., 2010; Fitzgerald et al., 2015). The modifications introduced by chemical coatings depend on the particle mineralogy, transport pathway and exposure duration (Matsuki et al., 2005; Sullivan et al., 2007; Rodríguez et al., 2011). Our results suggest that the IN activity of dust aerosols not only depend on their composition but also on their chemical exposure history. In Part 1 (Kumar et al., 2018a) we discussed in detail the fate of microcline in atmospheric solution droplets (especially (NH4)2SO4 and H2SO4) following various atmospheric air parcel trajectories with increasing moisture. This discussion is applicable to the aluminosilicates shown in this study and can hence be extended. A coating of aqueous (NH4)2SO4 solution may enhance the IN efficiency in condensation mode of aluminosilicates in general, but only when sulfuric acid and ammonia are deposited concomitantly. Aluminosilicates, especially feldspars, are sensitive to highly acidic conditions due to enhanced dissolution. This might hamper their relevance in the case of long-range transport when they are exposed to acidic air masses (e.g., acquiring sulfuric acid coatings prior to neutralization by ammonia). Moreover, in Part 2 (Kumar et al., 2019) we have shown that the relevance of quartz particles as atmospheric INPs is uncertain. To assess the IN activity of naturally eroded quartz, IN experiments need to be carried out with quartz-rich natural dust samples that are just sieved and not milled.
The data for freshly prepared sanidine, andesine and kaolinite suspensions in water or aqueous solutions (Figs. 2–3) and aging tests on kaolinite (Fig. 6) presented in this publication are available at the following repository: https://doi.org/10.3929/ethz-b-000260067 (Kumar et al., 2018b).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-6059-2019-supplement.
AK and CM planned the experiments. AK conducted the experiments and prepared the initial paper draft. AK, CM, and TP contributed to the interpretation of the results and the discussion.
This work was supported by the Swiss National Foundation, project number 200020_156251. We thank the following colleagues from ETH Zürich: Annette Röthlisberger and Marion Rothaupt for help in carrying out BET and XRD measurements and Michael Plötze for carrying out detailed XRD analysis; Fabian Mahrt for providing the SMPS and the APS for size distribution measurements; Peter Brack for providing various minerals. We would also like to thank Alexei Kiselev from the Institute of Meteorology and Climate Research (Karlsruhe Institute of Technology) for providing valuable feedback on this paper.
This paper was edited by Ryan Sullivan and reviewed by two anonymous referees.
Abdelmonem, A., Backus, E. H. G., Hoffmann, N., Sánchez, M. A., Cyran, J. D., Kiselev, A., and Bonn, M.: Surface-charge-induced orientation of interfacial water suppresses heterogeneous ice nucleation on a-alumina (0001), Atmos. Chem. Phys., 17, 7827–7837, https://doi.org/10.5194/acp-17-7827-2017, 2017.
Abendroth, R. P.: Behavior of a pyrogenic silica in simple electrolytes, J. Colloid Interface Sci., 34, 591–596, https://doi.org/10.1016/0021-9797(70)90223-7, 1970.
Anim-Danso, E., Zhang, Y., and Dhinojwala, A.: Surface charge affects the structure of interfacial ice, J. Phys. Chem. C, 120, 3741–3748, https://doi.org/10.1021/acs.jpcc.5b08371, 2016.
Ansmann, A., Tesche, M., Seifert, P., Althausen, D., Engelmann, R., Fruntke, J., Wandinger, U., Mattis, I., and Müller, D.: Evolution of the ice phase in tropical altocumulus: SAMUM lidar observations over cape verde, J. Geophys. Res.-Atmos., 114, D17208, https://doi.org/10.1029/2008JD011659, 2009.
Archuleta, C. M., DeMott, P. J., and Kreidenweis, S. M.: Ice nucleation by surrogates for atmospheric mineral dust and mineral dust/sulfate particles at cirrus temperatures, Atmos. Chem. Phys., 5, 2617–2634, https://doi.org/10.5194/acp-5-2617-2005, 2005.
Atkinson, J. D., Murray, B. J., Woodhouse, M. T., Whale, T. F., Baustian, K. J., Carslaw, K. S., Dobbie, S., O'Sullivan, D., and Malkin, T. L.: The importance of feldspar for ice nucleation by mineral dust in mixed-phase clouds, Nature, 498, 355–358, https://doi.org/10.1038/nature12278, 2013.
Auerbach, S. M., Carrado, K. A., and Dutta, P. K.: Handbook of zeolite science and technology, CRC Press, 2003.
Augustin-Bauditz, S., Wex, H., Kanter, S., Ebert, M., Niedermeier, D., Stolz, F., Prager, A., and Stratmann, F.: The immersion mode ice nucleation behavior of mineral dusts: A comparison of different pure and surface modified dusts, Geophys. Res. Lett., 41, 7375–7382, https://doi.org/10.1002/2014GL061317, 2014.
Augustin-Bauditz, S., Wex, H., Denjean, C., Hartmann, S., Schneider, J., Schmidt, S., Ebert, M., and Stratmann, F.: Laboratory-generated mixtures of mineral dust particles with biological substances: characterization of the particle mixing state and immersion freezing behavior, Atmos. Chem. Phys., 16, 5531–5543, https://doi.org/10.5194/acp-16-5531-2016, 2016.
Banfield, J. F. and Eggleton, R. A.: Analytical transmission electron microscope studies of plagioclase, muscovite, and K-feldspar weathering, Clays Clay Miner., 38, 77–89, https://doi.org/10.1346/CCMN.1990.0380111 1990.
Barker, D. S.: Ammonium in alkali feldspars, Am. Mineral., 49, July–August, 1964.
Bear, F. E.: Chemistry of the soil, 2nd edn., Reinhold Publishing, New York, 1965.
Belchinskaya, L., Novikova, L., Khokhlov, V., and Ly Tkhi, J.: Contribution of ion-exchange and non-ion-exchange reactions to sorption of ammonium ions by natural and activated aluminosilicate sorbent, J. Appl. Chem., 2013, 789410, https://doi.org/10.1155/2013/789410, 2013.
Berger, G., Cadore, E., Schott, J., and Dove, P. M.: Dissolution rate of quartz in lead and sodium electrolyte solutions between 25 and 300 ∘C: Effect of the nature of surface complexes and reaction affinity, Geochim. Cosmochim. Acta, 58, 541–551, https://doi.org/10.1016/0016-7037(94)90487-1, 1994.
Bibi, I., Icenhower, J., Niazi, N. K., Naz, T., Shahid, M., and Bashir, S.: Clay minerals: Structure, chemistry, and significance in contaminated environments and geological CO2 sequestration, chap. 21, in: Environmental materials and waste, edited by: Prasad, M. N. V. and Shih, K., Academic Press, 543–567, 2016.
Bleam, W. F., Welhouse, G. J., and Janowiak, M. A.: The surface coulomb energy and proton coulomb potentials of pyrophyllite {010}, {110}, {100}, and {130} edges, Clays Clay Miner., 41, 305–316, https://doi.org/10.1346/CCMN.1993.0410305, 1993.
Bolland, M. D. A., Posner, A. M., and Quirk, J. P.: pH-independent and pH-dependent surface charges on kaolinite, Clays Clay Miner., 28, 412–418, 1980.
Boose, Y., Welti, A., Atkinson, J., Ramelli, F., Danielczok, A., Bingemer, H. G., Plötze, M., Sierau, B., Kanji, Z. A., and Lohmann, U.: Heterogeneous ice nucleation on dust particles sourced from nine deserts worldwide – Part 1: Immersion freezing, Atmos. Chem. Phys., 16, 15075–15095, https://doi.org/10.5194/acp-16-15075-2016, 2016.
Bower, W. R., Pearce, C. I., Smith, A. D., Pimblott, S. M., Mosselmans, J. F. W., Haigh, S. J., McKinley, J. P., and Pattrick, R. A. D.: Radiation damage in biotite mica by accelerated α-particles: A synchrotron microfocus X-ray diffraction and X-ray absorption spectroscopy study, Am. Mineral., 101, 928–942, https://doi.org/10.2138/am-2016-5280CCBYNCND, 2016.
Brady, P. V. and Walther, J. V.: Controls on silicate dissolution rates in neutral and basic pH solutions at 25 ∘C, Geochim. Cosmochim. Ac., 53, 2823–2830, https://doi.org/10.1016/0016-7037(89)90160-9, 1989.
Brady, P. V. and Walther, J. V.: Kinetics of quartz dissolution at low temperatures, Chem. Geol., 82, 253–264, https://doi.org/10.1016/0009-2541(90)90084-K, 1990.
Brady, P. V., Cygan, R. T., and Nagy, K. L.: Molecular controls on kaolinite surface charge, J. Colloid Interface Sci., 183, 356–364, https://doi.org/10.1006/jcis.1996.0557, 1996.
Braggs, B., Fornasiero, D., Ralston, J., and St. Smart, R.: The effect of surface modification by an organosilane on the electrochemical properties of kaolinite, Clays Clay Miner., 42, 123–136, https://doi.org/10.1346/CCMN.1994.0420203, 1994.
Bray, A. W., Oelkers, E. H., Bonneville, S., Wolff-Boenisch, D., Potts, N. J., Fones, G., and Benning, L. G.: The effect of pH, grain size, and organic ligands on biotite weathering rates, Geochim. Cosmochim. Ac., 164, 127–145, https://doi.org/10.1016/j.gca.2015.04.048, 2015.
Brown, W. L. and Parsons, I.: Alkali feldspars: Ordering rates, phase transformations and behaviour diagrams for igneous rocks, Mineral. Mag., 53, 25–42, https://doi.org/10.1180/minmag.1989.053.369.03, 1989.
Bryant, G. W., Hallett, J., and Mason, B. J.: The epitaxial growth of ice on single-crystalline substrates, J. Phys. Chem. Solids, 12, 189-IN118, https://doi.org/10.1016/0022-3697(60)90036-6, 1959.
Burkert-Kohn, M., Wex, H., Welti, A., Hartmann, S., Grawe, S., Hellner, L., Herenz, P., Atkinson, J. D., Stratmann, F., and Kanji, Z. A.: Leipzig Ice Nucleation chamber Comparison (LINC): intercomparison of four online ice nucleation counters, Atmos. Chem. Phys., 17, 11683–11705, https://doi.org/10.5194/acp-17-11683-2017, 2017.
Busenberg, E. and Clemency, C. V.: The dissolution kinetics of feldspars at 25 ∘C and 1 atm CO2 partial pressure, Geochim. Cosmochim. Ac., 40, 41–49, https://doi.org/10.1016/0016-7037(76)90192-7, 1976.
Campbell, J. M., Meldrum, F. C., and Christenson, H. K.: Is ice nucleation from supercooled water insensitive to surface roughness?, J. Phys. Chem. C, 119, 1164–1169, https://doi.org/10.1021/jp5113729, 2015.
Carroll, S. A. and Walther, J. V.: Kaolinite dissolution at 25 degrees, 60 degrees, and 80 degrees C, Am. J. Sci., 290, 797–810, https://doi.org/10.2475/ajs.290.7.797, 1990.
Cashen, G. H.: Electric charges of kaolin, Trans. Faraday Soc., 55, 477–486, https://doi.org/10.1039/TF9595500477, 1959.
Chardon, E. S., Livens, F. R., and Vaughan, D. J.: Reactions of feldspar surfaces with aqueous solutions, Earth-Sci. Rev., 78, 1–26, https://doi.org/10.1016/j.earscirev.2006.03.002, 2006.
Cho, Y. and Komarneni, S.: Cation exchange equilibria of cesium and strontium with K-depleted biotite and muscovite, Appl. Clay Sci., 44, 15–20, https://doi.org/10.1016/j.clay.2008.12.015, 2009.
Christenson, H. K. and Thomson, N. H.: The nature of the air-cleaved mica surface, Surf. Sci. Rep., 71, 367–390, https://doi.org/10.1016/j.surfrep.2016.03.001, 2016.
Cox, S. J., Raza, Z., Kathmann, S. M., Slater, B., and Michaelides, A.: The microscopic features of heterogeneous ice nucleation may affect the macroscopic morphology of atmospheric ice crystals, Faraday Discuss., 167, 389–403, https://doi.org/10.1039/C3FD00059A, 2013.
Croteau, T., Bertram, A. K., and Patey, G. N.: Adsorption and structure of water on kaolinite surfaces: Possible insight into ice nucleation from Grand Canonical Monte Carlo calculations, J. Phys. Chem. A, 112, 10708–10712, https://doi.org/10.1021/jp805615q, 2008.
Croteau, T., Bertram, A. K., and Patey, G. N.: Simulation of water adsorption on kaolinite under atmospheric conditions, J. Phys. Chem. A, 113, 7826–7833, https://doi.org/10.1021/jp902453f, 2009.
Croteau, T., Bertram, A. K., and Patey, G. N.: Water adsorption on kaolinite surfaces containing trenches, J. Phys. Chem. A, 114, 2171–2178, https://doi.org/10.1021/jp910045u, 2010a.
Croteau, T., Bertram, A. K., and Patey, G. N.: Observations of high-density ferroelectric ordered water in kaolinite trenches using Monte Carlo simulations, J. Phys. Chem. A, 114, 8396–8405, https://doi.org/10.1021/jp104643p, 2010b.
Crundwell, F. K.: The mechanism of dissolution of the feldspars: Part I. Dissolution at conditions far from equilibrium, Hydrometallurgy, 151, 151–162, https://doi.org/10.1016/j.hydromet.2014.10.006, 2015.
Cziczo, D. J., Froyd, K. D., Hoose, C., Jensen, E. J., Diao, M., Zondlo, M. A., Smith, J. B., Twohy, C. H., and Murphy, D. M.: Clarifying the dominant sources and mechanisms of cirrus cloud formation, Science, 340, 1320–1324, 2013.
de Boer, G., Morrison, H., Shupe, M. D., and Hildner, R.: Evidence of liquid dependent ice nucleation in high-latitude stratiform clouds from surface remote sensors, Geophys. Res. Lett., 38, L01803, https://doi.org/10.1029/2010GL046016, 2011.
de Poel, W., Vaessen, S. L., Drnec, J., Engwerda, A. H. J., Townsend, E. R., Pintea, S., de Jong, A. E. F., Jankowski, M., Carlà, F., Felici, R., Elemans, J. A. A. W., van Enckevort, W. J. P., Rowan, A. E., and Vlieg, E.: Metal ion-exchange on the muscovite mica surface, Surf. Sci., 665, 56–61, https://doi.org/10.1016/j.susc.2017.08.013, 2017.
Dietzel, M. and Böhme, G.: The dissolution rates of gibbsite in the presence of chloride, nitrate, silica, sulfate, and citrate in open and closed systems at 20 ∘C, Geochim. Cosmochim. Ac., 69, 1199–1211, https://doi.org/10.1016/j.gca.2004.08.027, 2005.
Döbelin, N. and Kleeberg, R.: Profex: A graphical user interface for the rietveld refinement program BGMN, J. Appl. Crystallogr., 48, 1573–1580, https://doi.org/10.1107/S1600576715014685, 2015.
Eastwood, M. L., Cremel, S., Wheeler, M., Murray, B. J., Girard, E., and Bertram, A. K.: Effects of sulfuric acid and ammonium sulfate coatings on the ice nucleation properties of kaolinite particles, Geophys. Res. Lett., 36, L02811, https://doi.org/10.1029/2008GL035997, 2009.
Edwards, G. R. and Evans, L. F.: Effect of surface charge on ice nucleation by silver iodide, Trans. Faraday Soc., 58, 1649–1655, https://doi.org/10.1039/TF9625801649, 1962.
Ehre, D., Lavert, E., Lahav, M., and Lubomirsky, I.: Water freezes differently on positively and negatively charged surfaces of pyroelectric materials, Science, 327, 672–675, https://doi.org/10.1126/science.1178085, 2010.
Fitzgerald, E., Ault, A. P., Zauscher, M. D., Mayol-Bracero, O. L., and Prather, K. A.: Comparison of the mixing state of long-range transported Asian and African mineral dust, Atmos. Environ., 115, 19–25, 2015.
Fitzgerald, J. J., Hamza, A. I., Bronnimann, C. E., and Dec, S. F.: Studies of the solid/solution “interfacial” dealumination of kaolinite in HCl(aq) using solid-state 1h CRAMPS and SP/MAS 29si NMR spectroscopy, J. Am. Chem. Soc., 119, 7105–7113, https://doi.org/10.1021/ja970305m, 1997.
Fleet, M. E., Deer, W. A., Howie, R. A., and Zussman, J.: Rock-forming minerals: Micas, Geological Society, London, 2003.
Fletcher, N. H.: Active sites and ice crystal nucleation, J. Atmos. Sci., 26, 1266–1271, https://doi.org/10.1175/1520-0469(1969)026<1266:asaicn>2.0.co;2, 1969.
Freedman, M. A.: Potential sites for ice nucleation on aluminosilicate clay minerals and related materials, J. Phys. Chem. Lett., 6, 3850–3858, https://doi.org/10.1021/acs.jpclett.5b01326, 2015.
Giese, R. F. and van Oss, C. J.: The surface thermodynamic properties of silicates and their interactions with biological materials, in: Health effects of mineral dust, edited by: George, D. G. and Brooke, T. M., Reviews in Mineralogy, Mineralogical Society of America, Washington, DC, 327–346, 1993.
Glatz, B. and Sarupria, S.: Heterogeneous ice nucleation: Interplay of surface properties and their impact on water orientations, Langmuir, 34, 1190–1198, https://doi.org/10.1021/acs.langmuir.7b02859, 2018.
Greenwood, N. N. and Earnshaw, A.: Silicon, chap. 9, in: Chemistry of elements, 2nd edn., Elsevier, UK, 357 pp., 1998.
Grim, R. E.: Clay mineralogy, 2nd edn., McGraw-Hill, New York, NY, 1968.
Gudbrandsson, S., Wolff-Boenisch, D., Gislason, S. R., and Oelkers, E. H.: Experimental determination of plagioclase dissolution rates as a function of its composition and pH at 22 ∘C, Geochim. Cosmochim. Ac., 139, 154–172, https://doi.org/10.1016/j.gca.2014.04.028, 2014.
Gupta, V. and Miller, J. D.: Surface force measurements at the basal planes of ordered kaolinite particles, J. Colloid Interface Sci., 344, 362–371, https://doi.org/10.1016/j.jcis.2010.01.012, 2010.
Hallett, J.: The growth of ice crystals on freshly cleaved covellite surfaces, The Philosophical Magazine: A Journal of Theoretical Experimental and Applied Physics, 6, 1073–1087, https://doi.org/10.1080/14786436108239669, 1961.
Harrison, A. D., Whale, T. F., Carpenter, M. A., Holden, M. A., Neve, L., O'Sullivan, D., Vergara Temprado, J., and Murray, B. J.: Not all feldspars are equal: a survey of ice nucleating properties across the feldspar group of minerals, Atmos. Chem. Phys., 16, 10927–10940, https://doi.org/10.5194/acp-16-10927-2016, 2016.
Hiemstra, T., Yong, H., and Van Riemsdijk, W. H.: Interfacial charging phenomena of aluminum (hydr)oxides, Langmuir, 15, 5942–5955, https://doi.org/10.1021/la981301d, 1999.
Hofmeister, A. M. and Rossman, G. R.: The chemistry, structure and nomenclature of feldspars, in: Feldspar mineralogy, edited by: Ribbe, P. H., Mineralogical Society of America, Washington, DC, 1983.
Hoose, C., Lohmann, U., Erdin, R., and Tegen, I.: The global influence of dust mineralogical composition on heterogeneous ice nucleation in mixed-phase clouds, Environ. Res. Lett., 3, 025003, https://doi.org/10.1088/1748-9326/3/2/025003, 2008.
Hoose, C., Kristjánsson, J. E., Chen, J.-P., and Hazra, A.: A classical-theory-based parameterization of heterogeneous ice nucleation by mineral dust, soot, and biological particles in a global climate model, J. Atmos. Sci., 67, 2483–2503, https://doi.org/10.1175/2010jas3425.1, 2010.
Hoose, C. and Möhler, O.: Heterogeneous ice nucleation on atmospheric aerosols: a review of results from laboratory experiments, Atmos. Chem. Phys., 12, 9817–9854, https://doi.org/10.5194/acp-12-9817-2012, 2012.
Hu, X. L. and Michaelides, A.: Ice formation on kaolinite: Lattice match or amphoterism?, Surf. Sci., 601, 5378–5381, 2007.
Huertas, F. J., Chou, L., and Wollast, R.: Mechanism of kaolinite dissolution at room temperature and pressure part II: Kinetic study, Geochim. Cosmochim. Ac., 63, 3261–3275, https://doi.org/10.1016/S0016-7037(99)00249-5, 1999.
IPCC: Climate change 2013: The physical science basis, Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change, Cambridge University Press, Cambridge, UK, New York, NY, USA, 1535 pp., 2013.
James, D. W. and Harward, M. E.: Mechanism of NH3 adsorption by montmorillonite and kaolinite, Clays Clay Miner., 11, 301–320, https://doi.org/10.1346/CCMN.1962.0110131, 1962.
Jepson, W. B.: Kaolins: Their properties and uses, Philos. T. R. Soc. A, 311, 411–432, https://doi.org/10.1098/rsta.1984.0037, 1984.
Johari, G. P., Fleissner, G., Hallbrucker, A., and Mayer, E.: Thermodynamic continuity between glassy and normal water, J. Phys. Chem., 98, 4719–4725, https://doi.org/10.1021/j100068a038, 1994.
Kanji, Z. A., Ladino, L. A., Wex, H., Boose, Y., Burkert-Kohn, M., Cziczo, D. J., and Krämer, M.: Overview of ice nucleating particles, Meteor. Mon., 58, 1.1–1.33, https://doi.org/10.1175/amsmonographs-d-16-0006.1, 2017.
Kanji, Z. A., Sullivan, R. C., Niemand, M., DeMott, P. J., Prenni, A. J., Chou, C., Saathoff, H., and Möhler, O.: Heterogeneous ice nucleation properties of natural desert dust particles coated with a surrogate of secondary organic aerosol, Atmos. Chem. Phys., 19, 5091–5110, https://doi.org/10.5194/acp-19-5091-2019, 2019.
Karagüzel, C., Can, M. F., Sönmez, E., and Çelik, M. S.: Effect of electrolyte on surface free energy components of feldspar minerals using thin-layer wicking method, J. Colloid Interface Sci., 285, 192–200, https://doi.org/10.1016/j.jcis.2004.11.018, 2005.
Kaufmann, L., Marcolli, C., Hofer, J., Pinti, V., Hoyle, C. R., and Peter, T.: Ice nucleation efficiency of natural dust samples in the immersion mode, Atmos. Chem. Phys., 16, 11177–11206, https://doi.org/10.5194/acp-16-11177-2016, 2016.
Kaufmann, L., Marcolli, C., Luo, B., and Peter, T.: Refreeze experiments with water droplets containing different types of ice nuclei interpreted by classical nucleation theory, Atmos. Chem. Phys., 17, 3525–3552, https://doi.org/10.5194/acp-17-3525-2017, 2017.
Kiselev, A., Bachmann, F., Pedevilla, P., Cox, S. J., Michaelides, A., Gerthsen, D., and Leisner, T.: Active sites in heterogeneous ice nucleation – the example of K-rich feldspars, Science, 355, 367–371, https://doi.org/10.1126/science.aai8034, 2017.
Knopf, D. A., Alpert, P. A., Wang, B., and Aller, J. Y.: Stimulation of ice nucleation by marine diatoms, Nature Geosci., 4, 88–90, 2011.
Knopf, D. A. and Forrester, S. M.: Freezing of water and aqueous NaCl droplets coated by organic monolayers as a function of surfactant properties and water activity, J. Phys. Chem. A, 115, 5579–5591, https://doi.org/10.1021/jp2014644, 2011.
Knopf, D. A. and Alpert, P. A.: A water activity based model of heterogeneous ice nucleation kinetics for freezing of water and aqueous solution droplets, Faraday Discuss., 165, 513–534, https://doi.org/10.1039/C3FD00035D, 2013.
Kolb, C. E., Cox, R. A., Abbatt, J. P. D., Ammann, M., Davis, E. J., Donaldson, D. J., Garrett, B. C., George, C., Griffiths, P. T., Hanson, D. R., Kulmala, M., McFiggans, G., Pöschl, U., Riipinen, I., Rossi, M. J., Rudich, Y., Wagner, P. E., Winkler, P. M., Worsnop, D. R., and O' Dowd, C. D.: An overview of current issues in the uptake of atmospheric trace gases by aerosols and clouds, Atmos. Chem. Phys., 10, 10561–10605, https://doi.org/10.5194/acp-10-10561-2010, 2010.
Koop, T., Luo, B., Tsias, A., and Peter, T.: Water activity as the determinant for homogeneous ice nucleation in aqueous solutions, Nature, 406, 611–614, 2000.
Koop, T. and Zobrist, B.: Parameterizations for ice nucleation in biological and atmospheric systems, Phys. Chem. Chem. Phys., 11, 10839–10850, https://doi.org/10.1039/B914289D, 2009.
Korolev, A. and Field, P. R.: The effect of dynamics on mixed-phase clouds: Theoretical considerations, J. Atmos. Sci., 65, 66–86, https://doi.org/10.1175/2007jas2355.1, 2008.
Kosmulski, M.: Compilation of pzc and iep of sparingly soluble metal oxides and hydroxides from literature, Adv. Colloid Interface Sci., 152, 14–25, https://doi.org/10.1016/j.cis.2009.08.003, 2009.
Kulkarni, G., Sanders, C., Zhang, K., Liu, X., and Zhao, C.: Ice nucleation of bare and sulfuric acid-coated mineral dust particles and implication for cloud properties, J. Geophys. Res.-Atmos., 119, 9993–10011, https://doi.org/10.1002/2014JD021567, 2014.
Kumar, A., Marcolli, C., Luo, B., and Peter, T.: Ice nucleation activity of silicates and aluminosilicates in pure water and aqueous solutions – Part 1: The K-feldspar microcline, Atmos. Chem. Phys., 18, 7057–7079, https://doi.org/10.5194/acp-18-7057-2018, 2018a.
Kumar, A., Marcolli, C., Luo, B., and Peter, T.: Research Data supporting “Enhanced ice nucleation efficiency of K & Na/Ca feldspar, kaolinite and micas immersed in dilute NH3 and -containing solutions”, https://doi.org/10.3929/ethzb-000260067, 2018b.
Kumar, A., Marcolli, C., and Peter, T.: Ice nucleation activity of silicates and aluminosilicates in pure water and aqueous solutions – Part 2: Quartz and amorphous silica, Atmos. Chem. Phys., 19, 6035–6058, https://doi.org/10.5194/acp-19-6035-2019, 2019.
Kumar, N., Zhao, C., Klaassen, A., van den Ende, D., Mugele, F., and Siretanu, I.: Characterization of the surface charge distribution on kaolinite particles using high resolution atomic force microscopy, Geochim. Cosmochim. Ac., 175, 100–112, https://doi.org/10.1016/j.gca.2015.12.003, 2016.
Kumar, N., Andersson, M. P., van den Ende, D., Mugele, F., and Siretanu, I.: Probing the surface charge on the basal planes of kaolinite particles with high-resolution atomic force microscopy, Langmuir, 33, 14226–14237, https://doi.org/10.1021/acs.langmuir.7b03153, 2017.
Lammers, K., Smith, M. M., and Carroll, S. A.: Muscovite dissolution kinetics as a function of pH at elevated temperature, Chem. Geol., 466, 149–158, https://doi.org/10.1016/j.chemgeo.2017.06.003, 2017.
Layton, R. G. and Harris, F. S.: Nucleation of ice on mica, J. Atmos. Sci., 20, 142–148, https://doi.org/10.1175/1520-0469(1963)020<0142:NOIOM>2.0.CO;2, 1963.
Lee, M. R., Hodson, M. E., Brown, D. J., MacKenzie, M., and Smith, C. L.: The composition and crystallinity of the near-surface regions of weathered alkali feldspars, Geochim. Cosmochim. Ac., 72, 4962–4975, https://doi.org/10.1016/j.gca.2008.08.001, 2008.
Lee, S. S., Fenter, P., Nagy, K. L., and Sturchio, N. C.: Real-time observation of cation exchange kinetics and dynamics at the muscovite-water interface, Nat. Commun., 8, 15826, https://doi.org/10.1038/ncomms15826, 2017.
Liu, J., Sandaklie-Nikolova, L., Wang, X., and Miller, J. D.: Surface force measurements at kaolinite edge surfaces using atomic force microscopy, J. Colloid Interface Sci., 420, 35–40, https://doi.org/10.1016/j.jcis.2013.12.053, 2014.
Liu, J., Wang, X., Lin, C.-L., and Miller, J. D.: Significance of particle aggregation in the reverse flotation of kaolinite from bauxite ore, Miner. Eng., 78, 58–65, https://doi.org/10.1016/j.mineng.2015.04.009, 2015.
Liu, X., Lu, X., Sprik, M., Cheng, J., Meijer, E. J., and Wang, R.: Acidity of edge surface sites of montmorillonite and kaolinite, Geochim. Cosmochim. Ac., 117, 180–190, https://doi.org/10.1016/j.gca.2013.04.008, 2013.
Lohmann, U. and Diehl, K.: Sensitivity studies of the importance of dust ice nuclei for the indirect aerosol effect on stratiform mixed-phase clouds, J. Atmos. Sci., 63, 968–982, https://doi.org/10.1175/jas3662.1, 2006.
Lüönd, F., Stetzer, O., Welti, A., and Lohmann, U.: Experimental study on the ice nucleation ability of size-selected kaolinite particles in the immersion mode, J. Geophys. Res.-Atmos., 115, D14201, https://doi.org/10.1029/2009JD012959, 2010.
Marcolli, C., Gedamke, S., Peter, T., and Zobrist, B.: Efficiency of immersion mode ice nucleation on surrogates of mineral dust, Atmos. Chem. Phys., 7, 5081–5091, https://doi.org/10.5194/acp-7-5081-2007, 2007.
Marcolli, C.: Deposition nucleation viewed as homogeneous or immersion freezing in pores and cavities, Atmos. Chem. Phys., 14, 2071–2104, https://doi.org/10.5194/acp-14-2071-2014, 2014.
Marcolli, C., Nagare, B., Welti, A., and Lohmann, U.: Ice nucleation efficiency of AgI: review and new insights, Atmos. Chem. Phys., 16, 8915–8937, https://doi.org/10.5194/acp-16-8915-2016, 2016.
Marshall, C. E.: Reactions of feldspars and micas with aqueous solutions, Econ. Geol., 57, 1219–1227, https://doi.org/10.2113/gsecongeo.57.8.1219, 1962.
Matsuki, A., Iwasaka, Y., Shi, G. Y., Zhang, D. Z., Trochkine, D., Yamada, M., Kim, Y. S., Chen, B., Nagatani, T., and Miyazawa, T.: Morphological and chemical modification of mineral dust: Observational insight into the heterogeneous uptake of acidic gases, Geophys. Res. Lett., 32, L22806, https://doi.org/10.1029/2005GL024176, 2005.
Min, Y., Kubicki, J. D., and Jun, Y.-S.: Plagioclase dissolution during CO2–SO2 cosequestration: Effects of sulfate, Environ. Sci. Tech., 49, 1946–1954, https://doi.org/10.1021/es504586u, 2015.
Miranda, P. B., Xu, L., Shen, Y. R., and Salmeron, M.: Icelike water monolayer adsorbed on mica at room temperature, Phys. Rev. Lett., 81, 5876, https://doi.org/10.1103/PhysRevLett.81.5876, 1998.
Muir, I. J., Bancroft, G. M., Shotyk, W., and Wayne Nesbitt, H.: A SIMS and XPS study of dissolving plagioclase, Geochim. Cosmochim. Ac., 54, 2247–2256, https://doi.org/10.1016/0016-7037(90)90049-Q, 1990.
Murray, B. J., Broadley, S. L., Wilson, T. W., Atkinson, J. D., and Wills, R. H.: Heterogeneous freezing of water droplets containing kaolinite particles, Atmos. Chem. Phys., 11, 4191–4207, https://doi.org/10.5194/acp-11-4191-2011, 2011.
Murray, B. J., O'Sullivan, D., Atkinson, J. D., and Webb, M. E.: Ice nucleation by particles immersed in supercooled cloud droplets, Chem. Soc. Rev., 41, 6519–6554, https://doi.org/10.1039/C2CS35200A, 2012.
Murray, H. H.: Overview – clay mineral applications, Appl. Clay Sci., 5, 379–395, https://doi.org/10.1016/0169-1317(91)90014-Z, 1991.
Naderi Khorshidi, Z., Tan, X., Liu, Q., and Choi, P.: Molecular dynamics study of the dissolution mechanism of kaolinite basal surfaces in alkali media, Appl. Clay Sci., 152, 29–37, https://doi.org/10.1016/j.clay.2017.10.025, 2018.
Nash, V. E. and Marshall, C. E.: Cationic reactions of feldspar surfaces, Soil Sci. Soc. Am. J., 21, 149–153, https://doi.org/10.2136/sssaj1957.03615995002100020005x, 1957.
Negi, A. S. and Anand, S. C.: A textbook of physical chemistry, New Age International (P) Limited, India, 442–467, 1985.
Niedermeier, D., Hartmann, S., Clauss, T., Wex, H., Kiselev, A., Sullivan, R. C., DeMott, P. J., Petters, M. D., Reitz, P., Schneider, J., Mikhailov, E., Sierau, B., Stetzer, O., Reimann, B., Bundke, U., Shaw, R. A., Buchholz, A., Mentel, T. F., and Stratmann, F.: Experimental study of the role of physicochemical surface processing on the IN ability of mineral dust particles, Atmos. Chem. Phys., 11, 11131–11144, https://doi.org/10.5194/acp-11-11131-2011, 2011.
Niedermeier, D., Augustin-Bauditz, S., Hartmann, S., Wex, H., Ignatius, K., and Stratmann, F.: Can we define an asymptotic value for the ice active surface site density for heterogeneous ice nucleation?, J. Geophys. Res.-Atmos., 120, 5036–5046, https://doi.org/10.1002/2014JD022814, 2015.
Oelkers, E. H. and Schott, J.: Experimental study of anorthite dissolution and the relative mechanism of feldspar hydrolysis, Geochim. Cosmochim. Ac., 59, 5039–5053, https://doi.org/10.1016/0016-7037(95)00326-6, 1995.
Oelkers, E. H., Schott, J., Gauthier, J.-M., and Herrero-Roncal, T.: An experimental study of the dissolution mechanism and rates of muscovite, Geochim. Cosmochim. Ac., 72, 4948–4961, https://doi.org/10.1016/j.gca.2008.01.040, 2008.
Oelkers, E. H., Golubev, S. V., Chairat, C., Pokrovsky, O. S., and Schott, J.: The surface chemistry of multi-oxide silicates, Geochim. Cosmochim. Ac., 73, 4617–4634, https://doi.org/10.1016/j.gca.2009.05.028, 2009.
Oxburgh, R., Drever, J. I., and Sun, Y.-T.: Mechanism of plagioclase dissolution in acid solution at 25 ∘C, Geochim. Cosmochim. Ac., 58, 661–669, https://doi.org/10.1016/0016-7037(94)90496-0, 1994.
Pachana, K., Zuddas, P., and Censi, P.: Influence of pH and temperature on the early stage of mica alteration, Appl. Geochem., 27, 1738–1744, https://doi.org/10.1016/j.apgeochem.2012.02.009, 2012.
Peckhaus, A., Kiselev, A., Hiron, T., Ebert, M., and Leisner, T.: A comparative study of K-rich and Na/Ca-rich feldspar ice-nucleating particles in a nanoliter droplet freezing assay, Atmos. Chem. Phys., 16, 11477–11496, https://doi.org/10.5194/acp-16-11477-2016, 2016.
Pedevilla, P., Fitzner, M., and Michaelides, A.: What makes a good descriptor for heterogeneous ice nucleation on OH-patterned surfaces, Phys. Rev. B, 96, 115441, https://doi.org/10.1103/PhysRevB.96.115441, 2017.
Pinti, V., Marcolli, C., Zobrist, B., Hoyle, C. R., and Peter, T.: Ice nucleation efficiency of clay minerals in the immersion mode, Atmos. Chem. Phys., 12, 5859–5878, https://doi.org/10.5194/acp-12-5859-2012, 2012.
Pruppacher, H. R. and Klett, J. D.: Microphysics of clouds and precipitation, Kluwer Academic Publishers: Dordrecht, the Netherlands, 1994.
Reitz, P., Spindler, C., Mentel, T. F., Poulain, L., Wex, H., Mildenberger, K., Niedermeier, D., Hartmann, S., Clauss, T., Stratmann, F., Sullivan, R. C., DeMott, P. J., Petters, M. D., Sierau, B., and Schneider, J.: Surface modification of mineral dust particles by sulphuric acid processing: implications for ice nucleation abilities, Atmos. Chem. Phys., 11, 7839–7858, https://doi.org/10.5194/acp-11-7839-2011, 2011.
Rigg, Y. J., Alpert, P. A., and Knopf, D. A.: Immersion freezing of water and aqueous ammonium sulfate droplets initiated by humic-like substances as a function of water activity, Atmos. Chem. Phys., 13, 6603–6622, https://doi.org/10.5194/acp-13-6603-2013, 2013.
Rodríguez, S., Alastuey, A., Alonso-Pérez, S., Querol, X., Cuevas, E., Abreu-Afonso, J., Viana, M., Pérez, N., Pandolfi, M., and de la Rosa, J.: Transport of desert dust mixed with North African industrial pollutants in the subtropical Saharan Air Layer, Atmos. Chem. Phys., 11, 6663–6685, https://doi.org/10.5194/acp-11-6663-2011, 2011.
Rogers, R. R. and Yau, M. K.: A short course in cloud physics, Elsevier Science & Technology Books, 1989.
Salam, A., Lohmann, U., and Lesins, G.: Ice nucleation of ammonia gas exposed montmorillonite mineral dust particles, Atmos. Chem. Phys., 7, 3923-3931, https://doi.org/10.5194/acp-7-3923-2007, 2007.
Salam, A., Lesins, G., and Lohmann, U.: Laboratory study of heterogeneous ice nucleation in deposition mode of montmorillonite mineral dust particles aged with ammonia, sulfur dioxide, and ozone at polluted atmospheric concentrations, Air Qual. Atmos. Health, 1, 135–142, https://doi.org/10.1007/s11869-008-0019-6, 2008.
Sassen, K. and Benson, S.: A midlatitude cirrus cloud climatology from the facility for atmospheric remote sensing. Part II: Microphysical properties derived from lidar depolarization, J. Atmos. Sci., 58, 2103–2112, https://doi.org/10.1175/1520-0469(2001)058<2103:Amcccf>2.0.Co;2, 2001.
Schoonheydt, R. A. and Johnston, C. T.: Surface and interface chemistry of clay minerals, chapt. 3,in: Developments in clay science, edited by: Bergaya, F., Theng, B. K. G., and Lagaly, G., Elsevier, 87–113, 2006.
Schoonheydt, R. A. and Johnston, C. T.: Surface and interface chemistry of clay minerals, chap. 5, in: Developments in clay science, edited by: Bergaya, F. and Lagaly, G., Elsevier, 139–172, 2013.
Seifert, P., Ansmann, A., Mattis, I., Wandinger, U., Tesche, M., Engelmann, R., Müller, D., Pérez, C., and Haustein, K.: Saharan dust and heterogeneous ice formation: Eleven years of cloud observations at a central european earlinet site, J. Geophys. Res., 115, D20201, https://doi.org/10.1029/2009JD013222, 2010.
Shen, J. H., Klier, K., and Zettlemoyer, A. C.: Ice nucleation by micas, J. Atmos. Sci., 34, 957–960, https://doi.org/10.1175/1520-0469(1977)034<0957:INBM>2.0.CO;2, 1977.
Sihvonen, S. K., Schill, G. P., Lyktey, N. A., Veghte, D. P., Tolbert, M. A., and Freedman, M. A.: Chemical and physical transformations of aluminosilicate clay minerals due to acid treatment and consequences for heterogeneous ice nucleation, J. Phys. Chem. A, 118, 8787–8796, https://doi.org/10.1021/jp504846g, 2014.
Sosso, G. C., Li, T., Donadio, D., Tribello, G. A., and Michaelides, A.: Microscopic mechanism and kinetics of ice formation at complex interfaces: Zooming in on kaolinite, J. Phys. Chem. Lett., 7, 2350–2355, https://doi.org/10.1021/acs.jpclett.6b01013, 2016a.
Sosso, G. C., Tribello, G. A., Zen, A., Pedevilla, P., and Michaelides, A.: Ice formation on kaolinite: Insights from molecular dynamics simulations, J. Chem. Phys., 145, 211927, https://doi.org/10.1063/1.4968796, 2016b.
Speedy, R. J.: Thermodynamic properties of supercooled water at 1 atm, J. Phys. Chem., 91, 3354–3358, https://doi.org/10.1021/j100296a049, 1987.
Steinke, I.: Ice nucleation properties of mineral dusts, Doctor of Natural Sciences, Combined Faculties for the Natural Sciences and for Mathematics, Ruperto-Carola University of Heidelberg, Heidelberg, Germany, 2013.
Stillings, L. L. and Brantley, S. L.: Feldspar dissolution at 25 ∘C and pH 3: Reaction stoichiometry and the effect of cations, Geochim. Cosmochim. Ac., 59, 1483–1496, https://doi.org/10.1016/0016-7037(95)00057-7, 1995.
Sullivan, R. C., Guazzotti, S. A., Sodeman, D. A., and Prather, K. A.: Direct observations of the atmospheric processing of Asian mineral dust, Atmos. Chem. Phys., 7, 1213–1236, https://doi.org/10.5194/acp-7-1213-2007, 2007.
Sullivan, R. C., Miñambres, L., DeMott, P. J., Prenni, A. J., Carrico, C. M., Levin, E. J. T., and Kreidenweis, S. M.: Chemical processing does not always impair heterogeneous ice nucleation of mineral dust particles, Geophys. Res. Lett., 37, L24805, https://doi.org/10.1029/2010GL045540, 2010a.
Sullivan, R. C., Petters, M. D., DeMott, P. J., Kreidenweis, S. M., Wex, H., Niedermeier, D., Hartmann, S., Clauss, T., Stratmann, F., Reitz, P., Schneider, J., and Sierau, B.: Irreversible loss of ice nucleation active sites in mineral dust particles caused by sulphuric acid condensation, Atmos. Chem. Phys., 10, 11471–11487, https://doi.org/10.5194/acp-10-11471-2010, 2010b.
Sun, Z. and Shine, K. P.: Studies of the radiative properties of ice and mixed-phase clouds, Q. J. Roy. Meteor. Soc., 120, 111–137, https://doi.org/10.1002/qj.49712051508, 1994.
Teng, H. H., Fenter, P., Cheng, L., and Sturchio, N. C.: Resolving orthoclase dissolution processes with atomic force microscopy and X-ray reflectivity, Geochim. Cosmochim. Ac., 65, 3459–3474, https://doi.org/10.1016/S0016-7037(01)00665-2, 2001.
Turci, F., Pavan, C., Leinardi, R., Tomatis, M., Pastero, L., Garry, D., Anguissola, S., Lison, D., and Fubini, B.: Revisiting the paradigm of silica pathogenicity with synthetic quartz crystals: The role of crystallinity and surface disorder, Part. Fibre Toxicol., 13, 32 pp., https://doi.org/10.1186/s12989-016-0136-6, 2016.
Twohy, C. H., DeMott, P. J., Pratt, K. A., Subramanian, R., Kok, G. L., Murphy, S. M., Lersch, T., Heymsfield, A. J., Wang, Z., Prather, K. A., and Seinfeld, J. H.: Relationships of biomass-burning aerosols to ice in orographic wave clouds, J. Atmos. Sci., 67, 2437–2450, https://doi.org/10.1175/2010jas3310.1, 2010.
Usher, C. R., Michel, A. E., and Grassian, V. H.: Reactions on mineral dust, Chem. Rev., 103, 4883–4940, https://doi.org/10.1021/cr020657y, 2003.
Vali, G.: Interpretation of freezing nucleation experiments: singular and stochastic; sites and surfaces, Atmos. Chem. Phys., 14, 5271–5294, https://doi.org/10.5194/acp-14-5271-2014, 2014.
Vali, G., DeMott, P. J., Möhler, O., and Whale, T. F.: Technical Note: A proposal for ice nucleation terminology, Atmos. Chem. Phys., 15, 10263–10270, https://doi.org/10.5194/acp-15-10263-2015, 2015.
Vidyadhar, A. and Hanumantha Rao, K.: Adsorption mechanism of mixed cationic/anionic collectors in feldspar-quartz flotation system, J. Colloid Interface Sci., 306, 195–204, https://doi.org/10.1016/j.jcis.2006.10.047, 2007.
Wang, B., Knopf, D. A., China, S., Arey, B. W., Harder, T. H., Gilles, M. K., and Laskin, A.: Direct observation of ice nucleation events on individual atmospheric particles, Phys. Chem. Chem. Phys., 18, 29721–29731, https://doi.org/10.1039/C6CP05253C, 2016.
Welti, A., Lohmann, U., and Kanji, Z. A.: Ice nucleation properties of K-feldspar polymorphs and plagioclase feldspars, Atmos. Chem. Phys. Discuss., https://doi.org/10.5194/acp-2018-1271, in review, 2019.
Wex, H., DeMott, P. J., Tobo, Y., Hartmann, S., Rösch, M., Clauss, T., Tomsche, L., Niedermeier, D., and Stratmann, F.: Kaolinite particles as ice nuclei: learning from the use of different kaolinite samples and different coatings, Atmos. Chem. Phys., 14, 5529–5546, https://doi.org/10.5194/acp-14-5529-2014, 2014.
Whale, T. F., Holden, M. A., Kulak, A. N., Kim, Y.-Y., Meldrum, F. C., Christenson, H. K., and Murray, B. J.: The role of phase separation and related topography in the exceptional ice-nucleating ability of alkali feldspars, Phys. Chem. Chem. Phys., 19, 31186–31193, https://doi.org/10.1039/C7CP04898J, 2017.
Whale, T. F., Holden, M. A., Wilson, T. W., O'Sullivan, D., and Murray, B. J.: The enhancement and suppression of immersion mode heterogeneous ice-nucleation by solutes, Chem. Sci., 9, 4142–4151, https://doi.org/10.1039/C7SC05421A, 2018.
Xiao, Y. and Lasaga, A. C.: Ab initio quantum mechanical studies of the kinetics and mechanisms of silicate dissolution: catalysis, Geochim. Cosmochim. Ac., 58, 5379–5400, https://doi.org/10.1016/0016-7037(94)90237-2, 1994.
Yan, L., Englert, A. H., Masliyah, J. H., and Xu, Z.: Determination of anisotropic surface characteristics of different phyllosilicates by direct force measurements, Langmuir, 27, 12996–13007, https://doi.org/10.1021/la2027829, 2011.
Yan, L., Masliyah, J. H., and Xu, Z.: Interaction of divalent cations with basal planes and edge surfaces of phyllosilicate minerals: Muscovite and talc, J. Colloid Interface Sci., 404, 183–191, https://doi.org/10.1016/j.jcis.2013.04.023, 2013.
Yang, Y., Min, Y., and Jun, Y.-S.: Effects of Al/Si ordering on feldspar dissolution: Part II. The pH dependence of plagioclases' dissolution rates, Geochim. Cosmochim. Ac., 126, 595–613, https://doi.org/10.1016/j.gca.2013.10.049, 2014a.
Yang, Y., Min, Y., Lococo, J., and Jun, Y.: Effects of Al/Si ordering on feldspar dissolution: Part I. Crystallographic control on the stoichiometry of dissolution reaction, Geochim. Cosmochim. Ac., 126, 574–594, 2014b.
Yin, X., Gupta, V., Du, H., Wang, X., and Miller, J. D.: Surface charge and wetting characteristics of layered silicate minerals, Adv. Colloid Interface Sci., 179–182, 43–50, https://doi.org/10.1016/j.cis.2012.06.004, 2012.
Yukselen-Aksoy, Y. and Kaya, A.: A study of factors affecting on the zeta potential of kaolinite and quartz powder, Environ. Earth Sci., 62, 697–705, https://doi.org/10.1007/s12665-010-0556-9, 2011.
Zhang, L. and Lüttge, A.: Al,Si order in albite and its effect on albite dissolution processes: A Monte Carlo study, Am. Mineral., 92, 1316–1324, https://doi.org/10.2138/am.2007.2471, 2007.
Zhao, H., Bhattacharjee, S., Chow, R., Wallace, D., Masliyah, J. H., and Xu, Z.: Probing surface charge potentials of clay basal planes and edges by direct force measurements, Langmuir, 24, 12899–12910, https://doi.org/10.1021/la802112h, 2008.
Zhu, C., Liu, Z., Zhang, Y., Wang, C., Scheafer, A., Lu, P., Zhang, G., Georg, R. B., Yuan, H.-L., and Rimstidt, J. D.: Measuring silicate mineral dissolution rates using Si isotope doping, Chem. Geol., 445, 146–163, https://doi.org/10.1016/j.chemgeo.2016.02.027, 2016.
Zielke, S. A., Bertram, A. K., and Patey, G. N.: Simulations of ice nucleation by kaolinite (001) with rigid and flexible surfaces, J. Phys. Chem. B, 120, 1726–1734, 2015.
Zobrist, B., Marcolli, C., Koop, T., Luo, B. P., Murphy, D. M., Lohmann, U., Zardini, A. A., Krieger, U. K., Corti, T., Cziczo, D. J., Fueglistaler, S., Hudson, P. K., Thomson, D. S., and Peter, T.: Oxalic acid as a heterogeneous ice nucleus in the upper troposphere and its indirect aerosol effect, Atmos. Chem. Phys., 6, 3115–3129, https://doi.org/10.5194/acp-6-3115-2006, 2006.
Zobrist, B., Marcolli, C., Peter, T., and Koop, T.: Heterogeneous ice nucleation in aqueous solutions:? The role of water activity, J. Phys. Chem. A, 112, 3965–3975, https://doi.org/10.1021/jp7112208, 2008.
Zolles, T., Burkart, J., Häusler, T., Pummer, B., Hitzenberger, R., and Grothe, H.: Identification of ice nucleation active sites on feldspar dust particles, J. Phys. Chem. A, 119, 2692–2700, https://doi.org/10.1021/jp509839x, 2015.
Zuberi, B., Bertram, A. K., Cassa, C. A., Molina, L. T., and Molina, M. J.: Heterogeneous nucleation of ice in (NH4)2SO4−H2O particles with mineral dust immersions, Geophys. Res. Lett., 29, 142–141, https://doi.org/10.1029/2001GL014289, 2002.
Zuend, A., Marcolli, C., Luo, B. P., and Peter, T.: A thermodynamic model of mixed organic-inorganic aerosols to predict activity coefficients, Atmos. Chem. Phys., 8, 4559–4593, https://doi.org/10.5194/acp-8-4559-2008, 2008.
Zuend, A., Marcolli, C., Booth, A. M., Lienhard, D. M., Soonsin, V., Krieger, U. K., Topping, D. O., McFiggans, G., Peter, T., and Seinfeld, J. H.: New and extended parameterization of the thermodynamic model AIOMFAC: calculation of activity coefficients for organic-inorganic mixtures containing carboxyl, hydroxyl, carbonyl, ether, ester, alkenyl, alkyl, and aromatic functional groups, Atmos. Chem. Phys., 11, 9155–9206, https://doi.org/10.5194/acp-11-9155-2011, 2011.
- Article
(3333 KB) - Full-text XML
atmospherically relevantchemical species on fairly abundant mineral surfaces like feldspars and clays. We of course discuss these chemical interactions from the perspective of fate of airborne mineral dust but the same interactions could be interesting for studies on minerals at the ground level.





