the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Timescales of secondary organic aerosols to reach equilibrium at various temperatures and relative humidities
Secondary organic aerosols (SOA) account for a substantial fraction of air particulate matter, and SOA formation is often modeled assuming rapid establishment of gas–particle equilibrium. Here, we estimate the characteristic timescale for SOA to achieve gas–particle equilibrium under a wide range of temperatures and relative humidities using a state-of-the-art kinetic flux model. Equilibration timescales were calculated by varying particle phase state, size, mass loadings, and volatility of organic compounds in open and closed systems. Model simulations suggest that the equilibration timescale for semi-volatile compounds is on the order of seconds or minutes for most conditions in the planetary boundary layer, but it can be longer than 1 h if particles adopt glassy or amorphous solid states with high glass transition temperatures at low relative humidity. In the free troposphere with lower temperatures, it can be longer than hours or days, even at moderate or relatively high relative humidities due to kinetic limitations of bulk diffusion in highly viscous particles. The timescale of partitioning of low-volatile compounds into highly viscous particles is shorter compared to semi-volatile compounds in the closed system, as it is largely determined by condensation sink due to very slow re-evaporation with relatively quick establishment of local equilibrium between the gas phase and the near-surface bulk. The dependence of equilibration timescales on both volatility and bulk diffusivity provides critical insights into thermodynamic or kinetic treatments of SOA partitioning for accurate predictions of gas- and particle-phase concentrations of semi-volatile compounds in regional and global chemical transport models.
- Article
(2693 KB) -
Supplement
(1824 KB) - BibTeX
- EndNote
Secondary organic aerosols (SOA) play a central role in climate, air quality, and public health. Accurate descriptions of formation and evolution of SOA remain a grand challenge in climate and air quality models (Kanakidou et al., 2005; Shrivastava et al., 2017a). Current chemical transport models usually employ instantaneous equilibrium partitioning of semi-volatile oxidation products into the particle phase (Pankow, 1994), assuming that SOA partitioning is rapid compared to the timescales of other major atmospheric processes associated with SOA formation. The timescale of SOA to reach equilibrium with their surrounding condensable vapors needs to be evaluated under different ambient conditions to validate this assumption.
SOA particles can adopt liquid (dynamic viscosity η<102 Pa s), semi-solid (10 Pa s), or glassy or amorphous solid states (η>1012 Pa s), depending on chemical composition, temperature (T), and relative humidity (RH; Virtanen et al., 2010; Koop et al., 2011; Zhang et al., 2015; Reid et al., 2018). The occurrence of glassy or amorphous solid states may lead to kinetic limitations and a prolonged equilibration timescale in SOA partitioning (Shiraiwa and Seinfeld, 2012; Booth et al., 2014; Zaveri et al., 2014; Mai et al., 2015), affecting evolution of particle size distribution upon SOA growth (Maria et al., 2004; Shiraiwa et al., 2013a; Zaveri et al., 2018). A number of experimental studies have indeed observed kinetic limitations of the bulk diffusion of organic molecules (Vaden et al., 2011; Perraud et al., 2012; J. Ye et al., 2016; Zhang et al., 2018), while chamber experiments probing the intraparticle mixing did not find kinetic limitations at moderate and high RH and room temperature (Q. Ye et al., 2016; Gorkowski et al., 2017; Ye et al., 2018).
Recently, global simulations predicted that SOA particles are expected to be mostly in a glassy solid phase state in the middle and upper troposphere and also in dry lands in the boundary layer (Shiraiwa et al., 2017), which can lead to prolonged characteristic bulk diffusion timescales of organic molecules within SOA particles (Shiraiwa et al., 2011; Maclean et al., 2017). Slow bulk diffusion associated with a glassy phase state can prevent atmospheric oxidants from reacting with organic compounds such as polycyclic aromatic hydrocarbons (Shrivastava et al., 2017b; Mu et al., 2018), contributing to long-range transport of organic compounds. Recent ambient observations have shown that the condensation of highly oxygenated molecules (HOMs), which play an important role in new particle formation, can be governed by kinetic partitioning in the free troposphere (Bianchi et al., 2016). Diffusivity measurements of volatile organics in levitated viscous particles have shown strong temperature dependence of bulk diffusivity and the evaporation timescale (Bastelberger et al., 2017). Slow bulk diffusion may impact multiphase processes such as browning of organic particles (Liu et al., 2018), cloud droplet activation (Slade et al., 2017), and ice nucleation pathways (Knopf et al., 2018).
Given these observations and strong implications of SOA phase states, it is important to evaluate the common assumption of gas–particle partitioning equilibrium at different ambient conditions. In this study we provide theoretical analysis of partitioning kinetics of organic compounds using the kinetic multi-layer model of gas–particle interactions in aerosols and clouds (KM-GAP; Shiraiwa et al., 2012), which accounts for mass transport in both gas and particle phases. The equilibration timescale (τeq) of organic compounds partitioning into mono-dispersed particles is evaluated systematically under a wide range of temperatures and RH values, considering the effects of the particle phase state, particle size, mass loadings, and volatility of organic compounds in a closed system with finite amount of vapor. For comparison we also present simulations in an open system with vapor concentration maintained as a constant. This is the first study to directly relate the equilibration timescale of SOA partitioning to ambient temperature and relative humidity, which has important implications on the treatment of SOA evolution in chemical transport models.
We evaluate the timescale to achieve gas–particle equilibrium by simulating condensation of a compound Z into preexisting non-volatile mono-dispersed particles using the KM-GAP model. KM-GAP consists of multiple model compartments and layers: the gas phase, near-surface gas phase, sorption layer, surface layer, and a number of bulk layers (Shiraiwa et al., 2012). The following processes are treated as temperature-dependent in KM-GAP: gas phase diffusion, adsorption, desorption, surface–bulk exchange, and bulk diffusion (Fig. S1 in the Supplement). The physical and kinetic parameters are summarized in Table S1 in the Supplement. The gas-phase diffusion coefficient depends on temperature (T) and ambient pressure (P). P is calculated as a function of T based on the International Standard Atmosphere (International Organization for Standardization, 1975, https://www.iso.org/standard/7472.html, last access: 3 May 2019). The adsorption rate coefficient is related to the mean thermal velocity as a function of T and the surface accommodation coefficient, which is assumed to be 1 (Julin et al., 2014). The T dependence of desorption rate coefficient is described by an Arrhenius equation with an assumed typical adsorption enthalpy of 40 kJ mol−1.
Phase state and viscosity can be characterized by the glass transition temperature (Tg), at which phase transition between amorphous solid and semi-solid states occurs (Koop et al., 2011). When the Tg of organic particles under dry conditions (Tg,org) is known, the Tg of organic-water mixtures at given RH can be estimated considering hygroscopic growth combined with the Gordon–Taylor equation. In this work, we assumed the effective hygroscopicity parameter to be 0.1 (Petters and Kreidenweis, 2007; Gunthe et al., 2009) and the Gordon–Taylor constant to be 2.5 (Koop et al., 2011). Then, the T dependence of viscosity is calculated using the Vogel–Tammann–Fulcher equation (Angell, 1991; Rothfuss and Petters, 2017; DeRieux et al., 2018; Li and Shiraiwa, 2018).
Figure 1 shows the T- and RH-dependent viscosity of SOA particles with Tg,org of 240 K (Fig. 1a), 270 K (Fig. 1b), and 300 K (Fig. 1c). We chose these three Tg,org values to represent different phase states of liquid, semi-solid, and glassy states, respectively, at T of 298 K under dry conditions, and these values are within the range recently reported for monoterpene-derived SOA (Petters et al., 2019). The decrease in T leads to an increase in viscosity, while the increase in RH leads to a decrease in viscosity due to the plasticizing effect of water (Koop et al., 2011). For simplicity we assume that particles are ideally mixed, even though phase-separated particles are observed for ambient and laboratory-generated SOA particles under certain conditions (You et al., 2012; Renbaum-Wolff et al., 2016). The bulk diffusion coefficient Db (Fig. S2) is calculated by the Stokes–Einstein equation, which has been shown to work very well for organic molecules diffusing through materials with viscosity below ∼103 Pa s (Chenyakin et al., 2017). Note that the Stokes–Einstein equation may underpredict Db in highly viscous SOA; thus, it gives lower limits of Db (Price et al., 2015; Marshall et al., 2016; Bastelberger et al., 2017; Reid et al., 2018). Db is fixed at any given depth in the particle bulk in each simulation, assuming that condensation of Z would not alter particle viscosity and diffusivity, as only trace amounts of Z condense to preexisting particles in our simulations. Particle-phase reactions and their potential impacts on particle viscosity are also not considered in this study.
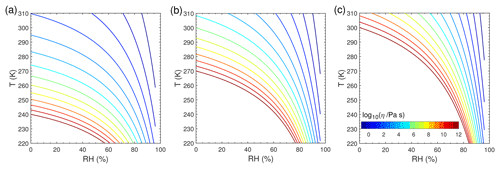
Figure 1Viscosity of preexisting particles as a function of temperature and relative humidity. The glass transition temperatures under dry conditions (Tg,org) are (a) 240 K, (b) 270 K, and (c) 300 K.
We mainly consider a closed system in which condensation of Z would lead to a decrease in its gas-phase mass concentration (Cg) and an increase in its particle-phase mass concentration (Cp). The particle diameter stays practically constant throughout each simulation, as the amount of condensing Z is set to be much smaller than the non-volatile preexisting particle mass (COA). The gas-phase mass concentration of Z right above the surface (Cs) is also calculated based on Raoult's law and partitioning theory (Pankow, 1994) in equilibrium with the near-surface bulk, which is resolved by KM-GAP (Shiraiwa and Seinfeld, 2012). We also calculate the mass fraction of Z in the near-surface bulk (fs) and the average mass fraction of Z in the entire bulk (fb) to infer the radial concentration profile (Fig. S3). The equilibration timescale (τeq) is calculated as the e-folding time t when the following criterion is met:
where Cp,0 and Cp,eq are the initial and equilibrium mass concentration of Z in the particle phase, respectively. Note that practically the same values can also be obtained by using initial and equilibrium gas-phase concentrations in Eq. (1), as the mass change of Z in the gas and particle phases is the same in these simulations.
3.1 Impacts of volatility and diffusivity on equilibration timescales
Figure 2 shows exemplary simulations of temporal evolution of Cg (blue line) and Cp (red line) of the compound Z in the closed system along with τeq, which is marked with red circles. The initial mass concentration of preexisting non-volatile mono-dispersed particles (COA) is assumed to be 20 µg m−3 with the number concentrations of 3×104 cm−3 and the initial particle diameter of 100 nm. Initial mass concentrations of Z in the gas (Cg,0) and particle (Cp,0) phases are set to 0.3 and 0 µg m−3, respectively. Tg,org is assumed to be 270 K. Figure 2a presents simulations for a semi-volatile organic compound (SVOC) with the pure compound saturation mass concentration (C0) of 10 µg m−3 condensing on particles with Db of 10−11 cm2 s−1 at RH = 60 % and T=298 K (Fig. S2). Upon condensation, Cg decreases while Cs and Cp increase, and the gas–particle equilibrium is reached within about 20 s, as indicated by τeq. For a low-volatile organic compound (LVOC) with C0=0.1 µg m−3, it takes a longer time to reach the equilibrium with a τeq of ∼30 s (Fig. 2b), as the partial pressure gradient between the gas phase and the particle surface (represented by the difference between Cg and Cs) is larger for lower C0. For both cases SOA growth is governed by gas-phase diffusion as indicated by Cs<Cg. The mass fraction of Z in the near-surface bulk is identical to the average mass fraction in the entire bulk (Fig. S3a and b), indicating that Z is homogeneously well-mixed in the particle without kinetic limitations of bulk diffusion in low viscous particles (Fig. 3a).
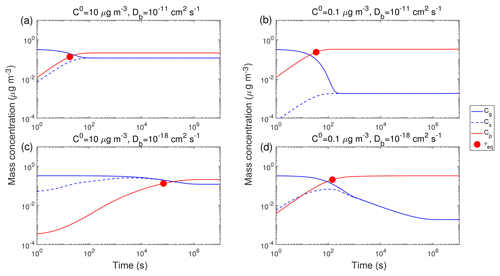
Figure 2Temporal evolution of mass concentrations of the condensing compound Z in the gas phase (Cg), just above the particle surface (Cs), and in the particle phase (Cp) in the closed system. τeq is marked with the red circle. RH is 60 % and T is (a, b) 298 K and (c, d) 250 K. The C0 of Z is (a, c) 10 µg m−3 and (b, d) 0.1 µg m−3. The glass transition temperature of preexisting particles under dry conditions (Tg,org) is set to 270 K, which leads to Db of (a, b) 10−11 cm2 s−1 and (c, d) 10−18 cm2 s−1. The initial mass concentration of preexisting particles is set to 20 µg m−3 with the number concentrations of 3×104 cm−3 and the initial particle diameter of 100 nm.
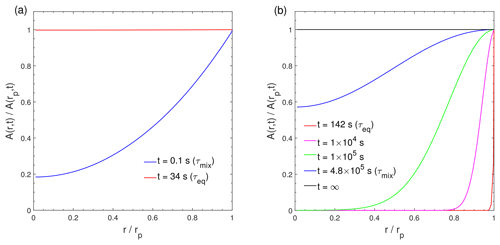
Figure 3Dimensionless radial concentration profiles in the particle for the condensation of the LVOC species (C0=0.1 µg m−3) at RH = 60 % and (a) T=298 K with cm2 s−1 and (b) T=250 K with cm2 s−1. The x axis indicates the radial distance from the particle center (r) normalized by the particle radius (rp), ranging from the particle core () to the surface (). The y axis indicates the bulk concentration of the condensing compound at a given position in the bulk (r) normalized by the bulk concentration at particle surface (rp).
At a lower T of 250 K, the phase state of preexisting particles that occurs is highly viscous with Db of cm2 s−1 (Fig. S2), resulting in much longer equilibration timescales (∼105 s) for SVOC with C0=10 µg m−3 (Fig. 2c). After Cg and Cs converge, they continue to decrease simultaneously while Cp increases slowly, showing that the particle undergoes quasi-equilibrium growth (Shiraiwa and Seinfeld, 2012; Zhang et al., 2012). For LVOC (C0=0.1 µg m−3) condensation, τeq is short (∼140 s) because a local thermodynamic equilibrium between the gas phase and the near-surface bulk is established relatively quickly (as mostly controlled by the condensation sink; Riipinen et al., 2011; Tröstl et al., 2016) due to very slow re-evaporation of the LVOC.
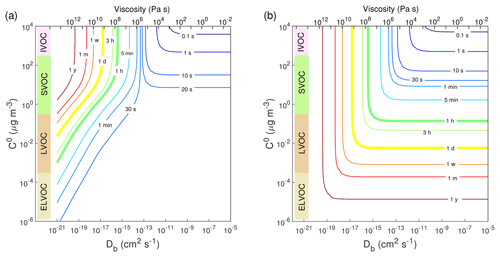
Figure 4Contour plot of equilibration timescale (τeq) as a function of bulk diffusivity (Db) and saturation mass concentration (C0) for (a) condensation in the closed system and (b) evaporation in the open system. The initial mass concentration of preexisting particles is set to 20 µg m−3 with the number concentrations of 3×104 cm−3 and the initial particle diameter of 100 nm. Viscosity is calculated from the Stokes–Einstein equation, assuming the effective molecular radius of 10−8 cm at T of 298 K.
The characteristic timescale of mass transport and mixing by molecular diffusion τmix can be calculated by , where rp is the particle radius (Seinfeld and Pandis, 2006). Figure 3 shows dimensionless radial concentration profiles of Z (C0=0.1 µg m−3) in the particle at (Fig. 3a) cm2 s−1 and (Fig. 3b) 10−18 cm2 s−1. For low viscous particles, τmix is very short and particles are homogeneously well-mixed at τeq, which is consistent with previous analytical calculations (Liu et al., 2013; Mai et al., 2015). In contrast, a large concentration gradient exists between the particle surface and the inner bulk (Figs. 3b and S3d) at τeq in highly viscous particles due to strong kinetic limitations of bulk diffusion (as indicated by a very long τmix), which prevents the entire particle bulk from reaching complete equilibrium. Thus, for LVOC condensation on highly viscous particles (Fig. 2d), τmix represents the timescale that establishes full equilibrium with homogeneous mixing in the entire particle bulk. These results are consistent with Mai et al. (2015) and Liu et al. (2016), who showed that an establishment of full equilibrium is limited by bulk diffusion in highly viscous particles, even though the local equilibrium of the LVOC may be achieved faster. Note that τmix is solely a function of particle size and bulk diffusivity, while τeq is also affected by volatility and mass loadings. At lower particle concentrations, the total accommodation of molecules to the particle surface decreases, resulting in longer equilibration timescales (Fig. S4).
We further computed τeq as a function of Db and C0 in the closed system. As shown in Fig. 4a, when Db is higher than cm2 s−1, τeq is insensitive to bulk diffusivity but sensitive to volatility: decreasing volatility increases τeq in this regime. In the regime with Db lower than cm2 s−1 and C0 higher than ∼10 µg m−3, τeq is controlled by bulk diffusivity: τeq increases from 30 s to longer than 1 year as Db decreases from 10−13 to 10−20 cm2 s−1. In the regime with cm2 s−1 and µg m−3, τeq depends on both diffusivity and volatility. Decreasing volatility would lead to shorter τeq due to an establishment of local equilibrium of the LVOC.
In an open system with fixed vapor concentration (Fig. S5), the τeq of SVOC is slightly longer but on the same order of magnitude as the τeq in the closed system, as relatively small amounts of SVOC need to condense to reach equilibrium. In contrast, the τeq of the LVOC in the open system become dramatically longer as the LVOC continues to condense into the particle phase because of low volatility (Pankow, 1994). For further simulations we focus mainly on the closed system, and the corresponding simulations for the open system are provided in the Supplement.
We also simulated evaporation in the closed system with the same parameters as in the condensation simulations (Table S2). Initially Cg=0 µg m−3 and trace amounts of semi-volatile or low-volatile species were assumed to be homogeneously well-mixed in preexisting particles. Figure S6 shows that for the evaporation of SVOC species with C0=10 µg m−3, decreasing Db from 10−11 to 10−18 cm2 s−1 would increase τeq from ∼20 to ∼105 s. These evaporation timescales are close to those derived from condensation (Fig. 2a and c) and consistent with previous kinetic simulations (Liu et al., 2016). In the closed system, the evaporation of a very small amount of LVOC species from the particle surface is already sufficient for reaching the particle-phase equilibrium concentration, resulting in a short τeq (Fig. S6b and d). For an open system with continuous removal of gas-phase compounds, which is often employed in evaporation experiments, the equilibrium timescale in the evaporation of the LVOC species from highly viscous particles can be longer than hours or days (Vaden et al., 2011; Liu et al., 2016). Figure 4b shows simulated evaporation timescales as a function of Db and C0 in an open system, which agrees very well with Fig. 3 in Liu et al. (2016). It shows that for less-viscous particles, τeq is limited by volatility, while for highly viscous particles, τeq is insensitive to volatility and controlled by bulk diffusivity.
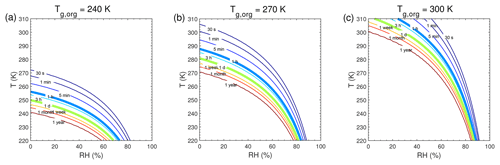
Figure 5Equilibration timescale (τeq) as a function of temperature and relative humidity in the closed system. The glass transition temperatures of preexisting particles at dry conditions (Tg,org) are (a) 240 K, (b) 270 K, and (c) 300 K. The saturation mass concentration (C0) of the condensing compound is 10 µg m−3 (SVOC). The mass concentration of preexisting particles is set to 20 µg m−3 with the number concentrations of 3×104 cm−3 and the initial particle diameter of 100 nm.
3.2 Equilibration timescales at different RH and T
We conducted further simulations to estimate τeq with a wide range of atmospherically relevant temperatures (220–310 K) and relative humidities (0 %–100 %). Figure 5 shows the temperature and humidity-dependent diagrams of τeq for SVOC (C0=10 µg m−3) condensation on particles with Tg,org of 240, 270, and 300 K, in the closed system. For particles with Tg,org of 240 K (Fig. 5a), τeq is on the order of seconds under boundary layer conditions (T>270 K). In these conditions particles are liquid with high bulk diffusivity (Figs. 1a and S2a); thus gas–particle partitioning is controlled by gas-phase diffusion and interfacial transport (Shiraiwa and Seinfeld, 2012; Mai et al., 2015). At low T (<260 K) with low or moderate RH (<70 %), τeq can increase from minutes to 1 year with decreasing T and RH mainly due to strong kinetic limitations of bulk diffusion with low Db (Fig. S2a). With Tg,org of 270 K (Fig. 5b) or 300 K (Fig. 5c), τeq is still on the order of minutes in most of boundary layer conditions. At low RH τeq can be extended to hours when particles may occur as semi-solid or amorphous solid. When T<270 K, τeq can be longer than months even at moderate RH, while τeq may stay very short at very high RH. The corresponding simulations of SVOC partitioning in the open system (Fig. S7) show a similar pattern to τeq in the closed system.
τeq for C0=103 and 0.1 µg m−3 in the closed system is presented in Fig. A1. In general, τeq would be shorter at higher C0 when particles are liquid, as the partial pressure gradient between the gas phase and the particle surface is smaller for higher C0 (Shiraiwa and Seinfeld, 2012; Liu et al., 2016). For example, the increase in C0 from 10 to 103 µg m−3 leads to τeq decrease from 30 to 1 s with Tg,org of 240 K at boundary layer conditions (Figs. 5a and A1a). At low T and RH (e.g., T<250 K and RH < 50 %), where particles are highly viscous, τeq is on the same order of magnitude for the condensation of the intermediate-volatility organic compound (IVOC) and the SVOC, as gas–particle partitioning is limited by bulk diffusion. Figure A2 shows bulk diffusion and mixing timescales (τmix) as a function of RH and T. It is interesting to note that τmix is very similar to the τeq of the IVOC (Fig. A1a–c), as gas diffusion and interfacial transport of the IVOC are fast. For the LVOC τeq is generally shorter than τmix, as its mass transfer to the particle surface is governed by condensation sink with negligible re-evaporation, while τmix still takes a long time to achieve homogeneous mixing in the particle phase if particles are viscous.
Previous studies have shown that τeq depends on particle size (Liu et al., 2013; Zaveri et al., 2014; Mai et al., 2015) and particle mass loadings (Shiraiwa and Seinfeld, 2012; Saleh et al., 2013). For further examination of these effects at the different T, Fig. 6 shows the dependence of τeq of the SVOC (C0=10 µg m−3) and LVOC (C0=0.1 µg m−3) on the mass concentration and the diameter of preexisting particles, over the range of 0.1–100 µg m−3 and 30–1000 nm, respectively, with the particle phase state being less viscous with cm2 s−1 at 298 K and highly viscous with cm2 s−1 at 250 K. In this comparison, when ambient particle mass concentration is held constant, increasing particle size will translate to a decrease in the number and surface area concentration of particles, and a decrease in total accommodation of molecules to the particle surface, thereby leading to an increase in τeq. When particle diameter is held constant, an increase in particle concentration leads to an increase in surface area concentration, resulting in a shorter τeq. When particles are less viscous at 298 K ( cm2 s−1) τeq of the SVOC is shorter than that of the LVOC for the same particle size and mass loadings. For partitioning into highly viscous particles at 250 K ( cm2 s−1), the SVOC takes a longer time than the LVOC to reach equilibrium.
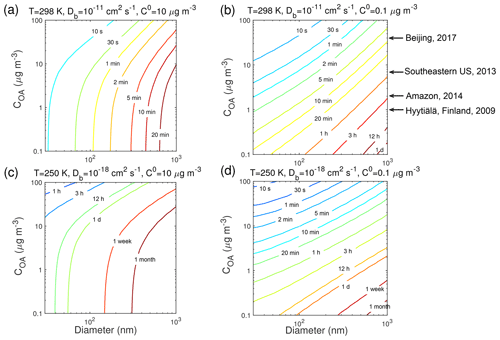
Figure 6Equilibration timescale (τeq) for (a, c) SVOC (C0=10 µg m−3) and (b, d) LVOC (C0=0.1 µg m−3) as a function of particle diameter (nm) and mass concentration (µg m−3) of preexisting particles at 60 % RH and T of (a, b) 298 K and (c, d) 250 K in the closed system. The glass transition temperature of preexisting particles under dry conditions (Tg,org) is set to 270 K, which leads to Db of (a, b) 10−11 cm2 s−1 and (c, d) 10−18 cm2 s−1. Ambient organic mass concentrations are indicated with arrows.
Typical ambient organic mass concentrations in Beijing, Centreville in the southeastern US, the Amazon Basin, and Hyytiälä, Finland, are indicated in Fig. 6. The particle phase state was observed to be mostly liquid in highly polluted episodes in Beijing (Liu et al., 2017), under typical atmospheric conditions in the southeastern US (Pajunoja et al., 2016), and under background conditions in Amazonia (Bateman et al., 2017). At these conditions τeq should be mostly less than 30 min (Fig. 6a and b). Particles were semi-solid or amorphous solid on clear days in Beijing (Liu et al., 2017), when influenced by anthropogenic emissions in Amazonia (Bateman et al., 2017), and in the boreal forest in Finland (Virtanen et a., 2010). Under these conditions and also when particles are transported to the free troposphere, τeq can be longer than 1 h, especially in remote areas with low mass loadings (Fig. 6c and d). Particles in the nucleation mode (diameter < 30 nm) are not considered in this study, as the particle size may affect the phase transition of these nanoparticles (Cheng et al., 2015). The role and impact of phase transition on nucleation and growth of ultrafine particles are beyond the scope of current simulations and need further investigation in future studies.
The timescale to reach equilibrium for SOA partitioning has been investigated in several laboratory experiments at room temperatures (Vaden et al., 2011; Saleh et al., 2013; Liu et al., 2016; J. Ye et al., 2016; Gong et al., 2018; Ye et al., 2018). These experiments monitored particle mass or composition, finding that equilibration timescales are longer at low RH, consistent with our model simulations. Note that, for condensation on highly viscous particles, even though particle mass or particle-phase concentrations appear to reach equilibrium, complete equilibrium with homogeneous mixing in the particle may not have been reached, driven by strong kinetic limitations and concentration gradients in the particle bulk (Figs. 2d and 3b). This is also supported by evaporation experiments showing that the local thermodynamic equilibrium established between the vapor and the near-surface bulk should be differentiated from the global equilibrium between the vapor and the entire bulk (Liu et al., 2016). Note that SOA evaporation is also influenced by volatility and oligomer decomposition (Roldin et al., 2014; Yli-Juuti et al., 2017). The timescale of gas–particle partitioning can be different in closed or open systems, especially for the LVOC (Figs. 4 and S5). The closed system simulations represent SOA partitioning in chamber experiments and in closed atmospheric air mass, which could be justified well within timescales of seconds to minutes and possibly up to hours, depending on meteorological conditions. The real atmosphere may be better approximated as an open system due to dilution and chemical production and loss, especially at longer timescales. Thus, particular care needs to be taken in comparing modeling results with different field observations or with experiments probing equilibration timescales (i.e., evaporation vs. condensation, open vs. closed system, and local vs. full equilibrium).
The simulated equilibration timescales of atmospheric SOA are mostly on the order of minutes to hours under conditions of the atmospheric boundary layer (Figs. 5 and A1). This agrees with previous experimental results that the gas–particle interactions can be regulated by both thermodynamic and kinetic partitioning (Booth et al., 2014; Liu et al., 2016; Saha and Grieshop, 2016; J. Ye et al., 2016; Gong et al., 2018), depending on several factors including particle phase state, size, mass loadings, and volatility. Organic particles containing high-molar-mass compounds tend to have high glass transition temperatures (Koop et al., 2011), and the occurrence of kinetic limitation will increase with higher Tg,org (Fig. 5). This is consistent with the results of intraparticle mixing experiments showing that as the carbon number of precursor (e.g. terpene) increased (that would lead to higher Tg,org), it took a longer time for the SVOC (evaporated from another type of SOA, e.g. toluene SOA) to partition into the terpene SOA, leading to slower molecular exchange among different types of SOA (Ye et al., 2018).
At low temperatures, the particles can occur as highly viscous at relatively high RH (Fig. 1), and τeq of SVOC partitioning can be longer than hours or days (Figs. 5 and S7). Equilibration timescales of LVOC condensation at low particle mass loadings (Fig. 6) may represent the clean conditions where new particle formation and growth often occur (Wang et al., 2016). It has been reported that highly oxygenated molecules play an important role in the initial growth of atmospheric particles in the free troposphere (Bianchi et al., 2016). Bulk diffusion would likely be a limiting step in the condensation of semi-volatile and low-volatility compounds at low temperatures, where particles may occur as highly viscous (Shiraiwa et al., 2017). In this case, particle growth would need to be treated kinetically, rather than thermodynamic equilibrium partitioning, as it would affect SOA growth kinetics and size distribution dynamics, with significant implications for the growth of ultrafine particles to climatically relevant sizes (Riipinen et al., 2011, 2012; Shiraiwa et al., 2013a; Zaveri et al., 2018). Chemical transport models usually have time steps on the order of minutes, in which the partitioning equilibrium may not be reached, for most SVOC species (C0>1 µg m−3) when Db is less than 10−15 cm2 s−1 (Fig. 4). Note that condensation of extremely low-volatility organic compounds (ELVOCs; Tröstl et al., 2016) into highly viscous particles may be governed by gas-phase diffusion, and timescales to reach local equilibrium could be shorter, as determined by the condensation sink (Riipinen et al., 2011; see also Fig. S4b), which may be more relevant for the practical application in chemical transport models.
In this study we assume that the bulk diffusivity within organic particles is independent of particle mixing state and morphology. Chamber experiments have demonstrated that evaporation of organic aerosol may be hindered if it is coated with organic aerosol from a different precursor (Loza et al., 2013; Boyd et al., 2017). Moreover, the phase separation has been observed in organic particles mixed with inorganic salts (You et al., 2014) and even without inorganic salts (Pöhlker et al., 2012; Riedel et al., 2016). Future simulations on equilibration timescales should consider the effects of the immiscibility (Barsanti et al., 2017; Liu et al., 2013) and the phase separation (Shiraiwa et al., 2013b; Pye et al., 2017; Fowler et al., 2018) as well as composition-dependent bulk diffusivity (O'Meara et al., 2016) and the evolution of the particle phase due to reactive uptake and condensed-phase chemistry (Hosny et al., 2016). Incorporation of the particle-phase formation of oligomers and other multifunctional high molar mass compounds can lead to a reduced bulk diffusivity (Pfrang et al., 2011; Hosny et al., 2016), which may prolong the equilibration timescales. Decomposition of highly oxidized molecules (e.g., organic hydroperoxides) in water may also affect gas–particle partitioning (Tong et al., 2016). Current simulations are focused on trace amount of the SVOC or LVOC condensing on mono-dispersed particles with negligible particle growth. Potential phase transition in the course of particle growth or evaporation should also be incorporated in future simulations. The shift in the particle phase state and gas–particle partitioning in response to temperature and RH may need to be considered in chemical transport models and laboratory experiments to better understand the fate of organic compounds.
The simulation data may be obtained from the corresponding author upon request.
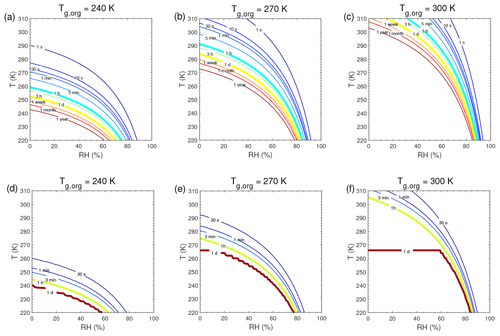
Figure A1Equilibration timescale (τeq) as a function of temperature and relative humidity in the closed system. The glass transition temperatures of preexisting particles at dry conditions (Tg,org) are set to (a, d) 240 K, (b, e) 270 K, and (c, f) 300 K. The mass concentration of preexisting particles is 20 µg m−3. The saturation mass concentration (C0) of the condensing compound is (a–c) 103 µg m−3 and (d–f) 0.1 µg m−3.
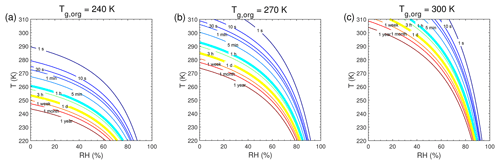
Figure A2Characteristic timescale of bulk diffusion or mixing timescale (τmix) as a function of temperature and relative humidity. The particle diameter is assumed to be 100 nm with the glass transition temperatures of preexisting particles at dry conditions (Tg,org) of (a) 240 K, (b) 270 K, and (c) 300 K.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-5959-2019-supplement.
YL and MS designed and conducted modeling and wrote the paper.
The authors declare that they have no conflict of interest.
This work was funded by the National Science Foundation (AGS-1654104) and the Department of Energy (DE-SC0018349).
This paper was edited by David Topping and reviewed by two anonymous referees.
Angell, C.: Relaxation in liquids, polymers and plastic crystals – strong/fragile patterns and problems, J. Non-Cryst. Solids, 131-133, 13–31, https://doi.org/10.1016/0022-3093(91)90266-9, 1991.
Barsanti, K. C., Kroll, J. H., and Thornton, J. A.: Formation of low-volatility organic compounds in the atmosphere: recent advancements and insights, J. Phys. Chem. Lett., 8, 1503–1511, https://doi.org/10.1021/acs.jpclett.6b02969, 2017.
Bastelberger, S., Krieger, U. K., Luo, B., and Peter, T.: Diffusivity measurements of volatile organics in levitated viscous aerosol particles, Atmos. Chem. Phys., 17, 8453–8471, https://doi.org/10.5194/acp-17-8453-2017, 2017.
Bateman, A. P., Gong, Z., Harder, T. H., de Sá, S. S., Wang, B., Castillo, P., China, S., Liu, Y., O'Brien, R. E., Palm, B. B., Shiu, H. W., Cirino, G. G., Thalman, R., Adachi, K., Alexander, M. L., Artaxo, P., Bertram, A. K., Buseck, P. R., Gilles, M. K., Jimenez, J. L., Laskin, A., Manzi, A. O., Sedlacek, A., Souza, R. A. F., Wang, J., Zaveri, R., and Martin, S. T.: Anthropogenic influences on the physical state of submicron particulate matter over a tropical forest, Atmos. Chem. Phys., 17, 1759–1773, https://doi.org/10.5194/acp-17-1759-2017, 2017.
Bianchi, F., Tröstl, J., Junninen, H., Frege, C., Henne, S., Hoyle, C. R., Molteni, U., Herrmann, E., Adamov, A., Bukowiecki, N., Chen, X., Duplissy, J., Gysel, M., Hutterli, M., Kangasluoma, J., Kontkanen, J., Kürten, A., Manninen, H. E., Münch, S., Peräkylä, O., Petäjä, T., Rondo, L., Williamson, C., Weingartner, E., Curtius, J., Worsnop, D. R., Kulmala, M., Dommen, J., and Baltensperger, U.: New particle formation in the free troposphere: A question of chemistry and timing, Science, 352, 1109–1112, https://doi.org/10.1126/science.aad5456, 2016.
Booth, A. M., Murphy, B., Riipinen, I., Percival, C. J., and Topping, D. O.: Connecting bulk viscosity measurements to kinetic limitations on attaining equilibrium for a model aerosol composition, Environ. Sci. Technol., 48, 9298–9305, https://doi.org/10.1021/es501705c, 2014.
Boyd, C. M., Nah, T., Xu, L., Berkemeier, T., and Ng, N. L.: Secondary organic aerosol (SOA) from nitrate radical oxidation of monoterpenes: effects of temperature, dilution, and humidity on aerosol formation, mixing, and evaporation, Environ. Sci. Technol., 51, 7831–7841, https://doi.org/10.1021/acs.est.7b01460, 2017.
Cheng, Y., Su, H., Koop, T., Mikhailov, E., and Pöschl, U.: Size dependence of phase transitions in aerosol nanoparticles, Nat. Commun., 6, 5923, https://doi.org/10.1038/ncomms6923, 2015.
Chenyakin, Y., Ullmann, D. A., Evoy, E., Renbaum-Wolff, L., Kamal, S., and Bertram, A. K.: Diffusion coefficients of organic molecules in sucrose–water solutions and comparison with Stokes–Einstein predictions, Atmos. Chem. Phys., 17, 2423–2435, https://doi.org/10.5194/acp-17-2423-2017, 2017.
DeRieux, W. S. W., Li, Y., Lin, P., Laskin, J., Laskin, A., Bertram, A. K., Nizkorodov, S. A., and Shiraiwa, M.: Predicting the glass transition temperature and viscosity of secondary organic material using molecular composition, Atmos. Chem. Phys., 18, 6331–6351, https://doi.org/10.5194/acp-18-6331-2018, 2018.
Fowler, K., Connolly, P. J., Topping, D. O., and O'Meara, S.: Maxwell–Stefan diffusion: a framework for predicting condensed phase diffusion and phase separation in atmospheric aerosol, Atmos. Chem. Phys., 18, 1629–1642, https://doi.org/10.5194/acp-18-1629-2018, 2018.
Gong, Z., Han, Y., Liu, P., Ye, J., Keutsch, F. N., McKinney, K. A., and Martin, S. T.: Influence of particle physical state on the uptake of medium-sized organic molecules, Environ. Sci. Technol., 52, 8381–8389, https://doi.org/10.1021/acs.est.8b02119, 2018.
Gorkowski, K., Donahue, N. M., and Sullivan, R. C.: Emulsified and liquid–liquid phase-separated states of α-pinene secondary organic aerosol determined using aerosol optical tweezers, Environ. Sci. Technol., 51, 12154–12163, https://doi.org/10.1021/acs.est.7b03250, 2017.
Gunthe, S. S., King, S. M., Rose, D., Chen, Q., Roldin, P., Farmer, D. K., Jimenez, J. L., Artaxo, P., Andreae, M. O., Martin, S. T., and Pöschl, U.: Cloud condensation nuclei in pristine tropical rainforest air of Amazonia: size-resolved measurements and modeling of atmospheric aerosol composition and CCN activity, Atmos. Chem. Phys., 9, 7551–7575, https://doi.org/10.5194/acp-9-7551-2009, 2009.
Hosny, N., Fitzgerald, C., Vyšniauskas, A., Athanasiadis, A., Berkemeier, T., Uygur, N., Pöschl, U., Shiraiwa, M., Kalberer, M., Pope, F., and Kuimova, M. K.: Direct imaging of changes in aerosol particle viscosity upon hydration and chemical aging, Chem. Sci., 7, 1357–1367, https://doi.org/10.1039/C5SC02959G, 2016.
International Organization for Standardization: Standard Atmosphere, ISO 2533:1975, available at: https://www.iso.org/standard/7472.html (last access: 3 May 2019), 1975.
Julin, J., Winkler, P. M., Donahue, N. M., Wagner, P. E., and Riipinen, I.: Near-unity mass accommodation coefficient of organic molecules of varying structure, Environ. Sci. Technol., 48, 12083–12089, https://doi.org/10.1021/es501816h, 2014.
Kanakidou, M., Seinfeld, J. H., Pandis, S. N., Barnes, I., Dentener, F. J., Facchini, M. C., Van Dingenen, R., Ervens, B., Nenes, A., Nielsen, C. J., Swietlicki, E., Putaud, J. P., Balkanski, Y., Fuzzi, S., Horth, J., Moortgat, G. K., Winterhalter, R., Myhre, C. E. L., Tsigaridis, K., Vignati, E., Stephanou, E. G., and Wilson, J.: Organic aerosol and global climate modelling: a review, Atmos. Chem. Phys., 5, 1053–1123, https://doi.org/10.5194/acp-5-1053-2005, 2005.
Knopf, D. A., Alpert, P. A., and Wang, B.: The role of organic aerosol in atmospheric ice nucleation: a review, ACS Earth Space Chem., 2, 168–202, https://doi.org/10.1021/acsearthspacechem.7b00120, 2018.
Koop, T., Bookhold, J., Shiraiwa, M., and Poschl, U.: Glass transition and phase state of organic compounds: dependency on molecular properties and implications for secondary organic aerosols in the atmosphere, Phys. Chem. Chem. Phys., 13, 19238–19255, https://doi.org/10.1039/C1CP22617G, 2011.
Li, Y. and Shiraiwa, M.: Molecular corridors, volatility and particle phase state in secondary organic aerosols, in: Multiphase Environmental Chemistry in the Atmosphere, edited by: Hunt S. W., Laskin A., and Nizkorodov S. A., ACS Symposium Ser., 1299, 209–244, https://doi.org/10.1021/bk-2018-1299.ch011, 2018.
Liu, C., Shi, S., Weschler, C., Zhao, B., and Zhang, Y.: Analysis of the dynamic interaction between SVOCs and airborne particles, Aerosol Sci. Tech., 47, 125–136, https://doi.org/10.1080/02786826.2012.730163, 2013.
Liu, P., Li, Y. J., Wang, Y., Gilles, M. K., Zaveri, R. A., Bertram, A. K., and Martin, S. T.: Lability of secondary organic particulate matter, P. Natl. Acad. Sci. USA, 113, 12643–12648, https://doi.org/10.1021/acscentsci.7b00452, 2016.
Liu, P., Li, Y. J., Wang, Y., Bateman, A. P., Zhang, Y., Gong, Z., Bertram, A. K., and Martin, S. T.: Highly viscous states affect the browning of atmospheric organic particulate matter, ACS Cent. Sci., 4, 207–215, https://doi.org/10.1021/acscentsci.7b00452, 2018.
Liu, Y., Wu, Z., Wang, Y., Xiao, Y., Gu, F., Zheng, J., Tan, T., Shang, D., Wu, Y., Zeng, L., Hu, M., Bateman, A. P., and Martin, S. T.: Submicrometer particles are in the liquid state during heavy haze episodes in the urban atmosphere of Beijing, China, Environ. Sci. Technol. Lett., 4, 427–432, https://doi.org/10.1021/acs.estlett.7b00352, 2017.
Loza, C. L., Coggon, M. M., Nguyen, T. B., Zuend, A., Flagan, R. C., and Seinfeld, J. H.: On the mixing and evaporation of secondary organic aerosol components, Environ. Sci. Technol., 47, 6173–6180, https://doi.org/10.1021/es400979k, 2013.
Maclean, A. M., Butenhoff, C. L., Grayson, J. W., Barsanti, K., Jimenez, J. L., and Bertram, A. K.: Mixing times of organic molecules within secondary organic aerosol particles: a global planetary boundary layer perspective, Atmos. Chem. Phys., 17, 13037–13048, https://doi.org/10.5194/acp-17-13037-2017, 2017.
Mai, H., Shiraiwa, M., Flagan, R. C., and Seinfeld, J. H.: Under what conditions can equilibrium gas–particle partitioning be expected to hold in the atmosphere?, Environ. Sci. Technol., 49, 11485–11491, https://doi.org/10.1021/acs.est.5b02587, 2015.
Maria, S. F., Russell, L. M., Gilles, M. K., and Myneni, S. C. B.: Organic aerosol growth mechanisms and their climate-forcing implications, Science, 306, 1921–1924, https://doi.org/10.1126/science.1103491, 2004.
Marshall, F. H., Miles, R. E., Song, Y.-C., Ohm, P. B., Power, R. M., Reid, J. P., and Dutcher, C. S.: Diffusion and reactivity in ultraviscous aerosol and the correlation with particle viscosity, Chem. Sci., 7, 1298–1308, https://doi.org/10.1039/C5SC03223G, 2016.
Mu, Q., Shiraiwa, M., Octaviani, M., Ma, N., Ding, A., Su, H., Lammel, G., Pöschl, U., and Cheng, Y.: Temperature effect on phase state and reactivity controls atmospheric multiphase chemistry and transport of PAHs, Sci. Adv., 4, eaap7314, https://doi.org/10.1126/sciadv.aap7314, 2018.
O'Meara, S., Topping, D. O., and McFiggans, G.: The rate of equilibration of viscous aerosol particles, Atmos. Chem. Phys., 16, 5299–5313, https://doi.org/10.5194/acp-16-5299-2016, 2016.
Pajunoja, A., Hu, W., Leong, Y. J., Taylor, N. F., Miettinen, P., Palm, B. B., Mikkonen, S., Collins, D. R., Jimenez, J. L., and Virtanen, A.: Phase state of ambient aerosol linked with water uptake and chemical aging in the southeastern US, Atmos. Chem. Phys., 16, 11163–11176, https://doi.org/10.5194/acp-16-11163-2016, 2016.
Pankow, J. F.: An absorption model of gas-particle partitioning of organic-compounds in the atmosphere, Atmos. Environ., 28, 185–188, https://doi.org/10.1016/1352-2310(94)90093-0, 1994.
Perraud, V., Bruns, E. A., Ezell, M. J., Johnson, S. N., Yu, Y., Alexander, M. L., Zelenyuk, A., Imre, D., Chang, W. L., Dabdub, D., Pankow, J. F., and Finlayson-Pitts, B. J.: Nonequilibrium atmospheric secondary organic aerosol formation and growth, P. Natl. Acad. Sci. USA, 109, 2836–2841, https://doi.org/10.1073/pnas.1119909109, 2012.
Petters, M. D. and Kreidenweis, S. M.: A single parameter representation of hygroscopic growth and cloud condensation nucleus activity, Atmos. Chem. Phys., 7, 1961–1971, https://doi.org/10.5194/acp-7-1961-2007, 2007.
Petters, S. S., Kreidenweis, S. M., Grieshop, A. P., Ziemann, P. J., and Petters, M. D.: Temperature- and humidity-dependent phase states of secondary organic aerosols, Geophys. Res. Lett., 46, 1005–1013, https://doi.org/10.1029/2018GL080563, 2019.
Pfrang, C., Shiraiwa, M., and Pöschl, U.: Chemical ageing and transformation of diffusivity in semi-solid multi-component organic aerosol particles, Atmos. Chem. Phys., 11, 7343–7354, https://doi.org/10.5194/acp-11-7343-2011, 2011.
Pöhlker, C., Wiedemann, K. T., Sinha, B., Shiraiwa, M., Gunthe, S. S., Smith, M., Su, H., Artaxo, P., Chen, Q., Cheng, Y., Elbert, W., Gilles, M. K., Kilcoyne, A. L. D., Moffet, R. C., Weigand, M., Martin, S. T., Pöschl, U., and Andreae, M. O.: Biogenic potassium salt particles as seeds for secondary organic aerosol in the Amazon, Science, 337, 1075–1078, https://doi.org/10.1126/science.1223264, 2012.
Price, H. C., Mattsson, J., Zhang, Y., Bertram, A. K., Davies, J. F., Grayson, J. W., Martin, S. T., O'Sullivan, D., Reid, J. P., Rickards, A. M., and Murray, B. J.: Water diffusion in atmospherically relevant α-pinene secondary organic material, Chem. Sci., 6, 4876–4883, https://doi.org/10.1039/c5sc00685f, 2015.
Pye, H. O. T., Murphy, B. N., Xu, L., Ng, N. L., Carlton, A. G., Guo, H., Weber, R., Vasilakos, P., Appel, K. W., Budisulistiorini, S. H., Surratt, J. D., Nenes, A., Hu, W., Jimenez, J. L., Isaacman-VanWertz, G., Misztal, P. K., and Goldstein, A. H.: On the implications of aerosol liquid water and phase separation for organic aerosol mass, Atmos. Chem. Phys., 17, 343–369, https://doi.org/10.5194/acp-17-343-2017, 2017.
Reid, J. P., Bertram, A. K., Topping, D. O., Laskin, A., Martin, S. T., Petters, M. D., Pope, F. D., and Rovelli, G.: The viscosity of atmospherically relevant organic particles, Nat. Commun., 9, 956, https://doi.org/10.1038/s41467-018-03027-z, 2018.
Renbaum-Wolff, L., Song, M., Marcolli, C., Zhang, Y., Liu, P. F., Grayson, J. W., Geiger, F. M., Martin, S. T., and Bertram, A. K.: Observations and implications of liquid–liquid phase separation at high relative humidities in secondary organic material produced by α-pinene ozonolysis without inorganic salts, Atmos. Chem. Phys., 16, 7969–7979, https://doi.org/10.5194/acp-16-7969-2016, 2016.
Riedel, T. P., Lin, Y. H., Zhang, Z., Chu, K., Thornton, J. A., Vizuete, W., Gold, A., and Surratt, J. D.: Constraining condensed-phase formation kinetics of secondary organic aerosol components from isoprene epoxydiols, Atmos. Chem. Phys., 16, 1245–1254, https://doi.org/10.5194/acp-16-1245-2016, 2016.
Riipinen, I., Pierce, J. R., Yli-Juuti, T., Nieminen, T., Hakkinen, S., Ehn, M., Junninen, H., Lehtipalo, K., Petaja, T., Slowik, J., Chang, R., Shantz, N. C., Abbatt, J., Leaitch, W. R., Kerminen, V. M., Worsnop, D. R., Pandis, S. N., Donahue, N. M., and Kulmala, M.: Organic condensation: a vital link connecting aerosol formation to cloud condensation nuclei (CCN) concentrations, Atmos. Chem. Phys., 11, 3865–3878, https://doi.org/10.5194/acp-11-3865-2011, 2011.
Riipinen, I., Yli-Juuti, T., Pierce, J. R., Petaja, T., Worsnop, D. R., Kulmala, M., and Donahue, N. M.: The contribution of organics to atmospheric nanoparticle growth, Nat. Geosci., 5, 453–458, https://doi.org/10.1038/ngeo1499, 2012.
Roldin, P., Eriksson, A. C., Nordin, E. Z., Hermansson, E., Mogensen, D., Rusanen, A., Boy, M., Swietlicki, E., Svenningsson, B., Zelenyuk, A., and Pagels, J.: Modelling non-equilibrium secondary organic aerosol formation and evaporation with the aerosol dynamics, gas- and particle-phase chemistry kinetic multilayer model ADCHAM, Atmos. Chem. Phys., 14, 7953–7993, https://doi.org/10.5194/acp-14-7953-2014, 2014.
Rothfuss, N. E. and Petters, M. D.: Characterization of the temperature and humidity-dependent phase diagram of amorphous nanoscale organic aerosols, Phys. Chem. Chem. Phys., 19, 6532–6545, https://doi.org/10.1039/C6CP08593H, 2017.
Saha, P. K. and Grieshop, A. P.: Exploring divergent volatility properties from yield and thermodenuder measurements of secondary organic aerosol from α-pinene ozonolysis, Environ. Sci. Technol., 50, 5740–5749, https://doi.org/10.1021/acs.est.6b00303, 2016.
Saleh, R., Donahue, N. M., and Robinson, A. L.: Time scales for gas-particle partitioning equilibration of secondary organic aerosol formed from alpha-pinene ozonolysis, Environ. Sci. Technol., 47, 5588–5594, https://doi.org/10.1021/es400078d, 2013.
Seinfeld, J. H. and Pandis, S. N.: Atmospheric chemistry and physics – From air pollution to climate change, John Wiley & Sons, Inc., New York, 2006.
Shiraiwa, M. and Seinfeld, J. H.: Equilibration timescale of atmospheric secondary organic aerosol partitioning, Geophys. Res. Lett., 39, L24801, https://doi.org/10.1029/2012GL054008, 2012.
Shiraiwa, M., Ammann, M., Koop, T., and Poschl, U.: Gas uptake and chemical aging of semisolid organic aerosol particles, P. Natl. Acad. Sci. USA, 108, 11003–11008, https://doi.org/10.1073/pnas.1103045108, 2011.
Shiraiwa, M., Pfrang, C., Koop, T., and Pöschl, U.: Kinetic multi-layer model of gas-particle interactions in aerosols and clouds (KM-GAP): linking condensation, evaporation and chemical reactions of organics, oxidants and water, Atmos. Chem. Phys., 12, 2777–2794, https://doi.org/10.5194/acp-12-2777-2012, 2012.
Shiraiwa, M., Yee, L. D., Schilling, K. A., Loza, C. L., Craven, J. S., Zuend, A., Ziemann, P. J., and Seinfeld, J. H.: Size distribution dynamics reveal particle-phase chemistry in organic aerosol formation, P. Natl. Acad. Sci. USA, 110, 11746–11750, https://doi.org/10.1073/pnas.1307501110, 2013a.
Shiraiwa, M., Zuend, A., Bertram, A. K., and Seinfeld, J. H.: Gas-particle partitioning of atmospheric aerosols: interplay of physical state, non-ideal mixing and morphology, Phys. Chem. Chem. Phys., 15, 11441–11453, https://doi.org/10.1039/C3CP51595H, 2013b.
Shiraiwa, M., Li, Y., Tsimpidi, A. P., Karydis, V. A., Berkemeier, T., Pandis, S. N., Lelieveld, J., Koop, T., and Pöschl, U.: Global distribution of particle phase state in atmospheric secondary organic aerosols, Nat. Commun., 8, 15002, https://doi.org/10.1038/ncomms15002, 2017.
Shrivastava, M., Cappa, C. D., Fan, J., Goldstein, A. H., Guenther, A. B., Jimenez, J. L., Kuang, C., Laskin, A., Martin, S. T., Ng, N. L., Petaja, T., Pierce, J. R., Rasch, P. J., Roldin, P., Seinfeld, J. H., Shilling, J., Smith, J. N., Thornton, J. A., Volkamer, R., Wang, J., Worsnop, D. R., Zaveri, R. A., Zelenyuk, A., and Zhang, Q.: Recent advances in understanding secondary organic aerosol: Implications for global climate forcing, Rev. Geophys., 55, 509–559, https://doi.org/10.1002/2016RG000540, 2017a.
Shrivastava, M., Lou, S., Zelenyuk, A., Easter, R. C., Corley, R. A., Thrall, B. D., Rasch, P. J., Fast, J. D., Simonich, S. L. M., Shen, H., and Tao, S.: Global long-range transport and lung cancer risk from polycyclic aromatic hydrocarbons shielded by coatings of organic aerosol, P. Natl. Acad. Sci. USA, 114, 1246–1251, https://doi.org/10.1073/pnas.1618475114, 2017b.
Slade, J. H., Shiraiwa, M., Arangio, A., Su, H., Pöschl, U., Wang, J., and Knopf, D. A.: Cloud droplet activation through oxidation of organic aerosol influenced by temperature and particle phase state, Geophys. Res. Lett., 41, 5297–5306, https://doi.org/10.1002/2014GL060582, 2017.
Tong, H., Arangio, A. M., Lakey, P. S. J., Berkemeier, T., Liu, F., Kampf, C. J., Brune, W. H., Pöschl, U., and Shiraiwa, M.: Hydroxyl radicals from secondary organic aerosol decomposition in water, Atmos. Chem. Phys., 16, 1761–1771, https://doi.org/10.5194/acp-16-1761-2016, 2016.
Tröstl, J., Chuang, W. K., Gordon, H., Heinritzi, M., Yan, C., Molteni, U., Ahlm, L., Frege, C., Bianchi, F., Wagner, R., Simon, M., Lehtipalo, K., Williamson, C., Craven, J. S., Duplissy, J., Adamov, A., Almeida, J., Bernhammer, A.-K., Breitenlechner, M., Brilke, S., Dias, A., Ehrhart, S., Flagan, R. C., Franchin, A., Fuchs, C., Guida, R., Gysel, M., Hansel, A., Hoyle, C. R., Jokinen, T., Junninen, H., Kangasluoma, J., Keskinen, H., Kim, J., Krapf, M., Kürten, A., Laaksonen, A., Lawler, M., Leiminger, M., Mathot, S., Möhler, O., Nieminen, T., Onnela, A., Petäjä, T., Piel, F. M., Miettinen, P., Rissanen, M. P., Rondo, L., Sarnela, N., Schobesberger, S., Sengupta, K., Sipilä, M., Smith, J. N., Steiner, G., Tomè, A., Virtanen, A., Wagner, A. C., Weingartner, E., Wimmer, D., Winkler, P. M., Ye, P., Carslaw, K. S., Curtius, J., Dommen, J., Kirkby, J., Kulmala, M., Riipinen, I., Worsnop, D. R., Donahue, N. M., and Baltensperger, U.: The role of low-volatility organic compounds in initial particle growth in the atmosphere, Nature, 533, 527–531, https://doi.org/10.1038/nature18271, 2016.
Vaden, T. D., Imre, D., Beránek, J., Shrivastava, M., and Zelenyuk, A.: Evaporation kinetics and phase of laboratory and ambient secondary organic aerosol, P. Natl. Acad. Sci. USA, 108, 2190–2195, https://doi.org/10.1073/pnas.1013391108, 2011.
Virtanen, A., Joutsensaari, J., Koop, T., Kannosto, J., Yli-Pirilä, P., Leskinen, J., Mäkelä, J. M., Holopainen, J. K., Pöschl, U., and Kulmala, M.: An amorphous solid state of biogenic secondary organic aerosol particles, Nature, 467, 824–827, https://doi.org/10.1038/nature09455, 2010.
Wang, J., Krejci, R., Giangrande, S., Kuang, C., Barbosa, H. M. J., Brito, J., Carbone, S., Chi, X., Comstock, J., Ditas, F., Lavric, J., Manninen, H. E., Mei, F., Moran-Zuloaga, D., Pöhlker, C., Pöhlker, M. L., Saturno, J., Schmid, B., Souza, R. A. F., Springston, S. R., Tomlinson, J. M., Toto, T., Walter, D., Wimmer, D., Smith, J. N., Kulmala, M., Machado, L. A. T., Artaxo, P., Andreae, M. O., Petäjä, T., and Martin, S. T.: Amazon boundary layer aerosol concentration sustained by vertical transport during rainfall, Nature, 539, 416–419, https://doi.org/10.1038/nature19819, 2016.
Ye, J., Gordon, C. A., and Chan, A. W. H.: Enhancement in secondary organic aerosol formation in the presence of preexisting organic particle, Environ. Sci. Technol., 50, 3572–3579, https://doi.org/10.1021/acs.est.5b05512, 2016.
Ye, Q., Robinson, E. S., Ding, X., Ye, P., Sullivan, R. C., and Donahue, N. M.: Mixing of secondary organic aerosols versus relative humidity, P. Natl. Acad. Sci. USA, 113, 12649–12654, https://doi.org/10.1073/pnas.1604536113, 2016.
Ye, Q., Upshur, M. A., Robinson, E. S., Geiger, F. M., Sullivan, R. C., Thomson, R. J., and Donahue, N. M.: Following particle-particle mixing in atmospheric secondary organic aerosols by using isotopically labeled terpenes, Chemistry, 4, 318–333, https://doi.org/10.1016/j.chempr.2017.12.008, 2018.
Yli-Juuti, T., Pajunoja, A., Tikkanen, O.-P., Buchholz, A., Faiola, C., Väisänen, O., Hao, L., Kari, E., Peräkylä, O., Garmash, O., Shiraiwa, M., Ehn, M., Lehtinen, K., and Virtanen, A.: Factors controlling the evaporation of secondary organic aerosol from α-pinene ozonolysis, Geophys. Res. Lett., 44, 2562–2570, https://doi.org/10.1002/2016GL072364, 2017.
You, Y., Renbaum-Wolff, L., Carreras-Sospedra, M., Hanna, S. J., Hiranuma, N., Kamal, S., Smith, M. L., Zhang, X., Weber, R. J., Shilling, J. E., Dabdub, D., Martin, S. T., and Bertram, A. K.: Images reveal that atmospheric particles can undergo liquid–liquid phase separations, P. Natl. Acad. Sci. USA, 109, 13188–13193, https://doi.org/10.1073/pnas.1206414109, 2012.
You, Y., Smith, M. L., Song, M., Martin, S. T., and Bertram, A. K.: Liquid–liquid phase separation in atmospherically relevant particles consisting of organic species and inorganic salts, Int. Rev. Phys. Chem., 33, 43–77, https://doi.org/10.1080/0144235X.2014.890786, 2014.
Zaveri, R. A., Easter, R. C., Shilling, J. E., and Seinfeld, J. H.: Modeling kinetic partitioning of secondary organic aerosol and size distribution dynamics: representing effects of volatility, phase state, and particle-phase reaction, Atmos. Chem. Phys., 14, 5153–5181, https://doi.org/10.5194/acp-14-5153-2014, 2014.
Zaveri, R. A., Shilling, J. E., Zelenyuk, A., Liu, J., Bell, D. M., D'Ambro, E. L., Gaston, C. J., Thornton, J. A., Laskin, A., Lin, P., Wilson, J., Easter, R. C., Wang, J., Bertram, A. K., Martin, S. T., Seinfeld, J. H., and Worsnop, D. R.: Growth kinetics and size distribution dynamics of viscous secondary organic aerosol, Environ. Sci. Technol., 52, 1191–1199, https://doi.org/10.1021/acs.est.7b04623, 2018.
Zhang, X., Pandis, S. N., and Seinfeld, J. H.: Diffusion-limited versus quasi-equilibrium aerosol growth, Aerosol Sci. Tech., 46, 874–885, https://doi.org/10.1080/02786826.2012.679344, 2012.
Zhang, Y., Sanchez, M. S., Douet, C., Wang, Y., Bateman, A. P., Gong, Z., Kuwata, M., Renbaum-Wolff, L., Sato, B. B., Liu, P. F., Bertram, A. K., Geiger, F. M., and Martin, S. T.: Changing shapes and implied viscosities of suspended submicron particles, Atmos. Chem. Phys., 15, 7819–7829, https://doi.org/10.5194/acp-15-7819-2015, 2015.
Zhang, Y., Chen, Y., Lambe, A. T., Olson, N. E., Lei, Z., Craig, R. L., Zhang, Z., Gold, A., Onasch, T. B., Jayne, J. T., Worsnop, D. R., Gaston, C. J., Thornton, J. A., Vizuete, W., Ault, A. P., and Surratt, J. D.: Effect of the Aerosol-Phase State on Secondary Organic Aerosol Formation from the Reactive Uptake of Isoprene-Derived Epoxydiols (IEPOX), Environ. Sci. Technol. Lett., 5, 167–174, https://doi.org/10.1021/acs.estlett.8b00044, 2018.





