the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Three-dimensional simulation of stratospheric gravitational separation using the NIES global atmospheric tracer transport model
Dmitry Belikov
Satoshi Sugawara
Shigeyuki Ishidoya
Fumio Hasebe
Shamil Maksyutov
Shuji Aoki
Shinji Morimoto
Takakiyo Nakazawa
A three-dimensional simulation of gravitational separation, defined as the process of atmospheric molecule separation under gravity according to their molar masses, is performed for the first time in the upper troposphere and lower stratosphere. We analyze distributions of two isotopes with a small difference in molecular mass (13C16O2 (Mi=45) and 12C16O2 (Mi=44)) simulated by the National Institute for Environmental Studies (NIES) chemical transport model (TM) with a parameterization of molecular diffusion. The NIES model employs global reanalysis and an isentropic vertical coordinate and uses optimized CO2 fluxes. The applicability of the NIES TM to the modeling of gravitational separation is demonstrated by a comparison with measurements recorded by high-precision cryogenic balloon-borne samplers in the lower stratosphere. We investigate the processes affecting the seasonality of gravitational separation and examine the age of air derived from the tracer distributions modeled by the NIES TM. We find a strong relationship between age of air and gravitational separation for the main climatic zones. The advantages and limitations of using age of air and gravitational separation as indicators of the variability in the stratosphere circulation are discussed.
Chapman and Milne (1920) proposed two different dynamical regimes: the homosphere (perfect mixing) in the lower part of the atmosphere and the heterosphere (diffusive equilibrium), where molecular diffusion leads to a separation of the atmospheric constituents according to their molecular mass. The process of atmospheric molecule separation according to their molar mass under gravity is termed “gravitational separation” (GS). The GS of atmospheric components is recognized as dominant in the atmosphere above a level of about 100 km called the turbopause (Warneck and Williams, 2012). Recently, the existence of GS of the major atmospheric components in the stratosphere was confirmed both experimentally using a precise cryogenic sampler and theoretically by two-dimensional numerical model simulations (Ishidoya et al., 2008, 2013).
The Brewer–Dobson circulation (BDC) is the global circulation in the stratosphere, consisting of air masses that rise across the tropical tropopause and then move poleward and descend into the extratropical troposphere (Butchart, 2014). Currently, the “mean age of air” (mean AoA), defined as the average time that an air parcel has spent in the stratosphere, is perhaps best known for being a proxy for the rate of the stratospheric mean meridional circulation and the whole BDC. The mean AoA provides an integrated measure of the net effect of all transport mechanisms on the tracers and air mass fluxes between the troposphere and stratosphere (Hall and Plumb, 1994; Waugh and Hall, 2002).
The increase in greenhouse gas abundance is leading to increased radiative forcing and therefore to warming of the troposphere and cooling of the stratosphere (Field et al., 2014). A strengthened BDC under climate change in the middle and lower stratosphere is robustly predicted by various chemistry–climate models (Butchart et al., 2006; Butchart, 2014; Garcia and Randel, 2008; Li et al., 2008; Stiller et al., 2012; Garfinkel et al., 2017). However, this is not in agreement with over 30 years of observations of the age of stratospheric air (Engel et al., 2009; Hegglin et al., 2014; Ray et al., 2014).
The sparse limited observations in the upper troposphere and lower stratosphere (UTLS) mean that chemical transport models (CTMs) are complementary and useful tools for widely diagnosing the BDC and representing the global transport and distribution of long-lived species. CTMs perform relatively well in the UTLS despite resolution issues. Confidence is high in the ability of models to reproduce many of the features, including the basic dynamics of the stratospheric BDC and the tropospheric baroclinic general circulation in the extratropics, the tropopause inversion layer, the large-scale zonal mean, and tropical and extratropical tropopause (Hegglin et al., 2010; Gettelman et al., 2011).
As future changes to the BDC are likely to be complex, a suite of methods, parameters, and tools is necessary to detect these changes. Leedham Elvidge et al. (2018) evaluated the capability of using seven trace gases to estimate stratospheric mean ages. Ishidoya et al. (2013) proposed using GS as an indicator of changes in the atmospheric circulation in the stratosphere. Analyses of GS, in addition to the CO2 and SF6 ages, may be useful for providing information on stratospheric circulation.
Ishidoya et al. (2013) also performed the first simulation of GS using the NCAR two-dimensional (2-D) SOCRATES model (Simulation Of Chemistry, Radiation, and Transport of Environmentally important Species, Huang et al., 1998), which is an interactive chemical, dynamical, and radiative model. The spatial domain of the model extends from the surface to 120 km in altitude. The vertical and horizontal resolutions are 1 km and 5∘, respectively. To extend the earlier work and overcome the inherent limitations of the 2-D model, we here present a more quantitative analysis using the National Institute for Environmental Studies (NIES) Eulerian three-dimensional (3-D) transport model (TM). The remainder of this paper is organized as follows. Overviews of the NIES TM, a method for modeling GS, and the simulation setup are provided in Sect. 2. In Sect. 3 we study modeled GS and compare vertical profiles with those observed. Finally, a summary and conclusions are provided in Sect. 4.
For further investigation of the GS process we redesigned and modified the NIES TM, which has previously been used to study the seasonal and inter-annual variability of greenhouse gases (i.e., CO2 and CH4 by Belikov et al., 2013b).
2.1 Model
The NIES model is an offline transport model driven by the Japanese Meteorological Agency Climate Data Assimilation System (JCDAS) datasets (Onogi et al., 2007). It employs a reduced horizontal latitude–longitude grid with a spatial resolution of near the equator (Maksyutov and Inoue, 2000) and a flexible hybrid sigma–isentropic (σ–θ) vertical coordinate, which includes 32 levels from the surface up to 5 hPa (Belikov et al., 2013b).
The model uses a revised version of hybrid isentropic grid. The original version used isentropic levels above the 350 K potential temperature level and sigma levels between the surface and 350 K level (Belikov et al., 2013b). A modified hybrid isentropic grid was introduced to simulate better vertical transport above the tropopause, extending the bottom level of the isentropic part to 295 K, as first used in the NIES TM simulation for the age-of-air intercomparison study (Krol et al., 2018). To limit application of the isentropic grid to the mid- to upper troposphere, for each potential temperature level between 295 and 350 K, a corresponding upper limit for pressure is set at fixed sigma level. For each theta level in a list [295, 300, 305, 310, 315, 320, 330, 340], the upper sigma limit is gradually changing from a sigma level of 0.6 for the 295 K level to 0.35 for the 340 K level, as [0.6, 0.54, 0.5, 0.47, 0.44, 0.41, 0.38, 0.35, 0.32]. For model levels between 295 and 340 K, once the sigma level reaches the prescribed maximum for this model level, vertical transport switches from one based on the diabatic heating rate to using vertical wind provided by reanalysis. Over the isentropic part of the grid, the vertical transport follows the seasonally varying climatological diabatic heating rate derived from reanalysis.
Following the approach by Hack et al. (1993), transport processes in the planetary boundary layer (height provided by the ECMWF ERA-Interim reanalysis; Dee et al., 2011) and in the free troposphere are separated with a turbulent diffusivity parameterization. The modified cumulus convection parameterization scheme computes the vertical mass fluxes in a cumulus cell using conservation of moisture derived from a distribution of convective precipitation in the reanalysis dataset (Austin and Houze Jr., 1973; Belikov et al., 2013a). To set cloud top and cloud bottom height a modified Kuo-type parameterization scheme (Grell et al., 1995) is used. Computation of entrainment and detrainment processes accompanying the transport by convective updrafts and downdrafts is as employed by Tiedtke (1989).
2.2 Molecular diffusion
According to Banks and Kockarts (1973), assuming a neutral gas, the equation for the vertical component of the diffusion velocity of gas 1 relative to gas 2 () in a binary mixture of gas 1 and gas 2 in a gravitational field can be written as
where n1 and n2 are the concentrations of particles 1 and 2, respectively; is the total concentration of the binary mixture; T is the absolute neutral gas temperature; p is the total pressure; M1 and M2 are the masses of particles 1 and 2; is the mean molecular mass; D12 is the molecular diffusion coefficient of gas 1 in gas 2; and αT is the thermal diffusion factor. The three terms in the brackets represent, from left to right, the effects of concentration gradient, pressure gradient, and temperature gradient, respectively, on the molecular diffusion velocity.
If component i is a multicomponent mix of minor constituents, then, using the hydrostatic equation, the perfect gas law, and Eq. (1), the diffusion velocity wi for the ith minor constituent can be written in time-independent form (for more details see pp. 33–34 in Banks and Kockarts, 1973):
where is the scale height, J K−1 is the Boltzmann constant, g=9.81 m s−2 is the standard acceleration due to gravity for Earth, and Di is the molecular diffusion coefficient. Here also ni and are the number density and the thermal diffusion factor for species i, respectively.
Similar to the SOCRATES model the vertical component of velocity is converted to the vertical component of the molecular diffusion flux of a minor constituent i relative to air (Huang et al., 1998):
The molecular diffusion coefficient is estimated from kinetic gas theory by Banks and Kockarts (1973) to be
where Mi and M are the mass of the minor constituent i and the mean molecular mass in atomic mass units, respectively, and n is the number density of air.
To derive a diffusive flux formulation consistent with the NIES model transport equation, the number density ni is substituted by the mixing ratio :
Here H is the atmospheric scale height, and is assumed to be zero since the thermal diffusion effect would be of no importance in the stratosphere (Ishidoya et al., 2013). The derived flux was added to the standard transport formulation for each species.
The eddy vertical diffusion in the stratosphere is often neglected in CTMs. However, it should be considered along with molecular diffusion for modeling GS. In the SOCRATES model two options are available for the parameterization of the gravity wave forcing and vertical diffusion coefficient (Huang et al., 1998). The default standard option uses the Lindzen–Holton gravity wave breaking scheme (Lindzen, 1981; Holton, 1982). A second option is to use the parameterization scheme developed primarily by Fritts and Lu (1993), which uses a general gravity wave spectral formulation provided by the observed gravity wave spectrum to deduce how the gravity wave energy flux responds to variation in the background environment. The first scheme was adopted in the current NIES TM simulation. In general, the eddy diffusion mixes concentrations in the volume, reduces vertical stratification, and thereby weakens the molecular diffusion effect, as discussed by Kockarts (2002).
2.3 Simulation setup
The study of GS requires considering two isotopes of atmospheric tracers with a small difference in molecular mass. Following the setup for the SOCRATES baseline-atmosphere run (Ishidoya et al., 2013), we calculated the distributions of 13C16O2 (Mi=45) and 12C16O2 (Mi=44). Firstly, a 20-year spin-up calculation with CO2 using biospheric and oceanic fluxes only and then a 29-year (1988–2016) simulation with total CO2 fluxes (biospheric, oceanic, and fossil fuel) were performed. The fluxes used were obtained with the GELCA-EOF (Global Eulerian–Lagrangian Coupled Atmospheric model with Empirical Orthogonal Function) inverse modeling scheme (Zhuravlev et al., 2013). This set of fluxes reproduces realistic time and spatial distributions of CO2 mixing ratio with strong seasonal variations in the Northern Hemisphere (NH) and weak variations in the Southern Hemisphere (SH). The period 1988–2014 is covered by the original JCDAS, which is extended by JRA-55 (an updated version of the Japanese reanalysis) remapped to the same horizontal and vertical grid, as JCDAS production discontinued after 2014. Use of JRA-55 for the whole simulated period is preferable; however, model redevelopment is required to take full advantage of the improved vertical and horizontal resolutions.
The 〈δ〉 value, a measure of the GS, is defined as the isotopic ratio of the CO2:
where subscripts strat and trop denote the stratospheric and tropospheric values, respectively. As the tropospheric value trop we selected the model tracer concentration from the third level, which corresponds to the lower boundary of the free troposphere. The tropospheric 〈δ〉 variations are very small and negligible compared with those in the stratosphere.
CO2 is a useful tracer of atmospheric dynamics and transport due to its long lifetime. It is chemically inert in the free troposphere and has only a small stratospheric source (up to 1 ppm) from methane oxidation (Boucher et al., 2009). Sufficiently accurate estimation of emissions and sinks, together with knowledge of their trend in combination with the good performance of the NIES model in simulating greenhouse gases, makes the selection of CO2 appropriate for this study.
3.1 Zonal mean distribution
The zonal mean distribution of CO2 in the upper part of the atmosphere is driven by the large-scale transport processes: fast quasi-isentropic mixing is combined with upwelling in the tropics and downwelling in the extratropical lowermost stratosphere. In the troposphere, vertical mixing is well developed. With height, the dynamic characteristics weaken, and the mass flux due to molecular diffusion increases (Eq. 3). At a certain level near the tropopause, vertical mixing is no longer able to suppress diffusion and the 〈δ〉 value becomes nonzero.
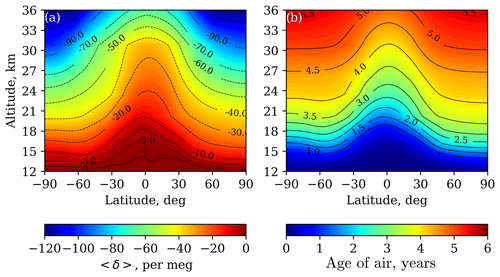
Figure 1Annual mean altitude–latitude distributions of 〈δ〉 value (per meg) (a) and the AoA (years) (b) calculated using the NIES TM. The unit (per meg) is typically used in isotope analysis and is the same as 10−3 ‰.
Along with the 〈δ〉 value we analyze the AoA (Fig. 1). For this, we used the idealized linearly growing “surface” tracer proposed in the age-of-air intercomparison project (Krol et al., 2018). To fit with our analysis period we extended the original simulation period (1988–2014) to 29 years (1988–2016) with a shorter (10 years) spin-up, as less time is required to reach equilibrium for the AoA analysis.
The processes creating the deformation of the zonal mean cross sections of the GS and the AoA are similar here: the tropical upwelling pumps in tropospheric air and stretches the parameter profile upward (Fig. 1). The NIES TM results shows strong subtropical mixing barriers in both hemispheres compared with the SOCRATES model.
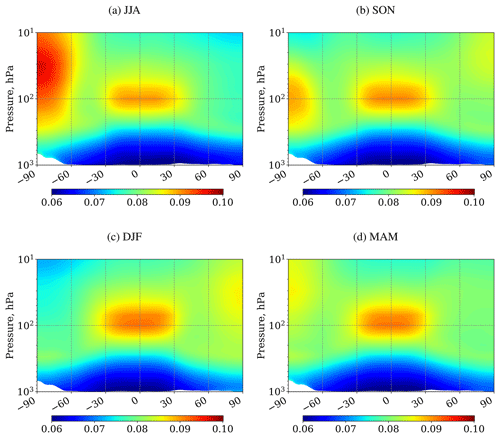
Figure 2Mean altitude–latitude distributions of the difference between the reciprocals of Hi and H ( [1 km−1], see text) for (a) JJA, (b) SON, (c) DJF, and (d) MAM. The results are averaged for 2000–2015.
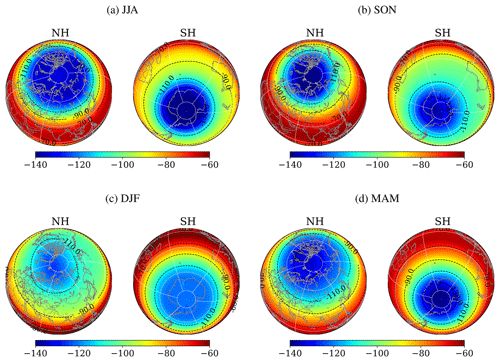
Figure 3Mean latitude–longitude distributions of 〈δ〉 value at the 10 hPa level in south polar and north polar projections for (a) JJA, (b) SON, (c) DJF, and (d) MAM. The results are averaged for 2000–2015.
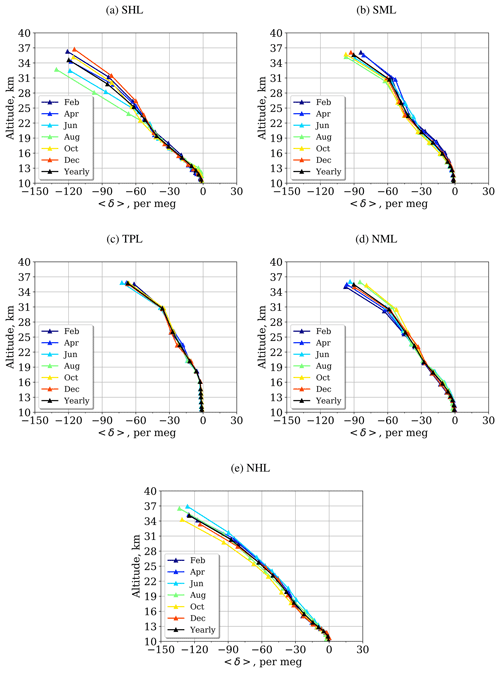
Figure 4Profiles of 〈δ〉 calculated by the model for February, April, June, August, October, December, and yearly mean averaged for 2000–2015 over the five latitudinal bands shown in Table 1
To estimate the contribution of atmospheric conditions to molecular diffusion, we consider the sum of the three terms in the square bracket of Eq. (5). Because the contribution of the first term (concentration gradient) is relatively small, the second term (originated from pressure gradient in Eq. 1) is the major contributor among the three terms. Therefore, the sum of the three terms can be approximated by the difference between the reciprocals of two scale heights (hereafter referred to as ). It has a dimension reciprocal to the length and is interpreted as a measure of the efficiency of vertical molecular diffusion under gravity. In view of the essentially one-dimensional nature of GS, it is interesting to consider how distributes in the troposphere and stratosphere. Figure 2 shows the latitude–height distribution of averaged in each season for the case of 12C16O2. Here the positive values indicate that 12C16O2 molecules descend relative to major constituents. The temperature fields necessary for the calculation are taken from the JCDAS reanalysis. Since is inversely proportional to temperature, it is generally small in the troposphere and has maxima in cold regions such as the tropical tropopause region and the winter time stratosphere.
The enhancement of does not readily result in a remarkable GS, because it is the difference of between 13C16O2 and 12C16O2 that creates GS in our case. We could expect that the enhancement of combined with the long stratospheric transit time in the polar stratosphere will be favorable for GS. Figure 3 compares the horizontal distributions of the seasonal mean 〈δ〉 on 10 hPa pressure surface in polar projections. We can see remarkable GS (small values of 〈δ〉) in both polar regions exhibiting surprisingly clear axial symmetry. In the present analysis, the physical processes that drive GS (Eq. 1) have been rearranged in the form of Eq. (5) to separate the contribution to GS in two factors, one the concentration gradient (the first term) and the other the temperature structure. A stronger seasonal variability of GS in the Southern Hemisphere is caused by changes in vertical pressure gradient (Eq. 1) reflected to those in scale height difference between species.
To minimize local temporal and spatial effects, the seasonal variation of vertical profiles was analyzed for five main climate zones: the southern and northern high latitudes, the southern and northern middle latitudes, and the tropics, as shown in Table 1 and averaged over time (2000–2015). It is clear from Fig. 4 that seasonal variation is evident from a level of about 12 km, except in the tropical region, where it starts from 20 km. The amplitude increases with height and reaches a maximum at the top of the model domain. It is quite obvious that seasonal variability is almost imperceptible in the tropics and increases towards the poles. The maximum and minimum values are reached in December–February and June–August for the South Pole and in April–June and October–December for the North Pole, respectively.
Probably the stronger polar vortex in the SH presumably leads to the enhanced GS (smaller values of 〈δ〉) in JJA in the SH (Figs. 3a and 4a light blue line) compared to that in DJF in the NH (Figs. 3c and 4e). In the NH, on the other hand, GS appears weakest during winter (Fig. 3c) in spite of the enhancement of (Fig. 2c).
Weak sensitivity to seasonal changes of the tracer concentration is a significant advantage of GS over AoA, which is the standard indicator of circulation in the stratosphere. On the other hand, this method requires more accurate sampling tools (i.e., balloon-borne cryogenic samplers) that are more difficult to deploy than other more common methods.
3.2 Vertical profiles
The modeled results are compared with measurements over the main climatic zones: the circumpolar regions, the temperate latitudes, and the tropical latitudes (Table 2). The collection of stratospheric air samples using a balloon-borne cryogenic sampler was initiated in 1985 at the Sanriku Balloon Center of the Institute of Space and Astronautical Science (Nakazawa et al., 1995, 2002; Aoki et al., 2003; Goto et al., 2017; Sugawara et al., 2018; Hasebe et al., 2018). The program has continued up to the present. In addition to observations over Japan, stratospheric air samples were also collected over the Scandinavian Peninsula, Antarctica, and Indonesia.
From those air samples, δ(15N) of N2, δ(18O) of O2, δ(O2∕N2), δ(Ar∕N2), and δ(40Ar) were derived to detect GS in the stratosphere (Ishidoya et al., 2006, 2008, 2013). The effect of GS on the isotopic ratio depends on Δm rather than on the atmospheric component, as follows from Eq. 6. Thus δ values from observations of various tracers and the current simulations can be compared.
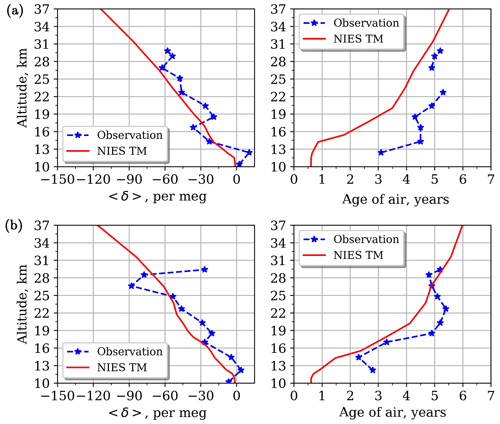
Figure 7Same as Fig. 5 but over the Syowa station for 3 January 1998 (a) and 5 January 2004 (b).
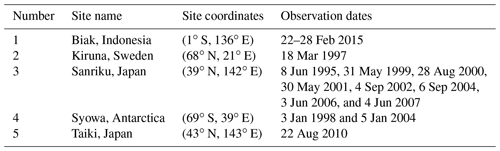
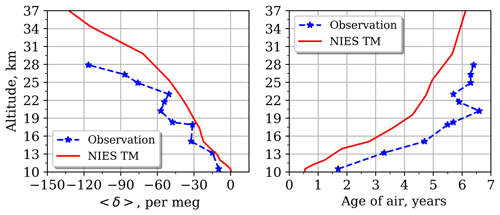
Most of the observations were collected in the northern part of Japan over Sanriku (eight profiles) and Taiki (one) in the warm season. Five profiles were observed at the beginning of summer (late May to early June) and four profiles at the end of summer (late August to early September). Typical spring and fall profiles are shown in Fig. 5. For this comparison, the modeled data are daily output at the nearest grid cell.
In the NH, the tropospheric CO2 is dominated by a strong seasonal cycle due to biospheric activity, which removes CO2 by photosynthesis during the growing phase to reach a minimum in August–September and releases it during boreal autumn and winter with a maximum in April–May. Due to steady growth and seasonal variation, CO2 concentrations in the atmosphere contain both monotonically increasing and periodic signals. Spring profiles are smoother, while in autumn they vary with height. The observed AoA shows a strong inversion in the lower altitudes due to seasonal uptake of CO2, as confirmed by CONTRAIL measurements (Machida et al., 2008; Sawa et al., 2008) and the Lagrangian transport model TRACZILLA (Diallo et al., 2017). The AoA calculated from the modeled surface tracer does not reproduce such effect.
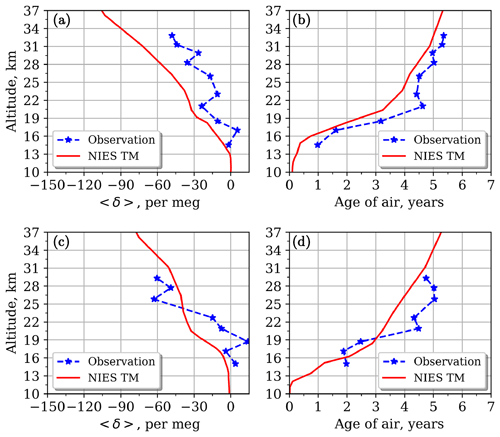
For the high-latitude sites Kiruna and Syowa (Figs. 6–7) the observed profiles are mainly smooth and have smaller vertical fluctuation, apart from the uppermost level over the Syowa station for 5 January 2004.
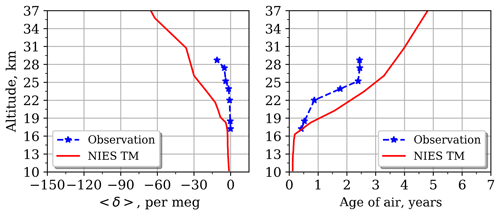
Due to the limited availability of balloon launching facilities, only one air sample has been conducted in the equatorial mid-stratosphere over Biak (Hasebe et al., 2018). The observed distribution can be explained by the mixing of large-scale NH and SH background values and long-range tracer transport with convective lifting (Inai et al., 2018). For this site, the 〈δ〉 value and the AoA variations with height are very small (Fig. 8), as vertical upwelling pumps young and well-mixed air upward.
Although this is not a model validation paper, it is necessary to evaluate the modeled results by comparison with observations, as the new parameterization for GS simulation was incorporated in the NIES TM. A detailed statistical analysis is summarized for the five observational sites in Table 3. This includes the standard deviation of the misfit between modeled and observed AoA and 〈δ〉 (σ(ΔAoA) and σ(Δ〈δ〉), respectively), the Pearson correlation coefficient between modeled and observed AoA and 〈δ〉 (r(AoA) and r(〈δ〉), respectively), and the Pearson correlation coefficient between AoA and 〈δ〉 from observation (r(AoA, 〈δ〉)o) and from the model (r(AoA, 〈δ〉)m). To calculate standard deviation and correlation coefficients only coincident points were selected.
The high values of the correlation coefficients between simulated and observed parameters prove the model efficiency with the implemented parameterization. The lower correlation for GS than for r(AoA) stresses the complexity of the high-precision cryogenic sampling required for GS. For example, most observed profiles show a tendency to have zones of very weak increase or even inversion of the parameters starting from a level of 20–25 km. Despite these limitations, the ability to study the physics underlying GS is a fundamental advantage of the 3-D simulation compared with the 2-D simulation as performed by SOCRATES.
The standard deviations σ(AoA) and σ(〈δ〉) quantify model–observation misfits. We stress a tendency of increase towards the high latitudes, although it seems that a larger gap is obtained for Biak. However, if we normalize the standard deviations by the value of the absolute maximum value of the characteristic, the error decreases towards high latitudes.
Table 3Standard deviation of misfit between modeled and observed AoA and 〈δ〉 value (σ(ΔAoA) and σ(Δ〈δ〉), respectively); the Pearson correlation coefficient between modeled and observed AoA and 〈δ〉 value (r(AoA) and r(〈δ〉), respectively); the Pearson correlation coefficient between AoA and 〈δ〉 from observation (r(AoA, 〈δ〉)o) and from the model (r(AoA, 〈δ〉)m).

GS and AoA are useful indicators of atmospheric transport processes. Two other correlations from Table 3 (r(AoA, 〈δ〉)o and r(AoA, 〈δ〉)m) quantify their relationship. Since one value increases with height and the other decreases, the correlation is negative. Modeled results show stronger anti-correlation than that observed, probably due to more straightforward connections in transport simulation; the parameterization used may not take into account additional factors affecting GS. We also do not exclude the influence of observational errors.
3.3 Relationship between age of air and 〈δ〉
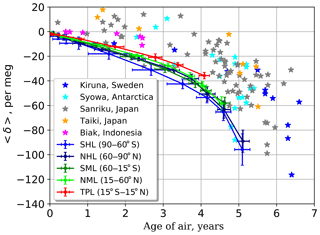
Further study of the relationship between the AoA and the 〈δ〉 value is useful for understanding the atmospheric processes, as both would be affected to some extent by changes in the stratospheric circulation. For comparison the modeled AoA and 〈δ〉 values were averaged over the same five broad-latitude bands as in Sect. 3.1 (see Table 1). Along with the modeled values (solid lines) the observed data are also depicted (symbols) in Fig. 9. Observation sites are quite evenly distributed across the selected latitude bands: Syowa in the southern high latitudes, Biak in the tropics, Sanriku and Taiki in the northern middle latitudes, and Kiruna in the northern high latitudes.
Figure 9 shows a near-one-to-one relationship between AoA and GS regardless of latitude and height. Although the model–observation discrepancy is significant for all layers, the distributions of observations show a similar pattern for the lower part of the stratosphere despite large scatter. The positive 〈δ〉 values obtained from observations are not reproducible according to the theory.
The 〈δ〉 value decreases rapidly for age values older than 4 years, as the molecular diffusion coefficient increases with increasing height due to its pressure dependence (Eq. 4), which causes the enhancement of gravitational separation with increasing height. This mechanism does not affect AoA significantly in the stratosphere (Ishidoya et al., 2008, 2013; Sugawara et al., 2018). This emphasizes a nonlinearity in the GS–AoA relationship in the stratosphere.
Another difference stressed the independence of the driving mechanisms of AoA, and GS is the influence of the seasonal variation. For younger air (0–2 years) the seasonal variability of AoA is maximal and falls with altitude, while the 〈δ〉 variability increases continuously upwards, as described in Sect. 3.1.
Sugawara et al. (2018) assumed that vertical upwelling in he tropical tropopause layer (TTL) acts to weaken and downwelling in high latitudes acts to strengthen the effect on the GS. To minimize the discrepancy between the model-calculated (with SOCRATES) and observed 〈δ〉 values over the equatorial region, a correction of the mean meridional circulation and the horizontal eddy diffusivity was performed. However, that correction cannot fully improve the simulation of the stratospheric circulation and hence the reproducibility of AoA and GS by the SOCRATES model. In this study the tracer simulation is based on reanalysis, which describes the atmospheric circulation in sufficient detail. As part of the global balanced air transport the upwelling and downwelling are limited by various constraints including mass flux conservation. The resulting tracer field distribution simultaneously describes AoA and GS, so both parameters can be used to describe the structure of the global atmospheric circulation. However, the limited set of observations and the limitations of the model do not yet allow us to investigate this mechanism and determine the structure of the AoA–GS relationship in more detail.
Chabrillat et al. (2018) presented a consistent intercomparison of AoA according to five modern reanalyses (ERA-Interim, JRA-55, MERRA, MERRA-2, and CFSR) and found significant diversity in the distributions which were obtained with the BASCOE (Belgian Assimilation System for Chemical Observations) transport model, depending on the input reanalysis. They have also found large disagreement between the five reanalyses with respect to the long-term trends of AoA. Thus, an ambitious multi-reanalyses approach is needed to distinguish what is robust in the current GS results from what is not.
A three-dimensional simulation of GS in the UTLS zone is performed for the first time using the NIES TM with a molecular diffusion parameterization. We consider the 〈δ〉 values derived from the distribution of two isotopes 12C16O2 and 13C16O2. The modeled 〈δ〉 values are compared to observations and the zonal mean distributions from the two-dimensional SOCRATES model.
In comparison with the SOCRATES simulation, the NIES model has a number of significant advantages: a three-dimensional tracer transport simulation driven by global JCDAS reanalysis and a vertical coordinate with isentropic levels. The model is optimized to run the greenhouse gas simulation, as confirmed through various validation and multi-model inter-comparisons. The use of optimized CO2 fluxes provided realistic tracer distribution and seasonality. Along with these strengths, some weaknesses are also revealed: coarse vertical resolution and the shallow top of the model domain.
The model-to-observation comparison shows that the model with this molecular diffusion parameterization is able to reproduce the mean value and the number of small-scale fluctuations recorded by high-precision cryogenic balloon-borne observations in the lower stratosphere. This reconstruction suggests that the tracer distribution can be explained by the properties of transport, as resolved by meteorological reanalysis and the representation of sub-grid-scale effects as diffusion. Overall, the implemented molecular diffusion parameterization in the NIES TM shows reasonable performance.
We found a strong relationship between the modeled GS and AoA, which is the main indicator of circulation in the stratosphere. However, in contrast to AoA, the GS has a lower sensitivity to seasonal variability, which is a significant issue in studies of atmospheric circulation. Thus, the modeled GS characteristics can provide useful insights and complement AoA information to give a more comprehensive evaluation of structure changes in the UTLS. However, due to the simplified approach and parameterizations, the presented simulation of the GS using the NIES model could not fully achieve the potential of 3-D modeling. Modern reanalysis dataset and recently developed transport models that effectively simulated the upper atmosphere can be employed to address these issues. Since this work is the first in 3-D modeling of GS, we believe this insight is useful for the scientific community working in the field of the UTLS studies.
Additional data requests should be addressed to Dmitry Belikov (dmitry.belikov@ees.hokudai.ac.jp).
DB carried out the NIES model simulations and the data analysis. SS, SI and FH contributed to the design of the analysis and theoretical description of the GS process. SM prepared the reanalysis data and contributed code of the NIES TM. SA, SM and TK provided the observational data. SS, SI, FH, SM, SA, SM and TK provided helpful discussion and comments. DB wrote the manuscript with contributions from all co-authors.
The authors declare that they have no conflict of interest.
We sincerely thank the balloon engineering group of the Institute of Space and Astronautical Science JAXA for their cooperation in our stratospheric air sampling. This work is partly supported by the Japan Society for Promotion of Science, Grant-in-Aid for Scientific Research (S) 26220101. We thank Masatomo Fujiwara, associated Professor at Hokkaido University for useful comments regarding the GS studies.
This paper was edited by Peter Haynes and reviewed by two anonymous referees.
Aoki, S., Nakazawa, T., Machida, T., Sugawara, S., Morimoto, S., Hashida, G., Yamanouchi, T., Kawamura, K., and Honda, H.: Carbon dioxide variations in the stratosphere over Japan, Scandinavia and Antarctica, Tellus B, 55, 178–186, 2003. a
Austin, P. M. and Houze Jr., R. A.: A technique for computing vertical transports by precipitating cumuli, J. Atmos. Sci., 30, 1100–1111, 1973. a
Banks, P. and Kockarts, G.: Aeronomy, Academic, New York, ISBN: 9781483260068, Academic Press, 372 pp., 1973. a, b, c
Belikov, D. A., Maksyutov, S., Krol, M., Fraser, A., Rigby, M., Bian, H., Agusti-Panareda, A., Bergmann, D., Bousquet, P., Cameron-Smith, P., Chipperfield, M. P., Fortems-Cheiney, A., Gloor, E., Haynes, K., Hess, P., Houweling, S., Kawa, S. R., Law, R. M., Loh, Z., Meng, L., Palmer, P. I., Patra, P. K., Prinn, R. G., Saito, R., and Wilson, C.: Off-line algorithm for calculation of vertical tracer transport in the troposphere due to deep convection, Atmos. Chem. Phys., 13, 1093–1114, https://doi.org/10.5194/acp-13-1093-2013, 2013a. a
Belikov, D. A., Maksyutov, S., Sherlock, V., Aoki, S., Deutscher, N. M., Dohe, S., Griffith, D., Kyro, E., Morino, I., Nakazawa, T., Notholt, J., Rettinger, M., Schneider, M., Sussmann, R., Toon, G. C., Wennberg, P. O., and Wunch, D.: Simulations of column-averaged CO2 and CH4 using the NIES TM with a hybrid sigma-isentropic (σ−Θ) vertical coordinate, Atmos. Chem. Phys., 13, 1713–1732, https://doi.org/10.5194/acp-13-1713-2013, 2013b. a, b, c
Boucher, O., Friedlingstein, P., Collins, B., and Shine, K. P.: The indirect global warming potential and global temperature change potential due to methane oxidation, Environ. Res. Lett., 4, 044007, https://doi.org/10.1088/1748-9326/4/4/044007, 2009. a
Butchart, N.: The Brewer-Dobson circulation, Rev. Geophys., 52, 157–184, 2014. a, b
Butchart, N., Scaife, A., Bourqui, M., De Grandpré, J., Hare, S., Kettleborough, J., Langematz, U., Manzini, E., Sassi, F., Shibata, K., Shindell, D., and Sigmond, M.: Simulations of anthropogenic change in the strength of the Brewer–Dobson circulation, Clim. Dynam., 27, 727–741, 2006. a
Chabrillat, S., Vigouroux, C., Christophe, Y., Engel, A., Errera, Q., Minganti, D., Monge-Sanz, B. M., Segers, A., and Mahieu, E.: Comparison of mean age of air in five reanalyses using the BASCOE transport model, Atmos. Chem. Phys., 18, 14715–14735, https://doi.org/10.5194/acp-18-14715-2018, 2018. a
Chapman, S. and Milne, E.: The composition, ionisation and viscosity of the atmosphere at great heights, Q. J. Roy. Meteorol. Soc., 46, 357–398, 1920. a
Dee, D. P., Uppala, S. M., Simmons, A., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M., Balsamo, G., Bauer, D. P., Bechtold, P., M. Beljaars, A. C., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L.,, Healy, Hersbah, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system, Q. J. Roy. Meteorol. Soc., 137, 553–597, 2011. a
Diallo, M., Legras, B., Ray, E., Engel, A., and Añel, J. A.: Global distribution of CO2 in the upper troposphere and stratosphere, Atmos. Chem. Phys., 17, 3861–3878, https://doi.org/10.5194/acp-17-3861-2017, 2017. a
Engel, A., Möbius, T., Bönisch, H., Schmidt, U., Heinz, R., Levin, I., Atlas, E., Aoki, S., Nakazawa, T., Sugawara, S., Moore, F., Hurst, D., Elkins, J., Schauffler, S., Andrews, A., and Boering, K.: Age of stratospheric air unchanged within uncertainties over the past 30 years, Nat. Geosci., 2, 28–31, 2009. a
Field, C. B., Barros, V. R., Mach, K., and Mastrandrea, M.: Climate change 2014: impacts, adaptation, and vulnerability, Vol. 1, Cambridge University Press Cambridge and New York, p. 1140, 2014. a
Fritts, D. C. and Lu, W.: Spectral estimates of gravity wave energy and momentum fluxes, Part II: Parameterization of wave forcing and variability, J. Atmos. Sci., 50, 3695–3713, 1993. a
Garcia, R. R. and Randel, W. J.: Acceleration of the Brewer–Dobson circulation due to increases in greenhouse gases, J. Atmos. Sci., 65, 2731–2739, 2008. a
Garfinkel, C. I., Aquila, V., Waugh, D. W., and Oman, L. D.: Time-varying changes in the simulated structure of the Brewer–Dobson Circulation, Atmos. Chem. Phys., 17, 1313–1327, https://doi.org/10.5194/acp-17-1313-2017, 2017. a
Gettelman, A., Hoor, P., Pan, L. L., Randel, W. J., Hegglin, M. I., and Birner, T.: The extratropical upper troposphere and lower stratosphere, Rev. Geophys., 49, RG3003, https://doi.org/10.1029/2011RG000355, 2011. a
Goto, D., Morimoto, S., Aoki, S., Sugawara, S., Ishidoya, S., Inai, Y., Toyoda, S., Honda, H., Hashida, G., Yamanouchi, T., and Nakazawa, T.: Vertical profiles and temporal variations of greenhouse gases in the stratosphere over Syowa Station, Antarctica, SOLA, 13, 224–229, 2017. a
Grell, G. A., Dudhia, J., and Stauffer, D. R.: A description of the fifth-generation Penn State/NCAR mesoscale model (MM5), NCAR Tech. Note, p. 122, 1995. a
Hack, J. J., Boville, B. A., Briegleb, B. P., Kiehl, J. T., Rasch, P. J., and Williamson, D. L.: Description of the NCAR community climate model (CCM2), NCAR Tech. Note, 382, p. 120, 1993. a
Hall, T. M. and Plumb, R. A.: Age as a diagnostic of stratospheric transport, J. Geophys. Res.-Atmos., 99, 1059–1070, https://doi.org/10.1029/93JD03192, 1994. a
Hasebe, F., Aoki, S., Morimoto, S., Inai, Y., Nakazawa, T., Sugawara, S., Ikeda, C., Honda, H., Yamazaki, H., Halimurrahman, Komala, N., Putri, F. A., Budiyono, A., Soedjarwo, M., Ishidoya, S., Toyoda, S., Shibata, T., Hayashi, M., Eguchi, N., Nishi, N., Fujiwara, M., Ogino, S.-Y., Shiotani, M., and Sugidachi, T.: Coordinated Upper-troposphere-to-stratosphere Balloon Experiment in Biak (CUBE/Biak), B. Am. Meteorol. Soc., 99, 1213–1230, 2018. a, b
Hegglin, M. I., Plummer, D. A., Shepherd, T. G., Scinocca, J. F., Anderson, J., Froidevaux, L., Funke, B., Hurst, D., Rozanov, A., Urban, J., von Clarmann, T., Walker, K. A., Wang, H. J., Tegtmeier, S., and Weigel, K.: Vertical structure of stratospheric water vapour trends derived from merged satellite data, Nat. Geosci., 7, 768–776, 2014. a
Hegglin, M. I., Gettelman, A., Hoor, P., Krichevsky, R., Manney, G. L., Pan, L. L., Son, S.-W., Stiller, G., Tilmes, S., Walker, K. A., Eyring, V., Shepherd, T. G., Waugh, D., Akiyoshi, H., Añel, J. A., Austin, J., Baumgaertner, A., Bekki, S., Braesicke, P., Brühl, C., Butchart, N., Chipperfield, M., Dameris, M., Dhomse, S., Frith, S., Garny, H., Hardiman, S. C., Jöckel, P., Kinnison, D. E., Lamarque, J. F., Mancini, E., Michou, M., Morgenstern, O., Nakamura, T., Olivié, D., Pawson, S., Pitari, G., Plummer, D. A., Pyle, J. A., Rozanov, E., Scinocca, J. F., Shibata, K., Smale, D., Teyssèdre, H., Tian, W., and Yamashita, Y.: Multimodel assessment of the upper troposphere and lower stratosphere: Extratropics, J. Geophys. Res.-Atmos., 115, D00M09, https://doi.org/10.1029/2010JD013884, 2010. a
Holton, J. R.: The role of gravity wave induced drag and diffusion in the momentum budget of the mesosphere, J. Atmos. Sci., 39, 791–799, 1982. a
Huang, T., Walters, S., Brasseur, G., Hauglustaine, D., and Wu, W.: Description of SOCRATES: A chemical dynamical radiative two-dimensional model, NCAR, p. 94, 1998. a, b, c
Inai, Y., Aoki, S., Honda, H., Furutani, H., Matsumi, Y., Ouchi, M., Sugawara, S., Hasebe, F., Uematsu, M., and Fujiwara, M.: Balloon-borne tropospheric CO2 observations over the equatorial eastern and western Pacific, Atmos. Environ., 184, 24–36, 2018. a
Ishidoya, S., Sugawara, S., Hashida, G., Morimoto, S., Aoki, S., Nakazawa, T., and Yamanouchi, T.: Vertical profiles of the O2∕N2 ratio in the stratosphere over Japan and Antarctica, Geophys. Res. Lett., 33, L13701, https://doi.org/10.1029/2006GL025886, 2006. a
Ishidoya, S., Sugawara, S., Morimoto, S., Aoki, S., and Nakazawa, T.: Gravitational separation of major atmospheric components of nitrogen and oxygen in the stratosphere, Geophys. Res. Lett., 35, L03811, https://doi.org/10.1029/2007GL030456, 2008. a, b, c
Ishidoya, S., Sugawara, S., Morimoto, S., Aoki, S., Nakazawa, T., Honda, H., and Murayama, S.: Gravitational separation in the stratosphere – a new indicator of atmospheric circulation, Atmos. Chem. Phys., 13, 8787–8796, https://doi.org/10.5194/acp-13-8787-2013, 2013. a, b, c, d, e, f, g
Kockarts, G.: Aeronomy, a 20th Century emergent science: the role of solar Lyman series, Ann. Geophys., 20, 585–598, 2002. a
Krol, M., de Bruine, M., Killaars, L., Ouwersloot, H., Pozzer, A., Yin, Y., Chevallier, F., Bousquet, P., Patra, P., Belikov, D., Maksyutov, S., Dhomse, S., Feng, W., and Chipperfield, M. P.: Age of air as a diagnostic for transport timescales in global models, Geosci. Model Dev., 11, 3109–3130, https://doi.org/10.5194/gmd-11-3109-2018, 2018. a, b
Leedham Elvidge, E., Bönisch, H., Brenninkmeijer, C. A. M., Engel, A., Fraser, P. J., Gallacher, E., Langenfelds, R., Mühle, J., Oram, D. E., Ray, E. A., Ridley, A. R., Röckmann, T., Sturges, W. T., Weiss, R. F., and Laube, J. C.: Evaluation of stratospheric age of air from CF4, C2F6, C3F8, CHF3, HFC-125, HFC-227ea and SF6; implications for the calculations of halocarbon lifetimes, fractional release factors and ozone depletion potentials, Atmos. Chem. Phys., 18, 3369–3385, https://doi.org/10.5194/acp-18-3369-2018, 2018. a
Li, F., Austin, J., and Wilson, J.: The strength of the Brewer–Dobson circulation in a changing climate: Coupled chemistry–climate model simulations, J. Clim., 21, 40–57, 2008. a
Lindzen, R. S.: Turbulence and stress owing to gravity wave and tidal breakdown, J. Geophys. Res.-Ocean., 86, 9707–9714, 1981. a
Machida, T., Matsueda, H., Sawa, Y., Nakagawa, Y., Hirotani, K., Kondo, N., Goto, K., Nakazawa, T., Ishikawa, K., and Ogawa, T.: Worldwide measurements of atmospheric CO2 and other trace gas species using commercial airlines, J. Atmos. Ocean. Technol., 25, 1744–1754, 2008. a
Maksyutov, S. and Inoue, G.: Vertical profiles of radon and CO2 simulated by the global atmospheric transport model, CGER report, CGER-I039-2000, CGER, NIES, Japan, 7, 39–41, 2000. a
Nakazawa, T., Machida, T., Sugawara, S., Murayama, S., Morimoto, S., Hashida, G., Honda, H., and Itoh, T.: Measurements of the stratospheric carbon dioxide concentration over Japan using a Balloon-borne cryogenic sampler, Geophys. Res. Lett., 22, 1229–1232, https://doi.org/10.1029/95gl01188,1995. a
Nakazawa, T., Aoki, S., Kawamura, K., Saeki, T., Sugawara, S., Honda, H., Hashida, G., Morimoto, S., Yoshida, N., Toyoda, S., and Makide, Y.: Variations of stratospheric trace gases measured using a balloon-borne cryogenic sampler, Adv. Space Res., 30, 1349–1357, 2002. a
Onogi, K., Tsutsui, J., Koide, H., Sakamoto, M., Kobayashi, S., Hatsushika, H., Matsumoto, T., Yamazaki, N., Kamahori, H., Takahashi, K., and Kadokura, S.: The JRA-25 reanalysis, J. Meteorol. Soc. Jpn. Ser. II, 85, 369–432, 2007. a
Ray, E. A., Moore, F. L., Rosenlof, K. H., Davis, S. M., Sweeney, C., Tans, P., Wang, T., Elkins, J. W., Bönisch, H., Engel, A., and Sugawara, S.: Improving stratospheric transport trend analysis based on SF6 and CO2 measurements, J. Geophys. Res.-Atmos., 119, 14110–14128, 2014. a
Sawa, Y., Machida, T., and Matsueda, H.: Seasonal variations of CO2 near the tropopause observed by commercial aircraft, J. Geophys. Res.-Atmos., 113, D23301, https://doi.org/10.1029/2008JD010568, 2008. a
Stiller, G. P., von Clarmann, T., Haenel, F., Funke, B., Glatthor, N., Grabowski, U., Kellmann, S., Kiefer, M., Linden, A., Lossow, S., and López-Puertas, M.: Observed temporal evolution of global mean age of stratospheric air for the 2002 to 2010 period, Atmos. Chem. Phys., 12, 3311–3331, https://doi.org/10.5194/acp-12-3311-2012, 2012. a
Sugawara, S., Ishidoya, S., Aoki, S., Morimoto, S., Nakazawa, T., Toyoda, S., Inai, Y., Hasebe, F., Ikeda, C., Honda, H., Goto, D., and Putri, F. A.: Age and gravitational separation of the stratospheric air over Indonesia, Atmos. Chem. Phys., 18, 1819–1833, https://doi.org/10.5194/acp-18-1819-2018, 2018. a, b, c
Tiedtke, M.: A comprehensive mass flux scheme for cumulus parameterization in large-scale models, Mon. Weather Rev., 117, 1779–1800, 1989. a
Warneck, P. and Williams, J.: The atmospheric Chemist's companion: numerical data for use in the atmospheric sciences, Springer Science & Business Media, 2012. a
Waugh, D. and Hall, T.: Age of stratospheric air: theory, observations, and models, Rev. Geophys., 40, p. 1010, https://doi.org/10.1029/2000RG000101, 1010, 2002. a
Zhuravlev, R., Ganshin, A., Maksyutov, S. S., Oshchepkov, S., and Khattatov, B.: Estimation of global CO2 fluxes using ground-based and satellite (GOSAT) observation data with empirical orthogonal functions, Atmos. Ocean. Opt., 26, 507–516, 2013. a