the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Solubility and solution-phase chemistry of isocyanic acid, methyl isocyanate, and cyanogen halides
James M. Roberts
Yong Liu
Condensed-phase uptake and reaction are important atmospheric removal processes for reduced nitrogen species, isocyanic acid (HNCO), methyl isocyanate (CH3NCO), and cyanogen halides (XCN, X = Cl, Br, I); yet many of the fundamental quantities that govern this chemistry have not been measured or are not well studied. These nitrogen species are of emerging interest in the atmosphere as they have either biomass burning sources, i.e., HNCO and CH3NCO, or, like the XCN species, have the potential to be a significant condensed-phase source of NCO− and therefore HNCO. Solubilities and the first-order reaction rate of these species were measured for a variety of solutions using a bubble flow reactor method with total reactive nitrogen (Nr) detection. The aqueous solubility of HNCO was measured as a function of pH and had an intrinsic Henry's law solubility of 20 (±2) M atm−1 and a Ka of 2.0 (±0.3) × 10−4 M (pKa = 3.7±0.1) at 298 K. The temperature dependence of HNCO solubility was very similar to other small nitrogen-containing compounds, such as HCN, acetonitrile (CH3CN), and nitromethane, and the dependence on salt concentration exhibited the “salting out” phenomenon. The rate constant of reaction of HNCO with 0.45 M , as NH4Cl, was measured at pH = 3 and found to be 1.2 (±0.1) × 10−3 M−1 s−1, faster than the rate that would be estimated from rate measurements at much higher pHs. The solubilities of HNCO in the non-polar solvents n-octanol (n-C8H17OH) and tridecane (C13H28) were found to be higher than aqueous solution for n-octanol (87±9 M atm−1 at 298 K) and much lower than aqueous solution for tridecane (1.7±0.17 M atm−1 at 298 K), features that have implications for multi-phase and membrane transport of HNCO. The first-order loss rate of HNCO in n-octanol was determined to be relatively slow, 5.7 (±1.4) × 10−5 s−1. The aqueous solubility of CH3NCO was found to be 1.3 (±0.13) M atm−1 independent of pH, and CH3NCO solubility in n-octanol was also determined at several temperatures and ranged from 4.0 (±0.5) M atm−1 at 298 K to 2.8 (±0.3) M atm−1 at 310 K. The aqueous hydrolysis of CH3NCO was observed to be slightly acid-catalyzed, in agreement with literature values, and reactions with n-octanol ranged from 2.5 (±0.5) to 5.3 (±0.7) × 10−3 s−1 from 298 to 310 K. The aqueous solubilities of XCN, determined at room temperature and neutral pH, were found to increase with halogen atom polarizability from 1.4 (±0.2) M atm−1 for ClCN and 8.2 (±0.8) M atm−1 for BrCN to 270 (±54) M atm−1 for ICN. Hydrolysis rates, where measurable, were in agreement with literature values. The atmospheric loss rates of HNCO, CH3NCO, and XCN due to heterogeneous processes are estimated from solubilities and reaction rates. Lifetimes of HNCO range from about 1 day against deposition to neutral pH surfaces in the boundary layer, but otherwise can be as long as several months in the middle troposphere. The loss of CH3NCO due to aqueous-phase processes is estimated to be slower than, or comparable to, the lifetime against OH reaction (3 months). The loss of XCNs due to aqueous uptake is estimated to range from being quite slow, with a lifetime of 2–6 months or more for ClCN and 1 week to 6 months for BrCN to 1 to 10 days for ICN. These characteristic times are shorter than photolysis lifetimes for ClCN and BrCN, implying that heterogeneous chemistry will be the controlling factor in their atmospheric removal. In contrast, the photolysis of ICN is estimated to be faster than heterogeneous loss for average midlatitude conditions.
- Article
(2100 KB) -
Supplement
(3457 KB) - BibTeX
- EndNote
The earth's atmosphere is a highly oxidizing environment in which chemical compounds are typically destroyed through radical pathways. The reduced nitrogen species, isocyanic acid (HNCO) and hydrogen cyanide (HCN), are an exception to this, as they have slow reactions with atmospheric radicals and have primarily condensed-phase sources and sinks (Li et al., 2000; Roberts et al., 2011). Cyanogen halides (XCN, where X = Cl, Br, I) are compounds that are present in the environment and whose atmospheric chemistry is of emerging interest. XCN compounds likewise have very slow reaction rates with radical species and, with the exception of ICN, very slow photolysis rates in the troposphere (Keller-Rudek et al., 2013). These general classes of reduced nitrogen species, isocyanates (R-NCO), cyanides (RCN), and cyanogen halides (XCN), have potential health impacts that are related to their condensed-phase chemistry (Boenig and Chew, 1999; Broughton, 2005; McMaster et al., 2018; Wang et al., 2007). Therefore, information on solubility and reaction rates is needed to understand the atmospheric fate of such compounds and to define their impact on human and ecosystem health. Five reduced nitrogen species will be focused on here: isocyanic acid (HNCO) and methyl isocyanate (CH3NCO), which are biomass burning products, and cyanogen chloride (ClCN), cyanogen bromide (BrCN), and cyanogen iodide (ICN), which could be condensed-phase sources of cyanate ion (NCO−) and therefore HNCO.
The isocyanate compounds are products of the pyrolysis or combustion of N-containing materials (biomass, polyurethanes) (Blomqvist et al., 2003; Koss et al., 2018), and the two simplest ones, HNCO and CH3NCO, have also been observed in interstellar and cometary media (Goesmann et al., 2015; Halfen et al., 2015). The atmospheric chemistry of HNCO has received considerable attention in the past few years as it has become clear that it is present in ambient air and could be related to health impacts through specific biochemical pathways (Roberts et al., 2011) involving the reaction of cyanate ions with proteins. There are relatively few observations of HNCO in ambient air, showing “background” mixing ratios that range from 10 pptv to over several ppbv, depending on the nature of regional sources, and peak mixing ratios approaching a few ppbv, observed in areas impacted by local biomass burning (Chandra and Sinha, 2016; Kumar et al., 2018; Mattila et al., 2018; Roberts et al., 2014; Sarkar et al., 2016; Wentzell et al., 2013; Woodward-Massey et al., 2014; Zhao et al., 2014). The aqueous-phase solubility of HNCO was examined by Roberts et al. (2011) and Borduas et al. (2016), wherein it was found that HNCO shows behavior typical of weak acids, where the effective Henry's coefficient Heff varies with pH, and so HNCO is only slightly soluble at pH characteristics of atmospheric aerosol (pH = 2–4) and is quite soluble at physiologic conditions (pH = 7.4). Attempts to model the global distribution of HNCO (Young et al., 2012) and the cloud water uptake of HNCO (Barth et al., 2013) used the limited solubility and hydrolysis data available at that time (Jensen, 1958; Roberts et al., 2011). Several aspects of HNCO solubility remain unknown, such as salt effects on aqueous solubility and solubility in non-aqueous solvents, a property important for predicting HNCO behavior in biological systems. The pH-dependent hydrolysis of HNCO was studied some time ago (Jensen, 1958); the mechanism for this process involves three separate reactions:
and Borduas et al. (2016) recently remeasured these rates under a wider range of conditions and found their measurements to be essentially consistent with the previous work at pHs of interest in the atmosphere. Rates of reaction of HNCO with other compounds in aqueous solution are not as well studied, especially under atmospheric conditions, e.g., low pH and relatively high ionic strength. Rates of reaction of with nitrogen bases have been measured only at the pKas of the BH+, which are typically pH 9–10 (Jensen, 1959; Williams and Jencks, 1974a, b).
Methyl isocyanate is most notable for its part in one of the largest industrial disasters in history, when a large quantity of CH3NCO was released from a chemical plant and fumigated the city of Bhopal, India. There are other, more common sources of CH3NCO to the atmosphere including combustion of biomass (Koss et al., 2018) and N-containing polymers, such as polyurethanes and isocyanate foams (Bengtstrom et al., 2016; Garrido et al., 2017), and cooking (Reyes-Villegas et al., 2018). Recent measurements of CH3NCO in laboratory wildfire studies have observed mixing ratios up to 10 ppbv or so in fuel characteristics of western North America (Koss et al., 2018). CH3NCO is also produced in photochemical reactions of methylisothiocyanate (CH3NCS), which is the main degradation product of the agricultural fungicide metam sodium (CH3NHCS2Na) (Geddes et al., 1995). In addition, CH3NCO has been observed in studies of the photooxidation of amides (Barnes et al., 2010; Borduas et al., 2015; Bunkan et al., 2015) and by extension will be formed in dimethyl amine oxidation. To the best of our knowledge there is only one reported set of ambient measurements of CH3NCO, conducted near a field where metam sodium was being used as a soil fumigant (Woodrow et al., 2014), and the resulting CH3NCO mixing ratios were as high as 1.7 ppbv. The California Office of Environmental Health Hazard Assessment has placed an inhalation reference exposure level of 0.5 ppbv (1 µg m−3) on CH3NCO due to its propensity to cause respiratory health effects (State of California, 2008).
There have only been a few studies on the gas-phase loss rates of CH3NCO including reaction with OH radicals, which appears to be slow based on the most recent measurements (Lu et al., 2014; Papanastasiou et al., 2019), reaction with chlorine atoms (Cl), which might be as much as 20 % of OH under some atmospheric conditions (Papanastasiou et al., 2019), and UV photolysis, which has a negligible contribution to atmospheric loss (Papanastasiou et al., 2019). Thus, heterogeneous uptake might compete with these gas-phase loss processes. The solubility of CH3NCO has not been previously determined experimentally but is probably low, < 2 M atm−1 by analogy to CH3NCS (3.7 M atm−1) (Geddes et al., 1995). In addition, there are no data on the solubility of CH3NCO in non-aqueous solvents. The hydrolysis of CH3NCO is acid-catalyzed, exhibiting the following overall reactions:
producing methyl amine and carbon dioxide. The rate constants for these reactions are fairly well established (Al-Rawi and Williams, 1977; Castro et al., 1985).
Cyanogen halides are less well studied as atmospheric species but have potentially important environmental sources. Cyanogen chloride was once produced as a chemical warfare agent; however its importance to the atmosphere is more related to its possible formation in the reaction of active chlorine species (, chloramines) with N-containing substrates such as amino acids and humic substances (Na and Olson, 2006; Shang et al., 2000; Yang and Shang, 2004). These reactions are known to be important in systems in which chlorination is used for disinfection such as swimming pools and water treatment (see, for example, Afifi and Blatchley III, 2015) and perhaps indoor surfaces (Chen Wang and Jonathan Abbatt, personal communication, 2018). We are not aware of any measurements of ClCN in ambient air. Cyanogen bromide can likewise be formed through reactions of with reduced nitrogen species, and there are observations of BrCN in bromide-containing waters that have received chlorine treatment (see, for example, Heller-Grossman et al., 1999). The formation results from the facile reaction of with bromide to make , which then reacts with nitrogen species in the water. In addition, there is a natural source of BrCN from at least one strain of marine algae (Vanelslander et al., 2012) that is thought to be related to allelopathic activity, i.e., secreted to control the growth of competing organisms. This marine algae source may be responsible for BrCN levels observed in remote atmospheres during the Atmospheric Tomography Mission-3 (NASA, 2019). Cyanogen iodide can also potentially be formed from the chlorination of water or wastewater because iodide is easily oxidized by ; however iodide is usually quite small in concentration, so the several studies that report total cyanogen halides report ClCN and BrCN but not ICN (Diehl et al., 2000; Yang and Shang, 2004). There are also biochemical pathways for ICN formation involving several enzymes that are part of the immune defense system (see, for example, Schlorke et al., 2016), but the extent to which ICN might be volatilized from those systems is not clear. There are also some observations of ICN in the remote marine troposphere (J. Andrew Neuman and Patrick R. Veres, personal communication, 2018), but their origin is currently unclear.
The possible gas-phase loss processes of cyanogen halides include reaction with radicals or ozone, and photolysis. Radical reaction rates (OH, Cl) have not been measured at room temperatures but are likely to be slow due to the strength of X–CN bonds (Davis and Okabe, 1968). The UV–visible absorption spectra of all three of these compounds have been measured (Barts and Halpern, 1989; Felps et al., 1991; Hess and Leone, 1987; Russell et al., 1987) and indicate a range of photolysis behavior, ranging from no tropospheric photolysis of ClCN to slight photolysis of BrCN and faster photolysis of ICN. The rates of photolysis need to be balanced against condensed-phase losses of XCN compounds to obtain a full picture of their atmospheric losses.
The aqueous-phase solution chemistry of cyanogen halides is not as well studied as the isocyanates. The aqueous solubilities of XCN compounds are not known with the exception of ClCN whose solubility is thought to be fairly low, 0.6–0.52 M atm−1 at 293–298 K (Weng et al., 2011; Yaws and Yang, 1992) as reported by Hilal et al. (2008). The hydrolysis of XCN compounds is known to be base-catalyzed and so involves the following reactions:
with R6 being fairly slow at medium to low pH (Bailey and Bishop, 1973; Gerritsen et al., 1993). The product, cyanic acid, HOCN, is unstable with respect to HNCO in aqueous solution (Belson and Strachan, 1982):
Thus, XCN compounds represent potential intermediates in the condensed-phase formation of HNCO, for which there is some observational evidence (Zhao et al., 2014). So, in addition to being active halogen species, XCN compounds represent a potential condensed-phase source of HNCO in systems in which there is halogen activation and there are reduced nitrogen species present, e.g., wildfire plumes, bio-aerosols, and indoor surfaces.
Measurements of solubility and reaction rates will be presented here for HNCO, CH3NCO, and the XCN species: ClCN, BrCN, and ICN. The aqueous solubility of HNCO was measured as a function of pH in the range pH 2–4, temperature in the range 279–310 K, and salt concentration up to 2.5 M NaCl. The rate of reaction of HNCO with was measured at pH 3 to examine the importance of this reaction to atmospheric uptake of HNCO. The solubilities of HNCO in the non-polar solvents n-octanol and tridecane were also measured as a function of temperature, in the range 298–310 K, and the first-order loss rate of HNCO in n-octanol was also determined. The aqueous solubility of CH3NCO was measured at several acidities, pH 2 and pH 7, and the solubility in n-octanol was also determined at several temperatures, 298 and 310 K. Finally, the aqueous solubility of ClCN, BrCN, and ICN was determined at room temperature, and at 273.15 K (ClCN, BrCN) and neutral pH, and the solubility and first loss of these compounds in n-octanol were also determined. These data will be used to estimate atmospheric lifetimes against aqueous uptake and to assess the relative bioavailability of these compounds.
Most of the techniques used for the work presented here have largely been presented elsewhere (Borduas et al., 2016; Kames and Schurath, 1995; Kish et al., 2013; Roberts, 2005) and will only be briefly summarized here. The basic principle is that the compound of interest is equilibrated with solution in a bubble flow reactor and then removed from the gas phase, and the exponential decay of the signal due to the loss of the compound is measured with a sensitive and selective method. The dependence of decay rates on the ratio of the flow rate to liquid volume can then be related to solubility and the first-order loss rate due to reaction in solution. This technique relies on being able to produce a consistent gas stream of the compound of interest and being able to selectively detect the compound exiting the reactor. This method has limitations in that the solubility must be within a certain range and the first-order loss rate slow enough that there are measurable amounts of compound exiting the reactor.
2.1 Preparation of gas-phase standards
The general system used for preparation of gas-phase streams of HNCO, CH3NCO, BrCN, and ICN was the capillary diffusion system described by Williams et al. (2000) and Roberts et al. (2010). Isocyanic acid was produced in a steady stream by heating the trimer, cyanuric acid (Sigma-Aldrich, USA), to 250 ∘C under N2 and establishing a constant diffusion rate through a short length of capillary tubing (1 mm ID × 5 cm length). Care was taken to condition the system for several days before use, by keeping the system under flow and at a minimum of 125 ∘C even when not in active use, to prevent the buildup of unwanted impurities, particularly NH3. Standards in the range of several ppmv in 40 SCCM could easily be prepared in this way.
The same capillary diffusion cells were used for CH3NCO preparation, starting with a sample of the pure liquid (Alinda Chemicals, UK). Fourier transform infrared (FTIR) analysis of samples of this material were found to contain small amounts of siloxanes (3 % by mole), which probably came from a chlorosilane added as a stabilizer, but no measurable presence of any other nitrogen compounds. The high volatility of CH3NCO (BP 38 ∘C) required that low concentration solution (1 % vol ∕ vol) of CH3NCO in n-tridecane (C13H28) solvent at a temperature of 0 ∘C be used in the diffusion cell. Under these conditions a 40 SCCM stream resulted in a mixing ratio of 10 ppmv. The output of the source was stable for long periods of time (days) and could be used for the solubility study and calibration of other instruments. The source was also analyzed by an H3O+ chemical ionization mass spectrometric system (H3O+ CIMS) (Koss et al., 2018; Yuan et al., 2016), which showed that it had no impurities detectable above the 1 % (as N) level.
The preparation of a gas-phase standard of ClCN is described by Stockwell et al. (2018) and is based on chemical conversion of a HCN calibration mixture. It has been known for some time that HCN reacts readily with active chlorine compounds to yield ClCN (Epstein, 1947), for example,
In fact, this reaction has been used as the basis for measuring HCN in the gas phase by conversion to ClCN with detection by gas chromatography with electron capture (Valentour et al., 1974). In those systems, Chloramine-T (N-Chloro-p-toluenesulfonamide sodium salt; Sigma-Aldrich) has proven useful. The method used in this work consisted of passing a small stream (5–10 SCCM) of a commercially prepared 10 ppmv gas-phase standard of HCN in N2 (GASCO, Oldsmar, FL, USA), combined with humidified zero air (ZA, 80 % RH, 30–50 SCCM) over a bed packed with glass beads coated with a solution of Chloramine-T. The glass beads were prepared by coating glass 3 mm OD beads with a 2 g/100 cm3 solution and packing ∼20 cm3 of them in a 12.7 mm OD PFA tube and flowing ZA over them until they appeared dry. The reaction was shown to be essentially 100 % (±10 %) when conducted in a humidified atmosphere (RH ≥ 60 %), (H3O+ CIMS) and FTIR analysis of the gas stream before and after passing through the chlorination bed. The ClCN source was also checked by measuring the total nitrogen content of the gas stream before and after the chlorination step, and the resulting signal was found to be 98±1 % of the original HCN standard. This means that the combination of the chlorination reaction and Nr conversion (see below) was at least 98 % efficient.
Preparation of BrCN and ICN gas streams was accomplished with the diffusion cell apparatus using commercially available samples of BrCN (98 % purity; Sigma-Aldrich) and ICN (97 % purity; Acros Organics), that were used without further purification. BrCN is a volatile solid so was kept on a diffusion cell at 0 ∘C while in use. ICN is a relatively non-volatile solid and so was placed in a diffusion cell and heated to 80 ∘C while in use. These resulted in sample streams that were on the order of 250–350 ppbv in 1 SLPM in the mixing ratio. Analysis using iodide ion chemical ionization mass spectrometry (Warneke et al., 2016) indicated traces of the molecular halogen species (Br2, I2), but no other significant N-containing species.
2.2 Detection of nitrogen compounds
The method for detection of the compounds studied in this work relies on the high temperature conversion of any N-containing species, except for N2 or N2O, to nitric oxide (NO) and detection of the resulting NO by O3 chemiluminescence (Williams et al., 1998). This technique, which we will refer to as total reactive nitrogen, Nr, has been shown to measure a wide range of reduced nitrogen species as well as the more familiar oxides of nitrogen (Hardy and Knarr, 1982; Saylor et al., 2010; Stockwell et al., 2018), provided care is taken to convert any nitrogen dioxide that is formed in the Pt converter back to NO prior to detection (Schwab et al., 2007). In this work, this was accomplished with a solid molybdenum tube operated at between 350 and 450 ∘C, with the addition of a small amount of pure H2 resulting in a 0.8 % mixing ratio in the catalyst flow. The detection system was routinely calibrated with a NO standard (Scott-Marrin, Riverside, CA, USA), and the conversion efficiency was confirmed with a low concentration (10 ppmv) HCN standard (GASCO, Oldsmar, FL, USA). The high conversion efficiencies (≥ 98 %) for HNCO and ClCN were confirmed by other methods as described by Stockwell et al. (2018). The conversion efficiencies for BrCN, and ICN are assumed to be equally high due to the fact the X–CN bond strengths of these compounds are lower than for H–CN and Cl–CN (Davis and Okabe, 1968) and the CH3–NCO bond is weaker than the H–NCO bond (Woo and Liu, 1935), so CH3NCO should be easily converted by the Nr catalyst. Although readily measured here, a solubility measurement of this kind does not require the determination of the absolute concentration of the analytes; it only requires that the measurement be linear (i.e., constant sensitivity) throughout the range of signals measured. The NO instrument is linear from the low pptv into the low ppmv range, the chief limitation being the ability to count photon rates above 5 MHz. The magnitude of the gas-phase sources used and the flow rate of the instrument (1 SLPM) insured that instrument signals did not reach the nonlinear range.
The requirement for the detection method to be selective could be an issue with a general method such as Nr. In practice, the reactions of the nitrogen species studied here form products that are not volatile under the conditions used in this work and so do not interfere with the measurement. In aqueous-phase reactions, HNCO produces , CH3NCO produces , and XCN compounds produce , all of which are non-volatile in the pH ranges at which those experiments were conducted. The products of the organic-phase reactions are not as well known: tridecane should not react with HNCO, n-octanol will form carbamyl or methyl carbamyl groups with n-octyl substituents which should be non-volatile. Possible reactions of XCN compounds with n-octanol are less well known, particularly in the absence of water in the solution; so those experiments will need to be interpreted with care.
The reactor used for the most of the experiments is a modification of the one described by Roberts (2005), the main modification being a reduction in volume to 125 cm3. Liquid volumes used in the experiments ranged from 20 to 50 cm3, and the volumetric flow rates used ranged from 170 to 1070 ambient cm3 min−1. Temperatures were measured using a calibrated mercury thermometer, and temperatures different than room temperatures were controlled using a water bath with either ice or water or a temperature control system. The uncertainties in the temperatures were ±0.5 ∘C.
The bubble flow reactor method relies on the rapid equilibration of a gas stream that contains the analyte of interest with solution by means of the creation of small, finely divided bubbles. In the system used here, these bubbles are created by passing the gas stream through a fine glass frit, situated at the bottom of the glass vessel. The main sample flow is passed through the bubbler and into the detector stream to establish a baseline. A small flow of the analyte is added upstream of the reactor by means of a PFA solenoid valve to start the measurement, and the effluent is monitored until the measured concentration attains equilibrium. At this point, the analyte entering the reactor is switched off, and the concentration exiting the reactor begins to decay. This decay is due to a combination of loss of the analyte as it re-equilibrates with the gas stream and first-order loss in the solution due to reaction. Under conditions of rapid equilibration, this decay takes the form of a single exponential equation, dependent on the ratio of flow rate (φ, cm3 s−1) to liquid volume (V, cm3), the effective Henry's law solubility Heff (M atm−1), and the first-order loss rate (k):
Measurements performed at a series of φ∕V should be linear with a slope of the decay rate (d ln(C0 ∕ Ct) ∕ dt) versus φ∕V of 1∕HeffRT, where R is the ideal gas constant, T the temperature (K), and an x intercept of k, the first-order loss rate (s−1). In practice, the linearity of this relationship and the performance of the measurement at different liquid volumes and flow rates that result in the same φ∕V provide a check on the assumption of rapid equilibration within the reactor. In practice we measure the effective Henry's coefficient in our experiments, but the distinction is only important for the weak acid, HNCO, as described in the Results and discussion section below.
Attempts to measure the solubility of ICN with the glass bubbler system described above were unsuccessful because ICN did not equilibrate at the levels and timescales typical of the other compounds measured in this work, and the decay profiles were not reproducible nor exponential. The possibility that this was due to higher solubility, faster reaction, or decomposition of ICN on glass surfaces was explored by using a smaller reactor fabricated from 12.7 mm O.D. PFA tubing and PFA compression fittings (see Supplement Fig. S1). In these experiments, liquid volumes of between 1.0 and 2.0 cm3 and flow rates of 100 to 600 ambient cm3 min−1 were used. This resulted in equilibration and decay profiles more similar to the other experiments, when the solubility of ICN in water was measured at room temperature. Attempts to measure ICN solubilities in n-octanol were not successful using either reactor.
Solution for the aqueous solubility and reaction experiments were prepared from reagent-grade materials. The pH 2–4 buffer solutions were commercial preparations, made from citric acid monohydrate with differing amounts of hydrochloric acid, sodium chloride, and sodium hydroxide (Fixanal, Fluka Analytical), with anion concentrations ranging from 0.08 to approximately 0.2 M. The manufacturer specifications (Fluka, Sigma-Aldrich) of the pH = 3 buffer showed a slight temperature dependence, with the pH ranging from 3.03 at 0 ∘C to 2.97 at 90 ∘C. An ammonium chloride solution of 0.45 M was prepared through addition of a measured amount of the solid to the pH = 3 buffer. Sodium chloride solutions ranging up to 2.5 M were prepared gravimetrically in the pH buffer solution. The pHs of NH4Cl and NaCl solutions were measured at room temperature with a pH meter and found to be within 0.1 pH unit of the nominal buffer pH value.
Examples of the data generated by equilibration experiments are shown in Figs. 1 and 2, which show the exponential decays for a series of gas flow rates (Fig. 1) and the correlation of the decay rates versus φ∕V (Fig. 2). Numerous other examples of both decay curves and decay rate versus φ∕V are shown in the Supplement for a range of different analytes and solutions. The uncertainties in Henry's coefficients are derived from a combination of the reproducibility of the decay rates, the agreement between decay rates at the same φ∕V (but different flows and liquid volumes), and the fits to the slope of relationships like those shown in Fig. 2 and were generally ±10 % or better. The uncertainties in first-order loss rate are the corresponding uncertainties in the intercepts. The results of the experiments with HNCO, CH3NCO, ClCN, BrCN, and ICN with the variety of solvents and conditions employed are summarized in Tables 1 and 2 and described below.
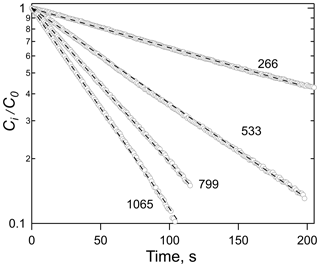
Figure 1Plots of the ratio of HNCO concentration at time t, Ci, to the initial concentration, Co, versus time for a series of flow rates, noted as ambient cm3 min−1. The solvent was tridecane (C13H28) at 299 K.
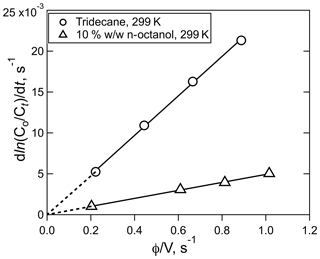
Figure 2Plots of HNCO loss rate versus the ratio of volumetric flow rate, φ, to solution volume, V, for the experiment shown in Fig. 1 (circles), and the experiment with 10 % w∕w n-octanol in tridecane at 299 K (triangles). The error bars in the individual rates were smaller than the width of the points.
3.1 Results for aqueous solution
3.1.1 Solubility and reactions of HNCO
Here we report results for pHs between 2 and 4 and for the temperature range 279.5 to 310.0 K at pH = 3. In addition, we report data for the effect of salt concentrations on the solubility at pH = 3 and the effect of ammonium concentrations on solubility and apparent first-order loss rate in solution. The dependence of aqueous solubility of HNCO on pH is expected given it is a weak acid, and its dissolution is accompanied by an acid-base equilibrium:
so that what is measured is the effective Henry's coefficient, Heff, which involves the sum of all forms of HNCO in solution:
Substituting for [NCO−] using the rearranged form of Eq. (3) and using Eq. (2) we get the relationship for Heff:
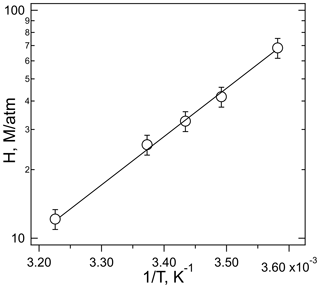
The plot of Heff versus is shown in Fig. 3, the slope of which is H×Ka, and the intercept is the intrinsic Henry's law constant, H. The resulting fit (R2= 0.99) gave a H = 20 (±2) M atm−1 and a Ka of 2.0 (±0.3) × 10−4 M (which corresponds to pKa = 3.7±0.1). The uncertainties in these numbers were derived from the standard deviations of the fitted parameters, where the value for Ka is the propagated uncertainty in both H and the slope. Figure 4 shows the comparison of the H measurements from this work with those of Borduas et al. (2016) plotted according to Eq. (5). There are approximately 20 % differences in the two data sets, which is just at the limits of the quoted uncertainties, when both the uncertainties in the intrinsic H and pKa are taken into account.
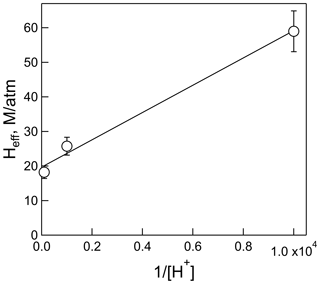
Figure 3Plot of the effective Henry's coefficient of HNCO versus for the measurements at pH = 2, pH = 3, and pH = 4 and 298 K.
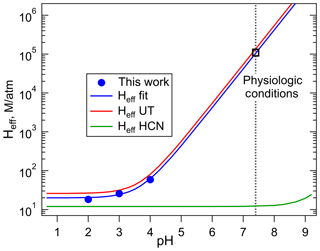
Figure 4Comparison of the effective Henry's coefficients of HNCO measured in this work (blue) with those reported by Borduas et al. (2016) plotted versus pH, according to Eq. (4). The error bars on our Heff values are smaller than the width of the symbols. The green line was calculated for HCN from the intrinsic H coefficient reported by Sander (2015), and its pKa, 9.3.
The temperature dependence of the solubility measured at pH = 3 obeys the simple Van't Hoff relationship:
shown in Fig. 5 as a linear relationship of log Heff versus 1∕T. These data were not corrected for the slight dependence of the buffer pH on temperature (3.02–2.99 pH units over this range). The slope of the correlation yields a ΔHsoln of kJ mole−1, calculated using dimensionless Henry's coefficients (HeffRT) (Sander, 2015). This enthalpy of solution agrees with that measured by Borduas et al. (2016) ( kJ mole−1) within the stated uncertainties. Moreover, this enthalpy is similar to that of other small N-containing molecules, HCN (−36.6 kJ mole−1), CH3CN (−34.1 kJ mole−1), and nitromethane (−33.3 kJ mole−1) (Sander, 2015) but different to that of formic acid (−47.4 kJ mole−1) which was used by the cloud uptake modeling study (Barth et al., 2013).
Often Henry's law solubility can depend on salt concentration of the solution, usually resulting in a lower solubility (salting out) but occasionally resulting in a higher solubility (salting in), with higher salt concentrations. These effects are most applicable to aerosol chemistry, in which ionic strengths can be quite high. This effect on HNCO solubility was measured at pH = 3 and 298 K for NaCl solutions between 0 and 2.5 M concentration. The results, shown in Fig. 6, exhibit the classic “salting out” effect, where HNCO was only about 60 % as soluble at 2.5 M compared to the standard pH = 3 buffer. The Setschenow constant, ks, can be determined by the relationship:
where Heff is Henry's coefficient at a given ionic strength, I, and Heff0 is Henry's coefficient in pure water. For a salt with two singly charged ions, I is equal to the salt concentration. In this experiment, ks was found to be 0.097±0.011 M−1. The magnitude of the salting out effect on HNCO is similar or slightly smaller than that found for other small organic compounds in NaCl, such as acetylene, ethane, and butane (Clever, 1983; Schumpe, 1993), Interestingly, Wang et al. (2014) found that Setschenow constants for ammonium sulfate are typically larger than those for NaCl, a feature which might impact the uptake of HNCO to aerosol particles with substantial (NH4)2SO4 content.
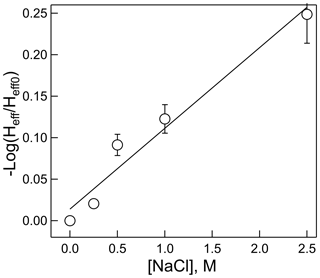
Figure 6Dependence of the effective Henry's coefficient (Heff) at a given salt concentration, relative to that with no added salt (Heff0) versus NaCl molarity. R2=0.960.
The net hydrolysis reaction rates observed in this study are listed in Table 1 and range from 0.22 to 4.15 × 10−3 s−1 and are both pH- and temperature-dependent. The main reactions of in aqueous solution are hydrolysis reactions that involve the acid or its conjugate anion, as detailed in Reactions (R1)–(R3) noted above. The expression for the net hydrolysis reaction is
as derived by Borduas et al. (2016). The rates of these reactions that were determined in several previous studies (Borduas et al., 2016; Jensen, 1958) are in reasonable agreement except for Reaction (R3), which is not atmospherically relevant. Equation (8) was used to calculate the values from those two studies that would correspond to the rates at pH = 3 measured in our work and are also listed in Table 1. The rate constants reported in this work agree within the range observed in the two previous studies, except for one temperature, and the relative standard deviations of mean values calculated from all three observations ranged from 5 % to 30 %.
Table 1Summary of solubility and loss rate measurements of HNCO and CH3NCO.

a Calculated from the temperature- and pH-dependent data reported by Borduas et al. (2016). b Calculated from the temperature- and pH-dependent data reported by Jensen (1958). c These were calculated from rates measured at higher pHs, assuming the mechanism is HNCO + NH3= > H2NC(O)NH2. d From and kw reported by Williams and Jencks (1974a). e From for HCl and kw reported by Castro et al. (1985).
The above hydrolysis reactions represent a lower limit on the condensed-phase loss of HNCO, so reaction with other species present in the condensed-phase might result in faster loss and produce unique chemical species. are known to react with a variety of organic compounds with an “active hydrogen” (a hydrogen attached to an O, N, or S atom) (Belson and Strachan, 1982), through simple addition across the N=C bond, where the active hydrogen ends up on the N and the other moiety ends up attached to the carbon. For example, alcohols react to yield carbamates, i.e., esters of carbamic acid:
Note that this is really the same mechanism as the neutral hydrolysis of HNCO, except that the addition of water forms carbamic acid, H2NC(O)OH, which is unstable and decomposes to NH3 and CO2. In the same fashion, can react with ammonia in solution to yield urea:
And in a more general sense, they react with amines to yield substituted ureas:
Reaction (R11) is known to be an equilibrium that lies far to the product side under all conditions pertinent to this work (Hagel et al., 1971). While the forward reaction rate for R11 has been measured under neutral to slightly basic conditions (Jensen, 1959; Williams and Jencks, 1974b), it has not been measured at pHs applicable to atmospheric aerosol or cloud droplets, i.e., pH = 2–4. These previous studies have assumed that the mechanism involves the reaction of the un-ionized species, e.g., NH3 and HNCO, although there is some evidence that Reaction (12) for some amines (RNH2) has a more complicated reaction mechanism (Williams and Jencks, 1974a). As a consequence of this assumption, the previous studies reported their reaction rates corrected for the acid-base equilibria of each species. The solubility and reaction experiment in this work was performed at pH = 3 and [] of 0.45 M, so a substantial correction of the literature values for the acid-base equilibria in the case of and a minor correction for the dissociation of HNCO was required in order to compare with our result. The results of our study (Table 1) show that the solubility of HNCO in NH4Cl solution at 292 K is essentially the same as that of the pH = 3 buffer alone (31.5±3 versus 32.6±3 M atm−1). This implies that Reaction (R11) does not impact the aqueous solubility. However, the measured first-order loss rate, 1.2 (±0.03) × 10−3 s−1, is faster than the hydrolysis at pH 3, 0.66 (±0.06) × 10−3 s−1. The reaction can be expressed as the sum of hydrolysis and reactions of HNCO and NCO− with (the predominant form at pH 3).
We calculate a value of 1.2 (±0.1) × 10−3 M−1 s−1 for k11 from our measurements which is much faster than the rate constants reported by previous studies, 5 × 10−6 M−1 s−1 (Jensen, 1959) and 1.5 × 10−5 M−1 s−1 (Williams and Jencks, 1974b), when corrected for acid-base equilibria.
3.1.2 Solubility and reactions of CH3NCO
The solubility and first-order loss rate of CH3NCO were measured at pH = 2 and pH = 7 at 298 K, and the results are listed in Table 1. Henry's coefficients, 1.3 (±0.13) and 1.4 (±0.14) M atm−1, were lower than those measured for HNCO, and independent of pH, within the uncertainties of the measurements. This is consistent with CH3NCO being a less polar compound, with no dissociation reactions that might be pH-dependent. In addition, these results imply that solution complexation due to the presence of anions does not affect CH3NCO solubility, at least the concentrations and anions present in the pH = 2 buffer solution, 0.2 M for the sum of citrate and chloride.
The first-order loss rates of CH3NCO, presumably due to hydrolysis, did show a pH dependence that implies acid catalysis. These hydrolysis rates were faster than the rates for HNCO at the same temperatures and pHs. The mechanism of CH3NCO hydrolysis and other solution chemistry is discussed by Al-Rawi and Williams (1977) and Castro et al. (1985). The hydrolysis of CH3NCO is thought to proceed first by formation of a methyl carbamic acid:
which is analogous to the way water adds across the N=C bond of HNCO. The methyl carbamic acid then either reacts with H3O+ (faster) or H2O (slower) to produce and CO2, or CH3NH2 and CO2, yielding the net reactions, Reactions (R4) and (R5):
Henry's law measurements in our work imply that if Reaction (R13) is happening, it must be to a quite minor extent, otherwise the H constant for CH3NCO would be much larger than it is. Solution-based studies of CH3NCO in the presence of strong acid anions (Al-Rawi and Williams, 1977; Castro et al., 1985) also imply that a complex mechanism takes place, involving a reversible complexation (shown here for ):
Rate constants for Reactions (R4) and (R5) were reported by Castro et al. (1985), but the precision of these was somewhat compromised by the presence of the Reaction (R14) equilibrium. Again, in this study, Henry's coefficient results imply a negligible role for complexation, so the following simplified expression for the pH dependence is used,
to derive the following values for k5=1.9 (±0.6) × 10−3 s−1 and k4= 0.13 (±0.07) M−1 s−1. These values are in reasonable agreement with the value for k5 given by Al-Rawi and Williams (1977), s−1 considering those measurements were at 1 M KCl, and the value for k4= 0.16 M−1 s−1 given by Castro et al. (1985) for reaction with HCl in the absence of a buffer.
3.1.3 Solubility and reactions of XCN compounds
The solubilities and first-order loss rates of XCN compounds were measured at room temperature and neutral pH in pure DI water and at ice–water temperature for ClCN and BrCN. The resulting Henry's coefficients are listed in Table 2. The ClCN solubility was essentially the same as that measured for CH3NCO at room temperature and is in reasonable agreement with the value of 0.52 M atm−1 at 298 K based on a model estimate (Hilal et al., 2008) and one reported measurement, 0.6 M atm−1 at 293 K (Weng et al., 2011). In contrast, BrCN was more soluble than ClCN, 8.2±0.8 M atm−1 at 296 ∘K, but fairly insoluble in an absolute sense. The temperature dependences of HClCN and HBrCN were as expected, showing higher solubility at lower temperatures; however, they had very different heats of solution, −27.8 kJ mole−1 for ClCN and −38.3 kJ mole−1 for BrCN, although there are only two data points for each compound. Both the higher solubilities and larger ΔHsoln, could be a result of the higher dipole moment and polarizability of BrCN relative to ClCN (Maroulis and Pouchan, 1997).
Table 2Summary of solubility and loss rate measurements of XCN compounds.
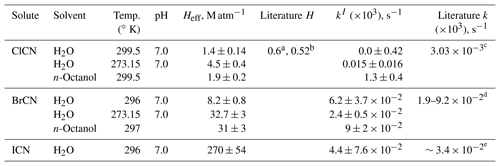
a Measured value at 293 K, reported by Weng et al. (2011). b Modeled value at 298 K, reported by Hilal et al. (2008). c From kw and kOH reported by Bailey and Bishop (1973). d Estimated from Heller-Grossman et al. (1999) and Vanelslander et al. (2012). e Estimated from Gerritsen et al. (1993).
The solubility of ICN was measured a room temperature using a combination of different flow rates (208–760 ambient cm3 min−1) and liquid volumes (1.95 and 0.95 cm3). A plot of the decay rates versus φ∕V for those runs is shown in Fig. 7. Where those data sets overlap, there is agreement to within about 15 %, implying that the equilibration could be fast enough to meet the criteria for these types of flow experiments. The resulting Henry's coefficient, 270 (±41) M atm−1, is significantly larger than the other two XCN compounds but is consistent with the trend of increasing solubility with dipole moment and polarizability. Attempts to use the small reactor to measure the solubility of ICN at ice–water temperatures was not successful; e.g., they did not yield simple single exponential decays with time under the same range of flow conditions as used in the room temperature experiment.
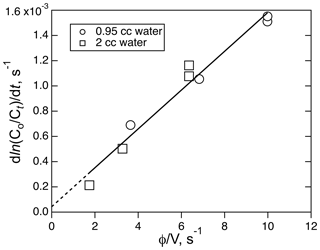
Figure 7The plot of ICN loss rate versus the ratio of volumetric flow rate, φ, to solution volume, V, for the experiment involving the solubility of ICN in water with the small reactor. The line is the least-square fit to the data (R2=0.968).
The hydrolysis of XCN compounds is known to be base-catalyzed and can be susceptible to anion complexation (Bailey and Bishop, 1973; Gerritsen et al., 1993) in a manner similar to CH3NCO:
This complexation can be ignored in our study for ClCN and BrCN since the experiment was performed in DI water; however, such complexation should be considered in future condensed-phase studies of XCN compounds. Accordingly, the expression for the ClCN and BrCN hydrolysis rate constant is
Bailey and Bishop (1973) found kw= 2.58 × 10−6 s−1 and kOH= 4.53 M−1 s−1 at 299.7 K, for ClCN, which corresponds to at pH7. This is consistent with the results of this study which found that the first-order loss rate was zero within the error of the linear fit (±4.2 × 10−4 s−1). The study of BrCN hydrolysis of Gerritsen et al. (1993) did not derive kw, nor did it present sufficient data for kw to be estimated. However, there are two other studies that presented data from which kw can be estimated, and those range from 1.9 to 9.2 × 10−5 s−1 (Heller-Grossman et al., 1999; Vanelslander et al., 2012).
The hydrolysis of ICN is slightly more complicated since there is some evidence that ICN might complex with iodide (Gerritsen et al., 1993). The room temperature hydrolysis rate observed in our experiment was not significantly different than zero, 4.4 (±7.6) × 10−5 s−1, but is in the same range of the rate constant estimated from the data given by Gerritsen et al. (1993) by extrapolating their rate constant versus [OH−] data to zero [OH−], assuming no complexation reactions.
3.2 Non-aqueous solution
Solubility in non-aqueous solvents is a standard indicator of how compounds will be distributed between different compartments in the environment, i.e., lipids in the body and organic aerosols in the atmosphere. In addition, the ratio of organic to aqueous solubility (Kow) is used to estimate membrane transport of a chemical species, a key factor in estimating physiologic effects of a pollutant. Several non-aqueous solvents were used in this study, tridecane to represent a completely non-polar solvent and n-octanol, which is used as a standard material for such studies. Tridecane was used because it is the heaviest n-alkane that is still a liquid at 273.15 K, and it has purely non-polar character, i.e., no functional groups, so is a slightly different model for non-polar matrices.
3.2.1 Solubility and reactions of HNCO
The experiments performed on HNCO were conducted with tridecane, 10 % (V∕V) n-octanol ∕ tridecane, and pure n-octanol, and the results are summarized in Table 1. HNCO is the least soluble in tridecane, 1.7 (±0.17) M atm−1, and increasingly soluble as the proportion of n-octanol is increased to pure n-octanol, 87 (±9) M atm−1 at 298 K. Experiments at two other temperatures were performed to confirm that these solubilities follow the expected temperature dependence and to obtain the solubility in pure n-octanol at human body temperature (310 K) to match data for the aqueous solubility. The lower solubility of HNCO in tridecane is expected since tridecane is completely non-polar and has no tendency to hydrogen bond or interact with the polarizable end of the HNCO molecule. In contrast, the increase in solubility of HNCO with increasing proportion of n-octanol is due to the polar –OH group at the end of the molecule.
The rate of reactions of HNCO with the non-aqueous solvents was below the limit of detection by this method for all combinations except for pure n-octanol at 310 K. Even so, the measured rate was quite a bit lower than the corresponding hydrolysis rate in aqueous solution at pH = 3. The manner in which these two factors (solubility and reaction) affect the net uptake and loss of HNCO will be discussed below.
3.2.2 Solubility and reactions of CH3NCO
The solubility of CH3NCO in n-octanol was measured at several temperatures, as summarized in Table 1. The value for 298 K is approximately 3 times higher than that of aqueous solubility and has the expected temperature dependence. In addition, the first-order reaction rates for CH3NCO in n-octanol were in the same range or slightly higher than the aqueous reactions. The reaction with n-octanol is expected to go via the carbamylation reaction, Reaction (R10), although there is some evidence that this reaction has a more complex mechanism, possibly involving multiple alcohol molecules (Raspoet et al., 1998). These rates are much faster than the corresponding rates for HNCO and may provide some guidance concerning the loss rates of CH3NCO to heterogeneous processes.
3.2.3 ClCN and BrCN
The solubilities of ClCN and BrCN in n-octanol were measured at room temperature. Cyanogen chloride and BrCN have about the same relative differences in solubility in n-octanol (a factor of 3–4) as they did H2O. The higher solubility of BrCN relative to ClCN could again be due to its higher dipole moment and polarizability (Maroulis and Pouchan, 1997). The first-order loss rates of ClCN and BrCN could be determined from the flow reactor experiments and were 1.3 (±0.4) × 10−3 and 9 (±2) × 10−5 s−1, respectively. Reactions of ClCN with alcohols are known (see, for example, Fuks and Hartemink, 1973), and form carbamates, in a mechanism that appears to be second-order in the alcohol and acid-catalyzed, but rate constants for ClCN-alcohol reactions have not been reported to the best of our knowledge. There are studies of rates of reactions of ClCN with nucleophiles, e.g., nitrogen bases, and those reactions appear to result in – CN substitution and formation of a Cl− ion (Edwards et al., 1986). In addition, BrCN has been used by protein chemists to selectively cleave disulfide bonds and has been used for some time by synthetic chemists to selectively convert tertiary amines to secondary amines (Siddiqui and Siddiqui, 1980; von Braun and Schwarz, 1902) and can carbamylate amino acids (Schreiber and Witkop, 1964). The importance of these reactions to the atmospheric fate of XCN compounds remains an open question, but it is important to note that they constitute losses of active halogen, i.e., the conversion of the halogen to a halide ion.
3.2.4 Octanol / water partition coefficients
The ratio of solubilities between a non-polar solvent and water is a fundamental quantity that is useful in predicting the fate of a compound in the environment and biological systems (Leo et al., 1971). This parameter is used to predict lipid solubility, membrane transport, and the potential of uptake of a particular compound by organic aerosol. n-Octanol is a standard non-polar solvent that is commonly used for this purpose, as it has an overall non-polar character with a substituent that is capable of hydrogen bonding. The data from this study can be used to calculate the octanol / water partition coefficients for HNCO, CH3NCO, ClCN, and BrCN as the ratio of the respective Henry's coefficients:
The results are listed in Table 4 along with Kows for some related small molecules. Both CH3NCO, and BrCN are fundamentally more soluble in n-octanol than in water, while ClCN has nearly the same solubility in both materials.
Table 4Octanol / water partition coefficients for HNCO, CH3NCO, ClCN, and BrCN and related compounds.
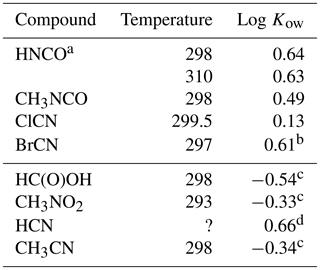
a This uses the intrinsic H calculated from Eq. (5) and our results. b Based on extrapolated at 297 K. c Sangster (1989). d EPA (1989).
The weak acid equilibrium of HNCO makes it more soluble in n-octanol at pH 3 but much more soluble in water at neutral pH. However, transport models of biological systems account for these acid base equilibria along with using the Kow to estimate transport rates (Missner and Pohl, 2009). Formic acid is a similarly weak acid (pKa = 3.77) and so is a good point of comparison to HNCO. The n-octanol partition coefficient of HNCO is a factor of 15 larger than that of HC(O)OH, so should have larger membrane permeabilities. Similarly, the n-octanol partition coefficient of CH3NCO is 6.8 times larger than that of CH3CN. The two cyanogen halides measured here had differing behavior, with ClCN showing almost no difference in solubility and BrCN having about the same increase in solubility in n-octanol as HNCO and CH3NCO.
3.3 Atmospheric and environmental chemistry implications
The atmospheric loss of the compounds studied here is either solely or predominantly through heterogeneous uptake and reaction for HNCO, CH3NCO, ClCN, and BrCN, or in the case of ICN due to both heterogeneous chemistry and photolysis. The aqueous solubility and reaction data from this study allow some prediction of uptake parameters and loss rates in some important systems, e.g., cloud water and natural water surfaces like oceans. In addition, some indications can be gained about the uptake of HNCO, CH3NCO, ClCN, and BrCN to organic aerosol, using n-octanol as a model. Finally, the n-octanol / water partition coefficient is often used as a key parameter in modeling cross-membrane transport, and the data from this study can be used to predict the behavior of these reduced-N compounds relative to other well-studied compounds.
The reactive uptake of HNCO, CH3NCO, and XCN on environmental surfaces, small particles, and aqueous droplets can be parameterized using the uptake coefficient, γ, defined as the fraction of collisions of a molecule with a surface that lead to incorporation of that molecule in the condensed phase. If solubility and reaction are the limiting processes, a good assumption for the species in this work, then γrxn can be estimated from the following equation (Kolb et al., 1995):
where Heff and k are Henry's coefficient and first-order loss rate in solution measured in this work, R is the gas constant, T is temperature, Da is the diffusion coefficient in aqueous solution (assumed here to be 1.9 × 10−5 cm2 s−1 for HNCO, cm2 s−1 for CH3NCO and ClCN, cm2 s−1 for BrCN, and cm2 s−1 for ICN at 298 K), and is the mean molecular speed. The results of these calculations are shown in Fig. 8 for the H measurements at 298 K reported here, khydr for HNCO reported by Borduas et al. (2016), khdyr for CH3NCO from this work, and khydr for ClCN from Bailey and Bishop (1973).
Deposition of a compound to the surface can be parameterized as essentially two processes taking place in series, physical transport within the planetary boundary layer to the surface and then chemical uptake on the surface (see, for example, Cano-Ruiz et al., 1993). In this formulation, the deposition velocity, vd (the inverse of the total resistance), is expressed as follows:
where 1∕vt is the resistance due to transport, and is the resistance due to chemical uptake. For a species for which uptake is rapid, e.g., a highly soluble acid, the chemical resistance becomes small and vd≅vt. This is the case for HNCO deposition to land or natural water surfaces (pHs ∼7–8). Typical vts are on the order of 0.5 to 1 cm s−1 for a reasonably mixed boundary layer (Wesely and Hicks, 2000). For compounds for which γ is quite small, the chemical term predominates.
The lifetime of a species within the planetary boundary layer then can be estimated as h∕vd, where h is the boundary layer height. The lifetime estimates for HNCO, CH3NCO, and XCN compounds are given in Table 3 and range from the short lifetime noted for HNCO to quite long lifetimes for the least soluble species, for example, ClCN.
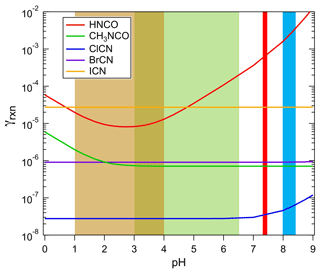
Figure 8The uptake coefficients of HNCO, CH3NCO, ClCN, BrCN, and ICN as a function of pH for aqueous solution at approximately 298 K. The shaded areas show the range of pH characteristics of aerosols (light brown), cloud/fog water (green), human physiology (red), and ocean surface water (light blue).
The loss rates due to uptake of species to atmospheric aerosol particles can be estimated from the pH-dependent uptake coefficients in Fig. 8, using parameterizations described in the literature (Davidovits et al., 2006; Sander, 1999). In the limited case of surface-controlled uptake, i.e., neglecting gas-phase diffusion, the loss of a species is
where A is the aerosol surface area. If we take the γs from Fig. 8, and assume highly polluted conditions to obtain a lower limit to the lifetime against this process, A = 1000 µm2 cm−3 and pHs between 1 and 2, then the lifetimes listed in Table 3 are arrived at. The values for HNCO and CH3NCO show a range because the uptake is pH-dependent, and it should be noted that the values for CH3NCO, ClCN, and BrCN are overestimated by this method, as their chemistry is slow enough that a volume-based estimate may be more appropriate. The more important effect here is that the γ values are based on hydrolysis losses, which are undoubtedly much slower than many of the solution-phase reactions that these species can undergo; hence the lifetimes against aerosol deposition are upper limits.
The loss of HNCO to cloud water is the subject of extensive work discussed by Barth et al. (2013), and no attempt will be made here to update that analysis. We can point out that our results yielded slightly lower Heff (∼22 %) at the lowest temperature we measured, compared to the values used by Barth et al. (2013); see Fig. S13. This would result in slightly slower removal rates in the Barth et al. model in low-temperature clouds. The fastest loss rates for HNCO were observed in warm dense clouds into which SO2 was also dissolving and adding considerable acidity; therefore the value for HNCO was included in Table 3. For the other compounds we use a simple parameterization of the cloud water reaction to estimate the in-cloud loss rates for CH3NCO and the XCN compounds. In the estimate of reaction rate,
where kl is the liquid-phase rate constant, Lc is the cloud liquid water content, and H is Henry's coefficient. If we assume a Lc of , and T≅298 K, and we use the H and k values measured in this work (the exception is that the literature value for CH3NCO at pH = 2 was used), then the values for lifetimes of CH3NCO and XCN compounds listed in Table 3 were obtained. Below we discuss the characteristic times obtained for each compound in the context of what else is known about their sources and atmospheric chemistry.
3.3.1 HNCO
The loss of HNCO via heterogeneous processes occurs in two separate regimes: in aerosols and cloud droplets at relatively low pH and in surface waters and on terrestrial surfaces that are neutral or slightly basic in pH. In the former case, HNCO solubility is relatively low, but hydrolysis is acid-catalyzed. In the latter case, solubility is high enough that uptake will be limited by the transport of HNCO to the surface, much like other strong acids such as HNO3. Ambient measurements of HNCO at surface sites are consistent with deposition of HNCO to the ground, exhibiting diurnal profiles similar to those of O3 or HNO3 (Kumar et al., 2018; Roberts et al., 2014; Mattila, et al., 2018; Zhao et al., 2014).
Several aspects of the aqueous solubility and hydrolysis and heterogeneous removal of HNCO have been examined in modeling studies. A global modeling study by Young et al. (2012) was a first attempt to model global HNCO by scaling the source to fire emissions of HCN. Loss of HNCO was assumed to be due to wet and dry deposition with efficiencies similar to HNO3 and HC(O)OH, and it was assumed that HNCO was lost once it was taken up by clouds. Young et al. (2012) concluded that HNCO had an average lifetime of about 37 days. Barth et al. (2013) addressed part of this analysis by modeling the cloud removal of HNCO using actual solubility and reaction data in a cloud parcel model; albeit, the hydrolysis rates used were from Jensen (1957), which were approximately 50 % higher than the Borduas results, and the temperature dependence of Heff was assumed to be equal to that of HC(O)OH and resulted in higher solubilities at low temperature. This cloud model showed that cloud water uptake was reversible in that in most cases hydrolysis was slow enough that some HNCO returned to the gas phase after cloud evaporation. The Barth et al. study estimated HNCO lifetimes as short as 1 h in warm polluted clouds (i.e., high SO2 and therefore H2SO4 formation). The results of our study and those of Borduas et al. (2016) add to these analyses in that now the measured temperature dependence of Heff can be used, and the hydrolysis rate constants can be updated.
The results in this paper allow for further refinement of HNCO loss estimates. For example, the salting out effect may be important for aerosol with high inorganic content, and high ammonium concentrations will result in reactive loss rates that are faster than hydrolysis. The solubility of HNCO in aerosol particles with substantial organic character can be higher or low depending on the nature of substituent groups, e.g., degree of −OH functionalization. Given that aerosol particles in most polluted atmospheres are at least half organic carbon by mass (Jimenez et al., 2009), it is useful to estimate what effect an increased solubility of HNCO might have on its removal lifetime. If we take our 1000 µm2 cm−3 surface area aerosol from the above calculation, assume a 50∕50 organic to aqueous distribution, and assume that the solubility of HNCO in the organic fraction is the same as n-octanol, we can arrive at a weighted average Henry's solubility of 55 M atm−1. If we combine that with the same reaction rate corresponding to pH 1, then the lifetime of HNCO against reaction to this aerosol drops to about 2 days, a significant effect.
In studies of the condensed-phase oxidation of dissolved N species, as well as biological processes that produce cyanate ions, there is a growing recognition that cyanate is part of the natural N cycle in the ocean (see Widner et al., 2013 and references therein). Observed near-surface cyanate levels often reached a few tens of nM in near-shore productive areas. The observations of cloud or aerosol source of HNCO presented in Zhao et al. (2014) on the coast of California might be explained by a combination of this NCO− seawater source and aerosol or cloud water acidification by local sources of strong acids, particularly HNO3. Specifically, acidification of sea spray containing about 10 nM NCO− to pH = 4 or so would correspond to Heff of around 50 M atm−1 and result in an equilibrium HNCO concentration of several hundred pptv. Such a source would most likely be limited by the concentration of sea-salt-derived aerosol but could easily account for the source implied by the measurements of Zhao et al. (2014).
3.3.2 CH3NCO
The atmospheric chemistry of CH3NCO is less well studied than HNCO. There is a single reported measurement of the reaction rate of CH3NCO with OH by relative rates which gave k = 3.6 × 10−12 cm3 mole−1 s−1 (Lu et al., 2014); however recent work indicates that secondary chemistry may have made this rate high by a significant amount (Papanastasiou et al., 2019). In addition, there are likely condensed-phase reactions that are faster than the simple hydrolysis reactions consider in this work. Nevertheless, it is useful to estimate the atmospheric loss rates implied by our work as a baseline against which future atmosphere observations can be judged, and the importance of other heterogeneous processes can be assessed. The uptake coefficients estimated for CH3NCO in Fig. 8 are relatively low, with only a slight increase at the lowest pHs in atmospheric media. As a consequence, atmospheric lifetimes of CH3NCO towards surface deposition are estimated to be quite long, 6 months or more if hydrolysis is the sole loss process. The loss due to aerosol of cloud water uptake is estimated to be slightly faster, due primarily to the slight acid catalysis of the CH3NCO hydrolysis rate.
3.3.3 ClCN, BrCN, and ICN
To date, we know of no observations of ClCN in the ambient atmosphere, but its formation in the chlorination of water, wastewater, and swimming pools (Afifi and Blatchley III, 2015; Daiber et al., 2016; Lee et al., 2006) indicates that there could be sources from human activities, including the use of chlorine bleach for cleaning indoor surfaces. In addition, there might also be a source from aerosol systems in which chlorine is being activated, i.e., oxidized from Cl− to ClNO2, Cl2, or HOCl (see, for example, Roberts et al., 2008) in the presence of reduced nitrogen. The results of our solubility measurements indicate that ClCN will volatilize from the condensed phase fairly readily, e.g., within seconds of the application of a thin film of chlorine bleach cleaning solution or the bubbling of air though a spa in which ClCN is dissolved. As a result, the atmospheric removal of ClCN should be considered. BrCN has been observed in systems in which bromide-containing water or wastewater were treated with halogens (Heller-Grossman et al., 1999), and there are biological mechanisms that make BrCN and ICN as well (Schlorke et al., 2016; Vanelslander et al., 2012). The potential for remote atmospheric sources of these compounds is currently being investigated, but BrCN could be the result of the same bromine activation chemistry that depletes ground-level ozone in that environment (Simpson et al., 2007).
Gas-phase radical reactions of XCN compounds have not been studied under atmospheric conditions. A few studies at higher temperatures and the studies of HCN and CH3CN can be used to roughly predict how fast the relevant reactions are. For example, the reactions of ClCN and BrCN with O atoms at 518–635 K are very slow (< 3 × 10−15 cm3 mole−1 s−1; Davies and Thrush, 1968), and the reaction of Cl atom with ClCN at high temperature is also quite slow (< 1.0 × 10−14 cm3 mole−1 s−1; Schofield et al., 1965). However, these observations do not preclude the presence of another reaction channel at low temperature, e.g., a mechanism involving addition to the CN group. The reactions of HCN and CH3CN with OH, Cl atoms, and O atoms at atmospherically relevant temperatures are all quite slow, implying that such addition channels are not likely to be substantially faster for these XCN compounds. We conclude that rate constants for the reactions of OH or Cl with X–CN compounds are likely quite low (< 2 × 10−14 cm3 mole−1 s−1), making the lifetimes of these compounds against these reactions on the order of a year or longer. The UV–visible absorption spectra of all three of these compounds have been measured (Barts and Halpern, 1989; Felps et al., 1991; Hess and Leone, 1987; Russell et al., 1987) and have maxima that range from < 200 nm for ClCN to 202 nm for BrCN and 250 nm for ICN, with absorption that tails into near-UV and visible wavelengths (see Fig. S13 in the Supplement). Extrapolation of the spectra, combined with photo fluxes estimated from the NCAR TUV model for midsummer 40∘ north at the surface, results in a range of photolysis behavior ranging from no tropospheric photolysis of ClCN to slight photolysis of BrCN (τ≅135 days) and faster photolysis of ICN (τ≅9 h). The above gas-phase processes provide the context in which to assess the importance of condensed-phase loss processes of ClCN, BrCN, and ICN. Rates of loss of XCN compounds due to surface deposition or cloud water or aerosol uptake would need to be faster than the gas-phase processes to be important in the atmosphere. In addition, condensed-phase reactions convert XCN to halide ions either by hydrolysis to cyanate or creation of a carbamyl functionalities. Only photolysis reforms the halogen atom and therefore maintains active halogen reaction chain. Estimated atmospheric lifetimes of XCN compounds against loss due to condensed-phase reactions listed in Table 3 show a general trend. The lifetimes become shorter as the halogen atom goes from Cl to Br to ICN, primarily due to higher solubilities. The actual condensed-phase losses are likely much shorter than those estimated here because of faster condensed-phase reactions that are not taken into account by the brief analysis presented here. Depending on the mechanism of condensed-phase XCN reactions, this chemistry could be a condensed-phase source of NCO− and therefore HNCO, similar to that observed by Zhao et al. (2014) in coastal clouds.
3.3.4 Solubility in non-polar media, uptake to organic aerosol, and membrane transport
The solubilities of HNCO, CH3NCO, and BrCN in n-octanol were roughly a factor of 4 larger than water, while that of ClCN was virtually the same. Reaction rates with n-octanol were the same as or slower than for aqueous solutions, except for ClCN which was faster than hydrolysis at pH = 7. As a result, loss due to uptake to organic aerosol will be only slightly faster for all of these species. Membrane transport is a key process in determining the extent to which a chemical species will impact biological systems. Simple membrane transport models parameterize this process as diffusion through a lipid bilayer according to a partition coefficient, Kp, which is the ratio of solubilities in lipid versus aqueous media (Missner and Pohl, 2009), and Kow is often used for this partition coefficient. The results of our work indicate that both HNCO and CH3NCO are more soluble in n-octanol than water, in contrast to other similar small organic acids and N-containing compounds (Table 4). These features will need to be accounted for in assessing the connection between environmental exposure to HNCO, CH3NCO, ClCN, and BrCN and resulting biochemical effects.
The data are available on request.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-4419-2019-supplement.
YL and JMR performed the laboratory experiments, and JMR and YL wrote the paper.
The authors declare that they have no conflict of interest.
Any mention of commercial products or brands was solely for identifying purposes and should not be construed as an endorsement.
We thank James B. Burkholder and Françios Bernard for help with the FTIR analysis and Patrick Veres and Bin Yuan for the CIMS analyses of XCN samples. We thank Dimitris Papanastasiou, J. Andrew Neuman, Patrick Veres, Chen Wang, and Jonathan Abbatt for communicating the results of their work prior to publication. This work was supported in part by NOAA's Climate and Health of the Atmosphere Initiatives.
This paper was edited by Sergey A. Nizkorodov and reviewed by two anonymous referees.
Afifi, M. Z. and Blatchley III, E. R.: Seasonal dynamics of water and air chemistry in an indoor chlorinated swimming pool, Water Res., 68, 771–783, 2015.
Al-Rawi, H. and Williams, A.: Elimination-addition mechanisms of acyl group transfer: the hydrolysis and synthesis of carbamates, J. Am. Chem. Soc., 99, 2671–2678, 1977.
Bailey, P. L. and Bishop, E.: Hydrolysis of cyanogen chloride, J. Chem. Soc., 912–916, https://doi.org/10.1039/dt9730000912, 1973.
Barnes, I., Solignac, G., Mellouki, A., and Becker, K. H.: Aspects of the atmospheric chemistry of amides, Chem. Phys. Chem., 11, 3844–3857, 2010.
Barth, M. C., Cochran, A. C., Fiddler, M. N., Roberts, J. M., and Bililign, S.: Numerical modeling of cloud chemistry effects on isocyanic acid (HNCO), J. Geophys. Res., 118, 8688–8701, 2013.
Barts, S. A. and Halpern, J. B.: Photodissociation of ClCN between 190 and 213 nm, J. Phys. Chem., 93, 7346–7351, 1989.
Belson, D. J. and Strachan, A. N.: Preparation and properties of isocyanic acid, Chem. Soc. Rev., 11, 41–56, 1982.
Bengtstrom, L., Salden, M., and Stec, A. A.: The role of isocyanates in fire toxicity, Fire Sci. Rev., 5, 1–23, 2016.
Blomqvist, P., Hertzberg, T., Dalene, M., and Skarping, G.: Isocyanates, aminoisocyanates, and amines from fires – a screening of common materials found in buildings, Fire Mater., 27, 275–294, 2003.
Boenig, D. W. and Chew, C. M.: A critical review: general toxicity and environmental fate of three aqueous cyanide ions and associated ligands, Water, Air Soil Pollut., 109, 67–79, 1999.
Borduas, N., da Silva, G., Murphy, J. G., and Abbatt, J. P. D.: Experimental and theoretical understanding of the gas phase oxidation of atmospheric amides with OH radicals: Kinetics, products, and mechanisms, J. Phys. Chem. A, 119, 4298–4308, 2015.
Borduas, N., Place, B., Wentworth, G. R., Abbatt, J. P. D., and Murphy, J. G.: Solubility and reactivity of HNCO in water: insights into HNCO's fate in the atmosphere, Atmos. Chem. Phys., 16, 703–714, https://doi.org/10.5194/acp-16-703-2016, 2016.
Broughton, E.: The Bhopal disaster and its aftermath: a review, Environ. Health, 4, 6–12, 2005.
Bunkan, A. J. C., Hetzler, J., Mikoviny, T., Wisthaler, A., Nielsen, C. J., and Olzmann, M.: The reactions of N-methylformamide and N,N-dimethylformamide with OH and their photo-oxidation under atmospheric conditions: experimental and theoretical studies, Phys. Chem. Chem. Phys., 17, 7046–7059, 2015.
Cano-Ruiz, J. A., Kong, D., Balas, R. B., and Nazaroff, W. W.: Removal of reactive gases at indoor surfaces: Combining mass transport and surface kinetics, Atmos. Environ. A, 27, 2039–2050, 1993.
Castro, E. A., Moodie, R. B., and Sansom, P. J.: The kinetics of hydrolysis of methyl and phenyl isocyanates, J. Chem. Soc. Perk. T., 2, 737–742, 1985.
Chandra, B. P. and Sinha, V.: Contribution of post-harvest agricultural paddy residue fires in the N.W. Indo-Gangetic Plain to ambient carcinogenic benzenoids, toxic isocyanic acid and carbon monoxide, Environ. Intl., 88, 187–197, 2016.
Clever, H. L.: Sechenov salt-effect parameter, J. Chem. Eng. Data, 28, 340–343, 1983.
Daiber, E. J., DeMarini, D. M., Ravuri, S. A., Liberatore, H. K., Cuthbertson, A. A., Thompson-Klemish, A., Byer, J. D., Schmid, J. E., Afifi, M. Z., Blatchley III, E. R., and Richardson, S. D.: Progressive increase in disinfection byproducts and mutagenicity from source to tap to swimming pool and spa water: Impact of human inputs, Environ. Sci. Technol., 50, 6652–6662, 2016.
Davidovits, P., Kolb, C. E., Williams, L. R., Jayne, J. T., and Worsnop, D. R.: Mass accommodation and chemical reactions at gas-liquid interfaces, Chem. Rev., 106, 1323–1354, 2006.
Davies, P. B. and Thrush, B. A.: Reactions of oxygen atoms with hydrogen cyanide, cyanogen chloride and cyanogen bromide, T. Faraday Soc., 64, 1836–1843, 1968.
Davis, D. D. and Okabe, H.: Determination of bond dissociation energies in hydrogen cyanide, cyanogen and cyanogen halides by the photodissociation method, J. Chem. Phys., 49, 5526–5531, 1968.
Diehl, A. C., Speitel Jr., G. E., Symons, J. M., Krasner, S. W., Hwang, C. J., and Barrett, S. E.: DBP formation during chloramination, J. Am. Water Works Ass., 92, 76–90, 2000.
Edwards, J. O., Erstfeld, T. E., Ibne-Rasa, K. M., Levey, G., and Moyer, M.: Reaction rates for nucleophiles with cyanogen chloride: Comparison with two other digonal carbon compounds, Int. J. Chem. Kinet., 18, 165–180, 1986.
Epstein, J.: Estimation of microquantities of cyanide, Anal. Chem., 19, 272–274, 1947.
Felps, W. S., Rupnik, K., and McGlynn, S. P.: Electronic spectroscopy of the cyanogen halides, J. Phys. Chem., 95, 639–656, 1991.
Fuks, R. and Hartemink, M. A.: The acid-catalyzed reaction of cyanogen chloride with aliphatic alcohols. A general synthesis of aliphatic carbamates, B. Soc. Chim. Belg., 82, 23–30, 1973.
Garrido, M. A., Gerecke, A. C., Heeb, N., Font, R., and Conesa, J. A.: Isocyanate emissions from pyrolysis of mattresses containing polyurethane foam, Chemosphere, 168, 667–675, 2017.
Geddes, J. D., Miller, G. C., and Taylor Jr., G. E.: Gas phase photolysis of methyl isothiocyanate, Environ. Sci. Technol., 29, 2590–2594, 1995.
Gerritsen, C. M., Gazda, M., and Margerum, D. W.: Non-metal redox kinetics: Hypobromite and hypoiodite reactions with cyanide and the hydrolysis of cyanogen halides, Inorg. Chem., 32, 5739–5748, 1993.
Goesmann, F., Rosenbauer, H., Bredehoft, J. H., Cabane, M., Ehrenfreund, P., Gautier, T., Giri, C., Kruger, H., Le Roy, L., MacDermott, A. J., McKenna-Lawlor, S., Meierhenrich, U. J., Munoz Caro, G. M., Raulin, F., Roll, R., Steele, A., Steininger, H., Sternberg, R., Szopa, C., Thiemann, W., and Ulamec, S.: Organic compounds on comet 67P/Churyumov-Gerasimenko revealed by COSAC mass spectrometry, Science, 349, aab0689-1 to aab0689-3, 2015.
Hagel, P., Gerding, J. J. T., Fieggen, W., and Bloemendal, H.: Cyanate formation in solutions of urea, 1. Calculation of cyanate concentrations at different temperature and pH, Biochim. Biophys. Acta, 243, 366–373, 1971.
Halfen, D. T., Ilyushin, V. V., and Ziurys, L. M.: Interstellar detection of methyl isocyanate CH3NCO in Sgr B2(N): A link from molecular clouds to comets, Astrophys. J. Lett., 812, 1–8, 2015.
Hardy, J. E. and Knarr, J. J.: Technique for measuring the total concentration of gaseous fixed nirogen species, J. Air Pollut. Contr. Assoc., 32, 376–379, 1982.
Heller-Grossman, L., Idin, A., Limoni-Relis, B., and Rebhun, M.: Formation of cyanogen bromide and other volatile DBPs in the disinfection of bromide-rich lake water, Environ. Sci. Technol., 33, 932–937, 1999.
Hess, W. P. and Leone, S. R.: Absolute I* quantum yields for the ICN Ã state by diode laser gain-vs-absorption spectroscopy, J. Chem. Phys., 86, 3773–3780, 1987.
Hilal, S. H., Ayyampalayam, S. N., and Carreira, L. A.: Air-liquid partition coefficient for a diverse set of organic compounds: Henry's law constant in water and hexadecane, Environ. Sci. Technol., 42, 9231–9236, 2008.
Jensen, M. B.: On the kinetics of the decomposition of cyanic acid, Acta Chem. Scand., 12, 1657–1670, 1958.
Jensen, M. B.: On the kinetics of the reaction of cyanic acid with amines, Acta Chem. Scand., 13, 289–300, 1959.
Jimenez, J. L., Canagaratna, M. R., Donahue, N. M., Prevot, A. S. H., Zhang, Q., Kroll, J. H., DeCarlo, P. F., Allan, J. D., Coe, H., Ng, N. L., Aiken, A. C., Docherty, K. S., Ulbrich, I. M., Grieshop, A. P., Robinson, A. L., Duplissy, J., Smith, J. D., Wilson, K. R., Lanz, V. A., Hueglin, C., Sun, Y. L., Tian, J., Laaksonen, A., Raatikainen, T., Rautiainen, J., Vaattovaara, P., Ehn, M., Kulmala, M., Tomlinson, J. M., Collins, D. R., Cubison, M. J., Dunlea, E. J., Huffman, J. A., Onasch, T. B., Alfarra, M. R., Williams, P. I., Bower, K., Kondo, Y., Schneider, J., Drewnick, F., Borrmann, S., Weimer, S., Demerjian, K., Salcedo, D., Cottrell, L., Griffin, R., Takami, A., Miyoshi, T., Hatakeyama, S., Shimono, A., Sun, J. Y., Zhang, Y. M., Dzepina, K., Kimmel, J. R., Sueper, D., Jayne, J. T., Herndon, S. C., Trimborn, A. M., Williams, L. R., Wood, E. C.,, Middlebrook, Kolb, C. E., Baltensperger, U., and Worsnop, D. R.: Evolution of organic aerosols in the atmosphere, Science, 326, 1525–1529, 2009.
Kames, J. and Schurath, U.: Henry's law and hydrolysis-rate constants for peroxyacetyl nitrates (PANs) using a homogeneous gas-phase source, J. Atmos. Chem., 21, 151–164, 1995.
Keller-Rudek, H., Moortgat, G. K., Sander, R., and Sörensen, R.: The MPI-Mainz UV/VIS Spectral Atlas of Gaseous Molecules of Atmospheric Interest, Earth Syst. Sci. Data, 5, 365–373, https://doi.org/10.5194/essd-5-365-2013, 2013.
Kish, J. D., Leng, C., Kelley, J., Hiltner, J., Zhang, Y., and Liu, Y.: An improved approach for measuering Henry's law coefficients of atmospheric organics, Atmos. Environ., 79, 561–565, 2013.
Kolb, C. E., Worsnop, D. R., Zahniser, M. S., Davidovits, P., Keyser, L. F., Leu, M.-T., Molina, M. J., Hanson, D. R., Ravishankara, A. R., Williams, L. R., and Tolbert, M. A.: Laboratory studies of atmospheric heterogeneous chemistry, in: Progress and Problems in Atmospheric Chemistry, edited by: Barker, J. R., Advanced Series in Physical Chemistry, 3, World Scientific, Singapore, 1995.
Koss, A. R., Sekimoto, K., Gilman, J. B., Selimovic, V., Coggon, M. M., Zarzana, K. J., Yuan, B., Lerner, B. M., Brown, S. S., Jimenez, J. L., Krechmer, J., Roberts, J. M., Warneke, C., Yokelson, R. J., and de Gouw, J.: Non-methane organic gas emissions from biomass burning: identification, quantification, and emission factors from PTR-ToF during the FIREX 2016 laboratory experiment, Atmos. Chem. Phys., 18, 3299–3319, https://doi.org/10.5194/acp-18-3299-2018, 2018.
Kumar, V., Chandra, B. P., and Sinha, V.: Large unexplained suite of chemically reactive compounds present in ambient air due to biomass fires, Sci. Rep., 8, 1–15, 2018.
Lee, J. H., Na, C., Ramirez, R. L., and Olsen, T. M.: Cyanogen chloride precursor analysis in chlorinated river water, Environ. Sci. Technol., 40, 1478–1484, 2006.
Leo, A., Hansch, C., and Elkins, D.: Partition coefficients and their uses, Chem. Rev., 71, 525–616, 1971.
Li, Q., Jacob, D. J., Bey, I., Yantosca, R. M., Zhao, Y., Kondo, Y., and Notholt, J.: Atmospheric hydrogen cyanide (HCN): Biomass burning sources, ocean sink?, Geophys. Res. Lett., 27, 357–360, 2000.
Lu, Z., Hebert, V. R., and Miller, G. C.: Gas-phase reaction of methyl isothiocyanate and methyl isocyanate with hydroxyl radicals under static relative rate conditions, J. Agr. Food Chem., 62, 1792–1795, 2014.
Maroulis, G. and Pouchan, C.: Dipole polarizability and hyperpolarizability of FCN, ClCN, BrCN and ICN, Chem. Phys., 216, 67–76, 1997.
Mattila, J. M., Brophy, P., Kirkland, J., Hall, S., Ullmann, K., Fischer, E. V., Brown, S., McDuffie, E., Tevlin, A., and Farmer, D. K.: Tropospheric sources and sinks of gas-phase acids in the Colorado Front Range, Atmos. Chem. Phys., 18, 12315–12327, https://doi.org/10.5194/acp-18-12315-2018, 2018.
McMaster, M. E., Ashley-Sing, C., Dos Santos Tavares, A. A., Corral, C. A., McGill, K., McNeil, D., Jansen, M. A., and Simpson, A. H. R. W.: The inhalation effects of by-products from chlorination of heated indoor swimming pools on spinal development in pup mice, Environ. Res., 166, 668–676, 2018.
Missner, A. and Pohl, P.: 110 Years of the Meyer–Overton rule: Predicting membrane permeability of gases and other small compounds, Chem. Phys. Chem., 10, 1405–1414, 2009.
Na, C. and Olson, T. M.: Mechanism and kinetics of cyanogen chloride formation from the chlorination of glycine, Environ. Sci. Technol., 40, 1469–1477, 2006.
NASA: ESPO Data Archive, https://espoarchive.nasa.gov/archive/browse/atom, last access: 14 February 2019.
Papanastasiou, D. K., Bernard, F., and Burkholder, J. B.: Atmospheric fate of methyl isocyanate, CH3NCO: OH and Cl reaction kinetics and identification of formyl isocyanate, HC(O)NCO, Manuscript in preparation, 2019.
Raspoet, G., Nguyen, M. T., McGarraghy, M., and Hegarty, A. F.: The alcoholysis reaction of isocyanates giving urethanes: Evidence for a multimolecular mechanism, J. Org. Chem., 63, 6878–6885, 1998.
Reyes-Villegas, E., Bannan, T., Le Breton, M., Mehra, A., Priestley, M., Percival, C., Coe, H., and Allan, J. D.: Online chemical characterization of food-cooking organic aerosols: Implications for source apportionment, Environ. Sci. Technol., 52, 5308–5318, 2018.
Roberts, J. M.: Measurement of the Henry's law coefficient and the first order loss rate of PAN in n-octanol, Geophys. Res. Lett., 31, L08803, https://doi.org/10.1029/2004GL022327, 2005.
Roberts, J. M., Osthoff, H. D., Brown, S. S., and Ravishankara, A. R.: N2O5 oxidizes chloride to Cl2 in acidic atmospheric aerosol, Science, 321, 1059, https://doi.org/10.1126/science.1158777, 2008.
Roberts, J. M., Veres, P., Warneke, C., Neuman, J. A., Washenfelder, R. A., Brown, S. S., Baasandorj, M., Burkholder, J. B., Burling, I. R., Johnson, T. J., Yokelson, R. J., and de Gouw, J.: Measurement of HONO, HNCO, and other inorganic acids by negative-ion proton-transfer chemical-ionization mass spectrometry (NI-PT-CIMS): application to biomass burning emissions, Atmos. Meas. Tech., 3, 981–990, https://doi.org/10.5194/amt-3-981-2010, 2010.
Roberts, J. M., Veres, P. R., Cochran, A. K., Warneke, C., Burling, I. R., Yokelson, R. J., Lerner, B. M., Gilman, J. B., Kuster, W. C., Fall, R., and de Gouw, J.: Isocyanic acid in the atmosphere and its possible link to smoke-related health effects, P. Natl. Acad. Sci. USA, 108, 8966–8971, 2011.
Roberts, J. M., Veres, P. R., VandenBoer, T. C., Warneke, C., Graus, M., Williams, E. J., Holloway, J. S., Lefer, B., Brock, C. A., Bahreini, R., Ozturk, F., Middlebrook, A. M., Wagner, N. L., Dube, W. P., and de Gouw, J. A.: New insights into atmospheric sources and sinks of isocyanic acid, HNCO, from recent urban and regional observations, J. Geophys. Res., 119, 1060–1072, 2014.
Russell, J. A., McLaren, I. A., Jackson, W. M., and Halpern, J. B.: Photolysis of BrCN between 193 and 266 nm, J. Phys. Chem., 91, 3248–3253, 1987.
Sander, R.: Modeling atmospheric chemistry: Interactions between gas-phase species and liquid cloud/aerosol particles, Surv. Geophys., 20, 1–31, 1999.
Sander, R.: Compilation of Henry's law constants (version 4.0) for water as solvent, Atmos. Chem. Phys., 15, 4399–4981, https://doi.org/10.5194/acp-15-4399-2015, 2015.
Sarkar, C., Sinha, V., Kumar, V., Rupakheti, M., Panday, A., Mahata, K. S., Rupakheti, D., Kathayat, B., and Lawrence, M. G.: Overview of VOC emissions and chemistry from PTR-TOF-MS measurements during the SusKat-ABC campaign: high acetaldehyde, isoprene and isocyanic acid in wintertime air of the Kathmandu Valley, Atmos. Chem. Phys., 16, 3979–4003, https://doi.org/10.5194/acp-16-3979-2016, 2016.
Saylor, R. D., Edgerton, E. S., Hartsell, B. E., Baumann, K., and Hansen, D. A.: Continuous gaseous and total ammonia measurements from the southeastern aerosol research and characterization (SEARCH) study, Atmos. Environ., 44, 4994–5004, 2010.
Schlorke, D., Flemming, J., Birkemeyer, C., and Arnhold, J.: Formation of cyanogen iodide by lactoperoxidase, J. Inorg. Biochem., 154, 35–41, 2016.
Schofield, D., Tsang, W., and Bauer, S. H.: Thermal decomposition of ClCN, J. Chem. Phys., 42, 2132–2137, 1965.
Schreiber, J. and Witkop, B.: The reaction of cyanogen bromide with mono- and diamino Acids, J. Am. Chem. Soc., 86, 2441–2445, 1964.
Schumpe, A.: The estimation of gas solubilities in salt solutions, Chem. Eng. Sci., 48, 153–158, 1993.
Schwab, J. J., Li, Y., Bae, M.-S., Demerjian, K. L., Hou, J., Zhou, X., Jensen, B., and Pryor, S.: A laboratory intercomparision of real-time gaseous ammonia measurement methods, Environ. Sci. Technol., 41, 8412–8419, 2007.
Shang, C., Gong, W.-L., and Blatchley III, E. R.: Breakpoint chemistry and volatile byproduct formation resulting from chlorination of model organic-N compounds, Environ. Sci. Technol., 34, 1721–1728, 2000.
Siddiqui, S. and Siddiqui, B. S.: Some extensions of von Braun (BrCN) reaction on organic bases, Z. Naturforsch., 35, 1049–1052, 1980.
Simpson, W. R., von Glasow, R., Riedel, K., Anderson, P., Ariya, P., Bottenheim, J., Burrows, J., Carpenter, L. J., Frieß, U., Goodsite, M. E., Heard, D., Hutterli, M., Jacobi, H.-W., Kaleschke, L., Neff, B., Plane, J., Platt, U., Richter, A., Roscoe, H., Sander, R., Shepson, P., Sodeau, J., Steffen, A., Wagner, T., and Wolff, E.: Halogens and their role in polar boundary-layer ozone depletion, Atmos. Chem. Phys., 7, 4375–4418, https://doi.org/10.5194/acp-7-4375-2007, 2007.
State of California: OEHHA Chemical Database – Air: https://oehha.ca.gov/air/chemicals/methyl-isocyanate, last access: 23 August 2017.
Stockwell, C. E., Kupc, A., Witkowski, B., Talukdar, R. K., Liu, Y., Selimovic, V., Zarzana, K. J., Sekimoto, K., Warneke, C., Washenfelder, R. A., Yokelson, R. J., Middlebrook, A. M., and Roberts, J. M.: Characterization of a catalyst-based conversion technique to measure total particulate nitrogen and organic carbon and comparison to a particle mass measurement instrument, Atmos. Meas. Tech., 11, 2749–2768, https://doi.org/10.5194/amt-11-2749-2018, 2018.
Valentour, J. C., Aggarwal, V., and Sunshine, I.: Sensitive gas chromatographic determination of cyanide, Anal. Chem., 46, 924–925, 1974.
Vanelslander, B., Paul, C., Grueneberg, J., Prince, E. K., Gillard, J., Sabbe, K., Pohnert, G., and Vyeverman, W.: Daily bursts of biogenic cyanogen bromide (BrCN) control biofilm formation around a marine benthic diatom, Proc. Natl Acad. Sci. USA, 109, 2412–2417, 2012.
von Braun, J. and Schwarz, R.: Die einwirkung von bromcyan auf tertiäre amine, Chem. Ber., 35, 1279–1285, 1902.
Wang, C., Lei, Y. D., Endo, S., and Wania, F.: Measuring and modeling the salting-out effect in ammonium sulfate solutions, Environ. Sci. Technol., 48, 13238–13245, 2014.
Wang, Z., Nicholls, S. J., Rodriguez, E. R., Kummu, O., Hörkko, S., Barnard, J., Reynolds, W. F., Topol, E. J., DiDonato, J. A., and Hazen, S. L.: Protein carbamylation links infammation, smoking, uremia, and atherogenesis, Nat. Med., 13, 1176–1184, 2007.
Warneke, C., Trainer, M., de Gouw, J. A., Parrish, D. D., Fahey, D. W., Ravishankara, A. R., Middlebrook, A. M., Brock, C. A., Roberts, J. M., Brown, S. S., Neuman, J. A., Lerner, B. M., Lack, D., Law, D., Hübler, G., Pollack, I., Sjostedt, S., Ryerson, T. B., Gilman, J. B., Liao, J., Holloway, J., Peischl, J., Nowak, J. B., Aikin, K. C., Min, K.-E., Washenfelder, R. A., Graus, M. G., Richardson, M., Markovic, M. Z., Wagner, N. L., Welti, A., Veres, P. R., Edwards, P., Schwarz, J. P., Gordon, T., Dube, W. P., McKeen, S. A., Brioude, J., Ahmadov, R., Bougiatioti, A., Lin, J. J., Nenes, A., Wolfe, G. M., Hanisco, T. F., Lee, B. H., Lopez-Hilfiker, F. D., Thornton, J. A., Keutsch, F. N., Kaiser, J., Mao, J., and Hatch, C. D.: Instrumentation and measurement strategy for the NOAA SENEX aircraft campaign as part of the Southeast Atmosphere Study 2013, Atmos. Meas. Tech., 9, 3063–3093, https://doi.org/10.5194/amt-9-3063-2016, 2016.
Weng, S.-C., Weaver, W. A., Blatchley, T. N., Cramer, J. S., Chen, J., and Blatchley III, E. R.: Dynamics of gas-phase trichloramine (NCl3) in chlorinated, indoor swimming pool facilities, Indoor Air, 21, 391–399, 2011.
Wentzell, J. B., Liggio, J., Li, S.-M., Vlasenko, A., Staebler, R., Lu, G., Poitras, M.-J., Chan, T., and Brook, J. R.: Measurements of gas phase acids in Diesel exhaust: A relevant source of HNCO?, Environ. Sci. Technol., 47, 7663–7671, 2013.
Wesely, M. L. and Hicks, B. B.: A review of the current status of knowledge on dry deposition, Atmos. Environ., 34, 2261–2282, 2000.
Widner, B., Mulholland, M. R., and Mopper, K.: Chromatographic determination of nanomolar cyanate concentrations in estuarine and sea waters by precolumn fluorescence derivatization, Anal. Chem., 85, 6661–6666, 2013.
Williams, A. and Jencks, W. P.: Acid and base catalysis of urea synthesis: Nonlinear Brønsted plots consistent with a diffusion-controlled proton-transfer mechanism and reactions of imidazole and N-methylimidazole with cyanic acids, J. Chem. Soc., 1760–1768, 1974a.
Williams, A. and Jencks, W. P.: Urea Synthesis from amines and cyanic acid: kinetic evidence for a zwitterionic intermediate, J. Chem. Soc., 1753–1759, 1974b.
Williams, E. J., Baumann, K., Roberts, J. M., Bertman, S. B., Norton, R. B., Fehsenfeld, F. C., Springston, S. R., Nunnermacker, L. J., Newman, L., Olszyna, K., Meagher, J., Hartsell, B., Edgerton, E., Pearson, J. R., and Rodgers, M. O.: Intercomparison of ground-based NOy measurement techniques, J. Geophys. Res.-Atmos., 103, 22261–22280, 1998.
Williams, J., Roberts, J. M., Bertman, S. B., Stroud, C. A., Fehsenfeld, F. C., Baumann, K., Buhr, M. P., Knapp, K., Murphy, P. C., Nowick, M., and Williams, E. J.: A method for the airborne measurement of PAN, PPN, and MPAN, J. Geophys. Res.-Atmos., 105, 28943–928960, 2000.
Woo, S.-C. and Liu, T.-K.: The absorption spectra and dissociation energies of cyanic acid and some isocyanates, J. Chem. Phys., 3, 544–546, 1935.
Woodrow, J. E., LePage, J. T., Miller, G. C., and Herbert, V. R.: Determination of methyl isocyanate in outdoor residential air near metam-sodium soil fumigations, J. Agr. Food Chem., 62, 8921–8927, 2014.
Woodward-Massey, R., Taha, Y. M., Moussa, S. G., and Osthoff, H. D.: Comparison of negative-ion proton-transfer with iodide ion chemical ionization mass spectrometry for quantification of isocyanic acid in ambient air, Atmos. Environ., 98, 693–703, 2014.
Yang, X. and Shang, C.: Chlorination byproduct formation in the presence of humic acid, model nitrogenous orgainc compounds, ammonia, and bromide, Environ. Sci. Technol., 38, 4995–5001, 2004.
Yaws, C. L. and Yang, H.-C.: Henry's law constant for compounds in water, in: Thermodynamic and physical properties, edited by: Yaws, C. L., Gulf Publishing Company, Houston, TX, 1992.
Young, P. J., Emmons, L. K., Roberts, J. M., Lamarque, J.-F., Wiedinmyer, C., Veres, P., and VandenBoer, T. C.: Isocyanic acid in a global chemistry transport model: Tropospheric distribution, budget, and identification of regions with potential health impacts, J. Geophys. Res.-Atmos., 117, 1–14, 2012.
Yuan, B., Koss, A., Warneke, C., Gilman, J. B., Lerner, B. M., Stark, H., and de Gouw, J. A.: A high-resolution time-of-flight chemical ionization mass spectrometer utilizing hydronium ions (H3O+ ToF-CIMS) for measurements of volatile organic compounds in the atmosphere, Atmos. Meas. Tech., 9, 2735–2752, https://doi.org/10.5194/amt-9-2735-2016, 2016.
Zhao, R., Lee, A. K. Y., Wentzell, J. J. B., McDonald, A. M., Toom-Sauntry, D., Leaitch, W. R., Modini, R. L., Corrigan, A. L., Russell, L. M., Noone, K. J., Schroder, J. C., Bertram, A. K., Hawkins, L. N., Abbatt, J. P. D., and Liggio, J.: Cloud partitioning of isocyanic acid (HNCO) and evidence of secondary source of HNCO in ambient air, Geophys. Res. Lett., 41, 1–8, 2014.