the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Unravelling the microphysics of polar mesospheric cloud formation
Mario Nachbar
Thomas Leisner
Polar mesospheric clouds are the highest water ice clouds occurring in the terrestrial atmosphere. They form in the polar summer mesopause, the coldest region in the atmosphere. It has long been assumed that these clouds form by heterogeneous nucleation on meteoric smoke particles which are the remnants of material ablated from meteoroids in the upper atmosphere. However, until now little was known about the properties of these nanometre-sized particles and application of the classical theory for heterogeneous ice nucleation was impacted by large uncertainties. In this work, we performed laboratory measurements on the heterogeneous ice formation process at mesopause conditions on small (r=1 to 3 nm) iron silicate nanoparticles serving as meteoric smoke analogues. We observe that ice growth on these particles sets in for saturation ratios with respect to hexagonal ice below Sh=50, a value that is commonly exceeded during the polar mesospheric cloud season, affirming meteoric smoke particles as likely nuclei for heterogeneous ice formation in mesospheric clouds. We present a simple ice-activation model based on the Kelvin–Thomson equation that takes into account the water coverage of iron silicates of various compositions. The activation model reproduces the experimental data very well using bulk properties of compact amorphous solid water. This is in line with the finding from our previous study that ice formation on iron silicate nanoparticles occurs by condensation of amorphous solid water rather than by nucleation of crystalline ice at mesopause conditions. Using the activation model, we also show that for iron silicate particles with dry radius larger than r=0.6 nm the nanoparticle charge has no significant effect on the ice-activation threshold.
Polar mesospheric clouds (PMCs) are water ice clouds occurring in the terrestrial atmosphere at an altitude of about 83 km (e.g. Rapp and Thomas, 2006; Thomas, 1991; Thomas and Olivero, 2001). The clouds form during the polar summer in the mesopause and were reported in the literature for the first time at the end of the 19th century (Leslie, 1885). They are optically very thin and can be seen from ground by the naked eye only after the sun has set below the horizon, which is why they are often called noctilucent clouds (NLCs). In recent years NLCs have been intensely studied using ground-based (e.g. Demissie et al., 2014; Kaifler et al., 2013; Kirkwood et al., 2008) and space-borne (e.g. DeLand et al., 2007; Hervig et al., 2016; Rong et al., 2015) methods. Additional studies have shown that during NLC season local temperatures are highly variable with mean temperatures of about 140 K and extremes as low as 100 K (Lübken et al., 2009; Rapp et al., 2002). Typical H2O concentrations of a few parts per million (Hervig et al., 2009; Seele and Hartogh, 1999) then lead to highly supersaturated conditions, i.e. saturation ratios exceeding Sh=100 are frequently observed (Lübken et al., 2009). It is commonly believed that such high supersaturations in the summer mesopause initiate the heterogeneous formation of crystalline ice on meteoric smoke particles (MSPs) (Gumbel and Megner, 2009; Keesee, 1989; Rapp and Thomas, 2006). MSPs are nanoparticles which form by re-condensation of material ablated from meteoroids entering the upper atmosphere (Plane et al., 2015). Recent studies estimated that about 40 t of cosmic material enters the atmosphere each day (Carrillo-Sánchez et al., 2016; Hervig et al., 2017). Approximately 20 % of this material ablates in the upper atmosphere with the major elemental species being Fe, Mg, and Si (Vondrak et al., 2008). The ablated elemental species then form oxide, hydroxide, and carbonate compounds below 85 km and polymerize into nanometre-sized particles (Plane et al., 2015), which are likely present in the form of magnetite (Fe3O4), wüstite (FeO), magnesiowüstite (MgxFe1−xO, x=0–0.6), or iron-rich olivine (Mg2xFe2−2xSiO4, x=0.4–0.5) (Hervig et al., 2017; Rapp et al., 2012). Strong atmospheric circulation limits the average lifetime of these particles in the summer mesopause such that they only reach sizes below about r=2 nm (Bardeen et al., 2008; Megner et al., 2008a, b; Plane et al., 2014). Model simulations have shown that about 10 % of these particles are negatively charged at NLC height and season (Plane et al., 2015, 2014).
Precise modelling of the formation process of NLCs is, however, hindered by a limited understanding of the microphysical processes involved in heterogeneous ice formation under mesopause conditions. Here, the main unknown parameters are the surface properties of MSPs (i.e. the ability of the material to serve as ice nuclei), the ice phase forming at mesopause conditions, and the effect the electrical charge of MSPs may have on the ice formation process. In order to improve our understanding of NLC formation we recently introduced an experimental set-up to study ice formation and growth processes on nanoparticles exposed to realistic mesopause conditions (Duft et al., 2015). We used this set-up in two previous studies to investigate ice growth rates on iron oxide and silica nanoparticles which served as analogues for MSPs (Nachbar et al., 2018b, c). We demonstrated that water vapour condenses in the form of compact amorphous solid water (ASW) at temperatures of the summer mesopause. In this study we follow up on our recent work and precisely measure onset conditions for the activation of ice growth on small meteoric smoke particle analogues at PMC formation conditions. We performed laboratory experiments by choosing conditions with saturation ratios below and above the activation threshold for ice growth. From these experiments, we determined critical saturations Scrit needed to activate ice growth. We analysed the data considering the formation of ASW and present a new adsorption-activation model, which highly reduces the current uncertainties in describing ice particle formation in the mesopause.
In this work we performed laboratory experiments using the MICE-TRAPS apparatus which was described earlier (Duft et al., 2015; Meinen et al., 2010; Nachbar et al., 2018b, 2016). In brief, sub-4 nm iron silicate nanoparticles of adjustable elemental composition are produced in a microwave plasma particle source as MSP analogues (Nachbar et al., 2018a). The nanoparticles are transferred continuously to the low pressure ( mbar) Trapped Reactive Atmospheric Particle Spectrometer (TRAPS) by means of an aerodynamic lens system. Within TRAPS the nanoparticles carrying a single positive charge are mass-selected and levitated in the molecular flow ice cell (MICE). MICE is a combination of a linear quadrupole ion trap and a water vapour supersaturation cell in which pressure, temperature, and humidity conditions of the polar summer mesopause can be established. The nanoparticles trapped in MICE are thermalized by collisions with a He background gas. The water vapour partial pressure in MICE is set by temperature-controlled sublimation from ice-covered surfaces which have been installed in addition to the ion trap electrodes. In this work, the saturation ratio S (short: saturation) is usually given with respect to the saturation vapour pressure of compact ASW (SASW). In some cases, and in order to facilitate comparison with previous studies, the saturation ratio is also given with respect to the saturation vapour pressure of hexagonal ice (Sh), for which we use the well-established parameterization given by Murphy and Koop (2005). The saturation SASW can be obtained from Sh using the following relation (Nachbar et al., 2018c):
We use the terms supersaturation and supersaturated conditions for cases in which the saturation is larger than 1.
A typical experiment in MICE starts by filling the particle trap with about 107 size-selected, singly charged nanoparticles in about 1 s. Water adsorption and condensation on the trapped nanoparticles is monitored by periodically extracting small fractions of the trapped nanoparticle population and measuring the nanoparticle mass as a function of the trapping time using a time-of-flight mass spectrometer. The saturation is usually varied by changing the particle temperature while keeping the water vapour density in MICE constant to facilitate comparison. In principle, water vapour density and particle temperature can be chosen independently within the limits of this experimental approach (Duft et al., 2015). Typical mass growth curves of iron oxide particles of initial radius rdry=1.87 nm are shown in Fig. 1 for various water vapour saturation ratios between SASW=1.4 and SASW=16.
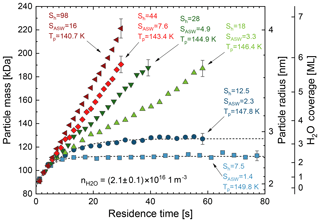
Figure 1Water vapour adsorption and depositional growth on Fe2O3 nanoparticles of initial radius rdry=1.87 nm under supersaturated conditions. Particle temperature varied between T=140.7 K at SASW=16 and T=149.8 K at SASW=1.4. Typical error bars are shown for the last point of each series.
We note that mass growth occurs independent of the saturation within the first few seconds when using a fixed water vapour concentration. At longer residence times two distinct regimes can be identified:
-
At low supersaturation (SASW=1.4 and SASW=2.3) the particle mass growth rate decreases with time after the initial growth. The mass accretion due to water adsorption is compensated by an increasing mass loss due to desorption from the particle surface. The particle mass then approaches a steady equilibrium state after about 25 s for the case shown. This behaviour is observed for all saturation ratios below a certain critical saturation threshold. In the following we will refer to the saturation regime below the critical threshold (i.e. in which the particle mass reaches a steady state) as the equilibrium regime. The mass of adsorbed water molecules mads in the steady state can be determined by fitting a simple exponential function of the following form to the data:
Here, m is the particle mass as a function of the residence time t, m0 is the initial particle mass, and τ is the characteristic time for reaching the steady state. Fits of Eq. (2) to the data for SASW=1.4 and SASW=2.3 are shown by the dashed curves in Fig. 1 resulting in mads=26 kDa and mads=41 kDa, respectively. These values for mads correspond to 2.3 and 3.2 monolayers of adsorbed water which significantly increases the size of the nanoparticles. A parameterization describing the amount of adsorbed water in the equilibrium regime and the method of calculating layer thickness from measured adsorbed water mass are described in Sect. 3.1.
-
At higher supersaturation (SASW=3.3 and above) a continuous particle growth is observed. In this growth regime, condensation always exceeds evaporation from the particle surface. The critical saturation for activation of ice growth Scrit is obtained in the experiment by monitoring the conditions at which the transition between equilibrium regime and growth regime occurs (i.e. between SASW=2.3 and SASW=3.3 in Fig. 1). By choosing finer temperature steps the critical saturation can be determined with higher accuracy. Measured critical saturations will be presented in Sect. 3.2 together with an ice-activation model which describes the measured data.
3.1 Adsorption in the equilibrium regime
In this section we present a parameterization for the water coverage on iron silicate particles under mesospheric conditions. Traditionally, the amount of water vapour adsorbed on a surface is described using adsorption isotherms where the water coverage is plotted as a function of the saturation ratio (e.g. Venables et al., 1984). The water coverage Θ is defined as the number of adsorbed water monolayers and is calculated using the wet and dry particle radius as . For dML we use the average distance of water molecules in the condensed state with molecular mass and the density of ice (ρ=930 kg m−3). For hydrophilic materials such as iron oxides and silica it is known that multilayer adsorption occurs (Mazeina and Navrotsky, 2007; Navrotsky et al., 2008; Sneh et al., 1996).
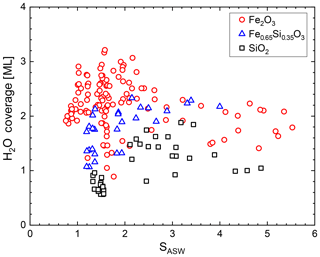
Figure 2Water coverage in monolayers H2O on iron silicate nanoparticles as a function of saturation.
We measured the mass of adsorbed water vapour in the equilibrium regime for iron oxide, silica, and mixed iron silicate particles (rdry=1.05–3.05 nm) covering the temperature range between 128 and 152 K in a total of 192 experiments. We converted the measured adsorbed mass to H2O coverages and plot the results in Fig. 2 as a function of SASW. The coverage on iron oxide particles is typically higher compared to iron silicate and silica particles which is in line with measurements showing that iron oxide exhibits a higher desorption energy than silica (e.g. Mazeina and Navrotsky, 2007; Sneh et al., 1996). We observe, however, that the data do not show the typical multilayer behaviour where coverage increases with saturation. This is a result of the curvature effect, which strongly influences the equilibrium coverage for nanometre-sized particles. Instead, we find that the adsorption model that we used recently (Nachbar et al., 2018a) to describe the water affinity of iron silicate particles describes the water coverage more adequately. In this work we modify this model to account for the influence of the curvature on the equilibrium coverage, which has not been done before.
The model was originally used to describe the surface concentration of adsorbed monomers at sub-monolayer coverage on a planar surface (Pruppacher and Klett, 2004). It assumes a homogeneous particle surface in which all surface binding sites for adsorbent molecules are characterized by the same surface desorption energy . The equilibrium between desorbing water molecule flux density jdes and adsorbing flux density jads yields
Here, n and vth are the number density and the mean thermal velocity of gas phase water molecules, respectively. The number of adsorbed water molecules is described by with the surface area of the dry particle . The other parameters are the vibrational frequency f=1013 Hz for H2O (Pruppacher and Klett, 2004), the universal gas constant R, and particle temperature T. Compared to our previous work (Nachbar et al., 2018a), we added a Kelvin-effect-like term,
to the flux density of desorbing molecules in order to take the increased desorption due to the curvature effect into account. Here, M is the molar mass of water, ρ is the density of the adsorbed water film which we assume is similar to the density of ice, and σ is the interfacial tension between the water film and air. We do not take into account the influence of the particle charge and of the collision radius of water molecules on the equilibrium saturation. Both effects are small compared to the Kelvin term and would make the parameterization unnecessarily complicated. Additionally, they would render Eq. (3) analytically unsolvable. By neglecting these effects we can re-arrange the equation to yield the following:
In Fig. 3 we plot the curvature-dependent desorption energy Edes as defined by the left-hand side of Eq. (5) versus the inverse of the dry particle radius using measured data for the adsorbed water vapour mass mads. From the intercept the curvature-independent desorption energy can be obtained while the slope is directly proportional to the surface tension of the water ad-layer–air interface. The figure shows that the three particle materials exhibit different desorption energies and that the water molecules are on average less strongly bound to the particle surface on smaller particles due to the curvature effect.
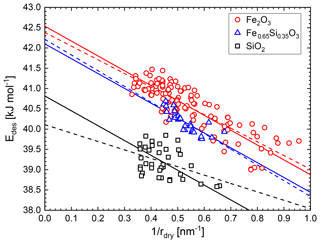
Figure 3Surface desorption energy of water molecules on iron silicate nanoparticles calculated from measured water coverages using Eq. (5). Dashed lines are independent linear fits and solid lines represent a combined linear fit resulting in σ=94 mN m−1.
In order to determine the surface tension of the water ad-layer we performed independent linear fits on the three data sets which are shown as dashed lines in Fig. 3. The determined surface tensions are σ (H2O-on-Fe2O3) = (87±5) mN m−1, σ (H2O-on-Fe0.65Si0.35O3) = (99±13) mN m−1, and σ (H2O-on-SiO2) = (53±18) mN m−1. To keep the intended parameterization for the water coverage as a function of the particle material as simple as possible, we refrained from using a material-dependent surface tension of the water ad-layer. We performed a combined fit with a single value for the surface tension for all three materials. The resulting fits yielded mN m−1, which compares very well to extrapolated values of the surface tension of supercooled liquid water (SLW) at these temperatures (σSLW (T=155 K) = 92 mN m−1 and σSLW (T=128 K) = 96 mN m−1) and which we recently proposed to use for lack of available surface tension data of ASW (Nachbar et al., 2018c). The combined fit is shown as solid lines in Fig. 3. From the intercepts of the linear fits we determined the curvature-independent desorption energies (Fe2O3) = (42.5±0.3) kJ mol−1, (Fe0.65Si0.35O3) = (42.1±0.2) kJ mol−1, and (SiO2) = (40.8±0.4) kJ mol−1. We also re-analysed the adsorption data for mixed iron silicate particles published in Nachbar et al. (2018a) using Eq. (5) and σ=94 mN m−1. The resulting curvature-independent desorption energies are shown in Fig. 4. Here, the three labelled data points are the intercepts from Fig. 3 while all other data points represent single measurements analysed using Eq. (5).
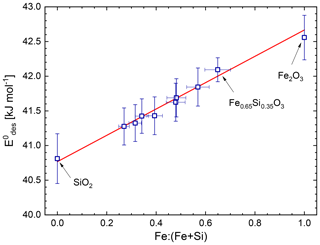
Figure 4Curvature-independent average desorption energy as a function of iron content of iron silicate particles. The red line represents a linear fit to the data. Based in part on original data from Nachbar et al. (2018a).
The average curvature-independent desorption energies follow the following linear relation:
where represents the relative iron content. Inserting this in Eq. (3), we arrive at a parameterization for the water coverage for iron silicate particles at mesopause conditions,
which can be used to predict the mass of adsorbed water for iron silicate particles as a function of the dry particle radius, temperature and water vapour concentration. The wet-particle radius rwet and the water coverage Θ can be calculated from mads using
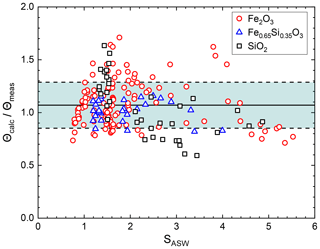
Figure 5Ratio of calculated water coverage using Eq. (7) and measured water coverage as a function of the saturation ratio.
In Fig. 5 we show the ratio of calculated to measured water coverages for all three materials. The average calculated water coverage deviates by about 7 % from the measurements (solid line) with a mean square deviation of about 22 % (dashed lines). The comparison shows that the measured water coverage is well represented by our water adsorption parameterization for particles between r=1–3 nm and temperatures between 128 and 152 K. Applied water vapour partial pressures range between about and 10−4 Pa.
3.2 Critical saturation for ice activation
We have measured the critical saturation for the activation of ice growth on small iron silicate nanoparticles (rdry=1.05–2.8 nm) in the temperature interval between 128 and 147 K for three different particle compositions in a total of 53 independent experiments. Figure 6a shows the measured critical saturations as a function of the initial dry particle radius for pure iron oxide (Fe2O3) particles at four different temperatures. Note that here we plot the saturation ratio with respect to the vapour pressure of hexagonal ice to facilitate comparison with other studies. Figure 6b compares the results at 139.6 K with measurements on silica and one mixed iron silicate with an elemental ratio . Note that in all measurements ice growth is activated below Sh=50, which compares to observations of saturation ratios exceeding Sh=100 when temperatures drop below 140 K on a regular basis during NLC season (Lübken et al., 2009). The solid lines in Fig. 6 are the results of an adsorption-activation model which we will present below.
We have shown previously that ASW is the initial form of condensed water that deposits on hydrophilic iron silicate nanoparticles at temperatures below 160 K (Nachbar et al., 2018c). It is well known that, depending on growth conditions, microporous ASW may be formed and that background gas molecules may be trapped during deposition. However, ASW samples produced above 100 K in the absence of a background gas were found to be compact or exhibited the same surface area as crystalline ice reference samples indicating the formation of compact ASW (Mayer and Pletzer, 1986; Stevenson et al., 1999; Westley et al., 1998). We thus argue that at the experimental conditions employed in our study (surface temperature of T≥128 K, maximum deposition rate 3Å s−1, or ∼1 ML s−1, Helium as a background gas) compact ASW is created on the nanoparticles with at maximum a marginal degree of porosity. Here, we will rely on a simple approach to describe ice formation in the mesopause by assuming that the nuclei are spherical and perfectly wettable (contact parameter close to 1, i.e. the activation barrier to form ASW is low). Under such conditions, and taking into account that the ice particle is charged, ice formation is likely to occur near the equilibrium saturation which is given by the Kelvin–Thomson equation for the particle radius including the adsorbed water rwet:
where Q is the particle charge, and ε0 and εr are the permittivity of vacuum and the relative permittivity of water, respectively. Above we showed that the MSP analogues are already covered with more than one monolayer of water at saturations below the ice-activation threshold. This water film is well described using bulk properties for the surface tension of ASW. For the surface tension of ASW we use σASW = (114.8–0.144⋅T) mN m−1 (where T is measured in kelvins, K), a parameterization which is based on a low-temperature extrapolation of measured data for supercooled water (Vinš et al., 2017). Our previous study on the vapour pressure of compact ASW indicates that this parameterization is consistent with the properties of ASW to within 10 % at the investigated temperatures between 133 and 147 K (Nachbar et al., 2018c). For the density of compact ASW we use a constant value of ρASW=0.93 g cm−3 (Brown et al., 1996; Loerting et al., 2011).
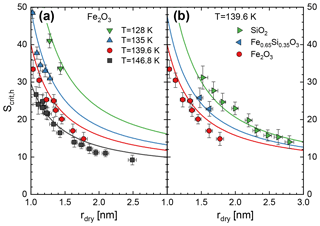
Figure 6Critical saturation as a function of the initial particle radius. Solid lines represent the ice-activation model (see text for details).
In the derivation of the Kelvin–Thomson equation, the vapour in equilibrium with the condensed phase is assumed to be an ideal gas. This also includes the assumption that the gas phase molecules are point-like. This assumption breaks down when the size of the particle becomes comparable to the size of the water molecules. When taking the size of water molecules into account using a hard sphere collision model the equilibrium saturation changes to the following:
The second term on the right-hand side represents the correction due to the finite size of the water molecules for which we use Å (Bickes et al., 1975). The right-hand side of Eq. (10) reduces to the Kelvin–Thomson term for . In our adsorption-activation model the onset conditions for ice growth are reached when the saturation in the environment of the particle surpasses the equilibrium saturation given by Eq. (10) (). The adsorption-activation model is illustrated in Fig. 7 for rdry=2 nm particles at T=140 K. Here, the Kelvin–Thomson radius represents the boundary between equilibrium and the ice growth regime (dashed–dotted line). For comparison, we also plotted the Kelvin–Thomson radius where we neglected the H2O collision radius (dashed line). Solid lines represent the wet-particle radius in the equilibrium regime according to Eqs. (7) and (8) for Fe2O3 in red and SiO2 in black. The onset conditions are defined in our model by the saturation ratio SASW for which the particle radius in the equilibrium regime intersects the Kelvin–Thomson radius.
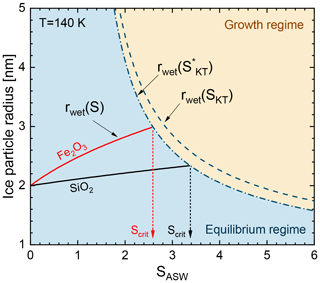
Figure 7Illustration of the adsorption-activation model. Solid lines represent the wet-particle radius in the equilibrium regime calculated using Eqs. (7) and (8). Dashed–dotted and dashed lines represent the Kelvin–Thomson radius (Q=1e) calculated with and without the H2O collision radius using Eq. (10), respectively.
We determined the critical saturation ratios using this method and plotted the results as solid lines in Fig. 6 for all temperatures and particle compositions shown. The model curves agree well with measured data, confirming the method as a good predictor for ice growth onset at mesopause conditions.
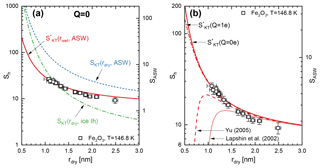
Figure 8Comparison of measured onset conditions for ice activation for Fe2O3 particles at T=146.8 K with different model calculations. (a) Comparison of the critical saturation given by the activation model excluding charge effects (Eq. 9, Q=0e). The red solid line represents calculations using the wet-particle radius while the blue dashed and green dashed–dotted lines represent calculations using the dry particle radius assuming compact ASW and hexagonal ice, respectively. (b) Comparison of the activation model for charged (dashed–dotted line, Q=1e) and neutral (solid line, Q=0e) particles. The dotted and dashed lines show the ice-activation model using modified versions of the Kelvin–Thomson equation (see text for details).
In Fig. 8a we plot the results of the adsorption-activation model (solid red curve) for iron oxide particles at 146.8 K. The blue dashed line was calculated using the adsorption-activation model but assuming that no water adsorbs prior to activation. The comparison of both model calculations shows that the equilibrium saturation is substantially reduced due to the adsorption of several monolayers of water near the activation threshold. Also shown as a green dashed–dotted line is the activation model assuming the formation of hexagonal ice and assuming that no water adsorbs prior to activation. These calculations represent the lowest critical saturations currently assumed in mesospheric models (e.g. Berger and Lübken, 2015; Schmidt et al., 2018). However, it is expected that the majority of MSPs in the mesopause is smaller than r=1.2 nm (Bardeen et al., 2008; Megner et al., 2008a, b; Plane et al., 2014). Ice formation on such small particles has to occur in order to explain observed ice particle concentrations in PMCs. According to our activation model, critical saturations are substantially smaller than currently assumed for particles with r<1.2 nm.
Figure 8b compares the critical saturation predicted by the activation model for neutral particles (solid curve) with singly charged particles (dashed–dotted curve). We note that the presence of several monolayers of water substantially increases the particle radius at the activation threshold which effectively decreases the influence of the particle charge. In our ice-activation model, the particle charge becomes significant only below rdry=0.6 nm. Note that such small iron oxide particles only consist of about 90 atoms. In Fig. 8b we also plot the critical saturation using modified versions of the Kelvin–Thomson equation according to Yu (2005) and Lapshin et al. (2002), which are in disagreement with our measurements below rdry=1.2 nm.
We measured the critical saturation for ice growth on iron silicate nanoparticles serving as meteor smoke substitutes under conditions of PMC formation. We found that ice growth initiates on iron silicate particles with dry particle radius r≥1 nm below Sh=50, a value which is commonly exceeded during NLC season. This affirms meteoric smoke particles as likely nuclei for heterogeneous ice formation in mesospheric clouds. The onset conditions for ice activation for iron oxide, silica, and iron silicates are well represented by the reduced equilibrium saturation of the wet-particle radius using the saturation vapour pressure and surface tension of ASW. This confirms our hypothesis of ASW activation and is in line with our previous observation of ASW depositional growth at mesopause conditions (Nachbar et al., 2018c). The activation threshold can be matched even more precisely by taking into account the collision radius of water molecules. Based on the ice-activation model we showed that due to the adsorbed water layer, charge effects play only a minor role in the ice activation of iron silicate particles larger than a dry size of r=0.6 nm. For smaller nanoparticles and clusters other competing effects may come into play which could potentially influence the equilibrium saturation, for instance the curvature dependence of the surface tension (Tolman, 1949), or long-range interactions between droplet surface and water molecules (Park et al., 2016; Vasil'ev and Reiss, 1996a, b). Our findings are parameterized in Eqs. (6), (7), and (10), which yield the wet-particle diameter and ice cloud activation threshold as a function of humidity, temperature, dry particle size, and iron content. Our results support our previous finding that amorphous solid water has to be considered as a relevant ice polymorph in polar mesospheric cloud formation.
During the summer season, iron-rich particles are heated by absorbed sunlight and it was argued that this would modify their ice-activation potential. In an accompanying article (Nachbar et al., 2018d) we show that this is a minor effect under typical mesospheric conditions.
All data are available on request from the corresponding author.
DD, MN, and TL designed the research. MN and DD performed the measurements and analysed the data. DD wrote the paper with contributions by the co-authors. TL supervised the project.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Layered phenomena in the mesopause region (ACP/AMT inter-journal SI)”. It is a result of the LPMR workshop 2017 (LPMR-2017), Kühlungsborn, Germany, 18–22 September 2017.
The authors thank the German Federal Ministry of Education and Research
(BMBF, grant number 05K13VH3 and 05K16VHB) and the German Research Foundation
(DFG, grant number LE 834/4-1) for financial support of this work. We
acknowledge support by the Deutsche Forschungsgemeinschaft and Open Access
Publishing Fund of Karlsruhe Institute of Technology.
The article processing charges for this open-access
publication were covered by a Research
Centre
of the Helmholtz Association.
Edited by:
Martin Dameris
Reviewed by: two anonymous referees
Bardeen, C. G., Toon, O. B., Jensen, E. J., Marsh, D. R., and Harvey, V. L.: Numerical simulations of the three-dimensional distribution of meteoric dust in the mesosphere and upper stratosphere, J. Geophys. Res.-Atmos., 113, D17202, https://doi.org/10.1029/2007JD009515, 2008.
Berger, U. and Lübken, F.-J.: Trends in mesospheric ice layers in the Northern Hemisphere during 1961–2013, J. Geophys. Res.-Atmos., 120, 11277–11298, 2015.
Bickes, R. W., Duquette, G., van den Meijdenberg, C. J. N., Rulis, A. M., Scoles, G., and Smith, K. M.: Molecular Beam Scattering Experiments with Polar Molecules: Measurement of Differential Collision Cross Sections for H2O+H2, He, Ne, Ar, H2O and NH3+H2, He, NH3, J. Phys. B-At. Mol. Opt., 8, 3034–3043, 1975.
Brown, D. E., George, S. M., Huang, C., Wong, E. K. L., Rider, K. B., Smith, R. S., and Kay, B. D.: H2O Condensation Coefficient and Refractive Index for Vapor-Deposited Ice from Molecular Beam and Optical Interference Measurements, J. Phys. Chem., 100, 4988–4995, 1996.
Carrillo-Sánchez, J. D., Nesvorný, D., Pokorný, P., Janches, D., and Plane, J. M. C.: Sources of cosmic dust in the Earth's atmosphere, Geophys. Res. Lett., 43, 11979–11986, 2016.
DeLand, M. T., Shettle, E. P., Thomas, G. E., and Olivero, J. J.: Latitude-dependent long-term variations in polar mesospheric clouds from SBUV version 3 PMC data, J. Geophys. Res.-Atmos., 112, D10315, https://doi.org/10.1029/2006JD007857, 2007.
Demissie, T. D., Espy, P. J., Kleinknecht, N. H., Hatlen, M., Kaifler, N., and Baumgarten, G.: Characteristics and sources of gravity waves observed in noctilucent cloud over Norway, Atmos. Chem. Phys., 14, 12133–12142, https://doi.org/10.5194/acp-14-12133-2014, 2014.
Duft, D., Nachbar, M., Eritt, M., and Leisner, T.: A Linear Trap for Studying the Interaction of Nanoparticles with Supersaturated Vapors, Aerosol Sci. Tech., 49, 683–691, 2015.
Gumbel, J. and Megner, L.: Charged meteoric smoke as ice nuclei in the mesosphere: Part 1 – A review of basic concepts, J. Atmos. Sol.-Terr. Phy., 71, 1225–1235, 2009.
Hervig, M. E., Stevens, M. H., Gordley, L. L., Deaver, L. E., Russell, J. M., and Bailey, S. M.: Relationships between polar mesospheric clouds, temperature, and water vapor from Solar Occultation for Ice Experiment (SOFIE) observations, J. Geophys. Res.-Atmos., 114, D20203, https://doi.org/10.1029/2009JD012302, 2009.
Hervig, M. E., Berger, U., and Siskind, D. E.: Decadal variability in PMCs and implications for changing temperature and water vapor in the upper mesosphere, J. Geophys. Res.-Atmos., 121, 2383–2392, 2016.
Hervig, M. E., Brooke, J. S. A., Feng, W., Bardeen, C. G., and Plane, J. M. C.: Constraints on Meteoric Smoke Composition and Meteoric Influx Using SOFIE Observations With Models, J. Geophys. Res.-Atmos., 122, 13495–13505, 2017.
Kaifler, N., Baumgarten, G., Fiedler, J., and Lübken, F.-J.: Quantification of waves in lidar observations of noctilucent clouds at scales from seconds to minutes, Atmos. Chem. Phys., 13, 11757–11768, https://doi.org/10.5194/acp-13-11757-2013, 2013.
Keesee, R. G.: Nucleation and Particle Formation in the Upper Atmosphere, J. Geophys. Res.-Atmos., 94, 14683–14692, 1989.
Kirkwood, S., Dalin, P., and Réchou, A.: Noctilucent clouds observed from the UK and Denmark – trends and variations over 43 years, Ann. Geophys., 26, 1243–1254, https://doi.org/10.5194/angeo-26-1243-2008, 2008.
Lapshin, V. B., Yablokov, M. Y., and Palei, A. A.: Vapor pressure over a charged drop, Russ. J. Phys. Ch., 76, 1727–1729, 2002.
Leslie, R. C.: Sky Glows, Nature, 32, 245, https://doi.org/10.1038/032245a0, 1885.
Loerting, T., Bauer, M., Kohl, I., Watschinger, K., Winkel, K., and Mayer, E.: Cryoflotation: Densities of Amorphous and Crystalline Ices, J. Phys. Chem. B, 115, 14167–14175, 2011.
Lübken, F. J., Lautenbach, J., Höffner, J., Rapp, M., and Zecha, M.: First continuous temperature measurements within polar mesosphere summer echoes, J. Atmos. Sol.-Terr. Phy., 71, 453–463, 2009.
Mayer, E. and Pletzer, R.: Astrophysical implications of amorphous ice – a microporous solid, Nature, 319, 298–301, 1986.
Mazeina, L. and Navrotsky, A.: Enthalpy of Water Adsorption and Surface Enthalpy of Goethite (α-FeOOH) and Hematite (α-Fe2O3), Chem. Mater., 19, 825–833, 2007.
Megner, L., Gumbel, J., Rapp, M., and Siskind, D. E.: Reduced meteoric smoke particle density at the summer pole – Implications for mesospheric ice particle nucleation, Adv. Space Res., 41, 41–49, 2008a.
Megner, L., Siskind, D. E., Rapp, M., and Gumbel, J.: Global and temporal distribution of meteoric smoke: A two-dimensional simulation study, J. Geophys. Res.-Atmos., 113, D03202, https://doi.org/10.1029/2007JD009054, 2008b.
Meinen, J., Khasminskaya, S., Ruehl, E., Baumann, W., and Leisner, T.: The TRAPS Apparatus: Enhancing Target Density of Nanoparticle Beams in Vacuum for X-ray and Optical Spectroscopy, Aerosol Sci. Tech., 44, 316–328, 2010.
Murphy, D. M. and Koop, T.: Review of the vapour pressures of ice and supercooled water for atmospheric applications, Q. J. Roy. Meteor. Soc., 131, 1539–1565, 2005.
Nachbar, M., Duft, D., Mangan, T. P., Martin, J. C. G., Plane, J. M. C., and Leisner, T.: Laboratory measurements of heterogeneous CO2 ice nucleation on nanoparticles under conditions relevant to the Martian mesosphere, J. Geophys. Res.-Planet., 121, 753–769, 2016.
Nachbar, M., Duft, D., Kiselev, A., and Leisner, T.: Composition, Mixing State and Water Affinity of Meteoric Smoke Analogue Nanoparticles Produced in a Non-Thermal Microwave Plasma Source, Z. Phys. Chem., 232, 635–648, 2018a.
Nachbar, M., Duft, D., and Leisner, T.: The vapor pressure over nano-crystalline ice, Atmos. Chem. Phys., 18, 3419–3431, https://doi.org/10.5194/acp-18-3419-2018, 2018b.
Nachbar, M., Duft, D., and Leisner, T.: Volatility of Amorphous Solid Water, J. Phys. Chem. B, 122, 10044–10050, 2018c.
Nachbar, M., Wilms, H., Duft, D., Aylett, T., Kitajima, K., Majima, T., Plane, J. M. C., Rapp, M., and Leisner, T.: The impact of solar radiation on polar mesospheric ice particle formation, Atmos. Chem. Phys. Discuss., https://doi.org/10.5194/acp-2018-1032, in review, 2018d.
Navrotsky, A., Mazeina, L., and Majzlan, J.: Size-Driven Structural and Thermodynamic Complexity in Iron Oxides, Science, 319, 1635–1638, https://doi.org/10.1126/science.1148614, 2008.
Park, Y., Tanimura, S., and Wyslouzil, B. E.: Enhanced growth rates of nanodroplets in the free molecular regime: The role of long-range interactions, Aerosol Sci. Tech., 50, 773–780, 2016.
Plane, J. M. C., Saunders, R. W., Hedin, J., Stegman, J., Khaplanov, M., Gumbel, J., Lynch, K. A., Bracikowski, P. J., Gelinas, L. J., Friedrich, M., Blindheim, S., Gausa, M., and Williams, B. P.: A combined rocket-borne and ground-based study of the sodium layer and charged dust in the upper mesosphere, J. Atmos. Sol.-Terr. Phy., 118, 151–160, 2014.
Plane, J. M. C., Feng, W., and Dawkins, E. C. M.: The Mesosphere and Metals: Chemistry and Changes, Chem. Rev., 115, 4497–4541, 2015.
Pruppacher, H. R. and Klett, J. D.: Microphysics of Clouds and Precipitation, Kluwer Academic Publishers, Dordrecht, 2004.
Rapp, M. and Thomas, G. E.: Modeling the microphysics of mesospheric ice particles: Assessment of current capabilities and basic sensitivities, J. Atmos. Sol.-Terr. Phy., 68, 715–744, 2006.
Rapp, M., Lübken, F. J., Müllemann, A., Thomas, G. E., and Jensen, E. J.: Small-scale temperature variations in the vicinity of NLC: Experimental and model results, J. Geophys. Res.-Atmos., 107, 4392, https://doi.org/10.1029/2001jd001241, 2002.
Rapp, M., Plane, J. M. C., Strelnikov, B., Stober, G., Ernst, S., Hedin, J., Friedrich, M., and Hoppe, U.-P.: In situ observations of meteor smoke particles (MSP) during the Geminids 2010: constraints on MSP size, work function and composition, Ann. Geophys., 30, 1661–1673, https://doi.org/10.5194/angeo-30-1661-2012, 2012.
Rong, P. P., Yue, J., Russell, J. M., Lumpe, J. D., Gong, J., Wu, D. L., and Randall, C. E.: Horizontal winds derived from the polar mesospheric cloud images as observed by the CIPS instrument on the AIM satellite, J. Geophys. Res.-Atmos., 120, 5564–5584, 2015.
Schmidt, F., Baumgarten, G., Berger, U., Fiedler, J., and Lübken, F.-J.: Local time dependence of polar mesospheric clouds: a model study, Atmos. Chem. Phys., 18, 8893–8908, https://doi.org/10.5194/acp-18-8893-2018, 2018.
Seele, C. and Hartogh, P.: Water vapor of the polar middle atmosphere: Annual variation and summer mesosphere Conditions as observed by ground-based microwave spectroscopy, Geophys. Res. Lett., 26, 1517–1520, 1999.
Sneh, O., Cameron, M. A., and George, S. M.: Adsorption and desorption kinetics of H2O on a fully hydroxylated SiO2 surface, Surf. Sci., 364, 61–78, 1996.
Stevenson, K. P., Kimmel, G. A., Dohnalek, Z., Smith, R. S., and Kay, B. D.: Controlling the morphology of amorphous solid water, Science, 283, 1505–1507, 1999.
Thomas, G. E.: Mesospheric clouds and the physics of the mesopause region, Rev. Geophys., 29, 553–575, 1991.
Thomas, G. E. and Olivero, J.: Noctilucent clouds as possible indicators of global change in the mesosphere, Adv. Space Res., 28, 937–946, 2001.
Tolman, R. C.: The Effect of Droplet Size on Surface Tension, J. Chem. Phys., 17, 333–337, 1949.
Vasil'ev, O. V. and Reiss, H.: Capture of vapor molecules by a realistic attraction potential of a drop, J. Chem. Phys., 105, 2946–2947, 1996a.
Vasil'ev, O. V. and Reiss, H.: Effect of the attractive potential of a drop in vapor phase nucleation, Phys. Rev. E, 54, 3950–3954, 1996b.
Venables, J. A., Spiller, G. D. T., and Hanbucken, M.: Nucleation and growth of thin films, Rep. Prog. Phys., 47, 399–459, https://doi.org/10.1088/0034-4885/47/4/002, 1984.
Vinš, V., Hošek, J., Hykl, J., and Hrubý, J.: Surface Tension of Supercooled Water: Inflection Point-Free Course down to 250 K Confirmed Using a Horizontal Capillary Tube, J. Chem. Eng. Data, 62, 3823–3832, 2017.
Vondrak, T., Plane, J. M. C., Broadley, S., and Janches, D.: A chemical model of meteoric ablation, Atmos. Chem. Phys., 8, 7015–7031, https://doi.org/10.5194/acp-8-7015-2008, 2008.
Westley, M. S., Baratta, G. A., and Baragiola, R. A.: Density and index of refraction of water ice films vapor deposited at low temperatures, J. Chem. Phys., 108, 3321–3326, 1998.
Yu, F.: Modified Kelvin–Thomson equation considering ion-dipole interaction: Comparison with observed ion-clustering enthalpies and entropies, J. Chem. Phys., 122, 084503, https://doi.org/10.1063/1.1845395, 2005.





