the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Understanding the catalytic role of oxalic acid in SO3 hydration to form H2SO4 in the atmosphere
Guochun Lv
Xiaomin Sun
Chenxi Zhang
Mei Li
The hydration of SO3 plays an important role in atmospheric sulfuric acid formation. Some atmospheric species can be involved in and facilitate the reaction. In this work, using quantum chemical calculations, we show that oxalic acid, the most common dicarboxylic acid in the atmosphere, can effectively catalyze the hydration of SO3. The energy barrier of the SO3 hydration reaction catalyzed by oxalic acid (cTt, tTt, tCt and cCt conformers) is a little higher or less than 1 kcal mol−1, which is lower than the energy barrier of 5.17 kcal mol−1 for water-catalyzed SO3 hydration. Compared with the rates of the SO3 hydration reaction catalyzed by oxalic acid and water, it can be found that in the upper troposphere the OA-catalyzed SO3 hydration can play an important role in promoting SO3 hydration. It leads us to conclude that the involvement of oxalic acid in SO3 hydration to form H2SO4 is significant in the atmosphere.
- Article
(1361 KB) -
Supplement
(241 KB) - BibTeX
- EndNote
In the atmosphere, hydrogen atom transfer (HAT) reactions play a significant role in many processes. The radical reaction (), as the most traditional HAT reaction, can be widely found in the atmosphere (Alvarez-Idaboy et al., 2001; Cameron et al., 2002; Steckler et al., 1997; Atkinson et al., 2006). The HAT process can also be found in some addition (Steudel, 1995; Williams et al., 1983; Courmier et al., 2005; Zhang and Zhang, 2002), decomposition (Rayez et al., 2002; Kumar and Francisco, 2015; Gutbrod et al., 1996), isomerization (Zheng and Truhlar, 2010; Atkinson, 2007) and abstraction reactions (Ji et al., 2013, 2017). These atmospheric HAT reactions display a main feature that the two-point hydrogen bond can occur and thus facilitates HAT (Kumar et al., 2016). Water molecules, acids and other catalysts, acting as hydrogen donors and acceptors, can contribute to the formation of two-point hydrogen bond (Vöhringer-Martinez et al., 2007; da Silva, 2010; Gonzalez et al., 2010; Bandyopadhyay et al., 2017). Thus, the effect of catalysts on promoting atmospheric HAT reactions has attracted more attention from atmospheric scientists.
The hydration of SO3 to form sulfuric acid (H2SO4) is a typical addition reaction involving the HAT. In the atmosphere, this hydration reaction is regarded as the main source of gas-phase sulfuric acid. For the reaction SO3 + H2O → H2SO4, the pre-reactive SO3… H2O complex is firstly formed, and the complex is then rearranged to produce H2SO4 (Holland and Castleman, 1978; Hofmann-Sievert and Castleman, 1984). But subsequent research found that this hydration reaction involving a single water molecule cannot take place in the atmosphere due to its high energy barrier (Hofmann and Schleyer, 1994; Morokuma and Muguruma, 1994; Steudel, 1995). The inclusion of a second water molecule in the above reaction has been proven to significantly reduce the hydration energy barrier (Morokuma and Muguruma, 1994; Loerting and Liedl, 2000; Larson et al., 2000). The promoting effect can be mainly attributed to the formation of the two-point hydrogen bond, which reduces the ring strain occurring in the pre-reactive complex, and facilitates the rearrangement of the pre-reactive complex via double HAT. It has also been shown that some other atmospheric molecules can serve as a catalyst to promote the hydration of SO3. To the best of our knowledge, the hydroperoxy radical (Gonzalez et al., 2010), formic acid (Hazra and Sinha, 2011; Long et al., 2012), sulfuric acid (Torrent-Sucarrat et al., 2012), nitric acid (Long et al., 2013) and ammonia (Bandyopadhyay et al., 2017) have been reported to replace the second water molecule to catalyze the hydration reaction of SO3.
Oxalic acid (OA), the most prevalent dicarboxylic acid in the atmosphere (Ho et al., 2015; Kawamura and Ikushima, 1993), is a water-soluble organic acid, so it has a high concentration in aerosols (Kawamura et al., 2013; van Pinxteren et al., 2014; Deshmukh et al., 2016; Wang et al., 2016). In addition to its accumulation in aerosols, OA, as an organic acid in the gas phase, has been found to enhance new particle formation (NPF; Xu et al., 2010, 2017; Weber et al., 2012, 2014; Xu and Zhang, 2012; Peng et al., 2015; Miao et al., 2015; Zhao et al., 2016; Chen et al., 2017; Arquero et al., 2017; Zhang, 2010). Theoretical studies about the effect of OA on atmospheric particle nucleation and growth have shown that it can generate stable complexes with water (Weber et al., 2012), sulfuric acid (Xu et al., 2010; Xu and Zhang, 2012; Miao et al., 2015; Zhao et al., 2016), ammonia (Weber et al., 2014; Peng et al., 2015) and amines (Chen et al., 2017; Xu et al., 2017; Arquero et al., 2017) via an intermolecular hydrogen bond. For OA, its potential to promote NPF is mainly attributed to its capability of forming hydrogen bonds with hydroxyl and/or carbonyl-type functional groups. Conversely to monocarboxylic acids, dicarboxylic acids such as OA have been proved to enhance nucleation in two directions because of its two acid moieties (Xu and Zhang, 2012). Thus, it can be believed that OA is a good candidate for catalyzing the HAT reaction in the atmosphere.
In this paper, we report the hydration reaction of SO3 in the presence of OA, aiming to study the catalytic effect and importance of OA in the hydration of SO3. It is known that OA can exist in several conformational forms (Buemi, 2009), which can be identified through the nomenclature used by Nieminen et al. (1992). Thus, five stable conformers of OA were considered in this work. The rate constants of OA-catalyzed SO3 hydration were calculated using kinetic analysis, and compared with that of the water-catalyzed hydration reaction. Finally, combining concentrations of reactants with the rate constants, we evaluated the importance of the hydration process involving the OA relative to the hydration of SO3 with the second water molecule as a catalyst to form sulfuric acid.
The Gaussian 09 software suite (Frisch et al., 2010) was used in this work to perform all electronic structure calculations. The geometric structures – including all reactants, complexes, transition states and products – were optimized using the M06-2X method (Zhao and Truhlar, 2008) with 6-311++G(3df,3pd) basis set. For the M06-2X method, the ultrafine integration grid was chosen to enhance calculation accuracy at reasonable additional cost. The frequency calculations were carried out at the same level after geometric optimization to verify the local minimum points and transition states through the criterion that there are no imaginary frequencies for the local minimum point and one imaginary frequency for transition states. According to frequency calculations, the zero-point energies (ZPEs) and thermal corrections can also be obtained. The intrinsic reaction coordinate (IRC) calculation (Fukui, 1981; Hratchian and Schlegel, 2004; Hratchian and Schlegel, 2005) was performed to ensure that the transition states are connected with the corresponding reactants and products. A high level ab initio method, CCSD(T) method (Purvis and Bartlett, 1982; Pople et al., 1987), with the cc-pV(T+d)Z basis set was used to refine the single-point energies of these optimized species. To obtain a more accurate conformational population of OA at different temperatures, the quantum chemistry composite method, Gaussian 4 (G4) theory (Curtiss et al., 2007), was also performed for OA conformers.
In the kinetic analysis, the electronic energies were based on the CCSD(T)/cc-pV(T+d)Z level of theory, while the partition functions were obtained from the M06-2X/6-311++G(3df,3pd) level of theory. The rate constants for the rearrangement process of the SO3 hydration reaction was estimated using conventional transition-state theory (TST; Truhlar et al., 1996) with Wigner tunneling correction. All kinetic analyses were executed in the KiSThelP program (Canneaux et al., 2014). The kinetic analyses are summarized as follows.
Based on the discussion in this paper, it can be concluded that SO3 hydration reactions begin with the formation of a pre-reactive complex, and then pass by a transition state to form a post-reactive complex. This process can be characterized by the following reaction:
Assuming that the complexes are in equilibrium with their reactants and that the steady-state approximation is applied to the pre-reactive complex, the reaction rate can be formulated as
where Keq1 and Keq2 are the equilibrium constants, and kuni is the rate constant for a unimolecular reaction from the pre-reactive complex to post-reactive complex.
In the water-catalyzed hydration process, two channels can be written as
The corresponding rates are
For the OA-catalyzed hydration reaction of SO3, there are two reaction channels and the same features as in the water-assisted hydration process. The two channels can be shown as follows:
Here, the symbol X in these two equations represents the different conformers of OA (namely, cTt, tTt, tCt and cCt conformer).
The corresponding rates of SO3 hydration involving OA can be obtained from the following equations:
To assess the importance of OA in SO3 hydration to H2SO4 in the atmosphere, the relative rate can be used as
It can be easily inferred from these equations that rate constants are the same for Eqs. (2, kw1) and (3, kw2), as well as for Eqs. (4, kX1) and (5, kX2) (for proof, see Supplement S1). Thus, the relative rate values in Eqs. (6) and (7) are the same. On account of these reasons, we will only compare the relative rate νX1∕νw1 in this paper.
3.1 Water-catalyzed hydration reaction of SO3
Although the hydration of SO3 involving two water molecules has been discussed many times, we still include it in our paper so as to compare it with the following SO3 hydration reactions catalyzed by OA at the same theoretical level, i.e., at the CCSD(T)/cc-pV(T+d)Z//M06-2X/6-311++G(3df,3pd) level. For the reactants SO3+2H2O, the existence of two pathways has become a consensus. One is that the water dimer reacts with SO3 to obtain the pre-reactive complex, then this complex is rearranged to form the H2SO4⋯H2O complex (channel 1); the other begins with the reaction of the SO3⋯H2O complex with water, and the following reaction process is the same as channel 1 (channel 2). In the hydration process, the additional water molecule serves as a catalyst that can promote the reaction by making a bridge in the HAT from water to SO3. The potential energy profile and geometric structures can be found in Fig. 1. Other results about the reaction in the Supplement in Table S1.
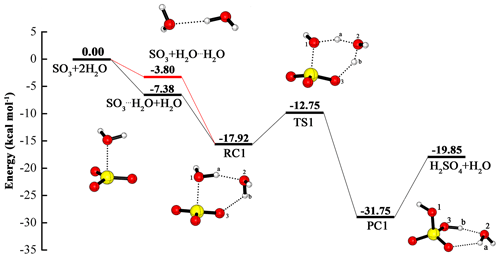
Figure 1Calculated potential energy profile for the hydration of SO3 with the second water molecule as a catalyst at the CCSD(T)/cc-pV(T+d)Z//M06-2X/6-311++G(3df,3pd) level.
From the two channels, it is clear that the binding energy of the water dimer is 3.80 kcal mol−1, and that of the SO3⋯H2O complex is 7.38 kcal mol−1. Moreover, the binding energy of the water dimer is consistent with its experimental value of 3.15±0.03 kcal mol−1 (Rocher-Casterline et al., 2011), and with theoretical results of 2.90 (Torrent-Sucarrat et al., 2012), 2.97 (Long et al., 2013), 3.14 (Hazra and Sinha, 2011) and 3.30 kcal mol−1 (Klopper et al., 2000). In the SO3⋯H2O complex, the binding energy of 7.38 kcal mol−1 in our paper agrees with that from theoretical estimates in the literature: 7.60 (Torrent-Sucarrat et al., 2012), 7.42 (Long et al., 2013), 7.25 (Hazra and Sinha, 2011) and 7.77 kcal mol−1 (Long et al., 2012). As shown in the Fig. 1, the two pathways involve the formation of the same pre-reactive complex (RC1) and the same subsequent processes. RC1 has a binding energy of 14.12 kcal mol−1 relative to SO3 + H2O⋯H2O, which is in accord with 13.60 (Torrent-Sucarrat et al., 2012) and 13.76 kcal mol−1 (Long et al., 2013). The RC1 consists of a six-membered ring structure, in which two hydrogen bonds (also called a two-point hydrogen bond) between Ha and O2, Hb and O3, can be found. The formation of sulfuric acid from the RC1 needs to go through the rearrangement process with a transition state, which is a rate-limiting step with the energy barrier of 5.17 kcal mol−1 with respect to RC1.
3.2 OA-catalyzed hydration reaction of SO3
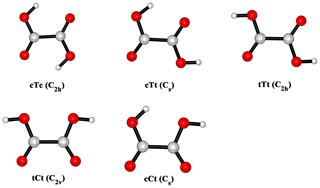
OA conformers, as shown in Fig. 2, are named according to the configurations of and dihedral angle: the lower-case letters refer to cis (c) or trans (t) configuration of ; the upper-case letters relate to cis (C) or tans (T) configuration of . The nomenclature about conformers of OA is proposed by Nieminen et al. (1992).
The calculated potential energy profile for the OA-catalyzed hydration reaction of SO3 is depicted in Fig. 3, and the corresponding geometry structures are shown in Fig. 4. Energies, enthalpies and free energies in all relevant species for the OA-catalyzed hydration of SO3 are summarized in the Supplement in Tables S2–S5. From the two figures, it is obvious that the cTc conformer cannot act as a catalyst in the hydration reaction because the HAT cannot occur. The transfer failure is attributed to the fact that the hydrogen and oxygen atom involved in the two-point hydrogen bond do not come from the same carboxyl group (see Fig. 4). The hydration reactions catalyzed by the remaining four conformers exhibit the same feature (Fig. 3), i.e., the pre-reactive complex formed from the SO3⋯H2O complex with OA or the OA⋯H2O complex with water can evolve into a product complex (H2SO4⋯OA complex) via the transition state of HAT. In this process, OA serves as a catalyst to promote the SO3 hydration reaction by making a bridge when the hydrogen atom transfers from H2O to SO3. In the reaction catalyzed by the cTt conformer, the binding energy of the cTt⋯H2O complex is 10.25 kcal mol−1. The binding energy of the pre-reactive complex is 10.95 kcal mol−1 compared to the cTt⋯H2O complex with SO3, while that relative to the SO3⋯H2O complex is 13.82 kcal mol−1 with cTt. The transformation from RCcTt to PCcTt (PC refers to post-reactive complex) corresponds to the HAT process, and has a transition state (TScTt) with an energy barrier of 1.19 kcal mol−1 with respect to RCcTt. PCcTt lies below the RCcTt by 13.32 kcal mol−1. It should be noted that the cTt conformer from RCcTt has transformed to the cCt conformer in PCcTt. The binding energy of PCcTt is 17.78 kcal mol−1 compared to H2SO4 and the cCt conformer.
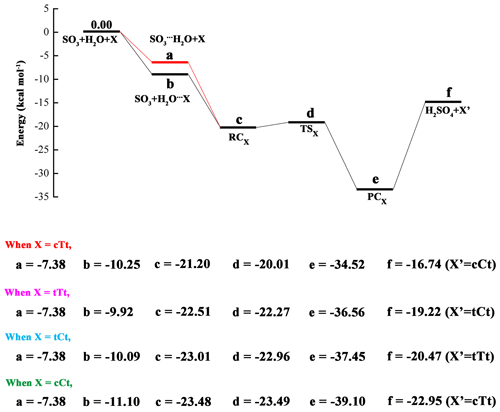
Figure 3Calculated potential energy profile for the hydration of SO3 with oxalic acid (OA) conformers (cTt, tTt, tCt and cCt) as catalysts at the CCSD(T)/cc-pV(T+d)Z//M06-2X/6-311++G(3df,3pd) level.
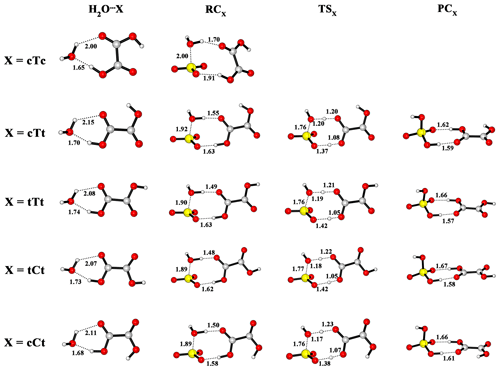
Figure 4Optimized M06-2X/6-311++G(3df,3pd) structures of reactant complexes, pre-reactive complexes, transition states and post-reactive complexes for the OA-catalyzed SO3 hydration reaction (distance unit: angstrom.
In hydration reactions involving the tTt conformer, the tTt⋯H2O complex is stabilized by 9.92 kcal mol−1, relative to tTt + H2O. Starting with the tTt⋯H2O + SO3 channel, the pre-reactive complex (RCtTt) can be formed with a binding energy of 12.59 kcal mol−1, whereas the binding energy of RCtTt is 15.13 kcal mol−1 when it comes from the SO3⋯H2O + tTt channel. The TStTt lies above the RCtTt by 0.24 kcal mol−1. And the reaction proceeds with the formation of PCtTt, which is more stable than RCtTt (14.05 kcal mol−1). The formed PCtTt needs to obtain an energy of 17.34 kcal mol−1 to disaggregate into H2SO4 and the tCt conformer.
For the tCt conformer, the binding energy of the tCt⋯H2O complex is 10.09 kcal mol−1. In the two channels, the same pre-reactive complex (RCtCt) can be formed with a binding energy of 12.92 kcal mol−1 relative to tCt⋯H2O + SO3, and 15.63 kcal mol−1 with respect to SO3⋯H2O + tCt. The RCtCt proceeds via the transition state (TStCt, with energy barrier of 0.05 kcal mol−1) into the post-reactive complex (PCtCt). The PCtCt complex can also be generated from the H2SO4 and tTt conformer releasing 16.98 kcal mol−1 of energy.
For the cCt conformer, the binding energy of the cCt⋯H2O complex is 11.10 kcal mol−1. Beginning with the cCt⋯H2O + SO3 and SO3⋯H2O + cCt channels, the hydration reactions undergo the same RCcCt complex, which is more stable than the two reactants (by 12.38 kcal mol−1, 16.10 kcal mol−1, respectively), and a transition state (TScCt), and then produces the H2SO4⋯cTt complex (PCcCt), which lies below the RCcCt complex by 15.62 kcal mol−1 and below H2SO4 + cTt by 16.15 kcal mol−1. The pre-reactive complex (RCcCt) is nearly iso-energetic with the transition state (TScCt).
In the light of the analysis above, it is obvious that the energy barrier of the hydration reaction catalyzed by OA is around 1.00 kcal mol−1 for the cTt conformer, and approximates to 0.00 kcal mol−1 for another three conformers. The result shows that OA is more effective than water in catalyzing the SO3 hydration because the hydration reaction catalyzed by water has an energy barrier of 5.17 kcal mol−1. Another point worth mentioning is that one OA conformer involved in SO3 hydration transfers to another conformer type after the completion of hydration reaction (cTt → cCt, tTt → tCt, tCt → tTt, cCt → cTt).
In addition, compared to formic acid (Millet et al., 2015; Bannan et al., 2017), the SO3 hydration reaction catalyzed by OA displays some specific characteristics. Both acids can obviously decrease the energy barrier of the hydration reaction. But because OA is a dicarboxylic acid, only one in the carboxylic groups participate in the hydration reaction and the other is free. This characteristic indicates that post-reactive complexes (PCtTt and PCtCt) can serve as a catalyst to continue to promote the SO3 hydration. For these post-reactive complexes (PCcTt, PCtTt, PCtCt and PCcCt), the above result has shown that these complexes are stable compared to the isolated H2SO4 and OA conformers. The free carboxylic group in these complexes can also provide the interaction site when these complexes interact with other species. The free carboxylic group of these stable post-reactive complexes indicates that these complexes have the potential to participate in nucleation.
3.3 Atmospheric implications
To evaluate the importance of OA in enhancing H2SO4 formation in the atmosphere, we calculated the rate constants of SO3 hydration catalyzed by OA and water, and compared the rate of OA-catalyzed hydration reactions with that of water-catalyzed hydration at different altitudes in the troposphere. The temperature, pressure, density of air and water vapor content at the corresponding altitude are taken from US Standard Atmosphere (1976, NASA and NOAA), and are shown in Table S6 in the Supplement.
According to these calculation methods, described in “Computational details” Sect. 2, it can be confirmed that both the ratio of rate constants and relative concentrations are important elements to estimate the effect of OA-catalyzed SO3 hydration. Thus, the rate constants for hydration reactions of SO3 catalyzed by OA and water at different altitudes are firstly analyzed and summarized in Table 1. The corresponding Keq and kuni are included in the Supplement (Table S7).
Table 1Rate constants (in cm6 molecule−2 s−1) of the SO3 hydration reaction catalyzed by water and by OA at different altitudes.
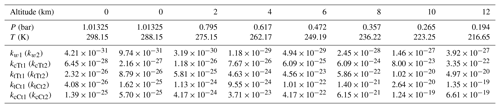
As shown in Table 1, the rate constant in Eq. (2) changes from cm6 molecule−2 s−1 (298.15 K at 0 km altitude) to cm6 molecule−2 s−1 (216.15 K at 12 km altitude). For Eq. (4), the transformation of rate constants within the range of altitudes can also be found (kcTt1: from to ; ktTt1: from to ; ktCt1: from to ; kcCt1: from to cm6 molecule−2 s−1). All corresponding rate constant ratios at various altitudes are described in Table 2. Obviously, the rate constant in the OA-catalyzed SO3 hydration reaction is about 103–108 times larger than that for the water-catalyzed SO3 hydration reaction within the range of altitudes. It can be seen from Table 2 that rate constant ratios increase with the temperature decreasing (i.e., with altitude increasing).
Table 2Relative rate constants of OA-catalyzed SO3 hydration with respect to water-catalyzed SO3 hydration at different altitudes.
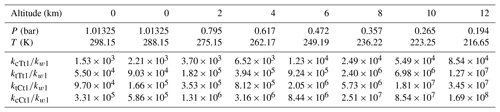
As seen from Table 2, at 298.15 K, the OA-catalyzed SO3 hydration reaction is 103–105 faster than the corresponding water-catalyzed reaction (kcTt1∕kw1: 1.53×103; ktTt1∕kw1: 5.50×104; ktCt1∕kw1: 9.70×104; kcCt1∕kw1: 3.31×105). In order to evaluate the catalytic effect of OA, we also list the rate constant ratio between other species and water-catalyzed SO3 hydration reactions. At 298 K, the nitric-acid-catalyzed rate constant is just 1.19 times larger than the water-catalyzed rate constant (Long et al., 2013). When sulfuric acid functions as an autocatalyst, the value of the rate constant ratio is around 102 (Torrent-Sucarrat et al., 2012). When formic acid acts as a catalyst, its rate constant is 104 greater than that of the water-catalyzed SO3 hydration at 300 K (Hazra and Sinha, 2011). The rate constant for ammonia-catalyzed SO3 hydration is 7 orders of magnitude larger than that for the water-catalyzed reaction at 298 K (Bandyopadhyay et al., 2017). These results indicate that the catalytic effect of OA in the SO3 hydration reaction is better than nitric acid and sulfuric acid, and similar to formic acid, but weaker than ammonia.
Table 4Concentrations (in molecules cm−3) of OA conformers involved in SO3 hydration and water at different altitudes.
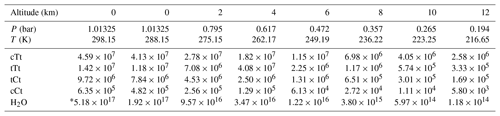
* The water vapor concentration at 0 km and 298.15 K are obtained from Torrent-Sucarrat et al. (2012). Other water vapor concentrations are taken from US Standard Atmosphere, 1976.
Table 5Relative rate of SO3 hydration reaction catalyzed by OA and by water at different altitudes.

* The rate νOA1 represents the sum of reaction rate for Eq. (4; X = cTt, tTt, tCt, cCt). The rate (νcTt1∕νw1, νtTt1∕νw1, νtCt1∕νw1, νcCt1∕νw1) are shown in Table S10 in the Supplement.
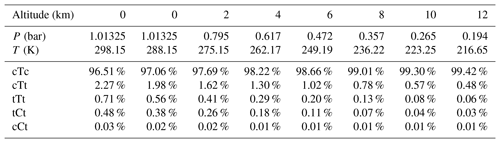
Based on the calculated Gibbs free energy at G4 level (see Table S8 in the Supplement) and the assumption of a Boltzmann distribution, mole fractions for OA conformers can be obtained (Table 3). The calculation method for the conformational population is shown in Supplement S2. The most stable conformer, cTc conformer, accounts for more than 95 % of OA at different altitudes ranging from 0 to 12 km. But this conformer cannot participate in catalyzing the hydration reaction of SO3. In other words, the conformers involved in catalyzing the SO3 hydration reaction do not exceed 5 % of OA. In some studies (Martinelango et al., 2007; Bao et al., 2012), observed concentrations of OA in the gas phase range from approximately 10 ng m−3 to close to 1 µg m−3. To obtain actual concentrations of OA conformers, we assumed 302 ng m−3 (2.02×109 molecules cm−3) for total OA at 298.15 K and an altitude of 0 km, which are measured by Bao et al. (2012). Combining mole fractions for conformers (cTt, tTt, tCt and cCt) and the total concentration of OA and considering the temperature and pressure effect using the idea gas equation (see Table S9 in the Supplement), the concentration of OA conformers involved in the hydration reaction at various altitudes can be calculated, which is tabulated in Table 4. The water vapor concentration is also included in Table 4.
As shown in Table 5, reaction rate ratios between the SO3 hydration reactions catalyzed by OA conformers (cTt, tTt, tCt and cCt) and the SO3 hydration reaction catalyzed by H2O are described. At an altitude of 0 km, the rate ratio for these two reactions is within the range of 10−5–10−6 at two temperatures (298.15 and 288.15 K), which indicates that the OA-catalyzed SO3 hydration is of minor importance at 0 km at different temperatures. However, as the altitude increases, the OA has an increasing impact on the SO3 hydration because of an obvious increase in the ratio. When the altitude increases to 10 km, the OA-catalyzed reaction is just 2 orders of magnitude slower than the water-catalyzed reaction. At 12 km altitude, the water-catalyzed hydration reaction is approximately 10 times faster than the OA-catalyzed SO3 hydration. To sum up, the comparison of relative rates shows that, in the upper troposphere, the OA can play a significant role in enhancing SO3 hydration to H2SO4.
It has been shown that some species including nitric acid, sulfuric acid, formic acid, ammonia, the hydroperoxy radical and OA in our study can catalyze the SO3 hydration reaction. By forming a two-point hydrogen bond, these species can make a bridge to promote the hydration reaction. It may be concluded that, as long as the species can form a two-point hydrogen bond with a water molecule and SO3, it has the potential to promote the SO3 hydration reaction. However, the real atmospheric importance of the species-catalyzed SO3 hydration reaction needs to be evaluated. That is, compared to the water-catalyzed SO3 hydration reaction, the species must have sufficient catalytic effect, leading to an increase in rate constants, so as to compensate for the high concentration difference between water vapor and the species.
The main conclusion of this work is that oxalic acid (OA), the most abundant dicarboxylic acid in the atmosphere, has the remarkable ability to catalyze SO3 hydration to H2SO4, and has a potential impact on H2SO4 formation in the atmosphere.
We have shown that the water-catalyzed hydration reaction of SO3 has an energy barrier of 5.17 kcal mol−1. For OA, four conformers (cTt, tTt, tCt and cCt) can be involved in the hydration reaction, whereas the most stable conformer (cTc) cannot catalyze the hydration reaction because the formed hydrogen bond structure rejects HAT. Other conformers can catalyze the hydration reaction and the corresponding energy barrier is a little higher or less than 1 kcal mol−1. The results demonstrate that OA has the stronger catalytic ability than water for SO3 hydration to form H2SO4.
According to the kinetic analysis, the rate constant of the OA-catalyzed hydration reaction is greater than that of the water-catalyzed reaction by orders of magnitude, which also reflects the obvious catalytic ability of OA. In addition to the rate constant, the reactant concentration is also an important factor to assess the effect of OA on SO3 hydration. Based on these two factors, our calculation shows that, in the upper troposphere, OA can play an important role in SO3 hydration to form H2SO4.
This work not only provides insight into the new mechanism of SO3 hydration in the atmosphere, but also has potential importance for investigating the catalytic effect of OA on other atmospheric reactions.
The data generated or analyzed in this study are available from the corresponding author upon request (sxmwch@sdu.edu.cn).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-2833-2019-supplement.
All authors conceived and designed the research. GL performed the calculation and analyzed the data, and wrote the main manuscript text. XS, CZ and ML revised the initial manuscript. All of the authors discussed the results, and contributed to the final manuscript.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Multiphase chemistry of secondary aerosol formation under severe haze”. It is not associated with a conference.
This work is supported by the National Natural Science Foundation of China
(21337001 and 21607056), the National Key Technology R&D Program (grant
no. 2014BAC21B01), the Natural Science Foundation of Guangdong Province
(2015A030313339) and the Fundamental Research Funds for the Central
Universities (21617455).
Edited by: Hang Su
Reviewed by: three anonymous referees
Alvarez-Idaboy, J. R., Mora-Diez, N., Boyd, R. J., and Vivier-Bunge, A.: On the Importance of Prereactive Complexes in Molecule-Radical Reactions: Hydrogen Abstraction from Aldehydes by OH, J. Am. Chem. Soc., 123, 2018–2024, https://doi.org/10.1021/ja003372g, 2001.
Arquero, K. D., Xu, J., Gerber, R. B., and Finlayson-Pitts, B. J.: Particle formation and growth from oxalic acid, methanesulfonic acid, trimethylamine and water: a combined experimental and theoretical study, Phys. Chem. Chem. Phys., 19, 28286–28301, https://doi.org/10.1039/C7CP04468B, 2017.
Atkinson, R.: Rate constants for the atmospheric reactions of alkoxy radicals: An updated estimation method, Atmos. Environ., 41, 8468–8485, https://doi.org/10.1016/j.atmosenv.2007.07.002, 2007.
Atkinson, R., Baulch, D. L., Cox, R. A., Crowley, J. N., Hampson, R. F., Hynes, R. G., Jenkin, M. E., Rossi, M. J., Troe, J., and IUPAC Subcommittee: Evaluated kinetic and photochemical data for atmospheric chemistry: Volume II – gas phase reactions of organic species, Atmos. Chem. Phys., 6, 3625–4055, https://doi.org/10.5194/acp-6-3625-2006, 2006.
Bandyopadhyay, B., Kumar, P., and Biswas, P.: Ammonia Catalyzed Formation of Sulfuric Acid in Troposphere: The Curious Case of a Base Promoting Acid Rain, J. Phys. Chem. A, 121, 3101–3108, https://doi.org/10.1021/acs.jpca.7b01172, 2017.
Bannan, T. J., Murray Booth, A., Le Breton, M., Bacak, A., Muller, J. B. A., Leather, K. E., Khan, M. A. H., Lee, J. D., Dunmore, R. E., Hopkins, J. R., Fleming, Z. L., Sheps, L., Taatjes, C. A., Shallcross, D. E., and Percival, C. J.: Seasonality of Formic Acid (HCOOH) in London during the ClearfLo Campaign, J. Geophys. Res.-Atmos., 122, 12488–12498, https://doi.org/10.1002/2017JD027064, 2017.
Bao, L., Matsumoto, M., Kubota, T., Sekiguchi, K., Wang, Q., and Sakamoto, K.: Gas/particle partitioning of low-molecular-weight dicarboxylic acids at a suburban site in Saitama, Japan, Atmos. Environ., 47, 546–553, https://doi.org/10.1016/j.atmosenv.2009.09.014, 2012.
Buemi, G.: DFT study of the hydrogen bond strength and IR spectra of formic, oxalic, glyoxylic and pyruvic acids in vacuum, acetone and water solution, J. Phys. Org. Chem., 22, 933–947, https://doi.org/10.1002/poc.1543, 2009.
Cameron, M., Sivakumaran, V., Dillon, T. J., and Crowley, J. N.: Reaction between OH and CH3CHO Part 1. Primary product yields of CH3 (296 K), CH3CO (296 K), and H (237–296 K), Phys. Chem. Chem. Phys., 4, 3628–3638, https://doi.org/10.1039/B202586H, 2002.
Canneaux, S., Bohr, F., and Henon, E.: KiSThelP: A program to predict thermodynamic properties and rate constants from quantum chemistry results, J. Comput. Chem., 35, 82–93, https://doi.org/10.1002/jcc.23470, 2014.
Chen, J., Jiang, S., Liu, Y.-R., Huang, T., Wang, C.-Y., Miao, S.-K., Wang, Z.-Q., Zhang, Y., and Huang, W.: Interaction of oxalic acid with dimethylamine and its atmospheric implications, RSC Adv., 7, 6374–6388, https://doi.org/10.1039/C6RA27945G, 2017.
Courmier, D., Gardebien, F., Minot, C., and St-Amant, A.: A computational study of the water-catalyzed formation of NH2CH2OH, Chem. Phys. Lett., 405, 357–363, https://doi.org/10.1016/j.cplett.2004.12.121, 2005.
Curtiss, L. A., Redfern, P. C., and Raghavachari, K.: Gaussian-4 theory, J. Chem. Phys., 126, 084108, https://doi.org/10.1063/1.2436888, 2007.
da Silva, G.: Carboxylic Acid Catalyzed Keto-Enol Tautomerizations in the Gas Phase, Angew. Chem. Int. Ed., 49, 7523–7525, https://doi.org/10.1002/anie.201003530, 2010.
Deshmukh, D. K., Kawamura, K., Lazaar, M., Kunwar, B., and Boreddy, S. K. R.: Dicarboxylic acids, oxoacids, benzoic acid, α-dicarbonyls, WSOC, OC, and ions in spring aerosols from Okinawa Island in the western North Pacific Rim: size distributions and formation processes, Atmos. Chem. Phys., 16, 5263–5282, https://doi.org/10.5194/acp-16-5263-2016, 2016.
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., Scalmani, G., Barone, V., Mennucci, B., Petersson, G. A., Nakatsuji, H., Caricato, M., Li, X., Hratchian, H. P., Izmaylov, A. F., Bloino, J., Zheng, G., Sonnenberg, J. L., Hada, M., Ehara, M., Toyota, K., Fukuda, R., Hasegawa, J., Ishida, M., Nakajima, T., Honda, Y., Kitao, O., Nakai, H., Vreven, T., Montgomery, J. A., Peralta, J. E., Ogliaro, F., Bearpark, M., Heyd, J. J., Brothers, E., Kudin, K. N., Staroverov, V. N., Kobayashi, R., Normand, J., Raghavachari, K., Rendell, A., Burant, J. C., Iyengar, S. S., Tomasi, J., Cossi, M., Rega, N., Millam, J. M., Klene, M., Knox, J. E., Cross, J. B., Bakken, V., Adamo, C., Jaramillo, J., Gomperts, R., Stratmann, R. E., Yazyev, O., Austin, A. J., Cammi, R., Pomelli, C., Ochterski, J. W., Martin, R. L., Morokuma, K., Zakrzewski, V. G., Voth, G. A., Salvador, P., Dannenberg, J. J., Dapprich, S., Daniels, A. D., Farkas, Foresman, J. B., Ortiz, J. V., Cioslowski, J., and Fox, D. J.: Gaussian 09, Revision B.01, Gaussian Inc. Wallingford CT, 2010.
Fukui, K.: The path of chemical reactions – the IRC approach, Acc. Chem. Res., 14, 363–368, https://doi.org/10.1021/ar00072a001, 1981.
Gonzalez, J., Torrent-Sucarrat, M., and Anglada, J. M.: The reactions of SO3 with HO2 radical and H2O⋯HO2 radical complex. Theoretical study on the atmospheric formation of HSO5 and H2SO4, Phys. Chem. Chem. Phys., 12, 2116–2125, https://doi.org/10.1039/B916659A, 2010.
Gutbrod, R., Schindler, R. N., Kraka, E., and Cremer, D.: Formation of OH radicals in the gas phase ozonolysis of alkenes: the unexpected role of carbonyl oxides, Chem. Phys. Lett., 252, 221–229, https://doi.org/10.1016/0009-2614(96)00126-1, 1996.
Hazra, M. K. and Sinha, A.: Formic Acid Catalyzed Hydrolysis of SO3 in the Gas Phase: A Barrierless Mechanism for Sulfuric Acid Production of Potential Atmospheric Importance, J. Am. Chem. Soc., 133, 17444–17453, https://doi.org/10.1021/ja207393v, 2011.
Ho, K. F., Huang, R.-J., Kawamura, K., Tachibana, E., Lee, S. C., Ho, S. S. H., Zhu, T., and Tian, L.: Dicarboxylic acids, ketocarboxylic acids, α-dicarbonyls, fatty acids and benzoic acid in PM2.5 aerosol collected during CAREBeijing-2007: an effect of traffic restriction on air quality, Atmos. Chem. Phys., 15, 3111–3123, https://doi.org/10.5194/acp-15-3111-2015, 2015.
Hofmann-Sievert, R. and Castleman, A. W.: Reaction of sulfur trioxide with water clusters and the formation of sulfuric acid, J. Phys. Chem., 88, 3329–3333, https://doi.org/10.1021/j150659a038, 1984.
Hofmann, M. and Schleyer, P. V. R.: Acid Rain: Ab Initio Investigation of the H2O⋅SO3 Complex and Its Conversion to H2SO4, J. Am. Chem. Soc., 116, 4947–4952, https://doi.org/10.1021/ja00090a045, 1994.
Holland, P. M. and Castleman, A. W.: Gas phase complexes: considerations of the stability of clusters in the sulfur trioxide–water system, Chem. Phys. Lett., 56, 511–514, https://doi.org/10.1016/0009-2614(78)89028-9, 1978.
Hratchian, H. P. and Schlegel, H. B.: Accurate reaction paths using a Hessian based predictor–corrector integrator, J. Chem. Phys., 120, 9918–9924, https://doi.org/10.1063/1.1724823, 2004.
Hratchian, H. P. and Schlegel, H. B.: Using Hessian Updating To Increase the Efficiency of a Hessian Based Predictor-Corrector Reaction Path Following Method, J. Chem. Theory Comput., 1, 61–69, https://doi.org/10.1021/ct0499783, 2005.
Ji, Y., Zhao, J., Terazono, H., Misawa, K., Levitt, N. P., Li, Y., Lin, Y., Peng, J., Wang, Y., Duan, L., Pan, B., Zhang, F., Feng, X., An, T., Marrero-Ortiz, W., Secrest, J., Zhang, A. L., Shibuya, K., Molina, M. J., and Zhang, R.: Reassessing the atmospheric oxidation mechanism of toluene, P. Natl. Acad. Sci. USA, 114, 8169, https://doi.org/10.1073/pnas.1705463114, 2017.
Ji, Y. M., Wang, H. H., Gao, Y. P., Li, G. Y., and An, T. C.: A theoretical model on the formation mechanism and kinetics of highly toxic air pollutants from halogenated formaldehydes reacted with halogen atoms, Atmos. Chem. Phys., 13, 11277–11286, https://doi.org/10.5194/acp-13-11277-2013, 2013.
Kawamura, K. and Ikushima, K.: Seasonal changes in the distribution of dicarboxylic acids in the urban atmosphere, Environ. Sci. Technol., 27, 2227–2235, https://doi.org/10.1021/es00047a033, 1993.
Kawamura, K., Tachibana, E., Okuzawa, K., Aggarwal, S. G., Kanaya, Y., and Wang, Z. F.: High abundances of water-soluble dicarboxylic acids, ketocarboxylic acids and α-dicarbonyls in the mountaintop aerosols over the North China Plain during wheat burning season, Atmos. Chem. Phys., 13, 8285–8302, https://doi.org/10.5194/acp-13-8285-2013, 2013.
Klopper, W., van Duijneveldt-van de Rijdt, J. G. C. M., and van Duijneveldt, F. B.: Computational determination of equilibrium geometry and dissociation energy of the water dimer, Phys. Chem. Chem. Phys., 2, 2227–2234, https://doi.org/10.1039/A910312K, 2000.
Kumar, M. and Francisco, J. S.: Red-Light-Induced Decomposition of an Organic Peroxy Radical: A New Source of the HO2 Radical, Angew. Chem. Int. Ed., 54, 15711–15714, https://doi.org/10.1002/anie.201509311, 2015.
Kumar, M., Sinha, A., and Francisco, J. S.: Role of Double Hydrogen Atom Transfer Reactions in Atmospheric Chemistry, Acc. Chem. Res., 49, 877–883, https://doi.org/10.1021/acs.accounts.6b00040, 2016.
Larson, L. J., Kuno, M., and Tao, F.-M.: Hydrolysis of sulfur trioxide to form sulfuric acid in small water clusters, J. Chem. Phys., 112, 8830–8838, https://doi.org/10.1063/1.481532, 2000.
Loerting, T. and Liedl, K. R.: Toward elimination of discrepancies between theory and experiment: The rate constant of the atmospheric conversion of SO3 to H2SO4, P. Natl. Acad. Sci. USA, 97, 8874–8878, https://doi.org/10.1073/pnas.97.16.8874, 2000.
Long, B., Long, Z.-W., Wang, Y.-B., Tan, X.-F., Han, Y.-H., Long, C.-Y., Qin, S.-J., and Zhang, W.-J.: Formic Acid Catalyzed Gas-Phase Reaction of H2O with SO3 and the Reverse Reaction: A Theoretical Study, Chem. Phys. Chem., 13, 323–329, https://doi.org/10.1002/cphc.201100558, 2012.
Long, B., Chang, C.-R., Long, Z.-W., Wang, Y.-B., Tan, X.-F., and Zhang, W.-J.: Nitric acid catalyzed hydrolysis of SO3 in the formation of sulfuric acid: A theoretical study, Chem. Phys. Lett., 581, 26–29, https://doi.org/10.1016/j.cplett.2013.07.012, 2013.
Martinelango, P. K., Dasgupta, P. K., and Al-Horr, R. S.: Atmospheric production of oxalic acid/oxalate and nitric acid/nitrate in the Tampa Bay airshed: Parallel pathways, Atmos. Environ., 41, 4258–4269, https://doi.org/10.1016/j.atmosenv.2006.05.085, 2007.
Miao, S.-K., Jiang, S., Chen, J., Ma, Y., Zhu, Y.-P., Wen, Y., Zhang, M.-M., and Huang, W.: Hydration of a sulfuric acid-oxalic acid complex: acid dissociation and its atmospheric implication, RSC Adv., 5, 48638–48646, https://doi.org/10.1039/C5RA06116D, 2015.
Millet, D. B., Baasandorj, M., Farmer, D. K., Thornton, J. A., Baumann, K., Brophy, P., Chaliyakunnel, S., de Gouw, J. A., Graus, M., Hu, L., Koss, A., Lee, B. H., Lopez-Hilfiker, F. D., Neuman, J. A., Paulot, F., Peischl, J., Pollack, I. B., Ryerson, T. B., Warneke, C., Williams, B. J., and Xu, J.: A large and ubiquitous source of atmospheric formic acid, Atmos. Chem. Phys., 15, 6283–6304, https://doi.org/10.5194/acp-15-6283-2015, 2015.
Morokuma, K. and Muguruma, C.: Ab initio Molecular Orbital Study of the Mechanism of the Gas Phase Reaction SO3 + H2O: Importance of the Second Water Molecule, J. Am. Chem. Soc., 116, 10316–10317, https://doi.org/10.1021/ja00101a068, 1994.
NASA and NOAA: Technical Report, available at: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19770009539.pdf (last access: 17 August 2018), 1976.
Nieminen, J., Rasanen, M., and Murto, J.: Matrix-isolation and ab initio studies of oxalic acid, J. Phys. Chem., 96, 5303–5308, https://doi.org/10.1021/j100192a024, 1992.
Peng, X.-Q., Liu, Y.-R., Huang, T., Jiang, S., and Huang, W.: Interaction of gas phase oxalic acid with ammonia and its atmospheric implications, Phys. Chem. Chem. Phys., 17, 9552–9563, https://doi.org/10.1039/C5CP00027K, 2015.
Pople, J. A., Gordon, M., and Raghavachari, K.: Quadratic configuration interaction. A general technique for determining electron correlation energies, J. Chem. Phys., 87, 5968–5975, https://doi.org/10.1063/1.453520, 1987.
Purvis, G. D. and Bartlett, R. J.: A full coupled cluster singles and doubles model: The inclusion of disconnected triples, J. Chem. Phys., 76, 1910–1918, https://doi.org/10.1063/1.443164, 1982.
Rayez, M.-T., Picquet-Varrault, B., Caralp, F., and Rayez, J.-C.: CH3C(O)OCH(O•)CH3 alkoxy radical derived from ethyl acetate: Novel rearrangement confirmed by computational chemistry, Phys. Chem. Chem. Phys., 4, 5789–5794, https://doi.org/10.1039/B207511N, 2002.
Rocher-Casterline, B. E., Ch'ng, L. C., Mollner, A. K., and Reisler, H.: Communication: Determination of the bond dissociation energy (D0) of the water dimer, (H2O)2, by velocity map imaging, J. Chem. Phys., 134, 211101, https://doi.org/10.1063/1.3598339, 2011.
Steckler, R., Thurman, G. M., Watts, J. D., and Bartlett, R. J.: Ab initio direct dynamics study of OH + HCl → Cl + H2O, J. Chem. Phys., 106, 3926–3933, https://doi.org/10.1063/1.473981, 1997.
Steudel, R.: Sulfuric Acid from Sulfur Trioxide and Water – A Surprisingly Complex Reaction, Angew. Chem. Int. Ed. Engl., 34, 1313–1315, https://doi.org/10.1002/anie.199513131, 1995.
Torrent-Sucarrat, M., Francisco, J. S., and Anglada, J. M.: Sulfuric Acid as Autocatalyst in the Formation of Sulfuric Acid, J. Am. Chem. Soc., 134, 20632–20644, https://doi.org/10.1021/ja307523b, 2012.
Truhlar, D. G., Garrett, B. C., and Klippenstein, S. J.: Current Status of Transition-State Theory, J. Phys. Chem., 100, 12771–12800, https://doi.org/10.1021/jp953748q, 1996.
Vöhringer-Martinez, E., Hansmann, B., Hernandez, H., Francisco, J. S., Troe, J., and Abel, B.: Water Catalysis of a Radical-Molecule Gas-Phase Reaction, Science, 315, 497–501, https://doi.org/10.1126/science.1134494, 2007.
van Pinxteren, D., Neusüß, C., and Herrmann, H.: On the abundance and source contributions of dicarboxylic acids in size-resolved aerosol particles at continental sites in central Europe, Atmos. Chem. Phys., 14, 3913–3928, https://doi.org/10.5194/acp-14-3913-2014, 2014.
Wang, G., Zhang, R., Gomez, M. E., Yang, L., Levy Zamora, M., Hu, M., Lin, Y., Peng, J., Guo, S., Meng, J., Li, J., Cheng, C., Hu, T., Ren, Y., Wang, Y., Gao, J., Cao, J., An, Z., Zhou, W., Li, G., Wang, J., Tian, P., Marrero-Ortiz, W., Secrest, J., Du, Z., Zheng, J., Shang, D., Zeng, L., Shao, M., Wang, W., Huang, Y., Wang, Y., Zhu, Y., Li, Y., Hu, J., Pan, B., Cai, L., Cheng, Y., Ji, Y., Zhang, F., Rosenfeld, D., Liss, P. S., Duce, R. A., Kolb, C. E., and Molina, M. J.: Persistent sulfate formation from London Fog to Chinese haze, P. Natl. Acad. Sci. USA, 113, 13630, https://doi.org/10.1073/pnas.1616540113, 2016.
Weber, K. H., Morales, F. J., and Tao, F.-M.: Theoretical Study on the Structure and Stabilities of Molecular Clusters of Oxalic Acid with Water, J. Phys. Chem. A, 116, 11601–11617, https://doi.org/10.1021/jp308499f, 2012.
Weber, K. H., Liu, Q., and Tao, F.-M.: Theoretical Study on Stable Small Clusters of Oxalic Acid with Ammonia and Water, J. Phys. Chem. A, 118, 1451–1468, https://doi.org/10.1021/jp4128226, 2014.
Williams, I. H., Spangler, D., Femec, D. A., Maggiora, G. M., and Schowen, R. L.: Theoretical models for solvation and catalysis in carbonyl addition, J. Am. Chem. Soc., 105, 31–40, https://doi.org/10.1021/ja00339a008, 1983.
Xu, J., Finlayson-Pitts, B. J., and Gerber, R. B.: Proton Transfer in Mixed Clusters of Methanesulfonic Acid, Methylamine, and Oxalic Acid: Implications for Atmospheric Particle Formation, J. Phys. Chem. A, 121, 2377–2385, https://doi.org/10.1021/acs.jpca.7b01223, 2017.
Xu, W. and Zhang, R.: Theoretical Investigation of Interaction of Dicarboxylic Acids with Common Aerosol Nucleation Precursors, J. Phys. Chem. A, 116, 4539–4550, https://doi.org/10.1021/jp301964u, 2012.
Xu, Y., Nadykto, A. B., Yu, F., Jiang, L., and Wang, W.: Formation and properties of hydrogen-bonded complexes of common organic oxalic acid with atmospheric nucleation precursors, J. Mol. Struct. Theochem., 951, 28–33, https://doi.org/10.1016/j.theochem.2010.04.004, 2010.
Zhang, D. and Zhang, R.: Mechanism of OH Formation from Ozonolysis of Isoprene: A Quantum-Chemical Study, J. Am. Chem. Soc., 124, 2692–2703, https://doi.org/10.1021/ja011518l, 2002.
Zhang, R.: Getting to the Critical Nucleus of Aerosol Formation, Science, 328, 1366, https://doi.org/10.1126/science.1189732, 2010.
Zhao, H., Zhang, Q., and Du, L.: Hydrogen bonding in cyclic complexes of carboxylic acid-sulfuric acid and their atmospheric implications, RSC Adv., 6, 71733–71743, https://doi.org/10.1039/C6RA16782A, 2016.
Zhao, Y. and Truhlar, D. G.: The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 120, 215–241, https://doi.org/10.1007/s00214-007-0310-x, 2008.
Zheng, J. and Truhlar, D. G.: Kinetics of hydrogen-transfer isomerizations of butoxyl radicals, Phys. Chem. Chem. Phys., 12, 7782–7793, https://doi.org/10.1039/B927504E, 2010.