the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A comprehensive study of hygroscopic properties of calcium- and magnesium-containing salts: implication for hygroscopicity of mineral dust and sea salt aerosols
Liya Guo
Wenjun Gu
Chao Peng
Weigang Wang
Yong Jie Li
Taomou Zong
Yujing Tang
Zhijun Wu
Qinhao Lin
Guohua Zhang
Xinhui Bi
Xinming Wang
Calcium- and magnesium-containing salts are important components for mineral dust and sea salt aerosols, but their physicochemical properties are not well understood yet. In this study, hygroscopic properties of eight Ca- and Mg-containing salts, including Ca(NO3)2•4H2O, Mg(NO3)2•6H2O, MgCl2•6H2O, CaCl2•6H2O, Ca(HCOO)2, Mg(HCOO)2•2H2O, Ca(CH3COO)2•H2O and Mg(CH3COO)2•4H2O, were investigated using two complementary techniques. A vapor sorption analyzer was used to measure the change of sample mass with relative humidity (RH) under isotherm conditions, and the deliquescence relative humidities (DRHs) for temperature in the range of 5–30 ∘C as well as water-to-solute ratios as a function of RH at 5 and 25 ∘C were reported for these eight compounds. DRH values showed large variation for these compounds; for example, at 25 ∘C DRHs were measured to be ∼ 28.5 % for CaCl2•6H2O and >95 % for Ca(HCOO)2 and Mg(HCOO)2•2H2O. We further found that the dependence of DRH on temperature can be approximated by the Clausius–Clapeyron equation. In addition, a humidity tandem differential mobility analyzer was used to measure the change in mobility diameter with RH (up to 90 %) at room temperature, in order to determine hygroscopic growth factors of aerosol particles generated by atomizing water solutions of these eight compounds. All the aerosol particles studied in this work, very likely to be amorphous under dry conditions, started to grow at very low RH (as low as 10 %) and showed continuous growth with RH. Hygroscopic growth factors at 90 % RH were found to range from 1.26 ± 0.04 for Ca(HCOO)2 to 1.79 ± 0.03 for Ca(NO3)2, and the single hygroscopicity parameter ranged from 0.09–0.13 for Ca(CH3COO)2 to 0.49–0.56 for Ca(NO3)2. Overall, our work provides a comprehensive investigation of hygroscopic properties of these Ca- and Mg-containing salts, largely improving our knowledge of the physicochemical properties of mineral dust and sea salt aerosols.
- Article
(2668 KB) -
Supplement
(128 KB) - BibTeX
- EndNote
Mineral dust, mainly emitted from arid and semiarid regions with an annual flux of ∼ 2000 Tg, is one of the most abundant types of aerosols in the troposphere (Textor et al., 2006; Ginoux et al., 2012). Mineral dust aerosol affects the climate system directly by scattering and absorbing solar and terrestrial radiation (Formenti et al., 2011; Ridley et al., 2016; Chen et al., 2017) and indirectly by serving as cloud condensation nuclei (CCN) and ice-nucleating particles (INPs) (Hoose and Möhler, 2012; Creamean et al., 2013; Cziczo et al., 2013; Tang et al., 2016a). In addition, deposition of mineral dust particles is an important source of several nutrient elements (Fe and P, for example) for many ecosystems around the globe, thus having significant impacts on biogeochemical cycles in these regions (Jickells et al., 2005; Mahowald et al., 2009, 2011; Zhang et al., 2015).
Mineral dust aerosol has an average lifetime of 2–7 days in the atmosphere and can thus be transported over thousands of kilometers (Textor et al., 2006; Uno et al., 2009). During transport mineral dust particles may undergo heterogeneous reactions with trace gases, impacting the abundance of a number of important reactive trace gases both directly and indirectly (Usher et al., 2003; Crowley et al., 2010; Romanias et al., 2012; Tang et al., 2017). These reactions can also lead to change in chemical composition of mineral dust particles (Usher et al., 2003; Li and Shao, 2009; Li et al., 2010; Tang et al., 2012; Romanias et al., 2016) and thereby modification of their physicochemical and optical properties (Krueger et al., 2003; Vlasenko et al., 2006; Liu et al., 2008b; Sullivan et al., 2009; Tang et al., 2016a; Pan et al., 2017). Mineral dust particles contain substantial amounts of carbonates, including CaCO3 (calcite) and CaMg(CO3)2 (dolomite) (Nickovic et al., 2012; Formenti et al., 2014; Jeong and Achterberg, 2014; Journet et al., 2014; Scanza et al., 2015). These carbonates are largely insoluble and have very low hygroscopicity (Sullivan et al., 2009; Tang et al., 2016a); however, their reactions with acidic gases in the troposphere can form Ca- and Mg-containing salts with higher hygroscopicity (Gibson et al., 2006; Liu et al., 2008b; Sullivan et al., 2009; Tang et al., 2016a), such as Ca(NO3)2 and Mg(NO3)2. For example, numerous laboratory and field studies have found that due to the formation of Ca(NO3)2 and CaCl2 from heterogeneous reactions with nitrogen oxides (Goodman et al., 2000; Liu et al., 2008a; Li et al., 2010; Tang et al., 2012; Tan et al., 2016) and HCl (Santschi and Rossi, 2006), solid CaCO3 particles could be converted to aqueous droplets under tropospheric conditions (Krueger et al., 2003; Laskin et al., 2005; Liu et al., 2008b; Shi et al., 2008; Tobo et al., 2010). In addition, MgCl2 and CaCl2 are important components in sea salt aerosol (as known as sea spray aerosol). The presence of MgCl2 and CaCl2, in addition to NaCl, can alter the hygroscopicity of sea salt aerosol (Gupta et al., 2015; Zieger et al., 2017); to be more specific, the hygroscopicity of sea salt was found to be significantly smaller than that of pure NaCl. Furthermore, the CCN activity of saline mineral dust was explored (Gaston et al., 2017), and good correlations were found between the CCN activities of saline mineral dust particles and the abundance of the soluble components (e.g., CaCl2) they contained.
Nevertheless, hygroscopic properties of Ca(NO3)2, Mg(NO3)2, CaCl2 and MgCl2 have not been completely understood, especially in the two following aspects. First, hygroscopic growth factors (GFs) were only measured by one or two previous studies for Ca(NO3)2 (Gibson et al., 2006; Jing et al., 2018), Mg(NO3)2 (Gibson et al., 2006), CaCl2 (Park et al., 2009) and MgCl2 aerosols (Park et al., 2009). Considering the importance of these compounds in the troposphere, additional measurements of their hygroscopic growth are clearly warranted. In addition, tropospheric temperatures range from ∼ 200 to ∼ 300 K; however, the effects of temperature on their phase transitions and hygroscopic growth remain largely unclear (Kelly and Wexler, 2005), due to lack of experimental data below room temperature.
Small carboxylic acids, such as formic and acetic acids, are abundant in the troposphere (Khare et al., 1999), and previous studies suggested that heterogeneous reactions of mineral dust with formic and acetic acids are efficient (Hatch et al., 2007; Prince et al., 2008; Tong et al., 2010; Ma et al., 2012; Tang et al., 2016b). It was shown that calcium and magnesium acetates were formed in heterogeneous reactions of gaseous acetic acid with MgO and CaCO3 particles, leading to a significant increase in particle hygroscopicity (Ma et al., 2012). However, only a few previous studies explored hygroscopic growth of Mg(CH3COO)2 and Ca(CH3COO)2, using techniques based on bulk samples (Wang et al., 2005; Ma et al., 2012; Pang et al., 2015). To our knowledge, hygroscopic GFs have never been reported for Ca(HCOO)2, Mg(HCOO)2, Ca(CH3COO)2 and Mg(CH3COO)2 aerosol particles.
To better understand hygroscopic properties of these Ca- and Mg-containing salts, two complementary techniques were employed in this work to investigate their phase transitions and hygroscopic growth. A vapor sorption analyzer (VSA), which measured the sample mass as a function of relative humidity (RH), was used to determine the deliquescence relative humidity (DRH) and solute-to-water ratios for Ca(NO3)2•4H2O, Mg(NO3)2•6H2O, CaCl2•6H2O, MgCl2•6H2O, Ca(HCOO)2, Mg(HCOO)2•2H2O, Ca(CH3COO)2•H2O and Mg(CH3COO)2•4H2O at different temperatures (5–30 ∘C). Furthermore, hygroscopic GFs of Ca(NO3)2, Mg(NO3)2, CaCl2, MgCl2, Ca(HCOO)2, Mg(HCOO)2, Ca(CH3COO)2 and Mg(CH3COO)2 aerosol particles were determined at room temperature up to 90 % RH, using a humidity tandem differential mobility analyzer (H-TDMA). This work would significantly increase our knowledge of the hygroscopicity of these compounds, hence leading to a better understanding of the physicochemical properties of mineral dust and sea salt aerosols.
Hygroscopic growth of Ca- and Mg-containing salts was investigated using two complementary techniques, i.e., a H-TDMA and a VSA. Eight salts, all supplied by Aldrich, were investigated in this work, including Ca(NO3)2•4H2O (>99 %), Mg(NO3)2•6H2O (99 %), CaCl2•6H2O (>99 %), MgCl2•6H2O (>99 %), Ca(HCOO)2 (>99 %), Mg(HCOO)2•2H2O (98 %), Ca(CH3COO)2•H2O (>99 %) and Mg(CH3COO)2•4H2O (99 %).
2.1 H-TDMA experiments
H-TDMA measurements were carried out at the Institute of Chemistry, Chinese Academy of Sciences, and the experimental setup was detailed in previous work (Lei et al., 2014; Peng et al., 2016). Hygroscopic growth of size-selected aerosol particles was determined by measuring their mobility diameters at different RHs. An atomizer (MSP 1500) was used to generate aerosol particles. Solutions used for atomization were prepared using ultrapure water, and their typical concentrations were 0.3–0.4 g L−1. After exiting the atomizer, an aerosol flow (300 mL min−1) was passed through a Nafion dryer and then a diffusion dryer filled with silica gel to reach a final RH of <5 %. The aerosol flow was then delivered through a neutralizer and the first differential mobility analyzer (DMA) to produce quasi-monodisperse aerosol particles with a mobility diameter of 100 nm. After that, the aerosol flow was transferred through a humidification section with a residence time of ∼ 27 s to be humidified to a given RH. The humidification section was made of two Nafion humidifiers (MD-700-12F-1, Perma Pure) connected in series. The RH of the resulting aerosol flow was monitored using a dew-point meter, which had an absolute uncertainty of ±0.8 % in RH measurement as stated by the manufacturer (Michell, UK). After humidification, the size distribution of aerosol particles was measured using a scanning mobility particle sizer (SMPS), which consisted of the second DMA coupled with a condensation particle counter (TSI 3776). For the second DMA, the aerosol flow and the sheath flow were always maintained at the same RH. The flow rate ratios of the aerosol flow to the sheath flow were set to 1:10 for both DMAs.
In our work, the hygroscopic GF is defined as the ratio of measured mobility diameters at a given RH to that at dry conditions:
where d0 and d are the measured mobility diameters at <5 % RH and at a given RH, respectively. In our work the dry mobility diameter selected using the first DMA was always 100 nm, and no shape factors were used to correct the dry particle diameters. Size distributions of all eight types of aerosol particles, measured using the SMPS, were found to be unimode, as illustrated by Fig. S1 (in the Supplement) in which size distributions of Ca(NO3)2 aerosols at 4 %, 50 % and 90 % RH are displayed as an example. The TDMAinv algorithm (Gysel et al., 2009) was applied to the H-TDMA data.
All the experiments were carried out at room temperature (298 ± 1 K), and in each experiment hygroscopic growth of aerosol particles was determined at 12 different RHs, i.e., <5 %, 10 %, 20 %, 30 %, 40 %, 50 %, 60 %, 70 %, 75 %, 80 %, 85 % and 90 %. The absolute uncertainties in RH were estimated to be within ±2 %. Hygroscopic growth of each compound was measured three times. The performance of the H-TDMA setup was routinely checked by measuring the hygroscopic growth of 100 nm (NH4)2SO4 and NaCl aerosol particles. Good agreement between measured hygroscopic growth curves with those predicted using the E-AIM model (Clegg et al., 1998) was always found for (NH4)2SO4 and NaCl aerosols, as detailed in our previous work (Jing et al., 2016; Peng et al., 2016).
2.2 VSA experiments
The VSA (Q5000SA), which measured the mass of a bulk sample as a function of RH under isotherm conditions, was manufactured by TA Instruments (New Castle, DE, USA). These experiments were performed at the Guangzhou Institute of Geochemistry, Chinese Academy of Sciences, and the instrument and experimental method are described elsewhere (Gu et al., 2017a, b; Jia et al., 2018). Experiments could be conducted in a temperature range of 5–85 ∘C with an accuracy of ±0.1 ∘C and a RH range of 0 %–98 % with an absolute accuracy of ±1 %. The mass measurement had a range of 0–100 mg, and its sensitivity was stated to be <0.1 µg. Initial mass of samples used in an experiment was usually in the range of 0.5–1 mg.
Two different types of experiments were carried out. The mass hygroscopic growth was studied in the first type of experiments: after the sample was dried at <1 % RH as a given temperature, RH was increased to 90 % stepwise with an increment of 10 % per step; after that, RH was set to 0 % (the actual RH was measured to be <1 %) to dry the sample again. The second type of experiments were conducted to measure DRH values: the sample was first dried at a given temperature, and RH was increased to a value which was at least 5 % lower than the expected DRH; RH was then increased stepwise with an increment of 1 % until a significant increase in sample mass was observed, and the RH at which the sample mass showed a significant increase was equal to its DRH. The measured relative change in sample mass due to signal noise and baseline drift was <0.5 % in our work; in each experiment when we suspected that the samples were undergoing deliquescence at a certain RH, we did not stop the experiment until the mass increase was >5 % to ensure the occurrence of deliquescence. At each RH the sample was considered to reach equilibrium with the environment when its mass change was <0.1 % within 30 min, and RH was changed to the next value only after the sample mass was stabilized. If the sample mass was increasing steadily but with a very small rate (e.g., <0.1 % in 30 min), the program we used may conclude erroneously that the system had reached the equilibrium; therefore, all the experimental data were inspected to check whether at each RH the sample mass reached the plateau (i.e., the system had reached the equilibrium). The time to reach a new equilibrium varied with compounds and largely depended on the dry sample mass, i.e., a sample with larger dry mass would take longer to reach the equilibrium. Each experiment was repeated at least three times, and the average value and standard deviation were reported.
3.1 Hygroscopicity of nitrates and chlorides
3.1.1 DRH at different temperature
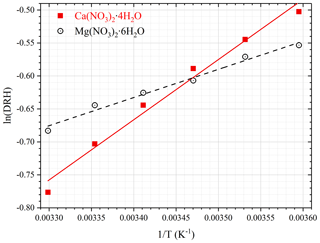
First we investigated the effect of temperature on the DRH of Ca(NO3)2•4H2O, Mg(NO3)2•6H2O and MgCl2•6H2O, which are the most stable forms of corresponding salts for the temperature range (5–30 ∘C) considered in this work (Kelly and Wexler, 2005). Figure 1a shows the change of RH and normalized sample mass as a function of time in an experiment to measure the DRH of Mg(NO3)2•6H2O at 25 ∘C. An abrupt and significant increase in sample mass was observed when RH was increased from 52 % to 53 %, suggesting that the deliquescence occurred between 52 % and 53 % RH. Therefore, its DRH was measured to be 52.5 ± 0.5 %; since RH for our VSA instrument had an absolute uncertainty of ±1 % (as stated in Sect. 2.2), in our work an uncertainty of ±1 %, instead of ±0.5 %, was assigned to the measured DRH. It should be noted that the mass change was >15 % when RH was increased from 52 % to 53 %, as shown in Fig. 1a; such a large mass increase cannot be solely caused by water adsorption since the mass of several monolayers of adsorbed water is estimated to be <1 % of the dry particle mass (Gu et al., 2017b). The continuous but small decrease in sample mass (about 1 % in total) with time (around 500–1000 min) before deliquescence took place, as shown in Fig. 1a, was likely caused by desorption of residual water contained by the sample under investigation.
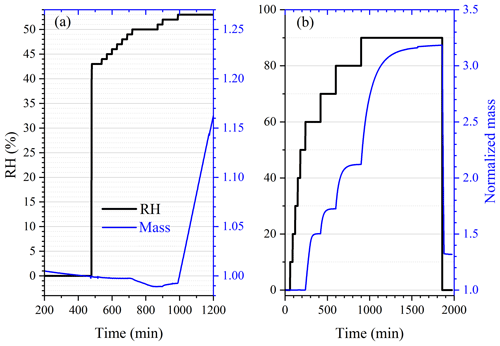
Figure 1Change of normalized sample mass (blue curve, right y axis) and RH (black curve, left y axis) as a function of time. (a) A typical experiment conducted to measure the DRH. (b) A typical experiment conducted to measure mass hygroscopic growth factors. In the two experiments shown here, Mg(NO3)2•6H2O was investigated at 25 ∘C. In this paper the sample mass was always normalized to its dry mass.
Table 1 summarizes our measured DRH of Ca(NO3)2•4H2O, Mg(NO3)2•6H2O and MgCl2•6H2O as a function of temperature (5–30 ∘C). DRH values show a strong dependence on temperature for Ca(NO3)2•4H2O (decreasing from 60.5 % at 5 ∘C to 46.0 % at 30 ∘C) and a weaker temperature dependence for Mg(NO3)2•6H2O (decreasing from 57.5 % at 5 ∘C to 50.5 % at 30 ∘C); in contrast, the DRH values of MgCl2•6H2O (31.5 %–32.5 %) exhibit little variation with temperature (5–30 ∘C). Several previous studies have reported the DRH of Ca(NO3)2•4H2O, Mg(NO3)2•6H2O and MgCl2•6H2O, and their results are compared with our work in the following paragraphs.
Table 1DRH (%) of Ca(NO3)2•4H2O, Mg(NO3)2•6H2O and MgCl2•6H2O measured in this work as a function of temperatures (5–30 ∘C). Solubility data (mol kg water−1) compiled by Kelly and Wexler (2005) were used to calculate solubilities in moles per mole of water. All the errors given in this work are standard deviations. The and ΔHs values were not estimated for MgCl2•6H2O because the difference in its measured DRH between 5 and 30 ∘C was very small or even insignificant. Please refer to Sect. 3.1.1 for further details.
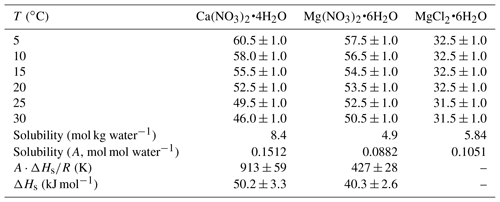
Ca(NO3)2•4H2O
RH of air in equilibrium with saturated Ca(NO3)2•4H2O solutions, i.e., the DRH values of Ca(NO3)2•4H2O, was measured to be 55.9 %, 55.4 %, 50.5 % and 46.7 % at 15, 20, 25 and 30 ∘C (Adams and Merz, 1929), and the absolute differences between DRH reported by Adams and Merz (1929) and those measured in our work are <3 %. The water vapor pressures of saturated Ca(NO3)2•4H2O solutions were measured to be 0.693, 0.920, 1.253, 1.591 and 1.986 kPa at 10, 15, 20, 25 and 30 ∘C (Apelblat, 1992), corresponding to DRH of 56 %, 54 %, 54 %, 50 % and 47 %, respectively; therefore, the absolute difference between DRHs measured in our work and those derived from Apelblat (1992) is <2 %. In another study (Al-Abadleh et al., 2003), RH over the saturated Ca(NO3)2•4H2O solution was measured to be 57 ± 5 % at room temperature; in other words, Al-Abadleh et al. (2003) reported a DRH of 57 ± 5 % for Ca(NO3)2•4H2O, slightly larger than that (49.5 ± 1.0 % at 25 ∘C) determined in our work.
Mg(NO3)2•6H2O
Water vapor pressures of saturated Mg(NO3)2•6H2O solutions were determined to be 0.737, 1.017, 1.390, 1.813 and 2.306 kPa at 10, 15, 20, 25 and 30 ∘C (Apelblat, 1992), giving DRHs of 60 %, 60 %, 59 %, 57 % and 54 % at corresponding temperatures. The vapor pressure of saturated Mg(NO3)2•6H2O solutions at 25 ∘C was reported to be 1.674 and 1.666 kPa by another two studies (Biggs et al., 1955; Robinson and Stokes, 1959), corresponding to DRH of ∼ 53 %. In addition, the water activity of the saturated Mg(NO3)2 solution was measured to be 0.528 at 25 ∘C (Rard et al., 2004), also suggesting a DRH value of ∼ 53 %; similarly, RH over the saturated Mg(NO3)2 solution was reported to be ∼ 53 % at 22–24 ∘C (Li et al., 2008b). Al-Abadleh and Grassian (2003) investigated the phase transition of the Mg(NO3)2•6H2O film, and its DRH was determined to be 49 %–54 % at 23 ∘C. As shown in Table 1, DRHs measured in our work agree very well with those reported by most previous studies (Biggs et al., 1955; Robinson and Stokes, 1959; Al-Abadleh and Grassian, 2003; Rard et al., 2004), but are always 3 %–5 % lower than those derived from Apelblat (1992). It is not clear why DRH values measured by Apelblat (1992) at different temperatures are always slightly higher than other studies.
MgCl2•6H2O
Kelly and Wexler (2005) calculated DRH of MgCl2•6H2O from vapor pressures of saturated MgCl2•6H2O solutions measured by previous work and found that DRH values were in the range of 33 %–34 % for temperatures at 0–40 ∘C. In addition, water activity of the saturated MgCl2 solution was reported to be 0.3278 at 25 ∘C (Rard and Miller, 1981), corresponding to a DRH value of ∼ 33 % for MgCl2•6H2O. The DRH values of MgCl2•6H2O measured in our work, as summarized in Table 1, show excellent agreement with those reported by previous work (Rard and Miller, 1981; Kelly and Wexler, 2005). Phase transition and deliquescence behavior of CaCl2•6H2O were also investigated in our work and found to be very complex, and the result will be discussed in Sect. 3.1.3.
Temperature in the troposphere varies from ∼ 200 to >300 K, and it is thus warranted to explore the effects of temperature on hygroscopic properties of atmospherically relevant particles. The dependence of DRH on temperature can usually be approximated by the Clausius–Clapeyron equation (Wexler and Seinfeld, 1991; Seinfeld and Pandis, 2016; Jia et al., 2018):
where T is temperature (K), DRH(T) and DRH(298) are the DRHs at T and 298 K, R is the gas constant (8.314 J mol−1 K−1), and ΔHs is the enthalpy of dissolution (J mol−1). The dimensionless constant, A, is numerically equal to the water solubility of the salt under investigation in the unit of moles per mole of water. Figure 2 shows the dependence of DRH values on temperature for Ca(NO3)2•4H2O and Mg(NO3)2•6H2O, confirming that Eq. (2) can indeed approximate the temperature dependence. The slope, which is equal to , was determined to be 913 ± 59 K for Ca(NO3)2•4H2O and 427 ± 28 K for Mg(NO3)2•6H2O, and thus ΔHs was derived to be 50.2 ± 3.3 kJ mol−1 for Ca(NO3)2•4H2O and 40.3 ± 2.6 kJ mol−1 for Mg(NO3)2•6H2O. It should be noted that for Eq. (2) to be valid, both the enthalpy of dissolution and the water solubility are assumed to be constant for the temperature range considered. The variation in DRH with temperature (5–30 ∘C) was very small and even insignificant for MgCl2•6H2O; as a result, we did not attempt to estimate the ΔHs value for MgCl2•6H2O since such an estimation would have large errors.
3.1.2 Water-to-solute ratios as a function of RH
The change of sample mass with RH (0 %–90 %) was measured at 5 and 25 ∘C for Ca(NO3)2•4H2O, Mg(NO3)2•6H2O and MgCl2•6H2O, using the VSA. The mass change, relative to that at 0 % RH, can be used to calculate water-to-solute ratios (WSRs, defined in this work as the molar ratio of H2O to Ca2+ or Mg2+) for deliquesced samples. Small increases in m∕m0 (typically <2 %) were observed for some compounds (as shown in Tables 2 and 6) when RH was below corresponding DRH values, mainly due to water adsorption or desorption and baseline drift. As summarized in Table 2, decrease in temperature would lead to increase in WSR at a given RH: at 90 % RH for example, WSRs were determined to be 28.78 ± 0.20 at 25 ∘C and 31.80 ± 0.96 at 5 ∘C for Ca(NO3)2•4H2O, 36.87 ± 0.23 at 25 ∘C and 41.40 ± 1.36 at 5 ∘C for Mg(NO3)2•6H2O, and 36.26 ± 1.76 at 25 ∘C and 39.55 ± 2.43 at 5 ∘C for MgCl2•6H2O. As discussed in Sect. 3.1.1, the enthalpies of dissolution (ΔHs) are negative for these compounds, suggesting that their dissolution processes in water are exothermic; therefore, dissolution is favored at lower temperatures and at a given RH, decrease in temperature would lead to increase in WSR in the aqueous solutions. Several previous studies have measured RH over aqueous Ca(NO3)2, Mg(NO3)2 and MgCl2 solutions at given concentrations, and their results are compared with our work, as discussed below.
Table 2Mass growth factors (m∕m0, defined as the ratio of sample mass at a given RH to that at 0 % RH) and water-to-solute ratios (WSRs) as a function of RH (0 %–90 %) at 25 and 5 ∘C for Ca(NO3)2•4H2O, Mg(NO3)2•6H2O and MgCl2•6H2O. WSRs were only calculated for RH exceeding the DRH (i.e., when the sample was deliquesced). All the errors given in this work are standard deviations.
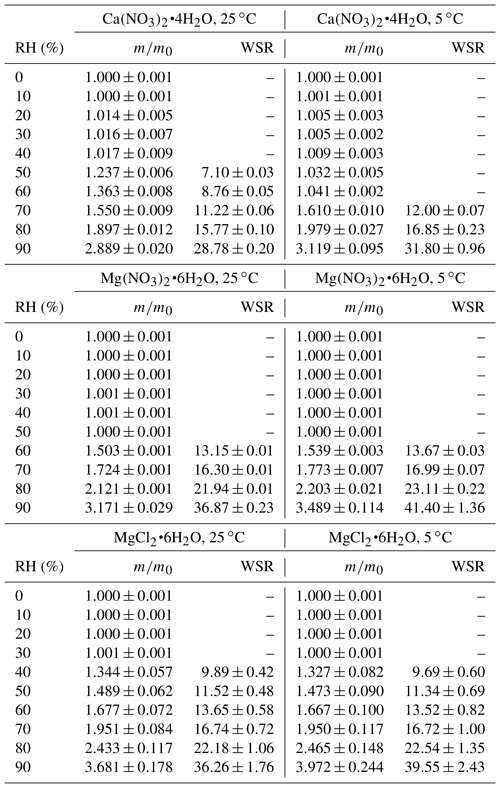
Ca(NO3)2
Water activities of Ca(NO3)2 solutions at 25 ∘C were measured to be 0.904, 0.812 and 0.712 when the concentrations were 2.0, 3.5 and 5.0 mol kg−1, respectively (El Guendouzi and Marouani, 2003). Since water activity of a solution is equal to the RH of air in equilibrium with the solution, it can be derived that the molality concentrations of Ca(NO3)2 solution were 2.0, 3.5 and 5.0 mol kg−1 when RH was 90.4 %, 81.2 % and 71.2 %; in other words, WSRs were found to be 11.1, 15.9 and 27.8 at 71.2 %, 81.2 % and 90.4 % RH, respectively (El Guendouzi and Marouani, 2003). As shown in Table 2, in our work WSRs were determined to be 11.22 ± 0.06, 15.77 ± 0.10 and 28.78 ± 0.20 at 70 %, 80 % and 90 % RH for Ca(NO3)2 solutions at the same temperature, suggesting good agreement with El Guendouzi and Marouani (2003).
Mg(NO3)2
Water activities of Mg(NO3)2 solutions were reported to be 0.897, 0.812 and 0.702 when the concentrations of the bulk solutions were 1.6, 2.5 and 3.5 mol kg−1 at 25 ∘C, respectively (Rard et al., 2004); this means that WSRs were equal to 15.9, 22.2 and 34.7 at 70.2 %, 81.2 % and 89.7 % RH. Ha and Chan (1999) fitted their measured water activities of Mg(NO3)2 as a function of molality concentration at 20–24 ∘C with a polynomial equation, and WSRs were derived to be 12.93, 16.12, 21.50 and 36.09 at 60 %, 70 %, 80 % and 90 % RH. As shown in Table 2, WSRs were measured to be 13.15 ± 0.01, 16.30 ± 0.01, 21.94 ± 0.01 and 36.87 ± 0.23 at 60 %, 70 %, 80 % and 90 % RH for deliquesced Mg(NO3)2 at 25 ∘C. Therefore, it can be concluded that for WSRs of Mg(NO3)2 solutions at ∼ 25 ∘C, our work shows good agreement with the two previous studies (Ha and Chan, 1999; Rard et al., 2004).
MgCl2
Water activities of MgCl2 solutions were reported to be 0.909, 0.800, 0.692, 0.491 and 0.408 when the concentrations were 1.4, 2.4, 3.2, 4.6 and 5.2 mol kg−1 (Rard and Miller, 1981); i.e., WSRs were equal to 10.7, 12.1, 17.4, 23.1 and 39.7 at 40.8 %, 49.1 %, 69.2 %, 80.0 % and 90.9 % RH. In another work (Ha and Chan, 1999), an electrodynamic balance was used to investigate hygroscopic growth of MgCl2 particles at 20–24 ∘C, and the measured molality concentrations of MgCl2 solutions as a function of water activity were fitted by a polynomial equation. It can be derived from Ha and Chen (1999) that WSRs were equal to 10.65, 12.34, 14.29, 17.04, 22.24 and 34.78 when RHs were 40 %, 50 %, 60 %, 70 %, 80 % and 90 %, respectively. WSRs measured in our work, as listed in Table 2, are 9.89 ± 0.42, 11.52 ± 0.48, 1.677 ± 0.072, 16.74 ± 0.72, 22.18 ± 1.06 and 36.26 ± 1.76 at 40 %, 50 %, 60 %, 70 %, 80 % and 90 % RH. As a result, our work agrees well with the two previous studies (Rard and Miller, 1981; Ha and Chan, 1999) for WSRs of MgCl2 solutions as a function of RH at ∼ 25 ∘C.
3.1.3 Phase transition of CaCl2⋅xH2O
The change in sample mass of CaCl2•6H2O with RH was also investigated at 25 ∘C. As shown in Fig. 3, when dried at 0 % RH, the sample mass was reduced by one-third (from ∼ 1.5 to ∼ 1.0), and it is speculated that CaCl2•6H2O was converted to CaCl2•2H2O. When RH was increased to 10 %, no significant increase in sample mass was observed. As RH was further increased to 20 %, the sample mass was increased by 48 ± 7 %; this may indicate that CaCl2•2H2O was converted to CaCl2•6H2O, as the ratio of molar mass of CaCl2•6H2O (219 g mol−1) to CaCl2•2H2O (147 g mol−1) is 1.49, approximately equal to the ratio of sample mass at 20 % RH to that at 10 % RH. Further increase in RH to 30 % would lead to additional increase in sample mass, implying the deliquescence of the sample and the formation of an aqueous CaCl2 solution.
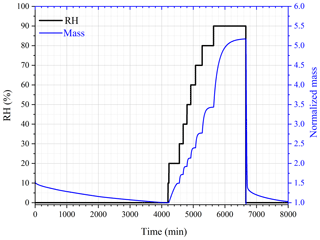
Figure 3Change of normalized sample mass (blue curve, right y axis) and RH (black curve, left y axis) as a function of time for CaCl2•xH2O at 25 ∘C.
Assuming that CaCl2•6H2O was converted to CaCl2•2H2O after being dried at 0 % RH, we could use the change of sample mass as a function of RH to calculate WSR (defined as molar ratio of H2O to Ca2+), and the results are listed in Table 3. Please note that we did not calculate WSR at 20 % RH since it is speculated that the significant mass increase at 20 % RH was caused by the transformation of CaCl2•2H2O to CaCl2•6H2O, as mentioned above. Water activities of aqueous CaCl2 solutions as a function of molality concentration reported in a previous study (Rard et al., 1977) were used to calculate WSR as a function of RH, and the results are also included in Table 3 for comparison. As evident from Table 3, at the same or similar RH, WSRs measured in our work are in good agreement with those derived from Rard et al. (1977), supporting our assertion that CaCl2•6H2O was converted to CaCl2•2H2O after being dried at 0 % RH. In fact, theoretical calculations (Kelly and Wexler, 2005) and experimental measurements (Gough et al., 2016) both suggested that when RH is gradually increased, solid–solid phase transition from CaCl2•2H2O to CaCl2•6H2O would occur before deliquescence takes place.
Table 3Mass growth factors (m∕m0, defined as the ratio of sample mass at a given RH to that at 0 % RH) and water-to-solute ratios (WSRs) as a function of RH (0 %–90 %) at 25 ∘C for CaCl2•xH2O. WSRs derived from RH over aqueous CaCl2 solutions as a function of concentration (mol kg−1) at 25 ∘C (Rard et al., 1977) are also included for comparison. All the errors given in this work are standard deviations.
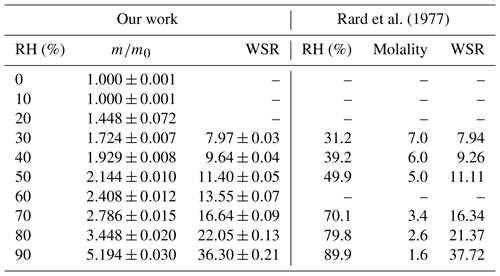
Additional experiments, in which RH was stepwise increased from 0 % with an increment of 1 % per step, were carried out in attempt to measure the DRH of CaCl2•xH2O at 25 ∘C. In all of these experiments, CaCl2•6H2O was always transformed to CaCl2•2H2O after being dried at 0 % RH. In some of these experiments the deliquescence took place at a RH of ∼ 28.5 %, which is consistent with the DRH of CaCl2•6H2O reported in the literature (Kelly and Wexler, 2005), suggesting that CaCl2•2H2O was first transformed to CaCl2•6H2O prior to deliquescence. However, in some other experiments the deliquescence occurred at a RH of ∼ 18.5 %, corresponding to the DRH of CaCl2•2H2O reported previously (Kelly and Wexler, 2005), implying that CaCl2•2H2O was deliquesced without being transformed to CaCl2•6H2O. The dual deliquescence processes, i.e., (1) transformation of CaCl2•2H2O to CaCl2•6H2O prior to deliquescence and (2) direct deliquescence of CaCl2•2H2O, were also observed using Raman spectroscopy at low temperatures (223–273 K) (Gough et al., 2016). It seems that the competition of these two mechanisms is both thermodynamically and kinetically dependent. Since phase transitions of CaCl2 are not only important for atmospheric aerosols but may also play a role in the existence of liquid water in some hyperarid environments (Gough et al., 2016), further investigation is being carried out by combining the VSA technique with vibrational spectroscopy.
3.1.4 Hygroscopic growth of aerosol particles
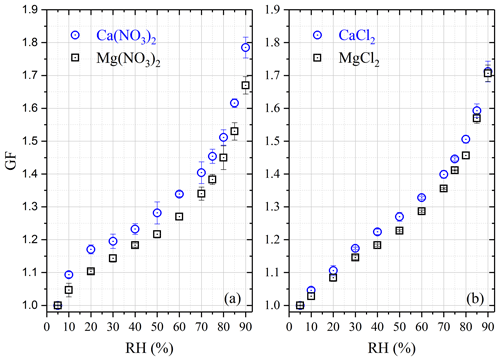
Hygroscopic GFs, which were measured using H-TDMA at room temperature, are displayed in Fig. 4 for Ca(NO3)2, CaCl2, Mg(NO3)2 and MgCl2 aerosols, and the results are also compiled in Table 4. It was found in our work that all four types of aerosols exhibit high hygroscopicity, with GF at 90 % RH being around 1.7 or larger. In addition, all the four types of aerosol particles, instead of having distinct solid–liquid phase transitions, showed significant hygroscopic growth at very low RH (as low as 10 %), and their GFs increased continuously with RH. This phenomenon is due to the fact that these aerosol particles, generated by drying aqueous droplets, were likely to be amorphous. It was also observed in previous work that some types of particles generated by drying aqueous droplets would be amorphous, such as Ca(NO3)2 (Tang and Fung, 1997; Gibson et al., 2006; Jing et al., 2018), Mg(NO3)2 (Zhang et al., 2004; Gibson et al., 2006; Li et al., 2008a), CaCl2 (Park et al., 2009; Tobo et al., 2009) and MgCl2 (Cziczo and Abbatt, 2000; Park et al., 2009).
Ca(NO3)2 and Mg(NO3)2 aerosols
Two previous studies (Gibson et al., 2006; Jing et al., 2018) employed H-TDMA to examine hygroscopic growth of 100 nm Ca(NO3)2 aerosol particles at room temperature. GF were determined to be 1.51 at 80 % RH and ∼ 1.77 at 85 % RH by Gibson et al. (2008). It should be pointed out that though the DMA-selected dry particle diameters were 100 nm for Ca(NO3)2 and Mg(NO3)2 aerosols, the dry diameters used by Gibson et al. (2006) were 89 nm for Ca(NO3)2 and 77 nm for Mg(NO3)2, being extrapolated to 0 % RH using the theoretical growth curve based on the Köhler theory. The Köhler theory is based on assumption of solution ideality and thus may not be applicable to highly concentrated aerosol droplets at low RH (Seinfeld and Pandis, 2016). If the dry diameter selected using the DMA (i.e., 100 nm) was used in GF calculation, GFs reported by Gibson et al. (2006) would be ∼ 1.34 at 80 % RH and ∼ 1.58 at 85 % RH; compared with our results (1.51 ± 0.02 at 80 % RH and 1.62 ± 0.01 at 85 % RH), GF reported by Gibson et al. (2006) are ∼ 11 % smaller at 80 % RH and only ∼ 3 % smaller at 85 %. In the second study (Jing et al., 2018), GFs were determined to be 1.56 at 80 % RH and 1.89 at 90 % RH; compared with our results (1.51 ± 0.02 at 80 % RH and 1.79 ± 0.03 at 90 % RH), GFs reported by Jing et al. (2018) were ∼ 3 % larger at 80 % RH and ∼ 6 % larger at 90 % RH. Overall, our results show reasonably good agreement with the two previous studies (Gibson et al., 2006; Jing et al., 2018).
Table 4Hygroscopic growth factors (GFs) of Ca(NO3)2, CaCl2, Mg(NO3)2 and MgCl2 aerosol particles measured at room temperature using a H-TDMA. The absolute uncertainties in RH were estimated to be within ±2 %. All the errors given in this work are standard deviations.
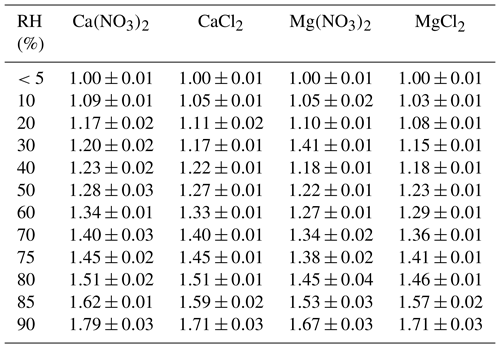
To our knowledge, only one previous study investigated the hygroscopic growth of Mg(NO3)2 aerosol (100 nm) using the H-TDMA (Gibson et al., 2006), and GF was measured to be 1.94 ± 0.02 at 83 % RH. As stated above, the theoretical extrapolated diameter (77 nm) at 0 % RH, instead of the dry diameter (100 nm) selected using the DMA, was used as the dry diameter to calculate their reported GFs (Gibson et al., 2006). If the DMA-selected dry diameter (100 nm) was used in calculation, the GF reported by Gibson et al. (2006) would be ∼ 1.49 at 83 % RH; for comparison, in our work GF were determined to be 1.45 ± 0.04 and 1.53 ± 0.03 at 80 % and 85 % RH, suggesting good agreement between the two studies if the DMA-selected dry diameter was used to calculate GF reported by Gibson et al. (2006).
CaCl2 and MgCl2 aerosols
Hygroscopic growth of CaCl2 and MgCl2 aerosol particles was explored using a H-TDMA (Park et al., 2009), and as far as we know, this was the only study which reported the H-TDMA-measured hygroscopic GFs of the two types of aerosols. Three dry diameters (20, 30 and 50 nm) were used for CaCl2 and MgCl2 aerosol particles (Park et al., 2009), and no significant size dependence of their hygroscopic properties was observed. GFs were measured to be around 1.27, 1.38, 1.48 and 1.59 at 60 %, 75 %, 80 % and 90 % RH for CaCl2 (Park et al., 2009). For comparison, GFs were determined in this work to be 1.33 ± 0.01, 1.45 ± 0.01, 1.51 ± 0.01 and 1.71 ± 0.03 at 60 %, 75 %, 80 % and 90 %, slightly larger than those reported by Park et al. (2009), and the differences were found to be <7 %.
At 50 %, 70 %, 80 %, 85 % and 90 % RH, GFs of MgCl2 aerosol were measured to be about 1.17, 1.29, 1.47, 1.59 and 1.79 by Park et al. (2009); for comparison, GFs were determined to be 1.23 ± 0.01, 1.36 ± 0.01, 1.46 ± 0.01, 1.57 ± 0.02 and 1.71 ± 0.03 in our work at the same RHs. The differences did not exceed 6 % at any given RH, suggesting good agreement between the two studies. Microscopy was used to investigate the hygroscopic growth of micrometer-size MgCl2 particles deposited on substrates (Gupta et al., 2015), and the ratios of 2-D particle areas, relative to that at <5 % RH, were measured to be around 1.65, 1.92, 2.02 and 2.28 at 60 %, 70 %, 75 % and 80 % RH, corresponding to diameter-based GFs of approximately 1.28, 1.38, 1.42 and 1.51, respectively. GFs of MgCl2 aerosol, as shown in Table 4, were determined to be 1.29 ± 0.01, 1.36 ± 0.01, 1.41 ± 0.01 and 1.46 ± 0.01 at 60 %, 70 %, 75 % and 80 % RH in our work; therefore, the differences between GFs reported in our work and those measured by Gupta et al. (2015) were <4 %.
Comparison between hygroscopic growth with CCN activities
GF measured using H-TDMA can be used to calculate the single hygroscopicity parameter, κGF, using Eq. (3a) (Petters and Kreidenweis, 2007; Kreidenweis and Asa-Awuku, 2014; Tang et al., 2016a):
where GF is the growth factor at a given RH; AK is a constant which describes the Kelvin effect and is equal to 2.1 nm for a surface tension of 0.072 J m−2 (pure water) and temperature of 298.15 K (Tang et al., 2016a). For a dry particle diameter (d0) of 100 nm, the denominator in the left term of Eq. (3a) is not larger than 1.02; therefore, the Kelvin effect is negligible and Eq. (3a) can be simplified to Eq. (3b):
Equation (4) can be derived by rearranging Eq. (3b):
In our work, GF data at 90 % RH were used to derive κGF, as usually done in many previous studies (Kreidenweis and Asa-Awuku, 2014). The single hygroscopicity parameter, κCCN, can also be derived from experimental measurements or theoretical calculations of CCN activities (Petters and Kreidenweis, 2007; Kreidenweis and Asa-Awuku, 2014). Ideally aerosol–water interactions under both subsaturation and supersaturation can be described by a constant single hygroscopicity parameter (Petters and Kreidenweis, 2007). Nevertheless, agreement and discrepancies between GF-derived and CCN-activity-derived κ have been reported (Petters and Kreidenweis, 2007; Petters et al., 2009; Wex et al., 2009), and several factors can contribute to such discrepancies. First of all, the solutions may not be ideal, and especially aerosol particles under subsaturation may consist of concentrated solutions; secondly, some of the compounds may have limited solubilities. As discussed previously (Petters and Kreidenweis, 2007; Prenni et al., 2007), both factors would lead to lower κGF, compared to κCCN. The effect of reduced surface tension, compared to pure water, should be negligible for the eight types of aerosol particles considered in our work since none of these compounds are known to be surface-active.
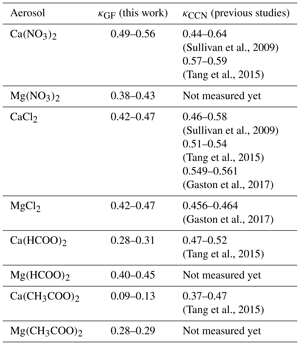
Comparison between κGF determined in our work and κCCN measured in previous studies is summarized in Table 5 and discussed below for Ca(NO3)2, CaCl2, Mg(NO3)2 and MgCl2 aerosols. In previous work which measured CCN activities (Sullivan et al., 2009; Tang et al., 2015; Gaston et al., 2017), the dry particle diameters used were typically in the range of 50–125 nm. The uncertainties in our derived κGF have taken into account the uncertainties in measured GF at 90 % RH.
-
For Ca(NO3)2 aerosol, κCCN values were measured to be 0.44–0.64 by Sullivan et al. (2009) and 0.57–0.59 by Tang et al. (2015); in our work GF at 90 % RH was measured to be 1.79 ± 0.03, giving a κGF of 0.49–0.56, in good agreement with κCCN reported by the two previous studies (Sullivan et al., 2009; Tang et al., 2015).
-
For CaCl2 aerosol, κCCN values were measured to be 0.46–0.58 by Sullivan et al. (2009), 0.51–0.54 by Tang et al. (2015) and 0.549–0.561 by Gaston et al. (2017). GF at 90 % RH was determined to be 1.71 ± 0.03 in the present work, giving a κGF of 0.42–0.47, slightly lower than κCCN values measured previously (Sullivan et al., 2009; Tang et al., 2015; Gaston et al., 2017).
-
In our work, GF was determined to be 1.71 ± 0.03 for MgCl2 at 90 % RH, giving a κGF of 0.42–0.47; a previous study (Gaston et al., 2017) measured the CCN activity of MgCl2 aerosol, and κCCN values were determined to be 0.456–0.464, in good agreement with κGF measured in our work.
-
For Mg(NO3)2 aerosol, GF and κGF were determined in our work to be 1.67 ± 0.03 and 0.38–0.43, respectively. To our knowledge, CCN activities of Mg(NO3)2 aerosol have not been experimentally explored yet, and κCCN values were predicted to be 0.8 for Mg(NO3)2 and 0.3 for Mg(NO3)2•6H2O (Kelly et al., 2007; Kreidenweis and Asa-Awuku, 2014), exhibiting large variation for the same compound with different hydrate states under dry conditions. These calculations were performed using the Köhler theory, assuming solution ideality (Kelly et al., 2007). As Kelly et al. (2007) pointed out, the hydration states, which are not entirely clear for Mg(NO3)2 aerosol particles under atmospherically relevant conditions, can have large impacts on their hygroscopicity and CCN activities.
3.2 Hygroscopicity of formates and acetates
3.2.1 DRH and water-to-solute ratios
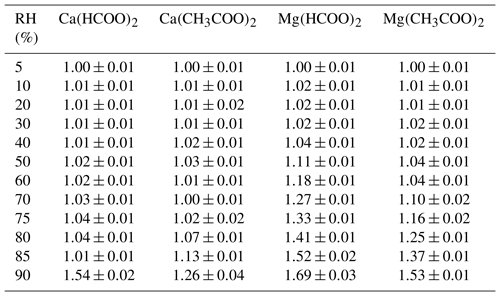
We measured the mass change of Ca(HCOO)2, Mg(HCOO)2•2H2O and Ca(CH3COO)2•H2O samples as a function of RH at 25 ∘C and found that the sample mass remained essentially constant for all three compounds when RH was increased from 0 % to 90 %. Therefore, a series of experiments in which RH was increased to 95 % were conducted, and for each compounds three duplicate experiments were carried out. As shown in Fig. 5a, when RH was increased from 0 % to 95 %, a significant while small increase in sample mass (∼ 10 %) was observed for Ca(HCOO)2. The average ratio of sample mass at 95 % RH to that at 0 % RH was determined to be 1.119 ± 0.036 for Ca(HCOO)2 and 1.064 ± 0.020 for Mg(HCOO)2•2H2O (not shown in Fig. 5), probably indicating that the DRH values were >95 % for both compounds at 25 ∘C.
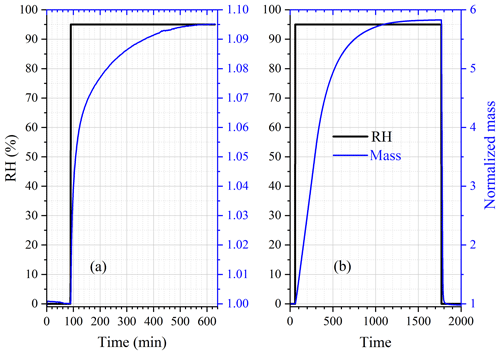
Figure 5Change of normalized sample mass (blue curve, right y axis) and RH (black curve, left y axis) as a function of time at 25 ∘C. (a) Ca(HCOO)2; (b) Ca(CH3COO)2•H2O.
When RH was increased from 0 % to 95 %, a large increase in sample mass (almost by a factor of 6), as shown in Fig. 5b, was observed for Ca(CH3COO)2•H2O. On average, the ratio of sample mass at 95 % RH to that at 0 % RH was measured to be 5.849 ± 0.064, corresponding to a WSR (defined as the molar ratio of H2O to Ca2+) of 48.42 ± 0.53 for the aqueous Ca(CH3COO)2 solution at 95 % RH. This observation suggested that the deliquescence of Ca(CH3COO)2•H2O at 25 ∘C occurred between 90 % and 95 % RH. In further experiments a significant increase in sample mass (by >10 %, and the sample was still increasing sharply when the experiment was terminated) was observed when RH was increased from 90 % to 91 % for Ca(CH3COO)2•H2O at 25 ∘C, suggesting a measured DRH of 90.5 ± 1.0 %. The DRHs of Ca(CH3COO)2 and internally mixed CaCO3∕Ca(CH3COO)2 particles were measured to be 85 % and 88 % at 5 ∘C (Ma et al., 2012), using a modified physisorption analyzer. Since in these two studies DRHs were measured at different temperatures (25 ∘C in our work and 5 ∘C by Ma et al., 2012) and the absolute difference in reported DRH was ∼ 5 %, the agreement in reported DRH can be considered to be quite good for Ca(CH3COO)2.
Table 6 summarizes the ratios of sample mass at a given RH to those at 0 % RH for Mg(CH3COO)2•4H2O as a function of RH at 25 ∘C. Being different from Ca(HCOO)2, Mg(HCOO)2•2H2O and Ca(CH3COO)2•H2O, for Mg(CH3COO)2•4H2O a large increase in sample mass was observed when RH was increased from 70 % to 80 %. This observation suggested that the deliquescence of Mg(CH3COO)2•4H2O occurred between 70 % and 80 % RH. Further experiments were carried out to measure its DRH, and a significant increase in sample mass occurred when RH was increased from 71 % to 72 %, giving a measured DRH of 71.5 ± 1.0 % at 25 ∘C. The RH over the saturated Mg(CH3COO2)2 solution at ∼ 23 ∘C was measured to be 65 % (Wang et al., 2005), slightly lower than the DRH determined in our work.
Table 6Mass growth factors (m∕m0, defined as the ratios of sample mass at a given RH to that at 0 % RH) and water-to-solute ratios (WSRs) as a function of RH (0 %–90 %) at 25 ∘C for Mg(CH3COO)2•4H2O. WSRs are only calculated for RH exceeding the DRH (i.e., when the sample was deliquesced). All the errors given in this work are standard deviations.

The ratios of sample mass, relative to that at 0 % RH, were measured to be 2.029 ± 0.013 and 3.100 ± 0.021 at 80 % and 90 % RH, corresponding to WSRs of 16.24 ± 0.11 at 80 % RH and 28.97 ± 0.20 at 90 % RH for aqueous Mg(CH3COO)2 solutions. A electrodynamic balance coupled to Raman spectroscopy was employed to study the hygroscopic growth of Mg(CH3COO)2 at ∼ 23 ∘C (Wang et al., 2005), and WSR was determined to be ∼ 15.6 at 80 % RH, in good agreement with our work. Ma et al. (2012) found that after heterogeneous reaction with CH3COOH(g) at 50 % RH for 12 h, the hygroscopicity of MgO particles, which was initially rather nonhygroscopic, was substantially increased due to the formation of Mg(CH3COO)2. The conclusion drawn by Ma et al. (2012) is qualitatively consistent with the results obtained in our work.
Table 6 also reveals that a small increase in sample mass (by ∼ 3 %, relative to that at 0 % RH) was observed for Mg(CH3COO)2•4H2O when RH was increased to 70 % before the deliquescence of Mg(CH3COO)2•4H2O took place. This could be due to the possibility that Mg(CH3COO)2•4H2O samples used in our work may contain a small fraction of amorphous Mg(CH3COO)2, which would take up some amount of water at a RH below the DRH of Mg(CH3COO)2•4H2O (Wang et al., 2005; Pang et al., 2015).
3.2.2 Hygroscopic growth of aerosol particles
Figure 6 and Table 7 display hygroscopic GFs of Ca(HCOO)2, Mg(HCOO)2, Ca(CH3COO)2 and Mg(CH3COO)2 aerosols, measured in our work using a H-TDMA. To the best of our knowledge, this is the first time that GFs of these four types of aerosols have been reported. For Mg(HCOO)2, aerosol particles showed gradual while small growth for RH of up to 30 %, and a further increase in RH led to significant growth; the average GF of Mg(HCOO)2 aerosol at 90 % RH was determined to be 1.69 ± 0.03, similar to those for Mg(NO3)2 (1.67 ± 0.03) and MgCl2 (1.71 ± 0.03) at the same RH. For RH up to 85 %, Ca(HCOO)2 aerosol particles exhibited gradual and small growth; when RH was increased to 90 %, abrupt and large growth was observed, with the GF being 1.54 ± 0.02, significantly smaller than that for Mg(HCOO)2 aerosol at the same RH. This is distinctively different from what was observed in VSA experiments, in which the mass of Ca(HCOO)2 and Mg(HCOO)2•2H2O powdered samples was only increased by ∼ 12 % and ∼ 6 % when RH was increased from 0 % to 95 %. This difference may be explained by different states of samples used in these two types of experiments (i.e., crystalline samples in VSA experiments, while likely amorphous aerosol particles in H-TDMA measurements), leading to different hygroscopic behaviors.
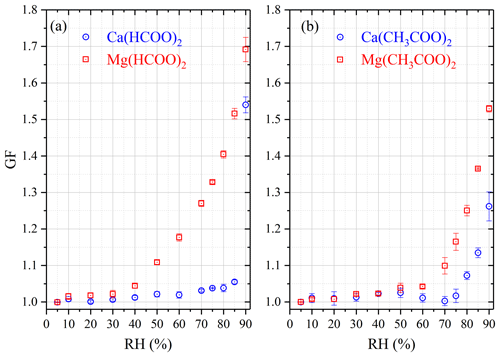
Figure 6Hygroscopic growth factors (GFs) of aerosol particles as a function of RH measured using HTDMA. (a) Ca(HCOO)2 and Mg(HCOO)2; (b) Ca(CH3COO)2 and Mg(CH3COO)2.
As shown in Fig. 6b, gradual and small growth was also observed for Ca(CH3COO)2 and Mg(CH3COO)2 aerosols at low RH. A fast increase in GF started at about 80 % RH for Ca(CH3COO)2 aerosol, and the GF was determined to be 1.26 ± 0.04 at 90 % RH. As discussed in Sect. 3.2.1, in VSA experiments no significant increase in sample mass was observed for Ca(CH3COO)2•H2O when RH was increased from 0 % to 90 %, which is different from H-TDMA results. This difference may again be explained (at least partly) by different states of particles used in these two types of experiments, as mentioned above. Careful inspection of Fig. 6b and Table 7 reveals a small decrease in GF from 1.03 ± 0.01 to 1.00 ± 0.01 for Ca(CH3COO)2 aerosol when RH was increased from 50 % to 70 %. The decrease in GF may be caused by restructuring of particles or change in particle morphology (Vlasenko et al., 2005; Koehler et al., 2009); in addition, the small change in GF (∼ 0.03) may not be significant when compared to the uncertainties in our H-TDMA measurements.
When RH increased from 0 % to 70 %, small and gradual growth occurred for Mg(CH3COO)2 aerosol particles, indicating that these particles may contain some amount of amorphous materials. It was also found in previous work (Li et al., 2008a, b) that Mg(NO3)2 particles generated by drying aqueous droplets were amorphous. Figure 6b reveals that a further increase in RH led to a large increase in GFs, and this is largely consistent with the occurrence of deliquescence at ∼ 71.5 % RH at 25 ∘C for Mg(CH3COO)2•4H2O, as mentioned in Sect. 3.2.1. At 90 % RH, the GF of Mg(CH3COO)2 aerosol was determined to be 1.53 ± 0.01, much larger than that for Ca(CH3COO)2 (1.26 ± 0.04).
At 90 % RH, for the four Ca-containing salts considered in our study and nitrate and chloride aerosols have very similar GFs (1.79 ± 0.03 vs. 1.71 ± 0.03), which are larger than that of formate (1.54 ± 0.02), and acetate has the smallest GF (1.26 ± 0.04). For comparison, the variation in GF at 90 % RH was found to be considerably smaller (from ∼ 1.53 to ∼ 1.71) for the four Mg-containing salts studied herein.
Table 7Hygroscopic growth factors of Ca(HCOO)2, Ca(CH3COO)2, Mg(HCOO)2 and Mg(CH3COO)2 aerosol particles measured using H-TDMA. The absolute uncertainties in RH were estimated to be within ±2 %. All the errors given in this work are standard deviations.
According to Eq. (4), GF measured at 90 % RH can be used to calculate κGF values, which were determined to be 0.28–0.31 for Ca(HCOO)2, 0.09–0.13 for Ca(CH3COO)2, 0.40–0.45 for Mg(HCOO)2 and 0.28–0.29 for Mg(CH3COO)2. A previous study (Tang et al., 2015) investigated the CCN activities of Ca(HCOO)2 and Ca(CH3COO)2 aerosols and reported their single hygroscopicity parameters (κCCN), while the CCN activities of Mg(HCOO)2 and Mg(CH3COO)2 have not been explored yet. As summarized in Table 5, κCCN was reported to be 0.47–0.52 for Ca(HCOO)2 (Tang et al., 2015), significantly larger than κGF (0.28–0.31) determined in our work; for Ca(CH3COO)2, Tang et al. (2015) reported κCCN to be in the range of 0.37–0.47, again much larger than κGF (0.09–0.13) derived from the present work.
As discussed in Sect. 3.1.4, for Ca(NO3)2 and CaCl2 aerosols, κGF values derived from H-TDMA experiments in the present work show fairly good agreement with κCCN derived from CCN activities measured in previous studies (Sullivan et al., 2009; Tang et al., 2015); in contrast, for Ca(HCOO)2 and Ca(CH3COO)2 aerosols, κGF values derived from our H-TDMA experiments are significantly smaller than κCCN reported by the previous study (Tang et al., 2015). This can be largely caused by the difference in water solubilities of Ca(NO3)2, CaCl2, Ca(HCOO)2 and Ca(CH3COO)2. Ca(NO3)2•4H2O and CaCl2•6H2O, with solubilities being 1983 and 1597 g kg−1 of water at 25 ∘C (Kelly and Wexler, 2005), can be considered to be highly soluble; for comparison, the solubilities were reported to be 166 g kg−1 of water for Ca(HCOO)2 at 25 ∘C and 347 g kg−1 of water for Ca(CH3COO)2•2H2O at 20 ∘C (Dean, 1973). Due to their limited water solubilities, Ca(HCOO)2 and Ca(CH3COO)2 aerosol particles may not be fully dissolved at 90 % RH in the H-TDMA experiments but would be dissolved to a larger extent (if not completely) for RH > 100 % in CCN activity measurements (Petters and Kreidenweis, 2008; Kreidenweis and Asa-Awuku, 2014). Therefore, for Ca(HCOO)2 and Ca(CH3COO)2 aerosols, κGF derived from H-TDMA measurements would be smaller than κCCN derived from CCN activity measurements. In fact, the observation that κGF appeared to be significantly smaller than κCCN, largely caused by limited water solubilities of compounds under investigation, has been well documented in the literature for laboratory-generated and ambient aerosol particles (Chang et al., 2007; Prenni et al., 2007; Wex et al., 2009; Good et al., 2010; Massoli et al., 2010).
3.3 Discussion
3.3.1 Comparison between H-TDMA and VSA measurements
In this work two complementary techniques were employed to investigate hygroscopic properties of Ca- and Mg-containing compounds. The mass change of bulk samples was measured as a function of RH using VSA, and the change in aerosol diameter with RH was determined using H-TDMA. Two major questions can be asked regarding the results obtained using the two different techniques. (1) How can the two types of results be reconciled? (2) What is the atmospheric relevance of each type of results? Below we use Ca(NO3)2 at room temperature as an example for discussion, and similar conclusions can be drawn for the other seven compounds.
As presented in Sect. 3.1, at 25 ∘C the deliquescence of Ca(NO3)2•4H2O took place at 52 %–53 % RH. In contrast, dry Ca(NO3)2 aerosol particles generated by atomizing aqueous solutions were likely to be amorphous (Tang and Fung, 1997; Al-Abadleh et al., 2003; Gibson et al., 2006); as a result, they exhibited continuous hygroscopic growth with increasing RH with no distinct solid–liquid phase transitions observed. When RH exceeds the DRH of Ca(NO3)2•4H2O, both Ca(NO3)2•4H2O bulk samples and Ca(NO3)2 aerosol particles are expected to deliquesce to form aqueous solutions. To directly link the mass change (measured using VSA) with diameter change (measured using H-TDMA), solution densities, which also vary with RH, are needed. Two important outputs of common aerosol thermodynamic models, such as E-AIM (Clegg et al., 1998) and ISORROPIA II (Fountoukis and Nenes, 2007) are volumes and WSRs as a function of RH (above DRH) for aqueous solutions. WSRs and particle diameters were both measured in our work at different RHs, and our experimental data, when compared with theoretical calculations, can be used to validate these thermodynamic models.
When RHs are lower than the DRH of Ca(NO3)2•4H2O, aerosol particles used in our H-TDMA experiments, instead of bulk samples used in the VSA measurements, are of direct atmospheric relevance, and hence the H-TDMA results should be used in atmospheric applications. There are still some open questions regarding Ca(NO3)2 aerosol particles (as well as other types of particles investigated in this work) for RH below DRH of Ca(NO3)2•4H2O. What is the phase state of aerosol particles at different RHs? Are they crystalline solid, amorphous solid (glassy) or supersaturated solutions? In this aspect, measurements of particle phase state of Ca(NO3)2 and other aerosols considered in our work, using the apparatus described previously (Li et al., 2017), can shed some light. Furthermore, how do WSRs change with RH for Ca(NO3)2 aerosol particles when RH is below the DRH of Ca(NO3)2•4H2O? This can be answered by determining particle mass as a function of RH for aerosol particles, and techniques are now available for this task (Vlasenko et al., 2017).
3.3.2 Atmospheric implications
Hygroscopicity of carbonate minerals, such as calcite and dolomite, is initially very low and can be largely enhanced due to formation of more hygroscopic materials via heterogeneous reactions during transport (Tang et al., 2016a). Our present work investigated the hygroscopic properties of eight Ca- or Mg-containing compounds which are aging products formed via heterogeneous reactions of carbonate minerals and revealed that the hygroscopicity of these products is significantly higher than original carbonate minerals. In addition, hygroscopicity was found to differ for different aging products, suggesting that heterogeneous reactions with different trace gases may have distinctive effects on the hygroscopicity of carbonate minerals. For example, the hygroscopicity of Ca(NO3)2 and CaCl2, formed through heterogeneous reactions with nitrogen oxides and HCl, is much higher than that for Ca(HCOO)2 and Ca(CH3COO)2, formed via heterogeneous reactions with formic and acidic acids. Our work also observed that significant hygroscopic growth of aerosol particles, such as Ca(NO3)2 and CaCl2, occurred at RHs as low as 10 %. This implies that aged carbonate particles can take up a significant amount of water even under very low RH, leading to changes in their diameters and morphology and thus impacting their optical properties and direct radiative effects (Pan et al., 2015, 2018).
Large amounts of saline mineral dust are emitted into the atmosphere from dry lake beds (Prospero et al., 2002), but these particles are usually assumed to be nonhygroscopic. Gaston et al. (2017) found that saline mineral dust particles from different sources exhibit very different CCN activities, and the measured κCCN varied from <0.01 to >0.8, depending on the abundance of soluble components (e.g., chlorides and sulfates) contained in these particles. Saline mineral dust particles from different sources are very likely to have different hygroscopic properties under subsaturation. To understand the hygroscopic growth of saline mineral dust particles, knowledge of hygroscopic growth as well as the abundance of soluble components they contain is needed. Since CaCl2 and MgCl2 have been identified as important components in saline mineral dust, their hygroscopicity data measured in our work will be useful for improving our knowledge in hygroscopic properties of saline mineral dust.
It is conventionally assumed that the hygroscopicity of sea salt is very similar to that of pure NaCl. However, a recent study (Zieger et al., 2017) suggested that the hygroscopic GF of sea salt aerosol at 90 % RH is 8 %–15 % lower than NaCl aerosol, and this difference is attributed to the presence of MgCl2 and CaCl2 hydrates in sea salt. GFs at 90 % RH were measured in our work to be ∼ 1.7 for MgCl2 and CaCl2 aerosols, significantly lower that for NaCl (2.29–2.46) (Zieger et al., 2017). Therefore, our work provides further experimental results to support the conclusion drawn by Zieger et al. (2017) and would help better understand the hygroscopicity of sea salt aerosol.
Ca- and Mg-containing salts, including nitrates, chlorides, formates and acetates, are important components for mineral dust and sea salt aerosols; however, their hygroscopic properties are not well understood yet. In this work, phase transition and hygroscopic growth of eight Ca- or Mg-containing compounds were systematically examined using a vapor sorption analyzer and a humidity tandem differential mobility analyzer. DRH values decreased from 60.5 ± 1.0 % at 5 ∘C to 46.0 ± 1.0 % at 30 ∘C for Ca(NO3)2•4H2O and from 57.5 ± 1.0 % at 5 ∘C to 50.5 ± 1.0 % at 30 ∘C for Mg(NO3)2•6H2O, both showing negative dependence on temperature, and this dependence can be approximated by the Clausius–Clapeyron equation. No significant dependence of DRH (around 31 %–33 %) on temperature (5 %–30 ∘C) was observed for MgCl2•6H2O. CaCl2•6H2O, found to deliquesce at ∼ 28.5 % RH at 25 ∘C, exhibited complex phase transition processes in which CaCl2•2H2O, CaCl2•6H2O and aqueous CaCl2 solutions were involved. Furthermore, DRH values were determined to be 90.5 ± 1.0 % for Ca(CH3COO)2•H2O and 71.5 ± 1.0 % for Mg(CH3COO)2•4H2O at 25 ∘C; for comparison, the sample mass was only increased by ∼ 12 % for Ca(HCOO)2 and ∼ 6 % for Mg(HCOO)2•2H2O when RH was increased from 0 % to 95 %, implying that the DRHs of these two compounds were probably >95 %.
We have also measured the change of sample mass as a function of RH up to 90 % to derive the water-to-solute ratios (WSRs) for deliquesced samples. WSRs were determined at 25 and 5 ∘C for deliquesced Ca(NO3)2•4H2O, Mg(NO3)2•6H2O and MgCl2•6H2O samples and at 25 ∘C for deliquesced CaCl2•6H2O and Mg(CH3COO)2•4H2O samples. We found that compared to that at 0 % RH, large increases in sample mass only occurred when RH was increased from 90 % to 95 % for Ca(CH3COO)2•H2O, and the WSR value was determined to be 5.849 ± 0.064 at 95 % RH. In addition, deliquescence was not observed even when RH was increased to 95 % for Ca(HCOO)2 and Mg(HCOO)2•2H2O, and the ratios of sample mass at 95 % to that at 0 % RH were determined to be 1.119 ± 0.036 for Ca(HCOO)2 and 1.064 ± 0.020 for Mg(HCOO)2•2H2O. Despite that compounds investigated in the present work are important components for tropospheric aerosols, in general they have not been included in widely used aerosol thermodynamic models, such as E-AIM (Clegg et al., 1998) and ISORROPIA II (Fountoukis and Nenes, 2007). The systematical and comprehensive datasets which we have obtained in this work are highly valuable and can be used to validate thermodynamic models if they are extended to include these compounds.
In addition, hygroscopic growth of aerosol particles was measured at room temperature for these eight compounds. Being different from solid samples for which the onset of deliquescence was evident, aerosol particles were found to grow in a continuous manner from very low RHs (as low as 10 %), implying that these dry aerosol particles generated from aqueous droplets were amorphous. Hygroscopic growth factors of aerosol particles at 90 % RH were determined to be 1.79 ± 0.03 and 1.67 ± 0.03 for Ca(NO3)2 and Mg(NO3)2, 1.71 ± 0.03 for both CaCl2 and MgCl2, 1.54 ± 0.02 and 1.69 ± 0.03 for Ca(HCOO)2 and Mg(HCOO)2, and 1.26 ± 0.04 and 1.53 ± 0.01 for Ca(HCOO)2 and Mg(HCOO)2. GFs at 90 % show significant variation (from ∼ 1.26 to ∼ 1.79) for the Ca-containing salts investigated here; among them nitrate and chloride have very similar GFs (1.79 ± 0.03 vs. 1.71 ± 0.03), which are larger than that of formate (1.54 ± 0.02), while acetate has the smallest GF (1.26 ± 0.04). Interestingly, for the four Mg-containing salts considered in this work, the variation in GF at 90 % RH was found to be much smaller (from ∼ 1.53 to ∼ 1.71).
GFs at 90 % RH were used to derive the single hygroscopicity parameters (κ), which were determined to be 0.49–0.56 and 0.38–0.43 for Ca(NO3)2 and Mg(NO3)2, 0.42–0.47 for both CaCl2 and MgCl2, 0.28–0.31 and 0.40–0.45 for Ca(HCOO)2 and Mg(HCOO)2, and 0.09–0.13 and 0.28–0.29 for Ca(HCOO)2 and Mg(HCOO)2 aerosols, respectively. Ca(NO3)2 and CaCl2 are very soluble in water, and thus their κ values derived from our H-TDMA experiments are consistent with those reported by previous CCN activity measurements (Sullivan et al., 2009; Tang et al., 2015); conversely, due to limited water solubilities, for Ca(HCOO)2 and Ca(CH3COO)2, κ values derived from our H-TDMA experiments are significantly smaller than those derived from CCN activities (Tang et al., 2015). Overall, the present work would significantly improve our knowledge of the hygroscopic properties of Ca- and Mg-containing salts, and thereby help better understand the physicochemical properties of mineral dust and sea salt aerosols.
All the data are available from Mingjin Tang (mingjintang@gig.ac.cn) upon request.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-2115-2019-supplement.
MT designed the research; LG, PC, TZ, QL and GZ performed the H-TDMA experiments and analyzed the results with the assistance and supervision of WW, ZW, MG, MH and XB; WG and YT carried out the VSA experiments and analyzed the data with the supervision of YJL, XW and MT; YJL and MT wrote the paper with contributions from all the other co-authors. LG and WG contributed equally to this work.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Regional transport and transformation of air pollution in eastern China”. It is not associated with a conference.
This work was funded by the National Natural Science Foundation of China
(91744204, 91644106 and 41675120), the Chinese Academy of Sciences
international collaborative project (132744KYSB20160036) and the special
fund of the State Key Joint Laboratory of Environment Simulation and Pollution
Control (17K02ESPCP). Mingjin Tang would also like to thank the CAS Pioneer
Hundred Talents program for providing a starting grant. Yujing Tang
contributed to this work as an undergraduate intern at Guangzhou Institute
of Geochemistry. This is contribution no. IS-2652 from GIGCAS.
Edited by: Hang Su
Reviewed by: three anonymous referees
Adams, J. R. and Merz, A. R.: Hygroscopicity of Fertilizer Materials and Mixtures, Ind. Eng. Chem., 21, 305–307, 1929.
Al-Abadleh, H. A. and Grassian, V. H.: Phase transitions in magnesium nitrate thin films: A transmission FT-IR study of the deliquescence and efflorescence of nitric acid reacted magnesium oxide interfaces, J. Phys. Chem. B, 107, 10829–10839, 2003.
Al-Abadleh, H. A., Krueger, B. J., Ross, J. L., and Grassian, V. H.: Phase transitions in calcium nitrate thin films, Chem. Commun., 2796–2797, 2003.
Apelblat, A.: The vapor pressures of water over saturated solutions of barium chloride, magnesium nitrate, calcium nitrate, potassium carbonate, and zinc sulfate at temperatures from 283 K to 323 K, J. Chem. Thermodyn., 24, 619–626, 1992.
Biggs, A. I., Parton, H. N., and Robinson, R. A.: The Constitution of the Lead Halides in Aqueous Solution, J. Am. Chem. Soc., 77, 5844–5848, 1955.
Chang, R. Y. W., Liu, P. S. K., Leaitch, W. R., and Abbatt, J. P. D.: Comparison between measured and predicted CCN concentrations at Egbert, Ontario: Focus on the organic aerosol fraction at a semi-rural site, Atmos. Environ., 41, 8172–8182, 2007.
Chen, S., Huang, J., Kang, L., Wang, H., Ma, X., He, Y., Yuan, T., Yang, B., Huang, Z., and Zhang, G.: Emission, transport, and radiative effects of mineral dust from the Taklimakan and Gobi deserts: comparison of measurements and model results, Atmos. Chem. Phys., 17, 2401–2421, https://doi.org/10.5194/acp-17-2401-2017, 2017.
Clegg, S. L., Brimblecombe, P., and Wexler, A. S.: Thermodynamic Model of the System H+--Na+---Cl−-H2O at 298.15 K, J. Phys. Chem. A., 102, 2155–2171, 1998.
Creamean, J. M., Suski, K. J., Rosenfeld, D., Cazorla, A., DeMott, P. J., Sullivan, R. C., White, A. B., Ralph, F. M., Minnis, P., Comstock, J. M., Tomlinson, J. M., and Prather, K. A.: Dust and Biological Aerosols from the Sahara and Asia Influence Precipitation in the Western U.S, Science, 339, 1572–1578, 2013.
Crowley, J. N., Ammann, M., Cox, R. A., Hynes, R. G., Jenkin, M. E., Mellouki, A., Rossi, M. J., Troe, J., and Wallington, T. J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Volume V – heterogeneous reactions on solid substrates, Atmos. Chem. Phys., 10, 9059–9223, https://doi.org/10.5194/acp-10-9059-2010, 2010.
Cziczo, D. J. and Abbatt, J. P. D.: Infrared observations of the response of NaCl, MgCl2, NH4HSO4, and NH4NO3 aerosols to changes in relative humidity from 298 to 238 K, J. Phys. Chem. A, 104, 2038–2047, 2000.
Cziczo, D. J., Froyd, K. D., Hoose, C., Jensen, E. J., Diao, M., Zondlo, M. A., Smith, J. B., Twohy, C. H., and Murphy, D. M.: Clarifying the Dominant Sources and Mechanisms of Cirrus Cloud Formation, Science, 340, 1320–1324, 2013.
Dean, J. A.: Lange's Handbook on Chemistry (Eleventh Edition), McGraw-Hill, Inc., New York, 1792 pp., 1973.
El Guendouzi, M. and Marouani, M.: Water activities and osmotic and activity coefficients of aqueous solutions of nitrates at 25 ∘C by the hygrometric method, J. Solution Chem., 32, 535–546, 2003.
Formenti, P., Rajot, J. L., Desboeufs, K., Saïd, F., Grand, N., Chevaillier, S., and Schmechtig, C.: Airborne observations of mineral dust over western Africa in the summer Monsoon season: spatial and vertical variability of physico-chemical and optical properties, Atmos. Chem. Phys., 11, 6387–6410, https://doi.org/10.5194/acp-11-6387-2011, 2011.
Formenti, P., Caquineau, S., Desboeufs, K., Klaver, A., Chevaillier, S., Journet, E., and Rajot, J. L.: Mapping the physico-chemical properties of mineral dust in western Africa: mineralogical composition, Atmos. Chem. Phys., 14, 10663–10686, https://doi.org/10.5194/acp-14-10663-2014, 2014.
Fountoukis, C. and Nenes, A.: ISORROPIA II: a computationally efficient thermodynamic equilibrium model for K+-Ca2+-Mg2+--Na+---Cl−-H2O aerosols, Atmos. Chem. Phys., 7, 4639–4659, https://doi.org/10.5194/acp-7-4639-2007, 2007.
Gaston, C. J., Pratt, K. A., Suski, K. J., May, N. W., Gill, T. E., and Prather, K. A.: Laboratory Studies of the Cloud Droplet Activation Properties and Corresponding Chemistry of Saline Playa Dust, Environ. Sci. Tech., 51, 1348–1356, 2017.
Gibson, E. R., Hudson, P. K., and Grassian, V. H.: Physicochemical properties of nitrate aerosols: Implications for the atmosphere, J. Phys. Chem. A, 110, 11785–11799, 2006.
Ginoux, P., Prospero, J. M., Gill, T. E., Hsu, N. C., and Zhao, M.: Global-scale Attribution of Anthropogenic and Natural Dust Sources and Their Emission Rates Based on MODIS Deep Blue Aerosol Products, Rev. Geophys., 50, RG3005, https://doi.org/10.1029/2012RG000388, 2012.
Good, N., Topping, D. O., Duplissy, J., Gysel, M., Meyer, N. K., Metzger, A., Turner, S. F., Baltensperger, U., Ristovski, Z., Weingartner, E., Coe, H., and McFiggans, G.: Widening the gap between measurement and modelling of secondary organic aerosol properties?, Atmos. Chem. Phys., 10, 2577–2593, https://doi.org/10.5194/acp-10-2577-2010, 2010.
Goodman, A. L., Underwood, G. M., and Grassian, V. H.: A Laboratory Study of the Heterogeneous Reaction of Nitric Acid on Calcium Carbonate Particles, J. Geophys. Res.-Atmos., 105, 29053–29064, 2000.
Gough, R. V., Chevrier, V. F., and Tolbert, M. A.: Formation of liquid water at low temperatures via the deliquescence of calcium chloride: Implications for Antarctica and Mars, Planet. Space Sci., 131, 79–87, 2016.
Gu, W. J., Li, Y. J., Tang, M. J., Jia, X. H., Ding, X., Bi, X. H., and Wang, X. M.: Water uptake and hygroscopicity of perchlorates and implications for the existence of liquid water in some hyperarid environments, RSC Adv., 7, 46866–46873, 2017a.
Gu, W., Li, Y., Zhu, J., Jia, X., Lin, Q., Zhang, G., Ding, X., Song, W., Bi, X., Wang, X., and Tang, M.: Investigation of water adsorption and hygroscopicity of atmospherically relevant particles using a commercial vapor sorption analyzer, Atmos. Meas. Tech., 10, 3821–3832, https://doi.org/10.5194/amt-10-3821-2017, 2017b.
Gupta, D., Eom, H. J., Cho, H. R., and Ro, C. U.: Gupta, D., Eom, H.-J., Cho, H.-R., and Ro, C.-U.: Hygroscopic behavior of NaCl-MgCl2 mixture particles as nascent sea-spray aerosol surrogates and observation of efflorescence during humidification, Atmos. Chem. Phys., 15, 11273–11290, https://doi.org/10.5194/acp-15-11273-2015, 2015.
Gysel, M., McFiggans, G. B., and Coe, H.: Inversion of tandem differential mobility analyser (TDMA) measurements, J. Aerosol. Sci., 40, 134–151, 2009.
Ha, Z. and Chan, C. K.: The Water Activities of MgCl2, Mg(NO3)2, MgSO4, and Their Mixtures, Aerosol Sci. Technol., 31, 154–169, 1999.
Hatch, C. D., Gough, R. V., and Tolbert, M. A.: Heterogeneous uptake of the C1 to C4 organic acids on a swelling clay mineral, Atmos. Chem. Phys., 7, 4445–4458, https://doi.org/10.5194/acp-7-4445-2007, 2007.
Hoose, C. and Möhler, O.: Heterogeneous ice nucleation on atmospheric aerosols: a review of results from laboratory experiments, Atmos. Chem. Phys., 12, 9817–9854, https://doi.org/10.5194/acp-12-9817-2012, 2012.
Jeong, G. Y. and Achterberg, E. P.: Chemistry and mineralogy of clay minerals in Asian and Saharan dusts and the implications for iron supply to the oceans, Atmos. Chem. Phys., 14, 12415–12428, https://doi.org/10.5194/acp-14-12415-2014, 2014.
Jia, X. H., Gu, W. J., Li, Y. J., Cheng, P., Tang, Y. J., Guo, L. Y., Wang, X. M., and Tang, M. J.: Phase transitions and hygroscopic growth of Mg(ClO4)2, NaClO4, and NaClO4•H2O: implications for the stability of aqueous water in hyperarid environments on Mars and on Earth, ACS Earth Space Chem., 2, 159–167, 2018.
Jickells, T. D., An, Z. S., Andersen, K. K., Baker, A. R., Bergametti, G., Brooks, N., Cao, J. J., Boyd, P. W., Duce, R. A., Hunter, K. A., Kawahata, H., Kubilay, N., laRoche, J., Liss, P. S., Mahowald, N., Prospero, J. M., Ridgwell, A. J., Tegen, I., and Torres, R.: Global Iron Connections between Desert Dust, Ocean Biogeochemistry, and Climate, Science, 308, 67–71, 2005.
Jing, B., Tong, S., Liu, Q., Li, K., Wang, W., Zhang, Y., and Ge, M.: Hygroscopic behavior of multicomponent organic aerosols and their internal mixtures with ammonium sulfate, Atmos. Chem. Phys., 16, 4101–4118, https://doi.org/10.5194/acp-16-4101-2016, 2016.
Jing, B., Wang, Z., Tan, F., Guo, Y., Tong, S., Wang, W., Zhang, Y., and Ge, M.: Hygroscopic behavior of atmospheric aerosols containing nitrate salts and water-soluble organic acids, Atmos. Chem. Phys., 18, 5115–5127, https://doi.org/10.5194/acp-18-5115-2018, 2018.
Journet, E., Balkanski, Y., and Harrison, S. P.: A new data set of soil mineralogy for dust-cycle modeling, Atmos. Chem. Phys., 14, 3801–3816, https://doi.org/10.5194/acp-14-3801-2014, 2014.
Kelly, J. T. and Wexler, A. S.: Thermodynamics of carbonates and hydrates related to heterogeneous reactions involving mineral aerosol, J. Geophys. Res.-Atmos, 110, D11201, https://doi.org/10.11029/12004jd005583, 2005.
Kelly, J. T., Chuang, C. C., and Wexler, A. S.: Influence of dust composition on cloud droplet formation, Atmos. Environ., 41, 2904–2916, 2007.
Khare, P., Kumar, N., Kumari, K. M., and Srivastava, S. S.: Atmospheric formic and acetic acids: An overview, Rev. Geophys., 37, 227–248, 1999.
Koehler, K. A., Kreidenweis, S. M., DeMott, P. J., Petters, M. D., Prenni, A. J., and Carrico, C. M.: Hygroscopicity and cloud droplet activation of mineral dust aerosol, Geophys. Res. Lett., 36, L08805, https://doi.org/10.01029/02009gl037348, 2009.
Kreidenweis, S. M. and Asa-Awuku, A.: Aerosol Hygroscopicity: Particle Water Content and Its Role in Atmospheric Processes, in: Treatise on Geochemistry (2 Edn.), edited by: Turekian, K. K., Elsevier, Oxford, 331–361, 2014.
Krueger, B. J., Grassian, V. H., Laskin, A., and Cowin, J. P.: The Transformation of Solid Atmospheric Particles into Liquid Droplets through Heterogeneous Chemistry: Laboratory Insights into the Processing of Calcium Containing Mineral Dust Aerosol in the Troposphere, Geophys. Res. Lett., 30, 1148, https://doi.org/10.1029/2002gl016563, 2003.
Laskin, A., Iedema, M. J., Ichkovich, A., Graber, E. R., Taraniuk, I., and Rudich, Y.: Direct Observation of Completely Processed Calcium Carbonate Dust Particles, Faraday Discuss., 130, 453–468, 2005.
Lei, T., Zuend, A., Wang, W. G., Zhang, Y. H., and Ge, M. F.: Hygroscopicity of organic compounds from biomass burning and their influence on the water uptake of mixed organic ammonium sulfate aerosols, Atmos. Chem. Phys., 14, 11165–11183, https://doi.org/10.5194/acp-14-11165-2014, 2014.
Li, H. J., Zhu, T., Zhao, D. F., Zhang, Z. F., and Chen, Z. M.: Kinetics and mechanisms of heterogeneous reaction of NO2 on CaCO3 surfaces under dry and wet conditions, Atmos. Chem. Phys., 10, 463–474, https://doi.org/10.5194/acp-10-463-2010, 2010.
Li, W. J. and Shao, L. Y.: Observation of nitrate coatings on atmospheric mineral dust particles, Atmos. Chem. Phys., 9, 1863–1871, https://doi.org/10.5194/acp-9-1863-2009, 2009.
Li, X.-H., Zhao, L.-J., Dong, J.-L., Xiao, H.-S., and Zhang, Y.-H.: Confocal Raman Studies of Mg(NO3)2 Aerosol Particles Deposited on a Quartz Substrate, Supersaturated Structures and Complicated Phase Transitions, J. Phys. Chem. B., 112, 5032–5038, 2008a.
Li, X., Dong, J., Xiao, H., Lu, P., Hu, Y., and Zhang, Y.: FTIR-ATR in situ observation on the efflorescence and deliquescence processes of Mg(NO3)2 aerosols, Sci. China-Chem., 51, 128–137, 2008b.
Li, Y. J., Liu, P. F., Bergoend, C., Bateman, A. P., and Martin, S. T.: Rebounding hygroscopic inorganic aerosol particles: Liquids, gels, and hydrates, Aerosol Sci. Tech., 51, 388–396, 2017.
Liu, Y., Gibson, E. R., Cain, J. P., Wang, H., Grassian, V. H., and Laskin, A.: Kinetics of heterogeneous reaction of CaCO3 particles with gaseous HNO3 over a wide range of humidity, J. Phys. Chem. A, 112, 1561–1571, 2008a.
Liu, Y. J., Zhu, T., Zhao, D. F., and Zhang, Z. F.: Investigation of the hygroscopic properties of Ca(NO3)2 and internally mixed Ca(NO3)2∕CaCO3 particles by micro-Raman spectrometry, Atmos. Chem. Phys., 8, 7205–7215, https://doi.org/10.5194/acp-8-7205-2008, 2008b.
Ma, Q. X., Liu, Y. C., Liu, C., and He, H.: Heterogeneous Reaction of Acetic Acid on MgO, α-Al2O3, and CaCO3 and the Effect on the Hygroscopic Behavior of These Particles, Phys. Chem. Chem. Phys., 14, 8403–8409, 2012.
Mahowald, N., Ward, D. S., Kloster, S., Flanner, M. G., Heald, C. L., Heavens, N. G., Hess, P. G., Lamarque, J.-F., and Chuang, P. Y.: Aerosol Impacts on Climate and Biogeochemistry, Annu. Rev. Env. Resour., 36, 45–74, 2011.
Mahowald, N. M., Engelstaedter, S., Luo, C., Sealy, A., Artaxo, P., Benitez-Nelson, C., Bonnet, S., Chen, Y., Chuang, P. Y., Cohen, D. D., Dulac, F., Herut, B., Johansen, A. M., Kubilay, N., Losno, R., Maenhaut, W., Paytan, A., Prospero, J. M., Shank, L. M., and Siefert, R. L.: Atmospheric Iron Deposition: Global Distribution, Variability, and Human Perturbations, Annu. Rev. Mar. Sci., 1, 245–278, 2009.
Massoli, P., Lambe, A. T., Ahern, A. T., Williams, L. R., Ehn, M., Mikkila, J., Canagaratna, M. R., Brune, W. H., Onasch, T. B., Jayne, J. T., Petaja, T., Kulmala, M., Laaksonen, A., Kolb, C. E., Davidovits, P., and Worsnop, D. R.: Relationship between aerosol oxidation level and hygroscopic properties of laboratory generated secondary organic aerosol (SOA) particles, Geophys. Res. Lett., 37, L24801, https://doi.org/10.21029/22010GL045258, 2010.
Nickovic, S., Vukovic, A., Vujadinovic, M., Djurdjevic, V., and Pejanovic, G.: Technical Note: High-resolution mineralogical database of dust-productive soils for atmospheric dust modeling, Atmos. Chem. Phys., 12, 845–855, https://doi.org/10.5194/acp-12-845-2012, 2012.
Pan, X., Uno, I., Hara, Y., Kuribayashi, M., Kobayashi, H., Sugimoto, N., Yamamoto, S., Shimohara, T., and Wang, Z.: Observation of the simultaneous transport of Asian mineral dust aerosols with anthropogenic pollutants using a POPC during a long-lasting dust event in late spring 2014, Geophys. Res. Lett., 42, 1593–1598, 2015.
Pan, X., Uno, I., Wang, Z., Nishizawa, T., Sugimoto, N., Yamamoto, S., Kobayashi, H., Sun, Y., Fu, P., Tang, X., and Wang, Z.: Real-time observational evidence of changing Asian dust morphology with the mixing of heavy anthropogenic pollution, Sci. Rep., 7, 335, https://doi.org/10.1038/s41598-41017-00444-w, 2017.
Pan, X., Ge, B., Wang, Z., Tian, Y., Liu, H., Wei, L., Yue, S., Uno, I., Kobayashi, H., Nishizawa, T., Shimizu, A., Fu, P., and Wang, Z.: Synergistic effect of water-soluble species and relative humidity on morphological changes in aerosol particles in the Beijing megacity during severe pollution episodes, Atmos. Chem. Phys., 19, 219–232, https://doi.org/10.5194/acp-19-219-2019, 2019.
Pang, S. F., Wu, C. Q., Zhang, Q. N., and Zhang, Y. H.: The structural evolution of magnesium acetate complex in aerosols by FTIR-ATR spectra, J. Mol. Struct., 1087, 46–50, 2015.
Park, K., Kim, J. S., and Miller, A. L.: A study on effects of size and structure on hygroscopicity of nanoparticles using a tandem differential mobility analyzer and TEM, J. Nanopart. Res., 11, 175–183, 2009.
Peng, C., Jing, B., Guo, Y. C., Zhang, Y. H., and Ge, M. F.: Hygroscopic Behavior of Multicomponent Aerosols Involving NaCl and Dicarboxylic Acids, J. Phys. Chem. A, 120, 1029–1038, 2016.
Petters, M. D. and Kreidenweis, S. M.: A single parameter representation of hygroscopic growth and cloud condensation nucleus activity, Atmos. Chem. Phys., 7, 1961–1971, https://doi.org/10.5194/acp-7-1961-2007, 2007.
Petters, M. D. and Kreidenweis, S. M.: A single parameter representation of hygroscopic growth and cloud condensation nucleus activity – Part 2: Including solubility, Atmos. Chem. Phys., 8, 6273–6279, https://doi.org/10.5194/acp-8-6273-2008, 2008.
Petters, M. D., Wex, H., Carrico, C. M., Hallbauer, E., Massling, A., McMeeking, G. R., Poulain, L., Wu, Z., Kreidenweis, S. M., and Stratmann, F.: Towards closing the gap between hygroscopic growth and activation for secondary organic aerosol – Part 2: Theoretical approaches, Atmos. Chem. Phys., 9, 3999–4009, https://doi.org/10.5194/acp-9-3999-2009, 2009.
Prenni, A. J., Petters, M. D., Kreidenweis, S. M., DeMott, P. J., and Ziemann, P. J.: Cloud droplet activation of secondary organic aerosol, J. Geophys. Res.-Atmos., 112, D10223, https://doi.org/10.11029/12006JD007963, 2007.
Prince, A. P., Kleiber, P. D., Grassian, V. H., and Young, M. A.: Reactive Uptake of Acetic Acid on Calcite and Nitric Acid Reacted Calcite Aerosol in an Environmental Reaction Chamber, Phys. Chem. Chem. Phys., 10, 142–152, 2008.
Prospero, J. M., Ginoux, P., Torres, O., Nicholson, S. E., and Gill, T. E.: Environmental characterization of global sources of atmospheric soil dust identified with the Nimbus 7 Total Ozone Mapping Spectrometer (TOMS) absorbing aerosol product, Rev. Geophys., 40, 1002, https://doi.org/10.1029/2000RG000095, 2002.
Rard, J. A. and Miller, D. G.: Isopiestic determination of the osmotic and activity coefficients of aqueous magnesium chloride solutions at 25 ∘C, J. Chem. Eng. Data, 26, 38–43, 1981.
Rard, J. A., Habenschuss, A., and Spedding, F. H.: A review of the osmotic coefficients of aqueous calcium chloride at 25 ∘C, J. Chem. Eng. Data, 22, 180–186, 1977.
Rard, J. A., Wijesinghe, A. M., and Wolery, T. J.: Review of the thermodynamic properties of Mg(NO3)2(aq) and their representation with the standard and extended ion-interaction (Pitzer) models at 298.15 K, J. Chem. Eng. Data, 49, 1127–1140, 2004.
Ridley, D. A., Heald, C. L., Kok, J. F., and Zhao, C.: An observationally constrained estimate of global dust aerosol optical depth, Atmos. Chem. Phys., 16, 15097–15117, https://doi.org/10.5194/acp-16-15097-2016, 2016.
Robinson, R. A. and Stokes, R. H.: Electrolyte Solutions (Second Revised Edition), Butterworths, London, UK, 608 pp., 1959.
Romanias, M. N., El Zein, A., and Bedjanian, Y.: Heterogeneous Interaction of H2O2 with TiO2 Surface under Dark and UV Light Irradiation Conditions, J. Phys. Chem. A, 116, 8191–8200, 2012.
Romanias, M. N., Zeineddine, M. N., Gaudion, V., Lun, X., Thevenet, F., and Riffault, V.: Heterogeneous Interaction of Isopropanol with Natural Gobi Dust, Environ. Sci. Tech., 50, 11714–11722, 2016.
Santschi, C. and Rossi, M. J.: Uptake of CO2, SO2, HNO3 and HCl on calcite (CaCO3) at 300 K: Mechanism and the role of adsorbed water, J. Phys. Chem. A, 110, 6789–6802, 2006.
Scanza, R. A., Mahowald, N., Ghan, S., Zender, C. S., Kok, J. F., Liu, X., Zhang, Y., and Albani, S.: Modeling dust as component minerals in the Community Atmosphere Model: development of framework and impact on radiative forcing, Atmos. Chem. Phys., 15, 537–561, https://doi.org/10.5194/acp-15-537-2015, 2015.
Seinfeld, J. H. and Pandis, S. N.: Atmospheric Chemistry and Physics: From Air Pollution to Climate Change (Third edition), Wiley Interscience, New York, 1152 pp., 2016.
Shi, Z., Zhang, D., Hayashi, M., Ogata, H., Ji, H., and Fujiie, W.: Influences of sulfate and nitrate on the hygroscopic behaviour of coarse dust particles, Atmos. Environ., 42, 822–827, 2008.
Sullivan, R. C., Moore, M. J. K., Petters, M. D., Kreidenweis, S. M., Roberts, G. C., and Prather, K. A.: Effect of chemical mixing state on the hygroscopicity and cloud nucleation properties of calcium mineral dust particles, Atmos. Chem. Phys., 9, 3303–3316, https://doi.org/10.5194/acp-9-3303-2009, 2009.
Tan, F., Tong, S., Jing, B., Hou, S., Liu, Q., Li, K., Zhang, Y., and Ge, M.: Heterogeneous reactions of NO2 with CaCO3-(NH4)2SO4 mixtures at different relative humidities, Atmos. Chem. Phys., 16, 8081–8093, https://doi.org/10.5194/acp-16-8081-2016, 2016.
Tang, I. N. and Fung, K. H.: Hydration and Raman scattering studies of levitated microparticles: Ba(NO3)2, Sr(NO3)2, and Ca(NO3)2, J. Chem. Phys., 106, 1653–1660, 1997.
Tang, M. J., Thieser, J., Schuster, G., and Crowley, J. N.: Kinetics and Mechanism of the Heterogeneous Reaction of N2O5 with Mineral Dust Particles, Phys. Chem. Chem. Phys., 14, 8551–8561, 2012.
Tang, M. J., Whitehead, J., Davidson, N. M., Pope, F. D., Alfarra, M. R., McFiggans, G., and Kalberer, M.: Cloud Condensation Nucleation Activities of Calcium Carbonate and its Atmospheric Ageing Products, Phys. Chem. Chem. Phys., 17, 32194–32203, 2015.
Tang, M. J., Cziczo, D. J., and Grassian, V. H.: Interactions of Water with Mineral Dust Aerosol: Water Adsorption, Hygroscopicity, Cloud Condensation and Ice Nucleation, Chem. Rev., 116, 4205–4259, 2016a.
Tang, M. J., Larish, W., Fang, Y., Gankanda, A., and Grassian, V. H.: Heterogeneous Reactions of Acetic Acid with Oxide Surfaces: Effects of Mineralogy and Relative Humidity, J. Phys. Chem. A, 120, 5609–5616, 2016b.
Tang, M., Huang, X., Lu, K., Ge, M., Li, Y., Cheng, P., Zhu, T., Ding, A., Zhang, Y., Gligorovski, S., Song, W., Ding, X., Bi, X., and Wang, X.: Heterogeneous reactions of mineral dust aerosol: implications for tropospheric oxidation capacity, Atmos. Chem. Phys., 17, 11727–11777, https://doi.org/10.5194/acp-17-11727-2017, 2017.
Textor, C., Schulz, M., Guibert, S., Kinne, S., Balkanski, Y., Bauer, S., Berntsen, T., Berglen, T., Boucher, O., Chin, M., Dentener, F., Diehl, T., Easter, R., Feichter, H., Fillmore, D., Ghan, S., Ginoux, P., Gong, S., Grini, A., Hendricks, J., Horowitz, L., Huang, P., Isaksen, I., Iversen, I., Kloster, S., Koch, D., Kirkevåg, A., Kristjansson, J. E., Krol, M., Lauer, A., Lamarque, J. F., Liu, X., Montanaro, V., Myhre, G., Penner, J., Pitari, G., Reddy, S., Seland, Ø., Stier, P., Takemura, T., and Tie, X.: Analysis and quantification of the diversities of aerosol life cycles within AeroCom, Atmos. Chem. Phys., 6, 1777–1813, https://doi.org/10.5194/acp-6-1777-2006, 2006.
Tobo, Y., Zhang, D. Z., Nakata, N., Yamada, M., Ogata, H., Hara, K., and Iwasaka, Y.: Hygroscopic mineral dust particles as influenced by chlorine chemistry in the marine atmosphere, Geophys. Res. Lett., 36, L05817, https://doi.org/10.01029/02008gl036883, 2009.
Tobo, Y., Zhang, D., Matsuki, A., and Iwasaka, Y.: Asian Dust Particles Converted into Aqueous Droplets under Remote Marine Atmospheric Conditions, P. Natl. Acad. Sci. USA, 107, 17905–17910, 2010.
Tong, S. R., Wu, L. Y., Ge, M. F., Wang, W. G., and Pu, Z. F.: Heterogeneous chemistry of monocarboxylic acids on a-Al2O3 at different relative humidities, Atmos. Chem. Phys., 10, 7561–7574, https://doi.org/10.5194/acp-10-7561-2010, 2010.
Uno, I., Eguchi, K., Yumimoto, K., Takemura, T., Shimizu, A., Uematsu, M., Liu, Z., Wang, Z., Hara, Y., and Sugimoto, N.: Asian Dust Transported One Full Circuit around the Globe, Nat. Geosci., 2, 557–560, 2009.
Usher, C. R., Michel, A. E., and Grassian, V. H.: Reactions on Mineral Dust, Chem. Rev., 103, 4883–4939, 2003.
Vlasenko, A., Sjogren, S., Weingartner, E., Gaggeler, H. W., and Ammann, M.: Generation of submicron Arizona test dust aerosol: Chemical and hygroscopic properties, Aerosol Sci. Technol., 39, 452–460, 2005.
Vlasenko, A., Sjogren, S., Weingartner, E., Stemmler, K., Gäggeler, H. W., and Ammann, M.: Effect of humidity on nitric acid uptake to mineral dust aerosol particles, Atmos. Chem. Phys., 6, 2147–2160, https://doi.org/10.5194/acp-6-2147-2006, 2006.
Vlasenko, S. S., Su, H., Pöschl, U., Andreae, M. O., and Mikhailov, E. F.: Tandem configuration of differential mobility and centrifugal particle mass analysers for investigating aerosol hygroscopic properties, Atmos. Meas. Tech., 10, 1269–1280, https://doi.org/10.5194/amt-10-1269-2017, 2017.
Wang, L. Y., Zhang, Y. H., and Zhao, L. J.: Raman spectroscopic studies on single supersaturated droplets of sodium and magnesium acetate, J. Phys. Chem. A, 109, 609–614, 2005.
Wex, H., Petters, M. D., Carrico, C. M., Hallbauer, E., Massling, A., McMeeking, G. R., Poulain, L., Wu, Z., Kreidenweis, S. M., and Stratmann, F.: Towards closing the gap between hygroscopic growth and activation for secondary organic aerosol: Part 1 – Evidence from measurements, Atmos. Chem. Phys., 9, 3987–3997, https://doi.org/10.5194/acp-9-3987-2009, 2009.
Wexler, A. S. and Seinfeld, J. H.: 2nd generation inorganic aerosol model, Atmos. Environ., 25, 2731–2748, 1991.
Zhang, Y. H., Choi, M. Y., and Chan, C. K.: Relating hygroscopic properties of magnesium nitrate to the formation of contact ion pairs, J. Phys. Chem. A, 108, 1712–1718, 2004.
Zhang, Y., Mahowald, N., Scanza, R. A., Journet, E., Desboeufs, K., Albani, S., Kok, J. F., Zhuang, G., Chen, Y., Cohen, D. D., Paytan, A., Patey, M. D., Achterberg, E. P., Engelbrecht, J. P., and Fomba, K. W.: Modeling the global emission, transport and deposition of trace elements associated with mineral dust, Biogeosciences, 12, 5771–5792, https://doi.org/10.5194/bg-12-5771-2015, 2015.
Zieger, P., Vaisanen, O., Corbin, J. C., Partridge, D. G., Bastelberger, S., Mousavi-Fard, M., Rosati, B., Gysel, M., Krieger, U. K., Leck, C., Nenes, A., Riipinen, I., Virtanen, A., and Salter, M. E.: Revising the hygroscopicity of inorganic sea salt particles, Nat. Commun., 8, 15883, https://doi.org/10.11038/ncomms15883, 2017.