the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The role of spring dry zonal advection in summer drought onset over the US Great Plains
Amir Erfanian
Rong Fu
This study addresses the role of the atmospheric moisture budget in determining the onset and development of summer droughts over the North American Great Plains (GP) using two state-of-the-art reanalysis datasets. We identified zonal moisture advection as the main cause of severe tropospheric drying during the extreme droughts in the southern GP in 2011 and northern GP in 2012. For both events, the eastward advection of anomalously dry and warm air in the free troposphere in spring set the stage for summer drought. This led to a sharp drop in relative humidity above the boundary layer, enhancing dry entrainment and suppressing deep convection. Further breakdown of the zonal advection into dynamic (caused by circulation anomalies) and thermodynamic (caused by moisture anomalies) contributions reveals dominance of thermodynamic advection in the tropospheric drying observed during the onset of both 2011 and 2012 droughts. The dependence of thermodynamic advection on the moisture gradient links springtime precipitation in the Rockies and southwestern US, the source region of the anomalous dry advection, to the GP summer precipitation (with correlations > 0.4 using gauge-based data). Identifying this previously overlooked precursor of the GP summer droughts improves our predictive understanding of drought onset mechanisms over the region.
- Article
(12897 KB) -
Supplement
(3498 KB) - BibTeX
- EndNote
The United States (US) Great Plains (GP) are prone to devastating droughts such as the infamous Dust Bowl of the 1930s (e.g., Brönnimann et al., 2009; Donat et al., 2016), the extended drought in the 1950s (e.g., Cook et al., 2011), the Texas drought of 2011 (e.g., Fernando et al., 2016), and the record-breaking drought of 2012 (e.g., Hoerling et al., 2013). Projections of the global climate models (GCMs) that participated in the Coupled Model Intercomparison Project Phase 5 (CMIP5) show a robust intensification of dry conditions over the GP under different global warming scenarios in the coming decades (Cook et al., 2015; Teng et al., 2016), which would damage agricultural and food industries throughout the region. The current dynamic prediction models have virtually zero prediction skill over the GP in summer (Quan et al., 2012; Hoerling et al., 2014). Improvement in our predictive understanding of drought onset and evolution mechanisms would provide the scientific foundation for more accurate and timely prediction of droughts over the region.
The GP drought and its underlying mechanisms have been studied extensively. Numerous studies have shown that, in the early stages of the GP droughts, the upper-level atmosphere features an anomalous high and anticyclonic vorticity over central North America (Chang and Wallace, 1987; Namias, 1991; Lyon and Dole, 1995; Cook et al., 2011; Donat et al., 2016; Fernando et al., 2016). A dynamical teleconnection between the height anomalies over the US and the North Pacific sea surface temperature (SST) anomalies has been considered as the main driver responsible for the onset of GP summer droughts in 1980 and 1988 (Trenberth et al., 1988; Lyon and Dole, 1995; Chen and Newman, 1998). Variability of Pacific and Atlantic SSTs has been considered an important driver of droughts in North America, with warm SST anomalies in the tropical Atlantic and cold SST anomalies in the tropical and eastern North Pacific favoring summer droughts over the GP (Namias, 1991; McCabe et al., 2004; Schubert et al., 2004; Kushnir et al., 2010; Wang et al., 2010; Feng et al., 2011; Zhao et al., 2017). However, the role of SST as a main driver of GP precipitation variability has been challenged by numerous studies arguing that atmospheric internal variability and land–atmosphere feedbacks are the dominant drivers of GP summer drought for both short- (Hoerling et al., 2013; Wang et al., 2014; Fernando et al., 2016; Pu et al., 2016) and long-term (Schubert et al., 2004; Ferguson et al., 2010) timescales. Despite the extensive research, it is still unclear whether SST anomalies in winter and spring significantly influence summer GP droughts. If so, what are the underlying physical mechanisms? This question is central to determining the predictability of GP summer droughts. As a first step, we need to understand the main cause of moisture deficits that initiate summer droughts in the GP. To our knowledge, a systematic moisture budget analysis to determine such causes has not been previously reported.
Moisture budget analysis has been attempted in the past to understand local and large-scale sources of moisture (Rasmusson, 1968; Yanai et al., 1973). The climatology, seasonal, and diurnal cycles of moisture budget terms have been analyzed over the US (Rasmusson, 1968) and over the US GP (Hao, 1987; Zangvil et al., 1993, 2001; Schubert et al., 1998; Lamb et al., 2012). For the southern GP (SGP), Lamb et al. (2012) calculated the vertically integrated moisture flux convergence (MFC) terms using the North American Regional Reanalysis in May–June for four selected years (1998, 2002, 2006, and 2007) and identified the horizontal advection and divergence terms, respectively, responsible for the moisture transport to and from the SGP. For the 1980 drought, Hao (1987) compared the vertically integrated horizontal advection and divergence terms of the 1980 and 1979 summers (calculated from radiosonde data over the SGP) and indicated that the horizontal divergence was the dominant contributor to the extreme drying in the summer of 1980. Schubert et al. (1998) identified the GP low-level jets (LLJ) as the dominant contributor to the summer mean moisture influx to the US interior and indicated a strong link between subseasonal variability of moisture influx from the Gulf of Mexico and warm-season precipitation over the central and eastern US. While these studies provide very useful information about the atmospheric moisture sinks and sources over the GP, they only focused on the warm-season vertically integrated budget terms in a few selected years/periods in their analysis. In order to understand the processes and feedbacks underlying GP droughts, the vertical structure of individual moisture tendencies, their seasonal evolution and year-to-year variability, and the relative importance of the moisture transport and evapotranspiration (ET) anomalies on precipitation variability must be investigated especially during the onset season (March, April, May).
In this paper, we provide a detailed examination of the atmospheric moisture budget terms using two state-of-the-art reanalysis datasets over the entire period of 1980–2018 (see Sect. 2 for details). Our diagnostic analyses present a comprehensive picture of GP tropospheric moisture sinks/sources by investigating the diurnal cycle and vertical structure of moisture budget terms and their temporal evolution before and during extreme droughts. A unique contribution of our study is the determination of physical processes that control the variability of moisture tendencies over the GP. This was achieved by separating the moisture transport anomalies into their thermodynamic and dynamic contributions, identifying the regional and remote drivers that modulate variability of these contributions, and measuring the relative importance of the individual terms in the onset and development of GP droughts. In the rest of the paper, we provide a detailed explanation of the implemented methods in Sect. 2, present the results in Sect. 3, provide a discussion of the results in Sect. 4, and summarize our main conclusions in Sect. 5.
2.1 Moisture budget
The conservation of water vapor () in pressure (p) coordinates can be written as Eq. (1) (Yanai et al., 1973; Trenberth and Guillemot, 1995):
where t, q, and p stand for time, specific humidity, and pressure respectively; v and ω are the horizontal wind vector and vertical wind velocity in pressure coordinates; e and c are the evaporation and condensation rates of the air parcel per unit mass, respectively.
Assuming a negligible contribution from the moisture tendency term (the first term in Eq. 1) for monthly and longer time averages (Trenberth and Guillemot, 1995), vertical integration of Eq. (1) from Pt=0 to Ps results in
where P and E are precipitation and evapotranspiration rates at the surface (in units of m s−1) and g and ρw stand for gravitational acceleration of the Earth and water density at the surface, respectively. The left side of Eq. (2) represents the negative of total moisture divergence flux, referred to as total moisture flux convergence (MFC) hereafter. Decomposing an arbitrary variable A into a stationary () and a transient term () (), and applying the covariance equation (), we can write Eq. (2) as the following:
where u and v are the zonal and meridional components of the horizontal wind, v. The first, second, and third terms on the left-hand side (LHS) represent the zonal, meridional, and vertical mean advections, respectively (“mean advection” for the stationary terms is abbreviated to “advection” hereafter); and the last term in the LHS refers to the eddy transient terms of the zonal, meridional, and vertical winds. In our analysis, the stationary and transient terms refer to the monthly mean and 6-hourly departure from the monthly mean (see Sect. 2.3 and 2.4 for more information on the temporal and spatial resolution of the input data and numerical calculations).
2.2 Thermodynamic versus dynamic contribution
Breaking up each term in Eq. (3) to a climatological mean and a monthly departure from climatology (e.g., ), Eq. 3 can be rewritten as (Chou and Lan, 2012; Li et al., 2016; Peng and Zhou, 2017):
where the anomalous precipitation (P′) is balanced by the anomalous advection, evaporation (E′), and residual (ε) which accounts for the submonthly transient eddy contribution. The transient advection terms in Eq. (4) can be further separated as
The first term in the right-hand side (RHS) of Eq. (5) is referred to as the thermodynamic contribution of the zonal advection which accounts for changes in humidity when setting the circulation to climatological wind, the second term in the RHS is referred to as the dynamic contribution which accounts for changes in wind given the climatological humidity, and the third term in RHS is the nonlinear term which accounts for the interannual anomalies of both wind and humidity (Seager et al., 2010; Chou and Lan, 2012; Li et al., 2016; Peng and Zhou, 2017). Separating all the advection terms into thermodynamic and dynamic contributions, Eq. (4) can be rewritten as the following:
2.3 Data
The moisture budget analysis in this study is based on the European Centre for Medium-Range Weather Forecasts (ECMWF) interim reanalysis (ERA-Interim) (Dee et al., 2011) which covers 6-hourly upper air parameters from 1979 to near-real time. The atmospheric model has 60 levels in a hybrid sigma-pressure vertical coordinate system and a T255 spectral horizontal resolution (∼79 km). The data are available online (http://apps.ecmwf.int/datasets/data/interim-full-daily/levtype=sfc/, last access: 3 November 2018). In addition to ERA-Interim, we also used the Modern-Era Retrospective Analysis for Research and Applications version 2 (MERRA2) (Gelaro et al., 2017) and repeated the moisture budget analysis to ensure that our conclusions were not sensitive to the choice of reanalysis product. MERRA2 is the latest atmospheric reanalysis of the National Aeronautics and Space Administration (NASA) Global Modeling and Assimilation Office (GMAO) covering the 1980 to near-present time period and is available online at the NASA GMAO website (https://gmao.gsfc.nasa.gov/reanalysis/MERRA-2/, last access: 6 September 2018). Their atmospheric model uses a cubed-sphere horizontal grid with a 0.5∘ × 0.625∘ resolution and a hybrid-eta vertical coordinate system with 72 model levels from the surface to 0.01 mbar.
For observed precipitation we used the National Centers for Environmental Prediction (NCEP) Climate Prediction Center (CPC) unified gauge-based analysis of daily precipitation over the continental US with a 0.25∘ × 0.25∘ resolution. The data are available from 1948 to present, provided by National Oceanic and Atmospheric Administration (NOAA) Earth System Research Laboratory (ESRL), Physical Sciences Division (PSD), Boulder, Colorado, USA, at https://www.esrl.noaa.gov/psd/ (last access: 17 July 2018).
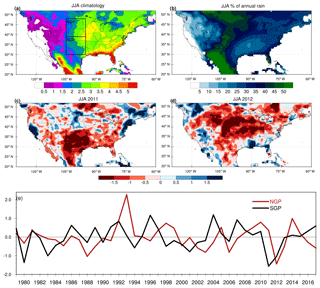
Figure 1Spatial maps of JJA precipitation (a) climatology (mm d−1), (b) JJA's percentage of the annual rain rate, and standardized anomalies (dimensionless) for the extreme droughts of (c) 2011 and (d) 2012. Monthly time series of the standardized anomalies of JJA precipitation are also shown (e) for the southern GP and northern GP regions (denoted by the boxes in a). The climatology and standardized anomalies were calculated using the CPC precipitation over the 1979–2018 period.
2.4 Computation
The moisture budget terms in Eq. (3) were calculated using the 6-hourly ERA-Interim reanalysis on a regular 0.75∘ grid and 14 selected pressure levels. The horizontal and vertical gradients were calculated using a centered finite-difference approach. The vertical integrals were performed by integrating the product of the moisture tendencies in each layer multiplied by the pressure thickness of each layer (dP) from surface to the 50 mbar level. The calculations were performed at 14 pressure levels (spanning 1000 to 50 mbar) where the lowest 6 levels (from 1000 to 850 mbar), which contain most of the atmospheric moisture, had a 25 mbar resolution and the thickness of the remaining levels grew to 50 mbar for the midtroposphere and 100 mbar for the upper troposphere. The vertically integrated moisture tendencies were divided by gρw and multiplied by a scale factor () to convert meters per second (m s−1) to millimeters per day (mm d−1). To determine the impacts of daytime and nocturnal anomalous circulation, we have separately computed daytime and nighttime composites. The daytime composites for the North American domain were calculated by averaging the reanalysis outputs at 18:00 and 00:00 Coordinated Universal Time (UTC), and the nighttime composites were obtained by averaging the reanalysis outputs at 06:00 and 12:00 UTC. More information on the benefits and limitations of the diagnostic computation of the atmospheric moisture budget with reanalysis is provided by Trenberth and Guillemot (1995) and Seager and Henderson (2013), including the impacts of several sources of errors, i.e., temporal, horizontal, and vertical resolution; numerical calculation of gradients and vertical integration; and reanalysis initialization.
2.5 Significance of correlation coefficients
There are 39 annual samples during our analysis period of 1979–2018. Accounting for the effective sample size by using the Livezey et al. (1983) method for a lag-1 autocorrelation of 0.2 for two time series ( and r1r2=0.04) (which is a conservative estimate for the annual time series of standardized anomalies of P, q, and zonal moisture advection) results in significance levels of 7.1 % and 1.4 % for the correlation coefficients of 0.3 and 0.4, respectively, using a two-tailed Student t distribution with N−2 degrees of freedom.
3.1 The Great Plains summer drought
The US GP, located east of the Rocky Mountains and west of the Mississippi River, are characterized by a semiarid climate with a land surface covered primarily by farmlands and temperate grasslands. On average, the region has an annual precipitation of 1–2 mm d−1, approximately half of which occurs during the boreal summer (Fig. 1b). The climatology of observed summer precipitation during 1979–2018 features a zonally asymmetric pattern with JJA precipitation less than 1 mm d−1 over the Rockies and US southwest, between 1 and 3 mm d−1 over the central plains, and greater than 3 mm d−1 over the US Midwest and eastern US (Fig. 1a). The GP have been subject to recurrent severe droughts and heat waves with two extreme droughts in 2011 and 2012 occurring during the most recent decade (Fig. 1e and also Cook et al., 2011; Hoerling et al., 2013; Fernando et al., 2016). Summer droughts over the region usually develop in the previous spring and peak in mid- to late summer. As indicated by the maps of JJA standardized precipitation anomalies (Fig. 1c and d), the drought of 2011 was confined to the SGP, especially Texas, while the 2012 event covered nearly the entire US GP with the drought epicenter over the northern GP (NGP). The temporal evolution of the 2011 drought shows a steady decline of precipitation and ET starting in February, extending throughout the spring and peaking during summer (−2 mm d−1) in both MERRA2 and ERA-Interim reanalysis data (Fig. 2a and b). The dry anomalies started recovering in the fall and the drought finally ended in late fall/early winter. Similarly, the NGP 2012 drought developed (somewhat rapidly) in spring as noted by a sharp decline in precipitation in March followed by a normal April and a large drop in precipitation and ET in May (Fig. 2c and d). The negative precipitation and ET anomalies extended through the 2012 summer and early fall with a gradual recovery of drought conditions closer to winter. As shown in Fig. 2, the amplitude of the anomalies and their temporal evolution is consistent between the two reanalysis datasets.
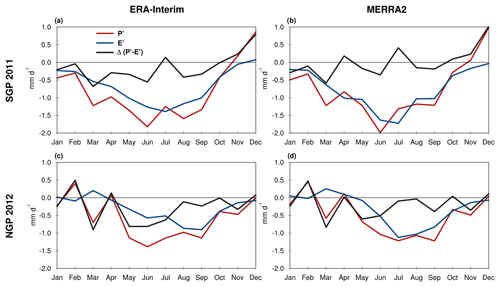
Figure 2Annual cycle of precipitation (red), evapotranspiration (blue), and P−E (black) anomalies (mm d−1) averaged over the SGP in 2011 (a, b) and the NGP in 2012 (c, d) using ERA-Interim (a, c: 1979–2018) and MERRA2 (b, d: 1980–2018) reanalysis.
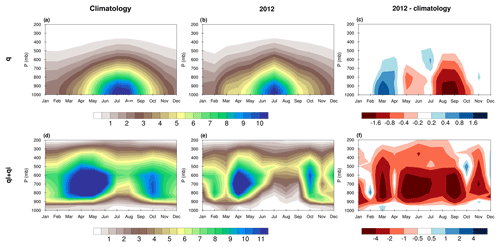
The atmospheric profiles of specific humidity (q) and cloud liquid and ice water content during the 2011 SGP and 2012 NGP droughts are compared against the 1979–2018 climatology in Figs. 3 and 4 (see Figs. S1 and S2 in the Supplement for relative humidity (RH) and fraction of cloud cover (FCC)). The q climatology for both the SGP and NGP indicates that the largest annual values occurred during summer, where the maximum humidity (larger than 10 g kg−1) was confined to the lower troposphere (1000–800 mbar) and gradually decreased to ∼5 and ∼3 g kg−1 in the mid- and upper troposphere (Figs. 3a and 4a). The climatological value of specific humidity at all levels starts decreasing in fall, with the lowest annual values (< 3 g kg−1) occurring during winter. The annual average values of the specific cloud ice and water content peak in fall and spring and reach the minimum values during summer over both the SGP and NGP, respectively (Figs. 3d and 4d). Over the NGP, annual minimum values also occur in winter (Fig. 4d). The springtime peak of specific cloud liquid and ice water is much greater than the peak values in fall, with the largest values (> 10 g kg−1) confined to the low- and midtroposphere (850–500 mbar) in the NGP and the lower free troposphere (850–650 mbar) in the SGP.
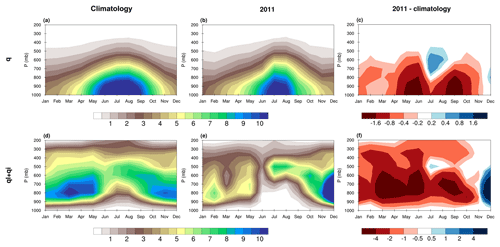
Figure 3Hovmöller diagram of the vertical profile of the ERA-Interim specific humidity (q) (a, b, c) and specific cloud liquid (ql) and ice (qi) water (d, e, f) averaged over the US southern Great Plains (30–39∘ N and 95–105∘ W) for the 1979–2018 climatology (a, d), 2011 (b, e), and the difference between the climatology and 2011 (c, f). The unit for q, ql, and qi is grams per kilogram (g kg−1).
The specific humidity and cloud liquid and ice water in both dry years were generally much smaller than their climatological values. However, the two variables reveal distinct temporal evolutions and vertical structures. As shown in Figs. 3c and 4c, large negative anomalies of q extending from the surface to the midtroposphere persisted year-round for the SGP 2011 event. The maximum dry anomalies of q were located in the near-surface levels and peaked during the May–June and August–September periods, indicating intensive drying of the boundary layer air during the drought peak. The dry anomalies in summer were preceded by an extended drier lower troposphere in the spring season. For the 2012 NGP event, however, the springtime anomalies of q remained reasonably wet during March–April before the drought intensified rapidly in May. The q anomalies remained negative during the entire summer and fall of 2012, with the largest negative anomalies occurring near the surface in August and September. Figure 4f shows that the negative anomalies of cloud liquid and ice water content over the NGP developed in winter and persisted throughout the year in 2012. The negative anomalies of cloud liquid and ice water content started 4 months before the negative q anomalies, highlighting the impact of warmer temperatures during the winter and spring of 2012, which reduced relative humidity (Fig. S2c), and consequently cloud liquid and ice water (Fig. 4f) and fractional coverage (Fig. S2f), and depleted soil moisture (Sun et al., 2015; Mo et al., 2016).
For both the 2012 NGP and 2011 SGP drought years, the cloud liquid and ice water content of dry years were much lower throughout the depth of the troposphere and over the course of the year, with the largest decline (∼40 %) occurring in the lower- and midtropospheric levels in spring and early summer (Figs. 3f and 4f). The drying of the low- and midtroposphere was linked to a sharp drop of mid- and upper-troposphere RH in spring as shown in Figs. S1c and S2c. A sharp decline of free-tropospheric RH intensifies the entrainment of dry air into the rising moist air above the boundary layer limiting the convective penetration depth and shifting the convection structure from predominantly deep convection to frequent shallow cumulus clouds (Derbyshire et al., 2004; Zhang et al., 2010; Del Genio, 2012). The FCC difference fields during the spring and early summer of both 2011 over the SGP and 2012 over the NGP indicate large negative anomalies extending from above the planetary boundary layer (PBL) to the upper troposphere, suggesting a strong suppression of deep convection during the onset season (Figs. S1f and S2f).
3.2 Moisture budget analysis
Summer in the GP is the warmest season of the year with the highest rate of seasonal evapotranspiration (ET). Despite its highest share of annual rain, JJA precipitation minus evapotranspiration (P−E) is negative, with the maximum deficit (greater than 3 mm d−1) over the GP and US Midwest. Such a P−E deficit is balanced by the atmospheric moisture flux convergence over monthly and seasonal timescales (see Sect. 2.1). Using ERA-Interim 6-hourly data over 1979–2018, we calculated the individual moisture tendencies in Eq. (3) and compared the sum of vertically integrated terms with the ERA-Interim-reported vertically averaged moisture convergence () to evaluate the accuracy of our numerical calculations. The spatial patterns of the JJA climatology of the MFC are very similar between our calculated values and those reported by ERA-Interim, for example, over the Intertropical Convergence Zone (ITCZ) between the Equator and 15∘ N and over the regions of subtropical anticyclones (Fig. 5a and b). Over land, the JJA climatology in the ERA-Interim MFC and that of the numerically calculated MFC from the 6-hourly atmospheric fields indicate near-zero differences over much of Alaska, western Canada, and the central and eastern US, except for over the complex terrain of the western US and northwestern Atlantic (Fig. 5d), where a relatively larger difference (between 0.5 and 1.5 mm d−1) occurs. These differences originate from multiple sources including the vertical resolution (14 pressure levels in our calculation versus the 60 model levels in ERA-Interim) and numerical calculation of the divergence and gradient terms (see Trenberth et al., 2011, and Seager and Henderson, 2013, for more details). Overall, our numerically calculated MFC maintains a desirable accuracy in comparison to the ERA-Interim MFC. The difference fields between MFC and P−E reveal moisture budget imbalances as large as 1.5 mm d−1 over the US central plains in JJA for both calculations of MFC (Fig. 5e and f). The imbalance is partially due to the (neglected) atmospheric moisture storage and in part due to the unclosed moisture budget in the reanalysis (Trenberth et al., 2011; Seager and Henderson, 2013).
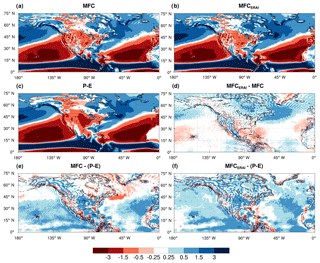
Figure 5JJA climatology (1979–2018) of the vertically integrated MFC (mm d−1) calculated diagnostically from the 6-hourly ERA-Interim output (a) and the monthly-mean MFC reported by ERA-Interim (b). JJA climatology of P−E (mm d−1) has been also calculated from the ERA-Interim monthly outputs over the same period (c). The difference between the ERA-Interim-reported and the calculated MFCs (d) represents the bias introduced by the numerical calculation of the budget terms in our analysis. The moisture budget imbalance is represented by subtracting the P−E climatology from those of the calculated MFC (e) and the ERA-Interim-reported MFC (f).
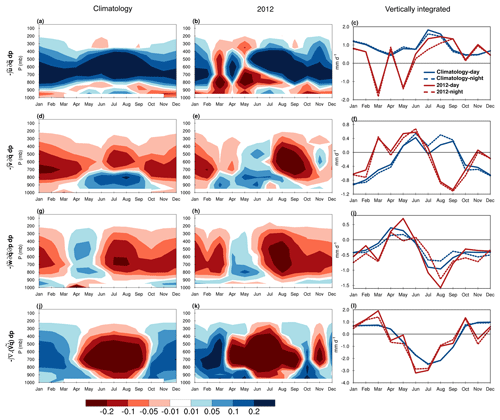
To investigate the GP summer droughts from a moisture budget perspective, we looked at the individual moisture tendencies, their vertical structure, annual cycle, and diurnal variability for both the 2011 and 2012 events compared with the 1979–2018 climatology in ERA-Interim. For the SGP (Fig. 6), all climatological tendencies indicate strong seasonal variability, with the vertically integrated tendencies (blue line) revealing positive values (moisture convergence) as large as 1 mm d−1 for the zonal advection during summer, meridional advection year-round, vertical advection during spring, and horizontal transient term during winter (Fig. 6c, f, i, and l). The major sources ( mm d−1) of negative tendencies (moisture divergence) are the transient term in spring and summer and the vertical advection term in fall and winter. For the summer season in particular, the eddy transient term features strong moisture divergence extending from the surface to the upper troposphere (Fig. 6j and l), whereas the meridional advection reveals strong positive tendencies that are confined to the lower troposphere and are much stronger during night featuring the moisture transport from the Gulf of Mexico through the GP LLJ (Fig. 6d and f). The zonal advection also indicates moderate to strong positive tendencies during summer that are confined to the mid- and upper troposphere (Fig. 6a and c). The difference between the daytime and nighttime moisture tendencies is quite large for the meridional advection term during spring and summer and the vertical advection term during late summer and fall, and it is negligible year-round for the zonal and meridional advection and horizontal transient terms. The annual cycle and the vertical structure of all moisture terms for the SGP in 2011 remained near or greater than the corresponding climatological values, with the exception of zonal advection. The zonal advection in 2011 indicates a major increase in dry tendencies (vertically integrated values mm d−1) extending from 900 mbar to the upper troposphere persisting from March to June (Fig. 6b and c). Meanwhile, all other moisture transport sources in Fig. 6 remained wetter than normal during the 2011 spring up until late summer, making the zonal advection of dry air solely responsible for the severe tropospheric drying during the drought onset, previously identified in Fig. 3.
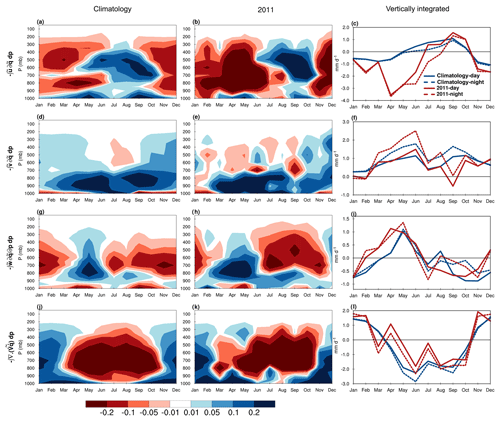
Figure 6Hovmöller diagram of the vertical profile of the atmospheric moisture budget components averaged over the US southern Great Plains for the 1979–2018 climatology (a, d, g, j) and 2011 (b, e, h, k). The first to fourth rows respectively represent the zonal advection, meridional advection, vertical advection, and horizontal transient terms in millimeters per day (mm d−1). The third column (c, f, j, l) represents the annual cycle of the corresponding terms (vertically integrated) for the climatology (blue) and 2011 (red) during the daytime (solid) and nighttime (dashed) steps using 6-hourly ERA-Interim reanalysis.
Over the NGP, zonal advection is the dominant moisture source year-round (vertically integrated values > 0.5 mm d−1), with positive tendencies extending from above the PBL to 300 mbar (Fig. 7a and c). The climatology of meridional advection reveals negative tendencies year-round throughout the troposphere, except during summer in lower tropospheric levels where the moisture convergence is noticeably larger overnight, highlighting the northerly moisture transport via the GP LLJ (Fig. 7d and f). The vertical advection term is moderately positive during April and May and strongly negative during the rest of the year (Fig. 7g and i). The horizontal transient terms reveal a vertical structure similar to that of the SGP with the strong negative tendencies confined to the May–September period (Fig. 7j and l). Similar to the 2011 SGP drought, the 2012 NGP drought onset is marked by strong advection of dry air in April and May concentrated in the lower free troposphere, which leads to the large ( mm d−1) decline in vertically integrated moisture tendencies during that period (Fig. 7b and c). Besides zonal advection, all other terms during the 2012 spring indicate normal or greater-than-normal moisture tendencies, characterizing the zonal advection term as the large-scale source of tropospheric drying during the 2012 drought onset. In the 2012 summer, both the vertical and meridional advection terms indicate large moisture divergence mostly due to considerable strengthening of the dry tendencies in the mid- and upper troposphere from July onward.
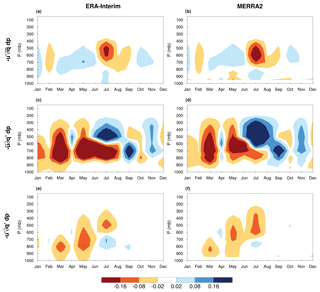
To identify potential drivers of the springtime tropospheric drying shown in Sect. 3.1 and 3.2, we decomposed the zonal, meridional, and vertical advection anomalies into their thermodynamic, dynamic, and nonlinear contributions (see Sect. 2.2). The results for the zonal advection term are presented in Figs. 8 and 9 for the SGP 2011 and NGP 2012 events, respectively. For both events, the contribution of dynamic and nonlinear terms to the anomalies of zonal advection are quite small (as compared to the thermodynamic term) during spring and early summer and nearly zero over the rest of the year in both ERA-Interim and MERRA2 reanalysis. During spring and early summer, the thermodynamic term reveals large negative moisture tendencies for both the SGP 2011 and NGP 2012 cases, with the vertical structure of the anomalous tendencies in the two reanalysis datasets consistently agreeing with one another (Figs. 8c, d, 9c, and d). Since the thermodynamic contribution is defined as the product of the climatological zonal wind (featuring large westerlies at 700 mbar) and the gradient of anomalous humidity, its variability is entirely controlled by the zonal gradient of q anomalies. As a result, the strong advection of dry lower- and midtropospheric tendencies during the 2011 and 2012 drought onsets was almost entirely forced by the zonal gradient of specific humidity or, more simply, by a relatively drier troposphere in the US SW and Rockies located upwind of the SGP and NGP.
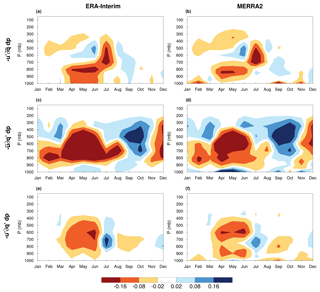
Figure 8Hovmöller diagram of the dynamic (a, b), thermodynamic (c, d), and nonlinear (e, f) contributions to the monthly anomalies of the zonal advection (mm d−1) in ERA-Interim (a, c, e) and MERRA2 (b, d, f) over the SGP in 2011. The monthly anomalies were calculated in respect to the 1979–2018 climatology for ERA-Interim and 1980–2018 climatology for MERRA2.
3.3 The relationship between anomalous moisture advection and the spring and summer dry/wet conditions
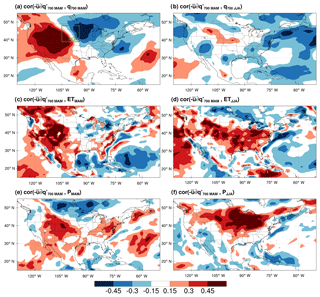
The relationship between the thermodynamic zonal moisture advection and anomalous dry/wet conditions was investigated using single-point lag/lead correlation maps between the tendency term over the SGP and NGP and multiple atmospheric variables over the US (Figs. 10 and 11). For both regions, the correlation between the MAM anomalies of the zonal thermodynamic advection and specific humidity at 700 mbar features a dipole pattern with strong positive (negative) correlations over the US west and southwest (east and northeast), highlighting the zonal gradient of humidity anomalies as the main driver of variability of the moisture term. At the surface, the correlation maps for MAM precipitation and ET indicate a similar pattern with significant positive correlations over the Rockies and US southwest and relatively weak negative correlations over the eastern US for both regions (the magnitude of positive correlations are stronger for SGP than NGP; Figs. 10c, e, 11c and e). The positive correlations indicate that the dry (wet) anomalies of ET and P over the upwind region are linked to the anomalous moisture divergence (convergence) over the SGP and NGP.
The springtime variability of thermodynamic advection over the GP is linked to the summertime surface and atmospheric conditions over the US interior plains. The correlation maps of JJA q for both SGP and NGP indicate positive correlations over the central US, east of the Rockies, and near-zero correlations elsewhere over the US. The correlations between the MAM moisture tendency in the SGP and JJA ET are strongly positive over the Rockies and central plains (Fig. 10d). A similar correlation pattern exists for the NGP tendency and JJA ET with the band of significant positive correlations extending from the eastern Rockies and central US to the US Midwest and east (Fig. 11d). Similar to ET maps, the correlations between the MAM moisture term over both the southern and northern GP and the JJA precipitation anomalies are strongly positive (> 0.45) over the US northern plains and Midwest and weakly positive over the southern plains and northwestern US (Figs. 10f and 11f). Similar correlation patterns were reproduced using the CPC gauge-based precipitation as an independent observational dataset in the lag/lead correlations with the MAM moisture term anomalies in the SGP and NGP (see Figs. S3 and S4).
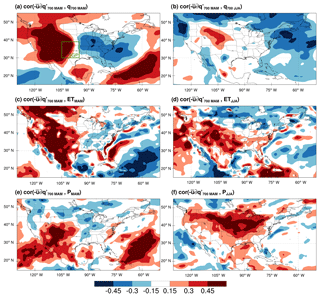
Figure 10Single-point correlation maps between the standardized time series (1979–2018) of the MAM zonal thermodynamic advection at 700 mbar averaged over the SGP (the box in a) and the standardized anomalies of ERA-Interim specific humidity at 700 mbar (a, b), evapotranspiration (c, d), and precipitation (e, f) for the MAM (a, c, e) and JJA (b, d, f) seasons. The correlation coefficients greater than 0.3 and 0.4 are statistically significant at the 10 % and 2 % levels, respectively (see Sect. 2.6).
The strength and spatial patterns of the correlations between the moisture term and both MAM and JJA precipitation (shown in Figs. 10 and 11) signal a potentially significant relationship between the MAM precipitation in the US SW and JJA precipitation in the GP. Using the CPC precipitation, we calculated single-point correlations between the standardized anomalies of MAM precipitation in the US SW and the JJA precipitation at each grid cell (Fig. 12a). The results indicate strong positive (> 0.3) correlations over the US West Coast, Rockies, and northern GP; weak positive correlations over the US Midwest; near-zero correlations over Arizona and the SGP; and weak negative correlations over the US east and southeast. The contours of positive correlations are especially strong over the NGP. The comparison of time series of JJA precipitation anomalies over the NGP against the MAM precipitation anomalies in the US SW (Fig. 12b) indicates a strong covariability between the two time series during the 1979–2018 period with a correlation coefficient of 0.41 (significant at 1 %). The correlation magnitude is surprisingly large as compared to the near-zero correlation between the standardized anomalies of MAM and JJA precipitation in the NGP.
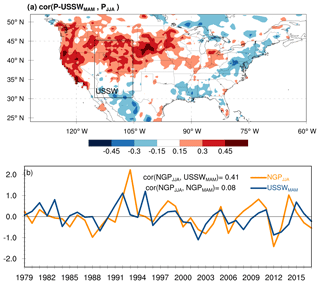
Figure 12Single-point correlation map between standardized anomalies of MAM precipitation over the US SW region (30–45∘ N and 105–115∘ W) and JJA precipitation at each grid cell (a). The time series of standardized anomalies of JJA precipitation over the NGP (yellow) and MAM precipitation in the US SW (blue) are shown in panel (b). The CPC gauge-based precipitation from 1979 to 2018 was used to derive both the correlation map and time series.
Our analyses of the variability and vertical structure of atmospheric moisture budget terms during the SGP 2011 and NGP 2012 extreme droughts identified severe lower-free-tropospheric drying over the US SW and the resulting dry zonal advection anomalies to the US GP in spring as the major drought onset mechanism for both events. The influence of lower-tropospheric humidity on GP precipitation grows continually in spring as the GP precipitation regime begins to shift from a dominantly frontal precipitation regime in winter toward convective precipitation in summer. Our results indicate that a drier lower free troposphere in the US GP, due to strong zonal advection of dry air in spring, is associated with a sharp drop of RH above the PBL which increases dry entrainment and decreases the buoyancy of a rising moist plume. The increased dry entrainment would decrease precipitation during spring and early summer by limiting the convective penetration depth and shifting the convection structure from predominantly deep convective towers toward frequent shallow cumulus clouds (Derbyshire et al., 2004; Zhang et al., 2010; Del Genio, 2012). For the SGP 2011 and NGP 2012 events, the suppressed convection in spring and early summer was supported by the severe decrease (∼30 %–40 %) of specific cloud liquid and iced water content above the PBL (Figs. 3f and 4f) and the FCC in the upper troposphere (Figs. S1f and S2f). The strong control of the free-tropospheric humidity on convective precipitation has already been demonstrated in both cloud-resolving model (CRM) simulations and observational studies (Derbyshire et al., 2004; Sherwood et al., 2010; Zhang et al., 2010; Zhuang et al., 2018). Meanwhile, the conventional convective parameterization schemes tend to severely underestimate the sensitivity of moist convection to environmental humidity largely due to underestimation of the turbulent entrainment of drier air into the rising convective cells (Derbyshire et al., 2004; Del Genio, 2012). This underestimation would lead to overestimation of deep convection in climate models implementing convection schemes and could be a potentially major source of uncertainty responsible for poor performance of the current dynamic models in predicting summer drought in the GP.
The temporal evolution of RH during the SGP 2011 and NGP 2012 droughts reveals a transition of the maximum dry anomalies of RH from the free-tropospheric levels in spring to the lower troposphere and boundary layer in summer. A positive land–atmosphere feedback could facilitate this shift by perpetuating the initial dry land surface conditions in spring to the severe drying and warming in summer. In this mechanism, an anomalously lower precipitation and lower FCC would lead to a relatively drier surface and enhanced insolation in late spring. As a result, ET would decline steadily in the following months, leading to a significant decrease in surface latent heat flux (estimated about 50 w m−2 for the 1988 summer by Lyon et al., 1995), which is largely balanced by an increase in upward sensible heat flux and air temperature. The hotter–drier surface would intensify the decline of boundary layer and lower-tropospheric humidity, causing further decrease in precipitation in summer. This feedback mechanism was found to be responsible for the intensification of several extreme cases of summer droughts and heat waves over the US interior plains (Chang and Wallace, 1987; Hao, 1987; Namias, 1991; Lyon and Dole, 1995; Saini et al., 2016). The anomalous warming of the PBL in summer can also increase the difference between the surface temperature and dew point (T−Td) resulting in elevation of the level of free convection (LFC), increase in convective inhibition energy (CIN), and suppression of deep convection (Hao, 1987; Myoung et al., 2010).
The breakdown of total MFC into its zonal, meridional, and vertical advection terms in our analysis shows the meridional and zonal advection terms to be the dominant sources of incoming moisture over the SGP and NGP, respectively. This is clear from the year-round strong positive tendencies of meridional advection over the SGP (confined to the lower troposphere; Fig. 6d) and zonal advection in the free-tropospheric levels over the NGP (Fig. 7a). While the role of meridional advection of moisture from the Gulf of Mexico to the US interior plains has received extensive attention in the literature (Schubert et al., 1998; Weaver et al., 2008; Berg et al., 2015), the importance of zonal advection as a major moisture transport mechanism has been overlooked. In the case of the NGP 2012 drought, for example, the severe moisture divergence during the drought onset has been attributed to the dry anomalies of meridional moisture advection as a result of weakening of the GP LLJ (Hoerling et al., 2013, 2014). Our close examination of the moisture budget terms, however, rejects this suggestion by revealing higher-than-normal moisture convergence for the meridional term during both the 2011 and 2012 events and attributing the observed tropospheric drying for the two events to the zonal advection term.
Further breakdown of moisture advection anomalies into their dynamic and thermodynamic contributions suggests that the thermodynamic contribution was almost entirely responsible for the extreme dry anomalies of zonal advection during the SGP 2011 and NGP 2012 droughts. By definition, the thermodynamic contribution is driven by the gradient of q, and the dominance of zonal thermodynamic advection in the onset of the 2011 and 2012 events signifies the importance of the west–east gradient of tropospheric moisture. The spatial patterns of MAM climatology of q indicate a relatively large meridional gradient where q decreases sharply moving northward from Mexico toward the GP and a smaller zonal gradient with higher q values over the Rockies gradually decreasing in the eastward direction toward the NGP and US Midwest (Fig. S5). Despite a relatively larger magnitude of the meridional gradient of humidity, the zonal advection tendency becomes much larger (2 to 3 times over the SGP and 4 to 5 times over the NGP) than the meridional advection in the free-tropospheric levels mainly due to the large zonal (westerly) and the near-zero meridional vectors of the horizontal wind over the GP at those levels. However, since the zonal gradient of moisture at the free-tropospheric levels is small, an anomalous dipole pattern (drier west–wetter east) or even a severe decline of q over the Rockies can change the direction of the climatological west–east moisture gradient diverting the zonal thermodynamic advection tendency from its climatological values (strongly positive over the NGP) to strong negative anomalies as large as those observed in the SGP 2011 and NGP 2012 MAM season.
The role of zonal thermodynamic advection in linking the dry/wet conditions over the GP and their upwind region is further supported by the lag/lead correlation analysis between the moisture term and multiple atmospheric and surface parameters in ERA-Interim reanalysis. Similar correlation analysis applied to the CPC-observed precipitation provided additional independent evidence indicating that the MAM precipitation anomalies in the US SW region lead the variability of JJA precipitation over the NGP (statistically significant at the 1 % level).
The year-to-year variability of spring conditions over the US SW is linked to the large-scale circulation and SST anomalies. The US SW and the Rockies are shown to have higher (drier) than normal precipitation during El Niño (La Niña) years (Redmond and Koch, 1991). Leathers et al. (1991) showed a significant positive correlation between the precipitation anomalies over the US SW and the Pacific/North American teleconnection index (PNA) during April to May. Previous studies have also identified an anomalous high and anticyclonic vorticity in the upper troposphere as an atmospheric driver of summer droughts over central North America (Chang and Wallace, 1987; Namias, 1991; Lyon and Dole, 1995; Cook et al., 2011; Donat et al., 2016; Fernando et al., 2016). For the two droughts of SGP 2011 and NGP 2012, the anomalies of 700 mbar (and also 350 mbar) height feature a dipole pattern with an anomalous low over northwestern North America and an anomalous high over the southeastern US (Fig. S5). This dipole pattern seems to be a part of a larger wave-like pattern extended over the North Pacific and was detected in correlation maps between the anomalies of (south and north) GP zonal thermodynamic advection and geopotential height at 700 mbar (not shown). A comprehensive analysis of the large-scale drivers of the zonal moisture advection over the GP can provide valuable information about the underlying mechanisms and predictability of the GP summer droughts and is a focus of our ongoing research.
We investigated the GP summer drought from a moisture budget perspective and looked at the subdaily, monthly, seasonal, and interannual variability of the moisture tendencies in two state-of-the-art reanalysis datasets. For the two extreme droughts (the SGP 2011 and NGP 2012) in our study period, we found that strong anomalies of dry zonal advection in the lower free troposphere (850 to 600 mbar) dominated the anomalously dry moisture flux convergence (MFC) at the early stage of the droughts. The severe free-tropospheric drying resulted in a sharp drop of RH above the boundary layer and an increase in dry entrainment which suppressed the deep convection during spring, setting the stage for extremely dry summers. The anomalies of moisture tendencies were further decomposed into their thermodynamic and dynamic contributions, with the former isolating the impact of the humidity gradient and the latter isolating the impact of wind circulation. The results from ERA-Interim and MERRA2 consistently attributed the observed dry anomalies of tropospheric moisture during the SGP 2011 and NGP 2012 drought onsets to the thermodynamic contribution of the zonal advection tendency. The thermodynamic advection tendency itself was strongly modulated by the springtime conditions over the upstream region (the US southwest) and significantly linked to the JJA precipitation and ET over the US GP. The NGP summer precipitation anomalies were found to be strongly correlated with MAM precipitation anomalies in the US SW, suggesting the springtime dry or wet anomalies over the US SW and the Rockies to be a precursor of the drier or wetter summer over the NGP.
The results of this study provide a comprehensive picture of atmospheric moisture supply over the GP as well as the major drivers of strong moisture divergence during drought onset in the GP. The importance of zonal moisture advection in spring to summer precipitation variability over the GP and the implication that spring dry conditions over the US SW may lead to summer rainfall deficits over the GP highlight the potential of these previously overlooked processes as an additional source of predictability for the hydrologic extremes over the GP.
All the data used in our analysis are publicly available. The ERA-Interim data were obtained from the ECMWF online data archive (http://apps.ecmwf.int/datasets/data/interimfull-daily/levtype=sfc/, last access: 3 November 2018). The MERRA2 data were downloaded through the NASA GMAO website (https://gmao.gsfc.nasa.gov/reanalysis/MERRA-2/, last access: 6 September 2018). The CPC precipitation data were obtained from the NOAA-ESRL website (https://www.esrl.noaa.gov/psd/, last access: 17 July 2018).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-15199-2019-supplement.
AE designed the study and conducted the analyses in close collaboration with RF. Both authors contributed to writing the manuscript, reviewing the results, and editing the paper.
The authors declare that they have no conflict of interest.
The authors thank Robert Dickinson of University of California, Los Angeles, for his constructive input and comments on this research.
This research has been supported by the National Oceanic and Atmospheric Administration Climate Program Office (NOAA-CPO) Modeling, Analysis, Predictions, and Projections (MAPP) Program (grant no. NA17OAR4310123).
This paper was edited by Timothy J. Dunkerton and reviewed by two anonymous referees.
Berg, L. K., Riihimaki, L. D., Qian, Y., Yan, H., Huang, M., Berg, L. K., Riihimaki, L. D., Qian, Y., Yan, H., and Huang, M.: The Low-Level Jet over the Southern Great Plains Determined from Observations and Reanalyses and Its Impact on Moisture Transport, J. Climate, 28, 6682–6706, https://doi.org/10.1175/JCLI-D-14-00719.1, 2015.
Brönnimann, S., Stickler, A., Griesser, T., Ewen, T., Grant, A. N., Fischer, A. M., Schraner, M., Peter, T., Rozanov, E., and Ross, T.: Exceptional atmospheric circulation during the “Dust Bowl”, Geophys. Res. Lett., 36, L08802, https://doi.org/10.1029/2009GL037612, 2009.
Chang, F.-C. and Wallace, J. M.: Meteorological Conditions during Heat Waves and Droughts in the United States Great Plains, Mon. Weather Rev., 115, 1253–1269, https://doi.org/10.1175/1520-0493(1987)115<1253:MCDHWA>2.0.CO;2, 1987.
Chen, P. and Newman, M.: Rossby wave propagation and the rapid development of upper-level anomalous anticyclones during the 1988 U.S. drought, J. Climate, 11, 2491–2504, https://doi.org/10.1175/1520-0442(1998)011<2491:RWPATR>2.0.CO;2, 1998.
Chou, C. and Lan, C. W.: Changes in the annual range of precipitation under global warming, J. Climate, 25, 222–235, https://doi.org/10.1175/JCLI-D-11-00097.1, 2012.
Cook, B. I., Seager, R., and Miller, R. L.: Atmospheric circulation anomalies during two persistent north american droughts: 1932–1939 and 1948–1957, Clim. Dynam., 36, 2339–2355, https://doi.org/10.1007/s00382-010-0807-1, 2011.
Cook, B. I., Ault, T. R., and Smerdon, J. E.: Unprecedented 21st century drought risk in the American Southwest and Central Plains, Sci. Adv., 1, e1400082, https://doi.org/10.1126/sciadv.1400082, 2015.
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., Mcnally, A. P., Monge-Sanz, B. M., Morcrette, J. J., Park, B. K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J. N., and Vitart, F.: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system, Q. J. Roy. Meteorol. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011.
Del Genio, A. D.: Representing the Sensitivity of Convective Cloud Systems to Tropospheric Humidity in General Circulation Models, Surv. Geophys., 33, 637–656, https://doi.org/10.1007/s10712-011-9148-9, 2012.
Derbyshire, S. H. S. H., Beau, I., Bechtold, P., Grandpeix, J.-Y. Y., Piriou, J.-M. M., Redelsperger, J.-L. L., and Soares, P. M. M. M. M.: Sensitivity of moist convection to environmental humidity, Q. J. Roy. Meteorol. Soc., 130, 3055–3079, https://doi.org/10.1256/qj.03.130, 2004.
Donat, M. G., King, A. D., Overpeck, J. T., Alexander, L. V., Durre, I., and Karoly, D. J.: Extraordinary heat during the 1930s US Dust Bowl and associated large-scale conditions, Clim. Dynam., 46, 413–426, https://doi.org/10.1007/s00382-015-2590-5, 2016.
Feng, S., Hu, Q., and Oglesby, R. J.: Influence of Atlantic sea surface temperatures on persistent drought in North America, Clim. Dynam., 37, 569–586, https://doi.org/10.1007/s00382-010-0835-x, 2011.
Ferguson, I. M., Dracup, J. A., Duffy, P. B., Pegion, P., and Schubert, S.: Influence of SST Forcing on Stochastic Characteristics of Simulated Precipitation and Drought, J. Hydrometeorol., 11, 754–769, https://doi.org/10.1175/2009JHM1132.1, 2010.
Fernando, D. N., Mo, K. C., Fu, R., Pu, B., Bowerman, A., Scanlon, B. R., Solis, R. S., Yin, L., Mace, R. E., Mioduszewski, J. R., Ren, T., and Zhang, K.: What caused the spring intensification and winter demise of the 2011 drought over Texas?, Clim. Dynam., 47, 3077–3090, https://doi.org/10.1007/s00382-016-3014-x, 2016.
Gelaro, R., McCarty, W., Suárez, M. J., Todling, R., Molod, A., Takacs, L., Randles, C. A., Darmenov, A., Bosilovich, M. G., Reichle, R., Wargan, K., Coy, L., Cullather, R., Draper, C., Akella, S., Buchard, V., Conaty, A., da Silva, A. M., Gu, W., Kim, G. K., Koster, R., Lucchesi, R., Merkova, D., Nielsen, J. E., Partyka, G., Pawson, S., Putman, W., Rienecker, M., Schubert, S. D., Sienkiewicz, M., and Zhao, B.: The modern-era retrospective analysis for research and applications, version 2 (MERRA-2), J. Climate, 30, 5419–5454, https://doi.org/10.1175/JCLI-D-16-0758.1, 2017.
Hao, W.: A Moisture Budget Analysis of the Protracted Heat Wave in the Southern Plains during the Summer of 1980, Weather Forecast., 2, 269–288, https://doi.org/10.1175/1520-0434(1987)002<0269:AMBAOT>2.0.CO;2, 1987.
Hoerling, M., Schubert, S., and Mo, K. C.: An Interpretation of the Origins of the 2012 Central Great Plains Drought Assessment Report, (March), 50, available at: ftp://ftp.oar.noaa.gov/CPO/pdf/mapp/reports/2012-Drought-Interpretation-final.web-041113.pdf (last access: 27 January 2018), 2013.
Hoerling, M., Eischeid, J., Kumar, A., Leung, R., Mariotti, A., Mo, K., Schubert, S., and Seager, R.: Causes and predictability of the 2012 great plains drought, B. Am. Meteor. Soc., 95, 269–282, https://doi.org/10.1175/BAMS-D-13-00055.1, 2014.
Kushnir, Y., Seager, R., Ting, M., Naik, N., and Nakamura, J.: Mechanisms of tropical atlantic SST influence on North American precipitation variability, J. Climate, 23, 5610–5628, https://doi.org/10.1175/2010JCLI3172.1, 2010.
Lamb, P. J., Portis, D. H., and Zangvil, A.: Investigation of Large-Scale Atmospheric Moisture Budget and Land Surface Interactions over U.S. Southern Great Plains including for CLASIC (June 2007), J. Hydrometeorol., 13, 1719–1738, https://doi.org/10.1175/JHM-D-12-01.1, 2012.
Leathers, D. J., Yarnal, B., Palecki, M. A., Leathers, D. J., Yarnal, B., and Palecki, M. A.: The Pacific/North American Teleconnection Pattern and United States Climate, Part I: Regional Temperature and Precipitation Associations, J. Climate, 4, 517–528, https://doi.org/10.1175/1520-0442(1991)004<0517:TPATPA>2.0.CO;2, 1991.
Li, L., Schmitt, R. W., Ummenhofer, C. C., Karnauskas, K. B., Li, L., Schmitt, R. W., Ummenhofer, C. C., and Karnauskas, K. B.: Implications of North Atlantic Sea Surface Salinity for Summer Precipitation over the U.S. Midwest: Mechanisms and Predictive Value, J. Climate, 29, 3143–3159, https://doi.org/10.1175/JCLI-D-15-0520.1, 2016.
Livezey, R. E., Chen, W. Y., Livezey, R. E., and Chen, W. Y.: Statistical Field Significance and its Determination by Monte Carlo Techniques, Mon. Weather Rev., 111, 46–59, https://doi.org/10.1175/1520-0493(1983)111<0046:SFSAID>2.0.CO;2, 1983.
Lyon, B. and Dole, R. M.: A diagnostic comparison of the 1980 and 1988 US summer heat wave- droughts, J. Climate, 8, 1658–1675, https://doi.org/10.1175/1520-0442(1995)008<1658:ADCOTA>2.0.CO;2, 1995.
McCabe, G. J., Palecki, M. A., and Betancourt, J. L.: Pacific and Atlantic Ocean influences on multidecadal drought frequency in the United States, P. Natl. Acad. Sci. USA, 101, 4136–4141, https://doi.org/10.1073/pnas.0306738101, 2004.
Mo, K. C., Lettenmaier, D. P., Mo, K. C., and Lettenmaier, D. P.: Precipitation Deficit Flash Droughts over the United States, J. Hydrometeorol., 17, 1169–1184, https://doi.org/10.1175/JHM-D-15-0158.1, 2016.
Myoung, B., Nielsen-Gammon, J. W., Myoung, B., and Nielsen-Gammon, J. W.: The Convective Instability Pathway to Warm Season Drought in Texas, Part II: Free-Tropospheric Modulation of Convective Inhibition, J. Clim., 23, 4474–4488, https://doi.org/10.1175/2010JCLI2947.1, 2010.
Namias, J.: Spring and Summer 1988 Drought over the Contiguous United-States – Causes and Prediction, J. Climate, 4, 54–65, https://doi.org/10.1175/1520-0442(1991)004<0054:SASDOT>2.0.CO;2, 1991.
Peng, D. and Zhou, T.: Why was the arid and semiarid northwest China getting wetter in the recent decades?, J. Geophys. Res.-Atmos., 122, 9060–9075, https://doi.org/10.1002/2016JD026424, 2017.
Pu, B., Fu, R., Dickinson, R. E., and Fernando, D. N.: Why do summer droughts in the Southern Great Plains occur in some La Niña years but not others?, J. Geophys. Res.-Atmos., 121, 1120–1137, https://doi.org/10.1002/2015JD023508, 2016.
Quan, X.-W., Hoerling, M. P., Lyon, B., Kumar, A., Bell, M. A., Tippett, M. K., Wang, H., Quan, X.-W., Hoerling, M. P., Lyon, B., Kumar, A., Bell, M. A., Tippett, M. K., and Wang, H.: Prospects for Dynamical Prediction of Meteorological Drought, J. Appl. Meteorol. Climatol., 51, 1238–1252, https://doi.org/10.1175/JAMC-D-11-0194.1, 2012.
Rasmusson, E. M.: Atmospheric Water Vapor Transport and the Water Balance of North America, Mon. Weather Rev., 96, 720–734, https://doi.org/10.1175/1520-0493(1968)096<0720:AWVTAT>2.0.CO;2, 1968.
Redmond, K. T. and Koch, R. W.: Surface Climate and Streamflow Variability in the Western United States and Their Relationship to Large-Scale Circulation Indices, Water Resour. Res., 27, 2381–2399, https://doi.org/10.1029/91WR00690, 1991.
Saini, R., Wang, G., Pal, J. S., Saini, R., Wang, G., and Pal, J. S.: Role of Soil Moisture Feedback in the Development of Extreme Summer Drought and Flood in the United States, J. Hydrometeorol., 17, 2191–2207, https://doi.org/10.1175/JHM-D-15-0168.1, 2016.
Schubert, S. D., Helfand, H. M., Wu, C. Y., and Min, W.: Subseasonal variations in warm-season moisture transport and precipitation over the central and eastern United States, J. Climate, 11, 2530–2555, https://doi.org/10.1175/1520-0442(1998)011<2530:SVIWSM>2.0.CO;2, 1998.
Schubert, S. D., Suarez, M. J., Pegion, P. J., Koster, R. D., and Bacmeister, J. T.: Causes of long-term drought in the U.S. Great Plains, J. Climate, 17, 485–503, https://doi.org/10.1175/1520-0442(2004)017<0485:COLDIT>2.0.CO;2, 2004.
Seager, R. and Henderson, N.: Diagnostic computation of moisture budgets in the ERA-interim reanalysis with reference to analysis of CMIP-archived atmospheric model data, J. Climate, 26, 7876–7901, https://doi.org/10.1175/JCLI-D-13-00018.1, 2013.
Seager, R., Naik, N., Vecchi, G. A., Seager, R., Naik, N., and Vecchi, G. A.: Thermodynamic and Dynamic Mechanisms for Large-Scale Changes in the Hydrological Cycle in Response to Global Warming, J. Climate, 23, 4651–4668, https://doi.org/10.1175/2010JCLI3655.1, 2010.
Sherwood, S. C., Roca, R., Weckwerth, T. M., and Andronova, N. G.: Tropospheric water vapor, convection, and climate, Rev. Geophys., 48, RG2001, https://doi.org/10.1029/2009RG000301, 2010.
Sun, Y., Fu, R., Dickinson, R., Joiner, J., Frankenberg, C., Gu, L., Xia, Y., and Fernando, N.: Drought onset mechanisms revealed by satellite solar-induced chlorophyll fluorescence: Insights from two contrasting extreme events, J. Geophys. Res.-Biogeo., 120, 2427–2440, https://doi.org/10.1002/2015JG003150, 2015.
Teng, H., Branstator, G., Meehl, G. A., and Washington, W. M.: Projected intensification of subseasonal temperature variability and heat waves in the Great Plains, Geophys. Res. Lett., 43, 2165–2173, https://doi.org/10.1002/2015GL067574, 2016.
Trenberth, K. E. and Guillemot, C. J.: Evaluation of the global atmospheric moisture budget as seen from analyses, J. Climate, 8, 2255–2272, https://doi.org/10.1175/1520-0442(1995)008<2255:EOTGAM>2.0.CO;2, 1995.
Trenberth, K. E., Branstator, G. W., and Arkin, P. A.: Origins of the 1988 North American drought, Science, 242, 1640–1645, https://doi.org/10.1126/science.242.4886.1640, 1988.
Trenberth, K. E., Fasullo, J. T., and Mackaro, J.: Atmospheric moisture transports from ocean to land and global energy flows in reanalyses, J. Climate, 24, 4907–4924, https://doi.org/10.1175/2011JCLI4171.1, 2011.
Wang, H., Schubert, S., Suarez, M., Koster, R., Wang, H., Schubert, S., Suarez, M., and Koster, R.: The Physical Mechanisms by Which the Leading Patterns of SST Variability Impact U.S. Precipitation, J. Climate, 23, 1815–1836, https://doi.org/10.1175/2009JCLI3188.1, 2010.
Wang, H., Schubert, S., Koster, R., Ham, Y.-G., and Suarez, M.: On the Role of SST Forcing in the 2011 and 2012 Extreme U.S. Heat and Drought: A Study in Contrasts, J. Hydrometeorol., 15, 1255–1273, https://doi.org/10.1175/JHM-D-13-069.1, 2014.
Weaver, S. J., Nigam, S., Weaver, S. J., and Nigam, S.: Variability of the Great Plains Low-Level Jet: Large-Scale Circulation Context and Hydroclimate Impacts, J. Climate, 21, 1532–1551, https://doi.org/10.1175/2007JCLI1586.1, 2008.
Yanai, M., Esbensen, S., and Chu, J.-H.: Determination of Bulk Properties of Tropical Cloud Clusters from Large-Scale Heat and Moisture Budgets, J. Atmos. Sci., 30, 611–627, https://doi.org/10.1175/1520-0469(1973)030<0611:DOBPOT>2.0.CO;2, 1973.
Zangvil, A., Portis, D. H., and Lamb, P. J.: Diurnal variations in the water vapor budget components over the Midwestern United States in summer 1979, 53–63, American Geophysical Union (AGU), 1993.
Zangvil, A., Portis, D. H., and Lamb, P. J.: Investigation of the large-scale atmospheric moisture field over the midwestern United States in relation to summer precipitation, Part I: Relationships between moisture budget components on different timescales, J. Climate, 14, 582–597, https://doi.org/10.1175/1520-0442(2001)014<0582:IOTLSA>2.0.CO;2, 2001.
Zhang, Y., Klein, S. A., Zhang, Y., and Klein, S. A.: Mechanisms Affecting the Transition from Shallow to Deep Convection over Land: Inferences from Observations of the Diurnal Cycle Collected at the ARM Southern Great Plains Site, J. Atmos. Sci., 67, 2943–2959, https://doi.org/10.1175/2010JAS3366.1, 2010.
Zhao, S., Deng, Y., and Black, R. X.: Observed and Simulated Spring and Summer Dryness in the United States: the Impact of the Pacific Sea Surface Temperature and Beyond, J. Geophys. Res.-Atmos., 122, 12713–12731, https://doi.org/10.1002/2017JD027279, 2017.
Zhuang, Y., Fu, R., Wang, H., Zhuang, Y., Fu, R., and Wang, H.: How Do Environmental Conditions Influence Vertical Buoyancy Structure and Shallow-to-Deep Convection Transition across Different Climate Regimes?, J. Atmos. Sci., 75, 1909–1932, https://doi.org/10.1175/JAS-D-17-0284.1, 2018.