the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Viscosities, diffusion coefficients, and mixing times of intrinsic fluorescent organic molecules in brown limonene secondary organic aerosol and tests of the Stokes–Einstein equation
Dagny A. Ullmann
Mallory L. Hinks
Adrian M. Maclean
Christopher L. Butenhoff
James W. Grayson
Kelley Barsanti
Jose L. Jimenez
Sergey A. Nizkorodov
Saeid Kamal
Viscosities and diffusion rates of organics within secondary organic aerosol (SOA) remain uncertain. Using the bead-mobility technique, we measured viscosities as a function of water activity (aw) of SOA generated by the ozonolysis of limonene followed by browning by exposure to NH3 (referred to as brown limonene SOA or brown LSOA). These measurements together with viscosity measurements reported in the literature show that the viscosity of brown LSOA increases by 3–5 orders of magnitude as the aw decreases from 0.9 to approximately 0.05. In addition, we measured diffusion coefficients of intrinsic fluorescent organic molecules within brown LSOA matrices using rectangular area fluorescence recovery after photobleaching. Based on the diffusion measurements, as the aw decreases from 0.9 to 0.33, the average diffusion coefficient of the intrinsic fluorescent organic molecules decreases from to cm2 s−1 and the mixing times of intrinsic fluorescent organic molecules within 200 nm brown LSOA particles increases from 0.002 to 14 s. These results suggest that the mixing times of large organics in the brown LSOA studied here are short (<1 h) for aw and temperatures often found in the planetary boundary layer (PBL). Since the diffusion coefficients and mixing times reported here correspond to SOA generated using a high mass loading (∼1000 µg m−3), biogenic SOA particles found in the atmosphere with mass loadings ≤10 µg m−3 are likely to have higher viscosities and longer mixing times (possibly 3 orders of magnitude longer). These new measurements of viscosity and diffusion were used to test the accuracy of the Stokes–Einstein relation for predicting diffusion rates of organics within brown LSOA matrices. The results show that the Stokes–Einstein equation gives accurate predictions of diffusion coefficients of large organics within brown LSOA matrices when the viscosity of the matrix is as high as 102 to 104 Pa s. These results have important implications for predicting diffusion and mixing within SOA particles in the atmosphere.
- Article
(3588 KB) -
Supplement
(320 KB) - BibTeX
- EndNote
Large amounts of volatile organic compounds, such as isoprene, limonene, and α-pinene from biogenic sources and aliphatic and aromatic compounds from anthropogenic sources, are released into the atmosphere. These compounds can be oxidized by a complex series of atmospheric reactions to form lower-volatility products that condense to form secondary organic aerosols (SOAs) (Hallquist et al., 2009; Kanakidou et al., 2005). SOA makes up approximately 30 %–70 % of the mass of atmospheric particles (Kanakidou et al., 2005; Jimenez et al., 2009). Due to the hygroscopic nature of SOA, an important component of SOA particles is water (Bateman et al., 2015; Hildebrandt Ruiz et al., 2015; Massoli et al., 2010). The amount of water in SOA particles is determined by the relative humidity (RH); as the RH increases, the water activity (aw) (and hence water content) in SOA particles increases to maintain equilibrium with the gas phase. SOA particles can influence climate either directly, by absorbing and scattering sunlight, or indirectly, by acting as cloud condensation nuclei (CCN) and ice nuclei (IN) (Kanakidou et al., 2005; Murray et al., 2010; Solomon, 2007; Wang et al., 2012). SOA particles can also influence air quality and public health (Baltensperger et al., 2008; Jang et al., 2006; Pöschl and Shiraiwa, 2015; Shiraiwa et al., 2017b).
Despite the importance of SOA particles in climate and air quality, their physicochemical properties remain poorly understood (Hallquist et al., 2009). This leads to uncertainties when predicting the role of SOA particles in atmospheric chemistry, climate, and air quality (Hallquist et al., 2009; Shiraiwa and Seinfeld, 2012; Shrivastava et al., 2017a; Zaveri et al., 2014). One physicochemical property that remains poorly known is the rate of diffusion of organics within SOA particles (Liu et al., 2016; Shiraiwa et al., 2013; Shrivastava et al., 2017a; Ye et al., 2016). Information on diffusion rates is needed to predict the reactivity and photochemistry of SOA particles (Chu and Chan, 2017; Davies and Wilson, 2015; Gržinić et al., 2015; Houle et al., 2015; Li et al., 2015; Lignell et al., 2014; Shiraiwa et al., 2011; Wang et al., 2015). Diffusion rates are also needed to predict the growth rates, size distributions, cloud condensation ability, and ice nucleating ability of SOA particles (Boyd et al., 2017; Huff Hartz et al., 2005; Murray et al., 2010; Perraud et al., 2012; Riipinen et al., 2011; Shiraiwa and Seinfeld, 2012; Solomon et al., 2007; Taina et al., 2017; Wagner et al., 2017; Wang et al., 2012; Zaveri et al., 2014, 2018). Slow diffusion of molecules in particles also has implications for the long-range transport of pollutants (Bastelberger et al., 2017; Shrivastava et al., 2017b; Zelenyuk et al., 2012; Zhou et al., 2012) and the optical properties of particles (Adler et al., 2013; Robinson et al., 2014).
To estimate diffusion rates of organics in SOA particles, it is common to use viscosity measurements together with the Stokes–Einstein relation (Booth et al., 2014; Hosny et al., 2013; Koop et al., 2000; Power et al., 2013; Renbaum-Wolff et al., 2013a; Shiraiwa et al., 2011, 2017a; Song et al., 2015, 2016),
where D is the diffusion coefficient of the diffusing species, k is the Boltzmann constant, T is the temperature, η is the dynamic viscosity, and RH is the hydrodynamic radius of the diffusing species. Until now, the accuracy of the Stokes–Einstein relation for predicting diffusion rates of organics in SOA particles has not been quantified, leading to uncertainties when estimating diffusion rates from viscosity measurements. Motivated primarily by the food industry, there have been a few tests of the Stokes–Einstein relation for predicting diffusion rates of organics in organic–water matrices, such as saccharide–water matrices (Bastelberger et al., 2017; Champion et al., 1997; Chenyakin et al., 2017; Corti et al., 2008; Price et al., 2016). In these cases, the matrices contained only two species (one organic and water), which is very different from SOA matrices that contain thousands of different species (Nozière et al., 2015).
In the future, researchers will likely continue to use viscosity data combined with the Stokes–Einstein relation to estimate diffusion rates of organics in SOA particles, because several techniques have been developed recently to measure the viscosities of SOA matrices and proxies of SOA matrices (Bateman et al., 2015; Grayson et al., 2016; Lee et al., 2017; Marsh et al., 2017; Price et al., 2015; Reid et al., 2018; Renbaum-Wolff et al., 2013a; Song et al., 2015; Zhang et al., 2015). As a result, the accuracy of the Stokes–Einstein relation for predicting diffusion rates of organics in SOA particles needs to be quantified.
In the following, we measured the viscosities of brown limonene SOA (brown LSOA) as a function of aw using the bead-mobility technique. The brown LSOA is a product of exposure of white limonene ozonolysis SOA to ppb levels of ammonia vapor (Laskin et al., 2010), and it is a model system for the formation of secondary brown carbon (Laskin et al., 2015). In addition, we measured diffusion coefficients of intrinsic fluorescent organic molecules within brown LSOA matrices using a technique called rectangular area fluorescence recovery after photobleaching. These new data, combined with viscosity data that already exist in the literature for brown LSOA–water matrices, were used to test the accuracy of the Stokes–Einstein relation for predicting diffusion rates of organics within SOA particles. We also used the measured diffusion coefficients to estimate mixing times of organics within 200 nm brown LSOA particles at RHs typically found in the planetary boundary layer (PBL; the region of the atmosphere from the surface to an altitude of up to 1 km). We focused on brown LSOA for the following reasons: first, brown LSOA contains light-absorbing molecules that are also fluorescent (here referred to as intrinsic fluorescent organic molecules) and capable of rapid photobleaching (Lee et al., 2013). These intrinsic fluorescent organic molecules offer a key advantage because one can measure diffusion coefficients within brown LSOA using rectangular area fluorescence recovery after photobleaching without the need to add a foreign tracer fluorescent molecule to the SOA matrix. Second, limonene accounts for roughly 10 % of the global emissions of monoterpenes (and is thus an important source of SOA in the atmosphere) (Kanakidou et al., 2005; Sindelarova et al., 2014).
2.1 Generation of brown LSOA
Brown LSOA was produced at the University of California, Irvine (UCI) following the procedure outlined in Hinks et al. (2016). First, particles consisting of limonene secondary organic material (LSOA) were generated in a 20 L flow tube by dark ozonolysis of d-limonene. Mixing ratios of ozone and d-limonene (97 % Sigma-Aldrich) were both 10 ppm prior to reaction. Ozone was produced externally to the flow tube by an electric discharge in pure O2 (ultra-high purity, Airgas). After the ozonolysis reaction, the mass concentration of LSOA particles within the flow tube was approximately 1000 µg m−3. At the exit of the flow tube, the carrier gas and LSOA particles were passed through a charcoal denuder to eliminate excess ozone and gas-phase organics, followed by collection of the LSOA particles on hydrophobic slides (Hampton Research; Aliso Viejo, CA, USA) using a Sioutas impactor with a single stage “D” (0.25 µm cut point at 9 SLM collection flow rate). After LSOA production, the hydrophobic slides containing the LSOA were placed within a small glass petri dish, which was left floating on the surface of a solution of 0.1 M ammonium sulfate (>99 %, EMD) in a larger, covered petri dish. Over a period of 3 to 5 days, the ammonia vapor in equilibrium with the ammonium sulfate solution (concentration estimated to be 300 ppb NH3 using the Extended AIM Aerosol Thermodynamics Model II) (Clegg et al., 1998) reacted with the fresh LSOA forming a visible brown color. After production of the brown LSOA, the samples were shipped to the University of British Columbia for viscosity and diffusion coefficient measurements.
2.2 Viscosity measurements
The viscosities of brown LSOA particles were determined at aw of approximately 0.7, 0.8, and 0.9, using the bead-mobility technique (Renbaum-Wolff et al., 2013b). At lower aw, the viscosities were too high for measurements with this technique. In short, small particles (5–50 µm in diameter) of brown LSOA were deposited on fluorinated glass slides (Knopf, 2003) from the samples received from UCI using the tip of a needle (BD PrecisionGlide™ Needle, 0.9 mm × 40 mm). A dilute solution containing hydrophilic melamine beads (actual diameter: (0.87±0.04) µm, Sigma Aldrich, no. 86296) was then nebulized over the fluorinated glass slides containing the brown LSOA particles. This resulted in melamine beads being incorporated into the brown LSOA particles. The fluorinated glass slides containing the brown LSOA particles were then placed in a flow cell (Renbaum-Wolff et al., 2013b). The RH within the flow cell was controlled by passing a nitrogen carrier gas through a water bubbler, which was located in a temperature-controlled bath. The dew point of the nitrogen gas flow was measured with a hygrometer (General Eastern; Model 1311DR), and the temperature of the flow cell was measured with a thermocouple. From the dew point and the temperature of the flow cell, the RH was determined. The RH was calibrated at the beginning of each set of measurements using the deliquescence point of ammonium sulfate.
Once the fluorinated glass slides containing the brown LSOA particles were placed in the flow cell, a constant flow (1100 to 1200 sccm) of humidified nitrogen gas (Praxair, ultrapure) was passed over the brown LSOA particles, which caused a shear stress on the surface of the particles and circulation of the beads within the particles. The velocity of the beads was determined using an optical microscope (Zeiss Axio Observer). For each aw studied, the speed of 7 to 16 beads in 2 to 5 brown LSOA droplets was measured and the bead speed was averaged. Once determined, the velocity of the beads was converted to viscosity using a calibration curve based on sucrose–water particles and glycerol–water particles from Grayson et al. (2017). Prior to measuring the velocity of the beads in an experiment, the brown LSOA particles were equilibrated with the RH within the flow cell for approximately 20 min, which should be long enough to ensure equilibration (Sect. S1 in the Supplement).
Viscosities for the same brown LSOA at aw of 0.05 and 0.3 are available from previous poke–flow measurements by Hinks et al. (2016). Briefly, in these studies brown LSOA was collected on hydrophobic glass surfaces using a procedure similar to the procedure described above. This resulted in supermicron particles with a spherical cap geometry. The particles were then poked with a sharp needle, generating a half-torus geometry. After poking, the material flowed and returned to its spherical cap geometry due to surface tension forces. From simulations of fluid flow, the viscosities of the material were determined. This technique is limited to viscosities ≥103 Pa s (Grayson et al., 2015). In addition, the upper and lower limits of viscosity from this technique differ by roughly a factor of 15 to 150. This uncertainty stems mainly from uncertainties in the parameters used when simulating the fluid flow.
2.3 Diffusion coefficient measurements
2.3.1 Generation of thin films of brown LSOA with a known aw for the diffusion coefficient measurements
Brown LSOA contains light-absorbing molecules that are also fluorescent and easily photobleachable (Lee et al., 2013). Diffusion coefficients of these intrinsic fluorescent organic molecules were determined using rectangle area fluorescent recovery after photobleaching (discussed below). For this technique, thin films (20–90 µm thick) containing brown LSOA with a known aw were needed. To produce thin films of brown LSOA with a known aw, particles of brown LSOA with diameters of 50–200 µm were deposited on hydrophobic slides from the samples received from the UCI using the tip of a needle (BD PrecisionGlide™ Needle, 0.9 mm × 40 mm). The super-micrometer brown LSOA particles were then located within a flow cell or sealed glass jar with controlled RH to set the aw within the brown LSOA (at equilibration, aw within the brown LSOA equals RH∕100). The times used to condition the brown LSOA particles to the controlled RH are given in Table S1 and discussed in Sect. S1. After equilibration, the brown LSOA particles were sandwiched between two hydrophobic glass slides to generate a thin film of brown LSOA with a thickness of 20–90 µm. Assembly of the films occurred within a glove bag that had a RH set to match the RH used for conditioning the brown LSOA particles in order to ensure the aw within the LSOA did not change during assembly of the films. The thickness of the films was controlled by aluminium spacers inserted between the two hydrophobic glass slides prior to assembly. After assembly, the brown LSOA within the thin films was isolated from the surrounding atmosphere using a layer of vacuum grease around the perimeter of the films. For further details, see Chenyakin et al. (2017) and Fig. S1.
2.3.2 Measurements of diffusion coefficients
Fluorescence recovery after photobleaching (FRAP) has often been used to determine diffusion rates of fluorescent molecules in biological samples such as in the cytoplasm and nuclei of cells (Axelrod et al., 1976; Deschout et al., 2010; Jacobson et al., 1976; Meyvis et al., 1999; Seksek et al., 1997). To determine diffusion coefficients of the intrinsic fluorophores in the brown LSOA, we used a version of FRAP, referred to as rectangular area fluorescence recovery after photobleaching (rFRAP) (Deschout et al., 2010). rFRAP was chosen over circular FRAP, since rFRAP has a closed-form expression for the recovery process. In rFRAP, a rectangular region of a thin film containing fluorescent molecules is photobleached with a high-intensity laser beam of a confocal laser scanning microscope (Fig. S2). After photobleaching, the fluorescence signal within the photobleached region recovers due to diffusion of fluorescent molecules from outside the photobleached region into the photobleached region. The recovery of the fluorescence signal over time is monitored and used to determine the diffusion coefficient of the fluorescent molecules.

Figure 1Images of brown limonene SOA films at three different aw (0.33, 0.6, and 0.9) recorded during a rectangular fluorescence recovery after photobleaching (rFRAP) experiment. Times shown in each panel correspond to times after photobleaching. The orange rectangles depict the area to be photobleached.
The rFRAP measurements were conducted with a laser scanning confocal microscope (Zeiss Axio Observer LSM 5 10 MP) with a low numerical aperture objective (Zeiss EC-Plan Neofluar 10×, 0.3 numerical aperture) to ensure near-uniform photobleaching in the z direction. One-dimensional scanning with a pixel dwell of 2.56 µs and an image scan time of 1.57 s were used. The images were acquired with 512×512 pixels with a pinhole set to 80 µm. The scanning laser power was varied between 17.0 and 42.6 µW depending on the fluorescence of the sample. In order to achieve a bleach depth (decrease in fluorescence intensity) of 30 %–50 %, as suggested by Deschout et al. (2010) for rFRAP experiments, the laser power for photobleaching was varied between 93 and 297 µW, depending on the sample (Deschout et al., 2010).
A rectangular area was used for photobleaching with length (x) and width (y). The recovery time in the rFRAP experiments were related to both the photobleaching area and diffusion rate. When the diffusion rate was fast (e.g., high water activities), we used a larger photobleaching area, and when the diffusion rate was slow (e.g., low water activities), we used a smaller photobleaching area to give experimentally accessible recovery times. The image sizes used in the rFRAP experiments were chosen in relation to the bleach size with larger image sizes used for larger bleach sizes. For example, at aw≥0.8, photobleached areas of 20 µm by 20 µm and image sizes of 199.6 µm by 199.6 µm were used, while at aw=0.33, photobleached areas of 5 µm by 5 µm and 3 µm by 3 µm and image sizes of 30 µm by 30 µm were used. All rFRAP experiments were carried out at a temperature of 294.5±1.0 K. Shown in Fig. 1 are examples of images of brown LSOA films with aw of 0.33, 0.6, and 0.9 recorded during rFRAP experiments.
2.3.3 Extraction of diffusion coefficients
Based on Fick's second law of diffusion, Deschout et al. (2010) developed the following equation to describe the fluorescence intensities in thin films after photobleaching a rectangular area with a confocal microscope (Deschout et al., 2010):
where is the fluorescence intensity at coordinate (x, y) and time t after photobleaching; F0(x, y) is the fluorescence intensity at coordinate (x, y) prior to photobleaching; K0 is the effective bleach depth, which describes the decrease in the fluorescence intensity within the photobleached area; lx and ly are the lengths of the photobleached area; r is the lateral resolution of the microscope; and D is the diffusion coefficient of the fluorescent molecules. The parameter is given by the following equation:
In a first step of the analysis for the extraction of diffusion coefficients, the images recorded after photobleaching were normalized to an image recorded prior to photobleaching using the open-source program ImageJ (Schneider et al., 2012). The resolution of the images was changed from 512×512 pixels to 128×128 pixels by averaging to reduce the noise. Then, Eq. (2) was used to extract from each image. In the fitting procedure used to extract , K0 and a normalization factor were left as free parameters. Next, was plotted as a function of t and a straight line was fit to the data. The diffusion coefficient, D, was calculated from the slope of the straight line using a linear fit to Eq. (3). Examples of plots of vs. t are shown in Fig. 2.
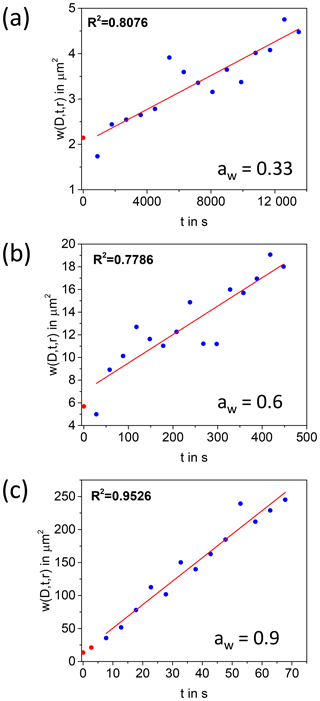
Figure 2Plot of as a function of time at aw of 0.9, 0.6, and 0.33. The red line is a linear fit to the data. The blue circles represent the data points that were included in the linear fit, and the red circles represent data that were not included because of possible reversible photobleaching. The diffusion coefficients were obtained from the slopes.
Equation (2) assumes that the only mechanism for recovery in the photobleached region is diffusion of unbleached molecules. The spontaneous recovery of the fluorescence signal without diffusion, referred to as reversible photobleaching, has been observed in previous studies at short timescales (Sinnecker et al., 2005; Stout and Axelrod, 1995; Verkman, 2003). To determine if this process occurred during our diffusion measurements with brown LSOA, a separate set of experiments was carried out. Particles of brown LSOA (40 to 90 µm in diameter) were conditioned to an aw of 0.6 and the entire particle was photobleached until the fluorescence intensity decreased by between 17 % and 47 %. The photobleaching was performed across the entire particle in order to rule out fluorescence intensity recovery due to diffusion of fluorescent molecules. Within the first 5 s after photobleaching a small amount of the fluorescent signal recovered (1 %–3 % of the photobleached signal), which we attribute to reversible photobleaching. To ensure this process did not impact our diffusion measurements, the data recorded during the first 5 s after photobleaching in the rFRAP experiments were not included when determining diffusion coefficients.
Possible heating of the sample during photobleaching by the laser was not expected to impact the diffusion measurements since local heating during photobleaching should be dissipated to the surroundings much faster than the time of the diffusion measurements. Nevertheless, to support this expectation, two experiments were carried out with different laser intensities but on the same sample conditioned to an aw of 0.9. A laser intensity of 139.9 µW was used for a bleach depth of 20 % and a laser intensity of 330 µW was used for a bleach depth of 50 %. Within uncertainty, the diffusion coefficients determined with both bleach depths were in agreement: cm2 s−1 was obtained for a laser intensity of 139.9 µW and cm2 s−1 was obtained for a laser intensity of 330 µW (uncertainties correspond to 95 % confidence intervals).
Equation (2) assumes that the fluorescence intensity is proportional to the concentration of the intrinsic fluorescent molecules, which is a valid assumption when the transmittance of light through the samples is ≥95 % (Fonin et al., 2014). In our experiments the transmittance of light through the samples was ≤93 %. To take into account the nonlinearity between the fluorescence signal and concentration, the measured fluorescence signal was first converted to concentration using the following equation:
where is the normalized concentration of the intrinsic fluorescent dye, is the normalized fluorescence signal, and T0 is the transmittance prior to the photobleaching process. Equation (4) is derived in Sect. S2. After the normalized concentrations were calculated, they were used in Eq. (2) in place of the normalized fluorescence signal. Note that the application of Eq. (4) to account for nonlinearity between the fluorescence signal and concentration changed the diffusion coefficients by less than the uncertainties in the measurements.
3.1 Viscosity of brown limonene SOA
Figure 3 shows the viscosity of brown LSOA as a function of aw measured with the bead-mobility technique. For comparison, the known viscosity of pure water and the viscosity of brown LSOA measured previously using the poke-and-flow technique are also included (Hinks et al., 2016). Overall, Fig. 3 shows that the viscosity increases by 3–5 orders of magnitude as the aw decreases from 0.9 to approximately 0.05. An increase in viscosity with a decrease in aw is expected due to the plasticizing effect of water (Koop et al., 2011; Power et al., 2013; Zobrist et al., 2011). A liquid has a viscosity of <102 Pa s, a semisolid has a viscosity between 102 and 1012 Pa s, and an amorphous solid has a viscosity of >1012 Pa s (Koop et al., 2011; Mikhailov et al., 2009; Shiraiwa et al., 2011). Based on Fig. 3, the brown LSOA studied here can be considered as a liquid above an aw of 0.7 and as a semisolid at aw below roughly 0.5.
3.2 Diffusion coefficients and mixing times of intrinsic fluorophores in brown limonene SOA
Figure 4a shows the measured diffusion coefficients of the intrinsic fluorophores in brown LSOA as a function of aw. The average diffusion coefficient decreases from to cm2 s−1 as the aw decreases from 0.9 to 0.33. The strong dependence on aw is due to the plasticizing effect of water as mentioned above (Koop et al., 2011; Power et al., 2013; Zobrist et al., 2011). Also included in Fig. 4 (secondary y axis) is the mixing time of the intrinsic fluorophores by molecular diffusion within a 200 nm brown SOA particle based on the measured diffusion coefficients. Mixing times were calculated with the following equation (Seinfeld and Pandis, 2016; Shiraiwa et al., 2011):
where Dp is the diameter of the particle and Dorg the measured diffusion coefficient of the intrinsic fluorophore. The mixing time is the time after which the concentration of the diffusing molecules at the center of the particle deviates by less than 1∕e from the equilibrium concentration (Shiraiwa et al., 2011). Based on the measured diffusion coefficients, for the brown LSOA studied here mixing times of the organics within 200 nm particles range from 0.002 to 14 s for aw from 0.9 to 0.33.
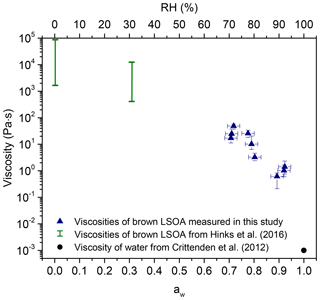
Figure 3Viscosity of brown LSOA as a function of aw (primary x axis) and RH (secondary x axis). The green bars show the viscosities that were measured by Hinks et al. (2016) and the blue triangles show the viscosities that were measured in this study using the bead-mobility technique. The black circle is the viscosity of water measured by Crittenden et al. (2012).
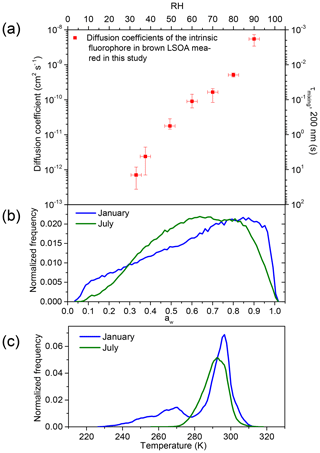
Figure 4(a) Measured diffusion coefficients of the intrinsic fluorophore in brown LSOA as a function of aw (primary x axis) and RH (secondary x axis). The secondary y axis shows the mixing time, which is the time that would be needed for intrinsic fluorophores to mix within a 200 nm brown limonene particle. The y error bars correspond to the highest and lowest diffusion coefficient measured. The x error bars correspond to uncertainty of the RH measurements (±2.5 %). (b) The aw distribution in January (blue line) and July (green line) in the planetary boundary layer (PBL) when monthly averaged concentrations of organic aerosol (OA) are >0.5 µg m−3 at the surface based on GEOS-Chem. (c) The temperature distribution in January and July in the PBL when monthly averaged concentrations of OA are >0.5 µg m−3 at the surface based on GEOS-Chem.
Also shown in Fig. 4 is the frequency distributions of aw (panel b) and temperatures (panel c) found in the planetary boundary layer for the months of January and July. We calculated these frequency distributions using GEOS-Chem version v10-01 (Pye et al., 2010), which was driven by 6 h average GEOS-5 meteorology fields. Following Maclean et al. (2017), when determining the frequency distributions of aw and temperatures within the PBL, we only included grid cells in a column up to the top of the PBL if the monthly averaged concentrations of organic aerosol (OA) were >0.5 µg m−3 at the surface, based on GEOS-Chem version v10-01 (Pye et al., 2010). Based on this model, OA concentrations were almost always <0.5 µg m−3 above the surface of the oceans. Hence, Fig. 4b, c do not include most conditions over the oceans. We excluded cases when OA concentrations were <0.5 µg m−3 at the surface since these concentrations are not expected to be important for climate or health. OA concentrations were >0.5 µg m−3 in all but one of the previous surface measurements of OA at remote locations (Spracklen et al., 2011).
Figure 4b shows that aw in the PBL is most often ≥0.33 when the organic mass concentrations are higher than 0.5 µg m−3 at the surface. Figure 4c shows that the temperature in the PBL is often within 5 K of the temperature used in our experiments (294.5 K). Based on Fig. 4, mixing times of intrinsic fluorophore in the brown LSOA studied here are often short (<1 h) for aw values and temperatures most often found in the PBL when the organic mass concentrations are higher than 0.5 µg m−3.
The diffusion coefficients and mixing times reported here correspond to brown LSOA generated using mass concentrations of 1000 µg m−3 in a flow reactor. For some types of SOA (SOA from ozonolysis of α-pinene, limonene, 3-hexenyl acetate and 3-hexen-1-ol) the viscosity of the SOA increases as the mass concentration used to generate the SOA decreases (Grayson et al., 2016; Jain et al., 2018). Since mass concentrations of biogenic SOA particles found in the atmosphere are most often ≤10 µg m−3 (Spracklen et al., 2011) the values reported here likely represent the lower limit for the viscosities and upper limit for the diffusion coefficients. Additional studies are needed to determine diffusion coefficients and mixing times for more atmospherically relevant mass concentrations. In addition, the brown LSOA was generated using a ratio of limonene to ozone ∼1, which suggests that not all double bonds in limonene were oxidized. Additional studies are also needed to determine if diffusion coefficients in brown LSOA are sensitive to the extent of oxidation of LSOA molecules.
Ye et al. (2018) studied the timescale for mixing of organics from toluene oxidation within limonene SOA particles using mass spectrometry (Ye et al., 2018). In these studies, the limonene SOA particles were generated with mass concentration of 16–22 µg m−3. Based on the studies by Ye et al. (2018) the mixing times of organics within limonene SOA particles are on the order of 3–4 h for RH values ranging from 10 % to 30 %, with little evidence for an RH dependence. At 33 % RH, we calculate a mixing time of approximately 14 s. This corresponds to a difference in diffusion coefficients of a factor of roughly 1000. A possible explanation for the apparent difference between the current results and the results reported by Ye et al. (2018) is the difference in the mass concentrations used to generate the SOA, and the low extent of oxidation of LSOA compounds, as discussed above.
3.3 Comparison between measured diffusion coefficients and Stokes–Einstein predictions
Shown in Fig. 5 are the measured diffusion coefficients and predicted diffusion coefficients based on viscosity measurements and the Stokes–Einstein relation. The viscosity measurements include our new bead-mobility viscosity results (Fig. 3) and previous poke–flow viscosity measurements by Hinks et al. (2016), as well as viscosity measurements of pure water for comparison (Crittenden et al., 2012; Hinks et al., 2016). To predict diffusion coefficients from the viscosity measurements and the Stokes–Einstein equation, the average dimension of the intrinsic fluorophores is needed. The exact molecular identities of the chromophores and fluorophores in brown LSOA is not known. Previous studies suggest that there is a distribution of chromophores with a broad range of molecular weights on the order of 500 g mol−1 (Nguyen et al., 2013). Therefore, we tested a range of molecular weights from 300 to 800 g mol−1, corresponding to hydrodynamic radii from 4.5 to 6.2 Å with an assumed density of 1.3 g cm−3 (Saathoff et al., 2009) and an assumed spherical geometry of the intrinsic fluorophores.
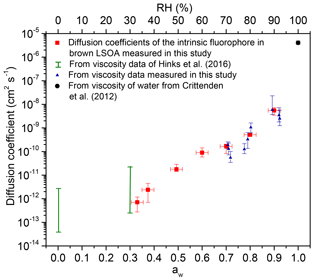
Figure 5Measured and calculated diffusion coefficients in brown LSOA as a function of aw (primary x axis) and RH (secondary x axis). The red squares show the measured diffusion coefficients of intrinsic fluorophores in brown LSOA. The blue triangles show the calculated diffusion coefficients of the intrinsic fluorophore in brown LSOA based on viscosities measured in this study using the bead-mobility technique and the Stokes–Einstein equation. The y error bars for the diffusion coefficients measured in this study (red squares) and the diffusion coefficients calculated from bead-mobility viscosity measurements (blue triangles) show the highest and lowest values measured. The green vertical bars depict the highest and the lowest limit of calculated diffusion coefficients of brown LSOA based on viscosity measurements from Hinks et al. (2016) and the Stokes–Einstein equation. The black circle depicts the calculated diffusion coefficient of the intrinsic fluorophore in pure water based on viscosity measurements of Crittenden et al. (2012) and the Stokes–Einstein equation. The uncertainties for the calculated diffusion coefficients take into account the uncertainty of the hydrodynamic radii of the diffusing molecules (4.5 to 6.2 Å).
Figure 5 shows that the difference between the measured and predicted diffusion coefficients is less than the uncertainty of the measurements for diffusion coefficients as small as roughly 10−12 cm2 s−1, which corresponds to a viscosity of between 4×102 and 1.2×104 Pa s, based on Fig. 4. This conclusion is consistent with most previous studies that have investigated the accuracy of the Stokes–Einstein relation for predicting diffusion coefficients of large organic molecules in organic–water mixtures. For example, Chenyakin et al. (2017), Champion et al. (1997), and Price et al. (2016) showed that the Stokes–Einstein relation predicts diffusion coefficients of large organics in sucrose–water solution consistent with measurements (i.e., within the uncertainty of the measurements) when the viscosity is 1×104 Pa s (Champion et al., 1997; Chenyakin et al., 2017; Price et al., 2016). In contrast, Longinotti and Corti (2007) and Corti et al. (2008) found disagreement between measured and predicted diffusion coefficients of large organics in organic–water solutions at slightly lower viscosities (Corti et al., 2008; Longinotti and Corti, 2007).
One physicochemical property of SOA particles that remains poorly understood is the diffusion rates of representative organics within SOA particles. To estimate diffusion rates of organics in realistic models for SOA particles, we (as well as other researchers) have used viscosity measurements together with the Stokes–Einstein relation. Until now, the accuracy of the Stokes–Einstein relation for predicting diffusion coefficients of organics in SOA particles had not been quantified, leading to uncertainties when estimating diffusion rates from viscosity measurements. In this study, we measured the viscosity of brown LSOA using the bead-mobility technique. From these viscosity values, we calculated diffusion coefficients of large organic molecules in brown LSOA. These calculated diffusion coefficient values were compared to diffusion coefficients of large organic molecules that were measured directly in brown LSOA using fluorescence recovery after photobleaching. We found that the Stokes–Einstein relation gives diffusion coefficients within the uncertainty of the measurements for brown LSOA matrices with viscosities between 0.2 and 1.2×104 Pa s.
In addition, mixing times in a 200 nm sized brown LSOA particle were calculated based on the measured diffusion coefficients. Mixing times were found to vary between 0.001 s at an aw of 0.9 and 14 s at an aw of 0.3. These results suggest that the mixing times of large organics in the brown LSOA studied here are short (<1 h) for aw and temperatures often found in the PBL. However, since the mixing times reported here correspond to brown LSOA generated using mass loadings of 1000 µg m−3, the mixing times are likely to be longer in ambient biogenic SOA particles typically found at mass loadings below 10 µg m−3 (Spracklen et al., 2011). Additional studies are needed using more atmospherically relevant mass concentrations, as well as the use of a range of oxidation conditions from “fresh” to “highly aged” SOA. The measurements reported here can be extended to lower mass loading conditions by using a multi-orifice impactor, which concentrates collected material into spots, and by collecting material for extended periods of time (e.g., several days) (Grayson et al., 2016).
Underlying material and related items for this paper are located in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-1491-2019-supplement.
DAU performed the viscosity and diffusion measurement. MLH and SAN provided the samples for analysis. AMM, CLB, KB, and JLJ provided RH and temperature data for the planetary boundary layer. JWG and SK provided assistance with the viscosity and diffusion measurements. DAU and AKB wrote the manuscript. All authors contributed toward revising and improving the manuscript. All authors read and approved the final manuscript.
The authors declare that they have no conflict of interest.
This work was funded by the Natural Science and Engineering Research Council
of Canada. Jose L. Jimenez was supported by DOE (BER/ASR) DE-SC0016559. Support from the
MJ Murdock Charitable Trust (grant 2012183) for computing infrastructure at
Portland State University is acknowledged.
Edited by: Alexander Laskin
Reviewed by: two anonymous referees
Adler, G., Koop, T., Haspel, C., Taraniuk, I., Moise, T., Koren, I., Heiblum, R. H., and Rudich, Y.: Formation of highly porous aerosol particles by atmospheric freeze-drying in ice clouds, P. Natl. Acad. Sci. USA, 110, 20414–20419, https://doi.org/10.1073/pnas.1317209110, 2013.
Axelrod, D., Koppel, D. E., Schlessinger, J., Elson, E., and Webb, W. W.: Mobility measurement by analysis of fluorescence photobleaching recovery kinetics, Biophys. J., 16, 1055–1069, https://doi.org/10.1016/S0006-3495(76)85755-4, 1976.
Baltensperger, U., Dommen, J., Alfarra, M. R., Duplissy, J., Gaeggeler, K., Metzger, A., Facchini, M. C., Decesari, S., Finessi, E., and Reinnig, C.: Combined determination of the chemical composition and of health effects of secondary organic aerosols: the POLYSOA project, J. Aerosol. Med. Pulm. D., 21, 145–154, https://doi.org/10.1089/jamp.2007.0655, 2008.
Bastelberger, S., Krieger, U. K., Luo, B., and Peter, T.: Diffusivity measurements of volatile organics in levitated viscous aerosol particles, Atmos. Chem. Phys., 17, 8453–8471, https://doi.org/10.5194/acp-17-8453-2017, 2017.
Bateman, A. P., Bertram, A. K., and Martin, S. T.: Hygroscopic Influence on the Semisolid-to-Liquid Transition of Secondary Organic Materials, J. Phys. Chem. A, 119, 4386–4395, https://doi.org/10.1021/jp508521c, 2015.
Booth, A. M., Murphy, B., Riipinen, I., Percival, C. J., and Topping, D. O.: Connecting Bulk Viscosity Measurements to Kinetic Limitations on Attaining Equilibrium for a Model Aerosol Composition, Environ. Sci. Technol., 48, 9298–9305, https://doi.org/10.1021/es501705c, 2014.
Boyd, C. M., Nah, T., Xu, L., Berkemeier, T., and Ng, N. L.: Secondary Organic Aerosol (SOA) from Nitrate Radical Oxidation of Monoterpenes: Effects of Temperature, Dilution, and Humidity on Aerosol Formation, Mixing, and Evaporation, Environ. Sci. Technol., 51, 7831–7841, https://doi.org/10.1021/acs.est.7b01460, 2017.
Champion, D., Hervet, H., Blond, G., Le Meste, M., and Simatos, D.: Translational Diffusion in Sucrose Solutions in the Vicinity of Their Glass Transition Temperature, J. Phys. Chem. B, 101, 10674–10679, https://doi.org/10.1021/jp971899i, 1997.
Chenyakin, Y., Ullmann, D. A., Evoy, E., Renbaum-Wolff, L., Kamal, S., and Bertram, A. K.: Diffusion coefficients of organic molecules in sucrose-water solutions and comparison with Stokes-Einstein predictions, Atmos. Chem. Phys., 17, 2423–2435, https://doi.org/10.5194/acp-17-2423-2017, 2017.
Chu, Y. and Chan, C. K.: Reactive Uptake of Dimethylamine by Ammonium Sulfate and Ammonium Sulfate–Sucrose Mixed Particles, J. Phys. Chem. A, 121, 206–215, https://doi.org/10.1021/acs.jpca.6b10692, 2017.
Clegg, S. L., Brimblecombe, P., and Wexler, A. S.: Thermodynamic Model of the System H+–––NO3–H2O at Tropospheric Temperatures, J. Phys. Chem. A, 102, 2137–2154, https://doi.org/10.1021/jp973042r, 1998.
Corti, H. R., Frank, G. A., and Marconi, M. C.: An Alternate Solution of Fluorescence Recovery Kinetics after Spot-Bleaching for Measuring Diffusion Coefficients. 2. Diffusion of Fluorescein in Aqueous Sucrose Solutions, J. Solution Chem., 37, 1593–1608, https://doi.org/10.1007/s10953-008-9329-4, 2008.
Crittenden, J. C., Trussell, R. R., Hand, D. W., Howe, K. J., and Tchobanoglous, G.: Physical and Chemical Quality of Water, in: MWH's Water Treatment: Principles and Design, Third Edition, John Wiley & Sons, Inc., 17–71, 2012.
Davies, J. F. and Wilson, K. R.: Nanoscale interfacial gradients formed by the reactive uptake of OH radicals onto viscous aerosol surfaces, Chem. Sci., 6, 7020–7027, https://doi.org/10.1039/c5sc02326b, 2015.
Deschout, H., Hagman, J., Fransson, S., Jonasson, J., Rudemo, M., Lorén, N., and Braeckmans, K.: Straightforward FRAP for quantitative diffusion measurements with a laser scanning microscope, Opt. Express, 18, 22886–22905, https://doi.org/10.1364/oe.18.022886, 2010.
Fonin, A. V., Sulatskaya, A. I., Kuznetsova, I. M., and Turoverov, K. K.: Fluorescence of Dyes in Solutions with High Absorbance. Inner Filter Effect Correction, PLoS ONE, 9, e103878, https://doi.org/10.1371/journal.pone.0103878, 2014.
Grayson, J. W., Song, M., Sellier, M., and Bertram, A. K.: Validation of the poke-flow technique combined with simulations of fluid flow for determining viscosities in samples with small volumes and high viscosities, Atmos. Meas. Tech., 8, 2463–2472, https://doi.org/10.5194/amt-8-2463-2015, 2015.
Grayson, J. W., Zhang, Y., Mutzel, A., Renbaum-Wolff, L., Böge, O., Kamal, S., Herrmann, H., Martin, S. T., and Bertram, A. K.: Effect of varying experimental conditions on the viscosity of α-pinene derived secondary organic material, Atmos. Chem. Phys., 16, 6027–6040, https://doi.org/10.5194/acp-16-6027-2016, 2016.
Grayson, J. W., Evoy, E., Song, M., Chu, Y., Maclean, A., Nguyen, A., Upshur, M. A., Ebrahimi, M., Chan, C. K., Geiger, F. M., Thomson, R. J., and Bertram, A. K.: The effect of hydroxyl functional groups and molar mass on the viscosity of non-crystalline organic and organic-water particles, Atmos. Chem. Phys., 17, 8509–8524, https://doi.org/10.5194/acp-17-8509-2017, 2017.
Gržinić, G., Bartels-Rausch, T., Berkemeier, T., Türler, A., and Ammann, M.: Viscosity controls humidity dependence of N2O5 uptake to citric acid aerosol, Atmos. Chem. Phys., 15, 13615–13625, https://doi.org/10.5194/acp-15-13615-2015, 2015.
Hallquist, M., Wenger, J. C., Baltensperger, U., Rudich, Y., Simpson, D., Claeys, M., Dommen, J., Donahue, N. M., George, C., Goldstein, A. H., Hamilton, J. F., Herrmann, H., Hoffmann, T., Iinuma, Y., Jang, M., Jenkin, M. E., Jimenez, J. L., Kiendler-Scharr, A., Maenhaut, W., McFiggans, G., Mentel, Th. F., Monod, A., Prévôt, A. S. H., Seinfeld, J. H., Surratt, J. D., Szmigielski, R., and Wildt, J.: The formation, properties and impact of secondary organic aerosol: current and emerging issues, Atmos. Chem. Phys., 9, 5155–5236, https://doi.org/10.5194/acp-9-5155-2009, 2009.
Hildebrandt Ruiz, L., Paciga, A. L., Cerully, K. M., Nenes, A., Donahue, N. M., and Pandis, S. N.: Formation and aging of secondary organic aerosol from toluene: changes in chemical composition, volatility, and hygroscopicity, Atmos. Chem. Phys., 15, 8301–8313, https://doi.org/10.5194/acp-15-8301-2015, 2015.
Hinks, M. L., Brady, M. V., Lignell, H., Song, M., Grayson, J. W., Bertram, A. K., Lin, P., Laskin, A., Laskin, J., and Nizkorodov, S. A.: Effect of viscosity on photodegradation rates in complex secondary organic aerosol materials, Phys. Chem. Chem. Phys., 18, 8785–8793, https://doi.org/10.1039/C5CP05226B, 2016.
Hosny, N. A., Fitzgerald, C., Tong, C., Kalberer, M., Kuimova, M. K., and Pope, F. D.: Fluorescent lifetime imaging of atmospheric aerosols: a direct probe of aerosol viscosity, Faraday Discuss., 165, 343–356, https://doi.org/10.1039/c3fd00041a, 2013.
Houle, F. A., Hinsberg, W. D., and Wilson, K. R.: Oxidation of a model alkane aerosol by OH radical: the emergent nature of reactive uptake, Phys. Chem. Chem. Phys., 17, 4412–4423, https://doi.org/10.1039/c4cp05093b, 2015.
Huff Hartz, K. E., Rosenørn, T., Ferchak, S. R., Raymond, T. M., Bilde, M., Donahue, N. M., and Pandis, S. N.: Cloud condensation nuclei activation of monoterpene and sesquiterpene secondary organic aerosol, J. Geophys. Res.-Atmos., 110, D14208, https://doi.org/10.1029/2004jd005754, 2005.
Jacobson, K., Wu, E., and Poste, G.: Measurement of the translation mobility of concanavalin a in glycerol-saline solutions and on the cell surface by fluorescence recovery after photobleaching, BBA-Biomembranes, 433, 215–222, https://doi.org/10.1016/0005-2736(76)90189-9, 1976.
Jain, S., Fischer, K. B., and Petrucci, G. A.: The Influence of Absolute Mass Loading of Secondary Organic Aerosols on Their Phase State, Atmosphere, 9, 131, https://doi.org/10.3390/atmos9040131, 2018.
Jang, M., Ghio, A. J., and Cao, G.: Exposure of BEAS-2B Cells to Secondary Organic Aerosol Coated on Magnetic Nanoparticles, Chem. Res. Toxicol., 19, 1044–1050, https://doi.org/10.1021/tx0503597, 2006.
Jimenez, J. L., Canagaratna, M. R., Donahue, N. M., Prevot, A. S. H., Zhang, Q., Kroll, J. H., DeCarlo, P. F., Allan, J. D., Coe, H., Ng, N. L., Aiken, A. C., Docherty, K. S., Ulbrich, I. M., Grieshop, A. P., Robinson, A. L., Duplissy, J., Smith, J. D., Wilson, K. R., Lanz, V. A., Hueglin, C., Sun, Y. L., Tian, J., Laaksonen, A., Raatikainen, T., Rautiainen, J., Vaattovaara, P., Ehn, M., Kulmala, M., Tomlinson, J. M., Collins, D. R., Cubison, M. J., Dunlea, J., Huffman, J. A., Onasch, T. B., Alfarra, M. R., Williams, P. I., Bower, K., Kondo, Y., Schneider, J., Drewnick, F., Borrmann, S., Weimer, S., Demerjian, K., Salcedo, D., Cottrell, L., Griffin, R., Takami, A., Miyoshi, T., Hatakeyama, S., Shimono, A., Sun, J. Y., Zhang, Y. M., Dzepina, K., Kimmel, J. R., Sueper, D., Jayne, J. T., Herndon, S. C., Trimborn, A. M., Williams, L. R., Wood, E. C., Middlebrook, A. M., Kolb, C. E., Baltensperger, U., and Worsnop, D. R.: Evolution of Organic Aerosols in the Atmosphere, Science, 326, 1525–1529, https://doi.org/10.1126/science.1180353, 2009.
Kanakidou, M., Seinfeld, J. H., Pandis, S. N., Barnes, I., Dentener, F. J., Facchini, M. C., Van Dingenen, R., Ervens, B., Nenes, A., Nielsen, C. J., Swietlicki, E., Putaud, J. P., Balkanski, Y., Fuzzi, S., Horth, J., Moortgat, G. K., Winterhalter, R., Myhre, C. E. L., Tsigaridis, K., Vignati, E., Stephanou, E. G., and Wilson, J.: Organic aerosol and global climate modelling: a review, Atmos. Chem. Phys., 5, 1053–1123, https://doi.org/10.5194/acp-5-1053-2005, 2005.
Knopf, D. A.: Thermodynamic properties and nucleation processes of upper tropospheric and lower stratospheric aerosol particles, Diss. ETH No. 15103, Zurich, Switzerland, ETH Zürich, 2003.
Koop, T., Kapilashrami, A., Molina, L. T., and Molina, M. J.: Phase transitions of sea-salt/water mixtures at low temperatures: Implications for ozone chemistry in the polar marine boundary layer, J. Geophys. Res.-Atmos., 105, 26393–26402, https://doi.org/10.1029/2000jd900413, 2000.
Koop, T., Bookhold, J., Shiraiwa, M., and Pöschl, U.: Glass transition and phase state of organic compounds: dependency on molecular properties and implications for secondary organic aerosols in the atmosphere, Phys. Chem. Chem. Phys., 13, 19238–19255, https://doi.org/10.1039/c1cp22617g, 2011.
Laskin, A., Laskin, J., and Nizkorodov, S. A.: Chemistry of Atmospheric Brown Carbon, Chem. Rev., 115, 4335–4382, https://doi.org/10.1021/cr5006167, 2015.
Laskin, J., Laskin, A., Roach, P. J., Slysz, G. W., Anderson, G. A., Nizkorodov, S. A., Bones, D. L., and Nguyen, L. Q.: High-Resolution Desorption Electrospray Ionization Mass Spectrometry for Chemical Characterization of Organic Aerosols, Anal. Chem., 82, 2048–2058, https://doi.org/10.1021/ac902801f, 2010.
Lee, H. D., Ray, K. K., and Tivanski, A. V.: Solid, Semisolid, and Liquid Phase States of Individual Submicrometer Particles Directly Probed Using Atomic Force Microscopy, Anal. Chem., 89, 12720–12726, https://doi.org/10.1021/acs.analchem.7b02755, 2017.
Lee, H. J., Laskin, A., Laskin, J., and Nizkorodov, S. A.: Excitation–Emission Spectra and Fluorescence Quantum Yields for Fresh and Aged Biogenic Secondary Organic Aerosols, Environ. Sci. Technol., 47, 5763–5770, https://doi.org/10.1021/es400644c, 2013.
Li, Y. J., Liu, P., Gong, Z., Wang, Y., Bateman, A. P., Bergoend, C., Bertram, A. K., and Martin, S. T.: Chemical Reactivity and Liquid/Nonliquid States of Secondary Organic Material, Environ. Sci. Technol., 49, 13264–13274, https://doi.org/10.1021/acs.est.5b03392, 2015.
Lignell, H., Hinks, M. L., and Nizkorodov, S. A.: Exploring matrix effects on photochemistry of organic aerosols, P. Natl. Acad. Sci. USA, 111, 13780–13785, https://doi.org/10.1073/pnas.1322106111, 2014.
Liu, P., Li, Y. J., Wang, Y., Gilles, M. K., Zaveri, R. A., Bertram, A. K., and Martin, S. T.: Lability of secondary organic particulate matter, P. Natl. Acad. Sci. USA, 113, 12643–12648, https://doi.org/10.1073/pnas.1603138113, 2016.
Longinotti, M. P. and Corti, H. R.: Diffusion of ferrocene methanol in super-cooled aqueous solutions using cylindrical microelectrodes, Electrochem. Commun., 9, 1444–1450, https://doi.org/10.1016/j.elecom.2007.02.003, 2007.
Maclean, A. M., Butenhoff, C. L., Grayson, J. W., Barsanti, K., Jimenez, J. L., and Bertram, A. K.: Mixing times of organic molecules within secondary organic aerosol particles: a global planetary boundary layer perspective, Atmos. Chem. Phys., 17, 13037–13048, https://doi.org/10.5194/acp-17-13037-2017, 2017.
Marsh, A., Rovelli, G., Song, Y.-C., Pereira, K. L., Willoughby, R. E., Bzdek, B. R., Hamilton, J. F., Orr-Ewing, A. J., Topping, D. O., and Reid, J. P.: Accurate representations of the physicochemical properties of atmospheric aerosols: when are laboratory measurements of value?, Faraday Discuss., 200, 639–661, 2017.
Massoli, P., Lambe, A. T., Ahern, A. T., Williams, L. R., Ehn, M., Mikkilä, J., Canagaratna, M. R., Brune, W. H., Onasch, T. B., Jayne, J. T., Petäjä, T., Kulmala, M., Laaksonen, A., Kolb, C. E., Davidovits, P., and Worsnop, D. R.: Relationship between aerosol oxidation level and hygroscopic properties of laboratory generated secondary organic aerosol (SOA) particles, Geophys. Res. Lett., 37, L24801, https://doi.org/10.1029/2010gl045258, 2010.
Meyvis, T. L., De Smedt, S., Van Oostveldt, P., and Demeester, J.: Fluorescence Recovery After Photobleaching: A Versatile Tool for Mobility and Interaction Measurements in Pharmaceutical Research, Pharm. Res., 16, 1153–1162, https://doi.org/10.1023/a:1011924909138, 1999.
Mikhailov, E., Vlasenko, S., Martin, S. T., Koop, T., and Pöschl, U.: Amorphous and crystalline aerosol particles interacting with water vapor: conceptual framework and experimental evidence for restructuring, phase transitions and kinetic limitations, Atmos. Chem. Phys., 9, 9491–9522, https://doi.org/10.5194/acp-9-9491-2009, 2009.
Murray, B. J., Wilson, T. W., Dobbie, S., Cui, Z., Al-Jumur, S. M. R. K., Mohler, O., Schnaiter, M., Wagner, R., Benz, S., Niemand, M., Saathoff, H., Ebert, V., Wagner, S., and Karcher, B.: Heterogeneous nucleation of ice particles on glassy aerosols under cirrus conditions, Nat. Geosci., 3, 233–237, https://doi.org/10.1038/ngeo817, 2010.
Nguyen, T. B., Laskin, A., Laskin, J., and Nizkorodov, S. A.: Brown carbon formation from ketoaldehydes of biogenic monoterpenes, Faraday Discuss., 165, 473–494, https://doi.org/10.1039/c3fd00036b, 2013.
Nozière, B., Kalberer, M., Claeys, M., Allan, J., D'Anna, B., Decesari, S., Finessi, E., Glasius, M., Grgić, I., Hamilton, J. F., Hoffmann, T., Iinuma, Y., Jaoui, M., Kahnt, A., Kampf, C. J., Kourtchev, I., Maenhaut, W., Marsden, N., Saarikoski, S., Schnelle-Kreis, J., Surratt, J. D., Szidat, S., Szmigielski, R., and Wisthaler, A.: The Molecular Identification of Organic Compounds in the Atmosphere: State of the Art and Challenges, Chem. Rev., 115, 3919–3983, https://doi.org/10.1021/cr5003485, 2015.
Perraud, V., Bruns, E. A., Ezell, M. J., Johnson, S. N., Yu, Y., Alexander, M. L., Zelenyuk, A., Imre, D., Chang, W. L., Dabdub, D., Pankow, J. F., and Finlayson-Pitts, B. J.: Nonequilibrium atmospheric secondary organic aerosol formation and growth, P. Natl. Acad. Sci. USA, 109, 2836–2841, https://doi.org/10.1073/pnas.1119909109, 2012.
Pöschl, U. and Shiraiwa, M.: Multiphase Chemistry at the Atmosphere-Biosphere Interface Influencing Climate and Public Health in the Anthropocene, Chem. Rev., 115, 4440–4475, https://doi.org/10.1021/cr500487s, 2015.
Power, R. M., Simpson, S. H., Reid, J. P., and Hudson, A. J.: The transition from liquid to solid-like behaviour in ultrahigh viscosity aerosol particles, Chem. Sci., 4, 2597–2604, https://doi.org/10.1039/c3sc50682g, 2013.
Price, H. C., Mattsson, J., Zhang, Y., Bertram, A. K., Davies, J. F., Grayson, J. W., Martin, S. T., O'Sullivan, D., Reid, J. P., and Rickards, A. M.: Water diffusion in atmospherically relevant α-pinene secondary organic material, Chem. Sci., 6, 4876–4883, 2015.
Price, H. C., Mattsson, J., and Murray, B. J.: Sucrose diffusion in aqueous solution, Phys. Chem. Chem. Phys., 18, 19207–19216, https://doi.org/10.1039/C6CP03238A, 2016.
Pye, H. O. T., Chan, A. W. H., Barkley, M. P., and Seinfeld, J. H.: Global modeling of organic aerosol: the importance of reactive nitrogen (NOx and NO3), Atmos. Chem. Phys., 10, 11261–11276, https://doi.org/10.5194/acp-10-11261-2010, 2010.
Reid, J. P., Bertram, A. K., Topping, D. O., Laskin, A., Martin, S. T., Petters, M. D., Pope, F. D., and Rovelli, G.: The viscosity of atmospherically relevant organic particles, Nat. Commun., 9, 956, https://doi.org/10.1038/s41467-018-03027-z, 2018.
Renbaum-Wolff, L., Grayson, J. W., Bateman, A. P., Kuwata, M., Sellier, M., Murray, B. J., Shilling, J. E., Martin, S. T., and Bertram, A. K.: Viscosity of α-pinene secondary organic material and implications for particle growth and reactivity, P. Natl. Acad. Sci. USA, 110, 8014–8019, https://doi.org/10.1073/pnas.1219548110, 2013a.
Renbaum-Wolff, L., Grayson, J. W., and Bertram, A. K.: Technical Note: New methodology for measuring viscosities in small volumes characteristic of environmental chamber particle samples, Atmos. Chem. Phys., 13, 791–802, https://doi.org/10.5194/acp-13-791-2013, 2013b.
Riipinen, I., Pierce, J. R., Yli-Juuti, T., Nieminen, T., Häkkinen, S., Ehn, M., Junninen, H., Lehtipalo, K., Petäjä, T., Slowik, J., Chang, R., Shantz, N. C., Abbatt, J., Leaitch, W. R., Kerminen, V.-M., Worsnop, D. R., Pandis, S. N., Donahue, N. M., and Kulmala, M.: Organic condensation: a vital link connecting aerosol formation to cloud condensation nuclei (CCN) concentrations, Atmos. Chem. Phys., 11, 3865–3878, https://doi.org/10.5194/acp-11-3865-2011, 2011.
Robinson, C. B., Schill, G. P., and Tolbert, M. A.: Optical growth of highly viscous organic/sulfate particles, J. Atmos. Chem., 71, 145–156, https://doi.org/10.1007/s10874-014-9287-8, 2014.
Saathoff, H., Naumann, K.-H., Möhler, O., Jonsson, Å. M., Hallquist, M., Kiendler-Scharr, A., Mentel, Th. F., Tillmann, R., and Schurath, U.: Temperature dependence of yields of secondary organic aerosols from the ozonolysis of a-pinene and limonene, Atmos. Chem. Phys., 9, 1551–1577, https://doi.org/10.5194/acp-9-1551-2009, 2009.
Schneider, C. A., Rasband, W. S., and Eliceiri, K. W.: NIH Image to ImageJ: 25 years of image analysis, Nat. Methods, 9, 671–675, 2012.
Seinfeld, J. H. and Pandis, S. N.: Atmospheric chemistry and physics: from air pollution to climate change, John Wiley & Sons, Hoboken, NJ, USA, 2016.
Seksek, O., Biwersi, J., and Verkman, A. S.: Translational Diffusion of Macromolecule-sized Solutes in Cytoplasm and Nucleus, J. Cell. Biol., 138, 131–142, https://doi.org/10.1083/jcb.138.1.131, 1997.
Shiraiwa, M., Ammann, M., Koop, T., and Pöschl, U.: Gas uptake and chemical aging of semisolid organic aerosol particles, P. Natl. Acad. Sci. USA, 108, 11003–11008, https://doi.org/10.1073/pnas.1103045108, 2011.
Shiraiwa, M. and Seinfeld, J. H.: Equilibration timescale of atmospheric secondary organic aerosol partitioning, Geophys. Res. Lett., 39, L24801, https://doi.org/10.1029/2012gl054008, 2012.
Shiraiwa, M., Zuend, A., Bertram, A. K., and Seinfeld, J. H.: Gas–particle partitioning of atmospheric aerosols: interplay of physical state, non-ideal mixing and morphology, Phys. Chem. Chem. Phys., 15, 11441–11453, 2013.
Shiraiwa, M., Li, Y., Tsimpidi, A. P., Karydis, V. A., Berkemeier, T., Pandis, S. N., Lelieveld, J., Koop, T., and Pöschl, U.: Global distribution of particle phase state in atmospheric secondary organic aerosols, Nat. Commun., 8, 15002, https://doi.org/10.1038/ncomms15002, 2017a.
Shiraiwa, M., Ueda, K., Pozzer, A., Lammel, G., Kampf, C. J., Fushimi, A., Enami, S., Arangio, A. M., Frohlich-Nowoisky, J., Fujitani, Y., Furuyama, A., Lakey, P. S. J., Lelieveld, J., Lucas, K., Morino, Y., Pöschl, U., Takaharna, S., Takami, A., Tong, H. J., Weber, B., Yoshino, A., and Sato, K.: Aerosol Health Effects from Molecular to Global Scales, Environ. Sci. Technol., 51, 13545–13567, https://doi.org/10.1021/acs.est.7b04417, 2017b.
Shrivastava, M., Cappa, C. D., Fan, J., Goldstein, A. H., Guenther, A. B., Jimenez, J. L., Kuang, C., Laskin, A., Martin, S. T., Ng, N. L., Petaja, T., Pierce, J. R., Rasch, P. J., Roldin, P., Seinfeld, J. H., Shilling, J., Smith, J. N., Thornton, J. A., Volkamer, R., Wang, J., Worsnop, D. R., Zaveri, R. A., Zelenyuk, A., and Zhang, Q.: Recent advances in understanding secondary organic aerosol: Implications for global climate forcing, Rev. Geophys., 55, 509–559, https://doi.org/10.1002/2016rg000540, 2017a.
Shrivastava, M., Lou, S., Zelenyuk, A., Easter, R. C., Corley, R. A., Thrall, B. D., Rasch, P. J., Fast, J. D., Massey Simonich, S. L., Shen, H., and Tao, S.: Global long-range transport and lung cancer risk from polycyclic aromatic hydrocarbons shielded by coatings of organic aerosol, P. Natl. Acad. Sci. USA, 114, 1246–1251, https://doi.org/10.1073/pnas.1618475114, 2017b.
Sindelarova, K., Granier, C., Bouarar, I., Guenther, A., Tilmes, S., Stavrakou, T., Müller, J.-F., Kuhn, U., Stefani, P., and Knorr, W.: Global data set of biogenic VOC emissions calculated by the MEGAN model over the last 30 years, Atmos. Chem. Phys., 14, 9317–9341, https://doi.org/10.5194/acp-14-9317-2014, 2014.
Sinnecker, D., Voigt, P., Hellwig, N., and Schaefer, M.: Reversible Photobleaching of Enhanced Green Fluorescent Proteins, Biochemistry, 44, 7085–7094, https://doi.org/10.1021/bi047881x, 2005.
Solomon, S.: Climate change 2007 – the physical science basis: Working group I contribution to the fourth assessment report of the IPCC, Cambridge University Press, Cambridge, UK and New York, NY, USA, 2007.
Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K. B., Tignor, M., and Miller, H. L.: IPCC Fourth Assessment Report: Climate Change 2007: The Physical Science Basis: Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, UK and New York, NY, USA, 996 pp., 2007.
Song, M., Liu, P. F., Hanna, S. J., Li, Y. J., Martin, S. T., and Bertram, A. K.: Relative humidity-dependent viscosities of isoprene-derived secondary organic material and atmospheric implications for isoprene-dominant forests, Atmos. Chem. Phys., 15, 5145–5159, https://doi.org/10.5194/acp-15-5145-2015, 2015.
Song, M., Liu, P. F., Hanna, S. J., Zaveri, R. A., Potter, K., You, Y., Martin, S. T., and Bertram, A. K.: Relative humidity-dependent viscosity of secondary organic material from toluene photo-oxidation and possible implications for organic particulate matter over megacities, Atmos. Chem. Phys., 16, 8817–8830, https://doi.org/10.5194/acp-16-8817-2016, 2016.
Spracklen, D. V., Jimenez, J. L., Carslaw, K. S., Worsnop, D. R., Evans, M. J., Mann, G. W., Zhang, Q., Canagaratna, M. R., Allan, J., Coe, H., McFiggans, G., Rap, A., and Forster, P.: Aerosol mass spectrometer constraint on the global secondary organic aerosol budget, Atmos. Chem. Phys., 11, 12109–12136, https://doi.org/10.5194/acp-11-12109-2011, 2011.
Stout, A. L. and Axelrod, D.: Spontaneous recovery of fluorescence by photobleached surface-adsorbed proteins, Photochem. Photobiol., 62, 239–244, https://doi.org/10.1111/j.1751-1097.1995.tb05264.x, 1995.
Taina, Y. J., Aki, P., Olli-Pekka, T., Angela, B., Celia, F., Olli, V., Liqing, H., Eetu, K., Otso, P., Olga, G., Manabu, S., Mikael, E., Kari, L., and Annele, V.: Factors controlling the evaporation of secondary organic aerosol from α-pinene ozonolysis, Geophys. Res. Lett., 44, 2562–2570, https://doi.org/10.1002/2016GL072364, 2017.
Verkman, A. S.: [28] Diffusion in cells measured by fluorescence recovery after photobleaching, Method. Enzymol., 360, 635–648, https://doi.org/10.1016/S0076-6879(03)60132-1, 2003.
Wagner, R., Höhler, K., Huang, W., Kiselev, A., Möhler, O., Mohr, C., Pajunoja, A., Saathoff, H., Schiebel, T., and Shen, X.: Heterogeneous ice nucleation of α-pinene SOA particles before and after ice cloud processing, J. Geophys. Res.-Atmos., 122, 4924–4943, 2017.
Wang, B., Lambe, A. T., Massoli, P., Onasch, T. B., Davidovits, P., Worsnop, D. R., and Knopf, D. A.: The deposition ice nucleation and immersion freezing potential of amorphous secondary organic aerosol: Pathways for ice and mixed-phase cloud formation, J. Geophys. Res.-Atmos., 117, D16209, https://doi.org/10.1029/2012jd018063, 2012.
Wang, B., O'Brien, R. E., Kelly, S. T., Shilling, J. E., Moffet, R. C., Gilles, M. K., and Laskin, A.: Reactivity of Liquid and Semisolid Secondary Organic Carbon with Chloride and Nitrate in Atmospheric Aerosols, J. Phys. Chem. A, 119, 4498–4508, https://doi.org/10.1021/jp510336q, 2015.
Ye, Q., Robinson, E. S., Ding, X., Ye, P., Sullivan, R. C., and Donahue, N. M.: Mixing of secondary organic aerosols versus relative humidity, P. Natl. Acad. Sci. USA, 113, 12649–12654, https://doi.org/10.1073/pnas.1604536113, 2016.
Ye, Q., Upshur, M. A., Robinson, E. S., Geiger, F. M., Sullivan, R. C., Thomson, R. J., and Donahue, N. M.: Following Particle-Particle Mixing in Atmospheric Secondary Organic Aerosols by Using Isotopically Labeled Terpenes, Chem, 4, 318–333, https://doi.org/10.1016/j.chempr.2017.12.008, 2018.
Zaveri, R. A., Easter, R. C., Shilling, J. E., and Seinfeld, J. H.: Modeling kinetic partitioning of secondary organic aerosol and size distribution dynamics: representing effects of volatility, phase state, and particle-phase reaction, Atmos. Chem. Phys., 14, 5153–5181, https://doi.org/10.5194/acp-14-5153-2014, 2014.
Zaveri, R. A., Shilling, J. E., Zelenyuk, A., Liu, J., Bell, D. M., D'Ambro, E. L., Gaston, C. J., Thornton, J. A., Laskin, A., Lin, P., Wilson, J., Easter, R. C., Wang, J., Bertram, A. K., Martin, S. T., Seinfeld, J. H., and Worsnop, D. R.: Growth Kinetics and Size Distribution Dynamics of Viscous Secondary Organic Aerosol, Environ. Sci. Technol., 52, 1191–1199, https://doi.org/10.1021/acs.est.7b04623, 2018.
Zelenyuk, A., Imre, D., Beránek, J., Abramson, E., Wilson, J., and Shrivastava, M.: Synergy between Secondary Organic Aerosols and Long-Range Transport of Polycyclic Aromatic Hydrocarbons, Environ. Sci. Technol., 46, 12459–12466, https://doi.org/10.1021/es302743z, 2012.
Zhang, Y., Sanchez, M. S., Douet, C., Wang, Y., Bateman, A. P., Gong, Z., Kuwata, M., Renbaum-Wolff, L., Sato, B. B., Liu, P. F., Bertram, A. K., Geiger, F. M., and Martin, S. T.: Changing shapes and implied viscosities of suspended submicron particles, Atmos. Chem. Phys., 15, 7819–7829, https://doi.org/10.5194/acp-15-7819-2015, 2015.
Zhou, S., Lee, A. K. Y., McWhinney, R. D., and Abbatt, J. P. D.: Burial Effects of Organic Coatings on the Heterogeneous Reactivity of Particle-Borne Benzo[a]pyrene (BaP) toward Ozone, J. Phys. Chem. A, 116, 7050–7056, https://doi.org/10.1021/jp3030705, 2012.
Zobrist, B., Soonsin, V., Luo, B. P., Krieger, U. K., Marcolli, C., Peter, T., and Koop, T.: Ultra-slow water diffusion in aqueous sucrose glasses, Phys. Chem. Chem. Phys., 13, 3514–3526, https://doi.org/10.1039/C0CP01273D, 2011.





