the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Understanding aerosol–cloud interactions through modeling the development of orographic cumulus congestus during IPHEx
Yajuan Duan
Markus D. Petters
A new cloud parcel model (CPM) including activation, condensation, collision–coalescence, and lateral entrainment processes is used to investigate aerosol–cloud interactions (ACIs) in cumulus development prior to rainfall onset. The CPM was applied with surface aerosol measurements to predict the vertical structure of cloud development at early stages, and the model results were evaluated against airborne observations of cloud microphysics and thermodynamic conditions collected during the Integrated Precipitation and Hydrology Experiment (IPHEx) in the inner region of the southern Appalachian Mountains (SAM). Sensitivity analysis was conducted to examine the model response to variations in key ACI physiochemical parameters and initial conditions. The CPM sensitivities mirror those found in parcel models without entrainment and collision–coalescence, except for the evolution of the droplet spectrum and liquid water content with height. Simulated cloud droplet number concentrations (CDNCs) exhibit high sensitivity to variations in the initial aerosol concentration at cloud base, but weak sensitivity to bulk aerosol hygroscopicity. The condensation coefficient ac plays a governing role in determining the evolution of CDNC, liquid water content (LWC), and cloud droplet spectra (CDS) in time and with height. Lower values of ac lead to higher CDNCs and broader CDS above cloud base, and higher maximum supersaturation near cloud base. Analysis of model simulations reveals that competitive interference among turbulent dispersion, activation, and droplet growth processes modulates spectral width and explains the emergence of bimodal CDS and CDNC heterogeneity in aircraft measurements from different cloud regions and at different heights. Parameterization of nonlinear interactions among entrainment, condensational growth, and collision–coalescence processes is therefore necessary to simulate the vertical structures of CDNCs and CDSs in convective clouds. Comparisons of model predictions with data suggest that the representation of lateral entrainment remains challenging due to the spatial heterogeneity of the convective boundary layer and the intricate 3-D circulations in mountainous regions.
- Article
(10672 KB) -
Supplement
(30846 KB) - BibTeX
- EndNote
Atmospheric aerosols produced by dramatically increased industrialization and urbanization exert a large impact on the climate system and the hydrological cycle (Koren et al., 2008; Ramanathan et al., 2001; Tao et al., 2012). Aerosols influence the Earth–atmosphere system primarily via two mechanisms: a radiative (direct) effect and a microphysical (indirect) effect (Rosenfeld et al., 2008). The direct effect on the Earth's energy budget occurs via the scattering and absorption of shortwave and longwave radiation in the atmosphere, hence modulating the net radiation and climate (Haywood and Boucher, 2000; Ramanathan et al., 2001). The indirect effect is related to aerosols as cloud condensation nuclei (CCN) or ice nuclei (IN) alter microphysical properties and consequently affect cloud radiative properties and precipitation efficiency (Jiang et al., 2008; Lohmann and Feichter, 2005; McFiggans et al., 2006). In particular, an increase in aerosol concentration results in an enhanced cloud droplet number concentration (CDNC), smaller average drop size, and increased cloud albedo (Twomey, 1977). Smaller cloud droplets are associated with lower collection and coalescence efficiency, slower drop growth, and reduced precipitation, thus leading to longer cloud lifetimes (Albrecht, 1989; Andreae and Rosenfeld, 2008; Khain et al., 2005). Over complex terrain in California and Israel, Givati and Rosenfeld (2004) attributed a reduction in annual precipitation of 15 %–25 % to air-pollution aerosols from upwind urban areas. By comparing two scenarios of maritime and continental aerosols, Lynn et al. (2007) found that simulations with maritime aerosols with relatively lower aerosol number concentrations yielded 30 % more precipitation than continental aerosols over a mountain slope. Such local effects can translate into large spatial shifts in clouds and precipitation, as aerosol–cloud interactions (ACIs) inducing suppression of precipitation upwind could give rise to the enhancement of precipitation downwind (Muhlbauer and Lohmann, 2008), thus modifying the spatial distribution of orographic precipitation, transferring precipitation from one watershed to another, and strongly influencing the local and regional hydrology. Yang et al. (2016) examined the reasons for warm rain suppression due to increased air pollution in the Mt. Hua area in central China. They demonstrated that weakened valley–ridge circulations because of aerosol–radiation interactions and lower water vapor concentrations in the valley led to the suppression of convection and precipitation in the mountain. A study of thermally driven orographic clouds over a tropical island during the Dominica Experiment (DOMEX) field campaign found that atmospheric moisture was the predominant constraint in cloud and precipitation formation over the aerosol effect, and the surface aerosol source has the strongest influence on precipitation under unfavorable environmental conditions for cloud growth (Nugent et al., 2016). Barros et al. (2018) showed that model simulations using aerosol activation spectra from local sources and activation spectra from remote aerosol sources resulted in a significant spatial and temporal redistribution of precipitation in the central Himalayas, including changes in cloud dynamics and the vertical distribution of hydrometeors. The latter is the basis for remote sensing measurements of precipitation, and therefore understanding how ACIs modify precipitation structure is key to improving retrievals in mountainous regions (e.g., Duan et al., 2015).
In the southern Appalachian Mountains (SAM, Fig. 1), persistent low-level clouds and fog (LLCF) play a governing role in warm-season rainfall by increasing the frequency and duration of light rainfall and drizzle, and by enhancing storm rainfall via seeder–feeder interactions (SFIs; Wilson and Barros, 2014, 2015 and 2017; Duan and Barros, 2017). SFI refers to the modification of cloud and raindrop size distributions when precipitation from above (seeder clouds) falls through lower cloud layers (feeder clouds) to significantly enhance drop collision–coalescence efficiency and rainfall rates. Albeit with large spatial variability, microphysical observations and idealized model simulations of the dynamical evolution of raindrop size distributions (RDSDs) with height show that SFIs in the lower atmosphere can explain a 1 order of magnitude increase in rainfall rate at low elevations in the SAM similar to orographic enhancement at higher elevations. Understanding and modeling the spatial variability of the vertical microstructure of clouds in complex terrain is therefore key to understanding precipitation processes toward improving rainfall estimation and prediction. Whereas previous studies linked LLCF in the SAM to high biogenic aerosol loading produced locally with occasional influx from remote pollution sources (Link et al., 2015; Lowenthal et al., 2009), a quantitative understanding of the indirect effect of aerosols on clouds with implications for precipitation dynamics including SFIs is lacking. The purpose of this study is to investigate ACI-integrating models and observations collected during IPHEx (Integrated Precipitation and Hydrology Experiment; Barros et al., 2014) with a focus on the evolution of cloud droplet spectra (CDS) with height. This is an important first step toward understanding spatial variability in the vertical structure of cloud microphysics that underlies the observed spatial and temporal heterogeneity of SFIs.
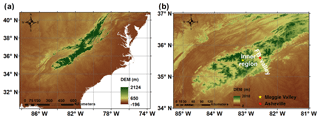
Figure 1(a) Study region of the IPHEx campaign in the SAM (highlighted in the black box), as shown in context of a large-scale map of the southeastern United States. (b) Topographic map of the SAM including the two ground-based IPHEx observation sites referred to in this study. FB valley denotes French Broad valley.
The representation of clouds and precipitation in numerical models relies on parameterizations of multi-scale processes with uncertainty that depends on the model temporal and spatial resolution (Khairoutdinov et al., 2005; Randall et al., 2003). For example, the characteristic timescale of condensational growth of submicron-size droplets is on the order of 1 ms, and length scales of individual drops range from micrometers to centimeters (Pinsky and Khain, 2002), which is a scale gap of 5 to 9 orders of magnitude with respect to the spatial resolution of cloud-resolving models (km). Detailed 2-D and 3-D models that explicitly resolve cloud formation and microphysical processes with varying degrees of completeness are available in the literature (Fan et al., 2009; Leroy et al., 2009; Muhlbauer et al., 2010). However, the wide range of length (µm–m) and timescales (ms–s) associated with aerosol–cloud–precipitation interactions (ACPIs) poses significant challenges for model spatial and temporal resolution. Analysis of high resolution (∼1 km) numerical weather prediction (NWP) simulations in the SAM for various hydrometeorological regimes using different Weather Research and Forecasting (WRF) physical parameterizations concluded that cloud development and cloud vertical microphysical structure are inadequate to predict the spatial and temporal variability of rainfall rate and rainfall microphysics at the ground (Wilson and Barros, 2015, 2017). In particular, WRF simulations using six different microphysical parameterization schemes were analyzed to characterize the spatiotemporal evolution of low-level moisture fields in the SAM under weak and strong synoptic conditions. The simulations could not capture persistent LLCF and, in particular, the midday rainfall peak observed in this region (Duan and Barros, 2017; Wilson and Barros, 2015). Furthermore, simulations exploring the use of different planetary boundary layer (PBL) parameterizations in WRF could not replicate the observed vertical structure of LLCF, thus failing to reproduce the reverse orographic enhancement linked to SFI and consequently underestimating surface rainfall intensity (Duan and Barros, 2017; Wilson and Barros, 2014, 2015, 2017).
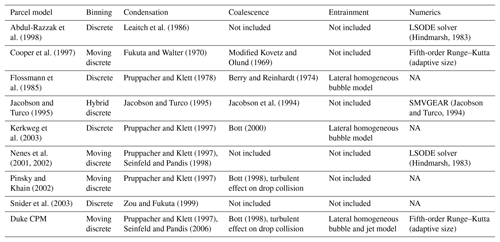
An alternative modeling approach to investigate ACI at fine resolution is the cloud parcel model (CPM). Typically, CPMs simulate aerosol activation and cloud droplet growth, as well as thermodynamic adaptation of ascending air parcels at micrometer and millisecond scales (Abdul-Razzak et al., 1998; Cooper et al., 1997; Flossmann et al., 1985; Jacobson and Turco, 1995; Kerkweg et al., 2003; Nenes et al., 2001; Pinsky and Khain, 2002; Snider et al., 2003). A synthesis of model formulations including spectral binning strategy, principal physical processes (i.e., condensational growth, collision–coalescence, entrainment), and numerical implementation is presented in Table 1 for CPMs frequently referred to in the peer-reviewed literature. The CPM used in this study (the Duke CPM, DCPM) explicitly solves the cloud microphysics of condensation, collision–coalescence, and lateral entrainment processes (first reported by Duan et al., 2017; Duan, 2017). The DCPM was formulated and implemented to be seamlessly coupled to an existing rainfall microphysics column model describing the stochastic dynamics of raindrop size distributions (bounce, collision–coalescence, and breakup mechanisms) (Prat and Barros, 2007b; Prat et al., 2012; Testik et al., 2011), which in turn is coupled to a radar model. The overarching motivation for the coupled parcel–rainshaft model is to simulate end-to-end ACPIs from the time of CN (condensation nuclei) activation to the time raindrops reach the ground. This framework enables investigating the impact of aerosol heterogeneity on the vertical structure of warm-season precipitation, and ultimately how this affects radar reflectivity measurements and quantitative precipitation estimation (QPE). Here, the focus is strictly on ACI leveraging IPHEx observations to drive, constrain, and evaluate the model.
Table 1Cloud parcel models with detailed microphysics from the literature and in this study (Duke CPM). NA denotes information is not described in the reference paper.
The paper is organized as follows. The mathematical formulation of the cloud parcel model is described in Sect. 2. Section 3 presents the IPHEx measurements relevant for the modeling study, followed by model sensitivity tests and a comparison of model results with in situ observations in Sect. 4. Finally, the main research findings and outlook of ongoing and future research are presented in Sect. 5.
A new cloud parcel model (or Duke CPM – DCPM – for specificity) was developed to explicitly solve key cloud microphysical processes and predict the evolution of cloud droplet spectra originating from aerosol distributions of uniform chemical composition (see the last row of Table 1 for details). The model synthesizes well-established theories and physical parameterizations in the literature. In particular, condensation and lateral homogeneous entrainment follow the formulations of Pruppacher and Klett (1997) and Seinfeld and Pandis (2006), modified to incorporate the single parameter representation of aerosol hygroscopicity (Petters and Kreidenweis, 2007). The representation of collision–coalescence processes takes into account the variation of collision efficiencies with height (Pinsky et al., 2001) and the effects of turbulence on drop collision efficiency as per Pinsky et al. (2008).
The model discretizes the CDS on a finite number of bins (nbin) using a discrete geometric volume-size distribution, spanning a large size range with fewer bins and a very fine discretization in the small droplet sizes to improve computational efficiency (Kumar and Ramkrishna, 1996; Prat and Barros, 2007a). The characteristic single-particle volumes in adjacent bins are expressed as , where Vrat is a constant volume ratio (Jacobson, 2005). When condensation and coalescence are solved simultaneously, a traditional stationary (time-invariant) grid structure often introduces artificial broadening of the droplet spectrum by reassigning droplets to fixed bins through interpolation that is numerical diffusion (Cooper et al., 1997; Pinsky and Khain, 2002). To eliminate numerical diffusion artifacts, the model implementation relies on a moving grid structure so that an initial size distribution can change with time according to condensational growth. This approach allows particles in each bin to grow by condensation to their exact transient sizes without partitioning between adjacent size bins. Subsequently, collision and coalescence are resolved on the moving bins that evolve from condensation. The DCPM predicts number and volume concentrations of cloud droplets and interstitial aerosols, liquid water content (LWC), effective drop radius, reflectivity, and other moments of the cloud droplet size distribution. It also tracks thermodynamic conditions (e.g., supersaturation, temperature, pressure) of the rising air parcel. The flowchart in Fig. 2 describes the key elements and linkages in the parcel model, including microphysical processes, and main inputs and outputs. The performance of the DCPM was first evaluated by comparing its dependence on different parameters with the results from the numerical simulations reported by Ghan et al. (2011) in Sect. S1 of the Supplement. Specifically, Figs. S1–S6 in the Supplement demonstrate that the simulated maximum supersaturation and number fraction activated from the DCPM are in good agreement with the numerical solutions in Ghan et al. (2011) for a wide range of updraft velocities, aerosol number concentrations, geometric mean radii, geometric standard deviations, hygroscopicity, and condensation coefficients. Model formulation of key processes is detailed below. A glossary of symbols as well as auxiliary formulae are given in Appendix A.
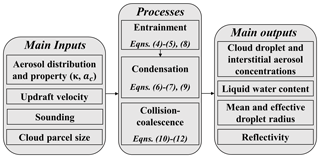
Figure 2Flowchart of the main inputs, microphysical processes, and main outputs of the DCPM. Equation numbers refer to formulae in Sect. 2.
2.1 Condensation growth with entrainment
The time variation of the parcel's temperature (T) can be written as
where the first two terms on the right-hand side represent the adiabatic cooling of a rising parcel, and the third term describes the modulation by entraining ambient dry air with entrainment rate μ. The vertical profiles of the ambient temperature (T′) and water vapor mixing ratio () can be interpolated from input sounding data from atmospheric model simulations or radiosonde observations.
The change of the water vapor mixing ratio (wv) in the parcel over time is described by
The change of the parcel's velocity (V) is given by
where γ=0.5 to include the effect of induced mass acceleration introduced by Turner (1963).
Due to significant uncertainties and complexities of entrainment and turbulent mixing (Khain et al., 2000), only lateral entrainment that mixes in ambient air instantaneously and is homogeneous in the parcel is considered in the DCPM. Based on observations from McCarthy (1974), the entrainment rate (μ) is represented by an empirical relationship that describes the influx of air and ambient particles into the parcel as varying inversely with cloud radius R. To predict the evolution of cloud radius, two conceptual models of lateral entrainment are available in the DCPM: the bubble model (Scorer and Ludlam, 1953) and the jet model (Morton, 1957).
For the bubble model, the change of the radius of a thermal bubble (RB) over time is given as
where and CB=0.6 (McCarthy, 1974).
For the jet model, the time variation of the radius of a jet plume (RJ) is expressed by
where and CJ=0.2 (Squires and Turner, 1962).
The condensational growth rate of droplets in the ith bin () is represented as
where droplet growth via condensation is driven by the difference between the ambient supersaturation (S) and the droplet equilibrium supersaturation (Seq, i, see Eq. A4 in Appendix A). The growth coefficient (G) depends on the physicochemical properties of aerosols (see Eq. A1 in Appendix A). Microscale perturbations in supersaturation due to air flow around individual hydrometeors, that is ventilation of the drop boundary layer, are implicitly parameterized by the modified diffusivity parameter used in the growth factor equation, which depends on particle size (Eq. A2, Appendix A).
Assuming S≪1, then , and the time variation of the supersaturation in the parcel can be expressed as
where α and γ depend on temperature and pressure (see Eqs. A5 and A6 in Appendix A; see also Korolev and Mazin, 2003).
During the parcel's ascent, entrainment mixes out cloud droplets and interstitial aerosols inside the parcel and brings in dry air and aerosol particles from the environment. Entrained aerosols are exposed to supersaturated conditions in the parcel; some become activated and continuously grow into cloud droplets. The rate of change in droplet number in the ith bin () due to entrainment alone is
where N′(z) is the number concentration of ambient aerosol particles (i.e., outside the cloud) at altitude z.
The rate of change in the liquid water mixing ratio (wL) in the parcel is calculated as follows:
2.2 Collision–coalescence growth
To describe droplet growth by collision–coalescence process, the stochastic collection equation (SCE) that solves for the time rate of change in the number concentration is written following Hu and Srivastava (1995):
where the first integral on the right-hand side of the equation describes the production of droplets of volume v resulting from coalescence of smaller drops, and the second integral accounts for the removal of droplets of volume v due to coalescence with other droplets. The continuous SCE is discretized and numerically solved by a linear flux method as outlined by Bott (1998). This method is mass conservative, introduces minimal numerical diffusion, and is highly computationally efficient (Kerkweg et al., 2003; Pinsky and Khain, 2002). As noted before, the collision–coalescence process is calculated on a moving grid with bins modified by condensational growth at each time step.
For two colliding drops of volume of v and v′, the coalescence kernel in Eq. (10) is computed as the product of the gravitational collision kernel and the coalescence efficiency ,
where Vt(V′t) is the terminal velocity of drop volume v(v′), and is the corresponding collision efficiency.
Ecoal is parameterized following Seifert et al. (2005), who applied the Beard and Ochs III method (1995) for small raindrops (dS<300 µm), the Low and List (1982) method for large raindrops (dS>600 µm), and used an interpolation formula for intermediate drops ( µm), where dS is the diameter of the small droplet. A simpler and faster option suggested by Beard and Ochs (1984) is also available in the model. The terminal velocity of hydrometeors is estimated following Beard (1976, 1977) in three ranges of the particle diameter (0.5–19 µm, 19 µm–1.07 mm, 1.07–7 mm), though droplets larger than 40 µm do not form in the early stages of cloud development. Another approximation by Best (1950) is also available as an option in the model. The table of drop–drop collision efficiencies at 1 µm resolution developed by Pinsky at al. (2001) is used for Ecoll. This table was created based on simulations of hydrodynamic droplet interactions over a broad range of droplet radii (1–300 µm), including collisions among small cloud droplets as well as between small cloud droplets and small raindrops. Moreover, Ecoll was derived at three pressure levels of 1000, 750, and 500 mb and can be interpolated at each level of a rising cloud parcel, thus taking the increase of Ecoll with height into account. Turbulence can significantly enhance collision rates especially for small droplets (below 10 µm in radii) as it increases swept volumes and collision efficiencies, and influences the collision kernels and droplet clustering (Khain and Pinsky, 1997; Pinsky et al., 1999, 2000). Considering different turbulent intensities for typical stratiform, cumulus, and cumulonimbus clouds, detailed tables of collision kernels and efficiencies in turbulent flow created by Pinsky et al. (2008) for cloud droplets with radii below 21 µm are also incorporated in the model.
2.3 Numerical formulation
The equations in Sect. 2.1 constitute a stiff system of nonlinear, first-order ordinary differential equations and involve state variables at very different scales. For the numerical integration of condensation growth, a fifth-order Runge–Kutta scheme with Cash–Karp parameters (Cash and Karp, 1990) using adaptive time steps (Press et al., 2007) is employed. At each time step, the error is estimated using the fourth-order and the fifth-order Runge–Kutta methods. Because dependent variables differ by several orders of magnitude, a fractional error (ε) is defined to scale the error estimate by the magnitude of each variable. Specifically, the time-step size is adaptive to satisfy a fractional tolerance of 10−7 for all variables. The initial time step to calculate condensational growth is s. The maximum time step is set as 10−3 s to ensure the diffusional growth of drops is precisely simulated and nonactivated particles reach equilibrium with the parcel supersaturation at each time step. For the collision–coalescence processes in Sect. 2.2, a simple Euler method is applied to integrate forward in time. The flux method for solving the discrete SCE was demonstrated to be numerically stable for various grid structures and integration time steps when the positive definiteness is maintained (Bott, 1998). Thus, a time increment of 0.2 s is adequate to ensure that the available mass in each bin is much larger than the change of mass in the bin during the redistribution of the mass at one time step. Relying on separate numerical integration methods for calculating condensation and collision–coalescence allows us to either include or exclude each process easily to examine its role individually in cloud formation.
Differential droplet sedimentation can be simulated explicitly in the DCPM using the Eulerian–Lagrangian framework described by Prat and Barros (2007b). For small cloud droplets (<40 µm) characteristic of the early stages of cloud formation and development considered in this study, terminal velocities aloft (e.g., Beard, 1977) are significantly smaller (≤0.06 m s−1) than the parcel updraft (≥0.5 m s−1). Further, the timescales of condensation and drop–drop interactions are very short compared to the timescales required to reach terminal velocity which are size dependent (Guzel and Barros, 2001; Barros et al., 2008). Exploratory tests with CPM model simulations with and without explicitly resolving sedimentation in the early stages of cloud formation and development showed no difference in simulated CDNC and CDS. Thus, explicit sedimentation is bypassed in the model simulations here, which reduces computational times by more than 3 orders of magnitude. Terminal velocity differences are, however, important to determine collision–coalescence outcomes (see Sect. 2.2).
The intense observing period (IOP) of the IPHEx field campaign took place during 1 May–15 June 2014. The study region was centered on the SAM extending to the nearby Piedmont and Coastal Plain regions of North Carolina (see maps in Fig. 1). IPHEx was one of the ground validation campaigns after the launch of NASA's Global Precipitation Measurement (GPM) core satellite. Further details can be found in the IPHEx science plan (Barros et al., 2014). Surface measurements in the inner region of the SAM were conducted in the Pigeon River basin (PRB, Fig. 1b) including a dense network of rain gauges and disdrometers. During the IPHEx IOP, measurements of surface aerosol concentrations and size distributions ranging from 0.01 to 10 µm were collected in Maggie Valley (MV), a tributary of the Pigeon River. Collocated with aerosol instruments at the MV supersite, the ACHIEVE (Aerosol, Cloud, Humidity, Interactions Exploring and Validating Enterprise) platform was also deployed, equipped with W-band (94 GHz) and X-band (10.4 GHz) radars, a ceilometer, and a microwave radiometer. Two aircraft were dedicated to the IPHEx campaign. The NASA ER-2 carried multifrequency radars (e.g., a dual-frequency Ka/Ku, W, X band) and radiometers, and functioned as the GPM core-satellite sampling simulator from high altitude. The University of North Dakota (UND) Citation aircraft was instrumented to characterize the microphysics and dynamical properties of clouds, including LWC and DSDs from cloud to rainfall drop sizes. Therefore, this data set offers a great opportunity to investigate ACIs tied to warm-season moist processes in complex terrain. A detailed description of the specific measurements relevant to this study is provided below and in Sect. S2.
3.1 Surface measurements
Aerosol observations were carried out at the MV supersite (marked as the yellow star in Fig. 1b) in the inner mountain region during the IPHEx IOP. The elevation of the MV site is 925 m above mean sea level (a.m.s.l.). The data set provides a clear characterization of the size distribution and hygroscopicity of surface aerosols in this inner mountain valley, which was not available previously. Nominal dry aerosol size distributions at the surface were measured by a scanning mobility particle sizer system (SMPS) for particles from 0.01 to 0.5 µm in diameter and a passive cavity aerosol spectrometer (PCASP; manufactured by Droplet Measurement Technologies, Inc., Boulder, CO, USA) for particle diameters in the size range of 0.1–10 µm. The SMPS consists of an electrostatic classifier (TSI Inc., 3081) and a condensation particle counter (CPC; TSI Inc., 3771). Note that the relative humidity (RH) of the differential mobility analyzer (DMA) column is well controlled and the average RH (±1 standard deviation) of the sheath and sample flows are 2.0±0.8 % and 3.2±0.5 %, respectively. In addition, a co-located ambient CPC (TSI Inc., 3772), which measures aerosol particles greater than 10 nm without resolving their size distributions, shows very close agreement with the SMPS measurements with regard to total number concentrations of aerosol particles (NCN).
A single column CCN counter (manufactured by Droplet Measurement Technologies, Inc., Boulder, CO, USA) operated in parallel to the SMPS–CPC to sample size-resolved CCN concentrations (NCCN). The CCN instrument cycles through six levels of supersaturation (S) in the range of 0.09 %–0.51 %. At a given S level, each CCN measurement cycle took approximately 8 min, corresponding to one SMPS scan and buffer time to adjust supersaturation. On average 178 measurement cycles were completed daily during the IPHEx IOP, except for occasional interruptions due to instrument maintenance. CN and CCN distributions were inverted as described previously (Nguyen et al., 2014; Petters and Petters, 2016). Supersaturation was calibrated using dried ammonium sulfate and a water activity model (Christensen and Petters, 2012; Petters and Petters, 2016). The midpoint activation diameter (D50) is derived from the inverted CN and CCN distributions (Petters et al., 2009). The hygroscopicity parameter (κ) is obtained from D50 and instrument supersaturation (Petters and Kreidenweis, 2007). Detailed time series and diurnal cycles of CN and CCN measurements are illustrated n in Sect. S2 (Figs. S7–S9). The data show that the average total number concentration (±1 standard deviation) of dry aerosol particles is 2487±1239 cm−3 for particles with diameters between 0.01 and 0.5 µm and 1106±427 cm−3 for particles with diameters between 0.1 and 10 µm in diameter. No significant diurnal variability in number concentration or hygroscopicity was present. In addition, a co-located Vaisala weather transmitter (WXT520) recorded local meteorological conditions continuously (e.g., wind speed, wind direction, relative humidity, temperature, and pressure) at 1 s intervals. Diurnal cycles of these local meteorological variables during the IPHEx IOP are displayed in Fig. S10. The average meteorological conditions at the sampling site are 0.8±0.6 m s−1 in wind speed, 172±115∘ in wind direction, 77±18 % in relative humidity, and 19±4 ∘C in ambient temperature (arithmetic mean ±1 standard deviation).
3.2 Aircraft measurements
Airborne observations from the UND Citation aircraft, equipped with meteorological (e.g., temperature, pressure, humidity) sensors and microphysical instruments, are used in this study (Poellot, 2015). Vertical velocity was obtained from a gust probe, and bulk LWC values were retrieved from two hot-wire probes (a King-type probe and a Nevzorov probe). Size-resolved concentrations were measured using three optical probes, covering droplet diameter from 50 µm to 3 cm: a PMS two-dimensional cloud (2D-C) probe, a SPEC two-dimensional stereo (2D-S) probe, and a SPEC high-volume precipitation spectrometer 3 (HVPS-3) probe. The cloud droplet probe (CDP) measures cloud drop concentrations and size distributions for particles with diameters between 2 and 50 µm in 30 bin sizes. The droplet sizes are determined by measuring the forward scattering intensity when droplets transit the sample area of the CDP. Coincidence errors cause CDP measurements to underestimate droplet concentrations and broaden droplet spectra. This type of error occurs when two or more droplets pass through the CDP laser beam simultaneously, and is highly dependent on droplet concentrations (Lance et al., 2010). The methodology to correct CDP observations is described in Sect. S2.2 (Fig. S11). The corrected CDP cloud droplet spectra are used in this study to evaluate model simulated CDNC and CDS. The corrections slightly shift the measurements to smaller drop sizes (not shown here), thus providing confidence in the performance of the CDP probe during the IPHEx campaign.
3.3 IPHEx case study: 12 June 2014
On 12 June 2014, the W-band radar observations at MV (see Fig. S12) indicate the formation of cumulus congestus clouds before 12:30 local time (LT) and further growth into cumulonimbus clouds. Near the MV site, a coordinated aircraft mission of both the UND Citation and NASR ER-2 was conducted from 12:14 to 15:51 LT on 12 June. Cloud droplet concentrations and size distributions were sampled at multiple heights above cloud base by conducting successively higher constant-altitude flight transects through clouds. The CDP sampled at 1 Hz frequency (corresponding to approximately 90 m in flight distance), and coincidence errors were taken into account by applying the correction as described in Sect. S2.1. In particular, the investigation is limited to the lowest horizontal leg (see the flight track in Fig. 3a, altitude around 2770–2800 m a.m.s.l.) through the cloud to avoid the influence of substantial mixing at cloud top that is not treated in the DCPM currently. The flight period of the first horizontal leg (∼2800 m a.m.s.l.) is from 12:17 to 12:28 LT (See Fig. S13a). In rising updrafts, in-cloud samples (white plus signs in Fig. 6a and green crosses in Fig. S13) are defined with a minimum LWC of 0.25 g m−3 from the CDP. The number of precipitation-size drops in CDNC from the 2-DC probe (measuring hydrometeors with diameter between 105 µm and 2 mm) is negligible in these cloudy regions (Fig. S14d), thus confirming that the aircraft sampled cumulus congestus clouds at the development stage. Significant topographic heterogeneity (terrain transect indicated by the thick black line in Fig. 3b) can exert a considerable influence on cloud formation across this region. As shown in Fig. 3c and d, a pronounced variability in drop number distributions is manifest in the in-cloud samples clustered by low (0–1 m s−1) and high (1–2 m s−1) updrafts. Along the first leg, three cloudy regions are identified near the eastern ridges (ER, highlighted in the blue dashed box in Fig. 3), over the inner valley region (in-cloud, IC) region, highlighted by the blue circle, and near the Eastern Cherokee Reservation (ECR, highlighted in the blue dashed box). Measurements of in-cloud samples for the three regions are discussed in Sect. S2.2.
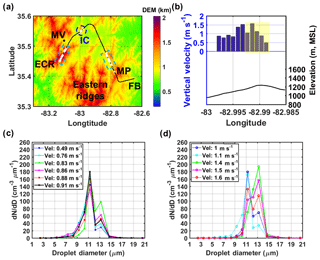
Figure 3(a) Lowest cloud transect of the UND Citation flight track on 12 June 2014. The in-cloud observations are identified as white plus signs and the black asterisk marks MV. From left to right in the map, ECR denotes Eastern Cherokee Reservation, MP denotes Mount Pisgah, and FB denotes French Board valley. (b) Updraft velocity variations of the targeted in-cloud region, denoted by IC in panel updrafts are shown in (a). The in-cloud samples were collected at 1 Hz (∼90 m in flight distance) resolution. Cloud droplet concentrations of the in-cloud samples in IC (b) with low (0–1 m s−1) and high (1–2 m s−1) updrafts are shown in panels (c) and (d), respectively. The updraft velocity of each sample is indicated in the legend. Dotted lines represent the droplet spectra in the reference subregion within the IC region, within the yellow shaded region in panel (b).
Eleven samples were collected along ∼1 km flight distance in cloud region IC (circled in Fig. 3a, vertical velocities shown as blue bars in Fig. 3b). The droplet spectra in stronger updrafts (see Fig. 3d) have higher number concentrations and a narrower size range compared to the samples in the weaker updrafts at the edge of the cloud (see Fig. 3c). This is because in the stronger (faster) updrafts, the timescale of vertical motion is very short, thus thwarting entrainment and collision–coalescence processes with condensation alone governing droplet growth. In the slower updrafts, the longer timescale of vertical motion enhances entrainment leading to replenishment of CN, and more importantly collision–coalescence processes to produce larger droplets, thus broadening the distribution. Aerosol size distributions are not resolved in the CPC measurements from UND Citation, and thus surface aerosol measurements at MV (marked as the black asterisk in Fig. 3a) are used as model input at IC.
4.1 Model initialization and reference simulation
Dry aerosol concentrations measured by the SMPS and PCASP at MV were averaged over the first 10 min (averaging interval: 12:14–12:24 LT) of the 12 June flight and then merged into a single size distribution as shown in Fig. 4. The combined aerosol distribution at the surface is fit by the superimposition of four lognormal functions using least-squares minimization. Table 2 summarizes parameters (total number concentration, geometric mean diameter, and geometric standard deviation) that characterize the four lognormal distributions. Notice that aerosol number concentrations below 0.03 µm are underestimated by the fitted cumulative distribution (cyan curve in Fig. 4). Table 3a summarizes the CPM numerical configuration parameters, and Table 3b provides model physiochemical parameters and initial conditions. These particles in such small diameters mostly remain nonactivated under the supersaturated conditions typical of the atmosphere, thus, underestimation of their concentrations does not affect cloud development in the model. The aerosol distribution is discretized into up to 1000 bins, initially covering the size range of 0.01–10 µm. The grid evolves in time with new bins added as larger particles form by condensational growth. The grid's high resolution is sufficient to simulate the partitioning of growing droplets and interstitial aerosols in the parcel. The aerosols are assumed to be internally mixed so that the hygroscopicity does not vary with particle size. A constant κ value of 0.14 is prescribed for each aerosol bin, derived from the average κ from MV measurements during the first 10 min of the 12 June flight.
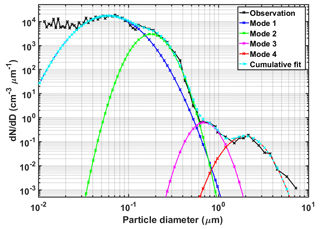
Figure 4Mean surface aerosol size distribution fitted by four lognormal functions. Observations are merged from the SMPS and PCASP, and are averaged during the first 10 min (12:14–12:24 LT) of the 12 June flight. Fitted parameters (total number concentration, geometric mean diameter, and geometric standard deviation) for each mode are summarized in Table 2.
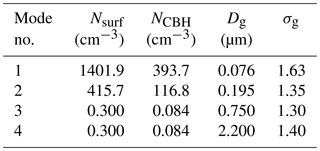
Table 2Lognormal fit parameters characterizing the aerosol number distribution of four modes. Note N is the total number of aerosol particles per cm3, Dg is the geometric mean diameter (µm), and σg is the geometric standard deviation for each mode. Nsurf and NCBH represent total aerosol number concentrations at the surface and cloud base height (CBH: 1270 m), respectively.
During the IPHEx IOP, daytime radiosondes were launched every 3 h at Asheville, NC (red star in Fig. 1b). This location is on the eastern slopes of the SAM in the French Broad valley outside of the inner mountain region far away from the targeted in-cloud region. In addition, the closest sounding (11:00 LT) was launched much earlier than the flight take-off time on 12 June 2014. To address the lack of sounding observations needed for CPM input, high-resolution (0.25 km grid size) WRF simulations were conducted to extract model soundings in the IC region (highlighted in Fig. 3a). The detailed configuration of the WRF model for these simulations (see Fig. 5a for nested grid domains) is described in Sect. S3. Upon inspection of model results 15 min prior to the flight time, the ensemble mean of six simulated soundings in valley locations within the IC region was used to specify environmental conditions at 12:15 LT in CPM simulations (Fig. 5b). The cloud base height (CBH) is the level where simulated RH is approximately 100 %. As marked by the horizontal black line in Fig. 5b, CBH =1270 m above ground level (a.g.l.). at 12:15 LT when the parcel is released from cloud base. The vertical distribution of simulated horizontal winds along the aircraft flight path is highly heterogeneous and anisotropic due to the complex 3-D structure of winds in the complex terrain of the inner mountain region. This includes shallow thermal upslope winds between the main valley and surrounding ridges, and ridge–valley circulations with multiple orientations in lateral valleys as illustrated by the supplementary animations SA1 (near surface), SA2 (at ridge level), SA3 (at CBH), and SA4 (along the first aircraft flight leg). The animations show southerly mesoscale horizontal transport above ridges, upslope flows along the topography in the inner region, and a mesoscale honeycomb-like structure of weak to moderate updrafts and downdrafts with short-lived intensification linked to overturning processes across the entire region.
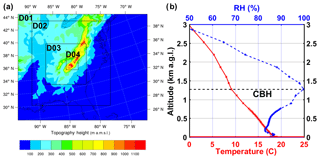
Figure 5(a) WRF model configuration of four one-way nested domains at a 15, 5, 1.25, 0.25 km grid resolution, respectively. (b) Vertical profile of temperature (red solid line) and relative humidity (dashed blue line) from the spatially averaged WRF sounding columns at IC (see its location in Fig. 3a). The horizontal dashed line depicts CBH =1270 m a.g.l.
At the IC cloud base, aerosol size distributions are estimated by assuming that total number concentrations at the surface decay exponentially with a scale height (HS) of 1000 m (representative of the effectiveness of the vertical venting mechanism), and geometric mean diameters and corresponding geometric standard deviations remain constant with height. The reference HS selected for the control simulation is the height above ground level where the lifting condensation level (LCL) and the convective boundary layer (CBL) are the same (i.e., ) in the SAM inner valley region under the flight path. The initial dry aerosol distribution at cloud base input to the model is the sum of four lognormal distributions with fitting parameters reported in Table 2. Following Kokhanovsky and de Leeuw (2009), the number concentration of entrained ambient aerosol particles (N′(z), see Eq. 8) is calculated based on the assumption that the initial aerosol distribution at the surface N(0) decays exponentially with height (, where z is the height above ground level).
The initial air parcel excess temperature with respect to the environment is 1.0 K, and the initial pressure and RH of the parcel at cloud base adapt to cloud surroundings. Vertical velocity measurements at cloud base are not available. The initial updraft velocity (V0) is assumed to be uniformly distributed and equal to 0.5 m s−1, consistent with vertical velocities observed by the W-band radar (see Fig. S12b) and simulated by the model around the same altitude (2.5 km a.m.s.l.). In summary, the air parcel in the reference simulation is launched with an initial radius (R) of 500 m, an initial updraft of 0.5 m s−1, and initial aerosol spectra that are in equilibrium with the humid air at cloud base. When the parcel is rising, the bubble parameterization with the characteristic length scale R=500 m is used to simulate lateral entrainment (see Eq. 4 in Sect. 2.1). Ambient aerosol particles penetrate through lateral parcel boundaries with number concentrations that decrease exponentially with height (HS=1000 m). The turbulent kinetic energy dissipation rate is specified as 200 cm2 s−3, typical of cumulus clouds at early stages. The parcel reaches cloud top when vertical velocity is near zero. Sensitivity to parcel radius R, scale height HS, and hygroscopicity κ will be explored in Sect. 4.2.
4.2 Parameter sensitivity analysis
In the past, CPM process studies principally targeted the aerosol–CDNC closure between model simulations and field observations. For example, Conant et al. (2004) conducted an aerosol–cloud droplet number closure study against observations from NASA's Cirrus Regional Study of Tropical Anvils and Cirrus Layers–Florida Area Cirrus Experiment (CRYSTAL-FACE) using the adiabatic CPM by Nenes et al. (2001, 2002) that solves activation and condensation processes only (see Table 1 for details). Using a condensation coefficient (ac) value of 0.06, they reported that predicted CDNC was on average within 15 % of the observed CDNC in adiabatic cloud regions. Fountoukis et al. (2007) used the same CPM as Conant et al. (2004) under extremely polluted conditions during the 2004 International Consortium for Atmospheric Research on Transport and Transformation (ICARTT) experiment. They report that the optimal closure of cloud droplet concentrations was achieved when the condensation coefficient was 0.06. For marine stratocumulus clouds sampled during the second Aerosol Characterization Experiment (ACE-2), Snider et al. (2003) applied the University of Wyoming parcel model to simulate condensation processes in adiabatic ascent (see Table 1) and experimented with various condensation coefficients in the range of 0.01–0.81. They hypothesized but did not demonstrate that CDNC overestimation errors (20 % to 30 % for ac=0.1) in their CPM simulations could be mitigated by varying the condensation coefficient as a function of dry particle size instead of using one value for the entire distribution.
The condensation coefficient of water ac is a key ACI physical parameter in parcel models that has a strong influence on activation and droplet growth, as it expresses the probability that vapor molecules impinge on the water droplet when they strike the air–water interface (McFiggans et al., 2006). Experimental measurements reviewed by Marek and Straub (2001) exhibit a strong inverse relationship between pressure and ac values ranging from 1000 to 100 hPa and from 0.007 to 0.1, respectively (their Fig. 4). Chodes et al. (1974) measured condensation coefficients in the range of 0.02–0.05, with a mean of 0.033 from measurements of individual droplets grown in a thermal diffusion chamber for four different supersaturation levels. Garnier et al. (1987) repeated the Chodes et al. (1974) experiments and found that the average condensation coefficient is closer to 0.02 after correcting their supersaturation calculations. Shaw and Lamb (1999) conducted extensive simultaneous measurements of the condensation coefficient and thermal accommodation coefficients (aT) for individual drops in a levitation cell and reported values for ac and aT in the ranges of 0.04–0.1 and 0.1–1 with most probable values of 0.06 and 0.7, respectively. Errors in aerosol–cloud droplet number closure studies using adiabatic CPMs with laboratory-based condensation coefficients are well above 10 % and often around 20 %–30 %, mostly due to overestimation (McFiggans et al., 2006).
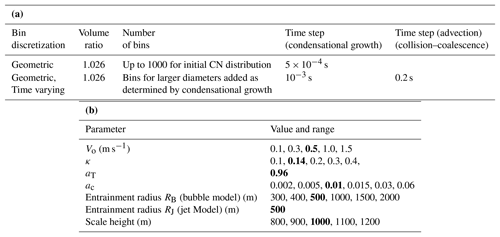
This section presents sensitivity tests to assess changes in DCPM simulations to variations in key inputs and assumptions. Test results are compared with in-cloud observations from the aircraft to assess the role of individual state variables and processes for the cumulus congestus' case on 12 June during IPHEx. Selected parameters are perturbed one at a time while other assumptions and input parameters remain unchanged as specified in Sect. 4.1. Table 3b presents a summary of the ranges of physiochemical parameters and initial conditions tested in the sensitivity analysis.
Table 3(a) Summary of model numerical configuration parameters used in simulations presented here. (b) Summary of physiochemical parameter ranges used in sensitivity simulations (reference value in bold).
4.2.1 Condensation coefficient
Condensation plays a dominant role in the early stages of cloud formation, and one key factor in this process is the condensation coefficient (ac) that governs activation and condensational growth. A laboratory study by Chuang (2003) reported ac values ranging from to 1, and experimental values from field campaigns and from chamber studies of individual droplet growth also differ over a wide range (0.007–0.1) as reviewed in Sect. 1. Here, ac was made to vary in the range [0.001,1.0] as per Fountoukis and Nenes (2005). For the targeted IC region, Fig. 6 shows simulated profiles of updraft velocity, supersaturation, total CDNC, LWC, and their sensitivity to selected ac values in comparison with the airborne observations (denoted by black crosses). Measurements from the IC region along the lowest cloud transect (blue circle in Fig. 3a) are used to evaluate model performance since no observations are available in the upper unmixed cloudy areas to assess the entire vertical profiles simulated by the CPM. Only simulations with reasonable agreement with the observations are discussed here, and thus results ac from 0.06 to 1.0 are not shown. Particles larger than 1 µm in diameter are considered cloud droplets and are included in the integration to calculate LWC. Note that ground elevations under the IC region vary from 928 m to 1184 m a.m.s.l. (see Fig. 3b), and the region is on a small hill in the middle of the valley and surrounded by much higher ridges (terrain elevation ∼1500 m a.m.s.l.). Hereafter, aircraft measurement altitudes are expressed as above ground level (a.g.l.) to facilitate comparison with model results.
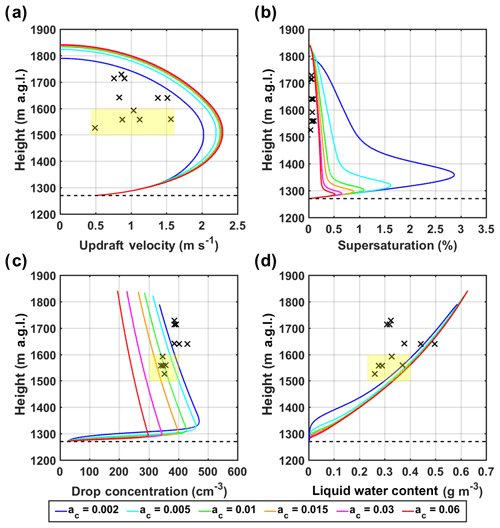
Figure 6Sensitivity of the updraft velocity (a), supersaturation (b), total drop concentration (c), and LWC (d) to the variations in the condensation coefficient (ac) as compared to the airborne observations (marked by black crosses). The horizontal dashed line depicts CBH. In panel (b), the quasi-steady approximation of supersaturation is calculated based on observed temperature. It should be kept in mind that airborne measurements of temperature in clouds are subject to large uncertainties, thus rendering the derivation of supersaturation unreliable.
Large values of ac (>0.01) have negligible influence on the vertical velocity profiles shown in Fig. 6a, and it is apparent that ac has a significant impact on the simulated supersaturation profiles (Fig. 6b). The black crosses indicate the quasi-steady approximation of supersaturation (Sqs) calculated according to Eq. (A8) (also Eq. 3 in Pinsky et al., 2013). Note that large uncertainties can be associated with aircraft temperature measurements used to estimate Sqs. Low values of ac strongly inhibit the phase transfer of water vapor molecules onto aerosol particles (aerosol wetting), slowing the depletion of water vapor in the parcel and thus substantially increasing maximum supersaturation (Smax). Consequently, smaller aerosol particles with high concentrations are activated for higher Smax values, resulting in a direct increase in cloud droplet numbers with lower values of ac (Fig. 6c). Overall, these results are in agreement with earlier studies (Nenes et al., 2002; Simmel et al., 2005) that investigated the dependence of cloud droplet number concentrations on the condensation coefficient. Moreover, Fig. 6c shows that the simulation with ac=0.01 (green line) captures the observed drop concentrations well between 1500 m and 1600 m a.g.l. (highlighted in yellow shade), whereas a condensation coefficient that is 1 order of magnitude lower (ac=0.002, blue line) yields better results for the observations above 1600 m. As summarized in Table 4, the simulated CDNC for the region between 1500 m and 1600 m a.g.l. on the hillslope (shaded in Fig. 6b, reference subregion within the IC region) attains an average CDNC of 354 cm−3 for ac=0.01, which is only ∼1.3 % higher than the observed average between 1500 m and 1600 m (349.4 cm−3). The corresponding LWC is also in reasonable agreement with the range of observed values (Fig. 6d). The simulated CDNCs are underestimated in the cluster between 1600 and 1750 m (397.5 cm−3), and the average CDNC simulated using a much lower condensation coefficient (0.002) is ∼8 % lower than the average CDNC from observations. Inspection of Fig. 6c suggests that within the IC region there are two clusters of air parcels at different levels above ground. Model simulations are closer to observations overlaying the lower terrain (Fig. 3b) using a lower condensation coefficient. A higher condensation coefficient improves simulations in the region that includes the maximum updrafts near the hilltop. Good agreement between the model results and airborne observations for the lower cluster provides confidence in the conclusions from the sensitivity tests. Thus, the lower cluster over higher terrain (Fig. 3b and d) is considered the reference region within the IC region for this study.
Table 4Evaluation of the predicted CDNC from simulations using various condensation coefficients against the averaged observation from the CDP.
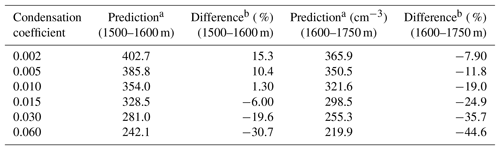
aThe averaged CDNC in the predictions for the indicated altitudes. The DCPM uses above ground level (a.g.l.) as the altitude coordinate. bDifference (%) (Prediction − Observation)/Observation. Note that observations between 1500 and 1600 m a.g.l. (349.4 cm−3) over the higher terrain (Fig. 3d) and between 1600 and 1750 m a.g.l. (397.5 cm−3) over the lower terrain (Fig. 3c) are calculated by averaging the cluster of five consecutive CDNC measurements. A shown in Fig. 3b, the two altitudes are approximately the same with respect to mean sea level (m.s.l.).
The sensitivity of predicted spectra at 1500 m (in solid lines, Fig. 7a) to ac varying from 0.002 to 0.06 is very high. The observed spectrum (black dotted line) is the average from five individual CDP measurements (dotted lines in Fig. 3c and d, also highlighted in the yellow shaded area in Fig. 3b) between 1500 m and 1600 m a.g.l. (see Fig. 6d for their LWC in shade). Generally, spectra simulated with lower values of ac are broader with higher numbers of small droplets, while simulations with large values of ac yield narrower spectra shifted to larger droplet sizes. The differences in drop size range and spectra shape can be explained by inspecting the vertical profiles of the parcel supersaturation and Seq for six illustrative aerosol particle diameters (Daero) depicted in Fig. S19. Growth by water vapor condensing on different sizes of cloud droplets is determined by the difference between S and Seq (Eq. 6 in Sect. 2.1). At low S, small particles become interstitial aerosols, and their corresponding Seq remains in equilibrium with the parcel supersaturation (). At high S, because of low ac values, activation of small aerosols contributes to significant spectra broadening, produces larger CDNC, and shifts the CDS toward smaller diameters due to slower condensational growth. This is consistent with Warner (1969), who found that low condensation coefficients (<0.05) were required to capture the observed dispersion of droplet spectra in natural clouds, especially for small sizes (i.e., left-hand side of the spectra). Figure 7b displays the simulated CDS at different levels for ac=0.01 in comparison with the individual droplet spectra measured by the CDP. The simulated spectra are representative of the evolution of cloud droplet distributions in one parcel at different cloud development stages. The observed spectrum at 1559 m a.g.l. (black dotted line) and its CDNC (357 cm−3) and LWC (0.37 g m−3) are selected for comparison based on the agreement between measurements and DCPM simulations. The results are also consistent with the parameterizations of CDNC and cloud droplet spectra at different heights, given the updraft velocity and the number of CCN that can be activated at moderate supersaturation levels as per Kuba and Fujiyoshi (2006). Simulated spectra at 1500 and 1600 m altitude show very good agreement with the observed number concentration and drop size range. Below 1600 m, a shift of the unimodal spectra to larger drop sizes suggests that the condensation process currently dominates the growth of cloud droplets. Larger drops above 1700 m can grow by coalescence, leading to the formation of a second mode at larger sizes in the upper portion of the cloud. For the analyses presented hereafter, we consider ac=0.01 together with other initial conditions prescribed for the reference simulation (Sect. 4.1, grey line in the following figures).
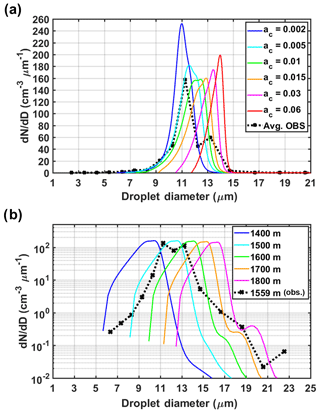
Figure 7(a) Sensitivity of simulated droplet spectra at 1500 m (solid lines) to the variations in ac. The black dotted line reflects the average of five droplet spectra observed by the CDP (dotted lines in Fig. 3c and d) between 1500 m and 1600 m a.g.l. (b) Simulated evolution of cloud droplet spectra at 1400, 1500, 1600, 1700, and 1800 m altitude assuming ac=0.01. The black dotted line denotes the observed droplet spectrum at 1559 m that has similar total CDNC and LWC as the simulation with ac=0.01 at the same altitude.
Further examination using data from other cloud and precipitation probes suggests that concentrations of droplets larger than 30 µm in diameter are negligible during the first horizontal flight leg. Considering that droplets with diameters larger than 30–32 µm are required to trigger effective droplet collisions (Pinsky and Khain, 2002), we conclude that the collision–coalescence process is not important in the sampled IC region, and it is unlikely that it contributes to the wide bimodal spectra observed at early stages of cloud growth. It is noteworthy that small drops are absent in the simulated spectra, in contrast to the observed spectrum that exhibits a broad drop size range and two distinct modes (see Fig. 7b). One possible explanation is that the moving bin grid determined by the condensation process tends to widen the spectral gap between the growing droplets and nonactivated aerosol particles in the ascending parcel. A geometric size distribution with 1000 bins is utilized herein to further refine the discretization for small particle sizes. Another explanation relates to the uncertainties of the input sounding extracted from the WRF simulation. Even though ambient aerosols are entrained continuously through lateral boundaries, most of them remain as interstitial aerosol particles because the low supersaturation in the parcel is insufficient to enable activation (see Fig. 6b). The WRF sounding in Fig. 5b exhibits a lapse rate of −4.1 ∘C km−1 from 1270 m (CBH) to 2200 m, corresponding to stable atmospheric conditions unfavorable for cloud development. To assess the impact of the environmental conditions on cloud growth, an additional model simulation was performed by altering the lapse rate at lower levels (see Appendix B1). The results show that uncertainties in the assumed environmental thermodynamic conditions (e.g., temperature) impose significant constraints in the vertical development of clouds, thus posing as a significant challenge in cloud modeling studies.
4.2.2 Entrainment strength
To access the influence of entrainment on cloud drop concentrations and LWC, different strengths of lateral entrainment are examined by altering the initial cloud parcel size R at the cloud base. Figure 8 displays the vertical profiles of total CDNC and LWC. Cloud droplet spectra formed at three altitudinal levels (1500 m: solid line, 1600 m: dotted line, and 1700 m: dashed line) for simulations using different initial parcel radii are compared to the CDP observations in the IC region (denoted by black crosses in Fig. 8a and b and the black dotted line in Fig. 8c). Entrainment appears to have a dominant influence on the cloud vertical structure as small rising parcels associated with higher entrainment dissipate faster by intensive mixing of dry ambient air through lateral cloud boundaries. Stronger entrainment strength results in a direct decrease in drop concentrations and LWC, while it has little influence on the droplet size range. The best agreement on droplet numbers is between the reference simulation (R=500 m, ac=0.01; grey line in Fig. 13a) and the reference subregion within the IC region (between 1500 m and 1600 m a.g.l.), whereas results for R=1500 m better capture the higher cluster of cloudy samples (above 1600 m a.g.l.). Recall that when R was held constant, the higher cluster is better reproduced using ac values 1 order of magnitude smaller than the reference value. Thus, the sensitivity analysis illuminates a competitive trade-off with weaker entrainment for higher condensation coefficients (R=1500 m and ac=0.01, the orange line in Fig. 8a) when other parameters in the reference simulation remain the same.
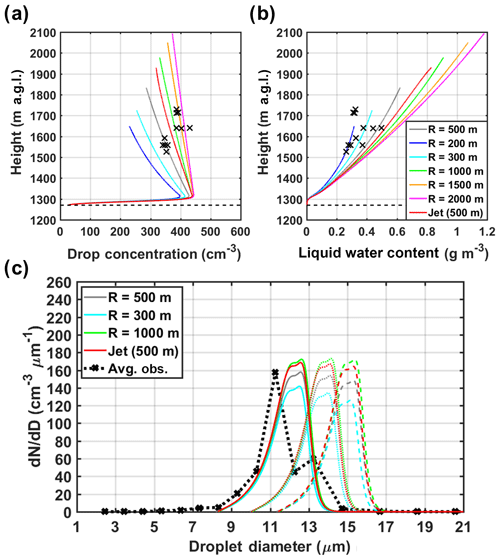
Figure 8Sensitivity of the total drop concentration (a) and LWC (b) to the variations in the initial parcel radius (R) considering lateral entrainment as a bubble model and a jet model. In panels (a) and (b), the airborne observations are marked by black crosses, and the horizontal dashed line depicts CBH. (c) Predicted droplet spectra at three altitudinal levels (1500 m: solid line, 1600 m: dotted line, and 1700 m: dashed line) using two parameterization schemes for lateral entrainment: the bubble model with R=500 m (base case, grey lines), R=300 m (cyan lines), and R=1000 m (green lines); and the jet model with R=500 m (red lines). The black dotted line reflects the average of five droplet spectra observed by the CDP (dotted lines in Fig. 3c and d) between 1500 m and 1600 m a.g.l.
Given R=500 m, an additional test was conducted using the jet model parameterization of lateral entrainment (Eq. 5 in Sect. 2.1). A comparison of results using the two entrainment parameterizations indicates that the bubble model (grey line) has stronger entrainment strength than the jet model (red line) given the same initial parcel size (R=500 m). Nevertheless, continuous increases in simulated LWC in the upper portion of the cloud (see Fig. 8b) for both parameterizations are unrealistic (Paluch, 1979). This problem is attributed to uncertainty in the environmental conditions based on the WRF sounding. As noted in Fig. B1, decreases in LWC are manifest at the upper portion of the cloud, as indicated in the simulations with modified sounding inputs. The lack of sufficient mixing with dry ambient air near cloud top is an inherent deficiency in the simple parameterization of lateral homogenous entrainment, assuming decreasing entrainment strength with height, but this assumption does not significantly affect our conclusions for in-cloud regions below cloud top.
4.2.3 Initial aerosol concentration
The initial aerosol concentration at cloud base can also have significant effects on cloud development. Because aerosol size distributions were not sampled by the aircraft during IPHEx, they are estimated by extrapolating surface aerosol number concentrations according to an exponential decay with a given scale height (HS). To probe and characterize the dependence of droplet formation on aerosol concentrations available at cloud base, sensitivity to HS was explored by varying its values from 800 to 1200 m in the range of LCL at valley locations along the flight (Sects. S3 and S4). Figure 9 shows the simulated profiles of the total CDNC and LWC, and cloud droplet spectra formed at three altitudinal levels (1500 m: solid line, 1600 m: dotted line, and 1700 m: dashed line). It is not surprising that aerosol concentrations at cloud base have a substantial influence on the resulting droplet concentrations. Higher aerosol concentrations, inferred from larger HS, lead to larger drop numbers with smaller average droplet sizes, which is known as the first indirect effect of aerosols (Twomey, 1977). Yet, here, LWC appears insensitive to the initial aerosol concentration as it is constrained by moisture content available in the parcel. The best agreement in CDNC between the DCPM simulations and the average droplet spectra observed by the CDP (black dotted line in Fig. 9c, see reference subregion within the IC region shaded in Fig. 3b) is achieved for HS=1000 m, thus within the typical HS range (550–1100 m) of aerosol number concentration measurements for remote continental types (Jaenicke, 1993).
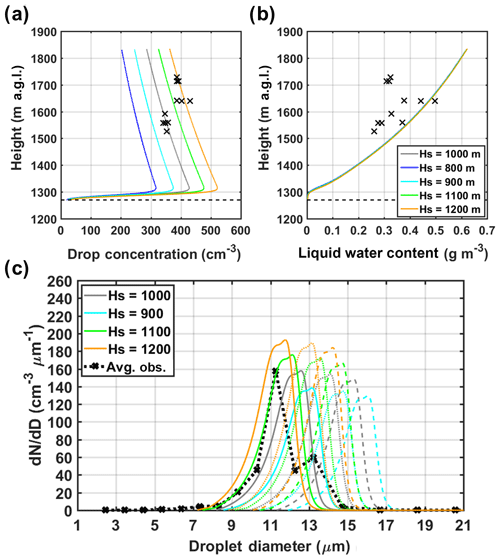
Figure 9Sensitivity of the total drop concentration (a), LWC (b), and droplet spectra (c) at three altitudinal levels (1500 m: solid line, 1600 m: dotted line, and 1700 m: dashed line) to the variations in initial aerosol concentrations at cloud base, as represented by different values of the scale height (HS). In panels (a) and (b), the airborne observations are marked by black crosses, and the horizontal dashed line depicts CBH. The black dotted line in panel (c) reflects the average of five droplet spectra observed by the CDP (dotted lines in Fig. 6c and d) between 1500 m and 1600 m a.g.l.
Because of the uncertainty in the characterization of environmental conditions due to the lack of soundings and the complexity of 3-D circulations in the inner mountain region, additional CPM simulations were conducted assuming a well-developed and well-mixed CBL and uniform distribution of dry aerosol concentrations below CBH. This enables contrasting the results using the well-mixed CBL and the vertical venting mechanism to pump low-level aerosol to the atmosphere above the mountain ridges. These modeling results are discussed in Sect. S4. The surface aerosol concentration at MV (see Fig. 4) is used as model input at cloud base, and other input parameters remain as specified in Sect. 4.1. Although there is good agreement in CDNC between simulations with surface aerosols at cloud base and the airborne observations using a conservative CPM, there are large discrepancies between the observed and simulated CDS with respect to spectral width, peak diameter, and peak concentration number above CBH. More generally, aerosols exhibit large space–time variability, especially persistent in regions of complex terrain, with heterogeneous mixing by different ventilation processes in addition to remote transport (see Figs. 3, 5, and 11 in De Wekker and Kossmann, 2015), all of which can contribute to the diversity of cloud droplet spectra across the cloud transect (see Fig. S15a–c). CPMs are column models and cannot capture lateral heterogeneity.
4.2.4 Hygroscopicity
Another key element in the condensation process is the hygroscopic property that governs the influence of aerosol chemical composition on CCN activity. To account for its temporal variability observed during IPHEx, a κ value varying from 0.1 to 0.4 (within the typical range measured at the surface site, see Figs. S8a and S9c) is applied uniformly for all particle sizes. Simulated profiles of total CDNC and LWC are weakly dependent on hygroscopicity, with only a slightly increase in total CDNC with more hygroscopic aerosols (Fig. 10). Predicted droplet spectra at three altitudinal levels (1500 m: solid line, 1600 m: dotted line, and 1700 m: dashed line) also show little sensitivity to variations in κ. Previous studies (Sect. S2) report that hygroscopic properties of aerosols vary with particle size and with height, and consequently hygroscopicity derived from surface measurements may not be representative of aerosols beneath the cloud (Pringle et al., 2010). These effects are not accounted for.
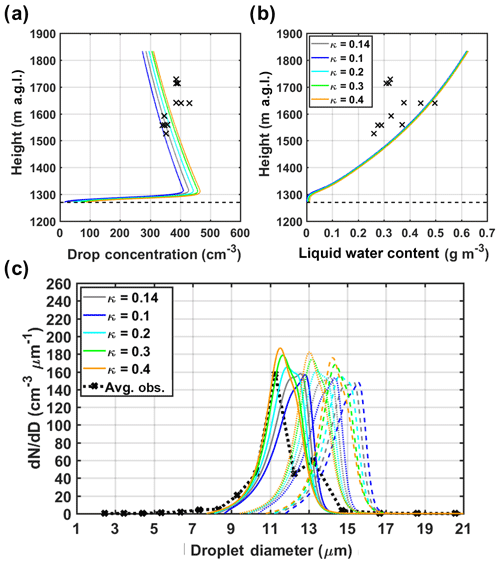
Figure 10Sensitivity of the total drop concentration (a), LWC (b), and droplet spectra (c) at three altitudinal levels (1500 m: solid line, 1600 m: dotted line, and 1700 m: dashed line) to variations in the hygroscopicity parameter (κ). In panels (a) and (b), the airborne observations are marked by black crosses, and the horizontal dashed line depicts CBH. The black dotted line in panel (c) reflects the average of five droplet spectra observed by the CDP (dotted lines in Fig. 3c and d) between 1500 m and 1600 m a.g.l.
4.2.5 Summary of sensitivity analysis
Under realistic assumptions, the total number concentration and size distributions from the airborne observations are captured by the reference simulation well. Sensitivity tests by changing ac in the range of 0.001–1.0 suggest that the predicted CDNC, CDS, LWC, and thermodynamic conditions are highly dependent on the condensation coefficient. At early stages of cloud development, the condensation coefficient plays a key role in the simulated spectra width and shape, with increases in ac yielding a shift towards larger droplet sizes and narrower spectral widths. Entrainment has a substantial impact on the cloud depth, droplet numbers, and LWC, whereas initial aerosol concentrations have a strong effect on number concentrations and size distributions of cloud droplets but induce little effects on LWC. Hygroscopicity has negligible influence on simulated total CDNC and LWC. Additional tests regarding the sounding inputs and initial updraft velocity are reported in Appendix B.
Due to the limited data set from the campaign, a specific set of initial conditions are inferred from surface and airborne observations and reasonable assumptions are made based on the literature and WRF model results. It is important to keep in mind the uncertainties associated with the determination of CBH, which is estimated from the WRF model simulations as concurrent soundings are not available during IPHEx. If the CBH is lifted by 100 m, simulations using different ac values (0.002–0.06) are in better agreement with the airborne measurements of LWC. The CDNC in the reference region (yellow shade, Fig. 6c) is captured better with a higher ac value (0.015) but narrower spectra results are associated with increasing ac values, inconsistent with the observed spectra (not shown here). These caveats highlight the need for comprehensive concerted observations of end-to-end processes in future field campaigns.
In previous field campaign follow-up studies, condensation coefficients close to the modal values from Shaw and Lamb (1999) were specified in adiabatic CPM simulations of activation and condensation processes to improve CDNC estimates against near-cloud-base aircraft measurements. This includes ac=0.06 for warm cumulus during CRYSTAL-FACE (Conant et al., 2004), ac=0.042 for stratocumulus during the Coastal Stratocumulus Imposed Perturbation Experiment (CSTRIPE, Meskhidze et al., 2005), and ac=0.06 for cumuliform and stratiform clouds during ICARTT (Fountoukis et al., 2007). In the present study, CPM simulations with entrainment and collision–coalescence processes are performed to predict CDNC from aircraft measurements several hundred meters above cloud base. Based on sensitivity tests, model simulations using a relatively low value of ac (0.01) exhibit CDNC and CDS consistent with the observed cloud spectra in the inner region of the SAM for early development of cumulus congestus on 12 June. Exploratory simulations increasing aerosol number concentrations at cloud base (HS=1200 m, Fig. B3b) show a highly nonlinear response to changes in ac and R, with the best agreement in CDNC being achieved with higher ac values (0.03 and 0.06) for weak entrainment environments (R=1500 m). Further, the corresponding spectra simulated with higher ac values exhibit larger discrepancies in spectral width and shape against the observations within the IC region (not shown here) and thus result in predictions of inferior skill with regard to cloud vertical development. These results illustrate the importance of nonlinear trade-offs between entrainment and condensation for realistic cloud environments (e.g., stronger entrainment with R=500 m and lower ac=0.01 in the reference simulation, Sect. 4.2.2).
Finally, the lower value of ac, which is in good agreement with aircraft observations above cloud base in the present study, is consistent with diffusion-kinetic theory, which accounts for the feedbacks between latent heat and temperature in the boundary layer of growing droplets (Fukuta and Myers, 2007). The entrainment–condensation feedbacks revealed by the DCPM explain ac values around 0.01 in earlier laboratory experiments of direct contact condensation on aerosols in ventilated cloud chambers with horizontal or vertical moist flows (Garnier et al., 1987; Hagen et al., 1989) in contrast with the most probable value (0.06) found in the levitation cell by Shaw and Lamb (1999).
The vertical microphysical structure of clouds plays a key role in modulating the rainfall intensity via seeder–feeder interactions in regions of complex terrain (e.g., Barros and Lettenmaier, 1994). In this study, a new entraining cloud parcel model (DCPM) with explicit bin microphysics is presented. Evaluation against classical cloud parcel models for a range of input parameters showed that the implementation correctly captures the known microphysics encoded in the supersaturation balance equation. The DCPM is then applied to investigate dominant factors in the microphysical development of clouds in the complex terrain of the inner southern Appalachian Mountains using observations from the Integrated Precipitation and Hydrology Experiment in 2014 (IPHEx) (Barros et al., 2014). In particular, the model was applied to simulate the development of midday cumulus congestus on 12 June 2014 when aircraft measurements are available during IPHEx. Although the aircraft sampled three distinct cloud regions along the lowest flight transect above cloud base, the target in-cloud region for this study is near the IPHEx supersite at Maggie Valley in the inner mountain region. Thus, a detailed modeling study could be conducted leveraging ground-based aerosol measurements and W-band radar profiles available at Maggie Valley to inform model initialization. Besides Maggie Valley observations, initial conditions and model parameters were specified based on a review of the literature when measurements of key input parameters were not available or cannot be measured by current sensor technology. Despite observing large variability in cloud microphysical properties at sub-kilometer scale (∼90 m is the spatial averaging resolution of the measurements along the flight track), modeling results are in good agreement with the cloud droplet number concentration spectra and liquid water content from measurements in the center of the cloud 300–500 m above cloud base.
In the framework of the cloud parcel model, sensitivity of the simulated cloud microphysical characteristics to variations in key parameters was investigated within the context of in situ measurements. Results from sensitivity tests show that the condensation coefficient (ac) exerts a profound influence on the droplet concentration, size distribution, liquid water content, and thermodynamic conditions inside the parcel. Decreases in ac lead to increases in cloud droplet number, broader droplet spectra, and higher maximum supersaturation near cloud base. The case-study during IPHEx reveals that the observed cloud features in the inner mountain region of the SAM are better captured by a low value of ac (0.01) and strong entrainment corresponding to parcel radius R=500 m using the bubble parameterization (Sect. 2.1). Lateral entrainment is found to play an important role on the vertical structure of CDNC, CDS and LWC in the cloud. Further, it was shown that with other input parameters remaining the same as those for the reference simulation, there is a trade-off between the CDNC sensitivity to entrainment strength and the condensation coefficient: strong entrainment (meaning the characteristic scale R in the bubble parameterization is small) is compensated by lower ac values and vice versa. This competitive interference explains higher values of ac in previous aerosol–cloud droplet closure studies using adiabatic parcel models that neither include entrainment nor collision–coalescence. Initial aerosol concentrations at cloud base also have a large impact on droplet numbers but negligible influence on liquid water content. The sensitivity analysis indicates that the cloud droplet growth is generally insensitive to hygroscopicity (Sect. 4.2.4), and thus the constant κ value used in this study does not significantly affect the simulated profiles of droplet number concentration and liquid water content. Analysis of the effect of the interdependence of initial aerosol concentration, condensation coefficient, and entrainment strength on the droplet number concentration revealed ambiguous behavior that could only be resolved by assessing the properties of the simulated droplet spectra (shape, range) against the aircraft measurements at different altitudes throughout the clouds (i.e., well above cloud base). Overall, these findings provide new insights into key parameters of aerosol–cloud interactions (ACIs) to inform physical parameterizations of convective cloud development.
Nevertheless, a review of data and model limitations is warranted. First, regarding data limitations to constrain and force the CPM, reasonable assumptions were made based on the literature to complement surface and airborne observations from IPHEx and WRF model simulations due to the lack of near-cloud-base measurements and soundings. Second, the lateral homogeneous entrainment assumption in the model implies that entrained aerosols are mixed instantly across the parcel. This disregards inhomogeneous supersaturation and microphysical structure inside the cloud associated with discrete entrainment events on different spatial scales (Baker et al., 1980; Khain et al., 2000). Turbulent mixing (Krueger et al., 1997) breaks down entrained blobs of air into smaller scales to form small bounded regions with uniform yet distinct properties on account of molecular diffusion, thus potentially leading to considerable spectrum broadening. In addition, entrainment with dry air at cloud top is an important element to cloud vertical development (Telford et al., 1984) currently not treated in the model. Downdrafts induced by the penetration of dry air at cloud top can sink and mix with updrafts, effectively diluting number concentrations and broadening droplet spectra in clouds (Telford and Chai, 1980). Another limitation is the assumption of constant and uniform hygroscopic properties for all particle sizes. That is, κ is treated as a bulk hygroscopicity parameter. In reality, the aerosol distribution is an aggregate of particles with different physicochemical properties, including different shapes, solubility, and chemical species (Kreidenweis et al., 2003; Nenes et al., 2002). Even if specified initial aerosol characteristics were to capture the variation of κ with size, how to track the evolution of κ as particles among different bins undergo collision and coalescence remains a challenge. Further research is needed to elucidate the impact of heterogeneous chemical composition of aerosols and variations with particle size.
For unstable cloud layers, complexity of in-cloud vertical velocity fields with localized areas of much stronger updrafts has been found to support the formation of wide bimodal spectra in cumulus clouds due to in-cloud nucleation of new droplets from interstitial aerosols when the parcel supersaturation higher up in the cloud exceeds the cloud base maximum (Pinsky and Khain, 2002). As a result, this mechanism can lead to the formation of a secondary mode of small droplets in individual spectra, different from our observed spectra with a second mode centered at a larger droplet size (Figs. 3 and 7). In this study, however, supersaturation does not increase above the cloud base maximum under the conditions of the original and modified model environments, likely attributed to the ambiguities in the sounding input from WRF, even if direct aircraft measurements, albeit highly uncertain, suggest otherwise. Because the collision–coalescence efficiency kernels are dependent on particle size, nonlinear stochastic behavior can also lead to the development of a second mode of larger drops especially because collision-break-up mechanisms are not active in the range of drop diameters present during the initial stages of cloud formation and development (Prat et al., 2012).
Overall, a numerical experiment consisting of 30 different simulations corresponding to 30 different parameter combinations was conducted, and the results suggest that the ranges of parameters that lead to physically meaningful results consistent with observations are well defined. The results underline the importance of the nonlinear relationship between entrainment processes that determine the local- (microscale) and cloud-scale thermodynamic environment around individual particles on the one hand and the aerosol condensation coefficient that measures the effectiveness of condensation processes in the same thermodynamic environment on the other. Given the multi-scale thermodynamic structure of clouds, these interactions suggest that condensation coefficients in the natural environment are transient and spatially variable. Further research is therefore necessary to arrive at representative ensemble estimates toward reducing ACI uncertainties in quantitative assessments of the aerosol indirect effect. Future work will focus on exploring the sensitivity of the DCPM in a multidimensional parameter space to quantify multiple parameter interactions (Gebremichael and Barros, 2006; Yildiz and Barros, 2007) on ACI processes using the factorial design method (Box et al., 1978).
The IPHEx data are accessible at Global Hydrology Resource Center (GHRC) Distributed Active Archive Center (https://ghrc.nsstc.nasa.gov/home/field-campaigns/iphex) (Petersen and Barros, 2018).
A1 Glossary of symbols
| ac | condensation coefficient |
| aT | thermal accommodation coefficient |
| cp | specific heat of dry air |
| Dv, | diffusivity of water vapor in air, and modified |
| diffusivity of water vapor in air | |
| es | saturation vapor pressure |
| g | gravitational constant |
| G | growth coefficient |
| HS | scale height |
| ka, | thermal conductivity of air, and modified |
| thermal conductivity of air | |
| L | latent heat of evaporation |
| Ma, Mw | molecular weight of dry air, and of water |
| N, N′ | number concentration of cloud droplets, |
| and of ambient aerosol particles | |
| p | pressure |
| r, rc | radius of cloud droplet, and of dry aerosol |
| particle | |
| R | universal gas constant |
| Ra | specific gas constant for moist air |
| Rv | specific gas constant for water vapor |
| RB, RJ | radius of air bubble, and of convective jet |
| S | supersaturation |
| Seq | droplet equilibrium supersaturation |
| T (T′) | temperature of air parcel (ambient air) |
| V | parcel updraft velocity |
| v, v′ | droplet volumes |
| wL | mixing ratio of liquid water in parcel |
| wv () | mixing ratio of water vapor in parcel |
| (and in the environment) | |
| κ | hygroscopicity parameter |
| μ | entrainment rate |
| ρa, ρw | density of dry air, and of water |
| σw | droplet surface tension |
A2 Additional formulae
where the modified diffusivity () and thermal conductivity () of water vapor in air account for non-continuum effects (Seinfeld and Pandis, 2006) and are described as follows:
where the thermal accommodation coefficient (aT) is taken as 0.96 (Nenes et al., 2001). Additional sensitivity tests of CDNC to aT, ranging from 0.1 to 1 (Shaw and Lamb, 1999), were conducted, and the resulting droplet concentrations indicate little sensitivity to this input parameter (not shown here).
The hygroscopicity parameter (κ) is adopted to characterize the impact of aerosol chemical composition on CCN activity according to the κ-Köhler theory (Petters and Kreidenweis, 2007). Seq, i for droplets in the ith bin () can be written as
where rc, i and ri are the radius of the dry aerosol particle and the corresponding growing droplet, respectively. Droplet surface tension (σw) is a function of the parcel temperature (Pruppacher and Klett, 1997).
Liquid water content (g m−3) can be expressed as follows:
Quasi-steady approximation of supersaturation Sqs (Pinsky et al., 2013) can be expressed as follows:
where is the average droplet radius, and N is the total droplet number concentration.
B1 Sensitivity to environmental conditions
To account for the uncertainties associated with the environmental condition from WRF and examine its impact on cloud formation, one additional simulation was conducted with modified temperature profiles at the lowest 2 km above CBH (1270 m), as displayed in Fig. B1. Here, we adjusted the original lapse rate (−4.1 ∘C km−1 from the WRF sounding, Fig. 10b) to −7 ∘C km−1 (Γ1) for 1270–2200 m. The lapse rate for 2200–3200 m was changed to −4 ∘C km−1 to keep the ambient temperature below CBH and above 3200 m unchanged. Deeper clouds are formed in the modified environment, representing a conditionally unstable atmosphere. LWC is significantly enhanced by faster droplet growth under fast cooling conditions.
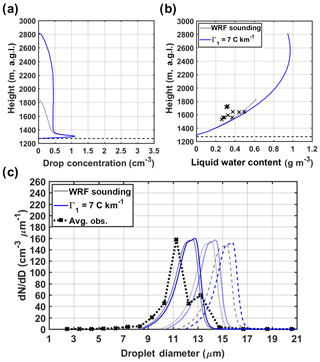
Figure B1Vertical profiles of the supersaturation (a) and LWC (b) for simulations with the original WRF sounding (grey lines) and modified ambient temperature (blue lines). In panel (b), the airborne observations are marked by black crosses, and the horizontal dashed line depicts CBH. (c) Predicted droplet spectra at three altitudinal levels (1500 m: solid line, 1600 m: dotted line, and 1700 m: dashed line) to the variations in the environmental conditions. The black dotted line reflects the average of five droplet spectra observed by the CDP (dotted lines in Fig. 3c and d) between 1500 m and 1600 m a.g.l.
B2 Sensitivity to initial updraft velocity
Cloud dynamics also play a crucial role in the microphysical evolution of cumulus clouds. One major parameter in the cloud dynamical field is the updraft velocity. In accordance with the observed vertical velocities by the aircraft and the W-band radar (see Fig. S12b), a reasonable variability in the initial updraft velocity at cloud base is introduced to assess its effects on the parcel supersaturation and cloud droplet concentrations, as shown in Fig. B2. By varying the initial updraft in a range of 0.1–1.5 m s−1, simulated results display similar vertical velocities at the observation levels, which are still higher than the measured range (not shown here). Slight increases in maximum supersaturation result from larger initial updraft velocities, thus leading to slight enhancement of total droplet numbers. The simulated spectra show a slightly shift towards larger drop sizes due to weaker updrafts, which allow more time for cloud droplets to grow in a rising parcel.
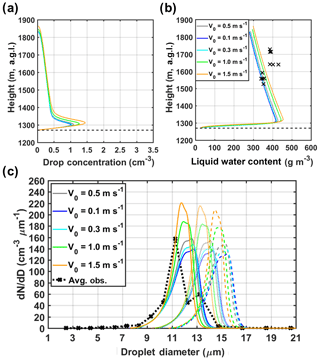
Figure B2Sensitivity of the supersaturation (a), total drop concentration (b), and droplet spectra (c) at three altitudinal levels (1500 m: solid line, 1600 m: dotted line, and 1700 m: dashed line) to the variations in the initial updraft velocity (V0) at cloud base. In panel (b), the airborne observations are marked by black crosses, and the horizontal dashed line depicts CBH. The black dotted line in panel (c) reflects the average of five droplet spectra observed by the CDP (dotted lines in Fig. 3c and d) between 1500 m and 1600 m a.g.l.
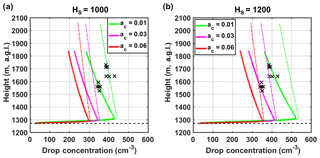
Figure B3Sensitivity of the total cloud drop concentration to the variations in condensation coefficient and entrainment strength (strong: R=500 m, solid thick lines; weak: R=1500 m, dash-dotted thin lines) assuming different initial aerosol concentrations at cloud base (a: HS=1000 m; b: HS=1200 m). The airborne observations are marked by black crosses, and the horizontal dashed line depicts CBH.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-1413-2019-supplement.
YD developed the Duke cloud parcel model (DCPM) and conducted the modeling study under the guidance of APB. MDP was the lead researcher operating the SMPS and CCN systems during IPHEx and provided level-2 data sets of SMPS and CCN measurements (Sect. 3.1). APB and YD wrote the manuscript, and MDP provided comments. APB handled the reviews and replies to reviewers with input from MDP and YD.
The authors declare that they have no conflict of interest.
The manuscript was revised after work originally submitted to ACP and
published in ACPD as Duan et al. (2017). The work was supported in part by
NASA grant NNX16AL16G and NSF Rapid Response Research (RAPID) Collaborative
IPHEx grant with Ana P. Barros (1442039) and Markus D. Petters (1442056). The
authors thank the UND Citation flight scientists, in particular Michael
Poellot, Andrew Heymsfield, and David J. Delene, for the flight data and
advice with airborne data analysis; Si-Chee Tsay and Adrian Loftus for the
deployment and operation of the ACHIEVE instruments and W-band radar
calibrated data; Anna M. Wilson for the deployment and maintenance of Duke's
H2F (Haze to Fog) mobility facility (including the PCASP and rain gauges),
data collection, and analysis; and Andrew Grieshop for loaning the X-ray
neutralizer for the duration of the study. We also thank Kyle Dawson and John
Hader for operating the SMPS and CCN systems in the field and Kyle Dawson for
help with the processing of SMPS and CCN data sets (Sect. 3.1). We also
acknowledge computing resources from Yellowstone
(ark:/85065/d7wd3xhc) at NCAR (allocated to the first author) used
for the WRF simulations. The authors are especially grateful to Neil
Carpenter from the Maggie Valley Sanitary District for his support of IPHEx
activities.
Edited by: Hailong Wang
Reviewed by: four anonymous referees
Abdul-Razzak, H., Ghan, S. J., and Rivera-Carpio, C.: A parameterization of aerosol activation: 1. Single aerosol type, J. Geophys. Res., 103, 6123–6131, https://doi.org/10.1029/97jd03735, 1998.
Albrecht, B. A.: Aerosols, cloud microphysics, and fractional cloudiness, Science, 245, 1227–1230, 1989.
Andreae, M. and Rosenfeld, D.: Aerosol–cloud–precipitation interactions. Part 1. The nature and sources of cloud-active aerosols, Earth-Sci. Rev., 89, 13–41, 2008.
Baker, M. B., Corbin, R. G., and Latham, J.: The influence of entrainment on the evolution of cloud droplet spectra: I. A model of inhomogeneous mixing, Q. J. Roy. Meteor. Soc., 106, 581–598, 1980.
Barros, A. P. and Lettenmaier, D. P.: Dynamic Modeling of Orographically-Induced Precipitation, Rev. Geophys., 32, 265–284, 1994.
Barros, A. P., Prat, O. P., and Shrestha, P.: Revisiting Low and List (1982); Evaluation of Raindrop Collision Parameterizations Using Laboratory Observations and Modeling, J. Atmos. Sci., 65, 2983–2993, https://doi.org/10.1175/2008JAS2630.1, 2008.
Barros, A. P., Petersen, W., Schwaller, M., Cifelli, R., Mahoney, K., Peters-Liddard, C., Shepherd, M., Nesbitt, S., Wolff, D., Heymsfield, G., and Starr, D.: NASA GPM-Ground Validation: Integrated Precipitation and Hydrology Experiment 2014 Science Plan, Duke University, Durham, NC, https://doi.org/10.7924/G8CC0XMR, 2014.
Barros, A. P., Shrestha, P., Chavez, S., and Duan, Y.: Modeling aerosol–cloud-precipitation interactions in mountainous regions – Challenges in the representation of indirect microphysical effects with impacts at sub-regional scales, in: Atmospheric Chemistry, IntechBookOpen (Pub.), https://doi.org/10.5772/intechopen.80025, 2018.
Beard, K. V.: Terminal velocity and shape of cloud and precipitation drops aloft, J. Atmos. Sci., 33, 851–864, 1976.
Beard, K. V.: Terminal velocity adjustment for cloud and precipiattion drops aloft, J. Atmos. Sci., 34, 1293–1298, 1977.
Beard, K. V. and Ochs, H. T.: Collection and coalescence efficiencies for accretion, J. Geophys. Res., 89, 7165–7169, 1984.
Beard, K. V. and Ochs III, H. T.: Collisions between small precipitation drops. Part II: Formulas for coalescence, temporary coalescence, and satellites, J. Atmos. Sci, 52, 3977–3996, 1995.
Berry, E. X. and Reinhardt, R. L.: An analysis of cloud drop growth by collection: Part I. Double distributions, J. Atmos. Sci., 31, 1814–1824, 1974.
Best, A. C.: Empirical formulae for the terminal velocity of water drops falling through the atmosphere, Q. J. Roy. Meteor. Soc., 76, 302–311, 1950.
Bott, A.: A flux method for the numerical solution of the stochastic collection equation, J. Atmos. Sci., 55, 2284–2293, 1998.
Bott, A.: A flux method for the numerical solution of the stochastic collection equation: Extension to two-dimensional particle distributions, J. Atmos. Sci., 57, 284–294, 2000.
Box, G. E., Hunter, W. G., and Hunter, J. S.: Statistics for experimenters: an introduction to design, data analysis, and model building, John Wiley & Sons, Hoboken, NJ, USA, 1978.
Cash, J. R. and Karp, A. H.: A variable order Runge-Kutta method for initial value problems with rapidly varying right-hand sides, ACM T. Math. Software, 16, 201–222, 1990.
Chodes, N., Warner, J., and Gagin, A.: A determination of the condensation coefficient of water from the growth rate of small cloud droplets, J. Atmos. Sci., 31, 1351–1357, 1974.
Christensen, S. I. and Petters, M. D.: The role of temperature in cloud droplet activation, J. Phys. Chem. A, 116, 9706–9717, https://doi.org/10.1021/jp3064454, 2012.
Chuang, P. Y.: Measurement of the timescale of hygroscopic growth for atmospheric aerosols, J. Geophys. Res., 108, 4282, https://doi.org/10.1029/2002jd002757, 2003.
Conant, W. C., VanReken, T. M., Rissman, T. A., Varutbangkul, V., Jonsson, H. H., Nenes, A., Jimenez, J. L., Delia, A. E., Bahreini, R., Roberts, G. C., Flagan, R. C., and Seinfeld, J. H.: aerosol–cloud drop concentration closure in warm cumulus, J. Geophys. Res., 109, D13204, https://doi.org/10.1029/2003jd004324, 2004.
Cooper, W. A., Bruintjes, R. T., and Mather, G. K.: Calculations pertaining to hygroscopic seeding with flares, J. Appl. Meteorol., 36, 1449–1469, 1997.
De Wekker, S. F. J. and Kossmann, M.: Convective Boundary Layer Heights Over Mountainous Terrain – A Review of Concepts, Front. Earth Sci., 3, 77, https://doi.org/10.3389/feart.2015.00077, 2015
Duan, Y.: Mapping the Impact of aerosol–cloud Interactions on Cloud Formation and Warm-season Rainfall in Mountainous Regions Using Observations and Models, PhD disertation, Duke University, 305 pp., 2017.
Duan, Y. and Barros, A. P.: Understanding How Low-Level Clouds and Fog Modify the Diurnal Cycle of Orographic Precipitation Using In Situ and Satellite Observations, Remote Sens., 9, 920, https://doi.org/10.3390/rs9090920, 2017.
Duan, Y., Wilson, A. M., and Barros, A. P.: Scoping a field experiment: error diagnostics of TRMM precipitation radar estimates in complex terrain as a basis for IPHEx2014, Hydrol. Earth Syst. Sci., 19, 1501–1520, https://doi.org/10.5194/hess-19-1501-2015, 2015.
Duan, Y., Petters, M. D., and Barros, A. P.: Understanding aerosol–cloud interactions in the development of orographic cumulus congestus during IPHEx, Atmos. Chem. Phys. Discuss., https://doi.org/10.5194/acp-2017-396, 2017.
Fan, J., Yuan, T., Comstock, J. M., Ghan, S., Khain, A., Leung, L. R., Li, Z., Martins, V. J., and Ovchinnikov, M.: Dominant role by vertical wind shear in regulating aerosol effects on deep convective clouds, J. Geophys. Res., 114, D22206, https://doi.org/10.1029/2009jd012352, 2009.
Flossmann, A. I., Hall, W. D., and Pruppacher, H. R.: A theoretical study of the wet removal of atmospheric pollutants. Part I: The redistribution of aerosol particles captured through nucleation and impaction scavenging by growing cloud drops, J. Atmos. Sci., 42, 583–606, 1985.
Fountoukis, C. and Nenes, A.: Continued development of a cloud droplet formation parameterization for global climate models, J. Geophys. Res., 110, D11212, https://doi.org/10.1029/2004jd005591, 2005.
Fountoukis, C., Nenes, A., Meskhidze, N., Bahreini, R., Conant, W. C., Jonsson, H., Murphy, S., Sorooshian, A., Varutbangkul, V., Brechtel, F., Flagan, R. C., and Seinfeld, J. H.: Aerosol–cloud drop concentration closure for clouds sampled during the International Consortium for Atmospheric Research on Transport and Transformation 2004 campaign, J. Geophys. Res., 112, D10S30, https://doi.org/10.1029/2006jd007272, 2007.
Fukuta, N. and Myers, M. N.: Simultaneous Measurement of Condensation and Thermal Accommodation Coefficients for Cloud Droplet Growth in Due Consideration of a New Moving Surface-Boundary Effect, J. Atmos. Sci., 64, 955–968, https://doi.org/10.1175/jas3834.1, 2007.
Fukuta, N. and Walter, L.: Kinetics of hydrometeor growth from a vaper-spherical model, J. Atmos. Sci., 27, 1160–1172, 1970.
Garnier, J. P., Ehrhard, P., and Mirabel, P.: Water droplet growth study in a continuous flow diffusion cloud chamber, Atmos. Res., 21, 41–51, 1987.
Gebremichael, M. and Barros, A.: Evaluation of MODIS Gross Primary Productivity (GPP) in tropical monsoon regions, Remote Sens. Environ., 100, 150–166, https://doi.org/10.1016/j.rse.2005.10.009, 2006.
Ghan, S. J., Abdul-Razzak, H., Nenes, A., Ming, Y., Liu, X., Ovchinnikov, M., Shipway, B., Meskhidze, N., Xu, J., and Shi, X.: Droplet nucleation: Physically-based parameterizations and comparative evaluation, J. Adv. Model. Earth Syst., 3, M10001, https://doi.org/10.1029/2011ms000074, 2011.
Givati, A. and Rosenfeld, D.: Quantifying precipitation suppression due to air pollution, J. Appl. Meteorol., 43, 1038–1056, 2004.
Guzel, H. and Barros, A. P.: Using Acoustic Emission Testing to Monitor Kinetic Energy of Raindrop and Rainsplash Erosion, in: Soil Erosion Research for the 21st Century, Proc. Int. Symp., 3–5 January 2001, Honolulu, HI, USA, edited by: Ascough II, J. C. and Flanagan, D. C., St. Joseph, MI, ASAE, 701P0007, 525–528, https://doi.org/10.13031/2013.4593, 2001.
Hagen, D. E., Schmitt, J., Trueblood, M., Carstens, J., White, D. R., and Alofs, D. J.: Condensation coefficient measurement for water in the UMR cloud simulation chamber, J. tmos. Sci., 46, 803–816, 1989.
Haywood, J. and Boucher, O.: Estimates of the direct and indirect radiative forcing due to tropospheric aerosols: A review, Rev. Geophys., 38, 513, https://doi.org/10.1029/1999rg000078, 2000.
Hindmarsh, A. C.: ODEPACK, a systematized collection of ODE solvers, Scientific Computing, edited by: Stepleman, R., North-Holland, New York, 1983.
Hu, Z. and Srivastava, R. C.: Evolution of raindrop size distribution by coalescence, breakup, and evaporation: Theory and observations, J. Atmos. Sci., 52, 1761–1783, 1995.
Jacobson, M. Z.: Fundamentals of atmospheric modeling, 2nd edn., Cambridge University Press, New York, NY, USA, 2005.
Jacobson, M. Z. and Turco, R. P.: SMVGEAR: A sparse-matrix, vectorized Gear code for atmospheric models, Atmos. Environ., 28, 273–284, 1994.
Jacobson, M. Z. and Turco, R. P.: Simulating Condensational Growth, Evaporation, and Coagulation of Aerosols Using a Combined Moving and Stationary Size Grid, Aerosol Sci. Technol., 22, 73–92, https://doi.org/10.1080/02786829408959729, 1995.
Jacobson, M. Z., Turco, R. P., Jensen, E. J., and Toon, O. B.: Modeling coagulation among particles of different composition and size, Atmos. Environ., 28, 1327–1338, 1994.
Jaenicke, R.: Tropospheric aerosols, in: aerosol–cloud-climate interactions, edited by: Hobbs, P. V., Academic Press, San Diego, CA, USA, 1–31, 1993.
Jiang, J. H., Su, H., Schoeberl, M. R., Massie, S. T., Colarco, P., Platnick, S., and Livesey, N. J.: Clean and polluted clouds: Relationships among pollution, ice clouds, and precipitation in South America, Geophys. Res. Lett., 35, L14804, https://doi.org/10.1029/2008gl034631, 2008.
Kerkweg, A., Wurzler, S., Reisin, T., and Bott, A.: On the cloud processing of aerosol particles: An entraining air-parcel model with two-dimensional spectral cloud microphysics and a new formulation of the collection kernel, Q. J. Roy. Meteor. Soc., 129, 1–18, https://doi.org/10.1256/qj.02.52, 2003.
Khain, A., Ovtchinnikov, M., Pinsky, M., Pokrovsky, A., and Krugliak, H.: Notes on the state-of-the-art numerical modeling of cloud microphysics, Atmos. Res., 55, 159–224, 2000.
Khain, A., Rosenfeld, D., and Pokrovsky, A.: Aerosol impact on the dynamics and microphysics of deep convective clouds, Q. J. Roy. Meteor. Soc., 131, 2639–2663, 2005.
Khain, A. P. and Pinsky, M. B.: Turbulence effects on the collision kernel. II: Increase of the swept volume of colliding drops, Q. J. Roy. Meteor. Soc., 123, 1543–1560, 1997.
Khairoutdinov, M., Randall, D., and DeMott, C.: Simulations of the atmospheric general circulation using a cloud-resolving model as a superparameterization of physical processes, J. Atmos. Sci., 62, 2136–2154, 2005.
Kokhanovsky, A. and de Leeuw, G.: Satellite Aerosol Remote Sensing Over Land, Environmental Sciences, Springer-Verlag Berlin Heidelberg, 2009.
Koren, I., Martins, J. V., Remer, L. A., and Afargan, H.: Smoke invigoration versus inhibition of clouds over the Amazon, Science, 321, 946–949, https://doi.org/10.1126/science.1159185, 2008.
Korolev, A. V. and Mazin, I. P.: Supersaturation of Water Vapor in Clouds, J. Atmos. Sci., 60, 2957–2974, 2003.
Kovetz, A. and Olund, B.: The effect of coalescence and condensation on rain formation in a cloud of finite vertical extent, J. Atmos. Sci., 26, 1060–1065, 1969.
Kreidenweis, S. M., Walcek, C. J., Feingold, G., Gong, W., Jacobson, M. Z., Kim, C. H., Liu, X., Penner, J. E., Nenes, A., and Seinfeld, J. H.: Modification of aerosol mass and size distribution due to aqueous-phase SO2 oxidation in clouds: Comparisons of several models, J. Geophys. Res., 108, 4213, https://doi.org/10.1029/2002JD002697, 2003.
Krueger, S. K., Su, C. W., and McMurtry, P. A.: Modeling entrainment and finescale mixing in cumulus clouds, J. Atmos. Sci., 54, 2697–2712, 1997.
Kuba, N. and Fujiyoshi, Y.: Development of a cloud microphysical model and parameterizations to describe the effect of CCN on warm cloud, Atmos. Chem. Phys., 6, 2793–2810, https://doi.org/10.5194/acp-6-2793-2006, 2006.
Kumar, S. and Ramkrishna, D.: On the solution of population balance equations by discretization – I. A fixed pivot technique, Chem. Eng. Sci., 51, 1311–1332, 1996.
Lance, S., Brock, C. A., Rogers, D., and Gordon, J. A.: Water droplet calibration of the Cloud Droplet Probe (CDP) and in-flight performance in liquid, ice and mixed-phase clouds during ARCPAC, Atmos. Meas. Tech., 3, 1683–1706, https://doi.org/10.5194/amt-3-1683-2010, 2010.
Leaitch, W. R., Strapp, J. W., Isaac, G. A., and Hudson, J. G.: Cloud droplet nucleation and cloud scavenging of aerosol sulphate in polluted atmospheres, Tellus B, 38, 328–344, 1986.
Leroy, D., Wobrock, W., and Flossmann, A. I.: The role of boundary layer aerosol particles for the development of deep convective clouds: A high-resolution 3D model with detailed (bin) microphysics applied to CRYSTAL-FACE, Atmos. Res., 91, 62–78, https://doi.org/10.1016/j.atmosres.2008.06.001, 2009.
Link, M., Zhou, Y., Taubman, B., Sherman, J., Morrow, H., Krintz, I., Robertson, L., Cook, R., Stocks, J., West, M., and Sive, B. C.: A characterization of volatile organic compounds and secondary organic aerosol at a mountain site in the Southeastern United States, J. Atmos. Chem., 72, 81–104, https://doi.org/10.1007/s10874-015-9305-5, 2015.
Lohmann, U. and Feichter, J.: Global indirect aerosol effects: a review, Atmos. Chem. Phys., 5, 715–737, https://doi.org/10.5194/acp-5-715-2005, 2005.
Low, T. B. and List, R.: Collision, coalescence and breakup of raindrops. Part I: Experimentally established coalescence efficiencies and fragment size distributions in breakup, J. Atmos. Sci., 39, 1591–1606, 1982.
Lowenthal, D., Zielinska, B., Mason, B., Samy, S., Samburova, V., Collins, D., Spencer, C., Taylor, N., Allen, J., and Kumar, N.: Aerosol characterization studies at Great Smoky Mountains National Park, summer 2006, J. Geophys. Res,, 114, D08206, https://doi.org/10.1029/2008jd011274, 2009.
Lynn, B., Khain, A., Rosenfeld, D., and Woodley, W. L.: Effects of aerosols on precipitation from orographic clouds, J. Geophys. Res., 112, D10225, https://doi.org/10.1029/2006JD007537, 2007.
Marek, R. and Straub, J.: Analysis of the evaporation coefficient and the condensation coefficient of water, Int. J. Heat Mass Tran., 44, 39–53, 2001.
McCarthy, J.: Field verification of the relationship between entrainment rate and cumulus cloud diameter, J. Atmos. Sci., 31, 1028–1039, 1974.
McFiggans, G., Artaxo, P., Baltensperger, U., Coe, H., Facchini, M. C., Feingold, G., Fuzzi, S., Gysel, M., Laaksonen, A., Lohmann, U., Mentel, T. F., Murphy, D. M., O'Dowd, C. D., Snider, J. R., and Weingartner, E.: The effect of physical and chemical aerosol properties on warm cloud droplet activation, Atmos. Chem. Phys., 6, 2593–2649, https://doi.org/10.5194/acp-6-2593-2006, 2006.
Meskhidze, N., Nenes, A., Conant, W. C., and Seinfeld, J. H.: Evaluation of a new cloud droplet activation parameterization with in situ data from CRYSTAL-FACE and CSTRIPE, J. Geophys. Res., 110, D16202, https://doi.org/10.1029/2004JD005703, 2005.
Morton, B. R.: Buoyant plumes in a moist atmosphere, J. Fluid Mech., 2, 127–144, 1957.
Muhlbauer, A. and Lohmann, U.: Sensitivity studies of the role of aerosols in warm-phase orographic precipitation in different dynamical flow regimes, J. Atmos. Sci., 65, 2522–2542, 2008.
Muhlbauer, A., Hashino, T., Xue, L., Teller, A., Lohmann, U., Rasmussen, R. M., Geresdi, I., and Pan, Z.: Intercomparison of aerosol–cloud–precipitation interactions in stratiform orographic mixed-phase clouds, Atmos. Chem. Phys., 10, 8173–8196, https://doi.org/10.5194/acp-10-8173-2010, 2010.
Nenes, A., Ghan, S., Abdul-Razzak, H., Chuang, P. Y., and Seinfeld, J. H.: Kinetic limitations on cloud droplet formation and impact on cloud albedo, Tellus B, 53, 133–149, 2001.
Nenes, A., Charlson, R. J., Facchini, M. C., Kulmala, M., Laaksonen, A., and Seinfeld, J. H.: Can chemical effects on cloud droplet number rival the first indirect effect?, Geophys. Res. Lett., 29, 1848, https://doi.org/10.1029/2002gl015295, 2002.
Nguyen, T. K. V., Petters, M. D., Suda, S. R., Guo, H., Weber, R. J., and Carlton, A. G.: Trends in particle-phase liquid water during the Southern Oxidant and Aerosol Study, Atmos. Chem. Phys., 14, 10911–10930, https://doi.org/10.5194/acp-14-10911-2014, 2014.
Nugent, A. D., Watson, C. D., Thompson, G., and Smith, R. B.: Aerosol Impacts on Thermally Driven Orographic Convection, J. Atmos. Sci., 73, 3115–3132, https://doi.org/10.1175/jas-d-15-0320.1, 2016.
Paluch, I. R.: The entrainment mechanism in Colorado cumuli, J. Atmos. Sci., 36, 2467–2478, 1979.
Petersen, W. and Barros, A.: GPM Ground Validation Integrated Precipitation and Hydrology Experiment (IPHEx) Field Campaign Data Collection, NASA EOSDIS Global Hydrology Resource Center Distributed Active Archive Center Huntsville, Alabama, USA, https://doi.org/10.5067/GPMGV/IPHEX/DATA101, 2018.
Petters, M. D. and Kreidenweis, S. M.: A single parameter representation of hygroscopic growth and cloud condensation nucleus activity, Atmos. Chem. Phys., 7, 1961–1971, https://doi.org/10.5194/acp-7-1961-2007, 2007.
Petters, M. D., Carrico, C. M., Kreidenweis, S. M., Prenni, A. J., DeMott, P. J., Collett, J. L., and Moosmüller, H.: Cloud condensation nucleation activity of biomass burning aerosol, J. Geophys. Res., 114, D22205, https://doi.org/10.1029/2009jd012353, 2009.
Petters, S. S. and Petters, M. D.: Surfactant effect on cloud condensation nuclei for two-component internally mixed aerosols, J. Geophys. Res.-Atmos., 121, 1878–1895, https://doi.org/10.1002/2015JD024090, 2016.
Pinsky, M., Khain, A., and Shapiro, M.: Collisions of small drops in a turbulent flow. Part I: Collision efficiency. Problem formulation and preliminary results, J. Atmos. Sci., 56, 2585–2600, 1999.
Pinsky, M., Khain, A., and Shapiro, M.: Stochastic effects of cloud droplet hydrodynamic interaction in a turbulent flow, Atmos. Res., 53, 131–169, 2000.
Pinsky, M., Khain, A., and Shapiro, M.: Collision efficiency of drops in a wide range of Reynolds numbers: Effects of pressure on spectrum evolution, J. Atmos. Sci., 58, 742–764, 2001.
Pinsky, M., Khain, A., and Krugliak, H.: Collisions of Cloud Droplets in a Turbulent Flow. Part V: Application of Detailed Tables of Turbulent Collision Rate Enhancement to Simulation of Droplet Spectra Evolution, J. Atmos. Sci., 65, 357–374, https://doi.org/10.1175/2007jas2358.1, 2008.
Pinsky, M., Mazin, I. P., Korolev, A., and Khain, A.: Supersaturation and Diffusional Droplet Growth in Liquid Clouds, J. Atmos. Sci., 70, 2778–2793, https://doi.org/10.1175/jas-d-12-077.1, 2013.
Pinsky, M. B. and Khain, A. P.: Effects of in-cloud nucleation and turbulence on droplet spectrum formation in cumulus clouds, Q. J. Roy. Meteor. Soc., 128, 501–534, 2002.
Poellot, M.: GPM Ground Validation UND Citation Cloud Microphysics IPHEx, Dataset, NASA Global Hydrology Resource Center Distributed Active Archive Center, Huntsville, Alabama, USA, https://doi.org/10.5067/GPMGV/IPHEX/DATA101, 2015.
Prat, O. P. and Barros, A. P.: A Robust Numerical Solution of the Stochastic Collection–Breakup Equation for Warm Rain, J. Appl. Meteorol. Clim., 46, 1480–1497, https://doi.org/10.1175/jam2544.1, 2007a.
Prat, O. P. and Barros, A. P.: Exploring the use of a column model for the characterization of microphysical processes in warm rain: results from a homogeneous rainshaft model, Adv. Geosci., 10, 145–152, https://doi.org/10.5194/adgeo-10-145-2007, 2007b.
Prat, O. P., Barros, A. P., and Testik, F. Y.: On the Influence of Raindrop Collision Outcomes on Equilibrium Drop Size Distributions, J. Atmos. Sci., 69, 1534–1546, https://doi.org/10.1175/jas-d-11-0192.1, 2012.
Press, W. H., Teukolsky, S. A., Vetterling, W. T., and Flannery, B. P.: Numerical Recipes: The art of scientific computing, 3rd edn., Cambridge University Press, Cambridge, MA, USA, 2007.
Pringle, K. J., Tost, H., Pozzer, A., Pöschl, U., and Lelieveld, J.: Global distribution of the effective aerosol hygroscopicity parameter for CCN activation, Atmos. Chem. Phys., 10, 5241–5255, https://doi.org/10.5194/acp-10-5241-2010, 2010.
Pruppacher, H. R. and Klett, J. D.: Microphysics of Clouds and Precipitation, Springer, Netherlands, 1978.
Pruppacher, H. R. and Klett, J. D.: Microphysics of Clouds and Precipitation, Atmos. Oceanogr. Sci. Libr., Kulwer Academic Publishers, Alphen aan den Rijn, The Netherlands, 1997.
Ramanathan, V., Crutzen, P., Kiehl, J., and Rosenfeld, D.: Aerosols, climate, and the hydrological cycle, Science, 294, 2119–2124, 2001.
Randall, D., Khairoutdinov, M., Arakawa, A., and Grabowski, W.: Breaking the Cloud Parameterization Deadlock, B. Am. Meteorol. Soc., 84, 1547–1564, https://doi.org/10.1175/bams-84-11-1547, 2003.
Rosenfeld, D., Lohmann, U., Raga, G. B., O'Dowd, C. D., Kulmala, M., Fuzzi, S., Reissell, A., and Andreae, M. O.: Flood or drought: how do aerosols affect precipitation?, Science, 321, 1309–1313, https://doi.org/10.1126/science.1160606, 2008.
Scorer, R. S. and Ludlam, F.: Bubble theory of penetrative convection, Q. J. Roy. Meteor. Soc., 79, 94–103, 1953.
Seifert, A., Khain, A., Blahak, U., and Beheng, K. D.: Possible effects of collisional breakup on mixed-phase deep convection simulated by a spectral (bin) cloud model, J. Atmos. Sci., 62, 1917–1931, 2005.
Seinfeld, J. H. and Pandis, S. N.: Atmospheric chemistry and physics, John Wiley, New York, 1998.
Seinfeld, J. H. and Pandis, S. N.: Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, 2nd edn., Wiley, New York, NY, USA, 2006.
Shaw, R. A. and Lamb, D.: Experimental determination of the thermal accommodation and condensation coefficients of water, J. Chem. Phys., 111, 10659–10663, https://doi.org/10.1063/1.480419, 1999.
Simmel, M., Diehl, K., and Wurzler, S.: Numerical simulation of the microphysics of an orographic cloud: Comparison with measurements and sensitivity studies, Atmos. Environ., 39, 4365–4373, https://doi.org/10.1016/j.atmosenv.2005.02.017, 2005.
Snider, J. R., Guibert, S., Brenguier, J. L., and Putaud, J. P.: Aerosol activation in marine stratocumulus clouds: 2. Köhler and parcel theory closure studies, J. Geophys. Res., 108, 8629, https://doi.org/10.1029/2002jd002692, 2003.
Squires, P. and Turner, J. S.: An entraining jet model for cumulo-nimbus updraughts, Tellus A, 14, 422–434, 1962.
Tao, W.-K., Chen, J.-P., Li, Z., Wang, C., and Zhang, C.: Impact of aerosols on convective clouds and precipitation, Rev. Geophys., 50, RG2001, https://doi.org/10.1029/2011rg000369, 2012.
Telford, J. W. and Chai, S. K.: A new aspect of condensation theory, Pure Appl. Geophys., 118, 720–742, 1980.
Telford, J. W., Keck, T. S., and Chai, S. K.: Entrainment at cloud tops and the droplet spectra, J. Atmos. Sci., 41, 3170–3179, 1984.
Testik, F. Y., Barros, A. P., and Bliven, L. F.: Toward a Physical Characterization of Raindrop Collision Outcome Regimes, J. Atmos. Sci., 68, 1097–1113, https://doi.org/10.1175/2010jas3706.1, 2011.
Turner, J. S.: The motion of buoyant elements in turbulent surroundings, J. Fluid Mech., 16, 1–16, 1963.
Twomey, S.: The influence of pollution on the shortwave albedo of clouds, J. Atmos. Sci., 34, 1149–1152, 1977.
Warner, J.: The Microstructure of Cumulus Cloud. Part II. The Effect on Droplet Size Distribution of the Cloud Nucleus Spectrum and Updraft Velocity, J. Atmos. Sci., 26, 1272–1282, 1969.
Wilson, A. M. and Barros, A. P.: An Investigation of Warm Rainfall Microphysics in the Southern Appalachians: Orographic Enhancement via Low-Level Seeder–Feeder Interactions, J. Atmos. Sci., 71, 1783–1805, https://doi.org/10.1175/jas-d-13-0228.1, 2014.
Wilson, A. M. and Barros, A. P.: Landform controls on low level moisture convergence and the diurnal cycle of warm season orographic rainfall in the Southern Appalachians, J. Hydrol., 531, 475–493, https://doi.org/10.1016/j.jhydrol.2015.10.068, 2015.
Wilson, A. M. and Barros, A. P.: Orographic Land-Atmosphere Interactions and the Diurnal Cycle of Low Level Clouds and Fog, J. Hydrometeorol., 18, 1513–1533, https://doi.org/10.1175/jhm-d-16-0186.1, 2017.
Yang, Y., Fan, J., Leung, L. R., Zhao, C., Li, Z., and Rosenfeld, D.: Mechanisms Contributing to Suppressed Precipitation in Mt. Hua of Central China. Part I: Mountain Valley Circulation, J. Atmos. Sci., 73, 1351–1366, https://doi.org/10.1175/jas-d-15-0233.1, 2016.
Yildiz, O. and Barros, A. P.: Elucidating vegetation controls on the hydroclimatology of a mid-latitude basin, J. Hydrol., 333, 431–448, https://doi.org/10.1016/j.jhydrol.2006.09.010, 2007.
Zou, Y. S. and Fukuta, N.: The effect of diffusion kinetics on the supersaturation in clouds, Atmos. Res., 52, 115–141, 1999.





