the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
On what scales can GOSAT flux inversions constrain anomalies in terrestrial ecosystems?
Brendan Byrne
Dylan B. A. Jones
Kimberly Strong
Saroja M. Polavarapu
Anna B. Harper
David F. Baker
Shamil Maksyutov
Interannual variations in temperature and precipitation impact the carbon balance of terrestrial ecosystems, leaving an imprint in atmospheric CO2. Quantifying the impact of climate anomalies on the net ecosystem exchange (NEE) of terrestrial ecosystems can provide a constraint to evaluate terrestrial biosphere models against and may provide an emergent constraint on the response of terrestrial ecosystems to climate change. We investigate the spatial scales over which interannual variability in NEE can be constrained using atmospheric CO2 observations from the Greenhouse Gases Observing Satellite (GOSAT). NEE anomalies are calculated by performing a series of inversion analyses using the GEOS-Chem adjoint model to assimilate GOSAT observations. Monthly NEE anomalies are compared to “proxies”, variables that are associated with anomalies in the terrestrial carbon cycle, and to upscaled NEE estimates from FLUXCOM. Statistically significant correlations (P<0.05) are obtained between posterior NEE anomalies and anomalies in soil temperature and FLUXCOM NEE on continental and larger scales in the tropics, as well as in the northern extratropics on subcontinental scales during the summer (R2≥0.49), suggesting that GOSAT measurements provide a constraint on NEE interannual variability (IAV) on these spatial scales. Furthermore, we show that GOSAT flux inversions are generally better correlated with the environmental proxies and FLUXCOM NEE than NEE anomalies produced by a set of terrestrial biosphere models (TBMs), suggesting that GOSAT flux inversions could be used to evaluate TBM NEE fluxes.
- Article
(2465 KB) -
Supplement
(1027 KB) - BibTeX
- EndNote
Organisms within terrestrial ecosystems have evolved to fit their climatic environment. Anomalous variations in temperature and precipitation about the mean climate can have significant impacts on the functioning of these organisms (Berry and Bjorkman, 1980; Gutschick and BassiriRad, 2003; Smith, 2011), which can be reflected in anomalies in the carbon balance of ecosystems. In fact, interannual variability (IAV) in the atmospheric growth rate of CO2 is largely explained by changes in the carbon balance of terrestrial ecosystems in response to climate variability (Keeling et al., 1976a, b; Conway et al., 1994; Keeling et al., 1995; Battle et al., 2000). The largest driver of IAV in the carbon cycle is El Niño–Southern Oscillation (ENSO) variability, which most strongly impacts tropical ecosystems (Bacastow, 1976; Bacastow et al., 1980; Bousquet et al., 2000; Ciais et al., 2013). During the warm phase of ENSO (El Niño) large areas of tropical land become drier and warmer, leading to a net emission of CO2 from the land to the atmosphere, which amplifies the atmospheric CO2 growth rate. During the cold phase of ENSO (La Niña), much of the tropical land is cooler and wetter than average, leading to anomalously low CO2 growth rates (Jones and Cox, 2005). Similarly, in extratropical regions, temperature and moisture anomalies drive variability in the carbon balance of ecosystems (Conway et al., 1994; Bousquet et al., 2000; Wunch et al., 2013; Zscheischler et al., 2014; He et al., 2018). Many studies have examined extreme heat waves or droughts in the extratropics, such as the 2003 European heat wave (Ciais et al., 2005) and the 2010 Russian heat wave and wildfires (Guerlet et al., 2013; Ishizawa et al., 2016). In these cases, positive temperature anomalies and drought conditions result in an anomalous release of CO2 from terrestrial ecosystems to the atmosphere.
Most previous studies that have investigated large-scale IAV in the carbon cycle using CO2 measurements have employed measurements from the global network of in situ instruments for observational constraints (Bousquet et al., 2000; Rödenbeck et al., 2003, 2018; Bruhwiler et al., 2011; Peylin et al., 2013; Marcolla et al., 2017; Shiga et al., 2018). This network provides by far the longest direct record of atmospheric CO2 measurements, with many sites functioning for decades. However, the spatial distribution of sites is inhomogeneous, with sites most densely located in North America and Europe and comparatively few elsewhere. Therefore, in situ observations from the global observation network are relatively insensitive to CO2 fluxes over much of Asia and in the tropics (Byrne et al., 2017), where IAV is the largest. Recently, space-based observations of atmospheric CO2 have provided expanded observational coverage for atmospheric CO2. One of the satellites, the Greenhouse Gases Observing Satellite (GOSAT), has been providing measurements of atmospheric CO2 since 2009. With multiple years of measurements, it is now possible to investigate IAV in the carbon cycle with GOSAT data.
In this study, we investigate interannual anomalies in NEE estimated from GOSAT measurements using the flux inversion method, wherein surface fluxes are estimated from atmospheric CO2 measurements using a tracer transport model and Bayesian inverse methods. A series of flux inversions using the GEOS-Chem four-dimensional variational (4D-Var) data assimilation system (Henze et al., 2007) are performed with different spatial resolutions, prior fluxes, and prior error covariances. NEE anomalies produced by the GEOS-Chem flux inversions are contrasted with two independent publicly available flux inversion estimates, the GOSAT level 4 product (Maksyutov et al., 2013) and CarbonTracker version CT2016 (Peters et al., 2007, with updates documented at https://www.esrl.noaa.gov/gmd/ccgg/carbontracker/), which is a flux inversion that assimilates CO2 observations from the surface network. In addition, we compare the flux inversion NEE anomalies with NEE anomalies simulated by several terrestrial biosphere models (TBMs). One of the primary goals of atmospheric flux inversions is to provide better constraints on NEE to evaluate these models. Therefore, it is necessary to first determine the ability of TBMs to represent IAV.
Anomalies in NEE from the inversions and TBMs are compared with “proxies”, variables that are known to be closely associated with IAV in the carbon cycle. Agreement between the anomalies in NEE and the proxies provides corroborating evidence that the inversions and TBMs are correctly recovering anomalies in NEE (Deng et al., 2016; Mabuchi et al., 2016; Liu et al., 2017). Three proxies are examined: soil temperature (Tsoil) anomalies from the Modern-Era Retrospective analysis for Research and Applications (MERRA-2) reanalysis (Reichle et al., 2011, 2017), the monthly self-calibrated Palmer Drought Severity Index (scPDSI) (Dai, 2017), and solar-induced chlorophyll fluorescence (SIF) observed by GOME-2 (Joiner et al., 2016). We also use flux data from FLUXCOM (http://www.fluxcom.org/, last access: 9 October 2019), which provides data-driven NEE anomaly estimates (Tramontana et al., 2016; Jung et al., 2017).
This study has two main objectives. The first is to quantify the correlation between GOSAT flux inversions and the flux proxies to determine the spatial scales over which the GOSAT inversions constrain monthly NEE anomalies in the tropics and summer anomalies in the northern extratropics. This is performed by examining the spatial scales over which there are correlations between the NEE anomalies and the proxies–FLUXCOM anomalies.
The second objective is to quantify the sensitivity of inversion–proxy correlations to the inversion setup. This is investigated with a series of GOSAT flux inversions with different model resolution, prior fluxes, and prior error covariances.
This paper is structured as follows. In Sect. 2, we describe the datasets used, flux inversions performed, and how anomalies are calculated. Section 3 presents the results of our analysis. Flux inversion NEE anomalies are compared with the proxies in the tropics and northern extratropics individually. We then present a series of observing system simulation experiments (OSSEs) to examine the smallest spatial scales for which NEE anomalies can be recovered from GOSAT observations. Section 4 discusses the agreement in anomalies between the GOSAT flux inversions and proxies, the scales constrained by GOSAT flux inversions, and the sensitivity of these results to the inversion setup. Finally, conclusions are given in Sect. 5.
2.1 FLUXCOM NEE data
FLUXCOM remote sensing and meteorological data (RS + METEO) products are generated at spatial resolution using upscaling approaches based on machine-learning methods that integrate FLUXNET (https://daac.ornl.gov/cgi-bin/dataset_lister.pl?p=9, last access: 9 October 2019; Baldocchi et al., 2001) site-level observations, satellite remote sensing, and meteorological data (Tramontana et al., 2016; Jung et al., 2017). Remote sensing measurements are used to produce a mean seasonal cycle (Tramontana et al., 2016) and the NEE IAV signal in this product results from the driving reanalysis (NCEP CRU). In particular, NEE IAV is driven by air temperature, incoming global radiation combined with the mean seasonal cycle of the normalized difference vegetation index (NDVI), and a model-based water availability index. Jung et al. (2017) generate NEE products using several machine-learning methods. We downloaded these products from the data portal of the Max Planck Institute for Biochemistry (https://www.bgc-jena.mpg.de, last access: 9 October 2019). We find that the different algorithms generally give similar results; therefore, we only present results using the multivariate regression spline (MARS) NEE in this study.
2.2 Proxies
2.2.1 Dai Global Palmer Drought Severity Index
The monthly self-calibrated Palmer Drought Severity Index (scPDSI) (Dai, 2017) provides a measure of drought severity on a grid. The scPDSI is computed using observed monthly surface air temperature and precipitation, and it provides a measure of surface aridity anomalies and changes on seasonal to longer timescales (Dai et al., 2004; Dai, 2011). We note that the scPDSI may not be a good proxy for soil moisture content over the high latitudes ().
2.2.2 SIF
We use the monthly gridded “SIF daily average” product from the NASA level 3 GOME-2 version 27 (V27) terrestrial chlorophyll fluorescence data (NASA-SIF, 2016; Joiner et al., 2013, 2016). SIF anomalies are multiplied by negative one to change the sign of the anomalies so that positive correlations will be obtained if negative SIF anomalies are correlated with positive NEE anomalies (emission of CO2 to the atmosphere).
2.2.3 Soil temperature
For the soil temperature proxy, we use soil temperatures from the MERRA-2 (Reichle et al., 2011, 2017) reanalysis. Specifically, we use the average soil temperature over levels 1–3 (TSOIL1, TSOIL2, and TSOIL3), which reaches a depth of 0.73 m.
2.2.4 Niño 3.4 index
For the phase of ENSO, we use the sea surface temperature (SST) anomaly in the Niño 3.4 region (5∘ S–5∘ N, 120∘ S–170∘ N) of the tropical Pacific Ocean. This region has been widely used to diagnose ENSO activity. The SST values are calculated from the Hadley Centre Sea Ice and Sea Surface Temperature (HadISST) dataset. The SST anomalies were downloaded from the National Oceanic and Atmospheric Administration (NOAA) Earth System Research Laboratory (ESRL) website (https://www.esrl.noaa.gov, last access: 9 October 2019).
2.3 Inversion analyses
2.3.1 CarbonTracker
We use optimized NEE from the NOAA CarbonTracker version CT2016 (Peters et al., 2007, with updates documented at https://www.esrl.noaa.gov/gmd/ccgg/carbontracker/, last access: 9 October 2019). CT2016 optimizes NEE by assimilating in situ observations of boundary layer atmospheric CO2. It employs the ensemble Kalman filter approach to assimilate CO2 with atmospheric chemical transport simulated by the TM5 offline atmospheric model (Krol et al., 2005). For CT2016, TM5 is driven by ERA-Interim assimilated meteorology from the European Centre for Medium-Range Weather Forecasts (ECMWF), with a horizontal resolution of globally and in a nested grid over North America. CT2016 also has IAV in biomass burning. Therefore, when analyzing posterior IAV in CT2016 we examine the IAV in NEE alone (referred to as CT2016) and IAV due to NEE and biomass burning combined (referred to as CT2016w∕BB).
2.3.2 GOSAT level 4 data
We use the GOSAT level 4 data product (Maksyutov et al., 2013) produced by the National Institute for Environmental Studies (NIES). This product is produced by assimilating NIES level 2 retrievals of into the NIES global atmospheric tracer transport model (NIES-TM) to optimize monthly CO2 fluxes for 64 subcontinental regions. The Vegetation Integrative SImulator for Trace gases (VISIT), a prognostic biosphere model (Ito, 2010; Saito et al., 2014), is used to generate prior biospheric fluxes for the inversion analyses. The GOSAT L4 product also has IAV in biomass burning. Therefore, when analyzing posterior IAV, we examine IAV in NEE alone (referred to as GOSAT L4) and IAV due to NEE and biomass burning combined (referred to as GOSAT L4w∕BB).
2.3.3 GEOS-Chem
We perform a series of flux inversions using the GEOS-Chem 4D-Var assimilation system (Henze et al., 2007). The GEOS-Chem forward model (http://acmg.seas.harvard.edu/geos/geos_overview.html, last access: 9 October 2019) is a global 3-D chemical transport model driven by assimilated meteorology from the Goddard Earth Observing System (GEOS-5) of the NASA Global Modeling and Assimilation Office (GMAO). The native resolution of the model is with 72 vertical levels from the surface to 0.01 hPa, but we run the model at lower resolution (either or , depending on the inversion) with 47 vertical layers. Our model configuration is based on the configuration of Nassar et al. (2011). To optimize surface fluxes, the 4D-Var cost function is minimized as described in Deng et al. (2014) to retrieve monthly scaling factors for prior ocean and terrestrial biosphere fluxes in each grid cell. We use an assimilation window of 9 months and keep posterior fluxes from the first 6 months, then shift the inversion widow forward 6 months. Using this method, we optimize NEE spanning 2010–2013 (in addition to a 6-month spin-up inversion starting in July 2009). Monthly ocean fluxes are from Takahashi et al. (2009), anthropogenic emissions are from Andres et al. (2016), and biomass burning emissions are from the Global Fire Emission Database GFEDv3 (van der Werf et al., 2006). We repeat the 2010 GFEDv3 biomass burning emissions for all years so that there is no prior NEE IAV. Error covariance matrices are taken to be diagonal such that there are no spatial or temporal covariances. Prior errors are assigned as a percentage of the prior flux estimate rather than an absolute value. We assign 16 % error to fossil fuels and 38 % error to biomass burning following Deng et al. (2014).
Table 1Setup of GEOS-Chem flux inversions. Differences are in model transport resolution, prior fluxes, and prior errors.
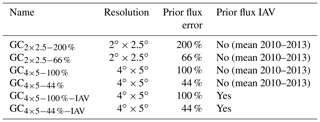
The GEOS-Chem flux inversions performed in this study are shown in Table 1. The flux inversions are performed with different model configurations to examine the sensitivity of the results to the inversion setup. We perform inversions at two spatial resolutions, and . The spatial resolution is varied to examine whether changes in model transport significantly impact our results. It has previously been shown that there are significant differences in tracer transport as model resolution is decreased in GEOS-Chem (Yu et al., 2018; Stanevich, 2018). In particular, Stanevich (2018) show that resolution-induced biases of up to 30 % can be introduced on the scale of TransCom regions for relative to for atmospheric methane (CH4) inversions.
The prior error statistics are varied between inversions. The prior error covariance provides a metric of the uncertainty in the prior fluxes. If prior fluxes are well known then small errors are applied. If they are poorly known then large prior errors are applied and the observations will have a larger impact on the posterior fluxes. However, in general, atmospheric CO2 observations under-constrain the fluxes and additional regularization considerations are required. To prevent the over-fitting of assimilated observations, prior flux errors are typically tighter than the true uncertainty in NEE fluxes. Therefore, the motivation for varying prior errors in this study is to examine the sensitivity of the posterior NEE anomalies to these prior constraints.
Finally, the prior NEE fluxes are varied between flux inversions. For all GEOS-Chem inversions, the prior NEE fluxes are based on the posterior fluxes from CT2016. CT2016 fluxes are used because they are informed by atmospheric CO2 observations and thus provide a seasonal cycle of NEE that is closer to observed atmospheric CO2 than a TBM forward run (Byrne et al., 2018). Using prior fluxes that are closer to the observed atmospheric CO2 then justifies tighter prior flux error covariances. We use two different setups of the CT2016 posterior fluxes in the inversions. For four inversions we remove the NEE IAV from the CT2016 fluxes. To do this, the fluxes are averaged over 4 years (2010–2013) to generate a mean seasonal cycle. We then repeat this climatology of NEE fluxes for each year of the inversion. The reason for removing prior NEE IAV is so that all posterior NEE anomalies will be introduced through the assimilation of GOSAT observations. This setup is different from many previous flux inversion studies that have included NEE IAV in the prior fluxes. Therefore, to examine the sensitivity of the posterior NEE IAV to prior NEE IAV, we also perform two inversions that employ 3-hourly CT2016 NEE fluxes over 2010–2013 unchanged from those available at https://www.esrl.noaa.gov/gmd/ccgg/carbontracker/, other than spatial interpolation to fit our grid, so that NEE IAV is present on the prior NEE for these inversions. The inversions are given names with a subscript following the convention “model resolution – percentage error applied to prior fluxes – presence of prior NEE IAV” such that an inversion analysis at resolution with 100 % uncertainty applied to prior fluxes and with prior NEE IAV is named GC.
For GOSAT observations, we use version 3.5 of the NASA Atmospheric CO2 Observations from Space (ACOS) GOSAT lite files from the CO2 Virtual Science Data Environment (https://co2.jpl.nasa.gov/, last access: 11 October 2019). Information on the ACOS retrieval algorithm is available in O'Dell et al. (2012) and Crisp et al. (2012). We selected all measurements from the TANSO-FTS shortwave infrared (SWIR) channel, including ocean glint as well as high-gain and medium-gain nadir, which pass the quality flag requirement and have warn levels less than or equal to 15. We generate “super-obs” from the GOSAT retrievals by aggregating the observations to the grid size of our inversion. We generate error estimates using the method described by Kulawik et al. (2016). The reduction in error with aggregation can be calculated using the expression , where a represents systematic errors that do not decrease with averaging, b represents random errors that decrease with averaging, and n represents the number of satellite observations that are averaged (Kulawik et al., 2016). Kulawik et al. (2016) give a=0.8 ppm and b=1.6 ppm as mean Northern Hemisphere geometric (colocated) values for GOSAT, and these are the values that we use.
2.3.4 Observing system simulation experiments
Five OSSEs are performed, for which pseudo-data are generated by simulating atmospheric CO2 with GEOS-Chem at spatial resolution and with year-specific NEE from the Joint UK Land Environment Simulator (JULES). The GEOS-Chem CO2 distribution is sampled according to the GOSAT observational coverage. We generate pseudo- using the GOSAT averaging kernel weighting and apply random errors to the pseudo-obs consistent with the error estimates described in Sect. 2.3.3. The inversion configuration for three of the OSSEs is identical to GC, GC, and GC, which use the posterior CT2016 fluxes as their prior NEE (see Table 1). These OSSEs are referred to as OSSECT2016−44 %, OSSECT2016−100 %, and OSSE, respectively. Two more OSSEs use the same setup as GC and GC, except that for these we use the 2010–2013 mean NEE fluxes from JULES as the prior fluxes. These two OSSEs are referred to as OSSEJULES−44 % and OSSEJULES−100 %.
2.4 Terrestrial biosphere models
2.4.1 JULES
JULES is a community land surface model that has evolved from the UK Met Office Surface Exchange Scheme. Phenology in JULES affects leaf growth rates and the timing of leaf growth and senescence based on temperature alone (Clark et al., 2011). Vegetation cover is predicted based on nine plant functional types that compete for space based on their relative productivity and height but are excluded from growing on agricultural land based on a fraction of agriculture in each grid cell (Harper et al., 2018). CRU-NCEP was used as model forcing data.
2.4.2 VISIT
VISIT is a prognostic biosphere model (Ito, 2010; Saito et al., 2014) that simulates carbon exchanges between the atmosphere and biosphere and among the carbon pools within terrestrial ecosystems at a daily time step. Modeling of plant CO2 assimilation in VISIT is based on a model of light extinction in the canopy, following the formulation of Monsi and Saeki (1953). Autotrophic respiration is formulated as the sum of growth respiration and maintenance respiration. Growth respiration is simulated as the cost to produce new biomass, while maintenance respiration is represented as a function of ground surface temperature. Heterotrophic respiration is the sum of respiration from two layers, litter and humus, which is regulated by soil temperature and soil moisture at each depth. VISIT is driven by reanalysis–assimilation climate datasets provided by the Japan Meteorological Agency (JMA): the Japan 25-year reanalysis (JRA-25) Climate Data Assimilation System JCDAS) (Onogi et al., 2007) for the period 1979 to present.
2.4.3 Carnegie–Ames–Stanford approach (CASA) Global Fire Emissions Database (GFED) carbon monitoring system (CMS) model
The version of the CASA model used here, referred to as CASA CMS, was modified from Potter et al. (1993) as described in Randerson et al. (1996), van der Werf et al. (2006), and Liu et al. (2014). It is driven by the MERRA reanalysis and the satellite-observed normalized difference vegetation index (NDVI) to track plant phenology. These flux estimates were computed at monthly time steps with 0.5∘ horizontal resolution. Monthly NEE fluxes were downloaded from the CarbonTracker ftp (ftp://aftp.cmdl.noaa.gov/products/carbontracker/co2/CT2016/fluxes/priors/, last access: 11 October 2019).
2.4.4 CASA GFED 4.1
The version of the CASA model used here, CASA GFED 4.1, was modified from Potter et al. (1993) as described in van der Werf et al. (2017). It is driven by ECMWF reanalysis and the satellite-observed NDVI to track plant phenology. These flux estimates were computed at monthly time steps with 0.25∘ horizontal resolution. Monthly NEE fluxes were downloaded from the CarbonTracker ftp (ftp://aftp.cmdl.noaa.gov/products/carbontracker/co2/CT2016/fluxes/priors/, last access: 11 October 2019).
2.5 Anomalies and correlations
Monthly anomalies are calculated by subtracting the mean 2010–2013 value for a given month from the monthly value for a specific year. For example, the NEE anomaly for a given month and year is calculated using
Anomalies are calculated over a range of spatial scales. In each case, the quantity of interest is first averaged into a spatial mean for each month, then anomalies are calculated. The same procedure is followed for June–July–August (JJA) anomalies except that the anomaly is calculated over the entire 3-month period instead of for a single month. It is worth noting that 4 years is a relatively short period to define a climatology, and some modes of climate variability occur on longer timescales. Ideally, a longer time period would be used to calculate a climatology, but we are limited by the availability of GOSAT data in this study.
In the tropics, temporal correlations are performed to quantify agreement between NEE anomalies and proxy–FLUXCOM anomalies. We want to test the hypothesis that the assimilation of CO2 observations will significantly increase the correlation between the posterior NEE IAV and the proxies relative to the prior NEE IAV and the proxies. We choose a null hypothesis in which the correlation is zero. This is the correct null hypothesis for flux inversions for which the prior NEE fluxes have no IAV. In flux inversions for which there is IAV in the prior NEE, the correlation between the proxies and prior NEE IAV should be used as the null hypothesis. However, this would be a significantly more difficult null hypothesis to test, so for simplicity we choose a null hypothesis of zero correlation for all cases. This is equivalent to testing whether the posterior NEE IAV is significantly correlated with the proxies, regardless of the prior IAV. The threshold for rejection of the null hypothesis (α) is chosen to be 0.05 such that the null hypothesis is rejected if the P value (P) is less than 0.05. We acknowledge that this α threshold is largely arbitrary but is widely used in the literature (Benjamin et al., 2018; Lakens et al., 2018). Throughout the paper, correlations that satisfy this criterion are called “strong”. In most cases a second test is performed, in which we test if the correlation between the flux inversion NEE IAV and the proxy is greater than that between the Niño 3.4 index and the proxy, and we conclude that the inversion and proxy only show good agreement if both of these thresholds are met. The coefficient of correlation is referred to as R.
We also perform a series of linear regressions. In the tropics, linear regressions are performed after aggregating over all tropical land such that the regression is performed on a single 48-point time series. In the northern extratropics, linear regressions are performed for the set of four JJA anomalies across five subcontinental regions, resulting in a 20-point dataset. For all regressions the y intercept is close to zero and is thus not reported. The slope of the regressions and coefficient of determination (R2) are reported.
3.1 Tropics
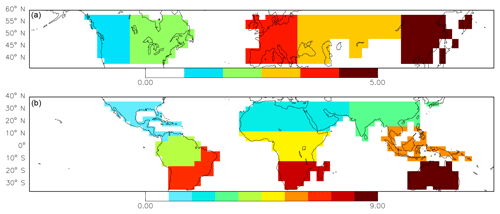
This section presents the correlations between monthly NEE anomalies and proxy–FLUXCOM anomalies in the tropics. The analysis is performed at five different spatial scales: , , subcontinental regions (shown in Fig. 1), continents, and the entire tropics. Figure 2 shows the mean correlation coefficient between the inversions and proxies–FLUXCOM on these scales in the tropics.
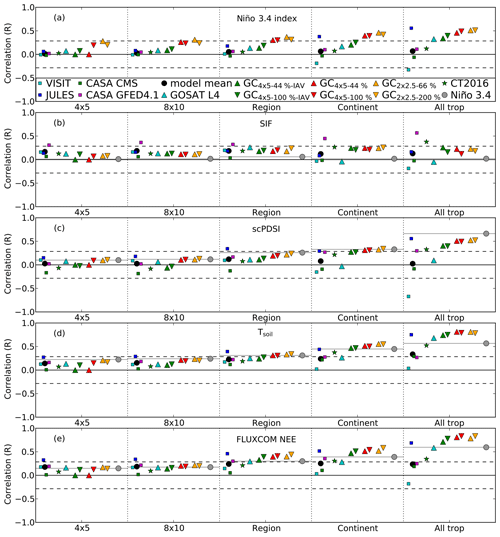
Figure 2Correlation in the tropics over a range of scales for models and inversions with (a) the Niño 3.4 index, (b) (−1) × SIF, (c) scPDSI, (d) Tsoil, and (e) FLUXCOM NEE. Squares represent correlations with terrestrial ecosystem model NEE IAV: VISIT (cyan), JULES (blue), CASA GFED CMS (green), and CASA GFED 4.1 (magenta); the black circle shows the mean correlation of the models. Triangles represent correlations with the GOSAT flux inversion NEE IAV: GOSAT L4 (cyan upward triangle), GC NEE IAV (green upward triangle), GC NEE IAV (green downward triangle), GC NEE IAV (red upward triangle), GC NEE IAV (red downward triangle), GC NEE IAV (orange upward triangle), and GC NEE IAV (orange downward triangle). The green stars show the correlation with CT2016 NEE IAV. The grey circle shows the correlation with the Niño 3.4 index. Dashed black lines indicate the correlation required for an α of 0.05; therefore, all correlations greater than the dashed black line indicate P<0.05.
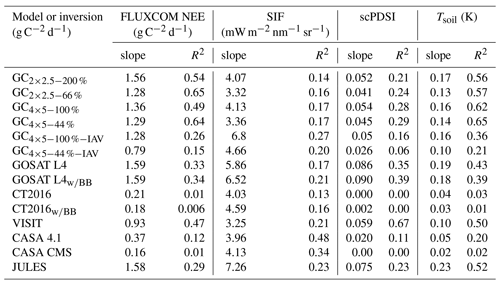
The correlation between posterior NEE anomalies and proxy–FLUXCOM anomalies increases with spatial aggregation (Fig. 2). This is expected as atmospheric CO2 observations are expected to best constrain fluxes on large spatial scales, such as the entire tropics. At smaller spatial scales, the atmospheric signal from variations in the fluxes becomes weaker and more difficult to constrain with the atmospheric CO2 observations. In general, the GEOS-Chem GOSAT inversions show strong correlations (P<0.05) with FLUXCOM and the Niño 3.4 index in subcontinental regions and on larger scales, as well as with Tsoil and scPDSI on continental and larger scales. We do not find strong correlations with GOME-2 SIF on any scale in the tropics.
The correlation coefficient is variable between GOSAT inversions, suggesting that the agreement between posterior fluxes and the proxies–FLUXCOM is sensitive to the inversion configuration. The inversions generally show slightly better agreement with the proxies and FLUXCOM than the inversions for subcontinental regions and continental scales. Correlations are stronger for the inversions without NEE IAV for subcontinental regions and continental scales. Larger prior errors generally result in larger correlations for subcontinental regions and larger scales.
The GOSAT L4 product tends to give weaker correlations with the proxies than the GEOS-Chem flux inversions, which is likely due to differences in the inversion configuration. For CT2016, which assimilates surface in situ and flask measurements, correlations with the proxies and FLUXCOM are generally weaker than for the GOSAT flux inversions.
For the TBMs, correlations are highly model dependent. Of the models, JULES shows the best agreement with the proxies and FLUXCOM. JULES shows strong correlations (P<0.05) at all scales for FLUXCOM NEE, for subcontinental regions and the entire tropics for Tsoil, and subcontinental regions for scPDSI. For the other models, less agreement is seen with the proxies and FLUXCOM. The one exception is CASA GFED 4.1, which shows strong correlations with SIF at all scales. This may be due to the fact that this model assimilates greenness indices to estimate gross primary production (GPP) fluxes. Anomalies in the greenness indices are likely well correlated with SIF anomalies; therefore, if anomalies in CASA NEE are driven by anomalies in GPP, it may explain the strong correlation.
Table 2Slope and coefficient of determination (R2) for linear regressions of inversion and TBM NEE anomalies against proxy–FLUXCOM anomalies across the entire tropics.
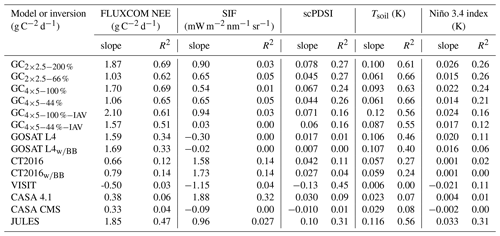
We now investigate the magnitude of tropical NEE IAV in the inversions and the TBMs. The magnitude of NEE IAV relative to the proxies and FLUXCOM can be obtained by performing linear regressions of the inversion and TBM NEE anomalies against proxy and FLUXCOM anomalies. Linear regressions are only calculated for the scale of the entire tropics, where the inversions and proxies–FLUXCOM agreed best. Table 2 shows the slope and coefficient of determination (R2) for the regressions. There is a large amount of variability in the slopes between inversions and TBMs for each proxy and FLUXCOM. The GOSAT inversion regressions are quite consistent with each other relative to those for CT2016 and the TBMs. The GOSAT inversions give slopes of 1.03–2.10 for FLUXCOM and 0.061–0.12 for Tsoil (note that FLUXCOM NEE is known to underestimate the magnitude of IAV; Jung et al., 2011, 2017). The largest differences between GEOS-Chem inversions are related to the magnitude of the prior error covariances. Looser prior constraints result in slopes that are 30 %–80 % larger. There are also large differences in the magnitude of posterior NEE IAV between the inversions with and without prior NEE IAV. For example, the slopes for the regression between FLUXCOM and the GEOS-Chem inversions with prior anomalies are 25 %–50 % larger than for GEOS-Chem inversions without prior NEE IAV. The GOSAT L4 product gives slopes that are consistent with the GEOS-Chem inversions. Furthermore, the agreement between the GOSAT L4 product and proxies (or FLUXCOM) is not sensitive to the inclusion of biomass burning. For CT2016, the best agreement is found with Tsoil (), for which CT2016 gives a smaller slope than the GOSAT inversions. The agreement between CT2016 and proxies–FLUXCOM is not sensitive to the inclusion of biomass burning. For the TBMs, JULES gives good fits with Tsoil (R2=0.56), and FLUXCOM (R2=0.47) and gives slopes that are similar in magnitude to the flux inversions. The rest of the TBMs have R2 that are too small to make meaningful comparisons. From this analysis we cannot make conclusions about the accuracy of the magnitude of IAV, and instead this is addressed with a series of OSSEs in Sect. 3.3.
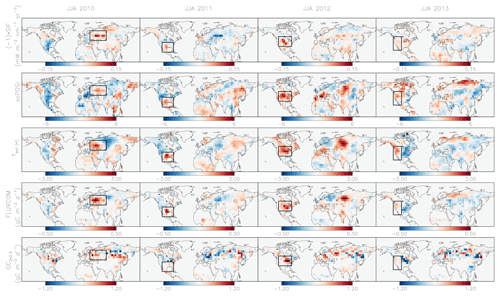
Figure 3Northern extratropical anomalies during JJA. Anomalies for (top row) SIF, (second) scPDSI, (third) Tsoil, (fourth) FLUXCOM NEE, and (bottom) GC NEE over JJA for (left to right) 2010–2013. Black boxes highlight major climate anomalies: the 2010 Russian heat wave, 2011 drought in Mexico and the southern USA, the 2012 North American drought, and the 2013 California drought.
3.2 Northern extratropics
In the northern extratropics, the observational coverage of GOSAT is highly seasonal, so we limit our analysis of anomalies in the northern extratropics to the summer (JJA) when observational coverage is the best (Liu et al., 2014; Byrne et al., 2017). Figure 3 shows the anomalies for the proxies, FLUXCOM NEE, and GC NEE across the Northern Hemisphere for JJA 2010–2013. The proxies and FLUXCOM generally show high coherence in anomalies. Events for which FLUXCOM NEE gives enhanced emissions to the atmosphere also show reduced SIF, increased scPDSI, and increased Tsoil. We have highlighted (with boxes) major climate anomalies over this time period: the 2010 Russian heat wave, the 2011 drought in Mexico and the southern USA, the 2012 North American drought, and the 2013 California drought. GC NEE indicates positive anomalies for all of these major events, suggesting that the inversion can recover subcontinental NEE IAV. However, there are also instances in which the inversion and proxies tend to disagree. For example, in 2010, GC indicates a positive anomaly in North America, whereas the proxies indicate near neutral or negative anomalies.
To examine agreement with the proxies on subcontinental regions, we have aggregated the inversions, the TBMs, proxies, and FLUXCOM into the five extratropical subcontinental regions shown in Fig. 1. The JJA anomalies in these regions over 2010–2013 provide 20 data points. We performed a linear regression of these anomalies against the proxies and FLUXCOM. Table 3 shows the slope and R2 values of the regressions. For the GOSAT inversions, the and with no prior NEE IAV show the closest agreement with FLUXCOM NEE and Tsoil (), while the inversions with prior NEE IAV show substantially poorer agreement (). This is a larger difference between the inversions with and without prior NEE IAV than was found for the tropics (see Sect. 4.4.3). The inversions with NEE IAV also give a smaller slope, indicating a smaller magnitude of NEE IAV, which is the opposite of what was found in the tropics. Comparing the inversions without prior NEE IAV, tight prior errors give , whereas loose prior constraints give . As with the tropics, the inversions with looser prior constraints give larger slopes, suggesting larger NEE IAV.
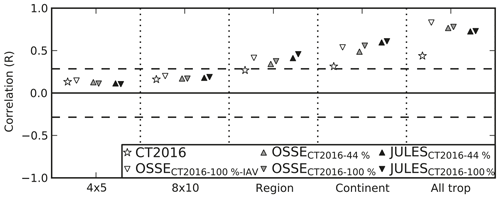
Figure 4Mean correlation coefficient (R) with the true OSSE NEE IAV over a range of spatial scales for CT2016 NEE IAV (white star), OSSE NEE IAV (white downward triangle), OSSECT2016−44 % NEE IAV (grey upward triangle), OSSECT2016−100 % NEE IAV (grey downward triangle), OSSEJULES−44 % NEE IAV (black upward triangle), and OSSEJULES−100 % (black downward triangle) NEE IAV.
Comparing the other inversions, the GOSAT L4 product shows agreement with FLUXCOM NEE (R2=0.33) and Tsoil (R2=0.43). CT2016 shows poor agreement with all proxies, indicating that this inversion is unable to isolate zonally asymmetric fluxes in the northern extratropics, which is surprising given the high sensitivity of the surface CO2 network to northern extratropical surface fluxes (Byrne et al., 2017). However, consistent with this result, Polavarapu et al. (2018) show that flux inversions assimilating measurements from the surface network are less able to recover zonally asymmetric flux signals than flux inversions assimilating GOSAT measurements. CT2016 also includes prior NEE IAV in the inversion, which may negatively impact the posterior NEE IAV, based on the GEOS-Chem inversion results.
For the TBMs, VISIT shows close agreement with FLUXCOM NEE, scPDSI, and Tsoil anomalies and to a lesser extent SIF anomalies. This is notable as VISIT generally showed poor agreement with the proxies in the tropics. JULES shows close agreement with Tsoil anomalies and some agreement with the other proxies. CASA GFED 4.1 shows good agreement with SIF anomalies but comparatively poorer agreement with the other proxies. CASA GFED CMS shows some agreement with SIF anomalies but little agreement with the other proxies.
3.3 Observing system simulation experiments
Strong correlations between the GOSAT flux inversions and proxies–FLUXCOM provide evidence that the GOSAT flux inversions give realistic constraints on NEE. However, the absence of strong correlations does not imply that the GOSAT flux inversions are not constraining IAV as there could be other causes (such as lagged effects within ecosystems) that can explain the absence of correlations. Therefore, to investigate the minimum spatial scales that can be constrained by GOSAT observations, we performed a series of OSSE experiments. In these experiments pseudo-observations were assimilated from a GEOS-Chem forward model run that had JULES NEE fluxes prescribed. See Sect. 2.3.4 for additional details of the OSSE setup.
3.3.1 Tropics
Strong correlations are obtained between the posterior and true anomalies for all OSSEs on subcontinental regional and larger scales, suggesting that subcontinental regions are the minimum scales that can be constrained by GOSAT measurements. Figure 4 shows the mean correlation coefficient between the posterior and true NEE anomalies in the tropics over a range of scales. The inversion setup has an impact on the correlations between the posterior and true NEE IAV. The largest differences between OSSEs are obtained on subcontinental regional and continental scales. On these scales, OSSEJULES−100 % has the largest correlation. The inclusion of prior NEE IAV (OSSE) does not appear to substantially degrade the correlation relative to a prior NEE without IAV (OSSECT2016−100 %), in contrast to what was found with the real-data GOSAT inversions. The prior error constraints generally have a large influence on the correlation with the true NEE IAV. Loose prior constraints give better agreement for all OSSEs, consistent with the GOSAT inversions.
Table 4Slope and coefficient of determination (R2) for linear regressions of OSSE posterior NEE anomalies against the true NEE IAV and OSSEJULES−100 %.
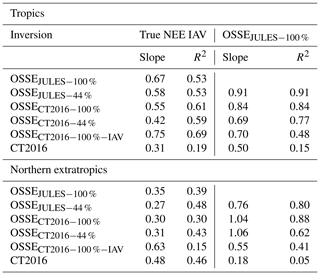
On the scale of the entire tropics, we performed linear regressions between the posterior and true anomalies, which are shown in Table 4. For all regressions, the magnitude of IAV in the posterior fluxes is less than the true NEE IAV (slope of 0.42–0.75). This suggests that the inversions do not recover the full magnitude of NEE IAV. In addition to comparing posterior and true anomalies, we examine the similarities in posterior anomalies between OSSEs. The right column of Table 4 shows the results of linear regressions between posterior and OSSEJULES−100 % NEE anomalies. The OSSEs without prior NEE IAV show better agreement with OSSEJULES−100 % posterior anomalies than the true anomalies. This suggests that the assimilation of pseudo-data is introducing NEE anomalies in a similar way for all OSSEs, and recovering the true NEE IAV is primarily limited by the observational coverage rather than the inversion setup. Overall, these OSSEs suggest that the real-data flux inversions underestimate IAV in NEE by 42 %–75 % and suggest that subcontinental regions are the minimum scale for which IAV can be recovered from GOSAT measurements.
3.3.2 Northern extratropics
The posterior NEE anomalies are generally correlated with the truth () but give slopes less than one, indicating that the OSSEs are not recovering the full magnitude of NEE IAV. Table 4 shows the slope and R2 for linear regressions of JJA NEE anomalies from the OSSEs against the true NEE IAV in subcontinental regions in the northern extratropics during JJA. Comparing the different OSSE setups, OSSE performs substantially worse than the OSSEs with no prior NEE IAV (R2=0.15 versus R2=0.30–0.48). This is consistent with comparisons between GOSAT inversions and proxies and suggests that employing prior NEE IAV in the northern extratropics degrades posterior NEE IAV on subcontinental scales during JJA. OSSEs with tighter prior constraints give larger R2, consistent with the GOSAT inversions. OSSEs with JULES mean seasonal cycle also agree better with the true NEE IAV than those that employ the mean seasonal cycle from CT2016.
4.1 Scales constrained by GOSAT
We investigated the agreement between monthly posterior NEE anomalies and proxy–FLUXCOM anomalies over a range of spatial scales. The results showed that the agreement between the inversions and the proxies–FLUXCOM were scale dependent. Here we synthesize these results and discuss the ability of GOSAT flux inversions to recover IAV in NEE over the range of scales examined in this study.
In the tropics, we find strong evidence that the GOSAT inversions are recovering the timing of NEE anomalies on the scale of the entire tropics; however, there is less agreement on the magnitude of monthly NEE anomalies over the tropics. The OSSEs suggest that GOSAT flux inversions underestimate the magnitude of NEE anomalies by about 50 %, depending on the inversion setup. On continental scales in the tropics, strong correlations with FLUXCOM NEE and Tsoil anomalies suggest that GOSAT flux inversion can constrain monthly NEE anomalies. On subcontinental regional scales in the tropics, the results were more ambiguous. The GOSAT inversions generally showed good agreement with FLUXCOM NEE IAV on subcontinental regional scales but only marginal agreement with Tsoil. The OSSEs also indicate marginal ability to recover subcontinental regional-scale fluxes. From these results, we caution against making conclusions about NEE IAV on subcontinental regional scales in the tropics using GOSAT flux inversions without corroborating evidence. On smaller scales, correlations do not meet the threshold of P<0.05.
In the northern extratropics during JJA, the results of this study suggest that subcontinental regional-scale constraints are possible. We found that large NEE anomalies due to major climate events are recovered in the inversion for GC (Fig. 3), while linear regressions showed close agreement for the GOSAT flux inversions with FLUXCOM NEE and Tsoil. However, we also found evidence that the posterior NEE IAV was sensitive to the inversion setup. The inversion analyses with prior NEE IAV (GC, GC, and GOSAT L4) showed weaker agreement with the proxies relative to the inversions without prior NEE IAV. Similarly, the OSSEs showed that prior NEE IAV reduced agreement between the posterior and the true NEE IAV in the northern extratropics during JJA.
4.2 Influence of ENSO
ENSO is the primary driver of large-scale NEE IAV in the tropics; therefore, it is useful to consider correlations between the inversions and TBMs and proxies–FLUXCOM within the context of ENSO variability. Here, we contrast correlations between the inversions and proxies to correlations between the Niño 3.4 index and proxies. Figure 2 shows correlations between the Niño 3.4 index and proxies over the range of spatial scales. Correlations between the proxies and the Niño 3.4 index increase with aggregation, as expected since the Niño 3.4 index reflects the large-scale ENSO-driven variability in the tropics. The GEOS-Chem GOSAT flux inversions show stronger correlations with the proxies than the Niño 3.4 index on subcontinental regions and at larger scales for correlations with FLUXCOM NEE and at continental and larger scales for Tsoil. For the GOSAT L4 inversion, the correlation only reaches this threshold for Tsoil at the largest aggregation scale. These results suggest that GOSAT observations provide more detailed flux information on continental and larger scales than the ENSO index. Thus, these data could provide insights into differences in the carbon dynamics between ENSO events and support the ability of space-based to inform continental-scale responses to ENSO variability as presented by Liu et al. (2017). Additional comparisons between posterior NEE fluxes and the Niño 3.4 index are provided in Sect. S1 of the Supplement.
4.3 Implications of correlations between flux inversions and proxies
The results of this study show varying degrees of agreement between anomalies in GOSAT flux inversions and anomalies in proxies and FLUXCOM. We consistently find that Tsoil and FLUXCOM NEE show the strongest agreement with the flux inversions, whereas scPDSI and SIF show weaker agreement. In this section, we discuss agreement between the proxies and flux inversions, as well as their implications.
4.3.1 Agreement with Tsoil and scPDSI
The results show high consistency in the timing of anomalies between Tsoil and GOSAT flux inversions on continental and larger scales in the tropics and on subcontinental scales in the northern extratropics during JJA. These results indicate that Tsoil is a useful proxy for corroborating NEE IAV in flux inversions in both the tropics and northern extratropics. The GOSAT flux inversion NEE IAV consistently shows closer agreement with Tsoil anomalies than with scPDSI in both the tropics and northern extratropics. This is consistent with previous research that has shown that NEE IAV is most closely related to temperature anomalies on large scales (Wang et al., 2013; Jung et al., 2017).
Although the results of this study indicate that Tsoil is a useful metric for corroborating NEE IAV in flux inversions, inferring the sensitivity of NEE anomalies to temperature anomalies directly is not advised for the fits given in Tables 2 and 3. This is because a number of factors have not been considered in this analysis. One factor is that temperature anomalies are also correlated with moisture and biomass burning anomalies. Keppel-Aleks et al. (2014) show that accounting for these covariances results in reduced sensitivity of NEE anomalies to temperature anomalies. A second factor is that the relationship between NEE anomalies and temperature and moisture anomalies is variable, depending on large-scale climate modes. For example, Fang et al. (2017) show that either temperature or precipitation anomalies can be the primary driver of NEE anomalies based on ENSO phase. A third factor is that the impact of temperature and moisture on NEE anomalies may be lagged (Braswell et al., 1997). Ecosystems can take a months to years to recover from droughts (Frank et al., 2015; Schwalm et al., 2017; Sippel et al., 2018). Baldocchi et al. (2018) found that NEE anomalies at a number of FLUXNET sites are negatively correlated with themselves after a 1-year lag, implying a highly oscillatory behavior in the net carbon fluxes from year to year.
This leaves many opportunities for future work to further investigate the relationship between NEE anomalies and climate variability in more detail. A further limit to the comparisons of flux inversions with Tsoil and scPDSI anomalies in the tropics is that we do not distinguish between seasons. The relationship between NEE, Tsoil, and scPDSI anomalies likely has substantial seasonal differences (Rödenbeck et al., 2018). We encourage future studies to examine seasonally dependent relationships using longer flux inversions, as well as studies that investigate lagged correlations and climate mode relationships between inversion NEE anomalies and temperature and water availability anomalies.
4.3.2 Agreement with SIF
It is notable that correlations with SIF are weaker than those with the other proxies. Linear regressions indicate that SIF anomalies show some correspondence to GOSAT flux inversion anomalies on subcontinental scales in the northern extratropics during JJA (), but little agreement is found in the tropics (R2≤0.05). These results are not all that surprising, as it is not clear that one should expect SIF and NEE to be highly correlated, since SIF is a proxy for GPP rather than NEE. It has previously been shown than NEE and GPP anomalies are only moderately correlated (Baldocchi et al., 2018). However, we also note that spurious trends have been found in the GOME-2 SIF observations (Zhang et al., 2018), which could impact the calculated anomalies. Furthermore, due to GOME-2's large field of view, clouds are almost always present for measurements in the tropics. We compared anomalies in GOME-2 SIF with FLUXCOM MARS GPP anomalies and found that correlations are generally positive over the majority of the globe, suggesting that IAV from GOME-2 SIF is reliable (Fig. S4 in the Supplement). However, the correlations are also spatially heterogeneous, with the closest agreement occurring over semiarid regions.
4.3.3 Agreement with FLUXCOM NEE
The GEOS-Chem GOSAT flux inversions with no prior NEE IAV showed close agreement with FLUXCOM NEE anomalies in the tropics on subcontinental regional and larger scales, as well as in the northern extratropics on subcontinental regional scales during JJA. This is a remarkable finding as these data-driven estimates of NEE IAV are independent, and agreement between the two estimates provides a strong indication that the results are robust. Therefore, comparisons with FLUXCOM NEE may provide a method for corroborating results from flux inversion studies. However, it should be noted that the net annual NEE fluxes produced by FLUXCOM are quite unrealistic (Tramontana et al., 2016; Jung et al., 2017), with annual net drawdown by the biosphere of 18–28 PgC yr−1.
It may also be possible to evaluate the magnitude of NEE IAV in FLUXCOM NEE through comparisons with flux inversions. Here we compare the magnitude of NEE IAV between the GOSAT flux inversions and FLUXCOM. The slope of the linear regression between the inversions indicates the relative magnitude of the inversion and FLUXCOM NEE anomalies. Over the entire tropics, the GOSAT inversions give slopes of 1.03–2.10 (mean of 1.56), suggesting that the magnitude of NEE anomalies is underestimated by FLUXCOM NEE. For JJA in the northern extratropics, the GOSAT inversions give slopes of 0.79–1.59 (mean of 1.31), again suggesting that the magnitude of NEE anomalies is underestimated by FLUXCOM. Furthermore, the OSSEs suggested that the inversions do not recover the full magnitude of NEE IAV, providing further evidence that FLUXCOM underestimates the magnitude of NEE IAV. This result is consistent with previous studies, which indicate that FLUXCOM underestimates the magnitude of NEE IAV (Jung et al., 2011, 2017).
4.4 Influence of the inversion configuration
4.4.1 Model horizontal resolution
The results of this study indicate that the spatial resolution of the model used in the inversion analysis ( or ) has a relatively minor impact on posterior NEE anomalies. This somewhat surprising since recent studies (Yu et al., 2018; Stanevich, 2018) have shown significant transport differences for different resolution versions of GEOS-Chem. Also, Deng et al. (2015) showed that there are large biases in CO2 in the upper troposphere and lower stratosphere in GEOS-Chem that impact inferred flux estimates. It is possible that, although the model transport errors influence the flux estimates, the resolution-dependent transport processes are not sensitive to NEE IAV for the time period considered here. However, both model resolutions examined in this study are quite coarse, and horizontal resolution becomes increasingly important at smaller spatial scales (Agustí-Panareda et al., 2019).
4.4.2 Prior error covariances
The magnitude of the prior error covariances generally had a significant impact on the posterior NEE IAV. In the tropics, inversions with loose prior constraints gave larger correlations with Tsoil and FLUXCOM NEE on subcontinental regional and continental scales. This suggests that the information content of the GOSAT observations is sufficiently large in the tropics that prior error covariances of 100 % for or 200 % for can be applied without degrading the posterior results by over-fitting the observations.
In the northern extratropics, the inversions with tighter prior constraints gave larger correlations with Tsoil and FLUXCOM NEE on subcontinental regional and continental scales, suggesting that loose prior constraints result in over-fitting of the GOSAT observations, which degrades the agreement with proxies. These results are the opposite of what was found for the tropics and suggest that tighter error constraints (as a percentage of NEE) should be applied in the northern extratropics than in the tropics.
The largest impact of varying the prior error covariances is in the magnitude of posterior NEE IAV. When loose prior constraints are applied the magnitude of NEE anomalies increases by 30 %–80 % (15 %–30 % for OSSEs) in the tropics and 5 %–60 % (0 %–30 % for OSSEs) in the northern extratropics. These results imply that care should taken when making conclusions about the magnitude of NEE anomalies from this analysis. Based on the OSSEs, it seems likely that the inversions underestimate the magnitude of NEE IAV on all scales, but the inversions with looser prior constraints result in a more realistic magnitude of NEE IAV. This suggests that there is a trade-off between obtaining a more realistic magnitude of IAV using looser constraints and obtaining more realistic timing of anomalies with tighter prior constraints.
4.4.3 Prior fluxes
The presence of IAV in prior NEE resulted in reduced correlations between NEE and the proxies in the northern extratropics, while the impact of prior NEE IAV was generally small in the tropics. The presence of prior NEE IAV likely degrades the posterior NEE IAV due to the fact that the observations under-constrain NEE IAV such that the prior NEE IAV strongly influences the spatiotemporal distribution of IAV in the posterior NEE. In fact, the posterior NEE IAV is generally more strongly correlated with the prior IAV than the proxies and FLUXCOM. Only on the scale of the entire tropics is the correlation with the prior NEE (R2=0.42) less than with the proxies (R2=0.61 for FLUXCOM NEE and R2=0.56 for Tsoil), indicating that the observations are influencing the posterior NEE IAV more than the prior NEE IAV (Sect. S2). This suggests that the impact of prior NEE IAV on the inversion is likely strongly dependent on how well the prior NEE IAV reflects the true NEE IAV. Realistic prior NEE IAV would likely improve the posterior NEE IAV; conversely, unrealistic prior NEE IAV will degrade the posterior NEE IAV. This implies that the realism of the prior NEE IAV should be investigated before including it in an inversion analysis. If the objective of the experiment is to examine the timing of posterior NEE IAV introduced through the assimilation of observations, then we recommend that annually repeating prior fluxes be used to investigate NEE IAV.
The impact of the prior mean seasonal cycle on posterior NEE IAV was investigated in a series of OSSEs. We found that correlations with the true NEE IAV were improved on continental scales when the mean seasonal cycle was closer to the true NEE IAV.
In this study, we examined the constraints on NEE IAV provided by GOSAT observations by performing a series of flux inversions. We addressed two main objectives in this analysis. The first objective was to quantify the agreement between GOSAT flux inversions and flux proxies, which are associated with IAV in the terrestrial carbon cycle, and FLUXCOM NEE. We found that posterior NEE anomalies were strongly correlated with FLUXCOM NEE and Tsoil anomalies but gave weaker correlations with scPDSI and SIF. Strong correlations (P<0.05) were found with FLUXCOM NEE and Tsoil on continental and larger scales in the tropics, suggesting that GOSAT flux inversions can capture NEE IAV on these spatial scales. In the northern extratropics, JJA posterior NEE anomalies were found to show strong agreement with anomalies in Tsoil () and FLUXCOM NEE () on subcontinental regions when no prior NEE IAV is used.
The second objective was to quantify the sensitivity of correlations between posterior NEE anomalies and proxy–FLUXCOM anomalies to the inversion setup. We found that the agreement between the flux inversions and proxies can be sensitive to the inversion setup. Posterior NEE anomalies were most sensitive to the prior fluxes and error covariances. The inclusion of prior NEE IAV had a substantial impact on the posterior NEE anomalies, and OSSEs showed that prior NEE IAV can degrade the correlation between the posterior and true NEE IAV. Therefore, if prior NEE IAV is included in future inversions, attempts should be made to test the realism of the prior NEE IAV. The magnitude of prior error covariances had a large impact on the magnitude of the posterior IAV, but the amplitude of NEE IAV is likely underestimated even if loose prior constraints are applied. Although not addressed in this study, correlated errors between GOSAT observations may introduce structures in the posterior NEE estimates, and thus we recommend that future work address the possibility of prescribing non-diagonal terms in the observational error covariance matrix.
The results of this study suggest that GOSAT measurements provide a useful constraint on IAV in the carbon cycle. Further study of the relationship between GOSAT-constrained NEE and environmental variables is merited given the results discussed here. In particular, the mechanisms driving these covariations should be further investigated. Lagged relationships between GOSAT-constrained NEE and environmental variables should also be investigated. Future research could also investigate differences in IAV between GOSAT-constrained NEE and that produced by TBMs. Given the better agreement with the proxies, GOSAT-constrained NEE IAV may provide a tool for evaluating the TBM-simulated NEE IAV in the future.
CarbonTracker CT2016 results were provided by NOAA ESRL, Boulder, Colorado, USA, from the website at https://www.esrl.noaa.gov/gmd/ccgg/carbontracker/ (National Oceanic and Atmospheric Administration (NOAA) Earth System Laboratory (ESRL), 2019a). CASA GFED 4.1 and CASA CMS NEE fluxes were also downloaded from the CT2016 website. The GOSAT L4 product and VISIT NEE were downloaded from the GOSAT Data Archive Service (https://data2.gosat.nies.go.jp; NIES, 2019). The Dai Global Palmer Drought Severity Index was downloaded from the Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory (https://doi.org/10.5065/D6QF8R93; Dai, 2017). NASA GOME-2 SIF products were obtained from the Aura Validation Data Center (https://avdc.gsfc.nasa.gov/; Aura Validation Data Center, 2019). FLUXCOM products were obtained from the data portal of the Max Planck Institute for Biochemistry (https://www.bgc-jena.mpg.de/geodb/projects/Home.php.; Max Plank Institue for Biogeochemistry, 2019). MERRA-2 products were downloaded from MDISC (https://gmao.gsfc.nasa.gov/reanalysis/MERRA-2/; Global Modeling and Assimilation Office, 2019), managed by the NASA Goddard Earth Sciences (GES) Data and Information Services Center (DISC). The GEOS-Chem forward and adjoint models are freely available to the public. Instructions for downloading and running the models can be found at http://wiki.seas.harvard.edu/geos-chem (Atmospheric Chemistry Modeling Group at Harvard University , 2019). ACOS GOSAT lite files were obtained from the CO2 Virtual Science Data Environment (https://co2.jpl.nasa.gov/; Jet Propulsion Laboratory, California Institute of Technology, 2019). The SST anomalies were downloaded from the National Oceanic and Atmospheric Administration (NOAA) Earth System Research Laboratory (ESRL) website (https://www.esrl.noaa.gov; National Oceanic and Atmospheric Administration (NOAA) Earth System Laboratory (ESRL), 2019b).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-13017-2019-supplement.
The study was designed by BB, DBAJ, KS, SMP, and DFB. BB performed flux inversions with the GEOS-Chem adjoint model and performed analysis between fluxes and proxies. ABH provided JULES NEE fluxes. SM provided GOSAT L4 NEE. BB wrote the paper with contributions from all other coauthors.
The authors declare that they have no conflict of interest.
We thank Martin Jung, Andy Jacobson, Joanna Joiner, Randy Kawa, and Jim Collatz for helpful comments on this paper.
This research has been supported by Environment and Climate Change Canada (grant no. GCXE17S037), the Natural Sciences and Engineering Research Council of Canada (grant no. RGPIN 197367-11), and the Canadian Space Agency (grant no. 11STFATO38).
This paper was edited by Thomas Karl and reviewed by Abhishek Chatterjee and two anonymous referees.
Agustí-Panareda, A., Diamantakis, M., Massart, S., Chevallier, F., Muñoz-Sabater, J., Barré, J., Curcoll, R., Engelen, R., Langerock, B., Law, R. M., Loh, Z., Morguí, J. A., Parrington, M., Peuch, V.-H., Ramonet, M., Roehl, C., Vermeulen, A. T., Warneke, T., and Wunch, D.: Modelling CO2 weather – why horizontal resolution matters, Atmos. Chem. Phys., 19, 7347–7376, https://doi.org/10.5194/acp-19-7347-2019, 2019. a
Andres, R., Boden, T., and Marland, G.: Monthly Fossil-Fuel CO2 Emissions: Mass of Emissions Gridded by One Degree Latitude by One Degree Longitude, Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, U.S. Department of Energy, Oak Ridge, Tenn., U.S.A, https://doi.org/10.3334/CDIAC/ffe.MonthlyMass.2016, 2016. a
Atmospheric Chemistry Modeling Group at Harvard University: GEOS-Chem Wiki, available at: http://wiki.seas.harvard.edu/geos-chem, last access: 12 October 2019. a
Aura Validation Data Center: NASA GOME-2 SIF, available at: https://avdc.gsfc.nasa.gov/, last access: 12 October 2019. a
Bacastow, R.: Modulation of atmospheric carbon dioxide by the Southern Oscillation, Nature, 261, 116–118, 1976. a
Bacastow, R., Adams, J., Keeling, C., Moss, D., Whorf, T., and Wong, C.: Atmospheric carbon dioxide, the Southern Oscillation, and the weak 1975 El Niño, Science, 210, 66–68, 1980. a
Baldocchi, D., Falge, E., Gu , L., Olson, R., Hollinger, D., Running, S., Anthoni, P., Bernhofer, C., Davis, K., Evans, R., Fuentes, J., Goldstein, A., Katul, G., Law, B., Lee, X., Malhi, Y., Meyers, M., Munger, W., Oechel, W., Paw, K. T., Pilegaard, K., Schmid, H. P., Valentini, R., Verma, S., Vesala, T., Wilson, K., and Wofsy, S.: FLUXNET: A new tool to study the temporal and spatial variability of ecosystem–scale carbon dioxide, water vapor, and energy flux densities, B. Am. Meteorol. Soc., 82, 2415–2434, 2001. a
Baldocchi, D., Chu, H., and Reichstein, M.: Inter-annual variability of net and gross ecosystem carbon fluxes: A review, Agr. Forest Meteorol., 249, 520–533, https://doi.org/10.1016/j.agrformet.2017.05.015, 2018. a, b
Battle, M., Bender, M., Tans, P. P., White, J., Ellis, J., Conway, T., and Francey, R.: Global carbon sinks and their variability inferred from atmospheric O2 and δ13C, Science, 287, 2467–2470, 2000. a
Benjamin, D. J., Berger, J. O., Johannesson, M., Nosek, B. A., Wagenmakers, E. J., Berk, R., Bollen, K. A., Brembs, B., Brown, L., Camerer, C., Cesarini, D., Chambers, C. D., Clyde, M., Cook, T. D., De Boeck, P., Dienes, Z., Dreber, A., Easwaran, K., Efferson, C., Fehr, E., Fidler, F., Field, A. P., Forster, M., George, E. I., Gonzalez, R., Goodman, S., Green, E., Green, D. P., Greenwald, A. G., Hadfield, J. D., Hedges, L. V., Held, L., Hua Ho, T., Hoijtink, H., Hruschka, D. J., Imai, K., Imbens, G., Ioannidis, J. P. A., Jeon, M., Jones, J. H., Kirchler, M., Laibson, D., List, J., Little, R., Lupia, A., Machery, E., Maxwell, S. E., McCarthy, M., Moore, D. A., Morgan, S. L., Munafó, M., Nakagawa, S., Nyhan, B., Parker, T. H., Pericchi, L., Perugini, M., Rouder, J., Rousseau, J., Savalei, V., Schönbrodt, F. D., Sellke, T., Sinclair, B., Tingley, D., Van Zandt, T., Vazire, S., Watts, D. J., Winship, C., Wolpert, R. L., Xie, Y., Young, C., Zinman, J., and Johnson, V. E.: Redefine statistical significance, Nat. Hum. Behav., 2, 6–10, https://doi.org/10.1038/s41562-017-0189-z, 2018. a
Berry, J. and Bjorkman, O.: Photosynthetic response and adaptation to temperature in higher plants, Ann. Rev. Plant Physio., 31, 491–543, 1980. a
Bousquet, P., Peylin, P., Ciais, P., Le Quéré, C., Friedlingstein, P., and Tans, P. P.: Regional changes in carbon dioxide fluxes of land and oceans since 1980, Science, 290, 1342–1346, 2000. a, b, c
Braswell, B., Schimel, D. S., Linder, E., and Moore, B.: The response of global terrestrial ecosystems to interannual temperature variability, Science, 278, 870–873, https://doi.org/10.1126/science.278.5339.870, 1997. a
Bruhwiler, L. M. P., Michalak, A. M., and Tans, P. P.: Spatial and temporal resolution of carbon flux estimates for 1983–2002, Biogeosciences, 8, 1309–1331, https://doi.org/10.5194/bg-8-1309-2011, 2011. a
Byrne, B., Jones, D. B. A., Strong, K., Zeng, Z.-C., Deng, F., and Liu, J.: Sensitivity of CO2 Surface Flux Constraints to Observational Coverage, J. Geophys. Res.-Atmos, 112, 6672–6694, https://doi.org/10.1002/2016JD026164, 2017. a, b, c
Byrne, B., Wunch, D., Jones, D. B. A., Strong, K., Deng, F., Baker, I., Köhler, P., Frankenberg, C., Joiner, J., Arora, V. K., Badawy, B., Harper, A. B., Warneke, T., Petri, C., Kivi, R., and Roehl, C. M.: Evaluating GPP and respiration estimates over northern midlatitude ecosystems using solar induced fluorescence and atmospheric CO2 measurements, J. Geophys. Res.-Biogeo., 123, 1–22, https://doi.org/10.1029/2018JG004472, 2018. a
Ciais, P., Reichstein, M., Viovy, N., Granier, A., Ogée, J., Allard, V., Aubinet, M., Buchmann, N., Bernhofer, C., Carrara, A., Chevallier, F., De Noblet, N., Friend, A. D., Friedlingstein, P., Grünwald, T., Heinesch, B., Keronen, P., Knohl, A., Krinner, G., Loustau, D., Manca, G., Matteucci, G., Miglietta, F., Ourcival, J. M., Papale, D., Pilegaard, K., Rambal, S., Seufert, G., Soussana, J. F., Sanz, M. J., Schulze, E. D., Vesala, T., and Valentini, R.: Europe-wide reduction in primary productivity caused by the heat and drought in 2003, Nature, 437, 529–533, 2005. a
Ciais, P., Sabine, C., Bala, G., Bopp, L., Brovkin, V., Canadell, J., Chhabra, A., DeFries, R., Galloway, J., Heimann, M., Jones, C., Le Quéré, C., Myneni, R., Piao, S., and Thornton, P.: Carbon and Other Biogeochemical Cycles, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, https://doi.org/10.1017/CBO9781107415324.015, 465–570, 2013. a
Clark, D. B., Mercado, L. M., Sitch, S., Jones, C. D., Gedney, N., Best, M. J., Pryor, M., Rooney, G. G., Essery, R. L. H., Blyth, E., Boucher, O., Harding, R. J., Huntingford, C., and Cox, P. M.: The Joint UK Land Environment Simulator (JULES), model description – Part 2: Carbon fluxes and vegetation dynamics, Geosci. Model Dev., 4, 701–722, https://doi.org/10.5194/gmd-4-701-2011, 2011. a
Conway, T. J., Tans, P. P., Waterman, L. S., Thoning, K. W., Kitzis, D. R., Masarie, K. A., and Zhang, N.: Evidence for interannual variability of the carbon cycle from the National Oceanic and Atmospheric Administration/Climate Monitoring and Diagnostics Laboratory global air sampling network, J. Geophys. Res.-Atmos., 99, 22831–22855, 1994. a, b
Crisp, D., Fisher, B. M., O'Dell, C., Frankenberg, C., Basilio, R., Bösch, H., Brown, L. R., Castano, R., Connor, B., Deutscher, N. M., Eldering, A., Griffith, D., Gunson, M., Kuze, A., Mandrake, L., McDuffie, J., Messerschmidt, J., Miller, C. E., Morino, I., Natraj, V., Notholt, J., O'Brien, D. M., Oyafuso, F., Polonsky, I., Robinson, J., Salawitch, R., Sherlock, V., Smyth, M., Suto, H., Taylor, T. E., Thompson, D. R., Wennberg, P. O., Wunch, D., and Yung, Y. L.: The ACOS CO2 retrieval algorithm – Part II: Global X−CO2 data characterization, Atmos. Meas. Tech., 5, 687–707, https://doi.org/10.5194/amt-5-687-2012, 2012. a
Dai, A.: Characteristics and trends in various forms of the Palmer Drought Severity Index during 1900–2008, J. Geophys. Res.-Atmos., 116, d12115, https://doi.org/10.1029/2010JD015541, 2011. a
Dai, A.: Dai Global Palmer Drought Severity Index (PDSI), Research Data Archive at the National Center for Atmospheric Research, Computational and Information Systems Laboratory, https://doi.org/10.5065/D6QF8R93, 2017. a, b, c
Dai, A., Trenberth, K. E., and Qian, T.: A global dataset of Palmer Drought Severity Index for 1870–2002: relationship with soil moisture and effects of surface warming, J. Hydrometeorol., 5, 1117–1130, 2004. a
Deng, F., Jones, D. B. A., Henze, D. K., Bousserez, N., Bowman, K. W., Fisher, J. B., Nassar, R., O'Dell, C., Wunch, D., Wennberg, P. O., Kort, E. A., Wofsy, S. C., Blumenstock, T., Deutscher, N. M., Griffith, D. W. T., Hase, F., Heikkinen, P., Sherlock, V., Strong, K., Sussmann, R., and Warneke, T.: Inferring regional sources and sinks of atmospheric CO2 from GOSAT XCO2 data, Atmos. Chem. Phys., 14, 3703–3727, https://doi.org/10.5194/acp-14-3703-2014, 2014. a, b
Deng, F., Jones, D. B. A., Walker, T. W., Keller, M., Bowman, K. W., Henze, D. K., Nassar, R., Kort, E. A., Wofsy, S. C., Walker, K. A., Bourassa, A. E., and Degenstein, D. A.: Sensitivity analysis of the potential impact of discrepancies in stratosphere–troposphere exchange on inferred sources and sinks of CO2, Atmos. Chem. Phys., 15, 11773–11788, https://doi.org/10.5194/acp-15-11773-2015, 2015. a
Deng, F., Jones, D., O'Dell, C. W., Nassar, R., and Parazoo, N. C.: Combining GOSAT XCO2 observations over land and ocean to improve regional CO2 flux estimates, J. Geophys. Res.-Atmos., 121, 1896–1913, https://doi.org/10.1002/2015JD024157, 2016. a
Fang, Y., Michalak, A. M., Schwalm, C. R., Huntzinger, D. N., Berry, J. A., Ciais, P., Piao, S., Poulter, B., Fisher, J. B., Cook, R. B., Hayes, D., Huang, M., Ito, A., Jain, A., Lei, H., Lu, C., Mao, J., Parazoo, N. C., Peng, S., Ricciuto, D. M., Shi, X., Tao, B., Tian, H., Wang, W., Wei, Y., and Yang, J.: Global land carbon sink response to temperature and precipitation varies with ENSO phase, Environ. Res. Lett., 12, 064007, https://doi.org/10.1088/1748-9326/aa6e8e, 2017. a
Frank, D., Reichstein, M., Bahn, M., Thonicke, K., Frank, D., Mahecha, M. D., Smith, P., Van der Velde, M., Vicca, S., Babst, F., Beer, C., Buchmann, N., Canadell, J. G., Ciais, P., Cramer, W., Ibrom, A., Miglietta, F., Poulter, B., Rammig, A., Seneviratne, S. I., Walz, A., Wattenbach, M., Zavala, M. A., and Zscheischler, J.: Effects of climate extremes on the terrestrial carbon cycle: concepts, processes and potential future impacts, Glob. Change Biol., 21, 2861–2880, 2015. a
Global Modeling and Assimilation Office: Modern-Era Retrospective analysis for Research and Applications, Version 2, available at: https://gmao.gsfc.nasa.gov/reanalysis/MERRA-2/, last access: 12 October 2019. a
Guerlet, S., Basu, S., Butz, A., Krol, M., Hahne, P., Houweling, S., Hasekamp, O., and Aben, I.: Reduced carbon uptake during the 2010 Northern Hemisphere summer from GOSAT, Geophys. Res. Lett., 40, 2378–2383, 2013. a
Gutschick, V. P. and BassiriRad, H.: Extreme events as shaping physiology, ecology, and evolution of plants: toward a unified definition and evaluation of their consequences, New Phytol., 160, 21–42, 2003. a
Harper, A. B., Wiltshire, A. J., Cox, P. M., Friedlingstein, P., Jones, C. D., Mercado, L. M., Sitch, S., Williams, K., and Duran-Rojas, C.: Vegetation distribution and terrestrial carbon cycle in a carbon cycle configuration of JULES4.6 with new plant functional types, Geosci. Model Dev., 11, 2857–2873, https://doi.org/10.5194/gmd-11-2857-2018, 2018. a
He, Z., Lei, L., Welp, L. R., Zeng, Z.-C., Bie, N., Yang, S., and Liu, L.: Detection of Spatiotemporal Extreme Changes in Atmospheric CO2 Concentration Based on Satellite Observations, Remote Sens., 10, 839, https://doi.org/10.3390/rs10060839, 2018. a
Henze, D. K., Hakami, A., and Seinfeld, J. H.: Development of the adjoint of GEOS-Chem, Atmos. Chem. Phys., 7, 2413–2433, https://doi.org/10.5194/acp-7-2413-2007, 2007. a, b
Ishizawa, M., Mabuchi, K., Shirai, T., Inoue, M., Morino, I., Uchino, O., Yoshida, Y., Belikov, D., and Maksyutov, S.: Inter-annual variability of summertime CO2 exchange in Northern Eurasia inferred from GOSAT XCO2, Environ. Res. Lett., 11, 105001, https://doi.org/10.1088/1748-9326/11/10/105001, 2016. a
Ito, A.: Changing ecophysiological processes and carbon budget in East Asian ecosystems under near-future changes in climate: implications for long-term monitoring from a process-based model, J. Plant Res., 123, 577–588, 2010. a, b
Jet Propulsion Laboratory, California Institute of Technology: CO2 virtual science data environment, available at: https://co2.jpl.nasa.gov/, last access: 12 October 2019. a
Joiner, J., Guanter, L., Lindstrot, R., Voigt, M., Vasilkov, A. P., Middleton, E. M., Huemmrich, K. F., Yoshida, Y., and Frankenberg, C.: Global monitoring of terrestrial chlorophyll fluorescence from moderate-spectral-resolution near-infrared satellite measurements: methodology, simulations, and application to GOME-2, Atmos. Meas. Tech., 6, 2803–2823, https://doi.org/10.5194/amt-6-2803-2013, 2013. a
Joiner, J., Yoshida, Y., Guanter, L., and Middleton, E. M.: New methods for the retrieval of chlorophyll red fluorescence from hyperspectral satellite instruments: simulations and application to GOME-2 and SCIAMACHY, Atmos. Meas. Tech., 9, 3939–3967, https://doi.org/10.5194/amt-9-3939-2016, 2016. a, b
Jones, C. D. and Cox, P. M.: On the significance of atmospheric CO2 growth rate anomalies in 2002–2003, Geophys. Res. Lett., 32, l14816, https://doi.org/10.1029/2005GL023027, 2005. a
Jung, M., Reichstein, M., Margolis, H. A., Cescatti, A., Richardson, A. D., Arain, M. A., Arneth, A., Bernhofer, C., Bonal, D., Chen, J., Gianelle, D., Gobron, N., Kiely, G., Kutsch, W. L., Lasslop, G., Law, B. E., Lindroth, A., Merbold, L., Montagnani, L., Moors, E. J., Papale, D., Sottocornola, M., Vaccari, F. P., and Williams, C.: Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations, J. Geophys. Res.-Biogeo., 116, G00J07, https://doi.org/10.1029/2010JG001566, 2011. a, b
Jung, M., Reichstein, M., Schwalm, C. R., Huntingford, C., Sitch, S., Ahlström, A., Arneth, A., Camps-Valls, G., Ciais, P., Friedlingstein, P., et al.: Compensatory water effects link yearly global land CO2 sink changes to temperature, Nature, 541, 516–520, 2017. a, b, c, d, e, f, g
Keeling, C. D., Adams Jr, J. A., Ekdahl Jr, C. A., and Guenther, P. R.: Atmospheric carbon dioxide variations at the South Pole, Tellus, 28, 552–564, 1976a. a
Keeling, C. D., Bacastow, R. B., Bainbridge, A. E., Ekdahl Jr, C. A., Guenther, P. R., Waterman, L. S., and Chin, J. F.: Atmospheric carbon dioxide variations at Mauna Loa observatory, Hawaii, Tellus, 28, 538–551, 1976b. a
Keeling, C. D., Whorf, T. P., Wahlen, M., and Van der Plichtt, J.: Interannual extremes in the rate of rise of atmospheric carbon dioxide since 1980, Nature, 375, 666–670, 1995. a
Keppel-Aleks, G., Wolf, A. S., Mu, M., Doney, S. C., Morton, D. C., Kasibhatla, P. S., Miller, J. B., Dlugokencky, E. J., and Randerson, J. T.: Separating the influence of temperature, drought, and fire on interannual variability in atmospheric CO2, Global Biogeochem. By., 28, 1295–1310, 2014. a
Krol, M., Houweling, S., Bregman, B., van den Broek, M., Segers, A., van Velthoven, P., Peters, W., Dentener, F., and Bergamaschi, P.: The two-way nested global chemistry-transport zoom model TM5: algorithm and applications, Atmos. Chem. Phys., 5, 417–432, https://doi.org/10.5194/acp-5-417-2005, 2005. a
Kulawik, S., Wunch, D., O'Dell, C., Frankenberg, C., Reuter, M., Oda, T., Chevallier, F., Sherlock, V., Buchwitz, M., Osterman, G., Miller, C. E., Wennberg, P. O., Griffith, D., Morino, I., Dubey, M. K., Deutscher, N. M., Notholt, J., Hase, F., Warneke, T., Sussmann, R., Robinson, J., Strong, K., Schneider, M., De Mazière, M., Shiomi, K., Feist, D. G., Iraci, L. T., and Wolf, J.: Consistent evaluation of ACOS-GOSAT, BESD-SCIAMACHY, CarbonTracker, and MACC through comparisons to TCCON, Atmos. Meas. Tech., 9, 683–709, https://doi.org/10.5194/amt-9-683-2016, 2016. a, b, c
Lakens, D., Adolfi, F., Albers, C., Anvari, F., Apps, M., Argamon, S., Baguley, T., Becker, R., Benning, S., Bradford, D., Buchanan, E., Caldwell, A., Van, C. B., Carlsson, R., Chen, S., Chung, B., Colling, L., Collins, G., Crook, Z., Cross, E., Daniels, S., Danielsson, H., Debruine, L., Dunleavy, D., Earp, B., Feist, M., Ferrell, J., Field, J., Fox, N., Friesen, A., Gomes, C., Gonzalez-Marquez, M., Grange, J., Grieve, A., Guggenberger, R., Grist, J., Van, H. A., Hasselman, F., Hochard, K., Hoffarth, M., Holmes, N., Ingre, M., Isager, P., Isotalus, H., Johansson, C., Juszczyk, K., Kenny, D., Khalil, A., Konat, B., Lao, J., Larsen, E., Lodder, G., Lukavský, J., Madan, C., Manheim, D., Martin, S., Martin, A., Mayo, D., McCarthy, R., McConway, K., McFarland, C., Nio, A., Nilsonne, G., De, O. C., De, X. J., Parsons, S., Pfuhl, G., Quinn, K., Sakon, J., Saribay, S., Schneider, I., Selvaraju, M., Sjoerds, Z., Smith, S., Smits, T., Spies, J., Sreekumar, V., Steltenpohl, C., Stenhouse, N., Swiatkowski, W., Vadillo, M., Van, A. M., Williams, M., Williams, S., Williams, D., Yarkoni, T., Ziano, I., and Zwaan, R.: Justify your alpha, Nat. Hum. Behav., 2, 168–171, https://doi.org/10.1038/s41562-018-0311-x, 2018. a
Liu, J., Bowman, K. W., Lee, M., Henze, D. K., Bousserez, N., Brix, H., Collatz, G. J., Menemenlis, D., Ott, L., Pawson, S., Jones, D. B. A., and Nassar, R.: Carbon monitoring system flux estimation and attribution: impact of ACOS-GOSAT sampling on the inference of terrestrial biospheric sources and sinks, Tellus B, 66, 22486, https://doi.org/10.3402/tellusb.v66.22486, 2014. a, b
Liu, J., Bowman, K. W., Schimel, D. S., Parazoo, N. C., Jiang, Z., Lee, M., Bloom, A. A., Wunch, D., Frankenberg, C., Sun, Y., O'Dell, C. W., Gurney, K. R., Menemenlis, D., Gierach, M., Crisp, D., and Eldering, A.: Contrasting carbon cycle responses of the tropical continents to the 2015–2016 El Niño, Science, 358, https://doi.org/10.1126/science.aam5690, 2017. a, b
Mabuchi, K., Takagi, H., and Maksyutov, S.: Relationships between CO2 flux estimated by inverse analysis and land surface elements in South America and Africa, J. Meteorol. Soc. Jpn, 94, 415–430, 2016. a
Maksyutov, S., Takagi, H., Valsala, V. K., Saito, M., Oda, T., Saeki, T., Belikov, D. A., Saito, R., Ito, A., Yoshida, Y., Morino, I., Uchino, O., Andres, R. J., and Yokota, T.: Regional CO2 flux estimates for 2009–2010 based on GOSAT and ground-based CO2 observations, Atmos. Chem. Phys., 13, 9351–9373, https://doi.org/10.5194/acp-13-9351-2013, 2013. a, b
Marcolla, B., Rödenbeck, C., and Cescatti, A.: Patterns and controls of inter-annual variability in the terrestrial carbon budget, Biogeosciences, 14, 3815–3829, https://doi.org/10.5194/bg-14-3815-2017, 2017. a
Monsi, M. and Saeki, T.: Uber den Lichtfaktor in den Pflanzengesellschaften und seine Bedeutung für die Stoffproduktion, Jpn. J. Bot., 14, 22–52, 1953. a
Max Plank Institue for Biogeochemistry: Data Exchange Portal, available at: https://www.bgc-jena.mpg.de/geodb/projects/Home.php, last access: 12 October 2019. a
NASA-SIF: NASA GOME-2 Solar Induced Fluoresence product, http://avdc.gsfc.nasa.gov/, last access: 25 June 2016. a
Nassar, R., Jones, D. B. A., Kulawik, S. S., Worden, J. R., Bowman, K. W., Andres, R. J., Suntharalingam, P., Chen, J. M., Brenninkmeijer, C. A. M., Schuck, T. J., Conway, T. J., and Worthy, D. E.: Inverse modeling of CO2 sources and sinks using satellite observations of CO2 from TES and surface flask measurements, Atmos. Chem. Phys., 11, 6029–6047, https://doi.org/10.5194/acp-11-6029-2011, 2011. a
National Oceanic and Atmospheric Administration (NOAA) Earth System Laboratory (ESRL): carbontracker, available at: https://www.esrl.noaa.gov/gmd/ccgg/carbontracker/, last access: 9 October 2019a. a
National Oceanic and Atmospheric Administration (NOAA) Earth System Laboratory (ESRL): Earth System Laboratory (ESRL), available at: https://www.esrl.noaa.gov, last access: 12 October 2019b. a
National Institute for Environmental Studies (NIES): GOSAT Data Archive Service, available at: https://data2.gosat.nies.go.jp, last access: 12 October 2019. a
O'Dell, C. W., Connor, B., Bösch, H., O'Brien, D., Frankenberg, C., Castano, R., Christi, M., Eldering, D., Fisher, B., Gunson, M., McDuffie, J., Miller, C. E., Natraj, V., Oyafuso, F., Polonsky, I., Smyth, M., Taylor, T., Toon, G. C., Wennberg, P. O., and Wunch, D.: The ACOS CO2 retrieval algorithm – Part 1: Description and validation against synthetic observations, Atmos. Meas. Tech., 5, 99–121, https://doi.org/10.5194/amt-5-99-2012, 2012. a
Onogi, K., Tsutsui, J., Koide, H., Sakamoto, M., Kobayashi, S., Hatsushika, H., Matsumoto, T., Yamazaki, N., Kamahori, H., Takahashi, K., Kadokura, S., Wada, K., Kato, K., Oyama, R., Ose, T., Mannoji, N., and Taira, R.: The JRA-25 reanalysis, J. Meteorol. Soc. Jpn., 85, 369–432, 2007. a
Peters, W., Jacobson, A. R., Sweeney, C., Andrews, A. E., Conway, T. J., Masarie, K., Miller, J. B., Bruhwiler, L. M., Pétron, G., Hirsch, A. I., Worthy, D. E. J., van der Werf, G. R., Randerson, J. T., Wennberg, P. O., Krol, M. C., and Tans, P. P.: An atmospheric perspective on North American carbon dioxide exchange: CarbonTracker, P. Natl. Acad. Sci. USA, 104, 18925–18930, https://doi.org/10.1073/pnas.0708986104, 2007. a, b
Peylin, P., Law, R. M., Gurney, K. R., Chevallier, F., Jacobson, A. R., Maki, T., Niwa, Y., Patra, P. K., Peters, W., Rayner, P. J., Rödenbeck, C., van der Laan-Luijkx, I. T., and Zhang, X.: Global atmospheric carbon budget: results from an ensemble of atmospheric CO2 inversions, Biogeosciences, 10, 6699–6720, https://doi.org/10.5194/bg-10-6699-2013, 2013. a
Polavarapu, S. M., Deng, F., Byrne, B., Jones, D. B. A., and Neish, M.: A comparison of posterior atmospheric CO2 adjustments obtained from in situ and GOSAT constrained flux inversions, Atmos. Chem. Phys., 18, 12011–12044, https://doi.org/10.5194/acp-18-12011-2018, 2018. a
Potter, C. S., Randerson, J. T., Field, C. B., Matson, P. A., Vitousek, P. M., Mooney, H. A., and Klooster, S. A.: Terrestrial ecosystem production: a process model based on global satellite and surface data, Global Biogeochem. Cy., 7, 811–841, https://doi.org/10.1029/93GB02725, 1993. a, b
Randerson, J. T., Thompson, M. V., Malmstrom, C. M., Field, C. B., and Fung, I. Y.: Substrate limitations for heterotrophs: Implications for models that estimate the seasonal cycle of atmospheric CO2, Global Biogeochem. Cy., 10, 585–602, https://doi.org/10.1029/96GB01981, 1996. a
Reichle, R. H., Koster, R. D., De Lannoy, G. J., Forman, B. A., Liu, Q., Mahanama, S. P., and Touré, A.: Assessment and enhancement of MERRA land surface hydrology estimates, J. Climate, 24, 6322–6338, 2011. a, b
Reichle, R. H., Draper, C. S., Liu, Q., Girotto, M., Mahanama, S. P., Koster, R. D., and De Lannoy, G. J.: Assessment of MERRA-2 land surface hydrology estimates, J. Climate, 30, 2937–2960, 2017. a, b
Rödenbeck, C., Houweling, S., Gloor, M., and Heimann, M.: CO2 flux history 1982–2001 inferred from atmospheric data using a global inversion of atmospheric transport, Atmos. Chem. Phys., 3, 1919–1964, https://doi.org/10.5194/acp-3-1919-2003, 2003. a
Rödenbeck, C., Zaehle, S., Keeling, R., and Heimann, M.: How does the terrestrial carbon exchange respond to inter-annual climatic variations? A quantification based on atmospheric CO2 data, Biogeosciences, 15, 2481–2498, https://doi.org/10.5194/bg-15-2481-2018, 2018. a, b
Saito, M., Ito, A., and Maksyutov, S.: Optimization of a prognostic biosphere model for terrestrial biomass and atmospheric CO2 variability, Geosci. Model Dev., 7, 1829–1840, https://doi.org/10.5194/gmd-7-1829-2014, 2014. a, b
Schwalm, C. R., Anderegg, W. R., Michalak, A. M., Fisher, J. B., Biondi, F., Koch, G., Litvak, M., Ogle, K., Shaw, J. D., Wolf, A., Huntzinger, D. N., Schaefer, K., Cook, R., Wei, Y., Fang, Y., Hayes, D., Huang, M., Jain, A., and Tian, H.: Global patterns of drought recovery, Nature, 548, 202–205, https://doi.org/10.1038/nature23021, 2017. a
Shiga, Y. P., Michalak, A. M., Fang, Y., Schaefer, K., Andrews, A. E., Huntzinger, D. H., Schwalm, C. R., Thoning, K., and Wei, Y.: Forests dominate the interannual variability of the North American carbon sink, Environ. Res. Lett., 13, 084015, https://doi.org/10.1088/1748-9326/aad505, 2018. a
Sippel, S., Reichstein, M., Ma, X., Mahecha, M. D., Lange, H., Flach, M., and Frank, D.: Drought, Heat, and the Carbon Cycle: a Review, Current Climate Change Reports, 1–21, 2018. a
Smith, M. D.: An ecological perspective on extreme climatic events: a synthetic definition and framework to guide future research, J. Ecol., 99, 656–663, 2011. a
Stanevich, I.: Characterizing model errors in chemical transport modelling of methane: Impact of coarse model resolution, 2018. a, b, c
Takahashi, T., Sutherland, S. C., Wanninkhof, R., Sweeney, C., Feely, R. A., Chipman, D. W., Hales, B., Friederich, G., Chavez, F., Sabine, C., Watson, A., Bakker, D. C. E., Schuster, U., Metzl, N., Yoshikawa-Inoue, H., Ishii, M., Midorikawa, T., Nojiri, Y., Körtzinger, A., Steinhoff, T., Hoppema, M., Olafsson, J., Arnarson, T. S., Tilbrook, B., Johannessen, T., Olsen, A., Bellerby, R., Wong, C. S., Delille, B., Bates, N. R., and Baar, H. J. W. D.: Climatological mean and decadal change in surface ocean pCO2, and net sea–air CO2 flux over the global oceans, Deep Sea Res. Pt. II, 56, 554–577, 2009. a
Tramontana, G., Jung, M., Schwalm, C. R., Ichii, K., Camps-Valls, G., Ráduly, B., Reichstein, M., Arain, M. A., Cescatti, A., Kiely, G., Merbold, L., Serrano-Ortiz, P., Sickert, S., Wolf, S., and Papale, D.: Predicting carbon dioxide and energy fluxes across global FLUXNET sites with regression algorithms, Biogeosciences, 13, 4291–4313, https://doi.org/10.5194/bg-13-4291-2016, 2016. a, b, c, d
van der Werf, G. R., Randerson, J. T., Giglio, L., Collatz, G. J., Kasibhatla, P. S., and Arellano Jr., A. F.: Interannual variability in global biomass burning emissions from 1997 to 2004, Atmos. Chem. Phys., 6, 3423–3441, https://doi.org/10.5194/acp-6-3423-2006, 2006. a, b
van der Werf, G. R., Randerson, J. T., Giglio, L., van Leeuwen, T. T., Chen, Y., Rogers, B. M., Mu, M., van Marle, M. J. E., Morton, D. C., Collatz, G. J., Yokelson, R. J., and Kasibhatla, P. S.: Global fire emissions estimates during 1997–2016, Earth Syst. Sci. Data, 9, 697–720, https://doi.org/10.5194/essd-9-697-2017, 2017. a
Wang, W., Ciais, P., Nemani, R. R., Canadell, J. G., Piao, S., Sitch, S., White, M. A., Hashimoto, H., Milesi, C., and Myneni, R. B.: Variations in atmospheric CO2 growth rates coupled with tropical temperature, P. Natl. Acad. Sci. USA, 110, 13061–13066, 2013. a
Wunch, D., Wennberg, P. O., Messerschmidt, J., Parazoo, N. C., Toon, G. C., Deutscher, N. M., Keppel-Aleks, G., Roehl, C. M., Randerson, J. T., Warneke, T., and Notholt, J.: The covariation of Northern Hemisphere summertime CO2 with surface temperature in boreal regions, Atmos. Chem. Phys., 13, 9447–9459, https://doi.org/10.5194/acp-13-9447-2013, 2013. a
Yu, K., Keller, C. A., Jacob, D. J., Molod, A. M., Eastham, S. D., and Long, M. S.: Errors and improvements in the use of archived meteorological data for chemical transport modeling: an analysis using GEOS-Chem v11-01 driven by GEOS-5 meteorology, Geosci. Model Dev., 11, 305–319, https://doi.org/10.5194/gmd-11-305-2018, 2018. a, b
Zhang, Y., Joiner, J., Gentine, P., and Zhou, S.: Reduced solar-induced chlorophyll fluorescence from GOME-2 during Amazon drought caused by dataset artifacts, Glob. Change Biol., 24, 2229–2230, 2018. a
Zscheischler, J., Mahecha, M. D., Von Buttlar, J., Harmeling, S., Jung, M., Rammig, A., Randerson, J. T., Schölkopf, B., Seneviratne, S. I., Tomelleri, E., Zaehlel, S., and Reichstein, M.: A few extreme events dominate global interannual variability in gross primary production, Environ. Res. Lett., 9, 035001, https://doi.org/10.1088/1748-9326/9/3/035001, 2014. a