the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Trapping of HCl and oxidised organic trace gases in growing ice at temperatures relevant to cirrus clouds
Matthias Kippenberger
Gerhard Schuster
Jos Lelieveld
John N. Crowley
The uptake of hydrochloric acid (HCl), ethanol (C2H5OH), 1-butanol (1-C4H9OH), formic acid HC(O)OH and trifluoroacetic (CF3C(O)OH) acid to growing ice surfaces was investigated at temperatures between 194 and 228 K. HCl displayed extensive, continuous uptake during ice growth, which was strongly dependent on the ice growth velocity, the temperature of the ice surface and the gas phase concentration of HCl. Trifluoroacetic acid was also observed to be trapped in growing ice, albeit approximately an order of magnitude less efficiently than HCl, whereas the adsorption and desorption kinetics of ethanol, 1-butanol, formic acid on ice were not measurably different to those for non-growing ice, even at very high ice growth rates. We present a parameterisation of the uptake coefficient for HCl on growing ice films (γtrap) and compare the results to an existing framework that describes the non-equilibrium trapping of trace gases on ice. The trapping of HCl in growing ice crystals in the atmosphere is assessed and compared to the gas and ice phase partitioning resulting from equilibrium surface adsorption and solubility.
- Article
(1284 KB) -
Supplement
(113 KB) - BibTeX
- EndNote
Ice clouds, which represent a surface area that exceeds that of the underlying earth by about an order of magnitude, have a significant influence on the chemical composition of the atmospheric gas and condensed phases. They can reversibly remove trace gases by physical adsorption (non-reactive uptake) or provide a surface to catalyse heterogeneous processes which are otherwise too slow to be of importance for the atmosphere. Examples of physical adsorption are the uptake of HNO3 and H2O2 to cirrus clouds, which can result in the repartitioning from the gas to the particle phase and to a vertical redistribution of the trace gases, for example by evaporating hydrometeors during gravitational sedimentation (Popp et al., 2004, 2007; von Kuhlmann and Lawrence, 2006; Marécal et al., 2010; Pouvesle et al., 2010). The best known example of reactive uptake is the interaction between HCl and ClONO2 on ice particles, which plays a central role in polar ozone destruction in the lower stratosphere (Solomon et al., 1986; Molina et al., 1987).
The nonreactive uptake of trace gases to atmospheric ice particles is often described using Langmuir adsorption isotherms. Whilst there is a priori no reason why the Langmuir isotherm should be applicable to trace gas uptake to an ice surface, which at atmospheric temperatures is extremely dynamic (Girardet and Toubin, 2001), it can be used to parameterise experimental observations for a large variety of atmospheric trace gases reasonably well (Abbatt, 2003; Crowley et al., 2010). Furthermore, for substances which hydrogen bond to the ice surface, the Langmuir partition coefficient can be related to the free energy of condensation (Sokolov and Abbatt, 2002; Pouvesle et al., 2010), though this relationship breaks down for strong acids such as HNO3 and HCl. Due to their important roles in atmospheric chemistry, the interaction between HCl and HNO3 with ice surfaces has been studied intensively over the past three decades. With very few exceptions, the vast majority of these studies, reviewed by the International Union of Pure and Applied Chemistry (IUPAC) (Crowley et al., 2010), were performed under equilibrium conditions where the ice neither grows nor evaporates. This situation does not always apply to atmospheric ice which frequently experiences sub- and supersaturation (Gao et al., 2004; Lee et al., 2004; Popp et al., 2007; Comstock et al., 2008) resulting in episodes of net evaporation and growth, respectively.
A trace gas colliding with a growing ice surface may be considered to have a finite probability of being “trapped” in the advancing ice crystal before it can desorb, effectively removing it from the gas phase until the ice particle evaporates. Trapping can thus change the gas-to-particle partitioning of a trace gas, and, as the trace gas moves into (not onto) the particle, it may not be readily available for heterogeneous reactions with other trace gases colliding with the ice surface.
Evidence for the efficient trapping of a trace gas in growing ice crystals is provided by analysis of results from several airborne field campaigns, which, by measurement of the gas and particle phase nitrate led to the conclusion that the uptake of HNO3 is efficiently enhanced during ice growth events (Kärcher and Voigt, 2006). However, the inherent variability in atmospheric conditions (temperature, ice growth rates and nitric acid concentrations) complicates the analysis of such datasets. To aid in the inclusion of trapping trace gases into atmospheric and climate models, Kärcher and co-workers (Kärcher and Basko, 2004; Kärcher et al., 2009) have developed a framework (“trapping model”) that considers the surface physical processes involved in transferring a molecule colliding with the ice surface to the bulk. The trapping model was developed in order to understand aircraft-based observations of large HNO3 concentrations in ice crystals. The validation of this semiempirical model and especially its extrapolation to other trace gases has to date not been possible owing to a lack of laboratory experimental data under controlled conditions and covering sufficient parameter space. The limited experimental work (Diehl et al., 1995; Santachiara et al., 1995; Dominé and Rauzy, 2004; Huthwelker et al., 2004) that is available on the uptake of HCl to growing ice surfaces has been conducted under conditions that do not allow for the evaluation of the trapping model. These studies are discussed in detail in Sect. 3.1.1
We present a detailed laboratory study that investigates the trapping efficiency for several different atmospheric trace gases under varying conditions of ice surface temperature T, ice growth velocity VIG and HCl concentration [HCl].
The experiments were conducted using a newly designed apparatus that enables generation of a well-defined water supersaturation during trace gas uptake to an ice surface growing at a constant, known rate. The apparatus (Fig. 1) consists of three chambers made of stainless steel. The cylindrical, lower chamber containing the ice sample (“ice chamber”; diameter = 4.86 cm, height = 1.3 cm) is isolated from the “upper chamber” (volume = 155 cm3) by a moveable quartz plate. The bottom of the ice chamber and the lowest 4 mm of its walls are in thermal contact with a copper block, which is cooled by a flow of ethanol from a cryostat. A thermocouple, located just under the ice surface, is used to obtain the approximate temperature of the ice. To reduce heat transfer to the ice and ensure a sharp temperature gradient between the reactor walls in contact with the ice and the rest of the reactor, the cylindrical parts of the ice chamber were constructed from very thin stainless steel (0.4 mm). Additionally, the upper chamber and the upper section of the walls of the ice chamber were heated resistively to keep them at room temperature. The upper chamber hosts the gas inlets through which He, water and the trace gas of interest are introduced as well as a pressure gauge (10 Torr, 1 Torr = 1.333 mbar; MKS Baratron) and the connection to a quadrupole mass spectrometer (QMS, see below). Interaction between the trace gas and ice surface is achieved when the quartz plate is withdrawn into a third chamber, which is continuously flushed with 100 cm3 (standard temperature and pressure; STP) min−1 (sccm) of He during experiments.
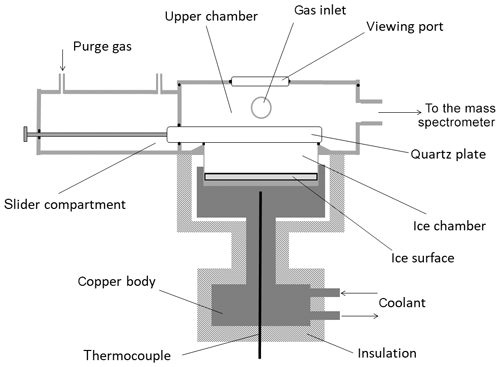
Figure 1Schematic representation of the reactor used during the trapping experiments. An electrical heating element (not shown) is wrapped around the slider compartment and upper chamber to keep them at room temperature.
All experiments reported here were conducted at a total pressure of 1.33 mbar (mainly He) and at ice surface temperatures between 194 and 227 K. The pressure in the reactor was chosen as a compromise between detection sensitivity (related to the differential pumping of the mass spectrometer (MS) and reaction time in the ion–molecule reactor of the mass spectrometer, see below) and the need to stay above the vapour pressure of ice (∼0.1 Torr at −40 ∘C) whilst avoiding severe limitations of mass transport to the ice surface at higher pressures (see below). The HCl concentrations were kept low to ensure that all experiments were conducted in the HCl–ice stability regions of the phase diagram (Thibert and Dominé, 1997). In accordance, irreversible uptake (e.g. due to the formation of stable hydrates of HCl) was never observed when the ice growth rate was zero.
The gas phase temperature was 298 K during all experiments. The flow rate of He was between 700 and 800 sccm. The walls of upper and lower chambers were coated with very thin Teflon films (Chemours, fluorinated ethylene propylene dispersion (FEPD) 121).
2.1 Preparation and characterisation of the ice surface
Ice was prepared by freezing 0.6–1.2 mL of liquid water (high-performance liquid chromatography (HPLC) grade, Merck) in the ice compartment at 243 K and subsequently cooling it down to the temperature of the experiment. The ice substrate had a geometric surface area of 18.6 cm2, a thickness of 1–2 mm, and appeared translucent and smooth upon visual inspection. Occasionally some cracks formed during cooling, presumably due to thermal stress in the relatively thick ice. The temperature on the ice surface was calculated from the vapour pressure of water at which net evaporation or condensation was zero. This was achieved in an iterative procedure in which the water vapour concentration (monitored by the QMS in electron impact mode, see below) was adjusted via a flow controller until the concentration no longer changed upon opening and isolating the ice chamber. The sensitivity of the QMS to water vapour was determined by flowing a known amount of pure H2O through a calibrated mass flow controller and diluting this with an accurately known He flow before passing the combined flow through the upper chamber (with the ice chamber closed). Subsequently, the measured water vapour pressure above the ice was then converted to the ice surface temperature using vapour pressure data from the literature (Wagner, 1994). The ice surface temperature was generally higher than that measured by the thermocouple in the bottom plate of the ice chamber. The largest difference (≈5 K) was found at the lowest temperatures and when using the thickest ice films. At 235 K, the difference was ≈0.5 K for thin films and 1.5 K for thick films. However, the temperature registered by the thermocouple is only used as a guide to the ice surface temperature, and this observation has no impact on our results or analysis. The uncertainty in the ice surface temperature measured via the water vapour concentration is ±2 K.
The net H2O flux to the ice surface during periods of supersaturation, , was calculated from the difference in the calibrated mass signal at m∕z 20 with the ice chamber isolated (“without ice”) and open (“with ice”) at different water vapour concentrations. The difference in signal intensity was assumed to arise solely from the uptake of H2O molecules by the ice surface. The ice growth velocity (VIG, m s−1) was derived from the measured flux of H2O molecules from the gas phase onto the ice surface and assuming an ice density of 0.92 g cm−3. The growth velocities were found to increase linearly with ice supersaturation (i.e. water vapour concentration in the reactor) in the range relevant to the growth experiments. The calibration was also periodically performed on HCl-covered ice and ice that had grown for several hours in an atmosphere containing HCl at normal experimental concentrations. The deviation between the different calibrations was usually less than 1 %, indicating that the presence of HCl did not alter the growth velocity of the ice significantly. Ice growth velocities during the uptake experiments were between and m s−1, which is typical of cirrus clouds with ice supersaturations between 1 % and 20 % (Bailey and Hallett, 2012).
2.2 Detection of trace gases
All gases were detected online using a quadrupole mass spectrometer (Balzers QMA 410) which was coupled to the ice–trace gas interaction chamber via a glass tube coated with Teflon (Chemours, FEPD, 121). Details of the mass spectrometer, which can use either electron impact or chemical ionisation, are given in Winkler et al. (2002) and von Hessberg et al. (2008). Water (, m∕z 20), ethanol and 1-butanol (both CH3O+, m∕z 31), and trifluoroacetic acid (TFA) (, m∕z 69) were detected using electron impact; HCl and HC(O)OH were detected in chemical ionisation mode using ions. The latter were formed by passing a 0.2 % mixture of SF6 in N2 (Air Liquide) through a 210Po-radioactive source (model P-2021-1000, NRD). reacts with HC(O)OH and HCl to form product ions at m∕z 65 (HC(O)OHF−) and 162 (SF5Cl−) (Huey et al., 1995; Lovejoy and Wilson, 1998).
The detection limits (based on the background noise levels at the respective signals) in electron impact mode for the organic trace gases were calculated to be in the range 7.5 to 9.5×109 molecules cm−3 (0.17 s signal integration). For chemical ionisation, the detection limits for HC(O)OH and HCl were 1.9×109 (0.30 s) and 3.2×109 molecules cm−3 (0.17 s), respectively. The mass spectrometric signals were calibrated by monitoring the pressure drop in a calibrated volume which contained a manometrically prepared mixture of the trace gas of interest in He 5.0 (Westfalen). An HCl mixture of 3.95 vol % in He was used as a stock supply (Air Liquide) and further diluted to mixing ratios of . The concentration of the stock mixture was determined by passing a known amount through two wash bottles, each containing 250 mL of pure water. The resulting aqueous solutions were then titrated with a 0.01 N volumetric standard solution of sodium hydroxide in water (Carl Roth) with phenolphthalein as an indicator. The standard deviation of different titrations was 0.1 % to 2 % between runs.
Owing to diffusion limitations, the excess water vapour during supersaturation does not completely condense on the ice. This results in an increase in gas phase H2O reaching the detector during phases of ice growth, which resulted in an increase in QMS sensitivity to HCl (usually less than 10 %). The dependence of the HCl detection scheme on [H2O] was linear and was taken into account when converting QMS signals to HCl concentrations during ice growth.
Whilst experiments were conducted for all of the trace gases listed above, only HCl and, to a lesser extent, TFA displayed evidence for trapping in growing ice. We therefore first present a typical dataset for HCl to illustrate the data analysis.
3.1 HCl uptake
A representative dataset showing the uptake of HCl onto a growing ice surface is displayed in Fig. 2. Initially, HCl is introduced into the reactor with the quartz plate closed, and a stable concentration was established (t<150 s). At t=150 s the quartz plate was withdrawn, exposing the fresh ice surface to HCl. The concentration of HCl drops immediately as HCl adsorbs to the fresh ice surface and then gradually returns towards its initial value as the surface saturates. This first uptake takes place at ice–water vapour equilibrium (supersaturation = 0 %). At t∼1040 s a supersaturation of 41 % was created by increasing the water concentration in the reactor, resulting in growth of the ice surface at 2 nm s−1. The permanent decrease of the HCl gas phase concentration during this ice growth phase is evidence for continuous uptake (and thus trapping) of HCl. At t∼1200 and 1320 s further increases in the ice supersaturation (to 82 % and 122 %, respectively) lead to enhanced continuous uptake. At t∼1520 s the equilibrium conditions were restored (supersaturation of 0 %) and the HCl signal returns to its initial value. The effective uptake coefficient during trapping (γtrap) was calculated using
where V and Aice are the volume of the reactor (≈161.3 cm3) and the ice surface area, respectively, and is the mean molecular velocity of HCl at 298 K (≈42 000 cm s−1). tice refers to the time the HCl is in contact with the ice surface and varied between ≈18 and 21 ms, depending on the total flow. The right-hand y axis indicates the flux of HCl (molecules s−1) passing through the reactor. The net flux of HCl (JHCl) to the surface is calculated from the difference in signal when the HCl exposure to the ice is modulated by withdrawing the sliding isolator.
The molar fraction of HCl in the growing ice surface, MHCl, is calculated from the relative flux of HCl and condensing water.
Datasets such as those exemplified in Fig. 2 were obtained for a number of temperatures (T, which varied between 194 and 227 K), HCl concentrations ([HCl], which varied between 6.4×109 and 2.2×1011 cm−3) and ice growth velocities (VIG, varied between 1 and 68 nm s−1).
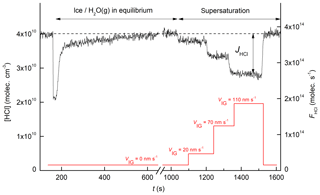
Figure 2The black line represents the time series of the HCl concentration (left y axis) or flux (right y axis) during an experiment at 213 K. Prior to t=1040 s, the ice was in equilibrium with the gas phase H2O concentration. After t=1040 s, the ice was supersaturated with respect to the gas phase, and the red line indicates the ice growth velocity, VIG (based on the H2O signal at m∕z 20), during the experiment.
Figure 3b shows the variation of γtrap with the growth velocity (VIG) at two different HCl concentrations (2.3×1010 and 7.1×1010 molecules cm−3) and an ice temperature of 210±1 K. In each case, γtrap depends linearly on the growth velocity of the ice surface. As ice growth was initiated only after HCl had returned to its concentration prior to exposure (i.e. when γtrap=0), we expect a direct proportionality between VIG and γtrap. This was observed in most experiments, with the intercept in plots such as those in Fig. 3, deviating insignificantly from zero. In some cases, however, the deviation of the intercept from zero was significant and relates to an offset in VIG, which was calculated relative to the mass spectrometer signal before HCl exposure began (e.g. at t=0 s in Fig. 1). A drift in mass spectrometer sensitivity or the ice temperature between t=0 s and the onset of H2O supersaturation (often > 1000 s later) may shift the plot of γtrap versus VIG, but this should not impact the values of dγtrap∕dVIG, which were obtained in quick succession and are therefore less susceptible to drifts.
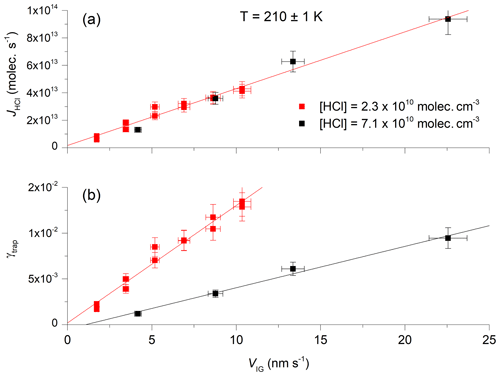
Figure 3The trapping coefficient (γtrap) as a function of ice growth velocity at 210 K using two different concentrations of HCl. The solid, straight lines are least-squares fits to the data. The error bars represent total uncertainty in γtrap and the ice growth velocity.
A linear relationship between γtrap and VIG was observed for values of γtrap up to ∼0.02. At larger ice growth velocities some datasets indicated a fall-off in the slope of γtrap versus VIG, the cause of which may have been a transport-related limitation to the uptake of HCl to the ice, whereby gradients in the HCl concentration close to the ice surface result in a reduction in mass transfer of HCl to the ice. As no simple scheme for the correction of the diffusive limitation to uptake exists for the complex geometry of the reactor, values of γtrap greater than 0.018 (10 % less that the maximum value (0.02) at which linear behaviour was still observed) were neglected in the final analysis.
In Fig. 3a, taking the same dataset, we plot the flux of HCl (JHCl in molecules s−1) to the surface during ice growth. JHCl is calculated from the difference between the flux observed by the mass spectrometer with and without interaction between HCl and the ice surface, as illustrated in Fig. 2. In contrast to γtrap, the two sets of measurements of JHCl at different HCl concentrations show the same dependence on VIG. As γtrap represents the efficiency of HCl removal from the gas phase on a per-collision basis and JHCl is the absolute number of HCl lost, we can conclude that, in our HCl concentration range, the trapping process is not limited by the collision rate of HCl with the ice surface or the net absorption rate because the same absolute flux is observed at a given ice growth rate for both high and low HCl concentrations and thus high and low collision and adsorption rates.
Returning to Fig. 3b, we see that, for a given ice growth velocity, the trapping efficiency depends on the HCl concentration. For example, an ice growth velocity of 10 nm s−1 results in values of γtrap that increase by a factor of 4 when the HCl concentration is reduced from 7.1×1010 to 2.3×1010 molecules cm−3. The HCl concentration can be converted to a fractional surface coverage θHCl (i.e. the equilibrium coverage which would have prevailed if the ice were not supersaturated) according to the Langmuir adsorption model.
where KLang is the Langmuir constant that describes the partitioning between molecules in the gas phase and those adsorbed on the surface and Nmax is the maximum surface coverage at equilibrium. We converted our gas phase HCl concentrations into surface coverages that would have been obtained under equilibrium conditions using the latest evaluation of adsorption isotherms (IUPAC, 2019) with cm3 molecule−1, independent of temperature in the range of our experiments. We recognise that the calculated values of θHCl during ice growth do not reflect actual surface coverages, but we find this a more useful parameter than the HCl concentration when interpreting and parameterising the values of γtrap obtained during growth (see below). Fractional surface coverages are also used in the trapping model (Kärcher and Basko, 2004; Kärcher et al., 2009), which we return to later.
Figure 4b presents the dependence of γtrap on VIG at three different ice temperatures, 195 K (with [HCl] = 2.2×1010 molecules cm−3), 211 K (with [HCl] = 2.5×1010 molecules cm−3) and 227 K (with [HCl] = 3.3×1010 molecules cm−3). The concentration–temperature pairs result in comparable, fractional equilibrium surface coverage of HCl on ice, with . The dataset indicates that the slope of γtrap versus the velocity of ice growth is largest at the lowest temperature. This result is expected, as the lifetime of an adsorbed [HCl] molecule on the ice surface will be longest at low temperatures, where the rate of thermally activated desorption is low. Longer surface residence times should increase the probability of trapping for any given ice growth velocity as the ratio of the rate of H2O uptake to the rate of HCl desorption increases. In Fig. 4a we plot JHCl instead of γtrap for the same dataset. Both the absolute flux and the efficiency of uptake of HCl show a similar dependence on temperature.
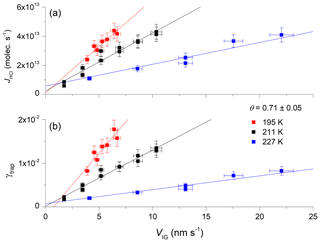
Figure 4Dependence of the trapping coefficient, γtrap, on the ice growth velocity (VIG) at three different temperatures and a comparable equilibrium surface coverage (θ) of HCl. The solid, straight lines are least-squares fits to the data. The error bars represent total uncertainty in γtrap and the ice growth velocity.
In order to facilitate the implementation of the experimental results into calculations of HCl interaction with growing ice surfaces under varying atmospheric conditions, we parameterised the data based on the dependence of γtrap on VIG, T and [HCl]. The basis of the parameterisation is the linear dependence of γtrap on VIG with values of (γtrap∕VIG) calculated for each dataset at constant temperature and [HCl]. The dependence of (γtrap∕VIG) on the HCl concentration (in the form of the calculated surface coverage, θ) is displayed in Fig. 5 where data at the five different experimental temperatures are plotted. The uptake coefficients tend to zero when the equilibrium surface coverage approaches unity and the fits to the data were forced through the origin. The rationale for this is the inherent assumption in the Langmuir isotherm that for θHCl=1, increasing the HCl concentration increases the collision frequency of HCl with the ice surface. The number of trapped HCl molecules is however limited by the ice growth velocity (Fig. 3a) and the efficiency of trapping (the number of trapped molecules divided by the collision frequency (Eq. 1) must tend to zero as [HCl] tends to infinity).
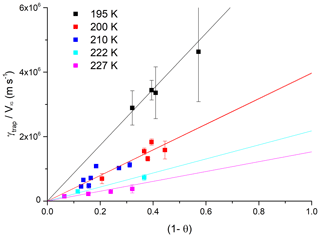
Figure 5Plot of γtrap∕VIG (as derived from data in Fig. 4) versus (1-θ) at different temperatures. The solid lines are proportional fits to the data at each temperature. The error bars represent total uncertainty.
The temperature-dependent slopes of (γtrap∕VIG) (1-θHCl)−1 are plotted versus inverse temperature in Arrhenius form in Fig. 6. enabling the dataset to be parameterised with Eq. (5).
Equation (5) is valid for low ice growth rates where the uptake of HCl is not limited by gas phase diffusion. The negative temperature dependence () indicates that the trapping of HCl in growing ice is associated with a net energy change of ∼17 kJ mol−1. The fact that the fit line does not pass through all of the data points plus the experimental uncertainty reflects the fact that the data were obtained on different ice surfaces. Although we attempted to make the ice as reproducible as possible, some scatter in γtrap was observed for different ice surface even under apparently identical conditions. This phenomenon has often been observed in studies of trace gas interaction with ice surfaces (Crowley et al., 2010) and may be related to the (variable) presence of grain boundaries in the ice substrate.
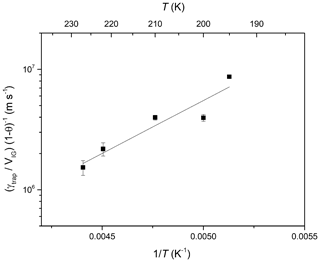
Figure 6Arrhenius plot of (γtrap∕VIG) (1-θ)−1 derived from data in Fig. 5 versus inverse temperature. The solid line is a least-squares fit to the data.
A physical framework (trapping model) describing the irreversible, nonreactive uptake of trace gases by growing ice particles has been developed by Kärcher and colleagues (Kärcher and Basko, 2004; Kärcher et al., 2009). The trapping model enables the calculation of γtrap, J and M from parameters n* (the maximum possible number density of molecules trapped in the ice) and vesc (an escape velocity which is connected to the surface desorption rate constant). Although the trapping model was originally developed for nitric acid, it can in principle be used to describe the trapping of any molecule in growing ice. Kärcher et al. (2009) consider the uptake of trace gases to growing ice surfaces to be a two-step process involving initial accommodation at the surface followed by trapping as new monolayers of water condense on the growing ice. The model distinguishes between different limiting cases which are characterised by different ratios of vesc to VIG. If (vesc∕VIG) is smaller than 0.1, i.e. the ice grows very rapidly or the desorption velocity is very small, γtrap approaches the mass accommodation coefficient (α) of the respective trace gas such that every molecule that accommodates also gets trapped (“burial limit”). If (vesc∕VIG) is larger than 10, most accommodated molecules will desorb from the ice surface rather than be trapped, and γtrap will be much smaller than α (“adsorption limit”). The experiments presented here may be considered to be at the adsorption limit since the maximum value of the uptake coefficient was ∼0.018, more than an order of magnitude lower than the mass accommodation coefficient of HCl on ice (α∼0.3, Crowley et al. 2010). At the adsorption limit, γtrap and JHCl are predicted to scale with VIG, which is in agreement with the experimental results of this study (Fig. 3). Also, if HCl concentrations are sufficiently high, the flux of HCl to the surface is limited by n* so that JHCl is independent of [HCl] but γtrap decreases as [HCl] increases, also in accord with our observations.
To assess the trapping model, we derive n* and vesc from our experimental datasets obtained at different temperatures and HCl concentrations. At the adsorption limit, the maximum number density of HCl in ice during trapping (n*) can be calculated from the mole fraction MHCl (Kärcher and Basko, 2004; Kärcher et al., 2009).
where vw is the volume occupied by an ice molecule in ice. Using mean values of MHCl from datasets obtained at a constant ice surface temperature and constant HCl concentration (variation of VIG only), we derive temperature-dependent values of n* which are plotted in Arrhenius form in Fig. 7 and described by
which is represented by the solid fit line through the data points. n* thus displays a significant, negative dependence on temperature. We also plot (right-hand y axis) the solubility of HCl in ice (as a mole fraction for an HCl partial pressure similar to those used in the present study) as measured by Thibert and Dominé (1997). Although their parameterisation was derived in a different temperature range (265–238 K) and using single-crystalline ice, the temperature dependence is very similar. This highlights the fact that although n* cannot be equated to a solubility (which infers thermodynamic equilibrium), it is a related parameter.
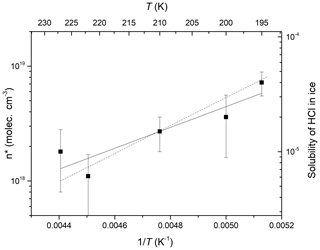
Figure 7Arrhenius plot of n* versus inverse temperature. The error bars represent the 1σ standard deviation of the mean values derived from MHCl. The solid line is a fit to the data according to Eq. (7). The dotted line (right-hand y axis) represents the solubility of HCl in ice (as a unitless mole fraction for an HCl partial pressure similar to those used in the present study) as measured by Thibert and Dominé (1997). The left and right y axes have the same relative span to enable the comparison of slopes.
Using Eq. (7), n* can be derived for any experimental temperature enabling vesc to be calculated from Kärcher and Basko (2004) and Kärcher et al. (2009).
where kB is the Boltzmann constant. Taking the present recommendations (IUPAC, 2019) for the Langmuir partition coefficient and accommodation coefficient (see above), we can derive m s−1.
At 229 K Eq. (7) indicates a value of n* equal to 1.1×1018 cm−3, which is significantly larger (by approximately a factor of 10) than that calculated by Kärcher et al. (2009) for HNO3 trapping during ice growth ( molecules cm−3). Our value of vesc at the same temperature is cm s−1, which can be compared to the value of cm s−1 calculated by Kärcher et al. (2009). The values of n* and vesc derived in this work are based on an extensive laboratory dataset for HCl whereas those calculated by Kärcher et al. (2009) are derived from a very limited number of data for HNO3 obtained under non-optimal conditions using a flow tube reactor in which the ice growth rate was poorly characterised and probably non-homogeneous. A more detailed comparison of the values of n* and vesc between these studies is therefore not warranted. However, in the following, we compare uptake coefficients of HCl (γtrap) based on our Eq. (5) with those calculated using the trapping model adapted for HCl by using values of n* and vesc derived from our data (Eq. 7 and 8).
We calculate the trapping model predictions of γtrap under conditions of planar flow (no diffusive limitation to uptake) at the adsorption limit and considering the limiting cases of high HCl partial pressures (surface saturation, ) and low HCl partial pressures (no surface saturation, ) whereby, according to Kärcher et al. 2009),
and
The values of γtrap from Eq. (5) and the trapping model are displayed in Fig. 8, which plots γtrap as a function of the HCl partial pressure for two different temperatures (200 and 230 K) and at an ice growth velocity of 10 nm s−1. The trapping model accurately reproduces the empirical Eq. (5) once values of n* have been multiplied by a factor 1.3 (and thus vesc decreased by the same factor, see Eq. 8). The parameters used to calculate n* include the ice growth velocity, the HCl concentration and the resultant fractional coverage of HCl on the surface so that a factor of 1.3 can be considered to be within experimental uncertainty. The fact that the trapping model and the empirical parameterisation of our experimental data agree so well reflects the fact that common values of the partition coefficient (KLang) have been used and that both the trapping model and our data analysis implicitly assume a common mechanism which involves surface accommodation and a trapping process that competes with desorption. Our data serve to confirm the concept of a limiting, maximum concentration of HCl in growing ice that is related to but significantly larger than the solubility of HCl in single ice crystals and thus provide validation of the underlying physical processes in the trapping model (Kärcher and Basko, 2004; Kärcher et al., 2009).
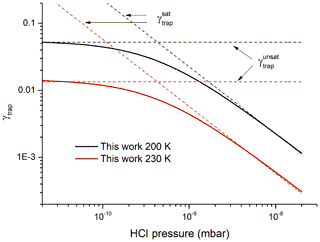
Figure 8Comparison of γtrap from the present dataset, parameterised according to Eq. (5) with the results of the modified trapping model from Kärcher et al. (2009) for the limiting cases of saturated and unsaturated uptake. The values of n* derived from our data and used to calculate vesc and γtrap have been multiplied by a factor of 1.3 to improve agreement (see text).
Previous experimental data on the uptake of HCl to growing ice surfaces
The uptake of HCl to equilibrium ice surfaces has been extensively studied, and the results are summarised by the IUPAC panel (Crowley et al., 2010; IUPAC, 2019). A limited number of laboratory studies have explored the uptake of HCl trace gases during ice growth, though generally not under conditions that enable detailed comparison with the present dataset or analysis with the trapping model.
Santachiara et al. (1995) studied the trapping of HCl during ice growth at 260 K, whereby ice crystals were grown on a metal surface via the Wegener–Bergeron process by transferring water from supercooled water droplets which contained hydrochloric acid. Analysis of the HCl content of the ice particles indicated up to 100 % transfer of HCl from the evaporating aqueous droplets to the growing ice crystals, with HCl mole fractions in ice (MHCl) of to . At 260 K, such concentrations are in an area of the HCl–ice phase diagram where the solid HCl–ice solution coexists with an aqueous phase (Thibert and Dominé, 1997). While these experiments indicate that HCl is incorporated efficiently into growing ice, quantitative comparison with our data is precluded by a lack of information pertaining to the HCl concentration in the gas phase, the temperature of the ice or the rate of ice growth.
Diehl et al. (1995) grew ice crystals directly from the gas phase onto a cooled filament. The ice was grown for 9–18 h at 258 K and at 15 % supersaturation with HCl concentrations in the gas phase between 2.8×1011 and 9.9×1012 molecules cm−3. Analysis of the ice phase indicates that, up to a value of , MHCl was linearly proportional to the concentration of HCl, increasing further to a maximum value of as the HCl concentration was increased further. The fact that the rate of ice growth is unknown and that high pressures and diffusion-limited uptake were used in the experiments of Diehl et al. (1995) preclude a more quantitative comparison.
Dominé and Rauzy (2004) studied HCl trapping in ice under conditions similar to those employed by Diehl et al. (1995) and were thus subject to the same limitations regarding diffusion, precluding a kinetic analysis. In their work, the lowest growth velocity was about 1000 nm s−1 and thus 25 times higher than the highest growth velocity in our experiments. A combination of fast ice growth and high pressure in their experiments resulted in substantial depletion of gas phase HCl close to the ice surface, effectively limiting the transfer of HCl to the surface and thus reducing MHCl. In accordance, the authors report a decrease in MHCl with increasing growth velocity.
Huthwelker et al. (2004) investigated the uptake of HCl on growing ice using a Knudsen reactor at temperatures of 190 and 203 K. The gas phase concentrations of HCl were between 1×108 and 1×1011 molecules cm−3, while ice growth velocities were between 0.2 and 100 nm s−1. As in the present study, the mass spectrometric detection of HCl and H2O enabled the real-time measurement of γtrap and MHCl. In qualitative agreement with this study, Huthwelker et al. (2004) measured comparable values of JHCl under similar conditions and observed that γtrap and MHCl increase with VIG. However, while we find that JHCl is proportional to VIG, Huthwelker et al. (2004) found , which makes MHCl approximately proportional to . Another major difference between the two studies is the temperature dependence of γtrap. While Huthwelker et al. (2004) found no statistically significant variation in γtrap between 190 and 203 K, our data suggest that γtrap doubles in this temperature range. Though the reason for these discrepancies is obscure, we note that a major difference between the two experiments lies in the mode of preparation of the ice film. The vapour-deposited ice films of Huthwelker et al. (2004) are rough and porous, and, under equilibrium, the dominant fraction of HCl uptake was attributed to bulk diffusion rather than surface adsorption. In contrast, the ice used in this study, prepared from the liquid phase, is thought to be smooth on a microscopic level and exhibited hardly any diffusive uptake. It remains unclear if and how the different ice formation modes and ice morphologies modify the trapping process.
3.2 Uptake of oxidised organics: ethanol, 1-butanol, formic acid and trifluoroacetic acid
Analogous to the experiments with HCl described above, we examined the uptake of ethanol, 1-butanol, formic acid and trifluoroacetic acid to growing ice surfaces. Despite the use of high values of VIG, no sign of trapping (i.e. a net reduction in the flux of molecules to the mass spectrometer during ice growth) was observed for ethanol, 1-butanol or formic acid. Trifluoroacetic acid represents an intermediate case, exhibiting continuous uptake during ice growth (213 and 223 K) with γtrap positively correlated to VIG and the largest value of γtrap obtained at the lowest temperature. The derivation of γtrap for trifluoroacetic acid is however associated with large uncertainty as the change in concentration is small, and small baseline drifts and/or changes in the mass spectrometer sensitivity increase the uncertainty to a factor of ∼2. For this reason, we restrict our discussion of the trifluoroacetic acid dataset (intermediate γtrap) to a qualitative comparison with HCl (large γtrap) and the other oxidised organic trace gases (low γtrap).
Table 1Summary of results.

a pKa value from Becker (2001). b pKa value from Haynes and Lide (2001). c pKa value from Riedel (2002). The HCl desorption lifetime, τdes, was calculated from the recommended IUPAC values of KLang and α; for trifluoroacetic acid, the data of Symington et al. (2010) were used.
The results for the organic trace gases are summarised along with those for HCl in Table 1, which also lists VIG, the range of fractional surface coverages and the approximate average lifetime (τdes) with respect to desorption for each trace gas at the respective experimental temperature.
Values of KLang and α (0.3) were taken from an evaluation (Crowley et al., 2010; IUPAC, 2019). Despite the deposition of hundreds to thousands of monolayers of water on the ice surface during the desorption lifetime, no trapping of ethanol, 1-butanol or formic acid could be observed with , i.e. more than 2 orders of magnitude lower than for HCl for similar ice growth rates and surface residence times. In qualitative agreement with our results, Abbatt et al. (2008) were unable to observe the trapping of ethanol during ice growth. Huffman and Snider (2004) studied the uptake of ethanol and 1-butanol to ice at 249 to 269 K which was growing with velocities of 24 to 110 nm s−1. The volume uptake coefficients were reported (amount of gas taken up per partial pressure and ice mass), and they displayed a positive T dependence and were independent of the ice growth velocity. The positive T dependence of the uptake observed by Huffman and Snider (2004) points to an uptake mechanism that is different from the one we observe for HCl, with dissolution of the organic trace gases in a quasi-liquid layer on the ice surface or in grain boundaries and triple junctions playing a potentially dominant role as the ice temperature approached the melting point. Taking the trace gas partial pressures used by Huffman and Snider (2004) and extrapolating their T-dependent uptake coefficient to 228 K results in mole fractions of for ethanol and for 1-butanol in the ice. The differences in gas phase concentrations leading to such low molar fractions would have been too small to be quantifiable with the methods used in this study.
The differences in γtrap between these trace gases provide an important clue to which factors may drive the trapping of a physi-adsorbed trace gas on a growing ice surface at temperatures far below the melting point. Studies of the equilibrium partitioning of ethanol, butanol and formic acid (and other oxidised organics) between ice and the gas phase indicate that they are adsorbed in molecular form via hydrogen bonds (Compoint et al., 2002; Jedlovszky et al., 2006; Pártay et al., 2007; Jedlovszky et al., 2008) and that the uptake is fully reversible (Sokolov and Abbatt, 2002; Peybernès et al., 2004; Kerbrat et al., 2007; von Hessberg et al., 2008). In contrast, the uptake of HCl to ice is known to be partially irreversible, and there is overwhelming experimental and theoretical evidence that HCl dissociates upon adsorption (Gertner and Hynes, 1998; Svanberg et al., 2000; Toubin et al., 2002; Park and Kang, 2005; Ayotte et al., 2011; Parent et al., 2011). For trifluoroacetic acid the adsorption is partially dissociative (Symington et al., 2010) and displays similar features to HCl, including partially non-reversible adsorption on pristine ice surfaces and partitioning coefficients that are independent of temperature (Symington et al., 2010; Zimmermann et al., 2016). Table 1 lists the acid dissociation constants (pKa) for several of the trace gases investigated in this study, highlighting the significant difference between the acidity of HCl (pKa = −7) per fluoro acetic acid (pKa = 0.52) and formic acid (pKa = 3.75).
We thus conclude that, following surface accommodation, the dissociative formation of ions is a prerequisite for the efficient trapping at the temperatures and ice growth rates of our study. This implies that ice lattice formation around solvated hydronium cations and acid anions is thermodynamically favoured, whereas physi-adsorbed trace gases impede the growth of ice at the adsorption site. While such dynamical effects are not included in the trapping model (see above), they are empirically incorporated in the parameters n* and vesc.
3.3 HCl trapping on atmospheric ice particles
Our laboratory dataset and the parameterisation of the trapping of HCl in growing ice surface enable us to calculate the particle phase HCl concentration associated with an ice cloud at a given ice particle growth rate and different ice particle diameters. This can be compared to the particle phase concentration of HCl resulting from the partitioning of HCl to the surface of ice crystals and to the solubility of HCl in ice under equilibrium conditions when the ice growth velocity is zero. In each case we calculate the mole fraction of HCl associated with the ice phase for a given gas phase concentration and temperature.
As HCl uptake to the ice is a non-equilibrium effect described by an effective uptake coefficient, we need to consider the limiting effect of gas phase diffusion to the surface. To do this, we modify the values of γtrap obtained in Eq. (5) using Eq. (12).
where Kn is the Knudsen number and is equal to 3 . DHCl is the temperature- and pressure-dependent diffusion coefficient of HCl in air and r is the particle radius. DHCl was calculated using the Fuller equation (Fuller et al., 1966) and values from the literature for the diffusion volumes of HCl and air (Tang et al., 2014).
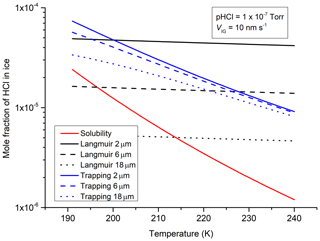
Figure 9Molar fraction of HCl (gas phase partial pressure Torr) associated with ice particles (with a radius of 2, 6 and 18 µm) considering either surface adsorption (Langmuir; zero ice growth) or trapping (ice growth velocity = 10 nm s−1).
Figure 9 compares the contributions of surface adsorption (VIG=0, black lines) and the trapping of HCl (VIG=10 nm s−1, blue lines) to the mole fraction of particulate HCl for prescribed conditions of HCl partial pressure ( Torr) and total pressure (100 Torr) at temperatures that may be found in the upper troposphere and at the tropopause. The HCl mole fractions associated with particles with a radius of 2, 6 and 18 µm resulting from surface adsorption were calculated using the Langmuir isotherm with cm3 molecule−1, independent of temperature (IUPAC, 2019). The contribution of the initial “pure” ice particle to the mole fraction of water was neglected during these calculations as the initial particle volume is small compared to that obtained after several minutes of growth in the presence of HCl. We also plot the mole fraction of HCl resulting from bulk solubility in ice (red curve), according to Thibert and Dominé (1997).
Figure 9 illustrates several key differences in the kinetically controlled trapping process compared to the equilibria associated with surface adsorption or solubility. The HCl mole fraction associated with trapping displays a strong dependence on temperature but only a weak dependence on particle diameter. In contrast, Langmuir adsorption, a surface-only effect, displays no dependence on temperature but a strong negative dependence on diameter, the latter reflecting the fact that the volume of a growing particle increases proportionally to r3, whereas the surface area increases proportional to r2. Trapping can therefore greatly enhance the overall uptake of HCl for particles with a radius larger than 6 µm and thus strongly influence the gas-to-particle partitioning during particle growth. The surface contribution to the HCl mole fraction is relatively more important only for smaller particles and for periods when the ice growth rate is low.
The solubility limit for HCl imbedded in an ice single crystal (Thibert and Dominé, 1997) is shown in red for reference. The values for the mole fraction of HCl in ice obtained during our experiments clearly exceed the thermodynamic limit. This likely reflects the fact that the timescale required to acquire equilibrium (i.e. diffusion of trapped HCl back to the gas phase) is much longer than the timescales of our experiments. The diffusion coefficient of HCl in ice is < 10−12 cm2 s−1 (see Thibert and Dominé, 1997, and references therein) implying timescales for a relaxation to equilibrium of > 105 s for particles with a m radius, which are longer than the timescales associated with atmospheric temperature fluctuations which control ice growth (and evaporation) rates.
An important difference between the uptake of HCl via equilibrium surface partitioning and trapping is the potential, fractional depletion of gas phase HCl. In the case of surface adsorption, the system will relax to the equilibrium state in which the rates of adsorption and desorption of HCl to/from the ice surface are equal; the fraction of HCl remaining in the gas phase depends on the initial concentration and the particle number density. In the case of non-equilibrium trapping, the complete transfer of the HCl to the particle phase during ice growth can occur. Consider a cirrus cloud (230 K) with an initial ice particle surface area density (A) of cm2 cm−3 (see e.g. Popp et al., 2004) and ice particles growing at 10 nm s−1. The uptake coefficient for HCl ( Torr) is γtrap , which converts (via Eq. 13) to a lifetime for gas phase HCl (τ) of only a few minutes.
The efficient removal of HCl from the gas phase in ice clouds via the trapping mechanism can have important repercussions for heterogeneous reactions taking place on the ice surface. While surface-adsorbed HCl is available for reactions with e.g. ClONO2, HOCl and N2O5, which liberate photochemically active forms of chlorine (Crowley et al., 2010), HCl that is trapped in the bulk of the ice will likely not participate in these reactions until the ice starts to evaporate. This may influence the spatial and temporal activation of chlorine and may likewise influence the development of the polar ozone hole.
Our experiments have clearly demonstrated that HCl is incorporated (trapped) efficiently in growing ice surfaces. The coefficient (γtrap) describing the uptake of HCl to an ice surface during growth was proportional to the velocity of ice growth and was largest at low temperatures when the desorption lifetime of HCl accommodated at the ice surface is longest. γtrap was found to be reduced at high HCl partial pressures and our experimental results are entirely consistent with the framework for trapping developed by Kärcher and colleagues (Kärcher and Basko, 2004; Kärcher et al., 2009).
No experimental evidence for the trapping of several oxidised organics that bind to the ice surface via H bonds could be found, whereas trifluoroacetic acid, which partially dissociates on the ice surface, was an intermediate case. We infer that the efficient trapping of HCl is related to its dissociation and solvation in the growing ice lattice, with the mole fraction of HCl exceeding the thermodynamic solubility limit. Experiments using ice single crystals would be useful to constrain the role (if any) of HCl uptake to grain boundaries on our polycrystalline ice substrate.
Our parameterisation of the experimental data enabled us to compare the relative importance of HCl trapping during ice growth with equilibrium partitioning only due to surface uptake, and it will facilitate the incorporation of HCl trapping in atmospheric models. The trapping of HCl in ice particles during their growth can represent a highly efficient route to removal of HCl from the gas phase in ice clouds, which, in contrast to surface-only uptake, does not make HCl available for heterogeneous surface reactions.
The underlying data (Figs. 3–7) are tabulated in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-11939-2019-supplement.
MK carried out the experiments and analysed the data. JNC, MK and JL wrote the paper. GS designed and built the reactor for investigating trace gas uptake to growing ice surfaces and helped with data interpretation.
The authors declare that they have no conflict of interest.
This study was carried out in partial fulfilment of a doctoral dissertation (by Matthias Kippenberger) at the University of Mainz and was partially funded by the International Max Planck Research School. This work contributes to the MaxWater initiative of the Max Planck Society. We thank Chemours for the provision of the FEP sample (FEPD 121) used to coat the reactor.
The article processing charges for this open-access publication were covered by the Max Planck Society.
This paper was edited by Thorsten Bartels-Rausch and reviewed by J. Paul Devlin and one anonymous referee.
Abbatt, J. P. D.: Interactions of atmospheric trace gases with ice surfaces: Adsorption and reaction, Chem. Rev., 103, 4783–4800, 2003.
Abbatt, J. P. D., Bartels-Rausch, T., Ullerstam, M., and Ye, T. J.: Uptake of acetone, ethanol and benzene to snow and ice: effects of surface area and temperature, Environ. Res. Lett., 3, 045008, https://doi.org/10.1088/1748-9326/3/4/045008, 2008.
Ayotte, P., Marchand, P., Daschbach, J. L., Smith, R. S., and Kay, B. D.: HCl Adsorption and Ionization on Amorphous and Crystalline H2O Films below 50 K, J. Phys. Chem. A, 115, 6002–6014, https://doi.org/10.1021/jp110398j, 2011.
Bailey, M. and Hallett, J.: Ice Crystal Linear Growth Rates from −20 degrees to −70 degrees C: Confirmation from Wave Cloud Studies, J. Atmos. Sci., 69, 390–402, https://doi.org/10.1175/jas-d-11-035.1, 2012.
Becker, H. G. O.: Organikum, 21. edn., Wiley-WCH, Weinheim, 2001.
Compoint, M., Toubin, C., Picaud, S., Hoang, P. N. M., and Girardet, C.: Geometry and dynamics of formic and acetic acids adsorbed on ice, Chem. Phys. Lett., 365, 1–7, 2002.
Comstock, J. M., Lin, R. F., Starr, D. O., and Yang, P.: Understanding ice supersaturation, particle growth, and number concentration in cirrus clouds, J. Geophys. Res.-Atmos., 113, D23211, https://doi.org/10.1029/2008jd010332, 2008.
Crowley, J. N., Ammann, M., Cox, R. A., Hynes, R. G., Jenkin, M. E., Mellouki, A., Rossi, M. J., Troe, J., and Wallington, T. J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Volume V – heterogeneous reactions on solid substrates, Atmos. Chem. Phys., 10, 9059–9223, https://doi.org/10.5194/acp-10-9059-2010, 2010.
Diehl, K., Mitra, S. K., and Pruppacher, H. R.: A laboratory study of the uptake of HNO3 and HCl vapor by snow crystals and ice spheres at temperatures between 0 and −40 ∘C, Atmos. Environ., 29, 975–981, 1995.
Domine, F. and Rauzy, C.: Influence of the ice growth rate on the incorporation of gaseous HCl, Atmos. Chem. Phys., 4, 2513-2519, https://doi.org/10.5194/acp-4-2513-2004, 2004.
Fuller, E. N., Schettle, P. D., and Giddings, J. C.: A new method for prediction of binary gas-phase diffusion coeffecients, Ind. Eng. Chem., 58, 19–27, 1966.
Gao, R. S., Popp, P. J., Fahey, D. W., Marcy, T. P., Herman, R. L., Weinstock, E. M., Baumgardner, D. G., Garrett, T. J., Rosenlof, K. H., Thompson, T. L., Bui, P. T., Ridley, B. A., Wofsy, S. C., Toon, O. B., Tolbert, M. A., Karcher, B., Peter, T., Hudson, P. K., Weinheimer, A. J., and Heymsfield, A. J.: Evidence that nitric acid increases relative humidity in low-temperature cirrus clouds, Science, 303, 516–520, 2004.
Gertner, B. J. and Hynes, J. T.: Model molecular dynamics simulation of hydrochloric acid ionization at the surface of stratospheric ice, Faraday Discuss., 301–322, 1998.
Girardet, C. and Toubin, C.: Molecular atmospheric pollutant adsorption on ice: a theoretical survey, Surf. Sci. Rep., 44, 163–238, 2001.
Haynes, W. M. and Lide, D. R.: CRC Handbook of Chemistry and Physics, 91. online edn., 2001.
Huey, L. G., Hanson, D. R., and Howard, C. J.: Reactions of Sf6- and I- with Atmospheric Trace Gases, J. Phys. Chem., 99, 5001–5008, 1995.
Huffman, W. A. and Snider, J. R.: Ice-oxyhydrocarbon interactions in the troposphere, J. Geophys. Res.-Atmos., 109, D01302, https://doi.org/10.1029/2003JD003778, 2004.
Huthwelker, T., Malmstrom, M. E., Helleis, F., Moortgat, G. K., and Peter, T.: Kinetics of HCI uptake on ice at 190 and 203 K: implications for the microphysics of the uptake process, J. Phys. Chem. A, 108, 6302–6318, https://doi.org/10.1021/jp0309623, 2004.
IUPAC: Task Group on Atmospheric Chemical Kinetic Data Evaluation, (Ammann, M., Cox, R. A., Crowley, J. N., Herrmann, H., Jenkin, M. E., McNeill, V. F., Mellouki, A., Rossi, M. J., Troe, J. and Wallington, T. J.), available at: http://iupac.pole-ether.fr/index.html (last access: June 2019), 2019.
Jedlovszky, P., Partay, L., Hoang, P. N. M., Picaud, S., von Hessberg, P., and Crowley, J. N.: Determination of the adsorption isotherm of methanol on the surface of ice. An experimental and Grand Canonical Monte Carlo simulation study, J. Am. Chem. Soc., 128, 15300–15309, 2006.
Jedlovszky, P., Hantal, G., Neuróhr, K., Picaud, S., Hoang, P. N. M., von Hessberg, P., and Crowley, J. N.: Adsorption isotherm of formic acid on the surface of ice, as seen from experiments and Grand Canonocal Monte Carlo simulation, J. Phys. Chem. C, 112, 8976–8987, 2008.
Kärcher, B. and Basko, M. M.: Trapping of trace gases in growing ice crystals, J. Geophys. Res.-Atmos., 109, D22204, https://doi.org/10.1029/2004JD005254, 2004.
Kärcher, B. and Voigt, C.: Formation of nitric acid/water ice particles in cirrus clouds, Geophys. Res. Lett., 33, L08806, https://doi.org/10.1029/2006GL025927, 2006.
Kärcher, B., Abbatt, J. P. D., Cox, R. A., Popp, P. J., and Voigt, C.: Trapping of trace gases by growing ice surfaces including surface-saturated adsorption, J. Geophys. Res.-Atmos., 114, D13306, https://doi.org/10.1029/2009JD011857, 2009.
Kerbrat, M., Le Calve, S., and Mirabel, P.: Uptake measurements of ethanol on ice surfaces and on supercooled aqueous solutions doped with nitric acid between 213 and 243 k, J. Phys. Chem. A, 111, 925–931, 2007.
Lee, S. H., Wilson, J. C., Baumgardner, D., Herman, R. L., Weinstock, E. M., LaFleur, B. G., Kok, G., Anderson, B., Lawson, P., Baker, B., Strawa, A., Pittman, J. V., Reeves, J. M., and Bui, T. P.: New particle formation observed in the tropical/subtropical cirrus clouds, J. Geophys. Res.-Atmos., 109, D20209, https://doi.org/10.1029/2004jd005033, 2004.
Lovejoy, E. R. and Wilson, R. R.: Kinetic studies of negative ion reactions in a quadrupole ion trap: Absolute rate coefficients and ion energies, J. Phys. Chem. A, 102, 2309–2315, 1998.
Marécal, V., Pirre, M., Rivière, E. D., Pouvesle, N., Crowley, J. N., Freitas, S. R., and Longo, K. M.: Modelling the reversible uptake of chemical species in the gas phase by ice particles formed in a convective cloud, Atmos. Chem. Phys., 10, 4977–5000, https://doi.org/10.5194/acp-10-4977-2010, 2010.
Molina, M. J., Tso, T. L., Molina, L. T., and Wang, F. C. Y.: Antarcctic stratospheric chemistry of chlorine nitrate, hydrogen chloride and ice – Release of active chlorine, Science, 238, 1253–1257, https://doi.org/10.1126/science.238.4831.1253, 1987.
Parent, P., Lasne, J., Marcotte, G., and Laffon, C.: HCl adsorption on ice at low temperature: a combined X-ray absorption, photoemission and infrared study, Phys. Chem. Chem. Phys., 13, 7111–7117, https://doi.org/10.1039/c0cp02864a, 2011.
Park, S. C. and Kang, H.: Adsorption, ionization, and migration of hydrogen chloride on ice films at temperatures between 100 and 140 K, J. Phys. Chem. B, 109, 5124–5132, https://doi.org/10.1021/jp045861z, 2005.
Pártay, L. B., Jedlovszky, P., Hoang, P. N. M., Picaud, S., and Mezei, M.: Free-energy profile of small solute molecules at the free surfaces of water and ice, as determined by cavity insertion widom calculations, J. Phys. Chem. C, 111, 9407–9416, 2007.
Peybernès, N., Marchand, C., Le Calvé, S., and Mirabel, P.: Adsorption studies of acetone and 2,3-butanedione on ice surfaces between 193 and 223 K, Phys. Chem. Chem. Phys., 6, 1277–1284, 2004.
Popp, P. J., Gao, R. S., Marcy, T. P., Fahey, D. W., Hudson, P. K., Thompson, T. L., Karcher, B., Ridley, B. A., Weinheimer, A. J., Knapp, D. J., Montzka, D. D., Baumgardner, D., Garrett, T. J., Weinstock, E. M., Smith, J. B., Sayres, D. S., Pittman, J. V., Dhaniyala, S., Bui, T. P., and Mahoney, M. J.: Nitric acid uptake on subtropical cirrus cloud particles, J. Geophys. Res.-Atmos., 109, D06302, https://doi.org/10.1029/2003JD004255, 2004.
Popp, P. J., Marcy, T. P., Watts, L. A., Gao, R. S., Fahey, D. W., Weinstock, E. M., Smith, J. B., Herman, R. L., Troy, R. F., Webster, C. R., Christensen, L. E., Baumgardner, D. G., Voigt, C., Karcher, B., Wilson, J. C., Mahoney, M. J., Jensen, E. J., and Bui, T. P.: Condensed-phase nitric acid in a tropical subvisible cirrus cloud, Geophys. Res. Lett., 34, L24812, https://doi.org/10.1029/2007GL031832, 2007.
Pouvesle, N., Kippenberger, M., Schuster, G., and Crowley, J. N.: The interaction of H2O2 with ice surfaces between 203 and 233 K, Phys. Chem. Chem. Phys, 12, 15544–15550, 2010.
Riedel, E.: Anorganische Chemie, 5. edn., de Gruyter, Berlin, 2002.
Santachiara, G., Prodi, F., and Vivarelli, F.: Scavanging of SO2 and HCl during growth of ice crystals by vapour diffusion, Atmos. Environ., 29, 983–987, https://doi.org/10.1016/1352-2310(95)00023-r, 1995.
Sokolov, O. and Abbatt, J. P. D.: Adsorption to ice of n-alcohols (ethanol to 1-Hexanol), acetic acid and hexanal, J. Phys. Chem., 106, 775–782, 2002.
Solomon, S., Garcia, R. R., Rowland, F. S., and Wuebbles, D. J.: On the depletion of Antarctic ozone, Nature, 321, 755–758, 1986.
Svanberg, M., Pettersson, J. B. C., and Bolton, K.: Coupled QM/MM molecular dynamics simulations of HCl interacting with ice surfaces and water clusters – Evidence of rapid ionization, J. Phys. Chem. A, 104, 5787–5798, 2000.
Symington, A., Cox, R. A., and Fernandez, M. A.: Uptake of Organic Acids on Ice Surfaces: Evidence for Surface Modification and Hydrate Formation, Z. Phys. Chemie-Int. J. Res. Phys. Chem. Chem. Phys., 224, 1219–1245, https://doi.org/10.1524/zpch.2010.6149, 2010.
Tang, M. J., Cox, R. A., and Kalberer, M.: Compilation and evaluation of gas phase diffusion coefficients of reactive trace gases in the atmosphere: volume 1. Inorganic compounds, Atmos. Chem. Phys., 14, 9233–9247, https://doi.org/10.5194/acp-14-9233-2014, 2014.
Thibert, E. and Dominé, F.: Thermodynamics and kinetics of the solid solution of HCl in ice, J. Phys. Chem. B, 101, 3554–3565, 1997.
Toubin, C., Picaud, S., Hoang, P. N. M., Girardet, C., Demirdjian, B., Ferry, D., and Suzanne, J.: Structure and dynamics of ice Ih films upon HCl adsorption between 190 and 270 K, II, Molecular dynamics simulations, J. Chem. Phys., 116, 5150–5157, 2002.
von Hessberg, P., Pouvesle, N., Winkler, A. K., Schuster, G., and Crowley, J. N.: Interaction of formic and acetic acid with ice surfaces between 187 and 227 K, Investigation of single species- and competitive adsorption, Phys. Chem. Chem. Phys., 10, 2345–2355, 2008.
von Kuhlmann, R. and Lawrence, M. G.: The impact of ice uptake of nitric acid on atmospheric chemistry, Atmos. Chem. Phys., 6, 225–235, https://doi.org/10.5194/acp-6-225-2006, 2006.
Wagner, W.: International equations for the pressure along the melting and along the sublimation curve of ordinary water substance, J. Phys. Chem. Ref. Data, 23, 515–525, 1994.
Winkler, A. K., Holmes, N. S., and Crowley, J. N.: Interaction of acetone, formaldehyde and methanol with ice surfaces between 198 and 223 K, Phys. Chem. Chem. Phys., 4, 5270–5275, 2002.
Zimmermann, S., Kippenberger, M., Schuster, G., and Crowley, J. N.: Adsorption isotherms for hydrogen chloride (HCl) on ice surfaces between 190 and 220 K, Phys. Chem. Chem. Phys., 18, 13799–13810, https://doi.org/10.1039/c6cp01962e, 2016.





