the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Light absorption properties and potential sources of particulate brown carbon in the Pearl River Delta region of China
Zhujie Li
Haobo Tan
Li Liu
Yiming Qin
Nan Wang
Yongjie Li
Mingfu Cai
Yan Ma
Chak K. Chan
Brown carbon (BrC) is a special type of organic aerosol (OA), capable of absorbing solar radiation from near-ultraviolet (UV) to visible wavelengths, which may lead to an increased aerosol radiative effect in the atmosphere. While high concentrations of OAs have been observed in the Pearl River Delta (PRD) region of China, the optical properties and corresponding radiative forcing of BrC in the PRD are still not well understood. In this work, we conducted a set of comprehensive measurements of atmospheric particulate matter from 29 November 2014 to 2 January 2015 to investigate aerosol compositions, optical properties, source origins, and radiative forcing effects at a suburban station in Guangzhou. The particle absorption Ångström exponent (AAE) was deduced and utilized to distinguish light absorption by BrC from that by black carbon (BC). The results showed that the average absorption contributions of BrC were 34.1±8.0 % at 370 nm, 23.7±7.3 % at 470 nm, 16.0±6.7 % at 520 nm, 13.0±5.4 % at 590 nm, and 8.7±4.3 % at 660 nm. A sensitivity analysis of the evaluation of the absorption Ångström exponent of BC (AAEBC) was conducted based on the Mie theory calculation assuming that the BC-containing aerosol was mixed with the core–shell and external configurations. The corresponding uncertainty in AAEBC was acquired. We found that variations in the imaginary refractive index (RI) of the BC core can significantly affect the estimation of AAEBC. However, AAEBC was relatively less sensitive to the real part of the RI of the BC core and was least sensitive to the real part of the RI of the non-light-absorbing shell. BrC absorption was closely related to aerosol potassium cation content (K+), a common tracer of biomass burning emissions, which was most likely associated with straw burning in the rural area of the western PRD. Diurnal variation in BrC absorption revealed that primary organic aerosols had a larger BrC absorption capacity than secondary organic aerosols (SOAs). Radiative transfer simulations showed that BrC absorption may cause 2.3±1.8 W m−2 radiative forcing at the top of the atmosphere (TOA) and contribute to 15.8±4.4 % of the aerosol warming effect. A chart was constructed to conveniently assess the BrC radiative forcing efficiency in the studied area with reference to certain aerosol single-scattering albedo (SSA) and BrC absorption contributions at various wavelengths. Evidently, the BrC radiative forcing efficiency was higher at shorter wavelengths.
- Article
(4406 KB) -
Supplement
(1513 KB) - BibTeX
- EndNote
Black carbon (BC) and organic carbon (OC) are dominant carbonaceous aerosol components that mainly originate from biomass burning on a global scale (Bond et al., 2004) and have caused great environmental concern in rapidly developing regions. Carbonaceous aerosols can not only exert adverse impacts on public health, similar to other particulate matters, but also significantly affect the terrestrial radiation balance with enormous uncertainties. In previous studies, BC was often considered to be the only light-absorbing species (Andreae and Gelencser, 2006), and OC was believed to only be able to scatter light, i.e., causing a cooling effect (Bond et al., 2011). Nevertheless, it has been reported that a fraction of organic aerosols (OAs) may also specifically contribute to light absorption from the near-ultraviolet (UV) to visible wavelength range, which is referred to as brown carbon (BrC) (Kirchstetter et al., 2004). BrC optical properties are strongly affected by its chemical composition and physical structure, which are related to different BrC sources. BrC can originate not only from direct emissions, including smoldering, biomass burning, or any type of incomplete fuel combustion process (Cheng et al., 2011; T. C. Bond et al., 1999), but also from secondary organic aerosol formation processes, such as aqueous phase reactions in acidic solutions (Desyaterik et al., 2013) or volatile organic compound (VOC) oxidation (Laskin et al., 2015; Sareen et al., 2010). In addition, BrC could have a complicated molecular composition and intermix with other substances, such as BC, non-absorbing OAs, and other inorganic materials, making it complicated to investigate BrC optical properties.
BC absorption is commonly assumed to cover the full wavelength range. However, the light absorption property of BrC is believed to be more wavelength-dependent, which can be represented by distinct absorption Ångström exponent (AAE) values, i.e., the power exponent of the light absorption coefficient. A typical threshold for the AAE of BC (AAEBC) of 1.6 has been recommended to distinguish BrC from BC (Lack and Cappa, 2010), and the AAE of BrC has been reported as having a wider range (2 to 7) (Hoffer et al., 2006). Based on the difference in the wavelength dependence of light absorption between BC and BrC, previous studies have applied the AAE method to differentiate light absorption by BrC through multiwavelength optical measuring apparatus, such as a three-wavelength photoacoustic soot spectrometer (PASS-3) (Lack and Langridge, 2013) and a multiwavelength Aethalometer (Olson et al., 2015). Based on the AAE method, the BrC absorption contribution has been estimated to be approximately 6 % to 41 % of total aerosol light absorption at short wavelengths, e.g., at 370 and 405 nm (Washenfelder et al., 2015). A uniform AAEBC from ∼300 nm up to ∼700 nm (Moosmüller et al., 2011) is commonly used when evaluating the BrC absorption contribution using the AAE method. However, it has been reported that the AAEBC can be influenced by the mixing state, BC core size, and morphology (Lack and Cappa, 2010). The lensing effect of the coating shell may enhance BC light absorption, the magnitude of which may also depend on wavelength and can alter the value of AAEBC (Liu et al., 2018). Moreover, different values of AAEBC have been found in the near-infrared and UV ranges (Wang et al., 2018). Therefore, using the default value of AAEBC=1 may lead to uncertainty in BrC absorption coefficient estimation.
Quantifying BrC optical absorption accurately is essential to interpret aerosol optical depth (AOD), and the corresponding aerosol direct radiative forcing (DRF) on the atmosphere can also be evaluated if the single-scattering albedo (SSA) and extinction coefficient of aerosols are known. The estimation of the DRF of BrC has shown a distinct seasonal variation, indicating the influence of different absorption properties of BrC (Arola et al., 2015). A global simulation study indicated that the average warming effect at the top of the atmosphere (TOA) caused by BrC absorption can be up to 0.11 W m−2, corresponding to ∼25 % of that predicted from BC absorption only (Feng et al., 2013).
During the last 3 decades, rapid economic development has led to severe air pollution problems in the Pearl River Delta (PRD) region (Chan and Yao, 2008). With rapid increases in the automobile population and factories, high loadings of secondary organic aerosols (SOAs) have often been observed (Tan et al., 2016b). Biofuel usage may also play a significant role during wintertime air pollution events in the PRD, indicating that the contribution from BrC light absorption cannot be ignored (Wu et al., 2018). Recently, BrC light absorption has been quantified by Qin et al. (2018) using the AAE method in the PRD region. OA chemical composition was simultaneously measured by a high-resolution time-of-flight aerosol mass spectrometer, and it was found that organic aerosols originating from biomass burning possessed the most intense absorption capability and were largely responsible for BrC absorption. Qin et al. (2018) also suggested that correlations between OA chemical compositions and BrC absorption were wavelength-dependent.
In this paper, we applied the homologous AAE differentiation method to quantify the fraction of aerosol light absorption by BrC using the measurements from a seven-wavelength Aethalometer. The potential error incurred with this methodology was determined using Mie theory simulations, especially for various complex refractive indexes of the BC core and the coating material. The correlation between BrC light absorption and water-soluble ions, which is used as the source tracer, was employed to identify potential BrC sources. An atmospheric radiative transfer model has also been applied to evaluate the impact of BrC on direct radiative forcing using surface-based aerosol optical properties and satellite-based surface-albedo data. The magnitudes of aerosol radiative forcing at the top of the atmosphere due to BC and BrC were also individually quantified.
2.1 Sampling site
Field observations were conducted at the Panyu station (23∘00′ N, 113∘21′ E), which is a monitoring site of the Chinese Meteorological Administration (CMA) Atmospheric Watch Network (CAWNET) that is located on the summit of Dazhengang Mountain (approximately 150 m above sea level) in Guangzhou, China. Figure 1 shows the location of the Panyu site, which is situated at the center of the PRD and is separated from residential areas by at least 500 m. Some agricultural fields can be found to the west of the site. Although there were no significant pollution sources nearby, this suburban site was strongly affected by pollutants transported from the urban area of Guangzhou and crop residual fires transported from the rural area of the PRD. The field campaign was conducted from 29 November 2014 to 2 January 2015. During the measurement period, aerosol light scattering and extinction, BC concentration, particle number size distribution (PNSD), OC concentration, and the water-soluble ion concentrations of PM2.5 were continuously monitored.
2.2 Measurements and data analysis
All instruments were housed inside the second-floor measurement room of a ∼5 m tall, two-story building. The ambient sample was taken on the roof by a 2 m long, 12.7 mm OD stainless steel inlet, and a PM2.5 cyclone sampler was also used. The metal tubing was thermally insulated and maintained at a constant temperature of ∼25 ∘C. A diffusion drier was also used in-line to dry the relative humidity (RH) of the air sample to below 30 % before further analysis.
2.2.1 Measurements of relevant species
A TSI-3936 scanning mobility particle sizer (SMPS) and a TSI-3321 aerodynamic particle sizer (APS) were utilized to measure the 10 to 500 nm mobility diameter and 0.5 to 2.5 µm aerodynamic diameter of the PNSD, respectively. The aerodynamic diameters of the APS data were converted into mobility diameters using a material density of 1.7 g cm−3. A detailed data merging method has been described by Cheng et al. (2006). Furthermore, the pipe diffusion loss of SMPS has been corrected using the empirical formula proposed by Kulkarni et al. (1996).
An AE-33 Aethalometer (Magee Scientific Inc.) was utilized for BC mass concentration measurement, which was derived from optical attenuation using a mass absorption cross section (MAC) of 7.77 m2 g−1 at 880 nm. The sensitivity of AE-33 was approximately 0.03 µg m−3 for a 1 min time resolution and a 5.0 liter per minute (L min−1) sample flow rate.
The PM2.5 mass concentration was measured by an environmental dust monitor (model EDM180, GRIMM Inc.), which monitored the mass concentration of PM2.5 and PM10 simultaneously.
Water-soluble ions (potassium (K+), calcium (Ca2+), magnesium (Mg2+), chloride (Cl−), sulfate (), nitrate (), and ammonium () were measured with the Monitor for AeRosols and Gases in Air (MARGA) (Model ADI2080, Metrohm Inc.), which is an online analyzer for semicontinuous measurements of gases and water-soluble ions in aerosols (Li et al., 2010). The MARGA was automatically calibrated with standard internal solutions during field measurement. The MARGA utilized its own PM2.5 sampling system provided by the manufacturer.
The OC and elemental carbon (EC) were measured by a Sunset online OC/EC analyzer (Model RT-4) with a laser transmittance-based charring correction (Wu et al., 2018, 2019). The sample flow rate of the OC∕EC analyzer was maintained at 8 L min−1. For each measurement cycle (1 h), samples were collected onto a quartz filter within the first 45 min and then thermal–optically analyzed during the remaining 15 min. First, OC was completely volatized in oxygen-free helium with a temperature ramped stepwise (600 and 840 ∘C). In the second stage, the temperature was reduced to 550 ∘C, and then EC and pyrolyzed carbon (PC) were combusted in an oxidizing atmosphere (10 % oxygen in helium), while the temperature was increased up to 870 ∘C step by step. The CO2 converted from all of the carbon components was then quantified by a nondispersive infrared absorption CO2 sensor (Lin et al., 2009). An internal calibration peak made by 5 % methane in helium was applied to quantify OC and EC. To correct the PC converted from OC to EC, a tunable pulsed diode laser beam was used to monitor the laser transmittance through the quartz filter throughout the thermal–optical analysis (Bauer et al., 2012).
2.2.2 Measurements of optical properties
Light extinction by aerosols at 532 nm was detected using a cavity ring-down aerosol extinction spectrometer (CRDS) (Model XG-1000, Hexin Inc.) by measuring the decay times of laser intensity through the aerosol-containing sample and the filtered background air sample under the same conditions. The extinction coefficient (σext) was calculated using the procedure described by Khalizov et al. (2009).
Aerosol total scattering (σsp) was measured by a TSI-3563 integrated nephelometer at three wavelengths (i.e., 450, 550, and 700 nm) and was calibrated with CO2 following the manual instructions. Particle-free air was used to check the nephelometer background signal once every 2 h. The scattering coefficients at other wavelengths were extrapolated using the following equations:
where λ0=450 nm is for wavelengths less than 550 nm and λ0=700 nm is for wavelengths greater than 550 nm. The corresponding time series of extinction coefficients, scattering coefficients, and SSA at 532 nm are displayed in Fig. S1 in the Supplement.
The Aethalometer was also used for multi-wavelength light absorption measurements in this study. The seven-wavelength aerosol light attenuation coefficients (σATN) were converted into aerosol light absorption coefficients (σabs) using Eq. (3) (Coen et al., 2010), where k is the parameter that accounts for the loading effect, ATN is the light attenuation through the filter with sample loading, and Cref is a fixed multiple scattering parameter.
The real-time k value was retrieved using the dual-spot loading correction algorithm developed by Drinovec et al. (2015). The detailed formula of ATN can also be found in Drinovec et al. (2015). Cref is considered a constant that strongly depends on the filter matrix effect. However, some studies have suggested that Cref may vary with wavelength (Arnott et al., 2005; Segura et al., 2014). For internal combustion engines and biomass burning, Cref at 370 nm was expected to be approximately 12 % and 18 % less than Cref at 532 nm for the aerosol component, respectively (Schmid et al., 2006). Different ambient observations also showed that Cref may have regional specificity, even though it was retrieved by the same methodology (Coen et al., 2010). In this study, Cref=3.29 was used in Eq. (3) at each wavelength, and this value was derived from the slope of σATN measured by the Aethalometer vs. σabs, which was deduced from the CRDS and nephelometer measurements. This Cref was also very similar to the Cref of 3.48 determined from an intercomparison study between an Aethalometer and a photoacoustic soot spectrometer during a field campaign conducted in the PRD region in 2004 (Wu et al., 2009).
The BC light absorption at certain wavelengths was derived from the absorption coefficient σabs according to Beer–Lambert's law, and its variation between different pairs of wavelengths (i.e., is denoted by the absorption AAE equation developed by Ångström (1929):
It has been suggested that the AAE of BC may vary between short and long wavelength ranges (Lack and Cappa, 2010); hence, applying a wavelength-independent AAEBC may lead to uncertainties in the BC absorption calculation from one wavelength to another. In this work, the light absorptions of BC at various wavelengths were retrieved by a modified wavelength-dependent AAE differentiation method conducted by Wang et al. (2018):
Here, represents the absorption coefficient due to only BC greater than 520 nm, and represents the absorption coefficient of BC less than 520 nm. (i=1, 2, and 3) represents the AAE of BC between a longer and shorter wavelength at λi=880, 520, and 370 nm and was calculated as
Accordingly, BrC absorption at a certain wavelength λ ( was equal to the value of total aerosol absorption (σabs,λ) minus BC absorption (:
The light absorption data at 880 nm (σabs,880 nm) were selected to represent BC absorption (, which should not be affected by BrC (Drinovec et al., 2015). It has been reported that the dust-related contributions of PM2.5 were normally less than 5 % in wintertime in Guangzhou; therefore, the influence from dust could be negligible in this study (Huang et al., 2014).
2.2.3 Estimation of AAEBC
Traditionally, AAEBC was believed to be close to 1.0 (Bodhaine, 1995), which has been commonly used for BC measurements (Olson et al., 2015). However, studies have demonstrated that AAEBC can be affected by the refractive index of coating materials, mixing state, morphology, and BC core size (Liu et al., 2015). Therefore, using the default AAEBC=1 may lead to uncertainty in BrC absorption estimation. To obtain the correct AAEBC, a series of Mie theory calculations were conducted using a simplified core–shell model (Bohren and Huffman, 1983; Wang et al., 2018). We used a modified BHCOAT code and BHMIE code to calculate the aerosol optical properties of the core–shell and external mixture at different wavelengths (Cheng et al., 2006). In the Mie theory, a particle is taken as a perfect homogeneous sphere, and its extinction and scattering efficiencies, and , respectively, are expressed as (Mie, 1908; Seinfeld and Pandis, 1998)
where is the size parameter; an and bn are functions of the complex refractive index (RI) and α in the Riccati–Bessel form, respectively. Re in Eq. (8) denotes that only the real part of RI is taken. The absorption efficiency ( is thus the difference between the extinction and scattering efficiencies:
Then, the absorption coefficient was obtained by the following (Bricaud and Morel, 1986):
where N(log Dp) is the PNSD function. A two-component parameterization of dry particles, i.e., the BC core and the non-light-absorbing species, was applied to calculate aerosol optical properties here (Wex et al., 2002). represents the RI of the BC core, and represents the RI of non-light-absorbing particles.
In a realistic atmosphere, some non-light-absorbing particles may exist independently without BC (Liu et al., 2013; Cheung et al., 2016). In this work, the portion of non-light-absorbing particles at a certain size (Dp) was determined by our previous measurements at the same site using a volatility tandem differential mobility analyzer (V-TDMA), during which completely vaporized (CV) particles at 300 ∘C were referred to as non-light-absorbing particles that externally mixed with other BC-containing particles. Thus, the PNSD of CV particles (N(logDp)CV) and BC-containing particles (N(logDp)BC) can be given by the following equations:
where N(logDp)measure is the PNSD of the measured particles from SMPS and APS. Φ(Dp)N,CV was the number fraction of CV particles in different size bins.
A previous study applied three kinds of BC mixture models to calculate the aerosol optical properties, including external, homogeneously internal, and core–shell mixtures (Bohren and Huffman, 2007; Seinfeld and Pandis, 1998). To quantify the mixing state of BC, rext was defined as the mass fraction of externally mixed BC (Mext) in total BC (MBC):
Tan et al. (2016a) suggested that two extreme conditions of external and core–shell mixtures comprised the actual mixing state of BC in the PRD. Hence, we simply divided the PNSD of BC into the PNSD from an external mixture of BC and a core–shell mixture of BC. The PNSDs of externally mixed BC particles and core–shell mixed BC particles were referred to by the following equations with a given rext.
fBC was defined as the BC volume fraction in the BC-containing particle volume, which can be converted from the BC mass concentration:
where ρBC is the density of BC and is assumed to be 1.5 g cm−3 (Ma et al., 2012); MBC is the BC mass concentration derived from the multi-angle absorption photometer (MAAP), which was obtained by an empirical formula from the Aethalometer that measured the BC concentration (MBC,AE), as proposed by Wu et al. (2009):
The PNSDs of externally mixed non-light-absorbing particles and externally mixed BC particles were input into the BHMIE code, and the PNSD of the core–shell mixed particles was imported into the BHCOAT code. Another critical parameter for the core–shell model was the diameter of the BC core. For the simplified core–shell model we applied, the visualization was that a homogeneous BC core sphere was encapsulated in a shell of non-absorbing coating (Bohren and Huffman, 2007). Without size-resolved coating thickness measurements, core–shell mixed particles simply assumed that cores with the same diameter had the same coating thickness. Therefore, the diameter of the BC core was calculated as follows:
Dcore and Dp are inputted as parameters into an and bn, respectively, which was described by Bohren and Huffman (2007). The corresponding time series of size distribution of the derived external BC and internal BC core are illustrated in Fig. S2. Thus, the values of all six wavelengths were calculated through the Mie model, and then the AAEBC values of those five wavelengths were obtained using Eq. (6). The performance of this empirically determined calculation method has been compared with other possible BC mixing schemes in detail (see Table 1).
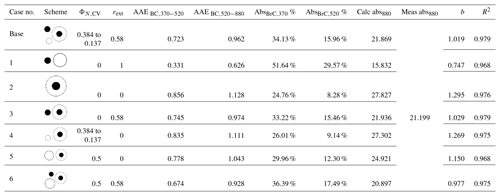
Table 1Intercomparison of the performance of various Mie-calculation schemes. Base Case is based on the empirical distribution function and mixing states of BC particles obtained from previous field measurements at the same site. ΦN,CV denotes the portion of non-BC particles, and rext is the mass portion of externally mixed BC with respect to total BC. AAEBC is the absorption Ångström exponent of BC, and the subscript represents the wavelength range. AbsBrC,370 % and AbsBrC,520 % are the BrC absorption contributions at 370 and 520 nm, respectively. Calcabs880 is the calculated absorption at 880 nm using the Mie model. Measabs880 is the measured absorption by an Aethalometer at 880 nm. b is the intercept of the regression analysis between Measabs880 and Calcabs880, i.e., Calcabs Measabs880. R2 is the correlation coefficient of the equation. The refractive index of BC core ( and non-light-absorbing particles ( is set to be 1.80–0.54i and 1.55–10−7i, respectively (Tan et al., 2016a).
2.2.4 Atmospheric radiative transfer model
In this work, the Santa Barbara DISORT Atmospheric Radiative Transfer (SBDART) model was employed to estimate the DRF of BrC absorption, i.e., its effects on the downward and upward fluxes (F in W m−2) of solar radiation at the TOA. SBDART is a software tool that can be used to compute plane-parallel radiative transfer under both clear and cloudy conditions within the atmosphere. More details about this model are found in Ricchiazzi et al. (1998). Both ground measurements and remote-sensing data were used in the simulation. The surface albedo was derived from a 500 m resolution Moderate Resolution Imaging Spectroradiometer (MODIS) Bidirectional Reflectance Distribution Function (BRDF) albedo model parameter product (MCD43A3, daily). The MCD43A3 products are the total shortwave broadband black-sky albedo (αBSA) and white-sky albedo (αWSA), while the actual surface albedo (α) was computed from a linear combination of αWSA and αBSA, which were weighted by the diffuse ratio (rd) and direct ratio (1−rd), respectively:
rd was obtained from an exponential fit of Eq. (21) based on empirical observations (Roesch, 2004; Stokes and Schwartz, 1994):
where μ0 is the cosine of the zenith angle, which is calculated by the model for any specified date, time, and latitude and longitude of the site. The surface-based aerosol optical properties, including the aerosol light absorption coefficients of both BC and BrC, i.e., differentiated from each other under the assumption of uniform AAEBC, along with the nephelometer-measured aerosol scattering coefficients, were used to calculate the SSA at different wavelengths according to Eq. (22):
This was then used in the model calculation. Finally, the AOD and asymmetry factor (ASY) at 440, 675, and 870 nm were derived from the Aerosol Robotic Network (AERONET) measurements at the Hong Kong Polytechnic University site (Holben et al., 1998), which is approximately 115 km to the southeast of the Panyu site. The tropical atmospheric profile was used in the SBDART model based on the prevailing weather conditions in the PRD. The aerosol DRF (ΔF) was calculated as the difference between the downward and upward radiation fluxes:
3.1 Aerosol light absorption
The AAEBC is widely defined as the uniform representation of the wavelength dependence of a BC particle (Olson et al., 2015). In reality, AAEBC may vary significantly with BC-containing aerosols of different sizes, mixing states, and morphologies (Lack and Langridge, 2013; Scarnato et al., 2013). In fact, some studies showed that the AAE of a large size, pure BC core may be less than 1.0 (Liu et al., 2018) and that the AAE of BC coated with a non-absorbing shell may be larger than that under uniformity (Lack and Cappa, 2010).
It has been suggested that a significant fraction of smaller size particles is non-BC-containing (Cheung et al., 2016; Ma et al., 2017). BC and non-BC materials can also be externally or internally mixed. Although size-resolved BC measurements were not available during this work, we conducted size-resolved V-TDMA measurements at 300 ∘C for 40, 80, 110, 150, 200, and 300 nm during an earlier field campaign (February 2014) at the same site as in this work. At 300 ∘C, all non-BC particles will be completely vaporized (CV), and thus the portion of non-BC particles at such size, denoted as ΦN,CV, can be determined. The average ΦN,CV values were 0.384, 0.181, 0.180, 0.158, 0.143, and 0.137, corresponding to 40, 80, 110, 150, 200, and 300 nm (see Fig. S3), respectively (Cheung et al., 2016; Tan et al., 2016a). The ΦN,CV values for other sizes were interpolated linearly from these six diameters. For particle sizes larger than 300 nm and less than 40 nm, ΦN,CV values were set to 0.137 and 0.384, respectively. Accordingly, the complete distribution of ΦN,CV for the whole PNSD was obtained. The mixing states of BC particles were also estimated here, i.e., the mass portion of externally mixed BC with respect to total BC, denoted as rext. The value of rext was taken as 0.58, which was obtained using an optical closure method during a previous field experiment at this site (Tan et al., 2016a). During the following Mie theory calculation, a fixed refractive index (–0.54i, –10−7i) was adopted for the whole size range. Accordingly, the calculated BC absorption at 880 nm (Abs880) was 21.869 Mm−1, which is reasonably close to the measured mean value of 21.199 Mm−1. To further validate our calculation scheme (Base Case), we have considered several extreme cases.
-
Case 1: BC is completely externally mixed with non-BC particles, i.e., and rext=1;
-
Case 2: BC is present in every size bin and BC is completely internally mixed with non-BC material, i.e., and rext=0;
-
Case 3: BC is both internally and externally mixed, but there are no non-BC-containing particles, i.e., and rext=0.58;
-
Case 4: BC is internally mixed with non-BC material and there are non-BC particles present, i.e., ΦN,CV ranges from 0.384 to 0.137 and rext=0;
-
Case 5: the same as Case 4 except assuming a fixed non-BC to BC ratio of 0.5, i.e., , rext=0;
-
Case 6: the same as Case 5 except that some externally mixed BC is also present, i.e., , rext=0.58.
The calculation results are listed in Table 1. Evidently, Case 1 (completely externally mixed) will significantly underestimate the measured Abs880, indicating that most BC particles were not likely externally mixed at the Panyu site. The complete internal mixing state (Cases 2, 4, and 5), by contrast, would substantially overestimate the BC absorption regardless of the form of the BC core distribution function. However, when the rext was considered (Base Case, Case 3, and Case 6), the calculated Abs880 values were all very close to the measured value, especially the Base Case.
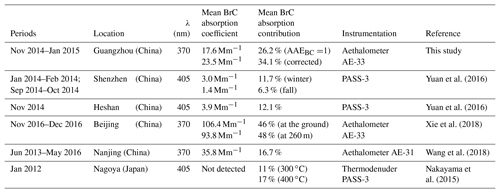
When the AAEBC was assumed to be uniform, the campaign-averaged σBrC values were 17.6±13.7 Mm−1 at 370 nm, 9.7±7.9 Mm−1 at 470 nm, 5.8±5.1 Mm−1 at 520 nm, 4.0±3.5 Mm−1 at 590 nm, and 2.3±2.1 Mm−1 at 660 nm. At the corresponding wavelengths, BrC absorption contributed 26.2 % ± 8.5 %, 20.0 % ± 7.3 %, 14.3 % ± 6.5 %, 11.7 % ± 5.3 %, and 7.8 % ± 4.1 % to the total aerosol absorptions. When the AAEBC was applied as the result of the Mie model calculation, the corrected campaign-averaged σabs,BrC values were 23.5±17.7 Mm−1 at 370 nm, 11.8±9.5 Mm−1 at 470 nm, 6.7±5.7 Mm−1 at 520 nm, 4.6±3.9 Mm−1 at 590 nm, and 2.6±2.3 Mm−1 at 660 nm. At the corresponding wavelengths, BrC absorption contributed 34.1 % ± 8.0 %, 23.7 % ± 7.3 %, 16.0 % ± 6.7 %, 13.0 % ± 5.4 %, and 8.7 % ± 4.3 % to the total aerosol absorption (see Fig. 2). Evidently, aerosol light absorption was predominantly due to BC; however, BrC also played a significant role, especially at shorter wavelengths. Table 2 shows the intercomparison of BrC light absorption in the near UV range between this work and other studies in the East Asian region. Clearly, the reported values vary substantially, and our result is toward the lower end of values. Figure S4 displays the time series of particle AAE measured by the Aethalometer, and AAEBC was derived from Mie model calculation. The AAEBC was almost always lower than AAE, indicating appreciable BrC light absorption at the Panyu site.
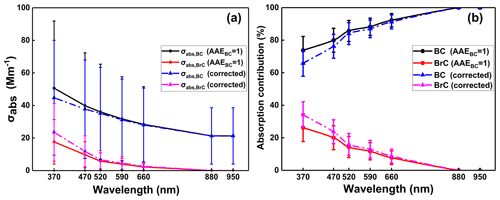
Figure 2(a) BC and BrC particle average light absorption coefficients at different wavelengths under different AAEBC assumptions; the whiskers represent an error of 1 standard deviation. (b) Contributions of BC and BrC to the total light absorption coefficient at different wavelengths under different AAEBC assumptions; the whiskers represent an error of 1 standard deviation.
3.2 Uncertainty in BC and BrC optical differentiation
Theoretically, the magnitude of BC absorptions can be affected by both parts of the complex RIs; thus, AAEBC may also vary with the RIs of both the BC core and coating shell. In fact, RI was also one of the least known properties of BC and other coating materials with negligible absorbing capabilities. The refractive index of the BC core ( displays a wide range of variations (Liu et al., 2018). Typically, the real and imaginary parts of the RI can vary from 1.5 to 2.0 and 0.5 to 1.1, respectively. In addition, the shell was assumed to consist of non-absorbing material in the core–shell model; i.e., its imaginary RI was set to be close to zero (10−7). The real part of the non-absorbing material RI ( may vary from 1.35 to 1.6 due to the presence of OA (Redmond and Thompson, 2011; Zhang et al., 2018) and inorganic salts (Erlick et al., 2011). Hence, it is necessary to investigate the uncertainties associated with the variations in AAEBC by varying the RIs of both the BC core and the non-absorbing materials.
Figure 3 shows the impacts of RI on the evaluations of AAEBC based on core–shell and external configuration, where the RI of the BC core was set to be constant, i.e., –0.54i, and the real part of varied from 1.35 to 1.6 at an interval of 0.05, with the imaginary part of set at 10−7. As shown in Fig. 3a, the calculated AAEBC for the core–shell model was higher than 1.0 at longer wavelengths (520 to 880 nm) and lower than 1.0 at shorter wavelengths (370 to 520 nm) (the red line in Fig. 3 denotes AAEBC=1). The averaged AAE ranged from 0.84 to 0.87, and the AAE ranged from 1.07 to 1.15, indicating that the AAE appeared to be more sensitive to the shell's real part than AAE. Even if the shell material was assumed to be non-absorbing, the variation in the real RI of the shell, which was referred to as the real part of , still led to changes in the shell's refractivity and correspondingly altered its lensing effect, causing a change in AAEBC. Meanwhile, AAE and AAE generally increased with an increasing real part of the shell. In Fig. 3b, under the externally mixed conditions, AAE and AAE were both less than 1.0. The average AAE was 0.33, and the average AAE was 0.63. These values were far less than the values under core–shell mixture conditions. In the external mixture model, the BC core and non-light-absorbing materials were assumed to exist dependently, and then the optical properties of these two components were considered separately. Therefore, altering the real part of the externally mixed non-absorbing material would not affect the light absorption property of the BC core or AAEBC.
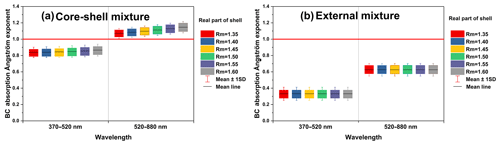
Figure 3Influence of the wavelength-independent refractive index of the non-absorbing materials on the (a) AAEs of the core–shell mixture and (b) AAEs of the external mixture with a constant BC core refractive index (–0.54i). The imaginary part of the non(less)-absorbing shell was set to 10−7, while the real part varied from 1.35 to 1.60. In each panel, the boundaries of the box represent the 75th and 25th percentiles; the whiskers above and below each box indicate an error of 1 standard deviation; the black lines in the boxes denote the average values. In panels (a) and (b), the red line indicates where AAEBC=1.
The impacts of the BC core on AAEBC are shown in Fig. 4, where the refractive index of non-light-absorbing materials was assumed to be and was wavelength-independent. Figure 4 was obtained with a core–shell mixture model (Fig. 4a and b) and an external mixture model (Fig. 4c and d) by varying the real part of from 1.5 to 2.0 with a step of 0.05 and varying the imaginary part of the from 0.4 to 1.0 with a step of 0.05. As shown in Fig. 4a and b, for the core–shell mixture, the averaged AAE ranged from 0.55 to 0.99 and the averaged AAE ranged from 0.84 to 1.27. The AAEBC at a certain wavelength generally increased when increasing the real part of but decreased when increasing the imaginary part of . The AAEBC appeared to be more sensitive to the imaginary part of than the real part of because the imaginary part of was directly related to the light-absorbing properties of particles. In Fig. 4c and d, for the external mixture, the averaged AAE ranged from 0.04 to 0.45 and the averaged AAE ranged from 0.28 to 0.79, while the averaged AAE and AAE were both less than 1.0. Similar to the core–shell mixture, the AAE increased when increasing the real part of but decreased when increasing the imaginary part of . However, the variation patterns of AAE were different from those of AAE. The AAE values were not changed by altering the real part of within the low imaginary part of , whereas the AAE values still increased when increasing the real part of within the high imaginary part of . A possible explanation was that the externally mixed BC core had weak light absorption within the low imaginary part of , causing the AAE values to be insensitive to the real part of . The AAE values were higher than the AAE values regardless of whether they were for the core–shell mixture or the external mixture. In addition, the AAEBC values conducted by the core–shell mixture were higher than those conducted by the external mixture.
Figure 4 demonstrated that the variation in the imaginary RI of the BC core had the most significant impact on the estimated AAEBC, indicating that the chemical component of BC emitted from different sources led to a large uncertainty in AAEBC estimation. At the same time, the influence arising from varying the real RI of the BC core was relatively moderate. Nevertheless, Fig. 3 shows that change in the real RI of the non-absorbing materials caused the least or no impact compared to the variations in the complex RI of the BC core.
It should be pointed out that most BC-containing particles are often observed as being fractal rather than spherical in shape (Katrinak et al., 1993). Because the Mie model assumes that all particles are spherical, it may lead to potential uncertainty for the estimation of AAEBC and BrC absorption contributions. Moreover, the externally mixed soot aggregates were “chain-like” or “puff-like” in the PRD dry season (Feng et al., 2010), in which the fractal dimension (Df) was between 1.5 and 2.0. Coating soot aggregates were likely spheres (Df approaches 3) from the high-resolution transmission electron microscopy (TEM) measurements taken in Hong Kong (Zhou et al., 2014). A soot aggregate sensitivity study with the superposition T-matrix method indicated that using the assumption of volume-equivalent spheres for the soot aggregates may result in an overestimation of approximately up to 15 % and an underestimation of approximately up to 50 % in the predicted 870 nm light absorption when the Df is between 1.5 and 3.0 (Liu et al., 2008). However, it should be recognized that the complex shapes or positions of the BC core inside the particle make it impractical to be numerically simulated in the exact details. By far the Mie model with a core–shell configuration would be the most practical and effective simulation scheme for BC particle optical property simulation.
Furthermore, we have performed Monte Carlo simulations to evaluate the uncertainties of the Mie calculation performed during this work. In the simulation, a sequence of random numbers or errors were applied to the input parameters, and then the corresponding uncertainties of particle light absorption and AAEBC were computed using the Mie model. Five hundred reiterations were conducted during the simulation such that the random errors will be normally distributed. The standard deviations (σ) of all input parameters are listed in Table S1. In order to cover the effect of extreme value, we used a range of ±3σ, or a confidence level of 99 %, in the Monte Carlo simulation. Table S2 lists the Monte Carlo simulation results, i.e., the average relative standard deviations (σMie) of the calculated BC light absorption at 880 nm (Abs880), AAE, and AAE. The uncertainties of the calculated Abs880, AAE, and AAE at two times of σMie, i.e., at a confidence level of 95 %, were approximately ±31 %, ±16 %, and ±13 %, respectively. Figure S5a shows the time series of the uncertainties of Abs880, AAE, and AAE from a Monte Carlo simulation for the campaign period. These uncertainties will certainly be propagated into the calculated BrC absorption contributions, too. Hence, we also estimated the corresponding uncertainties in the BrC absorption contribution results, as shown in Fig. S5b. Accordingly, the averaged lower limits of BrC absorption contributions were 26.8 % ± 9.1 % at 370 nm, 17.5 % ± 8.1 % at 470 nm, 10.1 % ± 7.3 % at 520 nm, 8.5 % ± 5.8 % at 590 nm, and 5.3 % ± 4.5 % at 660 nm, and the averaged upper limits of BrC absorption contribution ratios were 40.7 % ± 7.2 % at 370 nm, 29.5 % ± 6.7 % at 470 nm, 21.1 % ± 6.2 % at 520 nm, 17.3 % ± 5.2 % at 590 nm, and 12.0 % ± 4.1 % at 660 nm.
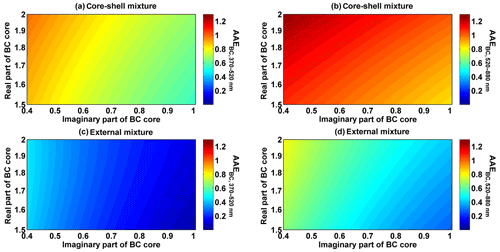
Figure 4Influence of the wavelength-independent refractive index of the BC core on AAEs with a constant shell refractive index (. A core–shell mixture was used for panels a and b, and an external mixture was used for panels c and d. The real part of varied from 1.5 to 2.0, with a step of 0.05, and the imaginary part of varied from 0.4 to 1.0, with a step of 0.05.
3.3 Characteristics of BrC light absorption, water-soluble ions, and OC concentrations
Globally, BrC has been observed to be highly correlated with biomass and biofuel burning emissions (Laskin et al., 2015). Since large quantities of sylvite are present in biomass burning particles, the K+ abundance has often been used as a biomass burning tracer (Levine, 1991). Figure 5 presents the time series of the OC mass concentration, K+ concentration, and BrC absorption from 29 November 2014 to 2 January 2015 at the Panyu site. The range of the OC concentrations obtained from the OC∕EC online analyzer was from 1.5 to 65.2 µg cm−3, and the campaign average was 12.5±7.3 µg cm−3. The BrC absorption hourly mean data were between 0.2 and 123.2 Mm−1, and the campaign average was 23.5±17.7 Mm−1. On the other hand, the average K+ concentration was 1.0±0.7 µg cm−3 (ranging from 0 to 5.4 µg cm−3). Clearly, similar trends among OC, K+, and BrC absorption can be seen during this field campaign (Fig. 5).
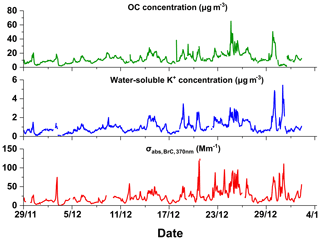
Figure 5Time series of the OC aerosol mass concentration (green line), water-soluble K+ mass concentration (blue line), and BrC light absorption (red line).
To investigate the origins of these observed OC, K+, and BrC, wind rose plots (as shown in Fig. 6) were generated for OC, K+, and BrC absorption, respectively. All three panels of Fig. 6 consistently show that the three substances were associated with the same wind pattern. For the entire campaign period, the highest values of OC, K+, and were mostly associated with southwesterly winds with a relatively low wind speed (∼2 m s−1). The relatively higher OC and K+ concentrations were highly related to the seasonal straw burning in the countryside of the PRD located to the west of the Panyu station. In contrast, OC and K+ concentrations during periods with easterly winds were substantially lower than those during periods with westerly winds. The wind rose plot of is shown in Fig. 6c. Similar to OC and K+, showed higher values under weak (<2 m s−1) westerly winds and lower values from the north and south, indicating that BrC absorption was likely attributed to local sources and was accumulated under calm wind conditions. Figure S6 shows the 3 d backward trajectory and the fire counts for 5 to 7 (Fig. S6a), 12 to 14 (Fig. S6b), and 24 to 26 (Fig. S6c) in November 2014, representing low-loading, moderate-loading, and high-loading period. Clearly, the high-loading period concurred with stagnant air movement and higher fire counts, indicating the contribution from open fire burning sources. However, there was a detectable difference among the three rose plots of Fig. 6 in the maximum concentration direction. A possible explanation was that although biomass burning emissions were believed to be the dominant and primary source of OC, K+, and BrC, their emission ratios were highly variable and may change with the type of biofuel and burning condition and may even vary during different stages of burning (Burling et al., 2012). Although biomass burning emissions contain substantial light-absorbing BrC, further atmospheric aging processes may significantly reduce its light-absorbing capability (Satish et al., 2017). Moreover, secondary formation may also lead to BrC formation inside these primary aerosols, such as humic-like substances formed through aqueous-phase reactions, which have been suggested to be an important component of BrC (Andreae and Gelencser, 2006).
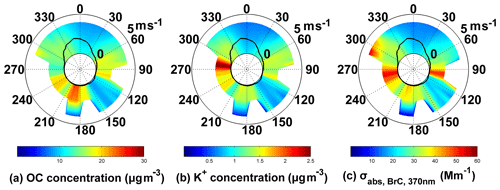
Figure 6Wind rose plots of OC (a), K+ (b), and (c). In each panel, the black solid lines denote the frequency of the wind direction. The shaded contour represents the average values of the corresponding species for that wind speed (radial length) and wind direction (transverse direction) in polar coordinates.
To further explore the possible sources of BrC optical absorption, the diurnal variations in OC, K+, , and /OC values are plotted in Fig. 7. The diurnal variation in OC at the Panyu site appeared to be dominated by the development of the planetary boundary layer (PBL) height; i.e., primary emissions accumulated at night and were swiftly diluted by vertical mixing in the morning. The slight increase in OC in the afternoon indicated that photochemistry may have still weakly contributed to SOA formation. Figure 7b shows the diurnal variation in K+. Unlike OC, K+ shows a small peak at approximately 06:00, which was consistent with breakfast time and was very likely due to cooking activities using biofuel. No lunch and dinnertime K+ peaks were observed. The most likely explanation is that the boundary layer height is much higher during lunch and dinnertime than in the early morning, providing a much better atmospheric diffusion condition for air pollutants. It is still a common practice to collect straw as biofuel in local rural areas, which can be visually spotted but is not heavily utilized in the region. However, the diurnal profile of (see Fig. 7c) shows the combined features of OC and K+ since both primary and secondary processes affect its intensity. The nighttime increasing trend was most likely attributed to straw burning activities in early winter in nearby rural areas that continued to accumulate within the shallow PBL (Jiang et al., 2013). /OC, i.e., the mass absorption coefficient of BrC (MACBrC) (Fig. 7d), showed a relatively flat pattern, with a pronounced dip in the afternoon and higher values at nighttime, which was likely due to enhanced primary emissions and stable stratification at nighttime. Declining trends during the late morning and afternoon hours indicated that the aging process and photochemical production may reduce the light-absorbing capacity of BrC (Qin et al., 2018).
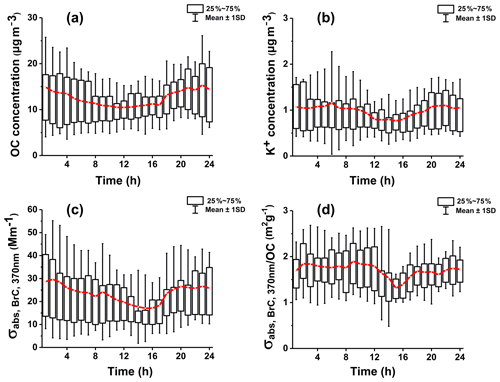
Figure 7Box–whisker plots of diurnal trends in the OC concentration (a), water-soluble K+ concentration (b), (c), and /OC (d). The red traces represent the variation in the average value. The upper and lower boundaries of the box represent the 75th and 25th percentiles, respectively; the whiskers above and below each box represent an error of 1 standard deviation.
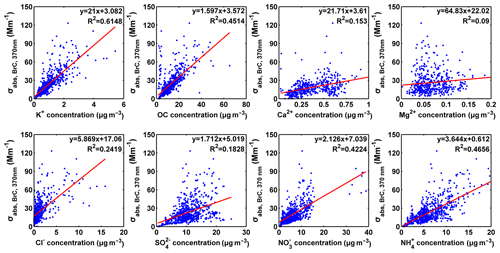
Furthermore, Fig. 8 shows the linear regression analysis results used to evaluate the correlations of with the OC, K+, Ca2+, Mg2+, Cl−, , , and concentrations. The best correlations can be found between and K+ (R2=0.6148), followed by those between and OC (R2=0.4514), (R2=0.4224), and (R2=0.4656). Source apportionment analysis of OA and BrC absorption in Beijing and Guangzhou illustrated that biomass burning organic aerosols (BBOAs) correlated well with BrC light absorption (Qin et al., 2018; Xie et al., 2019). Thus, the significant correlation between BrC absorption and K+ reaffirmed that biomass burning was the crucial emission source of BrC observed in this work. Although the geographic location of the observation site was situated in a coastal area and K+ could also be found in sea salt (Pio et al., 2008), it should be noted that the prevailing wind direction during winter was from the north (see Fig. S6), which drives maritime air parcels away from the site. Hence, the effect of sea salt and crustal materials to K+ was slight, which was demonstrated in the Supplement as shown in Fig. S7. Other earlier studies also suggested that the sea salt contribution to the K+ concentrations of PM2.5 was trivial in the PRD region during the winter (Lai et al., 2007). Another possible K+ source was coal combustion. The coal consumption in the PRD region was dominated by coal-fired power plants. The emission from power plants was usually very steady and was less likely to affect the diurnal correlation between K+ and BrC absorption. As shown in Fig. S8, the ratios of vary approximately from 0.015 and 0.020 and the diurnal profile of shows very little variation. Yu et al. (2018) have suggested that K+ usually accounted for 2.34 %–5.49 % of PM2.5 in the laboratory biomass burning study. However, K+ was normally lower than 1 % of coal combustion PM2.5. Therefore, the ratio range of K+ to PM2.5 observed in this work likely indicated aged biomass burning particles. Both nitrogen oxides (NOx) and ammonia (NH3) can be found in biomass burning plumes (Andreae and Merlet, 2001). For and , nitrate can be converted from NOx through atmospheric reactions, and ammonium may originate from NH3. However, similar to the diurnal variation in , diurnal variations in and also increased in the afternoon and appeared at nighttime in Fig. S8. However, and reached their peaks at noon, indicating that ammonium nitrate formed from the secondary reaction at this time. Along with the reduced boundary layer height and ambient temperature, was accumulated until the photochemical reaction stopped at night. The diurnal variation in was similar to that in due to the acid–base neutralization reaction. The overlapping of the , , and diurnal variations would lead to a significant correlation between BrC absorption and or . High concentrations of Ca2+ and Mg2+ are often found in dust-related aerosols (Lee et al., 1999). showed poor correlations with both Ca2+ and Mg2+, indicating that dust-related aerosol components contribute insignificantly to the total aerosol mass loading and, thus, dust may not affect the AAE differentiation method used in this work. Although sulfur dioxide (SO2) may also be emitted by biomass burning, is often believed to be secondary in nature, and the presence of other intense SO2 sources (e.g., automobile and industrial emissions) further reduces the correlation between BrC and . Sources of Cl− include both combustion and sea salt spray (Waldman et al., 1991). Although the prevailing wintertime wind direction was from the north, sea salt can still be carried to the site by a weak sea breeze, and thus Cl− may not show considerable correlation with BrC.
3.4 BrC radiative forcing efficiency
The radiative effects of aerosol scattering, BrC absorption, and BC absorption were investigated by the SBDART model. For each investigated variable under cloud-free conditions, we run the model twice to calculate the DRF at the TOA with and without the investigated variable. Accordingly, the difference of ΔF between the two simulations was considered as the radiative effect of the investigated variable. The results showed that the average radiative forcings at the TOA by scattering, BrC absorption, and BC absorption were W m−2, 2.3±1.8 W m−2, and 10.9±5.1 W m−2, respectively. Furthermore, BrC absorption was attributed to 15.8 % ± 4.4 % of the warming effect caused by aerosol light absorption, demonstrating the nonnegligible role of BrC in radiative forcing evaluation.
We also calculated the BrC radiative forcing efficiency (RFE) under various SSAs (ranging from 0.70 to 0.99) at three wavelengths, i.e., 440, 675, and 870 nm. The RFE was denoted as the radiative forcing normalized by the AOD. The average AOD and ASY at the three wavelengths were 0.365 and 0.691 at 440 nm, 0.212 and 0.632 at 675 nm, and 0.154 and 0.619 at 870 nm. A solar zenith angle of 55∘ and an average shortwave broadband surface albedo (0.119) were used in the calculation. The results were plotted as a set of RFE lookup charts as a function of the surface BrC absorption contribution (see Fig. 9).
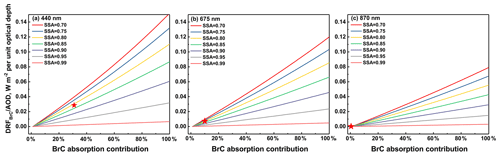
Figure 9BrC radiative forcing efficiencies, which are defined as the BrC TOA direct radiative forcing divided by the AOD, as a function of the BrC-to-total-aerosol absorption ratio and SSA measured at the surface. The average AOD of the three wavelengths, the average ASY of the three wavelengths, a solar zenith angle of 55∘, and average shortwave broadband surface albedo were used in the calculation. The red star corresponds to the average SSA and BrC absorption contributions determined from this campaign.
In general, for any wavelength, the RFE increased with increasing BrC absorption contribution for a certain SSA, indicating that BrC was a more efficient radiative forcing agent due to the preferential absorbance of BrC in a shorter wavelength range. However, for a certain BrC absorption contribution, the RFE increased with decreasing SSA; i.e., a higher portion of light-absorbing aerosol components can lead to more efficient radiative forcing. The trend among panels (a), (b), and (c) in Fig. 9 demonstrated that the effect of BrC absorption contribution on RFE was wavelength-dependent; i.e., BrC was a weaker radiative forcing agent at longer wavelengths, which is also consistent with the wavelength-dependent light-absorbing property of BrC. The red stars in Fig. 9 denote the average SSA and BrC absorption contribution conditions during this campaign, i.e., 0.029 W m−2 per unit AOD at 440 nm (Fig. 9a), 0.007 W m−2 per unit AOD at 675 nm (Fig. 9b), and 0.0002 W m−2 per unit AOD at 870 nm (Fig. 9c). These results suggested that the average value of RFE decreased distinctly from 440 to 870 nm not only because of the lower BrC absorption contribution but also because of the wavelength dependence of the BrC RFE. It should also be noted that the simulations were based on SSA measured under dry conditions. Under the typical ambient conditions of the PRD, the SSA might be markedly enhanced by aerosol water uptake (Jung et al., 2009), and then the BrC radiative forcing efficiency might be less. Moreover, Fig. 9 also serves as a lookup table to conveniently assess the BrC radiative forcing efficiency at different wavelengths with different BrC absorption contributions for a certain SSA.
In this work, light absorption due to BrC in the PRD region of China was quantitatively deduced during the winter season of 2014. The AAEs of ambient particles and BC core were derived from the measurements. For ambient particles, AAE370−520 nm and AAE520−880 nm ranged from 0.81 to 2.31 and 0.91 to 2.13, respectively. In the case of BC, AAE and AAE ranged from 0.59 to 0.98 and 0.82 to 1.15, respectively. Using the absorption coefficients of BC calculated according to the Mie theory and the observed total aerosol absorption coefficients, we estimated the AAEBC and hence the BrC absorption contribution for the optically equivalent mixture configuration. The average BrC light absorption contribution ranged from 8.7 % ± 4.3 % at 660 nm up to 34.1 % ± 8.0 % at 370 nm when AAEBC was set as uniform. The sensitivity of AAEBC estimation associated with different RI and mixing state assumptions was further investigated. The results showed that variations in the real RI of the non-absorbing material (1.35 to 1.6) may increase AAE from 0.84 to 0.87 and AAE from 1.07 to 1.15 for core–shell mixtures, with an AAE of 0.33 and AAE of 0.63 for external mixtures. Variations in the core's real RI (1.5 to 2.0) and imaginary RI (1.0 to 0.4) may increase AAE from 0.55 to 0.99 and AAE from 0.84 to 1.27 for the core–shell mixture and increase AAE from 0.04 to 0.45 and AAE from 0.28 to 0.79 for the external mixture. These results indicate that the optical properties of the BC core and non-absorbing material can significantly affect the accuracy of AAEBC and corresponding BrC absorption contribution estimations. Compared to the values of BrC light absorption coefficient and BrC light absorption contribution from other similar studies conducted in the East Asia region, the BrC measured in this work showed relatively lower values of light absorption coefficient but was found to be responsible for relatively higher portion of light absorption. It should be noted that the calculated BrC light absorption may vary exponentially with the value of AAEBC. According to Monte Carlo simulations under 95 % confidence level, we found that BrC light absorption contribution ratios in this work can range roughly from 18 % to 48 % at 370 nm, 10 % to 37 % at 470 nm, 3 % to 27 % at 520 nm, 3 % to 22 % at 590 nm, and 1 % to 16 % at 660 nm. Therefore, proper values of AAEBC have to be carefully obtained for a particular study area, especially needing to be constrained by the BC mass concentration, size distribution, and mixing state measurements.
Additionally, the measurements of major water-soluble inorganic ions (including K+, , and ) and particulate OC showed consistent features with those of , implying that BrC was associated with biomass burning emissions from nearby rural areas. Moreover, the diurnal trend in ∕OC indicated that primary biomass burning emissions can produce intense light-absorbing BrC, while the photochemical aging process may weaken the light-absorbing capability of BrC.
Using a radiative transfer model (i.e., SBDART), we estimated the BrC effects on aerosol radiative forcing. The average shortwave aerosol direct radiative forcings due to scattering, BrC absorption, and BC absorption at the TOA were evaluated to be W m−2, 2.3±1.8 W m−2, and 10.9±5.1 W m−2, respectively. BrC absorption accounted for 15.8 % ± 4.4 % of the total shortwave solar absorption warming effect at the TOA, indicating that BrC might be an important climate forcing agent, which is largely neglected in current climate models. To facilitate the estimation of the climate effects of BrC, a set of lookup charts was constructed for the investigated area based on the default tropical atmosphere profile, average surface albedo, average asymmetry factor, and surface-measured aerosol properties (i.e., BrC absorption contribution, SSA, and AOD). Therefore, the role of the BrC radiative forcing efficiency at three wavelengths can be conveniently assessed for certain SSA and BrC absorption contributions.
The field observation data and modeling parameters used in this study have been given as tables and time series plots in the Supplement. The sun photometer measurement data were acquired from the website of AERONET (https://aeronet.gsfc.nasa.gov/, last access: 3 August 2018; Nichol and Wong, 2005) and the surface albedo data were acquired from the website of MODIS (https://search.earthdata.nasa.gov/, last access: 23 August 2018; LP DAAC, 2000).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-19-11669-2019-supplement.
HT, JZ, YM, and CC designed the experiments, and ZL, LL, YQ, NW, FL, YL, and MC carried out the field measurements and data analysis. ZL and YQ performed Mie theory simulation. ZL, JZ, and HT prepared the paper with comments from all coauthors.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Multiphase chemistry of secondary aerosol formation under severe haze”. It is not associated with a conference.
This work is supported by the National Key Project of MOST (2016YFC0201901, 2016YFC0203305, and 2016YFC0202401), the National Natural Science Foundation of China (41575122 and 41730106), and the National Research Program for Key Issues in Air Pollution Control (no. DQGG0103). We are also deeply thankful for Cheng Wu and the staff at the Hong Kong Polytechnic University site of AERONET.
This research has been supported by the Ministry of Science and Technology of the People's Republic of China (grant nos. 2016YFC0201901, 2016YFC0203305, and 2016YFC0202401), the National Natural Science Foundation of China (grant nos. 41575122 and 41730106), and the National Research Program for Key Issues in Air Pollution Control (no. DQGG0103).
This paper was edited by Jingkun Jiang and reviewed by three anonymous referees.
Andreae, M. O. and Gelencsér, A.: Black carbon or brown carbon? The nature of light-absorbing carbonaceous aerosols, Atmos. Chem. Phys., 6, 3131–3148, https://doi.org/10.5194/acp-6-3131-2006, 2006.
Andreae, M. O. and Merlet, P.: Emission of trace gases and aerosols from biomass burning, Global Biogeochem. Cy., 15, 955–966, 2001.
Ångström, A.: On the Atmospheric Transmission of Sun Radiation and on Dust in the Air, Geograf. Annal., 11, 156–166, 1929.
Arnott, W. P., Hamasha, K., Moosmüller, H., Sheridan, P. J., and Ogren, J. A.: Towards Aerosol Light-Absorption Measurements with a 7-Wavelength Aethalometer: Evaluation with a Photoacoustic Instrument and 3-Wavelength Nephelometer, Aerosol Sci. Technol., 39, 17–29, https://doi.org/10.1080/027868290901972, 2005.
Arola, A., Schuster, G. L., Pitkänen, M. R. A., Dubovik, O., Kokkola, H., Lindfors, A. V., Mielonen, T., Raatikainen, T., Romakkaniemi, S., Tripathi, S. N., and Lihavainen, H.: Direct radiative effect by brown carbon over the Indo-Gangetic Plain, Atmos. Chem. Phys., 15, 12731–12740, https://doi.org/10.5194/acp-15-12731-2015, 2015.
Bauer, J. J., Yu, X.-Y., Cary, R., Laulainen, N., and Berkowitz, C.: Characterization of the Sunset Semi-Continuous Carbon Aerosol Analyzer, J. Air Waste Manag. Assoc., 59, 826–833, https://doi.org/10.3155/1047-3289.59.7.826, 2012.
Bodhaine, B. A.: Aerosol absorption measurements at Barrow, Mauna Loa and the south pole, J. Geophys. Res.-Atmos., 100, 8967–8975, 1995.
Bohren, C. F. and Huffman, D. R.: Wiley: Absorption and Scattering of Light by Small Particles – Craig F. Bohren, Donald R. Huffman, Optics & Laser Technology, 31, 328–328, 1983.
Bohren, C. F. and Huffman, D. R.: Absorption and Scattering of Light by Small Particles, WILEY-VCH Verlag GmbH & Co, KGaA, 328–328 pp., 2007.
Bond, T. C., Bussemer, M., Wehner, B., Keller, S., Charlson, R. J., A., and Heintzenberg, J.: Light Absorption by Primary Particle Emissions from a Lignite Burning Plant, Environ. Sci. Technol., 33, 3887–3891, 1999.
Bond, T. C., Streets, D. G., Yarber, K. F., Nelson, S. M., Woo, J. H., and Klimont, Z.: A technology-based global inventory of black and organic carbon emissions from combustion, J. Geophys. Res.-Atmos., 109, 43, https://doi.org/10.1029/2003jd003697, 2004.
Bond, T. C., Zarzycki, C., Flanner, M. G., and Koch, D. M.: Quantifying immediate radiative forcing by black carbon and organic matter with the Specific Forcing Pulse, Atmos. Chem. Phys., 11, 1505–1525, https://doi.org/10.5194/acp-11-1505-2011, 2011.
Bricaud, A. and Morel, A.: Light attenuation and scattering by phytoplanktonic cells: a theoretical modeling, Appl. Opt., 25, 571, https://doi.org/10.1364/ao.25.000571, 1986.
Burling, I. R., Yokelson, R. J., Akagi, S. K., Urbanski, S. P., Wold, C. E., Griffith, D. W. T., Johnson, T. J., Reardon, J., and Weise, D. R.: Corrigendum to “Airborne and ground-based measurements of the trace gases and particles emitted by prescribed fires in the United States” published in Atmos. Chem. Phys., 11, 12197–12216, 2011, Atmos. Chem. Phys., 12, 103–103, https://doi.org/10.5194/acp-12-103-2012, 2012.
Chan, C. K. and Yao, X.: Air pollution in mega cities in China, Atmos. Environ., 42, 1–42, https://doi.org/10.1016/j.atmosenv.2007.09.003, 2008.
Cheng, Y., He, K.-B., Zheng, M., Duan, F.-K., Du, Z.-Y., Ma, Y.-L., Tan, J.-H., Yang, F.-M., Liu, J.-M., Zhang, X.-L., Weber, R. J., Bergin, M. H., and Russell, A. G.: Mass absorption efficiency of elemental carbon and water-soluble organic carbon in Beijing, China, Atmos. Chem. Phys., 11, 11497–11510, https://doi.org/10.5194/acp-11-11497-2011, 2011.
Cheng, Y. F., Eichler, H., Wiedensohler, A., Heintzenberg, J., Zhang, Y. H., Hu, M., Herrmann, H., Zeng, L. M., Liu, S., Gnauk, T., Brüggemann, E., and He, L. Y.: Mixing state of elemental carbon and non-light-absorbing aerosol components derived from in situ particle optical properties at Xinken in Pearl River Delta of China, J. Geophys. Res.-Atmos., 111, D20204, https://doi.org/10.1029/2005JD006929, 2006.
Cheung, H. H. Y., Tan, H., Xu, H., Li, F., Wu, C., Yu, J. Z., and Chan, C. K.: Measurements of non-volatile aerosols with a VTDMA and their correlations with carbonaceous aerosols in Guangzhou, China, Atmos. Chem. Phys., 16, 8431–8446, https://doi.org/10.5194/acp-16-8431-2016, 2016.
Collaud Coen, M., Weingartner, E., Apituley, A., Ceburnis, D., Fierz-Schmidhauser, R., Flentje, H., Henzing, J. S., Jennings, S. G., Moerman, M., Petzold, A., Schmid, O., and Baltensperger, U.: Minimizing light absorption measurement artifacts of the Aethalometer: evaluation of five correction algorithms, Atmos. Meas. Tech., 3, 457–474, https://doi.org/10.5194/amt-3-457-2010, 2010.
Desyaterik, Y., Sun, Y., Shen, X., Lee, T., Wang, X., Wang, T., and Collett, J. L.: Speciation of “brown” carbon in cloud water impacted by agricultural biomass burning in eastern China, J. Geophys. Res.-Atmos., 118, 7389–7399, https://doi.org/10.1002/jgrd.50561, 2013.
Drinovec, L., Mocnik, G., Zotter, P., Prévôt, A. S. H., Ruckstuhl, C., Coz, E., Rupakheti, M., Sciare, J., Müller, T., Wiedensohler, A., and Hansen, A. D. A.: The “dual-spot” Aethalometer: an improved measurement of aerosol black carbon with real-time loading compensation, Atmos. Meas. Tech., 8, 1965–1979, https://doi.org/10.5194/amt-8-1965-2015, 2015.
Erlick, C., Abbatt, J. P. D., and Rudich, Y.: How Different Calculations of the Refractive Index Affect Estimates of the Radiative Forcing Efficiency of Ammonium Sulfate Aerosols, J. Atmos. Sci., 68, 1845–1852, https://doi.org/10.1175/2011jas3721.1, 2011.
Feng, X., Dang, Z., Huang, W., Shao, L., and Li, W.: Microscopic morphology and size distribution of particles in PM2.5 of Guangzhou City, J. Atmos. Chem., 64, 37–51, https://doi.org/10.1007/s10874-010-9169-7, 2010.
Feng, Y., Ramanathan, V., and Kotamarthi, V. R.: Brown carbon: a significant atmospheric absorber of solar radiation?, Atmos. Chem. Phys., 13, 8607–8621, https://doi.org/10.5194/acp-13-8607-2013, 2013.
Hoffer, A., Gelencsér, A., Guyon, P., Kiss, G., Schmid, O., Frank, G. P., Artaxo, P., and Andreae, M. O.: Optical properties of humic-like substances (HULIS) in biomass-burning aerosols, Atmos. Chem. Phys., 6, 3563–3570, https://doi.org/10.5194/acp-6-3563-2006, 2006.
Holben, B. N., Eck, T. F., Slutsker, I., Tanré, D., Buis, J. P., Setzer, A., Vermote, E., Reagan, J. A., Kaufman, Y. J., and Nakajima, T.: AERONET – A Federated Instrument Network and Data Archive for Aerosol Characterization, Remote Sens. Environ., 66, 1–16, 1998.
Huang, R.-J., Zhang, Y., Bozzetti, C., Ho, K.-F., Cao, J.-J., Han, Y., Daellenbach, K. R., Slowik, J. G., Platt, S. M., Canonaco, F., Zotter, P., Wolf, R., Pieber, S. M., Bruns, E. A., Crippa, M., Ciarelli, G., Piazzalunga, A., Schwikowski, M., Abbaszade, G., Schnelle-Kreis, J., Zimmermann, R., An, Z., Szidat, S., Baltensperger, U., Haddad, I. E., and Prevot, A. S. H.: High secondary aerosol contribution to particulate pollution during haze events in China, Nature, 514, 218–222, https://doi.org/10.1038/nature13774, 2014.
Jiang, D., Wang, C., Wu, D., Deng, X., Huang, X., Tan, H., Li, F., and Deng, T.: Diurnal variation of atmospheric boundary layer over Wushan station, Guangzhou using wind profiler radar (in Chinese), J. Trop. Meteorol., 29, 129–135, 2013.
Jung, J., Lee, H., Kim, Y. J., Liu, X., Zhang, Y., Gu, J., and Fan, S.: Aerosol chemistry and the effect of aerosol water content on visibility impairment and radiative forcing in Guangzhou during the 2006 Pearl River Delta campaign, J. Environ. Manage., 90, 3231–3244, https://doi.org/10.1016/j.jenvman.2009.04.021, 2009.
Katrinak, K. A., Rez, P., Perkes, P. R., and Buseck, P. R.: Fractal geometry of carbonaceous aggregates from an urban aerosol, Environ. Sci. Technol., 27, 225–238, 1993.
Khalizov, A. F., Xue, H., Wang, L., Zheng, J., and Zhang, R.: Enhanced light absorption and scattering by carbon soot aerosol internally mixed with sulfuric acid, The J. Phys. Chem. A, 113, 1066–1074, https://doi.org/10.1021/jp807531n, 2009.
Kirchstetter, T. W., Novakov, T., and Hobbs, P. V.: Evidence that the spectral dependence of light absorption by aerosols is affected by organic carbon, J. Geophys. Res.-Atmos., 109, D21208, https://doi.org/10.1029/2004jd004999, 2004.
Kulkarni, P., Baron, P. A., and Willeke, K.: Aerosol measurement : principles, techniques, and applications, Van Nostrand Reinhold, 807–808 pp., 1996.
Lack, D. A. and Cappa, C. D.: Impact of brown and clear carbon on light absorption enhancement, single scatter albedo and absorption wavelength dependence of black carbon, Atmos. Chem. Phys., 10, 4207–4220, https://doi.org/10.5194/acp-10-4207-2010, 2010.
Lack, D. A. and Langridge, J. M.: On the attribution of black and brown carbon light absorption using the Ångström exponent, Atmos. Chem. Phys., 13, 10535–10543, https://doi.org/10.5194/acp-13-10535-2013, 2013.
Lai, S.-C., Zou, S.-C., Cao, J.-J., Lee, S.-C., and Ho, K.-F.: Characterizing ionic species in PM2.5 and PM10 in four Pearl River Delta cities, South China, J. Environ. Sci., 19, 939–947, https://doi.org/10.1016/S1001-0742(07)60155-7, 2007.
Laskin, A., Laskin, J., and Nizkorodov, S. A.: Chemistry of atmospheric brown carbon, Chem. Rev., 115, 4335–4382, https://doi.org/10.1021/cr5006167, 2015.
Lee, E., Chan, C. K., and Paatero, P.: Application of positive matrix factorization in source apportionment of particulate pollutants in Hong Kong, Atmos. Environ., 33, 3201–3212, https://doi.org/10.1016/S1352-2310(99)00113-2, 1999.
Levine, J.: Biomass Burning Aerosols in a Savanna Region of the Ivory Coast, French Forum, 235–236, 1991.
Li, H., Han, Z., Cheng, T., Du, H., Kong, L., Chen, J., Zhang, R., and Wang, W.: Agricultural Fire Impacts on the Air Quality of Shanghai during Summer Harvesttime, Aerosol Air Qual. Res., 10, 95–101, https://doi.org/10.4209/aaqr.2009.08.0049, 2010.
Lin, P., Hu, M., Deng, Z., Slanina, J., Han, S., Kondo, Y., Takegawa, N., Miyazaki, Y., Zhao, Y., and Sugimoto, N.: Seasonal and diurnal variations of organic carbon in PM2.5 in Beijing and the estimation of secondary organic carbon, J. Geophys. Res., 114, D00G11, https://doi.org/10.1029/2008jd010902, 2009.
Liu, C., Chung, C. E., Yin, Y., and Schnaiter, M.: The absorption Ångström exponent of black carbon: from numerical aspects, Atmos. Chem. Phys., 18, 6259–6273, https://doi.org/10.5194/acp-18-6259-2018, 2018.
Liu, D., Allan, J., Whitehead, J., Young, D., Flynn, M., Coe, H., McFiggans, G., Fleming, Z. L., and Bandy, B.: Ambient black carbon particle hygroscopic properties controlled by mixing state and composition, Atmos. Chem. Phys., 13, 2015–2029, https://doi.org/10.5194/acp-13-2015-2013, 2013.
Liu, D., Taylor, J. W., Young, D. E., Flynn, M. J., Coe, H., and Allan, J. D.: The effect of complex black carbon microphysics on the determination of the optical properties of brown carbon, Geophys. Res. Lett., 42, 613–619, 2015.
Liu, L., Mishchenko, M. I., and Patrick Arnott, W.: A study of radiative properties of fractal soot aggregates using the superposition T-matrix method, J. Quant. Spectrosc. Ra. Transf., 109, 2656–2663, https://doi.org/10.1016/j.jqsrt.2008.05.001, 2008.
LP DAAC: MODIS/surface albedo daily 500 m, February 2000 to Present, available at: https://developers.google.cn/earth-engine/datasets/catalog/MODIS_006_MCD43A3 (last access: 3 August 2018), 2000.
Ma, N., Zhao, C. S., Müller, T., Cheng, Y. F., Liu, P. F., Deng, Z. Z., Xu, W. Y., Ran, L., Nekat, B., van Pinxteren, D., Gnauk, T., Müller, K., Herrmann, H., Yan, P., Zhou, X. J., and Wiedensohler, A.: A new method to determine the mixing state of light absorbing carbonaceous using the measured aerosol optical properties and number size distributions, Atmos. Chem. Phys., 12, 2381–2397, https://doi.org/10.5194/acp-12-2381-2012, 2012.
Ma, Y., Li, S. Z., Zheng, J., Khalizov, A., Wang, X., Wang, Z., and Zhou, Y. Y.: Size-resolved measurements of mixing state and cloud-nucleating ability of aerosols in Nanjing, China, J. Geophys. Res.-Atmos., 122, 9430–9450, https://doi.org/10.1002/2017jd026583, 2017.
Mie, G.: Beitrage Zur Optik Truber Medien, Speziell Kolloidaler Metallosungen, Ann. Phys., 25, 377, 1908.
Moosmüller, H., Chakrabarty, R. K., Ehlers, K. M., and Arnott, W. P.: Absorption Ångström coefficient, brown carbon, and aerosols: basic concepts, bulk matter, and spherical particles, Atmos. Chem. Phys., 11, 1217–1225, https://doi.org/10.5194/acp-11-1217-2011, 2011.
Nakayama, T., Ikeda, Y., Sawada, Y., Setoguchi, Y., Ogawa, S., Kawana, K., Mochida, M., Ikemori, F., Matsumoto, K., and Matsumi, Y.: Properties of light-absorbing aerosols in the Nagoya urban area, Japan, in August 2011 and January 2012: Contributions of brown carbon and lensing effect, J. Geophys. Res.-Atmos., 119, 12721–712739, 2015.
Nichol, J. E. and Wong, M.-S.: AERONET/aerosol optical depth measurements at Hong Kong Polytechnic University, November 2005 to September 2019, available at: https://aeronet.gsfc.nasa.gov/photo_db/Hong_Kong_PolyU.html (last access: 23 August 2018), 2005.
Olson, M. R., Victoria Garcia, M., Robinson, M. A., Van Rooy, P., Dietenberger, M. A., Bergin, M., and Schauer, J. J.: Investigation of black and brown carbon multiple-wavelength-dependent light absorption from biomass and fossil fuel combustion source emissions, J. Geophys. Res.-Atmos., 120, 6682–6697, https://doi.org/10.1002/2014jd022970, 2015.
Pio, C. A., Legrand, M., Alves, C. A., Oliveira, T., Afonso, J., Caseiro, A., Puxbaum, H., Sanchez-Ochoa, A., and Gelencsér, A.: Chemical composition of atmospheric aerosols during the 2003 summer intense forest fire period, Atmos. Environ., 42, 7530–7543, 2008.
Qin, Y. M., Tan, H. B., Li, Y. J., Li, Z. J., Schurman, M. I., Liu, L., Wu, C., and Chan, C. K.: Chemical characteristics of brown carbon in atmospheric particles at a suburban site near Guangzhou, China, Atmos. Chem. Phys., 18, 16409–16418, https://doi.org/10.5194/acp-18-16409-2018, 2018.
Redmond, H. and Thompson, J. E.: Evaluation of a quantitative structure-property relationship (QSPR) for predicting mid-visible refractive index of secondary organic aerosol (SOA), Phys. Chem. Chem. Phys., 13, 6872–6882, https://doi.org/10.1039/c0cp02270e, 2011.
Ricchiazzi, P., Yang, S., Gautier, C., and Sowle, D.: SBDART: A Research and Teaching Software Tool for Plane-Parallel Radiative Transfer in the Earth's Atmosphere, B. Am. Meteorol. Soc., 79, 2101–2114, https://doi.org/10.1175/1520-0477(1998)079<2101:Sarats>2.0.Co;2, 1998.
Roesch, A.: Use of Moderate-Resolution Imaging Spectroradiometer bidirectional reflectance distribution function products to enhance simulated surface albedos, J. Geophys. Res., 109, D12105, https://doi.org/10.1029/2004jd004552, 2004.
Sareen, N., Schwier, A. N., Shapiro, E. L., Mitroo, D., and McNeill, V. F.: Secondary organic material formed by methylglyoxal in aqueous aerosol mimics, Atmos. Chem. Phys., 10, 997–1016, https://doi.org/10.5194/acp-10-997-2010, 2010.
Satish, R., Shamjad, P., Thamban, N., Tripathi, S., and Rastogi, N.: Temporal Characteristics of Brown Carbon over the Central Indo-Gangetic Plain, Environ. Sci. Technol., 51, 6765–6772, https://doi.org/10.1021/acs.est.7b00734, 2017.
Scarnato, B. V., Vahidinia, S., Richard, D. T., and Kirchstetter, T. W.: Effects of internal mixing and aggregate morphology on optical properties of black carbon using a discrete dipole approximation model, Atmos. Chem. Phys., 13, 5089–5101, https://doi.org/10.5194/acp-13-5089-2013, 2013.
Schmid, O., Artaxo, P., Arnott, W. P., Chand, D., Gatti, L. V., Frank, G. P., Hoffer, A., Schnaiter, M., and Andreae, M. O.: Spectral light absorption by ambient aerosols influenced by biomass burning in the Amazon Basin. I: Comparison and field calibration of absorption measurement techniques, Atmos. Chem. Phys., 6, 3443–3462, https://doi.org/10.5194/acp-6-3443-2006, 2006.
Segura, S., Estellés, V., Titos, G., Lyamani, H., Utrillas, M. P., Zotter, P., Prévôt, A. S. H., Močnik, G., Alados-Arboledas, L., and Martínez-Lozano, J. A.: Determination and analysis of in situ spectral aerosol optical properties by a multi-instrumental approach, Atmos. Meas. Tech., 7, 2373–2387, https://doi.org/10.5194/amt-7-2373-2014, 2014.
Seinfeld, J. H. and Pandis, S. N.: Atmospheric Chemistry and Physics, John Wiley & Sons, Inc, New York, 1998.
Stokes, G. M. and Schwartz, S. E.: The Atmospheric Radiation Measurement (ARM) Program: Programmatic Background and Design of the Cloud and Radiation Test Bed, B. Am. Meteorol. Soc., 75, 1201–1221, 1994.
Tan, H., Liu, L., Fan, S., Li, F., Yin, Y., Cai, M., and Chan, P. W.: Aerosol optical properties and mixing state of black carbon in the Pearl River Delta, China, Atmos. Environ., 131, 196–208, https://doi.org/10.1016/j.atmosenv.2016.02.003, 2016a.
Tan, H., Yin, Y., Li, F., Liu, X., Chan, P. W., Deng, T., Deng, X., Wan, Q., and Wu, D.: Measurements of particle number size distributions and new particle formations events during winter in the Pearl River Delta region, China, J. Trop. Meteorol., 22, 191–199, 10.16555/j.1006-8775.2016.02.009, 2016b.
Waldman, J. M., Lioy, P. J., Zelenka, M., Jing, L., Lin, Y. N., He, Q. C., Qian, Z. M., Chapman, R., and Wilson, W. E.: Wintertime measurements of aerosol acidity and trace elements in Wuhan, a city in central China, Atmos. Environ. Part B., 25, 113–120, https://doi.org/10.1016/0957-1272(91)90045-G, 1991.
Wang, J., Nie, W., Cheng, Y., Shen, Y., Chi, X., Wang, J., Huang, X., Xie, Y., Sun, P., Xu, Z., Qi, X., Su, H., and Ding, A.: Light absorption of brown carbon in eastern China based on 3-year multi-wavelength aerosol optical property observations and an improved absorption Ångström exponent segregation method, Atmos. Chem. Phys., 18, 9061–9074, https://doi.org/10.5194/acp-18-9061-2018, 2018.
Washenfelder, R. A., Attwood, A. R., Brock, C. A., Guo, H., Xu, L., Weber, R. J., Ng, N. L., Allen, H. M., Ayres, B. R., and Baumann, K.: Biomass burning dominates brown carbon absorption in the rural southeastern United States, Geophys. Res. Lett., 42, 653–664, 2015.
Wex, H., Neusüß, C., Wendisch, M., Stratmann, F., Koziar, C., Keil, A., Wiedensohler, A., and Ebert, M.: Particle scattering, backscattering, and absorption coefficients: An in situ closure and sensitivity study, J. Geophys. Res.-Atmos., 107, LAC-1–LAC4-18, https://doi.org/10.1029/2000JD000234, 2002.
Wu, C., Wu, D., and Yu, J. Z.: Quantifying black carbon light absorption enhancement with a novel statistical approach, Atmos. Chem. Phys., 18, 289–309, https://doi.org/10.5194/acp-18-289-2018, 2018.
Wu, C., Wu, D., and Yu, J.: Estimation and Uncertainty Analysis of Secondary Organic Carbon Using One-Year of Hourly Organic and Elemental Carbon Data, J. Geophys. Res.-Atmos., 124, 2774–2795, https://doi.org/10.1029/2018JD029290, 2019.
Wu, D., Mao, J., Deng, X., Tie, X., Zhang, Y., Zeng, L., Li, F., Tan, H., Bi, X., Huang, X., Chen, J., and Deng, T.: Black carbon aerosols and their radiative properties in the Pearl River Delta region, Sci. China D, 52, 1152–1163, https://doi.org/10.1007/s11430-009-0115-y, 2009.
Xie, C., Xu, W., Wang, J., Wang, Q., Liu, D., Tang, G., Chen, P., Du, W., Zhao, J., Zhang, Y., Zhou, W., Han, T., Bian, Q., Li, J., Fu, P., Wang, Z., Ge, X., Allan, J., Coe, H., and Sun, Y.: Vertical characterization of aerosol optical properties and brown carbon in winter in urban Beijing, China, Atmos. Chem. Phys., 19, 165–179, https://doi.org/10.5194/acp-19-165-2019, 2019.
Yu, J., Yan, C., Liu, Y., Li, X., Zhou, T., and Zheng, M.: Potassium: A Tracer for Biomass Burning in Beijing?, Aerosol Air Qual. Res., 18, 2447–2459, https://doi.org/10.4209/aaqr.2017.11.0536, 2018.
Yuan, J.-F., Huang, X.-F., Cao, L.-M., Cui, J., Zhu, Q., Huang, C.-N., Lan, Z.-J., and He, L.-Y.: Light absorption of brown carbon aerosol in the PRD region of China, Atmos. Chem. Phys., 16, 1433–1443, https://doi.org/10.5194/acp-16-1433-2016, 2016.
Zhang, Y., Li, Z., Sun, Y., Lv, Y., and Xie, Y.: Estimation of atmospheric columnar organic matter (OM) mass concentration from remote sensing measurements of aerosol spectral refractive indices, Atmo. Environ., 179, 107–117, https://doi.org/10.1016/j.atmosenv.2018.02.010, 2018.
Zhou, S., Wang, T., Wang, Z., Li, W., Xu, Z., Wang, X., Yuan, C., Poon, C. N., Louie, P. K. K., Luk, C. W. Y., and Wang, W.: Photochemical evolution of organic aerosols observed in urban plumes from Hong Kong and the Pearl River Delta of China, Atmos. Environ., 88, 219–229, https://doi.org/10.1016/j.atmosenv.2014.01.032, 2014.