the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Simultaneous in situ measurements of small-scale structures in neutral, plasma, and atomic oxygen densities during the WADIS sounding rocket project
Martin Eberhart
Martin Friedrich
Jonas Hedin
Mikhail Khaplanov
Gerd Baumgarten
Bifford P. Williams
Tristan Staszak
Heiner Asmus
Irina Strelnikova
Ralph Latteck
Mykhaylo Grygalashvyly
Franz-Josef Lübken
Josef Höffner
Raimund Wörl
Jörg Gumbel
Stefan Löhle
Stefanos Fasoulas
Markus Rapp
Aroh Barjatya
Michael J. Taylor
Pierre-Dominique Pautet
In this paper we present an overview of measurements conducted during the WADIS-2 rocket campaign. We investigate the effect of small-scale processes like gravity waves and turbulence on the distribution of atomic oxygen and other species in the mesosphere–lower thermosphere (MLT) region. Our analysis suggests that density fluctuations of atomic oxygen are coupled to fluctuations of other constituents, i.e., plasma and neutrals. Our measurements show that all measured quantities, including winds, densities, and temperatures, reveal signatures of both waves and turbulence. We show observations of gravity wave saturation and breakdown together with simultaneous measurements of generated turbulence. Atomic oxygen inside turbulence layers shows two different spectral behaviors, which might imply a change in its diffusion properties.
The mesosphere–lower thermosphere (MLT) region is host to phenomena that are connected to dynamic and chemical processes that are still not fully understood. Thus, e.g., it is generally accepted that atmospheric gravity waves (GWs) play an essential role in the dynamics of this region and that they couple it with the lower and upper atmosphere (e.g., Becker and Schmitz, 2002; Fritts and Alexander, 2003; Alexander et al., 2010). When propagating, GWs might dissipate and thereby generate turbulence (e.g., Yamada et al., 2001; Selvaraj et al., 2016, and references therein). Apart from momentum deposition, which is a key coupling process, this also affects the mixing and redistribution of trace constituents (e.g., Fukao et al., 1994; Bishop et al., 2004). One of the most important trace constituents in the MLT is atomic oxygen (O), which plays an essential role in the chemistry and energy budget of the mesopause region (e.g., Mlynczak and Solomon, 1993). It is the major reactive trace constituent in the mesosphere–lower thermosphere (MLT) region and it plays a crucial role in different chemical reactions involved in airglow excitation or ion chemistry (e.g., Walterscheid et al., 1987; McDade et al., 1986; McDade, 1998; Marsh et al., 2006; Caridade et al., 2013; Lednyts'kyy et al., 2015). The lifetime of atomic oxygen varies with altitude from seconds at ∼50 km to months at ∼100 km (e.g., Torr, 1985; Smith et al., 2010).
Chemical heat released during exothermic reactions involving atomic oxygen is one of the main contributors to the energy budget of this region (e.g., Mlynczak and Solomon, 1991, 1993). These reactions yield chemical heating rates in the mesopause region of several Kelvin per day, which is comparable to (or even competitive with) those of turbulent heating (Lübken, 1997; Lübken et al., 2002), as well as direct heating due to solar radiation (e.g., Fomichev et al., 2004; Feofilov and Kutepov, 2012; Lübken et al., 2013, and references therein). Oxygen is involved in exothermic reactions with hydroxyl (OH), the emission bands of which have been extensively used to study the mesopause region temperature, gravity waves, and tides (e.g., Hines and Tarasick, 1987; Taylor et al., 1995, 1997, 2009; Snively, 2013; Fritts et al., 2014; Egito et al., 2017, and references therein).
It is believed that at altitudes at which the O lifetime is very long, i.e., roughly above 90 km, variations in O density mainly result from dynamical processes such as GWs, tides, and the large-scale circulation. But at lower heights chemical processes may play a crucial role in forming O-density variations. Such generalized conditions, however, can vary considerably from individual cases and are not suitable for case studies. It is also known that the mesopause region is very active dynamically. It is region where GWs break and a persistent turbulence field plays a crucial role in global circulation (e.g., Becker and Schmitz, 2002; Fritts and Alexander, 2003; Rapp et al., 2004). However, it is not known, for instance, how turbulence influences the O-density distribution or its diffusion properties and whether it can affect chemical heat release, e.g., by changing reaction rates.
This implies that in order to properly characterize the chemical and dynamical state of the mesopause region, it is important to know the altitude-resolved concentration of atomic oxygen along with the state of the background atmosphere, including its thermal structure and dynamical parameters. Also, a suitable justification of the chemical lifetime of atomic oxygen as well as characteristic times for dynamical processes have to be assessed for proper interpretation of measurements.
All these aspects stress the importance of common-volume measurements of the oxygen density together with the temperature and density of the background neutral atmosphere with a sufficiently high altitude resolution.
This paper aims at two things. The first is to provide an overview of the WADIS-2 sounding rocket campaign and measured parameters, and the second is to demonstrate that gravity wave motions and turbulence affect the distribution of atomic oxygen in the nighttime MLT region. We present results of in situ and some ground-based measurements obtained in the framework of the WADIS sounding rocket mission. We introduce new high-resolution O-density measurements in connection with other parameters of the atmosphere. The paper is structured as follows. In Sect. 2 we briefly describe the WADIS-2 mission and measurement techniques used in this study. In Sect. 3 we present measurement results followed by a more detailed analysis in Sect. 4. In Sect. 5 we critically discuss our findings, and in Sect. 6 we summarize the main results and give an outlook for our next rocket-borne measurements.
The WADIS sounding rocket mission, led by the Leibniz Institute of Atmospheric Physics (IAP) in Kühlungsborn, Germany, in partnership with the Institute of Space Systems (IRS) in Stuttgart and contributions from Austria, Sweden, the USA, and Norway, comprised two field campaigns conducted at the Andøya Space Center (ASC) in northern Norway (69∘ N, 16∘ E). The first campaign was conducted in June 2013 and the second in March 2015. WADIS stands for “Wave propagation and dissipation in the middle atmosphere: Energy budget and distribution of trace constituents”. The mission aimed to study the propagation and dissipation of gravity waves (GWs) and measuring the concentration of atomic oxygen simultaneously. Such measurements allow for the estimation of the contribution of chemical and turbulent heating to the energy budget of the MLT, as well as the transport of atomic oxygen by waves and turbulence. For a more detailed mission description the reader is referred to Strelnikov et al. (2017). The Arctic Lidar Observatory for Middle Atmosphere Research (ALOMAR; von Zahn et al., 1995) is located close to the launch site and was an integral part of the entire WADIS mission.
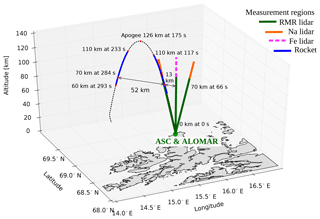
Figure 1Schematics of the WADIS-2 rocket experiment. Solid green and orange and dashed magenta lines show ALOMAR RMR, Na, and IAP Fe lidar measurement volumes, respectively. The black dashed line shows the rocket trajectory. Blue lines show the rocket measurement range used in this study.
The launch window for the second sounding rocket campaign was scheduled around local midnight to ensure full nighttime conditions. A large number of ground-based optical instruments supported the WADIS-2 rocket campaign. The ALOMAR Rayleigh–Mie–Raman (RMR), Na Weber, and IAP Fe lidar were running continuously throughout the campaign period whenever weather permitted. All three lidars measure temperature profiles along the beam direction as shown in Fig. 1. The instruments and temperature retrieval techniques for these lidars are described elsewhere (von Zahn et al., 2000; Hauchecorne and Chanin, 1980; She et al., 2002; Arnold and She, 2003; Höffner and Fricke-Begemann, 2005; Lautenbach and Höffner, 2004; Höffner and Lautenbach, 2009). Additionally, RMR and Na lidars measure line-of-sight wind speed in the altitude ranges 20–80 and 80–110 km, respectively (Baumgarten, 2010; Arnold and She, 2003).
The Advanced Mesospheric Temperature Mapper (AMTM) by Utah State University (Pautet et al., 2014) observed nightglow emissions at 1523.68 and 1542.79 nm. These observations yield measurements of the horizontal temperature field (see Fig. 4 and Wörl et al., 2019, for a detailed discussion of measurements during the WADIS-2 campaign).
The Middle Atmosphere ALOMAR Radar System, MAARSY (Rapp et al., 2011; Latteck et al., 2012), operated by the IAP, is located close to the rocket launch site and continuously running. MAARSY was used to detect polar mesospheric winter echoes (PMWEs) if they occurred (Latteck and Strelnikova, 2015).
The instrumented WADIS-2 payload was almost identical to the one launched during the first campaign (see Strelnikov et al., 2017, for details), except the instruments were tuned for polar night launch conditions.
The front and rear decks of the WADIS payloads were equipped with identical CONE (COmbined measurements for Neutrals and Electrons) ionization gauges to measure turbulence, neutral air density, and temperature on the upleg and downleg (Strelnikov et al., 2013). CONE measures the density of neutral air with an altitude resolution of ∼30 cm. Making use of laboratory calibrations allows us to derive the absolute density altitude profile. The measured density profile, in turn, can be integrated by assuming hydrostatic equilibrium to yield a temperature profile (see, e.g., Strelnikov et al., 2013, for details). The high sensitivity of the CONE instrument, which allows us to resolve density fluctuations of ∼0.01 %, makes it possible to derive turbulent parameters by analyzing the spectra of these fluctuations. The derivation technique of turbulent parameters is described in detail elsewhere (Lübken, 1992, 1997; Lübken et al., 1993; Strelnikov et al., 2003, 2013). Briefly, a theoretical spectral model of turbulence is fitted to a Fourier or wavelet spectrum of the measured relative density fluctuations, which are shown to be a conservative and passive turbulence tracer in the MLT (Lübken, 1992, 1997; Lübken et al., 1993). The key feature of this technique is that the theoretical model must reproduce the spectrum of the turbulent tracer (scalar) in both inertial (i.e., ) and viscous (or dissipation) subranges. The transition between these subranges takes place at the so-called inner scale, l0, which is related to the turbulence energy dissipation rate, ε, as , where ν is the kinematic viscosity and the constant C is of the order of 10. Also, Lübken et al. (1993) and Lübken (1997) showed that different spectral models, in particular those by Heisenberg (1948) and by Tatarskii (1971), yield close results for energy dissipation rates.
A positive ion probe (PIP) operated by the University of Technology in Graz (TUG), Austria, and a novel Langmuir probe (LP) developed and operated by Embry-Riddle Aeronautical University in Florida, USA, yielded high-resolution positive ion and electron density measurements, respectively. Both these plasma probes were mounted on booms located on the rear deck of the payload. Both WADIS payloads were also used to carry out a wave propagation experiment operated by TUG for precise measurements of absolute electron densities (Friedrich, 2016).
Two instruments, the Flux Probe Experiment (FIPEX) and an airglow photometer, were used to measure atomic oxygen densities. These instruments utilized entirely different measurement techniques. Photometers yield precise absolute density measurements, whereas FIPEX yields high-altitude-resolution data. The absolute values of the FIPEX measurements were validated by the photometers (see companion paper by Eberhart et al., 2019, for more details).
The FIPEX instruments developed by the IRS yield profiles of atomic oxygen densities with a high altitude resolution of ∼20 m (see Eberhart et al., 2015). Photometers operated by the Meteorological Institute at Stockholm University (MISU) measured oxygen densities using a well-established and reliable technique applied before on a large number of sounding rockets (e.g., Hedin et al., 2009).
FIPEX employs solid electrolyte sensors with gold electrodes that have selective sensitivity towards atomic oxygen. A low voltage is applied between the anode and cathode, pumping oxygen ions through the electrolyte ceramics (yttria-stabilized zirconia, YSZ). The current measured is proportional to the oxygen flux. A detailed description of measurements conducted by FIPEX during the WADIS mission is provided by Eberhart et al. (2015, 2019) for the first and second campaign, respectively.
The MISU airglow photometer measures emissions of the molecular oxygen atmospheric band around 762 nm from the overhead column, from which the volume emission rate is inferred by differentiation. The theory and application of oxygen density retrievals from the atmospheric band emissions are discussed in detail in the companion paper by Grygalashvyly et al. (2019).
The second MISU photometer on the payload measured emissions from the (0–0) band of the first negative band system centered at 391.4 nm. This emission is a sign of precipitating auroral electrons and thus a sensitive indicator of auroral activity.
The WADIS-2 sounding rocket was launched on 5 March 2015 at 01:44:00 UTC, which is during full nighttime conditions. Figure 1 shows the geometry of the WADIS-2 experiment. The black dashed parabola shows the actual rocket trajectory. The blue profiles show parts of the rocket trajectory that yielded measurements used in this paper. The solid green and orange and dashed magenta lines show the direction and altitude range for the RMR, Na, and Fe lidar, respectively. It is seen that the northwest-directed lidar beam was colocated with the ascending part of the rocket trajectory.
In this section we show data obtained by ground-based instruments around the rocket launch time and some profiles measured onboard the WADIS-2 sounding rocket. We start with measurements of the background state of the atmosphere as observed during the night of the rocket launch. Then we compare upleg and downleg density measurements collected by different instruments. These profiles are then used in Sect. 4 for a detailed fluctuation analysis. Finally, we demonstrate that the high-resolution FIPEX measurements yielded new, geophysically meaningful data.
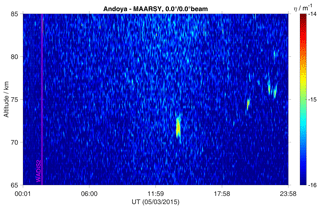
Figure 2Volume reflectivity measured by MAARSY on 5 March. Some short-living echoes were observed around noon and in the late evening but not around the WADIS-2 rocket launch.
3.1 Background
The background state of the atmosphere was continuously monitored by the ALOMAR lidars and radars. MAARSY did not observe any echoes during the night of the rocket launch. That is, the WADIS-2 rocket launch was under conditions of the confirmed absence of polar mesospheric winter echoes, or PMWEs. Figure 2 shows volume reflectivity measured by MAARSY during 5 March, i.e., the day of the rocket launch. Some short-living echoes were observed around noon and in the late evening but not in the morning when the WADIS-2 rocket was launched. We recall here that this sounding rocket mission did not aim to study PMWEs, so the presence of PMWEs was not a criterion for the rocket launch.
Thanks to favorable weather conditions, the lidars were able to measure both temperature and wind fields for several hours around the rocket launch time.
Figure 3 shows the temperature field measured by the IAP RMR and Fe lidars from 20 up to ∼100 km of altitude around the time of the WADIS-2 rocket launch. Figure 3 utilizes measurements by the vertical beam of the RMR lidar since the mobile Fe lidar only measures vertically. Also, the seeding temperature for the derivation of RMR temperatures was taken from Fe lidar measurements. Signatures of long-period waves are clearly seen above ∼65 km of altitude in both RMR and Fe lidar measurements.
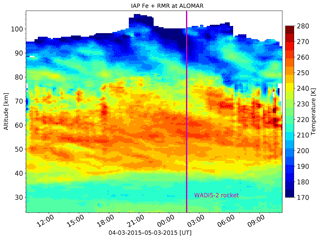
Figure 3Combined RMR and Fe lidar temperature measurements during the night of the WADIS-2 rocket launch, i.e., 4 to 5 March 2015.
The horizontal temperature field observed by the AMTM (Pautet et al., 2014) shown in Fig. 4 also reveals clear large-scale structures around the WADIS-2 launch time. Wörl et al. (2019) analyzed the colocated temperature measurements by both Fe lidar and AMTM in detail and concluded that the most pronounced wave signatures reveal periods of 24, 12, and 8 h; i.e., they are most probably created by tides.
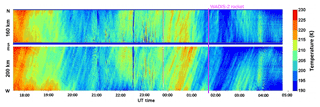
Figure 4NS and WE keogram summary of the AMTM temperature measurements obtained during the night of 4 to 5 March 2015.
Figure 5 shows measurements by the Na lidar conducted throughout the night of the WADIS-2 launch. Similar to Fe temperature, these measurements show prominent signatures of long-period waves above 80 km of altitude in both temperature and wind fields.
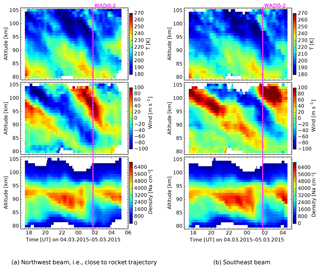
Figure 5Na lidar measurements during the night of the WADIS-2 rocket launch, i.e., 4 to 5 March 2015. The rocket was launched at 01:44 UTC.
All these data also contain smaller-scale fluctuations that result from gravity waves and turbulence. To see such small-scale fluctuations better and analyze them properly, one has to subtract the large-scale background (including tides) from the measurements shown in Figs. 3, 4, and 5 (see, e.g., Strelnikova et al., 2019). In the next section we focus on small-scale fluctuations of different quantities. We analyze rocket-borne instant measurements and further compare these with profiles measured by the ground-based instruments at the time of the rocket launch.
3.2 In situ measurements
The WADIS-2 rocket was launched at 01:44 UTC and reached an apogee of 126 km. The measurement phase started at about 60 km of altitude after nose cone and motor separation. However, the best-quality data were obtained above 70 km of height, mostly due to favorable aerodynamic conditions.
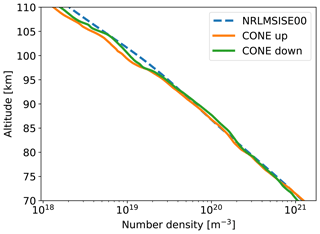
Figure 6Rocket-borne density measurements by the ionization gauge CONE for the upleg and downleg (orange and green lines, respectively). The blue dashed line shows the NRL-MSISE00 climatology for the time of the WADIS-2 launch, i.e., 5 March 2015 at 01:44:00 UTC.
Figures 6 and 7 show profiles of neutral air densities and temperatures measured in situ by the CONE instrument. Orange and green lines show upleg and downleg measurements, respectively. Blue dashed profiles represent NRLMSISE-00 reference atmosphere (Picone et al., 2002). The spin frequency of the WADIS-2 rocket of 3.27 Hz, which modulated the raw data, was filtered out by applying a notch filter. Additionally, the in situ measured densities shown were smoothed by a running average filter of a length of ∼200 m.
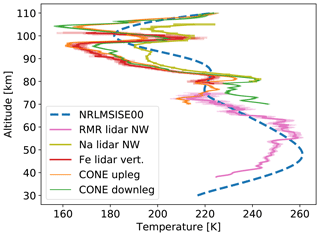
Figure 7Temperatures derived from the densities shown in Fig. 6 assuming hydrostatic equilibrium: orange and green for the upleg and downleg, respectively. Profiles in magenta, yellow, and red show measurements by RMR, Na, and Fe lidars, respectively. The blue dashed line shows the NRLMSISE-00 reference atmosphere for the time of the WADIS-2 launch (5 March 2015, 01:44:00 UTC).
Both the upleg and downleg profiles look very similar in terms of mean values and oscillations. The background atmosphere reveals a typical winter state (see, e.g., Strelnikov et al., 2013, wherein a collection of rocket-borne measurements for different seasons is shown). Also, the observed turbulence activity shown in Sect. 4 demonstrates typical winter behavior. The temperature profiles clearly show some GW signatures with amplitudes of up to 15 K at altitudes below 80 km. The height range between ∼83 and 90 km reveals very low GW amplitudes, i.e., temperature fluctuations of 1 K or less. A temperature increase of ∼40 K reminiscent of mesospheric inversion layers (MILs) similar to those analyzed by Szewczyk et al. (2013) is seen between 95 and 100 km and is discussed in Sect. 4. Some small-scale GWs, with amplitudes between 1 and 5 K and vertical wavelengths of the order of kilometers, are superposed on this large temperature disturbance. Figure 7 additionally shows temperature profiles in magenta, yellow, and red measured by RMR, Na, and Fe lidars, respectively.
The neutral density profiles in Fig. 6 also show some oscillations that can be attributed to gravity waves, which will be analyzed in detail in Sect. 4.
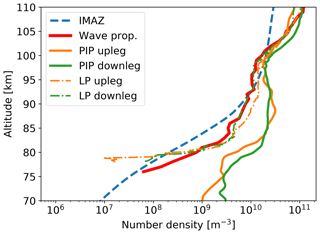
Figure 8Positive ion (solid orange and green lines) and electron (dash-dotted orange and green profiles) densities measured by the PIP and LP instruments, respectively. The bold solid red line shows results of the wave propagation experiment. The blue dashed line shows electron density from the empirical ionospheric model for the auroral zone, IMAZ, derived for the time of the WADIS-2 flight (see text for details).
In Fig. 8 we show profiles of electron and positive ion densities measured in situ on both the upleg and downleg. Dashed-dotted and solid profiles show electron and positive ion data, respectively. The bold solid red line shows measurement results of the wave propagation experiment. The two ion density profiles are also quite similar and also reveal some wave signatures. The two electron density profiles also demonstrate that the ionospheric background at the rocket upleg and downleg is rather similar. Comparison with the electron density profile from the empirical ionospheric model for the auroral zone, IMAZ (McKinnell and Friedrich, 2007), shown in Fig. 8 (blue dashed line), shows that the ionization level of the ionosphere was moderately high. This is in accord with the fact that some aurora was seen throughout the night of these observations. The inputs for IMAZ are an F10.7 solar flux index of 137.9 Jy (1 Jy = 10−26 W m−2 Hz−1), the planetary magnetic Ap index 5, and riometer absorption at 27.6 MHz of 0.076 dB. The two activity indices, the solar F10.7 and Ap index, were obtained from the GSFC–SPDF OMNIWeb interface at https://omniweb.gsfc.nasa.gov (last access: 28 August 2019). The integral riometer absorption was estimated from the electron density measurements by a wave propagation experiment based on Friedrich and Torkar (1983).
The overhead emission seen by the second MISU photometer varied (both increasing and decreasing at times) during the flight, indicating that the auroral emission was variable in time. The auroral emission was relatively weak, with peak total band radiances of 700–800 Rayleighs (around 6×107 photon × s−1 str−1 cm−2).
The PIP and LP instruments yield measurements of the relative densities of positive ions and electrons, respectively. The wave propagation experiment yields accurate measurements of absolute electron densities, which are used to normalize the PIP and LP measurements. The normalization was made at an altitude of ∼115 km, at which the quasi-neutrality condition is well satisfied for ionospheric plasma (see, e.g., Friedrich, 2016; Asmus et al., 2017, for more details). The large difference between positive ion and electron densities at altitudes ∼80–95 km was studied in detail by Asmus et al. (2017) and was shown to be due to charged dust particles.
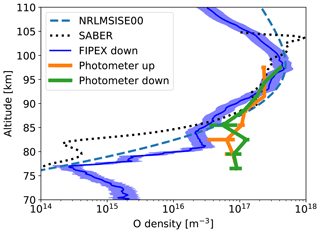
Figure 9Atomic oxygen density measurements. Bold orange and green lines with error bars show photometer measurements on the upleg and downleg, respectively. FIPEX downleg data are shown by the blue profile, with the shaded area showing measurement errors. The black dotted line shows SABER measurements (Level 2A, O event 20, orbit 71 729). The blue dashed line shows NRLMSISE-00 model data for the time of the rocket launch.
Figure 9 shows atomic oxygen density profiles measured by the photometer on the upleg and downleg in orange and green, respectively. The FIPEX measurements are only shown for the descending part of the WADIS-2 rocket flight because we are mostly confident in their absolute values and will use these data for further analysis. The blue dashed line shows NRLMSIS-00 data, and the black dotted line shows SABER (Sounding of the Atmosphere using Broadband Emission Radiometry) retrievals (orbit 71 729, event 20) at ∼230 km of distance and ∼4 h before the rocket launch. That is, the SABER measurements were not collocated and not simultaneous with the rocket flight and are only shown for qualitative comparison. However, the apparent density increase in SABER data above 100 km must be attributed to the observed auroral activity. We recall that the measurement principle of the FIPEX instrument is only sensitive to ambient O density and does not react to emissions.
We note here that the FIPEX is a new instrument that was first applied for oxygen density measurements on sounding rockets during the WADIS-1 rocket campaign (Eberhart et al., 2015). It showed good results and demonstrated the possibility of high-resolution O-density measurements in the MLT. The WADIS-2 rocket was additionally equipped with the MISU airglow photometer that indirectly measures O density from emissions of the molecular oxygen atmospheric band. Such measurements are also widely used from ground- and satellite-based platforms and are commonly accepted as reliable. The WADIS-2 sounding rocket comprised both measurement techniques on the same platform, which made it possible to closely compare their results. Both WADIS payloads (i.e., for the first and second campaigns) were equipped with several FIPEX sensors that were mounted at different angles relative to the rocket velocity (or rocket symmetry) axis. Such a multiple configuration aimed to find the most favorable aerodynamic orientation for the FIPEX sensors. We also note that because of the supersonic rocket velocity the measurement results of most instruments onboard sounding rockets require an aerodynamic correction (Gumbel et al., 1999; Gumbel, 2001; Rapp et al., 2001; Hedin et al., 2007; Staszak et al., 2015). By analyzing measurement conditions and comparing the measurement results, we chose the best-quality FIPEX data for further analysis. For a detailed discussion of all FIPEX measurements the reader is referred to the companion paper by Eberhart et al. (2019).
Figure 9 also reveals that below ∼85 km the differences between O densities measured by different techniques are very large. This is a manifestation of the disadvantages of the emission methods used for atomic oxygen retrieval. Thus, e.g., the technique for deriving O from OH∗ emissions (SABER) is based on the assumption of chemical equilibrium for ozone. Several recent works showed that below ∼80–87 km this assumption fails, in particular at high latitudes in March (Fig. 1 in Belikovich et al., 2018; Kulikov et al., 2018). Deviation from chemical equilibrium for ozone results in an underestimation of atomic oxygen density (Kulikov et al., 2019). Also, the photometric methods of atomic oxygen retrieval via atmospheric band observations (762 nm) are not free of disadvantages. The fitting coefficients for this method were calculated at the peak of atmospheric band emission (i.e., above ∼90 km) with an assumption that atomic oxygen recombination is a principal source of O2 (). Below this altitude, and in particular around the peak of the OH∗ layer, typically located at ∼80–88 km (e.g., Grygalashvyly et al., 2014), some additional mechanisms of O2 () population may occur (Witt et al., 1979; Kalogerakis, 2019). This leads to an overestimation of atomic oxygen calculated by the fit function of McDade et al. (1986).
It is already seen in Fig. 9 that the O-density profiles reveal some oscillations, with the largest amplitudes below approximately 83 km of altitude. It is worth mentioning that other FIPEX sensors yielded fluctuation data that show the same features (not shown here and discussed in detail in Eberhart et al., 2019).
The photometer measurements have an effective altitude resolution of 3 km, whereas the FIPEX sensors exhibit a height resolution of ∼20 m. In the next section we examine what advantages high-resolution measurements of atomic oxygen densities can bring and what the nature of the fluctuations in the FIPEX data is.
To extract small-scale fluctuations from the measured profiles, we subtract the mean background derived as a running average over a 5 km long vertical window. Similar results can be achieved by, e.g., applying a polynomial fit of the same vertical resolution, such as 5 km, or by means of other techniques (e.g., Strelnikova et al., 2019). We focus here on small vertical length scales <5 km comprising both turbulent fluctuations and part of the gravity wave spectrum. We note that choosing a particular cutoff wavelength always carries some degree of arbitrariness. For the small-scale structures in the MLT, especially those produced by turbulence, the background derivation does not affect the data analysis if residual fluctuation data contain all the scales below this limit (i.e., ∼5 km).
Fluctuations of horizontal wind derived from the lidar measurements for the time of the WADIS-2 rocket launch are shown in Fig. 10. It reveals an amplitude increase with height, z, according to the exponential law (), where H is scale height). It basically demonstrates that we observed gravity waves in the entire altitude range from near the ground up to ∼105 km. Wind fluctuation amplitude increases in the altitude range from 30 up to ∼70 km. Then the amplitude drops within the altitude range 70 to 80 km and increases again between 88 and 95 km. This is consistent with the behavior of temperature profiles that show larger wave amplitudes below 80 km of altitude, very low amplitudes above that height, and large wave amplitude again between 95 and 105 km (Figs. 5 and 7).
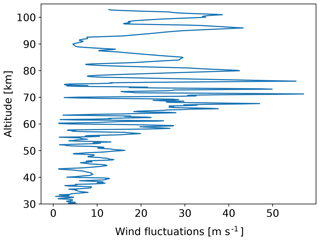
Figure 10Horizontal wind fluctuations (i.e., , where u′ and v′ are zonal and meridional wind fluctuations) derived from combined RMR and Na lidar measurements for the time of the WADIS-2 rocket flight.
In Fig. 11 we show relative density fluctuations (residuals) for neutrals, positive ions, and atomic oxygen in blue, orange, and green, respectively. These fluctuations were derived from the density profiles measured on the downleg of the WADIS-2 rocket flight. All three profiles show wave-like oscillations with (vertical) wavelengths in the range 1 to 5 km that can be attributed to gravity waves. Between 103 and 110 km of altitude all three profiles oscillate in phase. Below ∼103 km of height these density fluctuations reveal similar wavelengths but shifted in phase relative to each other.
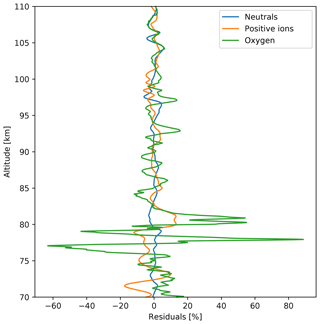
Figure 11Relative density fluctuations (residuals) of neutral air, positive ions, and atomic oxygen shown by blue, orange, and green profiles, respectively. These fluctuations were derived from the density profiles measured on the downleg of the WADIS-2 rocket flight by subtracting a running average over a 5 km long vertical window.
The density fluctuations of neutral gas shown in blue are used to derive turbulence energy dissipation rates, ε, as mentioned in Sect. 2. The resultant ε profiles for the upleg and downleg are shown in Fig. 12a and b, respectively.
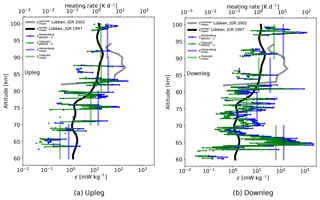
Figure 12In situ turbulence measurements by the WADIS-2 rocket launched on 1 March 2015 at 01:44:00 UTC. Blue and green represent turbulence energy dissipation rates, ε, derived using the spectral models of Heisenberg (1948) and Tatarskii (1971), respectively. Vertical lines show mean ε values over the 10 km height bins. Bold black and gray profiles show turbulence climatologies for winter and summer, respectively.
Blue and green profiles represent turbulence derivation utilizing different spectral models, i.e., that of Heisenberg (1948) and Tatarskii (1971), respectively (see also, e.g., Lübken et al., 1993). The difference between the green and blue values can be considered the method uncertainty. The black bold and gray profiles show climatologies, which indicate the mean seasonal values for winter (Lübken, 1997) and summer (Lübken et al., 2002), respectively. Figure 12 reveals, for instance, that we observed turbulence activity in the entire altitude range from 60 up to 100 km. This is a characteristic feature for the winter season. Also, the upleg and downleg turbulence data qualitatively agree with each other, except a small region observed between 63 and 67 km on the downleg. Thick vertical lines in Fig. 12 show mean values over the marked altitude regions (i.e., 10 km altitude bins). If compared with the results of our previous rocket campaign, WADIS-1, that was conducted in summer (Strelnikov et al., 2017), the observed winter turbulence field does not show a big difference between upleg and downleg measurements. If taking only mean values with their uncertainties into consideration, the height region 70 to 100 km looks very similar on both the upleg and downleg. The downleg turbulence measurements, however, reveal a patch of very strong turbulence around ∼65 km of height. The turbulence field in the summer MLT observed during the WADIS-1 campaign showed large oscillations in both space and time, so even mean ε values of upleg and downleg rocket measurements differed by orders of magnitude (Strelnikov et al., 2017). Turbulence variability in time was studied by analyzing MAARSY and EISCAT (European Incoherent SCATter Scientific Association) radar measurements that were properly scaled based on in situ data. MAARSY is only capable of measuring MLT parameters if some radar echo occurs, which means it requires the presence of PMSEs or PMWEs. The PMSE occurrence rate as observed by MAARSY is close to 100 % (Latteck and Bremer, 2017), which makes it easy to study the MLT in the summer season. The winter echoes, PMWEs, are much more rare; i.e., their occurrence rate is at most 30 % (Latteck and Strelnikova, 2015).
In Fig. 13 we show wavelet spectrograms of the neutral density fluctuations shown in Fig. 11. This spectrum was used to derive the ε profile shown in Fig. 12b (see Strelnikov et al., 2003, for details). We note that a qualitatively similar picture in terms of turbulent structures could be inferred by analyzing the upleg data, which are not shown here. In this spectrogram (Fig. 13) power decreases along the spatial-scale axis from large to small scales. The noise level corresponds to bluish colors. Turbulent layers can be recognized in this figure as regions of green that are extended to small scales of the order of 100 m or less. Note that this only gives a rough approximate visualization of the turbulence structure. A more close and detailed examination of individual spectra (power spectral densities, PSDs, vs. frequency) is required to derive the ε profile. Nevertheless, colored wavelet spectrograms like those shown in Fig. 13 help to identify power change at different scales in the spectrum. So, one can identify, for instance, two nearly parallel slopes in red between ∼80 and ∼98 km that extend approximately from scales of 5 to 3 km down to 1 km and slightly below. This region is marked with the blue dashed oval and tilted dashed lines in Fig. 13. This picture is reminiscent of a GW saturation process when the vertical wavelength of a GW becomes shorter (see, e.g., Fig. 5.3 in Nappo, 2002). Consistently, we observed a turbulence layer on top of this saturation region, i.e., in the 98 to 100 km range.
In Fig. 13 we further compare the neutral density spectrum derived from the CONE measurements with the spectrum of atomic oxygen density fluctuations derived from the FIPEX measurements. The black contour on top of the colored scalogram is a constant power line taken from a similarly derived wavelet spectrum (not shown here) of the O-density fluctuations that are shown in Fig. 11. The PSD value that represents the O spectra (black line) lies well within the inertial subrange (i.e., part) inside the regions where turbulence was observed. The contour line reproduces the small-scale structure of neutral density fluctuations quite well. So, all regions where neutral density structures extend to small scales are also present in the O-density spectra. This suggests that atomic oxygen is affected by turbulent mixing.
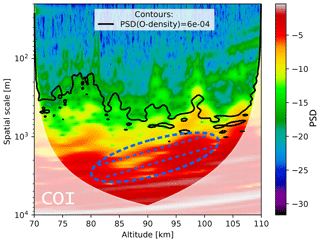
Figure 13Wavelet spectrum of neutral density fluctuations as color contours. Black contour shows a constant power line taken from the wavelet spectrum of atomic oxygen density fluctuations (not shown here). White shading shows the cone of influence (COI). The dashed oval and two lines mark regions where the power peak shifts from large to small scales, which can be attributed to a GW saturation process.
In order to directly compare the spectral content of neutral air and atomic oxygen fluctuations we further show in Fig. 14 two-dimensional slices of the corresponding wavelet spectrograms (i.e., for neutrals and oxygen). Figure 14 shows spectra of neutrals and O in black and blue, respectively. Additionally, in Fig. 14a we show a Fourier spectrum of the horizontal wind fluctuations (magenta) shown in Fig. 10. The wind spectrum only extends to ∼200 m, which is due to the limited altitude resolution of these measurements. The red dashed line marks the slope of k−3 (k is a wavenumber), which is commonly attributed to gravity waves (Fritts and Alexander, 2003). It is clearly seen that the spectrum of wind fluctuations closely follows the k−3 power law. The spectrum of neutrals is also very close to it, down to ∼15 m scales, at which white noise produced by instrument electronics dominates the signal. The spectrum of the instrumental noise is marked in Fig. 14 by a bold gray horizontal line. The dashed green line in Fig. 14a marks the slope, which is the famous Kolmogorov power law suggesting that turbulence acted on tracer distribution. It can be seen that the spectrum of O-density fluctuations might have been affected by turbulence.
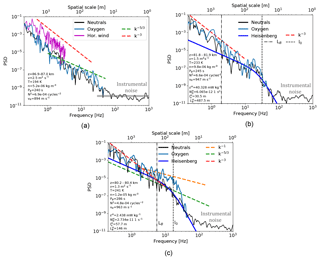
Figure 14Normalized power spectral densities (PSDs) of horizontal wind fluctuations (magenta), density fluctuations of neutral air (ΔNn ∕ Nn; black), and density fluctuations of atomic oxygen (Δ[O] ∕ [O]; blue) measured during the descent of the WADIS-2 sounding rocket. Dashed red, green, and orange lines show slopes with the k−3, , and k−1 power law, respectively. Vertical black dashed and dashed-dotted lines mark the inner and buoyancy scales of turbulence, l∘ and LB, respectively. Bold gray horizontal lines mark instrumental noise. (a) All spectra reveal a k−3 slope attributed to gravity waves; (b) all spectra reveal both waves and turbulence. The neutral and O spectra are nearly identical. (c) The small-scale part of the O spectrum reveals a k−1 slope.
Figure 14b shows spectra of neutral and oxygen density fluctuations taken from the region where moderate turbulence was observed near 82 km. The dark blue solid bold line also shows the fitted theoretical model of Heisenberg (1948). This model only describes two parts (or subranges) of the turbulence spectrum. Its left part, called the inertial subrange, follows the power law, whereas the dissipation part, often referred to as the viscous subrange, is described by the k−7 slope. One can see that the leftmost part of both spectra (i.e., for O and neutrals) follows the k−3, i.e., a GW-like slope (also marked by the red dashed line), which then smoothly transits into the turbulence spectrum well described by the Heisenberg model. The inertial subrange of both spectra spans over the same range of spatial scales, namely from the so-called buoyancy scale LB≈500 m down to the inner scale m. We recall here that the ε value is directly derived from the spatial scale l∘ defined as the transition between the inertial and viscous subranges.
Figure 14c shows spectra from the region just below the one described above. The ε value here drops by 1 order of magnitude and the inertial subrange shrinks to ∼100 m. Interestingly, the atomic oxygen spectrum reveals a somewhat different shape. Figure 14b and c demonstrate two types of spectral behavior of O-density fluctuations inside the turbulence layers observed during the WADIS-2 rocket experiment.
In this section we discuss the fluctuations shown above in different quantities measured with rocket-borne and ground-based instruments. First we focus on the large-scale morphology in the temperature field. Then we discuss fluctuations that might be attributed to gravity waves. Finally, we consider the observed smallest-scale structures due to turbulence.
Figure 7 shows a prominent temperature enhancement around ∼100 km of altitude. As mentioned in Sect. 3, Szewczyk et al. (2013) observed a similar temperature enhancement in the same altitude region. They showed that this signature was observed by the Microwave Limb Sounder (MLS) satellite instrument over a large region and was also seen in lidar data for a long time. These two facts led them to conclude that the observed temperature enhancement could be qualified as a mesospheric inversion layer (MIL). Their lidar temperature measurements also showed that the MIL descended together with the tide. A striking feature that accompanied the MIL studied by Szewczyk et al. (2013) was a very strong turbulence layer with ε=2 W kg−1 (equivalent to a heating rate of 200 K d−1) observed on top of their upper MIL. Interestingly, our downleg data reveal a very similar situation. Namely, on top of the temperature enhancement we also observe a vigorous turbulence layer with ε≃1 W kg−1 (or ∼100 K d−1). Our temperature enhancement (compare Figs. 7 and 3) also descends within a time period of several hours. Their temporal behavior is studied in Wörl et al. (2019), who found dominant periods of 24, 12, and 8 h. Its spatial extent is at least 60 km (distance between ascent and descent of the sounding rocket plus the distance to the southeast Na lidar beam, see Fig. 1). The upleg rocket data, however, are somewhat different. While the upleg measurements show similar temperature enhancement, the turbulence observed is 1 order of magnitude weaker. Szewczyk et al. (2013) argued that if turbulence itself did not produce the MIL, it might have amplified it. This statement is consistent with our observations. The local temperature maximum near 100 km reveals ∼10 K lower values for upleg measurements than for downleg (see Fig. 7). Also, turbulent energy dissipation rates measured on the upleg show values that are approximately 1 order of magnitude lower than those observed during the rocket descent (Fig. 12).
In the previous sections we showed ground-based wind and in situ density and temperature measurements that reveal signatures of gravity waves. Closer comparison of the density fluctuations of neutral gas, positive ions, and atomic oxygen in Fig. 11 shows at least two things. First, the amplitudes of GWs in these tracers are different. Second, the phases can be shifted relative to each other. Fritts and Thrane (1990) and Thrane et al. (1994) studied the relationship between ion and neutral density fluctuations due to gravity wave and turbulent motions both theoretically and experimentally. Their results indicated that this relationship in the middle atmosphere ranges between an adiabatic and a chemical equilibrium limit, depending on the characteristics of the wave or turbulent motion and the ion production and recombination rates. In a pure adiabatic limit case, which is when fully developed turbulence dominates in observed time series, the neutral and ion density fluctuations must be in antiphase, i.e., shifted by π relative to each other. Fritts and Thrane (1990) also noted that we should not expect the fluctuations of ions and neutrals to be either in or out of phase. Rather, they will have a phase shift that depends on the relative values of the intrinsic wave frequency, the mean ion number density, and the effective recombination rate.
Fritts and Thrane (1990) showed that the phase shift between fluctuations of different species depends on the relative magnitudes of wave and chemistry timescales. For low-frequency waves this phase shift is →0, indicating that the species are in chemical equilibrium. This situation is clearly observed just above the MIL-like temperature enhancement in the altitude range from 102 to 110 km (see Fig. 11), at which all three species, i.e., oxygen, ions, and neutrals, show nearly the same oscillations. This behavior is observed directly above the upper turbulence layer measured by rocket-borne instruments on both the upleg and downleg.
Next, we focus on the feature seen in the wavelet scalogram (Fig. 13), which is marked by the dashed lines. It suggests that waves with a vertical wavelength of ∼2–3 km saturated within the altitude range ∼80 to 98 km and broke producing turbulence layers (Fig. 12). That is, our new measurements suggest that turbulence produced by breaking GWs amplifies temperature fluctuations, producing MIL-like signatures in the temperature field. Note that the density fluctuations in Fig. 11 do not have this large MIL-like signature because of the background subtraction procedure, which filtered out waves longer than 5 km.
It is interesting to note that the altitude region below ∼82 km also reveals a feature similar to what is observed near 100 km of height: stronger turbulence activity on the downleg accompanies higher temperatures. Furthermore, right above this active region GW amplitudes seen in temperature data (Fig. 7) are very low. ε profiles (Fig. 12) also demonstrate lower turbulence activity (which might be connected to low GW amplitudes). Also, wind fluctuations (Fig. 10) are consistent with this picture. Their amplitude grows in the height region 30 to 70 km, and afterwards near 85 km it vanishes.
All these facts together suggest that we observed wave saturation and dissipation in the altitude range 70 to 80 km accompanied by turbulence production. Above these heights we observed GW amplitude growth and breakdown near 100 km. The latter can be attributed to either secondary GWs generated by turbulence (see, e.g., Becker and Vadas, 2018, and references therein) or just another wave package passing through our observation field.
The spatial scales considered in the discussion above are of the order of 1 km to a few kilometers. This range of vertical scales is characteristic for GWs in the MLT. If we look at these fluctuations in the spectral domain (e.g., shown in Fig. 14) we see that they follow the k−3 slope, usually attributed to GWs (see, e.g., Smith et al., 1987; Weinstock, 1990; Fritts and Alexander, 2003; Žagar et al., 2017, and references therein), in the range of scales from 5 km down to hundreds of meters. Now we discuss structures at smaller scales. A power increase in the spectrum, which appears at spatial scales below ∼500 m, must be attributed to the action of turbulence. If the spectrum reveals a clear shape that can be mathematically described by a model (e.g., Heisenberg, 1948; Tatarskii, 1971) we argue that we observed an active turbulence and derive its energy dissipation rate, ε. To do so, we have to make sure that the density fluctuations that we use for turbulence analysis are passive, which means that they do not influence the flow and are conservative; i.e., their value is not affected by the flow (see, e.g., Lübken, 1992, 1997; Lübken et al., 1993, 2002). It was also shown that plasma density fluctuations can satisfy this requirement and, under specific conditions, can be affected by nonturbulent processes like enhanced recombination of electrons with cluster ions (e.g., Röttger and La Hoz, 1990), the effect of charged ice particles in PMSE (e.g., Cho et al., 1992), or plasma instabilities (e.g., Blix et al., 1994; Strelnikov et al., 2009). If spectra at small scales reveal some enhanced power that cannot be described by a model, it might imply that we observed a residual structuring after the action of turbulence some time before. In such a case we cannot derive any parameters of turbulence from these data.
Recalling the above discussion about the relationship between density fluctuations of neutrals and ions, we note that our analysis results suggest that a similar relationship should also exist between small-scale atomic oxygen density fluctuations and other constituents, i.e., ionospheric plasma and neutral gas. So, e.g., earlier common-volume rocket-borne measurements of atomic oxygen and electron densities (Ne) by Friedrich et al. (1999) showed a clear correlation between the fine structure of O- and Ne-density profiles.
In the height range from ∼78 to ∼85 km in Fig. 11 fluctuations of ion density are in phase with those of O density and they are both almost in antiphase with the neutrals. This might imply that we observed O densities that are in chemical equilibrium with ion densities (phase shift close to zero) located inside turbulence layers (phase shift ∼π). The turbulence measurements indeed show turbulent layers in this altitude range (see Fig. 12b). On the one hand, this supports the theory of Fritts and Thrane (1990), but at the same time it raises the question of how O density behaves inside turbulence and whether turbulence affects the height distribution of atomic oxygen.
Now we discuss the power spectra shown in Fig. 14. This figure demonstrates three types of spectra found in the fluctuations measured during the WADIS-2 flight. As noted above, panel (a) shows spectra typical for gravity waves, whereas the other two panels (b and c) demonstrate turbulent spectra. Both spectra in panel (b), i.e., the PSD(ΔNn ∕ Nn) and the PSD(Δ[O] ∕ [O]) shown with black and blue lines, respectively, are nearly identical, suggesting that at these altitudes the chemical time constant is larger than the turbulent one. At the same time, just below this height, at which the chemical time constant is expected to be comparable, the PSD(Δ[O] ∕ [O]) shows different spectral behavior, revealing a k−1 slope at small scales (Fig. 14c).
A detailed analysis of all the regions where different types of O-density spectra occur is rather difficult for different reasons. One reason is that when turbulence is very strong, its spectrum extends down to scales below the current FIPEX resolution limit of ∼20 m; that is, the O-density spectrum appears not fully resolved. So far we can only identify three regions where the third type of spectrum (like in Fig. 14c) was observed in the downleg measurements at 90.9–91.2 km, 80.2–80.4 km, and 81.1–81.7 km.
Let us now discuss what processes could potentially contribute to the change in the diffusive properties of atomic oxygen as shown in Fig. 14c. Since satellite observations show that the horizontal (i.e., meridional and zonal) gradients of atomic oxygen at 70–100 km are much smaller than the vertical ones (e.g., Mlynczak et al., 2013, 2018), it is reasonable to assume that the meridional and zonal transport of atomic oxygen can be neglected in this case. Characteristic time due to vertical advection is of the order of 1 month (e.g., Brasseur and Solomon, 2005); hence, it is also negligible compared to, e.g., turbulent mixing. In order to clarify the relative significance of the chemical processes we compare characteristic times derived from in situ measurements in Fig. 15.
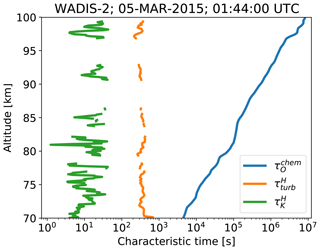
Figure 15Characteristic timescales derived from in situ measurements. – chemical lifetime of atomic oxygen, – characteristic timescale for the largest turbulent eddies derived based on the Heisenberg model, – Kolmogorov timescale derived based on the Heisenberg model.
The chemical lifetime of atomic oxygen, , shown in Fig. 15 by the blue line, was derived as the reciprocal of a loss term (Brasseur and Solomon, 2005, Eq. 5.30), omitting the loss due to reaction with ozone because in the mesopause region it is not significant (Smith et al., 2008). The Kolmogorov timescale, , wherein ν is the kinematic viscosity of air, was derived using results obtained with the model of Heisenberg (1948), i.e., , shown in blue in Fig. 12. The characteristic timescale for the largest turbulent eddies is / ωturb, wherein the turbulence buoyancy scale that characterizes the largest turbulence eddies was derived based on Weinstock (1978) as
where N is the buoyancy frequency, and the mean turbulent velocity that characterizes advection by the largest eddies was calculated as derived by Weinstock (1981) using results obtained with the model of Heisenberg (1948), i.e., . The Kolmogorov timescale characterizes the motion of the smallest turbulent eddies (i.e., of the size of the Kolmogorov scale, , and therefore the range describes all turbulent motions. Figure 15 thereby shows that during the WADIS-2 rocket flight turbulent advection was much faster than the chemical processes relevant for atomic oxygen. Such a situation, however, is most probably typical for the nighttime MLT at high northern latitudes.
Friedrich (2016) noted that O density should positively correlate with Ne for two reasons: (1) [O] inhibits the formation of water cluster ions (e.g., H+(H2O)n), which have significantly faster recombination rates than molecular ions (, NO+), and (2) [O] provides a reverse reaction by effectively detaching electrons from negative ions. In terms of density fluctuations, Ne is ultimately connected to the ambient ion density, Ni, which in turn at heights below ∼100 km is essentially governed by collisions with neutrals (e.g., Rapp et al., 2003). That is, the small-scale structures produced by turbulence must be observed in these species too. The difference in their response to turbulence arises due to differences in their diffusivity. Thus, the diffusion constant of charged constituents is affected by ambipolar forces resulting from electrostatic coupling between positively and negatively charged species (e.g., Chen, 2016). Moreover, it was shown that heavy charged aerosols, if present, can significantly reduce plasma diffusivity, allowing for the extension of eddy cascade in those species down to much smaller scales (e.g., Rapp et al., 2003). This, for instance, can lead to phenomena like polar mesosphere radar echoes in summer or winter, PMSEs or PMWEs, respectively (see, e.g., Rapp and Lübken, 2004; Lübken et al., 2006). Under conditions when the diffusivity, D, of plasma species is considerably reduced its spectral behavior can be described by a model that includes this parameter via, e.g., the Schmidt number, , wherein ν is the kinematic viscosity of ambient gas (e.g., Driscoll and Kennedy, 1985). Such models implement the theory of Batchelor (1958) and describe the small-scale part of the spectrum by a k−1 power law. In other words, if the spectrum of density fluctuations reveals the k−1 slope at scales smaller than those at which is present, this means that the diffusivity of this constituent is reduced. To summarize, spectra of O-density fluctuations that show the k−1 slope (one example is shown in Fig. 14c) may imply that atomic oxygen can show different diffusion properties inside turbulence layers. That is, to answer the question of whether turbulence affects the height distribution of atomic oxygen, we can definitely say yes. The observed k−1 spectral behavior, however, needs further in-depth investigation and lies out of the scope of this paper.
In this paper we present an overview of the entire scope of measurements conducted in the framework of the WADIS-2 sounding rocket campaign. We also demonstrate the important role of small-scale processes like gravity waves and turbulence in the distribution of O in the MLT region.
We show that all measured quantities, including winds, densities, and temperatures, reveal signatures of both waves and turbulence. Analysis of density fluctuations measured by rocket-borne instruments supported the theory by Fritts and Thrane (1990) but also suggested that a similar relationship might exist between atomic oxygen and other constituents, i.e., plasma and neutrals.
Atomic oxygen inside turbulent layers showed two different spectral behaviors at scales smaller than ∼300 m. Some of the O-density spectra reproduce spectra of neutral gas, but some of them show a k−1 slope. A more detailed study of such very small scales in O-density data is the subject of our future work. In particular, a somewhat higher altitude resolution and enhanced sensitivity of FIPEX sensors may yield a more detailed picture for our future rocket experiments.
The data can be obtained per request to the authors.
MR, FJL, and BS designed and directed the project; BS, MF, RL, JH, MK, JG, SL, SF, GB, JH, AB, and MJT designed and directed the subprojects and related instruments; ME, MF, JH, MK, GB, BPW, HA, RL, JH, RW, AB, MJT, and PDP performed the experiments; BS, ME, MF, JH, GB, BPW, TS, HA, IS, RL, MG, JH, RW, AB, MJT, and PDP analyzed the data; all authors contributed to the final paper.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Layered phenomena in the mesopause region (ACP/AMT inter-journal SI)”. It is a result of the LPMR workshop 2017 (LPMR-2017), Kühlungsborn, Germany, 18–22 September 2017.
The authors thank DLR-MORABA for their excellent contribution to the project by developing the complicated WADIS payload and campaign support together with the Andøya Space Center. The authors thank Hans-Jürgen Heckl and Torsten Köpnick for building the IAP rocket instrumentation.
This work was supported by the German Federal Ministry for Economic Affairs and Energy on the basis of a decision by the German Bundestag. The project WADIS was supported by the German Space Agency (DLR) under grant no. 50 OE 1001. The design and initial development of the AMTM was supported under an AFOSR DURIP grant to USU. The AMTM installation and operations at ALOMAR were supported under the NSF collaborative grant AGS-1042227. The sodium lidar observations and data analysis were supported by NSF grants AGS-1136269, AGS-1734693, and AGS-1829138. The ERAU Langmuir probe development was funded by Florida Space Grant Consortium.
The publication of this article was funded by the
Open-Access Fund of the Leibniz Association.
This paper was edited by Andreas Engel and reviewed by Selvaraj Dharmalingam and one anonymous referee.
Alexander, M. J., Geller, M., McLandress, C., Polavarapu, S., Preusse, P., Sassi, F., Sato, K., Eckermann, S., Ern, M., Hertzog, A., Kawatani, Y., Pulido, M., Shaw, T. A., Sigmond, M., Vincent, R., and Watanabe, S.: Recent developments in gravity-wave effects in climate models and the global distribution of gravity-wave momentum flux from observations and models, Q. J. Roy. Meteor. Soc., 136, 1103–1124, https://doi.org/10.1002/qj.637, 2010. a
Arnold, K. S. and She, C. Y.: Metal fluorescence lidar (light detection and ranging) and the middle atmosphere, Contemp. Phys., 44, 35–49, https://doi.org/10.1080/00107510302713, 2003. a, b
Asmus, H., Staszak, T., Strelnikov, B., Lübken, F.-J., Friedrich, M., and Rapp, M.: Estimate of size distribution of charged MSPs measured in situ in winter during the WADIS-2 sounding rocket campaign, Ann. Geophys., 35, 979–998, https://doi.org/10.5194/angeo-35-979-2017, 2017. a, b
Batchelor, G. K.: Small scale variation of convected quantities like temperature in turbulent field, J. Fluid Mech., 5, 113–133, 1958. a
Baumgarten, G.: Doppler Rayleigh/Mie/Raman lidar for wind and temperature measurements in the middle atmosphere up to 80 km, Atmos. Meas. Tech., 3, 1509–1518, https://doi.org/10.5194/amt-3-1509-2010, 2010. a
Becker, E. and Schmitz, G.: Energy Deposition and Turbulent Dissipation Owing to Gravity Waves in the Mesosphere., J. Atmos. Sci., 59, 54–68, https://doi.org/10.1175/1520-0469(2002)059<0054:EDATDO>2.0.CO;2, 2002. a, b
Becker, E. and Vadas, S. L.: Secondary gravity waves in the winter mesosphere: Results from a high-resolution global circulation model, J. Geophys. Res., 123, 2605–2627, https://doi.org/10.1002/2017JD027460, 2018. a
Belikovich, M., Kulikov, M., Grygalashvyly, M., Sonnemann, G., Ermakova, T., Nechaev, A., and Feigin, A.: Ozone chemical equilibrium in the extended mesopause under the nighttime conditions, Adv. Space Res., 61, 426–432, https://doi.org/10.1016/j.asr.2017.10.010, 2018. a
Bishop, R. L., Larsen, M. F., Hecht, J. H., Liu, A. Z., and Gardner, C. S.: TOMEX: Mesospheric and lower thermospheric diffusivities and instability layers, J. Geophys. Res.-Atmos., 109, D02S03, https://doi.org/10.1029/2002JD003079, 2004. a
Blix, T. A., Thrane, E. V., Kirkwood, S., and Schlegel, K.: Plasma instabilities in the lower E-region observed during the DYANA campaign, J. Atmos. Terr. Phys., 56, 1853–1870, 1994. a
Brasseur, G. P. and Solomon, S.: Aeronomy of the Middle Atmosphere: Chemistry and Physics of the Stratosphere and Mesosphere, 2005. a, b
Caridade, P. J. S. B., Horta, J.-Z. J., and Varandas, A. J. C.: Implications of the O + OH reaction in hydroxyl nightglow modeling, Atmos. Chem. Phys., 13, 1–13, https://doi.org/10.5194/acp-13-1-2013, 2013. a
Chen, F. F.: Introduction to Plasma Physics and Controlled Fusion, https://doi.org/10.1007/978-3-319-22309-4, 2016. a
Cho, J. Y. N., Hall, T. M., and Kelley, M. C.: On the role of charged aerosols in polar mesosphere summer echoes, J. Geophys. Res., 97, 875–886, 1992. a
Driscoll, R. J. and Kennedy, L. A.: A model for the spectrum of passive scalars in an isotropic turbulence field, Phys. Fluids, 28, 72–80, 1985. a
Eberhart, M., Löhle, S., Steinbeck, A., Binder, T., and Fasoulas, S.: Measurement of atomic oxygen in the middle atmosphere using solid electrolyte sensors and catalytic probes, Atmos. Meas. Tech., 8, 3701–3714, https://doi.org/10.5194/amt-8-3701-2015, 2015. a, b, c
Eberhart, M., Löhle, S., Strelnikov, B., Hedin, J., Khaplanov, M., Fasoulas, S., Gumbel, J., Lübken, F.-J., and Rapp, M.: Atomic oxygen number densities in the mesosphere–lower thermosphere region measured by solid electrolyte sensors on WADIS-2, Atmos. Meas. Tech., 12, 2445–2461, https://doi.org/10.5194/amt-12-2445-2019, 2019. a, b, c, d
Egito, F., Takahashi, H., and Miyoshi, Y.: Effects of the planetary waves on the MLT airglow, Ann. Geophys., 35, 1023–1032, https://doi.org/10.5194/angeo-35-1023-2017, 2017. a
Feofilov, A. G. and Kutepov, A. A.: Infrared Radiation in the Mesosphere and Lower Thermosphere: Energetic Effects and Remote Sensing, Surv. Geophys., 33, 1231–1280, https://doi.org/10.1007/s10712-012-9204-0, 2012. a
Fomichev, V. I., Ogibalov, V. P., and Beagley, S. R.: Solar heating by the near-IR CO2 bands in the mesosphere, Geophys. Res. Lett., 31, L21102, https://doi.org/10.1029/2004GL020324, 2004. a
Friedrich, M.: Handbook of the Lower Ionosphere, Verlag der Technischen Universität Graz, available at: https://lampx.tugraz.at/~karl/verlagspdf/ionosphere_friedrich_ebook.pdf (last access: 21 August 2019), https://doi.org/10.3217/ 978-3-85125-485-3, 2016. a, b, c
Friedrich, M. and Torkar, K.: High-latitude plasma densities and their relation to riometer absorption, J. Atmos. Terr. Phys., 45, 127–135, https://doi.org/10.1016/S0021-9169(83)80017-8, 1983. a
Friedrich, M., Gumbel, J., and Pilgram, R.: Atomic Oxygen in the Mesosphere and its Relevance for the Ionosphere: A Summary of Empirical Evidence, in: European Rocket and Balloon Programs and Related Research, edited by: Kaldeich-Schürmann, B., ESA Special Publication, 437, p. 287, 1999. a
Fritts, D. C. and Alexander, M. J.: Gravity wave dynamics and effects in the middle atmosphere, Rev. Geophys., 41, 1003, https://doi.org/10.1029/2001RG000106, 2003. a, b, c, d
Fritts, D. C. and Thrane, E. V.: Computation of the ion/neutral density ratio in the presence of wave and chemical effects, J. Atmos. Terr. Phys., 52, 827–834, https://doi.org/10.1016/0021-9169(90)90019-J, 1990. a, b, c, d, e
Fritts, D. C., Pautet, P.-D., Bossert, K., Taylor, M. J., Williams, B. P., Iimura, H., Yuan, T., Mitchell, N. J., and Stober, G.: Quantifying gravity wave momentum fluxes with Mesosphere Temperature Mappers and correlative instrumentation, J. Geophys. Res.-Atmos., 119, 13, https://doi.org/10.1002/2014JD022150, 2014. a
Fukao, S., Yamanaka, M., Ao, N., K Hocking, W., Sato, T., Yamamoto, M., Nakamura, T., Tsuda, T., and Kato, S.: Seasonal variability of vertical eddy diffusivity in the middle atmosphere 1. Three-year observations by the middle and upper atmosphere radar, J. Geophys. Res., 99, 18973–18987, https://doi.org/10.1029/94JD00911, 1994. a
Grygalashvyly, M., Sonnemann, G. R., Lübken, F.-J., Hartogh, P., and Berger, U.: Hydroxyl layer: mean state and trends at mid latitudes, J. Geophys. Res., 119, 12391–12419, https://doi.org/10.1002/2014JD022094, 2014. a
Grygalashvyly, M., Eberhart, M., Hedin, J., Strelnikov, B., Lübken, F.-J., Rapp, M., Löhle, S., Fasoulas, S., Khaplanov, M., Gumbel, J., and Vorobeva, E.: Atmospheric band fitting coefficients derived from a self-consistent rocket-borne experiment, Atmos. Chem. Phys., 19, 1207–1220, https://doi.org/10.5194/acp-19-1207-2019, 2019. a
Gumbel, J.: Aerodynamic influences on atmospheric in situ measurements from sounding rockets, J. Geophys. Res.-Space, 106, 10553–10563, https://doi.org/10.1029/2000JA900166, 2001. a
Gumbel, J., Rapp, M., and Unckell, C.: Aerodynamic Aspects of Rocket-Borne in situ Studies, in: European Rocket and Balloon Programs and Related Research, edited by: Kaldeich-Schürmann, B., ESA Special Publication, 437, p. 459, 1999. a
Hauchecorne, A. and Chanin, M.-L.: Density and temperature profiles obtained by lidar between 35 and 70 km, Geophys. Res. Lett., 7, 565–568, https://doi.org/10.1029/GL007i008p00565, 1980. a
Hedin, J., Gumbel, J., and Rapp, M.: On the efficiency of rocket-borne particle detection in the mesosphere, Atmos. Chem. Phys., 7, 3701–3711, https://doi.org/10.5194/acp-7-3701-2007, 2007. a
Hedin, J., Gumbel, J., Stegman, J., and Witt, G.: Use of O2 airglow for calibrating direct atomic oxygen measurements from sounding rockets, Atmos. Meas. Tech., 2, 801–812, https://doi.org/10.5194/amt-2-801-2009, 2009. a
Heisenberg, W.: Zur statistischen Theorie der Turbulenz, Z. Physik, 124, 628–657, 1948. a, b, c, d, e, f, g
Hines, C. O. and Tarasick, D. W.: On the detection and utilization of gravity waves in airglow studies, Planet. Space Sci., 35, 851–866, https://doi.org/10.1016/0032-0633(87)90063-8, 1987. a
Höffner, J. and Fricke-Begemann, C.: Accurate lidar temperatures with narrowband filters, Opt. Lett., 30, 890–892, https://doi.org/10.1364/OL.30.000890, 2005. a
Höffner, J. and Lautenbach, J.: Daylight measurements of mesopause temperature and vertical wind with the mobile scanning iron lidar, Opt. Lett., 34, 1351–1353, https://doi.org/10.1364/OL.34.001351, 2009. a
Kalogerakis, K. S.: A previously unrecognized source of the O2 Atmospheric band emission in Earth's nightglow, Sci. Adv., 5, https://doi.org/10.1126/sciadv.aau9255, 2019. a
Kulikov, M. Y., Belikovich, M. V., Grygalashvyly, M., Sonnemann, G. R., Ermakova, T. S., Nechaev, A. A., and Feigin, A. M.: Nighttime Ozone Chemical Equilibrium in the Mesopause Region, J. Geophys. Res.-Atmos., 123, 3228–3242, https://doi.org/10.1002/2017JD026717, 2018. a
Kulikov, M. Y., Nechaev, A. A., Belikovich, M. V., Vorobeva, E. V., Grygalashvyly, M., Sonnemann, G. R., and Feigin, A. M.: Boundary of Nighttime Ozone Chemical Equilibrium in the Mesopause Region From SABER Data: Implications for Derivation of Atomic Oxygen and Atomic Hydrogen, Geophys. Res. Lett., 46, 997–1004, https://doi.org/10.1029/2018GL080364, 2019. a
Latteck, R. and Bremer, J.: Long-term variations of polar mesospheric summer echoes observed at Andøya (69∘ N), J. Atmos. Sol.-Terr. Phy., 163, 31–37, 2017. a
Latteck, R. and Strelnikova, I.: Extended observations of polar mesosphere winter echoes over Andøya (69∘ N) using MAARSY, J. Geophys. Res.-Atmos., 120, 8216–8226, https://doi.org/10.1002/2015JD023291, 2015. a, b
Latteck, R., Singer, W., Rapp, M., Vandepeer, B., Renkwitz, T., Zecha, M., and Stober, G.: MAARSY: The new MST radar on Andøya-System description and first results, Radio Sci., 47, RS1006, https://doi.org/10.1029/2011RS004775, 2012. a
Lautenbach, J. and Höffner, J.: Scanning iron temperature lidar for mesopause temperature observation, Appl. Opt., 43, 4559–4563, https://doi.org/10.1364/AO.43.004559, 2004. a
Lednyts'kyy, O., von Savigny, C., Eichmann, K.-U., and Mlynczak, M. G.: Atomic oxygen retrievals in the MLT region from SCIAMACHY nightglow limb measurements, Atmos. Meas. Tech., 8, 1021–1041, https://doi.org/10.5194/amt-8-1021-2015, 2015. a
Lübken, F.-J.: On the extraction of turbulent parameters from atmospheric density fluctuations, J. Geophys. Res., 97, 20385–20395, 1992. a, b, c
Lübken, F.-J.: Seasonal variation of turbulent energy dissipation rates at high latitudes as determined by insitu measurements of neutral density fluctuations, J. Geophys. Res., 102, 13441–13456, 1997. a, b, c, d, e, f
Lübken, F.-J., Hillert, W., Lehmacher, G., and von Zahn, U.: Experiments revealing small impact of turbulence on the energy budget of the mesosphere and lower thermosphere, J. Geophys. Res., 98, 20369–20384, 1993. a, b, c, d, e
Lübken, F.-J., Rapp, M., and Hoffmann, P.: Neutral air turbulence and temperatures in the vicinity of polar mesosphere summer echoes, J. Geophys. Res., 107, 4273–4277, https://doi.org/10.1029/2001JD000915, 2002. a, b, c
Lübken, F.-J., Strelnikov, B., Rapp, M., Singer, W., Latteck, R., Brattli, A., Hoppe, U.-P., and Friedrich, M.: The thermal and dynamical state of the atmosphere during polar mesosphere winter echoes, Atmos. Chem. Phys., 6, 13–24, https://doi.org/10.5194/acp-6-13-2006, 2006. a
Lübken, F.-J., Berger, U., and Baumgarten, G.: Temperature trends in the midlatitude summer mesosphere, J. Geophys. Res.-Atmos., 118, 13, https://doi.org/10.1002/2013JD020576, 2013. a
Marsh, D. R., Smith, A. K., Mlynczak, M. G., and Russell, J. M.: SABER observations of the OH Meinel airglow variability near the mesopause, J. Geophys. Res.-Space, 111, A10S05, https://doi.org/10.1029/2005JA011451, 2006. a
McDade, I. C.: The photochemistry of the MLT oxygen airglow emissions and the expected influences of tidal perturbations, Adv. Space Res., 21, 787–794, https://doi.org/10.1016/S0273-1177(97)00674-1, 1998. a
McDade, I. C., Murtagh, D. P., Greer, R. G. H., Dickinson, P. H. G., Witt, G., Stegman, J., Llewellyn, E. J., Thomas, L., and Jenkins, D. B.: ETON 2 – Quenching parameters for the proposed precursors of O2 (b1Σ+g) and O(1S) in the terrestrial nightglow, Planet. Space Sci., 34, 789–800, https://doi.org/10.1016/0032-0633(86)90075-9, 1986. a, b
McKinnell, L.-A. and Friedrich, M.: A neural network-based ionospheric model for the auroral zone, J. Atmos. Sol.-Terr. Phy., 69, 1459–1470, https://doi.org/10.1016/j.jastp.2007.05.003, 2007. a
Mlynczak, M. G. and Solomon, S.: Middle atmosphere heating by exothermic chemical reactions involving odd-hydrogen species, Geophys. Res. Lett., 18, 37–40, https://doi.org/10.1029/90GL02672, 1991. a
Mlynczak, M. G. and Solomon, S.: A detailed evaluation of the heating efficiency in the middle atmosphere, J. Geophys. Res., 98, 10, https://doi.org/10.1029/93JD00315, 1993. a, b
Mlynczak, M. G., Hunt, L. A., Mast, J. C., Thomas Marshall, B., Russell III, J. M., Smith, A. K., Siskind, D. E., Yee, J.-H., Mertens, C. J., Javier Martin-Torres, F., Earl Thompson, R., Drob, D. P., and Gordley, L. L.: Atomic oxygen in the mesosphere and lower thermosphere derived from SABER: Algorithm theoretical basis and measurement uncertainty, J. Geophys. Res.-Atmos., 118, 5724–5735, https://doi.org/10.1002/jgrd.50401, 2013. a
Mlynczak, M. G., Hunt, L. A., Russell III, J. M., and Marshall, B. T.: Updated SABER Night Atomic Oxygen and Implications for SABER Ozone and Atomic Hydrogen, Geophys. Res. Lett., 45, 5735–5741, https://doi.org/10.1029/2018GL077377, 2018. a
Nappo, C. J.: An introduction to atmospheric gravity waves, 2002. a
Pautet, P.-D., Taylor, M. J., Pendleton, W. R., Zhao, Y., Yuan, T., Esplin, R., and McLain, D.: Advanced mesospheric temperature mapper for high-latitude airglow studies, Appl. Opt., 53, 5934, https://doi.org/10.1364/AO.53.005934, 2014. a, b
Picone, J. M., Hedin, A. E., Drob, D. P., and Aikin, A. C.: NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues, J. Geophys. Res.-Space, 107, 1468, https://doi.org/10.1029/2002JA009430, 2002. a
Rapp, M. and Lübken, F.-J.: Polar mesosphere summer echoes (PMSE): Review of observations and current understanding, Atmos. Chem. Phys., 4, 2601–2633, https://doi.org/10.5194/acp-4-2601-2004, 2004. a
Rapp, M., Gumbel, J., and Lübken, F.-J.: Absolute density measurements in the middle atmosphere, Ann. Geophys., 19, 571–580, 2001. a
Rapp, M., Lübken, F.-J., and Blix, T. A.: Small scale density variations of electrons and charged particles in the vicinity of polar mesosphere summer echoes, Atmos. Chem. Phys., 3, 1399–1407, https://doi.org/10.5194/acp-3-1399-2003, 2003. a, b
Rapp, M., Strelnikov, B., Müllemann, A., Lübken, F.-J., and Fritts, D. C.: Turbulence measurements and implications for gravity wave dissipation during the MaCWAVE/MIDAS rocket program, Geophys. Res. Lett., 31, L24S07, https://doi.org/10.1029/2003GL019325, 2004. a
Rapp, M., Latteck, R., Stober, G., Hoffmann, P., Singer, W., and Zecha, M.: First three-dimensional observations of polar mesosphere winter echoes: Resolving space-time ambiguity, J. Geophys. Res., 116, A11307, https://doi.org/10.1029/2011JA016858, 2011. a
Röttger, J. and La Hoz, C.: Characteristics of polar mesosphere summer echoes (PMSE) observed with the EISCAT 224 MHz radar and possible explanations of their origin, J. Atmos. Terr. Phys., 52, 893–906, 1990. a
Selvaraj, D., Patra, A. K., and Narayana Rao, D.: On the seasonal variations of reflectivity and turbulence characteristics of low-latitude mesospheric echoes over Gadanki, J. Geophys. Res.-Atmos., 121, 6164–6177, https://doi.org/10.1002/2015JD024283, 2016. a
She, C. Y., Vance, J. D., Williams, B. P., Krueger, D. A., Moosmüller, H., Gibson-Wilde, D., and Fritts, D.: Lidar studies of atmospheric dynamics near polar mesopause, EOS T. Am. Geophys. Un., 83, 289–293, https://doi.org/10.1029/2002EO000206, 2002. a
Smith, A. K., Marsh, D. R., Russell III, J. M., Mlynczak, M. G., Martin-Torres, F. J., and Kyrölä, E.: Satellite observations of high nighttime ozone at the equatorial mesopause, J. Geophys. Res.-Atmos., 113, D17312, https://doi.org/10.1029/2008JD010066, 2008. a
Smith, A. K., Marsh, D. R., Mlynczak, M. G., and Mast, J. C.: Temporal variations of atomic oxygen in the upper mesosphere from SABER, J. Geophys. Res.-Atmos., 115, D18309, https://doi.org/10.1029/2009JD013434, 2010. a
Smith, S. A., Fritts, D. C., and Vanzandt, T. E.: Evidence for a Saturated Spectrum of Atmospheric Gravity Waves., J. Atmos. Sci., 44, 1404–1410, https://doi.org/10.1175/1520-0469(1987)044<1404:EFASSO>2.0.CO;2, 1987. a
Snively, J. B.: Mesospheric hydroxyl airglow signatures of acoustic and gravity waves generated by transient tropospheric forcing, Geophys. Res. Lett., 40, 4533–4537, https://doi.org/10.1002/grl.50886, 2013. a
Staszak, T., Brede, M., and Strelnikov, B.: Open Source Software Openfoam as a New Aerodynamical Simulation Tool for Rocket-Borne Measurements, in: 22nd ESA Symposium on European Rocket and Balloon Programmes and Related Research, edited by: Ouwehand, L., ESA Special Publication, 730, p. 201, 2015. a
Strelnikov, B., Rapp, M., and Lübken, F.-J.: A new technique for the analysis of neutral air density fluctuations measured in situ in the middle atmosphere, Geophys. Res. Lett., 30, 2052, https://doi.org/10.1029/2003GL018271, 2003. a, b
Strelnikov, B., Rapp, M., Zecha, M., Blix, T. A., Friedrich, M., and Yeoman, T. K.: PMSE and E-region plasma instability: In situ observations, J. Atmos. Sol.-Terr. Phy., 71, 143–157, https://doi.org/10.1016/j.jastp.2008.10.003, 2009. a
Strelnikov, B., Rapp, M., and Lübken, F.: In-situ density measurements in the mesosphere/lower thermosphere region with the TOTAL and CONE instruments, Terrapub, 1–11, https://doi.org/10.5047/aisi.001, 2013. a, b, c, d
Strelnikov, B., Szewczyk, A., Strelnikova, I., Latteck, R., Baumgarten, G., Lübken, F.-J., Rapp, M., Fasoulas, S., Löhle, S., Eberhart, M., Hoppe, U.-P., Dunker, T., Friedrich, M., Hedin, J., Khaplanov, M., Gumbel, J., and Barjatya, A.: Spatial and temporal variability in MLT turbulence inferred from in situ and ground-based observations during the WADIS-1 sounding rocket campaign, Ann. Geophys., 35, 547–565, https://doi.org/10.5194/angeo-35-547-2017, 2017. a, b, c, d
Strelnikova, I., Baumgarten, G., and Lübken, F.-J.: Advanced hodograph-based analysis technique to derive gravity waves parameters from Lidar observations, Atmos. Meas. Tech. Discuss., https://doi.org/10.5194/amt-2019-79, in review, 2019. a, b
Szewczyk, A., Strelnikov, B., Rapp, M., Strelnikova, I., Baumgarten, G., Kaifler, N., Dunker, T., and Hoppe, U.-P.: Simultaneous observations of a Mesospheric Inversion Layer and turbulence during the ECOMA-2010 rocket campaign, Ann. Geophys., 31, 775–785, https://doi.org/10.5194/angeo-31-775-2013, 2013. a, b, c, d
Tatarskii, V. I.: The effects of the turbulent atmosphere on wave propagation, Jerusalem: Israel Program for Scientific Translations, 1971. a, b, c, d
Taylor, M. J., Bishop, M. B., and Taylor, V.: All-sky measurements of short period waves imaged in the OI(557.7 nm), Na(589.2 nm) and near infrared OH and O2(0,1) nightglow emissions during the ALOHA-93 Campaign, Geophys. Res. Lett., 22, 2833–2836, https://doi.org/10.1029/95GL02946, 1995. a
Taylor, M. J., Pendleton, W. R., Clark, S., Takahashi, H., Gobbi, D., and Goldberg, R. A.: Image measurements of short-period gravity waves at equatorial latitudes, J. Geophys. Res., 102, 26, https://doi.org/10.1029/96JD03515, 1997. a
Taylor, M. J., Pautet, P.-D., Medeiros, A. F., Buriti, R., Fechine, J., Fritts, D. C., Vadas, S. L., Takahashi, H., and São Sabbas, F. T.: Characteristics of mesospheric gravity waves near the magnetic equator, Brazil, during the SpreadFEx campaign, Ann. Geophys., 27, 461–472, https://doi.org/10.5194/angeo-27-461-2009, 2009. a
Thrane, E. V., Blix, T. A., Hoppe, U.-P., Lübken, F.-J., Hillert, W., Lehmacher, G., and Fritts, D. C.: A study of small-scale waves and turbulence in the mesosphere using simultaneous in situ observations of neutral gas and plasma fluctuations, J. Atmos. Terr. Phys., 56, 1797–1808, https://doi.org/10.1016/0021-9169(94)90011-6, 1994. a
Torr, D. G.: The photochemistry of the upper atmosphere, ISBN 978-0-12-444920-6, 165–278, 1985. a
Žagar, N., Jelićs , D., Blaauw, M., and Bechtold, P.: Energy Spectra and Inertia-Gravity Waves in Global Analyses, J. Atmos. Sci., 74, 2447–2466, https://doi.org/10.1175/JAS-D-16-0341.1, 2017. a
von Zahn, U., Thrane, E. V., and Skatteboe, R.: The ALOMAR facility: Status and outlook, in: Proceedings of the 12th ESA Symposium on European Rocket and Balloon Programmes and Related Research, edited by: Blix, T. A., ESA SP–370, Lillehammer, Norway, 379–385, 1995. a
von Zahn, U., von Cossart, G., Fiedler, J., Fricke, K. H., Nelke, G., Baumgarten, G., Rees, D., Hauchecorne, A., and Adolfsen, K.: The ALOMAR Rayleigh/Mie/Raman lidar: objectives, configuration, and performance, Ann. Geophys., 18, 815–833, https://doi.org/10.1007/s005850000210, 2000. a
Walterscheid, R. L., Schubert, G., and Straus, J. M.: A dynamical-chemical model of wave-driven fluctuations in the OH nightglow, J. Geophys. Res., 92, 1241–1254, https://doi.org/10.1029/JA092iA02p01241, 1987. a
Weinstock, J.: On the Theory of Turbulence in the Buoyancy Subrange of Stably Stratified Flows., J. Atmos. Sci., 35, 634–649, https://doi.org/10.1175/1520-0469(1978)035<0634:OTTOTI>2.0.CO;2, 1978. a
Weinstock, J.: Energy Dissipation Rates of Turbulence in the Stable Free Atmosphere., J. Atmos. Sci., 38, 880–880, https://doi.org/10.1175/1520-0469(1981)038<0880:EDROTI>2.0.CO;2, 1981. a
Weinstock, J.: Saturated and Unsaturated Spectra of Gravity Waves and Scale-Dependent Diffusion., J. Atmos. Sci., 47, 2211–2226, https://doi.org/10.1175/1520-0469(1990)047<2211:SAUSOG>2.0.CO;2, 1990. a
Witt, G., Stegman, J., Solheim, B., and Llewellyn, E.: A measurement of the O) atmospheric band and the OI(1S) green line in the nightglow, Planet. Space Sci., 27, 341–350, https://doi.org/10.1016/0032-0633(79)90111-9, 1979. a
Wörl, R., Strelnikov, B., Viehl, T. P., Höffner, J., Pautet, P.-D., Taylor, M. J., Zhao, Y., and Lübken, F.-J.: Thermal structure of the mesopause region during the WADIS-2 rocket campaign, Atmos. Chem. Phys., 19, 77–88, https://doi.org/10.5194/acp-19-77-2019, 2019. a, b, c
Yamada, Y., Fukunishi, H., Nakamura, T., and Tsuda, T.: Breaking of small-scale gravity wave and transition to turbulence observed in OH airglow, Geophys. Res. Lett., 28, 2153–2156, https://doi.org/10.1029/2000GL011945, 2001. a





