the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
New particle formation in the sulfuric acid–dimethylamine–water system: reevaluation of CLOUD chamber measurements and comparison to an aerosol nucleation and growth model
Andreas Kürten
Chenxi Li
Federico Bianchi
Joachim Curtius
António Dias
Neil M. Donahue
Jonathan Duplissy
Richard C. Flagan
Jani Hakala
Tuija Jokinen
Jasper Kirkby
Markku Kulmala
Ari Laaksonen
Katrianne Lehtipalo
Vladimir Makhmutov
Antti Onnela
Matti P. Rissanen
Mario Simon
Mikko Sipilä
Yuri Stozhkov
Jasmin Tröstl
Penglin Ye
Peter H. McMurry
A recent CLOUD (Cosmics Leaving OUtdoor Droplets) chamber study showed that sulfuric acid and dimethylamine produce new aerosols very efficiently and yield particle formation rates that are compatible with boundary layer observations. These previously published new particle formation (NPF) rates are reanalyzed in the present study with an advanced method. The results show that the NPF rates at 1.7 nm are more than a factor of 10 faster than previously published due to earlier approximations in correcting particle measurements made at a larger detection threshold. The revised NPF rates agree almost perfectly with calculated rates from a kinetic aerosol model at different sizes (1.7 and 4.3 nm mobility diameter). In addition, modeled and measured size distributions show good agreement over a wide range of sizes (up to ca. 30 nm). Furthermore, the aerosol model is modified such that evaporation rates for some clusters can be taken into account; these evaporation rates were previously published from a flow tube study. Using this model, the findings from the present study and the flow tube experiment can be brought into good agreement for the high base-to-acid ratios (∼ 100) relevant for this study. This confirms that nucleation proceeds at rates that are compatible with collision-controlled (a.k.a. kinetically controlled) NPF for the conditions during the CLOUD7 experiment (278 K, 38 % relative humidity, sulfuric acid concentration between 1 × 106 and 3 × 107 cm−3, and dimethylamine mixing ratio of ∼ 40 pptv, i.e., 1 × 109 cm−3).
The formation of new particles by gas-to-particle conversion (nucleation or new particle formation, NPF) is important for a variety of atmospheric processes and for human health.
It has been shown in numerous studies that sulfuric acid (H2SO4) is often associated with NPF (Weber et al., 1997; Kulmala et al., 2004; Fiedler et al., 2005; Kuang et al., 2008; Kirkby et al., 2011) and indeed it can explain some of the observed particle formation together with water vapor for neutral (uncharged) and ion-induced conditions when temperatures are low, e.g., in the free troposphere (Lee et al., 2003; Lovejoy et al., 2004; Duplissy et al., 2016; Ehrhart et al., 2016; Dunne et al., 2016). However, at least one additional stabilizing compound is required in order to explain boundary layer nucleation at warm temperatures. Acid–base nucleation, which involves a ternary compound, e.g., ammonia, in addition to sulfuric acid and water, can lead to much higher NPF rates compared to the binary system (Weber et al., 1998; Ball et al., 1999; Kürten et al., 2016a). Nevertheless, for most conditions close to the surface, the concentrations of H2SO4 and NH3 are too low, or temperatures are too high, to allow significant ternary nucleation of these compounds (Kirkby et al., 2011; Kürten et al., 2016a). However, the substitution of ammonia by amines, e.g., dimethylamine (DMA, (CH3)2NH), leads to NPF rates that can explain the atmospheric observations over a wide range of sulfuric acid concentrations, even when the amine mixing ratios are in the low parts per trillion volume range (Kurtén et al., 2008; Nadykto et al., 2011; Ortega et al., 2012; Chen et al., 2012; Almeida et al., 2013; Glasoe et al., 2015). A recent study even showed that NPF is collision-controlled, i.e., that it proceeds at the maximum possible speed (Rao and McMurry, 1989), when amine mixing ratios are above ∼ 20 pptv (5 × 108 cm−3) and sulfuric acid concentrations are between 1 × 106 cm−3 and 3 × 107 cm−3 at 278 K and 38 % relative humidity (Kürten et al., 2014). Indications that NPF can be collision-limited were reported more than 30 years ago based on the analysis of chamber nucleation experiments (McMurry, 1980), although the involvement of amines, which were probably present as a contaminant during those experiments, was not considered. Indications that atmospheric nucleation might occur through a collision-limited process have also been previously presented (Weber et al., 1996). Despite the strong evidence that sulfuric acid–amine nucleation is very efficient, it has rarely been observed in the atmosphere. Only one study has so far reported sulfuric acid–amine nucleation (Zhao et al., 2011) despite amine mixing ratios of up to tens of parts per trillion volume at some sites (Yu and Lee, 2012; You et al., 2014; Freshour et al., 2014; Yao et al., 2016). A global modeling study of sulfuric acid–amine nucleation has been carried out so far (Bergman et al., 2015), applying a nucleation parametrization based on the measurements of Almeida et al. (2013) and Glasoe et al. (2015).
Atmospheric boundary layer nucleation can also be explained by the existence of highly oxygenated organic molecules (Crounse et al., 2013; Ehn et al., 2014), e.g., from α-pinene. These highly oxygenated molecules have been found to nucleate efficiently in a chamber study even without the involvement of sulfuric acid, especially when ions take part in the nucleation process (Kirkby et al., 2016).
Even though oxidized organics seem to be globally important for NPF (Jokinen et al., 2015; Gordon et al., 2016; Dunne et al., 2016), the formation of new particles by sulfuric acid and amines should still be considered because sulfuric acid–amine nucleation rates exceed those from oxidized organics as soon as the concentrations of the precursor gases (sulfuric acid and amines) are high enough (Berndt et al., 2014). Therefore, at least locally or regionally, i.e., close to sources, amines should be relevant.
In this study, we reanalyze data from CLOUD (Cosmics Leaving OUtdoor Droplets) chamber experiments conducted at CERN during October–November 2012 (CLOUD7 campaign). NPF rates as a function of the sulfuric acid concentration from CLOUD7 were previously published (Almeida et al., 2013). However, these data are reanalyzed in the present study using an advanced method that takes into account the effect of self-coagulation in the estimation of NPF rates (Kürten et al., 2015a). The reanalyzed data and NPF rates obtained from scanning mobility particle sizer (SMPS) measurements are compared to results from a kinetic aerosol model. Modeling is also used for a comparison between results from a flow tube study (Jen et al., 2016a) and CLOUD.
The reanalyzed data cover sulfuric acid concentrations from ca. 1 × 106 to 3 × 107 cm−3, which fall into the range for most observations of atmospheric boundary layer NPF events (e.g., Kulmala et al., 2013). The DMA mixing ratio for most of the data shown in this study is ∼ 40 pptv (1 × 109 cm−3), which is within the rather wide range of observations (0.1 to 157 pptv, i.e., 2.5 × 106 to 4 × 109 cm−3) for C2-amines to which DMA belongs (Yao et al., 2016).
2.1 CLOUD experiment and instruments
The CLOUD experiment at CERN was designed to investigate nucleation and growth of aerosol particles in chemically diverse systems. Additionally, the influence of ions on NPF and growth can be studied inside the 26.1 m3 electro-polished stainless steel chamber (Kirkby et al., 2011). For the experiments discussed in this paper, NPF is initiated by illuminating the air inside the chamber with UV light by means of a fiber-optic system (Kupc et al., 2011), which produces sulfuric acid (H2SO4) photolytically from reactions involving O3, H2O, SO2, and O2. Diluted DMA and sulfur dioxide are taken from gas bottles; inside the chamber, these trace gases mix with clean synthetic air (i.e., O2 and N2 with a ratio of 21:79 from evaporated cryogenic liquids). To ensure homogenous conditions, the air is mixed with magnetically driven fans installed at the top and bottom of the chamber (Voigtländer et al., 2012). A thermal housing controls the chamber temperature to 278.15 K within several hundredths of a degree. The temperature was not varied for the experiments relevant for this study. The relative humidity was kept constant at 38 % by humidifying a fraction of the inflowing air with a humidification system (Duplissy et al., 2016). In order to keep the pressure inside the chamber at 1.005 bar, the air that is taken by the instruments has to be continuously replenished. Therefore, a flow of 150 L min−1 of the humidified air is continuously supplied to the chamber. For the sulfuric acid, DMA, and water system, ions do not have a strong enhancing effect on the nucleation rates for most conditions (Almeida et al., 2013); therefore, we do not distinguish between the neutral and charged pathways in such runs.
A suite of instruments is connected to the CLOUD chamber to measure particles, ions, clusters, and gas concentrations. A summary of these instruments is provided elsewhere (Kirkby et al., 2011; Duplissy et al., 2016). For this study, measured sulfuric acid and particle concentrations are relevant. A chemical-ionization atmospheric-pressure-interface time-of-flight mass spectrometer (CI-APi-TOF) was employed to measure sulfuric acid and its neutral clusters in this study (Jokinen et al., 2012; Kürten et al., 2014). The particle concentrations originate from a scanning mobility particle sizer (SMPS; Wang and Flagan, 1990), which measured the particle size distribution between ∼ 4 and ∼ 80 nm. The SMPS uses a differential mobility analyzer built by the Paul Scherrer Institute; it includes a Kr85 charger to bring the particles into charge equilibrium before they are classified. The retrieval of the particle size distributions requires corrections for the charging and the transmission efficiency, which were performed according to the literature (Wiedensohler and Fissan, 1988; Karlsson and Martinsson, 2003). The mixing ratio of DMA was determined using ion chromatography with a detection limit of 0.2 to 1 pptv (5 × 106 to 2.5 × 107 cm−3) at a time resolution between 70 and 210 min (Praplan et al., 2012; Simon et al., 2016).
2.2 Calculation of particle formation rates
Particle formation rates J (cm−3 s−1) are calculated from the measured size distributions (assumed to consist of n bins). For the size bin with the index m, the rate at which particles with a diameter equal to or larger than dm are formed can be calculated according to Kürten et al. (2015a):
This equation takes into account the time derivative of the number density of all particles for which dp≥dm, i.e., N≥m, and corrects for the effects of wall loss (size-dependent wall loss rates kw,i), dilution (dilution rate kdil), and coagulation (collision frequency function Ki,j), where Ni and Nj are the particle number densities in different size bins. The rate of losses to the chamber walls can be expressed using the equation from Crump and Seinfeld (1981):
where D(dp) is the diffusivity of a particle of diameter dp, which is given by the Stokes–Einstein relation (Hinds, 1999):
where kB, T, and η are the Boltzmann constant, the temperature, and the gas viscosity, respectively. The Cunningham slip correction factor, CC, is a function of the particle Knudsen number, , and λ is the mean-free path of the gas molecules. The empirically derived proportionality coefficient, Cw, depends upon the chamber dimensions and on the intensity of turbulent mixing. The rate of loss of sulfuric acid to the chamber walls is generally used to characterize Cw. The diffusivity of sulfuric acid is 0.0732 cm2 s−1 at 278 K and 38 % relative humidity (Hanson and Eisele, 2000).
The measured lifetime, determined from the decay of sulfuric acid when the UV light is turned off, was 554 s (wall loss rate 0.00181 s−1). With the experimentally determined diffusivity, this yields a Cw factor of 0.00667 cm−1 s−0.5. However, in this study diffusivities were calculated according to Eq. (3); thus, the calculated monomer diffusivity (for a monomer with a density of 1470 kg m−3 and a molecular weight of 0.143 kg mol−1; see Sect. 2.4) required a different scaling, resulting in a value of Cw=0.00542 cm−1 s−0.5 that was used throughout this study.
Dilution is taken into account by a loss rate that is independent of size and equals kdil=9.6 × 10−5 s−1. Correcting for particle–particle collisions requires the calculation of the collision frequency function. We used the method from Chan and Mozurkewich (2001). This method includes the effect of enhanced collision rates through van der Waals forces. A value of 6.4 × 10−20 J was used for the Hamaker constant (Hamaker, 1937), leading to a maximum enhancement factor of ∼ 2.3 for the smallest clusters, relative to the collision rate in the absence of van der Waals forces. The factor of 2.3 has previously been shown to give good agreement between measured and modeled cluster and particle concentrations for the chemical system of sulfuric acid and DMA (Kürten et al., 2014; Lehtipalo et al., 2016). In order to consider the collisions of particles in the same size bin, a scaling factor si,j is used in Eq. (1), which is 0.5 when i=j and 1 otherwise.
2.3 Reconstruction method
Recently a new method was introduced that makes it possible to retrieve NPF rates at sizes below the threshold of the instrument used to determine the particle number density. This method is capable of considering the effect of self-coagulation (Kürten et al., 2015a). It requires introducing new size bins below the threshold of the SMPS (termed dp2 in the following; dp2 corresponds to the index m=1). The method starts by calculating the number density in the first newly introduced smaller size bin (index m=0, diameter dp2− ddp):
Here, the particle growth rate (GR, nm s−1) as well as the difference between two adjacent size bins (ddp) needs to be used. Once the number density in the newly introduced bin is known this information can be used to calculate Jm−1. In the further steps, the numbers Nm−2 and Jm−2 are calculated and so on. In this way, the size distribution can be extrapolated towards smaller and smaller sizes in a stepwise process until eventually reaching the diameter dp1.
The method has so far only been tested against simulated data, not against measured size distributions (Kürten et al., 2015a). In this study the smallest measured SMPS diameter is dp2=4.3 nm; 26 new size bins with ddp=0.1 nm were introduced and this enabled the calculation of the NPF rates at dp1=1.7 nm in the smallest size bin. This size was chosen since previously published particle formation rates from the CLOUD experiment were reported for this diameter (e.g., Kirkby et al., 2011; Almeida et al., 2013; Riccobono et al., 2014).
The method introduced here explicitly takes into account losses that occur between particles with dp1 and dp2 (self-coagulation). These losses have not been taken into account by Almeida et al. (2013). Almeida et al. (2013) derived J3.2 nm from condensation particle counter (CPC) and SMPS measurements by including the corrections for wall loss, dilution, and coagulation above 3.2 nm (see also Kürten et al., 2016a). However, the extrapolation to 1.7 nm was made by using the Kerminen and Kulmala equation (Kerminen and Kulmala, 2002), which does not include the effect of self-coagulation. For the system of sulfuric acid and DMA, in which a significant fraction of particles reside in the small size range, this process is, however, important.
2.4 Kinetic new particle formation and growth model
The measured particle formation rates are compared to modeled formation rates assuming collision-limited particle formation, i.e., all clusters are not allowed to evaporate. McMurry (1980) was the first to show that number concentrations and size distributions of particles formed photochemically from SO2 in chamber experiments (Clark and Whitby, 1975) are consistent with collision-controlled nucleation; results from updated versions of this model have recently been presented (Kürten et al., 2014; McMurry and Li, 2017). The model used here has been described previously (Kürten et al., 2014, 2015a, b) but only brief introductions were reported; therefore, more details are provided in the following.
As outlined in Kürten et al. (2014), collision-controlled NPF accurately described the measured cluster distributions for the sulfuric acid–DMA system up to the pentamer (cluster containing five sulfuric acid molecules). In this model, it was assumed that the clusters consist of “monomeric” building blocks, each containing one DMA and one sulfuric acid molecule. Evidence that this 1:1 ratio between base and acid is approximately maintained for the small clusters was presented from neutral and charged cluster measurements (Almeida et al., 2013; Kürten et al., 2014; Bianchi et al., 2014; Glasoe et al., 2015). The molecular weight was, therefore, chosen as 0.143 kg mol−1 (sum of sulfuric acid with 0.098 kg mol−1 and DMA with 0.045 kg mol−1), and the density was chosen as 1470 kg m−3 (Qiu and Zhang, 2012).
During the reported experiments (CLOUD7 in fall 2012), DMA was always present at mixing ratios above ca. 20 pptv (5 × 108 cm−3). DMA was supplied from a certified gas bottle and diluted with synthetic air before it was introduced into the chamber to achieve the desired mixing ratios. Sulfuric acid was generated in situ from the reactions between SO2 and OH whenever the UV light was turned on (see Sect. 2.1). Since the UV light intensity and the gas concentrations were kept constant throughout each individual experiment, it is justified to assume a constant monomer production rate P1. The equation describing the temporal development of the monomer concentration, N1, is
and, for the clusters containing two or more sulfuric acid molecules (k≥2),
The same loss mechanisms (wall loss, dilution, and coagulation) as for the calculation of the particle formation rates (Sect. 2.2) are considered when modeling the cluster concentrations. In this study, the particle size distribution was calculated from the monomer up to a diameter of ∼ 84 nm, which corresponds to the upper size limit of the SMPS used in CLOUD7. Tracking each individual cluster or particle up to this large size would be computationally too demanding; thus, the size distribution was divided into so-called molecular size bins (tracking each individual cluster) and geometric size bins, in which the mid-point diameters of two neighboring size bins differ by a constant factor. The number of molecular size bins was set to 400 (which results in a diameter of ∼ 5 nm for the largest molecular bin), while the number of geometric size bins was set to 190 with a geometric factor of 1.015 (maximum diameter of the last bin is 83.7 nm). The treatment of the geometric size bins was similar to the molecular bins, except that the collision products were distributed between the two closest size bins. Two smaller particles with diameters dp,i and dp,j generate a cluster with size
If it is assumed that the collision product falls into the size range covered by the geometric bins, its diameter will be between two size bins dp,k and . The production rate of particles with diameter dp,x is
For the geometric size range, the resulting particles are distributed between the two bins to conserve mass, i.e.,
When the collision product falls into the molecular size bin regime the calculation is straightforward because the diameter of the product agrees exactly with a molecular bin and does not need to be distributed between two bins (see the production term in Eq. 6). In case the collision products exceed the largest bin diameter, the product is entirely assigned to the largest bin, while taking into account the scaling such that the total mass is conserved.
In the model, no free parameter is used as the concentration of monomers is constrained by the measurements. Therefore, the production rate P1 is adjusted such that the resulting monomer concentration in the model matches the measured sulfuric acid concentration. The model is used to simulate the experiments for a duration of 10 000 s with a time resolution of 1 s. For the small clusters and particles this leads to a steady state between production and loss; therefore, the resulting concentrations are essentially time independent.
The model introduced here was compared with the model described in McMurry and Li (2017) and yielded almost indistinguishable results for several scenarios when the same input parameters were used. We take this as an indication that both models correctly describe collision-controlled nucleation, especially since the models were independently developed and do not share the same code. The model in this paper is based on defining size bins according to their diameter, while the model by McMurry and Li (2017) uses particle volume.
2.5 Nucleation and growth model involving selected evaporation rates
Measured cluster concentrations for the sulfuric acid–DMA system from flow tube experiments indicated that finite evaporation rates exist for some clusters (Jen et al., 2014, 2016a). This was supported by the observation that diamines can yield even higher formation rates than amines for some conditions (Jen et al., 2016b). Within the flow tube experiments DMA was mixed into a gas flow containing a known amount of sulfuric acid monomers. The products, i.e., the sulfuric acid–DMA clusters, were measured after a short reaction time (≤ 20 s) with a chemical ionization mass spectrometer. From the measured signals, the cluster evaporation rates were retrieved from model calculations (Jen et al., 2016a). The main differences to the CLOUD study lie within the much shorter reaction time (20 s vs. steady state in CLOUD) and in the much wider range of base-to-acid ratios used by Jen et al. (2016a, b). This allowed them to retrieve even relatively slow evaporation rates for the sulfuric acid–DMA clusters. The measured cluster and particle concentrations increased with an increasing base-to-acid ratio, eventually approaching a plateau at a DMA-to-acid ratio of ∼ 1. Therefore, the high DMA-to-acid ratio used in the CLOUD7 experiment (∼ 100) can probably explain why our NPF rates are compatible with collision-controlled nucleation.
However, this was further tested by incorporating the evaporation rates from Jen et al. (2016a) in our model. For this purpose, the model described in Sect. 2.4 was modified in a way that allows the retrieval of the cluster concentrations of the monomer, dimer, trimer, and tetramer as functions of their DMA content (see Appendix A). The abbreviation AxBy denotes the concentration of a cluster containing x sulfuric acid (x=1 for the monomer) and y base (DMA) molecules. It is assumed that x≥y for all clusters, i.e., the number of bases, is always smaller than or equal to the number of acid molecules. The reported cluster concentrations (Fig. 3) refer to the number of acid molecules in the cluster, i.e., , and .
The evaporation rates considered are .1 s−1, s−1, and s−1 (Jen et al., 2016a). Jen et al. (2016a) suggested that the formation of stable tetramers requires at least two base molecules. In this case the evaporation rate of ke,A4B1 is infinity. In the model, this was solved by not taking into account the formation of clusters A4B1 (from A3B1 and A1) at all. Further details about the modeling involving evaporation rates can be found in Appendix A and in Table 1, which gives a summary of the different model studies.
3.1 Comparison between Almeida et al. (2013) and SMPS-derived NPF rates
Using the model described in Sect. 2.4, a comparison between the previously published NPF rates from Almeida et al. (2013) and the modeled rates was performed. Almeida et al. (2013) derived NPF rates for a particle mobility diameter of 1.7 nm. Using a density of 1470 kg m−3 and a molecular weight of 0.143 kg mol−1, it can be calculated that a spherical cluster containing nine monomers (nonamer) has a geometric diameter of ∼ 1.4 nm, i.e., a mobility diameter of 1.7 nm (Ku and Fernandez de la Mora, 2009; see also Appendix A); therefore, the modeled nonamer formation rates were used for the comparison.
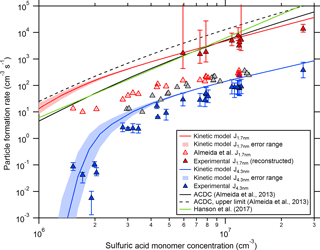
Figure 1Comparison between experimental and theoretical particle formation rates at different sizes (mainly at mobility diameters of 1.7 and 4.3 nm). The red and blue lines indicate calculated particle formation rates from the collision-controlled aerosol model described in Sect. 2.4 for CLOUD chamber conditions. The shaded regions show the model uncertainties when using an error of ±20 % for the wall loss coefficient (Cw; see Eq. 2). The open red symbols show previously published CLOUD7 data for the sulfuric acid–DMA–water system (Almeida et al., 2013), while the blue symbols show the rates derived from SMPS size distribution measurements (this study). The data shown by the closed red symbols were derived with the method introduced by Kürten et al. (2015a) by extrapolating the SMPS data starting at 4.3 nm. The black lines show the calculated formation rates from the ACDC model for a mobility diameter of 1.2 to 1.4 nm (Almeida et al., 2013). Equation (11) from Hanson et al. (2017) is used to generate the green line.
Figure 1 shows the modeled formation rates at 1.7 nm and the Almeida et al. (2013) data as functions of the sulfuric acid concentration (which is equivalent to the monomer concentration in the model (see Sect. 2.4) since it is assumed that all sulfuric acid is bound to DMA). It can be seen that the modeled NPF rates are significantly higher. This indicates that the previously published formation rates underestimate the true formation rates if sulfuric acid–DMA nucleation indeed proceeds at the collision limit. Previously published results indicated that this is the case (Kürten et al., 2014; Lehtipalo et al., 2016); however, we will provide further evidence that this assumption accurately describes the experiments in the present study and provide an explanation why Almeida et al. (2013) underestimated the formation rates.
It should be noted that the displayed experimental J1.7 nm values (open red triangles in Fig. 1) are identical to the values from Almeida et al. (2013), while the sulfuric acid concentration has been corrected. In Almeida et al. (2013) data were shown from CLOUD4 (spring 2011) and CLOUD7 (fall 2012). For consistency, the sulfuric acid concentrations from the chemical ionization mass spectrometer (Kürten et al., 2011) were used, as the CI-APi-TOF was not available during CLOUD4. Especially during CLOUD7, the chemical ionization mass spectrometer showed relatively high sulfuric acid concentrations even when no sulfuric acid was produced from the UV light system inside the CLOUD chamber; no correction was applied for this effect in Almeida et al. (2013). However, taking into account a subtraction of this instrumental background (sometimes reaching values above 1 × 106 cm−3) leads to a shallower slope for J1.7 nm vs. sulfuric acid and brings the corrected chemical ionization mass spectrometry values in good agreement with the sulfuric acid measured with the CI-APi-TOF. In the present study, the data from the CI-APi-TOF were used. The slope for J1.7 nm vs. sulfuric acid now yields a value of close to 2, while the previously reported value was ∼ 3.7 (Almeida et al., 2013). The higher value resulted from the bias in the sulfuric acid concentration and the consideration of data points at low sulfuric acid concentration, where NPF is significantly affected by losses to the chamber walls, which tends to bias the slope towards higher values (Ehrhart and Curtius, 2013).
3.2 Comparison between NPF rates from the kinetic model and SMPS measurements
The formation rates in Almeida et al. (2013) were calculated from measured particle number densities with a condensation particle counter that has a lower cutoff diameter of ∼ 3 nm. The derivation of particle formation rates at 1.7 nm therefore required an extrapolation to the smaller diameter (Kerminen and Kulmala, 2002). With the available model, we are now, in principle, able to calculate NPF rates for any particle diameter and compare the result to directly measured rates. This was done for the SMPS size channel corresponding to a mobility diameter of 4.3 nm (J4.3 nm) with the method described in Sect. 2.2. Using the SMPS data has the advantage that the size-dependent loss rates can be accurately taken into account, which is not possible when only the total (non-size-resolved) concentration from a condensation particle counter is available. Conversely, the smallest SMPS size channels need to be corrected by large factors to account for losses and charging probability (Sect. 2.1), which introduces uncertainty.
The result for J4.3 nm is shown in Fig. 1 together with the modeled particle formation rates for the same diameter. The agreement between modeled and measured NPF rates is very good, indicating that the collision-controlled model accurately describes 4.3 nm particle production rates for these experiments. This is further evidence that particles are formed at the collision limit. However, it is also an indication that the Almeida et al. (2013) data underestimate the NPF rates, which is further discussed in the following section.
3.3 Reconstruction model results
Recently, a new method was introduced, which allows the extrapolation of NPF rates determined at a larger size (dp2) to a smaller diameter (dp1). The advantage of that method is that the effect of cluster–cluster collisions (self-coagulation) can be accurately taken into account (Kürten et al., 2015a). So far, the method has not been tested for measured particle size distributions. However, the effect of cluster–cluster collisions should be largest in the case of collision-controlled nucleation since it results in the highest possible cluster (particle) concentrations for a given production rate of nucleating molecules. Therefore, the current data set is ideal for testing the new method. It requires the measured growth rate as an input parameter (Eq. 4); this growth rate was derived from fitting a linear curve to the mode diameter determined from the SMPS size distribution (Hirsikko et al., 2005). It was then used as a constant (i.e., it was assumed that it is independent of size) for the full reconstruction of the size distribution in order to obtain a formation rate at 1.7 nm. The growth rate could only be accurately determined for experiments with relatively high sulfuric acid concentration (above ∼ 5 × 106 cm−3); therefore, the reconstruction method was only tested for these conditions (Fig. 1). The comparison with the modeled formation rates at the same size (1.7 nm) shows that the reconstruction method yields quite accurate results, highlighting the importance of cluster–cluster collisions in this chemical system. This explains why the Almeida et al. (2013) data strongly underestimate the particle formation rates.
While the reconstruction method gives good results in the present study, it needs to be mentioned that the errors for this method can become quite large. Small inaccuracies in the growth rate can be blown up to very large uncertainties due to the nonlinear nature of the method. This can be seen for some of the data points with large error bars in the positive direction. The errors are calculated by repeating the reconstruction with growth rates GR ± dGR, where dGR (±20 %) is the error from the fitted growth rate. Therefore, the accuracy of the method strongly depends on good growth rate measurements and relies on the assumption that the growth rate does not change as a function of size. This seems to be a reasonable approximation for collision-controlled nucleation under the present conditions (Kürten et al., 2015a), but it could be different in other chemical systems.
The higher formation rates are also consistent with calculations from the ACDC (Atmospheric Cluster Dynamics Code) model (McGrath et al., 2012) that were previously published in Almeida et al. (2013). Figure 1 shows the rates calculated by the ACDC model (black lines). It should be noted that these values refer to a mobility diameter of 1.2 to 1.4 nm and therefore somewhat higher rates are expected due to the smaller diameter compared to J1.7 nm. However, the agreement between the measured and predicted rates from ACDC are now in much better agreement than before.
Hanson et al. (2017) recently reported an expression for the calculation of particle formation rates as a function of the sulfuric acid concentration, DMA concentration, and temperature. According to their formula the formation rate of tetramers (mobility diameter of ∼ 1.4 nm; see Appendix A) follows the expression
The formation rates J1.4 nm are shown in Fig. 1 (green line) for a DMA mixing ratio of 40 pptv (1 × 109 cm−3) and a temperature of 278 K. At first glance, the agreement between the experimental CLOUD data and Eq. (11) is remarkably good. However, one should note that Hanson et al. (2017) recommended using their equation only for DMA between 2 pptv (5 × 107 cm−3) and 16 pptv (4 × 108 cm−3) if sulfuric acid is present between 1 × 106 and 2 × 107 cm−3. Using the equation in this range avoids formation rates exceeding the kinetic limit. When using larger concentrations, the kinetic limit is eventually exceeded due to the power dependency of 3 regarding sulfuric acid and the 1.5 power dependency for DMA. Further comparison between Eq. (11) and the results from the present study are shown in Fig. 3 (lower panel).
3.4 Size distribution comparison between model and SMPS
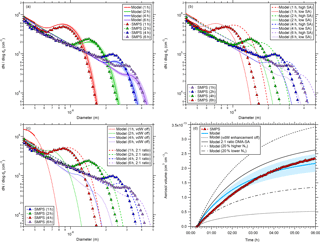
Figure 2Comparison between simulated and measured particle size distributions for one experiment (CLOUD7, run 1036.01). The comparison is shown for four different times (1, 2, 4, and 6 h) after the start of the experiment (panels a, b, and c). Panel (d) shows a comparison between modeled and measured aerosol volume as a function of time. The shaded regions in panel (a) show the model uncertainties when using an error of ±20 % for the wall loss coefficient (Cw; see Eq. 2). Panel (b) shows the change in the size distributions when the sulfuric acid monomer concentration is varied by ±20 %. The effect of van der Waals forces on the size distribution is shown in panel (c) along with the assumption that particles grow by the addition of two DMA molecules and one sulfuric acid molecule (2:1 ratio instead of 1:1 ratio). See text for further details.
Further comparison between modeled and measured data was performed for one experimental run (CLOUD7 run 1036.01) in which the particles were grown to sizes beyond 20 nm. Therefore, the time-dependent cluster and particle concentrations were modeled for a monomer production rate of 2.9 × 105 cm−3 s−1, which results in a steady-state monomer concentration of 1.07 × 107 cm−3 for the model; this is the same as the measured sulfuric acid concentration. The measured and modeled size distributions are shown in Fig. 2 (panels a, b, and c) at four different times, i.e., at 1, 2, 4, and 6 h after the start of the experiment. Given that there is no free parameter used in the model, the agreement between the base case simulation and the measurement is very good (Fig. 2a). For the earliest time shown (1 h) the modeled concentrations overestimate the measured concentrations by up to 30 %, whereas for the later times (≥ 4 h) the model underestimates the measured concentrations by up to 30 %. It is unclear whether these discrepancies are due to SMPS measurement uncertainties or if the model does not include or accurately describe all the relevant processes. If, for example, the SMPS would underestimate the concentrations of the smaller particles (< ca. 15 nm) and overestimate those of the larger particles, the observed difference between modeled and measured concentrations could also be explained.
A comparison between measured and modeled aerosol volume concentrations is shown in Fig. 2d. In order to enable direct comparison, the modeled size distribution was integrated starting at 4.3 nm since the SMPS did not capture smaller particles. In the beginning of the experiment the modeled aerosol volume is up to ∼ 40 % larger than the measured one, but, towards the end of the experiment (ca. 4 h after its start), the volumes agree quite well. This is possibly because the overestimated modeled particle number density at small diameters is compensated for by the underestimated particle concentration in the larger size range (see Fig. 2a).
This trend eventually leads to a slight underestimation of the aerosol volume by the model.
If one assumes that the SMPS is not responsible for the slight disagreement, then the following conclusions can be drawn regarding the accuracy of the model. The particle growth rate is represented well by the model given the good agreement between the positions of the local maxima in the size distribution and the intersections between the size distributions and the x axis. This good agreement between measured and modeled growth rates has already been demonstrated in Lehtipalo et al. (2016) for a particle diameter of 2 nm. The results shown here indicate that no significant condensation of other trace gases contributes to the growth of particles because, in this case, the measured particle size distributions would be shifted towards larger diameters compared to the model.
The good agreement between model and measurement is also a confirmation of the effect of van der Waals forces, when a Hamaker constant of 6.4 × 10−20 J is used, a value that has been demonstrated previously to represent particle size distribution dynamics correctly (McMurry, 1980; Chan and Mozurkewich, 2001; Kürten et al., 2014; Lehtipalo et al., 2016). Regarding the underestimation of the modeled size distribution for diameters of 15 nm, one explanation could be that the size-dependent particle loss rates in the CLOUD chamber are weaker than assumed (kw ∼ D0.5; see Eq. 2). A weaker size dependence would lead to higher predicted particle concentrations at larger sizes (Park et al., 2001). However, no evidence was found from the existing CLOUD data that this is the case. Dedicated wall loss experiments could be performed in the future to investigate this hypothesis further.
In order to quantitatively test the model sensitivity to certain variations, further simulations were performed (Fig. 2b and c). A variation in the steady-state sulfuric acid monomer concentration by ±20 % was achieved by using different monomer production rates for the high sulfuric acid case (P1=4.17 × 105 cm−3 s−1) and for the low sulfuric acid case (P1=2.01 × 105 cm−3 s−1, Fig. 2b). This rather small variation leads to significant mismatches between the modeled and measured size distributions that are also found for the aerosol volumes (Fig. 2d).
Two further scenarios were tested with the model. First, the enhancement due to van der Waals forces was turned off. This scenario results in significantly slower growth rates and the modeled size distributions do not match the measured ones at all anymore (Fig. 2c); the same is found when comparing modeled and measured aerosol volumes (Fig. 2d). Second, the aerosol density and the molecular weight of the condensing monomer were changed. In the base case simulations (Fig. 2a), the density of dimethylaminium bisulfate is 1470 kg m−3 and the molecular weight is 0.143 kg mol−1 because a one-to-one ratio between DMA and sulfuric acid is assumed. Since full neutralization of sulfuric acid by DMA would require a 2:1 ratio between base and acid, collision-controlled nucleation of (H2SO4)((CH3)2NH)2 monomers instead of (H2SO4)((CH3)2NH) was tested. Therefore, the density was decreased by 6 % to account for the density change between dimethylaminium bisulfate and dimethylaminium sulfate (see Qiu and Zhang, 2011), and the molecular weight was set to 0.188 kg mol−1. As expected, the particle growth is now slightly faster due to the additional volume added by the further DMA molecules (Fig. 2c). However, the changes are rather small and the modeled size distributions move a little further away from the measurements compared to the base case scenario (Fig. 2a).
Comparison between modeled and measured size distributions yielded similar results for other experiments from CLOUD7. However, the experiment shown in Fig. 2 was carried out over a relatively long time (6 h) at high sulfuric acid concentrations. Therefore, the particles could grow to large diameters and the comparison between model and experiment covers a wide size range.
3.5 Sensitivity of cluster concentrations and NPF rates regarding DMA
The data presented in the previous sections provide evidence that the NPF in the sulfuric acid–DMA system during CLOUD7 proceeds at rates that are consistent with collision-controlled nucleation, in agreement with results for this data set obtained using different approaches (Kürten et al., 2014; Lehtipalo et al., 2016). In this section, we compare whether for CLOUD conditions the collision-controlled assumption is consistent with the Jen et al. (2016a) results that showed that some clusters evaporate at the rates given in Sect. 2.5 and Table 1.
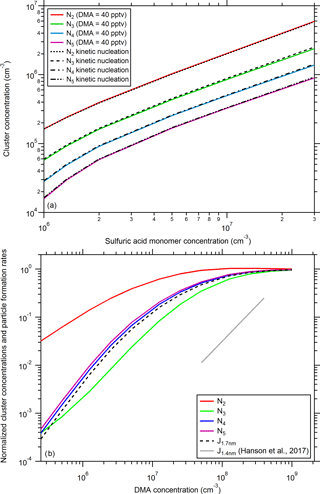
Figure 3(a) Comparison of modeled cluster (N2: dimer, N3: trimer, N4: tetramer, and N5: pentamer) concentrations using different scenarios. The dashed black lines use the collision-controlled nucleation scheme with all evaporation rates set to zero (Sect. 2.4); while the colored solid lines are calculated based on the model from Sect. 2.5 with a dimethylamine (DMA) mixing ratio of 40 pptv (1 × 109 cm−3), which was the average mixing ratio during the CLOUD7 campaign. (b) Variation in modeled cluster concentration and J1.7 nm as a function of the dimethylamine mixing ratio. The data were normalized to the values from the collision-controlled limit calculation (a). For the calculations, a sulfuric acid monomer concentration of N1= 5 × 106 cm−3 was used. An expression from Hanson et al. (2017) to calculate NPF rates as a function of DMA is shown by the grey line. See text for further details.
For the following discussion, both versions of the nucleation and growth model (Sect. 2.4 and 2.5) were used. Figure 3 shows a comparison between calculated cluster (dimer, trimer, tetramer, and pentamer) concentrations using collision-controlled nucleation (Sect. 2.4) and the model described in Sect. 2.5. When a DMA mixing ratio of 40 pptv (1 × 109 cm−3) is used (this was the average mixing ratio of DMA during the CLOUD7 experiments), there is almost no difference between the two scenarios. This indicates that, under the CLOUD7 conditions, NPF proceeded at almost the same rates that result for collision-controlled nucleation. Nevertheless, this does not imply that all cluster evaporation rates are zero. The conditions are only such that, due to the high DMA mixing ratio, most of the clusters (including the monomer) probably contain as many DMA molecules as sulfuric acid molecules; this results in very stable cluster configurations (Ortega et al., 2012). When DMA mixing ratios are low, most sulfuric acid clusters, however, contain only a small number of DMA molecules. As these clusters can evaporate more rapidly, the overall formation rate is slowed down (Ortega et al., 2012; Hanson et al., 2017). For low base-to-acid ratios, it can therefore matter whether a cluster is stabilized by a DMA, a diamine (Jen et al., 2016b), or by both an amine and an ammonia molecule (Glasoe et al., 2015). This can explain the more efficient NPF due to diamines or the synergistic effects involving amines and ammonia at low base-to-acid ratios. At high base-to-acid ratios, the differences in the effective evaporation rates become small (Jen et al., 2016b).
The effect of the DMA concentration on the cluster concentrations and on the particle formation rate was further investigated. The lower panel of Fig. 3 shows that the cluster concentrations and the NPF rate at 1.7 nm decrease with decreasing DMA levels. The figure shows the concentrations and the NPF rate normalized by the results for the collision limit. The NPF rate drops by about a factor of 3 when DMA is reduced to 2.5 × 107 cm−3 (∼ 1 pptv). Below that level, the reduction in J and in the trimer, tetramer, and pentamer concentrations is approximately linear with DMA. The dimer is less affected since, in the model, its evaporation rates are set to zero while the evaporating trimers contribute to the dimer concentration. From this perspective, very high particle formation rates should be observed even at DMA mixing ratios around 1 pptv (2.5 × 107 cm−3), which should be almost indistinguishable from rates calculated for collision-controlled nucleation. Possibilities for why such high rates have so far not been observed are discussed in Sect. 4.
For a comparison, the expected formation rates from Eq. (11) are shown in Fig. 3, lower panel, by the grey line. The values were scaled similar to the simulated data by setting the value for 40 pptv (1 × 109 cm−3) to 1. Although this DMA mixing ratio is outside the range for which the Hanson et al. (2017) formulation is recommended (between 5 × 107 and 4 × 108 cm−3), from Fig. 1 it can be concluded that both the Hanson et al. (2017) equation and the kinetic model agree quite well at this DMA mixing ratio. The slope of J vs. DMA seems, however, to be different in the relevant range of DMA (5 × 107 and 4 × 108 cm−3). This is due to the fact that the model predicts a steep slope (close to the value of 1.5 in Eq. 11) only for much lower DMA (< 2.5 × 106 cm−3); for higher DMA the slope flattens out and eventually reaches a plateau, when the value for collision-controlled nucleation is approached. This flatting of the curve is not reflected in the simple formulation from Hanson et al. (2017). However, in contrast to the three constant evaporation rates used in our modeling approach, Hanson et al. (2017) used a more sophisticated nucleation scheme involving many different evaporation rates, not only regarding sulfuric acid but also for DMA. This more complex scheme was, however, not implemented in our model.
Further experiments are required to derive accurate values for evaporation rates in the sulfuric acid–DMA system; these experiments should especially target DMA concentrations with low base-to-acid ratios (< 10).
This study confirms the results derived in previous studies that NPF in the sulfuric acid–DMA–water system can proceed at or close to the collision-controlled limit (Kürten et al., 2014; Lehtipalo et al., 2016). This is the case for sulfuric acid concentrations between 1 × 106 and 3 × 107 cm−3 and DMA mixing ratios around 40 pptv (1 × 109 cm−3) at 278 K and 38 % relative humidity. For these conditions particle formation rates and size distributions can be reproduced with high accuracy by an aerosol model that assumes that particle growth is exclusively due to the irreversible addition of H2SO4 ⋅ (CH3)2NH monomers and coagulation. Even when evaporation rates for the less stable clusters are introduced in the model (Jen et al., 2016a) the resulting particle formation rates are effectively indistinguishable from the kinetic model results for CLOUD7 conditions (i.e., at the high DMA-to-acid ratio of ∼ 100). The fact that the measured particle size distribution can be reproduced with good accuracy shows that neither water nor other species contribute significantly to particle growth during these CLOUD chamber experiments. Water could play a role at higher relative humidities, although quantum chemical calculations suggest that it plays only a minor role in NPF for the system of sulfuric acid and DMA (Olenius et al., 2017); this contrasts with the sulfuric acid–water system (see e.g., Zollner et al., 2012; Duplissy et al., 2016; Yu et al., 2017). In addition, it is not exactly known how temperature influences the cluster evaporation rates (Hanson et al., 2017). The evaporation rates from Jen et al. (2016a) were derived at temperatures close to 300 K; therefore, the simulation of nucleation in the CLOUD chamber (278 K) using the Jen et al. (2016a) rate parameters is likely to overestimate the effect of cluster evaporation.
It is not yet clear what exact base-to-acid ratio the particles have for a given diameter. The clusters and small particles (< ∼ 2 nm) seem to grow by maintaining a 1:1 ratio between base and acid, which follows from measurements using mass spectrometers (Almeida et al., 2013; Kürten et al., 2014; Bianchi et al., 2014). The larger particles could eventually reach a 2:1 ratio between base and acid, especially at the DMA mixing ratios relevant for this study (Ahlm et al., 2016). However, even when a 2:1 ratio is assumed in the model (Fig. 2c) the expected size distributions would not change significantly compared with the base case scenario (1:1 ratio). Therefore, it is not possible from our comparisons to find out if and at what diameter a transition from a 1:1 to 2:1 base-to-acid ratio takes place.
The question of why sulfuric acid–amine nucleation is rarely observed in the atmosphere is still open. Jen et al. (2016a) reported that clusters that contain equal numbers of DMA and sulfuric acid molecules are ionized at reduced efficiencies than more acidic clusters with the commonly used NO(HNO3)0−2 reagent ions. Still, Kürten et al. (2014) observed high concentrations for large clusters containing acid and base at an average ratio of 1:1. A reduced detection efficiency was also reported but the reduced sensitivity (in relation to the monomer) was only a factor of 3 for the trimer containing DMA. Using the model results from Sect. 3.5 the expected trimer concentration at 5 × 106 cm−3 of sulfuric acid and 1 pptv (2.5 × 107 cm−3) of DMA should be ∼ 1 × 105 cm−3. Even when the detection efficiency for the trimer was reduced by a factor of 3, such a concentration should still be well above the detection limit of a CI-APi-TOF. However, no sulfuric acid trimers could be detected in a field study in which amines were present at levels above 1 pptv (2.5 × 107 cm−3; Kürten et al., 2016b). It is therefore possible that any amines present were not suitable for nucleation. Therefore, application of methods capable of amine speciation should be applied more widely in atmospheric measurements (Place et al., 2017).
Several CLOUD papers reported particle formation rates for a diameter of 1.7 nm. Some of these published formation rates were derived from direct measurements using particle counters with cutoff diameters close to 1.7 nm (Riccobono et al., 2014; Duplissy et al., 2016), while other reported NPF rates were derived from process models describing the nucleation process in the CLOUD chamber (Kirkby et al., 2011, 2016). Therefore, no extrapolation of the NPF rates from a larger threshold diameter was performed, which could have led to an underestimation due to missing self-coagulation. In addition to Almeida et al. (2013), the data set reported by Dunne et al. (2016) and Kürten et al. (2016a) did make use of the NPF rate extrapolation method from 3.2 to 1.7 nm without taking into account the effect of self-coagulation. However, the reported formation rates are, in almost all cases, considerably slower than those for the collision-controlled limit at a given sulfuric acid concentration since no DMA was present in the CLOUD chamber (Dunne et al., 2016; Kürten et al., 2016a). The chemical system in these studies was the binary system (H2SO4 and H2O) and the ternary system involving ammonia. The conditions only approached the collision-controlled limit at the lowest temperature (210 K) when the highest ammonia mixing ratio of ∼ 6 pptv (1.5 × 108 cm−3) was investigated (Kürten et al., 2015b). However, even under these conditions, the reported rates are only about a factor of 2 slower than the collision-controlled limit (Kürten et al., 2016a). This is probably related to the low acid concentrations (≤ 3 × 106 cm−3) in these experiments, in which the self-coagulation effect is not as strong as at higher acid concentrations (see Fig. 1) when wall loss and dilution lead to decreased cluster concentrations relative to the monomer. This indicates that previously published CLOUD results, other than the Almeida et al. (2013) data, are most likely not significantly affected.
McMurry and Li (2017) have recently investigated the effect of the wall loss and dilution rate on NPF with their numerical model, which uses dimensionless parameters. In order to allow for a comparison between McMurry and Li (2017) and the present study, information on the dimensionless parameters W (describing wall loss) and M (describing dilution) is provided (see McMurry and Li, 2017, for the exact definitions). These parameters range from 0.04 to 0.7 (W) and 2 × 10−3 to 4 × 10−2 (M) for the experiments shown in this study (Fig. 1). The monomer production rate (P1) ranges from 7 × 103 to 2 × 106 cm−3 s−1.
New particle formation rates from CLOUD chamber measurements for the sulfuric acid–DMA–water system were reanalyzed. It was found that the previously published rates by Almeida et al. (2013) underestimate the NPF rates by up to a factor of ∼ 50 at high sulfuric acid concentrations (∼ 1 × 107 cm−3). The reason for this underestimation is the effect of self-coagulation that contributes efficiently to the loss of small particles in the size range relevant for the data analysis (between 1.7 and 3.2 nm). The previously used method for extrapolating the NPF rates from 3.2 to 1.7 nm did not include this effect and therefore the correction factors were too small. Using an advanced reconstruction method that accounts for the effect of self-coagulation yields much higher NPF rates (Kürten et al., 2015a). These corrected NPF rates are in good agreement with rates calculated from an aerosol model assuming collision-controlled nucleation and with measured NPF rates from SMPS data. Furthermore, the model can reproduce the measured size distribution with good accuracy up to ∼ 30 nm.
Extending the aerosol model by including evaporation rates for some clusters (see Jen et al., 2016a) still yields good agreement between modeled and measured CLOUD NPF rates and cluster concentrations. This indicates that the data for sulfuric acid–DMA from the flow tube study by Jen et al. (2016a) and from CLOUD (Kürten et al., 2014) are consistent for the high base-to-acid ratio relevant for this study (monomer ratio of DMA to sulfuric acid of ∼ 100).
The findings above raise some further conclusions and questions. These are in part related to the rare detection of sulfuric acid–amine nucleation in the atmosphere. Only one study has so far reported sulfuric acid–amine nucleation (Zhao et al., 2011). The nucleation of sulfuric acid–amines could, however, occur more often than currently thought.
-
It is unclear to what extent previously published atmospheric NPF rates are affected by incomplete J extrapolations. Some J measurements were made at diameters close to 3 nm and extrapolated to a smaller size. If self-coagulation were important, the formation rates at the small sizes could be significantly underestimated, and, therefore, in reality be much closer to rates consistent with collision-controlled nucleation than previously thought. In such a case, DMA (or other equally effective amines) could have been responsible for nucleation as they are among the most potent nucleation precursors (in combination with sulfuric acid). To avoid such ambiguities, the NPF rates should, in the future, be directly measured at small diameters whenever possible.
-
Better gas-phase amine (base) measurements are needed. Detection limits need to reach mixing ratios even below 0.1 pptv (2.5 × 106 cm−3); ideally the methods should also be capable of speciating the amines (discriminate DMA from ethylamine, which have the same mass when measured using mass spectrometry but probably behave differently in terms of their contribution to NPF). High time resolution (several minutes or better) for the amine measurements during nucleation events is also important. This can show whether amines can be significantly depleted during NPF. As amines are not produced in the gas phase (unlike sulfuric acid), their clustering with sulfuric acid monomers and small sulfuric acid clusters or particles can very likely lead to a significant reduction in the amine mixing ratios (Kürten et al., 2016b). This would indicate that NPF involving amines in the atmosphere could be self-limiting, i.e., after an initial burst of particles, NPF could be slowed down soon after when amine mixing ratios decrease.
-
It is not clear why no clusters containing three or more sulfuric acid molecules are frequently observed during atmospheric NPF when amines are expected to be present. This could be due to incorrect assumptions about the amine concentrations, the amine identities, or a reduced detection efficiency of chemical ionization mass spectrometers (Jen et al., 2016a). The potential formation of complex multi-species clusters (containing sulfuric acid, amines, ammonia, and oxidized organics) in the atmosphere could distribute the clusters over many different identities and therefore result in concentrations too low to be detected by the current instrumentation for the individual species.
The overall contribution of amines to atmospheric nucleation can only be quantified after these issues are understood. In addition to further atmospheric measurements, controlled laboratory measurements are necessary. Of special interest are the temperature-dependent evaporation rates of the relevant sulfuric acid–amine (and diamine) clusters.
Data used in this study can be obtained by sending an email to the corresponding author.
The kinetic model described in Sect. 2.4 was expanded in a way that allows the calculation of the concentrations of the monomer, dimer, trimer and tetramer as a function of their dimethylamine content. Here, AxBy denotes the concentration of a cluster containing x sulfuric acid (x=1 for the monomer) and y base (y=1 for dimethylamine monomer) molecules; x≥y for all clusters, i.e., the number of bases is always smaller than or equal to the number of acid molecules. When the total monomer concentration (N1) is fixed, i.e., at each time step, then the following equations result, i.e., for the A1B1 cluster:
for the two different identities of the sulfuric acid dimer
and for the three different identities of the sulfuric acid trimer
Since the formation of stable A4B1 clusters is not allowed (see Jen et al., 2016a), the loss due to the A1 and A3B1 collision is subtracted from the coagulation loss term in Eq. (A4).
Tetramers can be formed from trimers and dimers:
Note that the formation of A4B1 (from A3B1) is not included in the formation rate for tetramers (see also further below). The concentrations of larger clusters and particles are calculated with the same method as described in Sect. 2.4. The cluster concentrations reported in Sect. 3.5 refer to the number of acid molecules in the cluster, i.e., , , and .
The evaporation rates considered are .1 s−1, s−1, and s−1 (Jen et al., 2016a). Pure acid clusters are assumed to evaporate rapidly (at 278 K and higher) and are therefore not considered (Hanson and Lovejoy, 2006). Jen et al. (2016a) suggested that the formation of stable tetramers requires two base molecules. Therefore, this would indicate that the evaporation rate ke,A4B1 is infinity (or very fast), which is also shown by Hanson et al. (2017). However, the A4B1 formation (and its evaporation) is not explicitly treated in Eqs. (A4) and (A7).
In summary, three different evaporation rates were included in this model version (Eqs. A1 to A7), i.e., .1 s−1 (cluster A1B1), s−1 (cluster A3B1), and s−1 (cluster A3B2). All other evaporation rates were not explicitly included in the model, i.e., their rates were assumed to be zero (except for A4B1, which is assumed to be infinity). Table 1 gives an overview of the different model configurations used to generate the model data in the figures.
Calculation of particle mobility diameters
The mobility diameter of a cluster containing i sulfuric acid molecules (and i DMA molecules) can be calculated according to
Mw is the molecular weight of the monomer, i.e., 0.143 kg mol−1, ρ is the density of 1470 kg m−3 (see Sect. 2.4), and NA is the Avogadro number, i.e., 6.022 × 1023 mol−1. The addition of 0.3 nm in Eq. (A8) is used to convert the geometric diameter (first term in Eq. A8) to a mobility diameter (Ku and Fernandez de la Mora, 2009).
The authors declare that they have no conflict of interest.
Funding from the German Federal Ministry of Education and Research (grant
no. 01LK1222A) and the Marie Curie Initial Training Network “CLOUD-TRAIN”
(grant no. 316662) is gratefully acknowledged. Peter H. McMurry's and Chenxi Li's contributions
to this work were supported by the US Department of Energy's Atmospheric
System Research program and Office of Science, Office of Biological and
Environmental Research, under grant number DE-SC0011780. Federico Bianchi thanks the Swiss National Science Foundation (grant no. P2EZP2_168787). Richard C. Flagan acknowledges
funding from the NSF grants 1439551 and 1602086. Matti P. Rissanen appreciates funding
from the Academy of Finland (project no. 299574). Katrianne Lehtipalo thanks the European
Union's Horizon 2020 research and innovation program under the Marie
Skłodowska-Curie grant agreement no. 656994
(nano-CAVa).
Edited by: Farahnaz Khosrawi
Reviewed by: three anonymous referees
Ahlm, L., Yli-Juuti, T., Schobesberger, S., Praplan, A. P., Kim, J., Tikkanen, O.-P., Lawler, M. J., Smith, J. N., Tröstl, J., Acosta Navarro, J. C., Baltensperger, U., Bianchi, F., Donahue, N. M., Duplissy, J., Franchin, A., Jokinen, T., Keskinen, H., Kirkby, J., Kürten, A., Laaksonen, A., Lehtipalo, K., Petäjä, T., Riccobono, F., Rissanen, M. P., Rondo, L., Schallhart, S., Simon, M., Winkler, P. M., Worsnop, D. R., Virtanen, A., and Riipinen, I.: Modeling the thermodynamics and kinetics of sulfuric acid-dimethylamine-water nanoparticle growth in the CLOUD chamber, Aerosol Sci. Tech., 50, 1017–1032, https://doi.org/10.1080/02786826.2016.1223268, 2016.
Almeida, J., Schobesberger, S., Kürten, A., Ortega, I. K., Kupiainen-Määttä, O., Praplan, A. P., Adamov, A., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Dommen, J., Donahue, N. M., Downard, A., Dunne, E. M., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Guida, R., Hakala, J., Hansel, A., Heinritzi, M., Henschel, H., Jokinen, T., Junninen, H., Kajos, M., Kangasluoma, J., Keskinen, H., Kupc, A., Kurtén, T., Kvashin, A. N., Laaksonen, A., Lehtipalo, K., Leiminger, M., Leppä, J., Loukonen, V., Makhmutov, V., Mathot, S., McGrath, M. J., Nieminen, T., Olenius, T., Onnela, A., Petäjä, T., Riccobono, F., Riipinen, I., Rissanen, M., Rondo, L., Ruuskanen, T., Santos, F. D., Sarnela, N., Schallhart, S., Schnitzhofer, R., Seinfeld, J. H., Simon, M., Sipilä, M., Stozhkov, Y., Stratmann, F., Tomé, A., Tröstl, J., Tsagkogeorgas, G., Vaattovaara, P., Viisanen, Y., Virtanen, A., Vrtala, A., Wagner, P. E., Weingartner, E., Wex, H., Williamson, C., Wimmer, D., Ye, P., Yli-Juuti, T., Carslaw, K. S., Kulmala, M., Curtius, J., Baltensperger, U., Worsnop, D. R., Vehkamäki, H., and Kirkby, J.: Molecular understanding of sulphuric acid-amine particle nucleation in the atmosphere, Nature, 502, 359–363, https://doi.org/10.1038/nature12663, 2013.
Ball, S. M., Hanson, D. R., Eisele, F. L., and McMurry, P. H.: Laboratory studies of particle nucleation: Initial results for H2SO4, H2O, and NH3 vapors, J. Geophys. Res.-Atmos., 104, 23709–23718, https://doi.org/10.1029/1999JD900411, 1999.
Bergman, T., Laaksonen, A., Korhonen, H., Malila, J., Dunne, E. M., Mielonen, T., Lehtinen, K. E. J., Kühn, T., Arola, A., and Kokkola, H.: Geographical and diurnal features of amine-enhanced boundary layer nucleation, J. Geophys. Res.-Atmos., 120, 9606–9624, https://doi.org/10.1002/2015JD023181, 2015.
Berndt, T., Sipilä, M., Stratmann, F., Petäjä, T., Vanhanen, J., Mikkilä, J., Patokoski, J., Taipale, R., Mauldin III, R. L., and Kulmala, M.: Enhancement of atmospheric H2SO4∕ H2O nucleation: organic oxidation products versus amines, Atmos. Chem. Phys., 14, 751–764, https://doi.org/10.5194/acp-14-751-2014, 2014.
Bianchi, F., Praplan, A. P., Sarnela, N., Dommen, J., Kürten, A., Ortega, I. K., Schobesberger, S., Junninen, H., Simon, M., Tröstl, J., Jokinen, T., Sipilä, M., Adamov, A., Amorim, A., Almeida, J., Breitenlechner, M., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Hakala, J., Hansel, A., Heinritzi, M., Kangasluoma, J., Keskinen, H., Kim, J., Kirkby, J., Laaksonen, A., Lawler, M. J., Lehtipalo, K., Leiminger, M., Makhmutov, V., Mathot, S., Onnela, A., Petäjä, T., Riccobono, F., Rissanen, M. P., Rondo, L., Tomé, A., Virtanen, A., Viisanen, Y., Williamson, C., Wimmer, D., Winkler, P. M., Ye, P., Curtius, J., Kulmala, M., Worsnop, D. R., Donahue, N. M., and Baltensperger, U.: Insight into acid-base nucleation experiments by comparison of the chemical composition of positive, negative, and neutral clusters, Environ. Sci. Technol., 48, 13675–13684, https://doi.org/10.1021/es502380b, 2014.
Chan, T. W. and Mozurkewich, M.: Measurement of the coagulation rate constant for sulfuric acid particles as a function of particle size using tandem differential mobility analysis, J. Aerosol Sci., 32, 321–339, https://doi.org/10.1016/S0021-8502(00)00081-1, 2001.
Chen, M., Titcombe, M., Jiang, J., Jen, C., Kuang, C., Fischer, M. L., Eisele, F. L., Siepmann, J. I., Hanson, D. R., Zhao, J., and McMurry, P. H.: Acid–base chemical reaction model for nucleation rates in the polluted atmospheric boundary layer, P. Natl. Acad. Sci. USA, 109, 18713–18718, https://doi.org/10.1073/pnas.1210285109, 2012.
Clark, W. E., and Whitby, K. T.: Measurements of aerosols produced by the photochemical oxidation of SO2 in air, J. Colloid Interf. Sci., 51, 477–490, https://doi.org/10.1016/0021-9797(75)90144-7, 1975.
Crounse, J. D., Nielsen, L. B., Jørgensen, S., Kjaergaard, H. G., and Wennberg, P. O.: Autooxidation of organic compounds in the atmosphere, J. Phys. Chem. Lett., 4, 3513–3520, https://doi.org/10.1021/jz4019207, 2013.
Crump, J. G. and Seinfeld, J. H.: Turbulent deposition and gravitational sedimentation of an aerosol in a vessel of arbitrary shape, J. Aerosol Sci., 12, 405–415, https://doi.org/10.1016/0021-8502(81)90036-7, 1981.
Dunne, E. M., Gordon, H., Kürten, A., Almeida, J., Duplissy, J., Williamson, C., Ortega, I. K., Pringle, K. J., Adamov, A., Baltensperger, U., Barmet, P., Benduhn, F., Bianchi, F., Breitenlechner, M., Clarke, A., Curtius, J., Dommen, J., Donahue, N. M., Ehrhart, S., Flagan, R. C., Franchin, A., Guida, R., Hakala, J., Hansel, A., Heinritzi, M., Jokinen, T., Kangasluoma, J., Kirkby, J., Kulmala, M., Kupc, A., Lawler, M. J., Lehtipalo, K., Makhmutov, V., Mann, G., Mathot, S., Merikanto, J., Miettinen, P., Nenes, A., Onnela, A., Rap, A., Reddington, C. L. S., Riccobono, F., Richards, N. A. D., Rissanen, M. P., Rondo, L., Sarnela, N., Schobesberger, S., Sengupta, K., Simon, M., Sipilä, M., Smith, J. N., Stozkhov, Y., Tomé, A., Tröstl, J., Wagner, P. E., Wimmer, D., Winkler, P. M., Worsnop, D. R., and Carslaw, K. S.: Global atmospheric particle formation from CERN CLOUD measurements, Science, 354, 1119–1124, https://doi.org/10.1126/science.aaf2649, 2016.
Duplissy, J., Merikanto, J., Franchin, A., Tsagkogeorgas, G., Kangasluoma, J., Wimmer, D., Vuollekoski, H., Schobesberger, S., Lehtipalo, K., Flagan, R. C., Brus, D., Donahue, N. M., Vehkämäki, H., Almeida, J., Amorim, A., Barmet, P., Bianchi, F., Breitenlechner, M., Dunne, E. M., Guida, R., Henschel, H., Junninen, H., Kirkby, J., Kürten, A., Kupc, A., Määttänen, A., Makhmutov, V., Mathot, S., Nieminen, T., Onnela, A., Praplan, A. P., Riccobono, F., Rondo, L., Steiner, G., Tome, A., Walther, H., Baltensperger, U., Carslaw, K. S., Dommen, J., Hansel, A., Petäjä, T., Sipilä, M., Stratmann, F., Vrtala, A., Wagner, P. E., Worsnop, D. R., Curtius, J., and Kulmala, M.: Effect of ions on sulfuric acid-water binary particle formation II: Experimental data and comparison with QC-normalized classical nucleation theory, J. Geophys. Res.-Atmos., 121, 1752–1775, https://doi.org/10.1002/2015JD023539, 2016.
Ehn, M., Thornton, J. A., Kleist, E., Sipilä, M., Junninen, H., Pullinen, I., Springer, M., Rubach, F., Tillmann, R., Lee, B., Lopez-Hilfiker, F., Andres, S., Acir, I.-H., Rissanen, M., Jokinen, T., Schobesberger, S., Kangasluoma, J., Kontkanen, J., Nieminen, T., Kurtén, T., Nielsen, L. B., Jørgensen, S., Kjaergaard, H. G., Canagaratna, M., Dal Maso, M., Berndt, T., Petäjä, T., Wahner, A., Kerminen, V.-M., Kulmala, M., Worsnop, D. R., Wildt, J., and Mentel, T. F.: A large source of low-volatility secondary organic aerosol, Nature, 506, 476–479, https://doi.org/10.1038/nature13032, 2014.
Ehrhart, S. and Curtius, J.: Influence of aerosol lifetime on the interpretation of nucleation experiments with respect to the first nucleation theorem, Atmos. Chem. Phys., 13, 11465–11471, https://doi.org/10.5194/acp-13-11465-2013, 2013.
Ehrhart, S., Ickes, L., Almeida, J., Amorim, A., Barmet, P., Bianchi, F., Dommen, J., Dunne, E. M., Duplissy, J., Franchin, A., Kangasluoma, J., Kirkby, J., Kürten, A., Kupc, A., Lehtipalo, K., Nieminen, T., Riccobono, F., Rondo, L., Schobesberger, S., Steiner, G., Tomé, A., Wimmer, D., Baltensperger, U., Wagner, P. E., and Curtius, J.: Comparison of the SAWNUC model with CLOUD measurements of sulphuric acid-water nucleation, J. Geophys. Res.-Atmos., 121, 12401–12414, https://doi.org/10.1002/2015JD023723, 2016.
Fiedler, V., Dal Maso, M., Boy, M., Aufmhoff, H., Hoffmann, J., Schuck, T., Birmili, W., Hanke, M., Uecker, J., Arnold, F., and Kulmala, M.: The contribution of sulphuric acid to atmospheric particle formation and growth: a comparison between boundary layers in Northern and Central Europe, Atmos. Chem. Phys., 5, 1773–1785, https://doi.org/10.5194/acp-5-1773-2005, 2005.
Freshour, N. A., Carlson, K. K., Melka, Y. A., Hinz, S., Panta, B., and Hanson, D. R.: Amine permeation sources characterized with acid neutralization and sensitivities of an amine mass spectrometer, Atmos. Meas. Tech., 7, 3611–3621, https://doi.org/10.5194/amt-7-3611-2014, 2014.
Glasoe, W. A., Volz, K., Panta, B., Freshour, N., Bachman, R., Hanson, D. R., McMurry, P. H., and Jen, C.: Sulfuric acid nucleation: An experimental study of the effect of seven bases, J. Geophys. Res.-Atmos., 120, 1933–1950, https://doi.org/10.1002/2014JD022730, 2015.
Gordon, H., Sengupta, K., Rap, A., Duplissy, J., Frege, C., Williamson, C., Heinritzi, M., Simon, M., Yan, C., Almeida, J., Tröstl, J., Nieminen, T., Ortega, I. K., Wagner, R., Dunne, E. M., Adamov, A., Amorim, A., Bernhammer, A. K., Bianchi, F., Breitenlechner, M., Brilke, S., Chen, X., Craven, J. S., Dias, A., Ehrhart, S., Fischer, L., Flagan, R. C., Franchin, A., Fuchs, C., Guida, R., Hakala, J., Hoyle, C. R., Jokinen, T., Junninen, H., Kangasluoma, J., Kim, J., Kirkby, J., Krapf, M., Kürten, A., Laaksonen, A., Lehtipalo, K., Makhmutov, V., Mathot, S., Molteni, U., Monks, S. A., Onnela, A., Peräkylä, O., Piel, F., Petäjä, T., Praplan, A. P., Pringle, K. J., Richards, N. A. D., Rissanen, M. P., Rondo, L., Sarnela, N., Schobesberger, S., Scott, C. E., Seinfeld, J. H., Sharma, S., Sipilä, M., Steiner, G., Stozhkov, Y., Stratmann, F., Tomé, A., Virtanen, A., Vogel, A. L., Wagner, A. C., Wagner, P. E., Weingartner, E., Wimmer, D., Winkler, P. M., Ye, P., Zhang, X., Hansel, A., Dommen, J., Donahue, N. M., Worsnop, D. R., Baltensperger, U., Kulmala, M., Curtius, J., and Carslaw, K. S.: Reduced anthropogenic aerosol radiative forcing caused by biogenic new particle formation, P. Natl. Acad. Sci. USA, 113, 12053–12058, https://doi.org/10.1073/pnas.1602360113, 2016.
Hamaker, H. C.: The London–van der Waals attraction between spherical particles, Physica, 4, 1058–1072, https://doi.org/10.1016/S0031-8914(37)80203-7, 1937.
Hanson, D. R. and Eisele, F.: Diffusion of H2SO4 in humidified nitrogen: Hydrated H2SO4, J. Phys. Chem. A, 104, 1715–1719, https://doi.org/10.1021/jp993622j, 2000.
Hanson, D. R. and Lovejoy, E. R.: Measurement of the thermodynamics of the hydrated dimer and trimer of sulfuric acid, J. Phys. Chem. A, 110, 9525–9528, https://doi.org/10.1021/jp062844w, 2006.
Hanson, D. R., Bier, I., Panta, B., Jen, C. N., and McMurry, P. H.: Computational Fluid Dynamics Studies of a Flow Reactor: Free Energies of Clusters of Sulfuric Acid with NH3 or Dimethyl Amine, J. Phys. Chem. A, 121, 3976–3990, https://doi.org/10.1021/acs.jpca.7b00252, 2017.
Hinds, W. C.: Aerosol technology: Properties, behavior, and measurement of airborne particles, 2nd Edn., John Wiley & Sons, Inc., 150–153, 1999.
Hirsikko, A., Laakso, L., Hõrrak, U., Aalto, P. P., Kerminen, V.-M., and Kulmala, M.: Annual and size dependent variation of growth rates and ion concentrations in boreal forest, Boreal Environ. Res., 10, 357–369, 2005.
Jen, C., McMurry, P. H., and Hanson, D. R.: Stabilization of sulfuric acid dimers by ammonia, methylamine, dimethylamine, and trimethylamine, J. Geophys. Res.-Atmos., 119, 7502–7514, https://doi.org/10.1002/2014JD021592, 2014.
Jen, C. N., Zhao, J., McMurry, P. H., and Hanson, D. R.: Chemical ionization of clusters formed from sulfuric acid and dimethylamine or diamines, Atmos. Chem. Phys., 16, 12513–12529, https://doi.org/10.5194/acp-16-12513-2016, 2016a.
Jen, C. N., Bachman, R., Zhao, J., McMurry, P. H., and Hanson, D. R.: Diamine-sulfuric acid reactions are a potent source of new particle formation, Geophys. Res. Lett., 43, 867–873, https://doi.org/10.1002/2015GL066958, 2016b.
Jokinen, T., Sipilä, M., Junninen, H., Ehn, M., Lönn, G., Hakala, J., Petäjä, T., Mauldin III, R. L., Kulmala, M., and Worsnop, D. R.: Atmospheric sulphuric acid and neutral cluster measurements using CI-APi-TOF, Atmos. Chem. Phys., 12, 4117–4125, https://doi.org/10.5194/acp-12-4117-2012, 2012.
Jokinen, T., Berndt, T., Makkonen, R., Kerminen, V.-M., Junninen, H., Paasonen, P., Stratmann, F., Herrmann, H., Guenther, A. B., Worsnop, D. R., Kulmala, M., Ehn, M., and Sipilä, M.: Production of extremely low volatile organic compounds from biogenic emissions: Measured yields and atmospheric implications, P. Natl. Acad. Sci. USA, 112, 7123–7128, https://doi.org/10.1073/pnas.1423977112, 2015.
Karlsson, M. N. A. and Martinsson, B. G.: Methods to measure and predict the transfer function size dependence of individual DMAs, J. Aerosol Sci., 34, 603–625, https://doi.org/10.1016/S0021-8502(03)00020-X, 2003.
Kerminen, V.-M. and Kulmala, M.: Analytical formulae connecting the “real” and the “apparent” nucleation rate and the nuclei number concentration for atmospheric nucleation events, J. Aerosol Sci., 33, 609–622, https://doi.org/10.1016/S0021-8502(01)00194-X, 2002.
Kirkby, J., Curtius, J., Almeida, J., Dunne, E., Duplissy, J., Ehrhart, S., Franchin, A., Gagné, S., Ickes, L., Kürten, A., Kupc, A., Metzger, A., Riccobono, F., Rondo, L., Schobesberger, S., Tsagkogeorgas, G., Wimmer, D., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Dommen, J., Downard, A., Ehn, M., Flagan, R.C., Haider, S., Hansel, A., Hauser, D., Jud, W., Junninen, H., Kreissl, F., Kvashin, A., Laaksonen, A., Lehtipalo, K., Lima, J., Lovejoy, E. R., Makhmutov, V., Mathot, S., Mikkilä, J., Minginette, P., Mogo, S., Nieminen, T., Onnela, A., Pereira, P., Petäjä, T., Schnitzhofer, R., Seinfeld, J. H., Sipilä, M., Stozhkov, Y., Stratmann, F., Tomé, A., Vanhanen, J., Viisanen, Y., Vrtala, A., Wagner, P. E., Walther, H., Weingartner, E., Wex, H., Winkler, P. M., Carslaw, K. S., Worsnop, D. R., Baltensperger, U., and Kulmala, M.: Role of sulphuric acid, ammonia and galactic cosmic rays in atmospheric aerosol nucleation, Nature, 476, 429–435, https://doi.org/10.1038/nature10343, 2011.
Kirkby, J., Duplissy, J., Sengupta, K., Frege, C., Gordon, H., Williamson, C., Heinritzi, M., Simon, M., Yan, C., Almeida, J., Tröstl, J., Nieminen, T., Ortega, I. K., Wagner, R., Adamov, A., Amorim, A., Bernhammer, A.-K., Bianchi, F., Breitenlechner, M., Brilke, S., Chen, X., Craven, J., Dias, A., Ehrhart, S., Flagan, R. C., Franchin, A., Fuchs, C., Guida, R., Hakala, J., Hoyle, C. R., Jokinen, T., Junninen, H., Kangasluoma, J., Kim, J., Krapf, M., Kürten, A., Laaksonen, A., Lehtipalo, K., Makhmutov, V., Mathot, S., Molteni, U., Onnela, A., Peräkylä, O., Piel, F., Petäjä, T., Praplan, A. P., Pringle, K., Rap, A., Richards, N. A. D., Riipinen, I., Rissanen, M. P., Rondo, L., Sarnela, N., Schobesberger, S., Scott, C. E., Seinfeld, J. H., Sipilä, M., Steiner, G., Stozhkov, Y., Stratmann, F., Tomé, A., Virtanen, A., Vogel, A. L., Wagner, A., Wagner, P. E., Weingartner, E., Wimmer, D., Winkler, P. M., Ye, P., Zhang, X., Hansel, A., Dommen, J., Donahue, N. M., Worsnop, D. R., Baltensperger, U., Kulmala, M., Carslaw, K. S., and Curtius, J.: Ion-induced nucleation of pure biogenic particles, Nature, 533, 521–526, https://doi.org/10.1038/nature17953, 2016.
Ku, B. K. and Fernandez de la Mora, J.: Relation between electrical mobility, mass, and size for nanodrops 1–6.5 nm in diameter in air, Aerosol Sci. Tech., 43, 241–249, https://doi.org/10.1080/02786820802590510, 2009.
Kuang, C., McMurry, P. H., McCormick, A. V., and Eisele, F. L.: Dependence of nucleation rates on sulfuric acid vapor concentration in diverse atmospheric locations, J. Geophys. Res.-Atmos., 113, D10209, https://doi.org/10.1029/2007JD009253, 2008.
Kulmala, M., Vehkamäki, H., Petäjä, T., Dal Maso, M., Lauri, A., Kerminen, V.-M., Birmili, W., and McMurry, V.-M.: Formation and growth rates of ultrafine atmospheric particles: a review of observations, J. Aerosol Sci., 35, 143–176, https://doi.org/10.1016/j.jaerosci.2003.10.003, 2004.
Kulmala, M., Kontkanen, J., Junninen, H., Lehtipalo, K., Manninen, H. E., Nieminen, T., Petäjä, T., Sipilä, M., Schobesberger, S., Rantala, P., Franchin, A., Jokinen, T., Järvinen, E., Äijälä, M., Kangasluoma, J., Hakala, J., Aalto, P. P., Paasonen, P., Mikkilä, J., Vanhanen, J., Aalto, J., Hakola, H., Makkonen, U., Ruuskanen, T., Mauldin III, R. L., Duplissy, J., Vehkamäki, H., Bäck, J., Kortelainen, A., Riipinen, I., Kurtén, T., Johnston, M. V., Smith, J. N., Ehn, M., Mentel, T. F., Lehtinen, K. E. J., Laaksonen, A., Kerminen, V.-M., and Worsnop, D. R.: Direct observations of atmospheric aerosol nucleation, Science, 339, 943–946, https://doi.org/10.1126/science.1227385, 2013.
Kupc, A., Amorim, A., Curtius, J., Danielczok, A., Duplissy, J., Ehrhart, S., Walther, H., Ickes, L., Kirkby, J., Kürten, A., Lima, J. M., Mathot, S., Minginette, P., Onnela, A., Rondo, L., and Wagner, P. E.: A fibre-optic UV system for H2SO4 production in aerosol chambers causing minimal thermal effects, J. Aerosol Sci., 42, 532–543, https://doi.org/10.1016/j.jaerosci.2011.05.001, 2011.
Kürten, A., Rondo, L., Ehrhart, S., and Curtius, J.: Performance of a corona ion source for measurement of sulfuric acid by chemical ionization mass spectrometry, Atmos. Meas. Tech., 4, 437–443, https://doi.org/10.5194/amt-4-437-2011, 2011.
Kürten, A., Jokinen, T., Simon, M., Sipilä, M., Sarnela, N., Junninen, H., Adamov, A., Almeida, J., Amorim, A., Bianchi, F., Breitenlechner, M., Dommen, J., Donahue, N. M., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Hakala, J., Hansel, A., Heinritzi, M., Hutterli, M., Kangasluoma, J., Kirkby, J., Laaksonen, A., Lehtipalo, K., Leiminger, M., Makhmutov, V., Mathot, S., Onnela, A., Petäjä, T., Praplan, A. P., Riccobono, F., Rissanen, M. P., Rondo, L., Schobesberger, S., Seinfeld, J. H., Steiner, G., Tomé, A., Tröstl, J., Winkler, P. M., Williamson, C., Wimmer, D., Ye, P., Baltensperger, U., Carslaw, K. S., Kulmala, M., Worsnop, D. R., and Curtius, J.: Neutral molecular cluster formation of sulfuric acid-dimethylamine observed in real-time under atmospheric conditions, P. Natl. Acad. Sci. USA, 111, 15019–15024, https://doi.org/10.1073/pnas.1404853111, 2014.
Kürten, A., Williamson, C., Almeida, J., Kirkby, J., and Curtius, J.: On the derivation of particle nucleation rates from experimental formation rates, Atmos. Chem. Phys., 15, 4063–4075, https://doi.org/10.5194/acp-15-4063-2015, 2015a.
Kürten, A., Münch, S., Rondo, L., Bianchi, F., Duplissy, J., Jokinen, T., Junninen, H., Sarnela, N., Schobesberger, S., Simon, M., Sipilä, M., Almeida, J., Amorim, A., Dommen, J., Donahue, N. M., Dunne, E. M., Flagan, R. C., Franchin, A., Kirkby, J., Kupc, A., Makhmutov, V., Petäjä, T., Praplan, A. P., Riccobono, F., Steiner, G., Tomé, A., Tsagkogeorgas, G., Wagner, P. E., Wimmer, D., Baltensperger, U., Kulmala, M., Worsnop, D. R., and Curtius, J.: Thermodynamics of the formation of sulfuric acid dimers in the binary (H2SO4–H2O) and ternary (H2SO4–H2O–NH3) system, Atmos. Chem. Phys., 15, 10701–10721, https://doi.org/10.5194/acp-15-10701-2015, 2015b.
Kürten, A., Bianchi, F., Almeida, J., Kupiainen-Määttä, O., Dunne, E. M., Duplissy, J., Williamson, C., Barmet, P., Breitenlechner, M., Dommen, J., Donahue, N. M., Flagan, R. C., Franchin, A., Gordon, H., Hakala, J., Hansel, A., Heinritzi, M., Ickes, L., Jokinen, T., Kangasluoma, J., Kim, J., Kirkby, J., Kupc, A., Lehtipalo, K., Leiminger, M., Makhmutov, V., Onnela, A., Ortega, I. K., Petäjä, T., Praplan, A. P., Riccobono, F., Rissanen, M. P., Rondo, L., Schnitzhofer, R., Schobesberger, S., Smith, J. N., Steiner, G., Stozhkov, Y., Tomé, A., Tröstl, J., Tsagkogeorgas, G., Wagner, P. E., Wimmer, D., Ye, P., Baltensperger, U., Carslaw, K., Kulmala, M., and Curtius, J.: Experimental particle formation rates spanning tropospheric sulfuric acid and ammonia abundances, ion production rates and temperatures, J. Geophys. Res.-Atmos., 121, 12377–12400, https://doi.org/10.1002/2015JD023908, 2016a.
Kürten, A., Bergen, A., Heinritzi, M., Leiminger, M., Lorenz, V., Piel, F., Simon, M., Sitals, R., Wagner, A. C., and Curtius, J.: Observation of new particle formation and measurement of sulfuric acid, ammonia, amines and highly oxidized organic molecules at a rural site in central Germany, Atmos. Chem. Phys., 16, 12793–12813, https://doi.org/10.5194/acp-16-12793-2016, 2016b.
Kurtén, T., Loukonen, V., Vehkamäki, H., and Kulmala, M.: Amines are likely to enhance neutral and ion-induced sulfuric acid-water nucleation in the atmosphere more effectively than ammonia, Atmos. Chem. Phys., 8, 4095–4103, https://doi.org/10.5194/acp-8-4095-2008, 2008.
Lee, S.-H., Reeves, J. M., Wilson, J. C., Hunton, D. E., Viggiano, A. A., Miller, T. M., Ballenthin, J. O., and Lait, L. R.: Particle formation by ion nucleation in the upper troposphere and lower stratosphere, Science, 301, 1886–1889, https://doi.org/10.1126/science.1087236, 2003.
Lehtipalo, K., Rondo, L., Kontkanen, J., Schobesberger, S., Jokinen, T., Sarnela, N., Kürten, A., Ehrhart, S., Franchin, A., Nieminen, T., Riccobono, F., Sipilä, M., Yli-Juuti, T., Duplissy, J., Adamov, A., Ahlm, L., Almeida, J., Amorim, A., Bianchi, F., Breitenlechner, M., Dommen, J., Downard, A. J., Dunne, E. M., Flagan, R. C., Guida, R., Hakala, J., Hansel, A., Jud, W., Kangasluoma, J., Kerminen, V.-M., Keskinen, H., Kim, J., Kirkby, J., Kupc, A., Kupiainen-Määttä, O., Laaksonen, A., Lawler, M. J., Leiminger, M., Mathot, S., Olenius, T., Ortega, I. K., Onnela, A., Petäjä, T., Praplan, A., Rissanen, M. P., Ruuskanen, T., Santos, F. D., Schallhart, S., Schnitzhofer, R., Simon, M., Smith, J. N., Tröstl, J., Tsagkogeorgas, G., Tomé, A., Vaattovaara, P., Vehkamäki, H., Vrtala, A. E., Wagner, P. E., Williamson, C., Wimmer, D., Winkler, P. M., Virtanen, A., Donahue, N. M., Carslaw, K. S., Baltensperger, U., Riipinen, I., Curtius, J., Worsnop, D. R., and Kulmala, M.: The effect of acid–base clustering and ions on the growth of atmospheric nano-particles, Nat. Commun., 7, 11594, https://doi.org/10.1038/ncomms11594, 2016.
Lovejoy, E. R., Curtius, J., and Froyd, K. D.: Atmospheric ion-induced nucleation of sulfuric acid and water, J. Geophys. Res.-Atmos., 109, D08204, https://doi.org/10.1029/2003JD004460, 2004.
McGrath, M. J., Olenius, T., Ortega, I. K., Loukonen, V., Paasonen, P., Kurtén, T., Kulmala, M., and Vehkamäki, H.: Atmospheric Cluster Dynamics Code: a flexible method for solution of the birth-death equations, Atmos. Chem. Phys., 12, 2345–2355, https://doi.org/10.5194/acp-12-2345-2012, 2012.
McMurry, P. H.: Photochemical Aerosol Formation from SO2: A theoretical analysis of smog chamber data, J. Colloid Interf. Sci., 78, 513–527, https://doi.org/10.1016/0021-9797(80)90589-5, 1980.
McMurry, P. H. and Li, C.: The dynamic behavior of nucleating aerosols in constant reaction rate systems: Dimensional analysis and generic numerical solutions, Aerosol Sci. Tech., 51, 1057–1070, https://doi.org/10.1080/02786826.2017.1331292, 2017.
Nadykto, A. B., Yu, F., Jakovleva, M. V., Herb, J., and Xu, Y.: Amines in the Earth's atmosphere: A density functional theory study of the thermochemistry of pre-nucleation clusters, Entropy, 13, 554–569, https://doi.org/10.3390/e13020554, 2011.
Olenius, T., Halonen, R., Kurtén, T., Henschel, H., Kupiainen-Määttä, O., Ortega, I. K., Jen, C. N., Vehkamäki, H., and Riipinen, I.: New particle formation from sulfuric acid and amines: Comparison of monomethylamine, dimethylamine, and trimethylamine, J. Geophys. Res.-Atmos., 122, 7103–7118, https://doi.org/10.1002/2017JD026501, 2017.
Ortega, I. K., Kupiainen, O., Kurtén, T., Olenius, T., Wilkman, O., McGrath, M. J., Loukonen, V., and Vehkamäki, H.: From quantum chemical formation free energies to evaporation rates, Atmos. Chem. Phys., 12, 225–235, https://doi.org/10.5194/acp-12-225-2012, 2012.
Park, S. H., Kim, H. O., Han, Y. T., Kwon, S. B., and Lee, K. W.: Wall loss rate of polydispersed aerosols, Aerosol Sci. Tech., 35, 710–717, https://doi.org/10.1080/02786820152546752, 2001.
Place, B. K., Quilty, A. T., Di Lorenzo, R. A., Ziegler, S. E., and VandenBoer, T. C.: Quantitation of 11 alkylamines in atmospheric samples: separating structural isomers by ion chromatography, Atmos. Meas. Tech., 10, 1061–1078, https://doi.org/10.5194/amt-10-1061-2017, 2017.
Praplan, A. P., Bianchi, F., Dommen, J., and Baltensperger, U.: Dimethylamine and ammonia measurements with ion chromatography during the CLOUD4 campaign, Atmos. Meas. Tech., 5, 2161–2167, https://doi.org/10.5194/amt-5-2161-2012, 2012.
Qiu, C. and Zhang, R.: Physiochemical properties of alkylaminium sulfates: hygroscopicity, thermostability, and density, Environ. Sci. Technol., 46, 4474–4480, https://doi.org/10.1021/es3004377, 2012.
Rao, N. P. and McMurry, P. H.: Nucleation and Growth of Aerosol in Chemically Reacting Systems: A Theoretical Study of the Near-Collision-Controlled Regime, Aerosol Sci. Tech., 11, 120–132, https://doi.org/10.1080/02786828908959305, 1989.
Riccobono, F., Schobesberger, S., Scott, C. E., Dommen, J., Ortega, I. K., Rondo, L., Almeida, J., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Downard, A., Dunne, E. M., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Hansel, A., Junninen, H., Kajos, M., Keskinen, H., Kupc, A., Kürten, A., Kvashin, A. N., Laaksonen, A., Lehtipalo, K., Makhmutov, V., Mathot, S., Nieminen, T., Onnela, A., Petäjä, T., Praplan, A. P., Santos, F. D., Schallhart, S., Seinfeld, J. H., Sipilä, M., Spracklen, D. V., Stozhkov, Y., Stratmann, F., Tomé, A., Tsagkogeorgas, G., Vaattovaara, P., Viisanen, Y., Vrtala, A., Wagner, P. E., Weingartner, E., Wex, H., Wimmer, D., Carslaw, K. S., Curtius, J., Donahue, N. M., Kirkby, J., Kulmala, M., Worsnop, D. R., and Baltensperger, U.: Oxidation products of biogenic emissions contribute to nucleation of atmospheric particles, Science, 344, 717–721, https://doi.org/10.1126/science.1243527, 2014.
Simon, M., Heinritzi, M., Herzog, S., Leiminger, M., Bianchi, F., Praplan, A., Dommen, J., Curtius, J., and Kürten, A.: Detection of dimethylamine in the low pptv range using nitrate chemical ionization atmospheric pressure interface time-of-flight (CI-APi-TOF) mass spectrometry, Atmos. Meas. Tech., 9, 2135–2145, https://doi.org/10.5194/amt-9-2135-2016, 2016.
Voigtländer, J., Duplissy, J., Rondo, L., Kürten, A., and Stratmann, F.: Numerical simulations of mixing conditions and aerosol dynamics in the CERN CLOUD chamber, Atmos. Chem. Phys., 12, 2205–2214, https://doi.org/10.5194/acp-12-2205-2012, 2012.
Wang, S. C. and Flagan, R. C.: Scanning electrical mobility spectrometer, Aerosol Sci. Tech., 13, 230–240, https://doi.org/10.1080/02786829008959441, 1990.
Weber, R. J., Marti, J., McMurry, P. H., Eisele, F. L., Tanner, D. J., and Jefferson, A.: Measured atmospheric new particle formation rates: implications for nucleation mechanisms, Chem. Eng. Commun., 151, 53–64, https://doi.org/10.1080/00986449608936541, 1996.
Weber, R. J., Marti, J. J., McMurry, P. H., Eisele, F. L., Tanner, D. J., and Jefferson, A.: Measurements of new particle formation and ultrafine particle growth rates at a clean continental site, J. Geophys. Res.-Atmos., 102, 4375–4385, https://doi.org/10.1029/96JD03656, 1997.
Weber, R. J., McMurry, P. H., Mauldin, L., Tanner, D. J., Eisele, F. L., Brechtel, F. J., Kreidenweis, S. M., Kok, G. L., Schillawski, R. D., and Baumgardner, D.: A study of new particle formation and growth involving biogenic and trace gas species measured during ACE 1, J. Geophys. Res.-Atmos., 103, 16385–16396, https://doi.org/10.1029/97JD02465, 1998.
Wiedensohler, A. and Fissan, H. J.: Aerosol charging in high purity gases, J. Aerosol Sci., 19, 867–870, https://doi.org/10.1016/0021-8502(88)90054-7, 1988.
Yao, L., Wang, M.-Y., Wang, X.-K., Liu, Y.-J., Chen, H.-F., Zheng, J., Nie, W., Ding, A.-J., Geng, F.-H., Wang, D.-F., Chen, J.-M., Worsnop, D. R., and Wang, L.: Detection of atmospheric gaseous amines and amides by a high-resolution time-of-flight chemical ionization mass spectrometer with protonated ethanol reagent ions, Atmos. Chem. Phys., 16, 14527–14543, https://doi.org/10.5194/acp-16-14527-2016, 2016.
You, Y., Kanawade, V. P., de Gouw, J. A., Guenther, A. B., Madronich, S., Sierra-Hernández, M. R., Lawler, M., Smith, J. N., Takahama, S., Ruggeri, G., Koss, A., Olson, K., Baumann, K., Weber, R. J., Nenes, A., Guo, H., Edgerton, E. S., Porcelli, L., Brune, W. H., Goldstein, A. H., and Lee, S.-H.: Atmospheric amines and ammonia measured with a chemical ionization mass spectrometer (CIMS), Atmos. Chem. Phys., 14, 12181–12194, https://doi.org/10.5194/acp-14-12181-2014, 2014.
Yu, H. and Lee, S.-H.: Chemical ionisation mass spectrometry for the measurement of atmospheric amines, Environ. Chem., 9, 190–201, https://doi.org/10.1071/EN12020, 2012.
Yu, H., Dai, L., Zhao, Y., Kanawade, V. P., Tripathi, S. N., Ge, X., Chen, M., and Lee, S. N.: Laboratory observations of temperature and humidity dependencies of nucleation and growth rates of sub-3 nm particles, J. Geophys. Res.-Atmos., 122, 1919–1929, https://doi.org/10.1002/2016JD025619, 2017.
Zhao, J., Smith, J. N., Eisele, F. L., Chen, M., Kuang, C., and McMurry, P. H.: Observation of neutral sulfuric acid-amine containing clusters in laboratory and ambient measurements, Atmos. Chem. Phys., 11, 10823–10836, https://doi.org/10.5194/acp-11-10823-2011, 2011.
Zollner, J. H., Glasoe, W. A., Panta, B., Carlson, K. K., McMurry, P. H., and Hanson, D. R.: Sulfuric acid nucleation: power dependencies, variation with relative humidity, and effect of bases, Atmos. Chem. Phys., 12, 4399–4411, https://doi.org/10.5194/acp-12-4399-2012, 2012.