the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Surface impacts of the Quasi Biennial Oscillation
Lesley J. Gray
James A. Anstey
Yoshio Kawatani
Scott Osprey
Verena Schenzinger
Teleconnections between the Quasi Biennial Oscillation (QBO) and the Northern Hemisphere zonally averaged zonal winds, mean sea level pressure (mslp) and tropical precipitation are explored. The standard approach that defines the QBO using the equatorial zonal winds at a single pressure level is compared with the empirical orthogonal function approach that characterizes the vertical profile of the equatorial winds. Results are interpreted in terms of three potential routes of influence, referred to as the tropical, subtropical and polar routes. A novel technique is introduced to separate responses via the polar route that are associated with the stratospheric polar vortex, from the other two routes. A previously reported mslp response in January, with a pattern that resembles the positive phase of the North Atlantic Oscillation under QBO westerly conditions, is confirmed and found to be primarily associated with a QBO modulation of the stratospheric polar vortex. This mid-winter response is relatively insensitive to the exact height of the maximum QBO westerlies and a maximum positive response occurs with westerlies over a relatively deep range between 10 and 70 hPa. Two additional mslp responses are reported, in early winter (December) and late winter (February/March). In contrast to the January response the early and late winter responses show maximum sensitivity to the QBO winds at ∼ 20 and ∼ 70 hPa respectively, but are relatively insensitive to the QBO winds in between (∼ 50 hPa). The late winter response is centred over the North Pacific and is associated with QBO influence from the lowermost stratosphere at tropical/subtropical latitudes in the Pacific sector. The early winter response consists of anomalies over both the North Pacific and Europe, but the mechanism for this response is unclear. Increased precipitation occurs over the tropical western Pacific under westerly QBO conditions, particularly during boreal summer, with maximum sensitivity to the QBO winds at 70 hPa. The band of precipitation across the Pacific associated with the Inter-tropical Convergence Zone (ITCZ) shifts southward under QBO westerly conditions. The empirical orthogonal function (EOF)-based analysis suggests that this ITCZ precipitation response may be particularly sensitive to the vertical wind shear in the vicinity of 70 hPa and hence the tropical tropopause temperatures.
- Article
(13385 KB) -
Supplement
(33635 KB) - BibTeX
- EndNote
A modulation of the winter Northern Hemisphere (NH) stratospheric polar vortex by the equatorial Quasi Biennial Oscillation (QBO) has been well known for many years (Holton and Tan, 1980, 1982; Baldwin et al., 2001; Anstey and Shepherd, 2014). Potential mechanisms for this influence have been extensively explored. Modelling and observational studies suggest it is related to the influence of the equatorial winds (Ueq) on the stratospheric waveguide, which affects the vertically propagating planetary-scale waves from the troposphere. Nevertheless, the exact mechanisms are still under debate (Garfinkel et al., 2012; Watson and Gray, 2014; White et al., 2016). It is also evident that the Holton–Tan relationship between the QBO and NH polar vortex, with a stronger (weaker) polar vortex when the QBO winds in the lower–mid stratosphere are westerly (easterly), is more evident in some periods than in others (Lu et al., 2008, 2014; Anstey and Shepherd, 2008; Christiansen, 2010). This relationship has been shown to depend on the phase of the 11-year solar cycle (Labitzke et al., 2006) and the El Niño–Southern Oscillation (ENSO; Garfinkel and Hartmann, 2007; Wei et al., 2007; Calvo et al., 2009; Hansen et al., 2016). The majority of climate models currently employed to assess the impacts of climate change do not reproduce the QBO, and even those that do are often unable to reproduce the observed strength of the Holton–Tan correlation (Christiansen, 2014).
Variability of the stratospheric polar vortex is not only influenced by the QBO. Signals associated with the occurrence of explosive volcanic eruptions (Robock, 2000), ENSO events (e.g. Hansen et al., 2016, and references therein) and the 11-year solar cycle (Gray et al., 2010) have all been identified. There is, in addition, a strong influence of natural variability, both internally within the stratosphere and within the coupled ocean–atmosphere–land surface system that impacts the amplitude and propagation of vertically propagating waves from the troposphere. Because of this, there is currently limited predictability of, for example, sudden stratospheric warming (SSW) events in the stratosphere.
The mechanisms for stratospheric processes to influence the underlying troposphere and surface are currently not well understood, neither in the extra-tropics where polar vortex variability is a prime candidate (Kidston et al., 2015) nor at equatorial/subtropical latitudes where the direct impact of the QBO may be more relevant. Nevertheless, a large number of studies have demonstrated impact of stratospheric variability on the underlying tropospheric circulation, especially in the Atlantic sector (Baldwin and Dunkerton, 2001; Thompson et al., 2002; Scaife et al., 2014, 2016; Kidston et al., 2015; Hansen et al., 2017). An improved ability to simulate stratospheric processes and their impact on surface weather and climate has the potential to improve seasonal and decadal-scale forecasts of surface weather patterns such as the North Atlantic Oscillation (NAO; Marshall and Scaife, 2009; Scaife et al., 2016). Similarly, the direct impact of the QBO on the tropospheric circulation in the tropics and sub-tropics is of interest (Giorgetta et al., 1999; Collimore et al., 2003; Ho et al., 2009; Liess and Geller, 2012; Garfinkel and Hartmann, 2011a; Nie and Sobel, 2015). Recent studies have shown that the QBO modulates the amplitude of the Madden Julian Oscillation (MJO), and there is enhanced predictability of the MJO under QBO-E conditions (Yoo and Sonm, 2016; Marshall et al., 2017; Son et al., 2017; Nishimoto and Yoden, 2017).
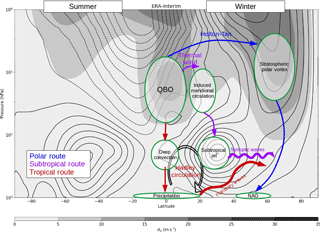
Figure 1Schematic summarizing the three primary routes (tropical, subtropical, polar) for QBO influence at the Earth's surface. Contours show the December–January–February averaged, zonally averaged zonal winds for 1979–2016 from ERA-Interim data. The contour interval is 5 ms−1; solid contours denote westerlies; dashed contours denote easterlies. Greyscale shows the standard deviation of the zonal winds in ms−1.
Three possible routes for QBO influence at the Earth's surface are identified and summarized in Fig. 1. One mechanism is through the modulation of vertical planetary wave propagation in winter by refraction or reflection of the waves towards (away from) high latitudes under QBO-E (QBO-W) conditions (Holton and Tan, 1980, 1982; Garfinkel et al., 2012; Watson and Gray, 2014; White et al., 2015). This influence route (the “polar route”) modulates the strength of the stratospheric polar vortex, which subsequently influences the underlying tropospheric circulation and surface temperature/pressure distributions (Baldwin and Dunkerton, 2001; Thompson et al., 2002; Mitchell et al., 2013). Changes in the mid–upper stratospheric zonal flow (particularly those that change the vertical and/or horizontal potential vorticity gradients) can also result in vertically reflected waves that can influence the surface without the direct mediation of a substantial change (or reversal) in the strength of the polar vortex (Perlwitz and Harnik, 2003, 2004; Shaw and Perlwitz, 2013; Lu et al., 2017).
The QBO also influences the temperature in the tropical and subtropical lower stratosphere. In order to maintain thermal wind balance in the presence of strong vertical wind shear, an adiabatic meridional circulation is induced, with anomalous upwelling (downwelling) over the Equator under QBO-E (QBO-W) conditions and a return circulation in the opposite sense at subtropical latitudes. At equatorial latitudes this results in a corresponding cold (warm) anomaly that influences tropical tropopause temperatures/static stability and hence deep convection (the “tropical route”). There is both modelling and observational evidence for a QBO signal in the characteristics of deep tropical convection and precipitation (Giorgetta et al., 1999; Collimore et al., 2003; Ho et al., 2009; Liess and Geller, 2012; Garfinkel and Hartmann, 2011b; Son et al., 2017).
At subtropical latitudes the induced meridional circulation also influences the horizontal temperature gradient/vertical wind shear in the vicinity of the tropospheric subtropical jet. This can then affect the growth and life-cycle of mid-latitude synoptic-scale and planetary-scale waves in the troposphere and thus extend the QBO anomaly down to the surface (the “subtropical route”; Ruti et al., 2006; Simpson et al., 2009; Garfinkel and Hartmann, 2011a).
These three possible routes (polar, subtropical, tropical) for QBO influence at the surface are unlikely to act in isolation, making it difficult to distinguish between them. For example, a QBO influence on the polar vortex will impact the surface not only at mid-to-high latitudes via the polar route, but also potentially in the tropics and subtropics via its impact on the strength of the upwelling branch of the Brewer–Dobson circulation. Conversely, QBO-related changes in tropical convection via the tropical route influence wave generation. This not only causes a feedback on to the QBO itself, by modulating the source of the vertically propagating waves that give rise to the QBO, but also affects the source of large-scale Rossby waves that propagate horizontally away from the tropics and interact with both the subtropical and eddy-driven mid-latitude jets (Hoskins and Karoly, 1981; Scaife et al., 2017).
In summary, there are multiple possible influence and feedback routes (teleconnections) between the QBO and the surface. While a data study alone is unable to establish cause and effect, nor isolate these individual routes of influence and feedbacks, it can nevertheless point to the primary QBO impacts at the surface and the potential contributors, and also provide hypotheses for climate model experiments to test.
In data studies that seek to investigate the influence of the QBO, a single time-series index to characterize the state of the QBO is desirable. The standard approach is to use the zonally averaged equatorial zonal wind Ueq at a selected level such as 40 or 50 hPa. However, this has the drawback of characterizing the behaviour at only one level and cannot provide information on the influence of the QBO winds from other levels. The selected level is often chosen on a trial-and-error basis to find the “best” level to employ, which has resulted in studies using a variety of different levels, usually between 30 and 70 hPa. A more objective approach employs empirical orthogonal function (EOF) analysis of the equatorial winds within a selected height range so that the height dependence of the QBO can also be captured (Wallace et al., 1993). Additionally, this approach allows examination of many more different states of the QBO evolution than is possible using the more traditional pressure level definition since observational data are usually only available on a handful of different pressure levels between 10 and 70 hPa. The EOF approach has been successfully employed in various previous studies (e.g. Baldwin and Dunkerton, 1998; hereafter denoted BD98; Crooks and Gray, 2005; Anstey et al., 2010; Rao and Ren, 2017).
In this study, the QBO influence on the NH stratospheric polar vortex and at the Earth's surface is investigated. The study mainly employs regression analysis instead of the usual composite analysis so that other sources of variability are more effectively accounted for. Both the traditional and EOF definitions of the QBO index are used to assess whether the extra complexity involved in the EOF approach is justified in terms of additional information or insight. A novel approach is also introduced to exclude the role of the polar vortex (i.e. the polar route) so that the remaining QBO variability associated with the tropical and subtropical routes can be more effectively characterized and analysed. The paper is organized as follows: Sect. 2 describes the datasets employed and the analysis approach. Section 3 describes and discusses the results of the analyses. Firstly, the polar vortex response is explored. A closer examination is then performed of the tropospheric response in the zonal winds. The same analysis techniques are then applied to the mslp and precipitation fields. Section 4 provides a summary of the results.
Zonal wind and precipitation fields for the period 1958–2016 are from the European Centre for Medium Range Weather Forecasting (ECMWF). The monthly averaged, zonally averaged and 3-D fields from ERA-40 (Uppala et al., 2005) and ERA-Interim (Dee et al., 2011) were obtained via the ECMWF public dataset web access (http://apps.ecmwf.int/datasets/, last access: 11 June 2018). The extracted fields were those interpolated on to standard pressure levels and 2.5∘ horizontal resolution. While we note the presence of jumps in the reanalysis fields due to the introduction of additional satellite data and the use of parallel processing streams (e.g. Long et al., 2017), these are primarily evident in the temperature fields and are much less evident in the zonal wind fields. The two datasets ERA-40 (1958–1979) and ERA-Interim (1979–2016) overlap in the period 1979–2001; we chose to employ the more recent data from ERA-Interim for this period, but tests showed that the results were not sensitive to this choice.
Precipitation fields from the Global Precipitation Climatology Project (GPCP; Adler et al., 2018) dataset at 2.5∘ latitude–longitude resolution for the period 1979–2016 were employed (http://gpcp.umd.edu/, last access: 11 June 2018).
The mslp data are from the Hadley Centre HadSLP2 dataset with spatial resolution of 5∘ (Allan and Ansell, 2006) for the period 1958–2004 together with the more recent data since 2004 from the HadSLP2r dataset.
The various QBO indices employed in the study were derived from radiosonde observations of Ueq issued by the Free University of Berlin (Naujokat, 1986; FUB, 2016). The FUB data are a combination from three different stations: Canton Island (3∘ S∕172∘ W; January 1953–August 1967), Gan/Maldives (1∘ S∕73∘ E; September 1967–December 1975) and Singapore (1∘ N∕104∘ E; since January 1976). The merged data are provided as monthly averages interpolated on the 70, 50, 40, 30, 20, 15 and 10 hPa levels. The FUB data, rather than the ERA data, were employed to avoid any possible degradation by the data assimilation process (Kawatani et al., 2016).
The composite difference analysis of the GPCC precipitation data was performed in a similar manner to that described in Liess and Geller (2012). Composites were compiled from those months where the equatorial wind Ueq at the selected pressure level was at least 3 ms−1 above or below the corresponding monthly average. Statistical significance of the composite differences was estimated using a two-sided Student's t-test.
The multivariate linear regression analysis is described in Gray et al. (2013, 2016): the time series at each grid point is fitted using a number of indices (time series) that characterize the observed variability associated with (1) volcanic eruptions, (2) El Niño–Southern Oscillation (ENSO), (3) solar radiative forcing, (4) the QBO and (5) a long-term trend. The GISS updated Sato Index (Sato et al., 1993) is used as the volcanic index. ENSO variability is characterized by a time series of averaged sea surface temperatures (SSTs) from the Nino 3.4 region (120–170∘ W, 5∘ N–5∘ S) using monthly averaged data on a 1∘ spatial grid from the Hadley Centre HadISST dataset (Rayner et al., 2003; https://www.esrl.noaa.gov/psd/gcos_wgsp/Timeseries/Nino34/, last access: 11 June 2018). Solar variability is characterized using the time series of sunspot numbers from WDC-SILSO (Royal Observatory of Belgium, Brussels; http://www.sidc.be/silso/, last access: 11 June 2018). A simple linear trend is used for the long-term trend index. The various indices used to characterize the QBO are described below. The best fit to the normalized anomalies is calculated by minimizing the residual term, which is modelled using an AR(1) to take into account any autocorrelation of the residual (see e.g. Press et al., 1992, Sect. 13.6). Statistical significances are determined using a Student's t-test with the null hypothesis that the contribution to the variability from a particular index is zero. The resulting regression coefficients are then re-scaled by multiplying the coefficients by the ratio of the max–min amplitude of the index and its standard deviation.
Sensitivity tests showed that the QBO regression coefficient results in the following sections are unaffected by inclusion or exclusion of the solar, volcanic, ENSO and/or trend terms. Sensitivity tests also confirmed that the data have not been overfitted by inclusion of too many indices since the QBO regression coefficients from the multivariate regression with all five indices were essentially identical to the univariate regression when only the QBO index was included (variability associated with the other indices was transferred to the residual in this latter case). Finally, tests were carried out to confirm that results using only the ERA-Interim period since 1979 were essentially the same as those from the whole period 1958–2016.
EOF analyses are performed to obtain a single time series to represent the QBO (Wallace et al., 1993). Figure S1 in the Supplement shows the height profile and principal component (PC) time series of the first two EOFs of the monthly averaged de-seasonalized FUB equatorial wind time series between 10 and 70 hPa for the period 1958–2016. The PC time series P1 and P2 are oscillations with an approximate 2-year period and are ∼ 90∘ out of phase. In the height region 15–70 hPa EOF1 characterizes the anti-correlation of the equatorial winds in the upper and lower stratosphere, whereas EOF2 captures the variability at the intermediate heights in the mid-stratosphere.
Figure S2 shows the reconstructed equatorial zonal wind field using only the first two EOFs. The main structure of alternating easterly and westerly shear zones is represented well, including the difference in the descent rates of the easterly and westerly shear zones. Some details such as the long stalling phases (Schenzinger et al., 2017), where the descent of the easterly shear zone can be halted for up to 6 months (e.g. in 2000), are smoothed out in the reconstruction, but comparison of results using the standard pressure level definition of the QBO index and the EOF-based definition does not show substantial differences, suggesting that this smoothing does not significantly affect the results.
The QBO phase space (Fig. 2) shows the amplitude of P1 (abscissa) versus P2 (ordinate) for each month of the time series, and forms an approximate circle around the origin. The phase angle of a particular point in time is defined as ψ= arctan (P2∕P1). Also shown are example profiles showing the height distribution for selected combinations of P1 and P2, at 30∘ intervals (Schenzinger, 2017). These are calculated as cos(ψ)e1+sin (ψ)e2, where e1 and e2 are the EOFs shown in Fig. S1. Note that at ψ= 0 and ψ= 90∘ the profiles are identical to EOF-1 and EOF-2 respectively, while at ψ= 180 and ψ= 270∘ they are the mirror image. Examining the plot in an anti-clockwise direction (with ψ increasing, starting from ψ= 0∘), a westerly phase in the upper stratosphere can be observed to steadily descend to the lower stratosphere by ψ= 90∘. This is gradually replaced by an easterly phase in the upper stratosphere by ψ= 180∘. Likewise, this easterly phase descends to the lower stratosphere by ψ= 270∘ and is replaced by a westerly phase at ψ= 360∘, thus completing the cycle. Note that for the descending easterlies (60∘ < ψ < 240∘) the phase space is more densely populated. This is consistent with the well-known slower descent of the easterly phase of the QBO, so that the observations progress more slowly through these phase angles.
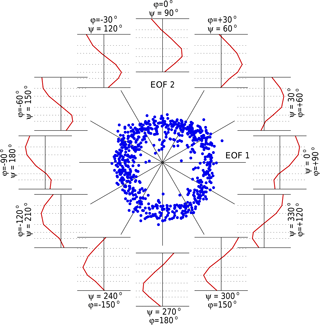
Figure 2EOF phase-space diagram. Each dot indicates a month in the period 1958–2016. The position (angle) of the dot indicates the closest combination of the two EOFs that characterize the vertical profile of the QBO zonal wind anomaly in that month. The distance from the origin represents the amplitude r (see text). Representative vertical profiles are provided to show the typical vertical wind profile for that value of ϕ. The pressure levels shown in each vertical profile panel are 70, 50, 40, 30, 20, 15 and 10 hPa.
Following BD98 the first two EOFs are combined to provide a single time series to characterize the QBO variations, by defining where r2= , ψ= arctan (P2∕P1) and ϕ is an arbitrary phase shift that can be interpreted as a rotation in phase space, and thus a projection onto a coordinate system that has been rotated by −ϕ compared to the one spanned by the original EOFs. For ϕ= 0∘, is the projection of a point (p1, p2) onto EOF-2. Addition of ϕ to the phase angle ψ gives , which is the projection onto a new axis, EOF-2*. This new axis can be interpreted as a combination of EOF-1 and EOF-2, so that EOF-2* = (sin(ϕ), cos(ϕ)) where the coordinate system is spanned by EOF-1 = (1, 0) and EOF-2 = (0, 1). As an illustration, Fig. S3 shows a sample period of the resulting time series u* for different phase angles ϕ. The figure also demonstrates that the phase shift ϕ can be interpreted as a shift in time. Given that the average cycle (2π) lasts for about 28 months, a step of ϕ = 10∘ is equivalent to a time shift of (28 × 10∕360) months (∼ 0.8 months). Note that a positive shift in ϕ denotes a negative shift in time (clockwise rotation in the Fig. 2 phase space).
A series of correlations is then performed between the time series of u* with various values of ϕ and the FUB Ueq time series at various heights to find the maximum correlation, and thus relate u* (and hence the phase shift ϕ) back to a particular QBO level of maximum influence. Figure S4 shows the correlation coefficients for the original zonal wind time series Ueq at each height between 10 and 70 hPa against u* at each phase shift between −180∘ < ϕ < 180∘. The maximum correlation coefficients exceed 0.9 for all but the lowermost (70 hPa) level, so the identification of the equatorial zonal wind Ueq at a certain level with u* at a specific phase shift ϕ appears to be well justified. Values of (a) ϕ= −60, (b) ϕ= 0 and (c) 60∘ can be broadly equated to using a QBO time-series index Ueq at 70, 40 and 20 hPa respectively.
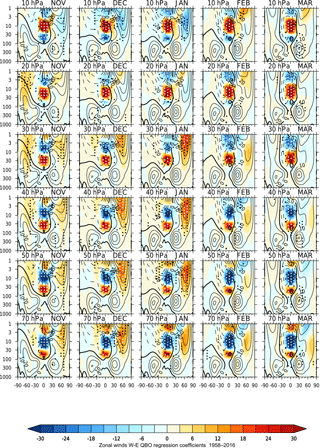
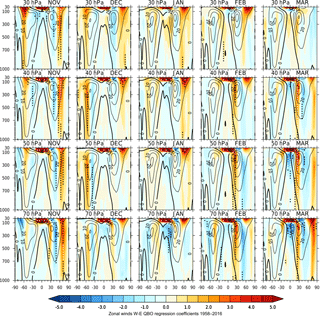
Figure 3Regression-based QBO-W minus QBO-E differences: height–latitude cross sections of zonally averaged zonal winds (ms−1) for November–March (columns) from the period 1958–2016. The rows show results for the QBO defined by equatorial zonal wind time series Ueq at different pressure levels from 10 to 70 hPa. Contours show the climatological values (interval of 10 ms−1 and the thick line is the zero value). White (black) dots indicate 99 % (95 %) statistical significance.
3.1 The polar vortex response
As described earlier, the standard approach that examines the difference between composite fields derived according to the phase of the equatorial QBO at a specified pressure level can be improved in two ways: firstly by employing regression analyses that take account of variability associated with ENSO, volcanic eruptions, the 11-year solar cycle plus a linear trend in addition to the QBO, and secondly by employing an EOF approach to encapsulate the height variations of the QBO. Figure 3 shows the scaled QBO regression coefficients of ERA-40/ERA-I zonally averaged zonal winds for November–March using the time series of FUB equatorial winds Ueq at different pressure levels from 10 to 70 hPa as the QBO index in the regression analysis. Each level represents a slightly different stage of the progression of the descending equatorial QBO. Scaling is applied so that the figures show typical amplitudes for QBO-W minus QBO-E differences (see Sect. 2). A statistically significant polar vortex response is evident over a relatively broad height range in each of the months, with maximum NH winter vortex response and greatest statistical significance in early winter (November–January) for the QBO defined by Ueq at 30–50 hPa. A very similar pattern of response is seen using the EOF approach, with maximum amplitude of the vortex response at around ϕ= 0∘, which is equivalent to Ueq at 40 hPa. Figure S5 shows results at selected values of (a) 60, (b) ϕ= 0 and (c) ϕ= −60∘ (which broadly equate to using a QBO time-series index Ueq at 20, 40 and 70 hPa respectively – see Sect. 2 and Fig. S4). The EOF results, based on 58 years, agree remarkably well with BD98 (who analysed only 18 years) in terms of the optimum value of ϕ to characterize the maximum vortex response (their optimum ϕ response correlated most closely with the Ueq time series at ∼ 45 hPa). A comparison of Fig. 3 and the full EOF results at all values of ϕ (not shown) suggests that the additional complexity of employing the EOF approach does not change the interpretation of the polar vortex response, but it does highlight that the peak vortex response occurs when there is a relatively deep equatorial QBO wind profile in the middle to lower stratosphere; the peak vortex response centred around ϕ= 0∘ is associated with a vertical QBO profile of equatorial winds having the same sign throughout the depth 15–70 hPa (see Fig. 2). This result supports the findings of Dunkerton et al. (1988), who concluded that “The most relevant QBO statistic does not appear to be the wind direction at any particular level, but rather the depth of the QBO wind regimes”.
These regression results confirm earlier studies (Baldwin et al., 2001; Anstey et al., 2010, 2014) that the primary influence of the QBO on the NH vortex is in early winter. There are some interesting similarities and differences between these results that employ regression analysis of the period 1958–2016 and the results of Anstey et al. (2010; hereafter A10), who employed composite analysis of only the ERA-40 dataset which covers the 1958–2001 period. The deep extension of the November signal into the NH troposphere is notable in both analyses. A10 note that a different EOF combination could be found to optimize an early winter response that peaked in November/December and a separate late winter response that peaked in February (see their Figs. 5 and 6). They found the greatest statistical significance in November, and this reduced as the winter progressed. In contrast, Figs. 3 and S5 indicate a maximum polar vortex response and greatest statistical significance in mid-winter (December/January). The February response is much weaker and is statistically insignificant at all values of Ueq and ϕ. There is better agreement with the analysis of Anstey and Shepherd (2014) and Lu et al. (2014), who analysed the longer period 1958–2011, suggesting that this difference is due to the additional years.
In the Southern Hemisphere (SH) the regression results also confirm the findings of BD98. The amplitude response of the SH vortex is found to be greatest (and statistically significant) in October/November. In contrast to the NH, this suggests that the QBO influence on the SH vortex is in late winter/spring; the QBO appears to primarily affect the timing of the final warming in the SH as opposed to the early/mid winter vortex strength in the NH. This supports the generally accepted mechanism of a QBO influence through the modulation of wave activity in the stratosphere. Wave forcing from the troposphere in the SH is much weaker than in the NH. The QBO thus has little influence on the SH vortex strength in early/mid winter and its influence on the polar vortex is only felt in late winter when the vortex begins to weaken through radiative processes. The SH vortex response maximizes for Ueq at 30 hPa in Fig. 3 and at approximately ϕ= 30∘ (not shown). ϕ= 30∘ is highly correlated with the Ueq time series at ∼ 30 hPa (see Fig. S4). This is a slightly higher level than the Ueq= 40 hPa level found to optimize the NH polar vortex response and is consistent with results of BD98 (and also A10, who analysed this hemispheric difference further).
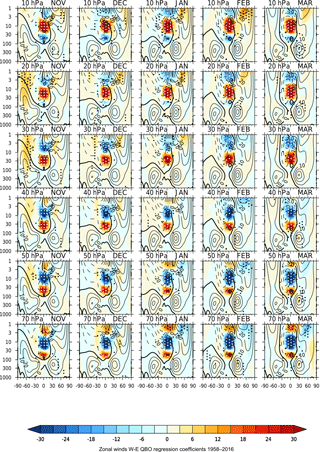
Figure 4As Fig. 3 but with an additional index included in the regression analysis to represent the polar vortex variations.
For Ueq= 20 hPa in November (Fig. 3), during the earlier stage in the descent of the anomaly, the main NH extra-tropical response is in the upper stratosphere, primarily over the subtropics in early winter. For Ueq= 30 hPa the anomaly strengthens and moves poleward throughout the course of the winter, although the response is only statistically significant in early winter. The NH subtropical response in the upper stratosphere in November resembles the QBO-induced meridional circulation anomaly (with an anomaly in the subtropics of opposite sign to that in the tropics; Plumb and Bell, 1982), but the amplitude enhancement and poleward extension throughout the winter suggest that it has been further amplified by wave–mean flow interaction (Gray et al., 2003). As an aside, we note the similarity between the evolution of the subtropical QBO feature in the upper stratosphere and the proposed mechanism for the response of the NH vortex to the 11-year solar cycle, which also involves the presence of a small early winter wind anomaly in the subtropical upper stratosphere that is amplified by wave–mean flow interaction and moves poleward and downward through the winter in a similar fashion (Kodera and Kuroda, 2002; Gray et al., 2010).
Figure 4 shows the corresponding QBO signal from a regression analysis in which an additional index was included to represent variations in the strength of the NH stratospheric polar vortex. The additional index consisted of the monthly time series of zonally averaged zonal winds at 10 hPa, 60∘ N. Including indices in the regression analysis that are not independent is inadvisable. The polar vortex index exhibits QBO variability (as Fig. 3 demonstrates) so both the QBO index and the vortex index include quasi 2-year variability. The QBO response is thus likely to change as a result of the inclusion of the vortex index. However, acknowledging this issue, we choose to turn it to our advantage to explore the possibility that the resulting changes in the response patterns can help to separate out the different influence paths discussed earlier (polar, subtropical, tropical). The QBO response shown in Fig. 4 is thus the response that the regression analysis determines to be more closely associated with the equatorial QBO wind index than with the polar vortex index.
Despite the known co-linearity between the QBO and the polar vortex indices, inclusion of the polar vortex index does not appear to adversely affect the efficacy of the fitting process of the linear regression model. Various sensitivity tests have been performed to check this. Firstly, we confirmed that the QBO results with and without the additional vortex index were not influenced by inclusion/exclusion of any of the other indices. Secondly, a stepwise approach was taken, in which variability associated with the polar vortex was first regressed out (using a univariate regression with just the vortex index) and then the standard multivariate analysis (with QBO, ENSO, solar, volcanic, and trend terms) was performed on the residual. Comparison of the results with the single-step process that included all indices at once found them to be essentially the same.
As expected, the polar vortex response previously associated with the QBO has disappeared in Fig. 4 since this is better captured by the vortex index. For example, a comparison of Fig. 4 for Ueq= 30–50 hPa in January with the corresponding plot in Fig. 3 shows that the statistically significant signal with a stronger polar vortex in the QBO-W phase than in the QBO-E phase has disappeared. Interestingly, there is an easterly anomaly evident in the NH subtropics in Fig. 3 between ∼ 5 and 70 hPa (see e.g. January at Ueq = 50 hPa), so the QBO anomaly extends into the mid-latitudes to ∼ 40∘ N. With the polar vortex index included (Fig. 4) this anomaly disappears, demonstrating that it is closely aligned to the see-saw pattern of anomalies that occur as a result of a polar vortex disturbance. As a result, the true width of the QBO wind anomaly can be seen, extending to ∼ 30 hPa. Similar comparisons with and without the vortex index will be employed in the following sections as a novel approach to explore whether the polar route is the primary route of QBO influence in the troposphere and at the Earth's surface.
3.2 Tropospheric zonal wind response
Figures 3 and 4 show highly statistically significant responses to the QBO that extend down into the troposphere for Ueq at all pressure levels, particularly in early and late winter. To better examine the tropospheric response, Figs. 5–6 reproduce Figs. 3–4 with a linear scale up to 30 hPa so that the tropospheric responses are highlighted (note that the colour scale has been altered accordingly; plots for Ueq= 10 and 20 hPa are omitted since they are virtually mirror images of those for Ueq= 50–70 hPa). In mid-winter, the influence of the polar vortex response extending down to the surface at mid-to-high NH latitudes is clearly evident in Fig. 5, and absent in Fig. 6, especially in January for Ueq= 30–50 hPa, although we note that the amplitude of the signal in mid-winter just below the polar vortex in Fig. 5 is relatively weak and barely significant.
In early winter, there is a strong, statistically significant NH negative/positive dipole structure, e.g. in November at 40∘ N∕60∘ N in Fig. 5, that shows a poleward progression as the QBO descends through the atmosphere from Ueq= 30 to Ueq= 70 hPa. This 40∘∕60∘ NH dipolar response in November is noticeably weakened when the polar vortex index is introduced (Fig. 6) e.g. for Ueq= 30–50 hPa, suggesting that a portion of this early winter dipolar response is connected to the stratospheric vortex variability. However, a 95 % statistically significant response nevertheless remains at around 50–70∘ N in November for Ueq= 30–40 and for Ueq= 70 hPa. This remaining high-latitude signal could be due to the choice of an imperfect vortex index that does not characterize the vortex behaviour sufficiently well, or it could be due to the presence of additional mechanisms that are active in early winter, such as planetary wave reflection from the upper stratosphere (Perlwitz et al., 2003, 2004; Shaw et al., 2014; Lu et al., 2017) that does not involve the mediation of large-scale variations of the polar vortex such as sudden stratospheric warming events (SSWs). It could also be a result of the tropical route, in which the QBO directly influences tropical convection and hence the source of planetary-scale waves propagating into the mid and high latitudes.
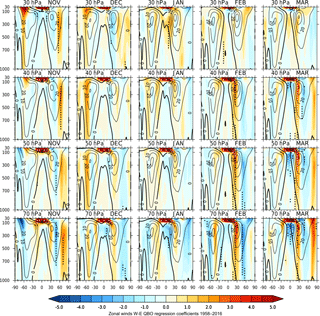
Figure 6As Fig. 4 but using a linear height scale between 30 and 1000 hPa to emphasize the tropospheric response. Note that the colour scale has been amended accordingly.
At the lower levels (Ueq= 40–70 hPa) in November there is a clear connection between the tropospheric anomaly and the QBO anomaly in the very lowermost levels of the equatorial stratosphere, giving a horseshoe shaped response in the subtropics. This horseshoe response is most evident for Ueq= 70 hPa in early winter (November) and in late winter/spring (February/March). At the same time as the development and strengthening of this horseshoe response an easterly anomaly develops in the upper tropospheric winds over the Equator, reaching 3 ms−1 (99 % statistical significance) in March at ∼ 200 hPa.
Inclusion of the additional polar vortex index (Fig. 6) strengthens the significance of the dipolar response e.g. at 30∘∕50∘ in February/March for Ueq= 70 hPa, suggesting the presence of a QBO influence via the tropical and/or sub-tropical route that is partially cancelled by the polar vortex influence. The negative anomaly in the tropical upper troposphere remains largely unaffected by the inclusion of the polar vortex index. This suggests a more local response of the tropical troposphere and the NH subtropical jet in late winter, either in response to the presence of the overlying QBO anomaly in the tropical lowermost stratosphere, for example through its impact on deep convection, or in response to the QBO-induced meridional circulation in the subtropics (or both).
An initial assessment of the horseshoe response for Ueq= 70 hPa might suggest a straightforward interpretation in terms of a modulation of the Hadley circulation strength by the QBO. In the stratosphere, the descending QBO-W phase gives rise to a local secondary meridional circulation anomaly in the tropics/subtropics with anomalous descent over the Equator, below the level of the maximum westerlies, which suppresses the background upwelling in the equatorial lower stratosphere (and vice versa under QBO-E conditions). QBO-W anomalies in the lower stratosphere also give rise to a weakened Brewer–Dobson (B–D) circulation as a result of reduced planetary wave forcing (White et al., 2016). Both impacts will thus weaken the upwelling branch of the B–D circulation in the tropical lower stratosphere. However, this simple interpretation in terms of a weakened B–D circulation response in the stratosphere extending down into the troposphere is incompatible with the response seen in Fig. 5, since it indicates a strengthening of the Hadley circulation under QBO-W conditions.
This apparent contradiction has been recognized by previous studies. One explanation has been sought in terms of the tropical route of influence via a QBO modulation of “deep convection”, i.e. the height to which equatorial tropical convective upwelling can extend. Previous studies have indeed found that QBO-W years are less favourable for deep convection and have investigated mechanisms for this in terms of the QBO modulation of the zonal wind vertical shear, cold-point (tropopause) temperatures and associated changes in static stability (Leiss and Geller, 2012; Nie and Sobel, 2015; Yoo and Son, 2016). On the other hand, the model study of Garfinkel and Hartmann (2011b) found a weakening of the subtropical jet under QBO-E conditions (consistent with our results), especially in the Pacific, and attributed this to the influence of the QBO-induced meridional circulation on the subtropical jet which interacts with high-frequency eddies and thus extends the anomaly to the surface. They also found the subtropical response was stronger in February than in January and noted that while there was a QBO response in modelled convection (with cloud tops rising in response to the QBO-E), the convective anomalies appeared to dampen, rather than drive, the QBO response in the extratropical troposphere.
3.3 Northern Hemisphere sea level pressure response
Figure 7 shows results for November–March from the regression analyses of mean sea level pressure over the NH for values of Ueq ranging from 10 to 70 hPa. The previously identified surface response in January over the Atlantic/European sector (e.g. Holton and Tan, 1982; Anstey and Shepherd, 2014 – see their Fig. 2) is evident for Ueq= 30–50 hPa and is statistically significant at the 95 % level for Ueq= 40–50 hPa. The response resembles a positive NAO response to QBO-W conditions, with anomalously low pressure over the pole and a strengthening of the subtropical high over the Azores (and vice versa under QBO-E conditions). The timing and range of Ueq values over which this response is maximized are approximately the same as the maximum response of the stratospheric polar vortex in Fig. 3. There is also a positive response over China and the Pacific, giving some suggestion of an annular mode response though neither of these responses is statistically significant. Results using the EOF approach show essentially the same pattern of response (Fig. S6).
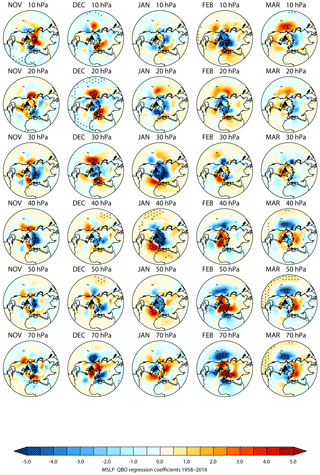
Figure 7Regression-based QBO-W minus QBO-E differences: latitude–longitude distribution of mean sea level pressure (hPa) for November–March (columns) from the period 1958–2016. The rows show results for the QBO defined by equatorial zonal wind time series Ueq at different pressure levels from 10 to 70 hPa. White (black) dots indicate 99 % (95 %) statistical significance.
Figure 8 shows the corresponding QBO signal when the additional NH vortex index was included. Note that we have not imposed a lag on the polar index to take into account any delay between changes in the polar vortex and the troposphere/surface response. Tests with imposed lags showed very little sensitivity, possibly because the data are monthly averaged and the averaging is therefore on the same timescale as the lag in the response. The positive NAO-like response in the QBO regression coefficients in January for Ueq= 30–50 hPa is substantially weakened by the inclusion of the polar vortex index and is no longer statistically significant, demonstrating that the QBO variability in the stratospheric polar vortex plays an important role in the January NAO-like response in mslp.
In December, there are also statistically significant mslp responses for Ueq= 20 and Ueq= 70 hPa (Fig. 7) that have not been previously reported. The response patterns have opposite signs at the two levels and resemble a positive (negative) annular mode for Ueq= 20 hPa (Ueq= 70 hPa) with substantial amplitudes (> 5 hPa difference between QBO-W and QBO-E) in both the North Pacific and the Atlantic/European sector. The statistical significance of the response over the Atlantic/European sector is greater than 99 % over a larger region than the previously identified NAO-like response in January, described above. However, the response is centred further eastward over Europe, so that it likely projects onto the eastern Atlantic pattern of variability rather than the NAO itself (it also likely projects onto the major centres of blocking events). The corresponding EOF analysis (Fig. S6) shows a similar pattern of response at 60 and ϕ= −60∘ (approximately equivalent to Ueq= 20 and Ueq= 70 hPa respectively), although at ϕ= −60∘ the Pacific response is not significant.
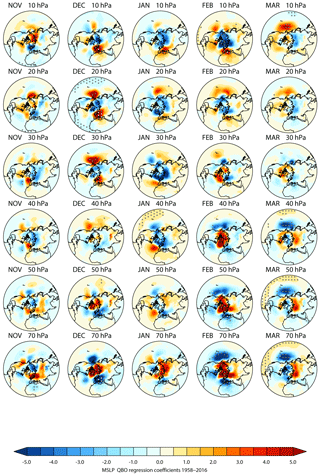
Figure 8As Fig. 7 but with an additional index included in the regression analysis to represent the polar vortex variations.
The December QBO surface responses appear to be unrelated to the January NAO response, not only in respect of the difference in the pattern of the response, but also with respect to their timing. Referring back to Fig. 2, the 60∘ QBO vertical wind profile is typical of a descending westerly phase in the upper stratosphere at around 20 hPa, i.e. at an earlier point in time than the ϕ= 0∘ profile (which is roughly equivalent to Ueq at 40 hPa). However, the December response at 20 hPa and the January response at ∼ 40 hPa are unlikely to be simply due to the gradual descent of the QBO winds from December to January in the same year. As discussed in Sect. 2, a change of ϕ= 10∘ is equivalent to a time shift of ∼ 0.8 months, so the time difference between 60 and ϕ=0∘ is at least 4 months (i.e. it takes on average at least 4 months for the QBO to descend from 20 to 40 hPa).
A likely reason that the December mslp response has not previously been identified is that the majority of previous studies have used Ueq= 40–50 hPa to characterize the QBO (and often only examine the DJF average). Figure 7 (and S6) shows clearly that the maximum December response is characterized using Ueq= 20 and Ueq= 70 hPa and there is a minimum response (and change of sign) around Ueq= 40 hPa, in contrast to the January response that peaks for Ueq= 40 hPa, so most previous studies will have missed it for this reason.
In the regression analysis in which the NH polar vortex index was included, the Ueq= 20 and Ueq= 70 hPa responses in December (Fig. 8) remain virtually unchanged. This suggests that they are not a direct result of the influence of vortex variability extending down to the surface, as was the case for the January response. We note that the early winter mslp sensitivity to QBO winds in the upper stratosphere shows similarity to the results of Lu et al. (2017), who examined the mslp response to the 11-year solar cycle in terms of downward wave reflection. In particular, they also found a dual response over the Aleutian Low region in the North Pacific and over the Atlantic/European sector in early winter, similar to Fig. 7 in December (see their Figs. 3 and 4). They also noted that the mslp anomaly pattern differs from the classical NAO pattern because it extends further eastward towards eastern Europe, again in a similar fashion to Fig. 7 in December.
While circumstantial, this similarity in mslp response suggests that a similar planetary wave reflection mechanism could be responsible for the highly significant QBO response seen for Ueq= 20 hPa in December, a possibility that requires further investigation. However, inclusion of a simple index in the regression analysis to represent years that are favourable for downward wave coupling, as proposed by Perlwitz and Harnik (2003), namely the difference of the zonal wind at 2 and 10 hPa averaged between 58 and 74∘ N, did not produce any notable changes to this December response (we would expect it to weaken substantially, in the same way as the NAO response in January weakens when the 10 hPa, 60∘ N vortex index is included). Nevertheless, this simple 2–10 hPa zonal wind index may not adequately represent downward wave coupling. Shaw et al. (2010) suggested that it may require a more complex index that includes information about both the vertical and meridional wavenumbers of the relevant waves.
On the other hand, there is also a similar response of the opposite sign for Ueq= 70 hPa, the mirror image of the Ueq= 20 hPa response, so it is not clear whether the December response indicates a sensitivity to the upper stratosphere or to the very lowermost stratosphere. The fact that the mslp signals are located near the major centres of blocking suggests that instability in the high-latitude upper troposphere and lower stratosphere may be involved, but more research is needed to explore this.
Later in the winter season (February/March) a statistically significant negative anomaly is also evident over the Aleutian Low region of the North Pacific for Ueq= 50–70 hPa (Fig. 7). This mslp anomaly remains unchanged when the polar vortex index is included, indicating that it is unlikely to be directly related to the variability of the polar vortex. This region of the Pacific is highly coupled to tropical variability, largely through the presence of Rossby wave trains generated by anomalous tropical heating, so the continued presence of the anomaly despite inclusion of the vortex index, together with its association with the QBO winds in the very lowermost region of the equatorial stratosphere, suggests that its origin lies in the tropics or subtropics. This is further confirmed if the regression analysis is repeated with an additional index to represent the strength of the subtropical jet in the Pacific sector (using the 200 hPa zonal winds at 30∘ N averaged between 160∘ E and 160∘ W). In this case, the Aleutian Low response was greatly reduced in amplitude and lost its statistical significance (not shown). We note that it was not sufficient to use a zonally averaged NH subtropical jet index; the removal of the Aleutian Low response in this way required an index based only on the Pacific Ocean subtropical jet, confirming the results of Garfinkel et al. (2011b), who showed that the response of the subtropical jet to the QBO differs between the Pacific and Atlantic basins.
In summary, significant QBO responses in mslp are seen in NH winter, with QBO W–E differences of up to ∼ 6 hPa. These responses are evident using both the EOF approach and the standard approach of characterizing the QBO by the equatorial winds at a selected equatorial pressure level Ueq. In mid-winter (January) the anomaly is closely associated with variations in the strength of the stratospheric polar vortex; maximum responses are found at values of Ueq between 30 and 50 hPa (Fig. 7) and at values of ϕ in the region of 0∘ (Fig. S6). The two approaches are thus consistent in showing sensitivity of both the stratospheric polar vortex and the mid-winter (January) mslp response to the presence of a vertical QBO wind profile that has the same sign anomaly throughout the depth of the stratosphere up to ∼ 20 hPa. In addition, there are significant early winter (December) and late winter (February/March) responses, with a 180∘ phase difference between the responses for Ueq= 20 and Ueq= 70 hPa and a minimum response for Ueq= 40–50 hPa. These early/late winter responses are therefore unlikely to be caused by the same mechanism as the January response.
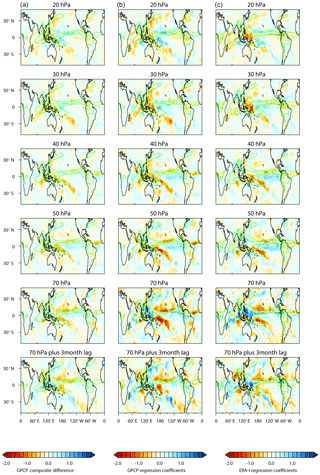
Figure 9Left column: latitude–longitude distributions of annually averaged W–E QBO composite differences in precipitation (mm day−1) using the GPCC dataset for 1979–2016. Middle column: corresponding regression analysis of the GPCC dataset for 1979–2016. Right column: corresponding regression analysis of total precipitation data from the ERA-I dataset for 1979–2016. The rows show results for the QBO defined by the equatorial zonal wind time series Ueq at different pressure levels from 20 to 70 hPa.
3.4 Precipitation response
Regression analysis results for precipitation are more uncertain, given the difficulty in accurately representing this quantity in the reanalysis models because of their reliance on parameterization of local processes that are too small to capture explicitly. Nevertheless, the results provide QBO response patterns that are generally consistent with previous studies of satellite observations, such as those of Leiss and Geller (2012; hereafter referred to as LG12), who performed an annual-mean composite analysis of the GPCP observations and Seo et al. (2013), who examined the QBO impact on rainfall in the western North Pacific in spring using the same dataset. As a preliminary assessment, Fig. 9 shows analysis of the GPCC observational dataset, for comparison with LG12. The left-hand column shows the annually averaged W–E composite difference based on the sign of Ueq at various pressure levels from 20 to 70 hPa. Composite differences are also shown for the QBO defined by the Ueq= 70 hPa time series lagged by 3 months (bottom panel), which was the QBO definition used by LG12 to account for the downward propagation of the QBO to the tropopause level (see their Sect. 3). The pattern and amplitude of the response at this level compares well with Fig. 7 of LG12; note that (a) LG12 show E–W differences, while Fig. 9 shows W–E differences, so the sign is reversed; (b) LG12 analysed the period 1979–2011, while Fig. 9 shows the analysis for 1979–2016, thus explaining some small differences in the response. For clarity, estimates of statistical significance are not shown in the figure, but they are similar to those of LG12, with rather limited regions of statistical significance.
The middle panel of Fig. 9 shows equivalent results from a multivariate regression analysis of the GPCC observations, where the influence of ENSO, the solar cycle, volcanic eruptions and a linear trend have been simultaneously accounted for. The regression analysis was first performed on the individual months and then averaged to obtain an estimate of the annually averaged response since it is not appropriate to annually average the data first when we are investigating a quasi 2-year oscillation. A similar averaging of the statistical significance estimates from the individual months is not appropriate, however, so these are not shown in Fig. 9 (but they are shown in later figures of the individual monthly averaged results).
The pattern of the annually averaged regression response is very similar to the composite differences, but the amplitudes are generally larger. As found by LG12, the basic pattern of the QBO response is unchanged when the ENSO is taken into account (and this is also true of the other potential influences: solar, volcanic and linear trends). In contrast to the results of LG12, the regression-based response for Ueq= 70 hPa has larger amplitude and is more clearly defined than when the 3-month lag is applied.
Finally, the right-hand column of Fig. 9 shows the equivalent regression-based results but using the ERA-I total precipitation reanalysis data for 1979–2016 instead of the GPCC observations. The pattern and amplitudes of the response are remarkably similar to the GPCC results, at all levels, giving confidence that the reanalysis precipitation data can be employed to investigate the QBO response. Figure S7 shows W–E QBO differences in total precipitation for each individual month from the regression analysis using Ueq= 70 hPa. While the individual monthly responses are much noisier, there are nevertheless statistically significant responses with coherent patterns from month to month that contribute to the annually averaged response shown in Fig. 9. Comparison between the traditional and EOF-based approaches also shows good agreement (Fig. S8).
These results all show an increase in total precipitation in the tropical western Pacific under QBO-W conditions in the very lowermost levels of the tropical stratosphere, in good agreement with previous studies, although the regression approach suggests maximum sensitivity for Ueq= 70 hPa (i.e. the 3-month lag employed by LG12 is not required). There is also a QBO influence on the main east–west band of precipitation across the Pacific and Atlantic oceans associated with the Inter-tropical Convection Zone (ITCZ), and this is evident for Ueq= 30–70 hPa. The response consists of a north–south dipole with reduced precipitation in the region of the climatological maximum at 5–10∘ N under QBO-W conditions and increased precipitation further south over the Equator, indicative of a southward shift of the ITCZ. The signal also clearly extends across into the Atlantic.
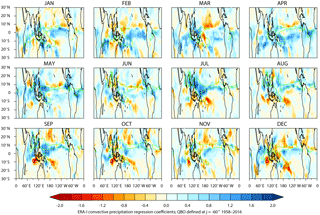
Figure 10Latitude–longitude distributions of monthly averaged W–E QBO differences from the regression analysis of convective precipitation data (mm per day) from the ERA-I dataset for 1958–2016. The EOF-based approach has been employed to define the QBO index, using ϕ= −60∘ (see text), which is approximately equivalent to defining the QBO by Ueq= 70 hPa.
Further insight into these QBO signals may be achieved by examining the combined ERA40/ERA-Interim dataset. While the observational data assimilated into the ERA40 reanalyses are less reliable, the overall signal patterns and amplitudes are consistent with the ERA-Interim period and their inclusion provides improved estimates of statistical significance. Additionally, the reanalysis datasets provide not only estimates of the total precipitation, but also the breakdown into its constituent parts. The latter includes convective precipitation, which is the component most likely influenced by the QBO. Similarly, additional insight can be gained using the EOF-based approach since it allows many more different configurations of the QBO to be explored (by taking different combinations of EOF1 and EOF2) and provides information on the typical vertical profile of the QBO at the angle ϕ where the maximum sensitivity is found.
Figure 10 shows results from a regression analysis of convective precipitation from the combined ERA dataset for each month, using ϕ= −60∘ (approximately equivalent to Ueq= 70 hPa) for the period 1958–2016. The pattern of response is similar to that of total precipitation in Fig. S8, confirming that convective precipitation dominates the QBO response in the tropics. The responses in the convective precipitation are more coherent, making it easier to extract the primary signals and their dependence on season. The responses compare well with the results of LG12, who concentrated their study on ISCCP weather states for developing and mature convection. The increased convective precipitation over the tropical western Pacific is particularly evident between May and September. The QBO response associated with the ITCZ is present all year around, but the signal has little statistical significance at this value of ϕ.
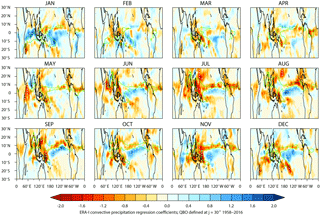
Figure 11As Fig. 10 but using 30∘, which is approximately equivalent to defining the QBO by Ueq= 30 hPa.
Examination of the QBO response at all values of ϕ shows that while ϕ= −60∘ maximizes the signal over the western Pacific, this is not the value that maximizes the ITCZ signal, as already noted in the discussion of Fig. 9. Figure 11 shows the W–E QBO differences in convective precipitation for each month from the regression analysis using 30∘ (approximately equivalent to Ueq= 30 hPa; see Fig. S4) for the period 1958–2016. In this case, the western Pacific signal is reversed in sign, is less coherent and has reduced statistical significance, but the north–south dipole response in the region of the ITCZ is much clearer and has extensive regions with 99 % significance over the tropical Pacific in all months from June through to December. Under QBO-W conditions there is a clear signal of increased precipitation over the Equator and reduced precipitation in the region of the climatological maximum associated with the ITCZ. This is in general agreement with the modelling results of Garfinkel and Hartmann (2011b), who found increased precipitation in the ITCZ over the Pacific under QBO-E conditions (note that their study was for perpetual February conditions).
Reference to Fig. 2 shows that the ϕ= −60 and ϕ= +30∘ QBO profiles both have the same sign (westerly) between 30 and 70 hPa, but the 30∘ profile is close to zero at 70 hPa. The reversal in sign of the tropical western Pacific response between ϕ = −60 and 30∘ therefore suggests that precipitation in this region is sensitive either to the equatorial winds above 30 hPa or, more likely, to the equatorial winds (or their vertical gradient) in the region of 70 hPa. The latter is more consistent with our understanding of the possible QBO mechanisms that influence deep tropical convection. The signal across the Pacific associated with the ITCZ is most sensitive to 30∘, which is characterized not only by an equatorial wind profile that has the same sign (westerly) throughout the stratosphere, but also by strong positive vertical wind shear near 70 hPa. Both of these results are consistent with an important role for tropical tropopause temperatures, which are closely linked with vertical wind shear (via thermal wind balance); the sensitivity to slightly different QBO wind profile and height of the vertical shear suggests directions for further investigation to identify the primary mechanism(s) of QBO influence on these two regions of convective precipitation. They also confirm the usefulness of employing the EOF approach to provide higher-resolution information on the QBO wind profile and its vertical shear.
QBO teleconnections with the NH stratospheric polar vortex, tropospheric zonal winds, mean sea level pressure and precipitation have been explored. Multivariate regression analysis was the main technique employed (composite difference analysis was employed where appropriate for comparison with previous studies). The analyses used both the traditional method of representing the QBO by the equatorial zonal wind Ueq at a single pressure level and also an EOF-based approach to better characterize the vertical profile of the QBO anomalies. The two approaches were found to give consistent results; the EOF approach provided additional insight, by highlighting responses that showed sensitivity to the vertical depth of the QBO wind anomaly or to the vertical shear of the QBO winds. Results of the analyses were interpreted in terms of three possible routes of QBO influence: tropical, subtropical and polar (see Fig. 1). A novel approach was employed to eliminate impacts associated with the polar route, by introducing an additional index into the regression analysis to characterize variations of the NH polar vortex. By including this index, any QBO influence on the troposphere that arises primarily via a modulation of the polar vortex (often through the occurrence of SSWs) was effectively removed, since this variability is better captured by the polar vortex index than the QBO index.
A stronger, undisturbed polar vortex was found to be associated with westerly QBO wind anomalies in the mid–lower stratosphere, in good agreement with previous studies. This polar vortex response was found for westerly QBO anomalies over a relatively deep range between 10 and 70 hPa.
The QBO response in zonal-mean zonal winds extends deep into the troposphere at subtropical, mid and high latitudes, particularly in early winter (November) and in late winter (March). As the QBO descends through to the lowermost levels of the stratosphere a horseshoe shaped response emerges in the subtropics, connecting the lowermost stratospheric QBO anomaly with an anomaly in the subtropical jet that extends deep into the troposphere. This subtropical response strengthens as the winter proceeds, reaching maximum amplitude and statistical significance in late winter/spring. At the same time, an easterly wind anomaly emerges in the tropical upper tropospheric winds for Ueq= 70 hPa, which also strengthens during the winter. A dipolar response at 40∘ N∕60∘ N is evident at all QBO levels from 30 to 70 hPa, particularly in early winter (November) and late winter/spring (February/March).
The horseshoe response in the sub-tropics and the easterly anomaly in the tropical upper troposphere were largely unaffected when the polar vortex index was introduced, which suggests they arise via the tropical or subtropical routes rather than the polar route. The early and late winter mid-latitude 40∘∕60∘ N dipolar responses are only partially removed when the polar index index is introduced. This suggests that either the additional polar vortex index has not completely captured (and removed) the tropospheric response associated with the polar route, or else there are additional mechanisms in early and late winter acting through the tropical or sub-tropical routes.
At the surface, several QBO signals in the mean sea level pressure were identified, with amplitudes up to ∼ 6 hPa. The previously reported positive NAO response in January to a westerly QBO phase in the lower stratosphere was confirmed and is closely associated with variations in the strength of the stratospheric polar vortex. In addition, two further mslp responses were found which have not previously been reported. In December a statistically significant anomaly was found over both Europe and the North Pacific in response to a QBO defined by Ueq = 20 hPa. The Atlantic/European response is shifted eastward compared with the NAO pattern. The QBO at 20 hPa is effectively a mirror image of the QBO at 70 hPa, so the response could be a result of sensitivity to the QBO at those lower levels. Neither the European nor Pacific responses were affected by inclusion of the stratospheric polar vortex index, suggesting early winter mechanisms that operate via the subtropical/tropical routes (or else a polar mechanism that does not involve large-scale variations in the polar vortex).
In March, a second mslp response is seen over the North Pacific, with a negative anomaly in response to a westerly QBO phase at Ueq= 50–70 hPa. This was shown to be closely associated with a strengthening of the Pacific subtropical jet.
Finally, the QBO impact on precipitation was examined, albeit with awareness of the difficulty of its representation in reanalysis models because of the challenges of parameterizing processes that occur at sub-grid scales. Identical analyses were performed using the ERA reanalysis datasets and GPCC observational data, and comparisons performed between composite and regression analyses, to ensure confidence in the results. An increase in precipitation was found over the tropical western Pacific in response to westerly QBO winds at Ueq= 70 hPa, particularly between May and September. Reduced precipitation was found in the east–west band of precipitation associated with the ITCZ in response to QBO westerlies, particularly between June and December, together with a corresponding increase equatorwards of this, suggesting a southward shift of the ITCZ. The ITCZ response maximized at 30∘. This QBO profile is most closely correlated with QBO winds at 30 hPa and has strong positive vertical wind shear around 70 hPa.
We note a number of caveats to this study. The most important is that the data study can only point to apparent relationships and does not demonstrate cause and effect. Secondly, the methodology assumes linearity, and in reality it is clear that significant non-linear responses can play an important role in the coupled climate system; nevertheless examination of these linear signals helps to identify and characterize the dominant signals and points to directions for future research. Finally, while the relevant known forcing factors are included in the regression analysis, there may be missing factors, and even those that are included may not be adequately represented. The representation of ENSO variability is a particular concern for the analysis of the precipitation responses since it dominates the variability at equatorial latitudes.
All analyses performed in this study were based on data publicly available, as described in Sect. 2. No additional datasets were produced in the process of this analysis.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-18-8227-2018-supplement.
The authors declare that they have no conflict of interest.
This article is part of the special issue “The SPARC Reanalysis Intercomparison Project (S-RIP) (ACP/ESSD inter-journal SI)”. It is not associated with a conference.
The authors wish to thank the two reviewers, Marvin Geller and
Chaim Garfinkel, for their very helpful and constructive comments that
resulted in a much improved manuscript. Lesley J. Gray, Hua Lu and
Scott Osprey acknowledge funding from the UK Natural Environment Research
Council (NERC) through support of the ACSIS (Atlantic Climate System
Integrated Study) Programmes at the National Centre for Atmospheric Science
(LG), the British Antarctic Survey (HL), and Belmont Grant NE/P006779/1 –
GOTHAM – 1505DC004/MW2 (SO). Yoshio Kawatani was supported by JSPS KAKENHI
grant numbers 26287117 and 15KK0178 and by the Environment Research and
Technology Development Fund (2-1503) of the Environmental Restoration and
Conservation Agency. Verena Schenzinger acknowledges doctoral study support
at Oxford through a Rhodes Scholarship.
Edited by: Gabriele Stiller
Reviewed by: Chaim Garfinkel and
Marvin A. Geller
Adler, R. F., Sapiano, M., Huffman, G. J., Wang, J.-J., Gu, G., Bolvin, D., Chiu, L., Schneider, U., Becker, A., Nelkin, E., Xie, P., Ferraro, R., and Shin, D.-B.: The Global Precipitation Climatology Project (GPCP) Monthly Analysis (New Version 2.3) and a Review of 2017 Global Precipitation, Atmosphere, 9, 138, https://doi.org/10.3390/atmos9040138, 2018.
Allan, R. and Ansell, T.: A new globally-complete monthly historical gridded mean sea level pressure data set (HadSLP2): 1850-2-004, J. Climate, 19, 5816–5842, 2006.
Anstey, J. A. and Shepherd, T. G.: Response of the northern stratospheric polar vortex to the seasonal alignment of QBO phase transitions, Geophys. Res. Lett., 35, L22810, https://doi.org/10.1029/2008GL035721, 2008.
Anstey, J. A. and Shepherd, T. G.: High-latitude influence of the quasi-biennial oscillation, Q. J. Roy. Meteor. Soc., 140, 1–21, 2014.
Anstey, J. A., Shepherd, T. G., and Scinocca, J. F.: Influence of the Quasi Biennial Oscillation on the Extratropical Winter Stratosphere in an Atmospheric Circulation Model and in Reanalysis Data, J. Atmos. Sci., 67, 1402–1419, https://doi.org/10.1175/2009JAS3292.1, 2010.
Baldwin, M. P. and Dunkerton, T. J.: Quasi-biennial modulation of the southern hemisphere stratospheric polar vortex. Geophys. Res. Letts, 25, 3343-3346, 1998.
Baldwin, M. P. and Dunkerton, T. J.: Stratospheric Harbingers of Anomalous Weather Regimes, Science, 294, 581–584, 2001.
Baldwin, M. P., Gray, L. J., Dunkerton, T. J., Hamilton, K., Haynes, P. H., Randel, W. J., Holton, J. R., Alexander, M. J., Hirota, I., Horinouchi, T., Jones, D. B. A., Kinnersley, J. S., Marquardt, C., Sato, K., and Takahashi, M.: The quasi-biennial oscillation, Rev. Geophys., 39, 179–229, 2001.
Calvo, N., Gioorgetta, M. A., Garcia-Herrera, R., and Manzini, E.: Nonlinearity of the combined warm ENSO and QBO effects of the Northern Hemisphere polar vortex in MAECHAM5 simulations, Geophys. Res. Lett., 34, D13109, https://doi.org/10.1029/2008JD011445, 2009.
Christiansen, B.: Stratospheric bimodality: can the equatorial QBO explain the regime behavior of the NH winter vortex?, J. Climate, 23, 3953–3966, 2010.
Christiansen, B.: The Holton-Tan relationship in the CMIP5 and CCMVal2 models, EGU General Assembley, Vienna, Austria, 27 April–2 May 2014, 2014EGUGA.16.5883C, 2014.
Collimore, C. C., Martin, D. W., Hitchman, M. H., Huesmann, A., and Waliser, D. E.: On the relationship between the QBO and tropical deep convection, J. Climate, 16, 2552–2568, 2003.
Crooks, S. A. and Gray, L. J.: Characterisation of the 11-year solar signal using a multiple regression analysis of the ERA-40 data set, J. Climate, 18, 996–1015, https://doi.org/10.1175/JCLI-3308.1, 2005.
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim reanalysis: configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, 2011.
Dunkerton, T. J., Delisi, D. P., and Baldwin, M. P.: Distribution of major stratospheric warmings in relation to the quasi-biennial oscillation, Geophys. Res. Lett., 15, 136–139, https://doi.org/10.1029/GL015i002p00136, 1988.
FUB: Freie Universität Berlin: The Quasi-Biennial-Oscillation (QBO) Data Series, available at: http://www.geo.fu-berlin.de/en/met/ag/strat/produkte/qbo/, last access: 11 March 2016.
Garfinkel, C. I. and Hartmann, D. L.: Effects of the El Nino – Southern Oscillation and the quasi biennial oscillation on polar temperatures in the stratosphere, J. Geophys. Res., 112, D19112, https://doi.org/10.1029/2007JD008481, 2007.
Garfinkel, C. I. and Hartmann, D. L.: The influence of the quasi-biennial oscillation on the troposphere in winter in a hierarchy of models. Part I: Simplified dry GCMs, J. Atmos. Sci., 68, 1273–1289, https://doi.org/10.1175/2011JAS3665.1, 2011a.
Garfinkel, C. I. and Hartmann, D. L.: The influence of the quasi-biennial oscillation on the troposphere in winter in a hierarchy of models. Part II: Perpetual winter WACCM runs, J. Atmos. Sci., 68, 2026–2041, 2011b.
Garfinkel, C. I., Shaw, T. A., Hartmann, D. L., and Waugh, D. W.: Does the Holton Tan Mechanism explain how the Quasi-Biennial Oscillation modulates the Arctic Polar Vortex?, J. Atmos. Sci., 69, 1713–1733, 2012.
Giorgetta, M. A., Bengtsson, L., and Arpe, K.: An investigation of QBO signals in the east Asian and Indian monsoon in GCM experiments, Clim. Dynam., 15, 435–450, https://doi.org/10.1007/s003820050292, 1999.
Gray, L. J.: The influence of the equatorial upper stratosphere on stratospheric sudden warmings, Geophys. Res. Lett., 30, 1166–1169, https://doi.org/10.1029/2002GL016430, 2003.
Gray, L. J., Beer, J., Geller, M., Haigh, J. D., Lockwood, M., Matthes, K., Cubasch, U., Fleitmann, D., Harrison, G., Hood, L., Luterbacher, J., Meehl, G. A., Shindell, D., van Geel, B., and White, W.: Solar influences on climate, Rev. Geophys., 48, RG4001, https://doi.org/10.1029/2009RG000282, 2010.
Gray, L. J., Scaife, A. A., Mitchell, D. M., Osprey, S., Ineson, S., Hardiman, S., Butchart, N., Knight, J., Sutton, R., and Kodera, K.: A lagged response to the 11 year solar cycle in observed winter Atlantic/European weather patterns, J. Geophys. Res.-Atmos., 118, 13405–13420, 2013.
Gray, L. J., Woollings, T. J., Andrews, M., and Knight, J.: Eleven-year solar cycle signal in the NAO and Atlantic/European blocking, Q. J. Roy. Meteor. Soc., 142, 1890–1903, 2016.
Hansen, F., Matthes, K., and Wahl, S.: Tropospheric QBO – ENSO interactions and differences between Atlantic and Pacific, J. Climate, 29, 1353–1368, https://doi.org/10.1175/JCLI-D-15-0164.1, 2016.
Hansen, F., Greatbatch, R. J., Gollan, G., Jung, T., and Weisheimer, A.: Remote control of North Atlantic Oscillation predictability via the stratosphere, Q. J. Roy. Meteorol. Soc., 143, 706–719, https://doi.org/10.1002/qj.2958, 2017.
Ho, C.-H., Kim, H.-S., Jeong, J.-H., and Son, S.-W.: Influence of stratospheric quasi-biennial oscillation on tropical cyclone tracks in western North Pacific. Geophys. Res. Lett., 36, L06702, https://doi.org/10.1029/2009GL037163, 2009.
Holton, J. R. and Tan, H.-C.: The Influence of Equatorial Quasi-Biennial Oscillation on the Global Circulation at 50 mb, J. Atmos. Sci., 37, 2200–2208, 1980.
Holton, J. R. and Tan, H.-C.: The quasi-biennial oscillation in the Northern Hemisphere lower stratosphere, J. Meteorol. Soc. Jpn., 60, 140–148, 1982.
Hoskins, B. J. and Karoly, D.: The steady linear response of a spherical atmosphere to thermal and orographic forcing, J. Atmos. Sci., 38, 1179–1196, 1981.
Kawatani, Y., Hamilton, K., Miyazaki, K., Fujiwara, M., and Anstey, J. A.: Representation of the tropical stratospheric zonal wind in global atmospheric reanalyses, Atmos. Chem. Phys., 16, 6681–6699, https://doi.org/10.5194/acp-16-6681-2016, 2016.
Kidston, J., Scaife, A. A., Hardiman, S. C., Mitchell, D. M., Butchart, N., Baldwin, M. P., and Gray, L. J.: Stratospheric influence on tropospheric jet streams, storm tracks and surface weather, Nat. Geosci., 8, 433–440, 2015.
Kodera, K. and Kuroda, Y.: Dynamical response to the solar cycle. J. Geophys. Res., 107, 4749–4761, https://doi.org/10.1029/2002JD002224, 2002.
Labitzke, K., Kunze, M., and Bronniman, S.: Sunsports, the QBO and the stratosphere in the north polar region – 20 years later, Meteorol. Z., 15, 355–363, 2006.
Liess, S. and Geller, M. A.: On the relationship between the QBO and distribution of tropical deep convection, J. Geophys. Res.-Atmos., 117, D03108, https://doi.org/10.1029/20117DO16317, 2012.
Long, C. S., Fujiwara, M., Davis, S., Mitchell, D. M., and Wright, C. J.: Climatology and interannual variability of dynamic variables in multiple reanalyses evaluated by the SPARC Reanalysis Intercomparison Project (S-RIP), Atmos. Chem. Phys., 17, 14593–14629, https://doi.org/10.5194/acp-17-14593-2017, 2017.
Lu, H., Baldwin, P. B., Gray, L. J., and Jarvis, M. J.: Decadal-scale changes in the effect of the QBO on the northern stratospheric polar vortex, J. Geophys. Res., 113, D10114, https://doi.org/10.1029/2007JD009647, 2008.
Lu, H., Bracegirdle, T. J., Phillips, T., Bushell, A., and Gray, L. J.: Mechanisms for the Holton – Tan relationship and its decadal variation, J. Geophys. Res.-Atmos., 119, 2811–2830, 2014.
Lu, H., Scaife, A. A., Marshall, G. J., Turner, J., and Gray, L. J.: Downward Wave Reflection as a Mechanism for the Stratosphere–Troposphere Response to the 11-Yr Solar Cycle, J. Climate, 30, 2395–2414, 2017.
Marshall, A. G. and Scaife, A. A.: Impact of the QBO on surface winter climate, J. Geophys. Res., 114, D18110, https://doi.org/10.1029/2009JD011737, 2009.
Marshall, A. G., Hendon, H. H., Son, S.-W., and Lim, Y.: Impact of the quasi-biennial oscillation on predictability of the Madden–Julian oscillation, Clim. Dynam., 49, 1365–1377, https://doi.org/10.1007/s00382-016-3392-0, 2017.
Mitchell, D. M., Gray, L. J., Anstey, J., Baldwin, M. P., and Charlton, A. J.: The influence of stratospheric vortex displacements and splits on surface climate, J. Climate, 26, 2668–2682, https://doi.org/10.1175/JCLI-D-12-00030.1, 2013.
Naujokat, B.: An Update of the Observed Quasi-Biennial Oscillation of the Stratospheric Winds over the Tropics, J. Atmos. Sci., 43, 1873–1877, 1986.
Nie, J. and Sobel, A. H.: Responses of tropical deep convection to the QBO: Cloud-resolving simulations, J. Atmos. Sci., 72, 3625–3638, https://doi.org/10.1175/JAS-D-15-0035.1, 2015.
Nishimoto, E. and Yoden, S.: Influence of the stratospheric quasi-biennial oscillation on the Madden–Julian oscillation during austral summer, J. Atmos. Sci., 74, 1105–1125, https://doi.org/10.1175/JAS-D-16-0205.1, 2017.
Perlwitz, J. and Harnik, N.: Observational evidence of a stratospheric influence on the troposphere by planetary wave reflection, J. Climate, 16, 3011–3026, 2003.
Perlwitz, J. and Harnik, N.: Downward coupling between the stratosphere and troposphere: The relative role of wave and zonal mean processes, J. Climate, 17, 4902–4909, https://doi.org/10.1175/JCLI-3247.1, 2004.
Plumb, R. A. and Bell, R. C.: A model of the quasi-biennial oscillation on an equatorial beta-plane, Q. J. Roy. Meteor. Soc., 108, 335–352, 1982.
Press, W. H., Teukolsky, S. A., Vettering, W. T., and Flannery, B. P.: Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd Edn., Cambridge University Press, Cambridge, 1992.
Rao, J. and Ren, R.: Varying stratospheric responses to tropical Atlantic SST forcing from early to late winterm, J. Climate, 1–18, https://doi.org/10.1007/s00382-017-3998-x, 2017.
Rayner, N. A., Parker, D. E., Horton, E. B., Folland, C. K., Alexander, L. V., and Rowell, D. P.: Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century, J. Geophys. Res., 108, 4407, https://doi.org/10.1029/2002JD002670, 2003.
Robock, A.: Volcanic eruptions and climate, Rev. Geophys., 38, 191–219, https://doi.org/10.1029/2007rg000232, 2000.
Ruti, P. M., Lucarini, V., Dell'Aquila, A., Calmanti, S., and Speranza, A.: Does the subtropical jet catalyze the midlatitude atmospheric regimes?, Geophys. Res. Lett., 33, L06814, https://doi.org/10.1029/2005GL024620, 2006.
Sato, M., Hansen, J. E., McCormick, M. P., and Pollack, J. B.: Stratospheric aerosol optical depths, 1850–1990, J. Geophys. Res.-Atmos., 98, 22987–22994, 1993.
Scaife, A. A., Athanassiadou, M., Andrews, M., Arribas, A., Baldwin, M., Dunstone, N., Knight, J., MacLachlan, C., Manzini, E., Müller, W. A., Pohlmann, H., Smith, D., Stockdale, T., and Williams, A.: Predictability of the quasi-biennial oscillation and its northern winter teleconnection on seasonal to decadal timescales. Geophys. Res. Lett., 41, 1752–1758, 2014.
Scaife, A. A., Karpechko, A. Y., Baldwin, M. P., Brookshaw, A., Butler, A. H., Eade, R., Gordon, M., MacLachlan, C., Martin, N., Dunstone, N., and Smith, D.: Seasonal winter forecasts and the stratosphere, Atmos. Sci. Lett., 17, 51–56, https://doi.org/10.1002/asl.598, 2016.
Scaife, A. A., Comer, R. E., Dunstone, N. J., Knight, J. R., Smith, D. M., MacLachlan, C., Martin, N., Peterson, K. A., Rowlands, D., Carroll, E. B., Belcher, S., and Slingo, J.: Tropical rainfall, Rossby waves and regional winter climate predictions, Q. J. Roy. Meteor. Soc., 143, 1–11, https://doi.org/10.1002/qj.2910, 2017.
Schenzinger, V.: Tropical stratosphere variability and extratropical teleconnections, DPhil, Thesis, Oxford University, 180 pp., 2017.
Schenzinger, V., Osprey, S., Gray, L., and Butchart, N.: Defining metrics of the Quasi-Biennial Oscillation in global climate models, Geosci. Model Dev., 10, 2157–2168, https://doi.org/10.5194/gmd-10-2157-2017, 2017.
Seo, J., Choi, W., Youn, D., Park, D.-S.R., Kim, J. Y.: Relationship between the stratospheric quasi-biennial oscillation and the spring rainfall in the western North Pacific, Geophys. Res. Lett., 40, 5949–5953, https://doi.org/10.1002/2013GL058266, 2013.
Shaw, T. A. and Perlwitz, J.: The life of Northern Hemisphere downward wave reflection between the stratosphere and troposphere, J. Climate, 26, 1745–1763, https://doi.org/10.1175/JCLI-D-12-00251.1, 2013.
Shaw, T. A., Perlwitz, J., and Harnik, N.: Downward wave reflection between the stratosphere and troposphere: The importance of meridional wave guiding and comparison with zonal-mean coupling, J. Climate, 23, 6365–6381, https://doi.org/10.1175/2010JCLI3804.1, 2010.
Shaw, T. A., Perlwitz, J., and Weiner, O.: Troposphere-stratosphere coupling: Links to North Atlantic weather and climate, including their representation in CMIP5 models, J. Geophys. Res. Atmos., 119, 5864–5880, https://doi.org/10.1002/2013JD021191, 2014.
Simpson, I. R., Blackburn, M., and Haigh, J. D.: The Role of Eddies in Driving the Tropospheric Response to Stratospheric Heating Perturbations, J. Atmos. Sci., 66, 1347–1365, 2009.
Son, S.-W., Lim, Y., Yoo, C., Hendon, H. H., and Kim, J.: Stratospheric Control of the Madden-Julian Oscillation, https://doi.org/10.1175/JCLI-D-16-0620.1, 2017.
Thompson, D. W. J., Baldwin, M. P., and Wallace, J. M.: Stratospheric connection to Northern Hemisphere wintertime weather: Implications for prediction, J. Climate, 15, 1421–1428, https://doi.org/10.1175/1520-0442(2002)015,1421:SCTNHW.2.0.CO;2, 2002.
Uppala, S. M., Kållberg, P. W., Simmons, A. J., Andrae, U., Bechtold, V. Da Costa, Fiorino, M., Gibson, J. K., Haseler, J., Hernandez, A., Kelly, G. A., Li, X., Onogi, K., Saarinen, S., Sokka, N., Allan, R. P., Andersson, E., Arpe, K., Balmaseda, M. A., Beljaars, A. C. M., Berg, L. Van De, Bidlot, J., Bormann, N., Caires, S., Chevallier, F., Dethof, A., Dragosavac, M., Fisher, M., Fuentes, M., Hagemann, S., Hólm, E., Hoskins, B. J., Isaksen, L., Janssen, P. A. E. M., Jenne, R., Mcnally, A. P., Mahfouf, J.-F., Morcrette, J.-J., Rayner, N. A., Saunders, R. W., Simon, P., Ster, A., Trenberth, K. E., Untch, A., Vasiljevic, D., Viterbo, P., and Woollen, J.: The ERA-40 re-analysis, Q. J. Roy. Meteor. Soc., 131, 2961–3012, 2005.
Wallace, J. M., Panetta, R. L., and Estberg, J.: Representation of the Equatorial Stratospheric Quasi-Biennial Oscillation in EOF Phase Space, J. Atmos. Sci., 50, 1751–1762, 1993.
Watson, P. A. G. and Gray, L. J.: How does the quasi-biennial oscillation affect the stratospheric polar vortex?, J. Atmos. Sci., 71, 391–409, https://doi.org/10.1175/JAS-D-13-096.1, 2014.
Wei, K., Chen, W., and Huang, R.: Association of tropical Pacific sea surface temperatures with the stratospheric Holton-Tan oscillation in the Northern Hemisphere, Geophys. Res. Lett., 34, L16814, https://doi.org/10.1029/2007GL030478, 2007.
White, I. P., Lu, H., Mitchell, N. J., and Phillips, T.: Dynamical Response to the QBO in the Northern Winter Stratosphere: Signatures in Wave Forcing and Eddy Fluxes of Potential Vorticity, J. Atmos. Sci., 72, 4487–4507, https://doi.org/10.1175/JAS-D-14-0358.1, 2015.
White, I. P., Lu, H., and Mitchell, N. J.: Seasonal evolution of the QBO-induced wave forcing and circulation anomalies in the northern winter stratosphere, J. Geophys. Res.-Atmos., 121, 10411–10431, https://doi.org/10.1002/2015JD024507, 2016.
Yoo, C. and Son, S.-W.: Modulation of the boreal wintertime Madden-Julian oscillation by the stratospheric quasi-biennial oscillation, Geophys. Res. Lett., 43, 1392–1398, 2016.