the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
On the origin of the mesospheric quasi-stationary planetary waves in the unusual Arctic winter 2015/2016
Manfred Ern
The midwinter 2015/2016 was characterized by an unusually strong polar night jet (PNJ) and extraordinarily large stationary planetary wave (SPW) amplitudes in the subtropical mesosphere. The aim of this study is, therefore, to find the origin of these mesospheric SPWs in the midwinter 2015/2016 study period. The study duration is split into two periods: the first period runs from late December 2015 until early January 2016 (Period I), and the second period from early January until mid-January 2016 (Period II). While the SPW 1 dominates in the subtropical mesosphere in Period I, it is the SPW 2 that dominates in Period II. There are three possibilities explaining how SPWs can occur in the mesosphere: (1) they propagate upward from the stratosphere, (2) they are generated in situ by longitudinally variable gravity wave (GW) drag, or (3) they are generated in situ by barotropic and/or baroclinic instabilities. Using global satellite observations from the Microwave Limb Sounder (MLS) and the Sounding of the Atmosphere using Broadband Emission Radiometry (SABER) the origin of the mesospheric SPWs is investigated for both time periods. We find that due to the strong PNJ the SPWs were not able to propagate upward into the mesosphere northward of 50∘ N but were deflected upward and equatorward into the subtropical mesosphere. We show that the SPWs observed in the subtropical mesosphere are the same SPWs as in the mid-latitudinal stratosphere. Simultaneously, we find evidence that the mesospheric SPWs in polar latitudes were generated in situ by longitudinally variable GW drag and that there is a mixture of in situ generation by longitudinally variable GW drag and by instabilities at mid-latitudes. Our results, based on observations, show that the abovementioned three mechanisms can act at the same time which confirms earlier model studies. Additionally, the possible contribution from, or impact of, unusually strong SPWs in the subtropical mesosphere to the disruption of the quasi-biennial oscillation (QBO) in the same winter is discussed.
- Article
(14066 KB) -
Supplement
(276 KB) - BibTeX
- EndNote
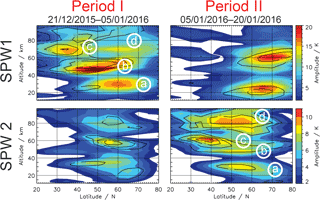
Figure 1Latitude–altitude cross sections of the SPW 1 and 2 derived from MLS temperature data. The amplitude as it occurred in the Arctic winter 2015/2016 is color coded, the deviation from the 12-year mean is presented by contour lines for the respective time period from MLS temperature data. The first half of the time period investigated here is hereafter referred to as Period I and the second half Period II.
The Arctic winter 2015/2016 was extraordinary in many respects regarding the middle atmosphere . Firstly, in early winter the polar vortex was the coldest and strongest it has been in 68 years (Matthias et al., 2016) with zonal mean wind speeds of over 80 m s−1 around the stratopause in mid-latitudes. Secondly, a significant disruption of the quasi-biennial oscillation (QBO) occurred, beginning at the end of December 2015 and fully completing by mid-April 2016 (Osprey et al., 2016; Newman et al., 2016; Coy et al., 2017). Thirdly, this particular winter was also characterized by one of the strongest El Niño events on record, with a strong polar stratospheric signature (Palmeiro et al., 2017). In addition to these global anomalies, there was a regional reversal in zonal wind from eastward to westward in the mesosphere over an altitude range of ∼ 10 km beginning at the end of December 2015 and lasting for four weeks, which was not connected to a sudden stratospheric warming (SSW) (Stober et al., 2017). Stober et al. (2017) found that this wind reversal, located only in polar latitudes, was caused by an unusually large stationary planetary wave (SPW) amplitude in the subtropical mesosphere leading to altered residual meridional circulation. The main aim of this paper is, therefore, to find the origin of the significantly enhanced SPW amplitude during this time period in the subtropical mesosphere.
The time period investigated here (21 December 2015 to 20 January 2016) can be split into two periods. While the amplitude of the SPW 1 dominates in the first half of the time period in the subtropical mesosphere, the amplitude of the SPW 2 is strongly increased in the second half (see Fig. 1). Thus we hereafter call the first half of the period where the SPW 1 dominates ”Period I”, and the second half where the SPW 2 dominates ”Period II”.
In Fig. 1 the latitude–altitude cross sections of the SPW 1 and 2 amplitude show four maxima in each period, denoted by the letters (a) to (d). In Period I, maximum (a) of the SPW 1 amplitude is located in the stratosphere between 40 and 75∘ N while maximum (b) is centered around the stratopause region and extends from 30 to 70∘ N. Maximum (c) is located between 60 and 80 km in altitude and between 20 and 50∘ N and is at least twice as large as the 12-year mean for this time period and beyond the standard deviation (not shown). Maximum (d) also extends between 60 and 80 km in altitude but between 50 and 80∘ N. Note that maxima (a) and (b) belong to the same wave when the geopotential height (GPH) is considered instead of temperature data (cf. Fig. S1 in the Supplement). The relationship between the double-peak structure in temperature and single-peak structure in GPH is based on the hydrostatic equilibrium T′ = , where H is the atmospheric scale height, R the gas constant of dry air, and subscript z indicates the vertical derivative (e.g., Sassi et al., 2002; Pancheva et al., 2009, 2016). We know that the GPH gives a more realistic view on planetary waves (PWs) in the middle atmosphere, however, we decided to show the temperature amplitudes instead due to the better visibility of the mesospheric SPWs and their upward propagation into the subtropical mesosphere. In the following we will treat the maxima (a) and (b) as one wave (a) + (b).
In Period II, maximum (a) of the SPW 2 amplitude is located in the stratosphere between 40 and 70∘ N; maximum (b) extends between 40 and 50 km from 35 to 65∘ N; while maximum (c) is located between 50 and 70 km and between 25 and 50∘ N. Maximum (c) is again at least twice as large as the 12-year mean for this time period, and beyond the standard deviation (not shown). Maximum (d) is located between 60 and 80 km in altitude and between 30 and 70∘ N. Similarly to the SPW 1 in Period I, the maxima (a) and (b) of the SPW 2 in Period II belong to the same wave when considering the GPH instead of temperature data (cf. Fig. S1). In the following we will once again treat the maxima (a) and (b) as one wave (a) + (b). Comparison of the temperature amplitude with that of the GPH (cf. Fig. S1) show that maximum (d) is not one single wave. Southward of 45∘ N wave (c) and (d) are actually the same wave (double-peak structure in temperature) while the polar part of wave (d) is a different wave. To avoid confusion in the following: we will call wave (c) and the southern part of wave (d) simply wave (c), and the northern part of wave (d) simply wave (d).
While the origin of maxima (d) of the SPW 1 and 2 in polar latitudes in both periods will play a secondary role in this study, the main focus is on the origin of maxima (c) in the subtropical mesosphere.
There are three possible mechanisms for the occurrence of SPWs in the mesosphere: (1) the stratospheric SPWs propagate vertically into the upper mesosphere, (2) the SPWs are generated in situ by breaking or dissipation of gravity waves (GWs) that were filtered in a longitudinally variable fashion in the stratosphere by SPWs (e.g., Holton, 1984; Smith, 2003; Lieberman et al., 2013) or (3) by barotropic and/or baroclinic instabilities (e.g., Siskind et al., 2010). Smith (1997) found that the first two mechanisms operate, however, the one that dominates depends on how favorable the conditions are in the middle atmosphere for vertical propagation. The third mechanism is well-known for the in situ generation of the quasi-2-day wave (e.g., Ern et al., 2013). A model study by Smith (2003) showed that vertical propagation of SPW dominates up to the lower mesosphere while in situ GW-generated SPWs dominate in the upper mesosphere. This result was confirmed by Lieberman et al. (2013) using satellite observations. In a model study, Siskind et al. (2010) discussed the possible in situ generation of SPWs in the mesosphere via a combination of forcing from below and in situ instability. The in situ generation of SPWs by instabilities in the lower mesosphere was confirmed by Iida et al. (2014) using satellite observations.
The vertical propagation of SPWs depends on the strength and structure of the zonal mean zonal wind in the middle atmosphere (Lin, 1982). The planetary wave guide (PWG) of SPWs are regions in the atmosphere where the background zonal wind supports the upward propagation of PWs (Dickinson, 1968). In midwinter the PWG is commonly split into a southern and a northern channel (e.g., Dickinson, 1968; Chapman and Miles, 1981; Li et al., 2007). While in the southern channel the SPWs preferably propagate equatorward towards the subtropical zero wind line and barely reach the upper stratosphere (Albers et al., 2013), the northern PWG channel in comparison follows the polar night jet (PNJ) sometimes even reaching up into the mesosphere (Lin, 1982).
We assume that the unusually strong PNJ in winter 2015/2016 guided the SPWs towards the subtropical mesosphere and that the conditions were favorable there for vertical propagation into the mesosphere.
In this paper we want to retrace SPWs occurring in the subtropical mesosphere between 21 December 2015 and 20 January 2016 to their origin. We therefore use different diagnostic tools applied to global satellite data, mainly Microwave Limb Sounder (MLS) data, as described in Sect. 2. The propagation properties of the SPWs are shown and discussed in Sects. 3 and 4 for Period I and II, respectively. The cause for the change in the wavenumber between Period I and II is discussed in Sect. 5 and followed by a short discussion on the origin of the polar mesospheric SPWs in Sect. 6. Finally, the results of this study are summarized in Sect. 7.
To find the origin of the quasi-stationary planetary waves (hereafter SPW) in each period we need to know the characteristics of the SPW (wavenumber and propagation direction) as well as the conditions required for propagation (zonal wind and refractive index squared) at all latitudes and altitudes of the Northern Hemisphere.
Since this is purely an observational study, we use global temperature and geopotential height (GPH) data from the Microwave Limb Sounder (MLS) on board the Aura satellite (Waters et al., 2006; Livesey et al., 2015). MLS has a global coverage from 82∘ S to 82∘ N on each orbit, and a usable height range from approximately 11 to 97 km (261–0.001 hPa) with a vertical resolution of ∼ 4 km in the stratosphere and ∼ 14 km at the mesopause. The temporal resolution is 1 day at each location, and data are available from August 2004 until the present (Livesey et al., 2015). Version 4 MLS data were used in this paper along with the application of the most recent recommended quality screening procedures from Livesey et al. (2015).
For our analyses the original orbital MLS data are accumulated in grid boxes with 20∘ grid spacing in longitude and 5∘ in latitude. Afterwards they are averaged at every grid box and for every day, generally resulting in a global grid with values at every grid point.
The estimation of the amplitude and phase of the SPWs as well as the filtering of the waves by atmospheric parameters is done by using the two-dimensional least squares method of Wu et al. (1995).
To estimate the propagation conditions and directions for SPWs the zonal and meridional winds are needed. From the GPH data from the MLS we calculate the geostrophic zonal (ug) and meridional (vg) wind by
where Φ is the geopotential, f is the Coriolis parameter, and x and y are used to denote the partial derivatives and where λ is longitude, ϕ is latitude and a is the radius of the earth.
A useful tool to distinguish regions of wave propagation from wave evanescence is the refractive index squared n2. Here we use the spherical form of the quasi-geostrophic refractive index squared (Andrews et al., 1987):
where
is the zonal mean potential vorticity gradient, z is the height, s the spherical wavenumber, c the phase velocity of the wave, N(z) is the buoyancy frequency, H is the scale height (= 7 km), ρ = is the standard density in log-pressure coordinates, Ω is the Earth's rotation frequency, overbars denote zonal mean quantities and subscripts denote derivatives with respect to the given variable. Planetary waves can propagate in regions where n2 > 0 and are evanescent in regions where n2 < 0.
The direction and strength of SPW propagation is measured by the Eliassen–Palm flux (EPF) vectors and their divergence (EPFD) which is locally parallel to the group velocity of SPW (Edmon et al., 1980). The quasi-geostrophic form of the EPF vectors (F) and its divergence (∇ ⋅ F) is defined as follows (e.g., Andrews et al., 1987):
where θ is the potential temperature and primes denote the perturbation from the zonal mean. Note, that an interaction of a SPW with the mean flow would result in EPFD convergence (negative) or divergence (positive) which results in a westerly wind deceleration or acceleration, respectively (Andrews et al., 1987).
Since it is well known, that an upward propagating SPW has a westward tilt with height (e.g., Smith, 2003) we are interested in the phase tilt with height at each latitude. We estimate the phase behavior with height by filtering the geostrophic zonal wind for the wavenumber of interest, choosing a minimum in the lower stratosphere and following it up into the mesosphere. If this minimum ends at −180∘ E before reaching the uppermost level the longitude–altitude cross section is copied and put to the left so that the minimum can be followed further upward.
To investigate the possible in situ generation of SPWs in the mesosphere by dissipating GWs longitudinally filtered in the stratosphere by SPWs, the absolute GW drag is calculated from SABER data. The SABER instrument, short for Sounding of the Atmosphere using Broadband Emission Radiometry, was launched onboard the TIMED satellite and measures temperatures at altitudes between 10 and 115 km (Mlynczak, 1997; Russell et al., 1999; Yee et al., 2003). SABER switches between southward-viewing (83∘ S–50∘ N) and northward-viewing (50∘ S–83∘ N) geometries about every 60 days. For the period of interest, until early January 2016 SABER was in the southward-viewing part of the yaw cycle and switched to northward-viewing on 4 January 2016. Thus we can only examine the possible in situ generation of polar mesospheric SPW by longitudinally variable GW drag for the second half of the investigation time period. The GW drag is calculated via a multi-step procedure (Ern et al., 2011, 2016).
This procedure is based on temperature–altitude profiles measured by SABER. Altitude profiles of temperature fluctuations due to atmospheric GWs are obtained by subtracting (separately for each measured temperature altitude profile) the zonal average background temperature profile, as well as the contribution of global-scale waves. Altitude profiles of GW amplitudes, vertical wavelengths and phases are derived for each altitude profile of temperature fluctuations using sliding windows of 10 km vertical extent From the vertical phase shift of GWs seen in both profiles of a pair of consecutive altitude profiles in the SABER measurement track the horizontal wavelength of observed GWs is estimated. Finally, GW momentum flux can be derived via Eq. (7) in Ern et al. (2004). Absolute values of GW drag are obtained from vertical gradients of absolute GW momentum flux (Ern et al., 2011). The end product is interpolated on a horizontal grid with a grid resolution of 10∘ in longitude and 2∘ in latitude. The vertical resolution is 10 km ranging from 30 to 90 km.
A detailed description of the observational filter of infrared limb sounders is given in Trinh et al. (2015). In particular, SABER can not observe the whole GW spectrum but is limited to GWs with horizontal wavelengths > 100 – 200 km and vertical wavelengths > 4 km. The SABER sensitivity function for observing GWs is given, for example, in Ern et al. (2018). Further, our estimates of horizontal wavelengths represent only the apparent horizontal wavelength parallel to the SABER measurement track and will usually overestimate the true horizontal wavelength of observed GWs (resulting in a low bias of their absolute GW momentum flux). For an illustration see Ern et al. (2018). Being limited by the sensitivity function, by the along-track sampling step that will undersample GWs with very short horizontal wavelengths, as well as by the fact that SABER only provides information along the single measurement track, SABER absolute GW momentum flux is low biased. Considerations by Ern et al. (2004) indicate a factor of about two or more. This will also affect the absolute GW drag. Also note that the absolute GW drag calculated from SABER data has no direction information which limits its significance. However, global distributions of absolute GW drag from SABER are a good tool to investigate the longitudinal distribution of GW breaking.
Using the synergy of the above-described analysis methods and satellite data sets, the origin of the mesospheric SPWs in each period is investigated in the following sections.
Figure 2a shows the latitude–altitude cross section of the zonal mean zonal wind (colored contour) and its deviation from the 12-year mean (contour lines). The PNJ is up to 25 m s−1 stronger in Period I than the 12-year mean and exceeds even the standard deviation (see Fig. S2). These stronger winds range from the mid-latitude stratosphere up into the subtropical mesosphere with the magnitude of the enhancement gradually decreasing towards the subtropical mesosphere.
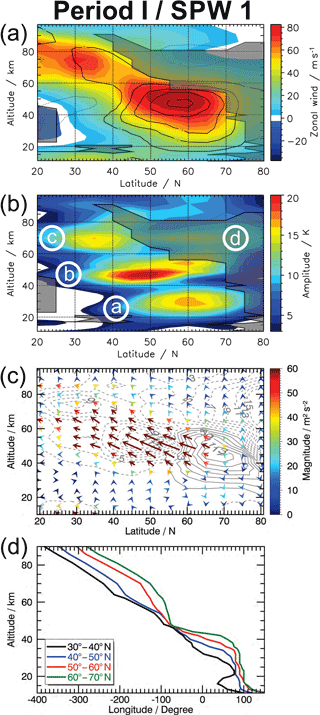
Figure 2Latitude–altitude cross sections of (a) the zonal mean zonal wind in colored contours, the deviation of each time period from its 12-year mean in black contour lines with steps of 5 m s−1 and the areas where the refractive index squared n2 is negative are shaded grey; (b) the amplitude of the SPW 1, areas where the refractive index squared n2 is negative are shaded grey; (c) Eliassen–Palm flux vectors of the SPW 1 with the magnitude of the flux is given by the length of the vector as well as by their color, contour lines present the EP-flux divergence in m s−1 per day; and (d) phase information of each SPW depending on the altitude and for different latitude bands. All data presented here are derived from MLS data.
The amplitude distribution of the SPW 1 matches the region of increased zonal wind (see Fig. 2b), i.e., the area of increased amplitudes shifts southward with height. This shift is in accordance with the area in which the SPW 1 can not propagate due to the negative refractive index squared (grey shaded areas in Fig. 2a and b). So there is a PWG from the mid-latitude lower stratosphere up into the subtropical upper mesosphere.
To solve the question as to whether wave (c) in Fig. 2b is the same as wave (a) + (b) which propagates into the subtropical mesosphere, we use the EPF vector. Figure 2c shows the EPF vectors of the SPW 1 for Period I; the magnitude of the vectors is given by the color coding as well as by the length of the vectors. The EPFD is given by grey contour lines in the background. While the vectors in the mid-latitude (40–60∘ N) lower and middle stratosphere point dominantly upward, they are downward facing in polar latitudes (60–80∘ N). In lower latitudes (20–40∘ N) the vectors are predominately equatorward pointed in the lower stratosphere and upward pointed above in the middle stratosphere. In the upper stratosphere and mesosphere the vectors face equatorward and upward in almost equal parts. This results in an increase of EPFD especially in the subtropical upper mesosphere where the magnitude is three times larger than the 12-year mean (not shown). In the upper mesosphere northward of 50∘ N the EPF vectors predominantly point upward. In other words the SPW 1 generated in the lower stratosphere could be propagated upward in midlatitudes to the upper stratosphere. The equatorward component then increases and the wave propagates upward and equatorward from the mid-latitude upper stratosphere into the subtropical upper mesosphere. So it seems that the origin of wave (c) in Period I is in the lower stratosphere, and that the conditions for vertical propagation were favorable in this period for the SPW 1.
It is known that an upward propagating SPW has a westward phase shift with height (e.g., Smith, 1997). The term phase jump is used here for very sharp changes in the longitudinal shift with height after which a vertical propagation of a SPW is not likely. The term phase kink is used for relatively smooth changes in the longitudinal shift with height after which a vertical propagation of a SPW is still likely, which is probably caused by changed propagation conditions. To finally prove that wave (a) + (b) and (c) are the same, Fig. 2d shows the phase location of the SPW 1 for different latitude bands. This confirms our assumption, there is a continuous westward phase shift in the vertical in the latitude band 40–50∘ N ranging from the lower stratosphere into the upper mesosphere. A similar characteristic is found in the southernmost latitude band 30–40∘ N above 22 km. In this latitude band (black line) there are two phase jumps below 22 km, each changing the direction of the longitudinal shift with height, caused by the subtropical jet and the area of negative refractive index at slightly higher altitudes (see Fig. 2a). Above 40 km the two southernmost latitude bands have an almost identical and steady increase with height. Thus the SPW 1 – wave (c) in Fig. 2b – is generated in the mid-latitude lower stratosphere and propagated upward all the way into the subtropical mesosphere.
The two northernmost latitude bands show a different behavior in the vertical propagation. In particular the latitude band 60–70∘ N displays a phase jump at 50 km. Above this altitude the westward propagation with height almost stops for around 15 km and slowly starts again above 65 km in altitude. This feature, together with the exclusively upward directed EPF vectors and the negative refractive index in that area, is strong evidence that wave (d) did not propagate from below into the upper polar mesosphere but was generated in situ by longitudinally variable dissipating GWs. Since we focus on the subtropical mesospheric SPW here, we will discuss the origin of the polar mesospheric wave (d) in more detail in Sect. 6.
In summary, the subtropical mesospheric SPW 1 – wave (c) – dominating in Period I propagates from the mid-latitude lower stratosphere into the subtropical upper mesosphere.
The PNJ in Period II is weaker than in Period I as is the area of strengthened zonal wind ranging from the polar stratosphere into the subtropical mesosphere (see Fig. 3a). Similarly to Period I, the PNJ is up to 25 m s−1 stronger than the 12-year mean and even though it does not exceed in the standard deviation in this particular case (see Fig. S2) it is still counted as a stronger PNJ. However, the area is narrower and slightly tilted compared to that in Period I. There is also an increased zonal wind in the subtropical mesosphere from 50 to 70 km which is up to 10 m s−1 stronger than the multi-year average. This region, however, is somewhat more separated from the PNJ than was the case in Period I.
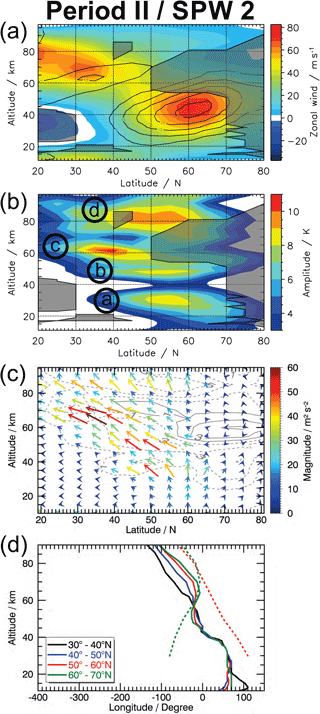
The amplitude of the SPW 2 shifts only slightly southward with height below 50 km and is much stronger above this altitude (see Fig. 3b). The area where no SPW propagation can occur (grey shaded area) is similar to that of SPW 1 during Period I northward of 50∘ N, but the tail into the subtropical upper mesosphere is replaced by a small area around 80 km between 40–45∘ N. The southward shift of the SPW 2 is again in accordance with the area in which the SPW 2 can not propagate. So there is a PWG from the mid-latitude lower stratosphere into the subtropical and mid-latitudinal upper mesosphere (the PWG is bounded by the grey shaded areas in Fig. 3a and b).
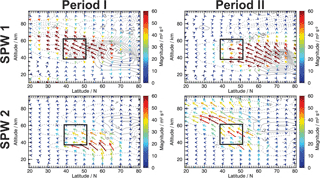
Figure 3c shows the EPF vectors of the SPW 2 for Period II. The vectors in the mid-latitude (50–65∘ N) lower and middle stratosphere point predominantly upward, while they are upward and poleward pointed at polar latitudes (65–80∘ N) and predominantly equatorward pointed at lower latitudes (20–45∘ N) in the lower and middle stratosphere. In the upper stratosphere and mesosphere the vectors face equatorward and upward in almost equal parts, southward of 60∘ N. This results in an increase of EPFD especially in the subtropical mesosphere where the magnitude is three times larger than the 12-year mean (not shown). Note that the magnitude of the EPF vectors and of the EPFD is small compared to that of the SPW 1 in Period I. In the upper mesosphere northward of 60∘ N the EPF vectors predominantly point upward. In other words the SPW 2, likely generated in the lower stratosphere, is able to propagate upward in mid-latitudes until the middle stratosphere. Then the equatorward component increases and the wave propagates upward and equatorward from the mid-latitude middle stratosphere into the subtropical mesosphere.
The westward phase tilt with the height of the SPW 2 in Period II is not as strong as it is for the SPW 1 in Period I (see Fig. 3d). Below 35 km, there is no westward shift in the vertical for the two northernmost latitude bands (50–70∘ N) meaning that the SPW 2 might be barotropic, and there is only a light westward phase tilt with height for the two southernmost latitude bands (30–50∘ N). Again, in the lower stratosphere the latitude band 30–40∘ N shows a phase jump with an eastward shift in the vertical caused by the subtropical jet. Above 40 km the magnitude of the westward phase tilt with height increases almost steadily for the two southernmost latitude bands, but again there is a phase kink at 60 km. Above this kink the two southernmost latitude bands split and the 30–40∘ N latitude band once more increases the westward shift with height. The 50–60∘ N latitude band has a phase kink at 50 km, followed by almost no longitudinal shift in the vertical for 20 km. The 60–70∘ N latitude band, in comparison, has a phase jump at 50 km resulting in an eastward shift with height for the overlying 20 km. Thus we assume that the northern part of wave (d) is generated in situ by longitudinally variable breaking GWs, which is supported by the positive EPFD in the polar mesosphere. Since we focus on the subtropical mesospheric SPW here, we will discuss the origin of wave (d) in more detail in Sect. 6.
Combining the information from the EPF vectors and the phase shift with height, it is shown that wave (c) is generated in the mid-latitude lower stratosphere and propagated upward all the way into the subtropical and mid-latitude mesosphere in Period II.
In summary, in both time periods the respective SPW was able to propagate from the mid-latitude lower stratosphere equatorward and upward into the subtropical upper mesosphere, guided by the strong PNJ. Surprisingly, in Period II the dominating wavenumber of the SPW changes from 1 to 2 in the subtropical mesosphere, although the conditions for upward propagation were also favorable for the SPW 1. This change in the dominating wavenumber is studied more closely in the next section.
To investigate the reason for the change in the wavenumber of the subtropical SPW in the mesosphere from Period I to II, Fig. 4 shows the EPF vectors and divergence of the SPW 1 (top) and SPW 2 (bottom) for Period I (left) and Period II (right). The magnitude of the EPF vectors of the SPW 1 in the subtropical mesosphere is much larger in Period I than in Period II as expected. The accumulation of large EPF vectors is shifted poleward in Period II compared to Period I and, especially in mid-latitudes, the upward component is almost completely missing in the former.
The behavior of the SPW 2 in the two considered time periods is the inverse of SPW 1. The magnitude of the EPF vectors of the SPW 2 in the subtropical mesosphere is much larger in Period II than in Period I, and the accumulation of enhanced EPF vectors is shifted southward in Period II compared to Period I. Similar to the SPW 1 in Period II, the upward component of the EPF vectors for the SPW 2 is missing in mid-latitudes in Period I. Combining these results, it seems that the region from 40–50∘ N and from 40 to 60 km in altitude (black rectangles in Fig. 4) is crucial for the upward propagation of the SPWs into the subtropical mesosphere.
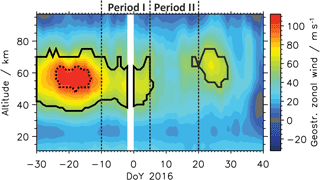
Figure 5Time–altitude cross sections of the zonal mean zonal wind averaged between 40 and 50∘ N. Areas enclosed by dotted (solid) black lines display areas with a negative refractive index squared n2 for the SPW 1 (2), i.e., areas where the vertical propagation of the SPW is prohibited. Data are derived from MLS.
Figure 5 shows the temporal evolution of the zonal mean zonal wind averaged between 40–50∘ N. The areas enclosed by the black dotted (solid) lines are characterized by a negative refractive index squared n2 for the SPW 1 (2). Focusing on the altitude range 40 to 70 km, the zonal mean zonal wind is very strong with values of up to 100 m s−1 in early and mid-December. During this period the conditions are not favorable for upward propagation of the SPW 1 and 2. Afterwards however, a two step weakening occurs starting shortly before Period I. In the first step the zonal wind decreases to approximately 70 m s−1 allowing the SPW 1 to propagate upward, but not SPW 2 since the refractive index squared is still negative for the SPW 2. In the second step the wind further decreases to 30 m s−1, allowing the SPW 1 and 2 to propagate upward. Thus the SPW 2 was not able to propagate upward during Period I due to the strong wind at 40–50∘ N between 40 and 60 km. The zonal wind weakening from Period I to Period II was caused by the SPW 1 in Period I. Looking again at Fig. 4 there is a strong EPF convergence of the SPW 1 in Period I decelerating the westerly wind especially in the area between 40–50∘ N and 40 and 60 km in altitude. This zonal wind deceleration paves the way for the upward propagation of the SPW 2 in Period II since the upward propagation of the SPW 2 is only possible in a weak zonal mean zonal wind. It is now clear why SPW 1 dominates in Period I in the subtropical mesosphere, but it is still not clear why SPW 2 dominates in Period II as it was also possible for the SPW 1 to propagate upward in Period II.
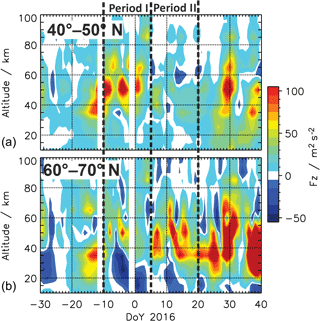
Figure 6Time–altitude cross sections of the vertical component of the EP-flux vector Fz for SPW 1 averaged between 40–50∘ N (a) and 60–70∘ N (b). Data are derived from MLS.
Figure 6 shows the temporal evolution of the vertical component of the EPF vector Fz for the SPW 1 averaged between 40–50∘ N (top) and 60–70∘ N (bottom). In Period I there is a strong enhancement in Fz at 40–50∘ N which vanishes in Period II. As expected, Fz is weak in Period I at 60–70∘ N but, surprisingly, it increases significantly in Period II. This means that in Period II the SPW 1 was able to propagate upward in polar latitudes, probably due to the weakened PNJ (cf. Figs. 2a and 3a). So it seems that when the SPW 1 can propagate upward in polar latitudes there is no longer the need to do so at lower latitudes. This stronger upward propagation of the SPWs in the northern channel of the PW guide compared to the southern channel is in accordance with the climatology (e.g., Albers et al., 2013).
Another possible cause for the SPW 2 strengthening in Period II is the previously mentioned disruption of the QBO (Osprey et al., 2016). Due to this disruption, the QBO is again/still in its westerly phase. From Holton and Tan (1980) we know that from January to March the SPW 2 is stronger during the westerly phase of the QBO. Thus the disruption of the QBO could also have an impact on the dominating SPW in the subtropical mesosphere.
In summary, the SPW 1 dominates in Period I in the subtropical mesosphere since the SPW 2 was not able to propagate upward due to the strong zonal wind at 40–50∘ N in the upper stratosphere and lower mesosphere. Both SPWs were theoretically able to propagate upward into the subtropical mesosphere in Period II since the convergence of the SPW 1 in Period I weakens the zonal mean zonal wind and therefore paves the way for upward propagation of the SPW 2 in Period II. Another cause for the change in the dominating wavenumber between Period I and II might be the disruption of the QBO, which remained in the westerly phase in January 2016 resulting in a stronger SPW 2. Due to the weaker PNJ in Period II the SPW 1 was able to propagate upward into the mesosphere at polar latitudes which, we assume, makes it unnecessary to do this at lower latitudes.
As previously mentioned, the 2015/2016 winter was also characterized by an outstandingly strong El Niño event (Palmeiro et al., 2017, and references therein). In principle there are two types of El Niño events which have different impact on the polar stratosphere: El Niño events confined to the eastern Pacific Ocean which result in a warm and weak polar vortex (Garcia-Herrera et al., 2006); El Niño events confined to the central Pacific Ocean which lead to a colder polar stratosphere and a stronger polar vortex (Iza and Calvo, 2015). Previous strong El Niño events have been confined to the eastern Pacific Ocean but in winter 2015/2016 extended to the central Pacific and west of the date line (e.g., Palmeiro et al., 2017). Thus the extraordinarily strong polar vortex in early winter 2015/2016 as reported by Matthias et al. (2016) might have been caused by the untypical structure of the strong El Niño during this particular period. Hence, this strong polar vortex affected by the strong El Niño event helped to guide the SPWs into the subtropical mesosphere.
The QBO is usually driven by a combination of drag exerted by global scale equatorial wave modes and by tropical GWs (Baldwin et al., 2001; Ern et al., 2014, and references therein). The unusual disruption of the QBO in winter 2015/2016, characterized by anomalous easterly acceleration occurring in the QBO westerlies (e.g., Osprey et al., 2016; Newman et al., 2016; Coy et al., 2017), begins at approximately the same time as the unusual strong SPW amplitude takes place in the subtropical mesosphere. Osprey et al. (2016) found an anomalous easterly acceleration of the equatorial winds at 40 hPa (approx. 23 km) caused by waves propagated to the equator from the Northern Hemisphere in the region below to be the primary source of the QBO disruption. For the SPW 1 we found an enhanced equatorward EPF at altitudes below 25 km and at latitudes 20–40∘ N during Period I together with an EPF convergence (cf. Fig. 4) resulting in an easterly acceleration of the zonal wind. In Period II, the magnitude of this equatorward EPF is lower compared to Period I and occurs at altitudes below 15 km in the EPF of the SPW 1 and SPW 2. So it seems that there is another PWG at lower latitudes vertically capped by the negative refractive index induced by the subtropical jet. This PWG guides the PWs into the equatorial region below 20 km. These findings confirm the model results of Osprey et al. (2016) but need further investigation.
However, Coy et al. (2017) also found large tropical momentum flux divergences in other years without a reversal of the QBO. Comparing the zonal mean zonal wind behavior in the subtropics between Period I and II (cf. Figs. 2a and 3a) shows that the westerly wind field in the mesosphere moved down by 5 km and that the stratospheric easterly wind field shrank about 5 km in the vertical. This downward movement and shrinking caused by the breaking SPWs in the subtropical mesosphere might have had an impact on the development of the QBO disruption. Thus, it is not clear whether the QBO disruption causes or is caused by the unusual SPW amplitude in the subtropical mesosphere. However, a detailed study and discussion of this hypothesis is beyond the scope of this paper.
Initially we want to focus on the origin of the SPW 1 wave (d) in Period I located between 50–70∘ N at 65 to 75 km with its maximum at 60∘ N at 70 km (see Fig. 2b). This wave is situated entirely in an area of negative refractive index (see Fig. 2b), which means that this wave can not propagate and is a more stationary wave-like structure caused by in situ processes than a physical SPW 1 which is vertically propagating. There are two possibilities for the development of this wave-like structure: one is the already mentioned in situ generation by longitudinally variable GW drag (Smith, 2003; Lieberman et al., 2013); the other was postulated but not proven by Siskind et al. (2010), who investigated an increased wave 1 amplitude above a region with easterly wind and a negative meridional gradient of the potential vorticity in the mesosphere. This negative meridional gradient of potential vorticity indicates potential instability which might generate a wave 1 structure.
Since SABER is in the southern yaw cycle until early January we are not able to investigate whether wave (d) is generated by longitudinally variable GW drag in Period I. However, the longitude–altitude cross section of the wavenumber 1 filtered zonal wind shows an anti-correlation between the stratospheric and mesospheric zonal wind disturbance (see Fig. 7c) at polar latitudes indicative of a SPW propagation from below or in situ generation by GWs (Smith, 2003). Since we have already ruled out SPW propagation from below due to the negative refractive index in that area and the downward pointing EPF vectors below, Smith's (2003) theory of in situ generation by longitudinally variable GW drag remains. This assumption is also supported by the phase jump at 50 km in the 60–70∘ N latitude band with almost no longitudinal propagation with height for 10 km (see Fig. 2d) and a non-uniform GW drag at 40–50∘ N with a dominating wave 1 structure (see Fig. 7a).
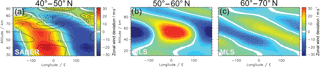
Figure 7(a) Longitude–altitude cross sections of the wavenumber 1 filtered geostrophic zonal wind amplitude (colored contour) and the absolute GW drag amplitude in m s−1 day−1 (contour lines) in Period I averaged between 40 and 50∘ N and derived from SABER data. (b) and (c) Longitude–altitude cross sections of the wavenumber 1 filtered geostrophic zonal wind amplitude in Period I averaged between 50 and 60∘ N and 60 and 70∘ N, respectively. Data are derived from MLS GPH data.
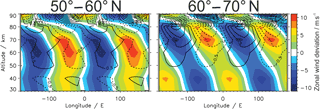
Figure 8Longitude–altitude cross sections of the geostrophic zonal wind amplitude (colored contour) and the absolute GW drag amplitude in m s−1 day−1 (contour lines) in Period II. The plots show the deviation from the zonal mean of the wavenumber 2 filtered atmospheric wind component and GW drag. Data are derived from SABER.
However, in the same area where wave (d) occurs in Period I the meridional gradient of the potential vorticity is negative (not shown) which is a necessary condition for barotropic and/or baroclinic instabilities. This might be indicative of the in situ generation of SPWs by instabilities (Siskind et al., 2010) especially between 50–60∘ N where there is no anti-correlation between the stratospheric and mesospheric zonal wind disturbance (see Fig. 7b). Iida et al. (2014) showed that instabilities forming SPWs might be brought about by an intensification of the PNJ in the stratosphere and the subtropical westerly jet in the mesosphere, which is the case in Period I (cf. Fig. 2a). Thus it is also possible that wave (d) in Period I is (partially) generated in situ by instabilities induced by the strong westerly jets in the mid-latitude stratosphere and subtropical mesosphere.
Since we can not prove whether wave (d) is generated in situ by longitudinally variable GW drag or by instabilities further investigations are needed but are beyond the scope of this paper.
The SPW 2 wave (d) in Period II ranges from 45 to 70∘ N between 70 and 90 km with its maximum between 50–60∘ N around 80 km (see Fig. 3b). Most of this wave lies above an area of negative refractive index n2 (see Fig. 3c). Additionally, the EPF vectors at 80 km around the maximum of wave (d) are very small throughout the whole Northern Hemisphere. Thus, wave (d) in Period II could not propagate from below into the mesosphere.
The northernmost part of the SPW 2 wave (d) in Period II is very likely generated in situ by longitudinally variable GW drag. Therefore we investigate the longitudinal structure of absolute GW drag that is obtained from vertical gradients of absolute GW momentum fluxes which are derived from SABER temperature observations (see also Ern et al., 2011, 2016, and references therein). This parameter does not provide directional information unless atmospheric background conditions allow for assumptions to be made and it can be used as a proxy for “real” GW drag. Figure 8 shows the zonal wind and SABER absolute GW drag each filtered for wavenumber 2 for the two northernmost latitude bands in Period II. Note that the filtering of wavenumber 2 is reasonable for these two latitude bands, since the zonal wind is westerly at all longitudes below 60 km (not shown). The GW spectrum should therefore be dominated by waves of westward directed phase speeds (opposite to the background wind). For this reason, as a working hypothesis, we assume that the GW drag is negative everywhere (similar to the simulations by Holton, 1984), and we show that this leads to an overall consistent picture. In the case of the two southernmost latitude bands, the zonal wind is predominantly westerly with some small areas of easterly wind (not shown). Thus, we cannot be sure about the sign of the GW drag in the mesosphere which makes it difficult to filter for wavenumber 2.
In the 60–70∘ N latitude band the maximum of the GW drag lies within the mesospheric minimum of zonal wind. In addition, the longitudinal phase tilt with altitude of the filtered GW drag is similar to the phase tilt of the SPW 2 (see Fig. 3d). At the same time the amplitude of the wavenumber 1 filtered GW drag is lower and somewhat out of phase with the zonal wind (see Fig. S4) which might be the reason why wavenumber 2 dominated here. On zonal average, GW drag decelerates the zonal wind and SPW 2 propagation is not possible. Therefore, the wave 2 structure in the polar mesosphere likely originates primarily from the longitudinally variable GW drag which is consistent with studies from Smith (2003) and Lieberman et al. (2013). Even though we can not prove in situ generation by longitudinally variable GW drag, all of the necessary preconditions are given: (1) the SPW can not propagate from below, (2) a non-uniform distribution of the GW drag is observed at the altitude where the SPW generation takes place, and (3) the forcing takes place in regions of weak background wind, which is in agreement with Smith (2003).
Note that our amplitudes of the filtered GW drag are much smaller than those of Smith (2003) (2.5 vs. 20 m s−1 day−1). Reasons for this discrepancy may be the much lower amplitude of the SPW 2 in Period II compared to the SPW 1 in Smith (2003), the fact that we average over 15 days, and that SABER can only measure a part of the GW spectrum and has a low bias in the observable GW drag (see Sect. 2, Ern et al., 2004).
In the other latitude band (50–60∘ N) there is no pure anti-correlation between the stratospheric and mesospheric zonal wind; the minimum of the zonal wind is westward shifted compared to the GW drag maximum at 70 to 80 km and the longitudinal phase tilt of the GW drag coincides with the SPW 2 phase tilt above 70 km. Thus in this latitude band the in situ generation is not only caused by longitudinally variable GW drag. We assume that the impact of the longitudinally variable GW drag decreases with decreasing latitude based on increasing uniformity with decreasing latitudes (see Fig. S4) and on the decreasing wavenumber 2 amplitude of the absolute GW drag with decreasing latitude at 70–80 km (see Fig. 8). Another possible in situ generation mechanism is barotropic and/or baroclinic instability. In Period II the meridional potential vorticity gradient is negative where the refractive index is negative, roughly speaking (see Fig. 3). This indicates in situ generation of SPWs by instabilities (Siskind et al., 2010). Furthermore, similarly to Iida et al. (2014) the stratospheric PNJ and the mesospheric subtropical jet were intensified, conceivably bringing about instabilities in the mesosphere, and hence the possibility of the generation of SPWs in the mesosphere.
The variety in the origins of mesospheric SPWs is in agreement with the model study of Smith (2003) and observational study of Lieberman et al. (2013), although these studies focused on the upward propagation and in situ generation by longitudinally variable GW drag only. Our study indicates that a mix of in situ generated SPW by longitudinally variable GW drag and barotropic and/or baroclinic instabilities is also possible.
This paper investigates the origin of mesospheric SPWs in a case study during one month in the Arctic midwinter 2015/2016 where an unusually strong SPW 1 and 2 amplitude was observed in the subtropical mesosphere. During the first half of the period (late December 2015 to early January 2016) SPW 1 dominates in the subtropical mesosphere, while SPW 2 dominates in the second half of the study period (early January to mid-January 2016). At the same time there is also an increased SPW amplitude of the respective SPW in both periods in the mid-latitude and polar mesosphere.
The origin of the subtropical mesospheric SPWs is located in the mid-latitudinal stratosphere in each period . We found that the SPW 1 in Period I as well as the SPW 2 in Period II propagated upward and equatorward from the mid-latitudinal stratosphere into the subtropical mesosphere, guided by the unusually strong PNJ (e.g., Matthias et al., 2016). While the strong PNJ might be influenced by the strong El Niño, the SPWs might be influenced by, or may impact on, the development of the disruption of the QBO starting during the same time period.
The change in the dominating wavenumber from Period I to Period II raises the question of why this change occurred at all. We pinpoint the area from 40 to 50∘ N and 40 and 60 km in altitude as being especially being crucial for upward propagation from the mid-latitude stratosphere into the subtropical mesosphere. In this area the upward propagation of the SPW 2 was prohibited in Period I due to strong westerly winds in the region. These strong westerly winds decelerated in Period I as the SPW 1 interacted with the mean flow, thereby paving the way for upward propagation of the SPW 2 in Period II. However, the upward propagation of the SPW 1 in Period II was much weaker in this crucial area compared to Period I, although an upward propagation was theoretically possible. This can be explained by a poleward shift of SPW 1 activity induced by the weakened zonal mean PNJ and thus strengthened polar channel of the PW guide. It is also possible that the increase in the SPW 2 amplitude in Period II is influenced by the disrupted QBO resulting in a recurring westerly phase which generally increases SPW 2 activity (Holton and Tan, 1980).
The polar mesospheric SPWs are generated in situ, likely by a mixture of longitudinally variable GW drag and barotropic and/or baroclinic instabilities. This mixture is possibly dominated by longitudinally variable GW drag towards polar latitudes and instabilities towards middle latitudes, which results in a smooth transition from pure in situ generation by longitudinally variable GW drag in polar latitudes and pure in situ generation by instabilities in the subtropical upper mesosphere. Note that our results do not prove in situ generation by GWs or instabilities but strongly support this assumption. With this observational study we have shown that the origin of mesospheric SPWs can be the upward propagation of SPWs, as well as in situ generation by longitudinally variable GW drag or instabilities, and that all three mechanisms can occur at the same time, which is partially in accordance with the model study of Smith (2003).
Jet Propulsion Laboratory/NASA provided access to the Aura/MLS level 2 retrieval products downloaded from http://mirador.gsfc.nasa.gov. SABER data were provided by GATS Inc. and are freely available at http://saber.gats-inc.com.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-18-4803-2018-supplement.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Sources, propagation, dissipation and impact of gravity waves (ACP/AMT inter-journal SI)”. It does not belong to a conference.
The work by Manfred Ern was partly supported by the Deutsche
Forschungsgemeinschaft (DFG, German Research Foundation) project ER 474/4-2
(MS-GWaves/SV) which is part of the DFG researchers group FOR 1898
(MS-GWaves). We thank the Jet Propulsion Laboratory/NASA for providing access
to the Aura/MLS level 2 retrieval products downloaded from
http://mirador.gsfc.nasa.gov. The authors would like to
thank the teams of the MLS and SABER instruments for their effort in
providing and continuously improving the high-quality data sets used in this
study. A big thanks goes to Axel Gabriel and Lena Schoon for their very
helpful discussions and comments. We also want to thank Dieter H. W. Peters
for helpful comments. The authors are also very grateful to the three anonymous
reviewers.
Edited by: Markus Rapp
Reviewed by: three anonymous referees
Albers, J. R., McCormack, J. P., and Nathan, T. R.: Stratospheric ozone and the morphology of the northern hemisphere planetary waveguide, J. Geophys. Res., 118, 563–576, https://doi.org/10.1029/2012JD017937, 2013. a, b
Andrews, D. G., Holton, J. R., and Leovy, C. B.: Middle atmosphere dynamics, Academic Press, London, 1987. a, b, c
Baldwin, M. P., Gray, L. J., Dunkerton, T. J., Hamilton, K., Haynes, P. H., Randel, W. J., Holton, J. R., Alexander, M. J., Hirota, I., Horinouchi, T., Jones, D. B. A., Kinnersley, J. S., Marquardt, C., Sato, K., and Takahashi, M.: The quasi-biennial oscillation, Rev. Geophys., 39, 179–229, https://doi.org/10.1029/1999RG000073, 2001. a
Chapman, W. and Miles, T.: Planetary-scale wave guides in the troposphere and stratosphere, Nature, 293, 108–112, 1981. a
Coy, L., Newman, P. A., Pawson, S., and Lait, L. R.: Dynamics of the Disrupted 2015/16 Quasi-Biennial Oscillation, J. Climate, 30, 5661–5674, https://doi.org/10.1175/JCLI-D-16-0663.1, 2017. a, b, c
Dickinson, R. E.: Planetary Rossby Waves Propagating Vertically Through Weak Westerly Wind Wave Guides, J. Atmos. Sci., 25, 984–1002, https://doi.org/10.1175/1520-0469(1968)025<0984:PRWPVT>2.0.CO;2, 1968. a, b
Edmon, H. J., Hoskins, B. J., and McIntyre, M. E.: Eliassen–Palm Cross Sections for the Troposphere, J. Atmos. Sci., 37, 2600–2616, https://doi.org/10.1175/1520-0469(1980)037<2600:EPCSFT>2.0.CO;2, 1980. a
Ern, M., Preusse, P., Alexander, M. J., and Warner, C. D.: Absolute values of gravity wave momentum flux derived from satellite data, J. Geophys. Res., 109, d20103, https://doi.org/10.1029/2004JD004752, 2004. a, b, c
Ern, M., Preusse, P., Gille, J. C., Hepplewhite, C. L., Mlynczak, M. G., Russell, J. M., and Riese, M.: Implications for atmospheric dynamics derived from global observations of gravity wave momentum flux in stratosphere and mesosphere, J. Geophys. Res.-Atmos., 116, D19107, https://doi.org/10.1029/2011JD015821, 2011. a, b, c
Ern, M., Preusse, P., Kalisch, S., Kaufmann, M., and Riese, M.: Role of gravity waves in the forcing of quasi two-day waves in the mesosphere: An observational study, J. Geophys. Res., 118, 3467–3485, https://doi.org/10.1029/2012JD018208, 2013. a
Ern, M., Ploeger, F., Preusse, P., Gille, J. C., Gray, L. J., Kalisch, S., Mlynczak, M. G., Russell, J. M., and Riese, M.: Interaction of gravity waves with the QBO: A satellite perspective, J. Geophys. Res., 119, 2329–2355, https://doi.org/10.1002/2013JD020731, 2014. a
Ern, M., Trinh, Q. T., Kaufmann, M., Krisch, I., Preusse, P., Ungermann, J., Zhu, Y., Gille, J. C., Mlynczak, M. G., Russell III, J. M., Schwartz, M. J., and Riese, M.: Satellite observations of middle atmosphere gravity wave absolute momentum flux and of its vertical gradient during recent stratospheric warmings, Atmos. Chem. Phys., 16, 9983–10019, https://doi.org/10.5194/acp-16-9983-2016, 2016. a, b
Ern, M., Trinh, Q. T., Preusse, P., Gille, J. C., Mlynczak, M. G., Russell III, J. M., and Riese, M.: GRACILE: A comprehensive climatology of atmospheric gravity wave parameters based on satellite limb soundings, Earth Syst. Sci. Data Discuss., https://doi.org/10.5194/essd-2017-109, in review, 2018. a, b
Garcia-Herrera, R., Calvo, N., Garcia, R. R., and Giorgetta, M. A.: Propagation of ENSO temperature signals into the middle atmosphere: A comparison of two general circulation models and ERA-40 reanalysis data, J. Geophys. Res., 111, D06101, https://doi.org/10.1029/2005JD006061, 2006. a
Holton, J. R.: The Generation of Mesospheric Planetary Waves by Zonally Asymmetric Gravity Wave Breaking, J. Atmos. Sci., 41, 3427–3430, https://doi.org/10.1175/1520-0469(1984)041<3427:TGOMPW>2.0.CO;2, 1984. a, b
Holton, J. R. and Tan, H.-C.: The Influence of the Equatorial Quasi-Biennial Oscillation on the Global Circulation at 50 mb, J. Atmos. Sci., 37, 2200–2208, https://doi.org/10.1175/1520-0469(1980)037<2200:TIOTEQ>2.0.CO;2, 1980. a, b
Iida, C., Hirooka, T., and Eguchi, N.: Circulation changes in the stratosphere and mesosphere during the stratospheric sudden warming event in January 2009, J. Geophys. Res., 119, 7104–7115, https://doi.org/10.1002/2013JD021252, 2014. a, b, c
Iza, M. and Calvo, N.: Role of Stratospheric Sudden Warmings on the response to Central Pacific El Niño, Geophys. Res. Lett., 42, 2482–2489, https://doi.org/10.1002/2014GL062935, 2015. a
Li, Q., Graf, H.-F., and Giorgetta, M. A.: Stationary planetary wave propagation in Northern Hemisphere winter – climatological analysis of the refractive index, Atmos. Chem. Phys., 7, 183–200, https://doi.org/10.5194/acp-7-183-2007, 2007. a
Lieberman, R. ., Riggin, D. M., and Siskind, D. E.: Stationary waves in the wintertime mesosphere: Evidence for gravity wave filtering by stratospheric planetary waves, J. Geophys. Res., 118, 3139–3149, https://doi.org/10.1002/jgrd.50319, 2013. a, b, c, d, e
Lin, B.-D.: The Behavior of Winter Stationary Planetary Waves Forced by Topography and Diabatic Heating, J. Atmos. Sci., 39, 1206–1226, https://doi.org/10.1175/1520-0469(1982)039<1206:TBOWSP>2.0.CO;2, 1982. a, b
Livesey, N. J., Read, W. G., Wagner, P. A., Froidevaux, L., Lambert, A., Manney, G. L., Millan, L., Pumphrey, H. C., Santee, M. L., Schwartz, M. J., Wang, S., Fuller, R. A., Jarnot, R. F., Knosp, B., and Martinez, E.: EOS MLS Version 4.2x Level 2 data quality and description document, Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA, 2015. a, b, c
Matthias, V., Dörnbrack, A., and Stober, G.: The extraordinarily strong and cold polar vortex in the early northern winter 2015/2016, Geophys. Res. Lett., 43, 12287–12294, https://doi.org/10.1002/2016GL071676, 2016. a, b, c
Mlynczak, M. G.: Energetics of the mesosphere and lower thermosphere and the SABER instrument, Adv. Space Res., 44, 1177–1183, 1997. a
Newman, P. A., Coy, L., Pawson, S., and Lait, L. R.: The anomalous change in the QBO in 2015–2016, Geophys. Res. Lett., 43, 8791–8797, https://doi.org/10.1002/2016GL070373, 2016. a, b
Osprey, S. M., Butchart, N., Knight, J. R., Scaife, A. A., Hamilton, K., Anstey, J. A., Schenzinger, V., and Zhang, C.: An unexpected disruption of the atmospheric quasi-biennial oscillation, Science, 353, 1424–1427, https://doi.org/10.1126/science.aah4156, 2016. a, b, c, d, e
Palmeiro, F. M., Iza, M., Barriopedro, D., Calvo, N., and Garcia-Herrera, R.: The complex behavior of El Nino winter 2015/2016, Geophys. Res. Lett., 44, 2902–2910, https://doi.org/10.1002/2017GL072920, 2017. a, b, c
Pancheva, D., Mukhtarov, P., Andonov, B., Mitchell, N. J., and Forbes, J. M.: Planetary waves observed by TIMED/SABER in coupling the stratosphere-mesosphere-lower thermosphere during the winter of 2003/2004: Part 2 – Altitude and latitude planetary wave structure, J. Atmos. Sol-Terr. Phy., 71, 75–87, https://doi.org/10.1016/j.jastp.2008.09.027, 2009. a
Pancheva, D., Mukhtarov, P., Siskind, D. E., and Smith, A. K.: Global distribution and variability of quasi 2-day waves based on the NOGAPS-ALPHA reanalysis model, J. Geophys. Res.-Space , 121, 11422–11449, https://doi.org/10.1002/2016JA023381, 2016. a
Russell, J. M., Mlynczak, M. G., Gordley, L. L., Tansock, J. J., and Esplin, R. W.: Overview of the SABER experiment and preliminary calibration results, in: Optical Spectroscopic Techniques and Instrumentation for Atmospheric and Space Research III, vol. 3756, Proc. SPIE, https://doi.org/10.1117/12.366382, 1999. a
Sassi, F., Garcia, R. R., Boville, B. A., and Liu, H.: On temperature inversions and the mesospheric surf zone, J. Geophys. Res.-Atmos., 107, 4380, https://doi.org/10.1029/2001JD001525, 2002. a
Siskind, D. E., Eckermann, S. D., McCormack, J. P., Coy, L., Hoppel, K. W., and Baker, N. L.: Case studies of the mesospheric response to recent minor, major, and extended stratospheric warmings, J. Geophys. Res., 115, D00N03, https://doi.org/10.1029/2010JD014114, 2010. a, b, c, d, e
Smith, A. K.: Stationary Planetary Waves in Upper Mesospheric Winds, J. Atmos. Sci., 54, 2129–2145, https://doi.org/10.1175/1520-0469(1997)054<2129:SPWIUM>2.0.CO;2, 1997. a, b
Smith, A. K.: The origin of stationary planetary waves in the upper mesosphere, J. Atmos. Sci., 60, 3033–3041, https://doi.org/10.1175/1520-0469(2003)060<3033:TOOSPW>2.0.CO;2, 2003. a, b, c, d, e, f, g, h, i, j, k
Stober, G., Matthias, V., Jacobi, C., Wilhelm, S., Höffner, J., and Chau, J. L.: Exceptionally strong summer-like zonal wind reversal in the upper mesosphere during winter 2015/16, Ann. Geophys., 35, 711–720, https://doi.org/10.5194/angeo-35-711-2017, 2017. a, b
Trinh, Q. T., Kalisch, S., Preusse, P., Chun, H.-Y., Eckermann, S. D., Ern, M., and Riese, M.: A comprehensive observational filter for satellite infrared limb sounding of gravity waves, Atmos. Meas. Tech., 8, 1491–1517, https://doi.org/10.5194/amt-8-1491-2015, 2015. a
Waters, J. W., Froidevaux, L., Harwood, R. S., Jarnot, R. F., Pickett, H. ., Read, W. G., Siegel, P. H., Cofield, R. E., Filipiak, M. J., Flower, D. A., Holden, J. R., Lau, G. K., Livesey, N. J., Manney, G. L., Pumphrey, H. C., Santee, M. L., Wu, D. L., Cuddy, D. T., Lay, R. R., Loo, M. S., Perun, V. S., Schwartz, M. J., Stek, P. C., Thurstans, R. P., Boyles, M. A., Chandra, K. M., Chavez, M. C., Chen, G.-S., Chudasama, B. V., Dodge, R., Fuller, R. A., Girard, M. A., Jiang, J. H., Jiang, Y., Knosp, B. W., LaBelle, R. C., Lam, J. C., Lee, K. A., Miller, D., Oswald, J. E., Patel, N. C., Pukala, D. M., Quintero, O., Scaff, D. M., Van Snyder, W., Tope, M. C., Wagner, P. A., and Walch, M. J.: The Earth Observing System Microwave Limb Sounder (EOS MLS) on the Aura Satellite, IEEE T. Geosci. Remote, 44, 1075–1092, https://doi.org/10.1109/TGRS.2006.873771, 2006. a
Wu, D. L., Hays, P. B., and Skinner, W. R.: A Least Squares Method for Spectral Analysis of Space-Time Series, J. Atmos. Sci., 52, 3501–3511, https://doi.org/10.1175/1520-0469(1995)052<3501:ALSMFS>2.0.CO;2, 1995. a
Yee, J. H., Talaat, E. R., Christensen, A. B., Killeen, T. L., Russell, J. M., and Woods, T. N.: TIMED instruments, Tech. Rep. 24, Johns Hopkins APL Technical Digest, Greenbelt, Maryland, 2003. a
- Abstract
- Introduction
- Instruments and methods
- The origin of the subtropical mesospheric SPW 1 in Period I
- The origin of the subtropical mesospheric SPW 2 in Period II
- Why does the SPW 2 dominate in Period II?
- Where is the origin of the polar mesospheric SPWs?
- Summary
- Data availability
- Competing interests
- Special issue statement
- Acknowledgements
- References
- Supplement
- Abstract
- Introduction
- Instruments and methods
- The origin of the subtropical mesospheric SPW 1 in Period I
- The origin of the subtropical mesospheric SPW 2 in Period II
- Why does the SPW 2 dominate in Period II?
- Where is the origin of the polar mesospheric SPWs?
- Summary
- Data availability
- Competing interests
- Special issue statement
- Acknowledgements
- References
- Supplement





