the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Model simulations with COSMO-SPECS: impact of heterogeneous freezing modes and ice nucleating particle types on ice formation and precipitation in a deep convective cloud
Karoline Diehl
Verena Grützun
In deep convective clouds, heavy rain is often formed involving the ice phase. Simulations were performed using the 3-D cloud resolving model COSMO-SPECS with detailed spectral microphysics including parameterizations of homogeneous and three heterogeneous freezing modes. The initial conditions were selected to result in a deep convective cloud reaching 14 km of altitude with strong updrafts up to 40 m s−1. At such altitudes with corresponding temperatures below −40 ∘C the major fraction of liquid drops freezes homogeneously. The goal of the present model simulations was to investigate how additional heterogeneous freezing will affect ice formation and precipitation although its contribution to total ice formation may be rather low. In such a situation small perturbations that do not show significant effects at first sight may trigger cloud microphysical responses. Effects of the following small perturbations were studied: (1) additional ice formation via immersion, contact, and deposition modes in comparison to solely homogeneous freezing, (2) contact and deposition freezing in comparison to immersion freezing, and (3) small fractions of biological ice nucleating particles (INPs) in comparison to higher fractions of mineral dust INP. The results indicate that the modification of precipitation proceeds via the formation of larger ice particles, which may be supported by direct freezing of larger drops, the growth of pristine ice particles by riming, and by nucleation of larger drops by collisions with pristine ice particles. In comparison to the reference case with homogeneous freezing only, such small perturbations due to additional heterogeneous freezing rather affect the total precipitation amount. It is more likely that the temporal development and the local distribution of precipitation are affected by such perturbations. This results in a gradual increase in precipitation at early cloud stages instead of a strong increase at later cloud stages coupled with approximately 50 % more precipitation in the cloud center. The modifications depend on the active freezing modes, the fractions of active INP, and the composition of the internal mixtures in the drops.
Deep convective clouds may cover a wide temperature range from +20 ∘C at ground level down to −40 ∘C at altitudes of 14 km. The high vertical updraft in these clouds transports moist air to high levels where most of the water vapor is condensed, leading to total water contents as high as 10 g m−3 (Wu et al., 2000). During early cloud stages, the condensed water is present in the form of liquid droplets, but after passing the zero degree level, mixed-phase conditions are established in which ice particles and supercooled liquid drops are present simultaneously (e.g., Rosenfeld and Woodley, 2000). Heterogeneous freezing may be active at temperatures below −2 ∘C with a dependence on the freezing mode and involved ice nucleating particles (INPs; Hoose and Möhler, 2012). When reaching altitudes with temperatures below −37 ∘C most of the liquid water is changed into ice by homogeneous freezing (e.g., Pruppacher and Klett, 2010). The ice mass increases further by growth processes such as the deposition of water vapor and supercooled droplets (i.e., riming) on ice particles and by the nucleation of supercooled drops via collisions with small ice particles. These processes lead to the formation of increasingly larger ice particles that eventually pass the melting layer and result in heavy precipitation.
The distribution of liquid and ice water mass is dependent on factors such as altitude, temperature, and in particular aerosol and ice nucleating particle concentrations and composition as well as on the active freezing modes (e.g., Khain et al., 2005; Leroy et al., 2006; Tao et al., 2007; Fan et al., 2013; Hiron and Flossmann, 2015). In deep convective clouds, a large fraction of ice is formed homogeneously; however, heterogeneous freezing at lower altitudes may have important effects on ice formation and thus precipitation (e.g., Gilmore et al., 2004; van den Heever et al., 2006; Ekman et al., 2007; Phillips et al., 2007; Lee et al., 2009).
The present model simulations address the question of how additional heterogeneous freezing will affect ice formation and precipitation although its contribution to total ice formation may be rather low. This situation may create so-called “small trigger effects”; i.e., small perturbations that do not show significant effects on first sight may trigger cloud microphysical responses.
For instance, a small number of ice particles is formed by a small amount of ice nucleating particles. They grow further by the deposition of water vapor, including the effects of the Bergeron–Findeisen process, i.e., at the expense of liquid drops. With increasing sizes of the ice particles collisions with supercooled drops become more likely (Pruppacher and Klett, 2010). The ice particles grow by riming when they collide with smaller supercooled drops that are deposited on the ice surface and subsequently freeze. When small ice particles collide with larger supercooled drops, the latter freeze by contact-induced nucleation of the ice particle. In this way even small amounts of ice particles may efficiently modify the distribution of ice and liquid water in a cloud. Thus, even when homogeneous freezing is dominant in deep convective clouds, additional heterogeneous freezing particularly taking place in lower cloud regions may have an essential impact on ice formation.
Small perturbations may also play a role within heterogeneous freezing processes themselves. Immersion freezing is assumed to represent the most important heterogeneous freezing process (e.g., Phillips et al., 2007). However, even small additional contributions from contact and deposition freezing may alter eventually precipitation. Another situation with small perturbations is the composition of ice nucleating particles (INPs). It was shown that certain aerosol types significantly modify cloud microphysics (e.g., Lohmann and Diehl, 2006; Phillips et al., 2008; Lee et al., 2009; DeMott et al., 2015; Hande et al., 2015). The most important atmospheric INP types are mineral dust and biological particles, but the latter are present in the atmosphere in much lower amounts than mineral dust particles (e.g., Phillips et al., 2009; Paukert and Hoose, 2014). Thus, the low fractions of biological particles may trigger significant effects.
Model simulations dealing with these issues were performed with the state-of-the-art model system COSMO-SPECS, a 3-D cloud model developed by Grützun et al. (2008). A follow-up version that was numerically more effective was provided by Lieber et al. (2012). COSMO-SPECS is well suited for the envisioned investigations as it provides a link between aerosol particles, cloud properties, and precipitation. It contains a detailed description of the cloud microphysical processes achieved by spectral bin microphysics that explicitly solves the microphysical equations. The last versions of COSMO-SPECS included parameterizations of immersion and contact freezing for several particle types such as mineral dust, soot, and biological particles from Diehl et al. (2006). Recently, in Diehl and Mitra (2015) the parameterizations of ice forming processes were extended and improved. They now include deposition nucleation and homogeneous freezing as new ice forming processes and advanced descriptions of immersion and contact freezing. For the present investigations, this new version of the microphysics was implemented in COSMO-SPECS.
The model simulations presented here are part of the German Science Foundation (DFG) research group INUIT (Ice Nuclei Research UnIT), which was established in 2012 to study heterogeneous ice formation in laboratory, field, and model studies. As an outcome of the experiments, joint parameterizations were derived to be fed into cloud models to simulate mixed-phase cloud microphysics. For more details see the INUIT website: http://www.ice-nuclei.de (INUIT Research group, 2018).
2.1 Previous version of COSMO-SPECS
The COSMO model (Consortium for Small-scale Modeling; Steppeler et al., 2003; Baldauf et al., 2011) is the regional part of the operational weather forecast system of the DWD. It is based on the primitive hydro-thermodynamic equations describing compressible non-hydrostatic flow in a moist atmosphere (http://www.cosmo-model.org).
The original COSMO model works with a Kessler-type cloud microphysics bulk scheme. This includes various states of water, such as cloud and rainwater and several forms of ice, but takes into account mass densities only (Kessler, 1995). Later, two-moment schemes were developed that additionally consider the hydrometeor number concentrations (e.g., Seifert and Beheng, 2006). Those schemes predict the evolution of the mass and number densities of several hydrometeor types. However, they offer only limited potential to include the aerosol particles. In spectral bin schemes the particle mass is discretized so that the hydrometeor spectra are divided into size bins for which number and mass are considered (e.g., Reisin et al., 1996; Khain et al., 2004). In those schemes initial aerosol particle spectra are explicitly included and the particle, drop, and ice particle spectra evolve freely. Thus, spectral microphysical schemes allow for detailed investigations of aerosol–cloud interactions. In particular, when the ice phase is included, explicit information about drop and ice particle sizes and the development of size spectra are given, allowing for conclusions about the correlations of ice formation and precipitation.
Grützun et al. (2008) completely replaced the formerly used microphysical scheme in the COSMO model with the spectral bin microphysics as described in Simmel and Wurzler (2006) and Diehl et al. (2006). The time integration of the coupling scheme between the COSMO model and the bin microphysics is performed with two different time steps because the microphysics operates on much smaller timescales than the concurrent dynamical processes. Within the COSMO model the horizontal and vertical winds as well as temperature and pressure are transported within a time step of 1 to 100 s, leading to dynamically updated values. These are used for the microphysical loop, which consists of time steps of 1 s or smaller during which changes in the hydrometeor spectra due to the included microphysical processes are calculated (Grützun et al., 2008). In the present simulations, the dynamical and the microphysical time steps were 4 and 1 s, respectively; i.e., within one dynamical time step, four microphysical time steps were calculated.
The spectral cloud microphysics describes all microphysical processes during the development of clouds and the subsequent initiation of precipitation. The entrainment of aerosol particles, drops, ice particles, temperature, and humidity is embedded (Simmel et al., 2005). A fixed bin structure is used in which in a first spectrum wetted aerosol particles and liquid drops are combined. An initially dry aerosol particle number size distribution is defined at which the particles are internally mixed with a soluble fraction, ε. The soluble and total mass fraction of aerosol particles is considered explicitly in each bin. By condensation, the particles grow into the droplet part of the spectrum. The size spectra are allowed to evolve freely, and they are not constrained by underlying distribution functions. Thus, the particles and drops move in this spectrum by processes such as growth by water vapor deposition, shrinking by evaporation, collision and coalescence of drops, and impaction scavenging of particles. Ice particles are formed from supercooled liquid drops via immersion and contact freezing described in parameterized form (Diehl and Wurzler, 2004; Diehl et al., 2006). Condensation freezing is included implicitly in immersion freezing: drops that are nucleated by aerosol particles entrained above the freezing level could freeze immediately by immersion freezing.
After freezing, the drops are removed from the first liquid spectrum and shifted into a second spectrum, which is used for mixed-phase particles. These consist of an ice core and a liquid shell; the liquid water mass may be zero to describe completely frozen particles. In the mixed-phase spectrum (with the same bins as the liquid spectrum) particles move by processes such as growth by water vapor deposition and by riming (i.e., collision with smaller supercooled droplets), collision and sticking of ice particles, ice nucleation of supercooled drops by collision with smaller ice particles, sublimation, and melting. This latter process is modeled by the possible existence of a liquid water shell. In this study, both spectra are divided into 66 categories, starting with 0.002 µm in diameter, with a mass doubling in every category.
Collision processes are described by the linear discrete method (Simmel et al., 2002) including the collision kernel of Kerkweg et al. (2003). By using the corresponding densities and terminal velocities, the collision kernel is appropriate for all collision processes between aerosol particles, drops, and ice particles such as the collision and coalescence of drops, impaction scavenging of particles by drops, contact freezing of supercooled drops after collisions with particles, riming of ice particles by collisions with supercooled liquid droplets, nucleation of supercooled drops by collisions with small ice particles, and sticking of ice particles after collision.
2.2 Improvements of ice parameterizations in COSMO-SPECS
2.2.1 Homogeneous freezing
In the new version of COSMO-SPECS, drops may freeze homogeneously at temperatures below −37 ∘C. This is determined by the soluble particle fraction dissolved in the drops together with the drop volume. A lower solute content and a larger drop volume affect higher freezing temperatures (Koop et al., 2000; Duft and Leisner, 2004). Homogeneous freezing is described in the model according to the approach of Koop et al. (2000). With their parameterization of the water activity criterion, the freezing temperatures of solution drops with a dependence on their molality are calculated (Diehl and Wurzler, 2004).
2.2.2 Immersion freezing
The parameterization of immersion freezing in Diehl and Mitra (2015) is an updated version related to the insoluble particle mass in drops. It is based on laboratory data of nm(T), the number of active sites per unit mass at temperature T. As shown in Fig. 1a, nm exponentially increases with T as described by
with nm in g−1, aimm and bimm as particle-related constants, , and T0= 0 ∘C, with T in ∘C. The constants are given in Diehl and Mitra (2015) together with two more parameters: Tini represents the onset of immersion freezing during experiments, and Tlim represents the temperature at which nm reaches a plateau value (Wex et al., 2015); see Fig. 1a. A new particle type is included here based on measurements of cellulose (Hiranuma et al., 2015), which represents a macro-tracer for plant debris (with the corresponding constants aimm= 7.86464, bimm= 0.560, Tini= −10 ∘C, Tlim= −36 ∘C). The freezing rate of drops containing insoluble ice nucleating material is given by Diehl and Mitra (2015):
with Nf as the number of frozen drops, Nliq the number of liquid drops, t the time, mpid the insoluble particle mass immersed in the drops, and FINP the mass fraction accounting for possible numbers of ice-active sites. K(T) stands for the cumulative nucleus spectrum per unit mass per unit temperature, which is related to nm by
As in the previous version, condensation freezing is included implicitly as it is also initiated by an INP immersed in a supercooled drop. The difference is a temporal separation (Cziczo and Froyd, 2014): if directly after drop activation the insoluble particle mass is sufficient for drop freezing at the actual temperature, the drop freezes immediately. If the ambient temperature is too high, it may freeze later at lower temperatures.
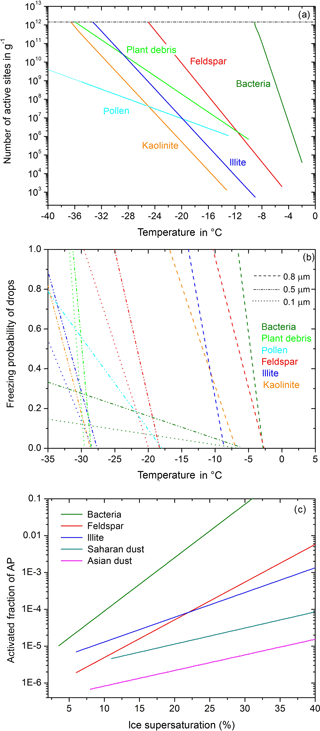
Figure 1Parameterizations of heterogeneous freezing. (a) Immersion freezing: numbers of active sites per unit mass as a function of temperature; from Diehl and Mitra (2015), with new data for plant debris based on Hiranuma et al. (2015). (b) Contact freezing: freezing probability of drops in the contact mode as a function of temperature; from Diehl and Mitra (2015), with new data for pollen and plant debris according to Hoffmann (2015) and Hiranuma et al. (2015). (c) Deposition nucleation: activated fraction of particles as a function of ice supersaturation; from Diehl and Mitra (2015).
2.2.3 Contact freezing and deposition nucleation
The description of contact freezing was modified by Diehl and Mitra (2015) so that it is also particle size resolved. A particle-type-dependent parameterization of deposition nucleation was newly added (Diehl and Mitra, 2015). Because of entrainment, inactivated interstitial particles are always present during the simulations with COSMO-SPECS and may serve as contact and deposition ice nucleating particles. If during the model simulations particles collide with supercooled drops the number of frozen drops formed by contact freezing is calculated according to
with Nf as the number of frozen drops, Nliq the number of liquid drops, T the temperature, acon and bcon the particle- and size-related constants (see Diehl and Mitra, 2015), and FINP the ice-active fraction of the aerosol particles. Figure 1b shows the freezing probability for different particle types and sizes. New particle types are plant debris and pollen based on laboratory measurements of Hoffmann (2015) and Hiranuma et al. (2015); their constants are listed in Table 1.
Interstitial particles may also serve for deposition nucleation. According to experimental findings the number of activated particles increases exponentially with ice supersaturation, which is shown in Fig. 1c and calculated by Diehl and Mitra (2015) using
with Nact as the number of activated particles, Ntotal the total particle number, FINP the fraction of ice-active particles, sice the ice supersaturation given in %, and adep and bdep the particle-related constants. The constants are given in Diehl and Mitra (2015) together with two more parameters: Tini and sini represent initial values of temperature and ice supersaturation for the onset of deposition freezing during experiments. The activated particles are shifted to the mixed-phase spectrum and grow further by water vapor deposition and riming, and they may initiate the freezing of supercooled drops by collision.
Table 1New values of contact freezing constants in Eq. (4) for pollen and plant debris based on data from Hiranuma et al. (2015; plant debris) and Hoffmann (2015; pollen).

For potential contact and deposition INP, minimum sizes are defined for mineral dust particles of 0.1 µm, for bacteria 0.3 µm, for plant debris 0.35 µm (Matthias-Maser and Jaenicke, 1995), and for pollen 0.4 µm. Complete pollen grains are large particles of 10 µm at least (Straka, 1975); however, Steiner et al. (2015) indicated the existence of so-called sub-pollen particles due to a pollen grain rupture after wetting.
3.1 Convective cloud, vertical profiles, and particle number size distribution
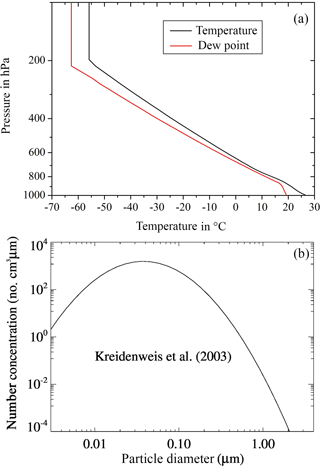
With COSMO-SPECS idealized test cases were simulated. A heat bubble over a flat terrain was initialized by a temperature disturbance of 1.5 K, which resulted in a deep convective cloud. The complete model domain covered 80 × 80 km2 with a horizontal resolution of 1 km. The model top reached an altitude of 18 km with a vertical resolution between 100 and 600 m (48 levels). The heat bubble was located in the domain center at 1.4 km of height and had a horizontal extension of 20 km and a vertical extension of 1.4 km. The initial wind was set to zero. The vertical profiles of temperature and dew point from Weisman and Klemp (1982), which are consistent with real conditions in convective situations, are shown in Fig. 2a.
As initial dry aerosol particles, the number size distribution of Kreidenweis et al. (2003) was selected. As can be seen from Fig. 2b, it is a mono-modal lognormal size distribution with N= 566 cm−3, d= 30 nm, and σ= 2 (with N the particle number, d the median diameter, and σ the standard deviation). After starting the simulation, the particle spectra evolved freely within the given size ranges. The soluble fraction ε of the aerosol particles was set to 0.5, which is a typical value of atmospheric particles (Busch et al., 2002). The ice nucleating particles are defined as part of the complete aerosol particle spectrum. The insoluble fraction of the particles entering drops via nucleation or impaction scavenging accounts for immersion freezing. Interstitial aerosol particles may serve as contact and deposition INPs. Because of the size conditions of the ice nucleating particles (see Sect. 2) one can note from Fig. 2b that the majority of the particles was not suited to initiate ice as is also the case in the real atmosphere.
3.2 Freezing processes and INP types and fractions
Process studies were performed including various ice forming processes and, in the case of heterogeneous freezing, different ice nucleating particle types in various fractions. First, a warm test case without freezing was simulated to characterize the behavior of the deep convective cloud. Afterwards, a case with homogeneous freezing only was performed that served as a reference case. To study the characteristic impacts of the individual heterogeneous freezing processes, simulations without homogeneous freezing were performed although these do not represent realistic cases. The next step was to couple one heterogeneous freezing process with homogeneous freezing, and afterwards two or all three heterogeneous freezing processes with homogeneous freezing. This kind of stepwise adding of ice forming processes allows for the study of the impact of small perturbations of less active freezing processes, such as contact and deposition freezing. More small perturbations are low numbers of ice nucleating particles, in particular biological particles. Therefore, for each type of simulation, the following parameters were varied:
-
ice nucleating particle type – biological particles and mineral dust; and
-
FINP, the ice-active fraction of aerosol particles.
As examples for the present paper only three types of mineral dust were selected: feldspar, kaolinite, and Saharan dust. Feldspar represents a very effective INP type contained in desert dusts and also in illite samples. Therefore, by scaling down it is representative for dust samples with a dependence on their composition (Atkinson et al., 2013). For example, African and Asian dust contains around 24 % feldspar, Arizona test dust (ATD) approximately 20 %, and illite NX 14 %. Kaolinite samples may also include up to 10 % feldspar, but the CMS kaolinite used for the experiments, which served as a base for the present parameterization, does not show detectable amounts (Murray et al., 2011). Therefore, it shows a significantly lower efficiency than feldspar in immersion and contact freezing (see Fig. 1a, b) and was used in these modes together with feldspar to indicate the lowest and highest effects. For deposition nucleation no parameterization of kaolinite is available, and therefore less efficient INPs are represented by Saharan dust (see Fig. 1c). Biological particles are represented by bacteria, plant debris, and pollen.
To reflect atmospheric conditions, the ice-active fractions of mineral dust were larger than the ones for biological particles. FINP values for mineral dust ranged from 0.1 to 10 % and for biological particles from 0.001 to 0.01 %. These values were used in Diehl and Mitra (2015) according to results from field measurements of cloud droplet residuals and background aerosols (e.g., Bauer et al., 2002; Twohy and Anderson, 2008; Kamphus et al., 2010; Hiranuma et al., 2013; Schmidt et al., 2017). In both cases the highest values are slightly overestimated, while the other values represent realistic situations.
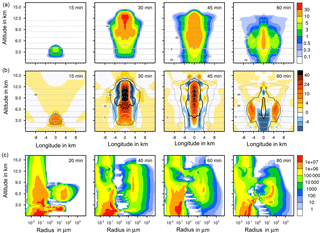
Figure 3(a, b) Temporal development of two parameters in the warm test case shown in a vertical cut through the cloud center. Horizontal dashed lines: temperature in ∘C. (a) Liquid water content in g kg−1; (b) vertical velocity in m s−1. Solid lines in (b) are contour lines of the total water content: 10 (black), 1 (dark gray), and 0.1 g kg−1 (light gray). (c) Temporal development of aerosol and drop size spectra in the center cell of the cloud. Number concentrations per m3.
4.1 Warm test case
As a first test case, a warm case was performed in which all freezing processes were switched off. This study demonstrated the formation of a deep convective cloud in which the cloud top reached 14 km of altitude with temperatures of −50 ∘C. Figure 3a and b illustrate the development of the liquid water content and the vertical velocity with time. The dotted lines give the temperature levels; note that they are lifted up inside the cloud because of the initial temperature disturbance and convective transport. After 15 min the cloud top passed the 0 ∘C level at 4 km of altitude, and after 30 min the cloud reached its maximal top height of 14 km. Precipitation set in after 45 min, and after 60 min the cloud started to dissipate as the cloud top height was decreasing. Correspondingly the strongest vertical updraft in the cloud was noted after 30 min with vertical velocities up to 40 m s−1 in the cloud center, which agrees with values found by Weisman and Klemp (1982). The complete aerosol and drop size spectra in the center cell of the cloud are given in Fig. 3c. The gap in the spectra at 1 µm radius indicates the distinction between aerosol particles and drops. Note that the majority of the drops stayed smaller than 100 µm, while parts of them grew to larger sizes in the millimeter range by collision and coalescence.
4.2 Single homogeneous and heterogeneous freezing
In a deep convective cloud as presented in Sect. 4.1 the major fraction of liquid water freezes homogeneously (Phillips et al., 2007). In the present study, for the reference case only homogeneous freezing was switched on and occurred at temperatures below −37 ∘C, i.e., at altitudes above 9 km. Afterwards, simulations were performed in which homogeneous freezing was switched off and only one single heterogeneous freezing process was switched on. To decide which cases to select for demonstrating the possible effects of small perturbations, the ice water fractions in the resulting clouds were determined for a number of cases.
4.2.1 Ice water fractions
Following the definition of Korolev et al. (2003) the ice water fraction decides whether a liquid, a mixed-phase, or an ice cloud has been formed. It is calculated from the integrated ice water content (IWC) and the integrated liquid water content (LWC) by using
A liquid cloud is defined by IWF < 0.1, a mixed-phase cloud by 0.1 ≤ IWF ≤ 0.9, and an ice cloud by IWF > 0.9 (Korolev et al., 2003).
Table 2List of simulated cases with single freezing modes resulting in mixed-phase or liquid clouds.
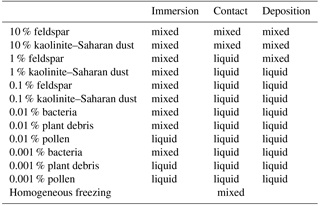
The resulting types of clouds are listed in Table 2. Homogeneous freezing resulted in a mixed-phase cloud and immersion freezing with mineral dust fractions as low as 0.1 % and biological fractions as low as 0.01 % except pollen. With 0.001 % biological fractions bacteria still formed a mixed-phase cloud but not plant debris and pollen. In contact and deposition modes, mixed-phase clouds were found only with 10 and 1 % feldspar and 10 % kaolinite–Saharan dust; in all other cases liquid clouds resulted, even with somewhat higher biological fractions of 0.01 %. Therefore, the biological particles were not included in simulations with contact and deposition freezing. The results in Table 2 indicate that cases representing small perturbations were those with 0.001 % biological material in the immersion mode and those with 1 % mineral dust in contact and deposition modes.
In the following sections, some example results from these simulations are presented for the reference case with homogeneous freezing, for immersion freezing with 1 % feldspar, and for contact and deposition freezing with 10 % feldspar. Figures 4 to 7 show the corresponding results of ice formation: ice water contents (Figs. 4a to 7a), ice particle numbers (Figs. 4b to 7b), and ice particle size spectra (Figs. 4c to 7c). The left columns of panels (b) and (c) indicate results from primary freezing only, i.e., from direct drop freezing (homogeneous, immersion, and contact freezing) or direct particle activation (deposition nucleation). The other columns in panels (b) and (c) give results from complete ice formation including growth by water vapor deposition, riming, collision and sticking of ice particles, and ice nucleation of drops by small ice particles (see Sect. 2.1).
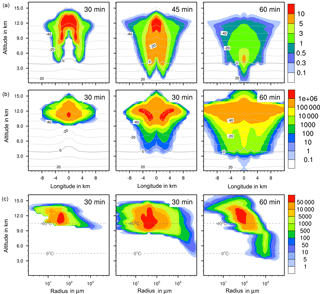
Figure 4Ice formation from the reference case with homogeneous freezing. (a, b) Temporal development of two parameters shown in a vertical cut through the cloud center. Horizontal dashed lines: temperature in ∘C. (a) Ice water contents in g kg−1 and (b) ice particle numbers per m3. (c) Ice particle size spectra in the center cell of the cloud at different times. Number concentrations per m3. Left pictures in (b) and (c) show primary homogeneous freezing only.
4.2.2 Ice water contents
The maximum ice water content (IWC) reached 10 g kg−1 in all cases (Figs. 4a to 7a). Thus, with contact and deposition freezing around 10 times more ice nucleating material as with immersion freezing was required to affect similar IWC. The homogeneous case, however, showed the largest regions with 10 g kg−1 IWC at altitudes above 10 km even after 45 min. Later, the region with more than 0.1 g kg−1 IWC was still enlarged.
In the cases of contact and deposition freezing, after 30 min the cloud regions with more than 0.1 g kg−1 IWC were smaller in comparison to homogeneous and immersion freezing. In particular, there was a gap in the center of the cloud. Because of high relative humidities in this cloud region, fewer interstitial (i.e., inactivated) aerosol particles were present that could have served as INPs. The same correlation between relative humidity and contact freezing effects was found in the model studies of Hande et al. (2017). After 45 min, melting ice particles arrived near the ground level in the case of contact and deposition freezing and also, but less, in the case of homogeneous freezing, but not with immersion freezing. In the latter case fewer ice particles were removed from the cloud, even at later cloud stages.
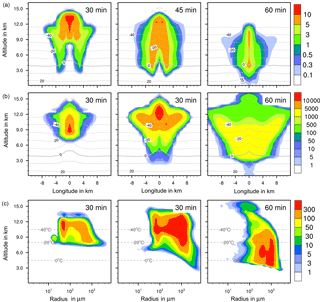
Figure 5Ice formation from immersion freezing with 1 % feldspar. (a, b) Temporal development of two parameters shown in a vertical cut through the cloud center. Horizontal dashed lines: temperature in ∘C. (a) Ice water contents in g kg−1 and (b) ice particle numbers per m3. (c) Ice particle size spectra in the center cell of the cloud at different times. Number concentrations per m3. Left pictures in (b) and (c) show primary immersion freezing only.
4.2.3 Ice particle numbers
Figures 4 to 7 (left columns, panels b and c) indicate the altitude at which primary ice formation proceeded. The maximum in the homogeneous case was between 10 and 12 km of altitude (−40 to −45 ∘C) and in the deposition case above 13 km due to high ice supersaturation and corresponding low temperatures (< −45 ∘C), which were present near cloud top. However, some particles were also nucleated at lower heights at the cloud edges. Immersion freezing was active in a wider range between 8 and 11 km with temperatures from −20 to −40 ∘C according to the insoluble particle mass in the drops. Contact freezing was dominant at lower altitudes from 6 to 9 km with temperatures between −10 and −25 ∘C due to the effects of large particles colliding with drops. Note from Fig. 6c the second maxima in the ice particle spectra at 12 km of altitude, which reflect the effects of small particles at low temperatures. Similar findings resulted from the model simulations performed by Hande and Hoose (2017) for convective clouds: immersion freezing was the most important heterogeneous freezing mode. In regions with temperatures below −35 ∘C homogeneous freezing was dominant, while there were fewer effects of deposition freezing; contact freezing was important at higher temperatures.
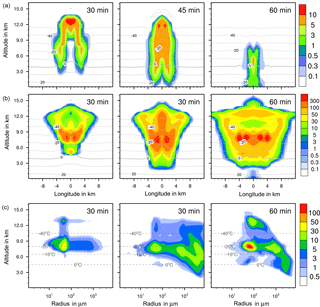
Figure 6Ice formation from contact freezing with 10 % feldspar. (a, b) Temporal development of two parameters shown in a vertical cut through the cloud center. Horizontal dashed lines: temperature in ∘C. (a) Ice water contents in g kg−1 and (b) ice particle numbers per m3. (c) Ice particle size spectra in the center cell of the cloud at different times. Number concentrations per m3. Left pictures in (b) and (c) show primary contact freezing only.
In homogeneous, immersion, and contact modes most primary frozen drops had radii around 40 µm; however, the complete ice particle spectra were rather different. Homogeneously frozen drops started with 1 µm radii, while the major fraction had radii between 10 and 100 µm. With immersion freezing the size spectrum was much broader, ranging from 40 µm to 1 mm radii; the smallest frozen drops had 10 µm because they had to sample sufficient ice nucleating material. The major fraction of drops frozen by contact freezing had radii from 20 to 80 µm, also starting with 10 µm. For smaller drops, the collision efficiency with INP is very low (Diehl et al., 2006). In contrast, primary formed ice particles from deposition nucleation had radii around 0.1 to 0.2 µm only due to the sizes of involved aerosol particles.
For the homogeneous and immersion case, the ice water contents and the ice particle numbers decreased between 30 and 60 min (Figs. 4a, b and 5a, b), while for the contact and deposition cases the IWC decreased but the ice particle numbers did not. This indicates that primary ice formation still continued at cloud stages after 60 min with contact and deposition freezing. Homogeneous and immersion freezing occurred mainly at altitudes above 9 km at which the numbers of available supercooled drops were reduced after 60 min (compare the warm test case in Sect. 4.1). The inactivated particles required for contact and deposition freezing were always present because of entrainment. Furthermore, for contact freezing taking place at lower altitudes supercooled drops were still available.
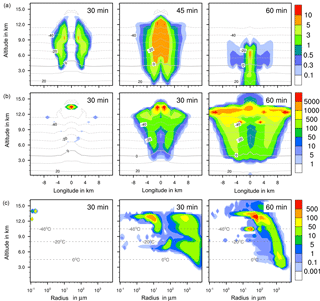
Figure 7Ice formation from deposition nucleation with 10 % feldspar. (a, b) Temporal development of two parameters shown in a vertical cut through the cloud center. Horizontal dashed lines: temperature in ∘C. (a) Ice water contents in g kg−1 and (b) ice particle numbers per m3. (c) Ice particle size spectra in the center cell of the cloud at different times. Number concentrations per m3. Left pictures in (b) and (c) show primary deposition freezing only.
With homogeneous and immersion freezing, high numbers of ice particles were formed (Figs. 4b to 7b), with up to 1 × 106 ice particles per m3 in the homogeneous case and up to 1 × 104 ice particles per m3 in the immersion mode. These numbers are in the range of those observed in atmospheric convective clouds (e.g., Frey et al., 2014). Similar numbers as with immersion freezing were reached with deposition nucleation but only in a limited area of the cloud where the IWC was low in contrast. This indicates that these ice particles were very small and contributed very little to the IWC. With contact freezing, at maximum only 300 ice particles per m3 were formed. Consider here that the INP fractions were 10 times higher in the contact and deposition cases than in the immersion case.
After 60 min in the homogeneous case, small ice particles were still present at high altitudes that were grown from the very small ones; larger ice particles moved downwards (Fig. 4c). In contrast, in the immersion case most of the smaller ice particles grew to larger sizes and moved downwards (Fig. 5c). With contact freezing, newly formed smaller ice particles were still present at lower altitudes after 60 min. In the deposition mode, an important process was the nucleation of larger drops by collisions with the pristine ice particles. These effects are visible in particular in Fig. 6c after 30 min when the ice particle spectrum was separated into two regions. All ice particles larger than 100 µm were the result of secondary ice formation, i.e., the collision of pristine ice particles with supercooled drops. In contrast, with homogeneous, immersion, and contact freezing, such large ice particles could be the result of primary ice formation (see Figs. 4c to 6c) but this was significant only for immersion freezing. With contact freezing a higher fraction of large ice particles was probably also the result of secondary ice formation considering the partially separated ice particle spectrum.
These results from single homogeneous and heterogeneous freezing indicate that there is probably no competition between the different freezing processes because they occur at different altitudes and regions in the cloud. As the primary effects have significantly different magnitudes one may assume that they do not affect each other; e.g., immersion freezing is not restricted by simultaneous contact freezing and vice versa. Because of the fast updraft in the cloud the drop numbers at higher altitudes are hardly reduced by the small effects of contact freezing occurring at lower altitudes.
4.3 Coupled homogeneous and heterogeneous freezing with effects on precipitation
4.3.1 Single heterogeneous modes combined with homogeneous freezing
As a first step model simulations were performed with simultaneous homogeneous freezing and one heterogeneous mode; i.e., homogenous freezing was always switched on plus one heterogeneous mode. The total precipitation after 180 min of modeling time was determined and compared to the value from the reference case with solely homogeneous freezing. Table 3 shows results for feldspar, kaolinite, and Saharan dust, as well as in the immersion mode additionally for bacteria, plant debris, and pollen. The results summarized in Table 3 indicate that in most cases the total precipitation amount was similar to homogeneous freezing, while there were some cases with more than 20 % deviations in both directions. In particular, enhanced precipitation after 180 min was found in the immersion mode for plant debris and pollen and in the deposition mode for 1 % Saharan dust. These cases represent situations in which small perturbations (in this case, small fractions of biological INP or few ice forming effects from deposition nucleation) trigger cloud microphysics so that eventually more precipitation is formed.
Similar observations were made by Hiron and Flossmann (2015), who studied the role of heterogeneous freezing modes in the framework of a 1.5-D bin-resolved cloud model. They simulated a convective cloud that reached an altitude of 9.5 km with temperatures near −40 ∘C. In single cases with solely contact and deposition freezing they found more accumulated rain than with solely immersion and homogeneous freezing.
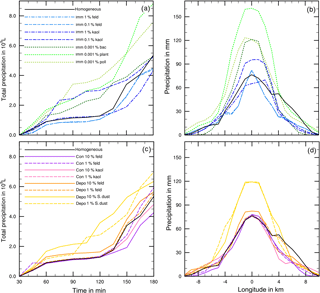
Figure 8(a, c) Temporal development of precipitation during 180 min of modeling time for coupled homogeneous and one heterogeneous freezing process. (b, d) Local distribution of precipitation through the cloud after 180 min. Black lines: reference case with homogeneous freezing. Colored lines mark the coupled heterogeneous freezing mode, and the line styles mark the fraction of ice-active material.
Figure 8 shows more precipitation details for the cases listed in Table 3. In Fig. 8a and c the development of total precipitation with time is given, and Fig. 8b and d indicate the local distribution of precipitation on a longitudinal line through the model domain after 180 min. In all cases precipitation set in after 45 min (Fig. 8a and c). Deviations were already visible at that time but became more obvious with proceeding time. In some cases precipitation stayed nearly constant during the next hour and increased at later times. This delayed increase in precipitation was noted for the reference case with homogeneous freezing (black solid line), for the cases with contact freezing (purple lines), and for mineral dust cases with immersion freezing except 0.1 % kaolinite (blue lines). In other cases, precipitation increased at early cloud stages, in particular with biological particles in the immersion mode (green lines) and with Saharan dust in the deposition mode (yellow lines).
From Fig. 8b and d one notes that in the cloud center precipitation ranged from 65 (immersion with 1 % kaolinite) to 160 mm (immersion with 0.001 % plant debris) with 75 mm in the reference case. Higher precipitation in the cloud center was observed for the cases with at least 20 % more total precipitation (see Table 3); however, it was also found for cases in which total precipitation was not significantly enhanced but precipitation was increased during early cloud stages, i.e., 10 % Saharan dust in the deposition mode and 0.001 % bacteria and 0.1 % kaolinite in the immersion mode.
To illustrate how ice formation influences the total condensed water in the deep convective cloud and thus precipitation, results from four example cases shown in Fig. 8 are considered in more detail. These are immersion with 1 % feldspar (case 1), immersion with 0.001 % plant debris (case 2), contact with 1 % feldspar (case 3), and deposition with 1 % Saharan dust (case 4). The amounts of total precipitation were 4.33 × 109, 8.81 × 109, 5.34 × 109, and 6.97 × 109 L, respectively (see Table 3). Figure 9 shows results from cases 1 to 4 in each panel for ice water contents (Fig. 9a) and ice particle numbers (Fig. 9b).
Differences between case 1 in which precipitation was mostly delayed and the other cases are significant. In case 1 more ice was present at middle and high altitudes after 60 min but less ice was near the ground level after 45 and 60 min and in mid-levels after 90 min. Thus, only a few melting ice particles precipitated from the cloud. The ice particle spectrum after 60 min indicates that there was a high contribution from immersion freezing to ice particles smaller than 500 µm in mid-levels between 4 and 9 km of height. The numbers of larger ice particles were reduced in comparison to the other cases; their formation was hindered by the competition of the many small ice particles.
In cases 2 to 4, the contributions from heterogeneous freezing to ice particles smaller than 500 µm in mid-levels between 4 and 9 km of height were rather low in contrast to case 1. However, more ice was present near ground level after 45 and 60 min and below 8 km of height after 90 min. This indicates the presence of larger ice particles, which strongly contribute to the ice water content. After 60 min, the numbers of ice particles larger than 500 µm were highest in cases 2 and 4 in which precipitation mostly increased in early cloud stages. In case 3 with contact freezing fewer larger ice particles were formed. From single contact freezing (Sect. 4.2.1) it was found that primary contact freezing also proceeded at later cloud stages, which hindered the growth of ice particles by competition.
The evaluation of the results indicates that the formation of precipitation-sized ice particles larger than 500 µm was essential to increase precipitation. The implications are advanced precipitation during early cloud stages, enhanced precipitation in the cloud center, and potentially higher total precipitation. Processes contributing mainly to the formation of larger ice particles are riming and the nucleation of supercooled drops by collision with pristine ice particles. The latter plays a major role with deposition freezing (see Sect. 4.2.1). In comparison to the reference case with homogenous freezing, additional heterogeneous ice formation by direct drop freezing affected by high INP fractions may delay precipitation because the growth of ice particles is hindered. On the other hand, small numbers of ice particles heterogeneously formed by low INP fractions trigger growth processes in the ice phase and thus may affect an increase in precipitation.
Table 4Total precipitation after 180 min of modeling time for coupled homogeneous and internally mixed immersion freezing. Marked in italics: cases with more than 20 % reduction of precipitation.
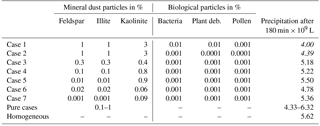
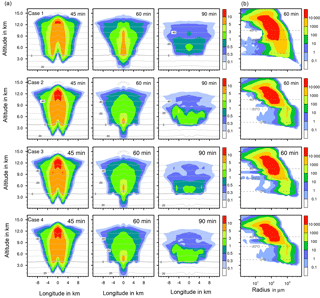
Figure 9Ice formation for different cases with coupled homogeneous and one heterogeneous freezing mode. Case 1: immersion freezing with 1 % feldspar; case 2: immersion freezing with 0.001 % plant debris; case 3: contact freezing with 1 % feldspar; case 4: deposition nucleation with 1 % Saharan dust. (a) Ice water content in g kg−1 at different times shown in a vertical cut through the cloud center. Horizontal dashed lines: temperature in ∘C. (b) Ice particle size spectra in the center cell of the cloud. Number concentrations per m3.
Internally mixed INP in the immersion mode
A number of cases were modeled with immersion freezing in which the insoluble mass contained in the drops did not consist of pure materials but was internally mixed. These mixtures contained higher fractions of mineral dust and small fractions of biological particles, as they reflect atmospheric conditions. Table 4 lists the compositions of seven cases together with the resulting amount of total precipitation; Fig. 10 shows the precipitation results.
In all mixed cases precipitation was lower than in the reference case with homogenous freezing. However, as can be seen from Fig. 10, the temporal development and the local distribution of precipitation were modified by the particle composition. In cases 1 and 2 with 5 % mineral dust fractions and in cases 3, 4, and 5 with 1 % mineral dust fractions, the development of precipitation was delayed below the reference line (homogeneous freezing) during early cloud stages (Fig. 10a). The lower the fraction of efficient dust INP, the earlier the increase in precipitation above the reference line. This was distinctly visible in case 7 with the lowest dust fractions. The 75 mm precipitation in the cloud center from homogeneous freezing was enhanced up to 100 to 120 mm in those cases. However, in comparison to the pure mineral dust cases no enhancement effects resulted from additional biological INP fractions. This indicates that the major fraction of composed INP decides ice formation and hence the development of precipitation.
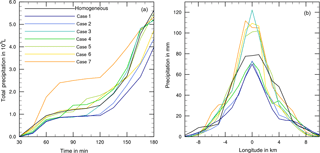
Figure 10(a) Temporal development of precipitation during 180 min of modeling time for coupled homogeneous and internally mixed immersion freezing. (b) Local distribution of precipitation through the cloud after 180 min. Black line: reference case with homogeneous freezing. Colored lines mark the different cases as listed in Table 4.
4.3.2 Several heterogeneous modes combined with homogeneous freezing
Finally, model simulations were performed in which contact and/or deposition freezing were switched on in addition to homogeneous and immersion freezing. In a first series of model simulations the FINP values were 1 % in all freezing modes. For these cases Table 5 gives the resulting precipitation after 180 min together with results from Sect. 4.3.1 for solely immersion, contact, and deposition freezing. In a second series of model simulations mixed coupled cases were performed with low INP fractions in the immersion mode and higher INP fractions in the contact and deposition modes. Here the immersion INPs were internally mixed. Table 6 summarizes five selected cases in which the INP fractions of approximately 0.1 % in the immersion mode contained mainly feldspar (cases 1, 2, and 3) or kaolinite (cases 4 and 5). In cases 3 and 5, the mixed immersion INPs additionally contained small fractions of biological particles. The INP fractions in the contact and deposition modes were 1 % mineral dust in cases 1, 2, and 4 and 0.1 % biological particles in cases 3 and 5.
Table 6Total precipitation after 180 min of modeling time for mixed cases with coupled homogeneous, immersion, contact, and deposition freezing. Marked in italics: cases with more than 20 % reduction of precipitation.
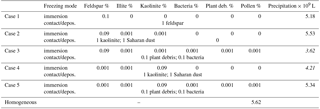
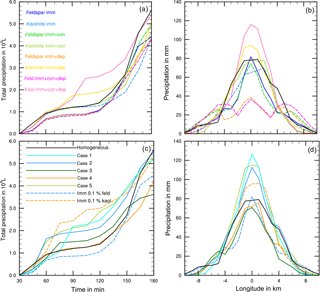
Figure 11(a, b) Results from solely immersion freezing and coupled with other freezing modes. Colored lines mark the different cases as listed in Table 5; broken solid lines: kaolinite. (c, d) Results from mixed cases with coupled freezing modes. Colored solid lines mark the different cases as listed in Table 6. Dashed lines: immersion freezing only. Black lines: reference case with homogeneous freezing. (a, c) Temporal development of precipitation during 180 min of modeling time. (b,d) Local distribution of precipitation through the cloud after 180 min.
The results in Table 5 indicate that in none of the investigated cases did additional contact and/or deposition freezing as small perturbations cause an increase in total precipitation. However, modifications of the temporal development and the local distribution of precipitation are visible and demonstrated in Fig. 11. In the case of feldspar, precipitation was delayed during early cloud stages with all combinations of freezing modes. The local distribution of precipitation was not modified by additional contact freezing but significantly changed by additional deposition freezing. Precipitation was reduced in the cloud center from 75 to 35 mm and was spread over a wider area with a 12 km diameter (instead of 4 km). This indicates the influence of deposition freezing on precipitation at the cloud edges. In contrast, for the kaolinite–Saharan dust cases, delayed precipitation from solely immersion freezing was slightly increased during later cloud stages by additional contact freezing and even more enhanced by additional contact and deposition freezing. Similarly, precipitation in the cloud center was increased from 70 mm with solely immersion freezing to 80 mm with additional contact freezing, to 95 mm with additional deposition freezing, and to 115 mm with both additional freezing modes. For the latter case Fig. 12 illustrates how additional contact and deposition modes altered the ice particle spectra. Although their impact on ice formation was rather low they modified the ice particle spectra so that higher numbers of larger ice particles were formed.
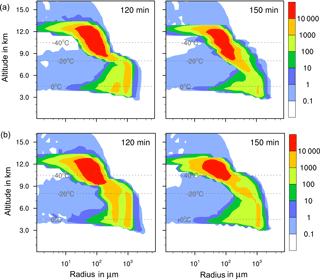
Figure 12Ice particle size spectra in the center cell of the cloud after 120 and 150 min for cases with 1 % kaolinite–Saharan dust. Number concentrations per m3. (a) Solely immersion freezing and (b) combined immersion, deposition, and contact freezing.
For the cases listed in Table 6 with lower internally mixed immersion INP fractions and higher contact and deposition INP fractions, an enhancement of total precipitation was not found, but again the development of precipitation and the local distribution were modified. In Fig. 11c and d results from solely immersion freezing are also shown. The 0.1 % feldspar in the immersion mode (dashed blue line) effected a delay in precipitation, while 1 % additional contact and deposition INP (solid blue lines, cases 1 and 2) as well as additional biological INP (solid green line, case 3) led to an increase during early cloud stages (Fig. 11c). However, with biological INP (case 3) this increase was less significant. In contrast, the enhancement of precipitation affected by 0.1 % kaolinite in the immersion mode (dashed orange line) was reduced by additional contact and deposition freezing (orange solid line, case 4) and by additional biological INP (solid light green line, case 5). Here the reduction was less significant with biological INP. Figure 11d again indicates that more precipitation during early cloud stages was coupled with a significant increase in precipitation in the cloud center although the total precipitation was not higher than in the reference case.
Thus, when contact and deposition freezing equally contribute to ice formation as immersion freezing (with higher INP fractions) they may work in both directions. They may enhance precipitation during early cloud stages, thereby counterbalancing the delaying effect of immersion freezing. On the other hand, when immersion freezing itself shows some “small trigger effects” these may be suppressed by contact and deposition freezing during early cloud stages. Additional biological particles counteract these tendencies.
The results presented in this section indicate that immersion freezing as the major ice forming process inhibits an increase in total precipitation above the amount from the reference case with homogeneous freezing. However, additional deposition nucleation and contact freezing as small perturbations have the chance to modify precipitation. With a dependence on the active INP types, possible changes are an increase in precipitation during early cloud stages coupled with more precipitation in the cloud center or no effect on the temporal development but a spread of precipitation over a wider area beyond the cloud. When contact and deposition freezing nearly equally contribute to ice formation as immersion freezing the effects do not show a clear trend. Their interactions may favor or suppress the formation of larger ice particles and thus an enhancement or a delay of precipitation. In comparison to pure dust cases no significant differences caused by additional biological particles are visible.
Growth processes in mixed-phase clouds are determined by the collision efficiencies of the involved drops and ice particles, which in turn are dependent on the sizes of the collision partners (Pruppacher and Klett, 2010; Diehl et al., 2006). Thus, the development of drop and ice particle spectra during cloud evolution determines the effectivity of growth processes and eventually the formation of precipitation-sized hydrometeors.
In this paper an improved version of the 3-D cloud modeling system COSMO-SPECS (Grützun et al., 2008) is presented, which allows for the study of the impact of aerosol particle types and three heterogeneous freezing modes on ice formation and precipitation. A deep convective cloud with a wide temperature range from +20 ∘C at the ground level and −50 ∘C at cloud top was simulated. The strong vertical updraft in this cloud lifted the nucleated drops within 10 min from the zero degree level to the cloud top where the major fraction of drops froze homogeneously. In this study it was investigated if under such conditions heterogeneous freezing may have a significant impact on ice formation and how this affects precipitation. In particular, we looked for so-called “small trigger effects”, i.e., if small perturbations such as low fractions of biological particles in the immersion mode or the less efficient processes of contact and deposition freezing could modify precipitation.
The following conclusions were drawn.
-
The different freezing processes hardly compete with and affect each other. Homogeneous, immersion, and contact freezing, which require supercooled drops, occur at different altitudes in the cloud. Deposition nucleation dominating at the highest altitudes is not in competition with homogeneous freezing because it is not coupled to supercooled drops. Also, contact and deposition freezing are not in competition; they are both coupled to inactivated particles but are dominant at different altitudes. Some deposition nucleation is possible at lower heights at the cloud edges, while contact freezing concentrates rather towards the cloud center where more drops are available.
-
Regarding the vertical velocity in the cloud, because of the release of latent heat during freezing the fields of highest vertical updraft were vertically extended in comparison to the warm case (see Fig. 3) by the additional release of latent heat during freezing. However, cases with different ice formation resulted in small local changes only (results not shown here).
-
Precipitation is modified by the formation of larger ice particles. This is suppressed in regions where homogeneous freezing is dominant because high numbers of small ice particles compete for growth via water vapor or drop deposition. It may also be suppressed in median regions when the impact of immersion freezing is high, i.e., with higher fractions of efficient INP. In such cases even small drops contain sufficient insoluble material to affect freezing. In lower regions where contact freezing is active growth processes are hindered because of shorter times until the ice particles reach the melting level.
-
In contrast, the formation of larger ice particles by growth processes is supported in median regions of the cloud when only small fractions of immersion INPs are active. Then larger drops freeze because higher masses of insoluble material in the drops are required. Additionally, supercooled drops are present for riming and the ice particles need some time to reach the melting level. Deposition nucleation primarily affects the formation of very small pristine ice particles; however, afterwards the formation of large ice particles by collision with supercooled drops is supported. In this way, deposition nucleation indirectly promotes the formation of large ice particles.
-
The results indicate so-called “small trigger effects” of heterogeneous freezing in comparison to homogeneous freezing and “small trigger effects” of deposition and contact freezing in comparison to immersion freezing. Therefore, although homogeneous freezing is dominant in a deep convective cloud, heterogeneous freezing processes should not be neglected. Aside from immersion freezing, contact and deposition freezing are also important. This finding is in contrast to the conclusion of Hiron and Flossmann (2015). From the fact that contact and deposition freezing contributed only low amounts of ice particles in comparison to the other freezing modes they concluded that these could be neglected in cloud models with less complexity.
-
“Small trigger effects” of biological particles in comparison to mineral dust particles were not found, and thus the role of biological particles in atmospheric clouds still remains unclear as was concluded earlier by Hiron and Flossmann (2015). They studied a case with solely bacterial INP (acting in a nonspecific ice nucleation mode), which resulted in significantly higher amounts of precipitation than in all other cases. However, when bacteria were added in a simulation in which all other INPs were also forming ice their influence became negligible.
-
In comparison to the reference case with homogeneous freezing, these small perturbations may affect an enhancement of total precipitation but mostly the effects are limited to modifications of the temporal development of precipitation, i.e., a gradual increase at early cloud stages instead of a strong increase at later cloud stages. The effects are coupled with changes in the local distribution of precipitation, i.e., approximately 50 % more precipitation in the cloud center. The modifications depend on the active freezing modes, the fractions of active INP, and the composition of the internal mixtures in the drops.
-
In general, precipitation from the simulated deep convective cloud did not show significant variations in the total precipitation amount. Changes in the local distribution of precipitation were more remarkable. Because of the strong vertical updraft in the present case precipitation is highly influenced by cloud dynamics but cloud microphysics still has an important impact.
Further simulations will switch to cloud situations with weaker cloud dynamics, i.e., reduced vertical velocity, slower ascent of the air, and reduced cloud top height. Thus, microphysical changes in the cloud may have more time to develop. Homogeneous freezing will have a smaller impact on ice formation, while heterogeneous freezing will show a higher impact.
The data are available from the corresponding author upon request.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Results from the ice nucleation research unit (INUIT) (ACP/AMT inter-journal SI)”. It is not associated with a conference.
This work is part of the research group INUIT (Ice Nuclei research UnIT)
FOR1525 and was supported by the Deutsche Forschungsgemeinschaft under grant
DI 1539/1-2. We appreciate the INUIT community for providing experimental
data as a base for parameterizations and for helpful discussions. We would like
to thank Ralf Wolke and Jens Stoll from TROPOS Leipzig for providing the
COSMO-SPECS code and for their support during restarting the model and
solving initial problems. Thanks to Martin Simmel from TROPOS Leipzig for
fruitful discussions and support. Karoline Diehl would like to thank Daniel Kunkel
from IPA Mainz for his aid in installing, starting, and performing
COSMO-SPECS model simulations on the high-performance cluster MOGON at the
University of Mainz.
Edited by: Barbara Ervens
Reviewed by: two anonymous referees
Atkinson, J. D., Murray, B. J., Woodhouse, M. T., Whale, T. F., Baustian, K. J., Carslaw, K. S., Dobbie, S., O'Sullivan, D., and Malkin, T. L.: The importance of feldspar for ice nucleation by mineral dust in mixed-phase clouds, Nature, 498, 355–358, https://doi.org/10.1038/nature12278, 2013.
Baldauf, M., Seifert, A., Förstner, J., Majewski, D., Raschendorfer, M., and Reinhardt, T.: Operational convective-scale numerical weather prediction with the COSMO model: Description and sensitivities, Mon. Weather Rev., 139, 3887–3905, 2011.
Bauer, H., Kasper-Giebl, A., Löflund, M., Giebl, H., Hitzenberger, R., Zibuschka, F., and Puxbaum, H.: The contribution of bacteria and fungal spores to the organics content of cloud water, precipitation and aerosols, Atmos. Res., 64, 109–119, 2002.
Busch, B., Kandler, K., Schütz, L., and Neusüß, C.: Hygroscopic properties and water soluble volume fraction of atmospheric particles in the diameter range from 50 nm to 3.8 µm during LACE 98, J. Geophys. Res., 107, LAC 2-1–LAC 2-11, https://doi.org/10.1029/2000JD000228, 2002.
Cziczo, D. J. and Froyd, K. D.: Sampling the composition of cirrus ice residuals, Atmos. Res., 142, 15–31, https://doi.org/10.1016/j.atmosres.2013.06.012, 2014.
DeMott, P. J., Prenni, A. J., McMeeking, G. R., Sullivan, R. C., Petters, M. D., Tobo, Y., Niemand, M., Möhler, O., Snider, J. R., Wang, Z., and Kreidenweis, S. M.: Integrating laboratory and field data to quantify the immersion freezing ice nucleation activity of mineral dust particles, Atmos. Chem. Phys., 15, 393–409, https://doi.org/10.5194/acp-15-393-2015, 2015.
Diehl, K. and Mitra, S. K.: New particle-dependent parameterizations of heterogeneous freezing processes: sensitivity studies of convective clouds with an air parcel model, Atmos. Chem. Phys., 15, 12741–12763, https://doi.org/10.5194/acp-15-12741-2015, 2015.
Diehl, K. and Wurzler, S.: Heterogeneous drop freezing in the immersion mode: Model calculations considering soluble and insoluble particles in the drops, J. Atmos. Sci., 61, 2063–2072, 2004.
Diehl, K., Simmel, M., and Wurzler, S.: Numerical simulations of the impact of aerosol properties and drop freezing modes on the glaciation, microphysics, and dynamics of clouds, J. Geophys. Res., 111, D07202, https://doi.org/10.1029/2005JD005884, 2006.
Duft, D. and Leisner, T.: Laboratory evidence for volume-dominated nucleation of ice in supercooled water microdroplets, Atmos. Chem. Phys., 4, 1997–2000, https://doi.org/10.5194/acp-4-1997-2004, 2004.
Ekman, A. M. L., Engström, A., and Wang, C.: The effect of aerosol composition and concentration on the development and anvil properties of a continental deep convective cloud, Q. J. Roy. Meteor. Soc., 133, 1439–1452, 2007.
Fan, J., Leung, L. R., Rosenfeld, D., Chen, Q., Li, Z., Zhang, J., and Yan, H.: Microphysical effects determine macrophysical response for aerosol impacts on deep convective clouds, P. Natl. Acad. Sci. USA, 110, E4581–E4590, https://doi.org/10.1073/pnas.1316830110, 2013.
Frey, W., Borrmann, S., Fierli, F., Weigel, R., Mitev, V., Matthey, R., Ravegnani, F., Sitnikov, N. M., Ulanovsky, A., and Cairo, F.: Tropical deep convective life cycle: Cb-anvil cloud microphysics from high-altitude aircraft observations, Atmos. Chem. Phys., 14, 13223–13240, https://doi.org/10.5194/acp-14-13223-2014, 2014.
Gilmore, M. S., Straka, J. M., and Rasmussen, E. N.: Precipitation and Evolution Sensitivity in Simulated Deep Convective Storms: Comparisons between liquid-only and simple ice and liquid phase microphysics, Mon. Weather Rev., 132, 1897–1916, 2004.
Grützun, V., Knoth, O., and Simmel, M: Simulation of the influence of aerosol particle characteristics on clouds and precipitation with LM-SPECS: Model description and first results, Atmos. Res., 90, 233–242, 2008.
Hande, L. B. and Hoose, C.: Partitioning the primary ice formation modes in large eddy simulations of mixed-phase clouds, Atmos. Chem. Phys., 17, 14105–14118, https://doi.org/10.5194/acp-17-14105-2017, 2017.
Hande, L. B., Engler, C., Hoose, C., and Tegen, I.: Seasonal variability of Saharan desert dust and ice nucleating particles over Europe, Atmos. Chem. Phys., 15, 4389–4397, https://doi.org/10.5194/acp-15-4389-2015, 2015.
Hande, L. B., Hoose, C., and Barthlott, C.: Aerosol- and droplet-dependent contact freezing: Parameterization development and case study, J. Atmos. Sci., 74, 2229–2245, https://doi.org/10.1175/JAS-D-16-0313.1, 2017.
Hiranuma, N., Brooks, S. D., Moffet, R. C., Glen, A., Laskin, A., Gilles, M. K., Liu, P., Macdonald, A. M., Strapp, J. W., and McFarquar, G. M.: Chemical characterization of individual particles and residuals of cloud droplets and ice crystals collected on board research aircraft in the ISDAC 2008 study, J. Geophys. Res., 118, 6564–6579, https://doi.org/10.1002/jgrd.50484, 2013.
Hiranuma, N., Möhler, O., Yamashita, K., Tajiri, T., Saito, A., Kiselev, A., Hoffmann, N., Hoose, C., Jantsch, E., Koop, T., and Murakami, M.: Ice nucleation by cellulose and its potential contribution to ice formation in clouds, Nat. Geosci., 8, 273–277, https://doi.org/10.1038/ngeo2374, 2015.
Hiron, T. and Flossmann, A. I.: A study of the role of the parameterization of heterogeneous ice nucleation for the modeling of microphysics and precipitation of a convective cloud, J. Atmos. Sci., 72, 3322–3339, https://doi.org/10.1175/JAS-D-15-0026.1, 2015.
Hoffmann, N.: Experimental Study on the Contact Freezing of Supercooled Micro-Droplets in Electrodynamic Balance, PhD Thesis, University of Heidelberg, Germany, https://doi.org/10.11588/heidok.00018744, 2015.
Hoose, C. and Möhler, O.: Heterogeneous ice nucleation on atmospheric aerosols: a review of results from laboratory experiments, Atmos. Chem. Phys., 12, 9817–9854, https://doi.org/10.5194/acp-12-9817-2012, 2012.
INUIT Research group: The INUIT research unit, available at: http://www.ice-nuclei.de, last access: 12 March 2018.
Kamphus, M., Ettner-Mahl, M., Klimach, T., Drewnick, F., Keller, L., Cziczo, D. J., Mertes, S., Borrmann, S., and Curtius, J.: Chemical composition of ambient aerosol, ice residues and cloud droplet residues in mixed-phase clouds: single particle analysis during the Cloud and Aerosol Characterization Experiment (CLACE 6), Atmos. Chem. Phys., 10, 8077–8095, https://doi.org/10.5194/acp-10-8077-2010, 2010.
Kerkweg, A., Wurzler, S., Reisin, T., and Bott, A.: On the cloud processing of aerosol particles: An entraining air parcel model with two-dimensional spectral cloud microphysics and a new formulation of the collection kernel, Q. J. Roy. Meteor. Soc., 129, 1–18, 2003.
Kessler, E.: On the continuity and distribution of water substance in atmospheric circulations, Atmos. Res. 38, 109–145, 1995.
Khain, A., Pokrovsky, A., Pinsky, M., Seifert, A., and Phillips, V.: Simulation of effects of atmospheric aerosols on deep turbulent convective clouds using a spectral microphysics mixed-phase cumulus cloud model. Part I: Model description and possible applications, J. Atmos. Sci., 61, 2963–2982, 2004.
Khain, A., Rosenfeld, D., and Pokrovsky, A.: Aerosol impact on the dynamics and microphysics of deep convective clouds, Q. J. Roy. Meteor. Soc., 131, 2639–2663, 2005.
Koop, T., Beiping, L., Tsias, A., and Peter, T.: Water activity as the determinant for homogeneous ice nucleation in aqueous solutions, Nature, 406, 611–614, 2000.
Korolev, A. V., Isaac, G. A., Cober, S. G., Strapp, J. W., and Hallett, J.: Microphysical characterization of mixed-phase clouds, Q. J. Roy. Meteor. Soc., 129, 39–65, 2003.
Kreidenweis, S. M., Walcek, C. J., Feingold, G., Gong, W., Jacobson, M. Z., Kim, C.-H., Liu, X., Penner, J. E., Nenes, A., and Seinfeld, J. H.: Modification of aerosol mass and size distribution due to aqueous-phase SO2 oxidation in clouds: Comparisons of several models, J. Geophyis. Res., 108, 4213, https://doi.org/10.1029/2002JD002697, 2003.
Lee, S. S., Donner, L. J., and Phillips, V. T. J.: Impacts of aerosol chemical composition on microphysics and precipitation in deep convection, Atmos. Res., 94, 220–237, 2009.
Leroy, D., Monier, M., Wobrock, W., and Flossmann, A. I.: A numerical study of the effects of the aerosol particle spectrum on the development of the ice phase and precipitation formation, Atmos. Res., 80, 15–45, https://doi.org/10.1016/j.atmosres.2005.06.007, 2006.
Lieber, M., Grützun, V., Wolke, R., Müller, M. S., and Nagel, W. E.: Highly scalable dynamic load balancing in the atmospheric modeling system COSMO-SPECS+FD4, in: Applied parallel and scientific computing, edited by: Jónasson, K., 7133, 131–141, Springer, Berlin, 2012.
Lohmann, U. and Diehl, K.: Sensitivity studies of the importance of dust nuclei for the indirect aerosol effect on stratiform mixed-phase clouds, J. Atmos. Sci., 63, 968–982, 2006.
Matthias-Maser, S. and Jaenicke, R.: Size distribution of primary biological aerosol particles with radii ≥ 0.2 µm, J. Atmos. Res., 39, 279–286, 1995.
Murray, B. J., Broadley, S. L., Wilson, T. W., Atkinson, J. D., and Wills, R. H.: Heterogeneous freezing of water droplets containing kaolinite particles, Atmos. Chem. Phys., 11, 4191–4207, https://doi.org/10.5194/acp-11-4191-2011, 2011.
Paukert, M. and Hoose, C.: Modeling immersion freezing with aerosol-dependent prognostic ice nuclei in Arctic mixed phase clouds, J. Geophys. Res.-Atmos., 119, 9073–9092, https://doi.org/10.1002/2014JD021917, 2014.
Phillips, V. T. J., Donner, L. J., and Garner, S. T.: Nucleation processes in deep convection simulated by a cloud-system-resolving model with double-moment bulk microphysics, J. Atmos. Sci., 64, 738–761, 2007.
Phillips, V. T. J., DeMott, P. J., and Andronache, C.: An empirical parameterization of heterogeneous ice nucleation for multiple chemical species of aerosol, J. Atmos. Sci., 65, 2757–2783, 2008.
Phillips, V. T. J., Andronache, C., Christner, B., Morris, C. E., Sands, D. C., Bansemer, A., Lauer, A., McNaughton, C., and Seman, C.: Potential impacts from biological aerosols on ensembles of continental clouds simulated numerically, Biogeosciences, 6, 987–1014, https://doi.org/10.5194/bg-6-987-2009, 2009.
Pruppacher, H. R. and Klett, J. D.: Microphysics of Clouds and Precipitation, 2nd rev. exp. Edn., Atmospheric and Oceanographic Sciences Library, 18, Springer Science & Business Media, 2010.
Reisin T., Levin, Z., and Tzivion, S.: Rain production in convective clouds as simulated in an axisymmetric model with detailed microphysics. Part I: Description of the model, J. Atmos. Sci., 53, 497–519, 1996.
Rosenfeld, D. and Woodley, W. L.: Deep convective clouds with sustained supercooled liquid water down to −37.5∘ C, Nature, 405, 440–442, 2000.
Schmidt, S., Schneider, J., Klimach, T., Mertes, S., Schenk, L. P., Kupiszewski, P., Curtius, J., and Borrmann, S.: Online single particle analysis of ice particle residuals from mountain-top mixed-phase clouds using laboratory derived particle type assignment, Atmos. Chem. Phys., 17, 575–594, https://doi.org/10.5194/acp-17-575-2017, 2017.
Seifert, A. and Beheng, K. D.: A two-moment cloud microphysics parameterization for mixed-phase clouds. Part I: Model description. Meteorol, Atmos. Phys., 92, 45–66, 2006.
Simmel, M. and Wurzler, S.: Condensation and nucleation in sectional cloud microphysical models based on the linear discrete method, Atmos. Res., 80, 218–236, 2006.
Simmel, M., Trautmann, T., and Tetzlaff, G.: Numerical solution of the stochastic collection equation – Comparison of the linear discrete method with other methods, Atmos. Res., 61, 135–148, 2002.
Simmel, M., Diehl, K., and Wurzler, S.: Numerical simulation of the microphysics of an orographic cloud: Comparison with measurements and sensitivity studies, Atmos. Environ., 39, 4365–4373, 2005.
Steiner, A. L., Brooks, S. D., Deng, C., Thornton, D. C. O., Pendleton, M. W., and Bryant, V.: Pollen as atmospheric cloud condensation nuclei, Geophys. Res. Lett., 42, 3596–3602, https://doi.org/10.1002/2015GL064060, 2015.
Steppeler, J., Doms, G., Schättler, U., Bitzer, H. W., Gassmann, A., Damrath, U., and Gregoric, G.: Meso-gamma scale forecast using the nonhydrostatic model LM, Meteorol. Atmos. Phys., 82, 75–96, 2003.
Straka, H.: Pollen- und Sporenkunde, Fischer Verlag, Stuttgart, Germany, 1975.
Tao, W.-K., Li, X., Khain, A., Matsui, T., Lang, S., and Simpson, J.: Role of atmospheric aerosol concentration on deep convective precipitation: Cloud-resolving model simulations, J. Geophys. Res., 112, D24S18, https://doi.org/10.1029/2007JD008728, 2007.
Twohy, C. H. and Anderson, J. R.: Droplet nuclei in non-precipitating clouds: composition and size matter, Environ. Res. Letters., 3, 045002, https://doi.org/10.1088/1748-9326/3/4/045002, 2008.
van den Heever, S. C., Carrió, G. G., Cotton, W. R., DeMott, P. J., and Prenni, A. J.: Impacts of nucleating aerosol on Florida storms. Part I: Mesoscale simulations, J. Atmos. Sci., 63, 1752–1775, 2006.
Weisman, M. and Klemp, J.: The dependence of numerically simulated convective storms on vertical wind shear and buoyancy, Mon. Weather Rev., 110, 504–520, 1982.
Wex, H., Augustin-Bauditz, S., Boose, Y., Budke, C., Curtius, J., Diehl, K., Dreyer, A., Frank, F., Hartmann, S., Hiranuma, N., Jantsch, E., Kanji, Z. A., Kiselev, A., Koop, T., Möhler, O., Niedermeier, D., Nillius, B., Rösch, M., Rose, D., Schmidt, C., Steinke, I., and Stratmann, F.: Intercomparing different devices for the investigation of ice nucleating particles using Snomax® as test substance, Atmos. Chem. Phys., 15, 1463–1485, https://doi.org/10.5194/acp-15-1463-2015, 2015.
Wu, B., Verlinde, J., and Sun, J.: Dynamical and microphysical retrievals from Doppler radar observations of a deep convective cloud, J. Atmos. Sci., 57, 262–283, 2000.