the Creative Commons Attribution 3.0 License.
the Creative Commons Attribution 3.0 License.
Heterogeneous reaction of HO2 with airborne TiO2 particles and its implication for climate change mitigation strategies
Daniel R. Moon
Giorgio S. Taverna
Clara Anduix-Canto
Trevor Ingham
Martyn P. Chipperfield
Paul W. Seakins
Maria-Teresa Baeza-Romero
One geoengineering mitigation strategy for global temperature rises resulting from the increased concentrations of greenhouse gases is to inject particles into the stratosphere to scatter solar radiation back to space, with TiO2 particles emerging as a possible candidate. Uptake coefficients of HO2, γ(HO2), onto sub-micrometre TiO2 particles were measured at room temperature and different relative humidities (RHs) using an atmospheric pressure aerosol flow tube coupled to a sensitive HO2 detector. Values of γ(HO2) increased from 0.021 ± 0.001 to 0.036 ± 0.007 as the RH was increased from 11 to 66 %, and the increase in γ(HO2) correlated with the number of monolayers of water surrounding the TiO2 particles. The impact of the uptake of HO2 onto TiO2 particles on stratospheric concentrations of HO2 and O3 was simulated using the TOMCAT three-dimensional chemical transport model. The model showed that, when injecting the amount of TiO2 required to achieve the same cooling effect as the Mt Pinatubo eruption, heterogeneous reactions between HO2 and TiO2 would have a negligible effect on stratospheric concentrations of HO2 and O3.
It has been suggested that injection of aerosols into the stratosphere in order to scatter solar radiation back to space could be a possible solar radiation management scheme (Shepherd and Working Group on Geoengineering the Climate, 2009). Such a scheme would have the effect of cooling the Earth's surface and serve as a measure to mitigate enhanced global warming. A possible candidate for stratospheric injection is sulfuric acid aerosols as these aerosols occur naturally in the stratosphere. These aerosols are formed by transport of precursors, e.g. SO2 and carbonyl sulfide (OCS), from the troposphere to the stratosphere (Holloway and Wayne, 2010), which form sulfuric acid vapour that condenses onto particles. However, injection of these particles could have important negative effects on the stratosphere through enhanced ozone depletion. Concentrations of sulfate aerosols can increase dramatically as the result of volcanic eruptions. Following the eruption of Mt Pinatubo in 1991, it was estimated that around 30 Tg of H2SO4 was injected in the stratosphere, dramatically increasing stratospheric aerosol loading and hence the available surface area for heterogeneous chemistry to occur (McCormick and Veiga, 1992). Following this volcanic event, the average global lower-tropospheric temperature decreased by 0.5 K (Dutton and Christy, 1992); however, stratospheric ozone concentrations reached a record low in northern mid-latitudes (Dutton and Christy, 1992; McCormick et al., 1995), showing that sulfate aerosols could be unsuitable for solar radiation management. The impact of sulfate geoengineering to stratospheric ozone concentrations is projected to decrease in time as concentrations of Br- and Cl-containing atmospheric species are expected fall, so much so that beyond 2050 the additional available surface area provided by sulfate geoengineering is predicted to enhance conversion of NOx (NOx = NO + NO2) to HNO3, resulting in an increase of stratospheric ozone (Visioni et al., 2017). Other candidates for particle types, such as TiO2, have been put forward due to their large refractive indices (Pope et al., 2012), meaning that less stratospheric aerosol loading would be necessary to achieve the same level of cooling. The refractive index of TiO2 at 550 nm is 2.5 compared to a value of 1.5 for naturally occurring sulfate aerosols (Tang et al., 2014). Assuming that the size of TiO2 particles can be optimised, it has been reported that, to achieve the same cooling effect that sulfate aerosols had during the Mt Pinatubo event, significantly less TiO2 than sulfuric acid would be required: approximately 3 times less in mass and 7 times less in volume (Pope et al., 2012). However, the impacts of the presence of TiO2 particles on stratospheric chemistry have to be determined before this kind of geoengineering solution can be considered. Mineral dust particles are commonly found in the troposphere and contribute the largest fraction to tropospheric aerosol loading in terms of mass (Textor et al., 2006; Huneeus et al., 2011). Typically TiO2 (which is classified as a mineral) constitutes from 0.1 to 10 % of overall atmospheric mineral dust loading, depending on the location of sources (Usher et al., 2003; Karagulian et al., 2006).
The heterogeneous chemistry of sulfate aerosols in the stratosphere is fairly well understood (Ammann et al., 2013) – for example the conversion of NOx to nitric acid in the aerosol via N2O5 adsorption and reaction, and also the activation of chlorine via the reaction of ClONO2 with HCl to form Cl2 and nitric acid within cold aerosols. However, the heterogeneous reactivity of mineral particles, in particular TiO2, is not as well understood. Removal and production of trace gases in the stratosphere may significantly perturb concentrations of O3; therefore it is important when assessing the potential impact of such a solar radiation management scheme to evaluate the kinetics of likely heterogeneous chemistry.
The hydroperoxyl radical, HO2, is an important species within the stratosphere, being present at about 5 parts per trillion by volume (pptv) around the tropopause, and is involved in a HOx catalytic cycle responsible for about 40 % of O3 depletion in the lower stratosphere via to the following reactions (Wennberg et al., 1994):
Moreover, HO2 can also react with stratospheric ClO and BrO to produce HOCl and HOBr respectively, which can be photolysed to produce further OH and atomic halogen species that can contribute to O3 loss. HO2 can undergo self-reaction upon surfaces of mineral dust, which is thought to result in the generation of H2O2 (Matthews et al., 2014), whose two predominant removal pathways are photolysis and reaction with OH (Versick et al., 2012):
Although the kinetics of the uptake of HO2 onto Arizona Test Dust (ATD), a proxy of mineral dust, has been previously investigated (Matthews et al., 2014; Bedjanian et al., 2013), the heterogeneous reaction of HO2 with TiO2 has not been studied. However, the kinetics of N2O5 uptake (Tang et al., 2014) and ClONO2 (Tang et al., 2016) onto TiO2 have been studied. The heterogeneous reaction of N2O5 results in the conversion to reactive nitrogen oxides (NO and NO2) involved in a catalytic cycle that leads to significant O3 depletion and non-reactive HNO3. The reactive uptake coefficient, γ, which is the probability that a species will collide with an aerosol and be removed by reaction, was measured to be more than an order of magnitude larger for HO2 onto ATD than for N2O5 and ClONO2 onto TiO2 sub-micron particles, and contrasting dependences of γ with relative humidities (RHs) were observed. Therefore, by analogy it is expected that HO2 uptake onto TiO2 may be faster than N2O5 uptake. ClONO2 uptake by TiO2 particles resulted in similar values of γ; however, no dependency of γ with RH between 7 and 33 % was observed.
In this investigation a borosilicate glass aerosol flow tube coupled with a sensitive HO2 detector based on chemical conversion followed by laser-induced fluorescence detection of OH (George et al., 2013) has been used to study the kinetics of the heterogeneous reaction of HO2 with airborne TiO2 nanoparticles at different RH. While it has been possible here to study such kinetics over a range of RHs representative to those typically found in the lower stratosphere (< 40 %) (Wennberg et al., 1994), experimental limitations meant that experiments were only conducted at room temperature (∼ 293 K). The TOMCAT three-dimensional (3-D) chemical transport model (CTM; Chipperfield, 1999) has also been used to predict the likely impact of HO2 uptake by TiO2 particles on the stratospheric concentrations of HO2 and O3.
2.1 Overview of experimental apparatus
The experimental setup deployed for this investigation is similar to other investigations of HO2 uptake by aerosols undertaken at the University of Leeds (George et al., 2013; Matthews et al., 2014; Lakey et al., 2016); therefore a detailed description of the components of the experiment is not given. A schematic diagram of the experiment is shown in Fig. 1, and all experiments were undertaken at room temperature (293 ± 3 K) and under normal laboratory levels of illumination. For some experiments the flow tube was covered with a black shield to eliminate light, and no differences in the results were observed.
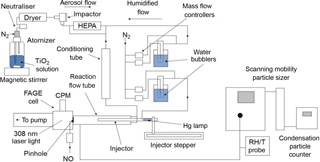
Figure 1Schematic diagram of the aerosol flow tube experiment. CPM: channel photomultiplier; HEPA: high-efficiency particulate air filter; FAGE: fluorescence assay by gas expansion; RH/T: relative humidity/temperature.
Compressed nitrogen – which had been passed through a gas purification system (TSI 3074B) consisting of particle filters, a dryer and a carbon filter – was used as the carrier gas for the experiments. A humidified flow of TiO2 particles was introduced through two inlets located at the rear of the aerosol flow tube, and the flow of HO2 radicals enters the flow tube via the movable injector. The total flow through the flow tube (107 cm length, 5.9 cm ID) was 5.4 L min−1, which resulted in a Reynolds number of 130 and therefore is considered laminar as confirmed by radial concentration gradient measurements of gases exiting the injector (George et al., 2013). Experiments consisted of moving the injector using a linear drive (BSL Engineering 15 KR4610A) to different fixed positions along the flow tube (30–70 cm from injector tip to HO2 detector inlet in steps of 5 cm) corresponding to reaction times between ∼ 8 and 20 s from the injector, with detection of HO2 at the end of the flow tube. All gas flows within the experiment were controlled using mass flow controllers (Brooks and MKS). The RH of the flow was measured using a probe (Rotronics) in the exhaust of the flow tube, which itself was calibrated against a dew point hygrometer (Buck Research Instruments CR-4).
2.2 Aerosol generation and detection
A solution of TiO2 (Aldrich Chemistry 718467, 99.5 % Degussa, i.e. a blend of TiO2 polymorphs 80 % anastase and 20 % rutile, 5 g in 500 mL of Milli-Q water) was placed in a commercial atomiser (TSI 3076) in order to produce a 1 L min−1 flow entrained with TiO2 particles, referred to as the aerosol flow. The aerosol flow was then passed through a neutraliser (Grimm 5522) to reduce static wall losses, a diffusion drier (TSI 3062) and an impactor (TSI 1035900) to ensure that larger aerosols, beyond the detection range of the Scanning Mobility Particle Sizer (SMPS, ∼ 750 nm diameter), do not enter the aerosol flow tube. A high-efficiency particulate air (HEPA, PALL Life Sciences) filter situated within a bypass loop was used to control the number concentration of particles entering the aerosol flow tube. The aerosol flow was then mixed with a humidified flow of nitrogen (3 L min−1) to control the RH within the system. The RH of the humidified flow was altered by changing the ratio of dry nitrogen and nitrogen passed through a water bubbler. This flow was then passed through a conditioning tube (residence time ∼ 6 s) before entering the aerosol flow tube to allow time for water adsorption onto the surface of the TiO2 particles to equilibrate at the given RH.
The total surface area of TiO2 particles available for heterogeneous reaction with HO2 was measured with a SMPS instrument from the flow exiting the aerosol flow tube. Previous experiments showed that there is a negligible loss of aerosols during the transit of the flow tube (George et al., 2013). The SMPS consisted of a differential mobility analyser (DMA, TSI 3080, 3081) that creates a monodisperse flow of aerosols based on their electrical mobility, which is related to their size. A condensation particle counter (CPC, TSI 3775) connected in parallel to the DMA quantified particle number concentrations. These two instruments connected in parallel can be used to create an aerosol size distribution from which the total surface area and average radius of particles can be calculated by making the assumption that particles are spherical (as demonstrated experimentally in Sect. 3.2 below). The average diameter of the particles is 136 and 173 nm at RH = 11 and 37 % respectively.
2.3 HO2 generation and detection
HO2 radicals were produced within the movable injector (110 cm length, 1.9 cm OD, 1.6 cm ID) by passing a 1.3 L min−1 humidified flow of nitrogen (consisting of a mixture of 0.9 L min−1 of dry N2 and 0.4 L min−1 N2 passed through a water bubbler) containing trace amounts of oxygen over a mercury lamp (L.O.T.-Oriel 6035) via the following reactions:
OH is also created by the photolysis of water vapour in Reaction (R5), but no OH was observed exiting the injector, presumably owing to rapid losses at the walls of the injector. HO2 was sampled by a 0.7 mm diameter pinhole at the end of the flow tube, and after chemical conversion to OH by addition of excess NO (50 sccm, BOC, 99.5 %) just inside the pinhole, laser-induced fluorescence (LIF) at low-pressure (the fluorescence assay by gas expansion (FAGE) technique; Heard and Pilling, 2003) was used to measure OH. The relative LIF signal from converted HO2 was calibrated using an established method (Winiberg et al., 2015) developed for field measurements of OH and HO2 radicals. Hence the experiment is able to measure the absolute concentration of HO2 during passage from the injector to the sampling inlet. The Q1(2) line of the OH ( = 0 − X2Πi − = 0) transition at ∼ 308 nm was used to detect OH. A Nd:YAG pumped dye laser (JDSU Q201-HD Q series, Sirah Cobra-Stretch) was used to produce the required 308 nm radiation (line width ∼ 0.1 cm−1) at a pulse repetition rate of 5 kHz. As the flows through the movable injector (1.3 L min−1) and mercury lamp current (20 mA) were kept constant, it is assumed that the initial HO2 concentration – [HO2]0 (defined in this investigation as [HO2] at the first injector position, i.e. 30 cm downstream of the injector), determined by calibration to be 1.6 × 109 molecule cm−3 – was the same for all experiments. These HO2 concentrations are ∼ 50 times higher than typical levels in the sunlit stratosphere (Wennberg et al., 1994). A reference fluorescence cell, in which a large concentration of OH was generated and detected by LIF, was used to facilitate the identification of OH lines and tune the laser wavelength. The FAGE cell was continuously evacuated using a combination of a rotary pump (Edwards, model E1M80) and a roots blower (EH1200), and was kept at 0.8–0.9 Torr, which was monitored using a capacitance monitor (Tylan General, CDC 11).
2.4 Experimental procedure and data analysis
The HO2 signal was measured at eight positions as the moveable injector was drawn back from 30 to 70 cm using the linear stepper drive and again as the moveable injector was pushed forwards back to its initial position. The HO2 signal was averaged over 20 s (average of twenty 1 s measurement points, each corresponding to 5000 laser shots) at each injector position with a 22 s delay between measurements at each injector position in order to allow time for mechanical vibrations to subside, and to ensure a full flush of the aerosol flow tube so that the LIF signal corresponds to HO2 emitted from the injector position being measured. The laser power was recorded for each injector position and used to normalise the HO2 signal to correct for any fluctuations in laser power (< 5 %). The HO2 signals with the injector moving forwards and backwards were then averaged, and this procedure was repeated six times with varying concentrations of aerosols present in the aerosol flow tube. The wall loss rate of HO2 (kwall) was determined by recording the HO2 decay in the absence of aerosols but at the same RH, and it was repeated four times for each experiment.
The HO2 concentration as a function of time along the flow tube can be expressed as
where [HO2]t and [HO2]0 are concentrations of HO2 at time t and t = 0 respectively, and kobs is the observed pseudo-first-order rate coefficient for HO2 uptake. As the HO2 signal is directly proportional to the concentration of HO2, the gradient of a plot of ln(HO2 signal) against time (calculated from the injector position and measured flow rate) yields kobs, as shown in Fig. 2.
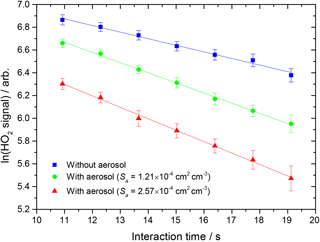
Figure 2Measured HO2 signal at different interaction times, in the presence of TiO2 particles (surface area density: 1.21 × 10−4 and 2.57 × 10−4 cm2 cm−3, green circles and red triangles respectively) and in their absence (blue squares). The RH in the aerosol flow tube was 11 %, the lowest used in this study. The lines represent linear least-squares fits to the data, yielding kobs = 0.079 ± 0.005 and kobs = 0.093 ± 0.003 s−1 (aerosols present, green circles and red triangles respectively) and 0.049 ± 0.003 s−1 (no aerosols, kwall).
The flow tube was coated with halocarbon wax (Halocarbon Products Corporation, Halocarbon Wax Series 600) to reduce HO2 wall loss rate (kwall), and an average of kwall from several determinations in the absence of aerosols was subtracted from kobs. A correction (typically about 30 %) to account for non-plug flow conditions in the aerosol flow tube using the procedure outlined by Brown (1978) was applied to yield k′, the pseudo-first-order loss of HO2 by heterogeneous reaction with TiO2 particles. The relationship between k′ and total surface area of TiO2 particles (Sa) can be expressed as (George et al., 2013)
where is the mean velocity of HO2 (∼ 435 ms−1 at 293 K) and γobs is the observed reactive uptake coefficient, obtained from a plot of k′ versus Sa, an example of which is given in Fig. 3. γobs was in turn corrected (typically ∼ 1 %) to account for the gas diffusion limitation (Fuchs and Sutugin, 1970), to yield γ(HO2).
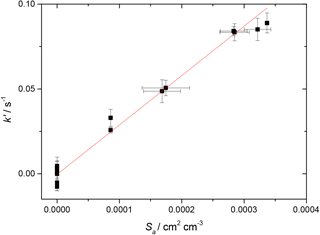
Figure 3First-order rate coefficient for loss of HO2 due to heterogeneous reaction with TiO2 particles at different total surface areas for T = 296 K and RH = 37 %. The gradient yielded a value of γ(HO2) = (2.68 ± 0.01) × 10−2, with the uncertainty representing 2σ random errors from the fit (95 % confidence limits).
2.5 TOMCAT model description
The TOMCAT offline 3-D CTM (Chipperfield, 1999, 2006) has been used to predict the impact of the heterogeneous reaction of TiO2 with HO2 to stratospheric concentrations of O3 and HO2. The model has been widely used in previous studies of stratospheric chemistry and performs well in reproducing stratospheric ozone and the trace species which control its distribution (Chipperfield et al., 2015). The model includes a detailed treatment of stratospheric chemistry of Ox, HOx, NOy, Cly and Bry species along with the main source gases. The model has a comprehensive gas-phase chemistry scheme and includes a number of heterogeneous reactions on stratospheric sulfate aerosols and polar stratospheric clouds (Chipperfield, 1999).
The loss rate of HO2 due to heterogeneous reaction with TiO2 was included in the model as
where Sa is the surface area density of TiO2, and and γ(HO2) are defined above. Three TOMCAT simulations were performed at a horizontal resolution of 5.6∘ × 5.6∘ and 32 levels from the surface to ∼ 60 km. The model was forced with wind and temperature fields from the European Centre for Medium-Range Weather Forecasts (ECMWF) ERA-Interim reanalyses and integrated for 2 years from January 2007 until December 2008, initialised with the output from a standard TOMCAT run which had spun up from 1977. More information on the model experiments is given in Sect. 3.3.
3.1 The reactive uptake coefficient dependence with relative humidity
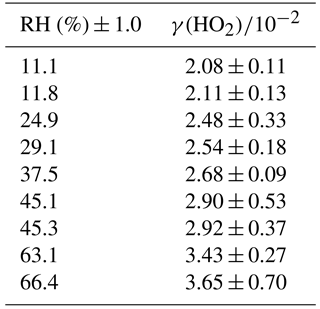
The reactive uptake coefficient for HO2 radicals, γ(HO2), onto TiO2 particles was determined at eight different RHs (11–66%), as shown in Fig. 4 and summarised in Table 1. The number of monolayers of water adsorbed onto the surface of TiO2 particles has been previously determined experimentally by transmission Fourier transform infrared (FTIR) spectroscopy (Goodman et al., 2001) and is also shown as a function of RH in Fig. 4.
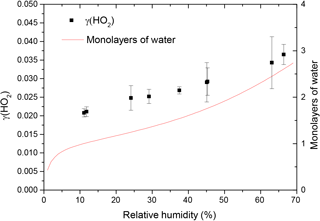
Figure 4Reactive uptake coefficients of HO2, γ(HO2), onto airborne TiO2 particles (black squares, left y axis) at different RH for T = 295 ± 2 K. The number of monolayers of the adsorbed water on TiO2 particles (red curve, right y axis) at 296 K is also plotted as a function of RH, determined using FTIR spectroscopy (Goodman et al., 2001).
The results clearly show a positive dependence of γ(HO2) across the range of RH investigated; as shown in Fig. 5, γ(HO2) correlates well with the number of monolayers of water adsorbed onto the TiO2 particles, V∕Vm, which was determined by Goodman et al. (2001) and parameterised by Eq. (4):
where V is the volume of gas (water vapour) adsorbed at equilibrium pressure P, Vm is volume of gas necessary to cover the surface of the adsorbent TiO2 particles with a complete monolayer, P is the equilibrium pressure of the adsorbing gas, P0 is the saturation vapour pressure of the adsorbing gas at that temperature, c is a temperature-dependent constant related to the enthalpies of adsorption of the first and higher layers, and n is the asymptotic limit of monolayers (∼ 8).
Wall losses of HO2 also increase as RH is increased within the aerosol flow tube; so in the absence of aerosols, the [HO2] for a given distance from the injector will decrease with RH. Previous work in this laboratory has shown that γ(HO2) for uptake on ATD aerosols increases as the [HO2] is lowered (Matthews et al., 2014), and hence some of the positive dependence of γ(HO2) with RH shown in Fig. 4 might be expected simply owing to the [HO2] impinging on the aerosol for a given injector position decreasing with RH. To investigate this further, uptake onto TiO2 at RH = 11 % was measured as a function of [HO2]0 exiting the injector, and γ(HO2) increased from 2.08 × 10−2 to 2.72 × 10−2 as [HO2]0 was decreased from 1.6 × 109 to 8.9 × 108 molecule cm−3. However, the wall loss rate for HO2 only increased from 0.049 to 0.079 s−1 across the entire range of RH (11 to 66 %), resulting in only a small change in [HO2]: decreases of ∼ 2.6 × 108 and ∼ 2.7 × 108 molecule cm−3 at the first and last injector position respectively. In previous studies of HO2 uptake onto ATD (Matthews et al., 2014) it was shown that the increase of γ(HO2) with decreasing [HO2] is linear. Therefore, when assuming the same behaviour for uptake onto TiO2 particles, the expected change in γ(HO2) as a result of RH increasing from 11 to 66 % due only to a change in initial HO2 concentration is only Δγ(HO2) = 0.0023 (or ∼ 6 % of the averaged measured γ(HO2) across this range). Hence the 75 % increase in γ(HO2) observed in Fig. 4 across this range of RH has a different cause.
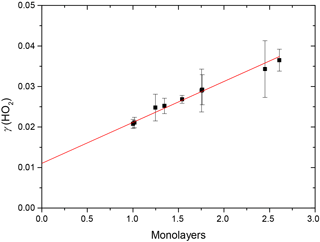
Figure 5Variation of the reactive uptake coefficient, γ(HO2), with the number of monolayers of water surrounding TiO2 particles (as determined by Goodman et al., 2001) for T = 295 ± 2 K. The red line represents a linear least-squares fit to the data (r2 = 0.987).
Figure 5 shows that, for the range of RH studied, γ(HO2) is a linear function of the number of monolayers of water surrounding a TiO2 particle, suggesting that water plays a role in the reactive HO2 uptake process on TiO2 particles. Studies using ambient pressure photoelectron spectroscopy (APPES) (Yamamoto et al., 2008) have shown that water adsorption on rutile, a polymorph of TiO2 (110), occurs in distinct steps, as illustrated in Fig. 6.
First, water molecules dissociate at O vacancies (Vbridge) at bridge sites, producing a stoichiometric amount of adjacent bridging OH groups (OHbridge) equal to twice the initial vacancy concentration upon initial exposure of rutile to water vapour (see Fig. 6):
This step takes place even at very low RH, with these bridging OH groups acting as nucleation sites for subsequent water adsorption by anchoring water molecules to form strongly bound OH–H2O complexes. The OH–H2O complexes continue to act as nucleation centres for further water adsorption. The wetting properties of TiO2 (110) are thus driven by moderate amounts of strongly attractive OH sites that nucleate water molecules. These OH–H2O complexes have a relatively high enthalpy of adsorption for water of −72 kJ mol−1 (Ketteler et al., 2007), whereas additional adsorption of water beyond a monolayer of water coverage is more characterised by enthalpies associated with the bulk enthalpy of water condensation (−45 kJ mol−1) (Chen et al., 2012), explaining the variation of the number of monolayers of water with RH shown in Fig. 4. Computational studies (Aloisio and Francisco, 1998) showed that in the gas phase HO2 can also readily form complexes with water through hydrogen bonding with a binding energy of 28.9 kJ mol−1. The observed correlation of γ(HO2) with the number of monolayers of water surrounding TiO2 particles could be explained by two effects: (1) an increase in the network of hydrogen bonding would increase the stability of a molecular system, ∼ 20.9 kJ mol−1, for each hydrogen bond (Joshi and Ghanty, 2013), or (2) simply more HO2 can adsorb onto the particle surface as the number of available sites for hydrogen bonding increases. An increase in the adsorption lifetime of HO2 owing to the more extended H-bonding network (Joshi and Ghanty, 2013) will result in an increased probability of HO2 reacting with another HO2, increasing the value of γ(HO2):
For up to ∼ 2 monolayers of H2O, an Eley–Rideal (ER) mechanism of a gas-phase HO2 molecule reacting with an adsorbed HO2 is more likely than for two adsorbed HO2 molecules diffusing together to react via a Langmuir–Hinshelwood (LH) mechanism. The coverage of Vbridge across the surface of TiO2 (110) is 0.125 monolayers (i.e. one vacancy for every eight unit cells) (Ketteler et al., 2007), meaning water will initially adsorb onto the surface of the particle in clusters. As the binding energy of the HO2 water complex is fairly high, the rate of HO2 diffusion across the surface after the initial adsorption at a bridging site will be slow, making a LH type mechanism seem unlikely. Above ∼ 2 monolayers, the adsorbed water clusters will begin to interact with each other via an extended H-bonded network more characteristic of bulk liquid water, allowing HO2 to diffuse around the thin surface film of water with thermodynamic properties similar to liquid water (Ketteler et al., 2007).
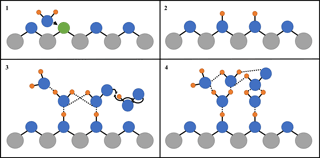
Figure 6Simplified diagram of the important steps of HO2 reactive uptake onto the surface of TiO2. Grey circles: Ti; blue circles: O; orange circles: H; green circles: oxygen vacancy (Vbridge): solid black lines: chemical bond; and dashed lines: hydrogen bond. (1) Diffusion of water molecule towards a bridging O vacancy. (2) Resultant formation of two neighbouring bridging OH groups at the original site of the O vacancy. (3) Bridging OH groups acting as anchoring sites for water and HO2 adsorption via hydrogen bonding, leading to multilayer water adsorption and HO2 self-reaction via an Eley–Rideal type mechanism. (4) The build-up of a more extensive hydrogen bonded network as more water molecules adsorb onto the particle, which stabilises HO2 increasing its desorption lifetime and hence probability that it will react.
The superoxide ion, O, which is the conjugate base of HO2, reacts with HO2 over 100 times quicker than with HO2 via
It is unlikely that O will form readily on the surface of the particle at low coverages of water. O can form on surfaces via direct surface–oxygen electron transfer, photo-induced electron transfer, surface intermolecular electron transfer or decomposition of hydrogen peroxide (H2O2) (Anpo et al., 1999). The dissociation of HO2 to O occurs in bulk liquid (pKa = 4.7; Thornton and Abbatt, 2005); however, water surrounding the particles only begins to acquire liquid-like properties once the coverage of water is greater than ∼ 2 monolayers. If significant formation of O does occur above ∼ 2 monolayers of H2O, then, owing to its much higher reactivity, some deviation from linearity of γ(HO2) versus monolayers of water (Fig. 5) might be expected. However, this was not observed, although the number of data points is very limited.
3.2 Comparison of γ(HO2) with literature values
There are previous studies of HO2 uptake onto ATD (Matthews et al., 2014), a proxy for mineral dust, and both N2O5 (Tang et al., 2014) and ClONO2 (Tang et al., 2016) uptake onto TiO2 particles. Values of γ(HO2) measured for ATD are comparable to those measured onto TiO2 particles at similar concentrations of HO2 in the aerosol flow tube (γ(HO2)ATD ∼ 0.008–0.030). For ATD, γ(HO2) was only determined at four values of RH, but a general increase with RH was observed (although there was a dip around RH = 50 % before a further increase), consistent with HO2 uptake being driven by the number of defects in the crystal lattice of mineral dust surfaces, which provides bridging OH groups upon exposure to water and subsequently by the number of monolayers of water adsorbed onto the surface of such aerosols. The number of monolayers of water on the ATD surface at different RH has been determined (Gustafsson et al., 2005) and also showed a general increase with RH but with a shoulder around RH = 50 %, where the observed γ(HO2) also contained a small dip.
Values of γ(N2O5) (Tang et al., 2014) and γ(ClONO2) (Tang et al., 2016) for uptake onto TiO2 particles were an order of magnitude lower than γ(HO2) and may be associated with the lower polarity of these molecules than that of HO2. It is likely that, as with uptake of HO2, both N2O5 and ClONO2 react with TiO2 via complexing with bridging OH groups and adsorbed H2O; therefore less polar molecules will be less bound to the surface and more likely to desorb back into the gas phase, leading to a smaller γ. The dependence upon RH for γ(N2O5) onto TiO2 is also different to that for HO2 observed here, with a small decrease of γ(N2O5) observed as the RH is increased from ∼ 5 to 23 %, where a minimum is reached; then beyond 23 %, γ(N2O5) increases as RH is increased (Tang et al., 2014). Competition between water and N2O5 for surface active OH groups was suggested for the initial observed decrease in γ(N2O5) with RH, whereas for RH > ∼ 23 % heterogeneous hydrolysis of N2O5 to form HNO3 starts to drive reactive uptake, resulting in an increase of γ(N2O5) (Tang et al., 2014). Measurements of γ(ClONO2) onto TiO2 particles were only made at two values of RH, insufficient to determine any systematic dependence, although Tang et al. (2016) expected γ(ClONO2) to increase as more water adsorbs onto the surface of TiO2 particles.
Measurements of γ(HO2) have been made onto sulfuric acid aerosols and thin films. These values are not consistent and range from > 0.1 to < 0.01 (Cooper and Abbatt, 1996; Thornton and Abbatt, 2005; Hanson et al., 1992; Gershenzon et al., 1995). The most recent measurement of γ(HO2) on aqueous-phase sulfuric acid aerosols was conducted at 35 % RH (Thornton and Abbatt, 2005). That study estimated a value of γ(HO2) = 0.006 ± 0.004, lower than onto TiO2 aerosols. Whilst the aerosols in that study are unlike sulfuric acid aerosols in the stratosphere, formed via condensation of sulfuric acid vapour onto existing solid aerosols, the relatively low value of γ(HO2) measured is consistent with the likely low partitioning of HO2 to its more reactive conjugate base, O, and a lower solubility of HO2 in aerosols with a low pH. The study concludes that heterogeneous uptake of HO2 onto sulfuric acid aerosols would show a strong negative temperature dependence driven by the temperature dependence of the Henry's Law coefficient. It is likely that at temperatures typical of the lower stratosphere (205–215 K) γ(HO2) for uptake onto sulfuric acid particles approach 1 (Gershenzon et al., 1995).
George et al. (2013) previously measured γ(HO2) onto dry salt aerosols. Values of γ(HO2) for NaCl and (NH4)2SO4 at RH values (33–54 %) below their deliquescence point were below the limit of detection (γ(HO2) < 0.004). Values of γ(HO2) for TiO2 reported here (Fig. 4 and Table 1) are more than an order of magnitude greater than that of solid salts, even for RH = 11 %. A possible explanation for the difference in γ(HO2) values could be that, even though the sizes of the aerosols determined by the SMPS are similar, dry salt aerosols are more spherical in shape than TiO2 particles, which may be more fractal in nature. As the SMPS indirectly measures the surface area of aerosols by measuring their mobility through an electric field, an assumption that the aerosol is spherical has to be made. If this is not the case, this may lead to a significant under-prediction of the surface area of non-spherical aerosols and therefore an over-prediction of γ(HO2). In order to measure the geometry of the TiO2 particles, a scanning electron microscope (SEM, FEI Nova NanoSEM 450) operating at 3 kV was used to image the TiO2 nanoparticles used within these experiments. Samples for the SEM were prepared by dispersing the nanoparticles in ethanol and allowing a drop of this solution to dry on a silicon wafer. The wafer with nanoparticles was then mounted on SEM stubs using conductive carbon tapes and coated with 2 nm of Ir, using a Cressington 208HR high-resolution sputter coater. Figure 7 shows an example of an SEM image providing evidence that the TiO2 particles are spherical and therefore that any error associated with SMPS measurements of surface area is minimal. A more likely explanation for the higher γ(HO2) for TiO2 particles is that dry salt aerosols do not adsorb a significant amount of water onto their surface until the deliquescence point is reached, whereas at RH = 11 % Fig. 4 shows that the TiO2 particles already have a monolayer coverage which can form relatively strongly bound complexes with HO2. Measurements of γ(HO2) for uptake onto aqueous salt aerosols show that γ(HO2) significantly increases above the deliquescence point (George et al., 2013) and is comparable to γ(HO2) measured for TiO2 (γ(HO2) ∼ 0.01).
3.3 Implications of HO2 uptake by TiO2 for stratospheric chemistry
The effect of HO2 uptake onto TiO2 particles upon the stratospheric concentrations of HO2 and O3 was assessed using the TOMCAT model (Chipperfield, 1999, 2006). At RH relevant to the lower stratosphere (<40%) the measurements showed that γ(HO2) is in the range 0.020–0.028 at 295 K. An inverse temperature dependence of γ(HO2) onto dry sea-salt aerosols has previously been observed (Remorov et al., 2002); although there have been no systematic experimental studies of the temperature dependence of γ(HO2), parameterisations have developed (Thornton et al., 2008; Macintyre and Evans, 2011). At stratospherically relevant temperatures (T = 200–220 K), γ(HO2) is likely to be considerably larger than observed at 295 K; however it is not possible to cool the aerosol flow tube/SMPS system to verify this experimentally. Therefore γ(HO2) = 1 was used in the model simulations representing an upper limit, with three TOMCAT simulations performed as follows. A control simulation, similar to that presented in Chipperfield et al. (2015), did not include TiO2 particles. A specified latitude–height distribution of TiO2 particles was then included in two simulations with an effective aerosol surface area density equal to that of sulfate aerosols in 1992, the year after the eruption of Mt Pinatubo. This is an assumption which allows for the fact that less TiO2 mass is needed in order to produce the same radiative impact as sulfate aerosol from Mt Pinatubo, but the TiO2 particle size is smaller. Hence these effects largely cancel (Tang et al., 2014). Stratospheric injection via a geoengineering solution will result initially in a different distribution of TiO2 particles compared with after the Mt Pinatubo eruption, but it is assumed that following mixing and transport the distributions would resemble one another and not lead to any significant difference in model behaviour and the conclusions drawn. Support from this assumption comes from a model run in which a globally uniform distribution of TiO2 was assumed initially and which yielded very similar results for the impact of γ(HO2).
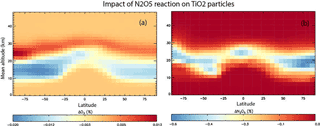
The first of these simulations included only the loss of N2O5 on TiO2 particles with γ(N2O5) = 0.005, the upper limit used in the modelling of Tang et al. (2014), which allows us to compare our results with their study. The second TiO2 simulation also included the loss of HO2 on TiO2 particles with a γ(HO2) = 1, as discussed above. Figure 8 shows the impact of including heterogeneous loss of N2O5 on TiO2 particles in the model.
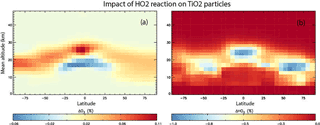
Figure 9Annual mean change (%) in atmospheric O3 (a) and HO2 (b) calculated using the TOMCAT 3-D model from inclusion of heterogeneous loss of HO2 on TiO2 particles for 2008, and using γ(HO2) = 1.
N2O5 is decreased by up to 0.5 % in the region of TiO2 particles, which is assumed to follow the distribution of sulfate particles after the Mt Pinatubo eruption, in order to follow the approach of previous modelling studies. Assuming a globally uniform distribution initially yielded results that were very similar. Inclusion of uptake is only a minor effect and considerably smaller than the impact of around −20 % modelled by Tang et al. (2004) for the same assumed γ(N2O5) = 0.005. The reasons for this are not clear, although it is noted that the effect modelled in our offline chemical transport model, with specified meteorology, is clearly confined to regions of high aerosol loading. The impacts modelled in the nudged chemistry–climate model study of Tang et al. (2004) are not confined to the region of high aerosol and even extend to the upper stratosphere. It is possible that their simulations, although nudged, also include some dynamical feedback which enhances an otherwise small signal. Figure 8 also shows that the resulting impact on O3 is small with changes less than 0.02 %. The model produces a region of slight decrease in the very low stratosphere, with a region of slight increase above.
Figure 9 shows results from the simulation which also included the loss of HO2 on stratospheric TiO2 particles, and using γ(HO2) = 1. It is evident that HO2 loss due to heterogeneous reaction between HO2 and TiO2 particles in 2008 is < 1 % and is confined to the lower stratosphere, where it is assumed TiO2 particles are located. Figure 9 also shows that the subsequent effect of the TiO2 particles on the O3 concentrations through the effects of this reaction is also small (< 0.1 %), with a small decrease in the tropical upper troposphere/lower stratosphere and a small increase at all latitudes in the lower stratosphere. This small effect of TiO2 particles on stratospheric HO2 and O3 concentrations is due to the reactive nature and short lifetime of HO2. The species readily reacts with other gas-phase species (e.g. O3), and so loss on TiO2 surfaces does not compete significantly.
The reactive uptake coefficients for the heterogeneous reaction of HO2 onto TiO2 particles were measured at different RH and at room temperature for the first time using an aerosol flow tube reactor coupled with a sensitive FAGE HO2 detection system. A range of HO2 uptake coefficients on TiO2 particles were measured varying from γ(HO2) = 0.021 ± 0.001 to 0.036 ± 0.007 for RH over the range 11 to 66 % respectively. The HO2 uptake coefficient showed a positive dependence on RH which correlated well with the number of monolayers of water adsorbed onto the TiO2 particle. These results suggest a mechanism by which HO2 adsorbs to the surface of the TiO2 particle by forming complexes with water molecules bound to bridging OH groups. As the number of water layers increases, so does the network of hydrogen bonds that stabilises HO2, leading to a longer adsorption lifetime and increased γ(HO2). The TOMCAT chemical transport model was used to evaluate the possible effects of HO2 uptake (using an upper limit of γ(HO2) = 1) onto the surface of TiO2 particles on the stratospheric concentrations of HO2 and O3. The amount of TiO2 used was chosen to achieve a similar cooling to that following the Mt Pinatubo eruption, but the model predicted a very small loss of both stratospheric HO2 and O3. TiO2 possesses photocatalytic properties, and water adsorbed onto its surface may dissociate under stratospheric illumination, providing a source of radicals (Chen et al., 2012; Romanias et al., 2012). Production of OH and HO2 from irradiated TiO2 surfaces should be evaluated in future studies together with studies of uptake at lower temperature to fully understand the consequences of injection of TiO2 particles into the stratosphere.
Data from the experiments and TOMCAT model simulations can be obtained by contacting Dwayne Heard (d.e.heard@leeds.ac.uk) and Martyn Chipperfield (m.chipperfield@leeds.ac.uk), respectively.
The authors declare that they have no conflict of interest.
We are grateful to the Natural Environment Research Council for funding a
studentship (Daniel R. Moon) and for funding the aerosol flow tube apparatus (grant
number NE/F020651/1). Trevor Ingham, Paul W. Seakins and Dwayne E. Heard are also grateful to the
NERC-funded National Centre for Atmospheric Science for ongoing support. The
TOMCAT modelling work was supported by the EU StratoClim project (FP7 grant
603557). We thank Wuhu Feng (NCAS Leeds) for help with the model. The model
simulations were performed on the University of Leeds and N8 HPC system.
Edited by: Allan Bertram
Reviewed by: two anonymous referees
Aloisio, S. and Francisco, J. S.: Existence of a hydroperoxy and water (HO2 center dot H2O) radical complex, J. Phys. Chem. A, 102, 1899–1902, https://doi.org/10.1021/jp972173p, 1998.
Ammann, M., Cox, R. A., Crowley, J. N., Jenkin, M. E., Mellouki, A., Rossi, M. J., Troe, J., and Wallington, T. J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Volume VI – heterogeneous reactions with liquid substrates, Atmos. Chem. Phys., 13, 8045–8228, https://doi.org/10.5194/acp-13-8045-2013, 2013.
Anpo, M., Che, M., Fubini, B., Garrone, E., Giamello, E., and Paganini, M. C.: Generation of superoxide ions at oxide surfaces, Top. Catalys., 8, 189–198, https://doi.org/10.1023/a:1019117328935, 1999.
Bedjanian, Y., Romanias, M. N., and El Zein, A.: Uptake of HO2 radicals on Arizona Test Dust, Atmos. Chem. Phys., 13, 6461–6471, https://doi.org/10.5194/acp-13-6461-2013, 2013.
Brown, R. L.: Tubular flow reactors with 1st-order kinetics, J. Res. Natl. Bureau Stand., 83, 1–8, 1978.
Chen, H., Nanayakkara, C. E., and Grassian, V. H.: Titanium Dioxide Photocatalysis in Atmospheric Chemistry, Chem. Rev., 112, 5919–5948, https://doi.org/10.1021/cr3002092, 2012.
Chipperfield, M. P.: Multiannual simulations with a three-dimensional chemical transport model, J. Geophys. Res.-Atmos., 104, 1781–1805, https://doi.org/10.1029/98jd02597, 1999.
Chipperfield, M. P.: New version of the TOMCAT/SLIMCAT off-line chemical transport model: Intercomparison of stratospheric tracer experiments, Q. J. Roy. Meteorol. Soc., 132, 1179–1203, https://doi.org/10.1256/qj.05.51, 2006.
Chipperfield, M. P., Dhomse, S. S., Feng, W., McKenzie, R. L., Velders, G. J. M., and Pyle, J. A.: Quantifying the ozone and ultraviolet benefits already achieved by the Montreal Protocol, Nat. Commun., 6, 8, https://doi.org/10.1038/ncomms8233, 2015.
Cooper, P. L. and Abbatt, J. P. D.: Heterogeneous interactions of OH and HO2 radicals with surfaces characteristic of atmospheric particulate matter, J. Phys. Chem., 100, 2249–2254, 1996.
Dutton, E. G. and Christy, J. R.: Solar radiative forcing at selected locations and evidence for global lower tropospheric cooling following the eruptions of El-Chichon and Pinatubo, Geophys. Res. Lett., 19, 2313–2316, https://doi.org/10.1029/92gl02495, 1992.
Fuchs, N. A. and Sutugin, A. G.: Highly dispersed aerosols, Ann Arbor Science, London, 1970.
George, I. J., Matthews, P. S., Whalley, L. K., Brooks, B., Goddard, A., Baeza-Romero, M. T., and Heard, D. E.: Measurements of uptake coefficients for heterogeneous loss of HO2 onto submicron inorganic salt aerosols, Phys. Chem. Chem. Phys., 15, 12829–12845, https://doi.org/10.1039/c3cp51831k, 2013.
Gershenzon, Y. M., Grigorieva, V. M., Ivanov, A. V., and Remorov, R. G.: O3 and OH sensitivity to heterogeneous sinks of HOx and CH3O2 on aerosol particles, Faraday Discuss., 100, 83–100, 1995.
Goodman, A. L., Bernard, E. T., and Grassian, V. H.: Spectroscopic study of nitric acid and water adsorption on oxide particles: Enhanced nitric acid uptake kinetics in the presence of adsorbed water, J. Phys. Chem. A, 105, 6443–6457, https://doi.org/10.1021/jp003722l, 2001.
Gustafsson, R. J., Orlov, A., Badger, C. L., Griffiths, P. T., Cox, R. A., and Lambert, R. M.: A comprehensive evaluation of water uptake on atmospherically relevant mineral surfaces: DRIFT spectroscopy, thermogravimetric analysis and aerosol growth measurements, Atmos. Chem. Phys., 5, 3415–3421, https://doi.org/10.5194/acp-5-3415-2005, 2005.
Hanson, D. R., Burkholder, J. B., Howard, C. J., and Ravishankara, A. R.: Measurement of hydroxyl and hydroperoxy radical uptake coefficients on water and sulfuric acid surfaces, J. Phys. Chem., 96, 4979–4985, https://doi.org/10.1021/j100191a046, 1992.
Heard, D. E. and Pilling, M. J.: Measurement of OH and HO2 in the troposphere, Chem. Rev., 103, 5163–5198, 2003.
Holloway, A. M. and Wayne, R. P.: Atmospheric Chemistry, RSC Publishing, Cambridge, UK, 2010.
Huneeus, N., Schulz, M., Balkanski, Y., Griesfeller, J., Prospero, J., Kinne, S., Bauer, S., Boucher, O., Chin, M., Dentener, F., Diehl, T., Easter, R., Fillmore, D., Ghan, S., Ginoux, P., Grini, A., Horowitz, L., Koch, D., Krol, M. C., Landing, W., Liu, X., Mahowald, N., Miller, R., Morcrette, J. J., Myhre, G., Penner, J., Perlwitz, J., Stier, P., Takemura, T., and Zender, C. S.: Global dust model intercomparison in AeroCom phase I, Atmos. Chem. Phys., 11, 7781–7816, https://doi.org/10.5194/acp-11-7781-2011, 2011.
Joshi, R. and Ghanty, T. K.: Hydrogen bonding interaction between HO2 radical and selected organic acids, RCOOH (R = CH3, H, Cl and F), Chem. Phys. Lett., 584, 43–48, https://doi.org/10.1016/j.cplett.2013.08.025, 2013.
Karagulian, F., Santschi, C., and Rossi, M. J.: The heterogeneous chemical kinetics of N2O5 on CaCO3 and other atmospheric mineral dust surrogates, Atmos. Chem. Phys., 6, 1373–1388, https://doi.org/10.5194/acp-6-1373-2006, 2006.
Ketteler, G., Yamamoto, S., Bluhm, H., Andersson, K., Starr, D. E., Ogletree, D. F., Ogasawara, H., Nilsson, A., and Salmeron, M.: The nature of water nucleation sites on TiO2(110) surfaces revealed by ambient pressure X-ray photoelectron spectroscopy, J. Phys. Chem. C, 111, 8278–8282, https://doi.org/10.1021/jp068606i, 2007.
Lakey, P. S. J., George, I. J., Baeza-Romero, M. T., Whalley, L. K., and Heard, D. E.: Organics Substantially Reduce HO2 Uptake onto Aerosols Containing Transition Metal ions, J. Phys. Chem. A, 120, 1421–1430, https://doi.org/10.1021/acs.jpca.5b06316, 2016.
Macintyre, H. L. and Evans, M. J.: Parameterisation and impact of aerosol uptake of HO2 on a global tropospheric model, Atmos. Chem. Phys., 11, 10965–10974, https://doi.org/10.5194/acp-11-10965-2011, 2011.
Matthews, P. S. J., Baeza-Romero, M. T., Whalley, L. K., and Heard, D. E.: Uptake of HO2 radicals onto Arizona test dust particles using an aerosol flow tube, Atmos. Chem. Phys., 14, 7397–7408, https://doi.org/10.5194/acp-14-7397-2014, 2014.
McCormick, M. P. and Veiga, R. E.: SAGE II measurements of early Pinatubo aerosols, Geophys. Res. Lett., 2, 155–158, 1992.
McCormick, M. P., Thomason, L. W., and Trepte, C. R.: Atmospheric effects of the Mt. Pinatubo eruption, Nature, 373, 399–404, https://doi.org/10.1038/373399a0, 1995.
Pope, F. D., Braesicke, P., Grainger, R. G., Kalberer, M., Watson, I. M., Davidson, P. J., and Cox, R. A.: Stratospheric aerosol particles and solar-radiation management, Nat. Clim. Change, 2, 713–719, https://doi.org/10.1038/nclimate1528, 2012.
Remorov, R. G., Gershenzon, Y. M., Molina, L. T., and Molina, M. J.: Kinetics and mechanism of HO2 uptake on solid NaCl, J. Phys. Chem. A, 106, 4558–4565, https://doi.org/10.1021/jp013179o, 2002.
Romanias, M. N., El Zein, A., and Bedjanian, Y.: Heterogeneous Interaction of H2O2 with TiO2 Surface under Dark and UV Light Irradiation Conditions, J. Phys. Chem. A, 116, 8191–8200, https://doi.org/10.1021/jp305366v, 2012.
Shepherd, J. G. and Working Group on Geoengineering the Climate: Geoengineering the climate: science, governance and uncertainty, RS Policy document 10/09, London, 2009.
Tang, M. J., Telford, P. J., Pope, F. D., Rkiouak, L., Abraham, N. L., Archibald, A. T., Braesicke, P., Pyle, J. A., McGregor, J., Watson, I. M., Cox, R. A., and Kalberer, M.: Heterogeneous reaction of N2O5 with airborne TiO2 particles and its implication for stratospheric particle injection, Atmos. Chem. Phys., 14, 8233–8234, https://doi.org/10.5194/acp-14-8233-2014, 2014.
Tang, M., Keeble, J., Telford, P. J., Pope, F. D., Braesicke, P., Griffiths, P. T., Abraham, N. L., McGregor, J., Watson, I. M., Cox, R. A., Pyle, J. A., and Kalberer, M.: Heterogeneous reaction of ClONO2 with TiO2 and SiO2 aerosol particles: implications for stratospheric particle injection for climate engineering, Atmos. Chem. Phys., 16, 15397–15412, https://doi.org/10.5194/acp-16-15397-2016, 2016.
Textor, C., Schulz, M., Guibert, S., Kinne, S., Balkanski, Y., Bauer, S., Berntsen, T., Berglen, T., Boucher, O., Chin, M., Dentener, F., Diehl, T., Easter, R., Feichter, H., Fillmore, D., Ghan, S., Ginoux, P., Gong, S., Grini, A., Hendricks, J., Horowitz, L., Huang, P., Isaksen, I., Iversen, I., Kloster, S., Koch, D., Kirkevåg, A., Kristjansson, J. E., Krol, M., Lauer, A., Lamarque, J. F., Liu, X., Montanaro, V., Myhre, G., Penner, J., Pitari, G., Reddy, S., Seland, Ø., Stier, P., Takemura, T., and Tie, X.: Analysis and quantification of the diversities of aerosol life cycles within AeroCom, Atmos. Chem. Phys., 6, 1777–1813, https://doi.org/10.5194/acp-6-1777-2006, 2006.
Thornton, J. and Abbatt, J. P. D.: Measurements of HO2 uptake to aqueous aerosol: Mass accommodation coefficients and net reactive loss, J. Geophys. Res.-Atmos., 110, D08309, https://doi.org/10.1029/2004jd005402, 2005.
Thornton, J. A., Jaeglé, L., and McNeill, V. F.: Assessing known pathways for HO2 loss in aqueous atmospheric aerosols: Regional and global impacts on tropospheric oxidants, J. Geophys. Res.-Atmos., 113, D05303, https://doi.org/10.1029/2007jd009236, 2008.
Usher, C. R., Michel, A. E., Stec, D., and Grassian, V. H.: Laboratory studies of ozone uptake on processed mineral dust, Atmos. Environ., 37, 5337–5347, https://doi.org/10.1016/j.atmosenv.2003.09.014, 2003.
Versick, S., Stiller, G. P., von Clarmann, T., Reddmann, T., Glatthor, N., Grabowski, U., Hoepfner, M., Kellmann, S., Kiefer, M., Linden, A., Ruhnke, R., and Fischer, H.: Global stratospheric hydrogen peroxide distribution from MIPAS-Envisat full resolution spectra compared to KASIMA model results, Atmos. Chem. Phys., 12, 4923–4933, https://doi.org/10.5194/acp-12-4923-2012, 2012.
Visioni, D., Pitari, G., and Aquila, V.: Sulfate geoengineering: a review of the factors controlling the needed injection of sulfur dioxide, Atmos. Chem. Phys., 17, 3879–3889, https://doi.org/10.5194/acp-17-3879-2017, 2017.
Wennberg, P. O., Cohen, R. C., Stimpfle, R. M., Koplow, J. P., Anderson, J. G., Salawitch, R. J., Fahey, D. W., Woodbridge, E. L., Keim, E. R., Gao, R. S., Webster, C. R., May, R. D., Toohey, D. W., Avallone, L. M., Proffitt, M. H., Loewenstein, M., Podolske, J. R., Chan, K. R., Wofsy, S. C.: Removal of stratospheric O3 by radicals – in situ measurements of OH, HO2, NO, NO2, ClO, and BrO, Science, 266, 398–404, https://doi.org/10.1126/science.266.5184.398, 1994.
Winiberg, F. A. F., Smith, S. C., Bejan, I., Brumby, C. A., Ingham, T., Malkin, T. L., Orr, S. C., Heard, D. E., and Seakins, P. W.: Pressure-dependent calibration of the OH and HO2 channels of a FAGE HOx instrument using the Highly Instrumented Reactor for Atmospheric Chemistry (HIRAC), Atmos. Meas. Tech., 8, 523–540, https://doi.org/10.5194/amt-8-523-2015, 2015.
Yamamoto, S., Bluhm, H., Andersson, K., Ketteler, G., Ogasawara, H., Salmeron, M., and Nilsson, A.: In situ x-ray photoelectron spectroscopy studies of water on metals and oxides at ambient conditions, J. Phys.-Condes. Matter, 20, 184025, https://doi.org/10.1088/0953-8984/20/18/184025, 2008.