the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Estimating the saturation vapor pressures of isoprene oxidation products C5H12O6 and C5H10O6 using COSMO-RS
Theo Kurtén
Noora Hyttinen
Emma Louise D'Ambro
Joel Thornton
Nønne Lyng Prisle
We have used COSMO-RS (the conductor-like screening model for real solvents), as implemented in the COSMOtherm program, to compute the saturation vapor pressures at 298 K of two photo-oxidation products of isoprene: the dihydroxy dihydroperoxide C5H12O6, and the dihydroperoxy hydroxy aldehyde, C5H10O6. The predicted saturation vapor pressures were significantly higher (by up to a factor of 1000) than recent experimental results, very likely due to the overestimation of the effects of intramolecular hydrogen bonds, which tend to increase saturation vapor pressures by stabilizing molecules in the gas phase relative to the liquid. Modifying the hydrogen bond enthalpy parameter used by COSMOtherm can improve the agreement with experimental results – however the optimal parameter value is likely to be system-specific. Alternatively, vapor pressure predictions can be substantially improved (to within a factor of 5 of the experimental values for the two systems studied here) by selecting only conformers with a minimum number of intramolecular hydrogen bonds. The computed saturation vapor pressures were very sensitive to the details of the conformational sampling approach, with the default scheme implemented in the COSMOconf program proving insufficient for the task, for example by predicting significant differences between enantiomers, which should have identical physical properties. Even after exhaustive conformational sampling, COSMOtherm predicts significant differences in saturation vapor pressures between both structural isomers and diastereomers. For C5H12O6, predicted differences in psat between structural isomers are up to 2 orders of magnitude, and differences between stereoisomers are up to a factor of 20 – though these differences are very likely exaggerated by the overestimation of the effect of intramolecular H-bonds. For C5H10O6, the maximum predicted differences between the three studied structural isomers and their diastereomer pairs are around a factor of 8 and a factor of 2, respectively, when only conformers lacking intramolecular hydrogen bonds are included in the calculations. In future studies of saturation vapor pressures of polyfunctional atmospheric oxidation products using COSMOtherm, we recommend first performing thorough conformational sampling and subsequently selecting conformers with a minimal number of intramolecular H-bonds.
- Article
(1278 KB) -
Supplement
(260 KB) - BibTeX
- EndNote
Atmospheric aerosol particles play a key role in regulating the Earth's climate, and are responsible for most air pollution-related mortality (Pachauri and Meyer, 2014; Brauer et al., 2016). A large fraction of these particles consists of secondary organic aerosol (SOA) material formed by oxidation reactions (Jimenez et al., 2009). Until recently, both the amount and the condensability of SOA were severely underestimated by atmospheric chemistry models, leading to large gaps in the understanding of atmospheric aerosols (Pierce et al., 2011; Zhang et al., 2014). A combination of field studies, laboratory work, and modeling has shown that a large part of the missing SOA may be explained by peroxyradical (RO2) autoxidation reactions, which rapidly convert hydrocarbons into highly oxidized multifunctional compounds (HOM; Ehn et al., 2014; Bianci et al., 2018). Unlike the sequential oxidation reactions which dominate the chemistry of simple “textbook” species with few functional groups, autoxidation only needs a single initial hydrocarbon–oxidant reaction; the subsequent cascade of RO2 hydrogen shift (H-shift) and O2 addition reactions can add up to 10 oxygen atoms to a hydrocarbon backbone without needing any additional low-concentration oxidants such as OH, O3, or NO3 (Ehn et al., 2014).
HOM compounds formed by RO2 H-shifts likely contain multiple hydroperoxide and/or peroxy acid functional groups, in addition to the alcohol, carbonyl, and carboxylic acid groups found in “conventional” atmospheric oxidation products (Bianci et al., 2018). This creates a challenge for evaluating the physical properties determining their atmospheric behavior and impact, such as pure-compound saturation vapor pressures (psat), solubilities (in various atmospherically relevant condensed phases), or activities. Until very recently, there were essentially no data on the volatility of polyfunctional peroxide compounds (defined here as compounds containing more than one hydroperoxide or peroxy acid group and at least one other non-alkyl functional group). Due to this limitation, empirical group contribution methods such as the generally successful Nannoolal (Nannoolal et al., 2008), SIMPOL (Pankow and Asher, 2008), or EVAPORATION (Compernolle et al., 2011) approaches cannot be expected to give reliable predictions for the properties of HOM compounds. In addition to this specific issue related to polyfunctional peroxides, there are also indications that group contribution methods may generally underestimate the volatility of highly functionalized compounds (Valorso et al., 2011; O'Meara et al., 2014). Both these issues may be related to limitations in the ability of these methods to describe intramolecular interactions, especially intramolecular hydrogen bonds. These tend to stabilize molecules in the gas phase relative to the condensed phase, thus leading to higher vapor pressures, as illustrated, for example, by the higher vapor pressure of 1,2-benzenediol (catechol), which can form intramolecular H-bonds, compared to 1,4-benzenediol (hydroquinone), which cannot (Chen et al., 2006). While intramolecular H-bonding is, in principle, described by cross terms in many of the group contribution methods, a lack of data has so far prevented the development of appropriate cross terms to describe for example H-bonds between multiple OOH groups.
Estimation methods based on quantum chemistry, most notably COSMO-RS (conductor-like screening model for real solvents; Eckert and Klamt, 2002), as implemented in the COSMOtherm program (COSMOtherm, 2018), require fewer system-specific empirical parameters and could thus be expected to be more accurate for compound classes for which there are limited measurement data. COSMOtherm has recently been applied to estimate both saturation vapor pressures, Henry's law constants, and partitioning coefficients for atmospherically relevant oxidized organic molecules, including some potential autoxidation products (Wania et al., 2014; Wang et al., 2015, 2017; Kurtén et al., 2016). Compared to group contribution methods, COSMOtherm has generally been found to predict significantly higher saturation vapor pressures and lower gas-aqueous partitioning coefficients (Wang et al., 2017) for polyfunctional oxidized species. In contrast, the disagreement between gas–organic-phase partitioning coefficients is considerably smaller, as the discrepancies in predicted saturation vapor pressures and activity coefficients in water-insoluble organic phases partially cancel each other (Wania et al., 2014). It is unclear whether the difference in predicted saturation vapor pressures is mainly due to an overestimation by COSMOtherm, an underestimation by the group contribution methods, or a combination of both. COSMOtherm is, in principle, able to account for intramolecular hydrogen bonding interactions between any types of functional groups as well as for the related conformational complexity of polyfunctional species. For treating large sets of compounds, the COSMOconf module for conformer sampling (COSMOconf, 2017) is an attractive add-on to COSMOtherm, as it allows for the rapid and automated prediction of properties using, for example, SMILES strings as input. However, due to the general lack of measurement data on low-volatility species (Bilde et al., 2015), neither the accuracy of the absolute psat (or partitioning coefficient) predictions nor the performance of the default approaches for conformational sampling implemented in COSMOconf have been evaluated for polyfunctional peroxide species. In this study we attempt to perform such evaluations, using two recently reported experimental saturation vapor pressure results as benchmarks.
D'Ambro et al. (2017) recently used thermal desorption measurements, combined with an iodide-based high-resolution time-of-flight chemical ionization mass spectrometer (HR-ToF-CIMS) coupled to the Filter Inlet for Gases and Aerosols (FIGAERO; Lopez-Hilfiker et al., 2014) to estimate the saturation vapor pressures of several products of isoprene photo-oxidation. Isoprene, C5H8, is the main hydrocarbon emitted to the air from vegetation, with a global mass flux estimated as 500 TgC yr−1 (Guenther et al., 2012). While the relative SOA yield from isoprene is low compared to larger hydrocarbons such as monoterpenes, the large emissions make isoprene one of the most important SOA precursors on a global scale (Wennberg et al., 2018). Two of the strongest signals detected in the particle phase from isoprene + OH (for both high and low NOx conditions) are C5H12O6 and C5H10O6 (Liu et al., 2016), tentatively identified as a dihydroxy dihydroperoxide (denoted ISOP(OOH)2) and a dihydroperoxy hydroxy aldehyde, with estimated saturation vapor pressures at 298 K of and Pa, respectively (D'Ambro et al., 2017). While technically not a “pure” autoxidation product, as its formation mechanism likely involves two OH oxidation steps (see D'Ambro et al., 2017 and Wennberg et al., 2018 for details), ISOP(OOH)2 shares many features of the proposed autoxidation products of larger alkenes such as monoterpenes; it has an O : C ratio above one, contains two OOH groups and two other functional groups, and potentially forms up to four intramolecular hydrogen bonds. At the same time, ISOP(OOH)2 is small enough that the uncertainty related to its chemical structure is relatively small (i.e., C5H12O6 is highly likely to be a dihydroxy dihydroperoxide, though multiple structural isomers may coexist); also, the computational cost of treating all possible structural isomers and conformers of ISOP(OOH)2 using quantum chemical methods is not prohibitive. To verify that our results are not specific to this particular molecule, we also performed calculations on the dihydroperoxy hydroxy aldehyde C5H10O6.
The saturation vapor pressures of the different ISOP(OOH)2 structural isomers and stereoisomers were estimated using the COSMOtherm program (Version C3.0, release 18), with the BP_TZVPD_FINE_18 parameterization. The input files for COSMOtherm were generated using the COSMOconf program, which uses multiple steps to generate the input files corresponding to a representative set of unique conformers. The program includes various conformer sampling and clustering methods (including elimination of similar structures) and various quantum chemical methods for geometry optimizations and single-point calculations in both the gas and the liquid phases. For the quantum chemical calculations, COSMOconf uses the TURBOMOLE program package (version 7.11; TURBOMOLE, 2018) and the Becke–Perdew (BP) density functional (Perdew, 1986; Becke, 1988), which is one variant of density functional theory (DFT).
We tested four different calculation schemes for generating and selecting the conformers for the final vapor pressure calculations:
-
Systematic. This is where the conformer sampling is done systematically using the Spartan'14 program (Wavefunction Inc., 2014) and the MMFF94 force field, rotating over all dihedral angles in 120∘ increments. Note that no solvent model was included in the Spartan calculations. The full set of conformers from Spartan'14 was then used as input for COSMOconf.
-
Best. This is where the conformer search, using the Balloon program (Vainio and Johnson, 2007; Puranen et al., 2010) implemented in COSMOconf, starts from a geometry that corresponds to the lowest COSMO-RS energy conformer calculated at the BP/def2-TZVPD//BP/def-TZVP level of theory. For this calculation scheme, all conformers were first generated using the systematic conformer sampling algorithm in the Spartan'14 program as described above and were subsequently optimized at the BP/def2-TZVPD//BP/def-TZVP level of theory (including COSMO solvation) using TURBOMOLE 7.11.
-
Worst. This is identical to Best, except with the COSMOconf search started from the highest-energy conformer found in the systematic sampling. The purpose of the Best and Worst schemes is to assess how much the vapor pressures depend on the arbitrary starting geometry provided to COSMOconf.
-
SMILES. This is where only COSMOconf was used to generate conformers, using the default settings of the program and creating the starting geometry from a SMILES string. This corresponds to results that would be obtained by a “casual” user or in automated runs of large numbers of compounds.
The detailed settings for each conformational sampling scheme are shown in Table S1 of the Supplement, together with additional computational details. The gas-phase calculations were performed similarly in all four conformational sampling schemes; gas-phase geometry optimizations were performed at the BP/def-TZVP level of theory and single-point calculations at the BP/TZVPD level of theory. In addition, COSMOconf maps the gas-phase conformers to the COSMO conformers to ensure that each COSMO conformer has a single corresponding gas-phase conformer. In the mapping, each gas-phase conformer is assigned to the geometrically closest COSMO conformer. If more than one gas-phase conformer corresponds to the same COSMO conformer, the gas-phase conformer with the lowest energy is chosen. Single-point gas-phase energies on the COSMO geometries are used for the COSMO conformers left without a corresponding gas-phase conformer after the mapping. The vapor pressure calculations were finally performed using 10 conformers in the SMILES scheme and 100 conformers in the other schemes. The choice of 100 conformers was governed by a compromise; on one hand the number is large enough that the saturation vapor pressure results are more or less “converged” (at least to within a few tens of percent, see Sect. 3.1.2 for a test case) with respect to the number of conformers, and on the other hand the number is small enough that the COSMOtherm calculations can be done within hours rather than days. (Also, COSMOtherm may sometimes run out of memory if the number of conformers is much larger than 100.) We note that for many applications, a much smaller number of conformers may be sufficient, provided that the initial conformational sampling is thorough.
3.1 Vapor pressure of C5H12O6
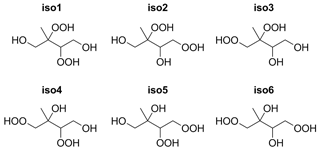
As illustrated in Fig. 1, there are, in principle, six different structural isomers of the dihydroxy dihydroperoxide C5H12O6 (assuming that the carbon backbone is identical to that of the parent isoprene). Each structural isomer has two chiral centers (carbon atoms with four non-equivalent substituents), giving rise to two pairs of enantiomeric structures. Based on the known mechanism of isoprene photo-oxidation, isomer 1 is likely to be the dominant form found in the atmosphere, with possible minor contributions from isomers 2, 3, and 4. In the recent review by Wennberg et al. (2018), the OH addition channels leading to isomer 1 (from the two main structural isomers of isoprene hydroxy hydroperoxide, ISOPOOH, after several reaction steps) are estimated to have yields of 95 %, compared to only 5 % for the channels leading to other isomers. However, it should be noted that the products of the minor addition channels may have larger yields for the reactions actually forming the dihydroxy hydroperoxides, which are themselves only relatively minor products of the overall isoprene photo-oxidation process. The precise distribution of the different atmospherically relevant isomers is impossible to accurately estimate at the moment, as many of the key branching ratios are highly uncertain.
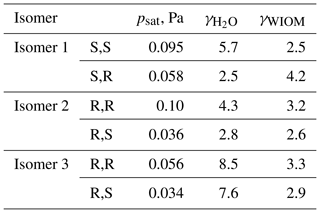
Table 1Saturation vapor pressures, in Pa, at 298.15 K, of different structural and stereoisomers of the dihydroxy dihydroperoxide C5H12O6, calculated using COSMOtherm version 18 and the BP_TZVPD_FINE_18 parameterization (based on BP/def2-TZVPD//BP/def-TZVP quantum chemical data). The experimental value (for an unknown mixture of isomers) is Pa.

The computed vapor pressures for different structural isomers and stereoisomers of C5H12O6 are shown in Table 1. For the first three structural isomers (isomers 1, 2, and 3), all four stereoisomers were studied. This provides an additional test for the configurational sampling methods, as the physical pure-compound properties of enantiomeric pairs (i.e., SS and RR or SR and RS stereoisomers) should be identical. For the three remaining isomers (4, 5, and 6), only one of each enantiomeric pair was included for computational reasons.
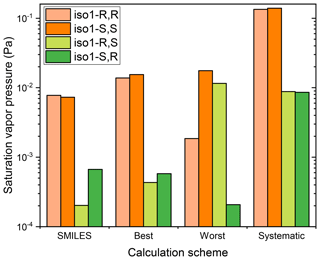
Figure 2Saturation vapor pressures, at 298.15 K, of different stereoisomers of structural isomer 1 of the dihydroxy dihydroperoxide C5H12O6, at 298.15 K, calculated using COSMOtherm version 18 and the BP_TZVPD_FINE_18 parameterization (based on BP/def2-TZVPD//BP/def-TZVP quantum chemical data), using different conformational sampling schemes.
Three main conclusions can be drawn from the data in Table 1. First, only the Systematic conformational sampling scheme results in enantiomers (mirror image pairs, i.e., RR/SS and RS/SR stereoisomers) having identical (or almost identical) saturation vapor pressures. This is illustrated in Fig. 2 for the case of isomer 1 (see Fig. S1–S3 in the Supplement for figures illustrating psat for the other isomers). The other conformational sampling schemes are thus incomplete, as they lead to physically inconsistent results. The SMILES scheme, which corresponds to using the default conformational sampling settings in the COSMOconf program, leads to especially inconsistent results, with differences of up to 2 orders of magnitude compared to the Systematic conformational sampling. The difference between Best and Worst schemes can also be up to 2 orders of magnitude, illustrating a worrying dependence of the COSMOconf results on the arbitrary input structure, even when a conformational sampling approach much more thorough than the default setting is used.
Second, the computed saturation vapor pressures are significantly higher than the measurement results. The values computed using the physically consistent Systematic scheme for the atmospherically relevant isomers (1, 2, 3, and 4) are between 25 and 1550 times higher than the experimental value. This discrepancy is larger than that reported recently for polyethylene glycol (PEG) vapor pressures (Krieger et al., 2018), where COSMOtherm was found to systematically overestimate the saturation vapor pressures of the first five PEG oligomers by a factor of 3–40. The larger disagreement may be related to the fact that the smallest PEG oligomers typically form one and the larger oligomers two intramolecular H-bonds, while ISOP(OOH)2 can form four. In many cases, the incomplete and inconsistent conformational sampling schemes (SMILES, Best, or Worst) actually lead to values closer to the experimental one – this is due to these schemes missing many of the lowest-energy conformers, which typically contain close to the maximum number (in this case, four) of intramolecular hydrogen bonds. Conformers with a smaller number of internal H-bonds typically lead to lower vapor pressures (as discussed in detail below) – supporting the hypothesis that the general overestimation of psat is due to an overestimation of the effects of internal H-bonds.
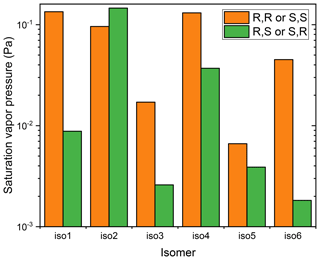
Figure 3Saturation vapor pressures, at 298.15 K, of different isomers of the dihydroxy dihydroperoxide C5H12O6, at 298.15 K, calculated using COSMOtherm version 18 and the BP_TZVPD_FINE_18 parameterization (based on BP/def2-TZVPD//BP/def-TZVP quantum chemical data), with the Systematic conformational sampling scheme.

Figure 4Lowest-energy conformers (at the BP/def2-TZVPD//BP/def-TZVP level, with COSMO solvation, using the Systematic configurational sampling scheme) of the S,S (a) and S,R (b) stereoisomers of structural isomer 1 of ISOP(OOH)2. The S,R stereoisomer only has two intramolecular H-bonds in the lowest-energy conformer, while the S,S isomer has three. Correspondingly, the saturation vapor pressure of the S,R stereoisomer is predicted to be lower by a factor of 15. Color coding: gray is C, red is O, and white is H.
Third, COSMOtherm predicts surprisingly large differences in vapor pressures, both between structural isomers and between different diastereomers (non-enantiomeric stereoisomers) of the same structural isomer, as illustrated in Fig. 3. The differences between diastereomers can be up to a factor of 20, even when using the Systematic conformer sampling scheme. For the structural isomers, a general trend can be discerned; isomers with OOH groups adjacent to each other (isomers 1, 3, and 5) tend to have lower vapor pressures than isomers with OOH groups further from each other (isomers 2, 4, and 6). This is likely caused by somewhat less-efficient intramolecular H-bonding in the former set of isomers, due to steric strain. The differences between diastereomers is similarly very likely related to subtle differences in H-bonding patterns. For example, the lowest-energy conformers of different diastereomers typically look quite different – see Fig. 4 for an example where the lowest-energy conformers of two diastereomers have different numbers of intramolecular H-bonds. Since COSMOtherm seems to overestimate the effect of intramolecular H-bonding, it is also likely that the differences between structural isomers and diastereomers are exaggerated. However, even if the true differences between diastereomers and/or structural isomers are significantly smaller than predicted by COSMOtherm, they may still be large enough to matter for atmospheric applications. Even differences on the order of some tens of percent between saturation vapor pressures of diastereomers would lead to different behavior with respect to condensation. Since different sources (including both different biogeochemical primary sources and different source reactions occurring in the atmosphere) can produce different distributions of stereoisomers, this could lead to seemingly inexplicable differences in behavior between “identical” chemical species. However, it should be noted that the thermal desorption profiles of these compounds (D'Ambro et al., 2017) appear Gaussian-like, or in other words, do not display bi- or multimodal desorption peaks which would indicate volatility differences between isomers of ISOP(OOH)2. We therefore conclude that either the isoprene photo-oxidation leads to only one specific (stereo)isomer of ISOP(OOH)2, or, more likely, that the differences in volatilities between the formed (stereo)isomers are too small to be measurable with the FIGAERO instrument (i.e., less than an order of magnitude).
3.1.1 Activity coefficients in water and water-insoluble organic matter
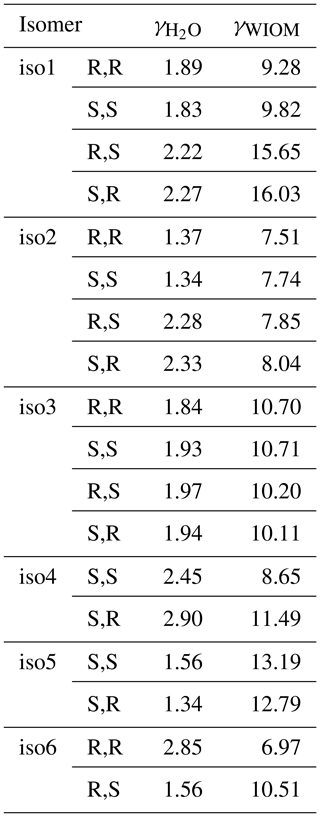
One potential reason for the difference between predicted and measured saturation vapor pressures is that the saturation vapor pressures reported by D'Ambro et al. (2017) are obtained by thermal desorption from aerosol particles containing a mixture of many different isoprene oxidation products, adsorbed on top of a solid ammonium sulfate core. If the activity coefficient of ISOP(OOH)2 in this mixture strongly deviates from unity, then the measured vapor pressure value (in effect, the equilibrium vapor pressure of ISOP(OOH)2 over the mixture; see, e.g., Bilde et al., 2015, for a detailed discussion) could be very different from the pure-compound psat. To test whether this could be the case, we computed the activity coefficients at infinite dilution of the different ISOP(OOH)2 isomers in an organic phase consisting of molecule “B”, proposed by Kalberer et al. (2004), as a good model for representing atmospheric water-insoluble organic matter (WIOM). We note that the actual organic phase used in the experiments is likely to be more polar than this model WIOM phase. We also compute activity coefficients in water for comparison, although these are unlikely to be relevant to the experiments by D'Ambro et al. due to the use of solid ammonium sulfate seed and moderate humidity (RH = 50 %). The calculations were done for the 100 best conformers, as selected by the Systematic scheme described above. The results are given in Table 2. The activity coefficients of the different ISOP(OOH)2 isomers vary between 1.37 and 2.90 in pure water and between 6.97 and 16.03 in the model WIOM phase. This suggests that the measured effective psat might possibly be up to 1 order of magnitude higher than the true pure-compound psat, but is very unlikely to be lower than the true value. Differences between the measured values and true pure-compound saturation vapor pressures cannot thus explain the discrepancy between COSMOtherm results and measurements.
Table 2Activities of ISOP(OOH)2 species computed in water and in a water-insoluble organic-phase model (WIOM) compound “Kalberer molecule B” (Kalberer et al., 2004), at infinite dilution and at 298.15 K, calculated using COSMOtherm version 18 and the BP_TZVPD_FINE_18 parameterization (based on BP/def2-TZVPD//BP/def-TZVP quantum chemical data).
3.1.2 Sensitivity of psat to H-bonding parameters
We next tested the effect of various adjustments to the treatment of H-bonds on the predicted psat values. First, we examined switching off intermolecular H-bonding entirely in the COSMO-RS treatment using the “nohb” setting. (Note that intramolecular H-bonds cannot be similarly switched off, as they are implicitly included in the quantum chemical energy calculations.) This resulted in a dramatic increase of the predicted saturation vapor pressures (by between a factor of 10 and 180 for all studied isomers, using the 100 best conformers selected by the Systematic scheme described above). This is reasonable, as H-bonds are the strongest intermolecular interactions between ISOP(OOH)2 molecules; ignoring them thus leads to significantly weaker intermolecular binding and higher saturation vapor pressures. While the effect of intramolecular H-bonds cannot be similarly switched off, the quantum chemical treatment of H-bonding can, in principle, be slightly improved by recomputing the gas-phase energies at a higher level of theory and using these higher-level energies in the Boltzmann weighting of conformers. We tested this approach by recomputing the electronic energies (at the BP/def-TZVP geometries) for the gas-phase conformers corresponding to the ten lowest-energy COSMO conformers of the R,S enantiomer of isomer 1 at the CCSD(T)-F12a/VDZ-F12 level (Adler et al., 2007; Werner et al., 2011) using the Molpro 2015.1 program (Werner et al., 2012, 2015). Of these 10 gas-phase conformers, nine contained (based on visual inspection) four intramolecular H-bonds, and one contained three H-bonds. The relative electronic energy of the conformer with only three H-bonds (compared to the lowest-energy conformer) was +10.5 kJ−1 at the BP/def2-TZVPD//BP/def-TZVP level but only +5.0 kJ−1 at the CCSD(T)-F12a/VDZ-F12//BP/def-TZVP level – suggesting that the BP method overestimates the favorability of intramolecular H-bonds. The vapor pressure computed for the set of 10 conformers accordingly decreased by a factor of 2 when the higher-level energies were used for weighting the gas-phase conformers. While this change is in the right direction, it is insufficient to reconcile predicted psat values with experiments, likely because the overestimation of intramolecular H-bonds is still present in the DFT-generated input files, despite the improved gas-phase conformer weighting. In principle, the problem might be resolved by generating all input files at a higher level of theory (for example, some variant of coupled cluster theory), but this would require an entirely new parameterization for COSMO-RS and would also result in significantly higher computational costs as well as much steeper scaling of the cost with respect to system size.
The newest release of COSMOtherm (version 18) provides some additional tools for adjusting the treatment of (intermolecular) H-bonds. Specifically, both enthalpic and entropic H-bonding parameters, as well as their temperature sensitivities, can be scaled. In principle this corresponds to four different parameters (labeled c0, c1, s0, and s1), but one of them (s1) is set to zero, leading, in practice, to three adjustable parameters. Test calculations (see Fig. S4 in the Supplement file) indicate that for the ISOP(OOH)2 saturation vapor pressures at 298 K, varying the c0 and s0 parameters had relatively small effects, while varying the c1 parameter (corresponding to the H-bonding enthalpy) had a large effect. We therefore tested the effect of varying c1 between arbitrarily chosen limits of 0.6 and 1.8 for all ISOP(OOH)2 isomers, using the 100 conformers from the Systematic sampling scheme (see Fig. S5 in the Supplement information file for results). In order to match the experimental value of about Pa solely by scaling the c1 parameter, scaling factors of 1.61 and 1.36 would be needed for the SS and RR and SR and RS enantiomer pairs of structural isomer 1, respectively.
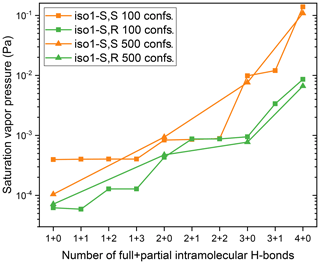
Figure 5Saturation vapor pressures, at 298.15 K, of the S,S and S,R stereoisomers of structural isomer 1 of the dihydroxy dihydroperoxide C5H12O6, calculated using COSMOtherm version 18 and the BP_TZVPD_FINE_18 parameterization (based on BP/def2-TZVPD//BP/def-TZVP quantum chemical data), including only conformers with less than n+m full and partial H-bonds (e.g., where “1+3” indicates one full and three partial H-bonds) and using either 100 or 500 conformers in the original conformer pool. For the calculations with 100 overall conformers, all gas-phase geometries were visually inspected, and the optimized gas-phase energy was replaced with a single-point gas-phase energy at the COSMO geometry whenever the optimized gas-phase structure had a different number of H-bonds than the COSMO structure. For the calculations with 500 overall conformers, the 100 lowest-energy gas-phase structures in each H-bond-restricted conformer subset were similarly inspected. In addition, duplicate gas-phase conformers within 10 kJ mol−1 of the lowest-energy optimized gas-phase structure were replaced with single-point gas-phase energies at the COSMO geometries. See Sect. S5 in the Supplement file for further details and discussion on gas-phase conformer selection.
Finally, we tested the effect on saturation vapor pressures of selecting only conformers with less than a certain number of full or partial intramolecular H-bonds, as identified by the COSMOtherm program (see the Supplement file for details). In order to ensure a sufficient number of conformers also for calculations using the more stringent selection criteria (e.g., choosing only conformers with one H-bond), we first performed a new conformational sampling for the S,S and S,R stereoisomers of structural isomer 1, using the Systematic approach but keeping 500 rather than 100 conformers in the overall conformer set. Next, saturation vapor pressures were computed for the two stereoisomers, but picking only conformers with less than n+m intramolecular H-bonds, where n refers to full bonds and is varied from 1 to 4, and m refers to partial bonds and is varied from 0 to 3, such that . (There were no conformers with zero full H-bonds for ISOP(OOH)2.) The results are shown in Fig. 5. Data are shown both for the original set of 100 conformers in total and for the larger set of 500 conformers. Since the data for 100 conformers indicate that the effect of partial bonds is minimal, only the full H-bonds were studied for the 500-conformer case. Note that additional care is required in picking the correct gas-phase conformers for these calculations. While the COSMOconf program maps gas-phase conformers to COSMO conformers, it subsequently reorders both sets by energy. Information on the original mapping is not contained in either set of files, though it can be found from the COSMOconf output. See Sect. S5 of the Supplement file for different options for picking gas-phase conformers based on a selected subset of COSMO conformers.
We can see from Fig. 5 that using 500 rather than 100 conformers results in a slight decrease in psat, even before the number of H-bonds are restricted: from 0.139 to 0.109 Pa for the S,S stereoisomer and from to Pa for the S,R stereoisomer. Restricting the number of full H-bonds has a dramatic effect on the saturation vapor pressure, especially for the S,S stereoisomer, which had a much higher vapor pressure than the S,R isomer when all conformers were included. Each reduction in the number of full H-bonds (n) causes a significant (between a factor of 1.6 and 14) decrease in saturation vapor pressures for both stereoisomers. The number of partial H-bonds has only a minor effect on the saturation vapor pressure. For the smallest value of n=1, the importance of sampling a sufficient number of conformers becomes evident, as the values corresponding to the sets containing 500 and 100 conformers diverge significantly for the S,S stereoisomer. The reason for this is that in the latter case, the n=1 restriction leads to only < 10 conformers being included in the psat calculations.
The psat values obtained with and Pa for the S,S and S,R stereoisomers, respectively, using the overall set of 500 conformers) are both much closer to each other and are much more close to the experimental value (around 10−4 Pa) than the psat values obtained using the full set of conformers. This confirms our hypothesis that the overestimation of vapor pressures by COSMOtherm, as well as the exaggerated differences between isomers, is very likely caused by an overestimation of the effects of intramolecular H-bonding. The fact that the values obtained with the n=1 setting match the experimental result so well (to within 30 %) may be fortuitous but could also indicate that including a single intramolecular H-bond (out of the maximum of four) accurately represents the real effect of intramolecular H-bonding for ISOP(OOH)2.
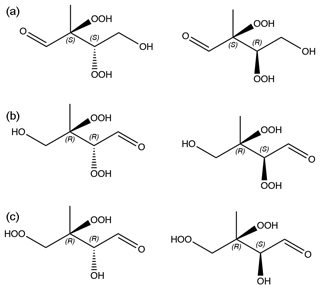
Figure 6C5H10O6 isomers and stereoisomers used in the calculations. (a) isomer 1. (b) isomer 2. (c) isomer 3. The chirality of stereocenters are indicated with S and R letters.
3.2 Vapor pressure of C5H10O6
We computed saturation vapor pressures for the three structural isomers of C5H10O6 that are likely to be atmospherically important (see Fig. 6). For each structural isomer, one of each enantiomeric pair was selected (as shown in Fig. 6). The Systematic conformer sampling scheme was used for the calculations, but with the last two cut-offs of 150 and 100 conformers (see Table S1 in the Supplement) replaced by 600 and 500, respectively. The best 100 conformers were then used in the psat calculation. Activities in water and a WIOM phase represented by molecule “B” from Kalberer et al. (2004) were also computed. The results are given in Table 3. Analogous to C5H12O6, the predicted saturation vapor pressures are around 50–150 times larger than the experimental value of Pa. The upper limit of this range is lower than for C5H12O6, possibly due to C5H10O6 having one less H-bond donor and thus one less intramolecular H-bond. The overestimation is consistent with an error of roughly a factor of 5 per intramolecular H-bond (as 53=125). The smaller number of H-bonds may also be the reason for the smaller differences between structural isomers and diastereomers (which are all less than a factor of 3), as well as the higher activity coefficients in water and lower activity coefficients in the WIOM phase, compared to C5H12O6. Another reason for the smaller differences may be that all three studied isomers have OOH groups on adjacent C atoms, possibly leading to somewhat weaker intramolecular H-bonding (and thus lower psat) due to steric strain, as discussed in Sect. 3.1.
Table 4Saturation vapor pressures, at 298.15 K, of C5H10O6 structural and stereoisomers, computed using COSMOtherm and the BP_TZVPD_FINE_18 parameterization (based on BP/def2-TZVPD//BP/def-TZVP quantum chemical data) with the Systematic conformer sampling scheme and with either modified values of the H-bonding enthalpy parameter c1 or using only conformers with a restricted number of full intramolecular H-bonds.
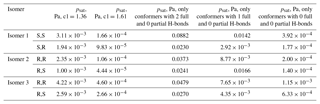
We also tested the effect of setting the H-bonding enthalpy parameter c1 to either 1.61 or 1.36 (the values needed to match experiments for the two diastereomers of isomer 1 of C5H12O6), as well as of restricting the number of intramolecular H-bonds to two, one, or zero full bonds. The effect of partial H-bonds was tested and found to be negligible, similar to C5H12O6. The results of these calculations are shown in Table 4. As expected, higher values of the c1 parameter lead to lower psat values, but neither of the scaling factors obtained for C5H12O6 leads to particularly good agreement with experiments for C5H10O6. With c1 set to 1.61, the predicted saturation vapor pressures are significantly smaller than the experimental value. This demonstrates the system-specific nature of the “optimal” scaling parameters and indicates that modifying H-bonding parameters in COSMOtherm is likely not a reliable approach for estimating properties of autoxidation products. As for C5H12O6, each decrease in the number of full H-bonds leads to a significant decrease in the saturation vapor pressure for all (stereo)isomers. When the number of H-bonds was restricted to zero, all of the predicted saturation vapor pressures were within a factor of 5 of the experimental value, and in all except one case they were below it. This indicates that completely removing intramolecular H-bonds may result in a slight underestimation in the vapor pressure of C5H10O6 – consistent with the observation that retaining one H-bond leads to an essentially perfect match (given the other error sources in both modeled and measured data) for C5H12O6. However, for C5H10O6, the vapor pressures predicted for conformers restricted to one intramolecular H-bond were between 4 and 25 times larger than the experimental value; the “true” effect of intramolecular H-bonding (as modeled by COSMOtherm) thus seems to be somewhere between the n=1 and n=0 cases modeled. While restricting the number of H-bonds to zero somewhat surprisingly increases the maximum difference between structural isomers from a factor of 3 to a factor of 8, it slightly decreases the maximum difference between diastereomers (from a factor of 2.8 to a factor of 2.2).
Our results confirm previous suggestions that COSMOtherm tends to overestimate the saturation vapor pressures of atmospheric oxidation products capable of forming multiple intramolecular H-bonds (Kurtén et al., 2016; Krieger et al., 2018). Based on the limited number of direct comparisons between predicted and experimental data, and further assuming that the effect is roughly proportional to the maximum number of intramolecular H-bonds, the overestimation seems to be on the order of a factor of 5 per H-bond. If applied to the data in Kurtén et al. (2016) on monoterpene autoxidation products, this would imply that the originally suggested approach of taking the geometric average of SIMPOL and COSMOtherm saturation vapor pressure predictions remains a reasonably good choice in the absence of other information. While COSMOtherm saturation vapor pressure predictions can be modified to agree better with experiments by scaling the hydrogen bond enthalpy parameter c1, the optimal value for this parameter is likely to depend on the system, and this approach can thus not generally be recommended. In contrast, computing saturation vapor pressures using only conformers with a limited number of hydrogen bonds (e.g., the smallest number possible for a given system) is likely to lead to more systematic improvements and can be recommended as a temporary solution until more accurate COSMO-RS H-bonding parameterizations become available.
For users of COSMOtherm and/or COSMOconf, our results suggest that extra caution is warranted when carrying out configurational sampling of flexible molecules, especially of compounds with multiple peroxy groups capable of strong intramolecular H-bonding and possessing a large number of low-energy conformers. While the default sampling approaches may sometimes lead to better agreement with experimental results (e.g., due to missing low-energy conformers with maximal numbers of intramolecular H-bonds), they also introduce a large potential error source, as the results are heavily dependent on the arbitrary input structure used to initiate the sampling. When computational resources permit, we therefore recommend performing Systematic configurational sampling (for example, using the approach described in Sect. 2), and correcting the results where necessary, for example, by selecting only conformers with a limited number of H-bonds from a sufficiently large overall set of conformers. We note that special care is required to ensure that the COSMO and gas-phase conformers in such calculations correspond to the same structures.
Finally, our results demonstrate that diastereomers of polyfunctional atmospheric oxidation products may have different intramolecular H-bonding patterns and thus potentially different saturation vapor pressures, solubilities, and activity coefficients. While the real differences are very likely smaller than those predicted by COSMOtherm (at least in the absence of corrections for the overestimation of H-bonds), they may still be large enough to matter in the atmosphere. Stereoisomerism should thus be kept in mind as a possible explanation in cases where nominally identical chemical compounds are observed to display different behavior, for example, with respect to condensation and aerosol formation.
The research data has been deposited in a reliable public data repository (the CERN Zenodo service) and can be accessed at: https://doi.org/10.5281/zenodo.1344890 (Kurtén et al., 2018).
Additional technical details on sampling and selection of conformers and figures illustrating vapor pressures for isomers 2–6 of C5H12O6 are available as a PDF file. COSMOtherm input files (.cosmo and .energy files) for all studied systems are provided in a zip file archived at: https://doi.org/10.5281/zenodo.1344890. The supplement related to this article is available online at: https://doi.org/10.5194/acp-18-17589-2018-supplement.
TK planned and supervised the study, with support from JT and NLP. NH, ELD, and TK performed the calculations, with support from NLP. TK wrote the paper with contributions from all co-authors.
The authors declare that they have no conflict of interest.
Theo Kurtén, Noora Hyttinen, and Emma Louise D'Ambro thank the Academy of Finland for funding. Emma Louise D'Ambro was supported
by the National Science Foundation Graduate Research Fellowship under grant
no. DGE-1256082. Nønne Lyng Prisle thanks the European Research Council under the European
Union's Horizon 2020 research and innovation programme (Project SURFACE,
grant agreement no. 717022) and the Academy of Finland (grant 308238) for
funding. We thank the CSC – IT Center for Science, Finland, for
computational resources and Frank Eckert from COSMOLogic GmbH for
technical support and helpful discussions. We thank Ben H. Lee and Felipe Lopez-Hilfiker
(UW) and John Shilling and Jiumeng Liu (PNNL) for their
contributions to the observations.
Edited by: Andreas Hofzumahaus
Reviewed by: two anonymous referees
Adler, T. B., Knizia, G., and Werner, H. J.: A simple and efficient CCSD(T)-F12 approximation, J. Chem. Phys., 127, 221106, https://doi.org/10.1063/1.2817618, 2007.
Becke, A. D.: Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A, 38, 3098–3100, 1988.
Bianchi, F., Kurtén, T., Riva, M., Mohr, C.,, Rissanen, M., Roldin, P.; Berndt, T., Crounse, J., Wennberg, P., Mentel, T., Wildt, J., Junninen, H., Jokinen, T., Kulmala, M., Worsnop, D., Thornton, J., Donahue, N. M., Kjaergaard, H. G., and Ehn, M.: Highly oxygenated molecules (HOM) from gas-phase autoxidation of organic peroxy radicals: A key contributor to atmospheric aerosol. Chem. Rev., in review, 2018.
Bilde, M., Barsanti, K., Booth, M., Cappa, C. D., Donahue, N. M., Emanuelsson, E. U., McFiggans, G., Krieger, U. K., Marcolli, C., Topping, D., Ziemann, P., Barley, M., Clegg, S., Dennis-Smither, B., Hallquist, M., Hallquist, Å. M., Khlystov, A., Kulmala, M., Mogensen, D., Percival, C. J., Pope, F., Reid, J. P., Ribeiro da Silva, M. A. V., Rosenörn, T., Salo, K., Soonsin, V. P., Yli-Juuti, T., Prisle, N. L., Pagels, J., Rarey, J., Zardini, A. A., and Riipinen, I.: Saturation Vapor Pressures and Transition Enthalpies of Low-Volatility Organic Molecules of Atmospheric Relevance: From Dicarboxylic Acids to Complex Mixtures, Chem. Rev., 115, 4115–4156, https://doi.org/10.1021/cr5005502, 2015.
Brauer, M., Freedman, G., Frostad, J., van Donkelaar, A., Martin, R. V., Dentener, F., van Dingenen, R., Estep, K., Amini, H., Apte, J. S., Balakrishnan, K., Barregard, L., Broday, D., Feigin, V., Ghosh, S., Hopke, P. K., Knibbs, L. D., Kokubo, Y., Liu, Y., Ma, S., Morawska, L., Texcalac Sangrador, J. L., Shaddick, G., Anderson, R., Forouzanfar, M. H., Burnett, R. T., and Cohen A.: Ambient Air Pollution Exposure Estimation for the Global Burden of Disease 2013, Environ. Sci. Tech. Lett., 50, 79–88, 2016.
Chen, X., Oja, V., Chan, W. G., and Hajaligol, M. R.: Vapor Pressure Characterization of Several Phenolics and Polyhydric Compounds by Knudsen Effusion Method, J.Chem. Eng. Data, 51, 386–391, 2006.
Compernolle, S., Ceulemans, K., and Müller, J.-F.: EVAPORATION: a new vapour pressure estimation methodfor organic molecules including non-additivity and intramolecular interactions, Atmos. Chem. Phys., 11, 9431–9450, https://doi.org/10.5194/acp-11-9431-2011, 2011.
COSMOconf: Version 4.2, COSMOlogic GmbH & Co KG, available at: http://www.cosmologic.de, last access: 7 May 2018, 2017.
COSMOtherm: version C3.0, Release 18.00, COSMOlogic GmbH & Co. KG, available at: http://www.cosmologic.de, last access: 7 May 2018.
D'Ambro, E. L., Lee, B. H., Liu, J., Shilling, J. E., Gaston, C. J., Lopez-Hilfiker, F. D., Schobesberger, S., Zaveri, R. A., Mohr, C., Lutz, A., Zhang, Z., Gold, A., Surratt, J. D., Rivera-Rios, J. C., Keutsch, F. N., and Thornton, J. A.: Molecular composition and volatility of isoprene photochemical oxidation secondary organic aerosol under low- and high-NOx conditions, Atmos. Chem. Phys., 17, 159–174, https://doi.org/10.5194/acp-17-159-2017, 2017.
Eckert, F. and Klamt, A.: Fast solvent screening via quantum chemistry: COSMO-RS approach, AlChE J., 48, 369–385, 2002.
Ehn, M., Thornton, J. A., Kleist, E., Sipila, M., Junninen, H., Pullinen, I., Springer, M., Rubach, F., Tillmann, R., Lee, B., Lopez-Hilfiker, F., Andres, S., Acir, I.-H., Rissanen, M., Jokinen, T., Schobesberger, S., Kangasluoma, J., Kontkanen, J., Nieminen, T., Kurten, T., Nielsen, L. B., Jorgensen, S., Kjaergaard, H. G., Canagaratna, M., Maso, M. D., Berndt, T., Petaja, T., Wahner, A., Kerminen, V.-M., Kulmala, M., Worsnop, D. R., Wildt, J., and Mentel, T. F.: A large source of low-volatility secondary or- ganic aerosol, Nature, 506, 476–479, https://doi.org/10.1038/nature13032, 2014.
Guenther, A. B., Jiang, X., Heald, C. L., Sakulyanontvittaya, T., Duhl, T., Emmons, L. K., and Wang, X.: The Model of Emissions of Gases and Aerosols from Nature version 2.1 (MEGAN2.1): an extended and updated framework for modeling biogenic emissions, Geosci. Model Dev., 5, 1471–1492, https://doi.org/10.5194/gmd-5-1471-2012, 2012.
Jimenez, J. L., Canagaratna, M. R., Donahue, N. M., Prevot, A. S. H., Zhang, Q., Kroll, J. H., DeCarlo, P. F., Allan, J. D., Coe, H., Ng, N. L., Aiken, A. C., Docherty, K. S., Ulbrich, I. M., Grieshop, A. P., Robinson, A. L., Duplissy, J., Smith, J. D., Wilson, K. R., Lanz, V. A., Hueglin, C., Sun, Y. L., Tian, J., Laaksonen, A., Raatikainen, T., Rautiainen, J., Vaattovaara, P., Ehn, M., Kulmala, M., Tomlinson, J. M., Collins, D. R., Cubison, M. J., Dunlea, E. J., Huffman, J. A., Onasch, T. B., Alfarra, M. R., Williams, P. I., Bower, K., Kondo, Y., Schneider, J. Drewnick, F., Borrmann, S., Weimer, S., Demerjian, K., Salcedo, D., Cottrell, L., Griffin, R., Takami, A., Miyoshi, T., Hatakeyama, S., Shimono, A., Sun, J. Y., Zhang, Y. M., Dzepina, K., Kimmel, J. R., Sueper, D., Jayne, J. T., Herndon, S. C., Trimborn, A. M., Williams, L. R., Wood, E. C., Middlebrook, A. M., Kolb, C. E., Baltensperger, U., and Worsnop, D. R.: Evolution of organic aerosols in the atmosphere, Science, 326, 1525–1529, https://doi.org/10.1126/science.1180353, 2009.
Kalberer, M., Paulsen, D., Sax, M., Steinbacher, M., Dommen, J., Prevot, A. S. H., Fisseha, R., Weingartner, E., Frankevich, V., Zenobi, R., and Baltensperger, U.: Identification of polymers as major components of atmospheric organic aerosols, Science, 303, 1659–1662, https://doi.org/10.1126/science.1092185, 2004.
Krieger, U. K., Siegrist, F., Marcolli, C., Emanuelsson, E. U., Gøbel, F. M., Bilde, M., Marsh, A., Reid, J. P., Huisman, A. J., Riipinen, I., Hyttinen, N., Myllys, N., Kurtén, T., Bannan, T., Percival, C. J., and Topping, D.: A reference data set for validating vapor pressure measurement techniques: homologous series of polyethylene glycols, Atmos. Meas. Tech., 11, 49–63, https://doi.org/10.5194/amt-11-49-2018, 2018.
Kurtén, T., Tiusanen, K., Roldin, P., Rissanen, M. P., Boy, M., Ehn, M., and Donahue, N. M. α-pinene Autoxidation Products May Not Have Extremely Low Saturation Vapor Pressures Despite High O : C Ratios, J. Phys. Chem. A, 120, 2569–2582, 2016.
Kurtén, T., Hyttinen, N., D'Ambro, E., Thornton, J., and Prisle, N.: Supplementary data for the manuscript “Estimating the saturation vapor pressures of isoprene oxidation products C5H12O6 and C5H10O6 using COSMO-RS”, submitted to Atmospheric Chemistry and Physics (Discussions) [Data set]. Zenodo, available at: https://doi.org/10.5281/zenodo.1344890, 2018.
Liu, J., D'Ambro, E. L., Lee, B. H., Lopez-Hilfiker, F. D., Zaveri, R. A., Rivera-Rios, J. C., Keutsch, F. N., Iyer, S., Kurtén, T., Zhang, Z., Gold, A., Surratt, J. D., Shilling, J. E., and Thornton, J. A.: Efficient Isoprene Secondary Organic Aerosol Formation from a Non-IEPOX Pathway, Environ. Sci. Tech. Lett. 50, 9872–9880, 2016.
Lopez-Hilfiker, F. D., Mohr, C., Ehn, M., Rubach, F., Kleist, E., Wildt, J., Mentel, Th. F., Lutz, A., Hallquist, M., Worsnop, D., and Thornton, J. A.: A novel method for online analysis of gas and particle composition: description and evaluation of a Filter Inlet for Gases and AEROsols (FIGAERO), Atmos. Meas. Tech., 7, 983–1001, https://doi.org/10.5194/amt-7-983-2014, 2014.
Nannoolal, Y., Rarey, J., and Ramjugernath, D.: Estimation of pure component properties, Part 3, Estimation of the vapor pressure of non-electrolyte organic compounds via group contributions and group interactions, Fluid Phase Equilibr., 269, 117–133, 2008.
O'Meara, S., Booth, A. M., Barley, M. H., Topping, D., and McFiggans, G.: An assessment of vapour pressure estimation methods, Phys. Chem. Chem. Phys., 16, 19453–19469, 2014.
Pachauri, R. K. and Meyer, L. A.: Climate Change 2014: Synthesis Report, Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, IPCC, Geneva, Switzerland, 2014.
Pankow, J. F. and Asher, W. E.: SIMPOL.1: a simple group contribution method for predicting vapor pressures and enthalpies of vaporization of multifunctional organic compounds, Atmos. Chem. Phys., 8, 2773–2796, https://doi.org/10.5194/acp-8-2773-2008, 2008.
Perdew, J. P.: Density-functional approximation for the correlation-energy of the inhomogenous electron gas, Phys. Rev. B, 33, 8822–8824, 1986.
Pierce, J. R., Riipinen, I., Kulmala, M., Ehn, M., Petäjä, T., Junninen, H., Worsnop, D. R., and Donahue, N. M.: Quantification of the volatility of secondary organic compounds in ultrafine particles during nucleation events, Atmos. Chem. Phys., 11, 9019–9036, https://doi.org/10.5194/acp-11-9019-2011, 2011.
Puranen, J. S., Vainio, M. J., and Johnson, M. S.: Accurate conformation-dependent molecular electrostatic potentials for high-throughput in silico drug discovery, J. Comput. Chem., 31, 1722-1732, https://doi.org/10.1002/jcc.21460, 2010.
TURBOMOLE V7.11: A development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available at: http://www.turbomole.com, last access: 7 May 2018.
Vainio, M. J. and Johnson, M. S.: Generation conformer ensembles using a multiobjective generic algorithm, J. Chem. Inf. Model., 47, 2462–2474, https://doi.org/10.1021/ci6005646, 2007.
Valorso, R., Aumont, B., Camredon, M., Raventos-Duran, T., Mouchel-Vallon, C., Ng, N. L., Seinfeld, J. H., Lee-Taylor, J., and Madronich, S.: Explicit modelling of SOA formation from α-pinene photooxidation: sensitivity to vapour pressure estimation, Atmos. Chem. Phys., 11, 6895–6910, https://doi.org/10.5194/acp-11-6895-2011, 2011.
Wang, C., Goss, K.-U., Lei, Y. D., Abbatt, J. P. D., and Wania, F. Calculating Equilibrium Phase Distribution during the Formation of Secondary Organic Aerosol using COSMOtherm, Environ. Sci. Technol 49, 8585–5894, 2015.
Wang, C., Yuan, T., Wood, S. A., Goss, K.-U., Li, J., Ying, Q., and Wania, F.: Uncertain Henry's law constants compromise equilibrium partitioning calculations of atmospheric oxidation products, Atmos. Chem. Phys., 17, 7529–7540, https://doi.org/10.5194/acp-17-7529-2017, 2017.
Wania, F., Lei, Y. D., Wang, C., Abbatt, J. P. D., and Goss, K.-U.: Novel methods for predicting gas–particle partitioning during the formation of secondary organic aerosol, Atmos. Chem. Phys., 14, 13189–13204, https://doi.org/10.5194/acp-14-13189-2014, 2014.
Wavefunction Inc.: Spartan'14 version 1.1.9, Irvine, CA, USA, 2014.
Wennberg, P. O., Bates, K. H., Crounse, J. D., Dodson, L. G., McVay, R. C., Mertens, L. A., Nguyen, T. B., Praske, E., Schwantes, R. H., Smarte, M. D., St. Clair, J. M., Teng, A. P., Zhang, X, and Seinfeld, J. H.: Gas-Phase Reactions of Isoprene and Its Major Oxidation Products, Chem. Rev., 118 3337-3390, https://doi.org/10.1021/acs.chemrev.7b00439, 2018.
Werner, H.-J., Knizia, G., and Manby, F. R.: Explicitly correlated coupled cluster methods with pair-specific geminals, Mol. Phys.. 109, 407–417, 2011.
Werner, H.-J., Knowles, P. J., Knizia, G., Manby, F. R., and Schütz, M.: Molpro: a general-purpose quantum chemistry program package, WIRES Comput. Mol. Sci. 2, 242–253, https://doi.org/10.1002/wcms.82, 2012.
Werner, H.-J., Knowles, P. J., Knizia, G., Manby, F. R., Schütz, M., Celani, P., Györffy, W., Kats, D., Korona, T., Lindh, R., Mitrushenkov, A., Rauhut, G., Shamasundar, K. R., Adler, T. B., Amos, R. D., Bernhardsson, A., Berning, A., Cooper, D. L., Deegan, M. J. O., Dobbyn, A. J., Eckert, F., Goll, R., Hampel, C., Hesselmann, A., Hetzer, G., Hrenar, T., Jansen, G., Köppl, C., Liu, Y., Lloyd, A. W., Mata, R. A., May, A. J., McNicholas, S. J., Meyer, W., Mura, M. E., Nicklass, A., O'Neill, D. P., Palmieri, P., Peng, D., Pflüger, K., Pitzer, R., Reiher, M., Shiozaki, T., Stoll, H., Stone, A. J., Tarroni, R., Thorsteinsson, T., and Wang, M. MOLPRO, version 2015.1, a package of ab initio programs, available at: http://www.molpro.net (last access: 5 December 2018), 2015.
Zhang, X., Cappa, C. D., Jathar, S. H., McVay, R. C., Ensberg, J. J., Kleeman, M. J., and Seinfeld, J. H.: Influence of vapor wall loss in laboratory chambers on yields of secondary organic aerosol, P. Natl. Acad. Sci. USA, 111, 5802–5807, 2014.