the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
H2SO4–H2O–NH3 ternary ion-mediated nucleation (TIMN): kinetic-based model and comparison with CLOUD measurements
Alexey B. Nadykto
Jason Herb
Kirill M. Nazarenko
Lyudmila A. Uvarova
New particle formation (NPF) is known to be an important source of atmospheric particles that impacts air quality, hydrological cycle, and climate. Although laboratory measurements indicate that ammonia enhances NPF, the physicochemical processes underlying the observed effect of ammonia on NPF are yet to be understood. Here we present a comprehensive kinetically based H2SO4–H2O–NH3 ternary ion-mediated nucleation (TIMN) model that is based on the thermodynamic data derived from both quantum-chemical calculations and laboratory measurements. NH3 was found to reduce nucleation barriers for neutral, positively charged, and negatively charged clusters differently, due to large differences in the binding strength of NH3, H2O, and H2SO4 to small clusters of different charging states. The model reveals the general favor of nucleation of negative ions, followed by nucleation on positive ions and neutral nucleation, for which higher NH3 concentrations are needed, in excellent agreement with Cosmics Leaving OUtdoor Droplets (CLOUD) measurements. The TIMN model explicitly resolves dependences of nucleation rates on all the key controlling parameters and captures the absolute values of nucleation rates as well as the dependence of TIMN rates on concentrations of NH3 and H2SO4, ionization rates, temperature, and relative humidity observed in the well-controlled CLOUD measurements well. The kinetic model offers physicochemical insights into the ternary nucleation process and provides a physics-based approach to calculate TIMN rates under a wide range of atmospheric conditions.
New particle formation (NPF), an important source of particles in the atmosphere, is a dynamic process involving interactions among precursor gas molecules, small clusters, and preexisting particles (Yu and Turco, 2001; Zhang et al., 2012). H2SO4 and H2O are known to play an important role in atmospheric particle formation (e.g., Doyle, 1961). In typical atmospheric conditions, the species dominating the formation and growth of small clusters is H2SO4. The contribution of H2O to the nucleation is related to the hydration of H2SO4 clusters (or, in the other words, modification of the composition of nucleating clusters), which reduces the H2SO4 vapor pressure and hence diminishes the evaporation of H2SO4 from the pre-nucleation clusters. NH3, the most abundant gas-phase base molecule in the atmosphere and a very efficient neutralizer of sulfuric acid solutions, has long been proposed to enhance nucleation in the lower troposphere (Coffman and Hegg, 1995), although it has been well recognized that earlier versions of the classical ternary nucleation model (Coffman and Hegg, 1995; Korhonen et al., 1999; Napari et al., 2002) significantly overpredict the effect of ammonia (Yu, 2006a; Merikanto et al., 2007; Zhang et al., 2010).
The impacts of NH3 on NPF have been investigated in a number of laboratory studies (Kim et al., 1998; Ball et al., 1999; Hanson and Eisele, 2002; Benson et al., 2009; Kirkby et al., 2011; Zollner et al., 2012; Froyd and Lovejoy, 2012; Glasoe et al., 2015; Schobesberger et al., 2015; Kürten et al., 2016) including those recently conducted at the European Organization for Nuclear Research (CERN) in the framework of the CLOUD (Cosmics Leaving OUtdoor Droplets) experiment that has provided a unique dataset for quantitatively examining the dependences of ternary H2SO4–H2O–NH3 nucleation rates on concentrations of NH3 ([NH3]) and H2SO4 ([H2SO4]), ionization rate (Q), temperature (T), and relative humidity (RH) (Kirkby et al., 2011; Kürten et al., 2016). The experimental conditions in the CLOUD chamber, a 26.1 m3 stainless steel cylinder, were well controlled, while impacts of potential contaminants were minimized (Schnitzhofer et al., 2014; Duplissy et al., 2016). Based on CLOUD measurements in H2SO4–H2O–NH3 vapor mixtures, Kirkby et al. (2011) reported that an increase in [NH3] from ∼0.03 ppb (parts per billion, by volume) to ∼0.2 ppb can enhance ion-mediated (or induced) nucleation (IMN) rate by 2–3 orders of magnitude and that the IMN rate is a factor of 2 to > 10 higher than that of neutral nucleation under a typical level of contamination by amines. In the presence of ionization, common highly polar atmospheric nucleation precursors such as H2SO4, H2O, and NH3 molecules tend to cluster around ions, and charged clusters are generally much more stable than their neutral counterparts with enhanced growth rates as a result of dipole–charge interactions (Yu and Turco, 2001).
Despite various laboratory measurements indicating that ammonia enhances NPF, the physicochemical processes underlying the observed different effects of ammonia on the formation of neutral, positively charged, and negatively charged clusters (Schobesberger et al., 2015) are yet to be understood. To achieve such an understanding, a nucleation model based on the first principles is needed. Such a model is also necessary to extrapolate data obtained in a limited number of experimental conditions to a wide range of atmospheric conditions, in which [NH3], [H2SO4], ionization rates, T, RH, and surface areas of preexisting particles vary widely depending on the region, pollution level, and season. The present work aims to address these issues by developing a kinetically based H2SO4–H2O–NH3 ternary IMN (TIMN) model that is based on the molecular clustering thermodynamic data. The model predictions are compared with relevant CLOUD measurements and previous studies.
2.1 Background
Most nucleation models developed in the past for H2SO4–H2O binary homogeneous nucleation (e.g., Vehkamäki et al., 2002), H2SO4–H2O ion-induced nucleation (IIN; e.g., Hamill et al., 1982; Raes et al., 1986; Laakso et al., 2003), and H2SO4–H2O–NH3 ternary homogeneous nucleation (Coffman and Hegg, 1995; Korhonen et al., 1999; Napari et al., 2002) have been based on the classical approach, which employs capillarity approximation (i.e., assuming that small clusters have the same properties as bulk) and calculates nucleation rates according to the free energy change associated with the formation of a “critical embryo”. Yu and Turco (1997, 2000, 2001) developed a neutral and charged binary H2SO4–H2O nucleation model using a kinetic approach that explicitly treats the complex interactions among small air ions, neutral and charged clusters of various sizes, precursor vapor molecules, and preexisting aerosols. The formation and evolution of cluster size distributions for positively and negatively charged cluster ions and neutral clusters affected by ionization, recombination, neutralization, condensation, evaporation, coagulation, and scavenging have been named IMN (Yu and Turco, 2000). The IMN theory significantly differs from classical IIN theory (e.g., Hamill et al., 1982; Raes et al., 1986; Laakso et al., 2003), which is based on a simple modification of the free energy for the formation of a critical embryo by including the electrostatic potential energy induced by the embedded charge (i.e., Thomson effect; Thomson, 1888). The classical approach does not properly account for the kinetic limitation to embryo development, enhanced stability and growth of charged clusters associated with dipole–charge interaction (Nadykto and Yu, 2003; Yu, 2005), and the important contribution of neutral clusters resulting from ion–ion recombination to nucleation (Yu and Turco, 2011). In contrast, these important physical processes are explicitly considered in the kinetic-based IMN model (Yu, 2006b).
Since the beginning of the century, nucleation models based on the kinetic approach have also been developed in a number of research groups (Lovejoy et al., 2004; Sorokin et al., 2006; Chen et al., 2012; Dawson et al., 2012; McGrath et al., 2012). Lovejoy et al. (2004) developed a kinetic ion nucleation model, which explicitly treats the evaporation of small neutral and negatively charged H2SO4–H2O clusters. The thermodynamic data used in their model were obtained from measurements of small ion clusters, ab initio calculations, the thermodynamic cycle, and some approximations (adjustment of Gibbs free energy for neutral clusters calculated based on liquid droplet model, interpolation, etc.). Lovejoy et al. (2004) did not consider the nucleation on positive ions. Sorokin et al. (2006) developed an ion cluster–aerosol kinetic (ICAK) model, which uses the thermodynamic data reported in Froyd and Lovejoy (2003a, b) and empirical correction terms proposed by Lovejoy et al. (2004). Sorokin et al. (2006) used the ICAK model to simulate dynamics of neutral and charged H2SO4–H2O cluster formation and compared the modeling results with their laboratory measurements. Chen et al. (2012) developed an approach for modeling NPF based on a sequence of acid–base reactions, with sulfuric acid evaporation rates (from clusters) estimated empirically based on measurements of neutral molecular clusters taken in Mexico City and Atlanta. Dawson et al. (2012) presented a semiempirical kinetics model for nucleation of methanesulfonic acid (MSA), amines, and water that explicitly accounted for the sequence of reactions leading to formation of stable particles. The kinetic models of Chen et al. (2012) and Dawson et al. (2012) consider only neutral clusters.
McGrath et al. (2012) developed the Atmospheric Cluster Dynamics Code (ACDC) to model the cluster kinetics by solving the birth–death equations explicitly, with evaporation rate coefficients derived from formation free energies calculated by quantum chemical methods (Almeida et al., 2013; Olenius et al., 2013). The ACDC model applied to the H2SO4–dimethylamine (DMA) system considers zero to four base molecules and zero to four sulfuric acid molecules (Almeida et al., 2013). Olenius et al. (2013) applied the ACDC model to simulate the steady-state concentrations and kinetics of neutral and negatively and positively charged clusters containing up to five H2SO4 and five NH3 molecules. In ACDC, the nucleation rate is calculated as the rate of clusters growing larger than the upper bounds of the simulated system (i.e., clusters containing four or five H2SO4 molecules) (Kürten et al., 2016).
The kinetic IMN model developed by Yu and Turco (1997, 2001) explicitly simulates the dynamics of neutral, positively charged, and negatively charged clusters, based on a discrete-sectional bin structure that covers the clusters containing 0, 1, 2,…, 15,…H2SO4 molecules to particles containing thousands of H2SO4 (and H2O) molecules. In the first version of the kinetic IMN model (Yu and Turco, 1997, 2001), due to the lack of thermodynamic data for the small clusters, the compositions of neutral and charged clusters were assumed to be the same and the evaporation of small clusters was accounted for using a simple adjustment to the condensation accommodation coefficients. Yu (2006b) developed a second-generation IMN model that incorporated newer thermodynamic data (Froyd, 2002; Wilhelm et al., 2004) and physical algorithms (Froyd, 2002; Wilhelm et al., 2004) and explicitly treated the evaporation of neutral and charged clusters. Yu (2007) further improved the IMN model by using two independent measurements (Marti et al., 1997; Hanson and Eisele, 2000) to constrain monomer hydration in the H2SO4–H2O system and by incorporating experimentally determined energetics of small neutral H2SO4–H2O clusters that became available then (Hanson and Lovejoy, 2006; Kazil et al., 2007). The first and second generations of the IMN model were developed for the H2SO4–H2O binary system, although the possible effects of ternary species such as the impact of NH3 on the stability of both neutral and charged pre-nucleation clusters have been pointed out in these previous studies (Yu and Turco, 2001; Yu, 2006b). The present work extends the previous versions of the IMN model in the binary H2SO4–H2O system to the ternary H2SO4–H2O–NH3 system, as described below.
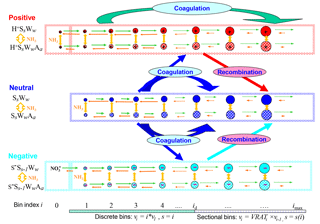
Figure 1Schematic illustration of kinetic processes controlling the evolution of positively charged (H+SsWwAa), neutral (SsWwAa), and negatively charged () clusters–droplets that are explicitly simulated in the ternary ion-mediated nucleation (TIMN) model. Here S, W, and A represent sulfuric acid (H2SO4), water (H2O), and ammonia (NH3), respectively, while s, w, and a refer to the number of S, W, and A molecules in the clusters–droplets, respectively. The TIMN model has been extended from an earlier version treating binary IMN (BIMN) by adding NH3 into the nucleation system and using a discrete-sectional bin structure to represent the sizes of clusters–particles starting from a single molecule up to background particles larger than a few micrometers.
2.2 Model representation of kinetic ternary nucleation processes
Figure 1 schematically illustrates the evolution of charged and neutral clusters–droplets explicitly simulated in the kinetic H2SO4–H2O–NH3 TIMN model. Here, H2SO4 (S) is the key atmospheric nucleation precursor driving the TIMN process while ions, H2O (W), and NH3 (A) stabilize the H2SO4 clusters and enhance H2SO4 nucleation rates in this way. Ions also enhance cluster formation rates due to the interaction with polar-nucleating species, leading to enhanced collision cross sections (Nadykto and Yu, 2003). The airborne ions are generated by galactic cosmic rays (GCRs) or produced by radioactive emanations, lightning, corona discharge, combustion, and other ionization sources. The initial negative ions, which are normally assumed to be , are converted into core ions (i.e., S−) and then to larger H2SO4 clusters in the presence of gaseous H2SO4. The initial positive ions H+Ww are converted into in the presence of NH3, H+Ss Ww in the presence of H2SO4, or H+Aa SsWw in the case that both NH3 and H2SO4 are present in the nucleating vapors. Some of the binary H2SO4–H2O clusters, both neutral and charged, transform into ternary ones by taking up NH3 vapors. The molar fraction of ternary clusters in nucleating vapors depends on [NH3], the binding strength of NH3 to binary and ternary pre-nucleation clusters, cluster composition, and ambient conditions such as T and RH.
Similar to the kinetic binary IMN (BIMN) model (Yu, 2006b), the kinetic TIMN model employs a discrete-sectional bin structure to represent clusters–particles. The bin index i represents the amount of core component (i.e., H2SO4) and id is the number of discrete bins. For small clusters (i≤id = 30 in this study), i is the number of H2SO4 molecules in the cluster (i.e., i=s) and the core volume of the ith bin , where v1 is the volume of one H2SO4 molecule. When i > id, vi = VRATi × vi−1, where VRATi is the volume ratio of the ith bin to the (i−1)th bin. The discrete-sectional bin structure enables the model to cover a wide range of sizes of nucleating clusters–particles with the highest possible size resolution for small clusters (Yu, 2006b). For clusters with a given bin i, the associated amounts of water and NH3 and thus the effective radius of each ternary cluster are calculated based on the equilibrium of clusters–particles with the water vapor and/or ammonia, as described in later sections.
The evolution of positive, negative, and neutral clusters due to the simultaneous condensation, evaporation, recombination, coagulation, and other loss processes is described by the following differential equations obtained by the modification of those describing the evolution of the binary H2SO4–H2O system (Yu, 2006b):
In Eqs. (1)–(6), the superscripts “+”, “−”, and “0” refer to positive, negative, and neutral clusters, respectively, while subscripts i, j, and k represent the bin indexes. and Q are the concentration of initial ions not containing H2SO4 (i.e., H+AaWw and ) and the ionization rate, respectively. Ni is the total number concentration (cm−3) of all cluster/particles (binary + ternary) in bin i. For small clusters (i≤id), Ni is the number concentration (cm−3) of all clusters containing i H2SO4 molecules. For example, is the total concentration of binary and ternary neutral clusters containing one H2SO4 molecule. Index i in Eq. (4) refers to the sum of H2SO4 and . The second term of Eq. (2) describes the reaction of + HNO3 → + H2SO4. Although the rate of this reaction is generally negligible, we keep the term there for completeness. is the gas-phase production rate of neutral H2SO4 molecules. is the loss rate due to scavenging by preexisting particles and wall and dilution losses in the laboratory chamber studies (Kirkby et al., 2011; Olenius et al., 2013; Kürten et al., 2016). is the volume fraction of intermediate particles (volume = vj + vk) partitioned into bin i with respect to the core component – H2SO4, as defined in Jacobson et al. (1994). is the volume fraction of intermediate particles of volume () partitioned into bin i. at j=2 and at j≠2. , , and are the mean (or effective) cluster evaporation coefficients for positive, negative and neutral clusters in bin i, respectively. , , and are the coagulation kernels for the neutral clusters–particles in bin j interacting with positive, negative, and neutral clusters–particles in bin i, respectively, which reduce to the condensation coefficients for H2SO4 monomers at j=1. and are coagulation kernels for clusters–particles of like sign from bin j and clusters–particles from bin k. It should be noted that the electrostatic repulsion is too strong for small clusters to gain more than one charge. However, small charged clusters can be scavenged by large preexisting particles of the same polarity. Large preexisting particles serve as the sink for small clusters in the model and the effect of multiple charge is small and thus is not tracked. is the recombination coefficient for positive clusters–particles in bin i interacting with negative clusters–particles in bin j, while is the recombination coefficient of negative clusters–particles from bin i interacting with positively charged clusters–particles from bin j.
The methods for calculating β, γ, η, and α for binary H2SO4–H2O clusters have been described in our previous publications (Yu and Turco, 2001; Nadykto and Yu, 2003; Yu, 2006b). Dipole–charge interaction (Nadykto and Yu, 2003), image capture, and three-body trapping effects (Hoppel and Frick, 1986) are considered in the calculation of these coefficients. Since β, η, and α depend on the cluster mass (or size) rather than on the cluster composition, schemes for calculating these properties in binary and ternary clusters are identical. In contrast, γ is quite sensitive to cluster composition. The evaporation rate coefficient of H2SO4 molecules from clusters containing i H2SO4 molecules (γi) is largely controlled by the stepwise Gibbs free energy change of formation of an i-mer from an (i−1)-mer (Yu, 2007)
where R is the molar gas constant, No is the arbitrary number concentration of a hypothetical gas consisting solely of the species for which the calculation is performed (generally under the reference vapor pressure P of 1 atm). ΔHo and ΔSo are enthalpy and entropy changes under the standard conditions (T=298 K, P=1 atm), respectively. The temperature dependence of ΔHo and ΔSo, which is generally small and typically negligible over the temperature range of interest (Nadykto et al., 2009), was not considered.
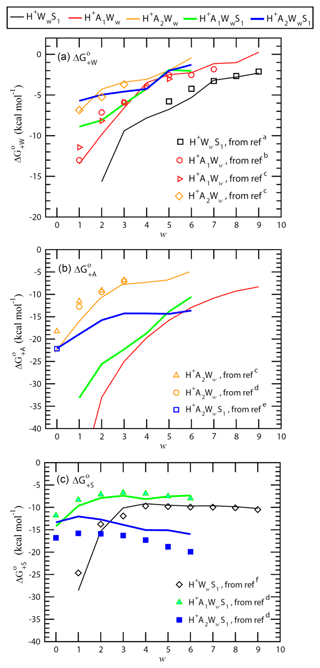
Figure 2Stepwise Gibbs free energy change under standard conditions for the addition of a water (), ammonia (), or sulfuric acid () molecule to form the given positively charged clusters as a function of the number of water molecules in the clusters (w). Lines are QC-based values, and symbols are experimental results or semi-experimental estimates (see notes under Table A2 for the references).
2.3 Thermochemical data of neutral and charged binary and ternary clusters
ΔH, ΔS, and ΔG values needed to calculate cluster evaporation rates (Eq. 7) for the TIMN model can be derived from laboratory measurements and computational quantum chemistry (QC) calculation. Thermochemical properties of neutral and charged binary and ternary clusters obtained using the computational chemical methods and comparisons of computed energies with available experimental data and semi-experimental estimates are given in Tables A1–A4 and discussed in the Appendix. As an example, Fig. 2 shows ΔG associated with the addition of water (), ammonia (), and sulfuric acid () to binary and ternary clusters as a function of the cluster hydration number w. H2O has high proton affinity and thus H2O is strongly bonded to all positive ions with low w. expectedly becomes less negative and binding of H2O to binary and ternary clusters weakens due to the screening effect as the hydration number w grows (Fig. 2a). The presence of NH3 in the clusters weakens binding of H2O to positive ions. For example, for H+A1WwS1 is ∼3–4 kcal mol−1 less negative than that for H+WwS1 at w=3–6. The addition of one more NH3 to the clusters to form H+A2Ww and H+A2WwS1 further weakens H2O binding by ∼1.5–6 kcal mol−1 at w=1–3, while exhibiting a much smaller impact on hydration free energies at w > 3. Both the absolute values and trends in derived from calculations are in agreement with the laboratory measurements within the uncertainty range of ∼1–2 kcal mol−1 for both QC calculations and measurements. This confirms the efficiency and precision of QC methods in calculating thermodynamic data needed for the development of nucleation models.
The proton affinity of NH3 is 204.1 kcal mol−1, which is 37.5 kcal mol−1 higher than that of H2O (166.6 kcal mol−1) (Jolly, 1991). The hydrated hydronium ions (H+Ww) are easily converted to H+A1Ww in the presence of NH3. The binding of NH3 and H2O molecules to H+Ww exhibits a similar pattern. In particular, binding of NH3 to H+Ww decreases as w is growing, with for H+A1Ww ranging from −52.08 kcal mol−1 at w=1 to −8.32 kcal mol−1 at w=9. The binding of NH3 to H+WwS1 ions is also quite strong, with for H+A1WwS1 ranging from −33.14 kcal mol−1 at w=1 and to −10.57 kcal mol−1 at w=6. The addition of the NH3 molecule to H+A1Ww (to form H+A2Ww) is much less favorable thermodynamically than that to H+Ww, with the corresponding being −22 and −6 kcal mol−1 at w=2 and w=6, respectively. The values for H+A2Ww are 3–5 kcal mol−1 more negative than the experimental values at w=0–1; however, they are pretty close to experimental data at w=2–3 (Fig. 2b and Table A2). While it is possible that the QC method overestimates the charge effect on the formation free energies of smallest clusters, the possible overestimation at w=0–1 will not affect nucleation calculations because most H+A2Ww clusters in the atmosphere contain more than two water molecules (i.e., w > 2) due to the strong hydration (see Table A2 and Fig. 2a).
A comparison of QC and semi-experimental estimates of values associated with the attachment of H2SO4 to positive ions shown in Fig. 2c indicates that computed values agree well with observations for H+WwS1 and H+A1WwS1 but differ by ∼2–4 kcal mol−1 from semi-experimental values for H+A2WwS1. As seen from Fig. 2a and c, the attachment of NH3 to H+WwS1 weakens the binding of both H2O and H2SO4 to the clusters. This suggests that the attachment of NH3 leads to the evaporation of H2SO4 and H2O molecules from the clusters. In other words, H2SO4 is less stable in H+A1WwS1 than in H+WwS1 (Fig. 2c). While this may be taken for the indication that NH3 inhibits nucleation on positive ions at the first look, further calculations show that binding of NH3 to H+A1WwS1 is quite strong (Fig. 2b) and that H2SO4 in the H+A2WwS1 cluster is much more stable than that in H+A1WwS1, with being more negative by ∼7 kcal mol−1 at w > 2. The H+A2WwS1 cluster can also be formed via the attachment of H2SO4 to H+A2Ww. In the presence of sufficient concentrations of NH3, a large fraction of positively charged H2SO4 monomers exist in the form of H+A2WwS1 and hence NH3 enhances nucleation of positive ions. Since positively charged H2SO4 dimers are expected to contain a large number of water molecules, we have not yet computed and derived quantum chemical data for these clusters. The CLOUD measurements do indicate that once H+A2WwS1 clusters are formed, they can continue to grow to larger H+AaWwSs clusters along pathway (Schobesberger et al., 2015).
Figure 2 clearly shows that the calculated values in most cases agree with measurements within the uncertainty range that justifies the application of QC values in the case that no reliable experimental data are available.
2.4 Nucleation barriers for neutral and charged clusters and size-dependent evaporation rates
Nucleation barriers and cluster evaporation rates are critically important for calculations of nucleation rates. This section describes the methods employed to calculate the evaporation rates of nucleating clusters of variable sizes and compositions (i.e., γ in Eqs. 1–6) in the TIMN model.
2.4.1 Equilibrium distributions of small binary and ternary clusters
In the atmosphere, [H2O] is much higher than [H2SO4] and thus H2SO4 clusters–particles are always in equilibrium with water vapor (Yu, 2007). In the lower troposphere, where most of the nucleation events were observed, [H2SO4] is typically at a sub-parts per trillion to parts per trillion level, while [NH3] is in the range of sub-parts per billion to parts per billion levels (Butler et al., 2016; Warner et al., 2016) (note that, in what follows, all references to vapor mixing ratios – parts per billion and parts per trillion – are by volume). This means that small ternary clusters can be considered to be in equilibrium with H2O and NH3 vapors. Like the previous BIMN model derived assuming equilibrium of binary clusters with water vapor, the present TIMN model treats small clusters containing a given number of H2SO4 molecules as being in equilibrium with both H2O and NH3. Their relative concentrations are calculated using the thermodynamic data shown in Tables A1–A4. It should be noted that the system may deviate from equilibrium and the model scheme is probably not suitable when [NH3] is less than or close to [H2SO4]. Under such cases, the equilibrium assumption may overestimate nucleation rates.
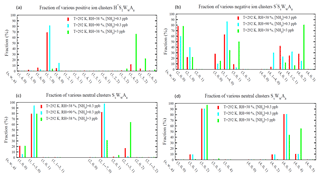
Figure 3Relative abundance (or molar fraction) of small clusters containing a given number of H2SO4 molecules for positive (a), negative (b), and neutral (c, d) cluster types at a temperature of 292 K and three different combinations of RHs (38 % and 90 %) and [NH3] (0.3 and 3 ppb). Some clusters with different numbers of water molecules were grouped together to make the plot more clear and neat. For the clusters shown in (d), there are no hydrate data and thus hydration for these clusters was not calculated.
Figure 3 shows the relative abundance (or molar fractions) of small positive, negative, and neutral clusters () containing a given number of H2SO4 molecules at the ambient temperature of 292 K and three different combinations of RH and [NH3] values. As a result of relative instability of H2SO4 in H+A1WwS1 compared to H+WwS1 or H+A2WwS1 (Fig. 2c), most of positive ions with one H2SO4 molecule exist in the form of either H+WwS1 or H+A2WwS1 (i.e, containing either zero or two NH3 molecules; Fig. 3a). When [NH3] = 0.3 ppb (with T=292 K), most of the positive ions containing one H2SO4 molecule do not contain NH3 and their composition is dominated by H+WwS1 (). At the given T and [NH3] = 0.3 ppb, around 17 % of positive ions with one H2SO4 molecule contain two NH3 molecules at RH = 38 %. The fraction of positive ions containing one H2SO4 and two NH3 molecules decreases to 0.9 %, when RH=90 %. At T=292 K and RH=38 %, the increase in [NH3] by a factor of 10 to 3 ppb leads to the domination of H+A2WwS1 (∼95 %) in the composition of positively charged H2SO4 monomers. As expected, the composition of positive ions and their contribution to nucleation depends on T, RH, and [NH3]. The incorporation of the quantum chemical and experimental clustering thermodynamics in the framework of the kinetic nucleation model enables us to study all these dependencies.
As a result of very weak binding of H2O and NH3 to small negative ions (Table A4), nearly all negatively charged clusters with s = 0–1 do not contain water and ammonia (not shown). In the case that s grows to 2, all S−S2AaWw clusters still do not contain NH3 (i.e., a=0), while only 20 %–40 % of them contain one water molecule (w=1) (Fig. 3b). As s further increases to 3, NH3 begins to enter some of the negatively charged ions. The fraction of S−S3AaWw clusters containing one NH3 molecule is 9 % at RH = 38 % and [NH3] = 0.3 ppb, 3 % at RH = 90 % and [NH3] = 0.3 ppb, and 50 % at RH = 38 % and [NH3] = 3 ppb. Most S−S3Ww clusters are hydrated while the fraction of S−S3AaWw clusters containing two NH3 molecules at these ambient conditions is negligible. The fraction of negative cluster ions containing two NH3 molecules becomes significant at s=4 (Fig. 3b) and increases from 28 % at [NH3] = 0.3 ppb to 80 % at [NH3] = 3 ppb at RH = 38 %. At [NH3] = 0.3 ppb, the increase in RH from 38 % to 90 % reduces the fraction of NH3-containing S−S3AaWw clusters (i.e, a > =1) from to 95 % to 70 %, demonstrating a significant impact of RH on cluster compositions and emphasizing the importance of accounting for the RH in calculations of ternary nucleation rates.
The equilibrium distributions of neutral clusters are presented in Fig. 3c (H2SO4 monomers and dimers) and Fig. 3d (H2SO4 trimers and tetramers). Hydration is accounted for in the case of monomers and dimers and not included, due to lack of thermodynamic data, in calculations for trimers and tetramers. Based on the thermodynamic data shown in Table A3, the dominant fraction of neutral monomers is hydrated (79 % at RH = 38 % and 94 % at RH = 90 %) while the fraction of monomers containing NH3 is negligible (0.02 % at [NH3] = 0.3 ppb and 0.2 % at [NH3] = 3 ppb, RH = 38 %). As a result of the growing binding strength of NH3 with the cluster size (Table A3), the fraction of neutral sulfuric acid dimers containing one NH3 molecule reaches 18 % at [NH3] = 0.3 ppb and 69 % at [NH3] = 3 ppb when T = 292 K and RH = 38 %. In the case of H2SO4 trimers and tetramers, data shown in Fig. 3d are limited to the relative abundance of unhydrated clusters only. Under the given conditions, most trimers contain two NH3 molecules while most tetramers contain three NH3 molecules. At [NH3] = 3 ppb, ∼2 % of trimers contain three NH3 molecules (i.e., ) and 55 % of tetramers contain four NH3 molecules (i.e., ). As a result of a significant drop of in the case that the a∕s ratio exceeds one (Table A3), the fraction of neutral clusters with is negligible. The cluster distributions clearly indicate that small sulfuric acid clusters are still not fully neutralized by NH3 even if [NH3] is at a parts per billion level and that the degree of neutralization (i.e., a:s ratio) increases with the cluster size.
2.4.2 Mean stepwise and accumulative Gibbs free energy change and impact of ammonia
In the TIMN model, the equilibrium distributions are used to calculate number-concentration-weighted stepwise Gibbs free energy change for adding one H2SO4 molecule to form a neutral, positively charged, and negatively charged cluster containing s H2SO4 molecules ():
where is the equilibrium fraction of a particular cluster within a cluster type as shown in Fig. 3.
In the atmosphere, where substantial nucleation is observed, the sizes of critical clusters are generally small (s < ∼5–10) (e.g., Sipilä et al., 2010) and nucleation rates are largely controlled by the stability (or γ) of small clusters with s < ∼5–10. QC calculations and experimental data on clustering thermodynamics available for clusters of small sizes (Tables A2–A4) are critically important as the formation of these small clusters is generally the limiting step for nucleation. Nevertheless, thermodynamics data for larger clusters are also needed to develop a robust nucleation model that can calculate nucleation rates under various conditions. Both measurements and QC calculations (Tables A2–A4) show significant effects of charge and charge signs (i.e., positive or negative) on the stability and composition of small clusters. These charge effects decrease quickly as the clusters grow due to the short-ranged nature of dipole–charge interaction and the quick decrease in electrical field strength around charged clusters as cluster sizes increase (Yu, 2005). Based on experimental data (Kebarle et al., 1967; Davidson et al., 1977; Wlodek et al., 1980; Holland and Castleman, 1982; Froyd and Lovejoy, 2003b), the stepwise ΔG values for clusters decrease exponentially as the cluster sizes increase and approach to the bulk values when clusters contain more than ∼8–10 molecules (Yu, 2005). Cluster compositions measured with an atmospheric pressure interface time-of-flight (APi-TOF) mass spectrometer during CLOUD experiments also show that the difference in the composition of positively and negatively charged clusters quickly decreases as the number of H2SO4 molecules increases from 1 to ∼10 and exhibits little further changes (Schobesberger et al., 2015).
In the present TIMN model, we assume that both neutral and charged clusters have the same composition when s≥10 and the following extrapolation scheme is used to calculate for clusters up to s=10:
where is the stepwise mean Gibbs free energy change for H2SO4 addition for a specific type (neutral, positive, or negative) of clusters at s=s1 that can be derived from QC calculation and/or experimental measurements, and is the corresponding value for clusters at s=s2 (= 10 in the present study) that is calculated in the capillarity approximation accounting for the Kelvin effect. c in Eq. (10) is the exponential coefficient that determines how fast approaches to bulk values as s increases. In the present study, c is estimated by fitting at s=2 and s=3 based on Eq. (10) to the corresponding from experimental (Hanson and Lovejoy, 2006; Kazil et al., 2007) or QC data (Table A3). Apparently the interpolation approximation Eq. (10) is subject to uncertainty. Nevertheless, it is a reasonable approach to connect thermochemical properties of QC data for small binary and ternary clusters that cannot be adequately described by the capillarity approximation with those for large clusters that can be adequately described by the very same capillarity approximation, and it is the best approach we can come up with at this point in order to develop a model that can be applied to all conditions. Further QC and experimental studies of the thermodynamics of relatively larger clusters can help to reduce the uncertainty.
For clusters with s≥s2, the capillarity approximation is used to calculate as
where P is the H2SO4 vapor pressure and Ps is the H2SO4 saturation vapor pressure over a flat surface with the same composition as the cluster. σ is the surface tension and v1 is the volume of one H2SO4 molecule. rs is the radius of the cluster and NA is the Avogadro's number.
The scheme to calculate bulk (s≥10) for H2SO4–H2O binary clusters has been described in Yu (2007). For ternary nucleation, both experiments (Schobesberger et al., 2015) and QC calculations (Table A4) indicate that the growth of relatively large clusters follows the s=a line (i.e, in the composition of ammonia bisulfate). In the present TIMN model, the bulk values for ternary clusters are calculated based on parameterized H2SO4 saturation vapor pressure over ammonia bisulfate as a function of temperature, derived by Marti et al. (1997) from vapor pressures measured at a temperature between 27 and 60 ∘C and surface tension measured at 298 K from Hyvärinen et al. (2005). The uncertainty in saturation vapor pressures and surface tension used in the calculation of the bulk values is another source of uncertainty in the TIMN model, although it is likely to be small compared to other uncertainties as the nucleation is generally limited by the formation of small clusters.
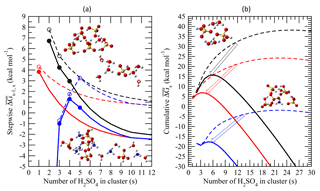
Figure 4(a) Average stepwise Gibbs free energy change for the addition of one H2SO4 molecule to form a neutral (black), positively charged (red), or negatively charged (blue) binary H2SO4–H2O (dashed lines or empty circles) or ternary H2SO4–H2O–NH3 (solid lines or filled circles) cluster containing s H2SO4 molecules (). (b) Same as (a) but for the cumulative (total) Gibbs free energy change in each case. Filled and empty circles in (a) refer to obtained using measurements and/or quantum-chemical calculations. for larger clusters with s ≥ 10, which approach the properties of the equivalent bulk liquid (20), is calculated using the capillarity approximation. Interpolation is used to calculate for clusters up to s=10 (Eq. 11). Calculations were carried out at T = 292 K, RH = 38 %, [H2SO4] = 3 × 108 cm−3, and [NH3] = 0.3 ppb. The inset diagrams represent equilibrium geometries for the most stable isomers of selected binary clusters ((H3O+)(H2SO4)(H2O)6, (H2SO4)2(H2O)4, and ()(H2SO4)4(H2O)2) and ternary clusters (()(H2SO4)(NH3)(H2O)4, ()(H2SO4)4(H2O)(NH3), (H2SO4)4(NH3)4).
Figure 4 presents stepwise () and cumulative (total) Gibbs free energy changes associated with the formation of neutral, positively charged, and negatively charged binary and ternary clusters containing s H2SO4 molecules under the conditions specified in the figure caption. The clusters are assumed to be in equilibrium with water (Yu, 2007) and ammonia (Fig. 3). As seen from Fig. 4, the presence of NH3 reduces the mean for larger clusters, which can be treated as the bulk binary H2SO4–H2O solution (Schobesberger et al., 2015), by ∼3 kcal mol−1, indicating a substantial reduction in the H2SO4 vapor pressure over ternary solutions (Marti et al., 1997). The comparison also shows that the influence of NH3 on of small clusters () is much lower than that on larger ones and bulk solutions. For example, at [NH3] = 0.3 ppb, the differences in between binary and ternary positive ions with s=1 and neutral clusters with s=2 are only 0.45 and ∼1 kcal mol−1, respectively. In the case of negative ions, zero and 0.27–0.45 kcal mol−1 differences at s≤2 and s=3–4, respectively, were observed. The reduced effect of ammonia on smaller clusters is explained (Tables A2–A4) by ammonia's weaker bonding to smaller clusters than to larger ones, which in turn yields lower average NH3-to-H2SO4 ratios (Fig. 3). It should be noted that QC data for positively charged clusters are very limited and the interpolation approximation is subject to large uncertainty. In order for the nucleation on positive ions to occur, the first step is for H2SO4 to attach to a positive ion that does not contain H2SO4. Unlike negative ions, the effect of charge on the bonding of H2SO4 with positive ions is much weaker and thus the stepwise Gibbs free energy change for the addition of one H2SO4 molecule to form a positively charged cluster is likely to be similar to that of neutral clusters, i.e., decreasing with cluster size. Therefore, the QC data for positively charged clusters containing one H2SO4 molecule provide a critical constraint. The success of the model in predicting the [NH3] needed for nucleation on positive ions to occur (see Sect. 3) shows the usefulness of the first-step data and approximation.
As seen from Fig. 4, bonding of H2SO4 to small negatively charged clusters (s < 3) is much stronger than that to neutrals and positive ions. As a result, at s < 3 the formation of negatively charged clusters is barrierless ( < 0). These small clusters cannot be considered nucleated particles because (Fig. 4a) first increases and then decreases with growing s, reaching the maximum barrier values at –6. can become positive for larger clusters due to the charge effect decreasing quickly as the clusters are growing. The effect of NH3 on negative ions becomes important at , when bonding between the clusters and NH3 becomes strong enough to contaminate a large fraction of binary clusters with ammonia (Fig. 3). In contrast, the impact of NH3 on neutral dimers and positively charged monomers of H2SO4, as well as on for both positively charged and neutral clusters, monotonically decreases for all s values, including s≤5.
for charged and neutral clusters converges into the bulk values at , when impact of the chemical identity of the core ion on the cluster composition becomes diffuse (Schobesberger et al., 2015) and when the contribution of the electrostatic effect to becomes less than ∼0.5 kcal mol−1. The comparison of cumulative (total) (Fig. 4b) indicates the lowest nucleation barrier for the case of negative ions, followed by positive ions and neutrals. The barrierless formation of clusters with s ranging from 1 to 3 substantially reduces the nucleation barrier for negatively charged ions and facilitates their nucleation. The presence of 0.3 ppb of NH3 lowers the nucleation barrier for negative, positive, and neutral clusters from ∼17, 24, and 38 kcal mol−1 to 2, 7, and 16 kcal mol−1, respectively. A relatively low nucleation barrier for charged ternary clusters is explained by the simultaneous effect of ionization and NH3, which also reduces the size of the critical cluster (s*).
It is important to note that the size of the critical cluster, commonly used to “measure” the activity of nucleation agents in the classical nucleation theory (Coffman and Hegg, 1995; Korhonen et al., 1999; Vehkamäki et al., 2002; Napari et al., 2002; Hamill et al., 1982) is no longer a valid indicator, when charged molecular clusters and small nanoparticles are considered. As seen from Fig. 4, positively charged ternary critical clusters (–4) are smaller than the corresponding negatively charged ones (–5); however, the nucleation barrier for ternary positive clusters under the condition specified in the figure caption is more than 3 times higher than that for ternary negatives ones.
2.4.3 Size- and composition-dependent H2SO4 evaporation rates
As we mentioned earlier, H2SO4 is the key atmospheric nucleation precursor driving the formation and growth of clusters in the ternary H2SO4–H2O–NH3 system while ions, H2O, and NH3 act to stabilize the H2SO4 clusters. The clustering thermodynamic data derived from QC calculations and measurements (Sect. 2.3) are used to constrain size- and composition- dependent Gibbs free energy changes and evaporation rates of H2SO4, which are critically important. Average or effective rates of H2SO4 molecule evaporation from positively charged, negatively charged, and neutral clusters containing s H2SO4 molecules () are calculated from as
where No is as defined in Eq. (6). The present model assumes only a single H2SO4 molecule evaporates, i.e., no water ligands, for instance, are attached to it. This is likely the dominant evaporation pathway as hydrated H2SO4 molecules are generally more stable.
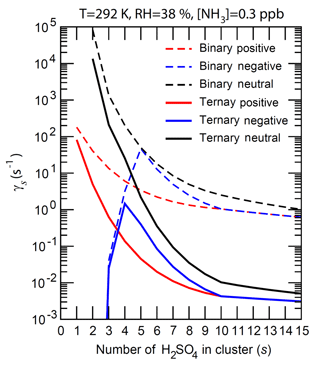
Figure 5The number-concentration-weighted mean evaporation rates () of H2SO4 molecules from neutral clusters (black), positively charged clusters (red), and negatively charged clusters (blue) for binary (H2SO4–H2O, dashed lines) and ternary (H2SO4–H2O–NH3, solid lines) nucleating systems containing s H2SO4 molecules (). T = 292 K, RH = 38 %, and [NH3] = 0.3 ppb for the ternary system.
Figure 5 gives the mean evaporation rate () of a H2SO4 molecule from these clusters under the conditions corresponding to Fig. 4. The shapes of curves are similar to those of (Fig. 4a) as values are largely controlled by (Eq. 12). The presence of ammonia, as expected, significantly reduces the vapor pressure of H2SO4 over bulk aerosol (Marti et al., 1997) and hence the H2SO4 evaporation rate. The evaporation rates of both neutral and positive clusters decrease as s increases, and the positive clusters are uniformly more stable than corresponding neutral clusters. for negative ions first increases and then decreases as s increases, peaking at around –6. The presence of NH3 reduces the evaporation rates of larger clusters by more than 2 orders of magnitude and the effect decreases for smaller clusters, as the binding of NH3 to small neutral and charged clusters is weaker compared to that for larger clusters (Fig. 4). [NH3] influences the average NH3 : H2SO4 ratio (Fig. 3) and the evaporation rates of these small clusters. The nucleation rates, limited by formation of small clusters (s < ∼5), depend strongly on the stability or evaporation rate of these small clusters. While the binding of NH3 to small neutral and charged clusters is weaker compared to that to larger clusters, small clusters containing NH3 are much more stable than those without (Fig. 4) and thus ammonia is important for nucleation.
The evolution of cluster/particle size distributions can be obtained by solving the dynamic Eqs. (1)–(6). Since the concentrations of clusters of all sizes are predicted, the nucleation rates in the kinetic model can be calculated for any cluster size larger than the critical size of neutral clusters (i > i*) (Yu, 2006b),
where , , and are nucleation rates associated with positive, negative, and neutral clusters containing i H2SO4 molecules. As a result of scavenging by preexisting particles or wall loss, the steady-state Ji decreases as i increases. To compare with CLOUD measurements, we calculate nucleation at a cluster mobility diameter of 1.7 nm (J1.7).
Many practical applications require information on the steady state nucleation rates. For each nucleation case presented in this paper, constant values of [H2SO4] (i.e., ), [NH3], T, RH, Q, and are assumed. The preexisting particles with fixed surface area or wall loss serve as a sink for all clusters. Under a given condition, cluster distribution and nucleation rate reach steady state after a certain amount of time. We calculate size-dependent coefficients for a given case and then solve Eqs. (1)–(6) to obtain the steady-state cluster distribution and nucleation rate, with the approach described in Yu (2006b).
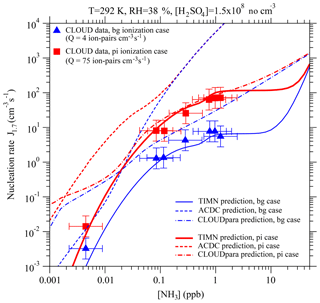
Figure 6Effect of ammonia concentrations ([NH3]) on effective nucleation rates calculated at a cluster mobility diameter of 1.7 nm (J1.7, lines) under the stated conditions with two ionization rates (Q) – background ionization, bg (blue), and ionization enhanced by a pion beam, pi (red). Also shown are predictions from the TIMN model, the Atmospheric Cluster Dynamics Code (ACDC) with thermochemistry obtained using the RI-CC2//B3LYP method (McGrath et al., 2012; Kürten et al., 2016), and an empirical parameterization of CLOUD measurements (CLOUDpara) (Dunne et al., 2016) indicated by solid, dashed, and dot-dashed lines, respectively. The symbols refer to CLOUD experimental data (Kirkby et al., 2011; Dunne et al., 2016), with the uncertainties in measured [NH3] and J1.7 shown by horizontal and vertical bars, respectively. To be comparable, the CLOUD data points given in Dunne et al. (2016) under the conditions of T = 292 K and RH = 38 % with [H2SO4] close to 1.5 × 108 cm−3 have been interpolated to the same [H2SO4] value (= 1.5 × 108 cm−3).
Figure 6 shows a comparison of the model TIMN rates J1.7 with CLOUD measurements, as a function of [NH3] under two ionization rates. It should be noted that Dunne et al. (2016) developed a simple empirical parameterization (denoted hereafter as “CLOUDpara”) of binary, ternary, and IIN rates in CLOUD measurements as a function of [NH3], [H2SO4], T, and negative ion concentration. The predictions of CLOUDpara (Dunne et al., 2016) and ACDC based on nucleation thermochemistry obtained using the RI-CC2//B3LYP method (McGrath et al., 2012; Kürten et al., 2016) are also presented in Fig. 6 for comparisons.
Like the CLOUD measurements, the TIMN predictions reveal a complex dependence of J1.7 on [NH3], and an analysis of the TIMN results shows this behavior can be explained by the differing responses of negative, positive, and neutral clusters to the presence of ammonia (Fig. 4). Under the conditions specified in Fig. 6, nucleation is dominated by negative ions for [NH3] < ∼0.5 ppb, by both negative and positive ions for [NH3] from ∼0.5 ppb to ∼10 ppb (with background ionization) or ∼20 ppb (with pion-enhanced ionization), and by neutrals at higher [NH3]. According to TIMN, [NH3] values of at least 0.6–1 ppb are needed before positive ions contribute significantly to nucleation rates – in good agreement with the threshold found in the CLOUD experiments (Kirkby et al., 2011; Schobesberger et al., 2015). TIMN simulations also extend CLOUD data at [NH3] of ∼1 ppb to include a “zero-sensitivity zone” in the region of 1–10 ppb, followed by a region of strong sensitivity of J1.7 to [NH3] commencing at [NH3] > ∼10–20 ppb. The latter zone may have important implications for NPF in heavily polluted regions, including much of India and China, where [NH3] may exceed 10–20 ppb (Behera and Sharma, 2010; Meng et al., 2018). It is noteworthy in Fig. 6 that the dependence of J1.7 on [NH3] and Q predicted by the ACDC model (McGrath et al., 2012) and the CLOUD data parameterization (Dunne et al., 2016) deviate substantially from the experimental data as well as the TIMN simulations. CLOUDpara does not consider impacts of positive ions and key controlling parameters such as RH and surface area of preexisting particles. Dunne et al. (2016) reported that CLOUDpara is also very sensitive to the approach to parameterize T dependence, showing that the contribution of ternary IIN to NPF below 15 km in altitude has grown from 9.6 % to 37.5 %, after the initial empirical temperature function was replaced with a simpler one.
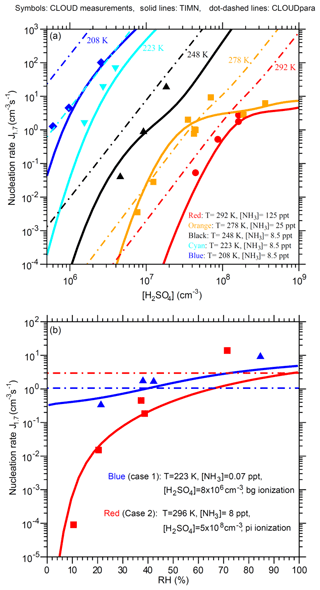
Figure 7Comparison of TIMN simulations (solid lines), CLOUDpara predictions (Dunne et al., 2016) (dot-dashed lines), and CLOUD measurements (symbols and data from Dunne et al., 2016) of the dependences of nucleation rates on (a) [H2SO4] at five different temperatures (T = 292, 278, 248, 223, and 208 K) and (b) RH at two sets of conditions as specified. [NH3] is in parts per trillion, by volume. Error bars for the uncertainties in measured [H2SO4] (−50 %, +100 %), [NH3] (−50 %, +100 %), and J1.7 (overall a factor of 2) are not shown. To be comparable, the CLOUD data points given in Dunne et al. (2016) under the conditions (T, RH, ionization rate) with [NH3] or [H2SO4] close to the corresponding values specified in the figure legends have been interpolated to the same [NH3] (Fig. 7a) or [H2SO4] (Fig. 7b) values.
Figure 7 presents a more detailed comparison of TIMN simulations with CLOUD measurements of J1.7 as a function of [H2SO4], T, and RH. The TIMN model reproduces both the absolute values of J1.7 and its dependencies on [H2SO4], T, and RH in a wide range of temperatures (T = 208–292 K) and [H2SO4] (5 × 105–5 × 108 cm−3). As expected, nucleation rates are very sensitive to [H2SO4] and T. For example, J1.7 increases by 3 to 5 orders of magnitude with an increase in [H2SO4] of a factor of 10 and by roughly 1 order of magnitude for a temperature decrease of 10 ∘C, except in cases in which the nucleation rate is limited by Q (for example, [H2SO4] = ∼108–109 cm−3 at T = 278 and 292 K, shown in Fig. 7a). The key difference between CLOUDpara and TIMN predictions is that the dlnJ1.7 ∕ dln[H2SO4] ratio predicted by CLOUDpara is nearly constant while TIMN shows that this ratio depends on both [H2SO4] and T. The CLOUD measurements taken at T = 278 K clearly show (in agreement with the TIMN) that dlnJ1.7 ∕ dln[H2SO4] is not constant. CLOUDpara overestimates J1.7 compared to both measurements and TIMN simulations, except for the case in which T = 278 K and [H2SO4] range from ∼7 × 106 to 5 × 107 cm−3, with a deviation of CLOUDpara from experimental data and TIMN growing with the lower temperature.
Both CLOUD measurements and TIMN simulations (Fig. 7b) show an important influence of RH on nucleation rates. In particular, CLOUD measurements indicate a 1–5 order of magnitude rise in J1.7 after RH increases from 10 % to 70 %–80 % and a stronger effect of RH on nucleation rates at higher temperatures under the conditions shown in Fig. 7b. The RH dependence of J1.7 predicted by the TIMN model is consistent with measurements, being slightly weaker than that measured at high RH.
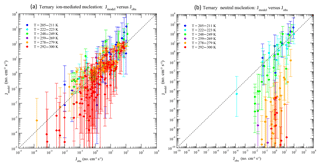
Figure 8Model predicted (Jmodel) versus observed (Jobs) nucleation rates under various conditions of all 377 data points of CLOUD measurements reported in Table S1 of Dunne et al. (2016), with (a) and without (b) the presence of ionization. The data points are grouped according to temperatures as specified in the legend. Vertical error bars show the range of Jmodel values calculated at 50 % and 200 % of measured [H2SO4], corresponding to the uncertainties in measured [H2SO4] (−50 %, +100 %). Error bars associated with the uncertainties in measured [NH3] (−50 %, +100 %) and Jobs (overall a factor of 2) are not shown.
Figure 8 compares TIMN model predictions with all 377 data points of CLOUD measurements reported in data Table S1 of Dunne et al. (2016). The vertical error bars show the range of Jmodel associated with the uncertainty in the [H2SO4] measured (−50 %, +100 %). The effect of uncertainty in measured [NH3] (−50 %, +100 %) is not included. In the presence of ionization (Fig. 8a), Jmodel agrees with CLOUD measurements within the uncertainties under mainly all conditions, although Jmodel tends to be slightly lower than Jobs when T = 292–300 K and Jobs is relatively small (< ∼1 cm−3 s−1). For the neutral nucleation (Fig. 8b), the model agrees well with observations at low T (T = 205–223 K) but deviates from observations as T increases. The underprediction of the model for neutral nucleation at T = 278–300 K cannot be explained by the uncertainties in measured [H2SO4] and [NH3]. Apparently for neutral nucleation the model predicts much stronger temperature dependence than the CLOUD measurements. The possible reasons for the difference include the uncertainties in both the model (especially the thermodynamics data and approximation) and measurements. It should be noted that under the conditions of high T and absence of ions, the role of cluster evaporation (i.e., thermodynamics) becomes more important (i.e., higher evaporation and/or generally less tightly bound clusters) and the effect of the possible biases of the used thermochemistry can be more clearly revealed. The contamination (by amines) in the CLOUD measurements (Kirkby et al., 2011) can be another possible reason. The level of contamination in the cloud chamber appears to increase with temperature (Kürten et al., 2016), which may explain the good agreement at low T and increased deviation at higher T. Further research is needed to identify the source of the difference for neutral ternary nucleation at high T.
A comprehensive kinetically based H2SO4–H2O–NH3 TIMN model, constrained with thermodynamic data from QC calculations and laboratory measurements, has been developed and used to shed new light on physicochemical processes underlying the effect of ammonia on NPF. We show that the stabilizing effect of NH3 grows with the cluster size and that the reduced effect of ammonia on smaller clusters is caused by weaker bonding that in turn yields lower average NH3-to-H2SO4 ratios. NH3 was found to impact nucleation barriers for neutral, positively charged, and negatively charged clusters differently due to the large difference in the binding energies of NH3, H2O, and H2SO4 to small clusters of different charging states. The lowest and highest nucleation barriers are observed in the case of negative ions and neutrals, respectively. Therefore, nucleation of negative ions is favorable, followed by nucleation of positive ions and neutrals. Different responses of negative, positive, and neutral clusters to ammonia result in a complex dependence of ternary nucleation rates on [NH3]. The TIMN model reproduces both the absolute values of nucleation rates and their dependencies on the key controlling parameters and agrees with the CLOUD measurements for all the cases at the presence of ionization. For the neutral ternary nucleation, the model agrees well with observations at low temperature but deviates from observations as temperature increases.
The TIMN model developed in the present study may be subject to uncertainties associated with the uncertainties in thermodynamic data and interpolation approximation for pre-nucleation clusters. Further measurements and quantum calculations, especially for relatively larger clusters, are needed to reduce the uncertainties. While the TIMN model predicts nucleation rates in a good overall agreement with the CLOUD measurements, its ability to explain the NPF events observed in the real atmosphere is yet to be quantified and will be investigated in further studies.
All relevant data are available in the article, or from the corresponding authors upon request.
Thermochemical data for small neutral and charged binary H2SO4–H2O and ternary H2SO4–H2O–NH3 clusters have been reported in a number of earlier publications (Bandy and Ianni, 1998; Ianni and Bandy, 1999; Torpo et al., 2007; Nadykto et al., 2008; Herb et al., 2011, 2013; Temelso et al., 2012a, b; DePalma et al., 2012; Ortega et al., 2012; Chon et al., 2014; Husar et al., 2014; Henschel et al., 2014, 2016; Kürten et al., 2015). The PW91PW91/6-311G(3df,3pd) method, which is a combination of the Perdue–Wang PW91PW91 density functional with the largest Pople 6-311G(3df,3pd) basis set, has thoroughly been validated and agrees well with existing experimental data. In earlier studies, this method has been applied to a large variety of atmospherically relevant clusters (Nadykto et al., 2006, 2007, 2008, 2014, 2015; Nadykto and Yu, 2007; Torpo et al., 2007; Zhang et al., 2009; Elm et al., 2012, 2013; Leverentz et al., 2013; Xu and Zhang, 2012, 2013; Zhu et al., 2014; Bork et al., 2014; Elm and Mikkelsen, 2014; Peng et al., 2015; Miao et al 2015; Ma et al., 2016) and has been shown to be well suited to study the H2SO4–H2O and H2SO4–H2O–NH3 clusters, as evidenced by a very good agreement of the computed values with measured cluster geometries, vibrational fundamentals, dipole properties, formation Gibbs free energies (Nadykto et al., 2007, 2008, 2014, 2015; Nadykto and Yu, 2007; Herb et al., 2013; Elm et al., 2012, 2013; Leverentz et al., 2013; Bork et al., 2014), and high-level ab initio results (Temelso et al., 2012a, b; Husar et al., 2012; Bustos et al., 2014).
Table A1Number of isomers successfully converged at the 6-311 level for selected clusters, along with the enthalpy, entropy, and Gibbs free energy of the most stable isomers (1 hartree = 627.5 kcal mol−1).
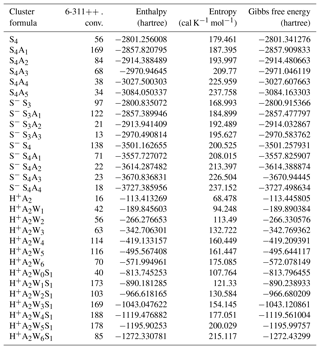
Table A2QC-based stepwise Gibbs free energy change (kcal mol−1) for the addition of one water (), ammonia (), or sulfuric acid () molecule to form the given positively charged clusters under standard conditions and the corresponding experimental data or semi-experimental estimates.

a Froyd and Lovejoy (2003a). b Meot-Ner
(Mautner) et al. (1984). c Payzant et al. (1973).
d Froyd (2002). e Froyd and Lovejoy (2012).
f The values given
here were calculated based on experimental
values at T = 270 K from Froyd and Lovejoy (2003a) and ΔS
values from quantum calculation.
Table A3Same as Table A2 except for neutral clusters.
a Nadykto and Yu (2007). b Torpo et al. (2007). c Ortega et al. (2012). d Chon et al. (2007). e Kürten et al. (2015).
We have extended the earlier QC studies of binary and ternary clusters to larger sizes. The computations have been carried out using a Gaussian 09 suite of programs (Frish et al., 2009). In order to ensure the quality of the conformational search we have carried out a thorough sampling of conformers. We have used both a basin-hopping algorithm, as implemented in Biovia Materials Studio 8.0, and locally developed sampling code. The sampling code is based on the following principle: mesh, with molecules to be added to the cluster placed in the mesh nodes, is created around the cluster, and a blind search algorithm is used to generate the guess geometries. The mesh density and orientation of molecules, as well as the minimum distance between molecules and cluster, are variable. Typically, for each cluster of a given chemical composition a thousand to several thousands of isomers have been sampled. We used a three-step optimization procedure, which includes
- i.
pre-optimization of initial and guess geometries using the semiempirical PM6 method, separation of the most stable isomers located within 15 kcal mol−1 of the intermediate global minimum and duplicate removal, followed by
- ii.
optimization of the selected isomers meeting the aforementioned stability criterion by the PW91PW91/CBSB7 method and
- iii.
the final optimization of the most stable isomers at the PW91PW91/CBSB7 level within 5 kcal mol−1 of the current global minimum using the PW91PW91/6-311G(3df,3pd) method.
Typically, only ∼4 %–30 % of initially sampled isomers reach the second (PW91PW91/CBSB7) level, at which ∼10 %–40 % of isomers optimized with PW91PW91/CBSB7 are selected for the final run. Typically, the number of equilibrium isomers of hydrated clusters is larger than that of unhydrated ones of similar chemical composition. Table A1 shows the numbers of isomers converged at the final PW91PW91/6-311G(3df,3pd) optimization step for selected clusters and HSG (enthalpy, entropy, and Gibbs free energy) values of the most stable isomers used in the present study. The number of isomers optimized at the PW91PW91/6-311G(3df,3pd) level of theory varies from case to case, typically being in the range of ∼10–200.
The computed stepwise enthalpy, entropy, and Gibbs free energies of cluster formation have been thoroughly evaluated and used to calculate the evaporation rates of H2SO4 from neutral, positively, and negatively charged clusters.
A1 Positively charged clusters
Table A2 presents the computed stepwise Gibbs free energy changes under standard conditions (ΔGo) for positive binary and ternary clusters, along with the corresponding experimental data or semi-experimental estimates. Figure 2 in the main text shows ΔG associated with the addition of water (), ammonia (), and sulfuric acid () to binary and ternary clusters as a function of the cluster hydration number w. Both the absolute values and trends in derived from calculations are in agreement with the laboratory measurements within the uncertainty range of ∼1–2 kcal mol−1 for both QC calculations and measurements. This confirms the efficiency and precision of QC methods in calculating thermodynamic data needed for the development of nucleation models. Nevertheless, it should be noted that the uncertainties in computed free energies of 1–2 kcal mol−1 may lead to large uncertainty in predicted particle formation rates. By increasing or decreasing all Gibbs free energies by 1 kcal mol−1, Kürten at al. (2016) showed that, depending on the conditions, the modeled particle formation rate can change from less than an order of magnitude to several orders of magnitude. Uncertainties estimated by Kürten at al. (2016) represent the upper limit because computed free energies may be overestimated for some clusters and underpredicted for others, which leads to partial or, in some case, full error cancelation.
A2 Neutral clusters
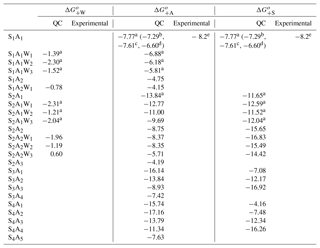
Table A3 presents the computed stepwise Gibbs free energy changes for the formation of ternary SsAaWw clusters under standard conditions. The corresponding binary electrically neutral clusters can be found in previous publications (e.g., Nadykto et al., 2008; Herb et al., 2011). The thermodynamic properties of the S1A1 have been reported in a number of computational studies (e.g., Herb et al., 2011; Kurtén et al., 2007; Nadykto and Yu, 2007). However, most of these studies, except for Nadykto and Yu (2007) and Henschel et al. (2014, 2016), did not consider the impact of H2O on cluster thermodynamics. We have extended the earlier studies of Nadykto and Yu (2007) and Herb et al. (2011) to larger clusters up to S4A5 (no hydration) and up to S2A2 (hydration included). The free energy of binding of NH3 to H2SO4 (or H2SO4 to NH3) obtained using our method is −7.77 kcal mol−1, which is slightly more negative than values reported by other groups (−6.6–7.61 kcal mol−1) and within less than 0.5 kcal mol−1 of the experimental value of −8.2 kcal mol−1 derived from CLOUD measurements (Kürten et al., 2015).
As it may be seen from Table A3, the NH3 binding to S1−2Ww weakens as w increases. The average for S1Ww formation derived from a combination of laboratory measurements and quantum chemical studies are −3.02, −2.37, and −1.40 kcal mol−1 for the first, second, and third hydrations, respectively (Yu, 2007). This indicates that a large fraction of H2SO4 monomers in the Earth's atmosphere are likely hydrated. Therefore, the decreasing NH3 binding strength to hydrated H2SO4 monomers implies that RH (and T) will affect the relative abundance of H2SO4 monomers containing NH3. Currently, no experimental data or observations are available to evaluate the impact of hydration (or RH) on . Table A3 shows that the presence of NH3 in H2SO4 clusters suppresses hydration and that for S2A2 falls below −2.0 kcal mol−1. This is consistent with earlier studies by our group (Herb et al., 2011) and others (Henschel et al., 2014, 2016) showing that large SnAn clusters (n > 2) are not hydrated under typical atmospheric conditions. In the present study, the hydration of neutral SnAn clusters at n > 2 is neglected, due to the lack of thermodynamic data.
The number of NH3 molecules in the cluster (or H2SO4 to NH3 ratio) significantly affects and values. For example, for S3Aa clusters increases from −7.08 to −16.92 kcal mol−1 and decreases from −16.14 to −8.93 kcal mol−1 as a grows from 1 to 3. For S4Aa clusters, increases from −7.48 to −16.26 kcal mol−1 and decreases from −17.16 to −11.34 kcal mol−1 as a increases from 2 to 4. for the S4A1 cluster is less negative by 1.38 kcal mol−1 than that for S4A2. for the S4A1 cluster is also quite low (−4.16 kcal mol−1), which might indicate the possible existence of a more stable S4A1 isomer, which is yet to be identified. In the presence of NH3, the uncertainty in the thermochemistry data for S4A1 will not significantly affect ternary nucleation rates because most S4 clusters contain three or four NH3 molecules.
For the SsAa clusters with s=a, increases as the cluster grows while first increases significantly as S1A1 is converted into S2A2 and then levels off as S2A2 is converted into S4A4. We also observe a significant drop in when the NH3 ∕ H2SO4 ratio exceeds 1. This finding is consistent with the ACDC model calculation showing that growth of neutral SsAa clusters follows the s=a pathway (Schobesberger et al., 2015).
A3 Negative ionic clusters
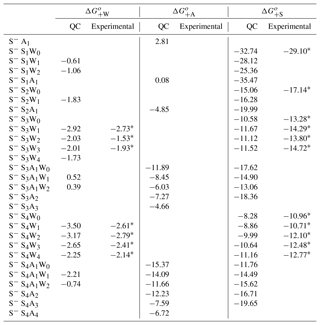
Table A4 shows ΔG+W, ΔG+A, and ΔG+S needed to form negatively charged clusters under standard conditions, along with available semi-experimental values (Froyd and Lovejoy, 2003b). H2O binding to negatively charged S−Ss clusters significantly strengths with increasing s, from = −0.61 – −1.83 kcal mol−1 at s=1–2 to = −3.5 kcal mol−1 at w=1 and −2.25 kcal mol−1 at w=4 at s=4. values at s=3 and 4 are slightly more negative (by ∼0.1–0.9 kcal mol−1) than those reported by Froyd and Lovejoy (2003b). Just like H2O binding, NH3 binding to S−Ss at s < 3 is very weak, with ranging from +2.81 kcal mol−1 at s=0 to −4.85 kcal mol−1 at s=2. However, it significantly increases as s grows. In particular, at ranges from −11.89 kcal mol−1 for S−S3A1 to −15.37 kcal mol−1 for S− S4A1. NH3 clearly cannot enter small negative ions. However, it can easily attach to larger negative ions with s≥3, which is consistent with CLOUD measurements (Schobesberger et al., 2015). Since hydration weakens NH3 binding in S−S3A1Ww and S−S4A1Ww clusters, its impacts on the cluster formation and nucleation rates may potentially be important.
In contrast to H2O and NH3, binding of H2SO4 to small negative ions (s < 3) is very strong. These ions are very stable even when they contain no NH3 or H2O molecules. High electron affinity of H2SO4 molecules results in the high stability of S−Ss at s=1–2. However, the charge effect reduces as s grows. In particular, of S−Ss drops from −32.74 kcal mol−1 at s=1 to −10.58 kcal mol−1 and −8.28 kcal mol−1 at s=3 and 4, respectively. At the same time, increases from 0.08 kcal mol−1 (s=1) to −11.89 kcal mol−1 (s=3) and −15.37 kcal mol−1 (s=4). The hydration of S−Ss at s=3 and 4 enhances the strength of H2SO4 binding, especially at s=4. values for S−S3−4Ww are consistently ∼1.5–3 kcal mol−1 less negative than the corresponding semi-experimental estimates (Table A4). The possible reasons behind the observed systematic difference are yet to be identified and include the use of the low-level ab initio Hartree–Fock method to compute reaction enthalpies and uncertainties in experimental enthalpies in studies by Froyd and Lovejoy (2003b).
NH3 binding to S−S3 significantly enhances the stability of H2SO4 in the cluster by ∼7 kcal mol−1 compared to for the corresponding binary counterpart. The binding of the second NH3 to S−S3A to form S−S3A2 is much weaker ( = −7.27 kcal mol−1) than that of the first NH3 molecule ( kcal mol−1). This indicates that most of S−S3Aa can only contain one NH3 molecule, in a perfect agreement with the laboratory study of Schobesberger et al. (2015). In the case of S−S4, binding of the first ( = −15.37 kcal mol−1) and second (and −12.23 kcal mol−1) NH3 molecules to the cluster is quite strong, while the attachment of NH3 leads to substantial stabilization of H2SO4 in the cluster, as evidenced by growing from −8.28 kcal mol−1 at a=0 to −11.76 kcal mol−1 and −16.71 kcal mol−1 at a=1 and a=2, respectively. The NH3 binding free energy to S−S4A2 (to form S−S4A3) drops to −7.59 kcal mol−1, indicating, in agreement with the CLOUD measurements (Schobesberger et al., 2015), that most S−S4 clusters contain one or two NH3 molecules.
FY designed the study, led the development of the TIMN model, analyzed results, and wrote a major part of the paper. ABN, JH, KMN, and LAU designed, carried out, and evaluated quantum calculations. ABN also contributed to the writing of the paper. GL contributed to the result analysis and discussion. All contributed to the reviewing and editing of the paper.
The authors declare that they have no conflict of interest.
The authors thank Richard Turco (Distinguished Professor Emeritus, UCLA) for
comments that helped to improve the paper. This study was supported by the
NSF under grant 1550816, NASA under grant NNX13AK20G, and NYSERDA under
contract 100416. ABN, KMN and LAU would like to thank the Russian Science Foundation
(under grant 18-11-00247) and
the Ministry of Science and Education of Russia (under grants 1.6198.2017/6.7
and 1.7706.2017/8.9) for support and the Center of Collective Use of MSTU
“STANKIN” for providing resources. Edited by: Veli-Matti
Kerminen
Reviewed by: three anonymous referees
Almeida, J., Schobesberger, S., Kürten, A., Ortega, I. K., Kupiainen-Määttä, O., Praplan, A. P., Adamov, A., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Dommen, J., Donahue, N. M., Downard, A., Dunne, E., Duplissy, J., Ehrhart, S., Flagan, R. C., Franchin, A., Guida, R., Hakala, J., Hansel, A., Heinritzi, M., Henschel, H., Jokinen, T., Junninen, H., Kajos, M., Kangasluoma, J., Keskinen, H., Kupc, A., Kurtén, T., Kvashin, A. N., Laaksonen, A., Lehtipalo, K., Leiminger, M., Leppä, J., Loukonen, V., Makhmutov, V., Mathot, S., McGrath, M. J., Nieminen, T., Olenius, T., Onnela, A., Petäjä, T., Riccobono, F., Riipinen, I., Rissanen, M., Rondo, L., Ruuskanen, T., Santos, F. D., Sarnela, N., Schallhart, S., Schnitzhofer, R., Seinfeld, J. H., Simon, M., Sipilä, M., Stozhkov, Y., Stratmann, F., Tomé, A., Tröstl, J., Tsagkogeorgas, G., Vaattovaara, P., Viisanen, Y., Virtanen, A., Vrtala, A., Wagner, P. E., Weingartner, E., Wex, H., Williamson, C., Wimmer, D., Ye, P., Yli-Juuti, T., Carslaw, K. S., Kulmala, M., Curtius, J., Baltensperger, U., Worsnop, D. R., Vehkamäki, H., and Kirkby, J.: Molecular understanding of sulphuric acid-amine particle nucleation in the atmosphere, Nature, 502, 359–363, 2013.
Ball, S. M., Hanson, D. R., Eisele, F. L., and McMurry, P. H., Laboratory studies of particle nucleation: Initial results for H2SO4, H2O, and NH3 vapors, J. Geophys. Res., 104, 23709–23718, https://doi.org/10.1029/1999JD900411, 1999.
Bandy, A. R. and Ianni, J. C.: Study of the hydrates of H2SO4 using density functional theory, J. Phys. Chem. A, 102, 6533–6539, 1998.
Behera, S. N. and Sharma, M.: Investigating the potential role of ammonia in ion chemistry of fine particulate matter formation for an urban environment, Sci. Total Environ., 408, 3569–3575, 2010.
Benson, D. R., Erupe, M. E., and Lee, S.-H.: Laboratory-measured H2SO4-H2O-NH3 ternary homogeneous nucleation rates: Initial observations, Geophys. Res. Lett., 36, L15818, https://doi.org/10.1029/2009GL038728, 2009.
Bork, N., Du, L., Reiman, H., Kurteìn, T., and Kjaergaard, H. G.: Benchmarking ab initio binding energies of hydrogen-bonded molecular clusters based on FTIR spectroscopy, J. Phys. Chem. A, 118, 5316–5322, 2014.
Bustos, D. J., Temelso, B., and Shields, G. C.: Hydration of the Sulfuric Acid–Methylamine Complex and Implications for Aerosol Formation, J. Phys. Chem. A, 118, 7430–7441, 2014.
Butler, T., Vermeylen, F., Lehmann, C. M., Likens, G. E., and Puchalski, M.: Increasing ammonia concentration trends in large regions of the USA derived from the NADP/AMoN network, Atmos. Environ., 146, 132–140, 2016.
Chen, M., Titcombe, M., Jiang, J., Kuang, C., Fischer, M. L., Edgerton, E., Eisele, F. L., Siepmann, J. I., Hanson, D. H., Zhao, J., and McMurry, P. H.: Acid-base chemical reaction model for nucleation rates in the polluted boundary layer, P. Natl. Acad. Sci. USA, 109, 18713–18718, 2012.
Chon, N. L., Lee, S. H., and Lin, H.: A theoretical study of temperature dependence of cluster formation from sulfuric acid and ammonia, Chem. Phys., 433, 60–66, 2014.
Coffman, D. J. and Hegg, D. A.: A preliminary study of the effect of ammonia on particle nucleation in the marine boundary layer, J. Geophys. Res., 100, 7147–7160, 1995.
Davidson, J. A., Fehsenfeld, F. C., and Howard, C. J.: The heats of formation of and association complexes with HNO3 and HBr, Int. J. Chem. Kinet., 9, 17–29, 1977.
Dawson, M. L., Varner, M. E., Perraud, V., Ezell, M. J., Gerber, R. B., and Finlayson-Pitts, B. J.: Simplified mechanism for new particle formation from methanesulfonic acid, amines and water via experiments and ab initio calculations, P. Natl. Acad. Sci. USA, 109, 18719–18724, 2012.
DePalma, J. W., Bzdek, B. R., Doren, D. J., and Johnston, M. V.: Structure and energetics of nanometer size clusters of sulfuric acid with ammonia and dimethylamine, J. Phys. Chem. A, 116, 1030–1040, 2012.
Doyle, G. J.: Self-nucleation in the sulfuric acid-water system, J. Chem. Phys., 35, 795–799, 1961.
Dunne, E. M., Gordon, H., Kürten, A., Almeida, J., Duplissy, J., Williamson, C., Ortega, I. K., Pringle, K. J., Adamov, A., Baltensperger, U., Barmet, P., Benduhn, F., Bianchi, F., Breitenlechner, M., Clarke, A., Curtius, J., Dommen, J., Donahue, N. M., Ehrhart, S., Flagan, R. C., Franchin, A., Guida, R., Hakala, J., Hansel, A., Heinritzi, M., Jokinen, T., Kangasluoma, J., Kirkby, J., Kulmala, M., Kupc, A., Lawler, M. J., Lehtipalo, K., Makhmutov, V., Mann, G., Mathot, S., Merikanto, J., Miettinen, P., Nenes, A., Onnela, A., Rap, A., Reddington, C. L. S., Riccobono, F., Richards, N. A. D., Rissanen, M. P., Rondo, L., Sarnela, N., Schobesberger, S., Sengupta, K., Simon, M., Sipilä, M., Smith, J. N., Stozkhov, Y., Tomé, A., Tröstl, J., Wagner, P. E., Wimmer, D., Winkler, P. M., Worsnop, D. R., and Carslaw, K. S.: Global particle formation from CERN CLOUD measurements, Science, 354, 1119–1124, https://doi.org/10.1126/science.aaf2649, 2016.
Duplissy, J., Merikanto, J., Franchin, A., Tsagkogeorgas, G., Kangasluoma, J., Wimmer, D., Vuollekoski, H., Schobesberger, S., Lehtipalo, K., Flagan, R. C., Brus, D., Donahue, N. M., Vehkämäki, H., Almeida, J., Amorim, A., Barmet, P., Bianchi, F., Breitenlechner, M., Dunne, E. M., Guida, R., Henschel, H., Junninen, H., Kirkby, J., Kürten, A., Kupc, A., Määttänen, A., Makhmutov, V., Mathot, S., Nieminen, T., Onnela, A., Praplan, A. P., Riccobono, F., Rondo, L., Steiner, G., Tome, A., Walther, H., Baltensperger, U., Carslaw, K. S., Dommen, J., Hansel, A., Petäjä, T., Sipilä, M., Stratmann, F., Vrtala, A.,Wagner, P. E., Worsnop, D. R., Curtius, J., and Kulmala, M.: Effect of ions on sulfuric acid-water binary particle formation II: Experimental data and comparison with QC-normalized classical nucleation theory, J. Geophys. Res.-Atmos., 121, 1752–1775, https://doi.org/10.1002/2015JD023539, 2016.
Elm, J. and Mikkelsen, K. V.: Computational approaches for efficiently modelling of small atmospheric clusters, Chem. Phys. Lett., 615, 26–29, 2014.
Elm, J., Bilde, M., and Mikkelsen, K. V.: Assessment of density functional theory in predicting structures and free energies of reaction of atmospheric prenucleation clusters, J. Chem. Theory Comput., 8, 2071–2077, 2012.
Elm, J., Bilde, M., and Mikkelsen, K. V.: Assessment of binding energies of atmospherically relevant clusters, Phys. Chem. Chem. Phys., 15, 16442–16445, 2013.
Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman, J. R., Scalmani, G., Barone, V., Mennucci, B., Petersson, G. A., Nakatsuji, H., Caricato, M., Li, X., Hratchian, H. P., Izmaylov, A. F., Bloino, J., Zheng, G., Sonnenberg, J. L., Hada, M., Ehara, M., Toyota, K., Fukuda, R., Hasegawa, J., Ishida, M., Nakajima, T., Honda, Y., Kitao, O., Nakai, H., Vreven, T., Montgomery, J. J. A., Peralta, J. E., Ogliaro, F., Bearpark, M., Heyd, J. J., Brothers, E., Kudin, K. N., Staroverov, V. N., Kobayashi, R., Normand, J., Raghavachari, K., Rendell, A., Burant, J. C., Iyengar, S. S., Tomasi, J., Cossi, M., Rega, N., Millam, J. M., Klene, M., Knox, J. E., Cross, J. B., Bakken, V., Adamo, C., Jaramillo, J., Gomperts, R., Stratmann, R. E., Yazyev, O., Austin, A. J., Cammi, R., Pomelli, C., Ochterski, J. W., Martin, R. L., Morokuma, K., Zakrzewski, V. G., Voth, G. A., Salvador, P., Dannenberg, J. J., Dapprich, S., Daniels, A. D., Farkas, O., Foresman, J. B., Ortiz, J. V., Cioslowski, J., and Fox, D. J.: Gaussian 09, Wallingford CT, 2009.
Froyd, K. D.: Ion induced nucleation in the atmosphere: Studies of NH3, H2SO4, and H2O cluster ions, Ph.D. thesis, Univ. of Colo., Boulder, 2002.
Froyd, K. D. and Lovejoy, E. R.: Experimental thermodynamics of cluster ions composed of H2SO4 and H2O. 1. Positive ions, J. Phys. Chem. A, 107, 9800–9811, 2003a.
Froyd, K. D. and Lovejoy, E. R.: Experimental thermodynamics of cluster ions composed of H2SO4 and H2O. 2. Measurements and ab initio structures of negative ions, J. Phys. Chem. A, 107, 9812–9824, 2003b.
Froyd K. D. and Lovejoy E. R.: Bond energies and structures of ammonia-sulfuric acid positive cluster ions, J. Phys. Chem. A, 116, 5886–5899, https://doi.org/10.1021/jp209908f, 2012.
Glasoe, W. A., Volz, K., Panta, B., Freshour, N., Bachman, R., Hanson, D. R., McMurry, P. H., and Jen, C.: Sulfuric acid nucleation: An experimental study of the effect of seven bases, J. Geophys. Res.-Atmos., 120, 1933–1950, 2015.
Hamill, P., Turco, R. P., Kiang, C. S., Toon, O. B., and Whitten, R. C.: An analysis of various nucleation mechanisms for sulfate particles in the stratosphere, J. Aerosol Sci., 13, 561–585, 1982.
Hanson, D. R. and Eisele, F.: Diffusion of H2SO4 in humidified nitrogen: Hydrated H2SO4, J. Phys. Chem. A, 104, 1715–1719, 2000.
Hanson, D. R. and Eisele, F. L.: Measurement of prenucleation molecular clusters in the NH3, H2SO4, H2O system, J. Geophys. Res., 107, 4158, https://doi.org/10.1029/2001JD001100, 2002.
Hanson, D. R. and Lovejoy, E. R.: Measurement of the thermodynamics of the hydrated dimer and trimers, J. Phys. Chem. A, 110, 9525–9538, https://doi.org/10.1021/jp062844w, 2006.
Henschel, H., Navarro, J. C. A., Yli-Juuti, T., Kupiainen-Määttä, O., Olenius, T., Ortega, I. K., Clegg, S. L., Kurtén, T., Riipinen, I., and Vehkamäki, H.: Hydration of atmospherically relevant molecular clusters: Computational chemistry and classical thermodynamics, J. Phys. Chem. A, 118, 2599–2611, 2014.
Henschel, H., Kurtén, T., and Vehkamäki, H.: Computational study on the effect of hydration on new particle formation in the sulfuric acid/ammonia and sulfuric acid/dimethylamine systems, J. Phys. Chem. A, 120, 1886–1896, https://doi.org/10.1021/acs.jpca.5b11366, 2016.
Herb, J., Nadykto, A., and Yu, F.: Large Ternary Hydrogen-Bonded Pre-Nucleation Clusters in the Earth's Atmosphere, Chem. Phys. Lett., 518, 7–14, https://doi.org/10.1016/j.cplett.2011.10.035, 2011.
Herb, J., Xu, Y., Yu, F., and Nadykto, A. B.: Large Hydrogen-Bonded Pre-Nucleation ()(H2SO4)m(H2O)k and ()(NH3)(H2SO4) m(H2O)k Clusters in the Earth's Atmosphere, J. Phys. Chem., A, 117, 133–152, https://doi.org/10.1021/jp3088435, 2013.
Holland, P. M. and Castleman Jr., A. W.: Thomson equation revisited in light of ion-clustering experiments, J. Phys. Chem., 86, 4181-4188, 1982.
Hoppel, W. A. and Frick, G. M.: Ion-aerosol attachment coefficients and the steady-state charge distribution on aerosols in a bipolar ion environment, Aerosol Sci. Technol., 1–21, 1986.
Husar, D. E., Temelso, B., Ashworth, A. L., and Shields, G. C.: Hydration of the bisulfate ion: atmospheric implications, J. Phys. Chem. A, 116, 5151–5163, 2012.
Hyvärinen, A., Raatikainen, T., Laaksonen, A., Viisanen, Y., and Lihavainen, H.: Surface tensions and densities of H2SO4 + NH3 + water solutions, Geophy. Res. Lett., 32, L16806, https://doi.org/10.1029/2005GL023268, 2005.
Ianni, J. C. and Bandy, A. R.: A Density Functional Theory Study of the Hydrates of NH3-H2SO4 and Its Implications for the Formation of New Atmospheric Particles, J. Phys. Chem. A, 103, 2801–2811, 1999.
Jacobson, M., Turco, R., Jensen, E., and Toon, O.: Modeling coagulation among particles of different composition and size, Atmos. Environ., 28, 1327–1338, 1994.
Jolly, W. L.: Modern Inorganic Chemistry (2nd Edn.), New York, McGraw-Hill, 1991.
Kazil, J., Lovejoy, E. R., Jensen, E. J., and Hanson, D. R.: Is aerosol formation in cirrus clouds possible?, Atmos. Chem. Phys., 7, 1407–1413, https://doi.org/10.5194/acp-7-1407-2007, 2007.
Kebarle, P., Searles, S. K., Zolla, A., Scarborough, J., and Arshadi, M.: J. Am. Chem. Soc., 89, 6393–6399, 1967.
Kim, T. O., Ishida, T., Adachi, M., Okuyama, K., and Seinfeld, J. H.: Nanometer-Sized Particle Formation from NH3 ∕ SO2 ∕ H2O ∕ Air Mixtures by Ionizing Irradiation, Aerosol Sci. Technol., 29, 112–125, 1998.
Kirkby, J., Curtius, J., Almeida, J., Dunne, E., Duplissy, J., Ehrhart, S., Franchin, A., Gagné, S., Ickes, L., Kürten, A., Kupc, A., Metzger, A., Riccobono, F., Rondo, L., Schobesberger, S., Tsagkogeorgas, G., Wimmer, D., Amorim, A., Bianchi, F., Breitenlechner, M., David, A., Dommen, J., Downard, A., Ehn, M., Flagan, R. C., Haider, S., Hansel, A., Hauser, D., Jud, W., Junninen, H., Kreissl, F., Kvashin, A., Laaksonen, A., Lehtipalo, K., Lima, J., Lovejoy, E. R., Makhmutov, V., Mathot, S., Mikkilä, J., Minginette, P., Mogo, S., Nieminen, T., Onnela, A., Pereira, P., Petäjä, T., Schnitzhofer, R., Seinfeld, J. H., Sipilä, M., Stozhkov, Y., Stratmann, F., Tomé, A., Vanhanen, J., Viisanen, Y., Vrtala, A., Wagner, P. E., Walther, H., Weingartner, E., Wex, H., Winkler, P. M., Carslaw, K. S., Worsnop, D. R., Baltensperger, U., and Kulmala, M.: Role of sulphuric acid, ammonia and galactic cosmic rays in atmospheric aerosol nucleation, Nature, 476, 429–435, 2011.
Korhonen, P., Kulmala, M., Laaksonen, A., Viisanen, Y., McGraw, R., and Seinfeld, J. H.: Ternary nucleation of H2SO4, NH3, and H2O in the atmosphere, J. Geophys. Res., 104, 26349–26353, 1999.
Kurtén, T., Torpo, L., Ding, C.-G., Vehkamäki, H., Sundberg, M. R., Laasonen, K., and Kulmala, M.: A density functional study on water-sulfuric acid-ammonia clusters and implications for atmospheric cluster formation, J. Geophys. Res., 112, D04210, https://doi.org/10.1029/2006JD007391, 2007.
Kürten, A., Münch, S., Rondo, L., Bianchi, F., Duplissy, J., Jokinen, T., Junninen, H., Sarnela, N., Schobesberger, S., Simon, M., Sipilä, M., Almeida, J., Amorim, A., Dommen, J., Donahue, N. M., Dunne, E. M., Flagan, R. C., Franchin, A., Kirkby, J., Kupc, A., Makhmutov, V., Petäjä, T., Praplan, A. P., Riccobono, F., Steiner, G., Tomé, A., Tsagkogeorgas, G., Wagner, P. E., Wimmer, D., Baltensperger, U., Kulmala, M., Worsnop, D. R., and Curtius, J.: Thermodynamics of the formation of sulfuric acid dimers in the binary (H2SO4-H2O) and ternary (H2SO4-H2O-NH3) system, Atmos. Chem. Phys., 15, 10701–10721, https://doi.org/10.5194/acp-15-10701-2015, 2015.
Kürten, A., Bianchi, F., Almeida, J., Kupiainen-Määttä, O., Dunne, E. M., Duplissy, J., Williamson, C., Barmet, P., Breitenlechner, M., Dommen, J., Donahue, N. M., Flagan, R. C., Franchin, A., Gordon, H., Hakala, J., Hansel, A., Heinritzi, M., Ickes, L., Jokinen, T., Kangasluoma, J., Kim, J., Kirkby, J., Kupc, A., Lehtipalo, K., Leiminger, M., Makhmutov, V., Onnela, A., Ortega, I. K., Petäjä, T., Praplan, A. P., Riccobono, F., Rissanen, M. P., Rondo, L., Schnitzhofer, R., Schobesberger, S., Smith, J. N., Steiner, G., Stozhkov, Y., Tomé, A., Tröstl, J., Tsagkogeorgas, G., Wagner, P. E., Wimmer, D., Ye, P., Baltensperger, U., Carslaw, K., Kulmala, M., and Curtius, J.: Experimental particle formation rates spanning tropospheric sulfuric acid and ammonia abundances, ion production rates and temperatures, J. Geophys. Res.-Atmos., 121, 12377–12400, 2016.
Laakso, L., Mäkelä, J. M., Pirjola, L., and Kulmala, M.: Model studies of ion-induced nucleation in the atmosphere, J. Geophys. Res., 107, 4427, https://doi.org/10.1029/2002JD002140, 2003.
Leverentz, H. R., Siepmann, J. I., Truhlar, D. G., Loukonen, V., and Vehkamaki, H.: Energetics of atmospherically implicated clusters made of sulfuric acid, ammonia, and dimethyl amine, J. Phys. Chem. A, 117, 3819–3825, 2013.
Lovejoy, E. R., Curtius, J., and Froyd, K. D.: Atmospheric ion-induced nucleation of sulfuric acid and water, J. Geophys. Res., 109, D08204, https://doi.org/10.1029/2003JD004460, 2004.
Ma, Y., Chen, J., Jiang, S., Liu, Y. R., Huang, T., Miao, S. K., Wang, C. Y., and Huang, W.: Characterization of the nucleation precursor (H2SO4–(CH3)2NH) complex: intra-cluster interactions and atmospheric relevance, RSC Adv., 6, 5824–5836, 2016.
Marti, J. J., Jefferson, A., Ping Cai, X., Richert, C., McMurry, P. H., and Eisele, F.: H2SO4 vapor pressure of sulfuric acid and ammonium sulfate solutions, J. Geophys. Res., 102, 3725–3736, 1997.
McGrath, M. J., Olenius, T., Ortega, I. K., Loukonen, V., Paasonen, P., Kurtén, T., Kulmala, M., and Vehkamäki, H.: Atmospheric Cluster Dynamics Code: a flexible method for solution of the birth-death equations, Atmos. Chem. Phys., 12, 2345–2355, https://doi.org/10.5194/acp-12-2345-2012, 2012.
Meng, Z., Xu, X., Lin, W., Ge, B., Xie, Y., Song, B., Jia, S., Zhang, R., Peng, W., Wang, Y., Cheng, H., Yang, W., and Zhao, H.: Role of ambient ammonia in particulate ammonium formation at a rural site in the North China Plain, Atmos. Chem. Phys., 18, 167–184, https://doi.org/10.5194/acp-18-167-2018, 2018.
Meot-Ner (Mautner), M.: The Ionic Hydrogen Bond and Ion Solvation. 2. Hydration of Onium Ions by 1–7 H2O Molecules. Relations Between Monomolecular, Specific and Bulk Hydration, J. Am. Chem. Soc., 106, 1265, https://doi.org/10.1021/ja00317a016, 1984.
Merikanto J., Napari, I., Vehkamäki, H., Anttila, T., and Kulmala, M.: New parameterization of sulfuric acid-ammonia-water ternary nucleation rates at tropospheric conditions, J. Geophys. Res., 112, D15207, https://doi.org/10.1029/2006JD007977, 2007.
Miao, S. K., Jiang, S., Chen, J., Ma, Y., Zhu, Y. P., Wen, Y., Zhang, M. M., and Huang, W.: Hydration of a sulfuric acid–oxalic acid complex: acid dissociation and its atmospheric implication, RSC Adv., 5, 48638–48646, 2015.
Nadykto, A. and Yu, F.: Uptake of neutral polar vapour molecules by charged particles: Enhancement due to dipole-charge interaction, J. Geophy. Res., 108, 4717, https://doi.org/10.1029/2003JD003664, 2003.
Nadykto, A. B. and Yu, F.: Strong hydrogen bonding between atmospheric nucleation precursors and common organics, Chem. Phys. Lett., 435, 14–18, 2007.
Nadykto, A. B., Al Natsheh, A., Yu, F., Mikkelsen, K. V., and Ruuskanen, J.: Quantum nature of the sign preference in the ion-induced nucleation, Phys. Rev. Lett., 96, 125701, https://doi.org/10.1103/PhysRevLett.96.125701, 2006.
Nadykto, A. B., Herb, J., Yu, F., and Xu, Y.: Enhancement in the production of nucleating clusters due to dimethylamine and large uncertainties in the thermochemistry of amine-enhanced nucleation, Chem. Phys. Lett., 609, 42–49, 2014.
Nadykto, A. B., Herb, J., Yu, F., Nazarenko, E. S., and Xu, Y.: Reply to the `Comment on “Enhancement in the production of nucleating clusters due to dimethylamine and large uncertainties in the thermochemistry of amine-enhanced nucleation” by Kupiainen-Maatta et al., Chem. Phys. Lett., 624, 111–118, 2015.
Nadykto, A. B., Al Natsheh, A., Yu, F., Mikkelsen, K. V., and Herb, J.: Computational Quantum Chemistry: A New Approach to Atmospheric Nucleation, Adv. Quantum Chem., 55, 449–478, 2008.
Nadykto, A. B., Du, H., and Yu, F.: Quantum DFT and DF–DFT study of vibrational spectra of sulfuric acid, sulfuric acid monohydrate, formic acid and its cyclic dimer, Vib. Spectrosc., 44, 286–296, 2007.
Nadykto, A. B., Yu, F., and Herb, J.: Theoretical analysis of the gas-phase hydration of common atmospheric pre-nucleation (HSO4−)(H2O)n and (H3O+)(H2SO4)(H2O)n cluster ions, Chem. Phys., 360, 67–73, https://doi.org/10.1016/j.chemphys.2009.04.007, 2009.
Napari, I., Noppel, M., Vehkamaki, H., and Kulmala, M.: An improved model for ternary nucleation of sulfuric acid–ammonia–water. J. Chem. Phys., 116, 4221–4227, https://doi.org/10.1063/1.1450557, 2002.
Olenius T., Kupiainen-Määttä, O., Ortega, I. K., Kurtén, T., and Vehkamäki, H.: Free energy barrier in the growth of sulfuric acid–ammonia and sulfuric acid–dimethylamine clusters, J. Chem. Phys., 139, 084312, https://doi.org/10.1063/1.4819024, 2013.
Ortega, I. K., Kupiainen, O., Kurtén, T., Olenius, T., Wilkman, O., McGrath, M. J., Loukonen, V., and Vehkamäki, H.: From quantum chemical formation free energies to evaporation rates, Atmos. Chem. Phys., 12, 225–235, https://doi.org/10.5194/acp-12-225-2012, 2012.
Payzant, J. D., Cunningham, A. J., and Kebarle, P.: Gas–Phase Solvation of Ammonium Ion by NH3 and H2O and Stabilities of Mixed Clusters (NH3)n(H2O)w, Can. J. Chem., 51, 3242–3249, 1973.
Peng, X. Q., Liu, Y. R., Huang, T., Jiang, S., and Huang, W.: Interaction of gas phase oxalic acid with ammonia and its atmospheric implications, Phys. Chem. Chem. Phys., 17, 9552–9563, 2015.
Raes, F., Janssens, A., and Dingenen, R. V.: The role of ion-induced aerosol formation in the lower atmosphere, J. Aerosol Sci., 17, 466–470, 1986.
Schnitzhofer, R., Metzger, A., Breitenlechner, M., Jud, W., Heinritzi, M., De Menezes, L.-P., Duplissy, J., Guida, R., Haider, S., Kirkby, J., Mathot, S., Minginette, P., Onnela, A., Walther, H., Wasem, A., Hansel, A., and the CLOUD Team: Characterisation of organic contaminants in the CLOUD chamber at CERN, Atmos. Meas. Tech., 7, 2159–2168, https://doi.org/10.5194/amt-7-2159-2014, 2014.
Schobesberger, S., Franchin, A., Bianchi, F., Rondo, L., Duplissy, J., Küfrten, A., Ortega, I. K., Metzger, A., Schnitzhofer, R., Almeida, J., Amorim, A., Dommen, J., Dunne, E. M., Ehn, M., Gagné, S., Ickes, L., Junninen, H., Hansel, A., Kerminen, V.-M., Kirkby, J., Kupc, A., Laaksonen, A., Lehtipalo, K., Mathot, S., Onnela, A., Petäjä, T., Riccobono, F., Santos, F. D., Sipilä, M., Tomé, A., Tsagkogeorgas, G., Viisanen, Y., Wagner, P. E., Wimmer, D., Curtius, J., Donahue, N. M., Baltensperger, U., Kulmala, M., and Worsnop, D. R.: On the composition of ammonia-sulfuric-acid ion clusters during aerosol particle formation, Atmos. Chem. Phys., 15, 55–78, https://doi.org/10.5194/acp-15-55-2015, 2015.
Sipilä, M., Berndt, T., Petäjä, T., Brus, D., Vanhanen, J., Stratmann, F., Patokoski, J., Mauldin, R. L., Hyvärinen, A. P., Lihavainen, H., and Kulmala, M.: The Role of Sulfuric Acid in Atmospheric Nucleation, Science, 327, 1243, https://doi.org/10.1126/science.1180315, 2010.
Sorokin, A., Arnold, F., and Wiedner, D.: Formation and growth of sulfuric acid–water cluster ions: Experiments, modelling, and implications for ion-induced aerosol formation, Atmos. Environ., 40, 2030–2045, 2006.
Temelso, B., Morrell, T. E., Shields, R. M., Allodi, M. A., Wood, E. K., Kirschner, K. N., Castonguay, T. C., Archer, K. A., and Shields, G. C.: Quantum mechanical study of sulfuric acid hydration: Atmospheric implications, J. Phys. Chem. A, 116, 2209–2224, 2012a.
Temelso, B., Phan, T. N., and Shields, G. C.: Computational study of the hydration of sulfuric acid dimers: Implications for acid dissociation and aerosol formation, J. Phys. Chem. A, 116, 9745–9758, 2012b.
Thomson, J. J.: Applications of Dynamics to Physics and Chemistry, 1st ed., Cambridge University Press, London, 1888.
Torpo, L., Kurtén, T., Vehkamäki, H., Laasonen, K., Sundberg, M. R., and Kulmala, M.: Significance of ammonia in growth of atmospheric nanoclusters, J. Phys. Chem. A, 111, 10671–10674, 2007.
Vehkamäki H., Kulmala, M., Napari, I., Lehtinen, K. E. J., Timmreck, C., Noppel, M., and Laaksonen, A.: An improved parameterization for sulfuric acid–water nucleation rates for tropospheric and stratospheric conditions, J. Geophys. Res., 107, 4622, https://doi.org/10.1029/2002JD002184, 2002.
Warner, J. X., Wei, Z., Strow, L. L., Dickerson, R. R., and Nowak, J. B.: The global tropospheric ammonia distribution as seen in the 13-year AIRS measurement record, Atmos. Chem. Phys., 16, 5467–5479, https://doi.org/10.5194/acp-16-5467-2016, 2016.
Wilhelm, S., Eichkorn, S., Wiedner, D., Pirjola, L., and Arnold, F.: Ion-induced aerosol formation: new insights from laboratory measurements of mixed cluster ions, (H2SO4)a(H2O)w and H+(H2SO4)a(H2O)w, Atmos. Environ., 38, 1735–1744, 2004.
Włodek, S., Łuczyński, Z., and Wincel, H.: Stabilities of gas-phase (HNO3)n, n≤6, clusters, Int. J. Mass Spectrom. Ion Phys., 35, 39–46, 1980.
Xu, W. and Zhang, R.: Theoretical investigation of interaction of dicarboxylic acids with common aerosol nucleation precursors, J. Phys. Chem. A, 116, 4539–4550, 2012.
Xu, W. and Zhang, R.: A theoretical study of hydrated molecular clusters of amines and dicarboxylic acids, J. Chem. Phys., 139, 064312, https://doi.org/10.1063/1.4817497, 2013.
Yu, F.: Modified Kelvin-Thomson equation considering ion-dipole interaction: Comparison with observed ion-clustering enthalpies and entropies, J. Chem. Phys., 122, 084503, https://doi.org/10.1063/1.1845395, 2005.
Yu, F.: Effect of ammonia on new particle formation: A kinetic H2SO4-H2O-NH3 nucleation model constrained by laboratory measurements, J. Geophys. Res., 111, D01204, https://doi.org/10.1029/2005JD005968, 2006a.
Yu, F.: From molecular clusters to nanoparticles: second-generation ion-mediated nucleation model, Atmos. Chem. Phys., 6, 5193–5211, https://doi.org/10.5194/acp-6-5193-2006, 2006b.
Yu, F.: Improved quasi-unary nucleation model for binary H2SO4-H2O homogeneous nucleation, J. Chem. Phys., 127, 054301, https://doi.org/10.1063/1.2752171, 2007.
Yu, F. and Turco, R. P.: The role of ions in the formation and evolution of particles in aircraft plumes, Geophys. Res. Lett., 24, 1927–1930, 1997.
Yu, F. and Turco, R. P.: Ultrafine aerosol formation via ion-mediated nucleation, Geophys. Res. Lett., 27, 883–886, 2000.
Yu, F. and Turco, R. P.: From molecular clusters to nanoparticles: The role of ambient ionization in tropospheric aerosol formation, J. Geophys. Res., 106, 47970–4814, 2001.
Yu, F. and Turco, R. P.: The size-dependent charge fraction of sub-3-nm particles as a key diagnostic of competitive nucleation mechanisms under atmospheric conditions, Atmos. Chem. Phys., 11, 9451–9463, https://doi.org/10.5194/acp-11-9451-2011, 2011.
Zhang, R., Wang, L., Khalizov, A. F., Zhao, J., Zheng, J., McGraw, R. L., and Molina, L. T.: Formation of nanoparticles of blue haze enhanced by anthropogenic pollution, P. Natl. Acad. Sci. USA, 106, 17650–17654, 2009.
Zhang, R., Khalizov, A. F., Wang, L., Hu, M., and Wen, X.: Nucleation and growth of nanoparticles in the atmosphere, Chem. Rev., 112, 1957–2011, https://doi.org/10.1021/cr2001756, 2012.
Zhang, Y., McMurry, P. H., Yu, F., and Jacobson, M. Z.: A Comparative Study of Homogeneous Nucleation Parameterizations, Part I. Examination and Evaluation of the Formulations, J. Geophys. Res., 115, D20212, https://doi.org/10.1029/2010JD014150, 2010.
Zhu, Y. P., Liu, Y. R., Huang, T., Jiang, S., Xu, K. M., Wen, H., Zhang, W. J., and Huang, W.: Theoretical study of the hydration of atmospheric nucleation precursors with acetic acid, J. Phys. Chem. A, 118, 7959–7974, 2014.
Zollner, J. H., Glasoe, W. A., Panta, B., Carlson, K. K., McMurry, P. H., and Hanson, D. R.: Sulfuric acid nucleation: power dependencies, variation with relative humidity, and effect of bases, Atmos. Chem. Phys., 12, 4399–4411, https://doi.org/10.5194/acp-12-4399-2012, 2012.
- Abstract
- Introduction
- Kinetic-based H2SO4–H2O–NH3 ternary ion-mediated nucleation (TIMN) model
- TIMN rates and comparisons with CLOUD measurements
- Summary
- Data availability
- Appendix A: Quantum-chemical studies of neutral and charged binary and ternary clusters
- Author contributions
- Competing interests
- Acknowledgements
- References
- Abstract
- Introduction
- Kinetic-based H2SO4–H2O–NH3 ternary ion-mediated nucleation (TIMN) model
- TIMN rates and comparisons with CLOUD measurements
- Summary
- Data availability
- Appendix A: Quantum-chemical studies of neutral and charged binary and ternary clusters
- Author contributions
- Competing interests
- Acknowledgements
- References