the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The impact of multi-species surface chemical observation assimilation on air quality forecasts in China
Zhen Peng
Lili Lei
Jianning Sun
Aijun Ding
Junmei Ban
Xingxia Kou
Kekuan Chu
An ensemble Kalman filter data assimilation (DA) system has been developed to improve air quality forecasts using surface measurements of PM10, PM2.5, SO2, NO2, O3, and CO together with an online regional chemical transport model, WRF-Chem (Weather Research and Forecasting with Chemistry). This DA system was applied to simultaneously adjust the chemical initial conditions (ICs) and emission inputs of the species affecting PM10, PM2.5, SO2, NO2, O3, and CO concentrations during an extreme haze episode that occurred in early October 2014 over East Asia. Numerical experimental results indicate that ICs played key roles in PM2.5, PM10 and CO forecasts during the severe haze episode over the North China Plain. The 72 h verification forecasts with the optimized ICs and emissions performed very similarly to the verification forecasts with only optimized ICs and the prescribed emissions. For the first-day forecast, near-perfect verification forecasts results were achieved. However, with longer-range forecasts, the DA impacts decayed quickly. For the SO2 verification forecasts, it was efficient to improve the SO2 forecast via the joint adjustment of SO2 ICs and emissions. Large improvements were achieved for SO2 forecasts with both the optimized ICs and emissions for the whole 72 h forecast range. Similar improvements were achieved for SO2 forecasts with optimized ICs only for the first 3 h, and then the impact of the ICs decayed quickly. For the NO2 verification forecasts, both forecasts performed much worse than the control run without DA. Plus, the 72 h O3 verification forecasts performed worse than the control run during the daytime, due to the worse performance of the NO2 forecasts, even though they performed better at night. However, relatively favorable NO2 and O3 forecast results were achieved for the Yangtze River delta and Pearl River delta regions.
Predicting and simulating air quality remains a challenge in heavily polluted regions (Wang et al., 2014; Ding et al., 2016). Chemical data assimilation (DA), which combines observations and model simulations, is recognized as one effective method to improve air quality forecasts. It has been widely used to assimilate aerosol measurements from both ground-based and spaceborne platforms, including surface PM10 observations (Jiang et al., 2013; Pagowski et al., 2014), surface PM2.5 observations (Li et al., 2013; Zhang et al., 2016), lidar observations (Yumimoto et al., 2007, 2008), aerosol optical depth products from AERONET (the AErosol RObotic NETwork) (Schutgens et al., 2010a, b, 2012), and various satellites (Sekiyama et al., 2010; Liu et al., 2011; Dai et al., 2014). These studies indicate that assimilating observations can substantially improve the spatiotemporal variations of aerosol in the simulation and forecasts.
Aerosols are not only primarily emitted; a larger portion of them is also formed secondarily through reactions with several gaseous-phase precursors and oxidants in the atmosphere (Huang et al., 2014; Nie et al., 2014; Xie et al., 2015). So, observations of trace gases are also useful in assimilating data for aerosol simulations and forecasts. Efforts to assimilate atmospheric-composition observations – like O3, SO2, NO, NO2, CO, and NH3 – have also been made. For example, Elbern et al. (1997, 2000, 2007) and Elbern and Schmidt (1999, 2001) developed a 4D-VAR (four-dimensional variational) system to assimilate surface measurements of O3, SO2, NO, and NO2 to improve air quality forecasts with the joint adjustment of initial conditions (ICs) and emission rates. Later, van Loon et al. (2000) assimilated O3 in the transport chemistry model LOTOS, based on an ensemble Kalman filter (EnKF). Heemink and Segers (2002) attempted to reconstruct NOx and volatile organic compound (VOC) emissions for O3 forecasting by assimilating O3. Carmichael et al. (2003, 2008a, b) developed 4D-VAR and EnKF systems to assimilate O3 and NO2 to improve ICs and emission sources for O3 forecasting. Hakami et al. (2005) constrained black carbon (BC) emissions during the Asian Pacific Regional Aerosol Characterization Experiment. Henze et al. (2007, 2009) estimated SOx, NOx, and NH3 emissions based on a 4D-VAR method by assimilating surface sulfate and nitrate aerosol observations. Other studies have estimated the NOx (van der A et al., 2006, 2017; Mijling and van der A, 2012; Mijling et al., 2009, 2013; Ding et al., 2015) and SO2 emissions (van der et A al., 2017) based on an extended Kalman filter by assimilating SO2 and NO2 retrievals from SCIAMACHY (SCanning Imaging Absorption spectroMeter for Atmospheric CHartographY) and OMI (Ozone Monitoring Instrument). Barbu et al. (2009) applied an EnKF to optimize the emissions and conversion rates using surface measurements of SO2 and sulfate. McLinden et al. (2016) constrained SO2 emissions using space-based observations.
In recent years, severe haze pollution episodes have begun to occur more frequently in China, especially in the megacity clusters of eastern China (e.g., Parrish and Zhu, 2009; Sun et al., 2015; Zhang et al., 2015). Thus, regional haze, especially when accompanied by extremely high PM2.5 concentrations, has drawn significant research interest. However, there are large uncertainties involved in the numerical prediction of atmospheric aerosols. During severe haze pollution episodes, air quality models often underestimate the extreme peak mass concentration of particulate matter (Wang et al., 2014). Previous studies have revealed that the assimilation of atmospheric-composition observations can improve air quality forecasts by constraining the uncertainties of both the chemical ICs and emissions (Tang et al., 2010, 2011, 2013, 2016; Miyazaki and Eskes, 2013; Miyazaki et al., 2012, 2014). Peng et al. (2017) demonstrated that significant improvements in forecasting PM2.5 can be achieved via the joint adjustment of ICs and source emissions using an EnKF to assimilate surface PM2.5 observations.
In 2013, China launched an atmospheric environmental monitoring system that provides real-time and online atmospheric chemical observations, including PM10, PM2.5, SO2, NO2, O3, and CO (http://113.108.142.147:20035/emcpublish/, last access: 26 November 2018). This dataset provides an opportunity to improve air quality forecasts using DA. However, such fruitful observations are less used in air quality forecasting even though a large discrepancy exists between the forecasts and observations. But it is now possible to estimate the impact on forecast improvement of simultaneously assimilating various surface observations. Thus, we developed an EnKF system that can simultaneously assimilate surface measurements of PM10, PM2.5, SO2, NO2, O3, and CO to correct WRF-Chem (Weather Research and Forecasting model with Chemistry) forecasts using the Goddard Chemistry Aerosol Radiation and Transport (GOCART) aerosol scheme. As an extension to Peng et al. (2017), the impact of simultaneously assimilating various surface aerosol and chemical observations was investigated.
Sections 2 and 3 briefly describe the DA system and observations used in this study, respectively. The experimental design is introduced in Sect. 4. Finally, the assimilation results are presented in Sect. 5, before a brief summary in Sect. 6.
The DA system in this study was the same as the one used in Peng et al. (2017). It can simultaneously analyze the chemical ICs and emissions with the assimilation of surface PM2.5 observations. A brief summary of the DA system is introduced here.
In every DA cycle, the ensemble emission scaling factors λf are first calculated by the forecast model of scaling factors MSF (see details of MSF in Sect. 2.2). Then, the ensemble forecast emissions Ef are calculated using the following equation:
where is the prescribed anthropogenic emission. The ensemble members of chemical fields Cf are forecasted using WRF-Chem, forced by the forecast emissions Ef whose ICs are previously analyzed concentration fields. Now, the background of the joint vector, , has been produced. Then, the analyzed state vector, , is optimized using an ensemble square root filter (EnSRF). Finally, the assimilated emissions Ea can be obtained using Eq. (1). It is noted that the optimized emissions are only the results of a mathematical optimum by utilizing observations. If the optimized emissions used in the EnSRF experiment run with pure concentrations as state vectors are identical to the emissions obtained from the joint EnSRF experiment run with concentrations and emission factors (representing emissions) as state vectors, identical results may be obtained.
2.1 WRF-Chem model
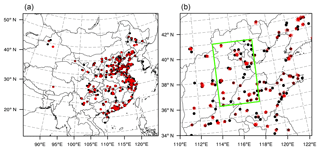
The model used to simulate the transport of aerosols and chemical species was the WRF-Chem (Grell et al., 2005). As in Peng et al. (2017), we used version 3.6.1; the physical and chemical parameterization options are listed in Table 1. The model computational domain covered almost the whole of China, and the horizontal resolution was 40.5 km. Figure 1b shows our area of interest, the North China Plain (NCP). The model included 57 vertical levels, and the model top was 10 hPa.
The hourly prior anthropogenic emissions were based on the Multi-resolution Emission Inventory for China (MEIC) (Li et al., 2014) for October 2010, instead of the regional emission inventory in Asia (Zhang et al., 2009) for the year 2006 in Peng et al. (2017). The reason we chose the MEIC-2010 was that the total emissions are reasonable for cities over the NCP (Zheng et al., 2015). The original resolution of the MEIC-2010 is , but it has been processed to match the model resolution (40.5 km) (Chen et al., 2016). No time variation was added to maintain objectivity in the prior anthropogenic emissions.
2.2 Forecast model of scaling factors
In this work, the primary sources to be optimized were the emissions of PM10, PM2.5, SO2, NO, NH3, and CO. The sources of NH3 were analyzed because they also impact greatly on the aerosols distribution. Thus, the emission scaling factors were prepared by the forecast model of scaling operator MSF before WRF-Chem integration.
We used the same persistence forecast operator MSF to forecast as in Peng et al. (2017). The forecast operator was developed by using the ensemble forecast chemical fields. Thus,
where is the ith ensemble member of the chemical fields at time t, and is the ensemble mean; κi,t is the ensemble concentration ratios and is the ensemble mean of κi,t with values of 1; β is the inflation factor to keep the ensemble spreads of κi,t at a certain level; and , , and are the previous assimilated emission scaling factors. It is noted that are spatially varying because they are calculated by using the spatially varying variables, the forecast chemical fields . Furthermore, there are very few negative values for (κi,t)inf after inflation. A quality control procedure is performed for (κi,t)inf before further appliance. All these negative data were set as 0 in this work. Then (κi,t)inf were re-centered to ensure the ensemble mean values of (κi,t)inf were all 1. Furthermore, another quality control procedure is performed for to keep them positive. Thus, all and could be positive.
In this study, the ensemble forecast chemical fields of PM25, PM10, SO2, NO, NH3, and CO of the previous assimilation cycle are respectively used to calculate the emission scaling factors . Previous works (Peng et al., 2015, 2017) showed that reasonable results can be obtained when the ensemble spread of the emission scaling factors range from 0.1 to 1. In order to keep the ensemble spread of the scaling factors at this level in most model area, β is chosen as 1.3, 1.4, 1.3, 1.2, 1.2, and 1.4 for the ensemble concentration ratios of P2.5, P10, SO2, NO, NH3, and CO, respectively, in Eq. (3).
Then, the sources = , , , , , are calculated using Eq. (1).
From the perspective of PM2.5 emissions, these include the unspeciated primary sources of PM2.5 , sulfate , and nitrate . We updated , , and (including the nuclei and accumulation modes) following Peng et al. (2017).
2.3 DA algorithm
The assimilation algorithm employed was the EnSRF proposed by Whitaker and Hamill (2002). The EnKF proposed by Evensen (1994) needs perturbations of observations in practice. Compared to the original EnKF, the EnSRF obviates the need to perturb the observations and avoids additional sampling errors introduced by perturbing observations.
We used the same EnSRF as in Schwartz et al. (2012, 2014). The ensemble member was chosen as 50. The localization radius was chosen as 607.5 km, so EnSRF analysis increments were forced to zero 607.5 km away from an observation (Gaspari and Cohn, 1999). The posterior (after assimilation) multiplicative inflation factor was chosen as 1.2 for all the concentration analysis.
2.4 State variables
The DA system provides joint analysis of ICs and emissions following Peng et al. (2017). Among them, 16 WRF-Chem/GOCART aerosol variables are included as the state variables. Furthermore, chemical species,such as SO2, NO2, and O3 are also included because they are the most important gas-phase precursors or oxidants of the secondary inorganic aerosols. CO is also assimilated because CO is an important tracer of combustion sources, as well as a precursor of O3 beyond NO2 (Parrish et al., 1991). The state variables of the emission scaling factors are .
Similar to weak-coupling DA, the DA system simultaneously updates both the ICs and the emissions, but with no cross-variable update, in order to avoid the effects of spurious multivariate correlations in the background error covariance that may develop due to the limited ensemble size and errors in both the model and observations (Miyazaki et al., 2012).
For the PM2.5 observations, the observation operator is expressed as (Schwartz et al., 2012)
where ρd is the dry-air density; P25 is the fine unspeciated aerosol contributions; S represents sulfate; OC1 and OC2 are hydrophobic and hydrophilic organic carbon, respectively; BC1 and BC2 are hydrophobic and hydrophilic black carbon, respectively; D1 and D2 are dusts with effective radii of 0.5 and 1.4 µm, respectively; and S1 and S2 are sea salts with effective radii of 0.3 and 1.0 µm, respectively. In fact, PM2.5 observations were only used to analyze P2.5, S, OC1, OC2 BC1, BC2, D1, D2, S1, S2, and . Since we had no NH3 observations, PM2.5 observations were also used to analyze (see Table 2). For other control variables, PM2.5 observations were not allowed to alter them.
For the PM10 observations, the PM10 observation operator is expressed as (Jiang et al., 2013)
Thus,
meaning that, in the assimilation experiments, we did not use the PM10 observations directly. In Eqs. (13) and (14), P10 denotes the coarse-mode unspeciated aerosol contributions; D3 and D4 are dusts with effective radii of 2.4 and 4.5 µm, respectively; and S3 is sea salt with an effective radius of 3.25 µm. We used the PM10−2.5 observations (the differences between the PM10 observations and the PM2.5 observations, to analyze P10, D3, D4, S3, and . In addition, PM10−2.5 observations were used to analyze D5 and S4, since they are coarse-mode mineral dust and sea salt aerosols. PM10−2.5 observations were not allowed to impact other control variables.
Moreover, as shown in Table 2, SO2 observations were used to analyze the SO2 concentration and . NO2 observations were used to estimate the NO, NO2 concentration and λNO. CO observations were used to analyze the CO concentration and λCO. And finally, O3 observations were only used to analyze the O3 concentration.
The surface chemical observations used in this study were obtained from the Ministry of Ecology and Environment of China. Altogether, there were 876 observational sites over the model domain (Fig. 1). At most sites, one measurement was selected randomly for the assimilation experiment on a grid. Altogether, 355 stations were kept for the model domain, where 133 assimilation stations were located on the NCP and 40 stations were located in the Beijing–Tianjin–Hebei (BTH) region. Other stations were used for verification purposes: 167 independent stations were located on the NCP, and 47 in the BTH region.
The observation error covariance matrix R included measurement errors and representation errors. We assumed that R is a diagonal matrix (without observation correlation).
Following Elbern et al. (2007), the measurement error ε0 is defined as
where Π0 represents the measurements for PM2.5, PM10−2.5, SO2, NO2, CO, or O3 (units: µg m−3). Values of a=1.5 and b=0.0075 were chosen for PM2.5, PM10−2.5, SO2, and NO2. For CO, a=10 and b=0.0075.
The representativeness error is defined as
where r=0.5, Δx=40.5 km (the model resolution), and L=3 km due to the lack of the information of the station type (Elbern et al., 2007).
Finally, the total error (εt) is defined as
In order to ensure data reliability, the observations were subjected to quality control before DA. Data values larger than a certain threshold were classified as unrealistic and were not assimilated. The threshold values were chosen as 700, 800, 300, 300, 400, and 4000 µg m−3 for PM2.5, PM10−2.5, SO2, NO2, O3, and CO, respectively. In addition, observations leading to innovations exceeding a certain value were also omitted. These threshold values were chosen as 70 µg m−3 for PM2.5, PM10−2.5, SO2, NO2, and O3. Also, 1500 µg m−3 was chosen for CO.
The DA experiment followed that of Peng et al. (2017), in which the assimilation of pure surface PM2.5 measurements with the EnKF was performed to correct finer aerosol variables and associated emissions. The experiment focused on an extreme haze event that occurred in October 2014 over northern China.
The 50-member ensemble spin-up forecasts were first performed from 1 to 4 October 2014 using the perturbed meteorological ICs, lateral boundary conditions (LBCs), and emissions. The perturbed meteorological ICs and LBCs are created by adding Gaussian random noise (Torn et al., 2006) to the temperature, water vapor, velocity, geopotential height, and dry surface pressure fields of the products of the National Centers for Environmental Prediction Global Forecast System (GFS) by WRFDA. The perturbed emissions were generated also by adding Gaussian random noise with a standard deviation of 10 % of the corresponding anthropogenic emissions. The aerosol ICs were zero, and the aerosol LBCs were idealized profiles embedded within the WRF-Chem model; neither of them was perturbed (Peng et al., 2017).
Then, the observed PM10, PM2.5, SO2, NO2, O3, and CO data starting from 5 to 16 October were assimilated hourly to adjust the ICs and the corresponding emissions. The ICs were the subject of analysis of the previous DA cycle. The meteorological LBCs were perturbed. The anthropogenic emissions – , , , ENO, , ECO, , and – are calculated by using the forecast emission scaling factors. Other species, such as the organic compounds Eorg and elemental compounds EBC, are perturbed by adding Gaussian random noise. Since the emissions are calculated by Eq. (1), their background uncertainties and the spatial correlations are completely dependent on those of the corresponding emission factors. The forecast scaling factors are calculated by Eqs. (2)–(5). And no other perturbations are added to the scaling factors; no other correlations are assumed for the scaling factors.
After that, two sets of 72 h forecasts were performed, each at 00:00 UTC from 6 to 15 October 2014, with hourly forecasting outputs for the assimilation experiment. These two sets of forecasting experiments were conducted using the ensemble mean of the concentration analysis as the ICs. One set of the experiments was forced by the optimized emissions (denoted as fcICsEs), and the other was forced by the prescribed anthropogenic emissions (denoted as fcICs). The aim was to use the difference between the fcICsEs and fcICs to indicate the impact of the optimized emissions.
Moreover, we also ran a control experiment. The ICs were based on the ensemble mean of the spin-up forecasts at 00:00 UTC on 5 October 2014. The emissions were the prescribed emissions.
5.1 Ensemble performance
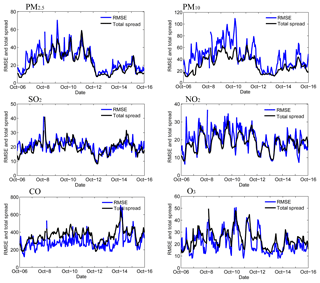
We begin by assessing the ensemble performance for the DA system. Figure 2 shows the time series of the prior total spreads and the prior root-mean-square errors (RMSEs) for PM2.5, PM10, and the four trace gases calculated against all observations in the BTH region. It shows that the magnitudes of the total spreads were close to the RMSEs, indicating that the DA system was well calibrated (Houtekamer et al., 2005).
Figure 3 shows the area-averaged time series extracted from the ensemble spread of the six emission scaling factors (, , , , , and in the BTH region. It shows that the ensemble spread of all the scaling factors were very stable throughout the ∼10-day experiment period, which indicates that MSF can generate stable artificial data to generate the ensemble emissions. The value of the emission scaling factors ranged from 0.2 to 0.6, indicating that the uncertainty of the assimilated emissions was about 20 %–60 %.
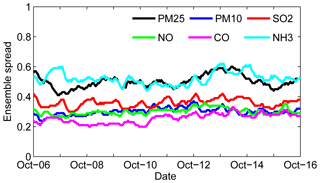
Figure 3Time series of the area-averaged ensemble spread for the emission scaling factors over the Beijing–Tianjin–Hebei region.
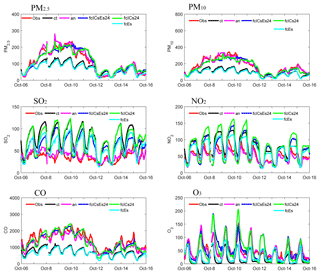
Figure 4Time series of the hourly pollutant concentrations in the Beijing–Tianjin–Hebei (BTH) region obtained from observations (red line), the control run (black line), the analysis (pink line), the first-day forecast from fcICsEs (fcICsEs24, blue line), and the first-day forecast from fcICs (fcICs24, blue line). The observations were obtained from the 47 independent sites in the BTH region. The modeled time series were interpolated to the 47 independent sites using the spatial bilinear interpolator method. The shaded backgrounds indicate the distribution of the observations, where the top edge represented the 90th percentile and the bottom edge the 10th percentile. Units: µg m−3.
5.2 Forecast improvements
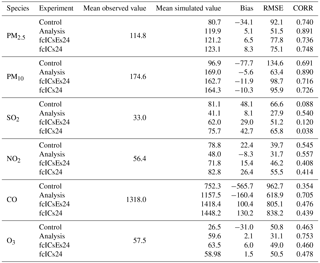
In order to evaluate the overall performance of the DA system, time series of the hourly pollutant concentrations from the control run, the analysis, and the first-day forecast of the two forecasting experiments were compared with the independent observations in the BTH region (Fig. 4). Furthermore, model evaluation statistics (Table 3) were calculated against independent observations from 6 to 16 October 2014. In addition, biases and RMSEs were presented as a function of forecast range for the control, analysis, and forecast experiments (Figs. 5–7).
The control run did not perform very well, although it was able to capture the synoptic variability and reproduce the overall pollutant levels when there was a severe haze event. The statistics show that there were larger systematic biases and RMSEs and a smaller correlation coefficient (CORR) for the control (see Table 3). The biases were −34.1, −77.7, −565.7, and −31 µg m−3 for PM2.5, PM10, CO, and O3, respectively, from 6 to 16 October – about 29.7 %, 44.5 %, 42.9 %, and 53.9 % lower than the corresponding observed concentrations. During the severe haze episode from 8 to 10 October in particular, when observed PM2.5 were larger than 200 µg m−3, the biases reached −90.5, −143.1, −911.8, and −39.1µg m−3, respectively – about 44.4 %, 51.9 %, 49.2 % and 55.7 % lower than the corresponding observed concentrations, suggesting a significant systematic underestimation of the WRF-Chem simulation. Additionally, a significant overestimation of 48.1 µg m−3 was obtained for SO2 – about 145.8 % higher than the observed concentrations. As for the NO2 simulation, WRF-Chem was able to realistically describe the diurnal and synoptic evolution of NO2 concentrations. The model bias was 22.4 µg m−3, which was about 39.7 % higher than the observed NO2. These results were similar to the simulations of Chen et al. (2016). Most of the WRF-Chem settings used here were the same as those used in Chen et al. (2016), except that they used CBMZ (Carbon Bond Mechanism, version Z) and MOSAIC (Model for Simulating Aerosol Interactions and Chemistry) as the gas-phase and aerosol chemical mechanisms.
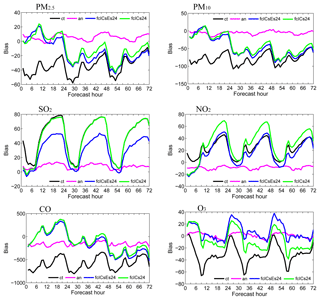
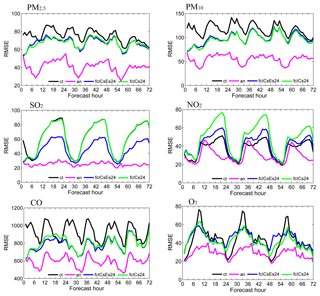
Figure 5Bias of surface PM2.5, PM10, SO2, NO2, CO, and O3 as a function of forecast range calculated against all the independent observations over the Beijing–Tianjin–Hebei region shown in Fig. 1. The 72 h forecasts were performed at each 00:00 UTC from 6 to 14 October 2014, and the statistics were computed from 6 to 14 October. Units: µg m−3.
After the assimilation of surface observations, the time series of the hourly pollutant concentrations from the analysis showed much better agreement with observations than those from the control. The magnitudes of the bias and the RMSEs decreased, and the CORRs increased for all six species. The biases were 5.1, −5.6, 8.1, −8.3, −160.4, and 2.1 µg m−3 for PM2.5, PM10, SO2, NO2, CO, and O3, respectively – about 4.4 %, −3.2 %, 24.5 %, −14.7 %, −12.17 %, and 3.7 % of the corresponding observed concentrations, indicating that the analysis fields were very close to the observations. The RMSEs were 51.5, 63.4, 27.9, 31.7, 618.9, and 31.1 µg m−3, respectively – about 44.1 %, 52.9 %, 58.1 %, 20.2 %, 35.7 %, and 38.78 % lower than the RMSEs of the control run. The CORRs reached 0.891, 0.890, 0.540, 0.557, 0.705, and 0.753, respectively. These statistics indicate that the DA system was able to adjust the chemical ICs efficiently.
The PM2.5, PM10, and CO concentrations from both sets of forecasting experiments benefitted substantially from the DA procedure, as expected. Smaller biases and RMSEs were obtained for almost the entire 72 h forecast range (see Figs. 5–7), as compared with the control run. For the first-day forecast in particular, the model performed almost perfectly. It faultlessly captured the diurnal and synoptic variability of the pollutant (see Fig. 4), in a manner that was very close to that of the analysis. The overall biases were 6.5, −11.9, and 100.4 µg m−3 for PM2.5, PM10, and CO, respectively, and the RMSEs were 77.8, 98.7, and 805.1 µg m−3, respectively, in fcICsEs24 (see Table 3). In fcICs24, the biases were 8.3, −10.3, and 130.2 µg m−3, respectively, and the RMSEs were 75.1, 95.9, and 838.2 µg m−3, respectively (see Table 3). However, with longer-range forecasts, the impact of DA quickly decayed. The relative reductions in RMSE mostly ranged from 30 % to 5 % for the second- and third-day forecast. From the perspective of the impact of the assimilated emissions, fcICs performed similarly to fcICsEs for PM2.5, PM10, and CO, indicating that ICs play key roles in aerosol and CO forecasts during severe haze episodes, while the impact of assimilated emissions seems negligible.
For the SO2 verification forecast, however, fcICsEs performed much better than both fcICs and the control run. Smaller biases and RMSEs were obtained for almost the entire 72 h forecast range. At nighttime in particular (from 18 to 23 h, 42 to 47 h, and 66 to 73 h), when there was significant systematic overestimation in the control run, both the biases and the RMSEs in fcICsEs were about 30 % lower than those of the control run. During the daytime (from 0 to 9 h, 24 to 33 h, and 48 to 57 h), fcICsEs still performed slightly better, although the control run did a near-perfect job. As for fcICs, smaller biases and RMSEs were obtained for only the first 3 h. Then, the performance was the same as the control run, indicating that the impact of the ICs had disappeared. These results demonstrate the superiority of the assimilated emissions, and that the joint adjustment of SO2 ICs and emissions is an efficient way to improve the SO2 forecast.
The NO2 DA results for the independent sites showed really poor performance (see Figs. 5–7). Smaller biases were gained in the daytime of the experiment trials. At nighttime, however, when the simulated NO2 deviated considerably from the observations in the control run, the biases of both sets of the validation forecasts became even larger. Furthermore, almost all the RMSEs of both sets of the validation forecasts were always larger than those of the control run.
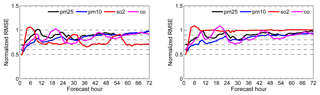
Figure 7Normalized RMSE (assimilation divided by control) for fcICsEs and fcICs for PM2.5, PM10, SO2, and CO.
The O3 DA results were dependent on the NO2 DA results in the daytime, due to chemical transformation. Both the biases and the RMSEs were larger, as compared with those of the control run (see Figs. 5–7). However, at nighttime, when there was significant systematic underestimation in the control run, the biases in fcICsEs had very similar values to those of the analysis. Also, the biases in fcICs ranged between the analysis and the control run, and the RMSEs of both sets of forecasting experiments were about 10 % smaller than those of the control run. All these results indicate that the DA system performed well at night.
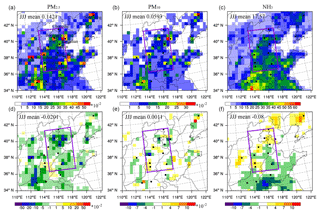
Figure 8Spatial distribution of the prescribed emissions (top panels) of PM2.5 (a, d), PM10 (b, e), and NH3 (c, f) and the corresponding time-averaged differences between the ensemble mean analysis and the prescribed values at the lowest model level averaged over all hours from 6 to 16 October 2014 in the NCP region. Units for PM2.5 and PM10 emissions: µg m−2 s−1; units for NH3 emissions: mol km−2 h−1.
5.3 Emission optimization results
Besides improved pollutant forecasts, improved estimates of emissions were expected from the joint DA procedure. The MEIC-2010 was constructed on the basis of annual statistical books in which the data were often 2–3 years older than the actual year (Chen et al., 2016). However, consistent efforts aimed at reducing and managing anthropogenic emissions have been made over the past decade to mitigate air pollution. Thus, there was a large difference between the emission year and our simulation year. Furthermore, the spatial allocations of these emissions over small spatial scales, and the monthly allocations, will also lead to some uncertainties. Lastly, the emissions inventory cannot fully capture the day-to-day variability or the actual daily variations, though its differentiation in terms of working days and weekend days, plus the daily variations, can be taken into account in practical applications. However, in this assimilation procedure, the differentiation in terms of working days and weekend days, plus the daily variations, was ignored. Therefore, the prescribed anthropogenic emissions were subject to large uncertainties.
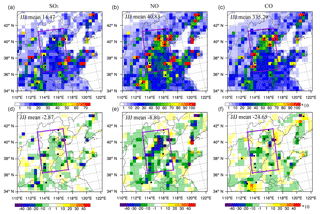
Figure 9As in Fig. 8 but for SO2 (a, d), NO (b, e), and CO (c, f). Units for SO2, NO, and CO emissions: mol km−2 h−1.
Figures 8 and 9 display the spatial distribution of the prescribed emission rates and the differences between the analysis and the prescribed emission rates of PM2.5, PM10, NH3, SO2, NO, and CO averaged over all hours from 6 to 16 October 2014 in the NCP region. The assimilated emission rates of PM2.5, SO2, NO, and CO were lower than the prescribed emissions on the whole. In the BTH region especially, the differences reached −0.02 µg m−2 s−1, −2.9, −8.8, and −24.65 mol km−2 h−1, which was a reduction of about 10 %–20 % of the prescribed emissions. For PM10 emissions, the assimilated values were very close to the prescribed ones, indicating that the prescribed PM10 emissions had small uncertainties for the NCP region. For NH3 emissions, the assimilated values were a little larger than the prescribed emissions in large industrial cities like Beijing, Tianjin, Baoding, Xingtai, Handan, and Taiyuan. However, they were smaller than the prescribed emissions in agricultural regions, especially in Shandong and Henan provinces. However, in the BTH region, the assimilated NH3 emissions were very close to the prescribed emissions on the whole.
Figure 10 shows the time series of the emission scaling factors and the emissions. As concluded in Peng et al. (2017), the forecast emission scaling factors changed with the analyzed emission scaling factors due to the use of the time-smoothing operator. Furthermore, although the prescribed emissions were constant when designing the assimilation experiment, the analyzed emission scaling factors showed obvious variation with time, as did the analyzed emissions. For the assimilated SO2 and NO emissions in particular, the diurnal variations were perfect. In addition, the difference between the assimilated emissions and the prescribed emissions were consistent with those in Figs. 8 and 9. The assimilated emissions of PM2.5, SO2, NO, and CO were apparently lower than the corresponding prescribed emissions, whereas the values of the assimilated emissions of PM10 and NH3 were very close to their corresponding prescribed emissions.
In order to investigate the impact of optimized emissions on chemical simulations, a simulation (fcEs) using the optimized emissions was performed from 5 to 16 October 2014. Just as in the control run, the ICs were the ensemble mean of the spin-up forecasts at 00:00 UTC on 5 October 2014. Thus the difference between the fcEs and the control run is the anthropogenic emissions. The results showed that the fcEs performed very similarly to the control run on the whole in the BTH region. For PM2.5, PM10, and CO, the values of the fcEs were a little smaller than those of the control run, which were consistent with the difference of the anthropogenic emissions. For SO2 and NO2, fcEs performed much better than the control run most of the time, though significant systematic overestimation still existed during the nighttime. For O3, minor improvements were also gained due to the better simulation in fcEs for NO2.
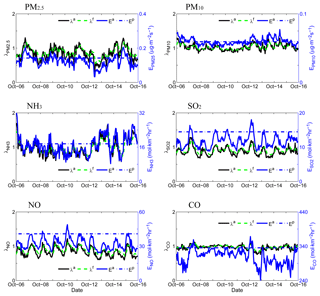
Figure 10Hourly area-averaged time series extracted from the analyzed emission scaling factors (black line), the forecast emission scaling factors (green dashed line), the analyzed emissions (blue line), and the prescribed emissions (blue dashed line) in the Beijing–Tianjin–Hebei region. Units for PM2.5 and PM10 emissions: µg m−2 s−1; units for NH3, SO2, NO, and CO emissions: mol km−2 h−1.
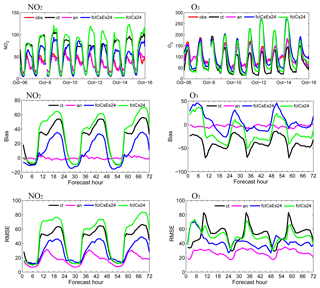
Figure 11NO2 and O3 time series of the hourly pollutant concentrations in the Pearl River delta region (PRD; 21–24∘ N, 112.5–115∘ E) obtained from observations (referred to as “obs”, red line), the control run (referred to as “ct”, black line), the analysis (referred to as “an”, pink line), the first-day forecast from fcICsEs (referred to as “fcICs24”, blue line), and the first-day forecast from fcICs (referred to as “fcICs24”, blue line). The bias and RMSEs of surface NO2 and O3 as a function of forecast range calculated against all the independent observations (34 sites) over the PRD region. Units: µg m−3.
5.4 Discussion
From the results presented above, it is clear that improvements were achieved for almost all the 72 h verification forecasts using the optimized ICs and emissions for PM2.5, PM10, SO2, and CO concentrations in the BTH region. However, the 72 h NO2 verification forecasts performed much worse than the control run, due to the assimilation. Plus, the 72 h O3 verification forecasts performed worse than the control run during the daytime, due to the worse performance of the NO2 forecasts, although they did perform better at night. However, relatively favorable NO2 and O3 forecast results were gained for the Yangtze River delta and Pearl River delta (PRD) regions (see Fig. 11). In the PRD region, during the daytime, the three NO2 forecasts (i.e., the control run, the fcICsEs, and the fcICs) performed similarly and had relatively small biases and RMSEs. At nighttime, when there was significant systematic overestimation in the control run, the biases and the RMSEs in fcICsEs were much smaller than those in the control run. For the O3 72 h verification forecasts, fcICsEs performed much better than the control run, except for the first 8 h. Also, fcICs improved the O3 forecasts to some extent in the 9–72 h forecast range. These results indicate that DA is still an effective way to improve NO2 and O3 forecasts.
Regarding the failure to improve the NO2 and O3 forecasts in the BTH region, there are three likely factors. Certainly, NO2 and O3 forecasts in other areas are also facing similar challenges.
Firstly, there are still some limitations for the EnKF method. EnKF assimilation is influenced greatly by model errors and observation errors. There are many sources of uncertainties in air quality forecasts that were not directly considered in this study (such as chemical schemes and parameterizations, meteorology, and emissions). And it is very difficult to accurately evaluate the uncertainties of models, though the covariance inflation technique was simply applied for all state variables to roughly compensate for model errors. Therefore, we can only obtain suboptimal results through EnKF assimilation. Furthermore, short-lived chemical reactive species, such as NO2 and O3, undergo highly complex nonlinear photochemical reactions, even on timescales of hours, such that the forecast accuracy is largely dependent on the chemical process as well as the physical transportation process, the ICs, and the emissions. However, those complex photochemical reaction processes are not precisely described in current chemical mechanisms, e.g., heterogeneous reactions (Yang et al., 2015), the photolysis of nitrous acid and ClNO2 during daytime (Zhang et al., 2017), and so on. Therefore, on the one hand, there are still large uncertainties for NO2 and O3 forecasts, while, on the other hand, it is very difficult for NO2 and O3 DA to accurately estimate the model errors with a limited ensemble size. Thus, NO2 and O3 assimilations do not perform well (Elbern et al., 2007; Tang et al., 2016). However, for SO2 and CO, which are representative of long-lived chemical reactive species, the chemical reaction process does not work on timescales of hours, meaning that to some extent hourly chemical DA has the potential to improve their forecasts. For CO in particular, due to its inertness, we might be able to obtain high-quality ICs and emissions through DA. The primary sources of aerosol are the dominant part of the atmospheric aerosol concentration. So, 72 h aerosol forecasts may perform similarly to CO, although there are large uncertainties in the chemical model.
Secondly, as stated in the above paragraph, the analysis ICs and emissions are only a mathematical optimum under the existing conditions. In addition, only part of the chemical ICs and emissions are involved in the DA experiment; VOC ICs and emissions, which may greatly influence the NO2 and O3 forecasts, were not included here because of the absence of VOC measurements. Although we carried out two DA sensitivity experiments to adjust the VOC ICs and emissions through the use of NO2 or O3 measurements, we were still unable to gain improved NO2 and O3 forecasts in the BTH region in both DA experiments. VOC measurements are needed to reduce uncertainties of VOC ICs and emissions. In addition, almost all available data were observed in cities, and no observation stations were located in rural areas. Thus, the atmospheric environmental monitoring system was still spatially heterogeneous.
Another important point is that there are still limitations to the current chemical mechanisms used in our model, such as the treatment of model error. NO is the primary species of NOx emissions in city areas and reacts directly with O3 to form NO2 (). Thus, O3 concentrations may inversely correlate with NO2 concentrations at night. Consequently, air quality models may systematically underestimate O3 concentrations. Currently, DA can only revise the ICs and the emissions in this work. It cannot change the model performance, especially when there are certain uncertainties for the meteorological simulation.
In this study, we developed an EnKF system to simultaneously assimilate surface measurements of PM10, PM2.5, SO2, NO2, O3, and CO via the joint adjustment of ICs and source emissions. This system was applied to assimilate hourly pollution data while modeling an extreme haze event that occurred in early October 2014 over northern China. In order to evaluate the impact of DA, two sets of 72 h verification forecasts were performed. One was conducted with the optimized ICs and emissions, and the other with only optimized ICs and the prescribed emissions. A control experiment without DA was also performed for comparison.
The results showed that both verification forecasts performed much better than the control simulations for PM2.5, PM10, and CO. Obvious improvements were achieved for almost the entire 72 h forecast range. For the first-day forecast especially, near-perfect forecasts results were achieved. However, with longer-range forecasts, the impact of DA quickly decayed. In addition, the forecasts with only optimized ICs and the prescribed emissions performed similarly to those with the optimized ICs and emissions, indicating that ICs play key roles in PM2.5, PM10, and CO forecasts during severe haze episodes.
Also, large improvements were achieved for SO2 forecasts with both the optimized ICs and emissions for the whole 72 h forecast range. However, similar improvements were achieved for SO2 forecasts with the optimized ICs only for the first 3 h, and then the impact of the ICs decayed quickly to zero. This demonstrates that the joint adjustment of SO2 ICs and emissions is an efficient way to improve SO2 forecasts.
Even though we failed to improve the NO2 and O3 forecasts in the BTH region, relatively favorable NO2 and O3 forecast results were gained in other areas. Also, the forecasts with both the optimized ICs and emissions performed much better than the forecasts with only optimized ICs and the prescribed emissions. These results indicate that there is still potential to improve NO2 and O3 forecasts via the joint adjustment of SO2 ICs and emissions.
However, only one case was investigated in this work. Thus it is uncertain if the conclusions about different performance of forecasts for various species would hold in a general. Therefore, more case studies are needed to obtain general conclusions in future works.
To reproduce the data presented in the draft, the WRF-Chem model version 3.6.1 can be downloaded at http://www2.mmm.ucar.edu/wrf/users/download/get_source.html (NCAR, 2018, last access: 26 November 2018); the meteorological background is provided by GFS data (0.5∘), which can be downloaded from https://www.ncdc.noaa.gov/data-access/model-data/model-datasets/global-forcast-system-gfs (NCEP, 2018, last access: 26 November 2018); and the observations are available from http://113.108.142.147:20035/emcpublish/ (MEP, 2018, last access: 26 November 2018).
ZP and ZL planned the research and developed the algorithm. ZP, JS, and AD designed the experiments. ZP, LL, and JB developed the model code. ZP and KC performed the simulations and analysis. DC provided the anthropogenic emissions for the model. XK performed the quality control procedure for the observations. ZP prepared the manuscript with contributions from all co-authors.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Regional transport and transformation of air pollution in eastern China”. It is not associated with a conference.
The authors are grateful to the two anonymous reviewers
for their valuable suggestions. This work was supported by the National Key
Technologies Research and Development program of China (2016YFC0202102) and
the National Natural Science Foundation of China (41875014, 41575141, and
41675052). The National Center for Atmospheric Research is sponsored by US
National Science Foundation. The numerical calculations in this paper were
carried out on the IBM BladeCenter cluster system in the High Performance
Computing Center (HPCC) of Nanjing University.
Edited by: Yuan Wang
Reviewed by: two anonymous referees
Barbu, A. L., Segers, A. J., Schaap, M., Heemink, A. W., and Builtjes, P. J. H.: A multi-component data assimilation experiment directed to sulphur dioxide and sulphate over Europe, Atmos. Environ., 43, 1622–1631, 2009.
Carmichael, G. R., Daescu, D. N., Sandu, A., and Chai, T.: Computational aspects of chemical data assimilation into atmospheric models, in: Science Computational ICCS 2003, Lecture Notes in Computer Science, Springer, Berlin, IV, 269–278, 2003.
Carmichael, G. R., Sandu, A., Chai, T., Daescu, D. N., Constantinescu, E. M., and Tang, Y.: Predicting air quality: improvements through advanced methods to integrate models and measurements, J. Comput. Phys., 227, 3540–3571, 2008a.
Carmichael, G. R., Sakuraib, T., Streetsc, D., Hozumib, Y., Uedab, H., Parkd, S. U., Funge, C., Hanb, Z., Kajinof, M., Engardtg, M., Bennetg, C., Hayamih, H., Sarteleti, K., Hollowayj, T., Wangk, Z., Kannaril, A., Fum, J., Matsudan, K., Thongboonchooa, N., and Amanno, M.: MICS-ASIA II: the model intercomaprison study for Asia phase II methodology and overview of findings, Atmos. Environ., 42, 3468–3490, 2008b.
Chen, D., Liu, Z., Fast, J., and Ban, J.: Simulations of sulfate-nitrate-ammonium (SNA) aerosols during the extreme haze events over northern China in October 2014, Atmos. Chem. Phys., 16, 10707–10724, https://doi.org/10.5194/acp-16-10707-2016, 2016.
Chen, F. and Dudhia, J.: Coupling an Advanced Land Surface–Hydrology Model with the Penn State–NCAR MM5 Modeling System – Part I: Model Implementation and Sensitivity, Mon. Weather Rev., 129, 569–585, https://doi.org/10.1175/1520-0493(2001)129<0569:Caalsh>2.0.Co;2, 2001.
Chin, M., Rood, R. B., Lin, S. J., Muller, J. F., and Thompson,A. M.: Atmospheric sulfur cycle simulated in the global model GOCART: Model description and global properties, J. Geophys. Res.-Atmos., 105, 24671–24687, 2000.
Chin, M., Ginoux, P., Kinne, S., Torres, O., Holben, B. N., Duncan, B. N., Martin, R. V., Logan, J. A., Higurashi, A., and Nakajima, J.: Tropospheric aerosol optical thickness from the GOCART model and comparisons with satellite and Sun photometer measurements, J. Atmos. Sci., 59, 461–483, 2002.
Chou, M.-D. and Suarez, M. J.: An efficient thermal infrared radiation parameterization for use in general circulation models, NASA Tech. Memo., NASA Goddard Space Flight Center, Greenbelt, MD, USA, TM 104606, vol. 3, 25 pp., 1994.
Dai, T., Schutgens, N. A. J., Goto, D., Shi, G. Y., and Nakajima, T.: Improvement of aerosol optical properties modeling over Eastern Asia with MODIS AOD assimilation in a global non-hydrostatic icosahedral aerosol transport model, Environ. Pollut., 195, 319–329, 2014.
Ding, A. J., Huang, X., Nie, W., Sun, J., Kerminen, V. M., Petaja, T., Su, H. L., Cheng, Y. F., Yang, X. Q., and Wang, M.: Enhanced haze pollution by black carbon in megacities in China, Geophys. Res. Lett., 43, 2873–2879, https://doi.org/10.1002/2016GL067745, 2016.
Ding, J., van der A, R. J., Mijling, B., Levelt, P. F., and Hao, N.: NOx emission estimates during the 2014 Youth Olympic Games in Nanjing, Atmos. Chem. Phys., 15, 9399–9412, https://doi.org/10.5194/acp-15-9399-2015, 2015.
Elbern, H. and Schmidt, H.: A 4D-Var chemistry data assimilation scheme for Eulerian chemistry transport modelling, J. Geophys. Res., 104, 18583–18598, 1999.
Elbern, H. and Schmidt, H.: Ozone episode analysis by four dimensional variational chemistry data assimilation, J. Geophys. Res., 106, 3569–3590, 2001.
Elbern, H., Schmidt, H., and Ebel, A.: Variational data assimilation for tropospheric chemistry modelling, J. Geophys. Res., 102, 15967–15985, 1997.
Elbern, H., Schmidt, H., Talagrand, O., and Ebel, A.: 4D-variational data assimilation with an adjoint air quality model for emission analysis, Environ, Model. Softw., 15, 539–548, 2000.
Elbern, H., Strunk, A., Schmidt, H., and Talagrand, O.: Emission rate and chemical state estimation by 4-dimensional variational inversion, Atmos. Chem. Phys., 7, 3749–3769, https://doi.org/10.5194/acp-7-3749-2007, 2007.
Evensen, G.: Sequential data assimilation with a nonlinear quasigeostrophic model using Monte Carlo methods to forecast error statistcs, J. Geophys. Res., 99, 10143–10162, 1994.
Gaspari, G. and Cohn S. E.: Construction of correlation functions in two and three dimensions, Q. J. Roy. Meteor. Soc., 125, 723–757, 1999.
Grell, G., Peckham, S. E., Schmitz, R., McKeen, S. A., Frost, G., Skamarock, W. C., and Eder, B.: Fully coupled “online” chemistry within the WRF model, Atmos. Environ., 39, 6957–6975, https://doi.org/10.1016/j.atmosenv.2005.04.027, 2005.
Hakami, A., Henze, D. K., Seinfeld, J. H., Chai, T., Tang, Y., Carmichael, G. R., and Sandu, A.: Adjoint inverse modeling of black carbon during the Asian Pacific Regional Aerosol Characterization Experiment, J. Geophys. Res.-Atmos., 110, D14301, https://doi.org/10.1029/2004JD005671, 2005.
Heemink, A. W. and Segers, A. J.: Modeling and prediction of environmental data in space and time using Kalman filtering, Stoch. Env. Res. Risk A., 16, 225–240, 2002.
Henze, D. K., Hakami, A., and Seinfeld, J. H.: Development of the adjoint of GEOS-Chem, Atmos. Chem. Phys., 7, 2413–2433, https://doi.org/10.5194/acp-7-2413-2007, 2007.
Henze, D. K., Seinfeld, J. H., and Shindell, D. T.: Inverse modeling and mapping US air quality influences of inorganic PM2.5 precursor emissions using the adjoint of GEOS-Chem, Atmos. Chem. Phys., 9, 5877–5903, https://doi.org/10.5194/acp-9-5877-2009, 2009.
Hong, S. Y., Noh, Y., and Dudhia, J.: A new vertical diffusion package with an explicit treatment of entrainment processes, Mon. Weather Rev., 134, 2318–2341, https://doi.org/10.1175/MWR3199.1, 2006.
Houtekamer, P. L., Mitchell, H. L., Pellerin, G., Buehner, M., Charron, M., Spacek, L., and Hansen, B.: Atmospheric data assimilation with an ensemble Kalman filter: Results with real observations, Mon. Weather Rev., 133, 604–620, 2005.
Huang, X., Song, Y., Zhao, C., Li, M., Zhu, T., Zhang Q., and Zhang, X. Y.: Pathways of sulfate enhancement by natural and anthropogenic mineral aerosols in China, J. Geophys. Res.-Atmos., 119, 14165–14179, 2014.
Jiang, Z., Liu, Z., Wang, T., Schwartz, C. S., Lin, H.-C., and Jiang, F.: Probing into the impact of 3DVAR assimilation of surface PM10 observations over China using process analysis, J. Geophys. Res.-Atmos., 118, 6738–6749, https://doi.org/10.1002/jgrd.50495, 2013.
Li, Z., Zang, Z., Li, Q. B., Chao, Y., Chen, D., Ye, Z., Liu, Y., and Liou, K. N.: A three-dimensional variational data assimilation system for multiple aerosol species with WRF/Chem and an application to PM2.5 prediction, Atmos. Chem. Phys., 13, 4265–4278, https://doi.org/10.5194/acp-13-4265-2013, 2013.
Li, M., Zhang, Q., Streets, D. G., He, K. B., Cheng, Y. F., Emmons, L. K., Huo, H., Kang, S. C., Lu, Z., Shao, M., Su, H., Yu, X., and Zhang, Y.: Mapping Asian anthropogenic emissions of non-methane volatile organic compounds to multiple chemical mechanisms, Atmos. Chem. Phys., 14, 5617–5638, https://doi.org/10.5194/acp-14-5617-2014, 2014.
Liu, Z., Liu, Q., Lin, H. C., Schwartz, C. S., Lee, Y. H., and Wang, T.: Three-dimensional variational assimilation of MODIS aerosol optical depth: implementation and application to a dust storm over East Asia, J. Geophys. Res., 116, D23206, https://doi.org/10.1029/2011JD016159, 2011.
McLinden, C. A., Fioletov, V., Shephard, M. W., Krotkov, N., Li, C., Martin, R. V., Moran, M. D., and Joiner, J.: Space-based detection of missing sulfur dioxide sources of global air pollution, Nat. Geosci., 9, 496–500, https://doi.org/10.1038/ngeo2724, 2016.
Mijling, B. and van der A, R. J.: Using daily satellite observations to estimate emissions of short-lived air pollutants on a mesoscopic scale, J. Geophys. Res., 117, D17302, https://doi.org/10.1029/2012JD017817, 2012.
Mijling, B., van der A, R. J., Boersma, K. F., Van Roozendael, M., De Smedt, I., and Kelder, H. M.: Reduction of NO2 detected from space during the 2008 Beijing Olympic Games, Geophys. Res. Lett., 36, L13801, https://doi.org/10.1029/2009GL038943, 2009.
Mijling, B., van der A, R. J., and Zhang, Q.: Regional nitrogen oxides emission trends in East Asia observed from space, Atmos. Chem. Phys., 13, 12003–12012, https://doi.org/10.5194/acp-13-12003-2013, 2013.
Ministry of Environmental Protection (MEP), Atmospheric environmental monitoring system of China, Ministry of Environmental Protection of China, available at: http://113.108.142.147:20035/emcpublish/, last access: 26 November 2018.
Miyazaki, K. and Eskes, H.: Constraints on surface NOx emissions by assimilating satellite observations of multiple species, Geophys. Res. Lett., 40, 4745–4750, https://doi.org/10.1002/grl.50894, 2013.
Miyazaki, K., Eskes, H. J., Sudo, K., Takigawa, M., van Weele, M., and Boersma, K. F.: Simultaneous assimilation of satellite NO2, O3, CO, and HNO3 data for the analysis of tropospheric chemical composition and emissions, Atmos. Chem. Phys., 12, 9545–9579, https://doi.org/10.5194/acp-12-9545-2012, 2012.
Miyazaki, K., Eskes, H. J., Sudo, K., and Zhang, C.: Global lightning NOx production estimated by an assimilation of multiple satellite data sets, Atmos. Chem. Phys., 14, 3277–3305, https://doi.org/10.5194/acp-14-3277-2014, 2014.
Mlawer, E. J., Taubman, S. J., Brown, P. D., Iacono, M. J., and Clough, S. A.: Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave, J. Geophys. Res.-Atmos., 102, 16663–16682, https://doi.org/10.1029/97jd00237, 1997.
National Center for Atmospheric Research (NCAR): WRF Source Codes and Graphics Software Downloads, available at: http://www2.mmm.ucar.edu/wrf/users/download/get_source.html, last access: 26 November 2018.
National Centers for Environmental Prediction (NCEP): Global Forecast System (GFS) Analysis, available at: https://www.ncdc.noaa.gov/data-access/model-data/model-datasets/global-forcast-system-gfs, last access: 26 November 2018.
Nie, W., Ding, A., Wang, T., Kerminen, V.-M., George, C., Xue, L., Wang, W., Zhang, Q., Petäjä, T., Qi, X., Gao, X., Wang, X., Yang, X., Fu, C., and Kulmala, M.: Polluted dust promotes new particle formation and growth, Sci. Rep., 4, 6634, https://doi.org/10.1038/srep06634, 2014.
Pagowski, M., Liu, Z., Grell, G. A., Hu, M., Lin, H.-C., and Schwartz, C. S.: Implementation of aerosol assimilation in Gridpoint Statistical Interpolation (v. 3.2) and WRF-Chem (v. 3.4.1), Geosci. Model Dev., 7, 1621–1627, https://doi.org/10.5194/gmd-7-1621-2014, 2014.
Parrish, D. D. and Zhu, T.: Clean Air for Megacities, Science, 326, 674–675, https://doi.org/10.1126/science.1176064, 2009.
Parrish, D. D., Trainer, M., Buhr, M. P., Watkins, B. A., and Fehsenfeld, F. C.: Carbon monoxide concentrations and their relation to concentrations of total reactive oxidized nitrogen at two rural U.S. sites, J. Geophys. Res., 96, 9309–9320, 1991.
Peng, Z., Zhang, M., Kou, X., Tian, X., and Ma, X.: A regional carbon data assimilation system and its preliminary evaluation in East Asia, Atmos. Chem. Phys., 15, 1087–1104, https://doi.org/10.5194/acp-15-1087-2015, 2015.
Peng, Z., Liu, Z., Chen, D., and Ban, J.: Improving PM2.5 forecast over China by the joint adjustment of initial conditions and source emissions with an ensemble Kalman filter, Atmos. Chem. Phys., 17, 4837–4855, https://doi.org/10.5194/acp-17-4837-2017, 2017.
Schutgens, N. A. J., Miyoshi, T., Takemura, T., and Nakajima, T.: Sensitivity tests for an ensemble Kalman filter for aerosol assimilation, Atmos. Chem. Phys., 10, 6583–6600, https://doi.org/10.5194/acp-10-6583-2010, 2010a.
Schutgens, N. A. J., Miyoshi, T., Takemura, T., and Nakajima, T.: Applying an ensemble Kalman filter to the assimilation of AERONET observations in a global aerosol transport model, Atmos. Chem. Phys., 10, 2561–2576, https://doi.org/10.5194/acp-10-2561-2010, 2010b.
Schutgens, N., Nakata, M., and Nakajima, T.: Estimating Aerosol Emissions by Assimilating Remote Sensing Observations into a Global Transport Model, Remote Sens., 4, 3528–3543, 2012.
Schwartz, C. S., Liu, Z., Lin, H. C., and McKeen, S. A.: Simultaneous three-dimensional variational assimilation of surface fine particulate matter and MODIS aerosol optical depth, J. Geophys. Res., 117, D13202, https://doi.org/10.1029/2011JD017383, 2012.
Schwartz, C. S., Liu, Z., Lin, H.-C., and Cetola, J. D.: Assimilating aerosol observations with a “hybrid” variational-ensemble data assimilation system, J. Geophys. Res.-Atmos., 119, 4043–4069, https://doi.org/10.1002/2013JD020937, 2014.
Sekiyama, T. T., Tanaka, T. Y., Shimizu, A., and Miyoshi, T.: Data assimilation of CALIPSO aerosol observations, Atmos. Chem. Phys., 10, 39–49, https://doi.org/10.5194/acp-10-39-2010, 2010.
Stockwell, W. R., Kirchner, F., Kuhn, M., and Seefeld, S: A new mechanism for regional atmospheric chemistry modeling, J. Geophys. Res., 102, 25847–25879, https://doi.org/10.1029/97JD00849, 1997.
Sun, Y. L., Wang, Z. F., Du, W., Zhang, Q., Wang, Q. Q., Fu, P. Q., Pan, X. L., Li, J., Jayne, J., and Worsnop, D. R.: Long-term real-time measurements of aerosol particle composition in Beijing, China: seasonal variations, meteorological effects, and source analysis, Atmos. Chem. Phys., 15, 10149–10165, https://doi.org/10.5194/acp-15-10149-2015, 2015.
Tang, X., Wang, Z. F., Zhu, J., Gbaguidi, A., Wu, Q. Z., Li, J., and Zhu, T.: Sensitivity of ozone to precursor emissions in urban Beijing with a Monte Carlo scheme, Atmos. Environ., 44, 3833–3842, 2010.
Tang, X., Zhu, J., Wang, Z. F., and Gbaguidi, A.: Improvement of ozone forecast over Beijing based on ensemble Kalman filter with simultaneous adjustment of initial conditions and emissions, Atmos. Chem. Phys., 11, 12901–12916, https://doi.org/10.5194/acp-11-12901-2011, 2011.
Tang, X., Zhu, J., Wang, Z. F., Wang, M., Gbaguidi, A., Li, J., Shao, M., Tang, G. Q., and Ji, D. S.: Inversion of CO emissions over Beijing and its surrounding areas with ensemble Kalman filter, Atmos. Environ., 81, 676–686, 2013.
Tang, X., Zhu, J., Wang, Z., Gbaguidi, A., Lin, C., Xin, J., Song, T., and Hu, B.: Limitations of ozone data assimilation with adjustment of NOx emissions: mixed effects on NO2 forecasts over Beijing and surrounding areas, Atmos. Chem. Phys., 16, 6395–6405, https://doi.org/10.5194/acp-16-6395-2016, 2016.
Torn, R. D., Hakim, G. J., and Snyder, C.: Boundary conditions for limited-area ensemble Kalman filters, Mon. Weather Rev., 134, 2490–2502, 2006.
van der A, R. J., Peters, D. H. M. U., Eskes, H., Boersma, K. F., Van Roozendael, M., De Smedt, I., and Kelder, H. M.: Detection of the trend and seasonal variation in tropospheric NO2 over China, J. Geophys. Res., 111, D12317, https://doi.org/10.1029/2005JD006594, 2006.
van der A, R. J., Mijling, B., Ding, J., Koukouli, M. E., Liu, F., Li, Q., Mao, H., and Theys, N.: Cleaning up the air: effectiveness of air quality policy for SO2 and NOx emissions in China, Atmos. Chem. Phys., 17, 1775–1789, https://doi.org/10.5194/acp-17-1775-2017, 2017.
van Loon, M., Builtjes, P. J. H., and Segers, A. J.: Data assimilation of ozone in the atmospheric transport chemistry model LOTOS, Environ. Model. Softw., 15, 603–609, 2000.
Wang, Z., Li, J., Wang, Z., Yang, W., Tang, X., Ge, B., Yan, P., Zhu, L., Chen, X., and Chen, H.: Modeling study of regional severe hazes over mid-eastern China in January 2013 and its implications on pollution prevention and control, Sci. China-Earth Sci., 57, 3–13, 2014.
Whitaker, J. S. and Hamill, T. M.: Ensemble data assimilation without perturbed observations, Mon. Weather Rev., 130, 1913–1924, 2002.
Wild, O., Zhu, X., and Prather, M. J.: Fast-j: Accurate simulation of in- and below-cloud photolysis in tropospheric chemical models, J. Atmos. Chem., 37, 245–282, https://doi.org/10.1023/A:1006415919030, 2000.
Xie, Y., Ding, A., Nie, W., Mao, H., Qi, X., Huang, X., Xu, Z., Kerminen, V.-M., Petäjä, T., Chi, X., Virkkula, A., Boy, M., Xue, L., Guo, J., Sun, J., Yang, X., Kulmala, M., and Fu, C.: Enhanced sulfate formation by nitrogen dioxide: Implications from in situ observations at the SORPES station, J. Geophys. Res.-Atmos., 120, 12679–12694, 2015.
Yang, Y. R., Liu, X. G., Qu, Y., An, J. L., Jiang, R., Zhang, Y. H., Sun, Y. L., Wu, Z. J., Zhang, F., Xu, W. Q., and Ma, Q. X.: Characteristics and formation mechanism of continuous hazes in China: a case study during the autumn of 2014 in the North China Plain, Atmos. Chem. Phys., 15, 8165–8178, https://doi.org/10.5194/acp-15-8165-2015, 2015.
Yumimoto, K., Uno, I., Sugimoto, N., Shimizu, A., and Satake, S.: Adjoint inverse modeling of dust emission and transport over East Asia, Geophys. Res. Lett., 34, L00806, https://doi.org/10.1029/2006GL02855, 2007.
Yumimoto, K., Uno, I., Sugimoto, N., Shimizu, A., Liu, Z., and Winker, D. M.: Adjoint inversion modeling of Asian dust emission using lidar observations, Atmos. Chem. Phys., 8, 2869–2884, https://doi.org/10.5194/acp-8-2869-2008, 2008.
Zhang, L., Shao, J. Y., Lu, X., Zhao, Y. H., Hu, Y. Y., Henze, D. K., Liao, H., Gong, S., and Zhang, Q.: Sources and processes affecting fine particulate matter pollution over North China: An adjoint analysis of the Beijing APEC period, Environ. Sci. Technol., 50, 8731–8740, https://doi.org/10.1021/acs.est.6b03010, 2016.
Zhang, L., Li, Q., Wang, T., Ahmadov, R., Zhang, Q., Li, M., and Lv, M.: Combined impacts of nitrous acid and nitryl chloride on lower-tropospheric ozone: new module development in WRF-Chem and application to China, Atmos. Chem. Phys., 17, 9733–9750, https://doi.org/10.5194/acp-17-9733-2017, 2017.
Zhang, Q., Streets, D. G., Carmichael, G. R., He, K. B., Huo, H., Kannari, A., Klimont, Z., Park, I. S., Reddy, S., Fu, J. S., Chen, D., Duan, L., Lei, Y., Wang, L. T., and Yao, Z. L.: Asian emissions in 2006 for the NASA INTEX-B mission, Atmos. Chem. Phys., 9, 5131–5153, https://doi.org/10.5194/acp-9-5131-2009, 2009.
Zhang, R., Wang, G., Guo, S., Zamora, M. L., Ying, Q., Lin, Y., Wang, W., Hu, M., and Wang, Y.: Formation of Urban Fine Particulate Matter, Chem. Rev., 115, 3803–3855, https://doi.org/10.1021/acs.chemrev.5b00067, 2015.
Zheng, B., Zhang, Q., Zhang, Y., He, K. B., Wang, K., Zheng, G. J., Duan, F. K., Ma, Y. L., and Kimoto, T.: Heterogeneous chemistry: a mechanism missing in current models to explain secondary inorganic aerosol formation during the January 2013 haze episode in North China, Atmos. Chem. Phys., 15, 2031–2049, https://doi.org/10.5194/acp-15-2031-2015, 2015.