2.1 Classical nucleation theory

Since CNT is the most widely used theoretical approach in atmospheric models we start by highlighting its main characteristic. Common CNT expressions use several assumptions to simplify the description of the interaction between water and the immersed particle (Hoose et al., 2010; Khvorostyanov and Curry, 2004; Zobrist et al., 2007). Typically the particle is assumed to have a negligible effect on the mobility and the thermodynamics of the vicinal water, i.e., $f_{\mathrm{het}}^{*}\approx f_{\mathrm{hom}}^{*}$. The latter is calculated assuming that the formation of clusters within the liquid phase mimics a first-order reaction in an ideal gas where every molecule that randomly jumps into the ice–liquid interface is incorporated within the ice lattice. Thus $f_{\mathrm{hom}}^{*}$ is the product of the frequency factor (derived from transition state theory) and the monomer concentration at the ice–liquid interface. This leads to (Kashchiev, 2000; Pruppacher and Klett, 1997)

where ΔG_act is the activation energy, i.e., the energy required for a water molecule to leave its equilibrium position in the bulk towards the vicinity of the ice germ (Pruppacher and Klett, 1997; Zobrist et al., 2007), h is Plank's constant, Ω the surface area of the ice germ and d₀ is the molecular diameter of water.

The work of ice nucleation results from the assumption that the ice germ has a hemispherical shape. Other assumptions include no surface stress (Cahn, 1980) and negligible mixing effects during germ formation (Barahona, 2014). These considerations lead to the expression (Turnbull and Fisher, 1949)

where ΔG_hom,CNT is the homogeneous work of nucleation, given by

where σ_iw is the ice–water interfacial energy and S_i is the saturation ratio with respect to ice. The effect of the immersed particle on J_het,CNT depends on the adsorption of water molecules on individual sites, and is characterized by the contact angle, θ, in the form

Equation (9) can be extended to account for line tension, curvature and misfit effects (Khvorostyanov and Curry, 2004), which, however, requires the usage of additional unconstrained parameters. Introducing Eqs. (6) and (7) into Eq. (5) we obtain the known expression,

where $\mathrm{\Omega }=\mathrm{4}\mathit{\pi }{r}_{\mathrm{g}}^{\mathrm{2}}$, and $r_{\mathrm{g}}={\left(\frac{\mathrm{3}{n}^{*}{v}_{\mathrm{w}}}{\mathrm{4}\mathit{\pi }}\right)}^{\mathrm{1}/\mathrm{3}}$ is the radius of the ice germ. Other symbols are defined in Table 1.

Due in part to the assumption of a negligible effect of the particle on the adjacent water the CNT framework does not provide a way to link the properties of the vicinal water to the nucleation rate. Another caveat of CNT is that fundamental parameters like ΔG_act, σ_iw and θ do not have a clear definition outside of the context of the theory. For example, ΔG_act is typically assumed the same as in bulk water, representing a barrier to bulk diffusion instead of interfacial transfer (Barahona, 2015; Kashchiev, 2000). Similarly σ_iw is not well defined for a diffuse interface, and it is difficult to measure away from equilibrium. Moreover, θ relies on a droplet-like picture of the nascent ice germ, which may not be appropriate for a germ forming within the dense liquid phase (Brukhno et al., 2008). Most studies thus treat ΔG_act, σ_iw and θ as empirical parameters, fitted to match measured nucleation rates. Many times this results in complex functional forms of T and S_i that may not be easily expanded to account for the modified properties of water near the immersed particle.

2.2 Negentropic nucleation framework

Some of the caveats of CNT are addressed in the negentropic nucleation framework (Barahona, 2014, 2015). In NNF simple thermodynamic arguments are used to approximate ΔG_hom and f_hom in terms of water properties that could, in principle, be independently estimated. This obviates the need for parameters that should be fitted to measured nucleation rates. At the same time, NNF is a relatively simple framework that can be easily implemented in large-scale atmospheric models and that has been shown to reproduce homogeneous freezing temperatures down to 180 K (Barahona, 2015; O and Wood, 2016). This section presents the main results of NNF for homogeneous ice nucleation.

In NNF the energy of formation of the interface, Φ_s, is an explicit function of the water activity and temperature in the form

where the constants Γ_w=1.46 and $s=\mathrm{1.105}{\mathrm{molec}}^{\mathrm{1}/\mathrm{3}}$ define the coverage of the ice–water interface and the lattice geometry of the ice germ, respectively, and Δh_f is the latent heat of fusion of water. Other symbols are defined in Appendix A. Equation (11) results from accounting for the finite character of the ice–liquid interface and from the assumption that, in joining the ice lattice, the water molecules lose most of their entropy (Barahona, 2014). The driving force for ice nucleation, Δμ_i, is given by

where a_w,eq is the equilibrium water activity. Equation (12) accounts for the work of “unmixing” affecting the bulk of the liquid when the ice germ is formed, which is proportional to ln(a_w) (Black, 2007). Using Eqs. (11) and (12), the critical germ size and the work of nucleation are obtained from the condition of mechanical equilibrium of the ice germ (Barahona, 2014), resulting in

and

In more recent work the kinetics of homogeneous ice nucleation have been re-examined in NNF to account for molecular rearrangement during the transfer of water molecules across the ice–liquid interface (Barahona, 2015). Within this approach $f_{\mathrm{hom}}^{*}$ is determined by the diffusion coefficient for interfacial transfer, D, in the form (Barahona, 2015; Kashchiev, 2000)

where Ω is the surface area of the ice germ. D represents contributions from purely diffusive process and from structural transformations required to incorporate water molecules into the ice germ. The latter originates because neighboring molecules need to be rearranged to accommodate new ones into the ice lattice, generating entropy and dissipating work. Using considerations from non-equilibrium thermodynamics D can be written in the form (Barahona, 2015)

where D_∞ is the bulk self-diffusion coefficient of water, and W_d is the average dissipated work during interface transfer. The latter is proportional to the excess free energy of solidification of water, i.e., $W_{\mathrm{d}}=-n_{\mathrm{t}}\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{s}}$, with n_t=16, the number of possible trajectories in which individual water molecules can make four-bonded water. Equation (16) shows explicitly that bulk diffusion (i.e., D_∞) as well as structural rearrangement are required for ice germ growth. Introducing Eq. (16) into Eq. (15) we obtain

Application of Eq. (17) to homogeneous ice nucleation shows agreement of J_hom with experimental data at very low T, where kinetic processes dominate the formation ice (Barahona, 2015).

NNF provides explicit dependencies of D and Φ_s on thermodynamic properties without depending on nucleation rate measurements. Thus it provides a suitable basis to study the thermodynamics and kinetics of ice formation in the vicinity of immersed particles. Doing so first requires building a model to describe the thermodynamics of the vicinal water.

2.3 Thermodynamics of the liquid–particle interface

The discussion presented in Sect. 1.1 suggests that the immersed particle enhances order near the particle–liquid interface, lowering the energy required to nucleate ice. The vicinal layer is thus described as a solution of hypothetical ice-like (IL) and liquid-like (LL) regions, with Gibbs free energy, given by

where ${\widehat{\mathit{\mu }}}_{\mathrm{LL}}$ and ${\widehat{\mathit{\mu }}}_{\mathrm{LL}}$ are the chemical potentials of the LL and IL species within the solution, respectively, and ζ is the fraction of IL regions in the layer. Increased order is represented by a higher fraction of IL regions, hence higher ζ. Equation (18) can also be written in terms of the chemical potentials of the “pure” LL and IL species, μ_LL and μ_IL, respectively, in the form

where $\mathrm{\Delta }{G}_{\mathrm{mix}}=({\widehat{\mathit{\mu }}}_{\mathrm{IL}}-{\mathit{\mu }}_{\mathrm{IL}})\mathit{\zeta }+(\mathrm{1}-\mathit{\zeta })({\widehat{\mathit{\mu }}}_{\mathrm{LL}}-{\mathit{\mu }}_{\mathrm{LL}})$ is the Gibbs energy of mixing. For a mechanical mixture of pure LL and IL species, ΔG_mix=0, whereas for an ideal solution, ΔG_mix is determined by the ideal entropy of mixing (Prausnitz et al., 1998). Reorganizing Eq. (19) we obtain,

where $\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{il}}={\mathit{\mu }}_{\mathrm{IL}}-{\mathit{\mu }}_{\mathrm{LL}}$. Δμ_il can be approximated using the equilibrium between bulk liquid and ice as a reference state (Kashchiev, 2000), making

and

where a_w,eff is termed the “effective water activity” and is the value of a_w associated with the LL regions in the vicinal water, and a_IL is the water activity in the IL regions. Assuming that, similarly to bulk ice, the solute does not significantly partition to the IL phase, then a_IL≈1. With this, and by combining Eq. (21) and Eq. (22) and rearranging, we obtain

The central assumption behind Eq. (23) is that a_w,eq corresponds to the equilibrium water activity between liquid and ice, or in other words, that near equilibrium Δμ_il≈Δμ_s. In reality Δμ_s corresponds to actual liquid and ice, instead of the hypothetical LL and IL substances. This difference can be accounted for by selecting a proper functional form for ΔG_mix, for which several empirical and semi-empirical interaction models, with varying degrees of complexity, exist (Prausnitz et al., 1998). In this work it is assumed that the vicinal water can be described as a regular solution. This is the simplest model that accounts for the interaction between solvent and solute during mixing and that is flexible enough to include corrections for the difference between Δμ_s and Δμ_il. Using this model Holten et al. (2013) were able to approximate the chemical potential of supercooled water. The authors also showed that taking into account clustering of water molecules led to a better agreement of the estimated water properties with MD simulations and experimental results.

According to the regular solution model, modified by clustering Holten et al. (2013),

The first term on the right-hand side corresponds to the usual definition of the ideal entropy of mixing, i.e., random ideal mixing and weak interaction between IL and LL regions, modified to account for clustering in groups of N molecules. N=6 corresponds to clustering in hexamers and is near the optimum fit between MD simulations and the solution model (Holten et al., 2013). It must be noted that Holten et al. (2013) recommended an alternative model termed “athermal solution”, where nonideality is ascribed to entropy changes upon mixing. In vicinal water some evidence points to nonideality originating from enthalpy changes near the particle (Etzler, 1983); hence a regular solution is more appropriate in this case. For N=6 the difference between the two models is negligible (Holten et al., 2013).

The second term on the right-hand side of Eq. (24) is an empirical functional form used to approximate the enthalpy of mixing, selected so that ΔG_mix=0 for both ζ=0 and ζ=1. A_w is a phenomenological interaction parameter, here assumed to implicitly correct the approximation Δμ_il≈Δμ_s. Typically A_w must be fitted to experimental observations. In this work A_w is calculated using an alternative approach, as follows.

An important aspect of the regular solution model is that it predicts that μ_vc has a critical temperature, T_c, defined by the conditions,

These conditions originate because $\frac{{\partial }^{\mathrm{2}}{\mathit{\mu }}_{\mathrm{vc}}}{\partial {\mathit{\zeta }}^{\mathrm{2}}}=\mathrm{0}$ represents a stability limit for the vicinal water. A solution would split into two phases, if doing so lowers its Gibbs free energy (Prausnitz et al., 1998). For a metastable solution μ_vc must be minimal, hence $\frac{\partial {\mathit{\mu }}_{\mathrm{vc}}}{\partial \mathit{\zeta }}=\mathrm{0}$. The condition $\frac{{\partial }^{\mathrm{2}}{\mathit{\mu }}_{\mathrm{vc}}}{\partial {\mathit{\zeta }}^{\mathrm{2}}}<\mathrm{0}$ indicates that any increase in ζ increases μ_vc (i.e., the curve μ_vc vs. ζ becomes concave downward), such that it is thermodynamically more favorable for the solution to split into distinct phases than to increase its concentration. The last condition, $\frac{{\partial }^{\mathrm{3}}{\mathit{\mu }}_{\mathrm{vc}}}{\partial {\mathit{\zeta }}^{\mathrm{3}}}=\mathrm{0}$, indicates that the metastable region reduces to a single point. Using Eq. (20) into Eq. (25) we obtain,

and

The last expression is only valid for ζ=0.5, indicating that a single critical temperature exists for a regular solution. Using this in Eq. (26) and solving for A_w gives, for T=T_c,

Physically, T_c represents the stability limit of the vicinal water, at which it spontaneously separates into IL and LL regions. For T<T_c the chemical potential of an equimolar solution of IL and LL would be larger than that of a simple mechanical mixture of the two species. Thus it is thermodynamically more favorable for the solution to split into its individual components, i.e., ice and liquid, leading to a stability limit of the system. Equation (28) thus provides an opportunity to theoretically determine A_w, since T_c should also correspond to a negligible work of nucleation. This further explained in Sect. 2.4.2.

Introducing Eqs. (23), (24) and (28) in Eq. (20), we obtain

By defining Λ_mix in the form,

Equation (29) can be written in the form

Equation (31) is the equation of state of the vicinal water. It describes the properties of the vicinal water in terms of the material-specific parameter ζ and the interaction parameters N and T_c. MD simulations indicate that N∼6 (Bullock and Molinero, 2013; Holten et al., 2013). T_c is thus the only remaining unknown in Eq. (31) and is calculated in Sect. 2.4.2.

2.4 Work of germ formation

The equation of state of vicinal water can be used to link ΔG_hom and ΔG_het as follows. In immersion freezing the particle remains within the droplet long enough that equilibrium is established. This condition is mathematically expressed by the equality, μ_vc=μ_w, where μ_w is the chemical potential of water in the bulk of the liquid, i.e., away from the particle. Using Eq. (31) this implies that

This expression indicates that the effect of the particle on its vicinal water can be understood as an enhancement of the chemical potential of the LL regions, a consequence of the tendency of the particle to lower μ_vc. Since Δμ_il<0, μ_LL must increase to maintain equilibrium. Using the equilibrium between bulk liquid and ice as reference state so that ${\mathit{\mu }}_{\mathrm{w}}={\mathit{\mu }}_{\mathrm{eq}}+k_B\ln \left(\frac{a_{\mathrm{w}}}{a_{\mathrm{w},\mathrm{eq}}}\right)$, we obtain the following after simplifying:

Or, equivalently,

Equation (34) suggests that, thermodynamically, immersion freezing can be described as homogeneous ice nucleation occurring at an enhanced water activity. This is because it is possible to create a path including homogeneous ice nucleation with the same change in Gibbs free energy as for heterogeneous freezing. Figure 1 shows that for a particle-droplet system in equilibrium, a_w,eff satisfies the condition

Equation (35) represents a thermodynamic relation between ΔG_het and ΔG_hom. It has the advantage that ΔG_het can be obtained without invoking assumptions on the mechanistic details of the interaction between the particle and the ice germ, which are parameterized by ζ. Since a_w is typically the controlled variable in ice nucleation, a_w,eff can be readily obtained by solving Eq. (34),

Although ascribing ice nucleation to the LL fraction of vicinal water agrees with the decisive role of free water in the formation of ice (Wang et al., 2016), caution must be taken in considering this to be the actual mechanism of ice nucleation, which could be quite complex. Equation (35), however, establishes a thermodynamic constrain for ΔG_het that should be met by any ice nucleation mechanism. It is also important to analyze the behavior of a_w,eff as ζ→1. It can be shown that the quotient $\frac{{\mathrm{\Lambda }}_{\mathrm{mix}}}{\mathit{\zeta }-\mathrm{1}}$ converges for ζ→1 as follows. From Eq. (30) we can write

Using $\ln \left(x\right)\to (x-\mathrm{1})$ for x→1, the last expression can be shown to converge to

The fact that ${lim}_{\mathit{\zeta }\to \mathrm{1}}\exp \left(-\frac{{\mathrm{\Lambda }}_{\mathrm{mix}}}{\mathrm{1}-\mathit{\zeta }}\right)\ne \mathrm{1}$ for T≠T_c stems from the simple interaction model used to define ΔG_mix (i.e., the regular solution approximation). T_c may depend on ζ, however the regular solution approximation predicts a unique critical temperature at ζ=0.5. This, however, does not lead to uncertainty in ΔG_hom since for ζ→1, the first term on the right-hand side of Eq. (36) is almost singular at $a_{\mathrm{w}}=a_{\mathrm{w},\mathrm{eq}}$. Thus if ${lim}_{\mathit{\zeta }\to \mathrm{1}}\exp \left(-\frac{{\mathrm{\Lambda }}_{\mathrm{mix}}}{\mathrm{1}-\mathit{\zeta }}\right)<\mathrm{1}$, then a_w must be just above a_w,eq to make $a_{\mathrm{w},\mathrm{eff}}=\mathrm{1}$. In other words, for all practical purposes, $a_{\mathrm{w},\mathrm{eff}}\to \mathrm{1}$ when the system approaches thermodynamic equilibrium.

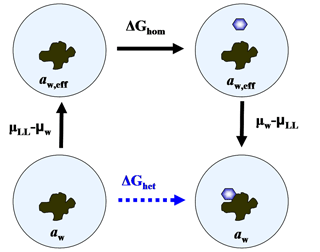
Figure 1Diagram representing a thermodynamic path, including homogeneous ice nucleation with the same work as heterogeneous freezing.

Download

2.4.1 Extension of the homogeneous model to the spinodal limit

In applying the homogeneous model to the heterogeneous problem in the form detailed in Sect. 2.4, caution must be taken in describing the limiting condition where the size of the ice germ becomes exceedingly small, i.e., n_hom→1, representing the vanishing of the energy barrier to ice nucleation. This is possible, since as ζ→1, a_w,eff becomes large (Eq. 36), and for ζ=1 it is only defined at thermodynamic equilibrium. Since for n_hom→1, thermodynamic potentials are not well defined, it is necessary to test the validity of NNF at such a limit. Moreover, in its original formulation (Sect. 2.2) NNF predicts a positive ΔG_hom for n_hom=1, at odds with the notion that the formation of a monomer-sized germ should carry no work.

At the limiting condition, n_hom=1, the work of nucleation is smaller than the thermal energy of the molecules and represents the onset of spontaneous phase separation (termed “spinodal decomposition”) during nucleation (Vekilov, 2010). Here it is argued that being a far-from-equilibrium process, ice nucleation always carries energy dissipation. When accounted for, the apparent inconsistency in NNF at n_hom=1 vanishes, since as shown below such a condition is not accessible. This approach differs from previous treatments, where this limit is associated with a negligible driving force for nucleation (Kalikmanov and van Dongen, 1993).

To account for the finite, albeit small, amount of work dissipated from the generation of entropy during spontaneous fluctuation, a simple approach is proposed. It involves writing the work of cluster formation in the form

$$\begin{array}{}\text{(39)}& {\displaystyle }\mathrm{\Delta }G=-n\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{i}}+n^{\mathrm{2}/\mathrm{3}}{\mathrm{\Phi }}_{\mathrm{s}}+W_{\mathrm{diss}},\end{array}$$

where W_diss represents work dissipation, assumed independent of the germ size, since it results from spontaneous fluctuations occurring in the liquid phase. Equation (39) is the typical expression for ΔG (Barahona, 2014) with an additional term accounting for irreversibility. The nucleation work is defined for n=n_hom in the form

$$\begin{array}{}\text{(40)}& {\displaystyle }\mathrm{\Delta }{G}_{\mathrm{hom}}=-n_{\mathrm{hom}}\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{i}}+n_{\mathrm{hom}}^{\mathrm{2}/\mathrm{3}}{\mathrm{\Phi }}_{\mathrm{s}}+W_{\mathrm{diss}},\end{array}$$

where n_hom is obtained from the mechanical stability condition, $\frac{\partial \mathrm{\Delta }G}{\partial n}=\mathrm{0}$, and is still given by Eq. (13), since W_diss is assumed independent of n. W_diss is then obtained from the conditions

$$\begin{array}{}\text{(41)}& {\displaystyle }\mathrm{\Delta }{G}_{\mathrm{hom}}{|}_{n_{\mathrm{hom}}=\mathrm{1}}=\mathrm{0},{\displaystyle \frac{{\partial }^{\mathrm{2}}\mathrm{\Delta }{G}_{\mathrm{hom}}}{\partial n_{\mathrm{hom}}^{\mathrm{2}}}}{|}_{n_{\mathrm{hom}}=\mathrm{1}}=\mathrm{0}.\end{array}$$

The first condition expresses the fact that the formation of a monomer-sized ice germ carries no work. The second condition establishes that n_hom=1 should correspond to a stability limit of the system where nucleation and spontaneous separation are analogous. This is referred as the spinodal point. From Eq. (40) we obtain

$$\begin{array}{}\text{(42)}& {\displaystyle \frac{{\partial }^{\mathrm{2}}\mathrm{\Delta }{G}_{\mathrm{hom}}}{\partial n_{\mathrm{hom}}^{\mathrm{2}}}}=-{\displaystyle \frac{\mathrm{2}}{\mathrm{9}}}{n}_{\mathrm{hom}}^{-\mathrm{4}/\mathrm{3}}{\mathrm{\Phi }}_{\mathrm{s}}=\mathrm{0}.\end{array}$$

Since n_hom only attains positive values, then only the trivial solution Φ_s=0 satisfies Eq. (42), i.e., the energy barrier to the formation of the ice germ vanishes at the spinodal. Using Φ_s=0 and $\mathrm{\Delta }{G}_{\mathrm{hom}}{|}_{n_{\mathrm{hom}}=\mathrm{1}}=\mathrm{0}$, Eq. (40) can be solved for W_diss in the form

$$\begin{array}{}\text{(43)}& {\displaystyle }{W}_{\mathrm{diss}}=\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{i}}.\end{array}$$

Thus the minimum amount of work dissipated during nucleation corresponds to a fluctuation relaxing Δμ_i. Replacing this expression within Eq. (40), we obtain

$$\begin{array}{}\text{(44)}& {\displaystyle }\mathrm{\Delta }{G}_{\mathrm{hom}}=-\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{i}}(n_{\mathrm{hom}}-\mathrm{1})+n_{\mathrm{hom}}^{\mathrm{2}/\mathrm{3}}{\mathrm{\Phi }}_{\mathrm{s}}\end{array}$$

Using Eq. (13) in Eq. (44) gives, after rearranging, the work of germ formation by homogeneous ice nucleation:

$$\begin{array}{}\text{(45)}& {\displaystyle }\mathrm{\Delta }{G}_{\mathrm{hom}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{i}}(n_{\mathrm{hom}}+\mathrm{2}).\end{array}$$

Equation (45) only differs from the NNF expression, Eq. (14), on the right-hand side, where it is implied that nucleation in a solution requires the coordination of at least two molecules, a condition that has been observed experimentally in the crystallization of proteins (Vekilov, 2010). It also suggests that dissipation effects are negligible for typical homogeneous nucleation conditions, i.e., $\mathrm{\Delta }{G}_{\mathrm{hom}}\approx \mathrm{\Delta }{G}_{\mathrm{hom},\mathrm{NNF}}$, since n_hom∼200 (Barahona, 2014). Moreover, the fact that ΔG_hom>0 even when n_hom→0 implies that ice nucleation always requires some work. Using Eq. (35) the heterogeneous work of nucleation can be readily written as

$$\begin{array}{}\text{(46)}& {\displaystyle }\mathrm{\Delta }{G}_{\mathrm{het}}\left(a_{\mathrm{w}}\right)={\left[{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\mathrm{\Delta }{\mathit{\mu }}_{\mathrm{i}}(n_{\mathrm{hom}}+\mathrm{2})\right]}_{a_{\mathrm{w},\mathrm{eff}}}.\end{array}$$

Equation (46) also suggests an operational definition for the critical ice germ in immersion freezing in the form

$$\begin{array}{}\text{(47)}& {\displaystyle }{n}_{\mathrm{het}}={\left(n_{\mathrm{hom}}+\mathrm{2}\right)}_{a_{\mathrm{w},\mathrm{eff}}}.\end{array}$$

The results of Eqs. (45) and (46) require further explanation, since in principle, an ice germ with only two molecules does not exist. Thus Eq. (45) must be interpreted in a different way. As ζ→1, or in deeply supercooled conditions, the fraction of ice-like regions in the vicinal water becomes large. Under such a scenario the reorientation of only two molecules may be enough to initiate ice nucleation. In other words, beyond the spinodal point ice nucleation is controlled by molecular motion within already formed ice-like regions. For homogeneous ice nucleation this would require extreme supercooling (T∼140 K, Fig. 2). In immersion ice nucleation it may occur at higher T, since the formation of a high fraction of ice-like regions in the vicinal water is facilitated by efficient INPs. This is further explored in Sect. 3.

Figure 2Work of heterogeneous ice nucleation. Color indicates different temperatures.

Download

NNF carries the assumption that thermodynamic potentials can be defined for the ice germ. In other words n_hom should be large enough that it represents a statistical ensemble of molecules. Of course this is not the case for n_hom=1, and it may cast doubt on the application of Eq. (39) to such limits. This possibility is, however, mitigated in two ways. Unlike CNT, which is based on the interfacial tension, the NNF framework is robust for small germs. Size effects impact ΔG mostly through Φ_s, since Δμ_i does not change substantially with the size of the system. In NNF the product Γ_wsΔh_f in Eq. (11) remains constant, and Φ_s is relatively insensitive to n. This is because Δh_f decreases with n as the total cohesive energy of the germ is inversely proportional to the number of molecules within the ice–liquid interfacial layer (Johnston and Molinero, 2012; Zhang et al., 1999). At the same time, the product Γ_ws, i.e., the ratio of the number of surface to interior molecules in the germ (Barahona, 2014; Spaepen, 1975), should increase for small ice germs, offsetting the decrease in Δh_f. Such behavior is supported by MD simulations (Johnston and Molinero, 2012). Equation (11) thus remains valid for small germs. A second mitigating factor is discussed in Sect. 3.1, where it is shown that conditions leading to n_het→1 are rare in the atmosphere, and J_het is largely independent of n_het for very small germs.

2.5 Kinetics of immersion freezing

Almost every theoretical approach to describe the effect of INPs on ice formation focuses on the thermodynamics of ice nucleation. However as discussed in Sect. 1.1, increased molecular ordering increases the viscosity of vicinal water, implying that the immersed particle modifies the flux of water molecules to the nascent ice germ, hence the kinetics of ice nucleation (Etzler, 1983; Feibelman, 2010). Since these structural changes are also related to modifications in the chemical potential of the vicinal water, it is likely that the same mechanism that decreases ΔG_het also controls the mobility of water molecules in the environment around the particle. Such a connection between the water thermodynamic properties and its molecular mobility is well established (Adam and Gibbs, 1965; Debenedetti and Stillinger, 2001; Scala et al., 2000), but it is generally neglected in nucleation theory (Ickes et al., 2017; Pruppacher and Klett, 1997). In this section a heuristic model is proposed to account for such effects.

Kinetic effects modify the value of the impingement factor, $f_{\mathrm{het}}^{*}$, which controls the flux of water molecules to the ice germ. In general the ice germ grows by diffusion and rearrangement of nearby water molecules across the ice–liquid interface, characterized by the interfacial diffusion coefficient, D. Increased ordering is characterized by a higher IL fraction, hence higher ζ. Thus, in immersion freezing, D must be a function of ζ. Using Eq. (15) this can be expressed in the form

Assuming that within the vicinal layer the ice germ grows following a similar mechanism as in the bulk of the liquid, then Eq. (16) can be applied to the heterogeneous process in the form

The last expression indicates that ice–liquid interfacial transfer requires a diffusional and a rearrangement component. D_∞(ζ) characterizes purely diffusional processes occurring within the particle–liquid interface. Molecular rearrangement during ice germ growth within the vicinal layer is determined by W_d(ζ). Since only molecules in the LL fraction of the vicinal water would rearrange to join the ice lattice then the latter is given by

Introducing the last expression in Eq. (49) we obtain

This expression is consistent with the thermodynamic model presented in Sect. 2.3, since as ζ increases, the vicinal water has a larger “ice” character, and fewer molecules need to rearrange to be incorporated into the growing ice germ.

2.6 Nucleation rate

The results of Sects. 2.3 to 2.5 provide the basis for writing an expression for the ice nucleation rate of droplets by immersion freezing. Before completing such a description we need to provide an expression for Z. The application of Eq. (2) typically leads to the known expression (Pruppacher and Klett, 1997)

On the other hand using Eq. (46) in Eq. (2), we obtain

where the subscript “d” indicates that energy dissipation is taken into account. For n_het>3 it is easily verifiable that Z_d≈Z. Indeed the discrepancy between Z_d and Z is only 30 % for n_het=3, and it is much smaller for larger ice germs. However for n_het=2, Z_d=0. This issue is rather fundamental and may represent the breaking of the assumption that each germ grows by the addition of a single molecule at a time. Hence Eq. (59) will be used keeping in mind that for very small ice germs, it represents only an approximation.

With the above considerations it is now possible to substitute Eqs. (46), (47), (58) and (59) into Eq. (5) to obtain the heterogeneous ice nucleation rate

where $d_{\mathrm{0}}=(\mathrm{6}{v}_{\mathrm{w}}/\mathit{\pi }{)}^{\mathrm{1}/\mathrm{3}}$ and $a_{\mathrm{0}}=\mathit{\pi }{d}_{\mathrm{0}}^{\mathrm{2}}/\mathrm{4}$ were used, and $\mathrm{\Omega }={\mathrm{\Gamma }}_{\mathrm{w}}s{n}_{\mathrm{het}}^{\mathrm{2}/\mathrm{3}}{a}_{\mathrm{0}}$ is the surface area of the ice germ. Other symbols and values used are listed in Appendix A.

2.7 The role of active sites

There is evidence that in dust and other INPs, ice is formed preferentially in the vicinity of surface patches, commonly referred as active sites. The existence of active sites has been established experimentally for deposition ice nucleation Kiselev et al. (2017), and they may be also important for immersion freezing Murray et al. (2012). In the classical view active sites have the property of locally reducing ΔG_het, increasing J_het. In the so-called singular hypothesis each active site has an associated characteristic temperature at which it nucleates ice. Current interpretation assigns J_het→∞ at each active site at its characteristic temperature, with some variability due to “statistical fluctuations” in the germ size (Vali, 2014). Some CNT-based approaches to describe immersion freezing account for the existence of active sites by assuming a distribution of contact angles for each particle. Hence each active site is assigned a characteristic contact angle instead of a characteristic temperature (Ickes et al., 2017; Zobrist et al., 2007).

The view of the role of active sites as capable of locally decreasing ΔG_het relies heavily on an interpretation of immersion freezing that mimics ice nucleation from the vapor phase (Fig. 3a). Such a description is, however, too limited for ice formation within the liquid phase. For example, it is implicitly assumed that the active site brings molecules together, similar to an adsorption site. However a particle immersed within a liquid is already surrounded by water molecules (Fig. 3b). In fact, nascent ice structures are associated with low-density regions within the liquid (Bullock and Molinero, 2013). Thus in the classical view the active site should be able to “pull molecules apart” instead of bringing them together. This creates a conceptual problem. To locally reduce ΔG_het active sites should be able to permanently create low-density regions within the liquid, which would require a large amount of energy. In other words, active sites would have the unusual property of creating a thermodynamic barrier maintaining their surrounding water in a non-equilibrium state. Such situation is unlikely in immersion freezing.

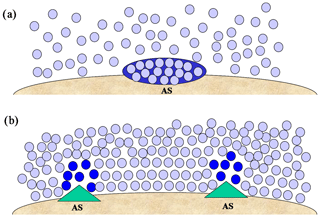
Figure 3Different representations of immersion freezing. (a) an ice germ (dark blue) forming on an active site (AS) by random collision of water molecules (light blue). (b) low-density regions (dark blue) forming in the vicinity of active sites within a dense liquid phase (light blue).

Download

The concept of a local nucleation rate also presents some difficulties. In the strict sense J_het is the velocity with which the size distribution of molecular clusters in an equilibrium population crosses the critical size (Kashchiev, 2000; Seinfeld and Pandis, 1998). In immersion freezing the domain of such a distribution is the whole volume of the droplet. Thus only a single value of J_het can be defined for a continuous liquid phase, independently of where the actual nucleation process is occurring, since no permanent spatial gradients of T or concentration exist within equilibrium systems. Having otherwise implies that parts of the system would need to be maintained in a non-equilibrium state, having their own cluster size distribution. This requires the presence of non-permeable barriers within the liquid, a condition not encountered in immersion freezing. Similarly, the characteristic temperature of an active site is an unmeasurable quantity, since a system in equilibrium has the same temperature everywhere. Hence it would be impossible to distinguish whether the particle as a whole or only the active site must reach a certain temperature before nucleation takes place.

These difficulties can be reconciled if, instead of promoting nucleation through a thermodynamic mechanism, active sites provide a kinetic advantage to ice nucleation. A way in which this can be visualized is shown in Fig. 3b. The vicinal water is in equilibrium with the particle and exhibits a larger degree of ordering near the interface. Since in immersion freezing the formation of ice in the liquid depends on molecular rearrangement, the active site should produce a transient structural transformation that allows the propagation of ice. These sites would be characterized by defects where templating is not efficient, allowing greater molecular movement, hence facilitating restructuring. Their presence is guaranteed, since particles are never uniform at the molecular scale. In this view active sites create ice by promoting fluctuation instead of by locking water molecules in strict configurations. It implies that for uniform systems (e.g., a single droplet with a single particle) ΔG_het depends on the equilibrium between the particle and the vicinal water, and active sites enhance fluctuation around specific locations. This obviates the need for the hypothesis of a well-defined characteristic temperature for each active site. It, however, does not mean that active sites are transient. They are permanent features of the particle and should have a reproducible behavior, inducing ice nucleation around the same place in repeated experiments (Kiselev et al., 2017).

Within the framework presented above, there can only be one J_het defined in the droplet volume. The presence of active sites introduces variability in J₀ instead of ΔG_het. The latter is determined by the thermodynamic equilibrium between the particle and its vicinal water. Although the theory presented here does not account for internal gradients in the droplet–particle system, in practice it is likely that the observed J_het corresponds to the site promoting the largest density fluctuations. Variability in J_het would be introduced by fluctuation in the cluster size distribution in the liquid and from the multiplicity of active sites in the particle population. In this sense the proposed view is purely stochastic.

3.1 Ice nucleation regimes

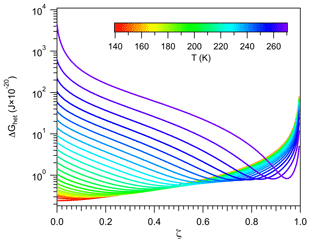
A consequence of the linkage between the properties of vicinal water and ΔG_het is the existence of distinct nucleation regimes. This was mentioned in Sect. 2.4.1, and here it is explored in detail. Recall from Fig. 2 that for a given temperature, ΔG_het passes by a minimum defined by the condition $\frac{{\partial }^{\mathrm{2}}\mathrm{\Delta }{G}_{\mathrm{het}}}{\partial n_{\mathrm{het}}^{\mathrm{2}}}=\mathrm{0}$. Figure 4b depicts a similar behavior when varying T. It shows that for a given ζ there is a temperature T_s at which ΔG_het is minimum. For T>T_s, ΔG_het increases with increasing T because n_het increases (Fig. 4a). This is the typical behavior predicted by the classical model (Khvorostyanov and Curry, 2005), hence such regime will be termed “germ-forming”, since ΔG_het is determined by the formation of the ice–liquid interface.

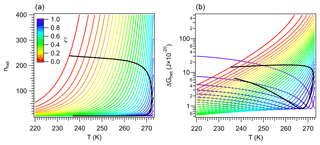
Figure 4Critical germ size (a) and work of heterogeneous ice nucleation (b) for different values of ζ (color). Black lines correspond to constant J_het=10⁶ m⁻² s⁻¹.

Download

A different behavior is found for T<T_s, where ΔG_het decreases with increasing T. In this regime n_het remains almost constant at very low values, ΔG_het is small and results mostly from the dissipation of work. Ice nucleation is not limited by the formation of the ice–liquid interface but rather by the propagation of small fluctuations in the vicinity of preformed ice-like regions. Therefore it is controlled by the diffusion of water molecules to such regions rather than by ΔG_het. This is akin to a spinodal decomposition process (Cahn and Hilliard, 1958) and will be termed “spinodal ice nucleation”. It is, however, not truly spinodal decomposition, since it requires a finite, albeit small, amount of work to occur.

Since for each value of ζ there is a minimum in ΔG_het (Fig. 4), theoretically all INPs are capable of nucleating ice in both regimes. In practice spinodal ice nucleation would only occur if T_s lies within the 233 K $<T<\mathrm{273}$ K range, where immersion freezing occurs. For example, for ζ=0.1, Fig. 4b shows that the minimum in ΔG_het occurs at T<220 K. Since homogeneous ice nucleation should occur above this temperature, INPs characterized by ζ=0.1 will not exhibit spinodal ice nucleation. These particles always nucleate ice in the classical germ-forming regime (T>T_s). The situation is, however, different for ζ=0.9, since T_s≈270 K. These INPs are capable of nucleating ice in both the spinodal (T<T_s) and the germ-forming (T>T_s) regimes. For the spinodal regime, ΔG_het is low and decreases slightly with increasing T, indicating that the thermodynamic barrier to nucleation is virtually removed. Ice formation is therefore almost entirely controlled by kinetics.

The existence of the spinodal nucleation regime signals the possibility of an interesting behavior in freezing experiments, where the same ΔG_het may correspond to two very different INPs. To show this the values of ΔG_het and n_het corresponding to J_het=10⁶ m⁻² s⁻¹ are depicted in Fig. 4 with black lines. These lines form semi-closed curves when plotted against temperature indicating that the same ΔG_het may correspond to two different values of ζ. The upper branch (with high ΔG_het) corresponds to the germ-forming regime and the lower branch to the spinodal regime. This picture may be convoluted by the fact that high ζ also implies strong kinetic limitations during ice nucleation and is further discussed in Sect. 3.3.

3.2 Pre-exponential factor

Kinetic effects on ice nucleation are typically analyzed in terms of the pre-exponential factor, which is proportional to $f_{\mathrm{het}}^{*}$ in the form

J₀ expresses the normalized flux of water molecules to the ice germ, corrected by Z. Figure 5 shows J₀ calculated using Eqs. (58) and (59). Results from CNT (Eq. 6) are also shown. In general J₀ varies with T and ζ. The sensitivity of J₀ to T is determined by D_∞ (Barahona, 2015), with J₀ increasing with T, since water molecules increase their mobility. Also, at higher T, less work is dissipated during interface transfer. These effects dominate the variation in J₀ for ζ<0.5, suggesting that the particle has a limited effect on the mobility of vicinal water. Ice nucleation around these particles would be reasonably well described by assuming a negligible effect of the particle on J₀, as done in CNT. This is evidenced by the CNT-derived values for $\mathit{\theta }=\mathrm{10}{}^{\circ }$ and $\mathit{\theta }=\mathrm{90}{}^{\circ }$, which represent particles with high and low particle–ice affinity, respectively, and correspond to the range of expected variability in CNT. The $\mathit{\theta }=\mathrm{90}{}^{\circ }$ and ζ∼0 lines in Fig. 5 are within 1 order of magnitude of each other and are in agreement with homogeneous nucleation results (Barahona, 2015). The $\mathit{\theta }=\mathrm{10}{}^{\circ }$ line is also close to the ζ∼0.5 curve. In both cases J₀ increases by about 2 orders of magnitude between 220 K and 273 K and decreases by about 2 orders of magnitude from ζ=0.0 to ζ=0.5, or from $\mathit{\theta }=\mathrm{90}{}^{\circ }$ to $\mathit{\theta }=\mathrm{10}{}^{\circ }$ in CNT. This reflects the effect of variation in Z on J₀.

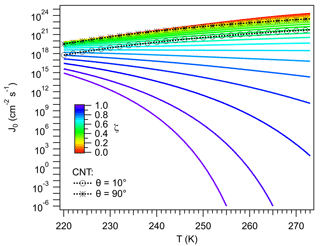
Figure 5Pre-exponential factor. Colored lines indicate different values of ζ. Black lines correspond to results calculated using CNT for different values of the contact angle, θ.

Download

The behavior of J₀ for ζ>0.5 dramatically differs from CNT. For ζ>0.5, and particularly for ζ>0.8, J₀ decreases strongly with increasing T. This is because as ζ→1 and T→273 K, the driving force for interfacial transfer, i.e., the separation of μ_vc from thermodynamic equilibrium, vanishes. As the system moves near these conditions D becomes very small. This is the result of the high IL fraction of the vicinal water limiting the number of configurations available to form cooperative regions, required to induce water mobility (Sect. 2.5.1). Such behavior cannot be reproduced by CNT, since no explicit dependency of D on the properties of the vicinal layer is accounted for. For ζ>0.99 J₀ decreases by more than 30 orders of magnitude from 220 K to 273K; molecular transport nearly stops. Ice nucleation may not be possible at such an extreme, despite the fact that these particles very efficiently reduce ΔG_het (Fig. 4); water may remain in the liquid state at very low temperatures. Such an effect has been experimentally observed in some biological systems (Wolfe et al., 2002).

3.3 Nucleation rate

The interplay between kinetics and thermodynamics determines the complex behavior of J_het in immersion ice nucleation. Particles highly efficient at decreasing ΔG_het also decrease the rate of interfacial diffusion to the point where they may effectively prevent ice nucleation. On the other hand, INPs with low ζ do not significantly affect J₀ but have a limited effect on ΔG_het. This is confounded with the presence of two thermodynamic nucleation regimes, one in which ΔG_het may be large and increases with T (“germ-forming”), and another in which ΔG_het is very small and decreases as T increases (“spinodal nucleation”). This picture can be simplified, since within the range $\mathrm{233}\mathrm{K}<T<\mathrm{273}$ K, where immersion freezing is relevant for atmospheric conditions, INPs with ζ>0.7 are, at the same time, more likely to nucleate ice in the spinodal regime and to exhibit strong kinetic limitations. Similarly for ζ<0.6 the transition to spinodal nucleation occurs below 233 K (Fig. 2). These INPs tend to nucleate ice in the germ-forming regime without significantly affecting J₀. Thus the thermodynamic regimes introduced in Sect. 3.1 loosely correspond to kinetic regimes. Roughly, ice nucleation in the spinodal regime is controlled by kinetics, and in the germ-forming regime, it is controlled by thermodynamics. This is a useful approximation, but it should be used with caution. Even in the germ-forming regime the particle affects the kinetics of ice–liquid interfacial transfer to some extent. Similarly, in the spinodal regime ΔG_het is small, but finite.

Figure 6 shows the behavior of J_het as T increases for different values of ζ. J_het in the germ-forming regime resembles the behavior predicted by CNT. J_het increases steeply with decreasing T and increasing ζ. Similarly for CNT, J_het increases for decreasing T and θ. This is characteristic of the thermodynamic control on J_het, where ΔG_het and $\frac{\mathrm{d}\mathrm{\Delta }{G}_{\mathrm{het}}}{\mathrm{d}T}$ are large (Fig. 4), and J₀ is relatively unaffected by the particle. In this regime it is always possible to find a contact angle (typically between 10 and 100^∘) that results in close agreement of J_het between CNT and NNF predictions (Fig. 6), particularly for $J_{\mathrm{het}}<{\mathrm{10}}^{\mathrm{12}}{\mathrm{cm}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$, which covers most values of atmospheric interest. This is also true for a_w=0.9 (Fig. 6), although the approximation to the equilibrium temperature signals a steeper behavior in CNT peaking at higher values than NNF. Since $\frac{\mathrm{d}{J}_{\mathrm{het}}}{\mathrm{d}T}$ is large, J_het may show threshold behavior, characteristic of ice nucleation mediated by some dust species like Chlorite and Montmorillonite (Atkinson et al., 2013; Hoose and Möhler, 2012; Murray et al., 2012).

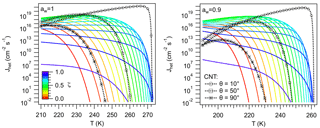
Figure 6Ice nucleation rate calculated using Eq. (61) for different values of ζ (color). Black lines were calculated using CNT for different values of the contact angle, θ.

Download

There is, however, no value of θ that would lead to overlap between CNT and NNF for ζ>0.7. These conditions largely correspond to spinodal ice nucleation. J_het is kinetically controlled, since ΔG_het is small, and J₀ varies widely with T (Fig. 5). As in the germ-forming regime J_het also reaches significant values but increases more slowly with decreasing T (Fig. 6). Higher ζ leads to J_het becoming significant at higher T. But unlike in the germ-forming case, curves with higher ζ tend to plateau at progressively lower values of J_het, since they become kinetically limited by their approximation to the thermodynamic equilibrium. For ζ∼0.7 some of the curves of Fig. 6 also display germ-forming behavior at high T and are characterized by a sudden decrease in $-\frac{\mathrm{d}{J}_{\mathrm{het}}}{\mathrm{d}T}$ as T decreases. The sudden change of slope corresponds to the region around the minimum ΔG_het (Fig. 4) and signals the transition from germ-forming to spinodal ice nucleation. Such behavior has been observed in some INPs of bacterial origin (Murray et al., 2012).

Figure 6 also indicates that nucleation regimes cannot be assigned based on the values of J_het or on the observed freezing temperature, T_f. In both regimes, J_het may reach substantial values, hence T_f may cover the entire range $\mathrm{233}\mathrm{K}<T<\mathrm{273}$ K. What is striking is that J_het curves with ζ>0.7 tend to cross those with ζ<0.7. This means that two INPs characterized by very different ζ can have the same freezing temperature. This result thus challenges the common notion that INPs with higher freezing temperatures are intrinsically more active at nucleating ice, or in other words, that by measuring T_f alone, it is possible to characterize the freezing properties of a given material. In reality, to discern whether the observed T_f corresponds to a good (in the thermodynamic sense) INP acting in the spinodal regime or a less active INP acting in the germ-forming regime, it is necessary to measure $\frac{\mathrm{d}{J}_{\mathrm{het}}}{\mathrm{d}T}$ along with T_f.

3.4 Application to the water activity-based nucleation rate

If a droplet is in equilibrium with its environment then a_w is a function of the relative humidity. Thus the relationship between a_w and the freezing temperature, T_f, conveys important information about the potential of a particle to catalyze the formation of ice and can be used to generate parameterizations of immersion ice nucleation for cloud models (Barahona and Nenes, 2009; Koop and Zobrist, 2009; Kärcher and Lohmann, 2003). A widely used class of parameterizations is based on the so-called water activity criterion (Koop and Zobrist, 2009; Koop et al., 2000), the condition that for a given material the water activity at which heterogeneous ice nucleation is observed, a_w,het, is related by a constant to a_w,eq (Koop and Zobrist, 2009; Koop et al., 2000). Here it is shown that the two-state thermodynamic model proposed in Sect. 2.3 implies the water activity criterion as a purely thermodynamic constraint to freezing.

3.4.1 Water activity shift

By definition the thermodynamic path shown in Fig. 1 operates between two equilibrium states. The relation between ΔG_het and ΔG_hom is therefore independent of the way the system reaches a_w,eff. In the absence of any kinetic limitations to the germ growth, Eq. (35) also represents a direct relationship between J_hom and J_het. (Knopf and Alpert, 2013; Koop and Zobrist, 2009; Kärcher and Lohmann, 2003; Marcolli et al., 2007). Thus one can imagine two separate experiments in which the environmental conditions are set to either a_w or a_w,eff, the former resulting in heterogeneous freezing and the latter in homogeneous ice nucleation. Under these conditions Eq. (34) implies that when heterogeneous ice nucleation is observed at $a_{\mathrm{w},\mathrm{het}}=a_{\mathrm{w}}$ there is a corresponding homogeneous process that would occur at $a_{\mathrm{w},\mathrm{hom}}=a_{\mathrm{w},\mathrm{eff}}$. Thus we can write an equivalent expression to Eq. (34), but in terms of a_w,het and a_w,hom, in the form

$$\begin{array}{}\text{(63)}& {\displaystyle }{a}_{\mathrm{w},\mathrm{het}}=a_{\mathrm{w},\mathrm{hom}}{\left({\displaystyle \frac{a_{\mathrm{w},\mathrm{eq}}}{a_{\mathrm{w},\mathrm{hom}}}}\right)}^{\mathit{\zeta }}\exp \left({\mathrm{\Lambda }}_{\mathrm{mix}}\right).\end{array}$$

Eq. (63) can be rewritten as

$$\begin{array}{}\text{(64)}& {\displaystyle }\ln \left(a_{\mathrm{w},\mathrm{het}}\right)=(\mathrm{1}-\mathit{\zeta })\ln \left(a_{\mathrm{w},\mathrm{hom}}\right)+\mathit{\zeta }\ln \left(a_{\mathrm{w},\mathrm{eq}}\right)+{\mathrm{\Lambda }}_{\mathrm{mix}}.\end{array}$$

Subtracting ln(a_w,eq) from each side of Eq. (64) gives

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\ln \left(a_{\mathrm{w},\mathrm{het}}\right)-\ln \left(a_{\mathrm{w},\mathrm{eq}}\right)=\\ \text{(65)}& {\displaystyle }& {\displaystyle }(\mathrm{1}-\mathit{\zeta })\left[\ln \left(a_{\mathrm{w},\mathrm{hom}}\right)-\ln \left(a_{\mathrm{w},\mathrm{eq}}\right)\right]+{\mathrm{\Lambda }}_{\mathrm{mix}}.\end{array}$$

Using the approximation $\ln \left(x\right)\approx x-\mathrm{1}$ for x∼1, Eq. (65) can be linearized in the form

$$\begin{array}{}\text{(66)}& {\displaystyle }\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{het}}=\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{hom}}(\mathrm{1}-\mathit{\zeta })+{\mathrm{\Lambda }}_{\mathrm{mix}},\end{array}$$

where $\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{hom}}=a_{\mathrm{w},\mathrm{hom}}-a_{\mathrm{w},\mathrm{eq}}$ and $\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{het}}=a_{\mathrm{w},\mathrm{het}}-a_{\mathrm{w},\mathrm{eq}}$ are the homogeneous and heterogeneous water activity shifts, respectively. Δa_w,hom has been found to be approximately constant for a wide range of solutes (Koop et al., 2000); therefore Eq. (66) suggests that Δa_w,het should be approximately constant, since Λ_mix∼0.02 and only depends on T. Thus, the two-state model presented in Sect. 2.3 implies the so-called water activity criterion (Koop et al., 2000) for heterogeneous ice nucleation, giving support to the hypothesis that increasing order near the particle surface drives ice nucleation.

Equations (63) to (66) are fundamental thermodynamic relationships of the system and can be used to analyze the effect of the immersed particle on ice formation independently of kinetic effects. To do so a_w,hom must be determined entirely by thermodynamics. This is because if a_w,hom is defined at some J_hom threshold then it (and by extension a_w,het) would also depend on the freezing kinetics. Fortunately, a thermodynamic definition of a_w,hom has been achieved by Baker and Baker (2004). The authors showed that, on average, freezing occurs below the temperature at which the compressibility of water reaches a maximum. At this point density fluctuations are wide enough to allow for structural transformations that facilitate the formation of ice-like regions within the droplet volume. Such a criterion does not depend on measured freezing rates and can be extended to the freezing of water solutions, coinciding with the results of Koop et al. (2000). Bullock and Molinero (2013) also derived a pure thermodynamic criterion for a_w,hom using the equilibrium between low-density regions and the bulk solution. Within these frameworks a_w,hom can be defined without reference to a J_hom threshold. By extension, Eq. (64) guarantees that a_w,het can be determined entirely by the thermodynamic properties of the system.

Equation (64) also implies that for a given a_w,hom there is a temperature for which $a_{\mathrm{w}}=a_{\mathrm{w},\mathrm{het}}$, referred as the “thermodynamic freezing temperature”, T_ft. Formally, T_ft represents the solution of

$$\begin{array}{ll}{\displaystyle }\ln \left(a_{\mathrm{w}}\right)& {\displaystyle }-(\mathrm{1}-\mathit{\zeta })\ln \left[a_{\mathrm{w},\mathrm{eq}}\left(T_{\mathrm{ft}}\right)+\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{hom}}\right]-\mathit{\zeta }\ln \left[a_{\mathrm{w},\mathrm{eq}}\left(T_{\mathrm{ft}}\right)\right]\\ \text{(67)}& {\displaystyle }& {\displaystyle }-{\mathrm{\Lambda }}_{\mathrm{mix}}\left(T_{\mathrm{ft}}\right)=\mathrm{0},\end{array}$$

or in the linearized form,

$$\begin{array}{}\text{(68)}& {\displaystyle }{a}_{\mathrm{w}}-a_{\mathrm{w},\mathrm{eq}}\left(T_{\mathrm{ft}}\right)-\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{hom}}(\mathrm{1}-\mathit{\zeta })-{\mathrm{\Lambda }}_{\mathrm{mix}}\left(T_{\mathrm{ft}}\right)=\mathrm{0}.\end{array}$$

Since Δa_w,hom is considered a thermodynamic property of the system (Baker and Baker, 2004), T_ft does not depend on the freezing kinetics. Thus T_ft can be interpreted as the highest temperature where it is likely to observe ice nucleation for a given thermodynamic state (determined by a_w, ζ and the system pressure).

Figure 7 shows the T_ft–a_w relationship defined by Eq. (67), calculated using $\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{hom}}=\mathrm{0.304}$ (Baker and Baker, 2004; Barahona, 2014; Koop et al., 2000). As expected, the figure resembles experimental results found by several authors (Alpert et al., 2011; Knopf and Alpert, 2013; Koop and Zobrist, 2009; Zobrist et al., 2008; Zuberi et al., 2002), where curves for ζ>0 align with constant water activity shifts to a_w,eq. To make this evident, lines were drawn using constant values of $\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{het}}=\mathrm{0.05},\mathrm{0.15}$ and 0.20, which coincide with lines corresponding to $\mathit{\zeta }=\mathrm{0.2},\mathrm{0.3}$ and 0.7, respectively. This shows that Eq. (66) is a good approximation to Eq. (63) and constitutes a theoretical derivation of the water activity criterion. The fact that such behavior can be reproduced by Eq. (63) validates the regular solution approximation used in Sect. 2.3 and supports the idea that the effect of the immersed particle on ice nucleation can be explained as a relative increase in the ice-like character of the vicinal water.

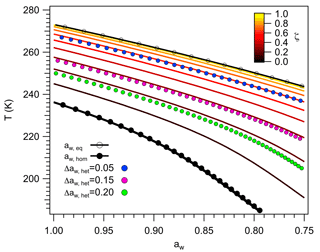
Figure 7Thermodynamic freezing temperature as a function of water activity. Colored lines correspond to $T_{\mathrm{ft}}(a_{\mathrm{w}}=a_{\mathrm{w},\mathrm{het}})$ for different values of ζ. Also shown are the water activities at equilibrium and at the homogeneous freezing threshold, a_w,eq and a_w,hom, respectively, and lines drawn applying constant water activity shifts, Δa_w,het, of 0.05, 0.15 and 0.20.

Download

It must be emphasized that T_ft only establishes the potential of an INP to induce freezing at $a_{\mathrm{w}}=a_{\mathrm{w},\mathrm{het}}$, regardless of whether a measurable J_het can be experimentally realized. Physically, it is plausible that as the particle increases the ice-like character of the vicinal water, it also increases the probability of wide density fluctuations. As a result low-density regions, wide enough to accommodate the ice gem, exist at higher T than in homogeneous ice nucleation. Following the argument of Baker and Baker (2004) this would also imply that the compressibility of water near the particle reaches a maximum at higher T than in the bulk. More research however is needed to elucidate this point. The presence of a spinodal regime would also mean that the observed freezing temperature may differ from T_ft, since at such a limit nucleation, it is no longer controlled by thermodynamics. This is illustrated in the next section.

3.4.2 Freezing by humic-like INPs

Δa_w,het has been determined in several studies and has been used to predict and parameterize J_het in atmospheric models (Knopf and Alpert, 2013; Zobrist et al., 2008). Thus it is useful in analyzing the conditions under which ζ (hence J_het) can be estimated using measured Δa_w,het values. Rearranging Eq. (66) we obtain

$$\begin{array}{}\text{(69)}& {\displaystyle }\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{het}}-\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{hom}}(\mathrm{1}-\mathit{\zeta })-{\mathrm{\Lambda }}_{\mathrm{mix}}=\mathrm{0}.\end{array}$$

If Δa_w,hom and Δa_w,het are known, ζ can be estimated iteratively by solving Eq. (69). Note that Λ_mix is temperature dependent (Eq. 34), implying a slight dependency of ζ on T when Δa_w,het is constant. However since Λ_mix is also typically small, ζ is almost equal to $\mathrm{1}-\frac{\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{het}}}{\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{hom}}}$.

To test Eq. (69) the data for leonardite (LEO) and Pahokee peat (PP) particles (humic-like substances) obtained by Rigg et al. (2013) are used. The authors reported $\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{het}}=\mathrm{0.2703}$ for LEO and $\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{het}}=\mathrm{0.2466}$ for PP. These values are assumed to be independent of a_w and T, with an experimental error in Δa_w,het of 0.025. The average J_het obtained from different samples and from repeated freezing and melting experiments for both materials is depicted in Fig. 8. Applying Eq. (69) over the T=210 K–250 K range and using $\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{hom}}=\mathrm{0.304}$ results in $\mathit{\zeta }=\mathrm{0.049}-\mathrm{0.058}$ for LEO and $\mathit{\zeta }=\mathrm{0.096}-\mathrm{0.121}$ for PP. Within this temperature range these values correspond to the germ-forming regime, hence J_het is thermodynamically controlled. A comparison against the experimentally determined J_het for three different values of a_w is shown in Fig. 8. Within the margin of error there is a reasonable agreement between the modeled and the experimental J_het.

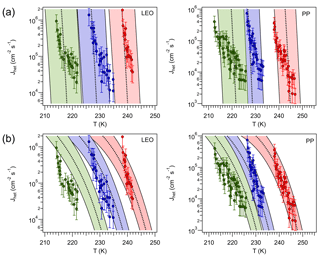
Figure 8(a) Heterogeneous ice nucleation rate calculated using a constant shift in a_w (black, dotted, lines) for leonardite (LEO, $\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{het}}=\mathrm{0.2703}$) and Pahokee peat (PP, $\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{het}}=\mathrm{0.2466}$). Red, blue and green colors correspond to a_w equal to 1.0, 0.931 and 0.872, respectively, for LEO, and 1.0, 0.901 and 0.862 for PP. Shaded area corresponds to $\mathrm{\Delta }{a}_{\mathrm{w},\mathrm{het}}\pm \mathrm{0.025}$. Markers correspond to experimental measurements reported by Rigg et al. (2013); error bars represent an order of magnitude deviation from the reported value. (b): J_het calculated for constant ζ=0.949 for LEO and ζ=0.952 for PP. The shaded area corresponds to a_w±0.01 and ζ±0.0015.

Download

The top panels of Figure 8, however, reveal that even if J_het becomes significant around the values predicted by Eq. (69), $-\frac{\mathrm{d}\ln J_{\mathrm{het}}}{\mathrm{d}T}$ is overestimated, particularly for PP. This may indicate that these INPs nucleate ice in the spinodal regime. To test this hypothesis J_het was fitted to the reported measurements by varying ζ within the range where spinodal nucleation would be dominant. To avoid agreement by design a single ζ was used for all experiments for each species resulting in ζ=0.949 for PP and ζ=0.952 for LEO (Fig. 8, bottom panels). For PP, J_het and $-\frac{\mathrm{d}\ln J_{\mathrm{het}}}{\mathrm{d}T}$ agree better with the experimental values, whereas for LEO the agreement improves at high T but worsens at low T. In this regime J_het seems to be slightly overestimated by the theory at the lowest a_w tested. This may be due to small uncertainties in a_w that play a large role in J_het (for example, the assumption of a T-independent a_w; Alpert et al., 2011). There is the possibility that the humic acid present in PP may slightly dissolve during the experiments (Daniel Knopf, personal communication, 2017), which would impact not only a_w but also may modify the composition of the particles, hence ζ.

The exercise above suggests that ice nucleation in PP may follow a spinodal mechanism. Using a single value of Δa_w,het to predict ζ, as expressed mathematically by Eq. (69), seems to work for LEO. Since Eq. (69) represents a thermodynamic relation between Δa_w,hom and Δa_w,het, it is expected to work well when nucleation is thermodynamically controlled, i.e., the germ-forming regime. However it may fail for spinodal ice nucleation, since it does not consider the effect of the particle on J₀. Δa_w,het however carries important information about J_het (Knopf and Alpert, 2013), but for spinodal ice nucleation, the relationship between Δa_w,het and ζ must be more complex than predicted by Eq. (69), since kinetic limitations play a significant role. Figure 8 also shows that similar T_f can be obtained by either high or low ζ. The particular regime in which an INP nucleates ice determines $-\frac{\mathrm{d}\ln J_{\mathrm{het}}}{\mathrm{d}T}$, hence the sensitivity of the droplet freezing rate to the particle size and to the cooling rate.

3.5 Limitations

It is important to analyze the effect of several assumptions introduced in Sect. 2 on the theory presented here. One of the limitations of the approach used in deriving Eq. (61) is that it employs macroscale thermodynamics in the formulation of the work of nucleation. The effect of this assumption is, however, minimized in several ways. First, unlike frameworks based on the interfacial tension, NNF is much more robust to changes in ice germ size, since the product Γ_wsΔh_f remains constant (Sect. 2.4). Second, in the spinodal regime ΔG_het is independent of n_het, and only for T>268 K and in the germ-forming regime, the approach presented here may lead to uncertainty (Sect. 3.1). Thus Eq. (61) remains valid for most atmospheric conditions, although caution must be taken when T_f>268 K. Alternatively the framework presented here could be extended to account explicitly for the effect of size on Δh_f and Γ_w (Zhang et al., 1999).

Further improvement could be achieved by implementing a more sophisticated equation of state of the vicinal water. Here a two-state assumption has been used, such that μ_vc is a linear combination of ice-like and liquid-like fractions. Such approximation has been used with success before (Etzler, 1983; Holten et al., 2013). However it is known that the structure of supercooled water represents an average of several distinct configurations (Stanley and Teixeira, 1980). These are, in principle, accounted for in the proposed approach, since ζ represents a relative, not an absolute, increase in the IL fraction. However there is no guarantee that such an increase can be linearly mapped in the way described in Sect. 2. Fortunately this would only mean, in practice, that the value of ζ for a given material is linked to the particular form of the equation of state used to describe the vicinal water.

Equation (61) is also blind to the surface properties of the immersed particle. The implicit assumption is that the effect of surface composition, charge, hydrophilicity and roughness on J_het can be parameterized as a function of ζ. The example shown in Sect. 3.4 suggests that this is indeed the case. Making such relations explicit must, however, lie at the center of future development of the proposed approach. Similarly, a heuristic approach was used to study the effect of irreversibility on the nucleation work. This can be improved substantially by making use of a generalized Gibbs approach (Schmelzer et al., 2006), which unfortunately may also increase the number of free parameters in the model. None of these limitations is expected to change the conclusions of this study, however they may affect the values of ζ fitted when analyzing experimental data. The approach proposed here, however, has the advantage of being a simple, one-parameter approximation that can be easily implemented in cloud models.