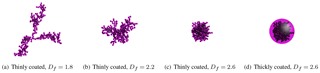the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Effects of brown coatings on the absorption enhancement of black carbon: a numerical investigation
Yongming Zhang
Feng Wang
Using the numerically exact multiple sphere T-matrix (MSTM) method, we explored the effects of brown coatings on absorption enhancement (Eabs) of black carbon (BC) at different wavelengths (λ). In addition, the ratio of the absorption of BC coated by brown carbon (BrC) to an external mixture of BrC and BC (Eabs_internal) is also investigated. In this work, thinly coated BC is defined as that with a BC volume fraction over 20 %, and other BC is considered to be thickly coated. Eabs increases with the absorption of coatings, while an opposite trend is observed for Eabs_internal. A much wider range of Eabs is observed for BC with brown coatings compared to that with non-absorbing coatings. As the mass ratio of BrC to BC (MR) is over 13.9, Eabs can exceed 5.4 for BC with brown coatings at λ=0.35 µm under a typical size distribution. Specifically, as MR increases to approximately 13.9, Eabs values of larger than 3.96 can be observed at 0.532 µm, which is a little higher than the commonly measured Eabs of 1.05–3.5 at this wavelength. Previous studies have focused on the lensing effects of coatings but neglected the blocking effects of absorbing coatings. Eabs_internal can be below 1 at an ultraviolet spectral region for BC with brown coatings, which indicates that the absorption of internally mixed BC is less than that of an external mixture of BrC and BC due to the blocking effects of outer coatings, and we named the blocking effect of absorbing coatings the “sunglasses effect”. In addition, the applicability of a core–shell sphere model is also evaluated for BC with brown coatings. The absorption cross section (Cabs) of thickly coated BC is underestimated by the core–shell sphere model for all wavelengths while the underestimation becomes negligible as the imaginary part of the refractive index of brown carbon (kBrC) becomes very large. The lensing effect and the sunglasses effect are clearly defined. Moreover, the effects of composition ratios and the size distribution are explored at different wavelengths. Our findings can improve the understanding of the absorption enhancement of BC with brown coatings.
- Article
(3941 KB) -
Supplement
(491 KB) - BibTeX
- EndNote
Recent modeling and field studies have indicated that aerosol light absorption is an important contributor to climate forcing (Bond et al., 2013; Jacobson, 2001; Krishnan and Ramanathan, 2002). Black carbon (BC), which is a product of incomplete combustion, is the strongest solar-absorbing aerosol in the atmosphere (Lack et al., 2009; Zhang et al., 2008b). BC radiative forcing from fossil fuels and biomass burning has been estimated to be approximately 0.4 W m−2, as the second anthropogenic contributor (after CO2) to climate forcing due to its strong absorption of solar radiation (Forster et al., 2007; Schwarz et al., 2008). Sensitivity tests suggest that the mixing state and morphology of BC aerosols can largely affect the absorption of BC (Ma et al., 2012; Zhang et al., 2018). Due to the large uncertainties of BC morphologies and mixing states, the understanding of BC absorption is still limited. Even when coated with non-absorbing materials, the BC absorption can be enhanced (Cappa et al., 2012; Liu et al., 2017). Many studies mainly attribute the absorption enhancements (Eabs) to the lensing effect (Bond et al., 2006; Fuller et al., 1999b).
For the estimation of BC absorption enhancements, many field measurements have been conducted. Naoe et al. (2009) presented factors of 1.1–1.4 for BC absorption enhancement at a suburban site in Japan, while Cui et al. (2016) indicated that the absorption enhancement factors increase from 1.4±0.3 during fresh combustions to ∼3 for aged BC at a rural site over the North China Plain (NCP). Liu et al. (2017) found that BC absorption enhancement is significantly influenced by the particle mixing state. The measured range of Eabs is approximately 1–1.5. You et al. (2016) observed the wavelength-dependent absorption enhancement of coated BC. In their measurements, Eabs increased up to 3 at the shortest measured wavelengths, while it was approximately 1.6 in the near-IR wavelength. A negligible absorption enhancement of only 6 % for ambient BC particles was reported by Cappa et al. (2012) based on direct measurements over California (USA). Chen et al. (2017) reported an average Eabs of 2.07±0.72 for the urban haze in winter in northern China. However, this result was time dependent. The absorption enhancement of BC during the urban PM2.5 pollution was 1.31±0.29 in the morning, while in the afternoon, it increased to approximately 2.23±1.05; then, it decreased to 1.52±0.75 in the evening. Recently, a larger Eabs value of 2.6–4.0 at Beijing, China, was reported by Xu et al. (2016). In summary, the reported Eabs values are not consistent in different studies due to the complex aging statuses.
Although the field measurements can provide referential absorption enhancement values for different aging statuses and regions, causes of these enhancements are not clear. For example, what is the main factor that causes complex absorption enhancements: morphology, the mixing states or the types of coatings? To our best knowledge, field measurements currently have difficulty answering these questions. Numerical simulation is a strong tool that reveals the mechanism responsible for the complex absorption enhancements. To improve the understanding of the complex absorption enhancements of BC, numerical studies have also been conducted. For instance, based on the core–shell Mie theory, the absorption enhancement factors have been estimated up to 3 (Bond et al., 2006). By the numerically exact multiple sphere T-matrix (MSTM) method, Zhang et al. (2017) presented the absorption enhancements of non-absorbing coatings for aged BC ranging from 1.1 to 2.4, and they were significantly influenced by the morphology and aging statuses but insensitive to the BC refractive index. However, previous studies have failed to uncover the effects of coating absorption. In their studies, coatings were considered to be non-absorptive, and BC absorption enhancements were completely caused by lensing effects. Nevertheless, in the atmosphere, there is a type of organic carbon (OC) that absorbs the radiation in the range of the ultraviolet and visible spectra, which is known well as brown carbon (BrC); BC can also be mixed with BrC. Compared with non-absorbing materials, the absorption of BrC is significantly wavelength dependent and the imaginary part of the refractive index for BrC has a wide range (Kirchstetter et al., 2004), which results in large uncertainties for the estimation of aerosol absorption. Therefore, the absorption of BrC has gained increasing interest (Kirchstetter et al., 2004; Shamjad et al., 2018).
Many studies have been conducted to evaluate the absorption of BrC. One typical method for the determination of BrC absorption is isolating BrC by extracting filtered samples (Cheng et al., 2017). This method can be used to determine the imaginary part of the BrC refractive index. However, it is difficult to understand the effects of BrC on the total aerosol absorption, as BrC is commonly mixed with other chemical compositions. The assumption of externally mixing can be used to evaluate the absorption of BrC and BC separately. Nevertheless, in many cases, BC is internally mixed with other materials. It is widely accepted that the absorption is underestimated by the external mixing assumption when BC is coated with non-absorbing materials due to lensing effects. However, whether this is true for BC with BrC coatings is not clear. To understand the effects of BrC coatings, the contributions of “lensing effects” and the total absorption enhancement of BC with BrC coatings should be analyzed individually.
Cheng et al. (2017) has conducted a numerical investigation on BC absorption enhancement, BrC absorption enhancement, and lensing effects on BC mixed with BrC by assuming a core–shell structure. While the internal mixing of BC is widely accepted, the core–shell structure is debated (Adachi et al., 2010; Bond et al., 2013; Cappa et al., 2012). He et al. (2015) developed a theoretical BC aging model and concluded that the evolution of coating thickness, morphology, and composition during the aging process could have significant impacts on BC absorption. Freshly emitted BC commonly presents fractal structures. As the BC ages in the atmosphere, BC becomes more compact and OC materials can condense onto the particles. Therefore, BC can be embedded in an OC shell (China et al., 2013; Wang et al., 2017). When the non-BC fraction is low, BC can still present a near-fractal structure (referred to as thinly coated BC in this study) (Wang et al., 2017). As BC is further coated, BC aggregates are collapsed into more compact and spherical clusters when fully engulfed in coating material (referred to as thickly coated BC in this study) (Coz and Leck, 2011a; Zhang et al., 2008a).
In this study, a numerical investigation was conducted to explore the factors that contribute to the complex absorption enhancement of BC with BrC coatings for different mixing states. Two types of mixing states were considered: thinly coated BC and thickly coated BC. Thinly coated BC is assumed to be those with a BC volume fraction over 20 %, and the other BC is considered to be thickly coated. The results would give further understanding for the causes of BC absorption enhancements and suggestions for the inferred BC mixing states.
2.1 Geometric properties of BC aerosols
In climate modeling, a spherical shape is commonly assumed for aerosols and can be calculated with high efficiency using the Mie theory (Mie, 1908). However, in many cases, this shape can introduce large errors compared with the measurements due to the oversimplification of the shape. Recently, the nonsphericity of aerosols has gained increasing interest (Bi and Yang, 2016; Yang et al., 2003). Specifically, observations have indicated that uncoated BC particles are commonly composed of numerous small spherical particles. Fractal aggregates can be greatly used to describe their geometric properties. Mathematically, the structure satisfies the well-known fractal law (Mishchenko et al., 2002):
where ns represents the number of the monomers in the cluster, R represents the mean radius of the monomers, k0 represents the fractal prefactor, Df represents the fractal dimension, Rg represents the radius of gyration, and li represents the distance from the ith monomer to the center of the cluster.
The fractal dimension is a key parameter that describes the compactness of BC aggregates (Luo et al., 2018a; Sorensen, 2001; Sorensen and Roberts, 1997). Generally, aggregates tend to be more compact with the increase in Df. A Df of 1 can describe an open-chain-type shape, while the aggregates tend to be spherical as Df approaches 3. Numerous experimental studies have been carried out to evaluate the Df of BC aggregates. Immediately after they are emitted, BC aggregates generally exhibit fluffy structures with a small fractal dimension (Df), that is normally less than 2, such as the Df of BC aggregates from biomass burnings (1.67–1.83) (Chakrabarty et al., 2006), the Df of BC from vehicle emissions (1.52–1.94) (China et al., 2014), and the Df of BC from diesel combustion (1.6–1.9) (Wentzel et al., 2003).
However, under the effects of atmospheric aging, the structures and chemical compositions of BC may change. Aged BC tends to be mixed with other chemical components, and the shape becomes more compact. Therefore, in the atmosphere, aggregates can have fractal dimensions of up to 2.6 (Chakrabarty et al., 2006). In some cases, BC aggregates are thinly coated with other materials and still exhibit a fractal structure. However, different from freshly emitted BC aggregates, both lacy and compact structures can exist. Therefore, for thinly coated BC, the Df was assumed to be in the range from 1.8 to 2.6. As BC becomes increasingly coated, BC aggregates may transform from highly agglomerated to nearly spherical particles. A Df=2.6 was assumed for thickly coated BC. Even though a fractal prefactor can also vary under different combustion and aging statuses, it has less significant effects on the absorption of BC compared to the Df. When fixing Df to be 1.82, Liu and Mishchenko (2005) demonstrated that the absorption cross section of BC aggregates does not change substantially as the fractal prefactor varies from 0.9 to 2.1. Therefore, a fixed fractal prefactor of 1.2 was assumed in this work.
The monomer radius and monomer number are two key parameters that determine the particle size. Even though the monomers' radii are polydispersed in the atmosphere, they vary within a narrow range. Monomer radii are commonly observed within ∼10–25 nm (Bond and Bergstrom, 2006). In addition, Kahnert (2010b) demonstrated that Cabs is insensitive to monomer radii when the monomer radii are within ∼10–25 nm. As a result, for convenient application, a fixed monomer radius of R=20 nm was assumed in this work. Based on transmission electron microscopy (TEM) and scanning electron microscopy (SEM) imaging, the monomer number ns can reach approximately 800 (Adachi and Buseck, 2008). Values of were considered in this work. For an aggregate with ns monomers, the equivalent radius was given by the equivalent volume sphere radius . The morphological parameters considered in this work are shown in Table 1.
2.2 Generation of BC aerosols
The morphologies of coated BC considered in this work are classified into two categories: thinly coated BC and thickly coated BC. The closed-cell structure, which is an example of where coating material that not only covers the outer layers of BC aggregates but also fills the internal voids among primary spherules, can be used to represent the thinly coated BC (Liou et al., 2011; Strawa et al., 1999). In addition, Kahnert (2017) demonstrated that the absorption of closed-cell structures and more realistic morphologies do not have large deviations. Therefore, it is reasonable to use the closed-cell model for calculating the absorption of thinly coated BC, while the thickly coated BC is commonly represented by a structure in which BC aggregates are encapsulated in a sphere (Cheng et al., 2014; Zhang et al., 2017). The typical morphologies are shown in Fig. 1.
Diffusion-limited algorithms (DLAs), including the particle–cluster aggregation (PCA) (Hentschel, 1984) and the cluster–cluster aggregation (CCA) methods (Thouy and Jullien, 1994), have been developed for the generation of aggregates. However, adjustable DLA codes are commonly applied due to their quick implementation and adjustable fractal parameters (Koylu et al., 1995). In this work, an adjustable DLA code developed by Woźniak (2012) was used. Compared with ordinary DLA codes, this code preserves fractal parameters during each step of the aggregation, which avoids the generation of multifractal aggregates (Jensen et al., 2002). After the generation of the aggregates, the coatings were added. More specifically, for thinly coated BC, the BrC shells were generated by the adjustable algorithm, and then the BC cores were added; the details are shown in previous studies (Luo et al., 2018c; Wu et al., 2014). The thickly coated BC is generated by covering the BrC spherical coatings on the BC aggregates, as shown in the study of Cheng et al. (2015).
2.3 Light scattering method
To calculate the radiative properties of BC in this work, numerical solution methods from Maxwell's equations, including the finite-difference time-domain (FDTD) method (Taflove and Hagness, 2005; Yee, 1966), generalized multiparticle Mie (GMM) method (Xu, 1997; Xu and Gustafson, 2001), MSTM method (Mackowski and Mishchenko, 2011; Mishchenko et al., 2004), the geometric-optics surface-wave (GOS) method (He et al., 2016; Liou et al., 2011), and discrete-dipole approximation (DDA) method (Draine and Flatau, 1994; Laczik, 1996; Yurkin and Hoekstra, 2007), can all be used. However, compared with other numerical methods, the MSTM has an advantage for the calculation of optical properties for randomly oriented particles analytically without numerically averaging over particle orientations. Therefore, this method has high efficiency to calculate optical properties of BC. In this work, the latest MSTM code, MSTM version 3.0 (Mackowski, 2013), was applied.
In this study, all the radiative properties of BC were calculated based on the assumption that BC particles and their mirror counterparts are present in equal numbers in the ensemble of randomly oriented particles. In the atmosphere, it is reasonable to assume that the possibility of each particle direction is identical, which mathematically satisfies the definition of random orientation (Mishchenko and Yurkin, 2017).
2.4 Calculating absorption enhancement of BC
The presence of non-BC-coated materials can result in the enhancement of BC absorption, referred to as BC absorption enhancement (Eabs). Therefore, Eabs can be defined as the amplification of BC absorption after BC being coated:
where Cabs_coated and Cabs_bare represent the absorption cross sections of coated BC and bare BC, respectively.
As BrC also absorbs solar radiation, it is also desirable to compare the absorption of BC coated by BrC coatings with BC and an external mixture of BrC and BC. The absorption of the BrC shell is calculated as
where Cabs_BrC(coated shape) and Cabs_BrC(bare shape) represent the absorption cross sections of BrC with morphologies that are identical to coated BC and bare BC, respectively. The calculation of the absorption of BrC shell is shown in Fig. S1 in the Supplement. In this process, we assume that the absorption of BrC with the same shape as the coated BC is identical to the external mixture of BrC that has the same shape as bare BC and BrC shell. We must clarify that this disposal method neglects the blocking effect and lensing effect of the outer BrC shell on the internal BrC. However, as the BrC absorption is significantly less than the BC absorption with an identical shape, the absorption caused by the blocking effect and lensing effect of outer BrC on the internal BrC is relatively small compared with the BC absorption. Therefore, it is reasonable to make some simplifications.
In this work, we defined a parameter (Eabs_internal) to represent the ratio between the absorption of BC coated by BrC coatings and an external mixture of BrC and BC:
2.5 Size distribution
The absorption of BC is significantly affected by the particle size (Kahnert, 2010b; Luo et al., 2018b). Therefore, the effects of the size distribution on BC absorption enhancement should be considered carefully. The shape of BC particles is commonly irregular. To describe the size of each BC particle, the radius of the corresponding equivalent volume sphere is typically used. Based on numerous measurements, a lognormal size distribution is observed to fit the realistic BC size distributions well (Bond et al., 2002; Chakrabarty et al., 2006; Wang et al., 2015), and it is widely used in climate models for the estimation of BC radiative forcing (Chung et al., 2012; Moffet and Prather, 2009). However, the mean size and standard deviation vary with the combustion status and aging status. In the atmosphere, geometric mean radii (rg) between 0.05 and 0.06 µm for BC are widely accepted (Alexander et al., 2008; Coz and Leck, 2011b; Li et al., 2016; Liu et al., 2018). The geometric standard deviation (σg) varies within a relatively narrow range. Consequently, bare BC with rg between 0.03 and 0.1 µm is considered for sensitivity analysis, an σg from 1.15 to 1.75. The minimum and maximum equivalent volume radii are rmin=0.02 µm and rmax=0.2 µm, respectively.
To estimate the effects of coating thickness on the absorption properties of BC, we assumed that BrC coating ratios are independent of BC size. The difference between the size distributions of bare BC and coated BC is attributed to the coating thickness. The size distribution of bare and coated BC is shown in Fig. S2. Even though the assumption does not completely agree with the real cases, it is reasonable to make some simplifications for the sensitivity analysis. Here, we must clarify that the size distribution parameters (rg and σg) mentioned in this work are applied for the bare BC, and the overall effective volume radius of coated BC is equal to the sum of coating thickness and radius of bare BC.
2.6 Calculation of bulk radiative properties of BC
To make our work more consistent with real circumstance, bulk optical properties are considered. These properties are calculated by averaging over a certain particle size distribution. In application, the equivalent volume radii (r) of BC are commonly assumed to follow a lognormal size distribution:
where rg and σg represent the geometric mean radius and geometric standard deviation, respectively. Given the size distribution, the bulk Cabs can be obtained using the following equation:
The bulk Eabs and Eabs_internal are calculated as those in Eqs. (3)–(5). The only difference is that the absorption cross section is now the bulk absorption cross section.
3.1 Effects of the imaginary part of the BrC refractive index: lensing effect and sunglasses effect
The refractive index of BC is commonly assumed to be wavelength independent over the visible and near-visible spectral regions, and the imaginary part kBC≈0.79 (Bond and Bergstrom, 2006; Moosmuller et al., 2009). In addition, Zhang et al. (2017) have demonstrated that the uncertainties of the BC refractive index have little impact on the absorption enhancement of coated BC aggregates. Therefore, a typical refractive index of BC was adopted in this study.
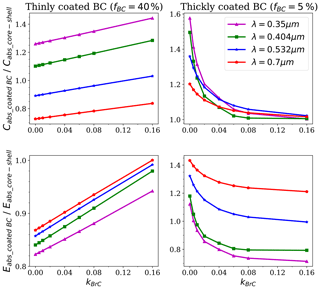
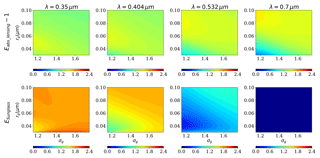
The real parts of the BrC refractive indices were assumed to have a constant value of 1.5 (Schnaiter et al., 2005), while the imaginary part of the refractive index (kBrC) was significantly dependent on wavelength at shorter visible and ultraviolet (UV) wavelengths (Alexander et al., 2008; Andreae and Gelencser, 2006; Moosmuller et al., 2009). Figure 2 shows the effects of kBrC on Eabs and Eabs_internal, where fBC represents the BC volume fraction. Large deviations in Eabs and Eabs_internal can be observed given different values of kBrC. Generally, Eabs increases with kBrC, while Eabs_internal decreases with increasing kBrC. Therefore, it is desirable to evaluate the effects of absorbing coatings on BC absorption enhancement. Given identical kBrC values, the absorption enhancements of thickly coated BC increase with wavelength. However, for BC that is internally mixed with BrC, wavelength-dependent absorption enhancements are measured to decrease with λ (You et al., 2016). This may be due to the wavelength-dependent kBrC. For thickly coated BC, Eabs_internal and Eabs decrease with wavelength, but they are not a strong function of λ for thinly coated BC. In addition, compared with BC with non-absorbing coatings, Eabs for thinly coated BC with absorbing coatings seems to be less wavelength dependent, while Eabs for thickly coated BC with absorbing materials is more sensitive to wavelength.
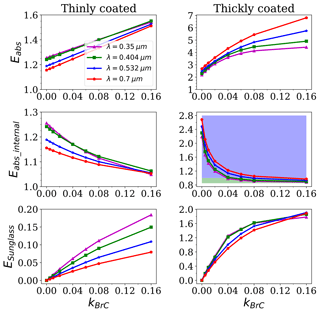
Figure 2Effects of kBrC on specific enhancement (ns=200). For thinly coated BC, Df=2.2 and fBC=40 %; for thickly coated BC, Df=2.6 and fBC=5 %. The blue shading represents the Eabs_internal of larger than 1, while the green shading describes the range of Eabs_internal of less than 1.
Many studies have noticed that the lensing effect can greatly enhance the absorption of BC. However, there is also an opposite effect, which is commonly neglected. As shown in Fig. 2, as kBrC increases, the value of Eabs_internal of thickly coated BC can be below 1. This indicates that the absorption of BC internally mixed with BrC coatings may be less than the sum of the absorption of an external mixture of BrC coatings and BC when kBrC is large. This phenomenon can be explained from physical insights. When the absorption of the coatings is weak, the light can penetrate the coatings of the BC materials, and the absorption of BC is significantly enhanced by the lensing effect. However, as the coating absorption increases, the light is blocked by the outer coatings. Therefore, the light cannot fully and deeply penetrate the absorbing coatings on BC. As a result, the total absorption is less than the sum of the absorption of coatings and BC that are calculated separately. Therefore, there is a need to classify the BrC coating effect into lensing effect (Eabs_lensing) and sunglasses effect (ESunglass), which represents the absorption enhancements and blocking effects of coatings, respectively.
Liu et al. (2017) defined the lensing effect as the absorption enhanced by the addition of non-black carbon. However, from a physical point, for BC with BrC coatings, the definition may not be clear as BrC also absorbs solar radiation, and it can be confused with Eabs. Therefore, here we redefine the lensing effect as the absorption enhanced by addition of non-absorbing materials. In addition, we assume that the lensing effect of BC with absorbing coatings is the same as those with non-absorbing coatings. Accordingly, Eabs_lensing can be calculated using
where Cabs_non-absorbing represents the absorption cross section of BC with non-absorbing coatings. The total Eabs should be contributed to the lensing effect, absorption of BrC shell, and the sunglasses effect. Therefore, Eabs can be expressed by
Combining Eqs. (3)–(9), we can obtain ESunglass, and the negative sign represents the fact that the sunglasses effect can cause a decrease in total absorption. According to the definition of ESunglass, we can easily obtain the relation that the absorption of BC coated with BrC is less than that of an external mixture of BrC and BC when ESunglass>Eabs_lensing−1.
The sensitivity of ESunglass to kBrC is shown in Fig. 2. For both thinly and thickly coated BC, ESunglass increases with kBrC. Fixing kBrC, ESunglass of thinly coated BC decreases with wavelength. However, for thickly coated BC, ESunglass can increase with wavelength at large kBrC values (such as kBrC=0.16). For the thinly coated BC, the blocking of ESunglass is less than the enhancement of Eabs_lensing (see Figs. 5 and 10); therefore, Eabs_internal of thinly coated BC is larger than 1. For thickly coated BC, the blocking of ESunglass can be larger than the enhancement of Eabs_lensing as kBrC is larger, which leads to Eabs_internal of less than 1. The threshold value of kBrC is dependent on particle size and mixing states. Generally, the threshold kBrC value decreases with particle size and coating thickness, as Eabs_internal of BC thickly coated with BrC coatings decreases with particle size and coating thickness in the ultraviolet region (see Figs. 6 and 9).
Although the core–shell sphere model has been debated for a long time, it is still widely used in climate models. By combining the electron tomography (ET) and DDA method, Adachi et al. (2010) found that the absorption of BC with fluffy structures is significantly enhanced by a core–shell structure at λ=0.55 µm. However, for thickly coated BC, BC absorption is underestimated at the UV, visible, and IR wavelengths (Kahnert et al., 2012). Mishchenko et al. (2014) have also demonstrated that the Cabs of thickly coated BC with non-absorbing coatings is significantly underestimated by a core–shell sphere and investigated the effects of off-center BC. Their results indicated that the Cabs values of aged BC covered with thick non-absorbing coatings are approximately 1.44 times higher than those calculated with a core–shell sphere model. Nevertheless, the effects of coating absorption on the applicability of the core–shell sphere model have not been evaluated. As shown in Fig. 3, Cabs for thinly coated BC is enhanced by a core–shell sphere structure in the visible spectral region, which agrees with the study of Adachi et al. (2010), while it is underestimated in the ultraviolet region. In addition, the ratio of Cabs of thinly coated BC to the core–shell sphere model increases with kBrC. However, the applicability of the core–shell sphere model to thickly coated BC is diverse. Consistent with Kahnert et al. (2012), thickly coated BC absorption is underestimated by the core–shell sphere model when coated with non-absorbing materials. Nevertheless, as kBrC increases, the underestimation becomes insignificant. The reason may be that less light can penetrate deeply into the BC as the kBrC increases, which leads to less variation in absorption. Therefore, the morphological effects of BC are relatively small.
The Eabs, compared with that for the core–shell sphere model, is also calculated. For thinly coated BC, the Eabs is significantly overestimated by the core–shell sphere model. However, this overestimation is alleviated by an increasing kBrC. For BC that is thickly coated with non-absorbing materials, the Eabs is underestimated by the core–shell sphere model at all wavelengths, while it decreases as kBrC becomes larger. The Eabs can be overestimated by the core–shell sphere model in the ultraviolet spectral region when kBrC is large. Therefore, the absorption characteristics of BC are significantly affected by the absorption of coatings. To agree with the measurements, typical kBrC values are assumed according to Kirchstetter et al. (2004), as shown in Fig. S2. In this work, kBrC values of 0.168, 0.114, 0.0354 and 0.001 were assumed for 4 typical wavelengths (λ=350, 404, 532 and 700 nm, respectively) via interpolation.
3.2 Bulk radiative properties: effects of the size distribution
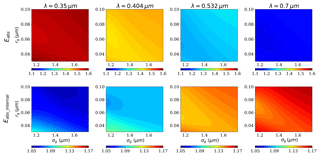
The sensitivity study conducted by Zhang et al. (2017) showed that the Eabs for aged BC was significantly affected by the size distribution. They reported different Eabs values of ∼1.7–2.4 and ∼2.0–2.7 for accumulated and coarse modes, respectively. By setting the fractal dimension to be 2.2 and fBC to be 40 %, the variations in BC absorption enhancements for different particle size distributions are shown in Fig. 4. Generally, weaker absorption enhancement can be observed by increasing λ from the ultraviolet region to the visible region, which is in agreement with the study of You et al. (2016). By defining the monomers' radii, Kahnert (2010a) demonstrated that the absorption cross section is significantly affected by the particle size, and the cubic fit can greatly describe the relations among equivalent volume radii for freshly emitted BC. However, for the absorption enhancement of thinly coated BC, the effects of size distribution are not obvious. With variations in rg and σg, the absorption enhancement changes at ranges of ∼1.563–1.603, ∼1.427–1.465, ∼1.2440–1.275, and ∼1.146–1.169 at λ=0.35, 0.404, 0.532, and 0.7 µm, respectively. The relative uncertainty in the absorption enhancements caused by the size distribution are 2.56 %, 2.66 %, 2.81 %, and 2.01 %, respectively. The effects of the size distribution on the absorption enhancement of thinly coated BC are similar at different wavelengths. Generally, Eabs has the largest value when both rg and σg are extremely small or extremely large.
The absorption of BrC and BC is considered separately in most cases. To investigate the difference between the absorption of internally mixed BC and the total absorption of BrC and BC (calculated separately), Eabs_internal is also calculated. Eabs_internal of thinly coated BC is greater in the visible region due to the insignificant sunglasses effects. The sensitivity of Eabs_internal is also not obvious to the size distribution. With the size distribution varying, Eabs_internal changes in the range of ∼1.055–1.099, ∼1.081–1.112, ∼1.132–1.147, and ∼1.140–1.165 for λ=0.35, 0.404, 0.532, and 0.7 µm, respectively, and the relative uncertainties are all below 2 %. In addition, Eabs_lengsing shares a dependence on size distribution similar to Eabs in the visible wavelengths. The reason is that the Eabs mainly derives from lensing effects due to the weak absorption of coatings. However, for ultraviolet wavelengths, there is a completely different pattern due to the sunglasses effect.
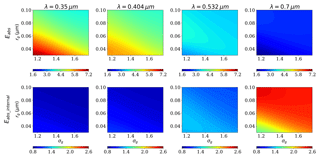
Figure 6Eabs and Eabs_internal of BC thickly coated with BrC at different size distributions (Df=2.6, fBC=6 %).
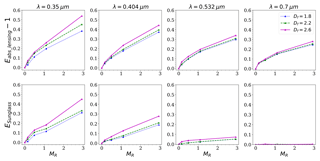
As both the lensing effect and sunglasses effect may affect the Eabs_internal, Eabs_lensing and ESunglass are also investigated, and the results are shown in Fig. 5. Here Eabs_lensing−1 represents the Eabs enhancement caused by the lensing effect, and ESunglass is the Eabs decrease caused by the sunglasses effect. For thinly coated BC, although both Eabs_lensing and ESunglass decrease with increasing λ, compared with ESunglass, Eabs_lensing has less spectral dependence. Eabs_lensing−1 is in the range of ∼0.205–0.283, ∼0.186–0.251, ∼0.163–0.2, and ∼0.147–0.171 for λ=0.35, 0.404, 0.532, and 0.7 µm, respectively. However, ESunglass can reach approximately 0.2 at λ=0.35 µm, but is about 0 at λ=0.7 µm. In addition, for thinly coated BC, the enhancements of the lensing effect are stronger than the blocking of the sunglasses effect. Therefore, Eabs_internal is above 1 for thinly coated BC (as shown in Figs. 2 and 4).
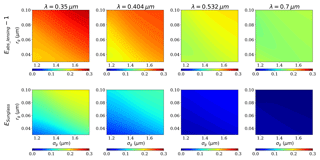
Figure 6 illustrates the effects of size distribution on Eabs and Eabs_internal of thickly coated BC. Compared with thinly coated BC, there is a different effect pattern for thickly coated BC. For ultraviolet wavelengths (e.g., λ=0.35 and 0.404 µm), absorption enhancements decrease as rg or σg increases. This indicates that as the particle becomes larger or the size distribution becomes wider, the absorption enhancements become weaker. However, for the visible wavelengths, the effects of the size distribution are quite complicated. The absorption enhancements are relatively small when both rg and σg are extremely large or small. The peak value commonly occurs when σg is extremely small. Zhang et al. (2017) concluded that the Eabs of aged BC is more sensitive to the size distribution in the accumulation mode (in which σg is relatively small), while the Eabs of coarsely coated BC aggregates (i.e., with large σg) show little variation with rg. This is precisely true for BC with weak absorbing coatings, as shown in the results for λ=0.7 µm. However, for BC with absorbing coatings, Eabs is sensitive to the size distribution for both modes. When fixing the fBC to be 6 %, as rg and σg vary, the absorption enhancements change in the ranges of ∼3.7–7.1, ∼3.85–5.80, ∼3.06–3.74, and ∼1.63–2.59 for λ=0.35, 0.404, 0.532, and 0.7 µm, respectively, and the uncertainties in Eabs can reach up to 91.9 %, 50.7 %, 22.2 %, and 60.7 %, respectively.
Eabs_internal of thickly coated BC is also significantly affected by the size distribution. With the rg varying in the range of 0.03–0.1 µm and σg varying in the range of 1.15–1.75, Eabs_internal varies in the range of 0.871–1.053, 0.891–1.121, 1.115–1.383, and 1.615–2.442 for λ=0.35, 0.404, 0.532, and 0.7 µm, respectively. In addition, effects of the size distribution on Eabs_internal and Eabs are related to wavelength. Eabs_internal decreases with particle size (i.e, increasing rg) at ultraviolet wavelengths, while it increases as the particles become larger at visible wavelengths (also see Fig. S6). Based on physical insights, the reason may be due to two aspects. When the wavelength is in the ultraviolet region, the absorption of the coatings is large; therefore, the blocking effects of the coatings are obvious. Given identical fBC values, the superficial area of the outer coating becomes lager as the particle size increases. As a result, the blocking effects of the outer coatings increase. Therefore, the Eabs_internal decreases. At visible wavelengths, the absorption of the coatings is negligible, and the light can penetrate deeply into BC. At that point, the main factor is the enhancement of the lensing effect, and the larger particles may cause a larger superficial area, which leads to the enhanced Eabs_internal. Eabs shares similar dependences on the size distribution for different wavelengths. In addition, Eabs_internal can be less than 1. This means that the enhancement of the lensing effect is less than the blocking of the sunglasses effect. In climate models, the σg is commonly assumed to be a fixed value, and the BC size distribution is commonly assumed to be in accumulation mode (Liu et al., 2012). The effects of the size distribution at fixed σg=1.5 are supplemented in Figs. S4–S7.
The effects of the size distribution on the lensing effect and sunglasses effect of thickly coated BC are shown in Fig. 7. Eabs_lensing is in the range of 2.197–2.514, 2.045–2.486, 1.844–2.526, and 1.6147–2.568 at λ=0.35, 0.404, 0.532, and 0.7 µm, respectively. It seems that Eabs_lensing is more sensitive to the size distribution in the visible region compared with the ultraviolet region. However, Eabs_lensing at different wavelengths does not deviate largely, and the uncertainty is within 25 %. However, effects of the size distribution on ESunglass largely depend on the wavelength. Fixing fBC=6 %, ESunglass is in the range between 1.586 and 2.062 at λ=0.35 µm and in the range between 0.001 and 0.027 at λ=0.7 µm. In addition, from Fig. 7, we can also see that the enhancement of the lensing effect (represented by Eabs_lensing−1) is less than the blocking of the sunglasses effect in the ultraviolet region for thickly coated BC, while the opposite phenomenon is observed in the visible region.
3.3 Bulk radiative properties: effects of the composition ratio
To make our calculation meaningful, we compare the calculated Eabs and mass absorption cross section (MAC) with the measurements of Liu et al. (2015b). The measurement results for Eabs and MAC are estimated from Fig. 1 and supplementary Fig. 2 of Liu et al. (2015b). MAC is calculated using
where mBC and ρBC represent the mass and mass density of BC, respectively. To agree with measurements, the coating thickness is determined by the mass ratio of BrC and BC components MR. In this study, MR is calculated by:
where ρBrC represents the mass density of BrC. In this work, we assume ambient BC mainly composed of primary organic matter with a low degree of oxidation. Based on the study of Nakao et al. (2013), an OC mass density range of 1–1.2 g cm−3 has been used by Liu et al. (2017). ρBrC=1.1 g cm−3 is assumed in this work. For the BC mass density, the study of Horvath (1993) gives values of ρBC=0.625 g cm−3 and ρBC=1.125 g cm−3. However, Fuller et al. (1999a) pointed out that the values may not be representative for BC in the atmosphere. Medalia and Richards (1972) and Janzen (1980) suggested ρBC in the range of 1.8–1.9 g cm−3, while Bergstrom (1972) found the ρBC value of 1.9–2.1 g cm−3. Bond and Bergstrom (2006) suggested using a value of 1.8 g cm−3. Figure S8 compares the computations with measurements by assuming ρBC=1.8 g cm−3. We assume that Eabs and MAC at λ=0.7 µm do not deviate largely with those at λ=0.781 µm. Modeled Eabs at λ=0.7 µm agrees well with the measurements. Although Eabs at λ=0.404 µm seems to be relatively higher than the measurements, it does not deviate largely from the measurements. However, modeled MAC is a little smaller than the measured MAC. Similar results were obtained for bare BC (Kahnert, 2010b; Liu and Mishchenko, 2005). Therefore, ρBC=1.8 g cm−3 may be a little high for estimation of MAC.
Bond and Bergstrom (2006) concluded that the MAC value of 7.5±1.2 m2 g−1 for bare BC can be assumed at λ=0.55 µm by reviewing 21 publications of MAC measurements. However, our calculated MAC of 6.02–6.2 m2 g−1 (see Table 2) at λ=0.532 µm lies below the range of MAC values suggested by Bond and Bergstrom (2006). Similar conclusions were drawn by Kahnert (2010b) and Liu and Mishchenko (2005). However, our calculated MAC agrees well with the calculated MAC of 6.0±0.1 m2 g−1 by Kahnert (2010b) at λ=0.55 µm. As MAC depends significantly on BC mass density, to agree with measurements, Liu and Mishchenko (2005) used ρBC=1.0 g cm−3. However, as pointed by Kahnert (2010b), the measured MAC and modeled MAC were not at the same wavelength, therefore leading to too low retrieved ρBC. To raise the computed MAC values to the average observed value of MAC = (7.5±1.2) m2 g−1, ρBC=1.3–1.4 g cm−3 was suggested by Kahnert (2010b). However, this ρBC value is rather drastically smaller than the value suggested by Bond and Bergstrom (2006). Therefore, Kahnert (2010b) suggested assuming ρBC=1.5–1.7 g cm−3 to raise the computational MAC results to the lower bound of the observations. By assuming ρBC=1.5 g cm−3, the comparison of modeled MAC and Eabs with measurements is shown in Fig. S9. Overall, the modeled MAC and Eabs agree relatively well with the measurement by assuming ρBC=1.5 g cm−3. Therefore, ρBC=1.5 g cm−3 is assumed in this study. In addition, according to the previous studies (Liu et al., 2015a; Zhang et al., 2016), the shell ∕ core ratio Dp∕Dc (equivalent particle diameter divided by BC core diameter) was observed to be commonly in the range of 1.1–2.7, and the corresponding MR is approximately 0.24–13.9. Therefore, MR of 0–13.9 is considered in this work.
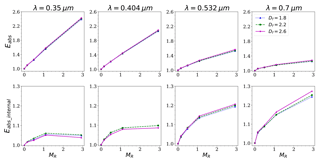
Figure 8Eabs and Eabs_internal of thinly coated BC with BrC coatings varying with MR for different Df values (rg=0.06 µm, σg=1.5).
Figure 8 compares the Eabs and Eabs_internal for thinly coated BC with different fractal dimensions at different composition ratios. Following Liu et al. (2018), a rg of 0.06 µm and a σ of 1.5 are assumed to reflect the real size distribution of BC. It is expected that as the coatings increase, Eabs becomes much stronger. With MR varying from 0 to 2.93, Eabs variations of ∼1–2.5, ∼1–2.2, ∼1–1.6, and ∼1–1.285 are obtained for λ=0.35, 0.404, 0.532, and 0.7 µm, respectively. The Eabs for thinly coated BC with weakly absorbing materials (i.e., λ=0.7 µm) is significantly lower than that for the core–shell sphere, as reported by Zhang et al. (2017), where Eabs can reach approximately 1.5 when the shell ∕ core ratio is 1.6 (MR=2.2709) at λ=0.55 µm. Even though the results are gained at two different wavelengths, the Eabs for BC that is coated with weakly absorbing coatings should not deviate substantially between λ=0.55 µm and λ=0.7 µm (see Fig. 12). Therefore, the differences from the previous study are mainly caused by the BC shape, as demonstrated in Fig. 3. When the relative contents of BC vary, substantial variations in Eabs_internal can also be observed. As MR varies in the range of 0–2.93, Eabs_internal increases from 1 to 1.07, 1 to 1.1, 1 to 1.22, and 1 to 1.285 for λ=0.35, 0.404, 0.532, and 0.7 µm, respectively. Eabs_internal of thinly coated BC increases with MR in the visible spectral region, while a little decrease in Eabs_internal can be observed in the ultraviolet region as MR increases when MR is larger than a threshold value. This is mainly caused by the blocking of the sunglasses effect.
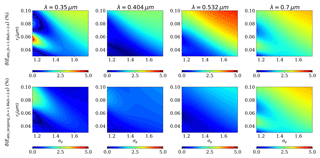
Figure 9The relative deviations of absorption properties between Df=1.8 and Df=2.6 for thinly coated BC with BrC coating (fBC=20 %).
At different wavelengths, the effects of Df may vary. Eabs_internal increases with Df in the visible wavelengths, as the more compact structure can lead to a greater lensing interaction. While in the ultraviolet region, as the structure becomes more compact, the interaction of absorbing coatings also increases; therefore, the blocking effects of outer coatings are greater. Therefore, the Eabs_internal can decrease with Df when Df is greater than a threshold value. Even though Cheng et al. (2014) and Luo et al. (2018b) showed that the effects of Df on Cabs are not obvious for thinly coated BC, for Eabs of thinly coated BC, the sensitivity of Df has not been investigated. To quantify the effects of Df, the relative deviations between Df=1.8 and Df=2.6 are also calculated for thinly coated BC. From Fig. 8, we found that the differences in Eabs and Eabs_internal among different values of Df are larger for thicker coatings. Therefore, to evaluate the maximum uncertainty, the fBC is fixed to be 20 %. As shown in Fig. 9, the differences in Eabs and Eabs_internal between Df=1.8 and Df=2.6 are all below 5 %. Eabs of BC thinly coated with non-absorbing coatings is more obviously affected by Df. However, the relative deviations between Df=1.8 and Df=2.6 do not exceed 12 % (as shown in Fig. S10.).
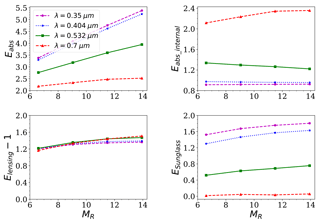
Figure 11Eabs and Eabs_lensing of thickly coated BC with BrC coatings varying with MR (rg=0.06 µm, σg=1.5).
To reveal the factors that contribute to the complex Eabs_internal, the effects of MR on Eabs_lensing and ESunglass of thinly coated BC are investigated at different wavelengths. Eabs_lensing increases with MR for all wavelengths. It seems that the sensitivity of Eabs_lensing to MR is more obvious in the ultraviolet region compared with the visible region. Fixing Df=2.2, with MR varying from 0 to 2.93, Eabs_lensing increases from 1 to 1.46, 1.4, 1.32, and 1.25 for λ=0.35, 0.404, 0.532, and 0.7 µm, respectively. In addition, more compact structure can result in stronger lensing interaction among monomers and thus leads to an Eabs_lensing increase with Df. Moreover, compared with the visible region, the effects of Df are more obvious at the ultraviolet region. ESunglass also increases with Df, as a more compact structure may lead to stronger blocking interaction among BC monomers. As expected, ESunglass is stronger in the ultraviolet region, while it tends to be 0 in the visible region. As MR reaches 2.93, ESunglass can reach approximately 0.46 at λ=0.35 µm, while ESunglass is below 0.02 at λ=0.7 µm.
Figure 11 demonstrates the absorption enhancements of thickly coated BC at different wavelengths for different composition ratios. Similar to thinly coated BC, Eabs increases with increasing MR or decreasing λ. When setting rg=0.06 µm and σg=1.5, as MR varies from 6.6 to 13.9, Eabs increases from 3.4 to 5.4 and 3.25 to 5.2 for λ=0.35 and λ=0.404 µm, respectively, while Eabs varies from 2.78 to 3.96 and 2.2 to 2.4 for λ=0.532 and 0.7 µm, respectively. In addition, the Eabs seems to be more sensitive to the composition ratios in the ultraviolet wavelengths. This may be caused by the absorption of coatings, which can substantially enhance the total absorption. In addition, the combined Eabs values of thinly coated and thickly coated BC range for BC with BrC coatings is much wider than that for BC with non-absorbing coatings (Eabs of ∼1–2.4) (Zhang et al., 2017, 2018).
At visible wavelengths, the Eabs_internal is greater than 1 due to the small blocking effects of BrC. Defining rg to be 0.06 µm and σg to be 1.5, as MR varies from 6.6 to 13.9, Eabs_lensing ranges from ∼1.222 to 1.337 and ∼2.115 to 2.357 for λ=0.532 and 0.7 µm, respectively. This indicates that the total absorption of BC and BrC can be substantially enhanced by the lensing effects. However, for ultraviolet wavelengths, the Eabs_internal is less than 1. Eabs_internal is within ∼0.913–0.924 and ∼0.956–0.974 for λ=0.35 and λ=0.404 µm, respectively. This demonstrates the absorbing coatings can significantly block the light into BC. Therefore, the total absorption is less than the sum of BrC absorption and BC absorption. In recent studies, the enhancements of lensing effects has gained increasing attention. However, few studies have investigated the blocking effects of absorbing coatings. As a matter of fact, the blocking effect of absorbing coatings is also a significant factor that affects the total absorption, as the Eabs_internal can be below 1. This indicates that the blocking effects of absorbing coatings may be greater than the enhancements of the lensing effects. Therefore, when BC is coated with BrC, we should not only focus on the enhancements of the lensing effects but also carefully consider the blocking effects of the coatings.
There is a different dependence on MR for Eabs_internal at different wavelengths. Eabs_internal increases with MR at relatively long wavelengths (eg. λ= 0.7 µm), while decreases as the coatings become thicker at relatively short wavelengths (0.404 and 0.532 µm). This phenomenon can also be explained from physical insights. When the wavelength is short, increased thickness of the coatings may lead to a greater sunglasses effect, which weakens the total absorption of the coatings and BC. However, at λ=0.7 µm, enhanced Eabs_internal can be obtained by increasing the coatings due to the negligible blocking effects of the coatings. In addition, Eabs_internal increases with wavelength due to the decrease in coating absorption (see Fig. 2). Eabs_internal of thickly coated BC is insensitive to MR at λ=0.35 µm due to the similar variations in Eabs_lensing and ESunglass with MR. As MR varies from 6.6 to 13.9, Eabs_lesnig increases from 2.204 to 2.363, 2.214 to 2.390, 2.216 to 2.473, and 2.165 to 2.509 at λ=0.35, 0.404, 0.532, and 0.7 µm, respectively. Meanwhile, ESunglass is largely affected by wavelengths. At λ=0.35 µm, ESunglass is in the range from 1.523 to 1.807, while ESunglass approaches 0 at λ=0.7 µm. It can also be seen from Fig. 11 that ESunglass>Eabs_lensing−1 at λ=0.35 and 0.404 µm. Therefore, Eabs_internal is less than 1.
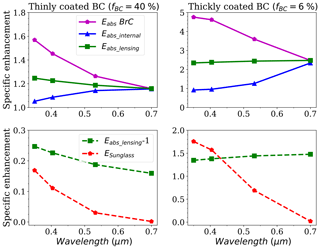
Figure 12Comparison of BC coated with non-absorbing materials and that coated with BrC (rg=0.06 µm, σg=1.5). Df=2.2 and Df=2.6 were assumed for thinly coated and thickly coated BC, respectively.
You et al. (2016) demonstrated that there are different wavelength dependencies for BC that is coated with absorbing and weakly absorbing materials. Eabs for BC coated with humic acid was observed to vary from 3.0 to approximately 1.6 as λ increased from 0.554 to 0.84 µm, while it seemed to be essentially wavelength independent for BC that is coated with sodium chloride. Figure 12 compares the wavelength dependencies of BC coated with non-absorbing materials and BrC. For thinly coated BC, there are substantial wavelength dependencies for BC coated with BrC. By setting fBC to be 40 %, Eabs increases from 1.15 to 1.57 with λ varying from 0.7 to 0.35 µm, which results in an approximately 49.6 % increase. However, when coated with non-absorbing materials, Eabs exhibits small wavelength dependences. This leads to approximate 8.7 % increases as λ decreases from 0.7 to 0.35 µm. Furthermore, for thickly coated BC, Eabs is significantly wavelength dependent for BC with BrC coatings. The decrease in λ from 0.7 to 0.35 µm would result in an approximately 100 % increase in Eabs, while Eabs seems to be essentially wavelength independent for BC with non-absorbing coatings (Eabs_lensing); it is approximately 2.4 when fBC=6 %, which is consistent with the value reported by Zhang et al. (2017). The differences of Eabs_lensing of thickly coated BC between λ=0.35 and 0.7 µm are below 6.2 %. Therefore, the variation in kBrC should be mainly responsible for the significant wavelength dependencies of Eabs for BC with BrC coatings when the wavelength is long. For ultraviolet wavelengths (λ from 0.35 to 0.404 µm), wavelength dependence of Eabs is relatively small, as the Eabs may increase with wavelength when kBrC is fixed at a large value (see Fig. 2), which can reduce the wavelength dependence. Therefore, the contribution of kBrC to the wavelength dependence should be further analyzed in ultraviolet wavelengths in the future.
In addition, the Eabs_internal of BC coated with BrC is also significantly wavelength dependent. Fixing fBC=40 % and 6 %, respectively, with λ varying from 0.35 to 0.7 µm, Eabs_internal increases from 1.05 to 1.18 and from approximately 0.92 to 2.3, respectively. Eabs_lensing−1 and ESunglass are also compared in Fig. 12. ESunglass decreases significantly with λ for both thinly and thickly coated BC. For thinly coated BC, Eabs_lensing−1 is larger than ESunglass for all wavelengths. However, ESunglass can be stronger than Eabs_lensing−1 in the ultraviolet region for thickly coated BC. This indicates that the total absorption of BC and BrC is weakened by internal mixing. Therefore, the sunglasses effect should also be noticed for the estimation of aerosol absorption.
Using the MSTM method, the Eabs and Eabs_lensing of BC with BrC coatings were investigated at λ=0.35, 0.404, 0.532, and 0.7 µm, respectively. The main findings of this work are as follows.
-
Generally, Eabs increases with kBrC while Eabs_interanl decreases as kBrC becomes larger. For the thinly coated BC, Eabs_internal is greater than 1 due to the enhancements of the lensing effects. However, for thickly coated BC, the Eabs_internal can be less than 1. This indicates the total absorption of BrC and BC is less than the sum of BrC and BC absorption individually, which is opposite to BC that is coated with weakly absorbing coatings. This phenomenon may be caused by the blocking effects of outer coatings. As the absorption of coatings increases, less light can penetrate into BC materials. Therefore, the total absorption of BrC and BC is weakened, resulting in Eabs_internal of less than 1. This effect is named the “sunglasses effect” in this study.
-
Cabs of thinly coated BC is underestimated by the core–shell sphere model in the ultraviolet region while it is overestimated in the visible region. In addition, the ratio of Cabs of thinly coated BC to that of the core–shell sphere model increases with kBrC. Eabs of thinly coated BC is enhanced by the core–shell sphere while the enhancements are alleviated by increasing kBrC. There are different dependencies for thickly coated BC. Cabs of thickly coated BC is underestimated by the core–shell sphere model for all wavelengths while the underestimation becomes negligible as kBrC becomes very large. Eabs of thickly coated BC with non-absorbing materials is underestimated by the core–shell assumption. However, the ratio of Eabs of thickly coated BC to the core–shell sphere model decreases with increasing kBrC, and Eabs is enhanced by the core–shell sphere in the visible region, when the absorption of coatings is large.
-
To make our calculation more consistent with real circumstance, the bulk absorption was calculated and the kBrC is selected by interpolation based on the study of Kirchstetter et al. (2004). For thinly coated BC, the effects of size distribution on Eabs are not obvious. The uncertainties of size distribution result in Eabs differences of less than 2.56 %, 2.52 %, 2.32 %, and 2.16 % for λ=0.35, 0.404, 0.532, and 0.7 µm, respectively. However, Eabs of thickly coated BC is quite sensitive to the size distribution. Eabs differences of approximately 92 % can be obtained as rg and σg vary for λ=0.35 µm. In addition, different from Eabs of 2.2–2.4 for thickly coated BC with weakly absorbing coatings, Eabs of 3.4–5.4 is observed for BC with BrC coatings at λ=0.35 µm as MR is in the range of ∼6.6–13.9. Specifically, as MR increases to approximately 13.9, Eabs of larger than 3.96 can be observed at 0.532 µm, which is a little higher than the commonly measured Eabs of 1.05–3.5 at this wavelength. For thinly coated BC, Eabs of BC with weakly absorbing coatings is in the range of approximately ∼1–1.3 for λ=0.7 µm (i.e., BC with weakly absorbing coatings) while a wider range of ∼1–2.5 is obtained for λ=0.35 µm. In summary, the Eabs range of BC with BrC coatings is much wider than that of BC with non-absorbing coatings.
-
The sunglasses effect and lensing effect are compared at different wavelengths. Esunglass is less than Eabs_lensing−1 for thinly coated BC. This indicates the blocking of the sunglasses effect is less than the enhancement of the lensing effect, so the Einternal>1 for thinly coated BC. However, Esunglass can be larger than Eabs_lensing−1 in the ultraviolet region for thickly coated BC, which leads to Einternal<1. Therefore, the absorption of BC thickly coated with BrC can be less than an external mixture of BC and BrC. In the visible region, Esunglass is less than Eabs_lensing−1 due to the small sunglasses effect.
-
Eabs of BC with BrC coatings is more wavelength dependent than that with non-absorbing coatings. For thinly coated BC, Eabs of BC with non-absorbing coatings leads to an approximately 8.7 % increase as λ decreases from 0.7 to 0.35 µm while the difference can reach approximately 50 % for BC with BrC coatings. For thickly coated BC, the decrease in λ from 0.7 to 0.35 µm would result in an approximately 100 % increase in Eabs for BC with BrC coatings. However, Eabs of BC with non-absorbing coatings seems to be to be essentially wavelength independent. In addition, for thinly coated BC, the effects of Df are not obvious for Eabs and Eabs_lensing. The uncertainties of Eabs and Eabs_internal caused by Df all are less than 5 %.
In this work, complex morphologies and mixing states are considered. Although current climate models do not simulate any morphological information of aerosols, many laboratory studies have been conducted to investigate the BC morphologies in different mixing states and in different regions. Therefore, our calculations can be applied according to specific mixing states (such as composition ratios) and regions. However, we acknowledge that the understanding of the relation between BC morphology and the composition ratio is still limited. Therefore, further laboratory investigations for the coated BC morphologies should be conducted in the future.
Our data are all exhibited in the figures. We have only a supplementary pdf file, which is available on the ACP website.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-18-16897-2018-supplement.
JL and QZ conceived the presented idea. JL developed the models, performed the computations, and wrote the paper. YZ and FW verified the simulation methods and results. QZ revised the paper and supervised the findings of this work. All authors discussed the results and contributed to the final paper.
The authors declare that they have no conflict of interest.
This work was financially supported by the National Key Research and
Development Plan (grant nos. 2016YFC0800100 and 2017YFC0805100), National
Natural Science Foundation of China (grant nos. 41675024 and U1733126), and
Fundamental Research Funds for the Central Universities (grant no.
WK2320000035). We particularly thank Daniel W. Mackowski and
Michael I. Mishchenko for the MSTM code. We also acknowledge the support of
the supercomputing center of USTC. We particularly thank the three anonymous
reviewers for their constructive suggestions.
Edited by: James Allan
Reviewed by: three anonymous referees
Adachi, K. and Buseck, P. R.: Internally mixed soot, sulfates, and organic matter in aerosol particles from Mexico City, Atmos. Chem. Phys., 8, 6469–6481, https://doi.org/10.5194/acp-8-6469-2008, 2008. a
Adachi, K., Chung, S. H., and Buseck, P. R.: Shapes of soot aerosol particles and implications for their effects on climate, J. Geophys. Res.-Atmos., 115, D15206, https://doi.org/10.1029/2009JD012868, 2010. a, b, c
Alexander, D. T. L., Crozier, P. A., and Anderson, J. R.: Brown carbon spheres in East Asian outflow and their optical properties, Science, 321, 833–836, 2008. a, b
Andreae, M. O. and Gelencsér, A.: Black carbon or brown carbon? The nature of light-absorbing carbonaceous aerosols, Atmos. Chem. Phys., 6, 3131–3148, https://doi.org/10.5194/acp-6-3131-2006, 2006. a
Bergstrom, R. W.: Predictions of the spectral absorption and extinction coefficients of an urban air pollution aerosol model, Atmos. Environ., 6, 247–258, https://doi.org/10.1016/0004-6981(72)90083-2, 1972. a
Bi, L. and Yang, P.: Tunneling effects in electromagnetic wave scattering by nonspherical particles: A comparison of the Debye series and physical-geometric optics approximations, J. Quant. Spectrosc. Ra., 178, 93–107, 2016. a
Bond, T. C. and Bergstrom, R. W.: Light absorption by carbonaceous particles: An investigative review, Aerosol Sci. Tech., 40, 27–67, 2006. a, b, c, d, e, f
Bond, T. C., Covert, D. S., Kramlich, J. C., Larson, T. V., and Charlson, R. J.: Primary particle emissions from residential coal burning: Optical properties and size distributions, J. Geophys. Res.-Atmos., 107, 8347, https://doi.org/10.1029/2001JD000571, 2002. a
Bond, T. C., Habib, G., and Bergstrom, R. W.: Limitations in the enhancement of visible light absorption due to mixing state, J. Geophys. Res.-Atmos., 111, D20211, https://doi.org/10.1029/2006JD007315., 2006. a, b
Bond, T. C., Doherty, S. J., Fahey, D. W., Forster, P. M., Berntsen, T., DeAngelo, B. J., Flanner, M. G., Ghan, S., Karcher, B., Koch, D., Kinne, S., Kondo, Y., Quinn, P. K., Sarofim, M. C., Schultz, M. G., Schulz, M., Venkataraman, C., Zhang, H., Zhang, S., Bellouin, N., Guttikunda, S. K., Hopke, P. K., Jacobson, M. Z., Kaiser, J. W., Klimont, Z., Lohmann, U., Schwarz, J. P., Shindell, D., Storelvmo, T., Warren, S. G., and Zender, C. S.: Bounding the role of black carbon in the climate system: A scientific assessment, J. Geophys. Res.-Atmos., 118, 5380–5552, 2013. a, b
Cappa, C. D., Onasch, T. B., Massoli, P., Worsnop, D. R., Bates, T. S., Cross, E. S., Davidovits, P., Hakala, J., Hayden, K. L., Jobson, B. T., Kolesar, K. R., Lack, D. A., Lerner, B. M., Li, S. M., Mellon, D., Nuaaman, I., Olfert, J. S., Petaja, T., Quinn, P. K., Song, C., Subramanian, R., Williams, E. J., and Zaveri, R. A.: Radiative Absorption Enhancements Due to the Mixing State of Atmospheric Black Carbon, Science, 337, 1078–1081, 2012. a, b, c
Chakrabarty, R. K., Moosmuller, H., Garro, M. A., Arnott, W. P., Walker, J., Susott, R. A., Babbitt, R. E., Wold, C. E., Lincoln, E. N., and Hao, W. M.: Emissions from the laboratory combustion of wildland fuels: Particle morphology and size, J. Geophys. Res.-Atmos., 111, D07204, https://doi.org/10.1029/2005JD006659, 2006. a, b, c
Chen, B., Bai, Z., Cui, X. J., Chen, J. M., Andersson, A., and Gustafsson, O.: Light absorption enhancement of black carbon from urban haze in Northern China winter, Environ. Pollut., 221, 418–426, 2017. a
Cheng, T. H., Wu, Y., and Chen, H.: Effects of morphology on the radiative properties of internally mixed light absorbing carbon aerosols with different aging status, Opt. Express, 22, 15904–15917, 2014. a, b
Cheng, T. H., Wu, Y., Gu, X. F., and Chen, H.: Effects of mixing states on the multiple-scattering properties of soot aerosols, Opt. Express, 23, 10808–10821, 2015. a
Cheng, Y., He, K. B., Engling, G., Weber, R., Liu, J. M., Du, Z. Y., and Dong, S. P.: Brown and black carbon in Beijing aerosol: Implications for the effects of brown coating on light absorption by black carbon, Sci. Total Environ., 599, 1047–1055, 2017. a, b
China, S., Mazzoleni, C., Gorkowski, K., Aiken, A. C., and Dubey, M. K.: Morphology and mixing state of individual freshly emitted wildfire carbonaceous particles, Nat. Commun., 4, 2122, https://doi.org/10.1038/ncomms3122, 2013. a
China, S., Salvadori, N., and Mazzoleni, C.: Effect of Traffic and Driving Characteristics on Morphology of Atmospheric Soot Particles at Freeway On-Ramps, Environ. Sci. Technol., 48, 3128–3135, 2014. a
Chung, C. E., Ramanathan, V., and Decremer, D.: Observationally constrained estimates of carbonaceous aerosol radiative forcing, P. Natl. Acad. Sci. USA, 109, 11624–11629, 2012. a
Coz, E. and Leck, C.: Morphology and state of mixture of atmospheric soot aggregates during the winter season over Southern Asia-a quantitative approach, Tellus B, 63, 107–116, 2011a. a
Coz, E. and Leck, C.: Morphology and state of mixture of atmospheric soot aggregates during the winter season over Southern Asia-a quantitative approach, Tellus B, 63, 107–116, 2011b. a
Cui, X. J., Wang, X. F., Yang, L. X., Chen, B., Chen, J. M., Andersson, A., and Gustafsson, O.: Radiative absorption enhancement from coatings on black carbon aerosols, Sci. Total Environ., 551, 51–56, 2016. a
Draine, B. T. and Flatau, P. J.: Discrete-Dipole Approximation for Scattering Calculations, J. Opt. Soc. Am., 11, 1491–1499, 1994. a
Forster, P., Ramaswamy, V., Artaxo, P., Berntsen, T., Betts, R., Fahey, D. W., Haywood, J., Lean, J., Lowe, D. C., Myhre, G., Nganga, J., Prinn, R., Raga, G., Schultz, M., and Van Dorland, R.: Changes in atmospheric constituents and in radiative forcing, Chap. 2, in: Climate Change 2007, The Physical Science Basis, Cambridge University Press, Cambridge, UK, 2007. a
Fuller, K. A., Malm, W. C., and Kreidenweis, S. M.: Effects of mixing on extinction by carbonaceous particles, J. Geophys. Res.-Atmos., 104, 15941–15954, 1999a. a
Fuller, K. A., Malm, W. C., and Kreidenweis, S. M.: Effects of mixing on extinction by carbonaceous particles, J. Geophys. Res.-Atmos., 104, 15941–15954, 1999b. a
He, C., Liou, K.-N., Takano, Y., Zhang, R., Levy Zamora, M., Yang, P., Li, Q., and Leung, L. R.: Variation of the radiative properties during black carbon aging: theoretical and experimental intercomparison, Atmos. Chem. Phys., 15, 11967–11980, https://doi.org/10.5194/acp-15-11967-2015, 2015. a
He, C. L., Takano, Y., Liou, K. N., Yang, P., Li, Q. B., and Mackowski, D. W.: Intercomparison of the GOS approach, superposition T-matrix method, and laboratory measurements for black carbon optical properties during aging, J. Opt. Soc. Am., 184, 287–296, 2016. a
Hentschel, H. G. E.: Fractal Dimension of Generalized Diffusion-Limited Aggregates, Phys. Rev. Lett., 52, 212–215, 1984. a
Horvath, H.: Atmospheric Light-Absorption – a Review, Atmos. Environ. A-Gen., 27, 293–317, 1993. a
Jacobson, M. Z.: Strong radiative heating due to the mixing state of black carbon in atmospheric aerosols, Nature, 409, 695–697, 2001. a
Janzen, J.: Extinction of Light by Highly Nonspherical Strongly Absorbing Colloidal Particles – Spectrophotometric Determination of Volume Distributions for Carbon-Blacks, Appl. Optics, 19, 2977–2985, 1980. a
Jensen, M. H., Levermann, A., Mathiesen, J., and Procaccia, I.: Multifractal structure of the harmonic measure of diffusion-limited aggregates, Phys. Rev. E, 65, 046109, https://doi.org/10.1103/PhysRevE.65.046109, 2002. a
Kahnert, M.: Modelling the optical and radiative properties of freshly emitted light absorbing carbon within an atmospheric chemical transport model, Atmos. Chem. Phys., 10, 1403–1416, https://doi.org/10.5194/acp-10-1403-2010, 2010a. a
Kahnert, M.: On the Discrepancy between Modeled and Measured Mass Absorption Cross Sections of Light Absorbing Carbon Aerosols, Aerosol Sci. Tech., 44, 453–460, 2010b. a, b, c, d, e, f, g, h
Kahnert, M.: Optical properties of black carbon aerosols encapsulated in a shell of sulfate: comparison of the closed cell model with a coated aggregate model, Opt. Express, 25, 24579–24593, 2017. a
Kahnert, M., Nousiainen, T., Lindqvist, H., and Ebert, M.: Optical properties of light absorbing carbon aggregates mixed with sulfate: assessment of different model geometries for climate forcing calculations, Opt. Express, 20, 10042–10058, https://doi.org/10.1364/OE.20.010042, 2012. a, b
Kirchstetter, T. W., Novakov, T., and Hobbs, P. V.: Evidence that the spectral dependence of light absorption by aerosols is affected by organic carbon, J. Geophys. Res.-Atmos., 109, D21208, https://doi.org/10.1029/2004JD004999, 2004. a, b, c, d
Koylu, U. O., Faeth, G. M., Farias, T. L., and Carvalho, M. G.: Fractal and Projected Structure Properties of Soot Aggregates, Combus. Flame, 100, 621–633, 1995. a
Krishnan, R. and Ramanathan, V.: Evidence of surface cooling from absorbing aerosols, Geophys. Res. Lett., 29, 1340, https://doi.org/10.1029/2002GL014687, 2002. a
Lack, D. A., Cappa, C. D., Cross, E. S., Massoli, P., Ahern, A. T., Davidovits, P., and Onasch, T. B.: Absorption Enhancement of Coated Absorbing Aerosols: Validation of the Photo-Acoustic Technique for Measuring the Enhancement, Aerosol Sci. Tech., 43, 1006–1012, 2009. a
Laczik, Z.: Discrete-dipole-approximation-based light-scattering calculations for particles with a real refractive index smaller than unity, Appl. Optics, 35, 3736–3745, 1996. a
Li, J., Liu, C., Yin, Y., and Kumar, K. R.: Numerical investigation on the Ångström Exponent of black carbon aerosol, J. Geophys. Res.-Atmos., 121, 3506–3518, 2016. a
Liou, K. N., Takano, Y., and Yang, P.: Light absorption and scattering by aggregates: Application to black carbon and snow grains, J. Quant. Spectrosc. Ra., 112, 1581–1594, 2011. a, b
Liu, C., Chung, C. E., Yin, Y., and Schnaiter, M.: The absorption Ångström exponent of black carbon: from numerical aspects, Atmos. Chem. Phys., 18, 6259–6273, https://doi.org/10.5194/acp-18-6259-2018, 2018. a, b
Liu, D. T., Taylor, J. W., Young, D. E., Flynn, M. J., Coe, H., and Allan, J. D.: The effect of complex black carbon microphysics on the determination of the optical properties of brown carbon, Geophys. Res. Lett., 42, 613–619, 2015a. a
Liu, D. T., Whitehead, J., Alfarra, M. R., Reyes-Villegas, E., Spracklen, D. V., Reddington, C. L., Kong, S. F., Williams, P. I., Ting, Y. C., Haslett, S., Taylor, J. W., Flynn, M. J., Morgan, W. T., McFiggans, G., Coe, H., and Allan, J. D.: Black-carbon absorption enhancement in the atmosphere determined by particle mixing state, Nat. Geosci., 10, 184–188, 2017. a, b, c, d
Liu, L. and Mishchenko, M. I.: Effects of aggregation on scattering and radiative properties of soot aerosols, J. Geophys. Res.-Atmos., 110, D11211, https://doi.org/10.1029/2004JD005649, 2005. a, b, c, d
Liu, S., Aiken, A. C., Gorkowski, K., Dubey, M. K., Cappa, C. D., Williams, L. R., Herndon, S. C., Massoli, P., Fortner, E. C., Chhabra, P. S., Brooks, W. A., Onasch, T. B., Jayne, J. T., Worsnop, D. R., China, S., Sharma, N., Mazzoleni, C., Xu, L., Ng, N. L., Liu, D., Allan, J. D., Lee, J. D., Fleming, Z. L., Mohr, C., Zotter, P., Szidat, S., and Prevot, A. S. H.: Enhanced light absorption by mixed source black and brown carbon particles in UK winter, Nat. Commun., 6, 8435, https://doi.org/10.1038/ncomms9435., 2015b. a, b
Liu, X., Easter, R. C., Ghan, S. J., Zaveri, R., Rasch, P., Shi, X., Lamarque, J.-F., Gettelman, A., Morrison, H., Vitt, F., Conley, A., Park, S., Neale, R., Hannay, C., Ekman, A. M. L., Hess, P., Mahowald, N., Collins, W., Iacono, M. J., Bretherton, C. S., Flanner, M. G., and Mitchell, D.: Toward a minimal representation of aerosols in climate models: description and evaluation in the Community Atmosphere Model CAM5, Geosci. Model Dev., 5, 709–739, https://doi.org/10.5194/gmd-5-709-2012, 2012. a
Luo, J., Zhang, Y., Wang, F., Wang, J., and Zhang, Q.: Applying machine learning to estimate the optical properties of black carbon fractal aggregates, J. Opt. Soc. Am., 215, 1–8, https://doi.org/10.1016/j.jqsrt.2018.05.002, 2018a. a
Luo, J., Zhang, Y., Zhang, Q., Wang, F., Liu, J., and Wang, J.: Sensitivity analysis of morphology on radiative properties of soot aerosols, Opt. Express, 26, A420–A432, https://doi.org/10.1364/OE.26.00A420, 2018b. a, b
Luo, J., Zhang, Y. M., and Zhang, Q. X.: A model study of aggregates composed of spherical soot monomers with an acentric carbon shell, J. Quant. Spectrosc. Ra., 205, 184–195, 2018c. a
Ma, X., Yu, F., and Luo, G.: Aerosol direct radiative forcing based on GEOS-Chem-APM and uncertainties, Atmos. Chem. Phys., 12, 5563–5581, https://doi.org/10.5194/acp-12-5563-2012, 2012. a
Mackowski, D. W.: MSTM Version 3.0: April 2013, available at: http://www.eng.auburn.edu/~dmckwski/scatcodes/ (last access: 10 October 2017), 2013. a
Mackowski, D. W. and Mishchenko, M. I.: A multiple sphere T-matrix Fortran code for use on parallel computer clusters, J. Quant. Spectrosc. Ra., 112, 2182–2192, 2011. a
Medalia, A. I. and Richards, L. W.: Tinting Strength of Carbon-Black, J. Colloid. Interf. Sci., 40, 233–252, https://doi.org/10.1016/0021-9797(72)90013-6, 1972. a
Mie, G.: Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen, Ann. Phys., 330, 377–445, https://doi.org/10.1002/andp.19083300302, 1908. a
Mishchenko, M. I. and Yurkin, M. A.: On the concept of random orientation in far-field electromagnetic scattering by nonspherical particles, Opt. Lett., 42, 494–497, 2017. a
Mishchenko, M. I., Travis, L. D., and Lacis, A. A.: Scattering, absorption, and emission of light by small particles, Cambridge university press, Cambridge, UK, 2002. a
Mishchenko, M. I., Liu, L., Travis, L. D., and Lacis, A. A.: Scattering and radiative properties of semi-external versus external mixtures of different aerosol types, J. Opt. Soc. Am., 88, 139–147, 2004. a
Mishchenko, M. I., Liu, L., Cairns, B., and Mackowski, D. W.: Optics of water cloud droplets mixed with black-carbon aerosols, Opt. Lett., 39, 2607–2610, 2014. a
Moffet, R. C. and Prather, K. A.: In-situ measurements of the mixing state and optical properties of soot with implications for radiative forcing estimates, P. Natl. Acad. Sci. USA, 106, 11872–11877, 2009. a
Moosmuller, H., Chakrabarty, R. K., and Arnott, W. P.: Aerosol light absorption and its measurement: A review, J. Quant. Spectrosc. Ra., 110, 844–878, 2009. a, b
Nakao, S., Tang, P., Tang, X. C., Clark, C. H., Qi, L., Seo, E., Asa-Awuku, A., and Cocker, D.: Density and elemental ratios of secondary organic aerosol: Application of a density prediction method, Atmos. Environ., 68, 273–277, 2013. a
Naoe, H., Hasegawa, S., Heintzenberg, J., Okada, K., Uchiyama, A., Zaizen, Y., Kobayashi, E., and Yamazaki, A.: State of mixture of atmospheric submicrometer black carbon particles and its effect on particulate light absorption, Atmos. Environ., 43, 1296–1301, 2009. a
Schnaiter, M., Linke, C., Mohler, O., Naumann, K. H., Saathoff, H., Wagner, R., Schurath, U., and Wehner, B.: Absorption amplification of black carbon internally mixed with secondary organic aerosol, J. Geophys. Res.-Atmos., 110, D19204, https://doi.org/10.1029/2005JD006046, 2005. a
Schwarz, J. P., Spackman, J. R., Fahey, D. W., Gao, R. S., Lohmann, U., Stier, P., Watts, L. A., Thomson, D. S., Lack, D. A., Pfister, L., Mahoney, M. J., Baumgardner, D., Wilson, J. C., and Reeves, J. M.: Coatings and their enhancement of black carbon light absorption in the tropical atmosphere, J. Geophys. Res.-Atmos., 113, D03203, https://doi.org/10.1029/2007JD009042, 2008. a
Shamjad, P. M., Satish, R. V., Thamban, N. M., Rastogi, N., and Tripathi, S. N.: Absorbing Refractive Index and Direct Radiative Forcing of Atmospheric Brown Carbon over Gangetic Plain, Acs Earth and Space Chemistry, 2, 31–37, 2018. a
Sorensen, C. M.: Light scattering by fractal aggregates: A review, Aerosol Sci. Tech., 35, 648–687, 2001. a
Sorensen, C. M. and Roberts, G. C.: The prefactor of fractal aggregates, J. Colloid. Interf. Sci., 186, 447–452, 1997. a
Strawa, A. W., Drdla, K., Ferry, G. V., Verma, S., Pueschel, R. F., Yasuda, M., Salawitch, R. J., Gao, R. S., Howard, S. D., Bui, P. T., Loewenstein, M., Elkins, J. W., Perkins, K. K., and Cohen, R.: Carbonaceous aerosol (Soot) measured in the lower stratosphere during POLARIS and its role in stratospheric photochemistry, J. Geophys. Res.-Atmos., 104, 26753–26766, 1999. a
Taflove, A. and Hagness, S. C.: Computational electrodynamics: the finite-difference time-domain method, Artech house, Norwood, MA, 2005. a
Thouy, R. and Jullien, R.: A Cluster-Cluster Aggregation Model with Tunable Fractal Dimension, J. Phys. A-Math. Gen., 27, 2953–2963, 1994. a
Wang, Q. Y., Huang, R.-J., Cao, J. J., Tie, X. X., Ni, H. Y., Zhou, Y. Q., Han, Y. M., Hu, T. F., Zhu, C. S., Feng, T., Li, N., and Li, J. D.: Black carbon aerosol in winter northeastern Qinghai-Tibetan Plateau, China: the source, mixing state and optical property, Atmos. Chem. Phys., 15, 13059–13069, https://doi.org/10.5194/acp-15-13059-2015, 2015. a
Wang, Y. Y., Liu, F. S., He, C. L., Bi, L., Cheng, T. H., Wang, Z. L., Zhang, H., Zhang, X. Y., Shi, Z. B., and Li, W. J.: Fractal Dimensions and Mixing Structures of Soot Particles during Atmospheric Processing, Environ. Sci. Tech. Lett., 4, 487–493, 2017. a, b
Wentzel, M., Gorzawski, H., Naumann, K. H., Saathoff, H., and Weinbruch, S.: Transmission electron microscopical and aerosol dynamical characterization of soot aerosols, J. Aerosol Sci., 34, 1347–1370, 2003. a
Woźniak, M.: Characterization of nanoparticle aggregates with light scattering techniques, Thesis, Aix-Marseille Université, Provence, France, available at: https://tel.archives-ouvertes.fr/tel-00747711 (last access: 19 November 2018), 2012. a
Wu, Y., Cheng, T. H., Gu, X. F., Zheng, L. J., Chen, H., and Xu, H.: The single scattering properties of soot aggregates with concentric core-shell spherical monomers, J. Opt. Soc. Am., 135, 9–19, 2014. a
Xu, X., Zhao, W., Zhang, Q., Wang, S., Fang, B., Chen, W., Venables, D. S., Wang, X., Pu, W., Wang, X., Gao, X., and Zhang, W.: Optical properties of atmospheric fine particles near Beijing during the HOPE-J3A campaign, Atmos. Chem. Phys., 16, 6421–6439, https://doi.org/10.5194/acp-16-6421-2016, 2016. a
Xu, Y. L.: Calculation of the addition coefficients in electromagnetic multisphere-scattering theory (vol. 127, p. 285, 1996), J. Comput. Phys., 134, 200–200, 1997. a
Xu, Y. L. and Gustafson, B. A. S.: A generalized multiparticle Mie-solution: further experimental verification, J. Quant. Spectrosc. Ra., 70, 395–419, 2001. a
Yang, P., Wei, H. L., Kattawar, G. W., Hu, Y. X., Winker, D. M., Hostetler, C. A., and Baum, B. A.: Sensitivity of the backscattering Mueller matrix to particle shape and thermodynamic phase, Appl. Optics, 42, 4389–4395, 2003. a
Yee, K.: Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media, IEEE T. Antenn. Propag., 14, 302–307, 1966. a
You, R., Radney, J. G., Zachariah, M. R., and Zangmeister, C. D.: Measured Wavelength-Dependent Absorption Enhancement of Internally Mixed Black Carbon with Absorbing and Nonabsorbing Materials, Environ. Sci. Technol., 50, 7982–7990, 2016. a, b, c, d
Yurkin, M. A. and Hoekstra, A. G.: The discrete dipole approximation: An overview and recent developments, J. Quant. Spectrosc. Ra., 106, 558–589, 2007. a
Zhang, R. Y., Khalizov, A. F., Pagels, J., Zhang, D., Xue, H. X., and McMurry, P. H.: Variability in morphology, hygroscopicity, and optical properties of soot aerosols during atmospheric processing, P. Natl. Acad. Sci. USA, 105, 10291–10296, 2008a. a
Zhang, R. Y., Khalizov, A. F., Pagels, J., Zhang, D., Xue, H. X., and McMurry, P. H.: Variability in morphology, hygroscopicity, and optical properties of soot aerosols during atmospheric processing, P. Natl. Acad. Sci. USA, 105, 10291–10296, 2008b. a
Zhang, X. L., Mao, M., Yin, Y., and Wang, B.: Absorption enhancement of aged black carbon aerosols affected by their microphysics: A numerical investigation, J. Opt. Soc. Am., 202, 90–97, 2017. a, b, c, d, e, f, g, h
Zhang, X. L., Mao, M., Yin, Y., and Wang, B.: Numerical Investigation on Absorption Enhancement of Black Carbon Aerosols Partially Coated With Nonabsorbing Organics, J. Geophys. Res.-Atmos., 123, 1297–1308, 2018. a, b
Zhang, Y., Zhang, Q., Cheng, Y., Su, H., Kecorius, S., Wang, Z., Wu, Z., Hu, M., Zhu, T., Wiedensohler, A., and He, K.: Measuring the morphology and density of internally mixed black carbon with SP2 and VTDMA: new insight into the absorption enhancement of black carbon in the atmosphere, Atmos. Meas. Tech., 9, 1833–1843, https://doi.org/10.5194/amt-9-1833-2016, 2016. a