the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Global streamflow and flood response to stratospheric aerosol geoengineering
Liren Wei
Duoying Ji
Chiyuan Miao
Helene Muri
John C. Moore
Flood risk is projected to increase under future warming climates due to an enhanced hydrological cycle. Solar geoengineering is known to reduce precipitation and slow down the hydrological cycle and may therefore be expected to offset increased flood risk. We examine this hypothesis using streamflow and river discharge responses to Representative Concentration Pathway 4.5 (RCP4.5) and the Geoengineering Model Intercomparison Project (GeoMIP) G4 scenarios. Compared with RCP4.5, streamflow on the western sides of Eurasia and North America is increased under G4, while the eastern sides see a decrease. In the Southern Hemisphere, the northern parts of landmasses have lower streamflow under G4, and streamflow of southern parts increases relative to RCP4.5. We furthermore calculate changes in 30-, 50-, and 100-year flood return periods relative to the historical (1960–1999) period under the RCP4.5 and G4 scenarios. Similar spatial patterns are produced for each return period, although those under G4 are closer to historical values than under RCP4.5. Hence, in general, solar geoengineering does appear to reduce flood risk in most regions, but the overall effects are largely determined by this large-scale geographic pattern. Although G4 stratospheric aerosol geoengineering ameliorates the Amazon drying under RCP4.5, with a weak increase in soil moisture, the decreased runoff and streamflow leads to an increased flood return period under G4 compared with RCP4.5.
- Article
(6735 KB) -
Supplement
(54244 KB) - BibTeX
- EndNote
Floods cause considerable damage every year (UNISDR, 2013), which increases with economic development and rate of climate change (Ward et al., 2017). Generally, people and assets exposed to extreme hydrology disasters, including flooding, increase under global warming (Alfieri et al., 2017; Arnell and Gosling, 2013; Tanoue et al., 2016; Ward et al., 2013). Previous studies have shown that flood risk covaries with runoff and streamflow (Arnell and Gosling, 2013; Hirabayashi et al., 2013, 2008). Hirabayashi et al. (2013) analyzed CMIP5 (Coupled Model Intercomparison Project Phase 5) projections for the RCP4.5 and RCP8.5 scenarios (Meinshausen et al., 2011) and found shortened return periods for floods, especially in Southeast Asia, India, and eastern Africa, especially under the RCP8.5 scenario.
Streamflow is a continuous variable and for convenience three quantities are commonly used to measure its distribution: Q5, the level of streamflow exceeding 5 % in a year; Q95, the level of streamflow exceeding 95 % in a year; and Qm, the annual mean flow. Koirala et al. (2014) analyzed the changes in streamflow conditions under the different RCP scenarios. Under RCP8.5 Q5 increases at high latitudes and in Asia and central Africa, while Qm and Q95 decrease in Europe and western parts of North and Central America. The spatial pattern under RCP4.5 is similar, and changes of Qm and Q5 streamflow are somewhat smaller than those under RCP8.5, while Q95 is about the same under both scenarios.
Other hydrologic indicators show similar results under future climate projections. For example, Arnell and Gosling (2013) used a global daily water balance hydrologic model (Mac-PDM.09; Gosling et al., 2010), forced by 21 climate models from the CMIP3 ensemble, and analyzed 10-year and 100-year return periods of maximum daily flood under various scenarios. They found that the uncertainty in projecting river streamflow is dominated by across-model differences rather than the climate scenario. Dankers et al. (2014) used a 30-year return period of 5-day average peak flows to study the changing patterns of flood hazard under the RCP8.5 scenario. They used nine global hydrology models together with five coupled climate models from CMIP5 and showed that simulated increases in flood risk occur in Siberia, Southeast Asia, and India, while decreases occur in northern and eastern Europe and northwestern North America.
River-routing models such as CaMa-Flood (Yamazaki et al., 2011) are important tools for simulating flood hazard. These models have been combined with high-resolution digital elevation models, flow direction maps (e.g., HYDRO1k and HydroSHEDS; Lehner et al., 2008), and hydrological models. Global-scale river models (GRMs) are typically structured to use the gridded runoff outputs from Earth system models (ESMs), land surface models (LSMs), or global hydrological models (GHMs) to simulate the lateral movement of water (Trigg et al., 2016). High-resolution offline river-routing models, such as CaMa-Flood, have contributed to improved simulation of river discharge (Yamazaki et al., 2009, 2013; Mateo et al., 2017). Zhao et al. (2017) used daily runoff from GHMs driving CaMa-Flood to produce monthly and daily river discharge and found that this approach results in better agreement between simulated and observed discharge compared with using native hydrological model routing. The CaMa-Flood model accounts for floodplain storage and backwater effects that are not represented in most GHM native routing methods, and these effects play a critical role in simulating peak river discharge (Yamazaki et al., 2014; Zhao et al., 2017; Mateo et al., 2017). Vano et al. (2014) analyzed several sources of uncertainty in future flood projections and suggested inter-model variability in forcing from ESMs is the major source of uncertainty in modeling the river discharge, although the model's ability to handle complex channels (e.g., deltas and floodplains) also has an important impact on simulation realism.
Solar radiation management (SRM) is geoengineering designed to reduce the amount of sunlight incident on the surface and so cool the climate. Stratospheric aerosol injection is one SRM method inspired by volcanic eruptions and utilizes the aerosol direct effect to scatter incoming solar radiation. Under the Geoengineering Model Intercomparison Project (GeoMIP; Robock et al., 2011; Kravitz et al., 2011, 2012, 2013a), the G4 experiment specifies a constant injection of 5 Tg sulfur dioxide (SO2) per year to the tropical lower stratosphere, or the equivalent aerosol burden, for the period of 2020–2069. This mimics about one-fourth of the stratospheric load injected by the 1991 eruption of Mount Pinatubo. Greenhouse gas forcing is specified by the RCP4.5 scenario. Nine ESMs have carried out the GeoMIP G4 experiment, with sulfate aerosols handled differently by each model. For example, BNU-ESM and MIROC-ESM use the prescribed meridional distribution of aerosol optical depth (AOD) recommended by the GeoMIP protocol; CanESM2 specifies a uniform sulfate AOD (Kashimura et al., 2017); GISS-E2-R and HadGEM2-ES adopt stratospheric aerosol schemes to simulate the AOD; NorESM1-M specifies the AOD and effective radius, calculated in previous simulations with the aerosol microphysical model ECHAM5-HAM (Niemeier et al., 2011; Niemeier and Timmreck, 2015). Indirect, potentially undesirable side effects of the injected sulfur aerosol include changing ice particle distributions in the upper troposphere and the distribution of ozone and water vapor in the stratosphere (Visioni et al., 2017). The direct radiative effects mainly result in the sharp reduction of the top-of-the-atmosphere (TOA) net radiative flux with a significant drop in global surface temperature and a concomitant decrease in global precipitation (Yu et al., 2015). The decline of precipitation under SRM is mainly due to increasing atmospheric static stability, together with a reduction of latent heat flux from the land surface to the atmosphere (Bala et al., 2008; Kravitz et al., 2013b; Tilmes et al., 2013). Both the reduction of latent heat flux and precipitation result in a slowdown of the global hydrological cycle (Niemeier et al., 2013; Kalidindi et al., 2014; Ferraro and Griffiths, 2016).
The spatial pattern of runoff roughly follows that of precipitation. Global spatially continuous and temporally variable observations of runoff are not available (Ukkola et al., 2018). Climate-model-simulated runoff is usually compared with observed downstream river discharge datasets, with the dataset collected by Dai (2016) and Dai et al. (2009) being the most complete. The Dai (2016) dataset represents historical monthly streamflow at the farthest downstream stations for the world's 925 largest ocean-reaching rivers from 1900 to early 2014, lacking global daily observations. As daily runoff is largely driven by daily precipitation, it is difficult to evaluate how good the runoff outputs from the climate models are at a daily scale. Over longer timescales, Alkama et al. (2013) found the CMIP5 models simulate mean runoff reasonably well (±25 % of observed) at the global scale. The CMIP5 models tend to slightly underestimate global runoff, with South American runoff being underestimated by all models. Koirala et al. (2014) found more CMIP5 model agreement on streamflow projections under RCP8.5 than under the RCP4.5 scenario, but the projected changes in low flow are robust in both scenarios with strong model agreement. Previous studies have shown that under RCP4.5, precipitation would decrease over southern Africa, the Amazon Basin, and Central America, and runoff follows these patterns. Over dry continental interiors, relatively large evaporation means that runoff does not follow precipitation (Dai, 2016). SRM affects both precipitation and evaporation and hence global patterns of runoff and streamflow. The risk of drought in dry regions under SRM appears to be reduced (Curry et al., 2014; Keith and Irvine, 2016; Ji et al., 2018). While many studies have looked at the impact of solar geoengineering on the hydrologic cycle, none have specifically considered the potential changes of river flow and flood frequency.
We investigate the potential change of streamflow using annual mean and extreme daily discharge and changes in the pattern of flooding using flood return period. Our study is organized as follows: Sect. 2 describes the models and methods used in this study; Sect. 3 presents the results of projected precipitation, evaporation, runoff, streamflow, and return period under the G4 and RCP4.5 simulations. Section 4 provides a discussion of mechanisms for the differences between G4 and RCP4.5 and uncertainties in the study. Finally, Sect. 5 summarizes the findings and mentions some social and economic implications from this study.
2.1 GeoMIP experiments
To analyze the potential changes of flood under stratospheric sulfate injection geoengineering, we compare the streamflow patterns under the RCP4.5 and G4 scenarios. Five ESMs were used here due to data availability (Table 1). We exclude the first decade of the G4 simulation from our analysis because it follows the abrupt increase in stratospheric aerosol forcing, which likely exerts a large perturbation to some parts of the climate system, and analyze the precipitation, evaporation, runoff, and streamflow pattern changes between each of model's G4 and RCP4.5 simulations during the period of 2030–2069. Using the last 40 years of G4 simulations is common to several previous studies (e.g., Curry et al., 2014; Ji et al., 2018). The historical simulation covering the period of 1960–1999 is used as the reference for the return period analysis. Equal weight is given to each model in the analysis, and streamflow and flood response are calculated for each model before multi-model ensemble averaging is carried out. For models with multiple realizations, streamflow and flood response are calculated for individual realization and then averaged for each model.
2.2 The river-routing model
The river-routing model used here is the Catchment-based Macro-scale Floodplain Model (CaMa-Flood; Yamazaki et al., 2011). CaMa-Flood uses a local inertial flow equation (Bates et al., 2010; Yamazaki et al., 2014) to integrate runoff along a high-resolution river map (HydroSHEDS; Yamazaki et al., 2013). Sub-grid characteristics such as slope, river length, river channel width, and river channel depth are parameterized in each grid box by using the innovative up-scaling method: Flexible Location of Waterways (FLOW) (Mateo et al., 2017; Yamazaki et al., 2014; Zhao et al., 2017). In addition, CaMa-Flood implements channel bifurcation and accounts for floodplain storage and backwater effects, which are not represented in most GHMs (Zhao et al., 2017). CaMa-Flood is able to reproduce relatively realistic flow patterns in complex river regions, such as deltas (Ikeuchi et al., 2015; Yamazaki et al., 2011, 2013). CaMa-Flood has been extensively validated and applied to many regional- and global-scale hydrological studies (e.g., Pappenberger et al., 2012; Hirabayashi et al., 2013; Mateo et al., 2014; Ikeuchi et al., 2015, 2017; Trigg et al., 2016; Zsótér et al., 2016; Emerton et al., 2017; Suzuki et al., 2018; Yamazaki et al., 2017).
We use only the daily runoff outputs from climate models to drive CaMa-Flood v3.6.2, which calculates the river discharge along the global river network. The spatial resolution of CaMa-Flood is set to 0.25∘ (∼25 km at midlatitudes). An adaptive time step scheme was applied in the model numerical integration, leading to a time step of about 10 min, while the model outputs are at daily temporal resolution. To conserve the input runoff mass, an area-weighted averaging method is used in CaMa-Flood to distribute the coarse input to the fine-resolution routing model (Mateo et al., 2017). CaMa-Flood performs a 1-year spin-up before simulating 40-year river discharge in our historical, RCP4.5, and G4 experiments. The runoff and river discharge from Antarctica and Greenland are not included in the simulations. For each streamflow level, grid cells with less than 0.01 mm day−1 are excluded from the analysis.
2.3 Indicators of streamflow
We analyze the streamflow change under the RCP4.5 and G4 scenarios using three streamflow indicators for the 2030–2069 period, that is, annual mean flow (Qm) and extreme high (Q5) or low flow (Q95). Qm, Q5, and Q95 are averaged over 40 years for each model, then averaged among models to obtain the multi-model mean response under the different scenarios. We compared the multi-model mean and multi-model median responses of the five models used in this study and found no obvious difference between the two averages.
We employ the two-sample Mann–Whitney U (MW-U) test to measure the significance of streamflow differences between G4 and RCP4.5. The MW-U test is a nonparametric test, which does not need the assumption of normal probability distributions. We use a bootstrap resampling method (Ward et al., 2016) with the MW-U test to increase sample size and to minimize the effects of outliers that can arise from the relatively short study period (Koirala et al., 2014). Specifically, we first apply the MW-U test to the G4 and RCP4.5 annual mean daily streamflow data for each model to obtain the value of the rank sum statistical value, U0. Then we generate 1000 random paired series of 40-year streamflow data from RCP4.5 and G4 simulations using the bootstrap resampling method and apply the MW-U test to each sample pair of generated streamflow data to obtain a series of statistical values: Uj, j = 1, 2...1000. The rank of U0 is then used to calculate the non-exceedance probability (Cunnane, 1978):
Here p0 is the non-exceedance probability and R0 is the rank of U0, and Nb is the number of the bootstrap samples. Finally, a non-exceedance probability less than 0.025 (or greater than 0.975) indicates a significant increase (or decrease) from RCP4.5 to G4.
2.4 Changes in flood frequency
The return period of a flood event is as an indicator of flood frequency (e.g., Dankers et al., 2014; Ward et al., 2017). The N-year return period indicates the probability of flood exceeding a given level in any given year of 1∕N. For each model, we choose the historical period of 1960–1999 as a reference for the return period calculation based on the annual maximum daily river discharge. We then analyze the return period change under RCP4.5 and G4 scenarios during the period of 2030–2069. In this study, we choose the 30-, 50-, and 100-year return period levels of river flow at each grid cell to study the change of flood probability. To estimate the return period, the time series of annual maximum daily discharge for the historical, RCP4.5, and G4 scenarios from each ESM are first arranged in ascending order and then fitted to a Gumbel probability distribution. The Gumbel distribution was used as a statistic of extreme flood events in previous studies (e.g., Hirabayashi et al., 2013; Ward et al., 2014). Using the Gumbel distribution, the cumulative distribution function, F(x), of river discharge (x) can be expressed as
where the two parameters a (scale) and b (location) are the parameters of Gumbel distribution (Gumbel, 1941). The parameters are estimated using an L-moments-based approach (Rasmussen and Gautam, 2003), where
and Xi is the annual maximum daily river discharge and is sorted in ascending order, and N is the number of sample years. Then
where c=0.57721 is Euler's constant. Changes in return period under SRM are expressed as differences G4 – RCP4.5 relative to the corresponding historical level.
3.1 Projected changes in precipitation, evaporation, and runoff
G4 stratospheric aerosol geoengineering lowers net radiation fluxes at the TOA by ∼0.36 W m−2, reduces mean global temperature by ∼0.5 K, and slows down the global hydrological cycle. Global precipitation decreases by 2.3±0.5 % per kelvin in response to G4 stratospheric aerosol injection (Ji et al., 2018). Precipitation and evaporation rates are strongly influenced by incoming radiation and the water vapor content of the troposphere. Solar geoengineering produces changes in both atmospheric circulation and thermodynamics. Several studies have analyzed changes in large-scale circulation under the G1 solar dimming experiment (e.g., Moore et al., 2014; Davis et al., 2016; Smyth et al., 2017; Guo et al., 2018), but the more subtle changes under G4 have not yet been analyzed in similar depth. Broadly speaking, increasing greenhouse gases tend to produce a stronger Hadley circulation and enhanced hydrological cycle, increasing precipitation in the tropics and lowering it in the subtropics (the wet gets wetter and dry gets drier) (Chou et al., 2013). Geoengineering, under both G1 solar dimming and G4 aerosol injection, counteracts this response, decreasing tropospheric temperatures and maintaining a higher pole–Equator meridional temperature gradient than under greenhouse gas forcing alone and tending to reverse the wet dry patterns under greenhouse gas forcing (Ji et al., 2018; Wang et al., 2018). Stratospheric aerosol injection geoengineering produces a more complex climate response than produced by simple solar dimming (e.g., G1), as the aerosol layer not only scatters shortwave radiation but also absorbs near-infrared and longer-wavelength radiation (Lohmann and Feichter, 2005; Niemeier et al., 2013; Ferraro et al., 2014). The net result of these changes in the GeoMIP experiments is model dependent (Wang et al., 2018; Ji et al., 2018).
Under G4, the global annual precipitation over land (excluding Greenland and Antarctic) decreases 9.3 mm relative to the reference RCP4.5 scenario. The tropical Africa and south Asia regions suffer large precipitation reduction, with values up to 37.1 and 52.3 mm per year (Fig. 1a); southeastern North America and Alaska also see large precipitation decreases. In contrast, precipitation increases significantly over southern Africa and eastern Brazil under G4. Previous studies based on Global Land–Atmosphere Climate Experiment–Coupled Model Intercomparison Project Phase 5 (GLACE-CMIP5) suggest strong coupling between local soil moisture and precipitation over southern Africa and eastern Brazil, both of which are simulated to experience large precipitation reduction under global warming (Seneviratne et al., 2013), which is reversed under G4. Although the precipitation increase under G4 over the Mediterranean region is not statistically significant, May et al. (2017) note soil moisture and precipitation both decrease under global warming. Lower temperatures under G4 result in a reduction of 6.9 mm in mean global land (excluding Greenland and Antarctic) evaporation relative to RCP4.5.
Under G4, there is large precipitation reduction over the Indian subcontinent and East Asia monsoon regions of 5.4 % and 5.0 %, respectively. Under G1, these reductions have been related to a reduced latitudinal seasonal amplitude of the Intertropical Convergence Zone (ITCZ) (Schmidt et al., 2012; Smyth et al., 2017) and a reduction in the intensity of the Hadley circulation (Guo et al., 2018). Precipitation over other monsoon regions in G4 sees less significant changes. Displacement of midlatitude westerlies and changes to the North Atlantic Oscillation, especially during winter, will change regional precipitation variations under G4. Ferraro et al. (2015) and Muri et al. (2018) found that tropical lower-stratospheric sulfate aerosol injection leads to a thermal wind response that affects the stratospheric polar vortices. The polar vortices guide winter midlatitude jets and cyclone paths across the midlatitudes. Under a warming climate, an earlier spring snowmelt over northeastern Europe and a later onset of the winter storm season would both alter flooding conditions (Blöschl et al., 2017). Both these will also be affected by G4 stratospheric aerosol geoengineering.
Increased evaporation forecast under RCP4.5 is suppressed under G4 geoengineering due to reduced downward surface radiation (Kravitz et al., 2013a; Yu et al., 2015). Evaporation decreases over a significantly (p<0.05) broader area than precipitation, especially in the Northern Hemisphere (Fig. 1b). The change of precipitation minus evaporation (P−E) basically follows the change of precipitation and evaporation, but is of a smaller magnitude (Fig. 1c), due to their simultaneous reductions. There are significant reductions in P−E over south Asia, tropical eastern Africa, and the Amazon Basin and significant increases over southern Africa and eastern Brazil. Increased P−E in northern Asia caused by global warming could be partly counteracted by solar geoengineering (Jones et al., 2018; Sonntag et al., 2018). The simulated precipitation and evaporation changes under G4 imply potentially significant changes in the terrestrial hydrological cycle. P−E can be used as a simplified measure of runoff and water availability. Under the G4 experiment, P−E increases over Europe during summertime, implying more water availability and a shortened return period of river discharge. Soil moisture also reflects local water mass balance, i.e., the difference between P−E and runoff. Soil moisture increases over southern Africa, southwestern North America, and several parts of South America, where P−E and runoff both increase. The regions with significant reductions in both P−E and runoff, such as tropical Africa, South Asia, and most of middle North America, also show decreases in soil moisture.
The spatial pattern of runoff change from RCP4.5 to G4 resembles that of P−E, with a broader area of significant changes (Fig. 1c, d). The annual runoff decreases by 2.4 mm, similar to the change in P−E. There are large runoff decreases over tropical Africa, South Asia, southeastern North America, the Amazon Basin, and Alaska. Runoff slightly increases over southern Africa, southwestern North America, and several regions of South America. Variability in runoff and streamflow is greater than for precipitation and evaporation (Figs. 1, 2) due to spatial heterogeneity in soil moisture and because streamflow spatially integrates runoff (Chiew and McMahon, 2002).
Precipitation, evaporation, and runoff changes show that land areas dry slightly, especially around the Equator, south Asia, and at northern high latitudes under G4. Increases in P−E are predicted in the western parts of Europe and North America, with their eastern sides becoming drier with decreasing P−E and runoff.
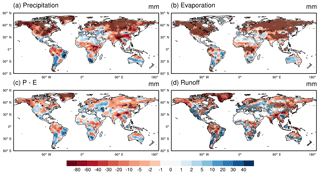
Figure 1Changes of annual precipitation (a), evaporation (b), precipitation minus evaporation (P−E, c), and runoff (d) between G4 and RCP4.5 during the period of 2030–2069. Hashed areas indicate locations where the changes are significant at the 95 % level using the two-sample MW-U test. For runoff (d), grid cells with less than 0.01 mm day−1 are masked out.
3.2 Projected changes in streamflow
Figure 2 shows the relative changes of three characteristic indicators of streamflow, while Fig. 3 presents the degree of across-model agreement. Figures S1–S5 in the Supplement show the results for each of the models listed in Table 1. Figures S6–S7 show the relative changes of three streamflow indicators under G4 and RCP4.5 relative to the historical period. In general, the streamflow indicators under G4 are less changed from the historical levels than under RCP4.5. In Fig. 2, positive values mean G4 streamflow is larger than RCP4.5 levels. Generally, decreases in Qm occur at high northern latitudes such as Siberia, northern Europe, and the Arctic Ocean coast of North America, along with Southeast Asia and middle and southern Africa. Qm increases in western Europe, central Asia, southwestern North America, and Central America (Fig. 2a). Significant changes are generally distributed around the globe. Based on the ensemble response of the five models analyzed here, 55 % of global continental area excluding Greenland, Antarctica, and masked cells shows decreases in Qm under G4 compared with RCP4.5, and about 45 % of global continental area shows increases. Figure 3 shows areas with robust agreement among models and allows the primary regions affected to be seen more clearly. Globally, only 21 % of global continental area exhibits robust decreases and 12 % increases in Qm under G4 (Fig. 3a). Despite the few grid cells with robust agreement among models, the general patterns are similar for the mean changes in Fig. 2a. Consistent decreases occur at high northern latitudes and in Papua New Guinea and the semiarid Sahel. Increases are mainly in the Southern Hemisphere but also parts of western Europe and the southwestern US. MIROC-ESM (Fig. S3) and NorESM1-M (Fig. S5) contradict the ensemble in having larger areas with increases in Qm under G4 than RCP4.5.
Figures 2b and 3b show that under G4, 52 % of unmasked land area is projected to increase its high flow Q5 levels under G4. Europe, western North America, central Asia, and central Australia show increases in Q5 under G4 compared with RCP4.5. Differences at the 95 % significance level are distributed fairly similarly to Qm in Fig. 2a. The Amazon Basin shows decreases in both Q5 and Qm and the southwestern US shows increases in both. Globally, 17 % of unmasked land area shows robust increases and 17 % shows decreases in Q5 under G4 (Fig. 3b). Robust increases are generally confined to the extratropics, while decreases are mainly, but not only, in the tropics. The projections of Q5 from CanESM2 under G4 show the largest differences in spatial pattern from the ensemble mean (Fig. S2) and it is the only model with more decreases than increases in Q5 under G4. Though high flow levels usually correspond with flood events (Ward et al., 2016), changes in flow levels do not necessarily translate into increases in flood frequency. We elaborate further on flood return period in Sect. 3.3.
Low flow (Q95, in Figs. 2c and 3c) has a noisier spatial pattern than for mean and high flow. Low flow shows a relatively uniform decrease around the globe. A total of 49 % of global unmasked land area shows increases in Q95 under G4. Despite the generally noisier pattern, the regions with differences significant at the 95 % level are more defined for Q95 than either Qm or Q5. The high northern latitudes become drier under G4, the southern high latitudes wetter. Robust increases cover about 11 % of global unmasked land area, mainly in Europe and South America. Robust decreases appear mainly in northern high-latitude regions, central Africa, and northern Asia and occupy about 20 % of global unmasked land area. Projections by NorESM1-M (Fig. S5) show different patterns from the ensemble mean (Fig. 2c), with bigger areas showing more increases than decreases in Q95 under G4.
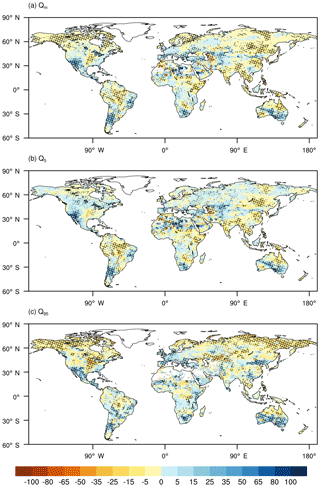
Figure 2Relative difference of three streamflow indicators between G4 and RCP4.5 during the period of 2030–2069, as percentages of RCP4.5: (G4-RCP4.5)/RCP4.5 × 100 %. (a) Annual mean flow (Qm); (b) annual high flow (Q5); (c) annual low flow (Q95). For each streamflow level, grid cells with less than 0.01 mm day−1 are masked out. Hashed areas indicate locations where the streamflow changes are significant at the 95 % level using the two-sample MW-U test.
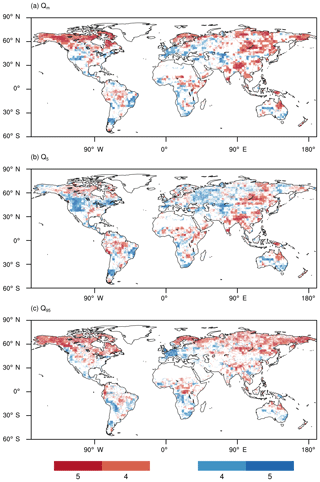
Figure 3Number of models agreeing on sign of change (red means G4-RCP4.5 < 0, blue means G4-RCP4.5 > 0) of streamflow indicator. (a) Annual mean flow (Qm); (b) annual high flow (Q5); (c) annual low flow (Q95). Shaded grid cells indicate a relatively robust response (at least four models show the same direction of change). For each streamflow level, grid cells with less than 0.01 mm day−1 are masked out.
Some of the regions show contrasting responses under G4 for high and low streamflow. Figure 4 shows regions where both high and low flow decrease under G4 cover about 30 % of global unmasked land area (regions in red), mainly in eastern and southeastern Asia, central Africa, and the Amazon Basin, together with central and eastern Siberia. In 20 % of global unmasked land area, high flows are projected to increase while low flows decrease (regions in yellow), mainly in the remaining parts of South Asia, central Africa, and South America. Increased high flow and simultaneous decrease in low flow suggests the potential for increased flood and drought frequencies. In 21 % of global unmasked land area, high flows decrease and low flows increase (regions in blue), which suggests these would see a decline in streamflow extremes, and are mainly at northern midlatitudes and high latitudes. Areas with both increased high and low flow also cover 29 % of the unmasked land surface (regions in green), mainly in Europe, Central America, and the Southern Hemisphere midlatitudes. Perhaps the clearest overall pattern is the streamflow generally increasing under G4 on the western sides of the large continents of Eurasia and North America, especially over Mexico, southern California, Spain, and western Europe, while streamflow decreases on the eastern sides of these continents. In the Southern Hemisphere, the pattern is meridional, with northern wetter parts of the landmasses having lower streamflow under G4, and southern drier parts increases.
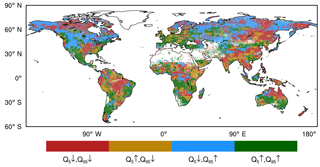
Figure 4The ensemble mean difference (G4 − RCP4.5) of high (Q5) and low (Q95) streamflow. The color bar is defined such that grid cells in which G4 is less than RCP4.5 for both Q5 and Q95 are in red (, both Q5 and Q95 greater in G4 than in RCP4.5 are in green (, Q5 greater in G4 and Q95 greater in RCP4.5 in yellow (), and vice versa in blue (). Grid cells with Q95 less than 0.01 mm day−1 are masked out.
3.3 Projected changes in return period
Changes in flooding between the RCP4.5 and G4 scenarios are measured by the changes in the return period of particular river discharge magnitude. Previous studies have used a 30-year return period as a relatively modest indicator of flood frequency (Dankers et al., 2014). We choose both the same flooding frequency indicator and also the more extreme 50- or 100-year return levels. The discharge for each model's 30-, 50-, and 100-year return periods in the simulated historical period defines the reference magnitudes at each grid cell. The return period of discharge corresponding to those levels are then found under the RCP4.5 and G4 scenarios. Dry regions, defined as mean annual streamflow during the historical period (1960–1999) less than 0.01 mm day−1, are masked out. The 40-year time series of the historical period (1960–1999) and 40-year future projections (2030–2069) are then fitted to the Gumbel probability distribution for each grid cell.
Figure 5a and b show the global distribution of the multi-model ensemble median return period of the historical 30-year return level under the RCP4.5 and G4 scenarios. Figures S8 and S9 show the relevant patterns for 50- and 100-year return periods. The elongation of return period in some regions (such as central Asia and the Amazon Basin) indicates relatively less-frequent flooding events compared with the past. Very close to half the global unmasked land area (49 %) shows increases in return period under the RCP4.5 scenario, while the other half experience decreases. Increases in return period are mainly in Asia and eastern Africa while decreases occur in Europe and North America. Our results agree with similar previous studies for RCP4.5 (e.g., Hirabayashi et al., 2013). Under G4 the spatial pattern is very similar to RCP4.5, with comparable large differences from the historical levels.
Figure 5c shows the difference of return period between the G4 and RCP4.5 scenarios. A negative value means a shorter return period under G4 than RCP4.5, which indicates an increase in flood frequency under G4. Decreasing flood frequency appears in India, China, Siberia, parts of the Amazon Basin, and northern Australia. Increasing flood frequencies are projected mainly in Europe, the southwestern US and much of Australia. The regions that are projected to experience an increased flood frequency under the RCP4.5 scenario, such as southern and southeastern Asia (Fig. 5a; Dankers et al., 2014; Hirabayashi et al., 2013), would experience a consistent decline of the flood frequency under G4. In general, the G4 return periods are less changed from the historical levels than under RCP4.5.
Figure 6 shows the regions of robust agreement among models in changes of 30-year return period under RCP4.5 and G4. Slightly fewer grid cells show robust responses under G4 than RCP4.5. As with Fig. 5, there is close agreement in spatial pattern of return period under the RCP4.5 and G4 scenarios. The spatial pattern of the changes in 50- and 100-year return levels shown in Figs. S8 and S9 is similar to that for the 30-year return level (Fig. 5), while the spread between two different return period levels is slightly different from the 30-year levels. These results suggest a consistent changing pattern of flood frequency as defined by the three return levels, but with different magnitudes of differences between RCP4.5 and G4, with G4 being closer to the historical levels.
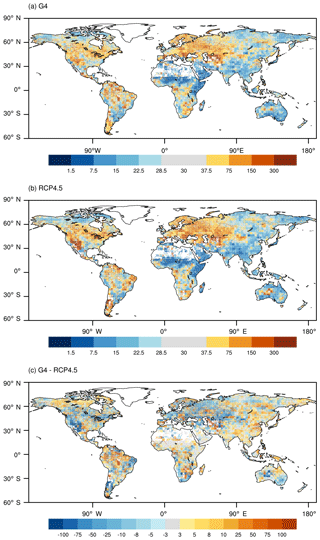
Figure 5Multi-model ensemble median of return periods for discharge that correspond to a 30-year return period level in the historical simulation (1960–1999) under (a) G4, (b) RCP4.5, and (c) the difference of G4 and RCP4.5. Grid cells in extremely dry regions in the historical simulation, i.e., Qm<0.01 mm day−1, are masked out.
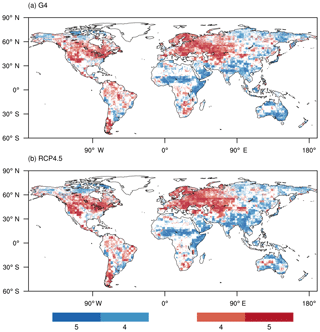
Figure 6The number of models agreeing on the sign of change in a 30-year return period under G4 (a) and RCP4.5 (b). Blue indicates decreases and red indicates increases relative to the historical simulation. Grid cells in extremely dry regions in the historical simulation, i.e., Qm<0.01 mm day−1, are masked out.
4.1 G4 changes relative to RCP4.5
G4 weakens the streamflow changes expected under RCP4.5 relative to the historical period (Koirala et al., 2014). For example, in southeastern Asia and India, both high flows and low flows are projected to increase under the RCP4.5 scenario, while both of them would increase less under G4. In contrast, southern Europe is projected to see decreases in both high and low flow under RCP4.5, while the projected streamflow shows fewer decreases under G4. However, in the Amazon Basin, both high and low streamflow decreases in both RCP4.5 and G4 relative to the historical period. In Siberia both high and low streamflow increases under RCP4.5 relative to the historical scenario, while the pattern is mixed under G4. This means that G4 offsets the impact introduced by anthropogenic climate warming in some regions, while in other regions such as the Amazon Basin and Siberia, it further enhances the decreasing trend in streamflow under the RCP4.5 scenario. The pattern seen is suggestive of the role of large-scale circulation patterns (Fig. 7), westerly flows over the Northern Hemisphere continents, and the Asian monsoon systems, with relative increases in midlatitude storm systems and decreases in monsoons under G4 compared with RCP4.5. These circulation changes result in, for example, more moist maritime air flowing into the Mediterranean region and weakened summertime monsoonal circulation under G4 in India and East Asia (Fig. 7e, f). Similar mechanisms may also account for the north–south pattern seen in Australia and South America. Monsoonal indicators do decrease under the much more extreme G1 experiment, in which solar dimming is designed to offset quadrupled CO2 levels (Tilmes et al., 2013).
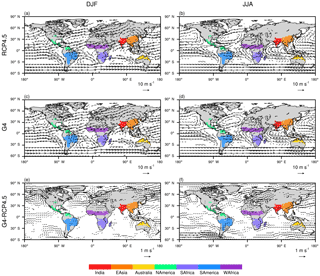
Figure 7Multi-model ensemble mean of 925 hPa wind field during December–January–February (DJF) and June–July–August (JJA). Panels (a) and (b) for RCP4.5, panels (c) and (d) for G4, and panels (e) and (f) for the difference between G4 and RCP4.5. Grid cells in which wind speed is less than 2.0 m s−1 are masked out in panels (a), (b), (c), and (d). Grids cells in which wind speed is less than 0.1 m s−1 are masked out in panels (e) and (f). Shaded monsoonal regions are derived using the criteria of Wang and Ding (2006) with the Global Precipitation Climatology Project (GPCP) dataset covering the years 1979–2010 (Adler et al., 2003).
There is a latitudinal dependence for streamflow: generally, the Qm decreases across all latitudes; high flow, Q5, decreases most in tropical regions; low flow, Q95, decreases most at high latitudes. The high latitudes display a complicated streamflow pattern with weakly increasing Q5 and significantly decreasing Q95. The decrease in the lower probability tail of streamflow is indicative of hydrological droughts, while the increases in the high streamflow tail indicate hydrological flooding (Keyantash and Dracup, 2002). Previous studies (Dankers et al., 2014; Hirabayashi et al., 2008) have noted that the flood frequency for rivers at high latitude (e.g., Alaska and Siberia) decreases under global warming, even in areas where the frequency, intensity of precipitation, or both are projected to increase. The annual hydrograph of these rivers is dominated by snowmelt, so changes of peak flow reflect the balance between length and temperature of winter season and the total amount of winter precipitation. The thawing of permafrost and changes in evapotranspiration also play an important role in the increase of runoff and streamflow (Dai, 2016). The combined effect of atmospheric circulation and land surface processes results in the complex change pattern in this cold region.
Under the G4 experiment, recent studies (Jones et al., 2018; Sonntag et al., 2018) have pointed out that the increased P−E in northern Asia caused by global warming could be partly counteracted by solar geoengineering. At the same time, solar geoengineering reduces polar temperatures and precipitation (Berdahl et al., 2014; Ji et al., 2018). The balance among precipitation, evaporation, and temperature accounts for the complex spatial pattern of streamflow and flood frequency under solar geoengineering, which has been previously related to soil moisture content (Dagon and Schrag, 2017). It is worth noting that the method for calculating potential evapotranspiration (ET) plays a significant role in determining simulated surface runoff changes (Haddeland et al., 2011; Thompson et al., 2013), which would influence the condition of streamflow. A recent study (Wartenburger et al., 2018) compared the ET spatial and temporal patterns simulated by GHMs in the second phase of the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP2a), which also confirmed that the ET scheme used affects model ensemble variance. The ET in this study is calculated by the ESMs (Table 1), not GHMs, and any biases in ET would feed into streamflow. For example, Mueller and Seneviratne (2014) found that climate models that participated in CMIP5 display an overall systematic overestimation of annual average ET over most regions, particularly in Europe, Africa, China, Australia, western North America, and part of the Amazon region.
The relatively drier streamflow pattern in the Amazon Basin under G4 is notable and consistent with changes in P−E (e.g., Jones et al., 2018). This drying pattern would increase the risk of a decline of the Amazon tropical rainforest (Boisier et al., 2015). Amazon Basin drying is complicated by various factors that are dependent on solar geoengineering. These include (i) the reduced seasonal movement of the ITCZ under solar geoengineering (Smyth et al., 2017; Guo et al., 2018); (ii) changes in sea surface temperature reflecting changes in frequency of El Niño–Southern Oscillation (Harris et al., 2008; Jiménez-Muñoz et al., 2016), although there is no evidence of such changes occurring under SRM (Gabriel and Robock, 2015); and (iii) changes to carbon cycle feedbacks (Chadwick et al., 2017; Halladay and Good, 2017), which would certainly be affected by changes in diffuse radiation under SRM (Bala et al., 2008; Muri et al., 2018).
4.2 Uncertainties
Previous studies suggest that the river-routing model CaMa-Flood can realistically reproduce peak river discharge because the floodplain storage and backwater effects are implemented (e.g., Zhao et al., 2017). In this study, the CaMa-Flood is driven by the runoff output directly from ESMs to simulate streamflow and flood response. Therefore, the uncertainty in runoff from the ESMs is also important. To drive the high-resolution CaMa-Flood model, the coarse-resolution runoff from ESMs was regridded using a first-order conservation method. Although the regridding method conserves the mass of runoff, distributing the runoff from coarse climate model grids to fine river-routing model grids introduces unavoidable errors. The relative magnitudes of this kind of error are dependent on the regional terrain and river-routing map. The uncertainty in runoff might be transformed by the river-routing model and overlap with the built-in bias of the river-routing model itself. Comparing the ratio between inter-model spread and multi-model ensemble mean, we find that runoff usually has large inter-model spread in arid regions, and streamflow has large inter-model spread over a broader area than that of runoff. This is due to the streamflow integrating the runoff spatially along the river-routing map; therefore it carries the uncertainties of runoff to a relatively large extent. Several studies have identified the uncertainty introduced by hydrological models (e.g., Chen et al., 2011; Prudhomme et al., 2014). We assume that systematic river-routing model bias relative to observations can be alleviated by subtracting historical simulations, and simulated runoff biases are not expected to change significantly under future scenarios. In addition to inherent model biases, there are natural processes that could change river routes and river network silt-up over time; these changes would impact local runoff and streamflow (Chezik et al., 2017), and we do not account for them in this study.
Gosling et al. (2017) compared the river runoff output from multiple global and catchment-scale hydrological models under three warming scenarios simulated by ESMs, finding that the across-model uncertainty overwhelmed the ensemble median differences among the scenarios. Yu et al. (2016) suggested model internal variability may be larger than across-model spread in eastern and southeastern Asia. In this study we use the offline hydrological model driven by runoff outputs from ESMs to calculate the streamflow; the uncertainty among ESMs is reflected in the range of return period based on streamflow change. Figure S10 shows the multi-model ensemble range of the 30-year return period level. Regions that have the shorter return period (i.e., higher flood frequency) from historical to future show a relatively small range among models (e.g., India and southeastern Asia). Regions that have the longer return period show a large range (e.g., Europe and North America). This reflects larger inter-model uncertainty over dry zones than over wetter ones. The return period change over dry zones is more meaningful when interpreted as the change of drought tendency. The 50- and 100-year return period level flow shows larger uncertainty than for the 30-year return period level, which is expected when estimating the low probability extreme tails of the flow probability density function from relatively short (40 year) sets of results.
We analyzed the streamflow response under stratospheric aerosol injection geoengineering, G4, and the RCP4.5 scenario using the daily total runoff from five climate models that participated in GeoMIP. We investigated the mean change patterns of annual mean and extreme high and low streamflow and analyzed the global flood frequency change in terms of return period. There is a pattern of generally increasing streamflow under G4 on the western sides of the major continents of Eurasia and North America, with decreasing streamflow on their eastern sides. In the Southern Hemisphere, the pattern is meridional, with northern parts of the landmasses having lower streamflow under G4, and southern parts increases. We further investigated the change of flooding corresponding to the magnitudes of the historical 30-, 50-, and 100-year return period levels; the flooding frequencies change dramatically from historical levels under both RCP4.5 and G4 and show similar spatial patterns. The projected return period pattern under the RCP4.5 scenario agrees well with previous studies, such as Dankers et al. (2014) and Hirabayashi et al. (2013). Generally, stratospheric aerosol injection geoengineering as simulated by G4 relieves flood stress, especially for Southeast Asia, and in turn increases the probability of flooding in the southwestern US, Mexico, and much of Australia – which are drought-prone places that might benefit from increased soil moisture and streamflow. The Amazon Basin shows a relative elongation of flood return period, while Europe shows shortening of return period under G4, and this was also implicit in streamflow characteristics in these regions.
CaMa-Flood does not consider anthropogenic infrastructure, such as dams or reservoirs, which some hydrological models do include. However, estimating future changes in human intervention on the natural system is highly uncertain. Technological advances over the century that may affect anthropogenic changes are by their nature entirely unknown at present. Hence integrating the human dimension into a model of the physical system is fraught with difficulty and uncertainty. Several studies can be used as a guide to the possible effects of anthropogenic impacts compared with natural changes that are captured in CaMa-Flood. Dai et al. (2009) argued that the direct human influence on the major global river streamflow is relatively small compared with climate forcing during the historical period. Mateo et al. (2014) suggested that dams regulate streamflow consistently in a basin study using CaMa-Flood combined with integrated water resources and reservoir operation models. Wang et al. (2017) shows that the reservoir would effectively suppress the flood magnitude and frequency. Recently, analyses of the role of human impact parameterizations (HIPs) in five hydrological models found that the inclusion of HIPs improves the performance of GHMs, in both managed and near-natural catchments, and simulates fewer hydrological extremes by decreasing the simulated high flows (Veldkamp et al., 2018; Zaherpour et al., 2018). These studies suggest that the high flows and flood response under G4 relative to RCP4.5 might be smaller when human intervention is considered and indicate the importance of considering human impacts in future hydrological response studies under geoengineering.
The accurate assessment of human impacts on flood frequency and magnitude depends not only on how anthropogenic effects are parameterized in hydrological models (Masaki et al., 2017) but also on how human activities are represented in geoengineering scenarios. As anthropogenic greenhouse gas emissions increase, human society would continually adapt to climate change and mitigate the related risk, including building new dams and reservoirs to withstand a strengthened global hydrological cycle. How society would respond to future streamflow and flood risk is an important topic both scientifically and in policy making. This is especially true for the developing world, where many cities are experiencing subsidence due to unsustainable rates of groundwater extraction. Subsidence accounted for up to one-third of 20th century relative sea level rise in and around China (Chen, 1991; Ren, 1993). Subsidence and sea level rise both increase flooding risks. However, in densely populated regions with much experience of irrigation management, such as Southeast Asia and India, reduced flood frequency under G4 stratospheric aerosol geoengineering might be further ameliorated.
Our results on streamflow and flood response are based on the GeoMIP G4 simulation and its reference RCP4.5 simulation. The generalizations of the work to other types and extents of solar geoengineering depends on the linearity of the streamflow response to both greenhouse gas and geoengineering. The linearity of response of radiative forcing and global temperatures in particular have been explored in CESM1 Stratospheric Aerosol Geoengineering Large Ensemble (GLENS; Tilmes et al., 2018). Many climate fields, such as temperature, are surprisingly linear under a very wide range of forcing, potentially allowing standard engineering control theory methods (e.g., MacMartin et al., 2014) to tailor a global response given the freedom to use different latitudinal input locations for the aerosol injection (MacMartin et al., 2017; Kravitz et al., 2017), or combinations of, for example, aerosol injection and marine cloud brightening (Cao et al., 2017). Nonlinearities are expected for systems that depend on ice/water phase changes, and these could affect global streamflow and flood responses in some regions, especially in the Arctic. Moreover, the type of solar geoengineering might be relevant as well. Ferraro et al. (2014) found that the tropical overturning circulation weakens in response to geoengineering with stratospheric sulfate aerosol injection due to radiative heating from the aerosol layer, but geoengineering simulated as a simple reduction in total solar irradiance does not capture this effect. A larger tropical precipitation perturbation occurs under equatorial injection scenarios (such as G4) than under simple solar dimming geoengineering, or the latitudinal varying injection schemes explored by GLENS, or a mix of different geoengineering strategies (such as aerosol injection and marine cloud brightening; Cao et al., 2017). Thus the response of streamflow and flood would be expected to differ, to some extent, under different types of solar geoengineering.
Floods are among the most costly natural disasters around the world, especially for more vulnerable developing countries (e.g., Bangladesh, India, and China). Our study suggests that solar geoengineering would exert nonuniform impacts on global flooding risk and hence local hydraulic infrastructure needs would vary if solar geoengineering of the G4 type were undertaken. Changes in flooding are strongly connected with the economic cost of damage due to climate change and sea level rise (Jevrejeva et al., 2016; Hinkel et al., 2014) and thorough studies should be made for further policy and decision making, especially applied to high-value economic or ecological entities. This may be carried out in the framework of specific impact models applied to local cities or regions and would hence benefit from local knowledge, especially in the developing world where resources for adaptation measures are scarce. Linkages between the developing world climate impacts researchers and the GeoMIP community will be encouraged and funded by the Developing Country Impacts Modelling Analysis for SRM (DECIMALS) project (Rahman et al., 2018). Scientists from developing countries are encouraged to apply DECIMALS to model the solar geoengineering impacts that matter most to their regions. DECIMALS promotes wider discussion of the implications of regional impact studies of solar geoengineering. These studies will be a helpful initial step in future decision making related to climate change adaptation and urban infrastructure design.
All output involved in the Coupled Model Intercomparsion Project Phase 5 (CMIP5) and the Geoengineering Model Intercomparison Project (GeoMIP) is publicly available, and much of it is accessible through the Earth System Grid Federation. Please see the CMIP5 website (http://esgf-node.llnl.gov, last access: 19 October 2018; Taylor et al., 2012). and the GeoMIP website (http://climate.envsci.rutgers.edu/GeoMIP/, last access: 19 October 2018; Kravitz et al., 2011) or contact the corresponding author for details. The Beijing Normal University Earth System Model (BNU-ESM) data is archived at http://climatemodeling.bnu.edu.cn (last access: 19 October 2018; Ji et al., 2014) and http://esg.bnu.edu.cn (last access: 19 October 2018; Ji et al., 2014). The Global Precipitation Climatology Project (GPCP) dataset is archived at https://www.ncdc.noaa.gov/cdr/atmospheric/precipitation-gpcp-daily (last access: 19 October, 2018; Adler et al., 2003).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-18-16033-2018-supplement.
DJ designed the research; LW carried out the simulations; LW, DJ, JCM, CM, and HM performed research and wrote the paper.
The authors declare that they have no conflict of interest.
This article is part of the special issue “The Geoengineering Model Intercomparison Project (GeoMIP): Simulations of solar radiation reduction methods (ACP/GMD inter-journal SI)”. It is not associated with a conference.
We thank all participants of the Geoengineering Model Intercomparison
Project and their model development teams, the CLIVAR/WCRP Working Group on
Coupled Modelling for endorsing GeoMIP, and the scientists managing the
Earth System Grid data nodes, who have assisted with making GeoMIP output
available. Research was funded by the National Basic Research Program of
China grant number 2015CB953600. Helene Muri was supported by Research
Council of Norway grant 229760/E10 and the following Sigma2 HPC resources: hexagon and
norstore (accounts nn9812k, nn9448k, NS9033K).
Edited by: Ben Kravitz
Reviewed by: two anonymous referees
Adler, R. F., Huffman, G. J., Chang, A., Ferraro, R., Xie, P.-P., Janowiak, J., Rudolf, B., Schneider, U., Curtis, S., Bolvin, D., Gruber, A., Susskind, J., Arkin, P., and Nelkin, E.: The Version-2 Global Precipitation Climatology Project (GPCP) Monthly Precipitation Analysis (1979–Present), J. Hydrometeorol., 4, 1147–1167, https://doi.org/10.1175/1525-7541(2003)004<1147:TVGPCP>2.0.CO;2, 2003.
Alfieri, L., Bisselink, B., Dottori, F., Naumann, G., de Roo, A., Salamon, P., Wyser, K., and Feyen, L.: Global projections of river flood risk in a warmer world, Earth's Futur., 5, 171–182, https://doi.org/10.1002/2016EF000485, 2017.
Alkama, R., Marchand, L., Ribes, A., and Decharme, B.: Detection of global runoff changes: Results from observations and CMIP5 experiments, Hydrol. Earth Syst. Sci., 17, 2967–2979, https://doi.org/10.5194/hess-17-2967-2013, 2013.
Arnell, N. W. and Gosling, S. N.: The impacts of climate change on river flow regimes at the global scale, J. Hydrol., 486, 351–364, https://doi.org/10.1016/j.jhydrol.2013.02.010, 2013.
Arora, V. K., Scinocca, J. F., Boer, G. J., Christian, J. R., Denman, K. L., Flato, G. M., Kharin, V. V., Lee, W. G., and Merryfield, W. J.: Carbon emission limits required to satisfy future representative concentration pathways of greenhouse gases, Geophys. Res. Lett., 38, L05805, https://doi.org/10.1029/2010GL046270, 2011.
Bala, G., Duffy, P. B., and Taylor, K. E.: Impact of geoengineering schemes on the global hydrological cycle, P. Natl. Acad. Sci. USA, 105, 7664–7669, https://doi.org/10.1073/pnas.0711648105, 2008.
Bates, P. D., Horritt, M. S., and Fewtrell, T. J.: A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling, J. Hydrol., 387, 33–45, https://doi.org/10.1016/j.jhydrol.2010.03.027, 2010.
Bentsen, M., Bethke, I., Debernard, J. B., Iversen, T., Kirkevåg, A., Seland, Ø., Drange, H., Roelandt, C., Seierstad, I. A., Hoose, C., and Kristjánsson, J. E.: The Norwegian Earth System Model, NorESM1-M – Part 1: Description and basic evaluation of the physical climate, Geosci. Model Dev., 6, 687–720, https://doi.org/10.5194/gmd-6-687-2013, 2013.
Berdahl, M., Robock, A., Ji, D., Moore, J. C., Jones, A., Kravitz, B., and Watanabe, S.: Arctic cryosphere response in the Geoengineering Model Intercomparison Project G3 and G4 scenarios, J. Geophys. Res.-Atmos., 119, 1308–1321, https://doi.org/10.1002/2013JD020627, 2014.
Blöschl, G., Hall, J., Parajka, J., Perdigão, R. A. P., Merz, B., Arheimer, B., Aronica, G. T., Bilibashi, A., Bonacci, O., Borga, M., Čanjevac, I., Castellarin, A., Chirico, G. B., Claps, P., Fiala, K., Frolova, N., Gorbachova, L., Gül, A., Hannaford, J., Harrigan, S., Kireeva, M., Kiss, A., Kjeldsen, T. R., Kohnová, S., Koskela, J. J., Ledvinka, O., Macdonald, N., Mavrova-Guirguinova, M., Mediero, L., Merz, R., Molnar, P., Montanari, A., Murphy, C., Osuch, M., Ovcharuk, V., Radevski, I., Rogger, M., Salinas, J. L., Sauquet, E., Šraj, M., Szolgay, J., Viglione, A., Volpi, E., Wilson, D., Zaimi, K., and Živković, N.: Changing climate shifts timing of European floods, Science, 80, 357, 588–590, https://doi.org/10.1126/science.aan2506, 2017.
Boisier, J. P., Ciais, P., Ducharne, A., and Guimberteau, M.: Projected strengthening of Amazonian dry season by constrained climate model simulations, Nat. Clim. Change, 5, 656–660, https://doi.org/10.1038/nclimate2658, 2015.
Cao, L., Duan, L., Bala, G., and Caldeira, K.: Simultaneous stabilization of global temperature and precipitation through cocktail geoengineering, Geophys. Res. Lett., 44, 7429–7437, https://doi.org/10.1002/2017GL074281, 2017.
Chadwick, R., Douville, H., and Skinner, C. B.: Timeslice experiments for understanding regional climate projections: applications to the tropical hydrological cycle and European winter circulation, Clim. Dynam., 49, 3011–3029, https://doi.org/10.1007/s00382-016-3488-6, 2017.
Chen, J., Brissette, F. P., Poulin, A., and Leconte, R.: Overall uncertainty study of the hydrological impacts of climate change for a Canadian watershed, Water Resour. Res., 47, 1–16, https://doi.org/10.1029/2011WR010602, 2011.
Chen, X. Q.: Sea level changes since the early 1920's from the long records of two tidal gauges in Shanghai, China. J. Coastal Res., 7, 787–799, 1991.
Chezik, K. A., Anderson, S. C., and Moore, J. W.: River networks dampen long-term hydrological signals of climate change, Geophys. Res. Lett., 44, 7256–7264, https://doi.org/10.1002/2017GL074376, 2017.
Chiew, F. H. S. and McMahon, T. A.: Global ENSO-streamflow teleconnection, streamflow forecasting and interannual variability, Hydrol. Sci. J., 47, 505–522, https://doi.org/10.1080/02626660209492950, 2002.
Chou, C., Chiang, J. C. H., Lan, C. W., Chung, C. H., Liao, Y. C., and Lee, C. J.: Increase in the range between wet and dry season precipitation, Nat. Geosci., 6, 263–267, https://doi.org/10.1038/ngeo1744, 2013.
Chylek, P., Li, J., Dubey, M. K., Wang, M., and Lesins, G.: Observed and model simulated 20th century Arctic temperature variability: Canadian Earth System Model CanESM2, Atmos. Chem. Phys. Discuss., 11, 22893–22907, https://doi.org/10.5194/acpd-11-22893-2011, 2011.
Cunnane, C.: Unbiased Plotting Position – A Review, J. Hydrol., 37, 205–222, 1978.
Curry, C. L., Sillmann, J., Bronaugh, D., Alterskjaer, K., Cole, J. N. S., Ji, D., Kravitz, B., Kristjánsson, J. E., Moore, J. C., Muri, H., Niemeier, U., Robock, A., Tilmes, S., and Yang, S.: A multimodel examination of climate extremes in an idealized geoengineering experiment, J. Geophys. Res.-Biogeosci., 119, 3900–3923, https://doi.org/10.1002/2013JD020648, 2014.
Dagon, K. and Schrag, D. P.: Regional Climate Variability Under Model Simulations of Solar Geoengineering, J. Geophys. Res.-Atmos., 122, 12106–12121, https://doi.org/10.1002/2017JD027110, 2017.
Dai, A.: Historical and Future Changes in Streamflow and Continental Runoff: A Review, Terr. Water Cycle Clim. Chang. Nat. Human-Induced Impacts, 1st Edn., edited by: Tang, Q. and Oki, T., 17–37, https://doi.org/10.1002/9781118971772.ch2, 2016.
Dai, A., Qian, T., Trenberth, K. E., and Milliman, J. D.: Changes in continental freshwater discharge from 1948 to 2004, J. Climate, 22, 2773–2792, https://doi.org/10.1175/2008JCLI2592.1, 2009.
Dankers, R., Arnell, N. W., Clark, D. B., Falloon, P. D., Fekete, B. M., Gosling, S. N., Heinke, J., Kim, H., Masaki, Y., Satoh, Y., Stacke, T., Wada, Y., and Wisser, D.: First look at changes in flood hazard in the Inter-Sectoral Impact Model Intercomparison Project ensemble, P. Natl. Acad. Sci. USA, 111, 3257–3261, https://doi.org/10.1073/pnas.1302078110, 2014.
Davis, N. A., Seidel, D. J., Birner, T., Davis, S. M., and Tilmes, S.: Changes in the width of the tropical belt due to simple radiative forcing changes in the GeoMIP simulations, Atmos. Chem. Phys., 16, 10083–10095, https://doi.org/10.5194/acp-16-10083-2016, 2016.
Emerton, R., Cloke, H. L., Stephens, E. M., Zsoter, E., Woolnough, S. J., and Pappenberger, F.: Complex picture for likelihood of ENSO-driven flood hazard, Nat. Commun., 8, 14796, https://doi.org/10.1038/ncomms14796, 2017.
Ferraro, A. J. and Griffiths, H. G.: Quantifying the temperature-independent effect of stratospheric aerosol geoengineering on global-mean precipitation in a multi-model ensemble, Environ. Res. Lett., 11, 34012, https://doi.org/10.1088/1748-9326/11/3/034012, 2016.
Ferraro, A. J., Highwood, E. J., and Charlton-Perez, A. J.: Weakened tropical circulation and reduced precipitation in response to geoengineering, Environ. Res. Lett., 9, 014001, https://doi.org/10.1088/1748-9326/9/1/014001, 2014.
Ferraro, A. J., Charlton-Perez, A. J., and Highwood, E. J.: Stratospheric dynamics and midlatitude jets under geoengineering with space mirrors and sulfate and titania aerosols, J. Geophys. Res.-Atmos., 120, 414–429, https://doi.org/10.1002/2014JD022734, 2015.
Gabriel, C. J. and Robock, A.: Stratospheric geoengineering impacts on El Niño/Southern Oscillation, Atmos. Chem. Phys., 15, 11949–11966, https://doi.org/10.5194/acp-15-11949-2015, 2015.
Gosling, S. N., Bretherton, D., Haines, K., and Arnell, N. W.: Global hydrology modelling and uncertainty: running multiple ensembles with a campus grid, Philos. Trans. R. Soc. A Math. Phys. Eng. Sci., 368, 4005–4021, https://doi.org/10.1098/rsta.2010.0164, 2010.
Gosling, S. N., Zaherpour, J., Mount, N. J., Hattermann, F. F., Dankers, R., Arheimer, B., Breuer, L., Ding, J., Haddeland, I., Kumar, R., Kundu, D., Liu, J., van Griensven, A., Veldkamp, T. I. E., Vetter, T., Wang, X., and Zhang, X.: A comparison of changes in river runoff from multiple global and catchment-scale hydrological models under global warming scenarios of 1 ∘C, 2 ∘C and 3 ∘C, Clim. Change, 141, 577–595, https://doi.org/10.1007/s10584-016-1773-3, 2017.
Gumbel, E. J.: The Return Period of Flood Flows, Ann. Math. Stat., 12, 163–190, https://doi.org/10.1214/aoms/1177731747, 1941.
Guo, A., Moore, J. C., and Ji, D.: Tropical atmospheric circulation response to the G1 sunshade geoengineering radiative forcing experiment, Atmos. Chem. Phys., 18, 8689–8706, https://doi.org/10.5194/acp-18-8689-2018, 2018.
Haddeland, I., Clark, D. B., Franssen, W., Ludwig, F., Voß, F., Arnell, N. W., Bertrand, N., Best, M., Folwell, S., Gerten, D., Gomes, S., Gosling, S. N., Hagemann, S., Hanasaki, N., Harding, R., Heinke, J., Kabat, P., Koirala, S., Oki, T., Polcher, J., Stacke, T., Viterbo, P., Weedon, G. P., and Yeh, P.: Multimodel Estimate of the Global Terrestrial Water Balance: Setup and First Results, J. Hydrometeorol., 12, 869–884, https://doi.org/10.1175/2011JHM1324.1, 2011.
Halladay, K. and Good, P.: Non-linear interactions between CO2 radiative and physiological effects on Amazonian evapotranspiration in an Earth system model, Clim. Dynam., 49, 2471–2490, https://doi.org/10.1007/s00382-016-3449-0, 2017.
Harris, P. P., Huntingford, C., and Cox, P. M.: Amazon Basin climate under global warming: the role of the sea surface temperature, Philos. Trans. R. Soc. B Biol. Sci., 363, 1753–1759, https://doi.org/10.1098/rstb.2007.0037, 2008.
Hinkel, J., Lincke, D., Vafeidis, A. T., Perrette, M., Nicholls, R. J., Tol, R. S. J., Marzeion, B., Fettweis, X., Ionescu, C., and Levermannet, A.: Coastal flood damage and adaptation costs under 21st century sea-level rise, P. Natl. Acad. Sci. USA, 111, 3292–3297, 2014.
Hirabayashi, Y., Kanae, S., Emori, S., Oki, T., and Kimoto, M.: Global projections of changing risks of floods and droughts in a changing climate, Hydrol. Sci. J., 53, 754–772, https://doi.org/10.1623/hysj.53.4.754, 2008.
Hirabayashi, Y., Mahendran, R., Koirala, S., Konoshima, L., Yamazaki, D., Watanabe, S., Kim, H., and Kanae, S.: Global flood risk under climate change, Nat. Clim. Chang., 3, 816–821, https://doi.org/10.1038/nclimate1911, 2013.
Ikeuchi, H., Hirabayashi, Y., Yamazaki, D., Kiguchi, M., Koirala, S., Nagano, T., Kotera, A., and Kanae, S.: Modeling complex flow dynamics of fluvial floods exacerbated by sea level rise in the Ganges–Brahmaputra–Meghna Delta, Environ. Res. Lett., 10, 124011, https://doi.org/10.1088/1748-9326/10/12/124011, 2015.
Ikeuchi, H., Hirabayashi, Y., Yamazaki, D., Muis, S., Ward, P. J., Winsemius, H. C., Verlaan, M., and Kanae, S.: Compound simulation of fluvial floods and storm surges in a global coupled river-coast flood model: Model development and its application to 2007 Cyclone Sidr in Bangladesh, J. Adv. Model. Earth Syst., 9, 1847–1862, https://doi.org/10.1002/2017MS000943, 2017.
Jevrejeva, S., Jackson, L. P., Riva, R. E. M., Grinsted, A., and Moore, J. C.: Coastal sea level rise with warming above 2∘ C, P. Natl Acad. Sci. USA, 113, 13342–13347, 2016.
Ji, D., Wang, L., Feng, J., Wu, Q., Cheng, H., Zhang, Q., Yang, J., Dong, W., Dai, Y., Gong, D., Zhang, R. H., Wang, X., Liu, J., Moore, J. C., Chen, D., and Zhou, M.: Description and basic evaluation of Beijing Normal University Earth System Model (BNU-ESM) version 1, Geosci. Model Dev., 7, 2039–2064, https://doi.org/10.5194/gmd-7-2039-2014, 2014.
Ji, D., Fang, S., Curry, C. L., Kashimura, H., Watanabe, S., Cole, J., Lenton, A., Muri, H., Kravitz, B., and Moore, J. C.: Extreme temperature and precipitation response to solar dimming and stratospheric aerosol geoengineering, Atmos. Chem. Phys., 18, 10133–10156, https://doi.org/10.5194/acp-18-10133-2018, 2018.
Jiménez-Muñoz, J. C., Mattar, C., Barichivich, J., Santamaría-Artigas, A., Takahashi, K., Malhi, Y., Sobrino, J. A., and Van Der Schrier, G.: Record-breaking warming and extreme drought in the Amazon rainforest during the course of El Niño 2015-2016, Sci. Rep., 6, 1–7, https://doi.org/10.1038/srep33130, 2016.
Jones, A. C., Hawcroft, M. K., Haywood, J. M., Jones, A., Guo, X., and Moore, J. C.: Regional climate impacts of stabilizing global warming at 1.5 K using solar geoengineering, Earth's Futur., 6, 230–251, https://doi.org/10.1002/2017EF000720, 2018.
Kalidindi, S., Bala, G., Modak, A., and Caldeira, K.: Modeling of solar radiation management: a comparison of simulations using reduced solar constant and stratospheric sulphate aerosols, Clim. Dynam., 44, 2909–2925, https://doi.org/10.1007/s00382-014-2240-3, 2014.
Kashimura, H., Abe, M., Watanabe, S., Sekiya, T., Ji, D., Moore, J. C., Cole, J. N. S., and Kravitz, B.: Shortwave radiative forcing, rapid adjustment, and feedback to the surface by sulfate geoengineering: Analysis of the Geoengineering Model Intercomparison Project G4 scenario, Atmos. Chem. Phys., 17, 3339–3356, https://doi.org/10.5194/acp-17-3339-2017, 2017.
Keith, D. W. and Irvine, P. J.: Solar geoengineering could substantially reduce climate risks – A research hypothesis for the next decade, Earth's Futur., 4, 549–559, https://doi.org/10.1002/2016EF000465, 2016.
Keyantash, J. and Dracup, J. A.: The quantification of drought: an evaluation of drought indices, B. Am. Meteorol. Soc., 83, 1167–1180, 2002.
Koirala, S., Hirabayashi, Y., Mahendran, R., and Kanae, S.: Global assessment of agreement among streamflow projections using CMIP5 model outputs, Environ. Res. Lett., 9, 64017, https://doi.org/10.1088/1748-9326/9/6/064017, 2014.
Kravitz, B., Robock, A., Boucher, O., Schmidt, H., Taylor, K. E., Stenchikov, G., and Schulz, M.: The Geoengineering Model Intercomparison Project (GeoMIP), Atmos. Sci. Lett., 12, 162–167, https://doi.org/10.1002/asl.316, 2011.
Kravitz, B., Robock, A., and Haywood, J. M.: Progress in climate model simulations of geoengineering, Eos (Washington, DC), 93, 340, https://doi.org/10.1029/2012EO350009, 2012.
Kravitz, B., Robock, A., Forster, P. M., Haywood, J. M., Lawrence, M. G., and Schmidt, H.: An overview of the Geoengineering Model Intercomparison Project (GeoMIP), J. Geophys. Res.-Atmos., 118, 13103–13107, https://doi.org/10.1002/2013JD020569, 2013a.
Kravitz, B., Caldeira, K., Boucher, O., Robock, A., Rasch, P. J., Alterskjær, K., Karam, D. B., Cole, J. N. S., Curry, C. L., Haywood, J. M., Irvine, P. J., Ji, D., Jones, A., Kristjánsson, J. E., Lunt, D. J., Moore, J. C., Niemeier, U., Schmidt, H., Schulz, M., Singh, B., Tilmes, S., Watanabe, S., Yang, S., and Yoon, J. H.: Climate model response from the Geoengineering Model Intercomparison Project (GeoMIP), J. Geophys. Res.-Atmos., 118, 8320–8332, https://doi.org/10.1002/jgrd.50646, 2013b.
Kravitz, B., MacMartin, D. G., Mills, M. J., Richter, J. H., Tilmes, S., Lamarque, J.-F., Tribbia, J. J., and Vitt, F.: First Simulations of Designing Stratospheric Sulfate Aerosol Geoengineering to Meet Multiple Simultaneous Climate Objectives, J. Geophys. Res.-Atmos., 122, 12616–12634, https://doi.org/10.1002/2017JD026874, 2017.
Lehner, B., Verdin, K., and Jarvis, K.: New global hydrograghy derived from spaceborne elevation data, Eos, Trans. AGU, 89, 93–94, https://doi.org/10.1029/2008EO100001, 2008.
Lohmann, U. and Feichter, J.: Global indirect aerosol effects: a review, Atmos. Chem. Phys., 5, 715–737, https://doi.org/10.5194/acp-5-715-2005, 2005.
MacMartin, D. G., Kravitz, B., Tilmes, S., Richter, J. H., Mills, M. J., Lamarque, J.-F., Tribbia, J. J., and Vitt, F.: The Climate Response to Stratospheric Aerosol Geoengineering Can Be Tailored Using Multiple Injection Locations, J. Geophys. Res.-Atmos., 122, 12574–12590, https://doi.org/10.1002/2017JD026868, 2017.
MacMartin, D. G., Kravitz, B., Keith, D. W., and Jarvis, A.: Dynamics of the coupled human-climate system resulting from closed-loop control of solar geoengineering, Clim. Dynam., 43, 243–258, https://doi.org/10.1007/s00382-013-1822-9, 2014.
Masaki, Y., Hanasaki, N., Biemans, H., Schmied, H. M., Tang, Q., Wada, Y., Gosling, S. N., Takahashi, K., and Hijioka, Y.: Intercomparison of global river discharge simulations focusing on dam operation - Multiple models analysis in two case-study river basins, Missouri-Mississippi and Green-Colorado, Environ. Res. Lett., 12, 055002, https://doi.org/10.1088/1748-9326/aa57a8, 2017.
Mateo, C. M., Hanasaki, N., Komori, D., Tanaka, K., Kiguchi, M., Champathong, A., Sukhapunnaphan, T., Yamazaki, D., and Oki, T.: Assessing the impacts of reservoir operation to floodplain inundation by combining hydrological, reservoir management, and hydrodynamic models, Water Resour. Res., 50, 7245–7266, https://doi.org/10.1002/2013WR014845, 2014.
Mateo, C. M. R., Yamazaki, D., Kim, H., Champathong, A., Vaze, J., and Oki, T.: Impacts of spatial resolution and representation of flow connectivity on large-scale simulation of floods, Hydrol. Earth Syst. Sci., 21, 5143–5163, https://doi.org/10.5194/hess-21-5143-2017, 2017.
May, W., Rummukainen, M., Chéruy, F., Hagemann, S., and Meier, A.: Contributions of soil moisture interactions to future precipitation changes in the GLACE-CMIP5 experiment, Clim. Dynam., 49, 1681–1704, https://doi.org/10.1007/s00382-016-3408-9, 2017.
Meinshausen, M., Smith, S. J., Calvin, K., Daniel, J. S., Kainuma, M. L. T., Lamarque, J-F., Matsumoto, K., Montzka, S. A., Raper, S. C. B., Riahi, K., Thomson, A., Velders, G. J. M., and van Vuuren, D. P. P.: The RCP greenhouse gas concentrations and their extensions from 1765 to 2300, Clim. Change, 109, 213, https://doi.org/10.1007/s10584-011-0156-z, 2011.
Moore, J. C., Rinke, A., Yu, X., Ji, D., Cui, X., Li, Y., Alterskjær, K., Kristjánsson, J. E., Muri, H., Boucher, O., Huneeus, N., Kravitz, B., Robock, A., Niemeier, U., Schulz, M., Tilmes, S., Watanabe, S., and Yang, S.: Arctic sea ice and atmospheric circulation under the GeoMIP G1 scenario, J. Geophys. Res.-Atmos., 119, 567–583, https://doi.org/10.1002/2013JD021060, 2014.
Mueller, B. and Seneviratne, S. I.: Systematic land climate and evapotranspiration biases in CMIP5 simulations, Geophys. Res. Lett., 41, 128–134, https://doi.org/10.1002/2013GL058055, 2014.
Muri, H., Tjiputra, J., Otterå, O. H., Adakudlu, M., Lauvset, S. K., Grini, A., Schulz, M., Niemeier, U., and Kristjánsson, J. E.: Climate response to aerosol geoengineering: a multi-method comparison, J. Climate, 31, 6319–6340, https://doi.org/10.1175/JCLI-D-17-0620.1, 2018.
Niemeier, U. and Timmreck, C.: What is the limit of climate engineering by stratospheric injection of SO2?, Atmos. Chem. Phys., 15, 9129–9141, https://doi.org/10.5194/acp-15-9129-2015, 2015.
Niemeier, U., Schmidt, H., and Timmreck, C.: The dependency of geoengineered sulfate aerosol on the emission strategy, Atmos. Sci. Lett., 12, 189–194, https://doi.org/10.1002/asl.304, 2011.
Niemeier, U., Schmidt, H., Alterskjær, K., and Kristjánsson, J. E.: Solar irradiance reduction via climate engineering: Impact of different techniques on the energy balance and the hydrological cycle, J. Geophys. Res.-Atmos., 118, 11905–11917, https://doi.org/10.1002/2013JD020445, 2013.
Pappenberger, F., Dutra, E., Wetterhall, F., and Cloke, H. L.: Deriving global flood hazard maps of fluvial floods through a physical model cascade, Hydrol. Earth Syst. Sci., 16, 4143–4156, https://doi.org/10.5194/hess-16-4143-2012, 2012.
Prudhomme, C., Giuntoli, I., Robinson, E. L., Clark, D. B., Arnell, N. W., Dankers, R., Fekete, B. M., Franssen, W., Gerten, D., Gosling, S. N., Hagemann, S., Hannah, D. M., Kim, H., Masaki, Y., Satoh, Y., Stacke, T., Wada, Y., and Wisser, D.: Hydrological droughts in the 21st century, hotspots and uncertainties from a global multimodel ensemble experiment, P. Natl. Acad. Sci. USA, 111, 3262–3267, https://doi.org/10.1073/pnas.1222473110, 2014.
Rahman, A. A., Artaxo, P., Asrat, A., and Parker, A.: Developing countries must lead on solar geoengineering research, Nature, 556, 22–24, https://doi.org/10.1038/d41586-018-03917-8, 2018.
Rasmussen, P. F. and Gautam, N.: Alternative PWM-estimators of the gumbel distribution, J. Hydrol., 280, 265–271, https://doi.org/10.1016/S0022-1694(03)00241-5, 2003.
Ren, M. E.: Relative sea level changes in China over the last 80 years, J. Coastal. Res., 9, 229–241, 1993.
Robock, A., Kravitz, B., and Boucher, O.: Standardizing experiments in geoengineering, Eos (Washington, DC), 92, 197, https://doi.org/10.1029/2011EO230008, 2011.
Schmidt, H., Alterskjær, K., Alterskjær, K., Bou Karam, D., Boucher, O., Jones, A., Kristjánsson, J. E., Niemeier, U., Schulz, M., Aaheim, A., Benduhn, F., Lawrence, M., and Timmreck, C.: Solar irradiance reduction to counteract radiative forcing from a quadrupling of CO2: Climate responses simulated by four earth system models, Earth Syst. Dyn., 3, 63–78, https://doi.org/10.5194/esd-3-63-2012, 2012.
Seneviratne, S. I., Wilhelm, M., Stanelle, T., van den Hurk, B., Hagemann, S., Berg, A., Cheruy, F., Higgins, M. E., Meier, A., Brovkin, V., Claussen, M., Ducharne, A., Dufresne, J.-L., Findell, K. L., Ghattas, J., Lawrence, D. M., Malyshev, S., Rummukainen, M., and Smith, B.: Impact of soil moisture-climate feedbacks on CMIP5 projections: First results from the GLACE-CMIP5 experiment, Geophys. Res. Lett., 40, 5212–5217, https://doi.org/10.1002/grl.50956, 2013.
Smyth, J. E., Russotto, R. D., and Storelvmo, T.: Thermodynamic and dynamic responses of the hydrological cycle to solar dimming, Atmos. Chem. Phys., 17, 6439–6453, https://doi.org/10.5194/acp-17-6439-2017, 2017.
Sonntag, S., Ferrer González, M., Ilyina, T., Kracher, D., Nabel, J. E. M. S., Niemeier, U., Pongratz, J., Reick, C. H., and Schmidt, H.: Quantifying and Comparing Effects of Climate Engineering Methods on the Earth System, Earth's Futur., 6, 149–168, https://doi.org/10.1002/2017EF000620, 2018.
Suzuki, T., Yamazaki, D., Tsujino, H., Komuro, Y., Nakano, H., and Urakawa, S.: A dataset of continental river discharge based on JRA-55 for use in a global ocean circulation model, J. Oceanogr., 74, 421–429, https://doi.org/10.1007/s10872-017-0458-5, 2018.
Tanoue, M., Hirabayashi, Y., and Ikeuchi, H.: Global-scale river flood vulnerability in the last 50 years, Sci. Rep., 6, 36021, https://doi.org/10.1038/srep36021, 2016.
Taylor, K. E., Stouffer, R. J., and Meehl, G. A.: An Overview of CMIP5 and the Experiment Design, B. Am. Meteorol. Soc., 93, 485–498, https://doi.org/10.1175/BAMS-D-11-00094.1, 2012.
Thompson, J. R., Green, A. J., Kingston, D. G., and Gosling, S. N.: Assessment of uncertainty in river flow projections for the Mekong River using multiple GCMs and hydrological models, J. Hydrol., 486, 1–30, 2013.
Tilmes, S., Fasullo, J., Lamarque, J. F., Marsh, D. R., Mills, M., Alterskjær, K., Muri, H., Kristjánsson, J. E., Boucher, O., Schulz, M., Cole, J. N. S., Curry, C. L., Jones, A., Haywood, J., Irvine, P. J., Ji, D., Moore, J. C., Karam, D. B., Kravitz, B., Rasch, P. J., Singh, B., Yoon, J. H., Niemeier, U., Schmidt, H., Robock, A., Yang, S., and Watanabe, S.: The hydrological impact of geoengineering in the Geoengineering Model Intercomparison Project (GeoMIP), J. Geophys. Res.-Atmos., 118, 11036–11058, https://doi.org/10.1002/jgrd.50868, 2013.
Tilmes, S., Richter, J. H., Kravitz, B., MacMartin, D. G., Mills, M. J., Simpson, I. R., Glanville, A. S., Fasullo, J. T., Phillips, A. S., Lamarque, J.-F., Tribbia, J., Edwards, J., Mickelson, S., and Gosh, S.: CESM1(WACCM) Stratospheric Aerosol Geoengineering Large Ensemble (GLENS) Project, B. Am. Meteorol. Soc., https://doi.org/10.1175/BAMS-D-17-0267.1, in press, 2018.
Tjiputra, J. F., Roelandt, C., Bentsen, M., Lawrence, D. M., Lorentzen, T., Schwinger, J., Seland, Ø., and Heinze, C.: Evaluation of the carbon cycle components in the Norwegian Earth System Model (NorESM), Geosci. Model Dev., 6, 301–325, https://doi.org/10.5194/gmd-6-301-2013, 2013.
Trigg, M. A., Birch, C. E., Neal, J. C., Bates, P. D., Smith, A., Sampson, C. C., Yamazaki, D., Hirabayashi, Y., Pappenberger, F., Dutra, E., Ward, P. J., Winsemius, H. C., Salamon, P., Dottori, F., Rudari, R., Kappes, M. S., Simpson, A. L., Hadzilacos, G., and Fewtrell, T. J.: The credibility challenge for global fluvial flood risk analysis, Environ. Res. Lett., 11, 94014, https://doi.org/10.1088/1748-9326/11/9/094014, 2016.
Ukkola, A. M., Pitman, A. J., De Kauwe, M. G., Abramowitz, G., Herger, N., Evans, J. P., and Decker, M.: Evaluating CMIP5 Model Agreement for Multiple Drought Metrics, J. Hydrometeorol., 19, 969–988, https://doi.org/10.1175/JHM-D-17-0099.1, 2018.
UNISDR (The United Nations International Strategy for Disaster Reduction): Global Assessment Report on Disaster Risk Reduction: From Shared Risk to Shared Value – The Business Case for Disaster Risk Reduction, Glob. Assess. Rep. Disaster Risk Reduct., 246, 2013.
Vano, J. A., Udall, B., Cayan, D. R., Overpeck, J. T., Brekke, L. D., Das, T., Hartmann, H. C., Hidalgo, H. G., Hoerling, M., McCabe, G. J., Morino, K., Webb, R. S., Werner, K., and Lettenmaier, D. P.: Understanding uncertainties in future Colorado River streamflow, Bull. Am. Meteorol. Soc., 95, 59–78, https://doi.org/10.1175/BAMS-D-12-00228.1, 2014.
Veldkamp, T. I. E., Zhao, F., Ward, P. J., de Moel, H., Aerts, J. C. J. H., Schmied, H. M., Portmann, F. T., Masaki, Y., Pokhrel, Y., Liu, X., Satoh, Y., Gerten, D., Gosling, S. N., Zaherpour, J., and Wada, Y.: Human impact parameterizations in global hydrological models improve estimates of monthly discharges and hydrological extremes: a multi-model validation study, Environ. Res. Lett., 13, 055008, https://doi.org/10.1088/1748-9326/aab96f, 2018.
Visioni, D., Pitari, G., and Aquila, V.: Sulfate geoengineering: A review of the factors controlling the needed injection of sulfur dioxide, Atmos. Chem. Phys., 17, 3879–3889, https://doi.org/10.5194/acp-17-3879-2017, 2017.
Wang, B. and Ding, Q.: Changes in global monsoon precipitation over the past 56 years, Geophys. Res. Lett., 33, 1–4, https://doi.org/10.1029/2005GL025347, 2006.
Wang, W., Lu, H., Leung, L. R., Li, H., Zhao, J., Tian, F., Yang, K., and Sothea, K.: Dam construction in Lancang-Mekong River Basin could mitigate future flood risk from warming-induced intensified rainfall, Geophys. Res. Lett., 44, 10378–10386, https://doi.org/10.1002/2017GL075037, 2017.
Wang, Q., Moore, J. C., and Ji, D.: A statistical examination of the effects of stratospheric sulfate geoengineering on tropical storm genesis, Atmos. Chem. Phys., 18, 9173–9188, https://doi.org/10.5194/acp-18-9173-2018, 2018.
Ward, P. J., Jongman, B., Weiland, F. S., Bouwman, A., van Beek, R., Bierkens, M. F. P., Ligtvoet, W., and Winsemius, H. C.: Assessing flood risk at the global scale: model setup, results, and sensitivity, Environ. Res. Lett., 8, 44019, https://doi.org/10.1088/1748-9326/8/4/044019, 2013.
Ward, P. J., Jongman, B., Kummu, M., Dettinger, M. D., Sperna Weiland, F. C., and Winsemius, H. C.: Strong influence of El Nino Southern Oscillation on flood risk around the world, P. Natl. Acad. Sci. USA, 111 15659–15664, https://doi.org/10.1073/pnas.1409822111, 2014.
Ward, P. J., Kummu, M., and Lall, U.: Flood frequencies and durations and their response to El Niño Southern Oscillation: Global analysis, J. Hydrol., 539, 358–378, https://doi.org/10.1016/j.jhydrol.2016.05.045, 2016.
Ward, P. J., Jongman, B., Aerts, J. C. J. H., Bates, P. D., Botzen, W. J. W., DIaz Loaiza, A., Hallegatte, S., Kind, J. M., Kwadijk, J., Scussolini, P., and Winsemius, H. C.: A global framework for future costs and benefits of river-flood protection in urban areas, Nat. Clim. Chang., 7, 642–646, https://doi.org/10.1038/nclimate3350, 2017.
Wartenburger, R., Seneviratne, S. I., Masaki, Y., Morfopoulos, C., and Christoph, M.: Evapotranspiration simulations in ISIMIP2a – Evaluation of spatio-temporal characteristics with a comprehensive ensemble of independent datasets, Environ. Res. Lett., 13, 1–49, https://doi.org/10.1088/1748-9326/aac4bb, 2018.
Watanabe, S., Hajima, T., Sudo, K., Nagashima, T., Takemura, T., Okajima, H., Nozawa, T., Kawase, H., Abe, M., Yokohata, T., Ise, T., Sato, H., Kato, E., Takata, K., Emori, S., and Kawamiya, M.: MIROC-ESM 2010: Model description and basic results of CMIP5-20c3m experiments, Geosci. Model Dev., 4, 845–872, https://doi.org/10.5194/gmd-4-845-2011, 2011.
Yamazaki, D., Oki, T., and Kanae, S.: Deriving a global river network map and its sub-grid topographic characteristics from a fine-resolution flow direction map, Hydrol. Earth Syst. Sci., 13, 2241–2251, https://doi.org/10.5194/hess-13-2241-2009, 2009.
Yamazaki, D., Kanae, S., Kim, H., and Oki, T.: A physically based description of floodplain inundation dynamics in a global river routing model, Water Resour. Res., 47, 1–21, https://doi.org/10.1029/2010WR009726, 2011.
Yamazaki, D., De Almeida, G. A. M., and Bates, P. D.: Improving computational efficiency in global river models by implementing the local inertial flow equation and a vector-based river network map, Water Resour. Res., 49, 7221–7235, https://doi.org/10.1002/wrcr.20552, 2013.
Yamazaki, D., Sato, T., Kanae, S., Hirabayashi, Y., and Bates, P. D.: Regional flood dynamics in a bifurcating mega delta simulated in a global river model, Geophys. Res. Lett., 41, 3127–3135, https://doi.org/10.1002/2014GL059744, 2014.
Yamazaki, D., Ikeshima, D., Tawatari, R., Yamaguchi, T., O'Loughlin, F., Neal, J. C., Sampson, C. C., Kanae, S., and Bates, P. D.: A high-accuracy map of global terrain elevations, Geophys. Res. Lett., 44, 5844–5853, https://doi.org/10.1002/2017GL072874, 2017.
Yu, M., Wang, G., and Chen, H.: Quantifying the impacts of land surface schemes and dynamic vegetation on the model dependency of projected changes in surface energy and water budgets, J. Adv. Model. Earth Syst., 8, 370–386, https://doi.org/10.1002/2015MS000492, 2016.
Yu, X., Moore, J. C., Cui, X., Rinke, A., Ji, D., Kravitz, B., and Yoon, J. H.: Impacts, effectiveness and regional inequalities of the GeoMIP G1 to G4 solar radiation management scenarios, Global Planet. Change, 129, 10–22, https://doi.org/10.1016/j.gloplacha.2015.02.010, 2015.
Zaherpour, J., Gosling, S. N., Mount, N., Schmied, H. M., Veldkamp, T. I. E., Dankers, R., Eisner, S., Gerten, D., Gudmundsson, L., Haddeland, I., Hanasaki, N., Kim, H., Leng, G., Liu, J., Masaki, Y., Oki, T., Pokhrel, Y., Satoh, Y., Schewe, J., and Wada, Y.: Worldwide evaluation of mean and extreme runoff from six global-scale hydrological models that account for human impacts, Environ. Res. Lett., 13, 1–23, https://doi.org/10.1088/1748-9326/aac547, 2018.
Zhao, F., Veldkamp, T. I. E., Frieler, K., Schewe, J., Ostberg, S., Willner, S., Schauberger, B., Gosling, S. N., Schmied, H. M., Portmann, F. T., Leng, G., Huang, M., Liu, X., Tang, Q., Hanasaki, N., Biemans, H., Gerten, D., Satoh, Y., Pokhrel, Y., Stacke, T., Ciais, P., Chang, J., Ducharne, A., Guimberteau, M., Wada, Y., Kim, H., and Yamazaki, D.: The critical role of the routing scheme in simulating peak river discharge in global hydrological models, Environ. Res. Lett., 12, 75003, https://doi.org/10.1088/1748-9326/aa7250, 2017.
Zsótér, E., Pappenberger, F., Smith, P., Emerton, R. E., Dutra, E., Wetterhall, F., Richardson, D., Bogner, K. and Balsamo, G.: Building a Multimodel Flood Prediction System with the TIGGE Archive, J. Hydrometeorol., 17, 2923–2940, https://doi.org/10.1175/JHM-D-15-0130.1, 2016.