the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A thermodynamic description for the hygroscopic growth of atmospheric aerosol particles
Dimitri Castarède
The phase state of atmospheric particulate is important to atmospheric processes, and aerosol radiative forcing remains a large uncertainty in climate predictions. That said, precise atmospheric phase behavior is difficult to quantify and observations have shown that “precondensation” of water below predicted saturation values can occur. We propose a revised approach to understanding the transition from solid soluble particles to liquid droplets, typically described as cloud condensation nucleation – a process that is traditionally captured by Köhler theory, which describes a modified equilibrium saturation vapor pressure due to (i) mixing entropy (Raoult's law) and (ii) droplet geometry (Kelvin effect). Given that observations of precondensation are not predicted by Köhler theory, we devise a more complete model that includes interfacial forces giving rise to predeliquescence, i.e., the formation of a brine layer wetting a salt particle at relative humidities well below the deliquescence point.
- Article
(6602 KB) -
Supplement
(459 KB) - BibTeX
- EndNote
The role of aerosols in the radiative budget of the planet is a source of large uncertainty in climate modeling and prediction (Stocker et al., 2013). One significant source of uncertainty comes from inadequate understanding of aerosol phase state in the atmosphere (Davis et al., 2015b). The phase behavior of atmospheric particles depends on both the environmental conditions (pressure, temperature, humidity, etc.) and the particle properties (Fig. 1).
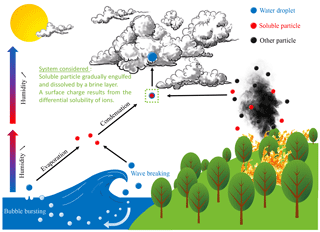
Figure 1Soluble particles are ubiquitous in the atmosphere, with primary sources including biomass burning and the sea surface illustrated here. Solid salt particles, which can be directly emitted or form when solution droplets evaporate and effloresce, provide hygroscopic surfaces for cloud condensation nucleation.
The phase state influences surface as well as bulk phase chemistry, cloud forming potential, particle deposition, and other aspects of the global water and bio- and geochemical cycles. Thus fundamental knowledge of aerosol particle phase behavior is a key aspect to understanding and modeling atmospheric processes. For example, mixed phase clouds in the Arctic demonstrate a surprising persistence that is not predicted by the current understanding of ice-water saturation vapor pressure gradients and the resulting competition for H2O (Wegener–Bergeron–Findeisen process) (Korolev, 2007; Martin et al., 2011; Morrison et al., 2012).
For soluble atmospheric particulate, Köhler theory is generally used to quantify and parameterize atmospheric phase state (Köhler, 1936). Köhler theory describes the equilibrium size of solution droplets in the atmosphere as determined by the saturation vapor pressure, which depends upon component mixing (Raoult's law) (Pruppacher and Klett, 1997) and the curvature of the interface (Kelvin or Gibbs–Thomson effect) (Orr et al., 1958; Thomson, 1871). For a fully soluble particle, implicit in the theory is a sudden transition from a dry (solid) particle to a saturated droplet. The relative humidity at the transition point is referred to as the deliquescence relative humidity (DRH). The Köhler model is useful because it provides a simple physical and mathematical description of nucleated condensation and can be modified to include compounds of limited solubility (Bilde and Svenningsson, 2004). As such it has remained the tool of choice in atmospheric models (Mirabel et al., 2000; Nenes and Seinfeld, 2003), although many measurements suggest that a precondensation of water even on pure soluble surfaces may occur below the DRH (Biskos et al., 2006; Cheng et al., 2015; Davis et al., 2015a; Hsiao et al., 2016; Hämeri et al., 2001; Montgomery et al., 2015; Zeng et al., 2013). For pure compounds, such observations are not predicted and thus hint that Köhler theory can be refined.
Here we suggest a theoretical refinement by considering the stability of a salt particle that is gradually engulfed and dissolved by a brine layer (Fig. 2). The model includes the understood bulk phase equilibria established by Köhler theory but invokes a transition region where metastable liquid layers exist on particle surfaces. The general shortcoming of Köhler theory for single component systems is the activated transition from dry particle to liquid droplet and the exclusion of an interfacial system that reduces the global free energy. The theory we propose herein evolves from previous explorations of wetting of soluble surfaces (Russell and Ming, 2002), where previous work has used bulk thermodynamics and ascribed disjoining pressures (also modeled using bulk properties or fitting parameters) to explore the stability of thin films on solvating particles (McGraw and Lewis, 2009; Shchekin and Rusanov, 2008; Shchekin et al., 2008, 2013). Other studies have used similar theoretical models to treat particle interfaces in the presence of substrate surfaces (Bruzewicz et al., 2011), or for terrestrial systems like brine crusts where geometric effects can be excluded (Hansen-Goos et al., 2014). In this treatment we include terms to explicitly account for the intermolecular origins of the interfacial forces in a manner akin to surface melting (Dash et al., 2006).
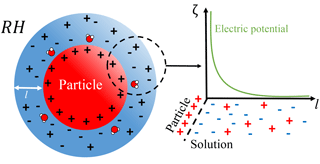
Figure 2Schematic of the system considered herein – an idealized solvating atmospheric particle. The use of an idealized spherical geometry is justified by previous findings that NaCl crystal corner and step sites dissolve preferentially to surface sites, in a manner that quickly roughens and rounds faceted crystals (Chen et al., 2014).
Thus we extend previous work to combine and define entropic, geometric, and explicit intermolecular interactions that result in modified equilibrium vapor pressures above particle surfaces. We do so in a manner wherein achievable analytic solutions help to illuminate the underlying physicochemical processes that control the system and may be used to benefit modeling at a range of scales. The implications of this work are far-reaching given that within the current state of understanding the existence of atmospheric aqueous surfaces is limited to deliquesced materials and/or coated insoluble particles. The model we propose herein suggests that aqueous surface layers may exist in some range of relative humidity (RH) below the DRH and thus resemble liquid droplet behavior for some processes and detection techniques.
Köhler theory considers and balances the effects on droplet stability due to the interfacial curvature and soluble components (Farmer et al., 2015; Lohmann et al., 2016; Ruehl et al., 2016). Thus the equilibrium vapor pressure pr at temperature T above a brine droplet of radius r is described by its departure from the analogous vapor pressure at the flat, pure water interface pb∞ at the same temperature,
where psol represents the equilibrium vapor pressure over the flat brine solution surface, also at temperature T. In detail the geometric term in Eq. (1) is given by the Kelvin equation,
where the surface free energy of the liquid–gas interface σ≡σ(ρsol) is a function of the bulk composition of the solution droplet as expressed by the solution density ρsol, Rg is the ideal gas constant, and vsol is the molar volume of the solution. Likewise the modified equilibrium due to the addition of soluble components is given by the water activity,
where a theoretical model (e.g., Van't Hoff – Zumdahl, 2005; E-AIM – Clegg et al., 1998; Friese and Ebel, 2010) or empirical parameterization can be chosen to best match the system of interest.
Thus from the combination of these effects the DRH is implicitly given when r=RDRH at the radius of the deliquesced droplet,
This traditional Köhler formulation (4) for a fully soluble particle predicts the deliquescence point and, when r is allowed to evolve above RDRH, the equilibrium relative humidity above the evolving brine droplet. However, in this formulation the sudden transition from a solid to liquid particle remains implicit.
Although the transition from solid to liquid solution may proceed quickly, it is important to consider whether or not there exists an intermediate state(s) of importance. Thus we consider whether a particle may be wetted by a thin film and what, if any, stability conditions may (de-)stabilize such a system. Such thin films are a common phenomenon and are generally treated within the rubric of adsorption or wetting (Schick, 1990), which are incorporated into applications in many fields from biology to surfactant physics (French et al., 2010).
Reformulating atmospheric particle dissolution as an interfacial problem leads to the system postulated in Fig. 2, where a charged soluble particle is engulfed and dissolved by a brine layer. However, in order for the interfacial system to endure it must yield some energetic benefit that can be captured by minimizing the global free energy of the system. Thus in addition to the bulk free energies tacit in Köhler theory (Eqs. 2–3) an interfacial contribution ζ(l) must be included. For thin films, Derjaguin–Landau–Verwey–Overbeek (DLVO) theory, which assesses the balance between short- and long-range intermolecular interactions, has been used to great success (Derjaguin and Landau, 1993; Luo, 2007; Verwey and Overbeek, 1948).
In the case of an ionic electrolyte a surface charge results from the differential solubility of ions (Kobayashi et al., 2014), while the solvated ions affect both the mixing entropy and the electric potential of the film. The ions in the brine layer are organized to offset the surface charge in a manner described by linearized Poisson–Boltzmann theory, where the characteristic falloff of the electric field is a Debye length , where ϵ0 is the vacuum permittivity, ϵ is the relative permittivity of the brine, kb is the Boltzmann constant, T is the absolute temperature, e is the elementary charge, and NA is Avogadro's constant. Thus the contribution to the free energy is
where qs is the surface charge and l is the thickness of the liquid layer. The colligative effect of the ions remains unchanged as in Eq. (3).
The long-range dipole fluctuations in the system are volume–volume interactions and can be depicted to first order as the nonretarded dispersion or van der Waals forces. Assuming that retardation is not important the van der Waals contribution to the free energy can be expressed as
where the Hamaker constant Ah is determined for a given layered system (French, 2000). This formulation assumes a planar geometry, which given the relative scales of the layering versus the system size is taken as accurate to first order (French, 2000). For small nanoparticles other considerations including the entire particle volume may become important, as we discuss later.
The combined effects of the short- and long-range interactions captured by Felec(l) and Fdisp(l) yield a total interaction potential,
whose derivative with respect to l, ζ′(l) represents the interfacial contribution to the free energy, and whose sign and strength will depend upon the material properties and geometry of the specific system.
To re-express Köhler theory including the effect of these intermolecular interactions we define an equilibrium vapor pressure over the curved brine surface pζ that includes the interfacial term, and thus in analogy to Eq. (1),
Assuming that the thermodynamic equilibrium condition at the solution–vapor interface is set by the free exchange of water molecules and that near deliquescence temperature is constant, an expression for pζ can be calculated by considering the difference in chemical potentials between the solvated and layered states,
where the details of the derivation as presented in Hansen-Goos et al. (2014, hereafter, HG14) (Hansen-Goos et al., 2014) are included in the Supplement for completeness. Thus Eq. (8) can be rewritten as
where
Thus at the system size evolves like , which captures the change in radius due to condensation and dissolution, where a linear solvation is assumed. The exact solution considering the volume–volume equivalence of dissolution requires numerically solving a third-degree polynomial and yields a negligible correction factor. The growth factor at DRH is , where the dry particle radius is Rs. At the entire particle is dissolved and thus r is the solution droplet's radius and the theory re-converges to classical Köhler theory as ζ′(l) vanishes.
Equation (10) is a general result describing the equilibrium vapor pressure over a dissolving salt particle, from the dry particle state to the totally dissolved state. Although herein we treat an idealized monovalent electrolyte system using modified DLVO theory to constrain the functional behavior of ζ′(l), natural systems may require more complex treatments that would likely yield a host of interesting behavior, and simultaneously strain the ability to achieve analytical and/or computational solutions.
It is instructive to use the refined Köhler formulation (Eq. 10) to model a NaCl particle, as this might represent an idealized marine aerosol. Although considerable information concerning bulk salt solutions is available it is difficult to assess the applicability of these values to thin brines. For example, the assumptions that the interfacial brine layer is a saturated solution whose thickness is controlled by electrostatic interactions may not be self-consistent. The ion availability within a saturated NaCl brine will allow efficient charge screening, and thus a very short Debye length should result. That said, the uncertain theoretical parameters (qs, Ah, κ−1, and brine concentration C) can also be used as fitting parameters in order to illuminate the range of possible physical behavior.
Here for an idealized case we choose to apply Eq. (10) to a sodium chloride particle of a representative atmospheric diameter ≃0.8 µm in the accumulation mode (Lewis and Schwartz, 2004; Lohmann et al., 2016). The growth factor is assumed such that the particle will lead to a solvated brine droplet of radius 1.36 µm, and for consistency with previous work we choose a temperature of 20 ∘C and a saturated concentration of [NaCl]sat=5.4 mol L−1 (Haynes, 2012), which is also used to calculate the Debye length. The value for surface charge qs=0.12 C m−2 is taken from Kobayashi et al. (2014), while the HG14 value is used, and the expression for the water activity of a NaCl solution is taken from Tang et al. (1997). The result is illustrated in Fig. 3, where both the classical Köhler behavior and the refined model of predeliquescent hygroscopic growth are captured. With the refined interfacial model the DRH is captured (≈75 % RH) as reported in many previous studies (Laskina et al., 2015; Metzger et al., 2012; Tang and Munkelwitz, 1994), but near the deliquescence transition (Fig. 3) a wetted interface is predicted below DRH when considering the balance of the intermolecular interactions.
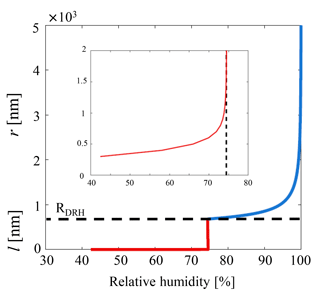
Figure 3Model of the growth of the solvating surface of a 0.8 µm accumulation mode NaCl particle as outlined in the text. Below deliquescence (≲75 % RH and and in the inset, zoomed plot) the metastable brine layer behavior is governed as in Eq. (10) – red curve. Above deliquescence the layer thickness l becomes the radius r of the growing solution droplet as is captured by classical Köhler theory (Eqs. 1–4 and Eq. 10 for , where the interfacial term has vanished – blue curve).
The result suggests that observations of precondensation in the existing literature (Biskos et al., 2006; Cheng et al., 2015; Hämeri et al., 2001) may also be explained by a metastable interfacial equilibrium. In Fig. 4 the theoretical model is compared to measurement data from Hämeri et al. (2001) and Biskos et al. (2006). Each of the solid lines in Fig. 4 correspond to nonlinear least-squares solutions to fit the data, where the identified fitting parameters are presented in Table 1.
(Kobayashi et al., 2014)(Haynes, 2012)Table 1Fitting parameters yielding curves in Fig. 4, where superscripted letters correspond to figure panels.

For physical consistency with the theoretical framework the best-fit solutions have been calculated excluding data points that preclude a full monolayer of water (l≤0.3 nm) and excluding the data points that represent the fully solvated particles (growth factor ≥1.2 in Fig. 4). Although sub-monolayer water adsorption is observed (Peters and Ewing, 1997), implicit in this theory is a bulk solution layer of uniform thickness. In all cases the data are well represented within a narrow window of the fitting parameters and the best-fit solutions also serve to demonstrate the impact of the parameters on the shapes of the curves. Furthermore, the best-fit solutions agree well with values extracted from the literature, listed in the first row of Table 1 and used previously to construct Fig. 3, where their sources are referenced.
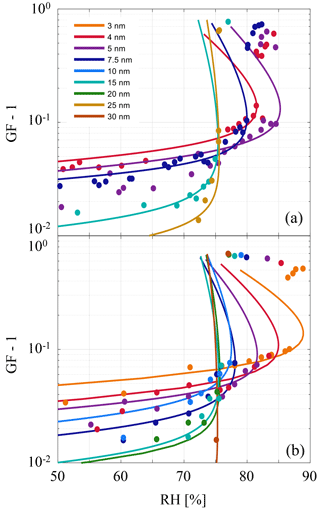
Figure 4Measurement data points of NaCl particle hygroscopic growth under incrementally increasing RH. Colors correspond to different initial dry particle radii indicated in the legend and the growth factor (GF) is the ratio of the measured radius to the dry radius (GF-1 scaling is used to suitably present data on logarithmic scales). (a) Lines represent theoretical fits to data presented by Hämeri et al. (2001). (b) Theoretical fits to data presented by Biskos et al. (2006). In all cases fitting parameters are presented in Table 1. Given the experimentally prescribed increasing humidities, particles that grow beyond the activation barrier set by the strong Kelvin effect (cf. Fig. 5) are observed at RH exceeding the equilibrium value.
For small particles (Rs≲5 nm) the Kelvin term is strong enough to compete with the intermolecular forces and thus the system retains an activation barrier until DRH or above (McGraw and Lewis, 2009), as shown in Figs. 4–5. In practice a small dry particle would be subjected to reversible uptake of water due to intermolecular attraction until it suddenly dissolves into a brine droplet when the deliquescence activation barrier is overcome. However, at short length scales the veracity of the bulk approximations and several other simplifying assumptions of this model must be questioned. For example, the high brine layer concentrations predicted for small particles may be indicative of the model limitations. Although the model represents the data remarkably well even where it might be expected to fail, in those cases it might be better to approach the activation problem in terms of adsorption theory (Langmuir, 1918) or using molecular dynamics simulations (Lovrić et al., 2016).
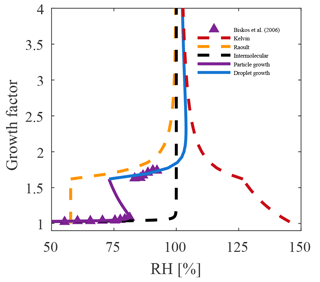
Figure 5The evolution of the individual terms in Eq. (10) are shown for a solvating 5 nm NaCl particle. For such small particles the Kelvin term dominates, yielding an activation barrier, as illustrated by the inflection in the layer growth (magenta) curve. One also observes that the Raoult term (yellow curve) changes only after the solid particle dissolves (RDRH) and that the intermolecular interactions are very short range (black curve).
The refinement of Köhler theory we have proposed yields a smooth metastable transition from solid- to aqueous-phase atmospheric particles. It captures observed behavior for specific compounds, yet remains general such that its application to more complex systems may yield deeper understandings of aerosol phase state and particle behavior.
Real particles in the atmosphere tend to be more complicated than idealized theories of solvation can easily capture. Atmospheric particulates that assist nucleation are often internally mixed and include varying quantities of soluble/insoluble, organic/inorganic materials etc. (Seinfeld et al., 2016; Zardini et al., 2008). Furthermore, theoretical adaptations of Köhler theory have been used to capture particle mixing state; for example “modified Köhler theory” (Bilde and Svenningsson, 2004) and “κ Köhler theory” (Petters and Kreidenweis, 2007). However, these remain limited to predicting critical supersaturations and droplet evolution. Our contribution is general in that it predicts the complete evolution from the dry particle through a metastable equilibrium characterized by a growing thin film, to the fully solvated droplet. Such films are not only consistent with droplet deliquescence but also with previous observations of water absorption and ionic mobility at RH far below the DRH () (Ewing, 2005; Verdaguer et al., 2005; Wise et al., 2008). The implication is that given the correct intermolecular force balance, the surface of any soluble-material-containing atmospheric particle may “predeliquesce” and thereby contribute to an as yet unquantified aqueous reservoir.
The formulation of continuous dry particle dissolution and droplet growth as represented by Eq. (10) and presented in the figures has several advantages over previous treatments of such systems. First we treat the intermolecular interactions explicitly in order to minimize the use of bulk parameters to model the interfacial system. The interfacial free energy minimization is then carried out and incorporated into Köhler theory as a simple additional term that continues to allow for analytical solutions. The approach is in contrast to other treatments of analogous systems that utilize ascribed or phenomenological descriptions of short-range interactions (Bruzewicz et al., 2011; Hellmuth and Shchekin, 2015; Shchekin and Rusanov, 2008; Shchekin et al., 2008, 2013) and/or do not account for the full particle geometry (Bruzewicz et al., 2011) and thus the atmospheric context. The model has the additional benefit of highlighting why, in practice, deliquescence is often observed to be an abrupt transition. The competition between the Kelvin term and the intermolecular forces results in an activation barrier (seen as the inflection points in Figs. 4 and 5), which when exceeded leaves a solvating particle in a highly supersaturated environment. As a result the particle grows suddenly until it reaches the new completely solvated equilibrium. Thus, there may be implications for nonequilibrium particle growth in the atmosphere.
Unfortunately, approximations remain inherent in the model, for example the fitted concentrations of the brine layers increase with decreasing particle size. These predicted equilibrium concentrations may seem physically unrealistic for very small particles, which could be due to the geometric limitations of our model – the dispersion forces are derived assuming interactions between flat, parallel interfaces. But it is also possible that the model is compensating for other physical effects not taken into account in this study (such as surface depletion), effects that could lower the chemical potential of the liquid phase for very small sizes. Applying the model to more complex systems will also yield hurdles and likely make further approximations necessary but, as previously stated, may also lead to deeper insight. This model may allow some assessment of the relative importance of the short- versus long-range interactions and which quantities limit surface phase behavior. However, for mixtures and other materials each term of Eq. (10) would need to be re-evaluated. If bulk parameters that feed into the Köhler behavior (e.g., surface energy, water activity) are poorly constrained, strict physical interpretations will remain challenging.
Given the importance of aerosol phase state there may also be significant implications to even a limited RH range where stable aqueous interfacial films exist. Most obvious is the significance for contributions to aqueous phase chemistry (Martin, 2000). However, there are also potential cloud- and climate-scale impacts that deserve some investigation. The radiative absorption cross section of predeliquescing particles may significantly change their optical properties, as has been shown for aerosol–particle mixtures (Ackerman and Toon, 1981), and especially for particles that include soot (Jacobson, 2000). There are also implications for understanding mixed phase cloud stability given that the equilibrium vapor pressure above a predeliquescence layer can be much lower than the analogous vapor pressure above a liquid droplet (Fig. 6).
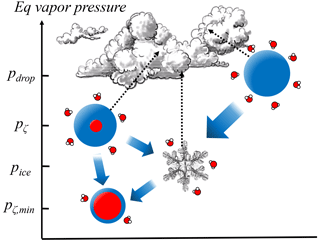
Figure 6Schematic of the equilibrium vapor pressures over droplets, predeliquesced particles, and ice particles, where gradients lead to Wegener–Bergeron–Findeisen processing. The range of equilibrium vapor pressures above predeliquesced thin films straddle the equilibrium vapor pressure over ice pice, resulting in a more stable coexistence between ice and predeliquesced particles, relative to liquid droplets.
Mixed phase clouds are inherently unstable given that air saturated with respect to water is supersaturated with respect to ice, and in fact most precipitation globally originates from mixed phase processes (Mülmenstädt et al., 2015). However, in the Arctic and sub-Arctic regions particularly, the unexplained persistence of mixed phase clouds has consequential climate impacts (Morrison et al., 2012). Simply put, the equilibrium vapor gradient innate between supercooled liquid droplets and ice crystals is greatly diminished if droplets are replaced by predeliquesced particles (Fig. 6), while to some observational techniques the two morphologies may be indistinguishable. A potential result is slower-growing ice crystals and thus a longer lifetime for mixed phase clouds. Although a complete understanding of the mixed phase must also involve particle dynamics (Sullivan et al., 2016), predeliquescing particles may play a contributing role and recent studies suggest that there exist more sources for dry soluble particles than previously thought (Davis et al., 2015b).
This study has introduced a refinement of Köhler theory that tracks a soluble atmospheric particle from its dry state to the solvated droplet equilibrium. The model presumes that from molecular scale adsorption to the growth of thin liquid films, the interface can be stabilized by the intermolecular interactions in a system. Although the details of real atmospheric systems would be subject to strict bookkeeping, even the highly simplified model proposed here captures many important parameters, like equilibrium vapor pressure and liquid layer thickness, that could contribute to better parameterizations for aerosol–cloud interaction modeling efforts.
All data utilized herein were extracted from the cited references.
The supplement related to this article is available online at: https://doi.org/10.5194/acp-18-14939-2018-supplement.
The authors have contributed equally to this work.
The authors declare that they have no conflict of interest.
This research was supported by the Swedish Research Council VR, the Swedish
Research Council FORMAS, the Nordic Top-Level Research Initiative CRAICC, and
the European Commission for ERASMUS mobility. Hendrik Hansen-Goos, Markus Petters,
Sarah Petters, Fabian Mahrt, and Robert McGraw are thanked for
helpful discussions. Special thanks to Merete Bilde whose contributions
significantly helped to improve the paper.
Edited by: Ashu Dastoor
Reviewed by: two anonymous referees
Ackerman, T. P. and Toon, O. B.: Absorption of visible radiation in atmosphere containing mixtures of absorbing and nonabsorbing particles, Appl. Optics, 20, 3661–3668, https://doi.org/10.1364/AO.20.003661, 1981. a
Bilde, M. and Svenningsson, B.: CCN activation of slightly soluble organics: the importance of small amounts of inorganic salt and particle phase, Tellus B, 56, 128–134, 2004. a, b
Biskos, G., Russell, L. M., Buseck, P. R., and Martin, S. T.: Nanosize effect on the hygroscopic growth factor of aerosol particles, Geophys. Res. Lett., 33, l07801, https://doi.org/10.1029/2005GL025199, 2006. a, b, c, d
Bruzewicz, D. A., Checco, A., Ocko, B. M., Lewis, E. R., McGraw, R. L., and Schwartz, S. E.: Reversible uptake of water on NaCl nanoparticles at relative humidity below deliquescence point observed by noncontact environmental atomic force microscopy, The Journal of Chemical Physics, 134, 044702, https://doi.org/10.1063/1.3524195, 2011. a, b, c
Chen, J.-C., Reischl, B., Spijker, P., Holmberg, N., Laasonen, K., and Foster, A. S.: Ab initio Kinetic Monte Carlo simulations of dissolution at the NaCl-water interface, Phys. Chem. Chem. Phys., 16, 22545–22554, https://doi.org/10.1039/C4CP02375G, 2014. a
Cheng, Y., Su, H., Koop, T., Mikhailov, E., and Pöschl, U.: Size dependence of phase transitions in aerosol nanoparticles, Nat. Commun., 6, 5923, https://doi.org/10.1038/ncomms6923, 2015. a, b
Clegg, S. L., Brimblecombe, P., and Wexler, A. S.: Thermodynamic Model of the System H+––––H2O at Tropospheric Temperatures, The Journal of Physical Chemistry A, 102, 2137–2154, https://doi.org/10.1021/jp973042r, 1998. a
Dash, J. G., Rempel, A. W., and Wettlaufer, J. S.: The physics of premelted ice and its geophysical consequences, Rev. Mod. Phys., 78, 695–741, 2006. a
Davis, R. D., Lance, S., Gordon, J. A., and Tolbert, M. A.: Long Working-Distance Optical Trap for in Situ Analysis of Contact-Induced Phase Transformations, Anal. Chem., 87, 6186–6194, https://doi.org/10.1021/acs.analchem.5b00809, 2015a. a
Davis, R. D., Lance, S., Gordon, J. A., Ushijima, S. B., and Tolbert, M. A.: Contact efflorescence as a pathway for crystallization of atmospherically relevant particles, P. Natl. Acad. Sci. USA, 112, 15815–15820, https://doi.org/10.1073/pnas.1522860113, 2015b. a, b
Derjaguin, B. and Landau, L.: Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes, Prog. Surf. Sci., 43, 30–59, https://doi.org/10.1016/0079-6816(93)90013-L, 1993. a
Ewing, G. E.: Intermolecular Forces and Clusters II, chap. H2O on NaCl: From Single Molecule, to Clusters, to Monolayer, to Thin Film, to Deliquescence, Springer Berlin Heidelberg, Berlin, Heidelberg, 1–25, https://doi.org/10.1007/430_012, 2005. a
Farmer, D. K., Cappa, C. D., and Kreidenweis, S. M.: Atmospheric Processes and Their Controlling Influence on Cloud Condensation Nuclei Activity, Chem. Rev., 115, 4199–4217, https://doi.org/10.1021/cr5006292, 2015. a
French, R. H.: Origins and Applications of London Dispersion Forces and Hamaker Constants in Ceramics, J. Am. Ceram. Soc., 83, 2117–2146, https://doi.org/10.1111/j.1151-2916.2000.tb01527.x, 2000. a, b
French, R. H., Parsegian, V. A., Podgornik, R., Rajter, R. F., Jagota, A., Luo, J., Asthagiri, D., Chaudhury, M. K., Chiang, Y.-m., Granick, S., Kalinin, S., Kardar, M., Kjellander, R., Langreth, D. C., Lewis, J., Lustig, S., Wesolowski, D., Wettlaufer, J. S., Ching, W.-Y., Finnis, M., Houlihan, F., von Lilienfeld, O. A., van Oss, C. J., and Zemb, T.: Long range interactions in nanoscale science, Rev. Mod. Phys., 82, 1887–1944, https://doi.org/10.1103/RevModPhys.82.1887, 2010. a
Friese, E. and Ebel, A.: Temperature Dependent Thermodynamic Model of the System H+––Na+–––Cl−–H2O, The Journal of Physical Chemistry A, 114, 11595–11631, https://doi.org/10.1021/jp101041j, 2010. a
Hämeri, K., Laaksonen, A., Väkevä, M., and Suni, T.: Hygroscopic growth of ultrafine sodium chloride particles, J. Geophys. Res.-Atmos., 106, 20749–20757, https://doi.org/10.1029/2000JD000200, 2001. a, b, c, d
Hansen-Goos, H., Thomson, E. S., and Wettlaufer, J.: On the edge of habitability and the extremes of liquidity, Planet. Space Sci., 98, 169–181, https://doi.org/10.1016/j.pss.2013.04.010, 2014. a, b
Haynes, W.: CRC Handbook of Chemistry and Physics, 93rd Edition, CRC Press Taylor & Francis, Boca Raton, FL, USA, 2012. a, b
Hellmuth, O. and Shchekin, A. K.: Determination of interfacial parameters of a soluble particle in a nonideal solution from measured deliquescence and efflorescence humidities, Atmos. Chem. Phys., 15, 3851–3871, https://doi.org/10.5194/acp-15-3851-2015, 2015. a
Hsiao, T.-C., Young, L.-H., Tai, Y.-C., and Chen, K.-C.: Aqueous film formation on irregularly shaped inorganic nanoparticles before deliquescence, as revealed by a hygroscopic differential mobility analyzer – Aerosol particle mass system, Aerosol Sci. Tech., 50, 568–577, https://doi.org/10.1080/02786826.2016.1168512, 2016. a
Jacobson, M. Z.: A physically-based treatment of elemental carbon optics: Implications for global direct forcing of aerosols, Geophys. Res. Lett., 27, 217–220, https://doi.org/10.1029/1999GL010968, 2000. a
Kobayashi, K., Liang, Y., Sakka, T., and Matsuoka, T.: Molecular dynamics study of salt–solution interface: Solubility and surface charge of salt in water, The Journal of Chemical Physics, 140, 144705, https://doi.org/10.1063/1.4870417, 2014. a, b, c
Köhler, H.: The nucleus in and the growth of hygroscopic droplets, T. Faraday Soc., 32, 1152–1161, 1936. a
Korolev, A.: Limitations of the Wegener–Bergeron–Findeisen Mechanism in the Evolution of Mixed-Phase Clouds, J. Atmos. Sci., 64, 3372–3375, https://doi.org/10.1175/JAS4035.1, 2007. a
Langmuir, I.: The adsorption of gases on plane surfaces of glass, mica and platinum, J. Am. Chem. Soc., 40, 1361–1403, https://doi.org/10.1021/ja02242a004, 1918. a
Laskina, O., Morris, H. S., Grandquist, J. R., Qin, Z., Stone, E. A., Tivanski, A. V., and Grassian, V. H.: Size Matters in the Water Uptake and Hygroscopic Growth of Atmospherically Relevant Multicomponent Aerosol Particles, The Journal of Physical Chemistry A, 119, 4489–4497, https://doi.org/10.1021/jp510268p, 2015. a
Lewis, E. R. and Schwartz, S. E.: Sea Salt Aerosol Production: Mechanisms, Methods, Measurements and Models – A Critical Review, American Geophysical Union, Washington DC, USA, https://doi.org/10.1029/GM152, 2004. a
Lohmann, U., Lüönd, F., and Mahrt, F.: An Introduction to Clouds: From the Microscale to Climate, Cambridge University Press, Cambridge, UK, https://doi.org/10.1017/CBO9781139087513, 2016. a, b
Lovrić, J., Duflot, D., Monnerville, M., Toubin, C., and Briquez, S.: Water-Induced Organization of Palmitic Acid at the Surface of a Model Sea Salt Particle: A Molecular Dynamics Study, The Journal of Physical Chemistry A, 120, 10141–10149, https://doi.org/10.1021/acs.jpca.6b07792, 2016. a
Luo, J.: Stabilization of Nanoscale Quasi-Liquid Interfacial Films in Inorganic Materials: A Review and Critical Assessment, CRC Cr. Rev. Sol. State, 32, 67–109, 2007. a
Martin, M., Chang, R. Y.-W., Sierau, B., Sjogren, S., Swietlicki, E., Abbatt, J. P. D., Leck, C., and Lohmann, U.: Cloud condensation nuclei closure study on summer arctic aerosol, Atmos. Chem. Phys., 11, 11335–11350, https://doi.org/10.5194/acp-11-11335-2011, 2011. a
Martin, S.: Phase transitions of aqueous atmospheric particles, Chem. Rev., 100, 3403–3453, https://doi.org/10.1021/cr990034t, 2000. a
McGraw, R. and Lewis, E. R.: Deliquescence and efflorescence of small particles, The Journal of Chemical Physics, 131, 194705, https://doi.org/10.1063/1.3251056, 2009. a, b
Metzger, S., Steil, B., Xu, L., Penner, J. E., and Lelieveld, J.: New representation of water activity based on a single solute specific constant to parameterize the hygroscopic growth of aerosols in atmospheric models, Atmos. Chem. Phys., 12, 5429–5446, https://doi.org/10.5194/acp-12-5429-2012, 2012. a
Mirabel, P., Reiss, H., and Bowles, R. K.: A comparison of Köhler activation with nucleation for NaCl–H2O, The Journal of Chemical Physics, 113, 8194–8199, https://doi.org/10.1063/1.1315992, 2000. a
Montgomery, J. F., Rogak, S. N., Green, S. I., You, Y., and Bertram, A. K.: Structural Change of Aerosol Particle Aggregates with Exposure to Elevated Relative Humidity, Environ. Sci. Technol., 49, 12054–12061, https://doi.org/10.1021/acs.est.5b03157, 2015. a
Morrison, H., de Boer, G., Feingold, G., Harrington, J., Shupe, M. D., and Sulia, K.: Resilience of persistent Arctic mixed-phase clouds, Nat. Geosci., 5, 11–17, 2012. a, b
Mülmenstädt, J., Sourdeval, O., Delanoë, J., and Quaas, J.: Frequency of occurrence of rain from liquid-, mixed-, and ice-phase clouds derived from A-Train satellite retrievals, Geophys. Res. Lett., 42, 6502–6509, https://doi.org/10.1002/2015GL064604, 2015. a
Nenes, A. and Seinfeld, J. H.: Parameterization of cloud droplet formation in global climate models, J. Geophys. Res.-Atmos., 108, 4415, https://doi.org/10.1029/2002JD002911, 2003. a
Orr, C., Hurd, F., and Corbett, W. J.: Aerosol size and relative humidity, J. Coll. Sci. Imp. U. Tok., 13, 472–482, https://doi.org/10.1016/0095-8522(58)90055-2, 1958. a
Peters, S. J. and Ewing, G. E.: Thin Film Water on NaCl(100) under Ambient Conditions: An Infrared Study, Langmuir, 13, 6345–6348, https://doi.org/10.1021/la970629o, 1997. a
Petters, M. D. and Kreidenweis, S. M.: A single parameter representation of hygroscopic growth and cloud condensation nucleus activity, Atmos. Chem. Phys., 7, 1961–1971, https://doi.org/10.5194/acp-7-1961-2007, 2007. a
Pruppacher, H. R. and Klett, J. D.: Microphysics of Coulds and Precipitation, Kluwer Academic Publ., Dordrecht, the Netherlands, 2nd edn., 1997. a
Ruehl, C. R., Davies, J. F., and Wilson, K. R.: An interfacial mechanism for cloud droplet formation on organic aerosols, Science, 351, 1447–1450, https://doi.org/10.1126/science.aad4889, 2016. a
Russell, L. M. and Ming, Y.: Deliquescence of small particles, The Journal of Chemical Physics, 116, 311–321, https://doi.org/10.1063/1.1420727, 2002. a
Schick, M.: Liquids at Interfaces, vol. Les Houches Lectures Session XLVIII, 1988, chap. Chapter 9: Introduction to Wetting Phenomena, Elesvier Science Publishers, New York, 1990. a
Seinfeld, J. H., Bretherton, C., Carslaw, K. S., Coe, H., DeMott, P. J., Dunlea, E. J., Feingold, G., Ghan, S., Guenther, A. B., Kahn, R., Kraucunas, I., Kreidenweis, S. M., Molina, M. J., Nenes, A., Penner, J. E., Prather, K. A., Ramanathan, V., Ramaswamy, V., Rasch, P. J., Ravishankara, A. R., Rosenfeld, D., Stephens, G., and Wood, R.: Improving our fundamental understanding of the role of aerosol–cloud interactions in the climate system, P. Natl. Acad. Sci. USA, 113, 5781–5790, https://doi.org/10.1073/pnas.1514043113, 2016. a
Shchekin, A. K. and Rusanov, A. I.: Generalization of the Gibbs–Kelvin–Köhler and Ostwald–Freundlich equations for a liquid film on a soluble nanoparticle, The Journal of Chemical Physics, 129, 154116, https://doi.org/10.1063/1.2996590, 2008. a, b
Shchekin, A. K., Shabaev, I. V., and Rusanov, A. I.: Thermodynamics of droplet formation around a soluble condensation nucleus in the atmosphere of a solvent vapor, The Journal of Chemical Physics, 129, 214111, https://doi.org/10.1063/1.3021078, 2008. a, b
Shchekin, A. K., Shabaev, I. V., and Hellmuth, O.: Thermodynamic and kinetic theory of nucleation, deliquescence and efflorescence transitions in the ensemble of droplets on soluble particles, The Journal of Chemical Physics, 138, 054704, https://doi.org/10.1063/1.4789309, 2013. a, b
Stocker, T. F., Qin, D., Plattner, G. K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M. (Eds.): IPCC, 2013 Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assesment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, https://doi.org/10.1017/CBO9781107415324, 2013. a
Sullivan, S. C., Lee, D., Oreopoulos, L., and Nenes, A.: Role of updraft velocity in temporal variability of global cloud hydrometeor number, P. Natl. Acad. Sci. USA, 113, 5791–5796, https://doi.org/10.1073/pnas.1514039113, 2016. a
Tang, I. N. and Munkelwitz, H. R.: Aerosol Phase Transformation and Growth in the Atmosphere, J. Appl. Meteorol., 33, 791–796, https://doi.org/10.1175/1520-0450(1994)033<0791:APTAGI>2.0.CO;2, 1994. a
Tang, I. N., Tridico, A. C., and Fung, K. H.: Thermodynamic and optical properties of sea salt aerosols, J. Geophys. Res.-Atmos., 102, 23269–23275, https://doi.org/10.1029/97JD01806, 1997. a
Thomson, W.: On the Equilibrium of Vapour at a Curved Surface of Liquid, Philos. Mag., 42, 448–452, 1871. a
Verdaguer, A., Sacha, G. M., Luna, M., Frank Ogletree, D., and Salmeron, M.: Initial stages of water adsorption on NaCl (100) studied by scanning polarization force microscopy, The Journal of Chemical Physics, 123, 124703, https://doi.org/10.1063/1.1996568, 2005. a
Verwey, E. J. W. and Overbeek, J. T. G.: Theory of the Stability of Lyophobic Colloids, Elsevier, Amsterdam, 1948. a
Wise, M. E., Martin, S. T., Russell, L. M., and Buseck, P. R.: Water Uptake by NaCl Particles Prior to Deliquescence and the Phase Rule, Aerosol Sci. Technol., 42, 281–294, https://doi.org/10.1080/02786820802047115, 2008. a
Zardini, A. A., Sjogren, S., Marcolli, C., Krieger, U. K., Gysel, M., Weingartner, E., Baltensperger, U., and Peter, T.: A combined particle trap/HTDMA hygroscopicity study of mixed inorganic/organic aerosol particles, Atmos. Chem. Phys., 8, 5589–5601, https://doi.org/10.5194/acp-8-5589-2008, 2008. a
Zeng, J., Zhang, G., Long, S., Liu, K., Cao, L., Bao, L., and Li, Y.: Sea salt deliquescence and crystallization in atmosphere: an in situ investigation using x-ray phase contrast imaging, Surf. Interface Anal., 45, 930–936, https://doi.org/10.1002/sia.5184, 2013. a
Zumdahl, S. S.: Chemical Principles, Houghton Mifflin Company, Boston, MA, 5th edn., 2005. a





