the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Influence of relative humidity on the heterogeneous oxidation of secondary organic aerosol
Katherine A. Smith
Secondary organic aerosol (SOA) is a complex mixture of hundreds of semi-volatile to extremely low-volatility organic compounds that are chemically processed in the atmosphere, including via heterogeneous oxidation by gas-phase radicals. Relative humidity (RH) has a substantial impact on particle phase, which can affect how SOA evolves in the atmosphere. In this study, SOA from dark α-pinene ozonolysis is heterogeneously aged by OH radicals in a flow tube at low and high RH. At high RH (RH =89 %) there is substantial loss of particle volume (∼60 %) at an equivalent atmospheric OH exposure of 3 weeks. In contrast, at low RH (RH =25 %) there is little mass loss (<20 %) at the same OH exposure. Mass spectra of the SOA particles were measured as a function of OH exposure using a vacuum ultraviolet aerosol mass spectrometer (VUV-AMS). The mass spectra observed at low RH overall exhibit minor changes with oxidation and negligible further changes above an OH exposure molecule cm−3 s suggesting limited impact of oxidation on the particle composition. In contrast, the mass spectra observed at high RH exhibit substantial and continuous changes as a function of OH exposure. Further, at high RH clusters of peaks in the mass spectra exhibit unique decay patterns, suggesting different responses of various species to oxidation. A model of heterogeneous oxidation has been developed to understand the origin of the difference in aging between the low- and high-RH experiments. Differences in diffusivity of the SOA between the low- and high-RH experiments alone can explain the difference in compositional change but cannot explain the difference in mass loss. Instead, the difference in mass loss is attributable to RH-dependent differences in the OH uptake coefficient and/or the net probability of fragmentation, with either or both larger at high RH compared to low RH. These results illustrate the important impact of relative humidity on the fate of SOA in the atmosphere.
- Article
(3394 KB) -
Supplement
(1110 KB) - BibTeX
- EndNote
Organic aerosol (OA) is ubiquitous in the atmosphere and makes up a large fraction of submicron particulate matter (Zhang et al., 2007). OA includes primary organic aerosol (POA) particles that are emitted directly into the atmosphere and secondary organic aerosol (SOA), which is formed in the atmosphere through oxidation of volatile organic compounds (VOCs) and yields less-volatile products that partition to the particle phase (Hallquist et al., 2009). SOA is often found to dominate OA mass (Jimenez et al., 2009) and thus can have a large impact on the ability of particles to affect climate and air quality. Despite the importance of SOA, understanding its full life cycle – involving formation, chemical evolution and removal processes – remains challenging due to its complex and variable composition (Hallquist et al., 2009).
Heterogeneous oxidation is an important process during the life cycle of OA in the atmosphere. Heterogeneous oxidation of OA involves the reaction of gas-phase oxidants, such as OH and O3, with compounds in the condensed phase. Heterogeneous oxidation can alter the composition of organic particles through two general pathways: functionalization and fragmentation (Kroll et al., 2009; Donahue et al., 2012; Lambe et al., 2012; Nah et al., 2013; Wiegel et al., 2015). Functionalization leads to formation of more oxygenated species in the particles (Smith et al., 2009; Ruehl et al., 2013) while fragmentation generally leads to production of more volatile species (Slade and Knopf, 2013). Heterogeneous oxidation can alter the optical properties (Cappa et al., 2011; Dennis-Smither et al., 2012), hygroscopicity (Petters et al., 2006; George et al., 2009; Cappa et al., 2011; Dennis-Smither et al., 2012; Harmon et al., 2013; Slade et al., 2015), density (George et al., 2007; Kroll et al., 2009; Nah et al., 2014), thermal properties (Emanuelsson et al., 2014; Hu et al., 2016) and the particle size (George et al., 2009; Dennis-Smither et al., 2012; Donahue et al., 2012; Kroll et al., 2015) of OA.
Various laboratory experiments have considered heterogeneous oxidation by OH of OA particles or films of OA proxies; these have typically focused on single compound systems (e.g., George et al., 2007; McNeill et al., 2008; Hennigan et al., 2010; Nah et al., 2013; Slade and Knopf, 2013; Chan et al., 2014; Davies and Wilson, 2015; Fan et al., 2015; Kroll et al., 2015; Lai et al., 2015). In general, heterogeneous oxidation leads to an increase in the bulk-average oxygen-to-carbon ratio (or the average carbon oxidation state) as a function of photochemical age (Kroll et al., 2015). Heterogeneous oxidation by OH can also lead to varying amounts of OA mass loss, from negligible to more than 30 % for OH exposures, equivalent to 1 week of typical ambient OH (Kroll et al., 2015).
One important consideration in understanding the impact of heterogeneous oxidation on OA properties is the influence of relative humidity and particle-phase water. The phase of OA particles depends on the OA composition and the relative humidity (RH) (Koop et al., 2011; Renbaum-Wolff et al., 2013). For SOA in general, particles at low RH tend to have very high viscosity, with the particles behaving as if solid or semi-solid, although the exact behavior depends on the SOA precursor gas, oxidant and concentration (Virtanen et al., 2010). At high RH, however, the viscosity of SOA is generally much lower, with the particle phase being more liquid-like (Bateman et al., 2015). Diffusion coefficient (Dorg) of molecules within particles are related to viscosity according to Stokes–Einstein relation, with lower diffusion coefficients corresponding to higher viscosity. The molecular diffusivity is further related to the mixing timescale (τ) of the particle. The relationship between Dorg and τ is approximately , where dp is the particle diameter. For reference, the τ of a 100 nm particle is ∼2.5 s when cm2 s−1, corresponding to a more “liquid-like” particle, while τ is ∼40 min when cm2 s−1, typical of “semi-solid” particles. Because RH impacts Dorg and mixing timescales, variations in RH have the potential to impact particle reactivity (Kuwata and Martin, 2012; Y. J. Li et al., 2015b; Wang et al., 2015) and thus the evolution of particles in the atmosphere.
To address this, recent experimental studies have considered the effect of RH on heterogeneous oxidation by OH radicals, typically using model (single-component) OA systems. Some studies have observed slower loss of the model compound (Chan et al., 2014; Davies and Wilson, 2015; Fan et al., 2015; Chim et al., 2017b), or smaller gas-phase uptake coefficients (Slade and Knopf, 2014) under lower-RH conditions. A number of model simulations have suggested the smaller OH uptake coefficient and longer photochemical lifetime of OA under dry conditions are driven by limited diffusion in highly viscous particles (Arangio et al., 2015; Houle et al., 2015). However, other single-component studies report no effect of RH or even a decrease in the loss of parent species and OH uptake (Park et al., 2008; Lai et al., 2014; Slade and Knopf, 2014), with suggestions that the existence of a water film at the surface hinders uptake of gas-phase oxidants. Given these contrasting results, it is difficult to extrapolate from these model systems to understand how RH might influence the reactivity of chemically complex SOA. We are aware of only one study that has probed the influence of RH on reactivity of SOA. Hu et al. (2016) examined the dependence on RH of heterogeneous oxidation of ambient isoprene-epoxydiol-derived (IEPOX) SOA by OH over the RH range 40 %–100 %. They observed mass loss of IEPOX-SOA upon heterogeneous oxidation at all RHs investigated. The extent of IEPOX-SOA loss was independent of RH for RH <90 %. However, at RH >90 % they found that the loss was somewhat enhanced, most likely as a result of an increase in particle surface area and not as a result of changes to particle phase, because viscosity of the IEPOX-SOA particles was likely sufficiently low that the particles exhibited liquid-like behavior at all RH conditions considered. Thus, the specific influence of SOA phase on heterogeneous reactivity remains unclear.
To address this gap, we have conducted heterogeneous OH oxidation experiments under low- and high-RH conditions using SOA formed from dark ozonolysis of α-pinene. We selected α-pinene SOA because oxidation of monoterpenes, including α-pinene, is an important source of SOA globally (Guenther et al., 1995, 2012; Ziemann and Atkinson, 2012). In addition, the composition, phase state and photochemical aging of α-pinene SOA have been extensively investigated, although the impact of phase on photochemical aging has not been characterized. Here we establish the effect of RH on the photochemical aging of the α-pinene SOA in terms of the influence on aerosol mass and compositional change. A simplified multiphase oxidation model that couples reaction and diffusion is used to understand the RH-dependent factors that impact photochemical aging.
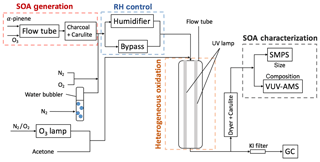
In the experiments here (Cappa et al., 2018), SOA is formed initially under dry conditions, and these SOA particles are then heterogeneously oxidized by OH at either a low or high RH. The experimental setup is shown in Fig. 1. Four parts are highlighted: SOA formation, RH control, heterogeneous oxidation and SOA measurements. SOA particles were first produced chemically in one flow tube under dry conditions (the SOA formation flow tube). The airstream was then humidified to the desired level, and the SOA particles were reacted heterogeneously with OH radicals in a second flow tube (the OH flow tube). The size distribution and chemical composition of the particles were then characterized. Each of these steps is described below.
2.1 SOA formation
SOA was formed from the homogeneous nucleation of products from dark ozonolysis of α-pinene in a stainless steel flow tube reactor in the absence of seed particles and NOx. α-pinene (98 %, Sigma-Aldrich) was constantly injected into a stream of clean, dry N2 (at 1.0 µL h−1) using two parallel syringe pumps. O3 was produced by passing the mixture through a cell lit by a Hg Pen-Ray lamp (UVP, LLC). These two flows were introduced into a 25 cm long, 1.2 cm diameter stainless steel tube containing two helical static mixers (StaMixCo LLC) and then passed into a 170 cm long, 2.5 cm diameter flow tube reactor. This step-wise increase in diameter facilitated the mixing of the reactants and limited dead volume in the main flow tube. The typical residence time of the flow tube was around 80 s. The O3 concentration was measured using an O3 monitor (Model 108L, 2B Technologies) while the α-pinene concentration is estimated based on flow rates and infusion rate. No OH scavenger was used during SOA formation. Detailed information of each experiment is summarized in Table 1. Downstream of the flow tube was a Carulite 200 (Carus Corporation) denuder followed by a charcoal denuder to remove residual hydrocarbons and oxidants in the gas phase. Previous experiments have shown negligible mass loss of SOA particles due to scavenging of vapors in denuders on the timescales relevant to our experiments (Cappa and Wilson, 2011). Therefore, the gas-phase oxidation of evaporated semi-volatile organics in the second flow tube is likely limited.
Table 1Experimental conditions for SOA generation and heterogeneous oxidation.
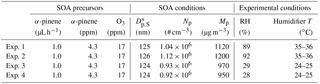
* Dp,S is the surface-weighted middle diameter of initial dry particles.
As shown in Table 1, mass concentrations of SOA were ∼1000 µg m−3, which is substantially higher than typical ambient aerosol concentrations by 2 orders of magnitude (depending on the environment). However, the high initial concentrations are needed to allow for robust chemical characterization of the particles by the VUV-AMS at the much lower concentrations encountered after particles have lost much of their mass at high OH exposures.
2.2 RH control
Particles were reacted with gas-phase OH radicals in a second flow tube at two distinct RH conditions: high RH and low RH. Grayson et al. (2016) summarize a variety of experimental observations of the influence of RH on the phase state of α-pinene SOA. Although there are discrepancies in the exact values of Dorg for α-pinene SOA in the literature, the observations generally indicate that cm2 s−1 below RH equalling 30 % and cm2 s−1 above RH equalling 70 %. Based on this, the experiments here were conducted at RH equalling 25 % for low-RH experiments and at RH equalling 89 % for high-RH experiments. A dry N2 stream, a N2 stream humidified by a water bubbler and the stream containing the SOA particles were combined after the denuders. Three steps were used to achieve the desired RH range in the OH flow tube. First, the fraction of dry and humidified N2 was varied, with no dry N2 for high-RH experiments. Second, the SOA particle stream was passed through a Nafion humidifier (Perma Pure LLC) for high-RH experiments, but through a bypass line for low-RH experiments. Third, the humidifier was heated to slightly above ambient temperatures (to ∼35–36 ∘C) to increase the absolute water vapor concentration in the flow for high-RH experiments. At this temperature and given the very short residence time in the humidifier, evaporation of SOA should be minimal (Kolesar et al., 2015). Condensation between the humidifier and the OH flow tube was avoided by maintaining the connecting tubing at the same temperature as the humidifier.
RH and temperature were monitored both at the inlet and outlet of the OH flow tube using Omega temperature controllers (CNi series, OMEGA Engineering, Inc.) and Newport humidity probes (iTHP-5, Newport Electronics), and temperature in the OH flow tube was measured by a thermocouple (5SC-TT-K-30-36, OMEGA Engineering, Inc.). Temperature in the OH flow tube was usually a few degrees higher than room temperature due to heating from the UV lamps, 26–27 ∘C compared to 24–25 ∘C, respectively. The temperature at the flow tube outlet was controlled to be equal to the temperature in the OH flow tube such that the RH measured at the outlet was representative of the RH in the OH flow tube.
2.3 Heterogeneous oxidation
The SOA was heterogeneously oxidized by OH radicals in a 130 cm long quartz flow tube. The residence time was 38 s at the flow rate of 1.0 L min−1. Four continuous output 130 cm long Hg lamps (λ=254 nm; Sankyo Denki) were positioned outside of the quartz flow tube. OH radicals were generated by the following reactions:
At a fixed condition (dry versus wet), the concentration of OH was varied by changing the input O3 concentration (Fig. S1 in the Supplement). O3 was generated using a corona discharger (Model Y, Ozone Services). The O3 concentration generated can be varied from 20 to 1000 ppm, which corresponds to 1–50 ppm after dilution into the OH flow tube. The O3 concentration was measured by an O3 monitor (Model 202M, 2B Technologies) before dilution into the flow tube.
To estimate the OH exposure in the flow tube, a tracer compound, acetone (H3CC(O)CH3), was added to the flow. Acetone reacts with OH along the length of the flow tube with a known rate coefficient, kAce+OH. We used the average temperature-dependent rate constant from Wollenhaupt et al. (2000) and Gierczak et al. (2003). The observed decay of acetone was used to calculate the OH exposure:
where [H3CC(O)CH3]0 and [H3CC(O)CH3] are the initial and final concentrations of acetone, respectively, [OH] is the time-dependent concentration of OH, 〈OH〉t is the time-averaged concentration of OH, and t is the residence time in the quartz flow tube, which is fixed at 38 s (Fig. S1). The acetone concentration was measured using a gas chromatograph (Model 8610C, SRI Instruments). A cylinder of 50 ppm acetone balanced in N2 was prepared and used. After dilution, the initial concentration of acetone entering the OH flow tube was ∼750 ppb.
Water vapor was removed from the airstream that exited the OH flow tube (after the RH was measured) by a diffusion dryer, and any remaining gas-phase hydrocarbons and oxidants were removed by a Carulite denuder.
2.4 SOA characterization
Both particle size and composition were characterized after the OH flow tube. The size distributions of the SOA particles were characterized by a scanning mobility particle sizer (SMPS; TSI Inc.), composed of a differential mobility analyzer (DMA; Model 3085, TSI Inc.) and a condensation particle counter (CPC; Model 3772, TSI Inc.). The SOA volume concentration at each OH exposure was calculated from the volume-weighted distribution. These volume concentrations (Vp) were normalized by the measured particle number concentration to account for variations in particle losses that result from changes in particle size upon heterogeneous oxidation. By comparing the number-normalized Vp values at a given OH exposure to that at no OH exposure, the extent of bulk volume (mass) loss as a function of OH exposure is obtained.
The composition of the SOA particles was characterized using the time-of-flight (ToF) vacuum ultraviolet aerosol mass spectrometry (VUV-AMS) at beamline 9.0.2 at the Advanced Light Source (ALS) at Lawrence Berkeley National Laboratory. A detailed description of the instrument has been reported elsewhere (Gloaguen et al., 2006). Briefly, particles are sampled into the instrument and focused into a particle beam through an aerodynamic lens. The particles impact onto a heater block that is maintained at 120–125 ∘C and evaporate. The evaporated molecules are photoionized using 10.5 eV radiation. The resulting ions are extracted and directed into a ToF mass spectrometer for detection. Each particle measurement is coupled with a background measurement. The background spectra are measured by sampling air into the VUV-AMS through a particle filter before the particle measurements. All the mass spectra reported here are background corrected. While the resolution of the VUV-AMS is m∕Δm ∼2000, the mass spectra reported here are in unit mass resolution.
2.5 Multilayer heterogeneous oxidation model
We developed a simplified multilayer heterogeneous oxidation model that is based on both the kinetic multi-layer models, KM-SUB, KM-GAP (Shiraiwa et al., 2010, 2012) and a stochastic model (Wiegel et al., 2015, 2017). The model is used to develop understanding of the factors that influence the particle bulk behavior and compositional change under different RH conditions. Our model treats particles as 2-D spheres having a fixed-depth surface layer and n variable-depth, subsurface bulk layers, as illustrated in Fig. 2. The depths of all subsurface layers are assumed to be equal. Diffusion and chemical reactions are coupled in the model to simulate evolution of SOA.
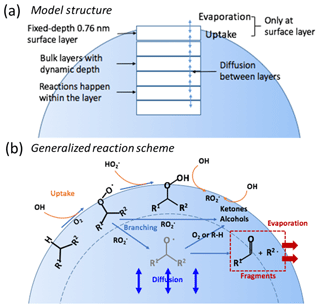
Figure 2Overview of the simplified model. (a) The particle is treated as a sphere stacked with a fixed-depth surface layer and multiple bulk layers with dynamic depths that evolve as the particle evaporates. (b) A generalized reaction scheme of the oxidation process. Oxidation is initiated by H-abstraction of parent compounds that generate organic peroxy radicals (RO2•) which react to form peroxides (ROOH), alcohols or ketones, or alkoxy radicals (RO•). RO• radicals can react to form fragments or stable functionalized products. The net probability of fragmentation is treated implicitly in the model by combining the probability of alkoxy radical formation and their fragmentation. Uptake of HOx radicals and evaporation of fragments occurs only at the surface layer.
Reactions of gas-phase HOx (OH and HO2) radicals with condensed-phase organic species are assumed to occur only in the surface layer. Unlike the KM-SUB model and the stochastic model, the physical processes of adsorption and desorption of HOx radicals are not explicitly simulated in the model. Production of HOx radicals from reactions that occur within the condensed phase is also not considered. Therefore, reactions involving HOx radicals are assumed to happen only at the surface, and not in the subsurface bulk layers. This is a reasonable assumption because HOx radicals are very reactive species, and they likely primarily react within 1 nm from the surface in organic aerosols (Arangio et al., 2015) with the probability of reaction falling off rapidly with distance into the particle (Houle et al., 2015). The OH and HO2 reaction rates are thus calculated by using a single uptake coefficient (γ) that characterizes the fraction of collisions that lead to reaction of HOx radicals with organic molecules at the surface, as illustrated by Eq. (2) (Smith et al., 2009):
where Y is any reactive stable organic species in the surface layer that can react with OH, is the uptake coefficient of OH radicals by species Y, fY is the fraction of Y molecules in the surface layer, Cp is the particle number concentration and A is the particle surface area of one particle. Jcoll is the OH radical flux at the particle surface, calculated as:
where is the mean speed of gas-phase OH and [OH]gs is the near-surface concentration of gas-phase OH. The relationship between [OH]gs and [OH]g, the concentration far away from the particle surface, can be described as:
where Cg,OH is a gas-phase diffusion correction factor suggested by Pöschl et al. (2007):
KnOH is the Knudsen number approximated as:
where Dg,OH is the OH gas-phase diffusion coefficient and Dp,s is the surface-weighted particle diameter. This correction is needed to account for gas-phase diffusion especially when high uptake of gas-phase OH leads to strong local depletion of OH near particle surface.
The same calculations for reaction rates are applied to reactions involving gas-phase HO2 radicals. The gas-phase concentrations of HOx radicals ([OH]g and [HO2]g) are assumed to be constant throughout the flow tube for a given OH exposure. At each OH exposure, the OH concentration is set equal to the time-averaged concentration as calculated from the specified OH exposure divided by total reaction time (38 s). The concentration of HO2 is assumed to be same as that of OH. Using the reaction scheme of R. Li et al. (2015) to simulate the more detailed gas-phase chemical reactions, it was determined that this was a reasonable assumption.
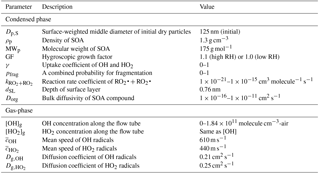
Since HOx radicals are assumed to react at the surface, the depth of the surface layer is set to 0.76 nm, corresponding to an effective molecular diameter of typical SOA components. This value is estimated assuming an average molecular weight of 175 g mole−1 and density of 1.3 g cm−3 for α-pinene SOA (Renbaum-Wolff et al., 2013). The depth of the surface layer is assumed to be independent of the total particle size, i.e., is constant.
A generalized reaction scheme of OH oxidation of alkanes suggested by Ruehl et al. (2013) and Wiegel et al. (2015) is used to simulate the compositional change of particles, as shown in Fig. 2b. It is assumed that all of the initial (unreacted) SOA molecules react identically. It is also assumed that all functionalized stable products formed are reactive towards OH, and up to three generations of products are considered. The general reaction scheme for both SOA parent species and for stable product species (written as Px, where x indicates the generation number, from 0 to 3) can be written as follows:
The stable product species that can go on to react are the ROOH and ROH species. The above scheme illustrates that oxidation is initiated by H-abstraction from a stable species (parent or product) by OH (Reaction R3), leading to production of an organic peroxy radical (RO2•). It is implicitly assumed that the alkyl radical (R•) that proceeds RO2• formation reacts rapidly with O2. The RO2• radicals can then react with either HO2 or RO2•. Reaction with HO2 (Reaction R4) leads to production of organic hydroperoxides (ROOH). Reaction of RO2• with another RO2• can lead to production of either functionalized stable products (alcohols or ketones; Reaction R5a) or alkoxy radicals (RO•; Reaction R5b). All stable product species produced from RO2• self-reactions are lumped into the generation-specific generic product species ROHx, where x indicates the generation. The RO• can either react with O2 (Reaction R6b) or other stable species (Reaction R6c) to produce stable products (ROH) or can decompose to produce two fragmentation products (F1 and F2; Reaction R6a). The fragmentation products are assumed to have low molecular weight and high volatility and thus evaporate from the particles, leading to mass loss. The stable products can further react with OH radicals in the surface layer and lead to the next generation of products. Formation of ROOH and ROH is known as functionalization. Here, the net effect of Reaction (R5) (RO2•+RO2• reactions) and Reaction (R6) (the fate of RO•) is treated in a simplified manner. In particular, RO• is not treated explicitly. Instead, the overall probability that RO2•+RO2• ultimately leads to production of functionalized products or fragmentation products is considered as a lumped probability (pfrag). The parameter pfrag accounts for both the branching ratio of RO2•+RO2• reactions and the fractional loss of RO• from decomposition (Reaction R6a) versus functionalization (Reactions R6b and R6c). The overall reaction for RO2•+RO2• can then be written as:
where F indicates all fragmentation products. The fragmentation products are assumed to be nonreactive towards OH and are the only species that can evaporate. This simplification of the reaction scheme serves to overcome the lack of knowledge regarding the actual branching ratios and rate coefficients associated with RO• decomposition and reaction with O2 and other stable species. The value of pfrag is not known a priori but can be varied to establish the sensitivity of the model to functionalization versus fragmentation, and how this might differ depending on the RH (and particle-phase state). It is assumed that γOH and , the rate coefficients for self-reaction of RO2• radicals (), and pfrag are the same for all generations. Generation-specific products are tracked through three generations of reaction. Subsequent reactions of third generation species are assumed to reform third generation species.
Reactions occur within layers, and diffusion occurs between neighbor layers. The diffusion rates are calculated based on the equations used in the KM-SUB model (Shiraiwa et al., 2010). The diffusion coefficient (Dorg) is assumed to be the same for parent compounds and functionalization products (both stable products and radical intermediates) and are dependent upon the RH. The Dorg for fragments is assumed to be 1.4 times larger than for the other species to account for their smaller sizes. The model results are not sensitive to reasonable variations in Dorg of the fragments.
Only fragmentation products are assumed to be sufficiently volatile to evaporate. All other species are assumed to be effectively nonvolatile. The evaporation of fragmentation products is treated in a simplified manner wherein once these compounds reach the surface layer (either because they are directly produced in that layer or diffuse up from lower layers), they evaporate instantaneously. The change of particle size is calculated based on loss of fragments, assuming a linear relation between molecule number and particle volume. As particles shrink, the thickness of the subsurface bulk layers (including the radius of the inner core) decreases based on the new particle size and constant total layer number, and the volume of each layer and molecular density of each species in each layer are recalculated. Density and averaged molecular weight of the aerosol are assumed to be constant over the process of oxidation.
Both the particle volume and composition after 38 s (the residence time of the quartz flow tube) of reaction are calculated as a function of OH concentration. The evolution of the particle volume and composition with OH exposure are then determined from the individual model results at each OH concentration. The simulated volume fraction remaining (VFR) of particles as a function of OH exposure can be directly and quantitatively compared to the observed VFR, while the simulated compositional changes can be qualitatively compared to the measurement of spectral change.
Water uptake affects the SOA in various ways. Water uptake can engender a change (decrease) in the SOA viscosity, cause the particle size to increase with a corresponding dilution of the organic molecules, impact the uptake of OH (i.e., γ) or alter the oxidation chemistry in the condensed phase (i.e., pfrag). The impact of viscosity changes are considered in the model by systematically varying the Dorg while assuming a constant, RH-independent size, composition, γ and pfrag (Sect. 3.3.1). The impact of the size increase and dilution are considered together by using an increased particle surface area and a decreased molecular density of organic compounds for high-RH simulations, where the extent of growth, characterized by the hygroscopic growth factor (GF) is constrained by literature observations (Sect. 3.3.2). In these simulations, the hygroscopicity of the products is assumed to be the same as the parent species, and thus the assumed growth factor is constant with oxidation. The impacts of variations in either γ or pfrag between low- and high-RH conditions are considered together (Sect. 3.3.3). These parameters are tuned one at a time for low- and high-RH conditions (using RH-dependent Dorg and size) to achieve good agreement with the measurements.
3.1 Bulk behavior
The heterogeneous oxidation of α-pinene SOA by OH leads to mass loss and particle shrinking for both the low- and high-RH condition. However, the extent of shrinkage at a given OH exposure differs between low and high RH (Fig. 3). An example of the change in the size distributions before and after heterogeneous oxidation at the same OH exposure ( molecule cm−3 s) is shown for both low and high RH (Fig. 3b). The general broadening of the size distribution after exposure to OH is due to the slower overall reaction for larger particles, resulting from their smaller surface-to-volume ratio. The variation in the volume loss with OH exposure between low and high RH is shown in Fig. 3a. At an OH exposure equalling 4.7×1012 molecule cm−3 s, only 20 % of particle volume (or mass assuming constant particle density) is lost at low RH, compared to more than 60 % volume loss at high RH. These observations clearly indicate that particles shrink to a much greater extent under high RH. These observations may have implications for the lifetime of SOA with respect to heterogeneous oxidation in the atmosphere. Assuming a typical atmospheric [OH] of 2×106 molecules cm−3, it would take 4 weeks for α-pinene SOA to lose 20 % of volume under dry conditions but only a few days to lose the same amount of volume under wet conditions. These observations suggest that SOA mass loss due to heterogeneous OH oxidation may vary substantially throughout the atmosphere, dependent on variations in ambient RH.
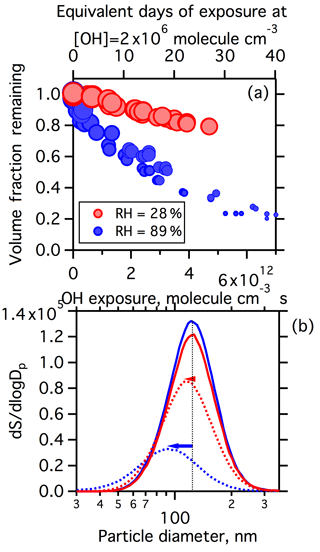
Figure 3Influence of photochemical aging on SOA volume for low-RH (red) or high-RH (blue) conditions. (a) The volume fraction remaining as a function of OH exposure. The sizes of markers correspond to particle size. (b) Example surface-weighted size distributions of particles before OH exposure (solid lines) and after oxidation at an OH exposure molecule cm−3 s (dashed lines).
Our observations for SOA can be compared to various single-component observations from the literature. Fan et al. (2015) reported the mass fraction remaining for methyl β-D-glucopyranoside (a cellulose oligomer surrogate) nanoparticles after photochemical aging by OH radicals at RH equalling 10–30 %. The extent of mass loss was observed to increase with RH to a small extent in this range. Chan et al. (2014) have also observed that aqueous (high RH) succinic acid particles lost volume to a greater extent than solid (low RH) succinic acid particles at the same OH exposure. However, they observed no further change in volume above OH exposure molecule cm−3 s for aqueous droplets, different from our observation of continuous volume loss at high RH. This is likely a result of the different chemical systems used. Davies and Wilson (2015) reported the change in diameter of citric acid particles as a function of OH lifetimes for RH equalling 20–90 %. For all RH conditions, they observed that the particle diameter initially increased but then peaked and decreased as the number of oxidation lifetimes was increased. Their oxidation lifetime values can be converted to equivalent, RH-dependent OH exposures using the reported rate constant. We find that there is a greater change in particle diameter for a given OH exposure for their experiments when RH is higher, with greater overall volume loss at high RH. Additionally, the initial small increase in diameter occurs at relatively low OH exposures ( molecules cm−3 s), and the general effects of RH on particle volume loss with OH exposure are reasonably consistent with our observations. In addition to the single-component studies, our results can also be compared to the observations of Hu et al. (2016), who reported the mass fraction remaining for IEPOX-SOA in the ambient environment as a function of OH exposure. As noted in the introduction, they observed faster decay of particle mass at 90–100 % RH compared to <90 % RH, but no further variation with RH at <90 %. However, they also observed a larger surface area concentration under 90 %–100 % RH due to particle growth, which was postulated to facilitate faster OH uptake. An increase in surface area is unlikely to explain our observation because the water uptake of α-pinene SOA at RH equalling 90 % is small (Varutbangkul et al., 2006), and the dry particle size distributions of our nonoxidized particles are nearly identical between the two RH conditions (Fig. 3b). Further, the increase in surface area is offset by a decrease in the mole fraction of the organic species due to the presence of water, which will be examined in Sect. 3.3.2.
3.2 Spectral changes
The composition of SOA generated from ozonolysis of α-pinene has been well-studied using both online and offline mass spectrometry (e.g., Tolocka et al., 2006; Shilling et al., 2009; Camredon et al., 2010; Putman et al., 2012; Yasmeen et al., 2012; Hall et al., 2013; Kristensen et al., 2014, 2016; Zhang et al., 2017). The mass spectrum obtained depends on the measurement method used. For example, mass spectra of α-pinene SOA obtained using high-temperature evaporation (>600 ∘C) coupled with electron impact ionization at 70 eV (the typical operating conditions of the Aerodyne AMS) have very few ions with having substantial intensity (Shilling et al., 2009). In contrast, mass spectra obtained using electrospray ionization (ESI), typically considered a softer ionization method, typically show that dimers or oligomers (nominally those compounds having molecular weights more than twice higher than that of the parent compound, 136 amu for α-pinene) comprise a substantial fraction of the particle (Kristensen et al., 2014; Zhang et al., 2017). Mass spectra for α-pinene SOA obtained using the VUV-AMS, used here, exhibit peaks spanning the range –300, although with much lower intensity ions at amu (Fig. 4). In the VUV-AMS spectra, ions in range –200 are likely a combination of monomers (especially above ), fragments of monomers (especially below ) and fragments of dimers. For example, characteristic fragment ions of monomers such as cis-pinonic acid and pinic acid, known products of α-pinene ozonolysis (Yu et al., 1999; Kristensen et al., 2014), have been previously identified in VUV-AMS mass spectra of nonoxidized particles (Mysak, 2006) and are observed here with high intensity in the nonoxidized particles. The characteristic ions are observed at , 114, 125, 166 for cis-pinonic acid () and at , 114, 140, 168 for pinic acid (), respectively. However, some of the odd-numbered, high-intensity ions that were observed in the nonoxidized particles, such as , 141 and 169 (Fig. 4), may be fragments of dimers based on Kristensen et al. (2016), although they used a different mass spectrometry technique (ESI). This is consistent with the peaks in the VUV-AMS spectrum of α-pinene SOA consisting of contributions of monomers, fragments of monomers and fragments of dimers. Dimers and oligomers are likely underrepresented in VUV-AMS spectra of α-pinene SOA, although they may comprise more than 50 % of the aerosol mass (Kristensen et al., 2016). This underrepresentation is probably attributable to substantial fragmentation of dimers during the ionization process and/or the slow desorption of dimers from the heater block, leading to low sensitivity of VUV-AMS towards dimers and oligomers.
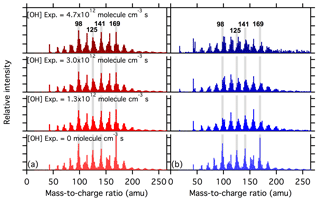
Figure 4Example mass spectra of SOA as a function of OH exposure for (a) low-RH (red, left panels) and (b) high-RH (blue, right panels) conditions. OH exposure increases from the bottom to the top panels, with values listed in the panels. Vertical gray bars highlight four ions that exhibited a dramatic decay at high RH, but only small changes at low RH. The mass-to-charge ratio of these four ions are indicated in the figure.
The relative changes of the α-pinene SOA mass spectra are considered as a function of OH exposure. We define nonoxidized particles as particles that passed through the OH flow tube with the lights on but with no added O3. As such, all changes to the observed spectra are attributable to chemical oxidation of the particles, not photolysis. We note that there is no difference in the mass spectra for nonoxidized particles for tests done with the lights on versus lights off in the absence of O3 for low-RH conditions (R2=0.997; Fig. S2). This indicates that direct photolysis of the SOA had no influence on the SOA spectra for the short exposure timescale (38 s) here. We also observe that the mass spectra of nonoxidized particles at low and high RH are identical (R2=0.999), indicating that photolysis does not differ between low- and high-RH conditions in these experiments. Thus, the differences in spectral changes between the two RH conditions are driven by chemical oxidation only.
The mass spectra observed at four different OH exposures are shown for low RH (Fig. 4a) and high RH (Fig. 4b). There are distinct RH-dependent differences in the spectral evolution. At low RH, the four most abundant ions in the nonoxidized particle spectra (, 125, 141 and 169) are still among the most abundant at the highest OH exposure. In contrast, at high RH the relative signal intensities of these four ions decreases substantially with increasing OH exposure.
The overall similarity of the oxidized spectra to the nonoxidized spectra can be considered by calculating the R2 between the spectra (Lanz et al., 2007). Smaller R2 values indicate greater spectral differences (lower similarity). The R2 between the mass spectra of oxidized particles and nonoxidized particles are calculated at each OH exposure for both the low- and high-RH experiments. Only ions that contribute more than 0.5 % to the total signals are included in the calculation. As shown in Fig. 5, changes in the R2 differ substantially between low and high RH. At low RH, the R2 decreases reasonably rapidly when the OH exposure is less than 2×1012 molecule cm−3 s. However, the R2 plateaus well above zero (to ca. R2=0.78), and the overall extent of decline is relatively small with limited changes above this OH exposure. In contrast, at high RH the R2 exhibits a rapid decrease to near zero when the OH exposure is less than 1×1012 molecule cm−3 s. The very small R2 values at high RH indicate that the composition of the oxidized particles differs substantially from the nonoxidized particles.
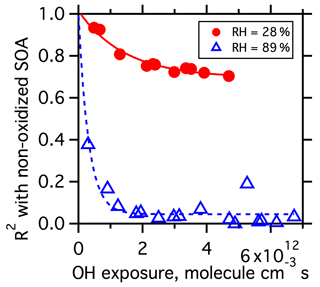
Figure 5Coefficient of determination (R2) between spectra of oxidized SOA and nonoxidized SOA as a function of OH exposure for dry (red circles) and wet (blue triangles) conditions. Spectra are filtered by excluding ions that have a percentage contribution to the total signal below 0.5 %. Lines are exponential fits and presented only as visual guides.
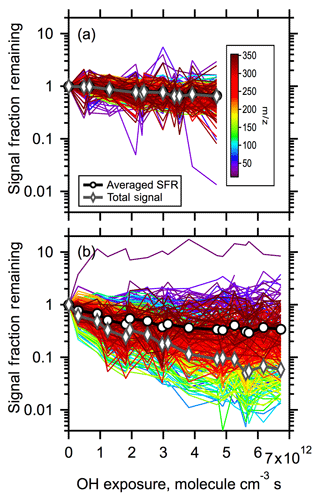
Figure 6Signal decay of all peaks observed above background in the mass-to-charge range of 15–350 amu as a function of OH exposure for (a) low-RH and (b) high-RH conditions. Colors denote mass-to-charge of a given peak. The black open circles and lines denote the unweighted, averaged decay of all the peaks. The dark gray open diamonds and lines denote the total signal fraction remaining (i.e., the signal weighted average of all peaks). Note the log scale for the y-axis.
The decay of each individual m∕z ion in the mass spectrum (from –350) with OH exposure is shown in Fig. 6. The intensity of each ion has been first normalized by the particle number concentration to account for changes in intensity due to variations in the physical loss of particles in the flow tube, which likely result from changes in the particle size distribution with OH exposure. The number-normalized intensities were then normalized by the observed intensity at zero OH exposure to assess the relative change. These resulting normalized intensities are also referred to here as the signal fraction remaining (SFR). The decay of the average SFR (calculated from the individual SFR curves) and the weighted-average SFR (equal to total signal fraction remaining) are also shown in Fig. 6. The differences in the average SFR decay between low- and high-RH conditions and the absolute magnitude of decay are consistent with the observed volume loss. However, the weighted-average SFR decays to a greater extent than the average SFR decay or mass loss under both low- and high-RH conditions. Ideally, loss of total signal should be equivalent to loss of particle mass if detection sensitivity towards all the species are the same. One possible explanation of this difference is that the VUV-AMS exhibits a lower sensitivity towards product species compared to parent species. Another possibility is the underrepresentation of dimers and oligomers in VUV-AMS spectra, as mentioned above. If the latter is true, it also indicates that dimers should decay more slowly than monomers to account for the difference between mass loss and total signal loss.
There is substantially greater spread in the SFR between individual ions at high RH compared to low RH at a given OH exposure. In other words, at low RH the intensities of the individual ions all decay to a similar extent. However, at high RH the intensity of some ions decrease by nearly a factor of 100 at the highest OH exposure, while the intensity of others remains similar to the nonoxidized particles. This is consistent with the differences in R2 versus OH exposure between low and high RH, indicating distinctly different compositional change.
We focus first on the high-RH ion decay curves. To further understand differences between ions that decay rapidly versus slowly under high-RH conditions, the ions have been grouped by their extent of decay (Fig. 7a). Four groups have been established. Group 1 includes ions that exhibit the fastest and most substantial decay, with the average SFR for this group equal to 0.04 at the highest OH exposure. This group contains most of the ions that have the greatest signal intensity in the nonoxidized particle spectrum and includes markers from known products of α-pinene ozonolysis, such as cis-pinonic acid and pinic acid. Also, the odd ions with , 141 and 169 that might be markers of oligomers as discussed above are also in Group 1. Nearly all of the ions in Group 1 have (Fig. 7b), suggesting that Group 1 primarily consists of either monomeric species or fragments thereof and signature fragments from dimers (or larger oligomers). That these ions exhibit a rapid, continuous decay indicates that they are chemically transformed, producing either new functionalized products or fragments that evaporated and are not produced during heterogeneous oxidation.
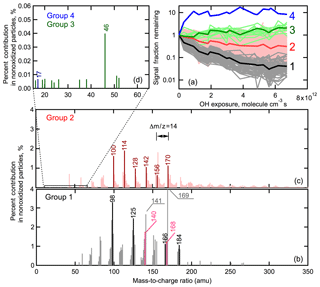
Figure 7(a) Categorization of peaks according to their decay with OH exposure for high-RH experiments. The peaks were classified into four groups. Peaks in Group 1 (gray) exhibit the fastest decay, with the average shown as the solid black curve. The peaks in Group 2 (red) exhibit the second fastest decay, with the average shown in dark red curve. The peaks in Group 3 (green) exhibit negligible decay, with the average shown in dark green. Group 4 (blue) contains only one peak. (b) Spectrum of the peaks in Group 1. Group 1 contains markers from cis-pinonic acid (black peaks) and pinic acid (pink peaks). (c) Spectrum of the peaks in Group 2. Group 2 contains patterns of repeating peaks separated by , illustrated by dark red peaks. (d) A zoomed-in view of the peaks of Group 3 and Group 4. These peaks have very small intensities.
Group 2 includes the ions that decay relatively slowly, albeit still to a substantial extent, with the average SFR equalling 0.3 at the highest OH exposure. Group 2 has the greatest number of ions, containing many ions with and, notably, almost all the ions with (Fig. 7c). The Group 2 ions with have generally smaller percentage contributions to the total signal in the nonoxidized particles than the Group 1 ions. This suggests that they are either less characteristic of minor ions for major parent compounds or characteristic of ions for minor parent compounds in the nonoxidized particles. The Group 2 ions with are contributed by very highly oxygenated products, dimer fragments and dimers. The comparably slow decay of Group 2 ions indicates either that they react substantially more slowly than the Group 1 species (which are likely monomers) or that production offsets some of the chemical loss during the aging process. It is difficult to determine which is more likely.
Group 3 includes ions that exhibited little decay with oxidation. The Group 3 ions all have (Fig. 7d), and thus are small ion fragments that could result from any of the particle-phase compounds, both parent and product species. The relative intensity of the Group 3 ions is overall extremely small. That their intensity remains relatively constant suggests that these ion fragments are produced to a greater extent from oxidation products than from the molecules comprising the nonoxidized SOA. In other words, production is offsetting loss. Group 4 includes the one ion () that exhibits an increase in signal intensity. The relative intensity of this ion is very small, contributing only 0.01 % to total signal in nonoxidized particles. However, at the highest OH exposure the percentage contribution of this ion increases to nearly 1 %. Since these experiments were performed under NOx free conditions, most likely corresponds to OH+ ions. In general, the formation of OH+ ions from photoionization is unfavorable, which explains the extremely low intensity of this ion in the mass spectra. However, the increase in the intensity of this ion with oxidation is likely still meaningful and could be a result of product species of increasing generation number having a greater number of −OH groups. Alternatively, it could indicate that the functional groups produced from oxidation are more likely to generate OH ions compared to the parent species due to differences in bond dissociation energies. Most likely, the increase in intensity of this ion is a result of functionalization.
Considering now the low-RH experiment (Fig. 6a), all the ions visually appear to decay to similar extents. However, building on the results from the high-RH experiment above, the mass spectrum has been split into the same m∕z groups (Fig. 8). It is found that the Group 1 ions collectively decay to the greatest extent for the low-RH experiment, consistent with the high-RH experiment. This provides additional evidence that Group 1 ions are mainly contributed from monomeric species that are chemically degraded and are not produced through heterogeneous oxidation. The Group 2 ions decay on average to a lesser extent than Group 1 ions at low RH, consistent with the high-RH experiment. There is, however, a fair amount of variability in the individual ions for this group (mainly driven by low intensity ions). The Group 3 ions exhibit, on average, slightly less decay than Group 2 ions, though with a fair amount of variability driven by the low ion intensities. The one Group 4 ion () may increase slightly with OH exposure, but the overall behavior is difficult to discern given the small change and low ion intensity.
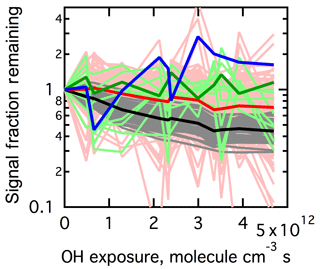
Figure 8Signal fraction remaining of all the individual ions observed above background in the range –350 under low-RH conditions. Ions are colored according to the groupings determined for the high-RH conditions (cf. Fig. 7a).
The mean SFR of Group 1 ions equals 0.4 at low RH compared to 0.05 at high RH at the same high OH exposure ( molecule cm−3 s). This difference is comparable to the observed differences in decay of parent ions for model (single-component) OA particles upon heterogeneous oxidation by OH under low- versus high-RH conditions (Chan et al., 2014; Davies and Wilson, 2015). As discussed above, ions in Group 1 are likely representative of monomeric species in parent compounds. With the assumption that Group 1 ions are only lost through heterogeneous oxidation and not formed, the mean signal decay of Group 1 ions could be considered as the lower limit of decay of parent species for α-pinene SOA. The lower limit of the reaction rate coefficient of α-pinene SOA with OH, kSOA+OH, can be estimated based on the signal loss rate of Group 1 ions by fitting the decay of the average SFR of Group 1 ions with an exponential function:
The derived kSOA+OH is cm3 molecule−1 s−1 for low-RH and cm3 molecule−1 s−1 for high-RH conditions. This difference in rate constants is similar to the difference reported by Davies and Wilson (2015) for citric acid and Hu et al. (2016) for IEPOX-SOA for a similar RH difference. The latter study reported an approximately linear relation between the rate coefficient and the wet particle surface area for the RH conditions examined. However, as discussed above, α-pinene SOA only takes up a small amount of water at RH equalling 90 %, leading to an increase in surface area of only ∼20 %, which cannot explain the more than 5 times higher rate constant under high RH.
Overall, it has been observed that substantially larger changes are observed at high RH than at low RH, both in terms of the extent of mass loss and the change in the particle composition with increasing OH exposure. It has also been observed that under low-RH conditions the composition of SOA stops changing (based on consideration of the R2) above a certain oxidation level, while mass loss continues slowly. In contrast, both compositional change and mass loss occur continuously and dramatically under high-RH conditions.
3.3 Model simulation: dependence on RH
The model is used here to establish the factors that primarily lead to the observed difference in heterogeneous oxidation under different RHs in terms of both mass loss and compositional change. Heterogeneous oxidation of organic aerosol has several key steps, as discussed above and shown in Fig. 2. These include sticking and uptake of gas-phase HOx radicals, chemical reactions of different species and diffusion of the species in the bulk. All of the steps can be affected by RH, and in particular the influence of RH on viscosity plays important roles in these steps.
For the uptake process, there are a variety of reasons that the reactivity of HOx radicals may differ between low- and high-RH conditions. The existence of water at the surface might lead to more efficient sticking of gas-phase HOx radicals due to enhanced hydrogen bonding to water (Chan et al., 2014). However, the greater abundance of water vapor at high RH also might decrease the available sites for adsorption of gas-phase HOx radicals due to competitive co-adsorption (Kaiser et al., 2011). After adsorbing and sticking to the surface, gas-phase HOx radicals are mobile on surfaces prior to reaction (Slade and Knopf, 2013). Since different sites have different reactivities depending on their bonding environment (Kwok and Atkinson, 1995), the reaction probability of gas-phase HOx radicals with surface species can be affected by molecular orientation and the mobility of the radicals. The orientation of the SOA molecules can potentially be affected by RH. At low RH the SOA molecules are likely less mobile and their particular orientation and alignment at the surface is relatively static compared to high RH (Moog et al., 1982). It is possible that a difference in the orientation and mobility of surface molecules between low and high RH affects the probability that an OH radical reacts versus desorbs after colliding with and sticking to the surface.
The viscosity of particles could also have an influence on the chemical pathways and products formed from RO2•+RO2• reactions within the bulk by affecting the (i) reaction probability, (ii) branching ratio or (iii) both. Denisov and Afanas'ev (2005) proposed that RO2•+RO2• react to form an unstable tetroxide, which then decomposes to produce a ketone and an alcohol (the Russell mechanism), two ketones and H2O2 (the Bennett–Summers mechanism), or two RO• radicals. They also indicated that the decomposition rate constant of the tetroxide intermediate decreases with an increase in viscosity of the surrounding phase. The products formed from decomposition of the tetroxide depend on the structure of the transition state and, in the condensed phase, on further reaction of radical products within a solvent cage. The presence of a solvent cage and the stability of the cage can potentially influence the branching ratio towards production of RO• radicals relative to stable, functionalized product species. This is important because RO• radicals are the only species that lead to fragmentation.
Another impact of an RH-dependent viscosity is on the mixing timescales for condensed-phase species. The mixing timescale for particles depends on the condensed-phase diffusivity, which is related to viscosity. For example, for cm2 s−1, the mixing timescale for a 100 nm particle is about 2 s (Koop et al., 2011). Thus, the particle can be generally considered well-mixed and liquid-like. However, for cm2 s−1 the mixing timescale for a 100 nm particle is ∼40 min. In this case, mixing is slow and the particle can be considered as having a more semi-solid phase. As discussed above, the diffusion coefficient (and viscosity) of α-pinene SOA vary continuously with RH. In general, at >70 % RH, the diffusivity of α-pinene SOA is large ( cm2 s−1), while at low RH the diffusivity is comparably small ( cm2 s−1). Given this, for our experiments it is expected that the particles at low RH (∼30 %) are semi-solid while at high RH (∼90 %) they are liquid-like. When the particles are more viscous (semi-solid), reaction of the organic radicals generated from reaction with OH will be primarily constrained to surface layers. In contrast, when the particles are less viscous (liquid-like), reaction of radicals may occur throughout the entire particle. Therefore, there is reason to think that the impact of heterogeneous oxidation on both distributions of parent and product species in the particles and mass loss should depend on RH.
In the model simulations, the influence of RH on the above processes is examined by systematically varying five input parameters: (i) the growth factor (GF), (ii) the OH uptake coefficient (γ), (iii) bulk diffusivity (Dorg), (iv) the RO2•+RO2• reaction rate constant () and (v) the combined branching ratio and fragmentation probability (pfrag). A summary of simulation parameters is shown in Table 2.
3.3.1 Impact of variations in bulk diffusivity
The ability of differences in the bulk diffusivity alone, and thus in the location of reactions, to explain the observed low- versus high-RH dependence is considered first. We perform simulations where γ, and pfrag are all held constant while Dorg is varied over a range constrained by the literature, from 10−16 to 10−11 cm2 s−1 by factors of 10 (Song et al., 2015). (The γ, and pfrag were all specified to produce model results generally consistent with the observations.) For these simulations it is assumed that the size of the particles is independent of RH (discussed in Sect. 3.3.2). We find that substantial differences in the extent of mass loss between simulations with low Dorg (corresponding to low RH) and high Dorg (corresponding to high RH), as was observed, can only be achieved if the is assumed to be cm3 molecule−1 s−1, an unreasonably low value (Fig. 9). When is this low, the RO2•+HO2 reaction (which leads to functionalization) becomes competitive in the surface layer at low RH and at high OH (HO2) exposure. This leads to a build-up for ROOH species in the surface layer and limits the fragmentation pathway. At high RH, the RO2• rapidly diffuse away from the surface into the bulk, where they primarily react with each other and can produce RO• radicals that can subsequently decompose, and the fragments can evaporate. This leads to a suppression of fragmentation at low RH compared to high RH, especially at higher OH (HO2) exposure. However, the in this case is orders of magnitude lower than reported in the literature for various RO2•+RO2• reactions (Denisov and Afanas'ev, 2005).
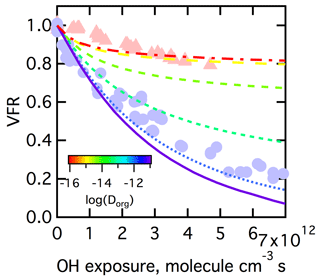
Figure 9Comparison between observations (points) and simulations (lines) at varying Dorg values of the dependence of the volume fraction remaining (VFR) versus OH exposure for SOA for low-RH (red triangles) and high-RH (blue circles) conditions. The simulations assumed γ=0.6, pfrag=0.5, GF =1.0 and cm3 molecule−1 s−1. The Dorg range from 10−16 to 10−11 cm2 s−1 is denoted by colored lines.
When a more reasonable value of is used ( cm3 molecule−1 s−1), only very small differences in the calculated VFR versus OH exposure curves between the two RH conditions (i.e., when Dorg is varied) are found no matter the values of γ and pfrag, assuming these are RH-independent (Fig. 10a). For these calculations, the γ and pfrag are selected to provide good model–measurement agreement with the VFR versus OH exposure curve for high-RH conditions. (A similar negligible dependence of the VFR on Dorg is predicted when γ and pfrag are selected to fit the low-RH observations.) It should be noted that the particular γ and pfrag used here do not provide a unique solution; various combinations give similar results. Thus, we conclude that differences in Dorg alone cannot explain the differences between the low- and high-RH experiments in terms of the overall mass loss. Simulations also show that the overall reaction rate of RO2•+RO2• in the particle is at least 3 orders of magnitude higher than the rate of RO2•+HO2, regardless of the bulk diffusivity or γ and pfrag used. Even if we assume that [HO2] [OH] instead of [HO2] = [OH], as suggested by some oxidation flow reactor studies (R. Li et al., 2015; Peng et al., 2015), loss of RO2• by reaction with HO2 is still negligible compared to loss by reaction with RO2•. This result suggests that the uptake of HO2 and formation of hydroperoxides are not particularly important during the heterogeneous oxidation of the SOA system considered here. This agrees with a previous study by Lakey et al. (2016), who put an upper limit of 0.001 on the uptake coefficient of HO2 by α-pinene SOA. However, although the VFR versus OH exposure curves using different Dorg values are very similar, there are substantial differences in terms of the calculated compositional changes for the different Dorg values considered (Fig. 10b). In particular, the fractional contribution of model parent species in the oxidized particles depends on Dorg, with larger contributions at smaller Dorg. For example, when cm2 s−1 (low RH), parent compounds make up more than 90 % of the total molecules at highest OH exposure (Fig. 10c). In contrast, when cm2 s−1 (high RH), oxidation products make up nearly all of the particles at the highest OH exposure (Fig. 10g). This is consistent with the observation of more dramatic spectral changes occurring under high-RH conditions when particles are expected to have low viscosity. The reason for this results from differences in the rate of exchange between the bulk and surface at the different RH values. At high RH, parent molecules exchange rapidly between the surface and the bulk layers. Therefore, OH can access all of the parent molecules in the particle, leading to rapid change of particle composition. In contrast, at low RH the OH radicals cannot effectively access parent molecules in below-surface layers due to the high viscosity and low diffusivity. In this case, the surface becomes highly oxidized while the bulk of the particle volume remains largely unoxidized, corresponding to minimal change of the spectra with OH exposure under dry conditions. Large differences in the overall particle composition between low- and high-RH conditions do not require additional differences in either γOH or the fragmentation probability, unlike for volume loss. This is because of the compensating effects of reaction location and oxidation extent of the products. Every time a stable species reacts with OH, there is a probability of fragmentation. Therefore, the net probability of fragmentation increases with higher generations of products, i.e., when species are more oxidized. At low RH, reactions are limited to the surface layer, leading to more highly oxidized products that have gone through more generations of reaction, with the difference more evident at lower OH exposures in particular (Fig. 10). While the net probability of fragmentation is therefore increased for these surface-layer molecules, they also inhibit reactions with the bulk of the particle and will be, on average, more oxidized. Ultimately, at low RH the volume loss proceeds through layer-by-layer oxidation and evaporation of the surface. In contrast, at high RH OH radicals can react with the entirety of the particle bulk as these molecules mix to the surface. The average extent of oxidation at high RH is therefore comparably lower than that in the surface-layer at low RH. However, a greater fraction of molecules have some probability of fragmenting and evaporating. The net effect is that the overall extent of volume loss is reasonably independent of RH and the particle bulk diffusivity, although clearly the reason for the volume loss (highly oxidized surface versus lightly oxidized bulk) depends on RH.
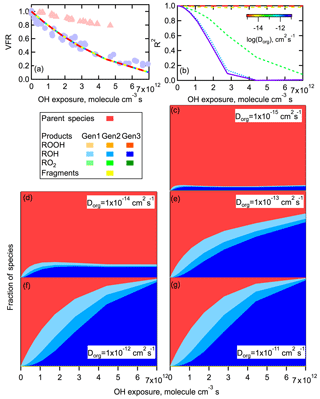
Figure 10Simulated effect of variations in the diffusion coefficient on mass loss and compositional change. For these simulations, the Dorg is allowed to vary from 10−11 to 10−15 cm2 s−1 while all other parameters are held constant and chosen to give good agreement with the high-RH observations (γ=0.50, pfrag=0.31). (a) The simulated volume fraction remaining (VFR) versus OH exposure. Observations (symbols) are shown for reference for low-RH (red triangles) and high-RH (blue circles) conditions. The simulation results overlap because diffusivity has no effect on bulk mass loss. (b) The calculated coefficient of determination (R2) between the molecular density of all simulated species as a function of OH exposure, referenced to the nonoxidized case. The Dorg is indicated by the line color, with the purple solid line denoting the fastest diffusion. (c–g) Simulated fractional concentrations of each species as a function of OH exposure for different Dorg values. Colors indicate different species and generation (see legend). Only the ROH species are readily visible.
The model results also indicate that there is a threshold Dorg above which bulk compositional changes are large and below which they are small, with the threshold cm2 s−1. Above or below this value the model results are relatively insensitive to further changes in Dorg (e.g., similar results are obtained for and 10−14 cm2 s−1, or for and 10−11 cm2 s−1). The particular threshold is related to the mixing timescale of the particles. For a 125 nm diameter particle (as used here), the mixing timescale when cm2 s−1 is about 40 s, which is comparable to the experimental timescale. Thus, above cm2 s−1 the particles are effectively well-mixed and further increases in Dorg have limited influence, and at lower Dorg the particles do not mix.
Our observations and modeling indicate that the phase state affects the distribution and oxidation level of the organic species in the particles upon photochemical aging. Slade et al. (2017) oxidized Suwannee River fulvic acid (SRFA) particles above and below the glass transition temperature (Tg) up to OH exposures of 7×1011 molecule cm−3 s−1, an order of magnitude lower than our highest value. Above Tg the Dorg is much larger than below the Tg, with an approximate transition from highly viscous to liquid-like around 295–300 K. As such, these T-dependent experiments are complementary to the RH-dependent experiments here. While they did not measure the particle composition, using the KM-GAP model (Shiraiwa et al., 2010, 2012) they concluded that oxidation at low temperatures (<295 K; semi-solid) engendered compositional changes primarily at the particle surface, while at high temperatures (>300 K; liquid-like) changes occurred throughout the particle, consistent with our results. Consequently, for the low-T experiments they predicted that the extent of oxidation of molecules in the near-surface layers, specifically, was much greater than what occurred throughout the entire particle in the high-T experiments, also consistent with our conclusions. Associated, we find that the concentration of highly oxidized (third or higher generation) species in the surface layer rapidly increases in the low-RH (low Dorg) simulations (Fig. S3). In contrast, for the high-RH simulations the concentration of highly oxidized molecules increases only slowly, but continuously, and ultimately reaches a higher concentration than for the low-RH simulations (Fig. S3). However, we note that these highly oxidized molecules in our low-RH experiments make up only a small fraction of the total molecules comprising the particle (Fig. 10), which is somewhat inconsistent with the conclusion of Slade et al. (2017) that large changes occur to the average molecular weight of the organic species comprising the particle.
3.3.2 Impact of size change
Besides affecting particle phase (i.e., Dorg), uptake of water at high RH also leads to an increase of particle size and dilution of organic compounds. The growth factor (GF) of α-pinene SOA at RH equalling 90 % is around 1.1 (Varutbangkul et al., 2006), corresponding to 21 % and 33 % increase in particle surface area and volume, respectively. The impact of this size increase is examined here by assuming that GF =1.1 for high-RH conditions and GF =1.0 for low-RH conditions, while all the other parameters are assumed to be RH independent. Multiple simulations are run for different combinations of γ, Dorg, and pfrag (Table 2). We find that there are negligible differences between simulations that account for size growth (GF =1.1) and those that do not (GF =1.0) in terms of both the volume loss and compositional change of the particles for all combinations of the other parameters (i.e., γ, Dorg, and pfrag) explored. Example results are shown in Fig. S4. The reason for the insensitivity to GF is that the increase in the surface area is offset by the decrease in the molecular density of organic compounds.
3.3.3 Influence of variations in OH uptake and condensed-phase reactions
Given that variations in Dorg alone cannot simultaneously explain the differences in observed mass loss and chemical changes at low versus high RH, coupled with the insight that the difference in hygroscopic growth for low and high RH has a negligible impact on the simulations, the impact of varying either γ or pfrag with RH is considered. For all calculations that follow it is assumed that cm2 s−1 for high RH and cm2 s−1 for low RH, based on the discussion in the Sect. 3.3.1. It is also assumed that GF =1.1 for high RH and that GF =1.0 for low-RH simulations. The model is successful in predicting bulk behavior, i.e., mass loss of particles over the full range of OH exposure (=0–7×1012 molecule cm−3 s), when RH-specific values of Dorg and GF are used along with RH-specific values of either γ or pfrag (Fig. 11a). For both conditions, cm3 molecule−1 s−1 is used. For each condition, various combinations of γ and pfrag yield the same VFR versus OH exposure curves. As shown in Fig. 11b, γ and pfrag have an inverse relationship, with increasing γ accompanied by decreasing pfrag (to achieve the same fit to the observations). It is also observed that slopes of linear fits to log(γ) versus log(pfrag) for high and low-RH conditions are identical, although the absolute values of γ and pfrag differ. This indicates that the relationship between either γdry and γwet or pfrag,dry and pfrag,wet required for good model–measurement agreement is independent of the absolute γ and pfrag. In other words, when pfrag is assumed to be RH-independent, the γOH always needs to be nearly 5 times faster at high-RH conditions to reproduce the observed greater mass loss compared to low RH. Alternatively, when γ is assumed RH-independent, the combined probability of fragmentation (pfrag) needs to be around 4 times higher at high RH to explain the difference in VFR between the two conditions.
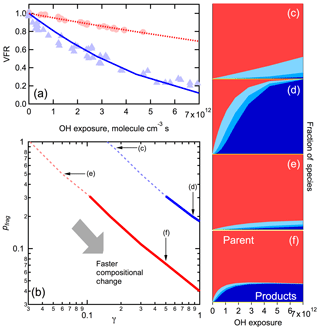
Figure 11(a) Observed (points) and modeled (lines) VFR versus OH exposure for the best-fit models for both low-RH (red) and high-RH (blue) conditions. (b) Illustration of the relationship between γ and pfrag that allow for a good fit to the observed VFR decay for low-RH (red) and high-RH (blue) conditions. The dashed lines show the full relationship, and the solid lines the best-estimate range. Four specific combinations of γ and pfrag are indicated for consideration of the associated composition change. (c–f) Simulated normalized composition change as a function of OH exposure for the γ and pfrag combinations indicated in panel (b). The colors correspond to different species, with red indicating precursor (parent) species and other colors indicating various oxidation products (cf. Fig. 10). Greater compositional changes for a given OH exposure result from combinations with larger γ and smaller pfrag for a given RH condition.
Although similar VFR versus OH exposure curves are obtained using various (RH-specific) combinations of γ and pfrag, the predicted variation in composition with OH exposure depends on the pair of γ and pfrag used. At high RH when γ is small and pfrag is large, the loss of parent molecules is relatively slow but most reactions with OH lead to the fragmentation and evaporation of the products. Consequently, there is little build-up of stable products in the particles (Fig. 11c). In contrast, when γ is large and pfrag is small the parent compounds react away faster but with a much larger fraction of stable products forming. Consequently, product species build up in the particles to a greater extent (Fig. 11d). However, the net production rate of fragments in these two cases are the same, with the decrease in reaction rate offsetting the increase in fragmentation probability (or vice versa). The covariation of γ and pfrag has a similar impact on the compositional changes for low-RH conditions (Fig. 11e, f), although the overall compositional changes are much smaller due to the high viscosity of the particles, as discussed above. Based on the above, we conclude that for high-RH conditions the γ must be greater than ca. 0.5 and pfrag must be less than ca. 0.3 to achieve both substantial changes in the particle composition and substantial volatilization, as observed. This range of γ, determined based on the overall bulk behavior, is generally supported by a comparison of the modeled decay of the parent compounds with the decay of the Group 1 ions (Fig. S5). If γwet is assumed to be ≤1, then pfrag,wet can be further constrained to be >0.18. Given that γwet ∼5γdry or , as established above, the parameters at low RH are constrained to be and .
3.4 Comparison with single-component studies
3.4.1 OH uptake
The results from our SOA experiments and model simulations can be compared with OH oxidation experiments performed on various single-component systems. Interestingly, some of these studies find that increasing RH can enhance the effective uptake coefficient, while others find that increasing RH reduces the effective uptake coefficient. The uptake coefficient can be calculated in two ways: (i) by measuring the loss rate of reacting particle-phase species, or (ii) by measuring the loss rate of gas-phase OH radicals. The first method may include loss due to secondary reactions in the condensed phase, in addition to direct loss from reaction with OH, and is generally referred to as the effective OH uptake coefficient, γOH,eff. The latter method characterizes loss of OH only and is referred to here as the OH uptake coefficient, γOH.
Some studies have observed a general increase in γOH or γOH,eff with RH when going from very dry conditions to higher RH (40–70 %). For example, Davies and Wilson (2015) reported that γOH,eff for citric acid particles increases by a factor of 3 when RH is increased from 20 % to 50 %, although there is a slight decrease in γOH,eff (by 30 %) as RH is increased further to 90 % RH. Chim et al. (2017b) similarly observed a continuous increase in γOH,eff from RH equalling 30 % to 70 % (from 1.9 to 2.6) and a small decrease at higher RH (to 2.4) for OH oxidation of particles composed of 2-methylglutaric acid (2-MGA). The increase in γOH,eff with RH at the lower-RH range was explained by a decrease in viscosity and faster mixing. This allows OH radicals to react directly more often with the parent species rather than producing highly oxidized molecules at the surface. The decrease of γOH,eff at the higher RH range was explained, in part, by a decrease in the relative concentration of parent compounds due to dilution by water. Nevertheless, both studies indicate γOH,eff is generally larger at high RH (∼90 %) than at low RH (∼30 %). Slade and Knopf (2014) determined that γOH (as opposed to γOH,eff) for levoglucosan particles increased with RH over the range 0–40 %, from approximately 0.2 to 0.7. While the exact reason for this increase was not identified – although it was suggested to result from differences in phase state and mixing timescale – if the reaction products formed are less reactive towards OH than the levoglucosan, this could explain the increase in γOH with RH because the products would build up to a lesser extent at the surface when particle mixing is faster. Alternatively, it may be that the reaction of OH with levoglucosan molecules at the particle surface depends on the orientation of the levoglucosan molecules. At very low RH the levoglucosan molecules may be fixed in unfavorable orientations (on average), and as RH is increased the levoglucosan may be able to adopt more favorable orientations. Finally, it may be that the sticking probability of OH radicals increases with RH. Regardless of the exact reason, the above single-component studies are consistent with our determination that kSOA+OH for the Group 1 (parent) ions is greater at high RH.
However, some single-component studies have reported a negative effect of RH on the uptake coefficient or reaction rate constant, with increasing RH leading to smaller γ or k. Slade and Knopf (2014) observed a decrease in γOH from 0.2 to 0.05 for methyl-nitrocatechol (MNC) particles when RH was increased from 0 % to 30 %. It was argued that because MNC has a low solubility in water, the decrease was likely a result of the competition for adsorption between OH radicals and water at the surface; this differs from levoglucosan, which is moderately soluble. The SOA here is moderately soluble, due to the highly oxygenated nature of the organic compounds, and thus most comparable to the levoglucosan experiments. Lai et al. (2014) reported a strong, negative effect of RH on the loss rate of levoglucosan after exposure to OH, in direct contrast to Slade and Knopf (2014). Lai et al. (2015) separately reported that the loss rate of cis-pinonic acid decreased, by a small amount, as RH increased from 20 to 80 %. However, there is an important distinction between the Lai et al. (2014, 2015) and Slade and Knopf (2014) experiments. Whereas Slade and Knopf (2014) used suspended particles, Lai et al. (2014, 2015) exposed thin films (<1 nm thickness) of the parent organic species to OH. Because the film was so thin the impact of diffusive exchange of molecules was effectively eliminated, and the increase in RH served only to dilute the levoglucosan and decrease the loss rate. These results suggest that the experimental method used (e.g., suspended particles versus thin films) can strongly impact the apparent influence of RH on heterogeneous oxidation processes. While experiments using suspended particles are more directly relevant to the atmosphere, the combination of thin film and suspended particle experiments can help to isolate the influence of mixing on reactive uptake and loss.
3.4.2 Reaction pathways
The influence of RH on the fate of the parent species from heterogeneous oxidation has also been considered by several studies. Following from faster loss of the parent species, Chan et al. (2014) observed faster formation of both functionalization and fragmentation products for reaction of succinic acid in aqueous droplets compared to solid aerosol, i.e., at high versus low RH. As a result, they observed a more dramatic change in the mass spectrum after OH exposure under high-RH conditions, consistent with our observation. However, the ions formed after oxidation were identical for the aqueous and solid succinic acid particles. That is, while the product species form faster at high RH, there was no indication that this had a major influence on the reaction pathways. Chim et al. (2017b) and Davies and Wilson (2015) similarly observed that, even though the reaction rates are different, the oxidation products formed are independent of RH. Furthermore, Chim et al. (2017b) observed that for 2-MGA the relative abundances of several important functionalization and fragmentation ions were independent of RH when considered at the same 2-MGA lifetime (which accounts for RH variations), indicating similar chemical pathways of oxidation regardless of RH.
In a chemical system containing carboxylic acids that are hydrophilic in nature, acid-base chemistry in the particles may need consideration in addition to free-radical chemistry when an aqueous phase is present. Liu et al. (2017) developed a model that couples both acid-base and free-radical chemistry in the oxidation of aqueous citric acid aerosol by OH radicals. They compared their simulation results to the observations of Davies and Wilson (2015). The inclusion of acid-base chemistry in the simulations did not alter the decay rate of citric acid nor the variation in hydrogen-to-carbon and oxygen-to-carbon ratios as a function of OH exposure. However, a significant increase in the abundance of fragmentation products were predicted only when acid-base chemistry is considered. One key reason is the enhanced unimolecular fragmentation rate of alkoxy radical anions compared to the neutral form. Hydration in the aqueous phase can also enable the decarboxylation of certain acyloxy radicals. Consistent with the simulations, Davies and Wilson (2015) reported that the abundance of Nc=6 product species (the same carbon number as citric acid) was smaller while the abundance of Nc=3–5 product species (fragments or decarboxylation compounds) was larger at RH equalling 65 % (corresponding liquid phase) compared to RH equalling 20 %, although the differences were not significant. It is possible that acid-base chemistry, which we do not include in our simulations, contributes to the difference in oxidation between the low- and high-RH SOA experiments here. Considering that acids can comprise a substantial fraction of α-pinene SOA, it is possible that the accelerated decomposition of alkoxy radicals in their anion form contributes to greater fragmentation under high-RH conditions in the chemically complex system studied here. However, citric acid is substantially more hygroscopic than α-pinene SOA. The growth factor for citric acid at RH equalling 20 % is similar to that of α-pinene SOA at RH equalling 90 %. As such, it is unclear to what extent acid-base chemistry might be playing a role in the oxidation of the α-pinene SOA at RH equalling 90 % and it may be negligible.
OH radicals can also be produced in the condensed phase through decomposition of organic peroxides (ROOH). ROOH molecules can contribute as much as 50 % to the total mass of α-pinene+O3 SOA (Docherty et al., 2005) but are unstable and with some observed to have half-lives of less than an hour with respect to decomposition at room temperature (Krapf et al., 2016). The decomposition products of ROOH – RO and OH radicals – both facilitate the formation of small molecular weight products that lead to volatilization. Although this chemical pathway is unlikely to contribute substantially to our experiments given the short timescale (38 s), it may influence the rate of aerosol mass loss under ambient conditions and longer timescales, especially under high-RH conditions where an appreciable amount of liquid water in the particles accelerates the decomposition of ROOH (Tong et al., 2016).
Regardless, RH-dependent differences in pfrag, and thus the oxidation products formed, can explain the difference in VFR and in the particle composition for SOA considered here based on our simulation results. Differences in viscosity of the particles have the potential to influence the reaction rate and product branching ratio, and the importance of this may differ in the more chemically complex SOA compared to the single-component experiments. Comparison with the single-component experiments suggests that the key difference between the low- and high-RH SOA experiments is more likely from the RH-dependence of γOH, although the role of variations in oxidation pathways (pfrag) cannot be completely ruled out.
The influence of RH on the heterogeneous oxidation of α-pinene SOA by gas-phase OH radicals is investigated for the first time. There is a substantial difference in the extent of aerosol volume loss that results from photochemical aging between experiments conducted at low versus high RH (28 % versus 90 %), with much greater loss for high-RH experiments. At low RH, the SOA particles are estimated to lose 80 % of their volume over ∼4 weeks of aging at typical atmospheric OH levels. In contrast, at high RH it takes only a few days for the same amount of shrinking to occur. At high RH, substantial changes are observed in the mass spectrum of the SOA as the particles are oxidized. Nearly all peaks in the spectrum decrease in intensity as aging occurs, although to varying extents. Grouping of the peaks in the mass spectrum according to their individual extents of decay suggests that monomeric parent species exhibit the fastest decay. The decay of peaks that are attributable to dimers (or higher order oligomers) is comparably slower, yet still substantial. Under low-RH conditions, limited changes in the mass spectrum with oxidation are observed for the SOA particles. However, if the decay groups identified for the high-RH experiment are applied to the low-RH experiments, there is a general consistency between the low- and high-RH results, with slightly faster decay of the monomeric compounds compared to the dimer compounds.
The RH dependence of the observed volume loss and compositional change of the SOA particles was assessed using a multiphase chemical-oxidation model in which variations in the bulk diffusivity, OH uptake coefficient and net probability of fragmentation were considered. Differences in the bulk diffusion coefficient alone, which affects mixing timescales within the particles, are found to have a negligible impact on the overall volume loss. However, the calculated variation in particle composition was highly sensitive to the bulk diffusion coefficient and whether it was larger or smaller than a threshold value of cm2 s−1. At Dorg values larger than the threshold value (faster mixing), substantial changes in the particle composition can occur as oxidation proceeds, whereas at Dorg values smaller than the threshold (slower mixing), the particle composition remains approximately constant. The difference in volume loss between low and high RH are shown to result from either the OH uptake coefficient or the net fragmentation probability (or both) being RH dependent, with larger values for high-RH conditions. Considering the volume loss and compositional changes together, these two parameters are constrained to be and for low-RH conditions and and for high-RH conditions when γOH is assumed to be less than 1. Comparison with studies of single compound systems suggests that variations in γOH is more likely responsible for the difference in low- versus high-RH experiments, although the possibility of different chemical pathways (i.e., differences in pfrag) due to differences in viscosity and the presence of water cannot be ruled out. Further work is necessary to establish which parameter, γ or pfrag, is more sensitive to variations in RH, especially in chemically complex systems.
Overall, our work indicates that RH has a substantial impact on the evolution of the size and composition, as well as potentially related physical properties, of α-pinene SOA upon photochemical aging. Particle phase-dependent differences in oxidation – including the importance of functionalization of fragmentation at the surface or throughout the bulk of a particle – can impact how the hygroscopicity of organic particles evolves (Chim et al., 2017a; Slade et al., 2017). Additionally, our observations suggest that the lifetime of SOA with respect to heterogeneous OH oxidation is significantly shorter at high RH and that this loss mechanism should be considered in regional and global models. Although the mass concentrations of SOA we use here are 1–3 orders of magnitude higher than ambient concentrations, the above conclusions are likely to hold true. Recent studies have demonstrated an increase in SOA viscosity with a decrease in mass loadings under low-RH conditions (Grayson et al., 2016; Jain et al., 2018). However, under high-RH conditions the SOA particles are likely to stay liquid-like independent of mass concentration. (Renbaum-Wolff et al., 2013; Kidd et al., 2014; Bateman et al., 2015). Thus, the difference in particle viscosity of several orders of magnitude between low- and high-RH conditions will almost certainly persist – and perhaps increase – at typical ambient SOA concentrations. Consequently, the influence of RH on SOA aging is likely important even at ambient SOA concentrations.
Ultimately, additional studies with other types of SOA (e.g., that formed from other biogenic or anthropogenic precursors) are needed to fully establish the effect of RH on SOA sensitivity to OH oxidation and to help further elucidate the underlying physical and chemical mechanisms. However, the results of the current study clearly point to the important role of RH in the heterogeneous oxidation of SOA.
The data and model code associated with this paper have been submitted for archiving at the UC Davis DASH data repository (https://dash.ucdavis.edu, last access: 8 October 2018) at https://doi.org/10.25338/B8ZK5X (Cappa et al., 2018).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-18-14585-2018-supplement.
ZL and CDC designed the experiments, ZL, KAS and CDC carried them out, and ZL performed the data analysis. ZL and CDC prepared the manuscript with contributions from all co-authors.
The authors declare that they have no conflict of interest.
We thank Kevin Wilson, Bruce Rude, Michael Jacob and Nadja Heine at the
Advanced Light Source for experimental assistance. Funding for this work was
provided by the National Science Foundation (ATM-1151062). This work was
performed at Beamline 9.0.2 at the Advanced Light Source at Lawrence
Berkeley National Laboratory. The Advanced Light Source is supported by the
director of the Office of Science, Office of Basic Energy Sciences, Chemical
Sciences Division of the U.S. Department of Energy under Contract No.
DE-AC02- 05CH1123.
Edited by: Markus Ammann
Reviewed by: two anonymous referees
Arangio, A. M., Slade, J. H., Berkemeier, T., Pöschl, U., Knopf, D. A., and Shiraiwa, M.: Multiphase chemical kinetics of OH radical uptake by molecular organic markers of biomass burning aerosols: humidity and temperature dependence, surface reaction, and bulk diffusion, J. Phys. Chem. A, 119, 4533–4544, https://doi.org/10.1021/jp510489z, 2015.
Bateman, A. P., Bertram, A. K., and Martin, S. T.: Hygroscopic Influence on the Semisolid-to-Liquid Transition of Secondary Organic Materials, J. Phys. Chem. A, 119, 4386–4395, https://doi.org/10.1021/jp508521c, 2015.
Camredon, M., Hamilton, J. F., Alam, M. S., Wyche, K. P., Carr, T., White, I. R., Monks, P. S., Rickard, A. R., and Bloss, W. J.: Distribution of gaseous and particulate organic composition during dark a-pinene ozonolysis, Atmos. Chem. Phys., 10, 2893–2917, https://doi.org/10.5194/acp-10-2893-2010, 2010.
Cappa, C. D. and Wilson, K. R.: Evolution of organic aerosol mass spectra upon heating: implications for OA phase and partitioning behavior, Atmos. Chem. Phys., 11, 1895–1911, https://doi.org/10.5194/acp-11-1895-2011, 2011.
Cappa, C. D., Che, D. L., Kessler, S. H., Kroll, J. H., and Wilson, K. R.: Variations in organic aerosol optical and hygroscopic properties upon heterogeneous OH oxidation, J. Geophys. Res., 116, D15204, https://doi.org/10.1029/2011jd015918, 2011.
Cappa, C. D., Li, Z., and Smith, K.: Influence of Relative Humidity on the Heterogeneous Oxidation of Secondary Organic Aerosol, UC Davis Dash, https://doi.org/10.25338/B8ZK5X, 8 October 2018.
Chan, M. N., Zhang, H., Goldstein, A. H., and Wilson, K. R.: Role of Water and Phase in the Heterogeneous Oxidation of Solid and Aqueous Succinic Acid Aerosol by Hydroxyl Radicals, J. Phys. Chem. C, 118, 28978–28992, https://doi.org/10.1021/jp5012022, 2014.
Chim, M. M., Cheng, C. T., Davies, J. F., Berkemeier, T., Shiraiwa, M., Zuend, A., and Chan, M. N.: Compositional evolution of particle-phase reaction products and water in the heterogeneous OH oxidation of model aqueous organic aerosols, Atmos. Chem. Phys., 17, 14415–14431, https://doi.org/10.5194/acp-17-14415-2017, 2017a.
Chim, M. M., Chow, C. Y., Davies, J. F., and Chan, M. N.: Effects of Relative Humidity and Particle Phase Water on the Heterogeneous OH Oxidation of 2-Methylglutaric Acid Aqueous Droplets, J. Phys. Chem. A, 121, 1667–1675, https://doi.org/10.1021/acs.jpca.6b11606, 2017b.
Davies, J. F. and Wilson, K. R.: Nanoscale interfacial gradients formed by the reactive uptake of OH radicals onto viscous aerosol surfaces, Chem. Sci., 6, 7020–7027, https://doi.org/10.1039/c5sc02326b, 2015.
Denisov, E. T. and Afanas'ev, I. B.: Oxidation and antioxidants in organic chemistry and biology, Taylor & Francis, Boca Raton, FL, 981 pp., 2005.
Dennis-Smither, B. J., Miles, R. E. H., and Reid, J. P.: Oxidative aging of mixed oleic acid/sodium chloride aerosol particles, J. Geophys. Res.-Atmos., 117, D20204, https://doi.org/10.1029/2012JD018163, 2012.
Docherty, K. S., Wu, W., Lim, Y. B., and Ziemann, P. J.: Contributions of organic peroxides to secondary aerosol formed from reactions of monoterpenes with O3, Environ. Sci. Technol., 39, 4049–4059, https://doi.org/10.1021/es050228s, 2005.
Donahue, N. M., Henry, K. M., Mentel, T. F., Kiendler-Scharr, A., Spindler, C., Bohn, B., Brauers, T., Dorn, H. P., Fuchs, H., Tillmann, R., Wahner, A., Saathoff, H., Naumann, K. H., Mohler, O., Leisner, T., Muller, L., Reinnig, M. C., Hoffmann, T., Salo, K., Hallquist, M., Frosch, M., Bilde, M., Tritscher, T., Barmet, P., Praplan, A. P., DeCarlo, P. F., Dommen, J., Prevot, A. S., and Baltensperger, U.: Aging of biogenic secondary organic aerosol via gas-phase OH radical reactions, P. Natl. Acad. Sci. USA, 109, 13503–13508, https://doi.org/10.1073/pnas.1115186109, 2012.
Emanuelsson, E. U., Mentel, T. F., Watne, A. K., Spindler, C., Bohn, B., Brauers, T., Dorn, H. P., Hallquist, A. M., Haseler, R., Kiendler-Scharr, A., Muller, K. P., Pleijel, H., Rohrer, F., Rubach, F., Schlosser, E., Tillmann, R., and Hallquist, M.: Parameterization of Thermal Properties of Aging Secondary Organic Aerosol Produced by Photo-Oxidation of Selected Terpene Mixtures, Environ. Sci. Technol., 48, 6168–6176, https://doi.org/10.1021/es405412p, 2014.
Fan, H., Tinsley, M. R., and Goulay, F.: Effect of Relative Humidity on the OH-Initiated Heterogeneous Oxidation of Monosaccharide Nanoparticles, J. Phys. Chem. A, 119, 11182–11190, https://doi.org/10.1021/acs.jpca.5b06364, 2015.
George, I. J., Vlasenko, A., Slowik, J. G., Broekhuizen, K., and Abbatt, J. P. D.: Heterogeneous oxidation of saturated organic aerosols by hydroxyl radicals: uptake kinetics, condensed-phase products, and particle size change, Atmos. Chem. Phys., 7, 4187–4201, https://doi.org/10.5194/acp-7-4187-2007, 2007.
George, I. J., Chang, R. Y. W., Danov, V., Vlasenko, A., and Abbatt, J. P. D.: Modification of cloud condensation nucleus activity of organic aerosols by hydroxyl radical heterogeneous oxidation, Atmos. Environ., 43, 5038–5045, https://doi.org/10.1016/j.atmosenv.2009.06.043, 2009.
Gierczak, T., Gilles, M. K., Bauerle, S., and Ravishankara, A. R.: Reaction of hydroxyl radical with acetone. 1. Kinetics of the reactions of OH, OD, and (OH)-O-18 with acetone and acetone-d(6), J. Phys. Chem. A, 107, 5014–5020, https://doi.org/10.1021/jp027301a, 2003.
Gloaguen, E., Mysak, E. R., Leone, S. R., Ahmed, M., and Wilson, K. R.: Investigating the chemical composition of mixed organic-inorganic particles by “soft” vacuum ultraviolet photoionization: The reaction of ozone with anthracene on sodium chloride particles, Int. J. Mass. Spectrom., 258, 74–85, https://doi.org/10.1016/j.ijms.2006.07.019, 2006.
Grayson, J. W., Zhang, Y., Mutzel, A., Renbaum-Wolff, L., Böge, O., Kamal, S., Herrmann, H., Martin, S. T., and Bertram, A. K.: Effect of varying experimental conditions on the viscosity of a-pinene derived secondary organic material, Atmos. Chem. Phys., 16, 6027–6040, https://doi.org/10.5194/acp-16-6027-2016, 2016.
Guenther, A., Hewitt, C. N., Erickson, D., Fall, R., Geron, C., Graedel, T., Harley, P., Klinger, L., Lerdau, M., Mckay, W. A., Pierce, T., Scholes, B., Steinbrecher, R., Tallamraju, R., Taylor, J., and Zimmerman, P.: A Global-Model of Natural Volatile Organic-Compound Emissions, J. Geophys. Res.-Atmos., 100, 8873–8892, https://doi.org/10.1029/94JD02950, 1995.
Guenther, A. B., Jiang, X., Heald, C. L., Sakulyanontvittaya, T., Duhl, T., Emmons, L. K., and Wang, X.: The Model of Emissions of Gases and Aerosols from Nature version 2.1 (MEGAN2.1): an extended and updated framework for modeling biogenic emissions, Geosci. Model Dev., 5, 1471–1492, https://doi.org/10.5194/gmd-5-1471-2012, 2012.
Hall, W. A., Pennington, M. R., and Johnston, M. V.: Molecular Transformations Accompanying the Aging of Laboratory Secondary Organic Aerosol, Environ. Sci. Technol., 47, 2230–2237, https://doi.org/10.1021/es303891q, 2013.
Hallquist, M., Wenger, J. C., Baltensperger, U., Rudich, Y., Simpson, D., Claeys, M., Dommen, J., Donahue, N. M., George, C., Goldstein, A. H., Hamilton, J. F., Herrmann, H., Hoffmann, T., Iinuma, Y., Jang, M., Jenkin, M. E., Jimenez, J. L., Kiendler-Scharr, A., Maenhaut, W., McFiggans, G., Mentel, Th. F., Monod, A., Prévôt, A. S. H., Seinfeld, J. H., Surratt, J. D., Szmigielski, R., and Wildt, J.: The formation, properties and impact of secondary organic aerosol: current and emerging issues, Atmos. Chem. Phys., 9, 5155–5236, https://doi.org/10.5194/acp-9-5155-2009, 2009.
Harmon, C. W., Ruehl, C. R., Cappa, C. D., and Wilson, K. R.: A statistical description of the evolution of cloud condensation nuclei activity during the heterogeneous oxidation of squalane and bis(2-ethylhexyl) sebacate aerosol by hydroxyl radicals, Phys. Chem. Chem. Phys., 15, 9679–9693, https://doi.org/10.1039/c3cp50347j, 2013.
Hennigan, C. J., Sullivan, A. P., Collett, J. L., and Robinson, A. L.: Levoglucosan stability in biomass burning particles exposed to hydroxyl radicals, Geophys. Res. Lett., 37, L09806, https://doi.org/10.1029/2010gl043088, 2010.
Houle, F. A., Hinsberg, W. D., and Wilson, K. R.: Oxidation of a model alkane aerosol by OH radical: the emergent nature of reactive uptake, Phys. Chem. Chem. Phys., 17, 4412–4423, https://doi.org/10.1039/c4cp05093b, 2015.
Hu, W., Palm, B. B., Day, D. A., Campuzano-Jost, P., Krechmer, J. E., Peng, Z., de Sá, S. S., Martin, S. T., Alexander, M. L., Baumann, K., Hacker, L., Kiendler-Scharr, A., Koss, A. R., de Gouw, J. A., Goldstein, A. H., Seco, R., Sjostedt, S. J., Park, J.-H., Guenther, A. B., Kim, S., Canonaco, F., Prévôt, A. S. H., Brune, W. H., and Jimenez, J. L.: Volatility and lifetime against OH heterogeneous reaction of ambient isoprene-epoxydiols-derived secondary organic aerosol (IEPOX-SOA), Atmos. Chem. Phys., 16, 11563–11580, https://doi.org/10.5194/acp-16-11563-2016, 2016.
Jain, S., Fischer, K. B., and Petrucci, G. A.: The Influence of Absolute Mass Loading of Secondary Organic Aerosols on Their Phase State, Atmosphere-Basel, 9, 131, https://doi.org/10.3390/atmos9040131, 2018.
Jimenez, J. L., Canagaratna, M. R., Donahue, N. M., Prevot, A. S. H., Zhang, Q., Kroll, J. H., DeCarlo, P. F., Allan, J. D., Coe, H., Ng, N. L., Aiken, A. C., Docherty, K. S., Ulbrich, I. M., Grieshop, A. P., Robinson, A. L., Duplissy, J., Smith, J. D., Wilson, K. R., Lanz, V. A., Hueglin, C., Sun, Y. L., Tian, J., Laaksonen, A., Raatikainen, T., Rautiainen, J., Vaattovaara, P., Ehn, M., Kulmala, M., Tomlinson, J. M., Collins, D. R., Cubison, M. J., Dunlea, E. J., Huffman, J. A., Onasch, T. B., Alfarra, M. R., Williams, P. I., Bower, K., Kondo, Y., Schneider, J., Drewnick, F., Borrmann, S., Weimer, S., Demerjian, K., Salcedo, D., Cottrell, L., Griffin, R., Takami, A., Miyoshi, T., Hatakeyama, S., Shimono, A., Sun, J. Y., Zhang, Y. M., Dzepina, K., Kimmel, J. R., Sueper, D., Jayne, J. T., Herndon, S. C., Trimborn, A. M., Williams, L. R., Wood, E. C., Middlebrook, A. M., Kolb, C. E., Baltensperger, U., and Worsnop, D. R.: Evolution of Organic Aerosols in the Atmosphere, Science, 326, 1525–1529, https://doi.org/10.1126/science.1180353, 2009.
Kaiser, J. C., Riemer, N., and Knopf, D. A.: Detailed heterogeneous oxidation of soot surfaces in a particle-resolved aerosol model, Atmos. Chem. Phys., 11, 4505–4520, https://doi.org/10.5194/acp-11-4505-2011, 2011.
Kidd, C., Perraud, V., Wingen, L. M., and Finlayson-Pitts, B. J.: Integrating phase and composition of secondary organic aerosol from the ozonolysis of alpha-pinene, P. Natl. Acad. Sci. USA, 111, 7552–7557, https://doi.org/10.1073/pnas.1322558111, 2014.
Kolesar, K. R., Li, Z., Wilson, K. R., and Cappa, C. D.: Heating-Induced Evaporation of Nine Different Secondary Organic Aerosol Types, Environ. Sci. Technol., 49, 12242–12252, https://doi.org/10.1021/acs.est.5b03038, 2015.
Koop, T., Bookhold, J., Shiraiwa, M., and Pöschl, U.: Glass transition and phase state of organic compounds: dependency on molecular properties and implications for secondary organic aerosols in the atmosphere, Phys. Chem. Chem. Phys., 13, 19238–19255, https://doi.org/10.1039/c1cp22617g, 2011.
Krapf, M., El Haddad, I., Bruns, E. A., Molteni, U., Daellenbach, K. R., Prevot, A. S. H., Baltensperger, U., and Dommen, J.: Labile Peroxides in Secondary Organic Aerosol, Chem-Us, 1, 603–616, https://doi.org/10.1016/j.chempr.2016.09.007, 2016.
Kristensen, K., Cui, T., Zhang, H., Gold, A., Glasius, M., and Surratt, J. D.: Dimers in a-pinene secondary organic aerosol: effect of hydroxyl radical, ozone, relative humidity and aerosol acidity, Atmos. Chem. Phys., 14, 4201–4218, https://doi.org/10.5194/acp-14-4201-2014, 2014.
Kristensen, K., Watne, A. K., Hammes, J., Lutz, A., Petaja, T., Hallquist, M., Bilde, M., and Glasius, M.: High-Molecular Weight Dimer Esters Are Major Products in Aerosols from alpha-Pinene Ozonolysis and the Boreal Forest, Environ. Sci. Tech. Let., 3, 280–285, https://doi.org/10.1021/acs.estlett.6b00152, 2016.
Kroll, J. H., Smith, J. D., Che, D. L., Kessler, S. H., Worsnop, D. R., and Wilson, K. R.: Measurement of fragmentation and functionalization pathways in the heterogeneous oxidation of oxidized organic aerosol, Phys. Chem. Chem. Phys., 11, 8005–8014, https://doi.org/10.1039/b905289e, 2009.
Kroll, J. H., Lim, C. Y., Kessler, S. H., and Wilson, K. R.: Heterogeneous Oxidation of Atmospheric Organic Aerosol: Kinetics of Changes to the Amount and Oxidation State of Particle-Phase Organic Carbon, J. Phys. Chem. A, 119, 10767–10783, https://doi.org/10.1021/acs.jpca.5b06946, 2015.
Kuwata, M. and Martin, S. T.: Phase of atmospheric secondary organic material affects its reactivity, P. Natl. Acad. Sci. USA, 109, 17354–17359, https://doi.org/10.1073/pnas.1209071109, 2012.
Kwok, E. S. C. and Atkinson, R.: Estimation of Hydroxyl Radical Reaction-Rate Constants for Gas-Phase Organic-Compounds Using a Structure-Reactivity Relationship – an Update, Atmos. Environ., 29, 1685–1695, https://doi.org/10.1016/1352-2310(95)00069-B, 1995.
Lai, C., Liu, Y., Ma, J., Ma, Q., and He, H.: Degradation kinetics of levoglucosan initiated by hydroxyl radical under different environmental conditions, Atmos. Environ., 91, 32–39, https://doi.org/10.1016/j.atmosenv.2014.03.054, 2014.
Lai, C., Liu, Y., Ma, J., Ma, Q., Chu, B., and He, H.: Heterogeneous Kinetics of cis-Pinonic Acid with Hydroxyl Radical under Different Environmental Conditions, J. Phys. Chem. A, 119, 6583–6593, https://doi.org/10.1021/acs.jpca.5b01321, 2015.
Lakey, P. S. J., Berkemeier, T., Krapf, M., Dommen, J., Steimer, S. S., Whalley, L. K., Ingham, T., Baeza-Romero, M. T., Pöschl, U., Shiraiwa, M., Ammann, M., and Heard, D. E.: The effect of viscosity and diffusion on the HO2 uptake by sucrose and secondary organic aerosol particles, Atmos. Chem. Phys., 16, 13035–13047, https://doi.org/10.5194/acp-16-13035-2016, 2016.
Lambe, A. T., Onasch, T. B., Croasdale, D. R., Wright, J. P., Martin, A. T., Franklin, J. P., Massoli, P., Kroll, J. H., Canagaratna, M. R., Brune, W. H., Worsnop, D. R., and Davidovits, P.: Transitions from functionalization to fragmentation reactions of laboratory secondary organic aerosol (SOA) generated from the OH oxidation of alkane precursors, Environ. Sci. Technol., 46, 5430–5437, https://doi.org/10.1021/es300274t, 2012.
Lanz, V. A., Alfarra, M. R., Baltensperger, U., Buchmann, B., Hueglin, C., and Prévôt, A. S. H.: Source apportionment of submicron organic aerosols at an urban site by factor analytical modelling of aerosol mass spectra, Atmos. Chem. Phys., 7, 1503–1522, https://doi.org/10.5194/acp-7-1503-2007, 2007.
Li, R., Palm, B. B., Ortega, A. M., Hlywiak, J., Hu, W. W., Peng, Z., Day, D. A., Knote, C., Brune, W. H., de Gouw, J. A., and Jimenez, J. L.: Modeling the Radical Chemistry in an Oxidation Flow Reactor: Radical Formation and Recycling, Sensitivities, and the OH Exposure Estimation Equation, J. Phys. Chem. A, 119, 4418–4432, https://doi.org/10.1021/jp509534k, 2015.
Li, Y. J., Liu, P. F., Gong, Z. H., Wang, Y., Bateman, A. P., Bergoend, C., Bertram, A. K., and Martin, S. T.: Chemical Reactivity and Liquid/Nonliquid States of Secondary Organic Material, Environ. Sci. Technol., 49, 13264–13274, https://doi.org/10.1021/acs.est.5b03392, 2015.
Liu, M. J., Wiegel, A. A., Wilson, K. R., and Houle, F. A.: Aerosol Fragmentation Driven by Coupling of Acid-Base and Free-Radical Chemistry in the Heterogeneous Oxidation of Aqueous Citric Acid by OH Radicals, J. Phys. Chem. A, 121, 5856–5870, https://doi.org/10.1021/acs.jpca.7b04892, 2017.
McNeill, V. F., Yatavelli, R. L. N., Thornton, J. A., Stipe, C. B., and Landgrebe, O.: Heterogeneous OH oxidation of palmitic acid in single component and internally mixed aerosol particles: vaporization and the role of particle phase, Atmos. Chem. Phys., 8, 5465–5476, https://doi.org/10.5194/acp-8-5465-2008, 2008.
Moog, R. S., Ediger, M. D., Boxer, S. G., and Fayer, M. D.: Viscosity Dependence of the Rotational Reorientation of Rhodamine-B in Mono-Alcohol and Poly-Alcohol – Picosecond Transient Grating Experiments, J. Phys. Chem.-Us, 86, 4694–4700, https://doi.org/10.1021/j100221a011, 1982.
Mysak, E. R.: Gentle photoionization of organic constituents using vacuum ultraviolet aerosol mass spectrometry, PhD Thesis, Department of Chemistry, University of North Carolina at Chapel Hill, Chapel Hill, NC, 2006.
Nah, T., Kessler, S. H., Daumit, K. E., Kroll, J. H., Leone, S. R., and Wilson, K. R.: OH-initiated oxidation of sub-micron unsaturated fatty acid particles, Phys. Chem. Chem. Phys., 15, 18649–18663, https://doi.org/10.1039/c3cp52655k, 2013.
Nah, T., Kessler, S. H., Daumit, K. E., Kroll, J. H., Leone, S. R., and Wilson, K. R.: Influence of molecular structure and chemical functionality on the heterogeneous OH-initiated oxidation of unsaturated organic particles, J. Phys. Chem. A, 118, 4106–4119, https://doi.org/10.1021/jp502666g, 2014.
Park, J. H., Ivanov, A. V., and Molina, M. J.: Effect of relative humidity on OH uptake by surfaces of atmospheric importance, J. Phys. Chem. A, 112, 6968–6977, https://doi.org/10.1021/jp8012317, 2008.
Peng, Z., Day, D. A., Stark, H., Li, R., Lee-Taylor, J., Palm, B. B., Brune, W. H., and Jimenez, J. L.: HOx radical chemistry in oxidation flow reactors with low-pressure mercury lamps systematically examined by modeling, Atmos. Meas. Tech., 8, 4863–4890, https://doi.org/10.5194/amt-8-4863-2015, 2015.
Petters, M. D., Prenni, A. J., Kreidenweis, S. M., DeMott, P. J., Matsunaga, A., Lim, Y. B., and Ziemann, P. J.: Chemical aging and the hydrophobic-to-hydrophilic conversion of carbonaceous aerosol, Geophys. Res. Lett., 33, L24806, https://doi.org/10.1029/2006GL027249, 2006.
Pöschl, U., Rudich, Y., and Ammann, M.: Kinetic model framework for aerosol and cloud surface chemistry and gas-particle interactions – Part 1: General equations, parameters, and terminology, Atmos. Chem. Phys., 7, 5989–6023, https://doi.org/10.5194/acp-7-5989-2007, 2007.
Putman, A. L., Offenberg, J. H., Fisseha, R., Kundu, S., Rahn, T. A., and Mazzoleni, L. R.: Ultrahigh-resolution FT-ICR mass spectrometry characterization of α-pinene ozonolysis SOA, Atmos. Environ., 46, 164–172, https://doi.org/10.1016/j.atmosenv.2011.10.003, 2012.
Renbaum-Wolff, L., Grayson, J. W., Bateman, A. P., Kuwata, M., Sellier, M., Murray, B. J., Shilling, J. E., Martin, S. T., and Bertram, A. K.: Viscosity of alpha-pinene secondary organic material and implications for particle growth and reactivity, P. Natl. Acad. Sci. USA, 110, 8014–8019, https://doi.org/10.1073/pnas.1219548110, 2013.
Ruehl, C. R., Nah, T., Isaacman, G., Worton, D. R., Chan, A. W., Kolesar, K. R., Cappa, C. D., Goldstein, A. H., and Wilson, K. R.: The influence of molecular structure and aerosol phase on the heterogeneous oxidation of normal and branched alkanes by OH, J. Phys. Chem. A, 117, 3990–4000, https://doi.org/10.1021/jp401888q, 2013.
Shilling, J. E., Chen, Q., King, S. M., Rosenoern, T., Kroll, J. H., Worsnop, D. R., DeCarlo, P. F., Aiken, A. C., Sueper, D., Jimenez, J. L., and Martin, S. T.: Loading-dependent elemental composition of a-pinene SOA particles, Atmos. Chem. Phys., 9, 771–782, https://doi.org/10.5194/acp-9-771-2009, 2009.
Shiraiwa, M., Pfrang, C., and Pöschl, U.: Kinetic multi-layer model of aerosol surface and bulk chemistry (KM-SUB): the influence of interfacial transport and bulk diffusion on the oxidation of oleic acid by ozone, Atmos. Chem. Phys., 10, 3673–3691, https://doi.org/10.5194/acp-10-3673-2010, 2010.
Shiraiwa, M., Pfrang, C., Koop, T., and Pöschl, U.: Kinetic multi-layer model of gas-particle interactions in aerosols and clouds (KM-GAP): linking condensation, evaporation and chemical reactions of organics, oxidants and water, Atmos. Chem. Phys., 12, 2777–2794, https://doi.org/10.5194/acp-12-2777-2012, 2012.
Slade, J. H. and Knopf, D. A.: Heterogeneous OH oxidation of biomass burning organic aerosol surrogate compounds: assessment of volatilisation products and the role of OH concentration on the reactive uptake kinetics, Phys. Chem. Chem. Phys., 15, 5898–5915, https://doi.org/10.1039/c3cp44695f, 2013.
Slade, J. H. and Knopf, D. A.: Multiphase OH oxidation kinetics of organic aerosol: The role of particle phase state and relative humidity, Geophys. Res. Lett., 41, 5297–5306, https://doi.org/10.1002/2014gl060582, 2014.
Slade, J. H., Thalman, R., Wang, J., and Knopf, D. A.: Chemical aging of single and multicomponent biomass burning aerosol surrogate particles by OH: implications for cloud condensation nucleus activity, Atmos. Chem. Phys., 15, 10183–10201, https://doi.org/10.5194/acp-15-10183-2015, 2015.
Slade, J. H., Shiraiwa, M., Arangio, A., Su, H., Pöschl, U., Wang, J., and Knopf, D. A.: Cloud droplet activation through oxidation of organic aerosol influenced by temperature and particle phase state, Geophys. Res. Lett., 44, 1583–1591, https://doi.org/10.1002/2016GL072424, 2017.
Smith, J. D., Kroll, J. H., Cappa, C. D., Che, D. L., Liu, C. L., Ahmed, M., Leone, S. R., Worsnop, D. R., and Wilson, K. R.: The heterogeneous reaction of hydroxyl radicals with sub-micron squalane particles: a model system for understanding the oxidative aging of ambient aerosols, Atmos. Chem. Phys., 9, 3209–3222, https://doi.org/10.5194/acp-9-3209-2009, 2009.
Song, M., Liu, P. F., Hanna, S. J., Li, Y. J., Martin, S. T., and Bertram, A. K.: Relative humidity-dependent viscosities of isoprene-derived secondary organic material and atmospheric implications for isoprene-dominant forests, Atmos. Chem. Phys., 15, 5145–5159, https://doi.org/10.5194/acp-15-5145-2015, 2015.
Tolocka, M. P., Heaton, K. J., Dreyfus, M. A., Wang, S. Y., Zordan, C. A., Saul, T. D., and Johnston, M. V.: Chemistry of particle inception and growth during alpha-pinene ozonolysis, Environ. Sci. Technol., 40, 1843–1848, https://doi.org/10.1021/es051926f, 2006.
Tong, H., Arangio, A. M., Lakey, P. S. J., Berkemeier, T., Liu, F., Kampf, C. J., Brune, W. H., Pöschl, U., and Shiraiwa, M.: Hydroxyl radicals from secondary organic aerosol decomposition in water, Atmos. Chem. Phys., 16, 1761–1771, https://doi.org/10.5194/acp-16-1761-2016, 2016.
Varutbangkul, V., Brechtel, F. J., Bahreini, R., Ng, N. L., Keywood, M. D., Kroll, J. H., Flagan, R. C., Seinfeld, J. H., Lee, A., and Goldstein, A. H.: Hygroscopicity of secondary organic aerosols formed by oxidation of cycloalkenes, monoterpenes, sesquiterpenes, and related compounds, Atmos. Chem. Phys., 6, 2367–2388, https://doi.org/10.5194/acp-6-2367-2006, 2006.
Virtanen, A., Joutsensaari, J., Koop, T., Kannosto, J., Yli-Pirila, P., Leskinen, J., Makela, J. M., Holopainen, J. K., Pöschl, U., Kulmala, M., Worsnop, D. R., and Laaksonen, A.: An amorphous solid state of biogenic secondary organic aerosol particles, Nature, 467, 824–827, https://doi.org/10.1038/nature09455, 2010.
Wang, B. B., O'Brien, R. E., Kelly, S. T., Shilling, J. E., Moffet, R. C., Gilles, M. K., and Laskin, A.: Reactivity of Liquid and Semisolid Secondary Organic Carbon with Chloride and Nitrate in Atmospheric Aerosols, J. Phys. Chem. A, 119, 4498–4508, https://doi.org/10.1021/jp510336q, 2015.
Wiegel, A. A., Wilson, K. R., Hinsberg, W. D., and Houle, F. A.: Stochastic methods for aerosol chemistry: a compact molecular description of functionalization and fragmentation in the heterogeneous oxidation of squalane aerosol by OH radicals, Phys. Chem. Chem. Phys., 17, 4398–4411, https://doi.org/10.1039/c4cp04927f, 2015.
Wiegel, A. A., Liu, M. J., Hinsberg, W. D., Wilson, K. R., and Houle, F. A.: Diffusive confinement of free radical intermediates in the OH radical oxidation of semisolid aerosols, Phys. Chem. Chem. Phys., 19, 6814–6830, https://doi.org/10.1039/c7cp00696a, 2017.
Wollenhaupt, M., Carl, S. A., Horowitz, A., and Crowley, J. N.: Rate coefficients for reaction of OH with acetone between 202 and 395 K, J. Phys. Chem. A, 104, 2695–2705, https://doi.org/10.1021/jp993738f, 2000.
Yasmeen, F., Vermeylen, R., Maurin, N., Perraudin, E., Doussin, J.-F., and Claeys, M.: Characterisation of tracers for aging of á-pinene secondary organic aerosol using liquid chromatography/negative ion electrospray ionisation mass spectrometry, Environ. Chem., 9, 236–246, https://doi.org/10.1071/en11148, 2012.
Yu, J. Z., Cocker, D. R., Griffin, R. J., Flagan, R. C., and Seinfeld, J. H.: Gas-phase ozone oxidation of monoterpenes: Gaseous and particulate products, J. Atmos. Chem., 34, 207–258, https://doi.org/10.1023/A:1006254930583, 1999.
Zhang, Q., Jimenez, J. L., Canagaratna, M. R., Allan, J. D., Coe, H., Ulbrich, I., Alfarra, M. R., Takami, A., Middlebrook, A. M., Sun, Y. L., Dzepina, K., Dunlea, E., Docherty, K., DeCarlo, P. F., Salcedo, D., Onasch, T., Jayne, J. T., Miyoshi, T., Shimono, A., Hatakeyama, S., Takegawa, N., Kondo, Y., Schneider, J., Drewnick, F., Borrmann, S., Weimer, S., Demerjian, K., Williams, P., Bower, K., Bahreini, R., Cottrell, L., Griffin, R. J., Rautiainen, J., Sun, J. Y., Zhang, Y. M., and Worsnop, D. R.: Ubiquity and dominance of oxygenated species in organic aerosols in anthropogenically-influenced Northern Hemisphere midlatitudes, Geophys. Res. Lett., 34, L13801, https://doi.org/10.1029/2007gl029979, 2007.
Zhang, X., Lambe, A. T., Upshur, M. A., Brooks, W. A., Be, A. G., Thomson, R. J., Geiger, F. M., Surratt, J. D., Zhang, Z. F., Gold, A., Graf, S., Cubison, M. J., Groessl, M., Jayne, J. T., Worsnop, D. R., and Canagaratna, M. R.: Highly Oxygenated Multifunctional Compounds in alpha-Pinene Secondary Organic Aerosol, Environ. Sci. Technol., 51, 5932–5940, https://doi.org/10.1021/acs.est.6b06588, 2017.
Ziemann, P. J. and Atkinson, R.: Kinetics, products, and mechanisms of secondary organic aerosol formation, Chem. Soc. Rev., 41, 6582–6605, https://doi.org/10.1039/c2cs35122f, 2012.