DMS oxidation and sulfur aerosol formation in the marine troposphere: a focus on reactive halogen and multiphase chemistry

Chen, Qianjie; Sherwen, Tomás; Evans, Mathew; Alexander, Becky

doi:https://doi.org/10.5194/acp-18-13617-2018

Articles | Volume 18, issue 18

https://doi.org/10.5194/acp-18-13617-2018

Articles | Volume 18, issue 18

Research article

27 Sep 2018

Research article |

| 27 Sep 2018

DMS oxidation and sulfur aerosol formation in the marine troposphere: a focus on reactive halogen and multiphase chemistry

Qianjie Chen, Tomás Sherwen, Mathew Evans, and Becky Alexander

Abstract

The oxidation of dimethyl sulfide (DMS) in the troposphere and subsequent chemical conversion into sulfur dioxide (SO₂) and methane sulfonic acid (MSA) are key processes for the formation and growth of sulfur-containing aerosol and cloud condensation nuclei (CCN), but are highly simplified in large-scale models of the atmosphere. In this study, we implement a series of gas-phase and multiphase sulfur oxidation mechanisms into the Goddard Earth Observing System-Chemistry (GEOS-Chem) global chemical transport model – including two important intermediates, dimethyl sulfoxide (DMSO) and methane sulphinic acid (MSIA) – to investigate the sulfur cycle in the global marine troposphere. We found that DMS is mainly oxidized in the gas phase by OH (66 %), NO₃ (16 %) and BrO (12 %) globally. DMS + BrO is important for the model's ability to reproduce the observed seasonality of surface DMS mixing ratio in the Southern Hemisphere. MSA is mainly produced from multiphase oxidation of MSIA by OH_(aq) (66 %) and O_3(aq) (30 %) in cloud droplets and aerosols. Aqueous-phase reaction with OH accounts for only 12 % of MSA removal globally, and a higher MSA removal rate is needed to reproduce observations of the MSA ∕ nss ${SO}_{4}^{2 -}$ ratio. The modeled conversion yield of DMS into SO₂ and MSA is 75 % and 15 %, respectively, compared to 91 % and 9 % in the standard model run that includes only gas-phase oxidation of DMS by OH and NO₃. The remaining 10 % of DMS is lost via deposition of intermediates DMSO and MSIA. The largest uncertainties for modeling sulfur chemistry in the marine boundary layer (MBL) are unknown concentrations of reactive halogens (BrO and Cl) and OH_(aq) concentrations in cloud droplets and aerosols. To reduce uncertainties in MBL sulfur chemistry, we should prioritize observations of reactive halogens and OH_(aq).

How to cite

How to cite.

Dates

Received: 24 Apr 2018 – Discussion started: 02 May 2018 – Revised: 07 Sep 2018 – Accepted: 07 Sep 2018 – Published: 27 Sep 2018

1 Introduction

The biogenic emission of dimethyl sulfide (DMS: CH₃SCH₃) from the ocean is the largest natural sulfur source to the atmosphere (Andreae, 1990). After emission, DMS is mainly oxidized in the troposphere, with a lifetime of 1–2 days (Chin et al., 1996; Boucher et al., 2003; Breider et al., 2010). The oxidation of DMS and subsequent formation of other sulfur species such as sulfuric acid (H₂SO₄) and methane sulfonic acid (MSA: CH₃SO₃H) are crucial for the formation and evolution of natural aerosols and clouds in the marine boundary layer (MBL) and thus have profound climate implications (Charlson et al., 1987; von Glasow and Crutzen, 2004; Thomas et al., 2010). In particular, Carslaw et al. (2013) pointed out that natural aerosols such as those that originate from DMS oxidation account for the largest uncertainty of aerosol radiative forcing in climate models.

The atmospheric fate of DMS determines the extent to which DMS affects our climate system. Production of H₂SO₄ and MSA from gas-phase oxidation of DMS-derived products can result in nucleation of new particles under favorable conditions (Kulmala et al., 2000; Chen et al., 2015), with implications for aerosol and cloud condensation nuclei (CCN) number concentrations. Sulfate and MSA formed in the aqueous phase will not result in new particle formation but will impact the aerosol size distribution, with implications for cloud microphysical properties (Kreidenweis and Seinfeld, 1988; Kaufman and Tanre, 1994). The oxidation mechanisms of DMS and subsequent formation of sulfate and MSA are, however, very complicated and still not well understood even after decades of research (Ravishankara et al., 1997; Barnes et al., 2006; Hoffmann et al., 2016). Large-scale models of atmospheric chemistry typically contain very simplified DMS chemistry and often ignore potentially important reaction intermediates. Most of these models include oxidation of DMS by OH and NO₃ radicals, directly producing SO₂ and MSA, and ignore the formation of dimethyl sulfoxide (DMSO: CH₃SOCH₃) and methane sulphinic acid (MSIA: CH₃SO₂H) intermediates (Chin et al., 1996, 2000; Gondwe et al., 2003; 2004; Berglen et al., 2004; Kloster et al., 2006). Nevertheless, previous large-scale modeling studies have suggested that BrO could be an important sink for DMS globally (up to 30 %), especially in the remote MBL where BrO mixing ratios can reach ppt levels (Boucher et al., 2003; von Glasow et al., 2004; Breider et al., 2010; Khan et al., 2016). Other oxidants that may be important for DMS oxidation include Cl radicals in the gas phase (von Glasow and Crutzen, 2004; Hoffmann et al., 2016) and O₃ in the gas and aqueous phase (Boucher et al., 2003; Hoffmann et al., 2016).

Some large-scale models have simulated the formation of the DMSO intermediate from DMS oxidation (Pham et al., 1995; Cosme et al., 2002; von Glasow et al., 2004; Castebrunet et al., 2009), which is important as DMSO is highly water soluble – Henry's law constant (H_DMSO) on the order of 10⁷ M atm⁻¹ – and can undergo dry and wet deposition in addition to gas- and aqueous-phase oxidation to MSA or SO₂ (Lee and Zhou, 1994; Campolongo et al., 1999; Barnes et al., 2006; Zhu et al., 2006; Hoffmann et al., 2016). In the cloud-free MBL, DMSO is mainly produced by DMS + BrO and DMS + OH_(g) via the addition channel and is oxidized by OH in the gas phase. In the cloudy MBL, DMSO is mainly produced via DMS + O_3(aq) and oxidized via DMSO + OH_(aq) in the aqueous phase (Hoffmann et al., 2016). Knowledge about aqueous-phase concentrations of OH in cloud droplets and aerosols is still very limited. Modeled OH_(aq) concentrations are on the order of 10⁻¹⁴–10⁻¹² M (Jacob, 1986; Matthijsen et al., 1995; Jacob et al., 1989; Herrmann et al., 2000). However, recent observations of OH_(aq), which are derived from the concentrations of dissolved organic compounds, are about 2 orders of magnitude lower (10⁻¹⁶–10⁻¹⁴ M) (Arakaki et al., 2013; Kaur and Anastasio, 2017). In addition to aqueous-phase oxidation of DMSO by OH_(aq), a box modeling study by Zhu et al. (2006) suggested that ${SO}_{4}^{-}$ and ${Cl}_{2}^{-}$ could contribute 34 % and 10 % of DMSO oxidation in the aqueous phase, respectively, with ${SO}_{4}^{-}$ and ${Cl}_{2}^{-}$ concentrations of $1 \times 10^{- 12}$ and $1 \times 10^{- 11}$ M (Herrmann et al., 2000), respectively. It should be noted that OH_(aq), ${SO}_{4}^{-}$ and ${Cl}_{2}^{-}$ concentrations are poorly known and the contribution of these species to DMSO oxidation will depend on their concentrations.

MSIA is generally not included in large-scale models, though it has been considered in some one-dimensional or box models (Lucas and Prinn, 2002; von Glasow and Crutzen, 2004; Zhu et al., 2006; Hoffmann et al., 2016). The Henry's law constant of MSIA has not been measured directly but is thought to be larger than that of DMSO and smaller than that of MSA, on the order of 10⁸ M atm⁻¹ (Barnes et al., 2006). MSIA is mainly produced from oxidation of DMSO by OH in both the gas and aqueous phase, and removed via further oxidation by OH and O₃ in both the gas and aqueous phase and ${Cl}_{2}^{-}$ in the aqueous phase (von Glasow and Crutzen, 2004; Zhu et al., 2006; Barnes et al., 2006; Hoffmann et al., 2016). Only oxidation of MSIA by OH in the gas phase produces SO₂; all other pathways lead to MSA formation. The contribution of each pathway towards MSIA oxidation depends on the concentration of each oxidant. Zhu et al. (2006) suggested ${Cl}_{2}^{-}$ is more important than OH_(aq) for MSIA oxidation in the aqueous phase when assuming a ${Cl}_{2}^{-}$ concentration of $1 \times 10^{- 11}$ M (Herrmann et al., 2000), while Hoffmann et al. (2016) suggested the opposite with a lower ${Cl}_{2}^{-}$ concentration ( $1.5 \times 10^{- 12}$ M).

The only source of MSA in the marine troposphere is from oxidation of DMS emitted from the marine biosphere. It thus contains information on both DMS emission flux and chemistry. It has been proposed as an ice core proxy for sea ice extent in past climates, as a result of melting sea ice releasing nutrients to stimulate phytoplankton growth to produce DMS (Curran et al., 2003; Abram et al., 2010). Other factors such as oxidation mechanisms of DMS and atmospheric circulation can also affect MSA abundance in ice core records (Becagli et al., 2009; Hezel et al., 2011). As DMS is the dominant sulfur source of both MSA and non-sea-salt sulfate (nss ${SO}_{4}^{2 -}$ ) in the remote marine troposphere, the MSA ∕ nss ${SO}_{4}^{2 -}$ molar ratio there reflects sulfur chemistry. In addition, the MSA ∕ nss ${SO}_{4}^{2 -}$ molar ratio has often been used as a measure of marine biogenic contribution to total atmospheric sulfate formation, as nss ${SO}_{4}^{2 -}$ has both anthropogenic and natural origins, while MSA is generally considered to have a predominant natural origin (Andreae et al., 1999; Savoie et al., 2002; Gondwe et al., 2004). MSA is very water soluble, with a Henry's law constant on the order of 10⁹ M atm⁻¹ (Campolongo et al., 1999), and is mainly removed from the atmosphere via wet and dry deposition with a lifetime of about a week (Pham et al., 1995; Chin et al., 1996, 2000; Cosme et al., 2002; Hezel et al., 2011). One-dimensional modeling studies by Zhu et al. (2006) and von Glasow and Crutzen (2004) suggested that the oxidation of MSA by OH_(aq) in the aqueous phase to form ${SO}_{4}^{2 -}$ in the MBL could also be a significant loss process of MSA (3 %–27 %) (Zhu et al., 2006; von Glasow and Crutzen, 2004), while a box modeling study by Hoffmann et al. (2016) found it negligible (2 %). The different conclusions regarding the role of reaction of MSA with OH_(aq) are due to different assumptions regarding OH_(aq) concentrations, which is highly uncertain.

In this study, we expand upon the current simplified DMS chemistry in a global chemical transport model, Goddard Earth Observing System-Chemistry (GEOS-Chem), including the DMSO and MSIA intermediates. We investigate the role of gas-phase and multiphase oxidation of DMS, DMSO, MSIA and MSA in determining their spatial distribution, seasonality and lifetime, and the implications for the MBL and global sulfur budget. Observations of DMS mixing ratios from four locations and MSA ∕ nss ${SO}_{4}^{2 -}$ ratios from 23 locations around the globe obtained from previous studies are used to assess the model performance. We conclude with recommendations for future laboratory experiments and field campaigns, and recommendations for sulfur chemistry that should be included in large-scale models of atmospheric chemistry and climate.

2 GEOS-Chem model

In this study, we use a global 3-D chemical transport model, GEOS-Chem v9-02 (http://acmg.seas.harvard.edu/geos/doc/archive/man.v9-02/index.html, last access: 19 September 2018), which is driven by assimilated meteorological data from the NASA Goddard Earth Observing System (GEOS-5, http://gmao.gsfc.nasa.gov, last access: 19 September 2018). It contains detailed HO_x–NO_x–VOC–ozone–BrO_x tropospheric chemistry originally described in Bey et al. (2001), with updated BrO_x and sulfate chemistry described in Parrella et al. (2012), Schmidt et al. (2016) and Chen et al. (2017). The sulfate–nitrate–ammonium aerosol simulation is fully coupled to gas-phase chemistry (Park et al., 2004), with aerosol thermodynamics described in Pye et al. (2009). The sea salt aerosol simulation is described in Jaeglé et al. (2011), and bulk cloud water pH is calculated as described in Alexander et al. (2012). The model contains detailed deposition schemes for both gas species and aerosols (Liu et al., 2001; Amos et al., 2012; Zhang et al., 2001; Wang et al., 1998). All simulations are performed at $4^{\circ} \times 5^{\circ}$ horizontal resolution and 47 vertical levels up to 0.01 hPa (≈81 km) after a model spin-up of 1 year. The vertical layer thickness ranges from 120–150 m for the first 12 layers to 200–800 m for the 13th–27th layers and >1000 m for the rest (http://acmg.seas.harvard.edu/geos/doc/archive/man.v9-01-02/appendix_3.html#A3.5.2, last access: 19 September 2018). The year 2007 is chosen as a reference year to be consistent with Schmidt et al. (2016) and Chen et al. (2017). The DMS emission flux from the ocean (F) is parameterized following Lana et al. (2011): F=k_TC_w, where gas transfer velocity k_T (m s⁻¹) is a function of sea surface temperature and wind speed and C_w (mol m⁻³) is the DMS concentrations in seawater obtained from Lana et al. (2011). In a sensitivity simulation, we used C_w from Kettle et al. (1999).

The standard model contains only three gas-phase DMS oxidation pathways in the original version, which produces SO₂ and MSA directly (Reaction R1–R3), following Chin et al. (1996) with updated reaction rate coefficients from Burkholder et al. (2015):

\begin{array}{l} (R1) & {DMS}_{(g)} + {OH}_{(g)} \overset{abstraction}{⟶} {SO}_{2 (g)} + {CH}_{3} O_{2} + {CH}_{2} O, \\ (R2) & {DMS}_{(g)} + {OH}_{(g)} \overset{addition}{⟶} 0.75 {SO}_{2 (g)} + 0.25 {MSA}_{(g)}, \\ (R3) & {DMS}_{(g)} + {NO}_{3 (g)} \to {SO}_{2 (g)} + {HNO}_{3} + {CH}_{3} O_{2} + {CH}_{2} O . \end{array}

The yields of SO₂ and MSA for the addition channel of the gas-phase DMS + OH reaction are originally from Chatfield and Crutzen (1990), who made simplified assumptions in their 2-D model based on previous laboratory experiments and modeling studies. It should be noted that only gas-phase chemistry was considered when they made the assumptions of the yields of SO₂ and MSA, which might not represent the real atmosphere as multiphase chemistry has been suggested to be the biggest source of MSA in the atmosphere (Zhu et al., 2006; Hoffmann et al., 2016).

Table 1Overview of sulfur chemistry in the full model run (R_all) with DMSO and MSIA intermediates and all 12 new reactions.

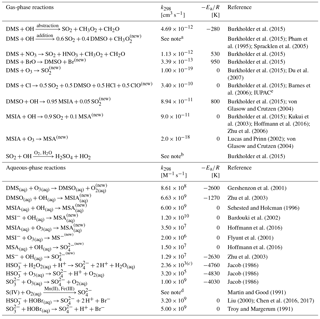
^new New reaction added in the model. ^a k(T, [O₂], [M]) = $8.2 \times 10^{- 39} [$ O₂ $] e^{5376 / T} / (1 + 1.05 \times 10^{- 5}$ ([O₂]/[M])e^3644∕T) cm³ molecule⁻¹ s⁻¹. ^b Low-pressure limit: $3.3 \times 10^{- 31} (300 / T)^{4.3}$ cm⁶ molecule⁻² s⁻¹; high-pressure limit: $1.6 \times 10^{- 12}$ cm³ molecule⁻¹ s⁻¹. ^c Rate constant of HS $O_{3}^{-}$ + H₂O₂(aq) at pH = 4.5. ^d The metal-catalyzed sulfate production rate is calculated from the following expression: $- \frac{d [{SO}_{4}^{2 -}]}{d t} = 750$ [Mn(II)][S(IV)] + 2600 [Fe(III)][S(IV)] + 1.0×10¹⁰ [Mn(II)][Fe(III)][S(IV)]; detailed description about [Mn(II)] and [Fe(III)] can be found in Alexander et al. (2009). ^e IUPAC: http://iupac.pole-ether.fr/htdocs/datasheets/pdf/SOx13_Cl_CH3SCH3.pdf (last access: 19 September 2018).

Download Print Version | Download XLSX

We add the DMSO and MSIA intermediates as two new advected chemical tracers, which undergo chemical production and loss, transport and deposition in the model. We add 12 new chemical reactions in the model, including gas-phase oxidation of DMS by OH (addition channel, modified to produce DMSO instead of MSA), BrO, Cl and O₃; multiphase oxidation of DMS by O₃; both gas-phase and multiphase oxidation of DMSO by OH; both gas-phase and multiphase oxidation of MSIA by OH and O₃; and multiphase oxidation of MSA by OH, as shown in Table 1. The rate coefficients for all gas-phase sulfur reactions are obtained from the most recent JPL report (Burkholder et al., 2015), except for MSIA_(g) + O_3(g) (Lucas and Prinn, 2002; von Glasow and Crutzen, 2004). The sulfur product yields for gas-phase reactions are obtained from various laboratory and modeling studies as indicated in Table 1. Product yields of 0.6 for SO₂ and 0.4 for DMSO have been commonly used in global models (Pham et al., 1995; Cosme et al., 2002; Spracklen et al., 2005; Breider et al., 2010) based on experiments described in Turnipseed et al. (1996) and Hynes et al. (1993). All oxidants (OH, O₃, H₂O₂, BrO, HOBr) are simulated in the full-chemistry scheme, except for Cl radicals. We used monthly mean Cl mixing ratios from Sherwen et al. (2016), which considered Cl–Br–I coupling but did not include chlorine production on sea salt aerosols, which was suggested to be the largest tropospheric chlorine source in Schmidt et al. (2016). We imposed a diurnal variation of Cl abundances based on solar zenith angle, similar to the offline simulation of OH abundances in GEOS-Chem (Fisher et al., 2017). The global distributions of tropospheric annual-mean concentrations of BrO, Cl, OH and O₃ are shown in Fig. 12. The high BrO abundances over the subtropics and polar regions are due to low deposition fluxes of reactive bromine (Schmidt et al., 2016), and the high BrO abundance over the Southern Ocean is due to its source from sea salt debromination (Chen et al., 2017). The high Cl abundance over coastal regions in the Northern Hemisphere is due to heterogeneous uptake of N₂O₅ on sea salt aerosols to produce reactive chlorine (Sherwen et al., 2016).

For the multiphase reactions DMS_(g) + O_3(aq), DMSO_(g) + OH_(aq), MSIA_(g) + OH_(aq), MSIA_(g) + O_3(aq) and MSA_(g) + OH_(aq) in cloud droplets and aerosols, we assume a first-order loss of the gas-phase sulfur species, following the parameterization described in Ammann et al. (2013) and Chen et al. (2017):

\begin{matrix} (1) & \frac{d [X_{(g)}]}{d t} = - \frac{c γ}{4} A [X_{(g)}], \end{matrix}

where X represents DMS, DMSO, MSIA or MSA; c is the average thermal velocity of X (m s⁻¹); A (m² m⁻³) is the total surface area concentration of aerosols or cloud droplets; and γ (unitless) is the reactive uptake coefficient of X that involves gas diffusion (γ_d), mass accommodation (α_b) and chemical reaction (Γ_b) in the aerosols or cloud droplets, as calculated in Eqs. (2)–(4).

\begin{array}{l} (2) & \frac{1}{γ} = \frac{1}{γ_{d}} + \frac{1}{α_{b}} + \frac{1}{Γ_{b}} \\ (3) & γ_{d} = \frac{4 D_{g}}{c r} \\ (4) & Γ_{b} = \frac{4 H_{X} R T \sqrt{D_{l, X} k_{X + Y} [Y]} f_{r}}{c} \end{array}

r is the radius of aerosols or cloud droplets (m); D_g is the gas-phase diffusion coefficient of X (m² s⁻¹), calculated as a function of air temperature and air density following Chen et al. (2017). H_X and D_l are the Henry's law constant (M atm⁻¹) and liquid-phase diffusion coefficient (m² s⁻¹) of X, which are summarized in Table 2; R ( $= 8.31 \times 10^{- 2}$ L bar mol⁻¹ K⁻¹) is the universal gas constant. T is air temperature (K); [Y] (= [OH_(aq)] or [O_3(aq)]) is the aqueous-phase concentration of the oxidant in aerosols or cloud droplets (M), where [O_3(aq)] is calculated assuming gas-liquid equilibrium and [OH_(aq)] is calculated following Jacob et al. (2005) ([OH_(aq)] =β[OH_(g)], $β = 1 \times 10^{- 19}$ M cm³ molecule⁻¹). This is about 2 orders of magnitude higher than [OH_(aq)] calculated indirectly from dissolved organic compound observations in Arakaki et al. (2013) and Kaur and Anastasio (2017). Thus, we conducted a sensitivity simulation reducing [OH_(aq)] in cloud droplets and aerosols by 2 orders of magnitude (Table 3). We conducted another sensitivity simulation by reducing the [OH_(aq)] in aerosols only by a factor of 20 (Herrmann et al., 2010) and found negligible changes (<2 %) in the global sulfur burden. Gas-phase sulfur species taken up by aerosols and cloud droplets will be oxidized in the aqueous phase. k_X+Y is the aqueous-phase reaction rate coefficient between aqueous-phase X and Y (M⁻¹ s⁻¹), as summarized in Table 1. f_r (= coth( $r / l) - l / r)$ is the reacto-diffusive correction term, which compares the radius of aerosols or cloud droplets (r) with the reacto-diffusive length scale of the reaction ( $l = \sqrt{D_{l} / (k_{X + Y} [Y])}$ ) (Ammann et al., 2013). The mass accommodation coefficients (α_b) of DMS, DMSO, MSIA and MSA are given in Table 2.

Table 2Henry's law constant at 298 K (H_X(298)); mass accommodation coefficient (α_b) and aqueous-phase diffusivity at 298 K (D_l(298 K)) for DMS, DMSO, MSIA and MSA; and acid dissociation constant (pK_a) for MSIA and MSA at 298 K.

^a CH₃SO₂H → ${CH}_{3} {SO}_{2}^{-}$ + H⁺; ^b CH₃SO₃H → ${CH}_{3} {SO}_{3}^{-}$ + H⁺.

Download Print Version | Download XLSX

Twelve model simulations were performed in order to investigate the importance of individual reactions for MBL sulfur chemistry and are described in Table 3. These simulations were designed to explore the role of DMS chemistry versus emissions for the DMS budget and the importance of gas-phase reactive halogen chemistry and multiphase chemistry for all sulfur-containing compounds.

Table 3Overview of model runs.

^* The product yield for the addition channel of the DMS + OH reaction is highly uncertain. Product yields of 0.6 for SO₂ and 0.4 for DMSO have been commonly used in global models (Pham et al., 1995; Cosme et al., 2002; Spracklen et al., 2005; Breider et al., 2010) based on experiments described in Turnipseed et al. (1996) and Hynes et al. (1993), and are used in this study (e.g., in R_all). Experiments under NO_x-free conditions suggest a DMSO yield near unity (Arsene et al., 1999; Barnes et al., 2006), as used in the sensitivity simulation R_add.

Download Print Version | Download XLSX

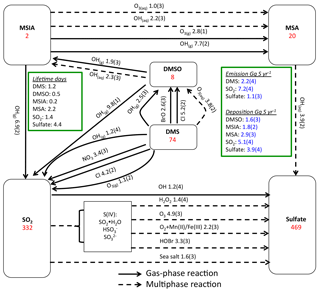
https://www.atmos-chem-phys.net/18/13617/2018/acp-18-13617-2018-f01

Figure 1Global sulfur budgets for R_all. Inventories (inside the boxes) are in units of Gg S. Solid arrows represent gas-phase reactions, while dashed arrows represent aqueous-phase reactions. Production and loss rates above arrows are in units of Gg S yr⁻¹. Read 1.9(3) as 1.9×10³ Gg S yr⁻¹.

Download

https://www.atmos-chem-phys.net/18/13617/2018/acp-18-13617-2018-f02

Figure 2Horizontal distribution of annual-mean surface mixing ratios (ppt) and vertical distribution of mixing ratios for (a) DMS, (b) DMSO, (c) MSIA, (d) MSA, (e) SO₂ and (f) sulfate. The dashed line indicates the climatological tropopause height.

Download

3 Results and discussion

3.1 DMS budget

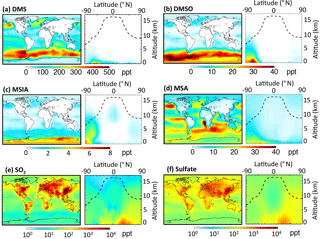
Figure 1 shows the global sulfur budgets for the model run, including DMSO and MSIA intermediates and all 12 new reactions (R_all). The DMS emission flux from the ocean to the atmosphere (F_DMS) is 22 Tg S yr⁻¹, which is similar to that (24 Tg S yr⁻¹) reported in Hezel et al. (2011) and within the range (11–28 Tg S yr⁻¹) reported in the literature (Spracklen et al., 2005, and references therein). F_DMS is 18 Tg S yr⁻¹ when using sea surface DMS concentrations from Kettle et al. (1999). The tropospheric burden of DMS is 74 Gg S, which is within the range of 20–150 Gg S reported in Faloona (2009), and is 40 % lower than the standard model run (R_std). The lifetime of DMS is 1.2 days in R_all, compared to 2.1 days in R_std. Surface DMS mixing ratios are highest over the Southern Ocean (≈400 ppt) (Fig. 2a), where DMS emissions are highest during summer (Lana et al., 2011) and DMS chemical destruction is small due to low OH abundance at high latitudes (DMS lifetime of 2–5 days over the Southern Ocean). DMS mainly resides in the lower troposphere, with 86 % of the tropospheric burden below 2 km. DMS is mainly oxidized in the gas phase by OH (37 % via abstraction channel and 29 % via addition channel), followed by NO₃ (16 %). The global contribution of OH and NO₃ to DMS oxidation from previous studies is 50 %–70 % and 20 %–30 %, respectively, depending mainly on which other oxidants are included (Boucher et al., 2003; Berglen et al., 2004; Breider et al., 2010; Khan et al., 2016). The oxidation of DMS by OH occurs mainly during daytime, while oxidation by NO₃ occurs mainly at night due to low nighttime OH production and rapid photolysis of NO₃ during daytime. Figure 3 shows the global annual-mean distribution of the fractional importance of different DMS oxidation pathways. The relative importance of OH for the oxidation of DMS ( $f_{[l] DMS + {OH}_{(g)}}$ ) is typically greater than 50 % over the oceans. The relative importance of NO₃ for the oxidation of DMS ( $f_{[l] DMS + {NO}_{3}}$ ) is typically low over the remote oceans (<10 %) but high over the continents and coastal regions (>40 %), where NO_x emissions are highest. It should be noted, however, that DMS abundance is low over continents (Fig. 2a).

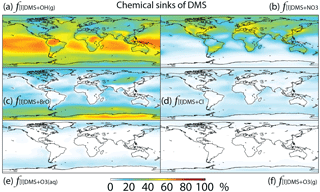
https://www.atmos-chem-phys.net/18/13617/2018/acp-18-13617-2018-f03

Figure 3Global tropospheric distribution of annual-mean percentage of DMS oxidized in the troposphere via (a) DMS + OH_(g) (f_[l]DMS+OH(g)), (b) DMS + NO₃ ( $f_{[l] DMS + {NO}_{3}}$ ), (c) DMS + BrO (f_[l]DMS+BrO), (d) DMS + Cl (f_[l]DMS+Cl), (e) DMS + O_3(aq) ( $f_{[l] DMS + O_{3 (aq)}}$ ) and (f) DMS + O_3(g) ( $f_{[l] DMS + O_{3 (g)}}$ ).

Download

The relative importance of BrO oxidation of DMS (f_[l]DMS+BrO) is 12 % (global annual mean), which is within the range suggested by Khan et al. (2016) (8 %) and Breider et al. (2010) (16 %). f_[l]DMS+BrO is highest (>30 %) over the Southern Ocean and Antarctica, especially during winter, due to high BrO (up to 0.5 ppt) and low OH and NO₃ abundance. The main uncertainty of the importance of BrO for DMS oxidation resides in the tropospheric BrO abundance, which is rarely measured and is still not well quantified in global models (von Glasow et al., 2004; Simpson et al., 2015). The BrO in our model generally underestimates satellite observations, especially over mid- and high latitudes (Chen et al., 2017), suggesting that our modeled estimate of the importance of DMS + BrO may be biased low. In order to quantify the contribution of BrO to DMS oxidation, we need to better quantify the BrO abundance through both observation and model development.

The fractional contribution of Cl to DMS oxidation (f_[l]DMS+Cl) is 4 % globally and generally less than 10 % everywhere. f_[l]DMS+Cl increases to 28 % in a sensitivity run, increasing Cl mixing ratios by an order of magnitude. In comparison, von Glasow and Crutzen (2004) calculated that about 8 % of DMS is oxidized by Cl in the cloud-free MBL during summer in a 1-D model. Hoffmann et al. (2016) estimated that about 18 % of DMS is oxidized by Cl under typical MBL conditions in a box model. Both studies used the same k_DMS+Cl as in our study, but Cl concentrations were not reported in either study. The annual-mean tropospheric Cl concentration used in this study is 1.1×10³ atoms cm⁻³, which is similar to that (1.3×10³ atoms cm⁻³) in another recent 3-D modeling study (Hossaini et al., 2016). As suggested by Sherwen et al. (2016), Cl concentration could be underestimated in our study, due at least in part to the missing chlorine source from sea salt aerosols and anthropogenic chloride emissions. The largest uncertainty for the importance of Cl for the oxidation of DMS resides in our limited knowledge of Cl concentrations in the troposphere. Due to the difficulty of directly observing Cl, estimates of its abundance are usually derived from non-methane hydrocarbon (NMHC) observations. Using this method, Cl concentration is estimated to be on the order of 10⁴ atoms cm⁻³ (0.2–80×10⁴ atoms cm⁻³) in the MBL and Antarctic boundary layer (Jobson et al., 1994; Singh et al., 1996; Wingenter et al., 1996, 2005; Boudries and Bottenheim, 2000; Arsene et al., 2007; Read et al., 2007), with highest concentrations over the tropical Pacific during autumn (Singh et al., 1996). However, a recent study suggests that this is an overestimate of tropospheric Cl abundance (Gromov et al., 2018). Another uncertainty in the atmospheric implications of DMS + Cl originates from its sulfur products, which are most likely CH₃SCH₂ via the abstraction channel and the (CH₃)₂S–Cl adduct via the addition channel (Barnes et al., 2006). The CH₃SCH₂ will likely be further oxidized into SO₂, similar to the abstraction channel of DMS + OH, while the (CH₃)₂S–Cl adduct could react with O₂ to produce DMSO. Atkinson et al. (2004) estimated that 50 % of DMS + Cl occurs through the abstraction channel and 50 % occurs through the addition channel at 298 K and 1 bar pressure, but the abstraction channel could account for more than 95 % at low pressure (Butkovskaya et al., 1995). Since DMS + Cl is neither a big sink of DMS nor a big source of DMSO in our study, the yield uncertainties have little influence on the modeled sulfur budgets. However, modeled estimates of DMS + Cl could be too low due to a potential low bias in modeled Cl abundance.

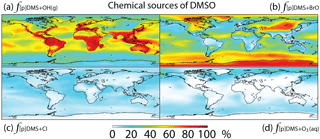
https://www.atmos-chem-phys.net/18/13617/2018/acp-18-13617-2018-f04

Figure 4Global tropospheric distribution of annual-mean percentage of DMSO produced via (a) DMS + OH_(g) ( $f_{[p] DMS + {OH}_{(g)}}$ ), (b) DMS + BrO (f_[p]DMS+BrO), (c) DMS + Cl (f_[p]DMS+Cl) and (d) DMS + O_3(aq) ( $f_{[p] DMS + O_{3 (aq)}}$ ).

Download

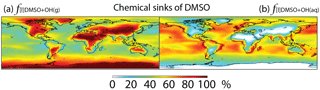
https://www.atmos-chem-phys.net/18/13617/2018/acp-18-13617-2018-f05

Figure 5Global tropospheric distribution of annual-mean percentage of DMSO oxidized via (a) DMSO + OH_(g) ( $f_{[l] DMSO + {OH}_{(g)}}$ ) and (b) DMSO + OH_(aq) ( $f_{[l] DMSO + {OH}_{(aq)}}$ ).

Download

In this study, DMS + O_3(aq) is the only multiphase DMS oxidation pathway, which accounts for only 2 % of DMS oxidation globally, reaching up to 5 % over high-latitude oceans (e.g., the Southern Ocean) (Fig. 3). In comparison, in a general circulation model Boucher et a. (2003) calculated that DMS + O_3(aq) accounts for about 6 % of DMS oxidation globally and 15 %–30 % over oceans north of 60^∘ N and in the 50–75^∘ S latitude band. The difference between the results from Boucher et al. (2003) and this study could be due to the differences in oxidant abundances such as O₃, OH, BrO and Cl. Using a 1-D model, von Glasow and Crutzen (2004) calculated that DMS + O_3(aq) accounts for 4 %–18 % of DMS oxidation in the cloudy MBL, which is similar to 5 %–10 % over the Southern Ocean MBL in our model results. The fraction of DMS oxidized by O₃ in the gas phase ( $f_{[l] DMS + O_{3 (g)}} = 0.5$ %) is smaller than $f_{[l] DMS + O_{3 (aq)}}$ , consistent with Boucher et al. (2003). Thus, both the gas-phase and multiphase oxidation of DMS by O₃ represent minor DMS sinks in the global troposphere.

3.2 DMSO budget

The modeled global tropospheric DMSO burden is 8 Gg S, which is 3–4 times larger than in the studies of Pham et al. (1995) and Cosme et al. (2002), which did not include production of DMSO from DMS + BrO. The modeled surface DMSO mixing ratio is highest over the Southern Ocean (≈30 ppt) (Fig. 2b), where the DMS mixing ratio is high and BrO is abundant. The high DMSO mixing ratio over Antarctica in our model is due to weak DMSO oxidation by OH in both the gas and aqueous phase. DMSO mainly resides in the lower troposphere, with 67 % of the tropospheric burden below 2 km.

Globally, we simulate DMS + BrO as the biggest source of DMSO (44 %), followed by the addition channel of DMS + OH (41 %), DMS + Cl (9 %) and DMS + O_3(aq) (6 %). The fraction of DMSO produced from DMS + BrO is highest over the high-latitude ocean, where OH abundance is low, and subtropical oceans, where BrO abundance is high, while DMS + Cl and DMS + O_3(aq) can account for up to 20 % of the DMSO production in coastal regions and the mid-latitude MBL, respectively (Fig. 4).

DMSO is removed from the atmosphere via gas-phase oxidation by OH (33 %), multiphase oxidation by OH in cloud droplets (37 %) and aerosols (3 %), and dry (16 %) and wet deposition (11 %). The lifetime of DMSO is about 11 h. Multiphase oxidation mainly occurs over regions where clouds are frequent and OH concentrations are high, e.g., low- to mid-latitude oceans (Fig. 5). Cosme et al. (2002) calculated 85 % of DMSO is lost via gas-phase oxidation by OH and the remaining 15 % via deposition in a global 3-D model, but they did not include heterogeneous loss of DMSO. It has been suggested that heterogeneous loss is the predominant loss process of DMSO in the cloudy MBL in box or 1-D models (Zhu et al., 2006; Hoffmann et al., 2016).

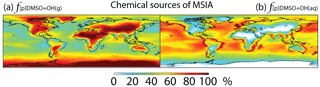
https://www.atmos-chem-phys.net/18/13617/2018/acp-18-13617-2018-f06

Figure 6Global tropospheric distribution of annual-mean percentage of MSIA produced in the troposphere via (a) DMSO + OH_(g) ( $f_{[p] DMSO + {OH}_{(g)}}$ ) and (b) DMSO + OH_(aq) ( $f_{[p] DMSO + {OH}_{(aq)}}$ ).

Download

https://www.atmos-chem-phys.net/18/13617/2018/acp-18-13617-2018-f07

Figure 7Global tropospheric distribution of annual-mean percentage of MSIA oxidized in the troposphere via (a) MSIA + OH_(aq) ( $f_{[l] MSIA + {OH}_{(aq)}}$ ), (b) MSIA + O_3(aq) ( $f_{[l] MSIA + O_{3 (aq)}}$ ), (c) MSIA + OH_(g) ( $f_{[l] MSIA + {OH}_{(g)}}$ ) and (d) MSIA + O_3(g) ( $f_{[l] MSIA + O_{3 (g)}}$ ).

Download

3.3 MSIA budget

MSIA is an important intermediate during the oxidation of DMSO to produce MSA, and it has a simulated tropospheric burden of 2 Gg S. The surface MSIA mixing ratio is higher over Antarctica than over the Southern Ocean (Fig. 2c) due to larger removal of MSIA by O_3(aq) and OH_(aq) in clouds over the Southern Ocean. Thirty-one percent of MSIA resides below 2 km altitude. The smaller fraction of MSIA below 2 km compared to DMSO is due to faster oxidation of MSIA by OH_(aq) and O_3(aq) in clouds and aerosols (Table 1).

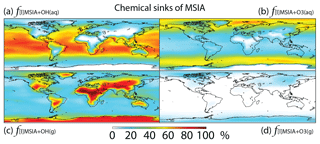
In R_all, MSIA is produced from both gas-phase (44 %) and multiphase (56 %) oxidation of DMSO by OH in cloud droplets and aerosols (Fig. 1). Multiphase production of MSIA mainly occurs over low- to mid-latitude oceans, where the OH abundance is high and clouds are frequent (Fig. 6).

MSIA is mainly removed in the troposphere via both gas-phase and multiphase oxidation by OH, with a lifetime of 4 h. Dry (2 %) and wet (2 %) deposition of MSIA accounts for 4 % of MSIA removal in the troposphere. Globally, multiphase oxidation in cloud droplets and aerosols by OH_(aq) (53 %) and O_3(aq) (24 %) is the biggest sink of MSIA, followed by gas-phase oxidation by OH (19 %). Multiphase oxidation by OH_(aq) is more important over low-latitude oceans, where OH abundance is high, reaching up to 70 % (Fig. 7). Multiphase oxidation by O_3(aq) is more important over high-latitude oceans, where OH abundance is low (Fig. 7). Over continents, including Antarctica, MSIA is mostly oxidized by OH in the gas phase.

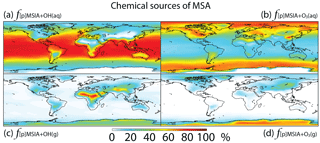
https://www.atmos-chem-phys.net/18/13617/2018/acp-18-13617-2018-f08

Figure 8Global tropospheric distribution of annual-mean percentage of MSA produced in the troposphere via (a) MSIA + OH_(aq) ( $f_{[p] MSIA + {OH}_{(aq)}}$ ), (b) MSIA +,O_3(aq) ( $f_{[p] MSIA + O_{3 (aq)}}$ ), (c) MSIA + OH_(g) ( $f_{[p] MSIA + {OH}_{(g)}}$ ) and (d) MSIA + O_3(g) ( $f_{[p] MSIA + O_{3 (g)}}$ ).

Download

In comparison, Hoffmann et al. (2016) also found that multiphase oxidation is the main sink of MSIA in the MBL in their box model, with O_3(aq), OH_(aq) and ${Cl}_{2}^{-}$ accounting for 42 %, 19 % and 10 % of MSIA removal, respectively. The rest of the MSIA (29 %) was removed by CH₃SO₂(O₂•) that was produced as an intermediate during the electron transfer reaction of MSIA with OH_(aq) and ${Cl}_{2}^{-}$ in cloud droplets and aerosols. By considering cloud droplets only, Hoffmann et al. (2016) suggested OH_(aq) is more important (1.5 times faster) than O_3(aq) for MSIA oxidation, which is consistent with our results. Since information such as OH_(aq) concentrations in aerosols, aerosol water content and cloud liquid water content was not provided in Hoffmann et al. (2016), we do not further compare our MSIA oxidation by O_3(aq) and OH_(aq) to Hoffmann et al. (2016). The modeling study by Hoffmann et al. (2016) is the only one that considered multiphase reaction of MSIA with both O_3(aq) and CH₃SO₂(O₂•). Zhu et al. (2006) found ${Cl}_{2}^{-}$ to be more important than OH_(aq) for MSIA oxidation when assuming ${Cl}_{2}^{-}$ concentration 6 times higher than that used in Hoffmann et al. (2016). Due to our limited knowledge about CH₃SO₂(O₂•) and ${Cl}_{2}^{-}$ production and concentrations in cloud droplets and aerosols, we do not include the multiphase reactions of MSIA with CH₃SO₂(O₂•) and ${Cl}_{2}^{-}$ in this study.

Gas-phase oxidation of MSIA by OH (18 %) has important implications for the MSA budget as MSIA + OH_(g) has a low yield for MSA formation (SO₂ yield of 0.9) (Kukui et al., 2003). Gas-phase oxidation of MSIA by O₃ is negligible globally (1 %). In contrast, Lucas and Prinn (2002) suggest MSIA + O_3(g) could compete with MSIA + OH_(g) for MSIA removal, but the rate coefficient of MSIA + OH_(g) is very small in their 1-D model (about 2 orders of magnitude smaller than ours).

3.4 MSA budget

In R_all, the global MSA burden is 20 Gg S, which is within the range of 13–40 Gg S reported in previous modeling studies (Pham et al, 1995; Chin et al., 1996, 2000; Cosme et al., 2002; Hezel et al., 2011). The largest MSA burden is from Hezel et al. (2011), in which DMSO was not included, while the smallest MSA burden is from Cosme et al. (2002), in which DMSO was included. Neglecting the DMSO intermediate in the model could result in an overestimate of MSA production as DMSO is also removed via dry and wet deposition. Note that none of these previous studies consider DMS + BrO and MSA + OH_(aq) in their models. Surface MSA mixing ratio is highest over the Southern Ocean, but the peak shifts north compared to DMS, DMSO and MSIA (Fig. 2d). This is due to larger production of MSA by O_3(aq) and OH_(aq) in clouds (due to higher O_3(aq) and OH_(aq) concentrations at lower latitudes) over the northern part of the Southern Ocean compared to the southern part of the Southern Ocean. Fifty-seven percent of MSA resides below 2 km altitude, suggesting that MSA is mainly produced in the MBL.

As shown in Fig. 1, MSA is mainly produced from multiphase oxidation of MSIA by OH (66 %) and O₃ (30 %). MSIA + OH_(aq) dominates over low-latitude oceans, while MSIA + O_3(aq) dominates over high-latitude oceans (Fig. 8). MSA formation occurs mainly in clouds (74 %), where the liquid water content is high. Our result is consistent with the general concept that gas-phase MSA formation is small compared to multiphase formation (Barnes et al., 2006; von Glasow and Crutzen, 2004; Zhu et al., 2006; Hoffmann et al., 2016). MSA + OH_(aq) accounts for 12 % of MSA removal in R_all, and the rest of the MSA is removed via dry (12 %) and wet (76 %) deposition. The lifetime of MSA is 2.2 days globally, which is relatively short compared to 5–7 days in previous studies (Pham et al, 1995; Chin et al., 1996, 2000; Cosme et al., 2002; Hezel et al., 2011) without MSA + OH_(aq). Information about the global distribution of MSA concentrations and deposition from these previous modeling studies is needed for comparison. The MSA lifetime is lowest (about 1 day) over tropical oceans, where clouds are frequent and OH abundance is high. It increases to 2–6 days over the Southern Ocean and subtropical oceans. To the best of our knowledge, this is the first study to report global MSA lifetime from a global 3-D model that considers MSA + OH_(aq). In the sensitivity run without MSA + OH_(aq) ( $R_{noMSA + {OH}_{(aq)}}$ ), the lifetime of MSA increases to 2.5 days. In the sensitivity run with a higher rate constant of MSA + OH_(aq) ( $R_{moreMSA + {OH}_{(aq)}}$ ), the lifetime of MSA decreases to 1.7 days.

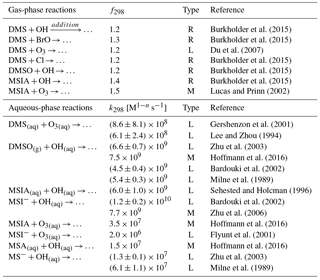
Table 4The uncertainties of the rate constants for the 12 reactions added in the model. The uncertainty factor f₂₉₈ means the reaction rate constant may be greater than or less than the recommended value by the factor f₂₉₈. Type “R”, “L” and “M” represent values obtained from “literature reviews”, “laboratory measurements” and “modeling studies”, respectively.

Download Print Version | Download XLSX

3.5 Uncertainties in rate constants

The uncertainties in the rate constants for the reactions added in the model are shown in Table 4. The uncertainty factor (f₂₉₈) used for gas-phase reaction rate constants at 298 K indicates that the reaction rate constant could be greater than or less than the recommended value by a factor of f₂₉₈. For all gas-phase reactions added in this study, f₂₉₈ varies from 1.2 to 1.5. f₂₉₈ is 1.3 for the DMS + BrO reaction, which adds to the uncertainty in oxidation of DMS by BrO. The global annual-mean tropospheric BrO burden varies from 3.6 to 5.7 Gg Br in three recent global modeling studies (Parrella et al., 2012; Schmidt et al., 2016; Chen et al., 2017), but all three of these modeling studies underestimate satellite observations of the tropospheric BrO column from Theys et al. (2011) (e.g., by 44 % over the Southern Ocean in Chen et al., 2017). Thus, further investigations are needed in both laboratory determination of the reaction rate constant for DMS + BrO and field observations of the BrO abundance in the troposphere. In addition, we need to better constrain the rate constants for the other two gas-phase reactions: DMS + OH (addition pathway) and DMSO + OH (f₂₉₈=1.2). Very few studies have determined the rate constants for the multiphase reactions added in the model (Table 4). The biggest uncertainty resides in the oxidation of MSA by OH_(aq) and the oxidation of MSIA by O_3(aq). The rate constant for the MS⁻ + OH_(aq) reactions differs by a factor of 4.7 in Milne et al. (1989) and Zhu et al. (2003), which results in about 30 % difference in global annual-mean tropospheric MSA burden. Only one box modeling study (Hoffmann et al., 2016) considered the oxidation of MSIA by O_3(aq) in clouds and aerosols, using the rate constant measured in Herrmann and Zellner (1997) for the MSIA_(aq) + O_3(aq) reaction and that in Flyunt et al. (2001) for the MSI⁻ + O_3(aq) reaction. As MSIA + O_3(aq) and MSA + OH_(aq) are important for MSA production and removal, more laboratory studies are needed to constrain the rate constants for these two reactions.

3.6 Model–observation comparison

3.6.1 Surface DMS mixing ratio

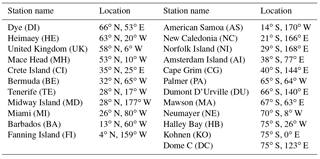
Monthly mean DMS mixing ratios measured at four stations around the globe are used to assess modeled DMS: Crete Island (CI; 35^∘24^′ N, 25^∘60^′ E) (Kouvarakis and Mihalopoulos, 2002), Amsterdam Island (AI; 37^∘50^′ S, 77^∘30^′ E) (Castebrunet et al., 2009), Cape Grim (CG; 40^∘41^′ S, 144^∘41^′ E) (Ayers et al., 1995) and Dumont D'Urville (DU; 66^∘40^′ S, 140^∘1^′ E) (Castebrunet et al., 2009). The DMS data covers the period 1997–1999 for CI, the period 1987–2006 for AI, the period 1989–1992 for CG and the period 1998–2006 for DU.

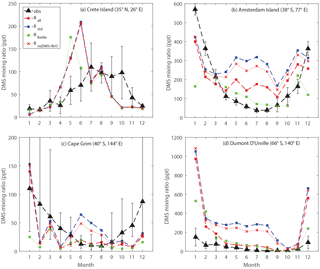
https://www.atmos-chem-phys.net/18/13617/2018/acp-18-13617-2018-f09

Figure 9Comparison between modeled and observed monthly mean surface DMS mixing ratios at (a) Crete Island (CI), (b) Amsterdam Island (AI), (c) Cape Grim (CG), and (d) Dumont D'Urville (DU) stations.

Download

Figure 9 shows the comparison between modeled and observed monthly-mean DMS mixing ratio at CI, AI, CG and DU stations. Comparing R_all with R_std, we can see that in general the modeled DMS mixing ratios match better with observations for the three stations in the Southern Hemisphere with the updated DMS chemistry, especially during Southern Hemisphere winter. Between June and August, the modeled DMS mixing ratios calculated from R_std overestimate observations by a factor of 6, 4 and 27 for AI, CG and DU, respectively. In comparison, during the same period, the modeled DMS mixing ratios calculated from R_all overestimate observations by a factor of 3 for AI, 50 % for CG and a factor of 4 for DU. The smaller discrepancy between modeled and observed DMS mixing ratio in R_all is largely due to DMS + BrO, as indicated by comparing R_all with a model run that includes all reactions except DMS + BrO (R_noDMS+BrO). It should be noted that BrO is underestimated in our model compared to satellite observations (underestimated by 44 % in terms of annual-mean tropospheric BrO column between 30^∘ S and 60^∘ S) (Chen et al., 2017), which might partly explain the remaining overestimate of DMS mixing ratios from R_all compared to observations.

In addition to DMS chemistry shown above, surface seawater DMS concentrations also affect the modeled DMS mixing ratio. The surface seawater DMS concentration was obtained from Kettle et al. (1999) in R_Kettle, instead of from Lana et al. (2011) in R_all. The global DMS emission flux from R_Kettle is 15 % lower than that from R_all. Overall, at CI, CG and DU, the modeled DMS mixing ratios from R_Kettle are similar to those from R_all during most of the year. Much lower DMS mixing ratios were calculated from R_Kettle at CI in June, at CG in January and at DU in December and January. At AI, however, the modeled DMS mixing ratios from R_Kettle are lower than those from R_all in general, which agree better with observations except in December and January. In this study, we focus on the chemistry aspects of the sulfur cycle and thus will not present further discussion on the impact of the DMS seawater climatology on atmospheric DMS abundance.

Table 5The locations of the 23 stations that provide annual-mean MSA ∕ nss ${SO}_{4}^{2 -}$ observations.

Download Print Version | Download XLSX

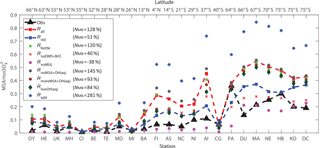
https://www.atmos-chem-phys.net/18/13617/2018/acp-18-13617-2018-f10

Figure 10Comparison between modeled (nine model runs described in Table 3) and observed (obs, black triangle) annual-mean surface MSA ∕ nss ${SO}_{4}^{2 -}$ ratios at 23 stations around the globe. The normalized mean bias $N_{MB} = \frac{\sum_{i = 1}^{23} (M_{i} - O_{i})}{\sum_{i = 1}^{23} O_{i}} \times 100$ %, where M_i and O_i are modeled value and observed value, respectively, is shown in inset.

Download

https://www.atmos-chem-phys.net/18/13617/2018/acp-18-13617-2018-f11

Figure 11Global distribution of annual-mean surface MSA ∕ nss ${SO}_{4}^{2 -}$ molar ratios from the full model run (R_all), overplotted with observed annual-mean surface MSA ∕ nss ${SO}_{4}^{2 -}$ ratios from 23 stations around the globe.

Download

3.6.2 Surface MSA ∕ nss ${SO}_{4}^{2 -}$ ratio

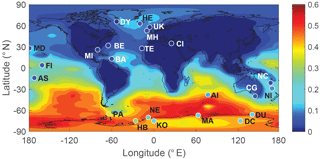
Figure 10 shows the comparison between modeled and observed annual-mean MSA ∕nss ${SO}_{4}^{2 -}$ ratio at 23 stations around the globe (Table 5). Data for all stations were obtained from Gondwe et al. (2004), except for CI from Kouvarakis and Mihalopoulos (2002) and AI, PA, KO and DC from Casterbrunet et al. (2009). The global distribution of annual-mean MSA ∕ nss ${SO}_{4}^{2 -}$ obtained from R_all, overplotted with observations for these 23 stations, is shown in Fig. 11. In addition to the four model runs described in Sect. 3.6.1 (R_alll, R_std, R_Kettle and R_noDMS+BrO), five additional model runs were performed by removing ( $R_{noMSA + {OH}_{(aq)}}$ ) or increasing ( $R_{moreMSA + {OH}_{(aq)}}$ ) aqueous-phase oxidation of MSA by OH; removing all multiphase chemistry involving DMS, DMSO, MSIA and MSA oxidation (R_noMUL); decreasing OH_(aq) concentrations in cloud droplets and aerosols by 2 orders of magnitude ( $R_{low {OH}_{(aq)}}$ ); and using a unity yield of DMSO for the addition channel of DMS oxidation by OH (R_add) (see Table 3).

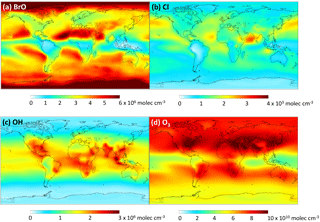
https://www.atmos-chem-phys.net/18/13617/2018/acp-18-13617-2018-f12

Figure 12Global tropospheric distribution of annual-mean gas-phase (a) BrO, (b) Cl, (c) OH and (d) O₃ concentration.

Download

Figures 10 and 11 show that modeled MSA ∕ nss ${SO}_{4}^{2 -}$ ratios calculated from R_all can generally reproduce the spatial variability of MSA ∕ nss ${SO}_{4}^{2 -}$ observations, especially the latitudinal trend of increasing ratios towards the south, where anthropogenic sources of nss ${SO}_{4}^{2 -}$ are less important. However, modeled MSA ∕ nss ${SO}_{4}^{2 -}$ ratios overestimate observations by a factor of 2 on average. The normalized mean bias N_MB ( $= \frac{\sum_{i = 1}^{23} (M_{i} - O_{i})}{\sum_{i = 1}^{23} O_{i}} \times 100$ %, where M_i and O_i are modeled value and observed value, respectively) for the comparison between modeled and observed MSA ∕ nss ${SO}_{4}^{2 -}$ ratios in R_all is 128 %. The large modeled MSA ∕ nss ${SO}_{4}^{2 -}$ over low-latitude oceans (13^∘ N–37^∘ S) is due to lower anthropogenic sources of nss ${SO}_{4}^{2 -}$ and to large multiphase MSA production as a result of high cloud liquid water content and oxidant abundance (OH and O₃). Over Antarctica (stations PA, DU, MA, NE, HB, KO and DC) where aqueous-phase oxidation of MSA is small, modeled MSA ∕ nss ${SO}_{4}^{2 -}$ ratios are about twice those of observations on average. In R_noDMS+BrO, the modeled MSA ∕ nss ${SO}_{4}^{2 -}$ ratios decrease compared to R_all, which is most evident over stations where DMS + BrO is a large source of DMSO and MSA (e.g., Southern Hemisphere ocean and Antarctica) (Fig. 4). Compared to R_all, the modeled MSA ∕ nss ${SO}_{4}^{2 -}$ ratios from R_noDMS+BrO match better with observations, with N_MB=40 %. However, as shown in Sect. 3.6.1, DMS observations were largely overestimated in R_noDMS+BrO (Fig. 9). If multiphase chemistry is switched off (R_noMUL), modeled MSA ∕ nss ${SO}_{4}^{2 -}$ ratios underestimate the observations by 49 % on average for all 23 stations. Thus, multiphase sulfur chemistry is important for the model simulation of MSA ∕ nss ${SO}_{4}^{2 -}$ observations. However, the OH_(aq) concentrations in cloud droplets and aerosols, which range from 10⁻¹⁴ to 10⁻¹² M in modeling studies (Jacob, 1986; Matthijsen et al., 1995; Jacob et al., 1989; Herrmann et al., 2000) and 10⁻¹⁶ to 10⁻¹⁴ M in observations (Arakaki et al., 2013; Kaur and Anastasio, 2017), are a large uncertainty in modeling multiphase sulfur chemistry. The model run reducing OH_(aq) concentrations by 2 orders of magnitude ( $R_{low {OH}_{(aq)}}$ ) results in a 25 % decrease in MSA ∕ nss ${SO}_{4}^{2 -}$ , with N_MB=84 %. Due to the small chemical loss of MSA in our model, MSA ∕ nss ${SO}_{4}^{2 -}$ in model runs without MSA + OH_(aq) ( $R_{noMSA + {OH}_{(aq)}}$ ) is similar to that in R_all. The model run with a larger reaction rate coefficient of MSA + O_(aq) ( $R_{moreMSA + {OH}_{(aq)}}$ ) results in a decrease in modeled MSA ∕ nss ${SO}_{4}^{2 -}$ (24 % on average) compared to R_all. This reveals the importance of MSA + OH_(aq) for MSA ∕ nss ${SO}_{4}^{2 -}$ observations, as suggested by von Glasow and Crutzen (2004), Zhu et al. (2006) and Mungall et al. (2018). The model run with a unity yield of DMSO from the addition channel of DMS oxidation by OH (R_add) largely overestimates MSA ∕ nss ${SO}_{4}^{2 -}$ observations, with N_MB=281 %.

Modeled MSA ∕ nss ${SO}_{4}^{2 -}$ from R_std without multiphase chemistry and DMS + BrO can generally reproduce the meridional trend of observations, with N_MB=51 %. However, R_std overestimates DMS observations (Fig. 9), suggesting that R_std produces comparable MSA ∕ nss ${SO}_{4}^{2 -}$ values for the wrong reasons.

4 Implications

Once emitted into the atmosphere through air–sea exchange, biogenic DMS undergoes complicated chemical processes to form SO₂ and MSA in the troposphere. SO₂ can then be oxidized to form sulfate aerosol. Sulfate and MSA produced in the gas phase can nucleate new particles under favorable conditions (Kulmala et al., 2000; Chen et al., 2015), while MSA and sulfate produced in the aqueous phase lead to the growth of existing particles (Kreidenweis and Seinfeld, 1988; Kaufman and Tanre, 1994). Global models such as general circulation models (GCMs) and chemical transport models (CTMs) generally consider very simplified gas-phase DMS chemistry, which could result in large biases in SO₂ and MSA prediction. Quantifying the yields of SO₂ and MSA from DMS oxidation is necessary to evaluate the climate impacts of DMS from the ocean ecosystem. Compared to the standard GEOS-Chem model run, the updated sulfur scheme in this study decreases the conversion yield of DMS to SO₂ ( $Y_{DMS \to {SO}_{2}}$ ) from 91 % to 75 % and increases the conversion yield of DMS to MSA (Y_DMS→MSA) from 9 % to 15 %. The remaining 10 % of DMS is lost via wet and dry deposition of DMSO and MSIA. In order to gain insight into the impacts of our updated sulfur scheme on global SO₂, MSA and sulfate burden, we conducted two sensitivity studies by allowing DMS as the only sulfur source for both the standard model run R_std (R_{std_onlyDMS}) and full model run R_all (R_{all_onlyDMS}). Compared to R_{std_onlyDMS}, the global DMS, SO₂, MSA and sulfate burden in R_{all_onlyDMS} decreases by 40 %, 17 %, 8 % and 12 %, respectively. The decrease in DMS is mainly due to DMS oxidation by BrO with the updated sulfur scheme. The decrease in SO₂ is due to a lower yield of SO₂ from DMS ( $Y_{DMS \to {SO}_{2}}$ ) but is partly compensated for by the increase in the DMS oxidation rate. MSA decreases despite an increase in the yield of MSA from DMS (Y_DMS→MSA) due to a shorter lifetime in R_{all_onlyDMS} (2.2 days in R_{all_onlyDMS} versus 4.1 days in R_{std_onlyDMS}) that is caused by the aqueous-phase sink of MSA via MSA + OH_(aq) and faster deposition of MSA produced in the MBL. The decrease in sulfate is caused by the decrease in SO₂ but is partly compensated for by the inclusion of MSA + OH_(aq) as a sulfate source, which accounts for 4 % of global sulfate production. The decrease in sulfate will be smaller if more MSA is oxidized into sulfate instead of being lost via deposition. In sum, climate models with a simplified DMS oxidation scheme (gas-phase oxidation by OH and NO₃ only) may overestimate SO₂, MSA and sulfate abundances in the pre-industrial environment, potentially leading to underestimates in sulfur aerosol radiative forcing calculations in climate models. Quantifying the impacts of our updated sulfur oxidation scheme on new particle formation is out of the scope of this study and should be addressed in the future.

MSA in Antarctic ice cores has been related to spring sea ice extent (Curran et al., 2003; Abram et al., 2010) as DMS is emitted in regions of sea ice melt. Our results show that, in addition to DMS emission, tropospheric sulfur chemistry is critical for MSA abundance in the troposphere, as also suggested by observations in inland East Antarctica (Legrand et al., 2017). Compared to the full model run R_all, sensitivity studies without DMS + BrO reaction (R_noDMS+BrO) and without multiphase oxidation of DMS, DMSO, MSIA and MSA (R_noMUL) reduce the global MSA burden by 15 % and 75 %, respectively. This indicates that reactive halogen and multiphase chemistry are important for the MSA budget in the troposphere, which should be considered when interpreting MSA abundance in ice cores, especially over time periods where the abundance of atmospheric oxidants may have changed.

5 Conclusions

In this study, we investigate the impacts of reactive halogen and multiphase chemistry on tropospheric DMS chemistry by adding two new chemical tracers (DMSO and MSIA) and 12 new reactions for both the gas-phase and multiphase oxidation of DMS, DMSO, MSIA and MSA into a global chemical transport model, GEOS-Chem. With the updated DMS chemistry, the DMS burden decreases by 40 % globally, mostly due to oxidation of DMS by BrO. BrO oxidation accounts for 12 % of DMS oxidation globally, which could be underestimated due to underestimates in BrO abundance in the model but is within the range of 8 %–16 % reported in previous studies. Cl is not important for DMS oxidation due to small Cl abundance, but this reaction should be revisited if modeled Cl budgets are substantially revised in the future. Neither gas-phase oxidation nor multiphase oxidation of DMS by O₃ is important for the global DMS budget, and both can be neglected in global models.

Dry and wet deposition accounts for 28 % of DMSO removal and 4 % of MSIA removal globally. The significant role of deposition as a sink for DMSO suggests that DMSO should be included in sulfur chemistry mechanisms, as exclusion of DMSO as an intermediate may result in an overestimate of MSA production from the oxidation of DMS. MSIA is an important intermediate between DMSO and MSA. MSA is mostly (97 % globally) produced through aqueous-phase oxidation of MSIA by O_3(aq) and OH_(aq) in cloud droplets and aerosols. Dry and wet deposition accounts for 88 % of MSA removal globally; multiphase oxidation by OH in cloud droplets and aerosols accounts for the rest. We note that the relative importance of deposition versus oxidation as a sink for MSA will depend on the OH_(aq) concentration in cloud droplets and aerosols, which is highly uncertain.

Modeled DMS mixing ratios agree better (mean square error between model and observation is 44 % smaller) with observations with the inclusion of DMS + BrO. The overestimate of MSA ∕ nss ${SO}_{4}^{2 -}$ observations using our updated sulfur oxidation scheme suggests MSA oxidation is underestimated in the model. The uncertainties of reactive halogen abundances, such as BrO and Cl, and the aqueous-phase oxidant concentrations, such as OH_(aq), have limited our ability to model DMS oxidation and MSA formation in the troposphere. Future studies should prioritize the measurements of reactive halogen abundances and OH_(aq) concentrations in cloud droplets, especially in the marine boundary layer.

Data availability

The DMS observational data in Fig. 9 were obtained from the referenced papers (Ayers et al., 1995; Kouvarakis and Mihalopoulos, 2002; Castebrunet et al., 2009). The MSA/nss ${SO}_{4}^{2 -}$ observational data in Fig. 10 were obtained from the referenced papers (Kouvarakis and Mihalopoulos, 2002; Gondwe et al., 2004; Casterbrunet et al., 2009).

Author contributions

QC and BA conceived the study. All authors contributed to model code development and interpretation of model results. QC wrote the manuscript with input from BA, TS and ME.

Competing interests

The authors declare that they have no conflict of interest.

Acknowledgements

We acknowledge Johan A. Schmidt for the discussions on tropospheric sulfur and halogen cycles, and providing support for the GEOS-Chem halogen chemistry scheme. We acknowledge Tom Breider for offering help with the DMSO simulation scheme. We acknowledge Paul Hezel for the help in searching for sulfur species observations and Giorgos Kouvarakis for providing DMS data on Crete. We acknowledge NSF AGS award 1343077 to Becky Alexander for support of this research.

Edited by: Jianzhong Ma
Reviewed by: two anonymous referees

References

Abram, N. J., Thomas, E. R., McConnell, J. R., Mulvaney, R., Bracegirdle, T. J., Sime, L. C., and Aristarain, A. J.: Ice core evidence for a 20th century decline of sea ice in the Bellingshausen Sea, Antarctica, J. Geophys. Res., 115, D23101, https://doi.org/10.1029/2010JD014644, 2010.

Alexander, B., Park, R. J., Jacob, D. J., and Gong S.: Transition metal-catalyzed oxidation of atmospheric sulfur: Global implications for the sulfur budget, J. Geophys. Res., 114, D02309, https://doi.org/10.1029/2008JD010486, 2009.

Alexander, B., Allman, D. J., Amos, H. M., Fairlie, T. D., Dachs, J., Hegg, D. A., and Sletten, R. S.: Isotopic constraints on the formation pathways of sulfate aerosol in the marine boundary layer of the subtropical northeast Atlantic Ocean, J. Geophys. Res., 117, D06304, https://doi.org/10.1029/2011JD016773, 2012.

Ammann, M., Cox, R. A., Crowley, J. N., Jenkin, M. E., Mellouki, A., Rossi, M. J., Troe, J., and Wallington, T. J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Volume VI – heterogeneous reactions with liquid substrates, Atmos. Chem. Phys., 13, 8045–8228, https://doi.org/10.5194/acp-13-8045-2013, 2013.

Amos, H. M., Jacob, D. J., Holmes, C. D., Fisher, J. A., Wang, Q., Yantosca, R. M., Corbitt, E. S., Galarneau, E., Rutter, A. P., Gustin, M. S., Steffen, A., Schauer, J. J., Graydon, J. A., Louis, V. L. St., Talbot, R. W., Edgerton, E. S., Zhang, Y., and Sunderland, E. M.: Gas-particle partitioning of atmospheric Hg(II) and its effect on global mercury deposition, Atmos. Chem. Phys., 12, 591–603, https://doi.org/10.5194/acp-12-591-2012, 2012.

Andreae, M. O.: Ocean-atmosphere interactions in the global biogeochemical sulfur cycle, Mar. Chem., 30, 1–29, https://doi.org/10.1016/0304-4203(90)90059-L, 1990.

Andreae, M. O., Elbert, W., Cai, Y., Andreae, T. W., and Gras, J.: Non-sea-salt sulfate, methanesulfonate, and nitrate aerosol concentrations and size distributions at Cape Grim, Tasmania, J. Geophys. Res., 104, 21695–21706, https://doi.org/10.1029/1999JD900283, 1999.

Arakaki, T., Anastasio, C., Kuroki, Y., Nakajima, H., Okada, K., Kotani, Y., Handa, D., Azechi, S., Kimura, T., Tsuhako, A., and Miyagi, Y.: A general scavenging rate constant for reaction of hydroxyl radical with organic carbon in atmospheric waters, Environ. Sci. Technol., 47, 8196–8203, https://doi.org/10.1021/es401927b, 2013.

Arsene, C., Barnes, I., and Becker, K. H.: FT-IR product study of the photo-oxidation of dimethyl sulfide: Temperature and O₂ partial pressure dependence, Phys. Chem. Chem. Phys., 1, 5463–5470, https://doi.org/10.1039/A907211J, 1999.

Arsene, C., Bougiatioti, A., Kanakidou, M., Bonsang, B., and Mihalopoulos, N.: Tropospheric OH and Cl levels deduced from non-methane hydrocarbon measurements in a marine site, Atmos. Chem. Phys., 7, 4661–4673, https://doi.org/10.5194/acp-7-4661-2007, 2007.

Atkinson, R., Baulch, D. L., Cox, R. A., Crowley, J. N., Hampson, R. F., Hynes, R. G., Jenkin, M. E., Rossi, M. J., and Troe, J.: Evaluated kinetic and photochemical data for atmospheric chemistry: Volume I – gas phase reactions of O_x, HO_x, NO_x and SO_x species, Atmos. Chem. Phys., 4, 1461–1738, https://doi.org/10.5194/acp-4-1461-2004, 2004.

Ayers, G. P., Bartley, S. T., Ivey, J. P., and Forgan, B. W.: Dimethylsulfide in marine air at Cape Grim, 41^∘ S, J. Geophys. Res., 100, 21013–21021, https://doi.org/10.1029/95JD02144, 1995.

Bardouki, H., Barcellos da Rosa, M., Mihalopoulous, N., Palm, W.- U., and Zetzsch, C.: Kinetics and mechanism of the oxidation of dimethylsulfoxide (DMSO) and methanesulfinate (MSI-) by OH radicals in aqueous medium, Atmos. Environ., 36, 4627–4634, https://doi.org/10.1016/S1352-2310(02)00460-0, 2002.

Barnes, I., Hjorth, J., and Mihalopoulos, N.: Dimethyl sulfide and dimethyl sulfoxide and their oxidation in the atmosphere, Chem. Rev., 106, 940-975, https://doi.org/10.1021/cr020529+, 2006.

Becagli, S., Castellano, E., Cerri, O., Curran, M., Frezzotti, M., Marino, F., Morganti, A., Proposito, M., Severi, M., and Traversi, R.: Methanesulphonic acid (MSA) stratigraphy from a Talos Dome ice core as a tool in depicting sea ice changes and southern atmospheric circulation over the previous 140 years, Atmos. Environ.,43, 1051–1058, https://doi.org/10.1016/j.atmosenv.2008.11.015, 2009.

Berglen, T. F., Berntsen, T. K., Isaksen, I. S. A., and Sundet, J. K.: A global model of the coupled sulfur/oxidant chemistry in the troposphere: The sulfur cycle, J. Geophys. Res., 109, D19310, https://doi.org/10.1029/2003JD003948, 2004.

Bey, I., Jacob, D. J., Yantosca, R. M., Logan, J. A., Field, B. D., Fiore, A. M., Li, Q., Liu, H. Y., Mickley, L. J., and Schultz, M. G.: Global modeling of tropospheric chemistry with assimilated meteorology: Model description and evaluation, J. Geophys. Res., 106, 23073–23095, https://doi.org/10.1029/2001JD000807, 2001.

Boucher, O., Moulin, C., Belviso, S., Aumont, O., Bopp, L., Cosme, E., von Kuhlmann, R., Lawrence, M. G., Pham, M., Reddy, M. S., Sciare, J., and Venkataraman, C.: DMS atmospheric concentrations and sulphate aerosol indirect radiative forcing: a sensitivity study to the DMS source representation and oxidation, Atmos. Chem. Phys., 3, 49–65, https://doi.org/10.5194/acp-3-49-2003, 2003.

Boudries, H. and Bottenheim, J. W.: Cl and Br atom concentrations during a surface boundary layer ozone depletion event in the Canadian High Arctic, Geophys. Res. Lett., 27, 517–520, https://doi.org/10.1029/1999GL011025, 2000.

Breider, T. J., Chipperfield, M. P., Richards, N. A. D., Carslaw, K. S., Mann, G. W., and Spracklen, D. V.: Impact of BrO on dimethylsulfide in the remote marine boundary layer, Geophys. Res. Lett., 37, L02807, https://doi.org/10.1029/2009GL040868, 2010.

Burkholder, J. B., Sander, S. P., Abbatt, J., Barker, J. R., Huie, R. E., Kolb, C. E., Kurylo, M. J., Orkin, V. L., Wilmouth, D. M., and Wine, P. H.: Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies, Evaluation No. 18, JPL Publication 15-10, Jet Propulsion Laboratory, Pasadena, availabel at: http://jpldataeval.jpl.nasa.gov (last access: 19 September 2018), 2015.

Butkovskaya, N. I., Poulet, G., and LeBras, G.: Discharge flow study of the reactions of chlorine and fluorine atoms with dimethyl sulfide, J. Phys. Chem., 99, 4536–4543, https://doi.org/10.1021/j100013a025, 1995.

Campolongo, F., Saltelli, A., Jensen, N. R., Wilson, J., and Hjorth, J.: The role of multiphase chemistry in the oxidation of dimethylsulfide (DMS) – A latitude dependent analysis, J. Atmos. Chem., 32, 327–356, https://doi.org/10.1023/A:1006154618511, 1999.

Carslaw, K. S., Lee, L. A., Reddington, C. L., Pringle, K. J., Rap, A., Forster, P. M., Mann, G. W., Spracklen, D. V., Woodhouse, M. T., Regayre, L. A., and Pierce, J. R.: Large contribution of natural aerosols to uncertainty in indirect forcing, Nature, 503, 67–71, https://doi.org/10.1038/nature12674, 2013.

Castebrunet, H., Martinerie, P., Genthon, C., and Cosme, E.: A three-dimensional model study of methanesulphonic acid to non sea salt sulphate ratio at mid and high-southern latitudes, Atmos. Chem. Phys., 9, 9449–9469, https://doi.org/10.5194/acp-9-9449-2009, 2009.

Charlson, R. J., Lovelock, J. E., Andreae, M. O., and Warren, S. G.: Oceanic phytoplankton, atmospheric sulphur, cloud albedo and climate, Nature, 326, 655–661, https://doi.org/10.1038/326655a0, 1987.

Chatfield, R. B. and Crutzen, P. J.: Are there interactions of iodine and sulfur species in marine air photochemistry?, J. Geophys. Res., 95, 22319–22341, https://doi.org/10.1029/JD095iD13p22319, 1990.

Chen, H., Ezell, M. J., Arquero, K. D., Varner, M. E., Dawson, M. L., Gerber, R. B., and Finlayson-Pitts, B. J.: New particle formation and growth from methanesulfonic acid, trimethylamine and water, Phys. Chem. Chem. Phys., 17, 13699–13709, https://doi.org/10.1039/c5cp00838g, 2015.

Chen, Q., Geng, L., Schmidt, J. A., Xie, Z., Kang, H., Dachs, J., Cole-Dai, J., Schauer, A. J., Camp, M. G., and Alexander, B.: Isotopic constraints on the role of hypohalous acids in sulfate aerosol formation in the remote marine boundary layer, Atmos. Chem. Phys., 16, 11433–11450, https://doi.org/10.5194/acp-16-11433-2016, 2016.

Chen, Q., Schmidt, J. A., Shah, V., Jaeglé, L., Sherwen, T., and Alexander, B.: Sulfate production by reactive bromine: Implications for the global sulfur and reactive bromine budgets, Geophys. Res. Lett., 44, 7069–7078, https://doi.org/10.1002/2017GL073812, 2017.

Chin, M., Jacob, D. J., Gardner, G. M., Foreman-Fowler, M. S., Spiro, P. A., and Savoie, D. L.: A global three-dimensional model of tropospheric sulfate, J. Geophys. Res., 101, 18667–18690, https://doi.org/10.1029/96JD01221, 1996.

Chin, M., Rood, R. B., Lin, S.-J., Muller, J. F., and Thompson, A. M.: Atmospheric sulfur cycle in the global model GOCART: Model description and global properties, J. Geophys. Res., 105, 24671–24687, 2000.

Clarke, J. H. R. and Woodward, L. A.: Raman spectrophotometric determination of the degrees of dissociation of methanesulphonic acid in aqueous solution at 25 ^∘C, T. Faraday Soc., 62, 2226–2233, 1966.

Cosme, E., Genthon, C., Martinerie, P., Boucher, O., and Pham, M.: The sulfer cycle at high-southern latitudes in the LMDZT General Circulation Model, J. Geophys. Res., 107, 4690, https://doi.org/10.1029/2002JD002149, 2002.

Curran, M. A. J., van Ommen, T. D., Morgan, V. I., Phillips, K. L., and Palmer, A. S.: Ice core evidence for Antarctic sea ice decline since the 1950s, Science, 302, 1203–1206, https://doi.org/10.1126/science.1087888, 2003.

Du, L., Xu, Y., Ge, M., Jia, L., Yao, L., and Wang, W.: Rate constant of the gas phase reaction of dimethyl sulfide (CH₃SCH₃) with ozone, Chem. Phys. Lett., 436, 36–40, https://doi.org/10.1016/j.cplett.2007.01.025, 2007.

Faloona, I.: Sulfur processing in the marine atmospheric boundary layer: A review and critical assessment of modeling uncertainties, Atmos. Environ., 43, 2841–2854, https://doi.org/10.1016/j.atmosenv.2009.02.043, 2009.

Fisher, J. A., Murray, L. T., Jones, D. B. A., and Deutscher, N. M.: Improved method for linear carbon monoxide simulation and source attribution in atmospheric chemistry models illustrated using GEOS-Chem v9, Geosci. Model Dev., 10, 4129–4144, https://doi.org/10.5194/gmd-10-4129-2017, 2017.

Flyunt, R., Makogon, O., Schuchmann, M. N., Asmus, K. D., and von Sonntag, C.: OH-Radical-induced oxidation of methanesulfinic acid. The reactions of the methanesulfonyl radical in the absence and presence of dioxygen, J. Chem. Soc. Perkin Trans., 2, 787–792, https://doi.org/10.1039/B009631H, 2001.

Gershenzon, M., Davidovits, P., Jayne, J. T., Kolb, C. E., and Worsnop, D. R.: Simultaneous uptake of DMS and ozone on water, J. Phys. Chem. A, 105, 7031–7036, https://doi.org/10.1021/jp010696y, 2001.

Gondwe, M., Krol, M., Gieskes, W., Klaassen, W., and de Baar, H.: The contribution of ocean-leaving DMS to the global atmospheric burdens of DMS, MSA, SO₂, and NSS ${SO}_{4}^{-}$ , Global Biogeochem. Cy., 17, 1056, https://doi.org/10.1029/2002GB001937, 2003.

Gondwe, M., Krol, M., Klassen, W., Gieskes, W., and De Baar, H.: Comparison of modeled versus measured MSA : nss ${SO}_{4}^{2 -}$ ratios: A global analysis, Global Biogeochem. Cy., 18, GB2006, https://doi.org/10.1029/2003GB002144, 2004.

Gromov, S., Brenninkmeijer, C. A. M., and Jöckel, P.: A very limited role of tropospheric chlorine as a sink of the greenhouse gas methane, Atmos. Chem. Phys., 18, 9831–9843, https://doi.org/10.5194/acp-18-9831-2018, 2018.

Herrmann, H. and Zellner, R.: Removal and interconversions of oxidants in the atmospheric aqueous phase, Part 2 (RINOXA 2), Universität Essen, Essen, Germany, 1997.

Herrmann, H., Ervens, B., Jacobi, H.-W., Wolke, R., Nowacki, P., and Zellner, R.: CAPRAM2.3: A Chemical Aqueous Phase Radical Mechanism for Tropospheric Chemistry, J. Atmos. Chem., 36, 231–284, https://doi.org/10.1023/A:1006318622743, 2000.

Hezel, P. J., Alexander, B., Bitz, C. M., Steig, . J., Holmes, C. D., Yang, X., and Sciare, J.: Modeled methanesulfonic acid (MSA) deposition in Antarctica and its relationship to sea ice, . Geophys. Res., 116, D23214, https://doi.org/10.1029/2011JD016383, 2011.

Hoffmann, E. H., Tilgner, A., Schrödner, R., Bräuer, P., Wolke, R., and Herrmann, H.: An advanced modeling study on the impacts and atmospheric implications of multiphase dimethyl sulfide chemistry, P. Natl. Acad. Sci. USA, 113, 11776–11781, https://doi.org/10.1073/pnas.1606320113, 2016.

Hossaini, R., Chipperfield, M. P., Saiz-Lopez, A., Fernandez, R., Monks, S., Feng, W., Brauer, P., and von Glasow, R.: A global model of tropospheric chlorine chemistry: Organic versus inorganic sources and impact on methane oxidation, J. Geophys. Res.-Atmos., 121, 14271–14297, https://doi.org/10.1002/2016JD025756, 2016.

Hynes, A. J., Stickel, R. E., Pounds, A. J., Zhao, Z., McKay, T., Bradshaw, J. D., and Wine, P. H.: Mechanistic studies of the OH-induced oxidation of dimethylsulfide, in: Proceedings of the International Symposium on Dimethylsulfide: Oceans, Atmosphere, and Climate, edited by: Restelli, G. and Angeletti, G., Kluwer Academic Publishers, Norwell, MA, USA, 211–221, 1993.

Jacob, D. J.: Chemistry of OH in remote clouds and its role in the production of formic acid and peroxymonosulfate, J. Geophys. Res., 91, 9807–9826, https://doi.org/10.1029/JD091iD09p09807, 1986.

Jacob, D. J., Gottlieb, E. W., and Prather, M. J.: Chemistry of a polluted cloudy boundary layer, J. Geophys. Res.-Atmos., 94, 12975–13002, https://doi.org/10.1029/JD094iD10p12975, 1989.

Jacob, D. J., Field, B. D., Li, Q., Blake, D. R., de Gouw, J., Warneke, C., Hansel, A., Wisthaler, A., Singh, H. B., and Guenther, A.: Global budget of methanol: Constraints from atmospheric observations, J. Geophys. Res., 110, D08303, https://doi.org/10.1029/2004JD005172, 2005.

Jaeglé, L., Quinn, P. K., Bates, T. S., Alexander, B., and Lin, J.-T.: Global distribution of sea salt aerosols: new constraints from in situ and remote sensing observations, Atmos. Chem. Phys., 11, 3137–3157, https://doi.org/10.5194/acp-11-3137-2011, 2011.

Jobson, B. T., Niki, H., Yokouchi, Y., Bottenheim, J., Hopper, F., and Leaitch, R.: Measurements of C₂–C₆ hydrocarbons during the Polar Sunrise 1992 Experiment: Evidence for Cl atom and Br atom chemistry, J. Geophys. Res., 99, 25355–25368, https://doi.org/10.1029/94JD01243, 1994.

Kaufman, Y. and Tanre, D.: Effect of variations in super-saturation on the formation of cloud condensation nuclei, Nature, 369, 45–48, https://doi.org/10.1038/369045a0, 1994.

Kaur, R. and Anastasio, C.: Light absorption and the photoformation of hydroxyl radical and singlet oxygen in fog waters, Atmos. Environ., 164, 387–397, https://doi.org/10.1016/j.atmosenv.2017.06.006, 2017.

Kettle, A., Andreae, M., Amouroux, D., Andreae, T., Bates, T., Berresheim, H., Bingemer, H., Boniforti, R., Curran, M., DiTullio, G., Helas, G., Jones, G., Keller, M., Kiene, R., Leck, C., Levasseur, M., Malin, G., Maspero, M., Matrai, P., McTaggart, A., Mihalopoulos, N., Nguyen, B., Novo, A., Putaud, J., Rapsomanikis, S., Roberts, G., Schebeske, G., Sharma, S., Simo, R., Staubes, R., Turner, S., and Uher, G.: A global database of sea surface dimethylsulfide (DMS) measurements and a procedure to predict sea surface DMS as a function of latitude, longitude, and month, Global Biogeochem. Cy., 13, 399–444, https://doi.org/10.1029/1999GB900004, 1999.

Khan, M. A. H., Gillespie, S. M. P., Razis, B., Xiao, P., DaviesColeman, M. T., Percival, C. J., Derwent, R. G., Dyke, J. M., Ghosh, M. V., Lee, E. P. F., and Shallcross, D. E.: A modelling study of the atmospheric chemistry of DMS using the global model, STOCHEM-CRI, Atmos. Environ., 127, 69–79, https://doi.org/10.1016/j.atmosenv.2015.12.028, 2016.

Kloster, S., Feichter, J., Maier-Reimer, E., Six, K. D., Stier, P., and Wetzel, P.: DMS cycle in the marine ocean-atmosphere system – a global model study, Biogeosciences, 3, 29–51, https://doi.org/10.5194/bg-3-29-2006, 2006.

Kouvarakis, G. and Mihalopoulos, N.: Seasonal variation of dimethylsulfide in the gas phase and of methanesulfonate and non-sea-salt sulfate in the aerosols phase in the eastern Mediterranean atmosphere, Atmos. Environ., 36, 929–938, https://doi.org/10.1016/S1352-2310(01)00511-8, 2002.

Kreidenweis, S. M. and Seinfeld, J. H.: Nucleation of sulfuric acid-water and methanesulfonic acid-water solution particles: implications for the atmospheric chemistry of organosulfur species, Atmos. Environ., 22, 283–296, https://doi.org/10.1016/0004-6981(88)90034-0, 1988.

Kukui, A., Borissenko, D., Laverdet, G., and Bras, G. L.: Gas phase reactions of OH radicals with dimethyl sulfoxide and methane sulfonic acid using turbulent flow reactor and chemical ionization mass spectrometry, J. Phys. Chem. A, 107, 5732–5742, https://doi.org/10.1021/jp0276911, 2003.

Kulmala, M., Pirjola, L., and Mäkelä, J. M.: Stable sulphate clusters as a source of new atmospheric particles, Nature, 404, 66–69, https://doi.org/10.1038/35003550, 2000.

Lana, A., Bell, T. G., Simó, R., Vallina, S. M., Ballabrera-Poy, J., Kettle, A. J., Dachs, J., Bopp, L., Saltzman, E. S., Ste- fels, J., Johnson, J. E., and Liss, P. S.: An updated climatology of surface dimethylsulfide concentrations and emission fluxes in the global ocean, Global Biogeochem. Cy., 25, GB1004, https://doi.org/10.1029/2010GB003850, 2011.

Lee, Y.-N. and Zhou, X.: Aqueous reaction kinetics of ozone and dimethylsulfide and its atmospheric implications, J. Geophys. Res., 99, 3597–3605, https://doi.org/10.1029/93JD02919, 1994.

Legrand, M., Preunkert, S., Weller, R., Zipf, L., Elsässer, C., Merchel, S., Rugel, G., and Wagenbach, D.: Year-round record of bulk and size-segregated aerosol composition in central Antarctica (Concordia site) – Part 2: Biogenic sulfur (sulfate and methanesulfonate) aerosol, Atmos. Chem. Phys., 17, 14055–14073, https://doi.org/10.5194/acp-17-14055-2017, 2017.

Liu, Q.: Kinetics of aqueous phase reactions related to ozone depletion in the arctic troposphere: bromine chloride hydrolysis, bromide ion with ozone, and sulfur(IV) with bromine and hypobromous acid, PhD thesis, Department of Chemistry, Purdue University, Purdue, USA, 253 pp., 2000.

Liu, H., Jacob, D. J., Bey, I., and Yantosca, R. M.: Constraints from ²¹⁰Pb and ⁷Be on wet deposition and transport in a global three-dimensional chemical tracer model driven by assimilated meteorological fields, J. Geophys. Res., 106, 12109–12128, https://doi.org/10.1029/2000JD900839, 2001.

Lucas, D. D. and Prinn, R. G.: Mechanistic studies of dimethylsulfide oxidation products using an observationally constrained model, J. Geophys. Res., 107, 1201–1226, https://doi.org/10.1029/2001JD000843, 2002.

Martin, L. R. and Good, T. W.: Catalyzed oxidation of sulfur dioxide in solution: The iron-manganese synergism, Atmos. Environ. A, 25, 2395–2399, https://doi.org/10.1016/0960-1686(91)90113-L, 1991.

Matthijsen, J., Builtjes, P. J. H., and Sedlak, D. L.: Cloud model experiments of the effect of iron and copper on tropospheric ozone under marine and continental conditions, Meteorol. Atmos. Phys., 57, 43–60, https://doi.org/10.1007/BF01044153, 1995.

Milne, P. J., Zika, R. G., and Saltzman, E. S.: Rate of reaction of dimethyl sulfoxide, and dimethyl sulfone with hydroxyl radical in aqueous solution, in: chap. 33, ACS Symposium Series, American Chemical Society, Washington, D.C., 518–528, 1989.

Mungall, E., Wong, J. P. S., and Abbatt, J. P. D.: Heterogeneous oxidation of particulate methane sulfonic acid by the hydroxyl radical: kinetics and atmospheric implications, ACS Earth Space Chem., 2, 48–55, https://doi.org/10.1021/acsearthspacechem.7b00114, 2018.

Park, R. J., Jacob, D. J., Field, B. D., Yantosca, R. M., and Chin, M.: Natural and transboundary pollution influences on sulfate-nitrate-ammonium aerosols in the United States: Implications for policy, J. Geophys. Res., 109, D15204, https://doi.org/10.1029/2003JD004473, 2004.

Parrella, J. P., Jacob, D. J., Liang, Q., Zhang, Y., Mickley, L. J., Miller, B., Evans, M. J., Yang, X., Pyle, J. A., Theys, N., and Van Roozendael, M.: Tropospheric bromine chemistry: implications for present and pre-industrial ozone and mercury, Atmos. Chem. Phys., 12, 6723–6740, https://doi.org/10.5194/acp-12-6723-2012, 2012.

Pham, M., Müller, J., Brasseur, G. P., Granier, C., and Mégie, G.: A three-dimensional study of the tropospheric sulfur cycle, J. Geophys. Res., 100, 26061–26092, https://doi.org/10.1029/95JD02095, 1995.

Pye, H. O. T., Liao, H., Wu, S., Mickley, L. J., Jacob, D. J., Henze, D. K., and Seinfeld, J. H.: Effect of changes in climate and emissions on future sulfate-nitrate-ammonium aerosol levels in the United States, J. Geophys. Res., 114, D01205, https://doi.org/10.1029/2008JD010701, 2009.

Ravishankara, A. R., Rudich, Y., Talukdar, R., and Barone, S. B.: Oxidation of atmospheric reduced sulphur compounds: perspective from laboratory studies, Philos. T. Roy. Soc. Lond. B., 352, 171–182, https://doi.org/10.1098/rstb.1997.0012, 1997.

Read, K. A., Lewis, A. C., Salmon, R. A., Jones, A. E., and Bauguitte, S.: OH and halogen influence on the variability of nonmethane hydrocarbons in the Antarctic Boundary Layer, Tellus B, 59, 22–38, https://doi.org/10.1111/j.1600-0889.2006.00227.x, 2007.

Saltzman, E. S., King, D. B., Holmen, K., and Leck, C.: Experimental determination of the diffusion coefficient of dimethylsulfide in water, J. Geophys. Res.-Oceans, 98, 16481–16486, https://doi.org/10.1029/93JC01858, 1993.

Savoie, D. L., Arimoto, R., Keene, W. C., Prospero, J. M., Duce, R. A., and Galloway, J. N.: Marine biogenic and anthropogenic contributions to non-sea-salt sulfate in the marine boundary layer over the North Atlantic Ocean, J. Geophys. Res., 107, AAC3-1–AAC3-21, https://doi.org/10.1029/2001JD000970, 2002.

Schmidt, J. A., Jacob, D. J., Horowitz, H. M., Hu, L., Sherwen, T., Evans, M. J., Liang, Q., Suleiman, R. M., Oram, D. E., Le Breton, M., Percival, C. J., Wang, S., Dix, B., and Volkamer, R.: Modeling the observed tropospheric BrO background: Importance of multiphase chemistry and implications for ozone, OH, and mercury, J. Geophys. Res.-Atmos., 121, 155–157, https://doi.org/10.1002/2015JD024229, 2016.

Schweitzer, F., Magi, L., Mirabel, P., and George, C.: Uptake rate measurements of methanesulfonic acid and glyoxal by aqueous droplets, J. Phys. Chem. A, 102, 593–600, https://doi.org/10.1021/jp972451k, 1998.

Sehested, K. and Holcman, J.: A pulse radiolysis study of the OH radical induced autoxidation of methanesulfinic acid, Radiat. Phys. Chem., 47, 357–360, https://doi.org/10.1016/0969-806X(95)00115-E, 1996.

Sherwen, T., Schmidt, J. A., Evans, M. J., Carpenter, L. J., Großmann, K., Eastham, S. D., Jacob, D. J., Dix, B., Koenig, T. K., Sinreich, R., Ortega, I., Volkamer, R., Saiz-Lopez, A., Prados-Roman, C., Mahajan, A. S., and Ordóñez, C.: Global impacts of tropospheric halogens (Cl, Br, I) on oxidants and composition in GEOS-Chem, Atmos. Chem. Phys., 16, 12239–12271, https://doi.org/10.5194/acp-16-12239-2016, 2016.

Simpson, W. R., Brown, S. S., Saiz-Lopez, A., Thornton, J. A., and von Glasow, R.: Tropospheric Halogen Chemistry: Sources, Cycling, and Impacts, Chem. Rev., 115, 4035–4062, https://doi.org/10.1021/cr5006638, 2015.

Singh, H. B., Gregory, G. L., Anderson, B., Browell, E., Sachse, G. W., Davis, D. D., Crawford, J., Bradshaw, J. D., Talbot, R., Blake, D. R., Thornton, D., Newell, R., and Merill, J.: Low ozone in the marine boundary layer of the tropical Pacific ocean: Photochemical loss, chlorine atoms, and entrainment, J. Geophys. Res., 101, 1907–1917, https://doi.org/10.1029/95JD01028, 1996.

Spracklen, D. V., Pringle, K. J., Carslaw, K. S., Chipperfield, M. P., and Mann, G. W.: A global off-line model of size-resolved aerosol microphysics: I. Model development and prediction of aerosol properties, Atmos. Chem. Phys., 5, 2227–2252, https://doi.org/10.5194/acp-5-2227-2005, 2005.

Theys, N., Van Roozendael, M., Hendrick, F., Yang, X., De Smedt, I., Richter, A., Begoin, M., Errera, Q., Johnston, P. V., Kreher, K., and De Mazière, M.: Global observations of tropospheric BrO columns using GOME-2 satellite data, Atmos. Chem. Phys., 11, 1791–1811, https://doi.org/10.5194/acp-11-1791-2011, 2011.

Thomas, M. A., Suntharalingam, P., Pozzoli, L., Rast, S., Devasthale, A., Kloster, S., Feichter, J., and Lenton, T. M.: Quantification of DMS aerosol–cloud–climate interactions using the ECHAM5-HAMMOZ model in a current climate scenario, Atmos. Chem. Phys., 10, 7425–7438, https://doi.org/10.5194/acp-10-7425-2010, 2010.

Troy, R. C. and Margerum, D. W.: Non-metal redox kinetics: Hypobromite and hypobromous acid reactions with iodide and with sulfite and the hydrolysis of bromosulfate, Inorg. Chem., 30, 3538–3543, https://doi.org/10.1021/ic00018a028, 1991.

Turnipseed, A. A. Barone, S. B., and Ravishankara, A. R.: Reaction of OH with dimethyl sulphide (DMS) – 2. Products and mechanisms, J. Phys. Chem., 100, 14703–14713, https://doi.org/10.1021/jp960867c, 1996.

von Glasow, R. and Crutzen, P. J.: Model study of multiphase DMS oxidation with a focus on halogens, Atmos. Chem. Phys., 4, 589–608, https://doi.org/10.5194/acp-4-589-2004, 2004.

von Glasow, R., von Kuhlmann, R., Lawrence, M. G., Platt, U., and Crutzen, P. J.: Impact of reactive bromine chemistry in the troposphere, Atmos. Chem. Phys., 4, 2481–2497, https://doi.org/10.5194/acp-4-2481-2004, 2004.

Wang, Y., Jacob, D. J., and Logan, J. A.: Global simulation of tropospheric O₃-NO_x-hydrocarbon chemistry: 1. Model formulation, J. Geophys. Res., 103, 10713–10725, https://doi.org/10.1029/98JD00158, 1998.

Wingenter, O. W., Kubo, M. K., Blake, N. J., Smith, T. W., Blake, D. R., and Rowland, F. S.: Hydrocarbon and halocarbon measurements as photochemical and dynamical indicators of atmospheric hydroxyl, atomic chlorine, and vertical mixing obtained during Lagrangian flights, J. Geophys. Res., 101, 4331–4340, https://doi.org/10.1029/95JD02457, 1996.

Wingenter, O. W., Sive, B. C., Blake, N. J., Blake, D. R., and Rowland, F. S.: Atomic chlorine concentrations derived from ethane and hydroxyl measurements over the equatorial Pacific Ocean: Implication for dimethyl sulphide and bromine monoxide, J. Geophys. Res., 110, D20308, https://doi.org/10.1029/2005JD005875, 2005.

Wudl, F., Lightner, D. A., and Cram, D. J.: Methanesulfinic acid and its properties, J. Am. Chem. Soc., 89, 4099–4101, 1967.

Zhang, L., Gong, S.-L., Padro, J., and Barrie, L.: A Size-segregated Particle Dry Deposition Scheme for an Atmospheric Aerosol Module, Atmos. Environ., 35, 549–560, https://doi.org/10.1016/S1352-2310(00)00326-5, 2001.

Zhu, L., Nicovich, J. M., and Wine, P. H.: Temperature-dependent kinetics studies of aqueous phase reactions of hydroxyl radicals with dimethylsulfoxide, dimethylsulfone, and methanesulfonate, Aquat. Sci., 65, 425–435, https://doi.org/10.1007/s00027-003-0673-6, 2003.

Zhu, L., Nenes, A., Wine, P. H., and Nicovich, J. M.: Effects of aqueous organosulfur chemistry on particulate methanesulfonate to non-sea salt sulfate ratios in the marine atmosphere, J. Geophys. Res., 111, D05316, https://doi.org/10.1029/2005JD006326, 2006.

Articles

Download

Article (10096 KB)
Full-text XML

Short summary

Uncertainty in the natural tropospheric sulfur cycle represents the largest source of uncertainty in radiative forcing estimates of sulfate aerosol. This study investigates the natural sulfur cycle in the marine troposphere using the GEOS-Chem model. We found that BrO is important for DMS oxidation and multiphase chemistry is important for MSA production and loss, which have implications for the yield of SO₂ and MSA from DMS oxidation and the radiative effect of DMS-derived sulfate aerosol.

DMS oxidation and sulfur aerosol formation in the marine troposphere: a focus on reactive halogen and multiphase chemistry

3.1 DMS budget

3.2 DMSO budget

3.3 MSIA budget

3.4 MSA budget

3.5 Uncertainties in rate constants

3.6 Model–observation comparison

3.6.1 Surface DMS mixing ratio

3.6.2 Surface MSA ∕ nssSO42- ratio

3.6.2 Surface MSA ∕ nss ${SO}_{4}^{2 -}$ ratio