the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Shortwave radiative impact of liquid–liquid phase separation in brown carbon aerosols
Mehrnoush M. Fard
Ulrich K. Krieger
Thomas Peter
Atmospheric aerosol particles may undergo liquid–liquid phase separation (LLPS) when exposed to varying relative humidity. In this study, we model how the change in morphology affects the shortwave radiative forcing, in particular for particles containing organic carbon as a molecular absorber, often termed “brown carbon” (BrC). Preferentially, such an absorber will redistribute to the organic phase after LLPS. We limited our investigation to particle diameters between 0.04 and 0.5 µm, atmospherically relevant organic-to-inorganic mass ratios typical for aged aerosol () and absorptivities ranging from zero (purely scattering) to highly absorbing brown carbon. For atmospherically relevant O : C ratios, core-shell morphology is expected for phase-separated particles. We compute the scattering and absorption cross sections for realistic eccentric core-shell morphologies. For the size range of interest here, we show that assuming the core-shell morphology to be concentric is sufficiently accurate and numerically much more efficient than averaging over eccentric morphologies. In the UV region, where BrC absorbs strongest, phase-separated particles may exhibit a scattering cross section up to 50 % larger than those of homogenously mixed particles, while their absorption cross section is up to 20 % smaller. Integrating over the full solar spectrum, due to the strong wavelength dependence of BrC absorptivity, limits the shortwave radiative impact of LLPS in the thin aerosol layer approximation. For particles with very substantial BrC absorption there will be a radiative forcing enhancement of 4 %–11.8 % depending on the Ångström exponent (AAE) of BrC absorptivity for the case of small surface albedos and a decrease of up to 18 % for surfaces with high reflectivity. However, for those of moderate absorptivity, LLPS will have no significant shortwave radiative impact.
Among many other impacts, atmospheric aerosols influence the radiation budget of the Earth directly through scattering and absorption (and less importantly emission) of incoming shortwave solar and outgoing infrared radiation. Aerosols can also affect climate indirectly through their interaction with clouds. Depending on their optical properties, size and albedo of the surface, aerosols mostly cool our planet (IPCC, 2013). However, those which are highly absorptive (e.g., soot particles) can lead to heating (e.g., Ramanathan et al., 2001; Bond et al., 2013). Anthropogenic aerosols are dominated by sulfate, organic carbon, black carbon (soot), nitrate and dust. According to the fifth Intergovernmental Panel on Climate Change report (IPCC, 2013), anthropogenic aerosols produce a net cooling effect, whereby radiative forcing due to aerosol–radiation interactions is assessed to be −0.35 (−0.85 to +0.15) Wm−2. Despite dedicated research efforts, aerosols remain one of the main sources of uncertainty for climate prediction.
Although organic aerosol particles are mainly characterized as only scattering as they are largely transparent in the visible region of the solar spectrum, a significant fraction of carbonaceous aerosols absorb solar and terrestrial radiation. Black carbon (BC) is by far the most well known absorbing component of the atmospheric aerosols, which strongly absorbs light over a broad wavelength range from UV to IR. It has only been in recent years that a new class of organic matter was identified, which exhibits significant though weaker absorptive properties compared to BC. This absorbing fraction of organic matter is referred to as brown carbon (BrC) (Pöschl, 2005; Andreae and Gelencser, 2006; Ramanathan et al., 2007; Laskin et al., 2015). In contrast to BC, the absorptivity of BrC has a very strong wavelength dependence with high absorption in the near-UV region, but absorption decreasing rapidly towards longer wavelengths (Andreae and Gelencser, 2006; Bond and Bergstrom, 2006; Ramanathan et al., 2007; Feng et al., 2013; Laskin et al., 2015). Several studies have suggested that at shorter wavelengths, BrC can significantly contribute to the total aerosol absorption or even dominate it in certain geographic regions (Yang et al., 2009; Bond et al., 2011; Zhang et al., 2011; Chung et al., 2012; Feng et al., 2013; Laskin et al., 2015). Despite recent interest and extensive research regarding the impact of BrC on radiative forcing (e.g., Arnott et al., 2003; Ramanathan et al., 2007; Alexander et al., 2008; Feng et al., 2013; Lack and Cappa, 2010; Lang-Yona et al., 2010; Lack et al., 2012; Ma and Thompson, 2012; Nakayama et al., 2010; Langridge et al., 2013; Saleh et al., 2013; Laskin et al., 2015; Tang et al., 2016), the magnitude of BrC absorption as well as its wavelength dependence is not yet well established and its assignment to different sources and its oxidation lifetime are far from being fully characterized.
In addition to the limited knowledge associated with the optical properties of organic carbon, our current understanding with respect to aerosol compositions, physical state and morphology is insufficient to accurately quantify the direct radiative effect of such aerosols. In particular, particle phase and morphology need to be investigated, since they influence the scattering and absorption of radiation (e.g., Baumgardner and Clarke, 1998; Martin et al., 2004; Lewis et al., 2009; Lack and Cappa, 2010). Experiments and modeling studies have shown that as ambient relative humidity (RH) decreases, deliquesced aerosols can exist not only as a one-phase system containing organics, inorganic salts and water in a homogeneous mixture, but often as two-phase systems, whereby one aqueous phase is dominated by the organic material while the other aqueous phase is predominantly inorganic, e.g., containing inorganic salts (Pankow, 2003; Marcolli and Krieger, 2006; Ciobanu et al., 2009, 2010; Bertram et al., 2011; Krieger et al., 2012). This phenomenon is referred to as liquid–liquid phase separation (LLPS). The separation relative humidity (SRH) at which the transition from well mixed to liquid–liquid phase separation occurs depends on the O : C ratio of the organic salts as well as on the nature of the inorganic salts but typically occurs in a range between 70 % and 95 % RH (Song et al., 2012a; You et al., 2012). In recent years, laboratory studies using model mixtures to represent tropospheric aerosols (Ciobanu et al., 2009; Bertram et al., 2011; Song et al., 2012a, b), or secondary organic aerosol (SOA) produced from smog chamber experiments (Smith et al., 2012) and filter samples collected during field measurement campaigns (You et al., 2012), imply that liquid–liquid phase separation (LLPS) is a common feature in mixed organic/inorganic particles. When two aqueous phases coexist in a particle, they may form different morphologies, such as core shell or partially engulfed, depending on which configuration yields the lowest total surface free energy (Kwamena et al. 2010; Qiu and Molinero, 2015). According to Song et al. (2012b, 2013), for aged aerosols with moderate to high oxygen-to-carbon (O : C) ratio, core shell is the dominated morphology. For further information, see the Faraday Discussions on this very topic (Song et al., 2013). Besides consequences for hygroscopicity (Hodas et al., 2015), a core-shell configuration alters the optical properties of the particles, in particular for organic phases containing absorbing molecules, such as BrC, since the absorbing BrC material will always reside in the organic shell.
Brown carbon refers to the light-absorbing fraction of the organic carbon that has a wavelength-dependent imaginary part of the refractive index, which increases towards shorter wavelengths. Emission sources of BrC are not very well characterized. The primary emissions are mainly linked to biomass burning, smoldering combustion and biogenic emissions from humic matter, plant debris and other bio-aerosols (Andreae and Gelencser, 2006; Alexander et al., 2008; Chakrabarty et al., 2010; Kirchstetter and Thatcher, 2012). Field measurements have also associated BrC with secondary organic aerosol (SOA) that forms by gas to particle partitioning of semi-volatile organic compounds present in the biomass burning smoke (Hecobian et al., 2010; Saleh et al., 2013). As SOA ages through oxidation processes, it may become significantly more absorbing in the near-UV region of the solar spectrum (Bones et al., 2010; Updyke et al., 2012; Laskin et al., 2015), implying that heterogeneous chemistry produces BrC in the condensed phase.
Despite the fact that the presence of LLPS has been observed and studied by a number of research groups, its impact on the radiative properties of mixed aerosol particles with molecular absorbers has so far not been quantified. In previous optical modeling studies, mostly focusing on the optical properties of particles containing soot inclusions, typically, volume mixing approximations for the optical properties were employed or the morphology was assumed to be that of a spherical symmetric, concentric core shell. In this paper, we apply a Mie code developed for calculating the scattering properties of a nonsymmetric cluster of spheres (Mackowski, 2013, http://eng.auburn.edu/users/dmckwski/scatcodes/, last access: 1 July 2018) to calculate the ratio in optical efficiencies between homogeneous and phase-separated particles. We vary the size and absorptivity of BrC and the organic to inorganic ratio over ranges typical of aged atmospheric aerosol in the accumulation mode, and show first that the average optical efficiencies of an ensemble of phase-separated particles with a random eccentric inclusion are well represented by those calculated for a simple concentric core-shell particle. Second, we take advantage of this finding and calculate the radiative forcing caused by phase-separated aerosol particles relative to aerosol particles homogenously mixed once in a thin aerosol layer approximation (Nemesure and Schwartz, 1998).
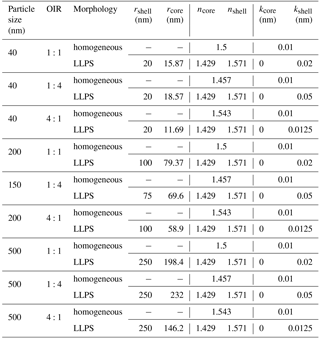
We first want to discuss the difference in scattering and absorption accounting for differences in morphology for liquid–liquid phase-separated particles. In particular, we investigate the difference between a symmetric core-shell morphology compared to one with an eccentric inclusion. To represent typical aged atmospheric aerosol containing BrC we choose the inorganic salt to be ammonium sulfate, representing the most abundant inorganic salt in continental aerosols, and light-absorbing organic carbon material, representing BrC. We choose to study three organics to inorganic ratios (OIR), 1:4, 1:1, and 4:1, from inorganic rich to organic rich, which cover the typical range observed using aerosol mass spectrometry (Zhang et al., 2007).
To account for the absorptivity of BrC, we take the imaginary part of the refractive index (k) for BrC spanning a wide range from non-absorbing organic material (k=0) to highly absorbing organic matter (k=0.168 at 355 nm). This range is based on various studies (Kirchstetter et al., 2004; Chen and Bond, 2010; Feng et al., 2013; Wang et al., 2014; Moise et al., 2015) that measured or collected data of k for different absorbing aerosol at different locations. The real part of the refractive index (n) for BrC at dry condition is taken as 1.65 (Hoffer et al., 2006). We use simple volume mixing to calculate the real part of BrC at 70 % RH, the size of the core relative to the shell for the different OIRs (see Fig. 1), as well as to calculate the refractive indices for the phase-separated particles (see Tables A1 and A2 in Appendix A). (Note, we use the volume mixing approximation just to illustrate the effect of morphology in this section; for this purpose any effective medium approximation could be used.)
For about 20 years, numerical calculations for scattering and absorption of a host sphere containing a non-concentrically positioned smaller sphere have been computationally feasible. In particular, the T-matrix approach of Mackowski and Mishchenko (1996, 2011) solves the problem of obtaining random-orientation properties of clusters of spheres in a numerically efficient manner. In our context, it has been applied in recent years for computing scattering and absorption of morphologically complex soot-containing aerosol (e.g., Mishchenko et al., 2013; Cheng et al., 2014). Here, we use the Multiple Sphere T-matrix (MSTM) version 3.0 (Mackowski, 2013, http://eng.auburn.edu/users/dmckwski/scatcodes/, last access: 1 July 2018) to compute fixed and random-oriented scattering and absorption cross sections as well as the asymmetry parameter for the eccentric core-shell liquid–liquid phase-separated aerosol with a molecular absorber in the organic phase.
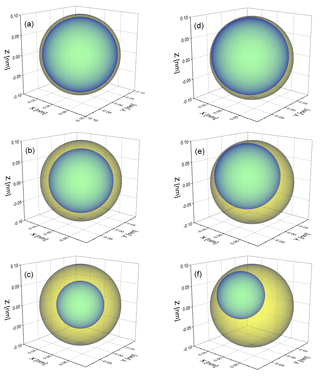
Figure 1Schematic of a phase-separated particle with a 100 nm radius to illustrate the thickness of the organic shell at (a) OIR , (b) OIR and (c) OIR for concentric core-shell morphologies. Panels (d–f) are the same for a single realization of an eccentric core-shell morphology. The calculations in this work typically use 500 such realizations, randomly oriented (with different distances of the inclusion from the center of the particles and different azimuth and polar angles). The direction of incoming light is along the z axis.
The computational costs of calculating cross sections increase substantially when going from highly symmetric core-shell morphology to a given eccentric core position relative to the incident light, and even more when random orientational averaging with random positioning of the core within the shell volume is required. Hence, we investigated systematically how the orientational averaged cross sections for the eccentric morphologies differ from the cross section for the concentric morphology. We performed this comparison for particles with properties ranging within the limits of OIR, size and absorptivity discussed above.
First, we used the MSTM code with random positioning of the center of the inorganic core within the organic shell to check how many realizations of fixed positions are needed for convergence of the mean cross sections. We did two types of randomized calculations for the position of the core within the shell.
-
Random position attached to inner surface. The core always remains attached to the inside surface of the particle; hence in a spherical coordinate system, the radial distance between the center of the core and the center of the particle remains fixed. We used a random number generator to draw random numbers for both the polar and the azimuthal angle to place the core within the particle in the spherical coordinate system. The light is always parallel to the z axis of a corresponding Cartesian coordinate system.
-
Random position within the volume. If the core was not attached, we also varied the distance between the core center and the particle center, i.e., the radial coordinate in the spherical coordinate system, by using a random number scaled such that the core accesses the volume within the particle with equal probability.
Figure 2a shows the distribution of scattering efficiency (Qscat) for a particular choice of particle parameters comparing 10 000 (locations) realizations (red columns, which refer to the Qscat of individual particles with their core located at random positions within the volume of the shell) with 500 realizations (green columns).
Scattering efficiency (Qscat) is the ratio of the scattering cross section, σscat, to the geometrical cross section of the particle, σgeometric:
For spherical particles with radius r, σgeometric=πr2.
As illustrated in Fig. 2b the mean of the scattering efficiencies converges rapidly with the number of the realizations used to calculate this mean. The same holds true for absorption efficiencies. Conservatively, in the following we use 500 different positions of the inclusion within the particle to determine the averaged Qscat and Qabs for the particles with eccentric core-shell morphology.
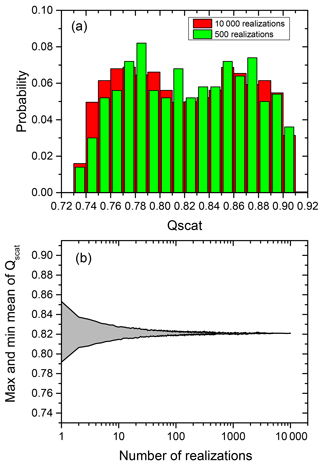
Figure 2(a) Probability distribution of Qscat for a phase-separated particle with the eccentric core positioned at 500 random locations (green columns) and 10 000 random locations (red column) within the volume of a 100 nm diameter particle at OIR , . (b) Maximum and minimum of the mean for Qscat for random realization of the position with the number of realizations used for the calculation.
It is evident from Fig. 2a that there is a considerable range in scattering efficiency with the position of the center of the inclusion as the width of the distribution is more than 20 % of the mean of the scattering efficiency. Figure 3 shows Qscat versus the core center perpendicular to the direction of the incoming radiation and along the direction of the radiation. (Please note that the incoming radiation is randomly polarized for all calculations.) Obviously, the scattering efficiency changes significantly with the position of the core along the incoming light axis. It is smallest for the core position facing the incoming light and largest with the core being located at the opposing position to the incoming light with an almost linear dependence for at least this particular set of parameters. The almost linear dependence of the efficiency along the light axis and random dependence perpendicular to it suggests that a concentric core-shell calculation of the scattering efficiency may be an excellent approximation for the mean of a monodisperse particle ensemble with random eccentric positions. In addition it suggests that the mean of the efficiency for an inclusion randomly distributed in the volume of the particle is not very different from one where the inclusion sticks to the surface of the particle at random positions.
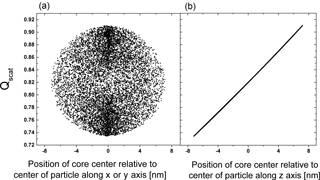
Figure 3The change in Qscat with the relative position of the core (rcore=92.8 nm) to the particle center perpendicular to the direction of light, x and y axis (a) and along the direction of light, z axis (b) for particle with OIR , k=0.168, rparticle=100 nm over 10 000 realizations.
For these particular particle parameter choices, this is really the case as Fig. 4 shows the mean scattering efficiency for the eccentric morphology as well as the one for a concentric core shell with the standard deviation on an enlarged scale. The mean values for the eccentric core shell, with its center randomly placed in the volume, and the eccentric core shell, with its center position randomly placed such that it touches the surface, are very similar and only differ in the fourth decimal place. The value for a concentric core shell is about 0.5 % lower. This emphasizes that the concentric core-shell model may be a good approximation for calculating the mean value for a distribution of particles with randomly located eccentric cores within either the volume or the surface for the OIR range and refractive indices typical of aged aerosol and particles in the accumulation size range. Let us note parenthetically that very similar behavior is exhibited when plotting the absorption efficiency instead of the scattering efficiency.
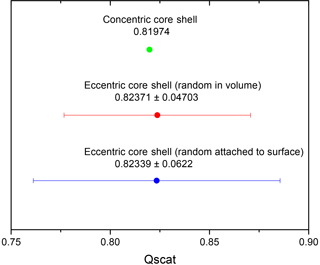
Figure 4Qscat mean value and standard deviation (SD) for eccentric core shell (over 10 000 realizations) within the volume (blue), Qscat mean value and SD for eccentric core shell (over 10 000 realizations) randomly attached to the inner surface (red), and Qscat for concentric core shell (green).
To test this hypothesis over a wide parameter range, we compare mean scattering and absorption efficiencies for particles with eccentric core-shell morphology (with the inorganic core randomly placed at 500 different positions within the volume of the particle) with the corresponding concentric core-shell morphology.
As the efficiencies for scattering and absorption are strongly dependent on the size of the particle (Bohren and Huffman, 2008; Van de Hulst, 1957) for accumulation-mode particles, we need to come up with a relative measure for the comparison of the two morphologies. The dependence is illustrated in Fig. 5 for a particle with k=0.168 and OIR . Here, the homogeneous particle is more efficient in absorbing the incoming light as particle size is increasing compared to the equivalent phase-separated one. In contrast, the phase-separated particle scatters light about 20 % more efficiently for particles above 400 nm diameter.
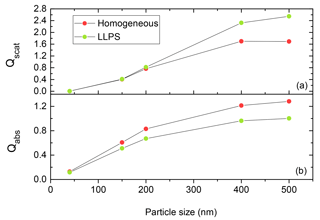
Figure 5Qscat (a) and Qabs (b) calculated for phase-separated (LLPS) and homogeneous particles ranging from 40 to 500 nm at OIR and k=0.168 using the eccentric core-shell Mie code at λ=355 nm. The red and green dots show the results for the same system at specific particle size for homogenous and phase-separated (LLPS) particles, respectively. The lines are only meant to guide the eye.
Since we are interested in the impact of LLPS on aerosol scattering and absorption, we take the internally mixed, homogeneous particle as a reference and in the following always plot the ratio of the LLPS morphology to the homogeneous particle for all calculated efficiencies. This way, the strong size dependence of the efficiencies seen in Fig. 5 for both morphologies cancels each other out and the emphasis is put instead on the effect of morphological change. These ratios may be understood as an empirical factor that could be used to correct calculations for homogeneous particles if those of equivalent phase-separated particles are needed.
In Figure 6, we have calculated the ratio of scattering efficiencies for the LLPS morphology over the ones for the homogenous morphology for both the eccentric case and the concentric case. As the computations for a concentric core-shell morphology are computationally very efficient, they were calculated for a small spacing in particle size, whereas the calculations for the eccentric morphologies were only done for a few particle sizes. The analogue ratios for absorption efficiencies are plotted in the right column.
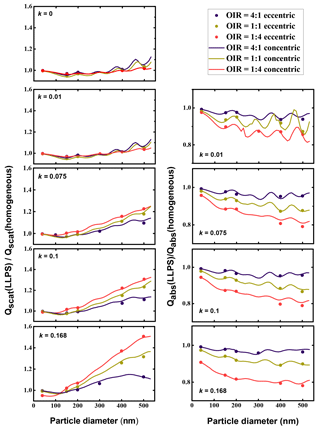
Figure 6Left column: ratio of Qscat for LLPS morphology over homogenous morphology as a function of particle diameter for OIR , 1:1 and 4:1, with increasing k from top to bottom, k=0, 0.01, 0.075, 0.1 and 0.168. Right column: corresponding absorption efficiency ratios. Dots represent calculations with random orientation of an eccentric core shell for the phase-separated particles; lines are calculations for the corresponding symmetric core-shell morphology (we used volume mixing to calculate refractive indices; see Tables A1 and A2).
Clearly, the effect of phase separation increases with particle size: the ratio of scattering efficiencies increases and is for all but the smallest sizes larger than 1, whereas the ratio of absorption efficiencies decreases and is always smaller than 1. All calculations have been performed for a wavelength of 355 nm; particles much smaller than this wavelength are close to Rayleigh scattering and become less sensitive to internal morphology. Hence, we expect all ratios to approach 1 for very small particle sizes. Also apparent are periodicities in both the ratio for scattering as well as the ratio of absorbing efficiencies showing a period with size of about 100 to 150 nm, presumably related to half-integral ratios of size to wavelength. These dampen out with increasing absorptivity.
However, the overall effect of increasing absorptivity is to enhance the differences between phase-separated particles relative to homogeneous ones.
The most significant trend is the dependence of the efficiency ratios on the organic to inorganic ratio. For the absorption efficiency, the particles with the lowest organic volume (OIR ) show the strongest deviation for the LLPS morphology relative to the homogenous particle. As the organic fraction decreases in the particle, the effect of redistribution of the absorbing molecules into the organic phase yields a stronger contrast in the imaginary part of the refractive index between the shell and the core. This increase in contrast influences both absorption and scattering efficiency ratios (see Appendix A).
Most importantly, the extensive comparison between the mean of eccentric core-shell realizations with the concentric core-shell calculations indicates that a concentric core-shell model is sufficient for estimating the ratios between scattering and absorption efficiencies for particles smaller than 500 nm in diameter and the ranges in OIR and absorptivity under consideration here. This approximation becomes less accurate with increasing particle size but stays within 2.8 % at maximum and is better than 1 % for most of the parameter range relevant here.
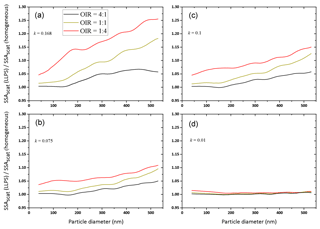
Figure 7Ratios of SSA for LLPS morphology over homogenous morphology as a function of particle diameter for OIR , 1:1 and 4:1, with decreasing absorption from (a) to (d), k=0.168, 0.1, 0.075 and 0.01 (same parameters as in Fig. 6; for details, see Tables A1 and A2). Here, we show only the data calculated for concentric core-shell morphologies.
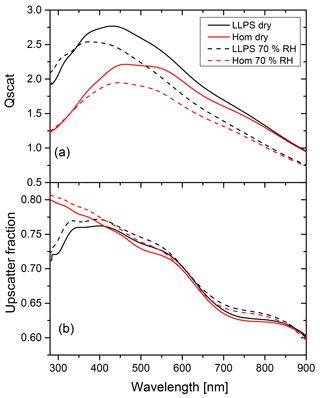
Figure 8Calculations for the limiting low albedo case are shown. OIR 1:4, diameter 200 nm and k=0.168 at 355 nm. Panel (a) shows the scattering efficiency for the homogeneous morphology (red) and LLPS morphology (black) under dry and wet conditions (solid and dashed line, respectively) for particles of identical diameter (200 nm) and AAE =2. Panel (b) shows the upscatter fraction for the homogeneous particle (red) and LLPS particle (black) under dry and wet conditions (solid and dashed line, respectively).
In the previous section, we showed that concentric core-shell calculations are sufficient to approximate the radiative impact of LLPS for a typical atmospheric aerosol containing a molecular absorber like brown carbon. Utilizing this insight allows us to perform integration over the UV–VIS part of the solar spectrum in a numerically efficient manner. In this section, we calculate the ratio of radiative forcing caused by a phase-separated aerosol versus a homogeneously mixed aerosol in the thin aerosol layer approximation for monodisperse aerosol.
According to Chýlek and Wong (1995) (see also Nemesure and Schwartz, 1998; compare to Charlson et al., 1991 for a purely scattering aerosol), the intrinsic properties that dictate the shortwave direct radiative forcing in the thin aerosol layer approximation for absorbing aerosol particles are their scattering and absorption cross sections and the fraction of radiation scattered by aerosol into the upper hemisphere, the upscattering fraction. Here, the ratio of scattering efficiency to extinction efficiency, the single scattering albedo (SSA), ω, determines the portion of total extinction due to scattering (e.g., Moosmüller and Sorensen, 2018):
For the examples of Fig. 6, the ratios of the single scattering albedos of the two morphologies are shown in Fig. 7.
For all OIR and absorptivities, a phase-separated particle has a larger single scattering albedo compared to a corresponding homogeneous particle, up to 25 % larger for the strong absorbing case and a large particle diameter. However, for weakly absorbing particles (k<=0.01) the effect is negligible, as expected. As in Fig. 6, the strongest enhancement is observed for the OIR 1:4 case, i.e., the one with the largest redistribution of absorbing molecules upon LLPS.
Following Chýlek and Wong's (1995) line of argumentation, we calculate the direct radiative forcing, ΔFR, of an optically thin aerosol layer in a cloud-free atmosphere (per unit area and unit vertical height, Δz) as
where is the globally averaged solar flux at the top of the scattering volume, σ the geometric cross section, a the surface albedo and β the upscatter fraction. The upscatter fraction, β, is a function of particle size and accounts for the asymmetry of the scattering phase function. It has a value of 0.5 for small particles in the Rayleigh regime and decreases as the size of the particle increases. The upscattering fraction for accumulation-mode particles (0.1 µm<r<1µm) that dominates aerosol mass and light scattering properties in the atmosphere, β, may be approximated for isotropic incoming radiation by (Wiscombe and Grams, 1976), with g being the asymmetry parameter, i.e., the average cosine of the scattering angle (, P being the normalized phase function). Since we are only interested in calculating the ratio of the radiative forcing for the LLPS morphology relative to homogenous morphology, we use this approximation for the upscatter fraction and calculate the ratio of the shortwave radiative forcing for the different morphologies as
Let us first discuss the case for a perfectly absorbing surface; i.e., albedo a is equal to zero. The last term in the curly bracket of Eq. (2) vanishes. The relevant factors of Eq. (2) for this albedo are shown in Fig. 8 for a particle for which we expect a significant effect of morphology based on the results presented in Fig. 6. Its OIR is equal to 1:4, it has a diameter of 200 nm and it has an imaginary part of the refractive index of k=0.168 at 355 nm. We take the wavelength dependence of the imaginary part of the refractive index (see Appendix B) into account by using a single Ångström exponent (AAE) in the following power law relationship (Moosmüller et al., 2011):
In the example shown in Fig. 8, AAE is equal to 2 (see Fig. B3 for k(λ) in Appendix B).
We also need to estimate the real part of the refractive index for a typical aged aerosol particle. Here, we assume it to consist of aqueous ammonium sulfate and secondary organic matter. The Lorentz–Lorenz relation (Born and Wolf, 1959) is utilized to estimate the real part of the refractive index based on parametrizations for the refractive index of ammonium sulfate and the organic matter for dry conditions and for 70 % RH as explained in detail in Appendix B.
Panel (a) in Fig. 8 shows the scattering efficiency for both dry conditions and at a relative humidity of 70 %. As discussed above, the LLPS morphology yields larger scattering efficiencies, especially at shorter wavelengths at which the differences in refractive indices are more significant. The upscatter fraction shown in panel (b) for LLPS morphology is about 10 % smaller than for the homogeneous morphology at near-UV wavelength (λ=290 nm) but they merge for the wavelengths above 400 nm.
For calculating the net ratio of the radiative forcing of phase-separated particles relative to homogeneously mixed ones, we utilize Eq. (3). Here, the product of upscatter fraction and scattering efficiency integrated over the shortwave solar spectrum for both LLPS morphology and homogeneous morphology yields the net ratio that quantifies the effect of morphology on direct radiative forcing. For the solar spectrum we used the spectral irradiance according to ASTM G173-03 (ASTM, 2012) and integrated Eq. (3) from 290 to 900 nm; see Appendix C.
The ratio is shown as a function of particle radius under dry and wet (70 % RH) conditions in Fig. 9a, b, respectively.
These calculations were done as in the example of Fig. 7 but for different scenarios with OIR , 1:1 and 4:1 and k=0, 0.1 and 0.168.
Figure 9 shows the results for the case in which AAE is equal to 2. This corresponds to highly absorbing BrC and will give the largest radiative forcing impact possible by mixed BrC particles. Figure 10 depicts the result for a less strongly absorbing BrC in the visible range of the solar spectrum, whereby AAE is chosen to be equal to 6.
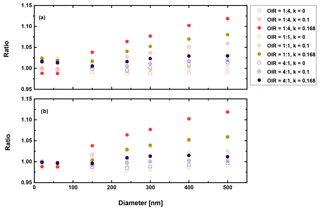
Figure 9Ratio of radiative forcing of LLPS to the homogenous case under 70 % RH (a) and dry conditions (0 % RH) (b) for AAE =2 and albedo a=0.
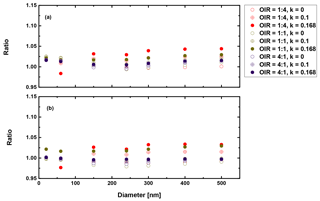
Figure 10Ratio of radiative forcing of LLPS to the homogenous case under 70 % RH (a) and dry conditions (b) for AAE =6 and albedo a=0.
First, we conclude from these calculations that the effect of morphology for purely scattering aerosol is negligible, smaller than 2 % for all sizes and organic to inorganic ratios. Second, there is not much difference between dry and moderately humid conditions (remember that at high RH (beyond SRH) we expect the particle to be homogeneously mixed). Third, as expected from the results discussed in the previous section, the greatest effect is calculated when the organic fraction is the lowest (OIR ), k has the largest value (0.168) and the size is on the upper size range of the accumulation mode. However, even here the increase is only about 12 %. For an AAE more likely to occur in aged aerosol, i.e., AAE =6, this increase reduces to 4 %. Based on the results shown in Figs. 9–10, the impact for cases where AAE is lower than 6 is negligible. Since even an AAE of 6 is considered to be characteristic of a strongly absorbing brown carbon, our overall conclusion is that liquid–liquid phase separation has no significant effect on direct shortwave aerosol forcing for low albedos.
Second, in a similar manner we may discuss the high albedo limit, i.e., a=1. Figures 11 and 12 show the corresponding results.
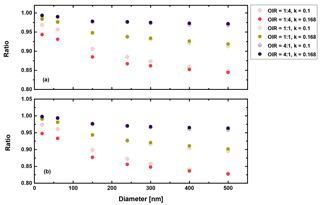
Figure 11Ratio of radiative forcing of LLPS to the homogenous case under 70 % RH (a) and dry conditions (0 % RH) (b) for AAE =2 and albedo a=1.
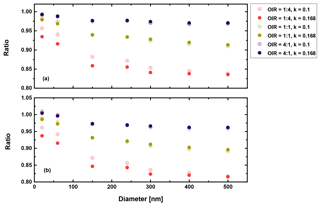
Figure 12Ratio of radiative forcing of LLPS to the homogenous case under 70 % RH (a) and dry conditions (b) for AAE =6 and albedo a=1.
Again, there are only small differences when comparing the humid and dry cases as well as the AAE =6 and AAE =2 cases. However, the LLPS morphology shows a smaller forcing compared to the homogeneous morphology because Qabs is the decisive parameter for a highly refractive surface (compare Eq. 3 and Fig. 6). Overall, the maximum reduction is 20 % for the largest sizes considered here and the OIR as expected from the discussion above.
Up to here, we have only compared ratios for the different morphologies. For a surface albedo close to zero, radiative forcing will be negative for a thin aerosol layer, whereas the forcing will turn positive for a highly reflecting surface for an absorbing aerosol. For intermediate albedos, the denominator of Eq. (3) (the forcing for the homogeneous morphology) will approach zero for a particular size and albedo combination, meaning that the effects of scattering and absorption at this surface albedo cancel out, resulting in a zero forcing. However, since the corresponding particles with LLPS morphology have a small but finite forcing, it results in a very large ratio of the shortwave radiative forcing for LLPS to homogenous morphology. This is illustrated in Fig. 13.
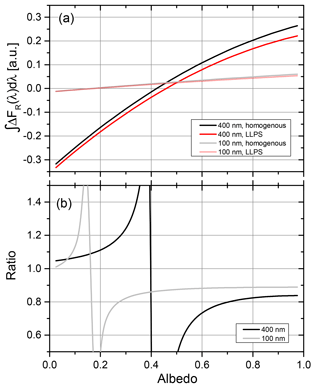
Figure 13(a) Direct radiative forcing integrated over the visible solar spectrum for particles with OIR 1:4, AAE =6 and k=0.168 at 355 nm. Results for two diameters are shown. (b) Ratio of forcing for LLPS morphology to homogeneous morphology; see Eq. (3) for the data of (a).
Panel (a) shows clearly that the albedo for which the direct radiative forcing vanishes depends on the size of the particle, shifting to larger albedos with increasing particle size. This leads to poles in the ratio of forcing for the two morphologies as seen in panel (b) of Fig. 12. However, for a more realistic atmospheric situation, whereby the thin aerosol layer will contain particles with sizes and refractive indices distributed over a significant range, these poles will level out. Hence, we expect a smooth transition for the ratio of radiative forcing with a larger negative forcing for LLPS morphology at low albedos to a smaller positive forcing at high albedos for LLPS morphology compared to homogeneous morphology.
Using both eccentric and concentric core-shell model calculations for scattering and absorption efficiencies of single aerosol particles with an inorganic non-absorbing core and an absorbing organic shell at different volume ratios, sizes and absorptivity revealed that a concentric core-shell model is a good approximation for calculating these efficiencies. Applied to liquid–liquid phase separation for atmospherically relevant OIR and sizes typical of the accumulation mode, we showed that the largest impact resulted from the case for which the organic fraction comprised the lowest contribution in the mixed particle (OIR ), formed a very thin shell around the inorganic core and was highly absorbing (k=0.168). Once integrated over the solar spectrum, taking into account the typical spectral dependence of BrC, the effect of morphology on radiative forcing substantially decreased to about a few percent. Overall, we conclude that the effect of liquid–liquid phase separation on shortwave radiative forcing is rather small and the correct value of AAE is the greatest source of uncertainty when estimating the impact.
All data shown in the figures can be obtained from the authors upon request.
Tables A1 and A2 show the values for the refractive indices, n+ik, at selected imaginary refractive indices (k=0.168 in Table A1 and k=0.01 in Table A2) set for the homogenous particle. The corresponding size of the core in the LLPS morphology as well as the refractive indices were calculated using simple volume mixing. These values are used as inputs for the calculations shown in Fig. 6.
Table A1Calculated values for relative size of the core to the shell for phase-separated particles and refractive indices (k=0.168) for homogenous and LLPS cases at different sizes and OIRs using volume mixing.
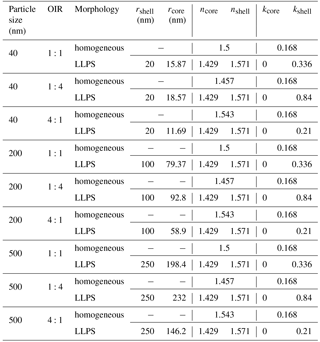
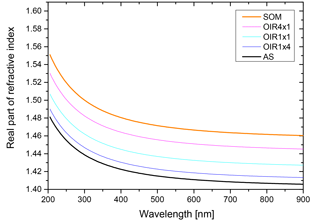
The real part of the refractive index for a liquid solution may be estimated in terms of the refractivity of the solution based on the Lorentz–Lorenz relation (Born and Wolf, 1959). The refractivity, to a good approximation, is a linear superposition of the molar refractivities of the solution's components. While refractive index data as well as density data are available for aqueous ammonium sulfate (AS) solutions (Tang and Munkelwitz, 1994), we choose the refractive index and density parametrizations of Lienhard et al. (2015) to be representative of the secondary organic matter (SOM) in our model calculations. As the molar refractivities depend strongly on wavelength, we parameterize the SOM molar refractivity wavelength dependence based on the parametrization given in Liu et al. (2013) and the ones for aqueous ammonium sulfate on the parametrization by Semmler et al. (2018). Finally, we use ideal mixing of the two binary systems to calculate the refractive index of the ternary system. The resulting refractive indices for the ternary system with different OIRs under dry conditions are shown in Fig. B1.
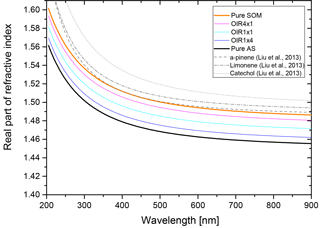
Figure B1Real part of the refractive index, n, for aqueous mixtures of ammonium sulfate (AS) and secondary organic matter (SOM) with varying OIRs extrapolated to dry conditions (lines in various colors). For comparison, the parametrizations of Liu et al. (2013) for SOM obtained by ozonolysis of α-pinene, limonene and catechol are given (gray lines).
To calculate the refractive indices at 70 % relative humidity we use the water activity of the binary aqueous solutions for AS (Tang and Munkelwitz, 1994) and SOM (Lienhard et al. 2015) and the Zdanovskii–Stokes–Robinson (ZSR) relation to calculate the water content of the AS–SOM mixture. This yields the refractive indices shown in Fig. B2.
Under humid conditions the real part of the refractive index decreases and, since AS takes up more water at 70 % compared to SOM, the difference in refractive index between AS-rich mixtures and SOM-rich mixtures increases when comparing humid to dry conditions.
The wavelength dependence of the imaginary part of the refractive index is taken into account by assuming the simple power law dependence of Eq. (4). In Fig. B3 we show the imaginary part of the refractive index as a function of wavelength for two Ångström exponents, with the k=0.168 at λ=355 nm. For comparison, we plot the parametrizations used by Wang et al. (2014) and the data collected in this reference as well.
Clearly, the AAE =2 case poses an upper limit of absorptivity, whereas the AAE =6 case is in between the parametrization for brown carbon primary organic aerosol and brown carbon secondary aerosol estimates of Wang et al. (2015).
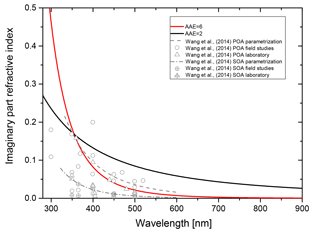
Figure B3Wavelength dependence of the imaginary part of the refractive index for AAE equal to 2 and 6 (solid black and red lines, respectively; k=0.168 for λ=355 nm). For comparison the parametrizations of Wang et al. (2014) for brown primary organic aerosol (POA, dashed gray line) and brown secondary organic aerosol (SOA, dashed-dotted gray line) are plotted as well as the data from laboratory and field studies collected by Wang et al. (2014).
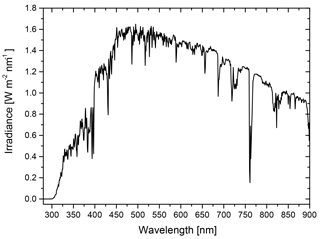
For calculating the shortwave radiative forcing ratio defined in Eq. (3), spectral irradiance is needed as an input for performing the integration. Since we are interested in estimating the relevance of LLPS for radiative forcing and only calculating a ratio, the particular choice of irradiance data is not very important. We use the ASTM G173-03 (ASTM, 2012) as spectral irradiance, which is plotted in Fig. C1.
The irradiance is for a solar zenith angle of 41.81∘; the atmospheric conditions are those of the standard US atmosphere with an ozone column of 340 DU and total column water vapor equivalent of 1.42 cm.
MMF and UKK performed the calculations, all three authors initiated the research and wrote the manuscript.
The authors declare that they have no conflict of interest.
We would like to thank Dan Mackowski for making his MSTM code publicly
available and an anonymous reviewer for insightful comments and suggestions.
This project was funded by the Swiss National Science Foundation (SNF; grant
no. 200020 146760/1).
Edited by: Sergey A. Nizkorodov
Reviewed by: two anonymous referees
Alexander, D. T., Crozier, P. A., and Anderson, J. R.: Brown carbon spheres in East Asian outflow and their optical properties, Science, 321, 833–836, 2008.
Andreae, M. O. and Gelencsér, A.: Black carbon or brown carbon? The nature of light-absorbing carbonaceous aerosols, Atmos. Chem. Phys., 6, 3131–3148, https://doi.org/10.5194/acp-6-3131-2006, 2006.
Arnott, W. P., Moosmüller, H., Sheridan, P. J., Ogren, J. A., Raspet, R., Slaton, W. V., Hand, J. L., Kreidenweis, S. M., and Collett, J. L.: Photoacoustic and filter-based ambient aerosol light absorption measurements: Instrument comparisons and the role of relative humidity, J. Geophys. Res.-Atmos., 108, 4034, https://doi.org/10.1029/2002JD002165, 2003.
ASTM: ASTM G173-12 Standard Tables for Reference Solar Spectral Irradiances: Direct Normal and Hemispherical on 37∘ Tilted Surface, ASTM International, Reference Solar Spectral Irradiance, available at: http://rredc.nrel.gov/solar/spectra/am1.5/ (last access: 1 April 2017), 2012.
Baumgardner, D. and Clarke, A.: Changes in aerosol properties with relative humidity in the remote southern hemisphere marine boundary layer, J. Geophys. Res.-Atmos., 103, 16525–16534, 1998.
Bertram, A. K., Martin, S. T., Hanna, S. J., Smith, M. L., Bodsworth, A., Chen, Q., Kuwata, M., Liu, A., You, Y., and Zorn, S. R.: Predicting the relative humidities of liquid-liquid phase separation, efflorescence, and deliquescence of mixed particles of ammonium sulfate, organic material, and water using the organic-to-sulfate mass ratio of the particle and the oxygen-to-carbon elemental ratio of the organic component, Atmos. Chem. Phys., 11, 10995–11006, https://doi.org/10.5194/acp-11-10995-2011, 2011.
Bohren, C. F. and Huffman, D. R.: Absorption and scattering of light by small particles, John Wiley & Sons, New York, USA, 2008.
Bond, T. C. and Bergstrom, R.: Light absorption by carbonaceous particles: An investigative review, Aerosol Sci. Tech., 40, 27–67, 2006.
Bond, T. C., Zarzycki, C., Flanner, M. G., and Koch, D. M.: Quantifying immediate radiative forcing by black carbon and organic matter with the Specific Forcing Pulse, Atmos. Chem. Phys., 11, 1505–1525, https://doi.org/10.5194/acp-11-1505-2011, 2011.
Bond, T. C., Doherty, S. J., Fahey, D. W., Forster, P. M., Berntsen, T., DeAngelo, B. J., Flanner, M. G., Ghan, S., Kärcher, B., Koch, D., Kinne, S., Kondo, Y., Quinn, P. K., Sarofim, M. C., Schultz, M. G., Schulz, M., Venkataraman, C., Zhang, H., Zhang, S., Bellouin, N., Guttikunda, S. K., Hopke, P. K., Jacobson, M. Z., Kaiser, J. W., Klimont, Z., Lohmann, U., Schwarz, J. P., Shindell, D., Storelvmo, T., Warren, S. G., and Zender, C. S.: Bounding the role of black carbon in the climate system: A scientific assessment, J. Geophys. Res.-Atmos., 118, 5380–5552, https://doi.org/10.1002/jgrd.50171, 2013.
Bones, D. L., Henricksen, D. K., Mang, S. A., Gonsior, M., Bateman, A. P., Nguyen, T. B., Cooper, W. J., and Nizkorodov, S. A.: Appearance of strong absorbers and fluorophores in limonene-O3 secondary organic aerosol due to NH4+-mediated chemical aging over long time scales, J. Geophys. Res.-Atmos., 115, D05203, https://doi.org/10.1029/2009JD012864, 2010.
Born, M. and Wolf, E.: Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, Pergamon Press Ltd, London, 1959.
Chakrabarty, R. K., Moosmüller, H., Chen, L.-W. A., Lewis, K., Arnott, W. P., Mazzoleni, C., Dubey, M. K., Wold, C. E., Hao, W. M., and Kreidenweis, S. M.: Brown carbon in tar balls from smoldering biomass combustion, Atmos. Chem. Phys., 10, 6363–6370, https://doi.org/10.5194/acp-10-6363-2010, 2010.
Charlson, R. J., Langner, J., Rodhe, H., Leovy, C. B., and Warren, S. G.: Pertubation of the northern hemisphere radiation balance by backscattering from anthropogenic sulfate aerosols, Tellus, 43, 152–163, 1991.
Chen, Y. and Bond, T. C.: Light absorption by organic carbon from wood combustion, Atmos. Chem. Phys., 10, 1773–1787, https://doi.org/10.5194/acp-10-1773-2010, 2010.
Cheng, T., Wu, Y., and Chen, H.: Effects of morphology on the radiative properties of internally mixed light absorbing carbon aerosols with different aging status, Opt. Express, 22, 15904–15917, 2014.
Chung, C. E., Ramanathan, V., and Decremer, D.: Observationally constrained estimates of carbonaceous aerosol radiative forcing, P. Natl. Acad. Sci. USA, 109, 116241–11629, 2012.
Chýlek, P. and Wong, J.: Effect of absorbing aerosols on global radiation budget, Geophys. Res. Lett., 22, 929–931, 1995.
Ciobanu, V. G., Marcolli, C., Krieger, U. K., Weers, U., and Peter, T.: Liquid-liquid phase separation in mixed arganic/inorganic Aerosol particles, J. Phys. Chem. A., 113, 10966–10978, https://doi.org/10.1021/jp905054d, 2009.
Ciobanu, V. G., Marcolli, C., Krieger, U. K., Zuend, A., and Peter, T.: Efflorescence of ammonium sulfate and coated ammonium sulfate particles: evidence for surface nucleation, J. Phys. Chem. A., 114, 9486–9495, https://doi.org/10.1021/jp103541w, 2010.
Feng, Y., Ramanathan, V., and Kotamarthi, V. R.: Brown carbon: a significant atmospheric absorber of solar radiation?, Atmos. Chem. Phys., 13, 8607–8621, https://doi.org/10.5194/acp-13-8607-2013, 2013.
Hecobian, A., Zhang, X., Zheng, M., Frank, N., Edgerton, E. S., and Weber, R. J.: Water-Soluble Organic Aerosol material and the light-absorption characteristics of aqueous extracts measured over the Southeastern United States, Atmos. Chem. Phys., 10, 5965–5977, https://doi.org/10.5194/acp-10-5965-2010, 2010.
Hodas, N., Zuend, A., Mui, W., Flagan, R. C., and Seinfeld, J. H.: Influence of particle-phase state on the hygroscopic behavior of mixed organic-inorganic aerosols, Atmos. Chem. Phys., 15, 5027–5045, https://doi.org/10.5194/acp-15-5027-2015, 2015.
Hoffer, A., Gelencsér, A., Guyon, P., Kiss, G., Schmid, O., Frank, G. P., Artaxo, P., and Andreae, M. O.: Optical properties of humic-like substances (HULIS) in biomass-burning aerosols, Atmos. Chem. Phys., 6, 3563–3570, https://doi.org/10.5194/acp-6-3563-2006, 2006.
IPCC: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G. K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge University Press, Cambridge, UK, New York, 2013.
Kirchstetter, T. W. and Thatcher, T. L.: Contribution of organic carbon to wood smoke particulate matter absorption of solar radiation, Atmos. Chem. Phys., 12, 6067–6072, https://doi.org/10.5194/acp-12-6067-2012, 2012.
Kirchstetter, T. W., Novakov, T., and Hobbs, P. V.: Evidence that the spectral dependence of light absorption by aerosols is affected by organic carbon, J. Geophys. Res.-Atmos, 109, D21208, https://doi.org/10.1029/2004JD004999, 2004.
Krieger, U. K., Marcolli, C., and Reid, J. P.: Exploring the complexity of aerosol particle properties and processes using single particle techniques, Chem. Soc. Rev., 41, 6631–6662, https://doi.org/10.1039/C2CS35082C, 2012.
Kwamena, N. O. A., Buajarern, J., and Reid, J. P.: Equilibrium morphology of mixed organic/inorganic/aqueous aerosol droplets: investigating the effect of relative humidity and surfactants, J. Phys. Chem. A., 114, 5787–5795, https://doi.org/10.1021/Jp1003648, 2010.
Lack, D. A. and Cappa, C. D.: Impact of brown and clear carbon on light absorption enhancement, single scatter albedo and absorption wavelength dependence of black carbon, Atmos. Chem. Phys., 10, 4207–4220, https://doi.org/10.5194/acp-10-4207-2010, 2010.
Lack, D. A, Langridge, J. M., Bahreini, R., Cappa, C. D., Middlebrook, A. M, and Schwarz, J. P.: Brown carbon and internal mixing in biomass burning particles, P. Natl. Acad. Sci. USA, 109, 14802–14807, 2012.
Langridge, J. M., Richardson, M. S., Lack, D. A., Brock, C. A., and Murphy, D. M.: Limitations of the photoacoustic technique for aerosol absorption measurement at high relative humidity, Aerosol Sci. Tech., 47, 1163–1173, 2013.
Lang-Yona, N., Abo-Riziq, A., Erlick, C., Segre, E., Trainic, M., and Rudich, Y.: Interaction of internally mixed aerosols with light, Phys. Chem. Chem. Phys., 12, 21–31, 2010.
Laskin, A., Laskin, J., and Nizkorodov, S. A.: Chemistry of atmospheric brown carbon, Chem. Rev., 115, 4335–4382, 2015.
Lewis, K. A., Arnott, W. P., Moosmüller, H., Chakrabarty, R. K., Carrico, C. M., Kreidenweis, S. M., Day, D. E., Malm, W. C., Laskin, A., Jimenez, J. L., Ulbrich, I. M., Huffman, J. A., Onasch, T. B., Trimborn, A., Liu, L., and Mishchenko, M. I.: Reduction in biomass burning aerosol light absorption upon humidification: roles of inorganically-induced hygroscopicity, particle collapse, and photoacoustic heat and mass transfer, Atmos. Chem. Phys., 9, 8949–8966, https://doi.org/10.5194/acp-9-8949-2009, 2009.
Lienhard, D. M., Huisman, A. J., Krieger, U. K., Rudich, Y., Marcolli, C., Luo, B. P., Bones, D. L., Reid, J. P., Lambe, A. T., Canagaratna, M. R., Davidovits, P., Onasch, T. B., Worsnop, D. R., Steimer, S. S., Koop, T., and Peter, T.: Viscous organic aerosol particles in the upper troposphere: diffusivity-controlled water uptake and ice nucleation?, Atmos. Chem. Phys., 15, 13599–13613, https://doi.org/10.5194/acp-15-13599-2015, 2015.
Liu, J., Bergin, M., Guo, H., King, L., Kotra, N., Edgerton, E., and Weber, R. J.: Size-resolved measurements of brown carbon in water and methanol extracts and estimates of their contribution to ambient fine-particle light absorption, Atmos. Chem. Phys., 13, 12389–12404, https://doi.org/10.5194/acp-13-12389-2013, 2013.
Ma, L. and Thompson, J. E.: Optical properties of dispersed aerosols in the near ultraviolet (355 nm): measurement approach and initial data, Anal. Chem., 84, 5611–5617, 2012.
Mackowski, D. W.: Multiple Sphere T-Matrix (MSTM) version 3.0, available at: http://eng.auburn.edu/users/dmckwski/scatcodes/ (last access: 1 April 2017), 2013.
Mackowski, D. W. and Mishchenko, M. I.: Calculation of the T matrix and the scattering matrix for ensembles of spheres, J. Opt. Soc. Am., 13, 2266–2278, 1996.
Mackowski, D. W. and Mishchenko, M. I.: A multiple sphere T-matrix Fortran code for use on parallel computer clusters, J. Quant. Spectrosc. Ra., 112, 2182–2192, 2011.
Marcolli, C. and Krieger, U. K.: Phase changes during hygroscopic cycles of mixed organic/inorganic model systems of tropospheric aerosols, J. Phys. Chem. A., 110, 1881–1893, https://doi.org/10.1021/Jp0556759, 2006.
Martin, S. T., Hung, H.-M., Park, R. J., Jacob, D. J., Spurr, R. J. D., Chance, K. V., and Chin, M.: Effects of the physical state of tropospheric ammonium-sulfate-nitrate particles on global aerosol direct radiative forcing, Atmos. Chem. Phys., 4, 183–214, https://doi.org/10.5194/acp-4-183-2004, 2004.
Mishchenko, M. I., Liu, L., and Mackowski, D. W.: T-matrix modeling of linear depolarization by morphologically complex soot and soot-containing aerosols, J. Quant. Spectrosc. Ra., 123, 135–144, 2013.
Moise, T., Flores, J. M., and Rudich, Y.: Optical properties of secondary organic aerosols and their changes by chemical processes, Chem. Rev., 115, 4400–4439, 2015.
Moosmüller, H. and Sorensen, C. M.: Small and large particle limits of single scattering albedo for homogeneous, spherical particles, J. Quant. Spectrosc. Ra., 204, 250–255, 2018.
Moosmüller, H., Chakrabarty, R. K., Ehlers, K. M., and Arnott, W. P.: Absorption Ångström coefficient, brown carbon, and aerosols: basic concepts, bulk matter, and spherical particles, Atmos. Chem. Phys., 11, 1217–1225, https://doi.org/10.5194/acp-11-1217-2011, 2011.
Nakayama, T., Matsumi, Y., Sato, K., Imamura, T., Yamazaki, A., and Uchiyama, A.: Laboratory studies on optical properties of secondary organic aerosols generated during the photooxidation of toluene and the ozonolysis of α-pinene, J. Geophys. Res.-Atmos., 115, D24204, https://doi.org/10.1029/2010JD014387, 2010.
Nemesure, S. and Schwartz S. E.: Effect of absorbing aerosol on shortwave radiative forcing of climate, 8th atmospheric radiation measurement (ARM), Science Team Meeting, Tucson, AZ, 23–26 March 1998.
Pankow, J. F.: Gas/particle partitioning of neutral and ionizing compounds to single and multi-phase aerosol particles. 1. unified modeling framework, Atmos. Environ., 37, 3323–3333, https://doi.org/10.1016/S1352-2310(03)00346-7, 2003.
Pöschl, U.: Atmospheric aerosols: composition, transformation, climate and health effects, Angew. Chem. Int. Edit., 44, 7520–7540, 2005.
Qiu, Y. and Molinero, V.: Morphology of liquid–liquid phase separated aerosols, J. Am. Chem. Soc., 137, 10642–10651, 2015.
Ramanathan, V., Crutzen, P. J., Lelieveld, J., Mitra, A. P., Althausen, D., Anderson, J., Andreae, M. O., Cantrell, W., Cass, G. R., Chung, C. E., and Clarke, A. D.: Indian ocean experiment: an integrated analysis of the climate forcing and effects of the great Indo-Asian haze, J. Geophys. Res.-Atmos., 106, 28371–28398, 2001.
Ramanathan, V., Li, F., Ramana, M. V., Praveen, P. S., Kim, D., Corrigan, C. E., Nguyen, H., Stone, E. A., Schauer, J. J., Carmichael, G. R., and Adhikary, B.: Atmospheric brown clouds: Hemispherical and regional variations in long-range transport, absorption, and radiative forcing, J. Geophys. Res.-Atmos., 112, D22S21, 10.1029/2006JD008124, 2007.
Saleh, R., Hennigan, C. J., McMeeking, G. R., Chuang, W. K., Robinson, E. S., Coe, H., Donahue, N. M., and Robinson, A. L.: Absorptivity of brown carbon in fresh and photo-chemically aged biomass-burning emissions, Atmos. Chem. Phys., 13, 7683–7693, https://doi.org/10.5194/acp-13-7683-2013, 2013.
Semmler, M., Luo, B. P., and Koop, T.: Refractive indices of H2SO4-(NH4)2SO4-H2O solutions at upper tropospheric conditions, in preparation, 2018.
Smith, M. L., Bertram, A. K., and Martin, S. T.: Deliquescence, efflorescence, and phase miscibility of mixed particles of ammonium sulfate and isoprene-derived secondary organic material, Atmos. Chem. Phys., 12, 9613–9628, https://doi.org/10.5194/acp-12-9613-2012, 2012.
Song, M., Marcolli, C., Krieger, U. K., Zuend, A., and Peter, T.: Liquid-liquid phase separation in aerosol particles: Dependence on O : C, organic functionalities, and compositional complexity, Geophys. Res. Lett., 39, L19801, https://doi.org/10.1029/2012GL052807, 2012a.
Song, M., Marcolli, C., Krieger, U. K., Zuend, A., and Peter, T.: Liquid-liquid phase separation and morphology of internally mixed dicarboxylic acids/ammonium sulfate/water particles, Atmos. Chem. Phys., 12, 2691–2712, https://doi.org/10.5194/acp-12-2691-2012, 2012b.
Song, M., Marcolli, C., Krieger, U. K., Lienhard, D. M., and Peter, T.: Morphologies of mixed organic/inorganic/aqueous aerosol droplets, Faraday discuss., 165, 289–316, https://doi.org/10.1039/C3FD00049D, 2013.
Tang, I. N. and Munkelwitz, H. R.: Water activities, densities, and refractive indices of aqueous sulfates and sodium nitrate droplets of atmospheric importance, J. Geophys. Res., 99, 18801–18818, 1994.
Tang, M., Alexander, J. M., Kwon, D., Estillore, A. D., Laskina, O., Young, M. A., Kleiber, P. D., and Grassian, V. H.: Optical and physicochemical properties of brown carbon aerosol: Light scattering, FTIR extinction spectroscopy, and hygroscopic growth, J. Phys. Chem. A., 24, 4155–4166, 2016.
Updyke, K. M., Nguyen, T. B., and Nizkorodov, S. A.: Formation of brown carbon via reactions of ammonia with secondary organic aerosols from biogenic and anthropogenic precursors, Atmos. Environ., 63, 22–31, 2012.
Van de Hulst, H. C.: Light Scattering by Small Molecules, Dover Publications Inc, New York, 1957.
Wang, X., Heald, C. L., Ridley, D. A., Schwarz, J. P., Spackman, J. R., Perring, A. E., Coe, H., Liu, D., and Clarke, A. D.: Exploiting simultaneous observational constraints on mass and absorption to estimate the global direct radiative forcing of black carbon and brown carbon, Atmos. Chem. Phys., 14, 10989–11010, https://doi.org/10.5194/acp-14-10989-2014, 2014.
Wiscombe, W. J. and Grams, G. W.: The backscattered fraction in two-stream approximations, J. Atmos. Sci., 33, 2440–2451, 1976.
Yang, M., Howell, S. G., Zhuang, J., and Huebert, B. J.: Attribution of aerosol light absorption to black carbon, brown carbon, and dust in China – interpretations of atmospheric measurements during EAST-AIRE, Atmos. Chem. Phys., 9, 2035–2050, https://doi.org/10.5194/acp-9-2035-2009, 2009.
You, Y., Renbaum-Wolff, L., Carreras-Sospedra, M., Hanna, S. J., Hiranuma, N., Kamal, S., Smith, M. L., Zhang, X., Weber, R. J., Shilling, J. E., Dabdub, D., Martin, S. T., and Bertram, A. K.: Images reveal that atmospheric particles can undergo liquid–liquid phase separations, P. Natl. Acad. Sci. USA, 109, 13188–13193, https://doi.org/10.1073/pnas.1206414109, 2012.
Zhang, Q., Jimenez, J. L., Canagaratna, M. R., Allan, J. D., Coe, H., Ulbrich, I., Alfarra, M. R., Takami, A., Middlebrook, A. M., Sun, Y. L., Dzepina, K., Dunlea, E., Docherty, K., DeCarlo, P. F., Salcedo, D., Onasch, T., Jayne, J. T., Miyoshi, T., Shimono, A., Hatakeyama, S., Takegawa, N., Kondo, Y., Schneider, J., Drewnick, F., Borrmann, S., Weimer, S., Demerjian, K., Williams, P., Bower, K., Bahreini, R., Cottrell, L., Griffin, R. J., Rautiainen, J., Sun, J. Y., Zhang, Y. M., and Worsnop, D. R.: Ubiquity and dominance of oxygenated species in organic aerosols in anthropogenically-influenced Northern Hemisphere midlatitudes, Geophys. Res. Lett., 34, L13801, https://doi.org/10.1029/2007GL029979, 2007.
Zhang, X., Lin, Y. H., Surratt, J. D., Zotter, P., Prévôt, A. S. H., and Weber, R. J.: Light-absorbing soluble organic aerosol in Los Angeles and Atlanta: A contrast in secondary organic aerosol, Geophys. Res. Lett., 38, L21810, https://doi.org/10.1029/2011GL049385, 2011.
- Abstract
- Introduction
- Eccentric versus concentric core-shell morphology
- Atmospheric implications
- Conclusions
- Data availability
- Appendix A: Calculating refractive indices for homogenous and phase-separated particles
- Appendix B: Estimating the refractive index for the calculations of Sect. 3.
- Appendix C: Spectral irradiance
- Author contributions
- Competing interests
- Acknowledgements
- References
- Abstract
- Introduction
- Eccentric versus concentric core-shell morphology
- Atmospheric implications
- Conclusions
- Data availability
- Appendix A: Calculating refractive indices for homogenous and phase-separated particles
- Appendix B: Estimating the refractive index for the calculations of Sect. 3.
- Appendix C: Spectral irradiance
- Author contributions
- Competing interests
- Acknowledgements
- References