the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Exploration of the influence of environmental conditions on secondary organic aerosol formation and organic species properties using explicit simulations: development of the VBS-GECKO parameterization
Victor Lannuque
Marie Camredon
Florian Couvidat
Alma Hodzic
Richard Valorso
Sasha Madronich
Bertrand Bessagnet
Bernard Aumont
Atmospheric chambers have been widely used to study secondary organic aerosol (SOA) properties and formation from various precursors under different controlled environmental conditions and to develop parameterization to represent SOA formation in chemical transport models (CTMs). Chamber experiments are however limited in number, performed under conditions that differ from the atmosphere and can be subject to potential artefacts from chamber walls. Here, the Generator for Explicit Chemistry and Kinetics of Organics in the Atmosphere (GECKO-A) modelling tool has been used in a box model under various environmental conditions to (i) explore the sensitivity of SOA formation and properties to changes on physical and chemical conditions and (ii) develop a volatility basis set (VBS)-type parameterization. The set of parent hydrocarbons includes n-alkanes and 1-alkenes with 10, 14, 18, 22 and 26 carbon atoms, α-pinene, β-pinene and limonene, benzene, toluene, o-xylene, m-xylene and p-xylene. Simulated SOA yields and their dependences on the precursor structure, organic aerosol load, temperature and NOx levels are consistent with the literature. GECKO-A was used to explore the distribution of molar mass, vaporization enthalpy, OH reaction rate and Henry's law coefficient of the millions of secondary organic compounds formed during the oxidation of the different precursors and under various conditions. From these explicit simulations, a VBS-GECKO parameterization designed to be implemented in 3-D air quality models has been tuned to represent SOA formation from the 18 precursors using GECKO-A as a reference. In evaluating the ability of VBS-GECKO to capture the temporal evolution of SOA mass, the mean relative error is less than 20 % compared to GECKO-A. The optimization procedure has been automated to facilitate the update of the VBS-GECKO on the basis of the future GECKO-A versions, its extension to other precursors and/or its modification to carry additional information.
- Article
(3663 KB) -
Supplement
(2192 KB) - BibTeX
- EndNote
Fine particulate matter impacts visibility (e.g. Han et al., 2012), human health (e.g. Lim et al., 2012; Malley et al., 2017) and climate (e.g. Boucher et al., 2013). A large fraction of fine particles is organic, representing between 20 % and 90 % of the total mass (e.g. Jimenez et al., 2009). This organic fraction can be directly emitted into the atmosphere (primary organic aerosol, POA) or formed by gas–particle partitioning of low-volatility species produced during the oxidation of gaseous organic compounds (secondary organic aerosol, SOA) (e.g. Mader et al., 1952; O'Brien et al., 1975; Grosjean, 1992). The secondary origin of organic aerosol (OA) dominates the primary fraction in most environments (e.g. Gelencsér et al., 2007). SOA is composed of a large number of compounds having various chemical structures and spanning therefore a wide range of physicochemical properties (reactivity, volatility, molar mass, solubility, optical absorption). The amount of SOA formed from a gaseous precursor depends mainly on its structure (carbon chain length, degree of unsaturation, number and type of functional groups, etc.) and on environmental conditions that influence (i) the concentration and the structure of organic compounds produced during gas-phase oxidation (oxidant concentrations and NOx levels, temperature, photolysis, humidity, etc.) and (ii) their partitioning between the gas and the condensed phase (pre-existing OA mass (Coa), temperature, etc.) (e.g. Kroll and Seinfeld, 2008; Ng et al., 2017; Shrivastava et al., 2017).
SOA formation is represented in chemical transport models (CTMs) using simplified parameterizations. These parameterizations describe the formation of secondary organic species from the oxidation of gaseous precursors and their consumptions through the use of surrogate species having different volatilities (e.g. Odum Jay et al., 1996; Pun et al., 2002, 2003, 2006; Tsigaridis and Kanakidou, 2003; Couvidat et al., 2012; Couvidat and Sartelet, 2015), sometimes discretized into decadal volatility bins (e.g. Robinson et al., 2007; Donahue et al., 2006, 2012; Jimenez et al., 2009; Zhang and Seinfeld, 2013). The gas–particle partitioning of a surrogate species or a given volatility bin is usually described considering an absorption process according to the theory described by Pankow (1994). Comparisons with field observations show that current CTMs have difficulties in reproducing the spatial and temporal variations of PM2.5 mass concentrations (e.g. de Gouw et al., 2005; Johnson et al., 2006; Volkamer et al., 2006; Heald et al., 2005; Hodzic et al., 2010; Shrivastava et al., 2011; Couvidat et al., 2012; Solazzo et al., 2012; Im et al., 2015), mainly because of the difficulties to represent the secondary organic fraction of the aerosol (Solazzo et al., 2012).
SOA parameterizations have typically been developed and optimized based on atmospheric chamber data. Atmospheric chambers have been widely used to study SOA formation from various precursors under different controlled environmental conditions. Experiments, being limited in number, do not cover the diversity of atmospheric chemical and physical conditions that influence SOA formation. Smog chamber experiments are also usually performed under conditions that differ from the atmosphere (high level of oxidants and precursors, different light spectrum and intensity, low humidity, short times of ageing, etc.). In addition, SOA formation experiments can be subject to potential artefacts from chamber wall surfaces, such as heterogeneous reactions or aerosol and vapour wall losses (e.g. McMurry and Grosjean, 1985; Matsunaga and Ziemann, 2010; La et al., 2016).
The objectives of this study are (i) to explore the influence of environmental conditions on SOA formation and the distribution of physicochemical properties (volatility, enthalpy of vaporization, molar mass, OH rate constant and water solubility) of the evolving molecular mixture and (ii) to optimize a volatility basis set (VBS)-type parameterization (e.g. Donahue et al., 2006) on the basis of a deterministic and explicit modelling of SOA formation. Deterministic and explicit simulations allow (i) taking into account the influence of various environmental conditions encountered in the atmosphere, (ii) simulating SOA formation under representative concentration regimes and timescales and (iii) accessing detailed properties of organic compounds in both gas and condensed phases. Nearly explicit representation of SOA formation under various environmental conditions is possible with the Generator for Explicit Chemistry and Kinetics of Organics in the Atmosphere (GECKO-A) (Aumont et al., 2005; Camredon et al., 2007). The environmental scenarios and the explicit representation of SOA formation are described in Sect. 2. Explicit simulations are used to explore the influence of environmental conditions on SOA formation and the distribution of the physicochemical properties of species produced during organic compound oxidation in Sect. 3. A VBS-type parameterization is optimized and evaluated using explicit simulations as a benchmark in Sect. 4.
2.1 The environmental scenarios
Scenarios were developed in a box model to represent the variability of SOA formation within the range of environmental conditions encountered in the atmosphere (temperature, relative humidity, solar zenith angle, aerosol mass concentration and chemical concentrations). Scenarios were built with various NOx concentrations to cover chemical regimes from low NOx to high NOx conditions (Table 1).
Table 1Constant environmental conditions used in the various scenarios. For each scenario, the concentrations of OH, HO2, NO and NO2 are at the stationary state induced by the constant conditions. Values in bold represent the conditions used in the reference scenario.
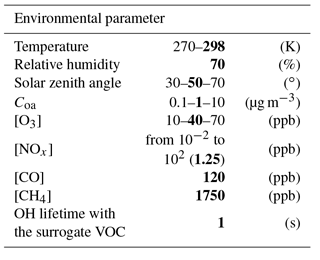
To examine the sensitivity of SOA formation to each parameter, chemical and physical conditions were fixed in each scenario. Physical parameters set in the simulations were temperature (270 and 298 K), relative humidity (70 %), zenith angle (30, 50 and 70∘) and Coa (0.1, 1 and 10 µg m−3). The chemistry considered was the reactivity of inorganic species (i.e. the chemistry) and the oxidation of CO and CH4. The influence of non-methane volatile organic compound (VOC) oxidation on the HOx and NOx cycles was included using a surrogate species. The OH lifetime with respect to reaction with the surrogate VOC was set to 1 s, in the range of what is observed in situ (Lou et al., 2010; Hansen et al., 2014). The oxidation of this surrogate VOC with OH leads to the formation of a surrogate peroxy radical, with a chemistry assumed to be similar to CH3O2. Dry deposition was considered for O3, H2O2 and HNO3 (with deposition rates of , and s−1, respectively). Chemical concentrations were fixed for CO (120 ppb), methane (1750 ppb), O3 (10, 40 and 70 ppb) and NOx (ranging from 10−2 to 102 ppb). Photolysis frequencies were computed for each fixed zenith angle at the surface using the Tropospheric Ultraviolet and Visible (TUV) radiation model (Madronich and Flocke, 1999) with rules for organic chromophores described in Aumont et al. (2005). Each simulation was run in a box model until the OH, HO2, NO and NO2 stationary state concentrations were reached. These stationary states were used as inputs for our SOA formation scenarios. In each scenario, the initial concentration of a given SOA precursor is set to a low enough value (10 pptC) to not affect significantly both the stationary state conditions of the simulations and the prescribed amount of pre-existing aerosol (Coa).
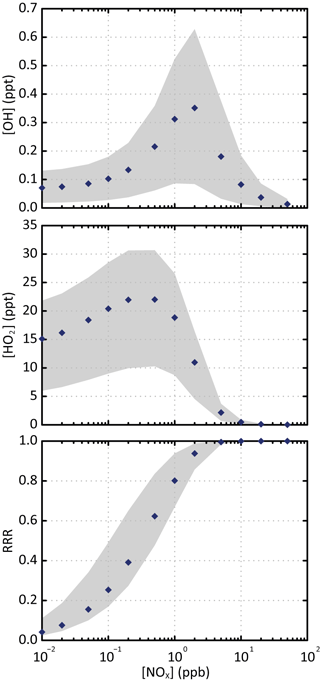
Figure 1Simulated stationary state concentration of OH and HO2 and corresponding reaction rate ratio (RRR) as a function of NOx concentrations for the various scenarios. The blue points are the simulated values for the scenario performed at a temperature of 298 K, a zenith angle of 50∘ and 40 ppb of ozone. The grey zone corresponds to the range of values simulated in all the scenarios.
Figure 1 shows the simulated stationary state concentrations of OH and HO2 as a function of NOx concentrations for the various scenarios. Simulated evolutions and concentrations of OH and HO2 with NOx are in agreement with the observations (e.g. Stone et al., 2012). The distribution of secondary species depends on the evolution of RO2 radicals. The branching ratio of RO2 reacting with NO, called hereafter RRR (for reaction rate ratio), is often used to characterize the chemical environment (e.g. Lane et al., 2008). In the scenarios, the loss of RO2 with CH3O2 (the major RO2 radical) represents less than 10 %. The RRR was therefore calculated here without considering the RO2 + RO2 reactions as
where and are the rate constants for the reactions of the peroxy radicals with NO and HO2, respectively, and [NO] and [HO2] the concentrations of the different radicals. Figure 1 also presents the variation of RRR with NOx. Rate constants of RO2 with NO and HO2 used to compute RRR are calculated at 298 K: = cm3 molec−1 s−1 (Jenkin et al., 1997) and = cm3 molec−1 s−1 (e.g. Boyd et al., 2003, assuming a large carbon skeleton for RO2). Figure 1 shows that most of the RO2 reacts with NO for NOx concentrations higher than 1 ppb. The NOx and HOx concentrations used in the various scenarios are consistent with typical chemical characteristics of low- to high-NOx environments. These stationary state scenarios are representative of the evolution of the tropospheric chemical system. They were used here to explore explicitly the formation of SOA under the ranges of NOx levels, oxidant concentrations, temperature, solar radiation and pre-existing OA mass encountered in the troposphere.
2.2 The explicit representation of SOA formation
Aromatic and long-chain aliphatic hydrocarbons emitted by anthropogenic activities, and isoprene and terpenic compounds emitted by biogenic sources, are known to be major SOA precursors (e.g. Carlton et al., 2009; Kroll and Seinfeld, 2008; Nordin et al., 2013; Tsigaridis et al., 2014; Zhao et al., 2016). Explicit oxidation chemical schemes were generated with the GECKO-A modelling tool for five linear alkanes (decane, tetradecane, octadecane, docosane and hexacosane), five linear 1-alkenes (decene, tetradecene, octadecene, docosene and hexacosene), five aromatic compounds (benzene, toluene, m-xylene, o-xylene and p-xylene) and three terpenic compounds (α-pinene, β-pinene and limonene). The GECKO-A modelling tool does not handle the polycyclic aromatic structures, and the current oxidation protocol is not up to date to represent SOA formation from isoprene oxidation. SOA formation from polycyclic aromatic hydrocarbons and isoprene oxidation has thus not been studied here.
The GECKO-A tool is a computer programme that automatically writes chemical schemes on the basis of a prescribed protocol. Elementary data are taken from laboratory studies if available and structure/property relationships if not. The protocol implemented in GECKO-A is described by Aumont et al. (2005), with chemistry updates for gas-phase oxidation performed by Valorso et al. (2011) and Aumont et al. (2012, 2013). The evolution of alkoxy radicals through decomposition and isomerization is estimated using the structure–property relationship developed by Vereecken et al. (2009, 2010), as described by La et al. (2016). In the current version, GECKO-A generates explicit chemical schemes for non-aromatic species and uses the Master Chemical Mechanism (MCM, version 3.3.1) to describe the chemistry of species including an aromatic structure (Jenkin et al., 2003; Bloss et al., 2005).
The explicit description of the oxidation of organic precursors involves millions of secondary species and reactions. Explicit chemical schemes cannot be solved for precursors having more than eight atoms of carbon, even in a box model. Simplifications are therefore needed. In this study, the gaseous reactivity of species having a saturation vapour pressure lower than 10−13 atm is not considered as these species are dominantly in the condensed phase. Lumping of position isomers is also allowed if the production yield of a species is lower than 10−3 (Valorso et al., 2011). RO2 mainly reacts with NO, HO2 and other RO2. In our scenario, the RO2 family is dominated by CH3O2. Among the self RO2 reactions, only the RO2+CH3O2 are considered when chemical schemes are generated. Furthermore, writing of the oxidation scheme is stopped after formation of the 15th-generation stable products.
The gas–particle partitioning of each stable organic compound was implemented as described in Camredon et al. (2007). Phase partitioning is described by an absorption process following Raoult's law (e.g. Pankow, 1994):
where and are the concentration of the species i in the particulate and the gas phase, respectively, R is the gas constant, T the temperature, the mean molar weight of the OA (250 g mol−1), the saturation vapour pressure of the species i and γi the activity coefficient of the species i in the condensed phase. The condensed phase is considered homogeneous, ideal (γi=1), inert and at equilibrium with the gas phase. Saturation vapour pressure of each organic compound is estimated using the Nannoolal method (Nannoolal et al., 2004, 2008). Equation (2) is solved for the set of organic species using a simple iterative method (Pankow, 1994). For the gas-phase oxidation, time integration is solved using the two-step solver (Verwer and VanLoon, 1994; Verwer et al., 1996).
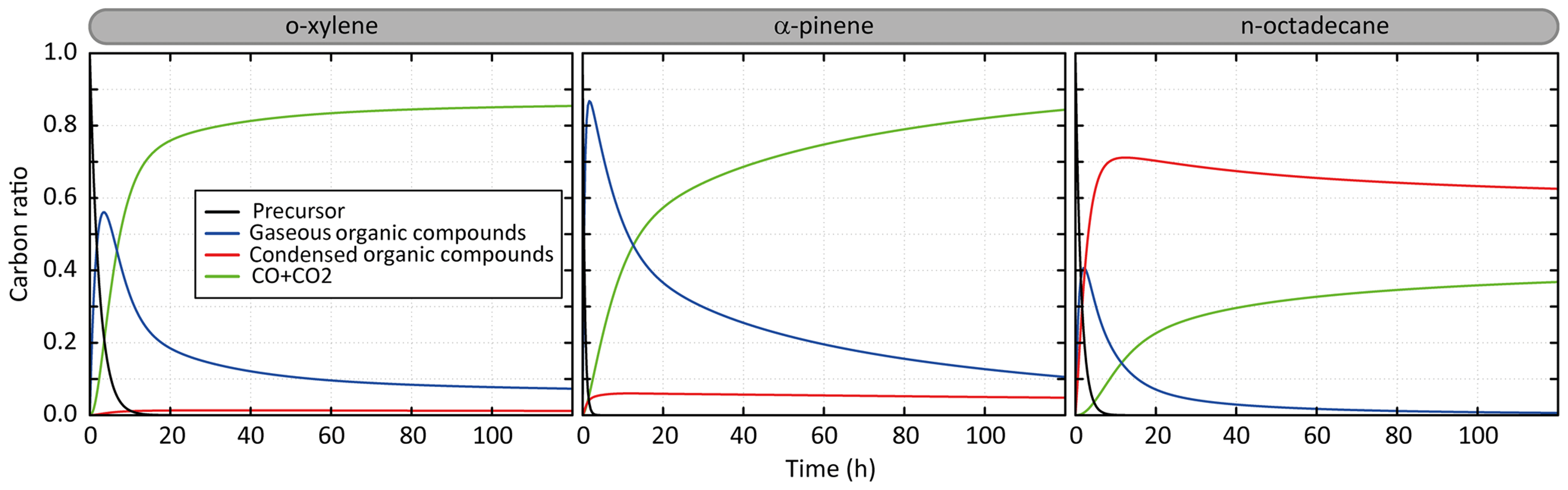
Figure 2Temporal evolution of the simulated carbon distribution between the precursor, CO and CO2, and gaseous and condensed organic compounds. Simulated results are shown for o-xylene, α-pinene and n-octadecane for the scenario performed at a temperature of 298 K, a zenith angle of 50∘, a Coa of 1 µg m−3, 40 ppb of ozone and a RRR of 90 %.
3.1 Carbon distribution and SOA formation
Figure 2 presents the temporal evolution of the carbon during the oxidation of a precursor in the scenario performed at a temperature of 298 K, a zenith angle of 50∘, a Coa of 1 µg m−3, 40 ppb of ozone and a RRR of 90 %. This scenario is called hereafter the “reference” scenario. Examples are shown for o-xylene, α-pinene and n-octadecane oxidation. Under these average conditions, the precursors are oxidized in 10, 6 and 2.5 h for o-xylene, n-octadecane and α-pinene, respectively. The carbon is first dominantly in the form of secondary gaseous organic compounds (around 55 %, 85 % and 40 % at the gaseous maximum for o-xylene, α-pinene and n-octadecane, respectively). For o-xylene, these gas-phase intermediates are mainly transformed into CO and CO2, with less than 1 % of the carbon present as secondary OA. After 5 days of oxidation, the carbon mainly ends in the form of CO and CO2 (∼85 %), the remaining fraction being mostly gas-phase organic carbon. The complete oxidation of α-pinene into CO and CO2 takes longer than for o-xylene. During the oxidation, up to 7 % of the carbon is in SOA. After 5 days, the carbon initially present as α-pinene mainly ends in the form of CO and CO2 (∼85 %); the remaining fraction of the carbon is gaseous at 10 % and condensed at 5 %. For n-octadecane, the full oxidation of the carbon into CO and CO2 is slow. Gas-phase intermediates produce dominantly low-volatility species which transfer to the condensed phase. A maximum carbon fraction of around 70 % is in the particle phase after 10 h of oxidation. The carbon fraction in SOA is slowly transferred back to the gas phase when gaseous oxidation proceeds, leading ultimately to the formation of CO and CO2. The oxidation of the carbon into CO and CO2 occurs only by gas-phase oxidation here as the particle phase is represented as inert in this model configuration. After 5 days of oxidation, the carbon is mainly in the aerosol (∼62 %) and in the form of CO and CO2 (∼38 %).
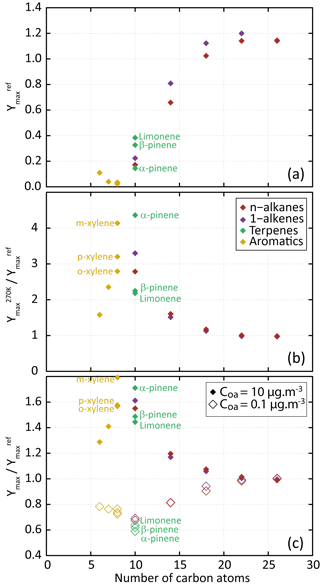
Figure 3(a) Dependence of Ymax on the precursor's carbon number for the scenario performed at a temperature of 298 K, a zenith angle of 50∘, a Coa of 1 µg m−3, 40 ppb of ozone and a RRR of 90 %. (b) Dependence of on the precursor's carbon number. (c) Dependence of (open symbols) and (filled symbols) on the precursor's carbon number.
3.2 Influence of environmental parameters on SOA formation
Figure 3a shows the evolution of the maximum SOA yield (Ymax, calculated as the mass ratio of the produced SOA to the reacted precursor quantity) as a function of the number of carbons in the parent compound. Results are shown for the reference scenario; the maximum SOA yield is noted . For a given 1-alkane or 1-alkene series, simulated SOA yield increases with the length of the precursor's carbon skeleton. This behaviour, as well as the simulated yields, is consistent with observations from chamber experiments during n-alkane and 1-alkene oxidation at ambient temperature and high NOx (e.g. Lim and Ziemann, 2009; Matsunaga et al., 2009). Ymax reaches a plateau of about 1.2 for precursor chain lengths higher than 18 carbons, independently of their carbon number. These precursors lead to the formation of first-generation compounds being dominantly in the condensed phase (e.g. Aumont et al., 2012). For aromatic compounds, simulated Ymax decreases with increasing number of methyl groups. This Ymax evolution with the aromatic precursor's structure is consistent with experimental trends observed in chambers (e.g. Ng et al., 2007; Li et al., 2016). For terpenes, simulated Ymax increases in the following precursor's order: α-pinene, β-pinene and limonene, in agreement with observed behaviours (e.g. Zhao et al., 2015).
The influence of temperature and pre-existing OA on Ymax is presented in Fig. 3b and c. Results are shown for a scenario in which one environmental parameter is changed from the reference scenario: the temperature from 298 to 270 K or the Coa from 1 to 0.1 or 10 µg m−3 (the maximum SOA yields are noted hereafter , and , respectively). As expected, simulation results show that aerosol yields increase when COA increases (e.g. Odum et al., 1996) and when the temperature decreases (e.g. Takekawa et al., 2003). In both cases, the highest sensitivity is simulated for species bearing between 6 and 14 carbon atoms. For these precursors, the secondary organic species contributing to SOA are semi-volatile and their partitioning depends largely on the temperature and Coa. A low sensitivity of Ymax is simulated for the species with the longest carbon skeleton (i.e. with nC>18). These low-volatility precursors rapidly form low-volatility compounds that partition dominantly to the condensed phase, regardless of environmental conditions.
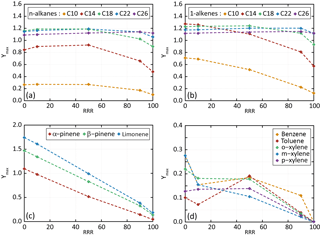
Figure 4Dependence of Ymax on RRR (here in percent) for n-alkanes (a), 1-alkene (b), terpenes (c) and aromatic species (d) for the scenarios performed at a temperature of 298 K, a zenith angle of 50∘, a Coa of 1 µg m−3 and 40 ppb of ozone. Points are connected with dashed lines to help in seeing trends of Ymax with RRR.
The influence of NOx on Ymax is presented in Fig. 4. Results are shown for the reference scenario (RRR of 90 %) and scenarios into which the RRR is changed from the reference scenario to 0 %, 10 %, 50 % and 100 %. Simulated results show that SOA yields generally decrease with the increase of NOx. These trends are in agreement with observations (e.g. Ng et al., 2007; Donahue et al., 2005). Again, a weak sensitivity to NOx is simulated for largest chain length species (i.e. with nC>18). These larger chain length compounds produce first oxidation products able to partition dominantly in the condensed phase at all NOx levels. The explicit simulations reproduce the observed tendencies of SOA yields with the precursor's structure, NOx levels, temperature and pre-existing OA mass. These agreements support their use to explore the physicochemical properties of organic compounds and as a reference for the development of reduced chemical schemes for SOA formation.
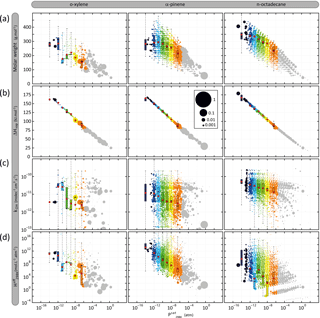
Figure 5Distribution of organic species (gaseous and particulate summed) in terms of volatility ( and (a) molar mass (Mw), (b) vaporization enthalpy (ΔHvap), (c) OH reactivity (kOH) and (d) solubility (. Simulated results are shown for o-xylene, α-pinene and n-octadecane after 6 h of oxidation for the scenario performed at a temperature of 298 K, a zenith angle of 50∘, a Coa of 1 µg m−3, 40 ppb of ozone and a RRR of 90 %. Each bubble is a species and the volume of the bubble is proportional to the carbon ratio represented by the species. The bubbles are coloured by volatility classes (see Table 2 for the bin bounds). The distribution of the properties weighted by the concentration in carbon atoms of the species in each volatility class at 6 h is represented as box plots showing the 25th, 50th and 75th percentiles, and the minimal and maximal values. Red points are the mean properties weighted by the concentration in carbon atoms of the species in each volatility class.
3.3 Physicochemical properties of organic compounds
The explicit simulations were used to explore the distribution of organic species physicochemical properties that influence OA formation, in particular
-
the molar mass (Mw), needed to convert the aerosol concentration of the species from molecular to mass units;
-
the volatility (i.e. saturation vapour pressure) that influences directly the gas–aerosol partitioning of a species. The saturation vapour pressure at a given temperature is calculated in GECKO-A using the Clausius–Clapeyron expression with Psat at 298 K and vaporization enthalpy (ΔHvap) estimated from the Nannoolal et al. method (2004, 2008);
-
the solubility (i.e. Henry's law coefficient) that influences the dry deposition of organic gases but also potentially its gas–aerosol partitioning for water-soluble species. The effective Henry's law coefficient (Heff) at 298 K is calculated in GECKO-A with the GROHME method (Raventos-Duran et al., 2010);
-
the reaction rate with OH (kOH) that drives the chemical lifetime of organic species. The OH reaction rate at 298 K of each organic compound is estimated in GECKO-A using the Kwok and Atkinson (1995) structure activity relationship with updates described by Aumont et al. (2012) if no experimental data are available.
Figure 5 presents the simulated distribution of (a) molar mass, (b) vaporization enthalpy, (c) OH reactivity and (d) solubility ( as a function of the volatility ( of organic species. Results are presented for a time step close to the maximum of secondary organic compound, after 6 h of oxidation, for the reference scenario. Examples are shown for o-xylene, α-pinene and n-octadecane oxidation. Thousands of secondary organic species spanning several orders of magnitude in properties are formed during the oxidation of a given precursor. The volatility distributions range from 10−15 to 1 atm, independently of the precursor structure. Molar mass increases with the decrease of the volatility of organic compounds, varying from around 50 to 400 g mol−1 for the highest and lowest volatile species. Simulated results show that species formed at high NOx have a molar mass higher than at low NOx (see Fig. S1 in the Supplement). Explicit simulation shows a ΔHvap increase of 12.5 kJ mol−1 per logarithm unit decrease of , independently of NOx levels (see Fig. S1). Rate constants of organic species with OH at 298 K vary between 10−13 and 10−10 molec−1 cm3 s−1. Simulations do not show a clear trend of kOH with the volatility of the species, neither with the level of NOx, kOH being scattered over 3 orders of magnitude for a given Psat and RRR. The effective Henry's law constant increases with the decrease of organic compound volatility, varying between around 1 and 1016 mol L−1 atm−1 for the highest and lowest volatile species. NOx levels do not have a significant influence on the Heff distribution of species with the volatility (see Fig. S1).
4.1 Structure of the parameterization
A VBS-type parameterization (e.g. Donahue et al., 2006) was developed on the basis of the explicit GECKO-A simulations. The parameterization, called VBS-GECKO, lumps the secondary organic compounds (SOCs) into bins of saturation vapour pressures at 298 K () and considers the following:
-
The formation of n volatility bins (VBk,i with i varying from 1 to n) from the gas-phase oxidation for each precursor k (precuk). The VBk,i values are considered to be formed from OH oxidation for all the precursors and also from O3 and NO3 oxidation for alkenes and terpenes. The reaction rate constants for the oxidation of a given precursor k (kprecuk+OH, and are taken from the GECKO-A database (see Table S1). Each VBk,i is formed with a molecular stoichiometric coefficient that depends on NOx via the RRR (, and for OH, O3 and NO3 reaction, respectively):
-
The ageing of the VBk,i from gaseous OH oxidation and photolysis redistributes the matter between the various VBk,i values.. The OH and photolysis gaseous ageing is considered for all the VBk,i values except for the lowest volatility bin, the gas-phase fraction of that bin being expected to be negligible under atmospheric conditions. The OH reaction rate constant, kOH, was set to the same value for each VBk,i. These VB reactions lead to the formation of the VBk,j with a stoichiometric coefficient depending on RRR ():
Each VBk,i (i≠n) is photolysed with a photolysis constant being proportional to the acetone one (Jacetone). The proportionality factor, ϕk, is considered to be the same for the VBk,i of a given precursor k. The VBk,i photolysis leads to a loss of matter ():
-
The partitioning of the precursor k and the VBk,i between the gas and the particle phase. The partitioning is described, as in the reference GECKO-A simulations, by an absorption process following Raoult's law and considering a homogeneous, ideal, inert condensed phase at equilibrium with the gas phase:
4.2 VBS-GECKO properties
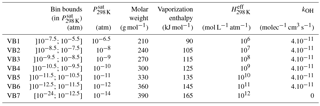
Explicit simulations were used to select the number and the range of the volatility bins and their properties (molar weight, kOH, vaporization enthalpy and Henry's law constant). Tests were performed to establish the best number and range of volatility bins to get a compromise between the reliability and the size of the VBS-GECKO parameterization. The partitioning of organic species having a lower than 10−12 atm is almost exclusively in the particulate phase under typical atmospheric conditions. Therefore, the lower volatility bin in the VBS-GECKO parameterization lumps all species having a lower than 10−12.5 atm. Similarly, organic species having a above 10−6 atm are dominantly in the gas phase under typical atmospheric conditions and volatility bin is included for species having a above 10−5.5 atm. Between these thresholds, the gas–particle partitioning of a species depends sensitively on temperature and OA load, so that a finer volatility discretization is desirable. A total of seven volatility bins were selected for the VBS-GECKO parameterization. The boundaries of the k volatility bins i, VBk,i, are the same for all the precursors k. Bin intervals at 298 K are shown in Table 2 and in Fig. 5 by the different colours of the SOC bubbles.
The properties of the k volatility bins i, VBk,i, are set to the same value for the various precursors k. Each of the VBk,i values has for assigned saturation vapour pressure the central value of its logarithmic interval (see Table 2). Molar weight, vaporization enthalpy and Henry's law constant for each bin i are set to the mean properties of the SOCs in this volatility bin (i.e. the SOC property weighted by its concentration) during the alkanes' explicit simulations (C10, C14, C18, C22 and C26). The same kOH value of 4.10−11 cm3 molec−1 s−1 is used for all the VBk,i values (except for the lowest volatility bin which is considered inert). This value is in the upper range of the SOC rate constants seen in Fig. 5 and is similar to that used earlier in VBS parameterization (e.g. Robinson et al., 2007; Grieshop et al., 2009; Hodzic et al., 2010). Note that the performance of the VBS-GECKO parameterization should only be weakly sensitive to the kOH value assigned to each VBk,i. Indeed, compensations occur during the optimization of the stoichiometric coefficients (i.e. an upper kOH value for the reactivity of the VBk,i will lead to high values of the associated with the production of the reacting VBk,i bin and low values of the associated with the production of the other bins). The properties assigned to each bin are summarized in Table 2.
In the published VBS-type parameterizations, molar weights are usually set to a value of 250 g mol−1 (e.g. Tsimpidi et al., 2010; Robinson et al., 2007). This value is smaller than the mean values provided by the explicit simulations for the less volatile bins. The vaporization enthalpy used for each bin is also generally smaller in the VBS parameterization, especially for the less volatile bins (e.g. Robinson et al., 2007; Grieshop et al., 2009; Hodzic et al., 2010; Tsimpidi et al., 2010). The difference reaches 40 kJ mol−1 for the less volatile bins. The vaporization enthalpies recently used by Hodzic et al. (2016) and derived from experimental data are however consistent with the VBS-GECKO values obtained here. Dry deposition of low-volatility organic compounds has been generally ignored in VBS models and no Henry's law coefficient was therefore assigned to volatility bins until Hodzic et al. (2014). Hodzic et al. (2014) provided Henry's law coefficient for the various volatility bins based on GECKO-A explicit simulations for anthropogenic and biogenic precursors. As expected, Henry's law coefficients provided in Table 2 agree with most of the values given in Hodzic et al. (2014), both being derived from similar types of simulations.
4.3 VBS-GECKO optimization
4.3.1 Optimization scenario and method
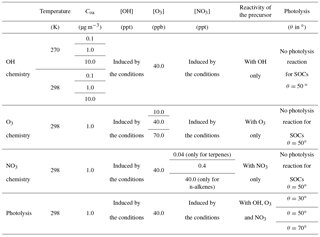
Explicit simulations were used to optimize stoichiometric coefficients and photolysis factors of the VBS-GECKO parameterization. A set of stoichiometric coefficients was optimized for each of the 18 precursors and for each RRR. The entire range of RRR is covered by linear interpolation of the stoichiometric coefficients. Each set (k, RRR) of stoichiometric coefficients is optimized using the explicit simulations presented in Sect. 2, with some reactions turned successively off in the GECKO-A chemical schemes to specifically evaluate the coefficients related to the reaction with each oxidant (OH, O3, NO3) and photolysis, as described hereafter and summarized in Table 3.
For each n-alkane and aromatic k and for each RRR, the seven () and 42 (; ) coefficients were optimized simultaneously using six explicit simulations performed with a zenith angle of 50∘, 40 ppb of ozone, at two temperatures (270 and 298 K) and for three values of Coa (0.1, 1 and 10 µg m−3). For these optimizations, the photolysis reactions of secondary organic compounds were removed in both the GECKO-A and the VBS-GECKO chemical schemes.
For each 1-alkene and terpene k, and for each RRR, the seven (), the seven (), the seven () and the 42 (; ) coefficients were optimized simultaneously on 11 explicit simulations and considering in each simulation the oxidation of the precursor k with a single oxidant only (either OH, O3 or NO3). For the simulations taking into account the precursor reaction with OH only, the same set of six simulations described above for alkanes and aromatics was used, i.e. a zenith angle of 50∘, 40 ppb of ozone, at two temperatures (270 and 298 K) and for three values of Coa (0.1, 1 and 10 µg m−3). For the simulations accounting only for the precursor reaction with O3, a set of three simulations was used with three O3 concentrations (10, 40 and 70 ppb), at 298 K and a Coa of 1 µg m−3. For the simulations accounting only for the precursor reaction with NO3, a set of two simulations was used with 40 ppb of ozone, at 298 K, a Coa of 1 µg m−3 and for two NO3 concentrations (0.04 and 0.4 ppt for the terpenes, 0.4 and 40 ppt for the 1-alkenes). For each oxidant case, the reactions of the precursor with the other oxidants and the photolysis reaction of secondary organic compounds were turned off in both the GECKO-A and the VBS-GECKO chemical schemes.
The set of 49 stoichiometric coefficients for the alkane and aromatic precursors and the 63 stoichiometric coefficients for the 1-alkenes and terpenes were optimized for five RRRs (0, 0.1, 0.5, 0.9 and 1). After the optimization of these coefficients, the photolysis factor ϕk was finally optimized for each of the 18 precursors k. Each photolysis factor ϕk does not depend on RRR and was optimized simultaneously using the 15 simulations performed for a precursor k with three values of zenith angle (30, 50 and 70∘) for the five RRRs, 40 ppb of ozone, at 298 K and a Coa of 1 µg m−3. The optimization was performed for different durations depending on the lifetime of the studied precursor with OH. For the less reactive species (aromatic compounds and n-alkanes), the optimization was realized for a duration of 5 days. For 1-alkenes and terpenes, the optimization duration was 2 and 1 days, respectively. The time step used for the optimization was set to 20 min.
The optimizations were performed minimizing the root mean square error (RMSE) between the GECKO-A and VBS-GECKO simulated evolutions of the total mass concentration of each of the seven volatility bins (particulate and gaseous summed). The RMSE was calculated on the entire duration of a set of reference simulations as
where and are the mass of the volatility bin i at the time step number j simulated with the GECKO-A and the VBS-GECKO, respectively, ntime the number of time steps over the reference simulations and n the total number of bins. The optimization was run following a bound optimization by quadratic approximation (BObyQA) method (Powell, M., 2009) under the R software (R Core Team, 2017). The fitted stoichiometric coefficients were bounded between 0 and 1, and the photolysis factors between 0 and 100. The iterative process to minimize the RMSE stops when none of the parameters vary more than 0.2 % between two successive iterations.
For each n-alkane or aromatic precursor, the 246 parameters (49 stoichiometric coefficients for each of the five RRRs plus one photolysis coefficient) were adjusted on a total of 45 learning simulations (six simulations for each of the five RRRs plus 15 simulations for the photolysis coefficient), leading to a total of 16 200 simulated time steps (45 simulation of 120 h each with three time steps per hour) providing distinct mass concentrations for the seven volatility bins. Similarly, for each 1-alkene or terpene, the 316 parameters (63 stoichiometric coefficients for each of the five RRRs plus one photolysis coefficient) were optimized on 70 learning simulations (11 simulations for each of the five RRRs plus 15 simulations for the photolysis coefficient) leading to a total 10 080 simulated time steps for 1-alkene (70 simulations of 48 h each with three time steps per hour) and 5040 for terpene (70 simulations of 24 h each with three time steps per hour). The fitted parameters of the VBS-GECKO parameterization are provided in Table S1.
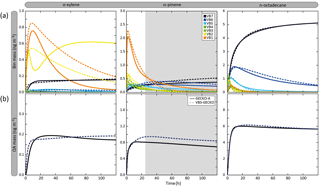
Figure 6Temporal evolution of volatility bin mass concentration (a) and organic aerosol mass (b) simulated with GECKO-A (continuous lines) and VBS-GECKO (dashed lines). Simulated results are shown for o-xylene, α-pinene and n-octadecane for the scenario performed at a temperature of 298 K, a zenith angle of 50∘, a Coa of 1 µg m−3, 40 ppb of ozone and a RRR of 90 %. Parameters have been optimized on duration represented by white background on the figure.
4.3.2 Optimization results
Figure 6 presents the temporal evolution of the mass concentration of each volatility bin (gas and particle summed) and of OA in the GECKO-A and VBS-GECKO simulations during the oxidation of a precursor. Results are shown for the simulations performed at a temperature of 298 K, a zenith angle of 50∘, a Coa of 1 µg m−3, 40 ppb of ozone and a RRR of 90 % (i.e. in the scenario previously called the reference scenario in Sect. 3.1). Examples are given for o-xylene, α-pinene and n-octadecane oxidations. Note that, in Fig. 6, organic species with values greater than the VBS-GECKO volatility bin upper boundary (i.e. 10−5.5 atm; see Fig. 5) are not reported. At the beginning of the oxidation, GECKO-A explicit simulations show that first oxidation species are mainly in the highest volatility bins of the VBS-GECKO volatility range: (1) in VB1 and VB2 for o-xylene, (2) mainly in VB1 but also in VB2, VB3 and VB4 for α-pinene and (3) in VB2 and VB3 for n-octadecane. The oxidation of these first oxidation species leads to the formation of further generation species with a lower volatility, increasing the VB5, VB6 and VB7 mass concentration. As oxidation proceeds, the concentration of the volatility bins generally increases to reach a maximum before decreasing. Nevertheless, this behaviour is not observed for
-
the VB7 temporal evolution. In this version of the GECKO-A tool, VB7 has no chemical sink (see above) and the concentration of the VB7 therefore increases to reach a plateau.
-
the VB2 temporal evolution of o-xylene. Two species contribute to most of this bin in the explicit simulations: a dinitrocresol and a dinitro-dimethyl-phenol. Under the conditions of this simulation, these second-generation species have long lifetimes with OH and NO3 (hundreds of hours), and therefore the chemical loss of VB2 cannot be observed on the timescale of the simulation.
Figure 6 shows that the structure of the VBS-GECKO parameterization reproduces the temporal evolution of the seven volatility bins' mass concentration during this learning simulation. The VBS-GECKO parameterization shows however discrepancies in representing the evolution of the highest volatility bins (VB1 and VB2). The temporal evolution of organic species in VB1 and VB2 is driven by the reactivity of species having values greater than 10−5.5 atm. As no volatility bin is included for these species in VBS-GECKO, the VB1 and VB2 mass evolution is less well reproduced than the bins of lower volatility. Species in VB1 and VB2 do not, however, partition substantially into the condensed phase except under heavy aerosol loading and low temperature for VB2. The reliability of the optimization was evaluated comparing the temporal evolution of OA mass (which is not directly optimized during the fitting process) between GECKO-A and VBS-GECKO simulations (see Fig. 6). The relative root mean square error (RRMSE) was calculated a posteriori for the aerosol mass concentration as
with and are the mass concentration of OA formed at each time step j with the GECKO-A and the VBS-GECKO, respectively, and ntime the total number of time steps. The temporal evolution of OA mass is well reproduced by the parameterization for o-xylene, α-pinene and n-octadecane, with a RRMSE lower than 20 % (10.2 %, 17.1 % and 1.8 % for o-xylene, α-pinene and n-octadecane, respectively).
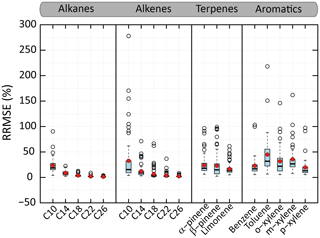
Figure 7Distributions of the RRMSE on organic aerosol mass concentration calculated between VBS-GECKO and GECKO-A on the learning simulations. The bottom and top of the boxes are the first and third quartiles; the bands inside the boxes represent the medians. The ends of the whiskers represent the lowest RRMSE still within 1.5 times the interquartile range (IQR) of the lower quartiles and the highest RRMSE still within 1.5 IQR of the upper quartiles. Red points represent the mean values and empty points the outliers. There are 45 simulations for n-alkane or aromatics and 70 for 1-alkene or terpene. Time steps for which the OA mass simulated with GECKO-A is under a threshold of µg m−3 (i.e. a SOA yield lower than around 1 %) are not considered in RRMSE calculation.
Figure 7 shows the distributions of the RRMSE for the OA mass concentration for the various learning simulations and for each precursor. For the n-alkanes and 1-alkenes, the RRMSE increases when the carbon chain length decreases. The mean RRMSE on OA mass evolutions is less than 5 % for n-alkanes and 1-alkenes bearing more than 14 carbon atoms. It reaches 23 % and 31 % for n-decane and 1-decene. For terpenes, the mean of RRMSEs are of 24 %, 23 % and 17 % for α-pinene, β-pinene and limonene, respectively. For the aromatic precursors, the mean of RRMSEs are of 23 %, 45 %, 32 %, 36 % and 20 % for benzene, toluene, o-, m- and p-xylene, respectively. The VBS-GECKO parameterization reproduces SOA masses with a RRMSE lower than 50 % for more than 90 % of the learning simulations.
4.4 VBS-GECKO evaluation
4.4.1 Evaluation scenario
Results of the GECKO-A simulations performed in the previous sections were used as a training dataset to fit the coefficients of the parameterization. Here, new simulations are conducted with GECKO-A to produce a validation dataset to assess VBS-GECKO. New box model scenarios were therefore designed for that purpose. These scenarios use a mixture of precursors and environmental conditions not encountered during the training phase, including variations of environmental parameters with time (Coa, temperature, photolysis and NOx levels). Scenarios were run for two constant COA values (2 and 20 µg m−3), two types of meteorological conditions for temperature, relative humidity and zenith angle (a “summer” and a “winter” case, called hereafter SUM and WIN, respectively) and two NOx conditions (a “high NOx” and a “low NOx” case, called hereafter HNOx and LNOx, respectively). A total of eight scenarios were run.
Diurnal temperature profiles were represented by a sinusoid function with a 5 K amplitude, a maximum reached at 14:00 LT and average values of 290 and 275 K for the SUM and WIN scenarios, respectively. Diurnal photolysis frequencies were computed for midlatitudes using the TUV model (Madronich and Flocke, 1999) with zenith angle variations corresponding to 1 July for the SUM case and 1 January for the WIN scenario. The relative humidity was set to 60 % and 85 % for the SUM and WIN scenarios, respectively. For the HNOx and LNOx cases, the initial concentration of NOx was set at 50 and 0.5 ppb, respectively. The OH lifetime with respect to the reaction with the surrogate VOC was again set to 1 s. Chemical concentrations were also fixed for CO, methane and O3 at 120, 1750 and 40 ppb, respectively. The evaluation scenarios started at 12:00 LT and lasted 5 days. Simulated evolutions of NO, NO2, NO3, OH, HO2 and O3 concentrations for the HNOx_WIN, HNOx_SUM, LNOx_WIN and LNOx_SUM scenarios are presented in Figs. S2–S5.
For each scenario, three mixtures of precursors summing up to an initial concentration of 10 pptC were considered: a “biogenic”, an “intermediate” and an “anthropogenic” case (called hereafter BIO, INT and ANT, respectively). In the BIO case, biogenic compounds (i.e. α-pinene, β-pinene and limonene) represent 90 % in carbon of the initial mixture and anthropogenic compounds (i.e. the five alkanes, the five alkenes and the five aromatic compounds) the remaining 10 %. In the INT and ANT cases, the biogenic∕anthropogenic ratio in carbon is 50 %∕50 % and 10 %∕90 %, respectively. In the biogenic or anthropogenic family, each species was arbitrarily set to the same level (in pptC units).
A total of 24 simulations (eight environmental scenarios using each three sets of initial mixture of precursors) were run with the GECKO-A chemical scheme and VBS-GECKO parameterization.
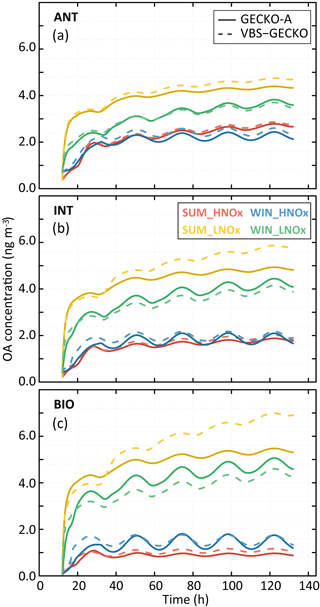
Figure 8Simulated organic aerosol (OA) mass with GECKO-A (continuous lines) and VBS-GECKO (dashed lines), for the different evaluation scenarios using Coa=2 µg m−3. Panel (a) presents results for the ANT cases, (b) for the INT cases and (c) for the BIO cases. The different colours represent the different scenarios (see text).
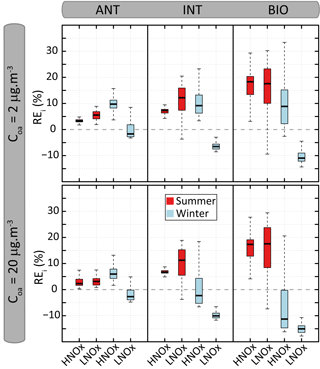
Figure 9Distribution of the relative errors (REi) on organic aerosol mass concentration calculated between VBS-GECKO and GECKO-A for the 24 evaluation scenarios. The bottom and top of the boxes are the first and third quartiles; the bands inside the boxes represent the medians. The ends of the whiskers represent the lowest and the highest REi values. There are 361 time steps for each evaluation scenario.
4.4.2 Evaluation results
Figure 8 shows the temporal evolution of the OA mass concentrations formed according to the GECKO-A and the VBS-GECKO, for the different evaluation scenarios performed with a Coa of 2 µg m−3. Temporal evolutions simulated with a Coa of 20 µg m−3 are presented in Fig. S6. Figure 9 presents the distribution of the relative errors on the OA mass concentrations for the 24 evaluation scenarios. The relative error (RE) is calculated at each time step i as
where and are the mass concentrations of OA formed at each time step i with the GECKO-A and the VBS-GECKO, respectively.
Reference GECKO-A simulations show generally (1) a fast increase of OA mass concentration during the first 10 h of oxidation, (2) a clear diurnal cycle of OA concentration linked to the temperature variations, with a larger amplitude for the WIN than for the SUM scenarios, (3) higher simulated OA concentrations for the LNOx scenarios with maximum concentration obtained during the summer, (4) a slight increase of OA concentrations with the increase of anthropogenic precursors in the HNOx scenarios and with the increase of biogenic precursors in the LNOx scenarios. These trends are well represented by the VBS-GECKO parameterization as well as the orders of magnitude of the OA concentrations (mean errors between ±20 %). Low errors are simulated for the ANT mixture (with %). The errors generally increase with the increase of biogenic precursors in the mixture (with % for the BIO mixture). In particular, for the summer LNOx scenarios, VBS-GECKO overestimates OA mass from the second day. This overestimation increases with the length of the simulation.
The origin of these errors is not entirely clear, as the role of many important driving variables is masked by the training and fitting procedures. It is, however, possible to list some of the major simplifications and approximations that were made in developing the VBS-GECKO parameterization: (i) discretization into seven decadal bins (rather than continuous vapour pressure distribution, for example); (ii) use of the same matrix of VB plus OH stoichiometric coefficients to represent the reactivity of organic species formed from the oxidation of the precursor with OH, O3 and NO3; (iii) use of a single photolytic scale factor (relative to acetone photolysis) to represent the overall photolysis of a complex mixture containing many photo-labile species; (iv) discretization into five RRRs with separate optimization and linear interpolation to cover the entire range; and (v) selected simulation duration used for the optimization that is expected to influence the weight given at first or further generation products. More detailed consideration of these important parameters presents a clear opportunity to further improve the parameterization.
The GECKO-A modelling tool was used to explore SOA formation from the oxidation of various hydrocarbons in a box model under stationary state scenarios representative of environmental conditions. The set of parent hydrocarbons includes n-alkanes and 1-alkenes with 10, 14, 18, 22 and 26 carbon atoms, α-pinene, β-pinene and limonene, benzene, toluene, o-xylene, m-xylene and p-xylene. The developed environmental scenarios allow investigation of the sensitivity of SOA formation to changes of physical (photolysis, Coa, T, relative humidity) and chemical () conditions. Simulated trends of maximum SOA yields are consistent with the literature data. In particular, Ymax increases with the carbon skeleton size of the parent the n-alkane or 1-alkenes, from 0.2 for the C10 to a plateau value of 1.2 for the C>18. For the aromatic compounds, Ymax slightly decrease with number of methyl groups with values below 0.15. For terpenes, simulated Ymax increases in the following precursor's order: α-pinene, β-pinene and limonene. As expected, Ymax increases when temperature decreases and COA increases. NOx conditions drive the distributions of secondary organic species and changes substantially the volatility distribution of the species. Simulated SOA yields generally decrease with the increase of NOx (or RRR). SOA yields from terpene are particularly sensitive to NOx levels, with values in the 1.1–1.75 range under low NOx conditions (RRR close to 0) to values in the 0.05–0.2 range under high NOx conditions (RRR close to 1). SOA yields for species having a large carbon skeleton (i.e. with nC>18) show a low sensitivity to temperature, COA and NOx regimes as they rapidly form compounds that partition dominantly to the condensed phase. Explicit simulations were used to explore the distribution of the millions of secondary organic species formed during the oxidation of the precursors in term of molar mass, vaporization enthalpy, OH reaction rate and Henry's law coefficient.
Simulation results obtained with the GECKO-A modelling tool were used as a reference to fit a VBS-type parameterization. The VBS-GECKO parameterization is designed for 18 selected hydrocarbons and includes OH oxidation for all the hydrocarbons, as well as NO3 and O3 oxidation for the terpenes and 1-alkenes. For each hydrocarbon, seven volatility bins are considered, ageing by reaction with OH, photolysis and partitioning according to Raoult's law. The dependence of SOA formation on NOx levels is represented by a linear interpolation of different sets of parameters optimized for various RRRs. Properties of the bins, i.e. molar weight, vaporization enthalpy, OH rate constants and Henry's law coefficient, are selected from the reference explicit simulations. The evaluation of the parameterization shows that VBS-GECKO captures the dynamic of SOA formation for a large range of conditions with a mean relative error on OA mass temporal evolution lesser than 20 % compared to explicit simulations.
Explicit simulations of organic compound oxidation provided by GECKO-A have been previously used to develop a reduced chemical scheme for the chemistry (Szopa et al., 2005) as well as to develop reduced parameterizations for SOA formation from semi-volatile and intermediate volatility n-alkanes (Hodzic et al., 2016). For the first time in this study, a reduction protocol has been developed and evaluated to optimize SOA parameterizations from explicit simulations for a large number of precursor species and under various environmental conditions. The optimization procedure has been automated to facilitate the update of the VBS-GECKO on the basis of the future GECKO-A versions, its extension to other precursors and/or its modification to carry additional information (e.g. optical properties, hygroscopicity, N∕C ratio). The implementation and the evaluation of VBS-GECKO in a 3-D model are the purpose of a companion paper.
The explicit GECKO-A dataset used to optimize the VBS-GECKO parameterization has been made available on Zenodo: https://zenodo.org/record/1402601/ (last access: 5 September 2018).
The supplement related to this article is available online at: https://doi.org/10.5194/acp-18-13411-2018-supplement.
VL conducted the simulations, the optimizations and the evaluations. AH contributed to the development of the methodology. All the authors contributed to design the research, to interpret the data and to write the article.
The authors declare that they have no conflict of interest.
This work was financially supported by the French Environment and Energy
Management Agency (ADEME) and INERIS. We also thank French Ministry of
Ecology for its financial support. This publication was developed under
assistance agreement no. 83587701-0 awarded by the U.S. Environmental
Protection Agency to A. Hodzic. It has not been formally reviewed by EPA.
The views expressed in this document are solely those of authors and do not
necessarily reflect those of the Agency.
Edited by: Markus Petters
Reviewed by: two anonymous referees
Aumont, B., Szopa, S., and Madronich, S.: Modelling the evolution of organic carbon during its gas-phase tropospheric oxidation: development of an explicit model based on a self generating approach, Atmos. Chem. Phys., 5, 2497–2517, https://doi.org/10.5194/acp-5-2497-2005, 2005.
Aumont, B., Valorso, R., Mouchel-Vallon, C., Camredon, M., Lee-Taylor, J., and Madronich, S.: Modeling SOA formation from the oxidation of intermediate volatility n-alkanes, Atmos. Chem. Phys., 12, 7577–7589, https://doi.org/10.5194/acp-12-7577-2012, 2012.
Aumont, B., Camredon, M., Mouchel-Vallon, C., La, S., Ouzebidour, F., Valorso, R., Lee-Taylor, J., and Madronich, S.: Modeling the influence of alkane molecular structure on secondary organic aerosol formation, Faraday Discuss., 165, 105, https://doi.org/10.1039/c3fd00029j, 2013.
Bloss, C., Wagner, V., Jenkin, M. E., Volkamer, R., Bloss, W. J., Lee, J. D., Heard, D. E., Wirtz, K., Martin-Reviejo, M., Rea, G., Wenger, J. C., and Pilling, M. J.: Development of a detailed chemical mechanism (MCMv3.1) for the atmospheric oxidation of aromatic hydrocarbons, Atmos. Chem. Phys., 5, 641–664, https://doi.org/10.5194/acp-5-641-2005, 2005.
Boucher, O., Randall, D., Artaxo, P., Bretherton, C., Feingold, G., Forster, P., Kerminen, V.-M., Kondo, Y., Liao, H., Lohmann, U., Rasch, P., Satheesh, S. K., Sherwood, S., Stevens, B., and Zhang, X. Y.: Clouds and Aerosols, in Climate Change 2013 – The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., 571–658, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA., 2013.
Boyd, A. A., Flaud, P. M., Daugey, N., and Lesclaux, R.: Rate constants for RO2 + HO2 reactions measured under a large excess of HO2, J. Phys. Chem. A, 107, 818–821, https://doi.org/10.1021/jp026581r, 2003.
Camredon, M., Aumont, B., Lee-Taylor, J., and Madronich, S.: The SOA/VOC/NOx system: an explicit model of secondary organic aerosol formation, Atmos. Chem. Phys., 7, 5599–5610, https://doi.org/10.5194/acp-7-5599-2007, 2007.
Carlton, A. G., Wiedinmyer, C., and Kroll, J. H.: A review of Secondary Organic Aerosol (SOA) formation from isoprene, Atmos. Chem. Phys., 9, 4987–5005, https://doi.org/10.5194/acp-9-4987-2009, 2009.
Couvidat, F. and Sartelet, K.: The Secondary Organic Aerosol Processor (SOAP v1.0) model: a unified model with different ranges of complexity based on the molecular surrogate approach, Geosci. Model Dev., 8, 1111–1138, https://doi.org/10.5194/gmd-8-1111-2015, 2015.
Couvidat, F., Debry, É., Sartelet, K., and Seigneur, C.: A hydrophilic/hydrophobic organic (H2O) aerosol model: Development, evaluation and sensitivity analysis, J. Geophys. Res., 117, D10304, https://doi.org/10.1029/2011JD017214, 2012.
de Gouw, J. A., Middlebrook, A. M., Warneke, C., Goldan, P. D., Kuster, W. C., Roberts, J. M., Fehsenfeld, F. C., Worsnop, D. R., Canagaratna, M. R., Pszenny, A. A. P., Keene, W. C., Marchewka, M., Bertman, S. B., and Bates, T. S.: Budget of organic carbon in a polluted atmosphere: Results from the New England Air Quality Study in 2002, J. Geophys. Res., 110, D16305, https://doi.org/10.1029/2004JD005623, 2005.
Donahue, N. M., Huff Hartz, K. E., Chuong, B., Presto, A. A., Stanier, C. O., Rosenhorn, T., Robinson, A. L., and Pandis, S. N.: Critical factors determining the variation in SOA yields from terpene ozonolysis: A combined experimental and computational study, Faraday Discuss., 130, 295–309, https://doi.org/10.1039/b417369d, 2005.
Donahue, N. M., Robinson, a. L., Stanier, C. O., and Pandis, S. N.: Coupled partitioning, dilution, and chemical aging of semivolatile organics, Environ. Sci. Technol., 40, 2635–2643, https://doi.org/10.1021/es052297c, 2006.
Donahue, N. M., Epstein, S. A., Pandis, S. N., and Robinson, A. L.: A two-dimensional volatility basis set: 1. organic-aerosol mixing thermodynamics, Atmos. Chem. Phys., 11, 3303–3318, https://doi.org/10.5194/acp-11-3303-2011, 2011.
Donahue, N. M., Kroll, J. H., Pandis, S. N., and Robinson, A. L.: A two-dimensional volatility basis set – Part 2: Diagnostics of organic-aerosol evolution, Atmos. Chem. Phys., 12, 615–634, https://doi.org/10.5194/acp-12-615-2012, 2012.
Gelencsér, A., May, B., Simpson, D., Sánchez-Ochoa, A., Kasper-Giebl, A., Puxbaum, H., Caseiro, A., Pio, C., and Legrand, M.: Source apportionment of PM2.5 organic aerosol over Europe: Primary/secondary, natural/anthropogenic, and fossil/biogenic origin, J. Geophys. Res., 112, D23S04, https://doi.org/10.1029/2006JD008094, 2007.
Grosjean, D.: In situ organic aerosol formation during a smog episode: Estimated production and chemical functionality, Atmos. Environ., 26A, 953–963, 1992.
Han, S., Bian, H., Zhang, Y., Wu, J., Wang, Y., Tie, X., Li, Y., Li, X., and Yao, Q.: Effect of Aerosols on Visibility and Radiation in Spring 2009 in Tianjin, China, Aerosol Air Qual. Res., 12, 211–217, https://doi.org/10.4209/aaqr.2011.05.0073, 2012.
Hansen, R. F., Griffith, S. M., Dusanter, S., Rickly, P. S., Stevens, P. S., Bertman, S. B., Carroll, M. A., Erickson, M. H., Flynn, J. H., Grossberg, N., Jobson, B. T., Lefer, B. L., and Wallace, H. W.: Measurements of total hydroxyl radical reactivity during CABINEX 2009 – Part 1: field measurements, Atmos. Chem. Phys., 14, 2923–2937, https://doi.org/10.5194/acp-14-2923-2014, 2014.
Heald, C. L., Jacob, D. J., Park, R. J., Russell, L. M., Huebert, B. J., Seinfeld, J. H., Liao, H., and Weber, R. J.: A large organic aerosol source in the free troposphere missing from current models, Geophys. Res. Lett., 32, L18809, https://doi.org/10.1029/2005GL023831, 2005.
Hodzic, A., Jimenez, J. L., Madronich, S., Canagaratna, M. R., DeCarlo, P. F., Kleinman, L., and Fast, J.: Modeling organic aerosols in a megacity: potential contribution of semi-volatile and intermediate volatility primary organic compounds to secondary organic aerosol formation, Atmos. Chem. Phys., 10, 5491–5514, https://doi.org/10.5194/acp-10-5491-2010, 2010.
Hodzic, A., Aumont, B., Knote, C., Lee-Taylor, J., Madronich, S., and Tyndall, G.: Volatility dependenceof Henry's law constants of condensableorganics: Application to estimatedepositional loss of secondary organicaerosols, Geophys. Res. Lett., 41, 4795–4804, https://doi.org/10.1002/2014GL060649, 2014.
Im, U., Bianconi, R., Solazzo, E., Kioutsioukis, I., Badia, A., Balzarini, A., Baró, R., Bellasio, R., Brunner, D., Chemel, C., Curci, G., Denier van der Gon, H., Flemming, J., Forkel, R., Giordano, L., Jiménez-Guerrero, P., Hirtl, M., Hodzic, A., Honzak, L., Jorba, O., Knote, C., Makar, P. A., Manders-Groot, A., Neal, L., Pérez, J. L., Pirovano, G., Pouliot, G., San Jose, R., Savage, N., Schroder, W., Sokhi, R. S., Syrakov, D., Torian, A., Tuccella, P., Wang, K., Werhahn, J., Wolke, R., Zabkar, R., Zhang, Y., Zhang, J., Hogrefe, C., and Galmarini, S.: Evaluation of operational online-coupled regional air quality models over Europe and North America in the context of AQMEII phase 2, Part II: Particulate matter, Atmos. Environ., 115, 421–441, https://doi.org/10.1016/j.atmosenv.2014.08.072, 2015.
Jenkin, M. E., Saunders, S. M., and Pilling, M. J.: The tropospheric degradation of volatile organic compounds: a protocol for mechanism development, Atmos. Environ., 31, 81–104, https://doi.org/10.1016/S1352-2310(96)00105-7, 1997.
Jenkin, M. E., Saunders, S. M., Wagner, V., and Pilling, M. J.: Protocol for the development of the Master Chemical Mechanism, MCM v3 (Part B): tropospheric degradation of aromatic volatile organic compounds, Atmos. Chem. Phys., 3, 181–193, https://doi.org/10.5194/acp-3-181-2003, 2003.
Jimenez, J. L., Canagaratna, M. R., Donahue, N. M., Prevot, A. S. H., Zhang, Q., Kroll, J. H., DeCarlo, P. F., Allan, J. D., Coe, H., Ng, N. L., Aiken, A. C., Docherty, K. S., Ulbrich, I. M., Grieshop, A. P., Robinson, A. L., Duplissy, J., Smith, J. D., Wilson, K. R., Lanz, V. A., Hueglin, C., Sun, Y. L., Tian, J., Laaksonen, A., Raatikainen, T., Rautiainen, J., Vaattovaara, P., Ehn, M., Kulmala, M., Tomlinson, J. M., Collins, D. R., Cubison, M. J., Dunlea, E. J., Huffman, J. A., Onasch, T. B., Alfarra, M. R., Williams, P. I., Bower, K., Kondo, Y., Schneider, J., Drewnick, F., Borrmann, S., Weimer, S., Demerjian, K., Salcedo, D., Cottrell, L., Griffin, R., Takami, A., Miyoshi, T., Hatakeyama, S., Shimono, A., Sun, J. Y., Zhang, Y. M., Dzepina, K., Kimmel, J. R., Sueper, D., Jayne, J. T., Herndon, S. C., Trimborn, A. M., Williams, L. R., Wood, E. C., Middlebrook, A. M., Kolb, C. E., Baltensperger, U., and Worsnop, D. R.: Evolution of organic aerosols in the atmosphere., Science, 326, 1525–1529, https://doi.org/10.1126/science.1180353, 2009.
Johnson, D., Utembe, S. R., Jenkin, M. E., Derwent, R. G., Hayman, G. D., Alfarra, M. R., Coe, H., and McFiggins, G.: Simulating regional scale secondary organic aerosol formation during the TORCH 2003 campaign in the southern UK, Atmos. Chem. Phys., 6, 419–431, https://doi.org/10.5194/acpd-5-7829-2005, 2006.
Kroll, J. H. and Seinfeld, J. H.: Chemistry of secondary organic aerosol: Formation and evolution of low-volatility organics in the atmosphere, Atmos. Environ., 42, 3593–3624, https://doi.org/10.1016/j.atmosenv.2008.01.003, 2008.
La, Y. S., Camredon, M., Ziemann, P. J., Valorso, R., Matsunaga, A., Lannuque, V., Lee-Taylor, J., Hodzic, A., Madronich, S., and Aumont, B.: Impact of chamber wall loss of gaseous organic compounds on secondary organic aerosol formation: Explicit modeling of SOA formation from alkane and alkene oxidation, Atmos. Chem. Phys., 16, 1417–1431, https://doi.org/10.5194/acp-16-1417-2016, 2016.
Lane, T. E., Donahue, N. M., and Pandis, S. N.: Effect of NOx on secondary organic aerosol concentrations, Environ. Sci. Technol., 42, 6022–6027, https://doi.org/10.1021/es703225a, 2008.
Li, L., Tang, P., Nakao, S., and Cocker III, D. R.: Impact of molecular structure on secondary organic aerosol formation from aromatic hydrocarbon photooxidation under low-NOx conditions, Atmos. Chem. Phys., 16, 10793–10808, https://doi.org/10.5194/acp-16-10793-2016, 2016.
Lim, S. S., Vos, T., Flaxman, A. D., et al.: A comparative risk assessment of burden of disease and injury attributable to 67 risk factors and risk factor clusters in 21 regions, 1990–2010: a systematic analysis for the Global Burden of Disease Study 2010, Lancet, 380, 2224–2260, https://doi.org/10.1016/S0140-6736(12)61766-8, 2012.
Lim, Y. B. and Ziemann, P. J.: Effects of molecular structure on aerosol yields from OH radical-initiated reactions of linear, branched, and cyclic alkanes in the presence of NO x, Environ. Sci. Technol., 43, 2328–2334, https://doi.org/10.1021/es803389s, 2009.
Lou, S., Holland, F., Rohrer, F., Lu, K., Bohn, B., Brauers, T., Chang, C. C., Fuchs, H., Häseler, R., Kita, K., Kondo, Y., Li, X., Shao, M., Zeng, L., Wahner, A., Zhang, Y., Wang, W., and Hofzumahaus, A.: Atmospheric OH reactivities in the Pearl River Delta - China in summer 2006: Measurement and model results, Atmos. Chem. Phys., 10, 11243–11260, https://doi.org/10.5194/acp-10-11243-2010, 2010.
Mader, P. P., MacPhee, R. D., Lofberg, R. T., and Larson, G.: Composition of organic prtion of atmospheric aerosols in the Los Angeles area, Indust. Eng. Chem., 44, 1352–1355, 1952.
Madronich, S. and Flocke, S.: The Role of Solar Radiation in Atmospheric Chemistry, in: Environmental Photochemistry, edited by: Boule, D. P., no. 2/2L, The Handbook of Environmental Chemistry, Springer Berlin Heidelberg, 1–26, 1999.
Malley, C. S., Kuylenstierna, J. C. I., Vallack, H. W., Henze, D. K., Blencowe, H., and Ashmore, M. R.: Preterm birth associated with maternal fine particulate matter exposure: A global, regional and national assessment, Environ. Int., 101, 173–182, https://doi.org/10.1016/j.envint.2017.01.023, 2017.
Matsunaga, A. and Ziemann, P. J.: Gas-Wall Partitioning of Organic Compounds in a Teflon Film Chamber and Potential Effects on Reaction Product and Aerosol Yield Measurements, Aerosol Sci. Technol., 44, 881–892, https://doi.org/10.1080/02786826.2010.501044, 2010.
Matsunaga, A., Docherty, K. S., Lim, Y. B., and Ziemann, P. J.: Composition and yields of secondary organic aerosol formed from OH radical-initiated reactions of linear alkenes in the presence of NOx: Modeling and measurements, Atmos. Environ., 43, 1349–1357, https://doi.org/10.1016/j.atmosenv.2008.12.004, 2009.
McMurry, P. H. and Grosjean, D.: Gas and aerosol wall losses in Teflon film smog chambers, Environ. Sci. Technol., 19, 1176–1182, https://doi.org/10.1021/es00142a006, 1985.
Nannoolal, Y., Rarey, J., Ramjugernath, D., and Cordes, W.: Estimation of pure component properties, Fluid Phase Equilib., 226, 45–63, https://doi.org/10.1016/j.fluid.2004.09.001, 2004.
Nannoolal, Y., Rarey, J., and Ramjugernath, D.: Estimation of pure component properties, Fluid Phase Equilib., 269, 117–133, https://doi.org/10.1016/j.fluid.2008.04.020, 2008.
Ng, N. L., Chhabra, P. S., Chan, a. W. H., Surratt, J. D., Kroll, J. H., Kwan, a. J., McCabe, D. C., Wennberg, P. O., Sorooshian, A., Murphy, S. M., Dalleska, N. F., Flagan, R. C., and Seinfeld, J. H.: Effect of NOx level on secondary organic aerosol (SOA) formation from the photooxidation of terpenes, Atmos. Chem. Phys., 7, 5159–5174, https://doi.org/10.5194/acpd-7-10131-2007, 2007.
Ng, N. L., Brown, S. S., Archibald, A. T., Atlas, E., Cohen, R. C., Crowley, J. N., Day, D. A., Donahue, N. M., Fry, J. L., Fuchs, H., Griffin, R. J., Guzman, M. I., Herrmann, H., Hodzic, A., Iinuma, Y., Kiendler-Scharr, A., Lee, B. H., Luecken, D. J., Mao, J., McLaren, R., Mutzel, A., Osthoff, H. D., Ouyang, B., Picquet-Varrault, B., Platt, U., Pye, H. O. T., Rudich, Y., Schwantes, R. H., Shiraiwa, M., Stutz, J., Thornton, J. A., Tilgner, A., Williams, B. J., and Zaveri, R. A.: Nitrate radicals and biogenic volatile organic compounds: Oxidation, mechanisms, and organic aerosol, Atmos. Chem. Phys., 17, 2103–2162, https://doi.org/10.5194/acp-17-2103-2017, 2017.
Nordin, E. Z., Eriksson, A. C., Roldin, P., Nilsson, P. T., Carlsson, J. E., Kajos, M. K., Hellén, H., Wittbom, C., Rissler, J., Löndahl, J., Swietlicki, E., Svenningsson, B., Bohgard, M., Kulmala, M., Hallquist, M., and Pagels, J. H.: Secondary organic aerosol formation from idling gasoline passenger vehicle emissions investigated in a smog chamber, Atmos. Chem. Phys., 13, 6101–6116, https://doi.org/10.5194/acp-13-6101-2013, 2013.
O'Brien, R. J., Crabtree, J. H., Holmes, J. R., Hoggan, M. C., and Bockian, A. H.: Formation of photochemical aerosols from hydrocarbons, Environ. Sci. Tech., 9, 577–582, 1975.
Odum Jay, R., Hoffmann, T., Bowman, F., Collins, D., Flagan Richard, C., and Seinfeld John, H.: Gas particle partitioning and secondary organic aerosol yields, Environ. Sci. Technol., 30, 2580–2585, https://doi.org/10.1021/es950943+, 1996.
Pankow, J. F.: An absorption model of gas/particle partitioning of organic compounds in the atmosphere, Atmos. Environ., 28, 185–188, https://doi.org/10.1016/1352-2310(94)90093-0, 1994.
Powell, M. J. D.: The BOBYQA algorithm for bound constrained optimization without derivatives, Technical Report DAMTP 2009/NA06, Centre for Mathematical Sciences, University of Cambridge, Cambridge, England, available at: http://www.damtp.cam.ac.uk/user/na/NA_papers/NA2009_06.pdf/ (last access: 5 September 2018), 2009.
Pun, B. K., Griffin, R. J., Seigneur, C., and Seinfeld, J. H.: Secondary organic aerosol 2. Thermodynamic model for gas/particle partitioning of molecular constituents, J. Geophys. Res.-Atmos., 107, AAC4/1-AAC4/15, https://doi.org/10.1029/2001JD000542, 2002.
Pun, B. K., Wu, S. Y., Seigneur, C., Seinfeld, J. H., Griffin, R. J., and Pandis, S. N.: Uncertainties in modeling secondary organic aerosols: Three-dimensional modeling studies in Nashville/Western Tennessee, Environ. Sci. Technol., 37, 3647–3661, https://doi.org/10.1021/es0341541, 2003.
Pun, B. K., Seigneur, C., and Lohman, K.: Modeling secondary organic aerosol formation via multiphase partitioning with molecular data, Environ. Sci. Technol., 40, 4722–4731, https://doi.org/10.1021/es0522736, 2006.
R Core Team: R: A language and environment for stastistical computing, R Found. Stat. Comput. Vienna, Austria [online], available at: http://www.r-project.org/ (last access: 5 September 2018), 2017.
Robinson, A. L., Donahue, N. M., Shrivastava, M. K., Weitkamp, E. A., Sage, A. M., Grieshop, A. P., Lane, T. E., Pierce, J. R., and Pandis, S. N.: Rethinking Organic Aerosols: Semivolatile Emissions and Photochemical Aging, Science, 80, 1259–1262, https://doi.org/10.1126/science.1133061, 2007.
Shrivastava, M., Fast, J., Easter, R., Gustafson, W. I., Zaveri, R. A., Jimenez, J. L., Saide, P., and Hodzic, A.: Modeling organic aerosols in a megacity: comparison of simple and complex representations of the volatility basis set approach, Atmos. Chem. Phys., 11, 6639–6662, https://doi.org/10.5194/acp-11-6639-2011, 2011.
Shrivastava, M., Cappa, C. D., Fan, J., Goldstein, A. H., Guenther, A. B., Jimenez, J. L., Kuang, C., Laskin, A., Martin, S. T., Ng, N. L., Petaja, T., Pierce, J. R., Rasch, P. J., Roldin, P., Seinfeld, J. H., Shilling, J., Smith, J. N., Thornton, J. A., Volkamer, R., Wang, J., Worsnop, D. R., Zaveri, R. A., Zelenyuk, A., and Zhang, Q.: Recent advances in understanding secondary organic aerosol: Implications for global climate forcing, Rev. Geophys., 55, 509–559, https://doi.org/10.1002/2016RG000540, 2017.
Solazzo, E., Bianconi, R., Pirovano, G., Matthias, V., Vautard, R., Moran, M. D., Wyat Appel, K., Bessagnet, B., Brandt, J., Christensen, J. H., Chemel, C., Coll, I., Ferreira, J., Forkel, R., Francis, X. V, Grell, G., Grossi, P., Hansen, A. B., Miranda, A. I., Nopmongcol, U., Prank, M., Sartelet, K. N., Schaap, M., Silver, J. D., Sokhi, R. S., Vira, J., Werhahn, J., Wolke, R., Yarwood, G., Zhang, J., Rao, S. T., and Galmarini, S.: Operational model evaluation for particulate matter in Europe and North America in the context of AQMEII, Atmos. Environ., 53, 75–92, https://doi.org/10.1016/j.atmosenv.2012.02.045, 2012.
Stone, D., Whalley, L. K., and Heard, D. E.: Tropospheric OH and HO2 radicals: field measurements and model comparisons, Chem. Soc. Rev., 41, 6348, https://doi.org/10.1039/c2cs35140d, 2012.
Szopa, S., Aumont, B., and Madronich, S.: Assessment of the reduction methods used to develop chemical schemes: building of a new chemical scheme for VOC oxidation suited to three-dimensional multiscale chemistry simulations, Atmos. Chem. Phys., 5, 2519–2538, https://doi.org/10.5194/acp-5-2519-2005, 2005.
Takekawa, H., Minoura, H., and Yamazaki, S.: Temperature dependence of secondary organic aerosol formation by photo-oxidation of hydrocarbons, Atmos. Environ., 37, 3413–3424, https://doi.org/10.1016/S1352-2310(03)00359-5, 2003.
Tsigaridis, K. and Kanakidou, M.: Global modelling of secondary organic aerosol in the troposphere: a sensitivity analysis, Atmos. Chem. Phys., 3, 1849–1869, https://doi.org/10.5194/acp-3-1849-2003, 2003.
Tsigaridis, K., Daskalakis, N., Kanakidou, M., Adams, P. J., Artaxo, P., Bahadur, R., Balkanski, Y., Bauer, S. E., Bellouin, N., Benedetti, A., Bergman, T., Berntsen, T. K., Beukes, J. P., Bian, H., Carslaw, K. S., Chin, M., Curci, G., Diehl, T., Easter, R. C., Ghan, S. J., Gong, S. L., Hodzic, A., Hoyle, C. R., Iversen, T., Jathar, S., Jimenez, J. L., Kaiser, J. W., Kirkeväg, A., Koch, D., Kokkola, H., H Lee, Y., Lin, G., Liu, X., Luo, G., Ma, X., Mann, G. W., Mihalopoulos, N., Morcrette, J. J., Müller, J. F., Myhre, G., Myriokefalitakis, S., Ng, N. L., O'donnell, D., Penner, J. E., Pozzoli, L., Pringle, K. J., Russell, L. M., Schulz, M., Sciare, J., Seland, Shindell, D. T., Sillman, S., Skeie, R. B., Spracklen, D., Stavrakou, T., Steenrod, S. D., Takemura, T., Tiitta, P., Tilmes, S., Tost, H., Van Noije, T., Van Zyl, P. G., Von Salzen, K., Yu, F., Wang, Z., Wang, Z., Zaveri, R. A., Zhang, H., Zhang, K., Zhang, Q., and Zhang, X.: The AeroCom evaluation and intercomparison of organic aerosol in global models, Atmos. Chem. Phys., 14, 10845–10895, https://doi.org/10.5194/acp-14-10845-2014, 2014.
Valorso, R., Aumont, B., Camredon, M., Raventos-Duran, T., Mouchel-Vallon, C., Ng, N. L., Seinfeld, J. H., Lee-Taylor, J., and Madronich, S.: Explicit modelling of SOA formation from α-pinene photooxidation: Sensitivity to vapour pressure estimation, Atmos. Chem. Phys., 11, 6895–6910, https://doi.org/10.5194/acp-11-6895-2011, 2011.
Vereecken, L., Peeters, J., Fracheboud, J. M., Orlando, J. J., Tyndall, G. S., Sehested, J., Møgelberg, T. E., Nielsen, O. J., and Troe, J.: Decomposition of substituted alkoxy radicals – part I: a generalized structure–activity relationship for reaction barrier heights, Phys. Chem. Chem. Phys., 11, 9062, https://doi.org/10.1039/b909712k, 2009.
Vereecken, L., Peeters, J., Ceulemans, K., Compernolle, S., Vereecken, L., Peeters, J., Jenkin, M. E., Rossi, M. J., and Troe, J.: A structure–activity relationship for the rate coefficient of H-migration in substituted alkoxy radicals, Phys. Chem. Chem. Phys., 12, 12608, https://doi.org/10.1039/c0cp00387e, 2010.
Verwer, J. G. and Van Loon, M.: An Evaluation of Explicit Pseudo-Steady-State Approximation Schemes for Stiff ODE Systems from Chemical Kinetics, J. Comput. Phys., 113, 347–352, https://doi.org/10.1006/jcph.1994.1141, 1994.
Verwer, J. G., Blom, J. G., Van Loon, M., and Spee, E. J.: A comparison of stiff ode solvers for atmospheric chemistry problems, Atmos. Environ., 30, 49–58, https://doi.org/10.1016/1352-2310(95)00283-5, 1996.
Volkamer, R., Jimenez, J. L., San Martini, F., Dzepina, K., Zhang, Q., Salcedo, D., Molina, L. T., Worsnop, D. R., and Molina, M. J.: Secondary organic aerosol formation from anthropogenic air pollution: Rapid and higher than expected, Geophys. Res. Lett., 33, L17811, https://doi.org/10.1029/2006GL026899, 2006.
Zhang, X. and Seinfeld, J. H.: A functional group oxidation model (FGOM) for SOA formation and aging, Atmos. Chem. Phys., 13, 5907–5926, https://doi.org/10.5194/acp-13-5907-2013, 2013.
Zhao, D. F., Kaminski, M., Schlag, P., Fuchs, H., Acir, I.-H., Bohn, B., Häseler, R., Kiendler-Scharr, A., Rohrer, F., Tillmann, R., Wang, M. J., Wegener, R., Wildt, J., Wahner, A., and Mentel, T. F.: Secondary organic aerosol formation from hydroxyl radical oxidation and ozonolysis of monoterpenes, Atmos. Chem. Phys., 15, 991–1012, https://doi.org/10.5194/acp-15-991-2015, 2015.
Zhao, Y., Nguyen, N. T., Presto, A. A., Hennigan, C. J., May, A. A., and Robinson, A. L.: Intermediate Volatility Organic Compound Emissions from On-Road Gasoline Vehicles and Small Off-Road Gasoline Engines, Environ. Sci. Technol., 50, 4554–4563, https://doi.org/10.1021/acs.est.5b06247, 2016.